2. 四川大学 计算机学院, 四川 成都 610207
2. College of Computer Science, Sichuan University, Chengdu 610207, China
在实时系统领域, 周期性实时任务调度是最核心的理论问题之一[1].最早截止期优先(earliest deadline first, 简称EDF)作为单处理器系统中最优的调度算法[2], 得到众多学者的广泛关注和研究.当前研究主要关注同步和异步两大类实时系统.所谓同步系统, 是指系统中所有任务释放首个作业的时刻均相同.与之相反, 异步系统则不要求任务同步地释放首个作业, 而是允许为每个任务释放首个作业定义一个特定的时刻, 称为相位.特殊地, 当异步系统中所有任务的初始相位均相同时, 该异步系统即退化为同步系统.因此, 同步系统可看作是异步系统的一个特例.同步和异步系统上的EDF可调度性分析问题十分经典又极具挑战性, 有些早已得到解决, 成为实时系统理论中里程碑式的成果; 更多问题则在提出后数十年间都未能突破, 直到近期才得以解决, 同时又衍生出新的开放性问题.
同步系统的EDF可调度性分析问题在20世纪70年代得到研究.Liu等人率先研究了任务截止期与周期相等(Di=Pi)的隐含截止期任务模型, 并给出了多项式时间的判定算法[3].注意到, 隐含截止期任务模型是实时系统的理想模型.在实际应用中, 实时任务的截止期和周期之间并没有必然联系.很多偶发性任务, 例如中断响应任务, 其特点是触发频率较低, 并且任务一旦触发就需要在很短时间内完成.这类任务可抽象为截止期小于周期的任务模型.对于截止期大于周期的任务模型, 常见于多媒体应用等事件流的处理中.这类系统通常设有缓存来暂存中间结果, 任务的截止期取决于缓存区的大小.例如, 缓存如果能够暂存3个中间结果, 则任务的截止期可以是周期的3倍.显然, 这类系统允许任务具有大于周期的截止期.另外, 在类似于基于stateflow[4]等同步语言的代码生成中, 也存在类似的任意截止期模型的应用.
对于任意截止期的同步任务系统(DiPi), 自20世纪80年代起就有学者着手研究[5, 6], 并发现这类一般化模型上的EDF可调度性分析异常困难, 问题的计算复杂性长期以来难以确定.直到2010年, Eisenbrand等人才最终从理论上证明同步系统上的EDF可调度分析问题是弱coNP困难的[7], 这意味着同步系统存在伪多项式时间的EDF可调度判定算法(pseudo-polynomail time decision algorithm, 简称PTDA).目前, PTDA的研究主要集中在利用率严格小于1的同步系统.Zhang等人[8]提出的QPA算法是当前最优秀的精确判定算法之一.尽管QPA在理论上仍属于伪多项式时间算法, 但大量实验结果表明, 与传统算法相比, QPA能够成指数级地降低计算时间, 具有接近常数的计算复杂度[8].本文应用文献[8]的方法生成了更大范围的随机算例样本, 并对QPA算法做进一步的实验(详见第5.3.1节).研究发现, QPA算法对于利用率U≤0.99的算例可保持常数的时间复杂度, 计算次数均不超过100, 但当U > 0.99时, 却迅速退化为指数计算时间.Baruah等人指出, 利用率U趋于1的同步系统可调度性判定仍然属于很困难的问题.该问题是否存在PTDA至今仍被列为实时系统调度领域的5个开放性课题之一[1].
更困难的是, 对于异步系统而言, 可调度性分析属于强coNP困难问题.该结论甚至对利用率U严格小于1的异步系统同样成立[5].这从理论上否定了异步系统存在PTDA算法的可能.同步系统中所有PTDA算法(包括QPA)均不再适用.目前异步系统的可调度性分析问题仅有充分判定条件的研究[5], 即当算法给出“可调度”的结论时, 异步系统一定可调度.但是, 当算法返回“不可调度”时, 系统的可调度性则不确定.
综上, U趋于1的同步系统以及异步系统中的可调度性分析问题均属于很困难的问题.为了更高效地求解这两类困难问题, 本文同时开展了同步和异步两类实时系统的整数规划模型和线性松弛方法的研究.首先, 本文为异步系统上的可调度性分析问题建立了一般化的整数规划模型.该模型中的变量和约束不等式具有多项式规模, 不依赖于利用率U的取值, 从根本上消除了U对算法复杂性的影响.在理论上, 本文对模型约束集合展开多面体分析, 证明了模型维数和极大诱导不等式, 并基于这些结果为可调度性分析问题提出了多项式时间的线性松弛求解方法.其次, 由于同步系统是异步系统的简单特例.因此, 异步系统的模型和方法很容易扩展到同步系统中, 并且异步系统中问题解空间的多面体结论在同步系统中同样成立.另外, 在同步系统中, 本文的线性松弛算法可以嵌入QPA算法中缩减解空间的策略, 这使得算法的计算性能又进一步得到提升.
本文随机生成了大量同步和异步系统的算例, 通过实验验证了本文方法的有效性.首先验证了极大诱导不等式的有效性.实验结果表明, 本文模型能够获得较紧的问题解下界.在异步和同步系统中, 线性松弛解与最优整数解之间的平均百分界差分别为0.78%和1.27%.另外, 分别从同步和异步两方面开展实验, 将本文算法与传统算法进行性能比较.一方面, 对于同步系统算例, 将本文算法与QPA算法进行比较.实验结果表明, 对于U > 0.99的算例, 本文算法能够对70%的算例给出可调度性的判定结果, 算法的迭代次数较QPA算法有指数级的降低.例如, 一个具有30个任务的算例, 应用QPA算法要迭代33 653次, 而本文算法只需迭代3次.另一方面, 对于异步系统, 通过实验比较了本文算法与文献[5]中传统算法的计算效率.实验结果表明, 对于整个随机异步算例集合, 本文算法能够对近96%的算例给出可调度性判定, 将传统算法[5]不能判定可调度性的算例比例平均降低了29.27%.对于剩余的4%的算例, 本文算法能够降低可调度性算法的时间上界.与传统上界结果相比, 新上界的值平均降低了近104倍.
本文第1节介绍可调度性分析问题的形式化定义.第2节介绍同步/异步系统EDF可调度分析的相关研究.第3节给出问题的整数规划模型以及相关的多面体理论结果.第4节提出用于可调度性判定的多项式时间线性松弛方法.第5节给出实验结果.第6节对全文进行总结, 并对未来工作进行展望.
1 问题的数学定义本节给出实时任务系统的形式化定义, 并阐述一些相关的基本术语和概念.实时调度理论与“传统”调度理论[9]研究的一个主要差异在于实时任务具有周期性复发的特征.一般地, 实时任务系统通常定义为由一组有限数量且相互独立的实时任务构成的集合T={τ1, …, τn}.其中, 每个实时任务τi都将产生无限数量的作业序列.本文考虑偶发实时任务系统, 即每个任务τi中任意两相邻作业的释放时间间隔不确定, 但两个释放动作间存在一个最小的时间间隔, 称为周期.
1.1 偶发性实时任务系统系统T中每个偶发实时任务通常定义为一个四元组τi=(φi, Ci, Di, Pi), 其中元素的具体含义描述如下.
• φi∈R+:任务τi中第1个作业的释放时刻(又称相位), 令Φ=max{φ1, …, φn}.
• Ci∈R+:任务τi中作业的最坏执行时间(WCET), 规定任务τi释放的所有作业具有相同的Ci.
• Di∈R+:任务τi的相对截止期, 规定任务τi释放的所有作业具有相同的Di; 若τi的某作业J在t时刻释放, 则该作业必须在t+Di时刻之前完成.换言之, 该作业在[t, t+Di]时间段内需占用Ci个时间单位的处理器资源.t+Di称为作业J的绝对截止期.
• Pi∈N+:任务τi的周期, 表示τi中任意两个连续释放作业间的最小时间间隔; 若τi在t时刻释放了一个作业, 则τi的下一个作业需在t+Pi时刻之后释放(含t+Pi时刻).
若任务系统T关联的最大相位Φ=0, 则T称为同步系统, 否则, T称为异步系统.显然, 同步系统是异步系统的特例.另外, 若T中每个任务τi的相对截止期Di和周期Pi相等(Di=Pi), 则称T为隐含截止期任务系统; 若T中每个任务τi关联的Di≤Pi, 则称T为约束截止期任务系统; 本文研究任意截止期的任务系统, 即T中每个任务τi关联的Di与Pi之间没有任何约束关系, Di可小于、等于甚至大于Pi.
接下来, 进一步给出文中将会用到的其他术语和相关定义.
• Ui=Ci/Pi:任务τi的利用率.
• U=
• lcm(P1, …, Pj):周期P1, …, Pj的最小公倍数.
• H=lcm(P1, …, Pn)为系统T的超周期.
• ηi(t1, t2)=max{⌊(t2-φi-Di)/Pi⌋-⌈(t1-φi)/Pi⌉+1, 0}:任务τi在时间段[t1, t2)内释放的作业数, 其中每个作业的释放时刻均大于等于t1, 其绝对截止期均小于等于t2[5].
1.2 基于EDF调度的实时任务系统运行行为对实时任务系统T的调度行为可抽象为一个指派函数s:R→TU{∅}.对于任意时间点t:(1) σ(t)=τi表示调度算法指派处理器在t时刻执行任务τi释放的作业; (2) σ(t)=∅说明在t时刻处理器不执行任何作业, 处于空闲状态.本文考虑单处理器上可抢占式调度方法, 即处理器可以随时中断当前正在执行的任务作业, 转而处理其他任务释放的作业, 被中断的作业会在未来的某个时间点恢复执行.在当前的研究中, 通常假设处理器上这种任务间的切换不产生额外的代价和开销.
目前, 实时系统中的调度算法主要分为静态优先级调度和动态优先级调度.本文关注一类应用最为广泛的动态优先级调度算法--最早截止期优先(EDF)算法[3, 10, 11].根据EDF调度策略, 在每个时间点, 处理器都会从那些已经释放但未完成的若干作业中挑选出绝对截止期最小的那个优先执行.直观上, EDF调度策略倾向于让那些最先可能错失截止期的作业抢占处理器资源, 从而使尽可能多的作业能够在其相应的绝对截止期之前完成.在EDF调度策略控制下, 如果系统中的每个任务释放的所有作业都能在其相应的绝对截止期之前完成, 则称系统可被EDF成功调度.1974年, Dertouzos[2]从理论上证明了EDF是最优的单处理器可抢占式调度算法.这意味着, 任意一个实时任务系统如果不能被EDF策略成功调度, 则该任务系统也不能被其他算法成功调度.因此, 将能够被EDF策略成功调度的任务系统简称为可调度的系统; 反之, 则称为不可调度的系统.
1.3 可调度性分析问题可调度性分析问题是指, 对于给定的任务系统T, 是否存在一个判定算法A:若T能够被某种策略成功调度, 则算法A回答“是”; 否则, 若T不能被任何调度策略成功调度, 则算法A回答“否”.根据第1.2节所述, 在单处理器系统中, EDF是最优的调度策略.因此, 单处理器上任务系统T的可调度性分析问题又等价为系统T是否可被EDF策略成功调度的判定问题.
可调度性判定问题的传统分析方法框架均建立在一种被称为处理器需求范式(processor demand criterion)的基础之上.下面首先给出处理器需求函数的定义.
定义1.处理器需求函数(processor demand function, 简称PDF)[5]df(t1, t2)表示任务系统T={τ1, …, τn}在给定的时间段[t1, t2)内可能产生的最大执行时间需求, 具体计算公式如下:
| $ df({t_1}, {t_2}) = \sum\limits_{i = 1}^n {{\eta _i}({t_1}, {t_2}){C_i}} . $ |
易知, 在时间段[t1, t2)内, 处理器至少要提供df(t1, t2)个时间单位的计算资源用来执行任务系统T中已释放的作业.否则, T中的任务就有错失截止期的危险.根据PDF的定义, 能够很自然地推导出系统可调度的一个必要条件, 即任务系统在任意时间段产生的时间需求量不能超过该时间段的长度, 其形式化描述如下:
| $ \forall 0 \le {t_1} < {t_2}:df({t_1}, {t_2}) \le {t_2}-{t_1}. $ |
接下来分别从异步和同步系统两个方面介绍可调度性分析理论的基本原理.
定理1[5].异步任务系统T在单处理器上是可调度的, 当且仅当U≤1, 且∀0≤t1 < t2≤Φ+2H:df(t1, t2)≤t2-t1.
以上定理实际上蕴含着一个异步系统可调度性分析算法[12]:在时间段[0, Φ+2H]中, 检查每个可能有作业释放的时间点t1, 计算t1对应的所有需求函数df(t1, t2), 其中时间点t2满足t2 > t1,代表系统可能释放的所有作业关联的绝对截止期.注意到, 超周期H是关于规模n的指数函数, 因此以上可调度性分析算法是指数时间的.Baruah等人[5]已经从理论上证明了异步系统可调度性分析问题是强NP困难的, 并且该结论对于利用率U严格小于1的系统也同样成立.目前, 异步系统的可调度性分析理论主要围绕着充分性判定条件展开研究[7], 致力于提出一些(伪)多项式时间的近似判定算法, 对于任意异步系统, 若算法回答“是”, 则说明系统可被EDF成功调度; 然而, 当算法回答“否”时, 却无法断定系统的可调度性.异步系统可调度性分析算法的相关研究详见第2节的介绍.
对于同步系统, 定理1中的结论可进一步简化, 如定理2所述.
定理2[5].同步任务系统T在单处理器上是可调度的, 当且仅当∀L≤L*:df(0, L)≤L.
与定理1相比, 定理2将需求函数由原先的二元参变量t1和t2降为一元参变量L, 并给定变量L的上界L*.根据定理2, 同步系统的可调度分析算法只需检查每个小于等于L*的L, 计算相应的一元需求函数df(0, L), 并判断df(0, L)≤L是否成立.在之前的文献中, 也有学者将L称为可调度性分析的上界[8], 将需求函数df(0, L)重新定义为需求上界函数(demand bound function, 简称DBF)
在过去的几十年间, 众多学者为实时任务系统建立了各式各样的形式化模型, 为调度算法分析提供了理论基础[1].这些形式化模型, 从偶发性任务模型[3]到任务图模型[13, 14], 再到时间自动机[15, 16], 无一不在易解性和可表达性之间寻求一个折中.之前的研究通常把是否具有PTDA算法作为衡量一个系统模型是否易解的标准.针对每一类系统模型, 专家学者大都致力于探究PTDA算法的存在性, 并努力尝试提出PTDA算法.本文所研究的偶发性实时任务模型(具体定义见第1.1节)是最经典的形式化模型之一, 迄今为止, 至少有数十位学者为此类系统上PTDA算法的研究做出贡献.
2.1 同步系统可调度性分析问题研究1990年, Baruah等人[5]研究发现, 利用率U < 1的任意截止期同步系统存在PTDA算法, 并最先确定了可调度分析上界L*的范围:
| $ {L^{\;*}} < L_a^{\;1} = \max \left\{ {{D_1}, ..., {D_n}, \mathop {\max }\limits_{1 \le i \le n} \{ {P_i}-{D_i}\} \frac{U}{{1-U}}} \right\}. $ |
1996年, Ripoll等人[17]在基于约束截止期的假设下, 进一步缩小了可调度性分析上界, 该上界很快被扩展到任意截止期的同步系统中[18]:
| $ {L^{\;*}} < L_a^{\;2} = \max \left\{ {{D_1}, ..., {D_n}, \frac{{\sum\nolimits_{i = 1}^n {({P_i}-{D_i}){U_i}} }}{{1-U}}} \right\}. $ |
另外, Spuri[19]和Ripoll等人[17]也给出了可调度性分析上界的递推方程形式:
| $ {\omega ^0} = \sum\limits_{i = 1}^n {{C_i}}, {\omega ^{m + 1}} = \sum\limits_{i = 1}^n {\left\lceil {\frac{{{\omega ^m}}}{{{P_i}}}} \right\rceil {C_i}}, $ |
以上公式从ω0开始迭代, 直到求得不动点ωm+1=ωm时停止, 并令可调度性分析上界L* < Lb=ωm+1.
2009年, Zhang等人[8]又改进了L*的上界值:
| $ {L^{\;*}} < L_a^{\;3} = \max \left\{ {({D_1}-{P_1}), ..., ({D_n}-{P_n}), \frac{{\sum\nolimits_{i = 1}^n {({P_i}-{D_i}){U_i}} }}{{1 - U}}} \right\}. $ |
注意到, 以上可调度性分析上界的值均限定在一个关于U的伪多项式界内.传统判定算法在最坏情况下需要检查小于等于L*的所有L, 并逐个计算需求上界函数dbf(L).尽管L*是伪多项式时间界的, 但实际计算时间依然庞大.Zhang等人[8, 20]充分利用DBF函数的非递减性质, 提出了一种能够跳跃搜索的快速处理器需求分析(QPA)方法, 从而避免对1~L*上界中所有可能的L进行枚举式的检查.实验结果表明[8], QPA算法能够成指数级地降低dbf(L)的迭代次数.如, 对于某个包含16个任务的算例, 传统枚举式算法需要迭代计算dbf(L)高达858 331次, QPA算法只需12次迭代即可完成可调度性判定.QPA算法是目前判定同步系统可调度性最优秀的算法.
我们研究发现, QPA算法的性能受到利用率U取值的影响, 且算法的时间复杂性存在一个常数-指数突变的临界点.对于U≤0.99的系统, QPA算法中需求上界函数dbf(L)的计算迭代次数不会超过100次, 算法具有接近常数时间的复杂度.然而, 当U > 0.99后, QPA计算dbf(L)的迭代次数呈指数增长, 算法迅速退化为指数时间的复杂度.有研究表明, 利用率U趋于1的同步系统可调度性分析属于弱coNP困难问题[7], 理论上存在PTDA算法, 但至今未有学者明确给出此类算法.该问题仍被列为实时调度领域的5大开放性课题之一[1].本文即针对这些困难问题开展研究, 实验结果表明, 第3节和第4节提出的模型和算法对大部分U > 0.99的困难算例都有效(约70%), 与QPA算法相比, 能够成指数倍地降低算法迭代次数.
2.2 异步系统可调度性分析问题研究异步实时任务中的可调度性分析问题是强coNP困难问题, 该结论甚至对于利用率U严格小于1的系统也成立[5].这意味着, 同步系统中所有在U < 1约束下建立起来的PTDA算法(包括QPA算法)均不再适用.目前, 异步系统可调度性分析的研究主要关注充分性判定条件[12].其中, 代表性的充分判定算法将每个任务τi的初始相位ϕi直接忽略, 进而将原系统当作同步系统考虑[5].Baruah等人[5]指出, 给定一个异步系统T, 若其相对应的同步系统T′是可调度的, 则原系统T也是可调度的.但是, 若T′是不可调度的, T的可调度性则不能确定.
注意到, 同步系统中PTDA的研究成果扩展到异步系统所面临的主要困难在于, 异步系统中不存在一个伪多项式界的可调度分析上界L*.即使将系统利用率限定为U < 1, 上界L*在理论上依然是指数规模(Φ+2H)[5].但是, 如果能从理论和实验上证明, 对于大多数的异步系统, 可调度性分析上界L*的取值实际上远远小于Φ+2H, 落在QPA等PTDA算法能够快速处理的范围内, 则同步系统中的众多PTDA算法结果均可应用于求解异步系统的可调度性分析问题.本文应用整数规划理论, 尝试为异步系统找到一个较小的可调度分析上界L, 可看作是将同步系统PTDA算法扩展到异步系统中的第1步研究.
3 整数规划模型及多面体分析根据第1.3节中介绍的可调度判定基本原理, 可调度性判定问题本质上是对解空间的搜索问题.即在一个时间域内不断搜索可能发生溢出(overflow)的时间段或时间点, 直到找到溢出点, 判定问题回答为“否”(不可调度); 或者穷尽了整个时间域也未发现溢出, 判定问题回答为“是”(可调度).为了更深刻地理解此类搜索问题, 本节应用整数规划(integer programming, 简称IP)模型重新刻画可调度性判定问题.整数规划理论在对问题解空间的描述和分析层面都具有独特优势.本节的工作将从优化理论角度给出可调度性判定问题的一些新性质.这些新的性质和实时调度领域的既有结论和算法相结合, 将有助于提出新的可调度性判定算法, 提高算法的求解效率.
与以往研究不同, 本文并非为可调度性判定问题直接建立IP模型, 而是基于分而治之的思想, 先对整个时间域[0, Φ+2H](异步系统)或[0, L*](同步系统)进行划分, 得到若干互不相交的时间子域[Q1, Q2), [Q2, Q3), …, [Ql, Ql+1], 其中Qi和Qi+1分别表示第i个子域的下界和上界(1≤i≤l).易知, Q1=0, Ql+1=Φ+2H(或L*).另外, Qi和Qi+1的选取还需满足:不存在任何任务τk, 使得Qi < Dk+φk < Qi+1成立.在每个时间子域[Qi, Qi+1)中, 判断是否存在时间点违背定理1(在同步系统中违背定理2)的问题将对应一个最优化问题.最优化问题的解与0的小于和大于关系分别蕴含原判定问题回答“是”或“否”.若所有时间域关联的最优解均小于0, 则说明系统可调度; 否则, 只要存在一个时间域关联的最优解大于等于0, 则说明系统不可调度.因此, 原可调度性判定问题被分解为若干个时间子域对应的最优化问题.这些子问题具有相似的解空间结构, 本文为所有子问题建立统一的整数规划模型.接下来分别从异步和同步系统两方面入手, 给出时间子域[Qi, Qi+1)上可调度性判定问题的IP模型.
3.1 异步系统中可调度判定问题的IP模型和理论分析在异步系统中, 给定时间域对应的可调度性判定子问题定义如下.
定义2.给定时间域[Qi, Qi+1), 异步系统中相应的可调度性判定问题是:在时间域中寻找两个时间点t1和t2, 满足(Qi≤t1 < t2 < Qi+1), 使得df(t1, t2) > t2-t1成立.若成功地查找到t1和t2, 则系统不可调度; 否则, 系统可调度.
接下来为定义2中的判定问题建立相应的IP模型, 即异步系统可调度性分析问题(schedulability test for asychronous system, 简称STAS)的IP模型, 简记为STAS-IP模型.首先, STAS-IP模型中用到的所有常量在本文第1.1节均已定义, 在此不再赘述.下面主要介绍STAS-IP模型中用到的3类变量, 及其相关的约束条件.
首先, 给出时间变量t1和t2.定义2中在时间域[Qi, Qi+1)内要寻找的两个时间点分别定义为t1和t2.在STAS-IP模型中, 时间变量被定义为非负实数变量:t1, t2∈R≥0.另外, 根据定义2可知, t1和t2需满足约束Qi≤t1 < t2 < Qi+1.因此, 构造以下约束:
| $ {t_1} < {t_{2{\kern 1pt} }} $ | (1) |
| $ {t_2} < {Q_{i + 1}} $ | (2) |
| $ {t_1} \ge {Q_i}{\kern 1pt} {\kern 1pt} $ | (3) |
约束条件(1)限定了时间点t1和t2的序关系, 即t1要严格小于t2.约束条件(2)保证了时间点t2在Qi+1之前取值.约束条件(3)保证t1取Qi之后的值.约束式(1)-(3)联立, 共同保证了t1和t2可以取遍时间域[Qi, Qi+1)内的所有时间点, 且满足t1 < t2.
注意到, 在划分时间域时, 本文规定Qi和Qi+1需满足条件:不存在任何任务τk, 使得Qi < Dk+φk < Qi+1成立.换句话说, 对于给定的Qi和Qi+1, 系统中任何任务τk均不满足Qi < Dk+φk < Qi+1.因此, 系统中的任务被划分为两个集合T1={τk|Dk+φk≤Qi}和T2={τk|Dk+φk≥Qi+1}.易知, T2中任务所释放的作业其截止期落在时间点Qi+1之外, 一定不会影响需求函数df(t1, t2)的值.故T2可以直接从STAS-IP模型中排除, 而只需考虑T1中的任务.
接下来, 给出xk变量.为T1中的每个任务τk(1≤k≤n)分配一个非负整数变量xk, 表示τk在时间段[0, t2-Dk]内应该完成的作业个数.易知, 在时间段[0, t2-Dk]内, 任务τk释放并且必须完成的作业个数至多为⌊(t2-φk-Dk)/Pk⌋.因此, 有xk≤⌊(t2-φk-Dk)/Pk⌋成立.更进一步地, 可知如下线性不等式成立.
| $ {P_k}{x_k} + {D_k} + {\varphi _k} \le {t_2}, {\rm{ }}\forall {\tau _k}:{D_k} + {\varphi _k} \le {Q_i} $ | (4) |
约束条件(4)给出了xk的线性上界xk≤(t2-φk-Dk)/Pk.由于xk是整数变量, 所以xk至多取到⌊(t2-φk-Dk)/Pk⌋.
最后, 给出yk变量.为T1中的每个任务τk(1≤k≤n)分配一个非负整数变量yk, 表示τk在时间段[0, t1]内最多释放的作业个数.易知, 任务τk在[0, t1]内最多释放⌈(t1-φk)/Pk⌉个作业, 即yk=⌈(t1-φk)/Pk⌉.易知, yk≥(t1-φk)/Pk成立, 如约束条件(5)所示.约束(5)给出了变量yk的线性下界.
| $ {P_k}{y_k} + {\varphi _k} \ge {t_1}, {\rm{ }}\forall {\tau _k}:{D_k} + {\varphi _k} \le {Q_i} $ | (5) |
注意到, 变量xk的整数上界和yk的整数下界分别为⌊(t2-φk-Dk)/Pk⌋和⌈(t1-φk)/Pk⌉.因此, max{xk-yk+1}=⌊(t2-φk-Dk)/Pk⌋-⌈(t1-φk)/Pk⌉+1.这恰好与ηk(t1, t2)定义中的第1项相对应.以下引理给出了STAS-IP模型中变量集合{xk, yk|Dk+φk≤Qi}与ηk(t1, t2)的联系.
引理3.在时间域[Qi, Qi+1)中, 对于任意给定的时间段[t1, t2], 有
证明:根据定义1, df(t1, t2)计算公式
•当Dk+φk≤Qi时, ⌊(t2-φk-Dk)/Pk⌋+1即为任务τk在时间段[0, t2]内释放并完成的最多作业个数, ⌈(t1-φk)/Pk⌉为任务τk在时间段[0, t1]内释放的最多作业个数, 例如图 1中的任务τ1.已知t1 < t2, 有⌊(t2-φk-Dk)/Pk⌋+1≥⌈(t1-φk)/Pk⌉成立.故ηk(t1, t2)=⌊(t2-φk-Dk)/Pk⌋-⌈(t1-φk)/Pk⌉+1.

|
Fig. 1 Illustration for the different two values of hk(t1, t2) 图 1 hk(t1, t2)两种取值情况的示意图 |
•当Dk+φk≥Qi+1时, ⌊(t2-φk-Dk)/Pk⌋+1≤0, 例如图 1中的任务τ2.易知, ⌊(t2-φk-Dk)/Pk⌋+1-⌈(t1-φk)/Pk⌉≤0.故ηk(t1, t2)=0.
注意到, 由于Qi和Qi+1的取值限制, Qi < Dk+φk < Qi+1的情况已被排除, 故无需讨论.
综上可得
易知, 当每个任务都尽可能多地释放作业时, 引理3中不等式取等.故有
基于以上变量和约束条件的定义, 给出STAS-IP模型的目标函数如下:
| $ \min \left( {{t_2}-{t_1}-\sum\nolimits_{{\tau _k}:{D_k} + {\varphi _k} \le {Q_i}} {{C_k}({x_k}-{y_k} + 1)} } \right) $ | (6) |
目标函数(6)的主体部分可看作两个子式的差.子式①t2-t1是时间段[t1, t2]的长度; 子式②
由定义1可知, df(t1, t2)由ηk(t1, t2)的线性加和构成(1≤k≤n).由于ηk(t1, t2)是非线性的, 故df(t1, t2)也是非线性的.在STAS-IP模型中, 非线性的df(t1, t2)被等价为线性式
注意到, 目标函数(6)即保证最优解对应的时间段长度与其相应的最大处理器需求之差最小.易知, 若STAS-IP模型求得最优解对应的目标值小于0, 即存在一个时间段[t1, t2], 使得df(t1, t2) > t2-t1成立, 则说明系统不可调度; 若最优解对应的目标值大于等于0, 则说明不存在产生溢出的时间段, 即系统可调度.
定理4. STAS-IP模型是多项式规模的整数线性规划模型.
证明:令m=|{τk|Dk+φk≤Qi}|.易知, STAS-IP模型中的变量个数是2m+2, 约束集合(1)~(5)中不等式的个数之和为2m+3.由于m是小于n的整数, 显然, STAS-IP模型是多项式规模的.另外, 目标函数(6)是线性的, 并且约束集合(1)~(5)均为线性不等式, 故STAS-IP模型属于整数线性规划模型.
接下来对STAS-IP模型的解空间进行精确理论分析.假设STAS-IP模型的变量规模为2m+2.STAS问题的任意可行解均关联一个整数向量f=(t1, t2, x1, ..., xm, y1, ..., ym), 其中, 非负整数t1和t2是f关联的时间段下界和上界值, 非负整数xk是f中第k个任务τk在时间段[0, t2-Dk]内完成的作业个数, 非负整数yk是任务τk在时间段[0, t1]内释放的作业个数(1≤k≤m).显然, STAS-IP模型中每个可行解的关联向量f满足约束不等式(1)~(5);反之, 每个满足约束不等式(1)~(5)的向量也一定是STAS-IP模型的可行解.因此, 可由约束不等式(1)~(5)定义STAS-IP模型的解空间多面体PSTAS(Tm), 其中Tm={τk|τk∈T Dk+φk≤Qi}.首先, 多面体PSTAS(Tm)对应的可行解集合F定义如下:
| $ F = \{ f \in {N^{2m}}^{ + 2}|f满足约束不等式\left( 1 \right) \sim \left( 5 \right)\} . $ |
以上表达说明, STAS-IP的多面体可定义为所有可行解构成的凸包(convex hull):PSTAS(Tm)=conv(F).下面给出PSTAS(Tm)的维数和极大诱导不等式的理论结果.
定理5.若∀τk∈Tm:Pk+Dk+φk≤Qi+1-1, 则STAS-IP多面体PSTAS(Tm)的维数为2m+2.
证明:欲证多面体维数等于2m+2, 只需在F中找出2m+3个仿射无关向量.首先, 给出基向量f0=(Qi, Qi+1-1, 0, ..., 0, K, ..., K)∈N2m+2, 其中K为变量yk的取值, 是一个使约束(5)成立的常数.另外, 0和K的个数为m.然后, 给出剩余的2m+2个可行解关联向量.
•集合F1由两个关联向量组成:F1={(Qi+1, Qi+1-1, 0, .., 0, K, ..., K), (Qi, Qi+1-2, 0, ..., 0, K, ..., K)}.
•集合F2包含m个向量:F2={(Qi, Qi+1-1, 1, 0, ..., 0, K, ..., K), (Qi, Qi+1, 0, 1, 0, ..., 0, K, ..., K), ..., (Qi, Qi+1-1, 0, ..., 1, K, ..., K)}, 其中, 第k个向量关联的xk变量取值为1.
•集合F3包含m个向量:F3={(Qi, Qi+1-1, 0, ..., 0, K+1, K, ..., K), (Qi, Qi+1-1, 0, ..., 0, K, K+1, K, ..., K), ..., (Qi, Qi+1-1, 0, ..., 0, K, ..., K+1)}, 其中, 第k个向量关联的yk变量取值为K+1.
易知, 将F1, F2和F3中的每个向量减去基向量f0后得到2m+2个线性无关的向量.所以, 向量集合{f0}UF1UF2UF3中的2m+3个关联向量仿射无关.
定理6.若存在两个时间点Qi≤t2 < t3 < Qi+1和一个任务τk∈Tm, 使得Pkxk+Dk+φk=t2 Pk(xk+1)+Dk+φk=t3, 并且∀τk∈Tm:Pk+Dk+φk≤t2, 则STAS-IP模型中约束不等式(4)是PSTAS(Tm)的极大诱导不等式.
证明:根据定理5, PSTAS(Tm)的维数为2m+2.对于约束(4)中的不等式Pkxk+Dk+φk≤t2, 只需在F中找出2m+2个令等号成立的仿射无关向量, 即可证明该不等式为极大诱导不等式.首先给出基向量f0=(Qi, t2, 0, ..., xk, ..., 0, K, ..., K).在f0的基础上, 构造向量f1=(Qi+1, t2, 0, ..., xk, ..., 0, K, ..., K).易知, f0, f1均使不等式取等.接下来, 分两步构造剩余的2m个使不等式取等的向量.
•集合F1包含m个向量:F1={(Qi, t2, 1, 0, ..., xk, ..., 0, K, ..., K), ..., (Qi, t3, 0, ..., xk+1, ..., 0, K, ..., K), ..., (Qi, t2, 0, ..., xk, ..., 1, K, ..., K)}.
•集合F2包含m个向量:F2={(Qi, t2, 0, ..., xk, ..., 0, K+1, K, ..., K), ..., (Qi, t2, 0, ..., xk, ..., 0, K, K+1, K, ..., K), ..., (Qi, t2, 0, ..., xk, ..., 0, K, ..., K+1)}.
将{f1}, F1和F2中每个向量减去基向量f0后得到2m+1个线性无关的向量.所以, 向量集合{f0, f1}UF1UF2中的2m+2个关联向量仿射无关.
应用类似的构造证明技术不难推出以下结论, 具体证明过程在此不再赘述.
推论7.若存在两个时间点Qi≤t1 < t′1 < Qi+1和一个任务τk∈Tm, 使得Pkyk+φk=t1 Pk(yk+1)+φk=t′1, 并且∀τk∈Tm:Pk+Dk+φk≤t1, 则STAS-IP模型中约束不等式(5)是PSTAS(Tm)的极大诱导不等式.
定理6和推论7说明, 约束(4)和(5)是可调度性判定问题非常紧的约束条件.在多面体理论中, 极大诱导不等式对应解空间的精确边界.根据最优化理论, 问题最优解总是在边界交叉点上取得.也就是说, 最优解很有可能在约束不等式(4)和(5)取等时取得.本文将在第5.1节通过实验验证这些约束不等式的有效性.
3.2 同步系统中可调度判定问题模型和理论分析上一节以异步系统为例, 给出了可调度性判定问题一般化的STAS-IP模型.本节应用相似的技术, 为同步系统建立IP模型.与STAS-IP模型相比, 本节模型将更加简化.下面先给出同步系统中可调度性判定问题的定义.
定义3.给定时间域[Qi, Qi+1), 同步系统中相应的可调度性判定问题是:在时间域中寻找时间点t, (Qi≤t < Qi+1), 使得dbf(t) > t成立.若成功查找到t, 则系统不可调度; 否则, 系统可调度.
根据定义3可知, 同步系统对应的IP模型只需两类变量:①时间点变量t:定义3中要寻找的时间点; ②每个任务τk对应一个变量xk, 表示τk在时间段[0, t-Dk]内应该完成的作业个数.
根据定理2, 建立同步系统可调度性分析问题(schedulability test for sychronous systems, 简称STSS)的IP模型如下.
Model STSS-IP:
| $ \min \left( {t-\sum\nolimits_{{\tau _k}:{D_k} \le {Q_i}} {{C_k}({x_k} + 1)} } \right){\kern 1pt} $ | (7) |
s.t.
| $ t < {Q_{i + 1}} $ | (8) |
| $ t \ge {Q_i} $ | (9) |
| $ {P_k}{x_k} + {D_k} \le t, {\rm{ }}\forall {\tau _k}:{D_k} \le {Q_i} $ | (10) |
| $ {x_k}, y \in {N^{ \ge 0}}, {\rm{ }}\forall {\tau _k}:{D_k} \le {Q_i} $ | (11) |
显然, STSS-IP模型是STAS-IP模型在考虑Φ=0时的简化.目标函数(7)使得时间段[0, t]的长度与其对应的需求上界dbf(t)的差值最小.约束(8)和(9)保证了时间点变量t落在时间域[Qi, Qi+1)中.约束(10)是STAS-IP模型中约束(4)考虑jk=0后的结果, 给出了变量xk的上界.易知, STSS-IP模型的变量和线性约束不等式的个数分别为m+1和m+2.另外, 采用类似的证明技术, 第3.1节中的多面体理论结果不难扩展到同步系统中, 具体证明过程略.
推论8.若∀τk∈Tm:Pk+Dk < Qi+1, 则STSS-IP多面体PSTSS(Tm)的维数为m+1.
推论9.若存在两个时间点Qi≤t < t′ < Qi+1和一个任务τk∈Tm, 使得Pkxk+Dk=t Pk(xk+1)+Dk+φk=t′, 并且∀τk∈Tm: Pk+Dk≤t, 则STSS-IP模型中约束不等式(10)是PSTSS(Tm)的极大诱导不等式.
4 线性松弛算法上一节将原可调度性判定问题分解为若干子问题, 为每个子问题建立了IP模型.本节将通过求解这一系列子问题的IP模型来给出原问题的判定结果.具体方法如算法1所示.
算法1.同/异步系统可调度性判定问题的线性松弛算法.
输入:任务系统T={τ1, …, τn}及可调度性分析上界:L(在同步系统中,
输出:任务系统T是否可调度.
BEGIN
1. 将任务按照Dk+φk递增顺序进行排列, 得到有序任务序列:τ[1], …, τ[n];
2. l:=1; Ql:=0;
3. REPEAT 1≤k≤n:
4. IFτ[k]关联的D[k]+φ[k] > Ql THEN l:=l+1; Ql:=D[k]+φ[k];
5. Ql+1:=L; feasible:=0;
6. FOR each [Ql, Ql+1):
7. 将时间段[Ql, Ql+1)上关联的STAS-IP/STSS-IP模型中整数约束拿掉, 求解其线性松弛模型;
8. 得到线性松弛解fl, 其对应的目标值为LPl;
9. 将松弛解fl取整, 得到原IP模型中的可行解, 其对应目标值为FSl;
10. IF LPl > 0 THEN feasible:=feasible+1;
11. ELSE IF FSl < 0 THEN RETURN系统T不可调度;
12. IF feasible=lTHEN RETURN系统T可调度;
13. ELSE RETURN系统可调度性不确定;
END
算法1为同步和异步两类实时任务系统的可调度性判定问题提供了统一的求解框架, 主要分为两部分.
①算法在第1行~第5行将时间域[0, L]划分为l个互不相交的子时间域.注意到, 每个子域[Qi, Qi+1)的下界和上界取值要么等于某个Dk+φk(见算法第3行和第4行), 要么等于0或L; 显然满足第3节中规定的约束条件:不存在任何任务τk, 使得Qi < Dk+φk < Qi+1成立.易知, 原可调度性判定问题可转化为l个定义在时间域[Qi, Qi+1)上的子问题(1≤i≤l).
②算法在第6行~第11行首先将每个子问题对应的IP模型进行线性松弛处理, 即去掉整数变量约束, 进而得到一个易于求解的线性规划(linear programming, 简称LP)模型.求解这个线性松弛模型, 得到一个松弛最优解fl, 其对应的解向量中可以包含小数.通过对fl向量取整, 可以得到原IP模型的一个可行解.根据最优化理论, 线性松弛解fl的值LPl一定小于等于IP模型的最优解, 可行解的值FSl一定大于等于IP模型的最优解.因此,
•若LPl > 0, 则IP模型最优解一定大于0, 可得系统T在时间域[Qi, Qi+1)内可调度.在算法中, 逐个验证每个子时间域, 只要发现系统T在该时间域内可调度, 变量feasible就会自增1(见算法第10行).如果系统T在l个子时间域内均可调度, 则feasible的值等于l, 即可判定系统T在整个时间域上可调度(见算法第12行).
•否则, 若LPl≤0, 则IP模型的最优解与0的关系不确定, 此时, 若fl取整得到的可行解的值FSl < 0, 则IP模型的最优解一定小于0, 可知系统T不可调度(见算法第11行).
定理10.算法1的计算复杂性是多项式时间的.
证明:由算法第3行和第4行可知, 原可调度性判定问题至多被划分为n个子问题, 每个子问题对应一个线性松弛问题.又知, 线性松弛问题是多项式时间可解的, 因此, 算法1是多项式时间的.
根据定理10, 算法1的迭代次数被限定在多项式规模内, 在最坏情况下, 至多需要迭代n次.注意到, 同步系统中存在很多优良的算法理论结果, 如QPA算法, 与这些已有理论成果相结合, 能够进一步减少算法1的迭代次数, 提高算法的执行效率.
4.1 同步系统中算法性能的优化策略在同步系统中, QPA算法能够在时间域[0, L]中实现跳跃式搜索.这主要是基于以下结论[8]:若时间点t关联的需求上界函数值dbf(t) < t, 则在时间域(dbf(t), t]内不可能存在溢出点.因此, 可以跳过这一区域, 在搜索过t点后, 直接对时间点dbf(t)进行搜索.可将该结论应用到算法1中, 以减少需求求解的子问题个数.改进后的算法如下.
算法2.同步系统中改进的可调度性判定算法.
输入:任务系统T={τ1, …, τn}及可调度性分析上界
输出:任务系统T是否可调度.
BEGIN
1. 将任务按照Dk递增顺序进行排列, 得到有序任务序列:τ[1], …, τ[n];
2. Qlow:=D[n]; Qhigh:=L; uncertain:=false;
3. WHILE Qhigh≥D[1] DO
4. 求解时间段[Qlow, Qhigh]关联的STSS线性松弛模型, 得到松弛解f, 其对应的目标值为LP;
5. 将松弛解f取整, 得到原STSS-IP模型中的可行解, 其对应目标值为FS;
6. IF LP < 0 & & FS < 0 THEN RETURN系统T不可调度;
7. ELSE IF LP < 0 & & FS > 0 THEN uncertain:=true;
8. Qhigh:=min{Qlow, dbf(Qlow)+1}; Qlow:=max{Dk|Dk < Qhigh};
9. IF uncertain=false THEN RETURN系统T可调度;
10. ELSE RETURN系统可调度性不确定;
END
算法2的第8行实现了本文方法与文献[8]中结论的结合.与算法1相比, 算法2排除了那些一定不存在溢出点的时间段.如图 2所示, 算法1会对l个时间段对应的线性松弛模型逐个进行求解; 算法2则可能在执行过程中跳过一些时间段, 或者缩小时间段的长度, 从而减少算法的迭代次数, 并缩小问题的解空间.在第5.3节, 将给出算法2与QPA算法的性能比较.
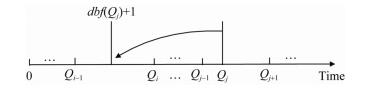
|
Fig. 2 Algorithm 2 will search in [Qi-1, dbf(Qj)+1] after the completion of searching in [Qj, Qj+1] 图 2 算法2在搜索完区域[Qj, Qj+1]之后, 搜索[Qi-1, dbf(Qj)+1] |
4.2 异步系统中对不确定情况的处理
注意到, 本文算法的返回结果分为两种情况, 一是明确指出系统T可调度或不可调度, 二是不能确定系统的可调度性.对于第1种返回情况的算例, 本文算法是精确判定算法; 对于第2种情况, 本文算法虽然不能判定算法的可调度性, 却能在一定程度上缩小可调度性分析上界.这在异步系统的可调度性分析中尤为明显.对于不能确定系统可调度性的算例, 进一步应用以下算法, 将给出一个较小的可调度性分析上界.
算法3.异步系统中对不确定情况的处理算法.
输入:可调度性不确定的任务系统T={τ1, …, τn}及可调度性分析上界L=Φ+2H.
输出:缩小的可调度性分析上界L.
BEGIN
1. 将任务按照Dk递增顺序进行排列, 得到有序任务序列:τ[1], …, τ[n];
2. Qlow:=D[n]; Qhigh:=L;
3. WHILE Qlow < Qhigh DO
4. 求解时间段[Qlow, Qhigh]关联的STSS线性松弛模型, 得到松弛解f=(t, x1, …, xm), 其目标值为LP;
5. IF LP≥0 Then Qhigh:=⌊(Qlow+t)/2⌋;
6. ELSE Qlow:=⌊(t+Qhigh)/2⌋;
7. L:=max{Qlow, Qhigh};
END
算法3应用折半法思想, 在时间域[D[n], Φ+2H]中确定离D[n]最近的时间点L, 使得时间段[L, Φ+2H]对应的线性松弛解的值LP≥0.易知, 当LP≥0时, 时间段[L, Φ+2H]中一定不存在溢出点, 即可排除出搜索范围.因此, 只有时间段[0, L]中才可能出现溢出点, L即为新的可调度性分析上界.易知, 算法3的计算复杂性为O(log (Φ+2H)), 即使H为指数规模, 算法3也是多项式时间界的.第5.4节将通过实验验证算法3在降低可调度性分析上界方面的有效性.
5 实验结果及分析为了验证本文算法的有效性, 本节针对大量随机任务测试集进行实验.本文算法由C++程序调用Gurobi 5.6[21]函数库实现, 程序运行环境为具有2.2GHz主频和1G内存的奔腾处理器.另外, 随机任务集算例的生成方法详见第5.1节.
5.1 随机任务集生成算法本节采用文献[8]中生成随机同步任务集的方法, 并将其扩展到异步系统中.
•任务利用率的生成策略:本节按照0-1间的均匀分布为任务集中的每个任务分配一个利用率U.具体生成算法参见文献[22]中的UUniFast算法.该算法已被证明可以有效地生成呈均匀分布的任务利用率[22].
•任务周期的生成策略:本文采用文献[23]的方法生成满足指数分布的任务周期.令Pmax:=max1≤i≤n{Pi}和Pmin:=min1≤i≤n{Pi}.为使所有任务的周期均匀分布在一个给定范围(如Pmax/Pmin的最大值)内, 首先将这个范围划分为k个子区域:e0~e1, e1~e2, …, ek-1~ek; 然后, 在每个子区域中, 随机生成⌊(n-1)/k⌋个任务周期.另外, 剩余的(n-1) mod k个任务周期则在e0~ek内随机分配.
•任务截止期和相位的生成策略:每个任务τi的截止期Di在区域[a, b]中随机生成.其中, 区域下界a的取值规则如下:当τi的执行时间Ci < 10时, a:=Ci; 当10≤Ci < 100时, a:=2×Ci; 当100≤Ci < 1000时, a:=3×Ci; 当Ci≥1000时, a:=4×Ci.区域上界b的默认值为1.2×Pi.另外, 在异步系统中, 每个任务τi的相位φi通过在区域[0, Di]中取随机数获得.
在本节所有实验中, 对于每种问题参数取值, 均生成了大约6 000个随机算例, 并统计算法运行的平均情况.
5.2 极大诱导不等式的有效性分析图 3给出了本文的STSS和STAS线性松弛模型对各自最优整数解的逼近程度.这种逼近程度可由百分比界差gap进行评估.gap的计算公式为|(OPT-LP)/LP|×100%, 其中, OPT为IP模型求得的最优整数解, LP为IP模型去掉整数约束后, 得到的松弛最优解.百分比界差是数学规划领域常用的评价参数[24, 25], 具体可视为在去除问题参数取值的影响后, 问题松弛解与最优解之间的绝对差距.注意到松弛模型中主要起作用的是极大诱导不等式约束, gap值能够在一定程度上反映极大诱导不等式的有效性.

|
Fig. 3 Values of gap affected by the problem parameters 图 3 问题参数对gap值的影响 |
本节对具有30个任务的测试集进行实验, 分别调用Gurobi的单纯形算法和分支切割算法求解[D[n], L]对应的线性松弛模型和IP模型.图 3(a)给出了同步和异步系统在Pmax/Pmin:=1000, b=1.2×Pi以及U=0.6~0.96时, gap的取值情况.平均情况下, 异步和同步系统的gap能够保持在0.78%和1.27%左右, 这说明, 线性松弛解距离最优解的偏差能够限制在一个很小的范围内.对于不确定的算例, 直接依据松弛解判定系统可调度性的可信度为99.23%(异步)和98.73%(同步).另外, 图 3(b)给出了同步和异步系统在U=0.9, b=1.2×Pi以及Pmax/Pmin:=10~1000000时, gap的取值情况.异步和同步系统的平均gap值分别为2.41%和3.37%.
5.3 同步系统中算法性能分析 5.3.1 问题参数对QPA算法的影响本节重现了QPA算法, 研究了可调度分析上界L取值和利用率U的变化对算法性能的影响.我们发现, 当QPA算法中L分别取
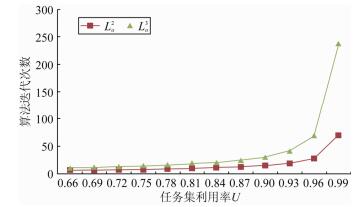
|
Fig. 4 Iteration times of QPA affected by values of upper bound L 图 4 上界L不同取值对QPA算法迭代次数的影响 |
另外, 对于U≤0.99的算例, QPA算法的迭代次数不超过100;当U > 0.99时, QPA算法的迭代次数呈指数增长, 如图 5所示(本节任务测试集的相关参数设定为:n=30, Pmax/Pmin:=1000, b=1.2×Pi).
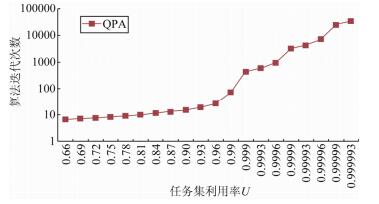
|
Fig. 5 Iteration times of QPA affected by utilization Us 图 5 利用率U对QPA算法迭代次数的影响 |
5.3.2 本文算法与QPA算法的性能比较
本文通过调用gurobi库函数中的单纯形算法实现了算法2.注意到, 若STSS-IP模型中目标函数值小于0, 则说明系统不可调度.因此, 在STSS-IP模型中增加约束
本文调用linux系统中的计时器接口clock_gettime (), 分别测量了算法2求解一次松弛问题的时间以及QPA算法求解一次需求函数h(t)的时间(任务测试集的相关参数设定为:n=30, U=0.9, Pmax/Pmin:=1000, b=1.2×Pi).我们发现, 两者耗时均在ms量级.因此, 本文将算法2求解一次松弛问题定义为一次迭代.图 6给出了算法2与QPA算法的迭代次数随问题参数的变化.其中, 图 6(a)给出了测试集的参数设定为n=30, Pmax/Pmin:=1000, b=1.2×Pi时, 利用率U对算法性能的影响.对于算法2可判定调度性的算例:当U≤0.99时, 算法2和QPA算法的迭代次数相差不大; 当U > 0.99后, QPA算法的迭代次数迅速增多, 平均情况下QPA算法迭代次数多达1 000次以上, 是本文算法的指数倍.

|
Fig. 6 Iteration times of QPA and Algorithm 2 affected by problem parameters 图 6 问题参数对QPA和算法2迭代次数的影响 |
QPA算法迭代次数随U增大的原因是, QPA算法跳跃式搜索的步长直观上与利用率U成反比.在QPA算法执行过程中, 假设当前检查的时间点为t, 则下一个时间点为min{t-1, dbf(t)}[8].QPA算法1次迭代的步长即为两相邻检查点的距离max{t-dbf(t), 1}.在时间域长度一定的条件下, QPA算法的步长越大, 则迭代次数越少, 反之亦然.U可看作任务在时间段内释放作业负载的密度.在时间段t固定时, 负载密度越大, 需求函数dbf(t)就可能越大, 进而t-dbf(t)的值越小, 步长也越短.这使得QPA算法的迭代次数随U增大而增多.同时注意到, QPA算法的迭代次数并非随U增大以线性速度增长.实验结果表明, U=0.99是QPA算法迭代次数的增长速度由线性到指数的分界点, 如图 6(a)所示.
另外, 在算法2中, 线性松弛方法的迭代次数与利用率U无关, 而只与任务数n相关.因此, 算法2的迭代次数并不会随着U增大而增大.注意到, 算法2的迭代次数在U > 0.99后不但没有增多, 反而有所下降, 如图 6(a)所示.经过统计得知, 在U > 0.99的算例集合中, 不可调度的算例比例接近80%.算法2在判定不可调度的算例时更加高效.算法2将整个时间域划分成n个子时间域.算法一次迭代就可以判定一个时间子域内是否存在溢出点.给定一个任务系统, 在n个时间子域中, 只要有一个存在溢出点, 就可以判定该系统不可调度.因此, 对于不可调度的算例, 算法2往往能够在最初的几个时间子域中迅速找到溢出点, 从而返回判定结果, 终止程序.
综上, 在U取值很大时, QPA算法的搜索步长变得很小, 算法退化为在整个时间域上逐个时间点检查溢出情况.然而, U增大也使得不可调度的算例比例增加, 算法2在判定不可调度的算例时, 往往能够经过最初几次迭代迅速终止.基于以上两方面考虑, 在U很大时, QPA算法的迭代次数迅速上升, 而算法2的迭代次数却有所下降, 如图 6(a)所示.
图 6(b)给出在测试集参数设为n=30, U=0.999, b=1.2×Pi时, 算法性能随Pmax/Pmin取值的变化.图 6(c)给出了在测试集参数U=0.999, Pmax/Pmin:=1000, b=1.2×Pi时, 任务个数对算法性能的影响趋势.最后, 图 7给出了算法2不能确定调度性的算例比例随问题参数的变化.我们发现, 对于小规模的算例, 能够判定可调度性的算例比例平均不低于72%, 如图 7(a)所示.当任务个数增多或者Pmax/Pmin值增大时, 可判定算例比例略有下降, 但仍不低于60%, 如图 7(b)和图 7(c)所示.
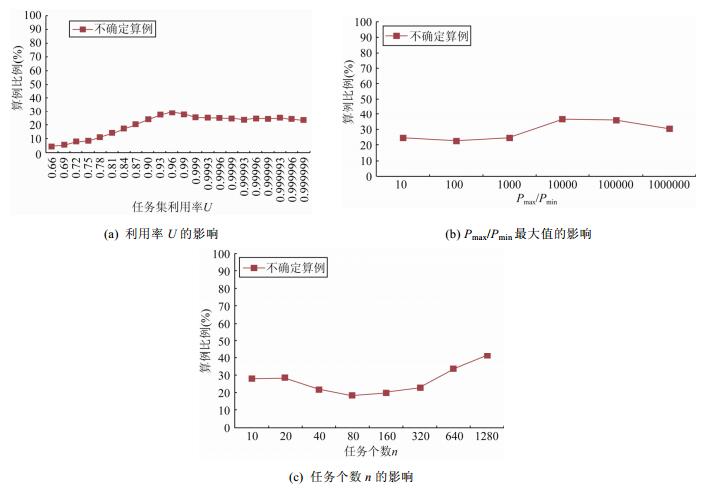
|
Fig. 7 Proportion of uncertain instances affected by problem parameters 图 7 问题参数对不确定算例比例的影响 |
5.4 异步系统中算法性能分析
针对异步系统, 本节将算法1和Baruah等人提出的传统算法[5]进行比较.注意到, 文献[5]中的方法回答“可调度”时, 说明异步系统一定是可调度的.但是, 当算法返回“不可调度”时, 则异步系统的可调度性不能确定.本节比较了本文算法和文献[5]中方法能够确切给出判定结果的算例比例.在问题参数为n=30, Pmax/Pmin:=1000, b=1.2×Pi, U=0.66~0.96时, 图 8给出了本文算法和传统算法[5]对同一随机算例集合给出的判定结果.实验结果表明, 本文算法对近96%的算例都能给出精确的判定结果, 将传统算法[5]不能给出判定结果的算例比例平均降低了29.27%.注意到, 当U≤0.9时, 本文算法不能给出判定结果的算例比例保持在6%以下.当U > 0.9之后, 该比例有明显上升趋势.这种现象产生的原因是, 算法1不能给出判定结果的算例比例与U成正比关系.由算法1第10行~第13行可知, 算法返回“可调度性不确定”结果的必要条件是:存在一个子问题的线性松弛解LPl≤0.不妨令l=n, 则
| $ \begin{array}{l} L{P_i} = \min \left( {{t_2}-{t_1}-\sum\nolimits_{{\tau _k}:{D_k} + {\varphi _k} \le {Q_i}} {{C_k}\left( {{x_k}-{y_k} + 1} \right)} } \right)\\ \;\;\;\;\;\;\left( {经过线性松弛, {x_k}和{y_k}允许取小数} \right)\\ \;\;\;\;\;\; = {t_2} - {t_1} - \sum\nolimits_{{\tau _k}:{D_k} + {\varphi _k} \le {Q_i}} {{C_k}\left( {\left( {{t_2} - {t_1} + {D_k}} \right)/{P_k} + 1} \right)} \\ \;\;\;\;\;\;\left( {根据约束(4)和(5), 将{x_k} \le \left( {{t_2} - {\varphi _k} - {D_k}} \right)/{P_k}和{y_k} \ge \left( {{t_1} - {\varphi _k}} \right)/{P_k}代入} \right)\\ \;\;\;\;\;\; = \left( {1 - U} \right)\left( {{t_2} - {t_1}} \right) - \sum\nolimits_{{\tau _k}:{D_k} + {\varphi _k} \le {Q_i}} {{u_k}\left( {{P_k} - {D_k}} \right).} \end{array} $ |
观察上式可知, 当利用率U增大时, 等号右边第1项(1-U)(t2-t1)减小, 同时, 第2项
针对判定结果不确定的算例, 应用算法3可将可调度性分析上界L降低到一个合理的范围.如图 9所示, 算法3得到的L较之原上界值Φ+2H有指数级的降低, 平均降低了近104倍(为了表述方便, 图 9直接将新的L值与超周期H进行比较).
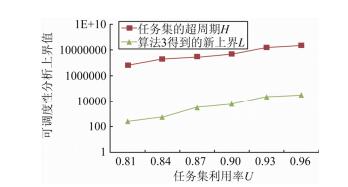
|
Fig. 9 Comparison between the new bound obtained by Algorithm 3 and the hyper-period H 图 9 算法3获得的界与超周期H的比较 |
6 总结与展望
本文研究了偶发性实时任务系统可调度性分析问题的整数规划方法, 为同步和异步两类任务系统提出了统一的求解模型和算法框架.第5节的实验结果表明, 该方法在利用率U较大的同步任务系统和较为困难的异步系统中更具优势.而且, 本文算法的性能比较稳定, 受测试集参数变化的影响较小.注意到, 本文算法尽管对某些困难算例能够指数倍地提升求解效率, 但并不是对所有算例都能给出明确的判定结果.尤其是对异步系统而言, 本文方法对U≤0.9的算例更加有效.因此, 下一步的工作是更加深入地分析本文IP模型的解空间, 提出更多的强有效不等式和更多能够从理论上严格证明的极大诱导不等式, 进一步缩小算法的gap值, 从而有效降低不确定算例的比例.另外, 偶发实时任务模型是实时系统领域中最基本的形式化模型之一, 绝大多数复杂实时系统模型的可调度性分析均基于偶发实时任务模型的基本原理和框架.偶发任务调度新的问题模型和算法框架的提出, 极有可能扩展到更复杂的实时系统模型中.因此, 充分结合图论和网络优化理论, 为DRT等更复杂的实时系统模型建立整数规划方法求解框架, 也是很有希望的未来工作方向之一.
| [1] | Baruah S, Pruhs K. Open problems in real-time scheduling. Journal of Scheduling, 2010, 13(6): 577–582 . [doi:10.1007/s10951-009-0137-5] |
| [2] | Davis RI, Burns A. A survey of hard real-time scheduling for multiprocessor systems. ACM Computing Surveys, 2011, 43(4): 88–87 . [doi:10.1145/1978802.1978814] |
| [3] | Liu CL, Layland JW. Scheduling algorithms for multiprogramming in a hard-real-time environment. Journal of the ACM, 1973, 20(1): 46–61 . [doi:10.1145/321738.321743] |
| [4] | Hamon G, Rushby J. An operational semantics for Stateflow. Int'l Journal on Software Tools for Technology Transfer, 2004, 9(5-6): 447–456 . [doi:10.1007/s10009-007-0049-7] |
| [5] | Baruah SK, Rosier LE, Howell RR. Algorithms and complexity concerning the preemptive scheduling of periodic, real-time tasks on one processor. Real-Time Systems, 1990, 2(4): 301–324 . [doi:10.1007/BF01995675] |
| [6] | Leung JYT, Merrill ML. A note on preemptive scheduling of periodic, real-time tasks. Information Processing Letters, 1980, 11(3): 115–118 . [doi:10.1016/0020-0190(80)90123-4] |
| [7] | Eisenbrand F, Rothvoß T. EDF-Schedulability of synchronous periodic task systems is coNP-hard. In:Proc. of the ACM-SIAM Symp. on Discrete Algorithms. 2010. 1029-1034. |
| [8] | Zhang F, Burns A. Schedulability analysis for real-time systems with EDF scheduling. IEEE Trans. on Computers, 2009, 58(9): 1250–1258 . [doi:10.1109/TC.2009.58] |
| [9] | Sun JH, Deng QX, Meng YK. Two-Stage workload scheduling problem on GPU architectures:Formulation and approximation algorithm. Ruan Jian Xue Bao/Journal of Software, 2014, 25(2): 298–313 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/4527.htm [doi:10.13328/j.cnki.jos.004527] |
| [10] | Zhang DS, Wu T, Chen FY, Jin SY. Global EDF-based on-line energy-aware real-time scheduling algorithm in multi-core systems. Ruan Jian Xue Bao/Journal of Software, 2012, 23(4): 996–1009 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/4054.htm [doi:10.3724/SP.J.1001.2012.04054] |
| [11] | Liu H, Fei SM. A fault-tolerant scheduling algorithm based on EDF for distributed control systems. Ruan Jian Xue Bao/Journal of Software, 2003, 14(8): 1371–1378 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/14/1371.htm |
| [12] | Pellizzoni R, Lipari G. A new sufficient feasibility test for asynchronous real-time periodic task sets. In:Proc. of the 16th Euromicro Conf. on Real-Time Systems (ECRTS 2004). IEEE, 2004. 204-211.[doi:10.1109/EMRTS.2004.1311022] |
| [13] | Stigge M, Ekberg P, Guan N, Yi W. The digraph real-time task model. In:Proc. of the 17th IEEE Real-Time and Embedded Technology and Applications Symp. (RTAS). IEEE, 2011. 71-80.[doi:10.1109/RTAS.2011.15] |
| [14] | Stigge M, Ekberg P, Guan N, Yi W. On the tractability of digraph-based task models. In:Proc. of the 23rd Euromicro Conf. on Real-Time Systems (ECRTS 2004). IEEE, 2011. 162-171.[doi:10.1109/ECRTS.2011.23] |
| [15] | Fersman E, Krcal P, Pettersson P, Yi W. Task automata:Schedulability, decidability and undecidability. Information and Computation, 2007, 205(8): 1149–1172 . [doi:10.1016/j.ic.2007.01.009] |
| [16] | Tan GZ, Sun JH, Wang BC, Yao WH. Solving Chinese postman problem on time varying network with timed automata. Ruan Jian Xue Bao/Journal of Software, 2011, 22(6): 1267–1280 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/4033.htm [doi:10.3724/SP.J.1001.2011.04033] |
| [17] | Ripoll I, Crespo A, Mok AK. Improvement in feasibility testing for real-time tasks. Real-Time Systems, 1996, 11(1): 19–39 . [doi:10.1007/BF00365519] |
| [18] | Hoang H, Buttazzo G, Jonsson M, Karlsson S. Computing the minimum EDF feasible deadline in periodic systems. In:Proc. of the 12th IEEE Int'l Conf. on Embedded and Real-Time Computing Systems and Applications. IEEE, 2006. 125-134.[doi:10.1109/RTCSA.2006.22] |
| [19] | Spuri M. Analysis of deadline scheduled real-time systems. Technical Report, 2772, INRIA, 1996. |
| [20] | Zhang F, Burns A. Schedulability analysis of EDF-scheduled embedded real-time systems with resource sharing. ACM Trans. on Embedded Computing Systems, 2013, 12(3): 1–19 . [doi:10.1145/2442116.2442117] |
| [21] | Optimization G. Gurobi optimizer reference manual. 2012. http://www.gurobi.com |
| [22] | Bini E, Buttazzo GC. Measuring the performance of schedulability tests. Real-Time Systems, 2005, 30(1-2): 129–154 . [doi:10.1007/s11241-005-0507-9] |
| [23] | Davis RI, Zabos A, Burns A. Efficient exact schedulability tests for fixed priority real-time systems. IEEE Trans. on Computers, 2008, 57(9): 1261–1276 . [doi:10.1109/TC.2008.66] |
| [24] | Tan G, Sun J, Hou G. The time-dependent rural postman problem:Polyhedral results. Optimization Methods and Software, 2013, 28(4): 855–870 . [doi:10.1080/10556788.2012.666240] |
| [25] | Sun JH, Meng YK, Tan GZ. An integer programming approach for the Chinese postman problem with time-dependent travel time. Journal of Combinatorial Optimization, 2014, 29(3): 565–588 . [doi:10.1007/s10878-014-9755-8] |
| [9] | 孙景昊, 邓庆绪, 孟亚坤. GPU上两阶段负载调度问题的建模与近似算法. 软件学报, 2014 , 25(2) : 298 –313. http://www.jos.org.cn/1000-9825/4527.htm [doi:10.13328/j.cnki.jos.004527] |
| [10] | 张冬松, 吴彤, 陈芳园, 金士尧. 多核系统中基于Global EDF的在线节能实时调度算法. 软件学报, 2012 , 23(4) : 996 –1009. http://www.jos.org.cn/1000-9825/4054.htm [doi:10.3724/SP.J.1001.2012.04054] |
| [11] | 刘怀, 费树岷. 基于EDF的分布式控制系统容错调度算法. 软件学报, 2003 , 14(8) : 1371 –1378. http://www.jos.org.cn/1000-9825/14/1371.htm |
| [16] | 谭国真, 孙景昊, 王宝财, 姚卫红. 时变网络中国邮路问题的时间自动机模型. 软件学报, 2011 , 22(6) : 1267 –1280. http://www.jos.org.cn/1000-9825/4033.htm [doi:10.3724/SP.J.1001.2011.04033] |
 2017, Vol. 28
2017, Vol. 28



