随着移动设备例如智能手机、传感器和穿戴设备的广泛使用, 相应的智能移动应用也随之产生, 包括人脸识别、视频应用等, 它们具有数据密集和时延敏感的特点, 如果计算延迟过高, 则会影响应用的服务质量. 边缘计算^[1]在网络边缘部署了计算基础设施, 可以提供较高的计算性能和低延迟的服务, 所以将计算任务从移动设备卸载到物理距离邻近服务器上执行是一种可行的方案. 通过卸载应用中部分或者全部任务, 可以提升移动应用的服务质量. 然而, 由于边缘服务器和基站的资源有限, 并且需要同时服务多个移动设备^[2-5], 当出现大量服务请求时任务处理的服务质量可能出现下降的情况^[3], 这主要体现在引起较长的任务等待时延以及任务超时失效.

在任务卸载到边缘服务器之后, 任务之间的调度顺序将会进一步影响到各个任务的处理时延以及是否超时. 特别是在用户数量比较多, 而可用资源有限的情况下, 任务排队等待时间的影响会更加显著. 一般而言, 先分配处理器的任务更有可能获得更短的完成时间. 对于时延敏感任务, 能够在截止期限之前完成并且返回结果是关键的服务质量评价依据^[6], 这对任务的资源分配提出了更高的要求. 此外, 卸载到边缘服务器上执行的任务可能来自不同的移动设备, 优化任务之间的调度顺序可以协调多个设备之间的优化目标. 通常使用的调度方法如先到先调度可能使得信道条件较稳定、传输数据量小的设备总是得到快速响应, 而信道状况较差、传输数据量大的设备所卸载的任务则总是无法在截止期限内完成, 从而无法很好地平衡多个设备的优化目标.

鉴于此, 本文主要研究可用资源受限的单基站、多个移动设备的典型边缘计算框架^{[6, 7]}, 并针对时延敏感任务提出了任务卸载和任务调度的联合优化策略. 该策略是一个基于强化学习的两步策略, 包括了带有替代回报的深度强化学习^[8]的任务卸载方案和基于组合多臂赌博机(combinatorial multi-armed bandit, CMAB)的任务调度方案. 在每一个决策时隙, 卸载决策单元首先产生每个设备是否卸载任务的控制信号, 移动设备根据控制信号将任务卸载到服务器执行或者置于本机执行; 服务器收集到来自设备的任务之后, 根据调度单元生成的调度优先级执行任务调度, 并将奖励信号反馈给任务调度单元, 用以持续优化任务调度策略. 本文的主要贡献如下.

• 针对带截止期限的任务, 解决了在边缘计算平台资源有限条件下多用户任务卸载问题. 基于任务在终端和服务器端执行的两种情况, 本文设立了决策模型和最小化系统整体代价的优化目标, 并在调度阶段加入卸载成功率约束来改进多用户之间的公平性.

• 提出了基于 CMAB 的动态任务调度算法. 对资源受限的边缘计算平台, 采用李亚普诺夫(Lyapunov)优化方程将长期的卸载成功率约束和费用最小化目标转化为多阶段在线优化问题. 然后将任务调度问题建模为 CMAB 模型, 采用改进的 CUCB (combinatorial upper confidence bound)方法求解.

• 提出了协作任务卸载策略. 考虑动态改变的调度顺序带来回报值不稳定问题, 改进了基于扰动回报的深度 Q 学习方法来进行任务卸载决策. 在训练过程中对回报值扰动噪声进行拟合, 使用估计的替代回报代替直接观测的回报值. 其中多个用户的协作体现在共同更新替代回报估计矩阵、采用共享参数的方式训练以及同时观测环境并做决策.

• 仿真实验结果表明: 对于带截止期限的多用户任务卸载, 本文所提出的改进方案在边缘计算平台资源受限的场景下具有良好的适应性和可靠性保证, 相比于已有方法在整体性能上具有明显优势.

本文第1节介绍相关研究工作. 第2节介绍边缘环境下系统模型和问题描述. 第3节介绍基于强化学习的任务卸载和调度联合优化方案. 第4节分别介绍卸载和调度策略性能分析. 第5节通过仿真实验对算法进行性能评估和结果分析. 第6节对本文工作进行总结.

1 相关工作

目前有很多学者从计算卸载和任务调度的优化角度进行了一些相关研究, 并且有一部分工作从不同角度出发探讨了资源受限的场景. 此外, 强化学习(reinforcement learning, RL)方法是一个广泛采纳的任务卸载解决方案. 本节从问题和解法两个角度出发, 介绍边缘环境下的任务卸载和任务调度的研究现状.

1.1 计算卸载和任务调度

现有的任务卸载方法一般考虑固定的边缘服务器中任务调度策略^[4]. 但是在计算资源受限的实际场景中, 任务在边缘服务器上的排队等待时间是影响服务质量不可忽视的因素, 传统的优化计算卸载决策的方法无法对服务器上任务处理时延进行优化. 因此有学者将任务调度和任务卸载进行联合优化或者针对计算卸载的任务特性设计优化的任务调度策略^{[7, 9-14]}. 任务的处理时延优化^{[15, 16]}以及兼顾各个用户的性能目标是计算卸载和任务调度联合优化中着重考虑的问题. 文献 [7] 中针对卸载任务异步到达边缘服务器的问题, 提出了服务器端的序列化的任务执行模型, 并且考虑了资源无限的理想化场景以及资源有限的实际场景. 文献 [11] 中研究了一个最小化移动设备能耗开销的任务卸载策略, 并且提出了在边缘服务器端基于动态优先级的任务调度策略. 文献 [14] 中不仅考虑了用户向MEC (multi-access edge computing)平台卸载任务的场景, 也考虑了用户之间进行任务卸载的可能. 在此模型下将问题建模为混合整数非线性规划问题. 他们首先提出了一个资源优化方案的闭式解, 然后基于块坐标下降方法导出较低计算复杂度的近似解.

已有一些研究工作致力于解决时延敏感任务的决策与调度问题^[17-22]. 例如文献[17]提出了一种时间任务调度算法, 以在应用延迟约束内调度所有任务. 文献[18]提出一种基于深度强化学习的方法来调度混合云中的实时作业. 文献[19]提出了如何通过在能耗和任务执行时间之间进行良好的权衡来调整任务放置和资源分配. 然而这些工作并非针对有限资源场景下的任务调度. 文献[20]提出了一种在有限资源边缘计算场景下的串行任务卸载策略, 但未考虑多个终端之间的卸载公平性. 在兼顾多用户性能方面, 现有研究采用了不同的公平性指标来保证多用户之间的公平性. 文献 [13] 中设计了关于吞吐量的公平性指标; 文献 [12] 保证了虚拟机之间的公平性; 文献 [4, 7, 23] 通过最小化最长任务执行时间以保证公平性. 但是以上方法都没有考虑如何平衡多个时延敏感任务的调度目标, 并且所采用的启发式解法专注于即时回报, 可能造成最终性能下降.

1.2 基于强化学习的卸载决策

不同于传统的基于即时回报的解法或是手工设计的启发式算法, 强化学习方法的优势在于可对长期目标进行优化, 并且具有更好的泛化性. 对于单基站多用户的任务卸载场景, 目前已有多种基于强化学习的解决方案. 文献 [24] 中采用了Q学习的方法来最小化所有用户的能耗, 同时考虑了任务的时延约束以及异构计算任务的动态资源需求. 作者将问题建模为一个混合整数非线性规划问题. 在每个决策时隙, MEC服务器需要决定每个任务是在设备终端还是在边缘服务器上执行以及信道资源分配. 该算法在多个不同场景下进行测试, 但其性能仅在小型基站下得到验证. 文献 [25] 中设计了一个基于强化学习的在线算法, 能在时变的无线信道状态下进行自适应计算卸载决策. 他们的方法将原优化问题解耦为卸载决策的子问题和资源分配的子问题, 并在连续的状态空间下起作用. 文献 [4] 中针对每个移动设备传输能力有限的场景, 导出优化的动态调度方法以最小化所有用户的最终能耗以及时延. 调度方法需要做出3类决策: 任务在终端还是服务器上执行; 对于需要进行任务卸载的设备, 需要分配多少传输能量; MEC服务器对每个任务分配多少计算资源. 文献 [3] 中基于基站中存在大规模用户的场景, 研究如何应对基站对卸载信号的检测出现遗漏的情况. 该策略令所有的用户轮流进行计算卸载, 而其他用户的动作在这一时隙是固定的. 为了避免网络的训练陷入局部最优, 以一定的概率随机作出动作. 实验结果表明这一方法可以在大规模用户场景下显现优势. 文献 [2] 中将用户分为多个组形成多个相互独立的MEC环境进行训练, 使用了分布式强化学习方法来提升训练的多样性. 方法基于A2C (advantage actor critic)的强化学习方法, 采用了自适应的n步训练方法来提升训练效率的同时避免由于分布式训练造成高偏差. 应对环境的不确定性, 文献 [2] 采用高斯噪声来增加策略的鲁棒性. 然而这些方法都无法处理有偏观测回报, 即真实的回报值因为环境扰动而在观测时改变为其他回报. 这种回报值的有偏性会使策略出现不可控的改变.

基于以上分析, 本文提出的策略针对时延敏感任务的卸载优化问题. 其中对于资源受限的边缘计算系统平衡系统总体性能和各个用户的性能指标, 并且采用带有替代回报值的强化学习方法提高卸载决策的鲁棒性.

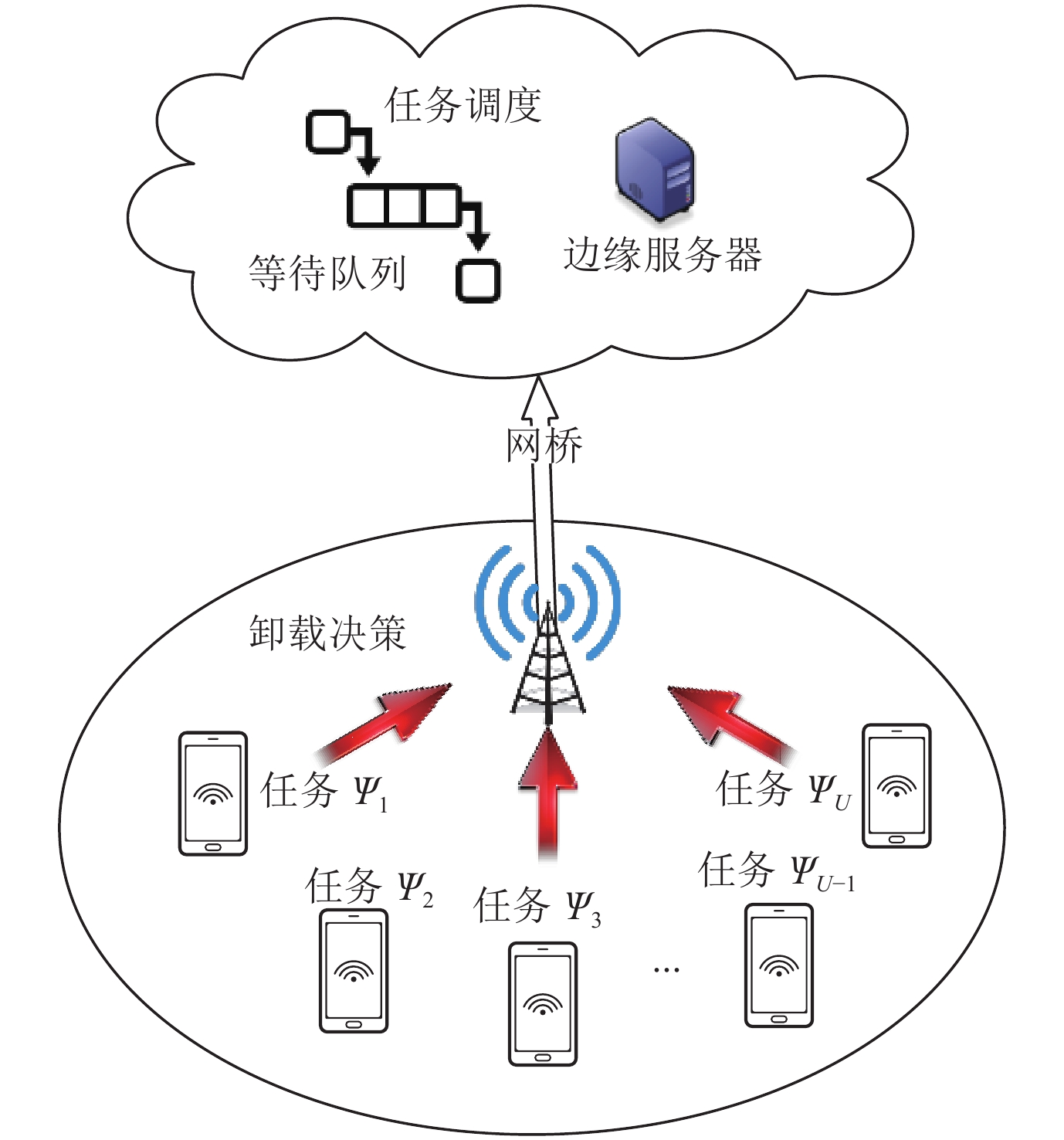
2 模型及问题描述

本节的场景介绍包括决策模型、任务处理时延约束模型、任务在本机设备和边缘服务器的执行模型, 然后对计算卸载和任务调度的联合优化问题做出描述. 单基站多用户的场景模型如图1所示, 其中红色箭头表示执行任务卸载. 令 ${\boldsymbol{U}} = \left\{ {1, 2, \ldots, U} \right\}$ 表示停留在基站覆盖范围内的移动设备, ${\boldsymbol{M}} = \left\{ {1, 2, \ldots, M} \right\}$ 作为无线信道的集合, 移动设备可以通过这些无线信道向基站传输任务执行所需的数据. 移动设备和边缘服务器都有一定的计算能力. 假设系统的操作是在固定长度的时隙 $\left\{ {1, 2, \ldots, T} \right\}$ 上进行, 并且每一个设备在每个时隙 $ t $ 都有一个新任务等待执行.

2.1 决策模型

为了在不损害总体性能的前提下兼顾多个用户的性能目标, 不仅需要对任务是否卸载进行决策来最小化设备的整体开销, 还需要保证每个设备所卸载的任务都能以一定概率在截止期限内完成. 而任务的时延和排队等待时间相关, 因此解决这一问题需要同时对卸载和调度顺序进行决策. 在每个决策时隙, 决策的执行分别基于卸载决策单元和任务调度单元. 本文采用文献 [2] 中的任务模型, 假设设备 $ i $ 在时隙 $ t $ 所产生的任务定义为 $ {\varPsi _i} = \left\{ {i, {k_i}, {c_i}, {d_i}} \right\} $ , $ i $ 是产生任务的设备索引, $ {k_i} $ 是输入数据规模, $ {c_i} $ 是完成该任务所需的CPU周期, $ {d_i} $ 是任务的截止期限, 任务之间相互独立. 当处理器被其他任务所占用时, 任务须在队列中等待.

在决策时隙开头, 卸载决策单元根据系统状态, 对每个设备产生的任务做出决策 $ \left\{ {\left( {{b_i}, {a_i}} \right)|i \in {\boldsymbol{U}}} \right\} $ , $ {b_i} = 0 $ 表示任务在本机处理, $ {b_i} = 1 $ 表示任务交给边缘服务器处理. 当任务由边缘服务器处理时, $ {a_i} \in {\boldsymbol{M}} $ 表示所选择的数据传输信道. 系统状态包括任务信息 $\left\{ {{\varPsi _1}, {\varPsi _2}, \ldots, {\varPsi _U}} \right\}$ 、各个设备的位置 $\left\{ {\left( {{x_1}, {y_1}} \right), \ldots, \left( {{x_U}, {y_U}} \right)} \right\}$ 、各设备内等待队列中任务完成所需时间之和 $\left\{ {{q_1}, \ldots, {q_U}} \right\}$ 以及服务器的等待队列中任务完成所需时间之和 $ {q_e} $ .

在卸载的任务( $ {b_i} = 1 $ )到达边缘服务器后, 这些任务将进入服务器的等待队列, 同时调度单元根据每个任务的截止期限以及服务质量指标产生调度优先级, 调度单元优先调度优先级高的任务, 当计算资源充足时才会调度低优先级的任务. 本节详细描述任务本地处理和卸载处理的开销, 其中省略标识时间的下标 $ t $ 来简化表达.

2.2 设备本地处理

如果任务 $ {\varPsi _i} $ 在设备本地处理, 那么任务将移交给本地的计算单元. 任务的执行时间取决于本地设备的计算能力 $ c{p_{{i}}} $ , 任务所需的CPU周期 $ {c_i} $ , 以及设备队列中的任务完成所需时间之和为 $ {q_i} $ . 任务初始化时间相对较短, 所以不纳入计算. 因此, 任务的时间开销计算如下:

$ \tau _{{i}}^l = \frac{{{c_i}}}{{c{p_i}}} + {q_i} $

(1)

能耗开销费用计算如下:

$ e_i^l = {c_i} \cdot {\beta _i} \cdot \lambda $

(2)

其中, $ \;{\beta _i} $ 是设备 $ i $ 平均每个CPU周期所产生的能耗开销, 大小和计算设备的特性相关. 在此采用实际的度量^[26]并将其设为 $ \;{\beta _i} = {10^{ - 27}} \cdot {\left( {c{p_i}} \right)^2} $ , $ \lambda $ 是单位能耗所产生的费用. 任务需要在截止期限内完成, 否则将产生一定的罚数返回给卸载决策单元, 增加任务执行的平均开销. 因此, 开销是由能耗费用和执行时间长度共同决定. 对于设备 $ {i}\text{} $ 所产生的任务, 本机处理的开销计算如下:

$ C_i^l = \left\{ \begin{array}{*{20}{l}} {e_i^l} , &{\tau _i^l \leqslant {d_i}} \\ \Xi , &{{\rm{otherwise}}} \end{array} \right.$

(3)

2.3 任务卸载处理

如果任务 $ {\varPsi _i} $ 卸载边缘服务器上处理, 任务就会通过无线通讯网传输到基站, 同时产生传输时延以及传输能耗开销. 任务 $ {\varPsi _i} $ 被分配到的传输功率表示为 $ {p_i} \in {\boldsymbol{P}} $ , P是可选的传输功率集合. 基于码分多址的无线电干扰模型, 设备 $ i $ 和基站之间的上行数据率计算如下:

$ {\sigma _i} = \omega \cdot {\log _2}\left(1 + \frac{{{p_i} \cdot {g_{i, e}}}}{{{\varpi _{i, e}} + \displaystyle\sum\nolimits_{j \in {\boldsymbol{U}}\backslash \left\{ i \right\};{a_i} \ne {a_j}} {{p_j} \cdot {g_{i, e}}} }}\right) $

(4)

其中, $ \omega $ 是信道带宽, $ {\varpi _{i, e}} $ 是背景噪声的功率. $ {g_{i, e}} = d_{i, e}^{ - \rho } $ 是设备 $ i $ 和基站之间的信道增益, $\; \rho $ 是路径损失指数而 $ {d_{i, e}} $ 是设备 $ i $ 和基站之间的距离. 此外, $ {\boldsymbol{U}}\backslash \left\{ i \right\}:{a_i} \ne {a_j} $ 包含了 $ {\boldsymbol{U}} $ 中除了 $ i $ 之外满足 $ {a_j} \ne {a_i} $ 的所有元素. 因此, 设备 $ i $ 上传数据的时间开销计算如下:

$ \tau _i^{tr, e} = \frac{{{k_i}}}{{{\sigma _i}}} $

(5)

由于基站到设备端的下行传输率相对上行传输率较高, 并且任务的结果数据量通常较小, 所以返回结果所产生的能耗以及结果数据的传输时间可忽略不计^[27].

类似于本机处理, 任务 $ {\varPsi _i} $ 在服务器上所需的时间为:

$ \tau _i^e = \tau _i^{tr, e} + \tau _i^{{\rm{comp}}, e} $

(6)

其中, $ {q_{i, e}} $ 是执行任务 $ {\varPsi _i} $ 的等待时间. 因此, 任务服务器上执行所需的总时延为:

$ \tau _i^e = \tau _i^{tr, e} + \tau _i^{{\rm{comp}}, e} $

(7)

边缘计算的能耗开销包含了因任务执行向边缘服务器支付的费用以及数据传输带来的能耗开销, 计算如下:

$ e_i^e = {c_i} \cdot {\beta _e} + \tau _i^{tr, e} \cdot {p_i} \cdot \lambda $

(8)

其中, $ \lambda $ 是边缘服务器的每个CPU周期的单位费用, β_e是边缘服务器平均每个CPU周期所产生的能耗开销.

和本机处理类似, 卸载到边缘服务器的任务也须在截止期限内完成. 因此任务卸载的开销计算如下:

$ C_i^e = \left\{ \begin{array}{*{20}{l}} {e_i^e} , &{\tau _i^e \leqslant {d_i}} \\ \Xi , &{{\rm{otherwise}}} \end{array} \right.$

(9)

2.4 长期时延约束模型

对于单基站多用户的计算卸载, 边缘服务器是共享资源, 所以对卸载任务的执行成功率建立约束以保证用户之间的公平性. 如果等待时间给任务执行带来明显影响, 并且影响到达一定程度导致任务过期, 那么任务即使完成也不再具有实际意义时则判定该任务执行失败. 反之, 任务在截止期限内完成则判定为成功执行. 为了权衡所有用户的性能目标, 我们对需要在服务器上等待的任务引入长期的卸载成功率约束, 即:

$ \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {{\boldsymbol{E}}\left[ {s_{i, t}^e} \right]} \geqslant \kappa $

(10)

其中, $ s_{i, t}^e = 1 $ 表示来自设备 $ i $ 所卸载的任务在时隙 $ t $ 执行成功, 否则 $ s_{i, t}^e = 0 $ . 这一约束是保证每个设备卸载任务的长期成功率不小于 $ \kappa $ .

2.5 优化目标

综合以上模型和评价指标, 优化问题可以表示为:

$ ({\rm{P}}1) \; \min \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^U {(1 - {b_{i, t}})} } \cdot C_{i, t}^e + {b_{i, t}} \cdot C_{i, t}^l \tag{11a}$

$ {\rm{s}}.{\rm{t}}. \; {{{b}}_i} \in \left\{ {0, 1} \right\},\;{i \in \boldsymbol{U}} \tag{11b} $

$ \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {{\boldsymbol{E}}\left[ {s_{i, t}^e} \right]} \geqslant \kappa \tag{11c}$

这是一个带约束的多目标优化问题.由于约束和时间紧密耦合, 因此难以用通常的离线算法进行求解. 因此把目标(P1)分解为计算卸载(SUB1-P1)和任务调度(SUB2-P1)两个子问题, 即:

$ ({\rm{SUB}}1\text{-}{\rm{P}}1) \; \min \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^U {\left( {1 - {b_{i, t}}} \right)} } \cdot C_{i, t}^l + {b_{i, t}} \cdot C_{i, t}^e \tag{12a}$

$ {\rm{s}}.{\rm{t}}. \; {b_{i, t}} \in \left\{ {0, 1} \right\}, \;{i \in {\boldsymbol{U}}} \tag{12b} $

和

$ ({\rm{SUB}}2\text{-}{\rm{P}}1) \; \min \sum\limits_{t = 1}^T {\sum\limits_{i = 1}^U {s_{i, t}^e} } \cdot {c_{i, t}} \cdot {\beta _e} \tag{13a}$

$ {\rm{s}}.{\rm{t}}. \; s_{i, t}^e \leqslant {b_{i, t}} \tag{13b}$

$ \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {{\boldsymbol{E}}\left[ {s_{i, t}^e} \right]} \geqslant \kappa \tag{13c}$

由于任务调度仅针对卸载到服务器端的任务, 假定调度单元可以根据调度顺序预估任务的处理时延, 对于无法在截止期限内完成的任务不予执行, 而是将资源腾出给其他需要执行的任务, 由此可以进一步减少任务执行所需的费用并提升任务成功执行的整体概率.

3 计算卸载与任务调度的联合优化 3.1 基于李亚普诺夫框架的调度优化问题转化

本文利用李亚普诺夫框架将调度问题转化为可求解的在线优化问题. 首先分别为每个设备引入一个虚拟队列, 在时隙 $ t $ 虚拟队列中存在的积压工作表示为 $ {Y_{i, t}} $ . 在整个决策过程, $ {Y_{i, t}} $ 按以下规则演化:

$ {Y_{i, t + 1}} = \max \left\{ {{Y_{i, t}} + {{\kappa}} - s_{i, t}^e, 0} \right\} $

(14)

接下来介绍定理1来证明这一规则的合理性.

定理1. 长期时延约束成立当且仅当在决策过程中虚拟队列保持稳定的平均比率.

证明: 根据排队论^[28], 如果所有的虚拟队列在决策过程中保持稳定的平均比率( $ {\lim _{T \to \infty }}{\boldsymbol{E}}\left[ {{Y_{i, T}}} \right]/T = 0 $ ), 则虚拟队列的平均到达率会小于服务率, 即:

$ \frac{1}{T}\mathop {\lim }\limits_{T \to \infty } \sum\limits_{t = 1}^T {{\boldsymbol{E}}\left[ {\left| {{{\boldsymbol{O}}_t}} \right| \cdot {{\kappa}} - \left| {{\boldsymbol{S}}_t^e} \right|} \right]} \leqslant 0 $

(15)

其中, $\left| {{\boldsymbol{S}}_t^e} \right| =\displaystyle \sum\nolimits_{i \in {{\boldsymbol{U}}}} {s_{i, t}^e \cdot {b_{i, t}}}$ 是时隙 $ t $ 卸载到服务器并且成功执行的任务集合大小, $ \left| {{{\boldsymbol{O}}_{{t}}}} \right| = \displaystyle \sum\nolimits_{i \in {\boldsymbol{U}}} {{b_{i, t}}} $ 是卸载到服务器的任务集合大小. 公式(15)与公式(10)等价. 证毕.

通过定理1, 时隙耦合的约束转化为在决策过程中保持虚拟队列具有稳定的平均比率. 为达到这一目的, 一个直接的方式就是限定虚拟队列的每一次增长. 基于此, 我们通过李亚普诺夫优化技术来限制虚拟队列长度的增加, 同时最小化SUB2-P1的目标. 建立的李亚普诺夫二次方程如下:

$ L\left( {{\boldsymbol{\varTheta }}\left( t \right)} \right) = \frac{1}{2}\sum\limits_{i \in {\boldsymbol{U}}} {Y_{i, t}^2} $

(16)

其中, $ {\boldsymbol{\varTheta }}\left( t \right) \triangleq {\left\{ {{Y_{i, t}}} \right\}_{i \in {\boldsymbol{U}}}} $ 包含了所有虚拟队列的积压工作.

为限制每个时隙虚拟 $ L\left( {{\boldsymbol{\varTheta }}\left( t \right)} \right) $ 值的期望增量, 本文首先通过李亚普诺夫漂移方程来度量这一增量, 即:

$ \Delta L ( {\boldsymbol{\varTheta }}( t ) ) = {\boldsymbol{E}}\left[ L ( {\boldsymbol{\varTheta }( {t + 1} )} ) - L( {{\boldsymbol{\varTheta }}( t )} )|{\boldsymbol{\varTheta }}\left( t \right) \right] $

(17)

合并考虑SUB2-P1目标即最小化任务执行的总费用, 可以得到如下方程:

$ f\left( {{\boldsymbol{S}}_t^e} \right) = \Delta L\left( {{\boldsymbol{\varTheta }}\left( t \right)} \right) + X \cdot {\boldsymbol{E}}\left[ {\sum\limits_{i \in {\boldsymbol{U}}} {s_{i, t}^e \cdot {c_i} \cdot {\beta _e}|{\boldsymbol{\varTheta }}\left( t \right)} } \right] $

(18)

其中, $ X $ 是用于平衡费用目标和超时约束的惩罚因子. 对于任务调度单元而言, 每个设备是否执行任务卸载是一个可观测的随机事件, 而条件期望与每个设备是否执行任务卸载有关. 因此需要导出方程的上界, 结果如定理2所示.

定理2. $ f\left( {{\boldsymbol{S}}_t^e} \right) $ 的值约束形式如下:

$ \Delta L\left( {{\boldsymbol{\varTheta }}\left( t \right)} \right) + X \cdot {\boldsymbol{E}}\left[ {\sum\limits_{i \in {\boldsymbol{U}}} {s_{i, t}^e \cdot {c_i} \cdot {\beta _e}|{\boldsymbol{\varTheta }}\left( t \right)} } \right] \\ \leqslant \Gamma + \sum\limits_{i = 1}^U {{Y_{i, t}} \cdot {\boldsymbol{E}}\left[ {\kappa - s_{i, t}^e|{\boldsymbol{\varTheta }}\left( t \right)} \right] + X \cdot {\boldsymbol{E}}\left[ {\sum\limits_{i = 1}^U {s_{i, t}^e \cdot {c_i} \cdot {\beta _e}} |{\boldsymbol{\varTheta }}\left( t \right)} \right]} $

(19)

其中, $ \Gamma = U \cdot \left( {1 + {\kappa ^2}} \right)/2 $ 为常数.

证明: 将演化方程求平方, 可得:

$ Y_{i, t + 1}^2 = Y_{i, t}^2 + 2 \cdot {Y_{i, t}} \cdot \left( {\kappa - s_{i, t}^e} \right) + {\left( {\kappa - s_{i, t}^e} \right)^2} $

(20)

$\left( \dfrac{1}{2} \right) \cdot Y_{i, t + 1}^2$ 和 $\left( \dfrac{1}{2} \right) \cdot Y_{i, t}^2$ 的差值为:

$ \frac{1}{2} \cdot \left( {Y_{i, t + 1}^2 - Y_{i, t}^2} \right) = \frac{1}{2} \cdot {\left( {\kappa - s_{i, t}^e} \right)^2} + {Y_{i, t}} \cdot \left( {\kappa - s_{i, t}^e} \right) \leqslant \frac{1}{2} \cdot \left( {{\kappa ^2} + {{\left( {s_{i, t}^e} \right)}^2}} \right) + {Y_{i, t}} \cdot \left( {\kappa - s_{i, t}^e} \right) \leqslant \frac{1}{2} \cdot \left( {{\kappa ^2} + 1} \right) + {Y_{i, t}} \cdot \left( {\kappa - s_{i, t}^e} \right) $

(21)

由此可得:

$ \Delta L\left( {{\boldsymbol{\varTheta }}\left( t \right)} \right) \leqslant \Gamma + \sum\limits_{i \in {\boldsymbol{U}}} {{Y_{i, t}} \cdot {\boldsymbol{E}}\left[ {\kappa - s_{i, t}^e|{\boldsymbol{\varTheta }}\left( t \right)} \right]} $

(22)

将 $X \cdot {\boldsymbol{E}}\left[ {\displaystyle\sum\nolimits_{i \in {\boldsymbol{U}}} {s_{i, t}^e} \cdot {c_i} \cdot {\beta _e}|{\boldsymbol{\varTheta }}\left( t \right)} \right]$ 插入公式(22), 即可转化为公式(19). 证毕.

因此, 在线调度问题形式化为:

$ ({\rm{SUB}}2\text{-}{\rm{P}}2) \; {\min _{{{\boldsymbol{S}}}_t^e}}\Gamma + \sum\limits_{i \in {\boldsymbol{U}}} {{Y_{i, t}} \cdot \left( {\kappa - s_{i, t}^e} \right)} + X \cdot \sum\limits_{i \in {\boldsymbol{U}}} {s_{i, t}^e \cdot {c_i} \cdot {\beta _e}}\tag{23a}$

${\rm{s}}.{\rm{t}}. \; s_{i, t}^e \leqslant {b_{i, t}} \tag{23b}$

$ s_{i, t}^e \in \left\{ {0, 1} \right\}\tag{23c} $

为简化表达式, 我们将常数项去除, 可得:

$({\rm{SUB}}2\text{-}{\rm{P}}3) \; {\min _{{{\boldsymbol{S}}}_t^e}}\sum\limits_{i \in {\boldsymbol{U}}} {{Y_{i, t}} \cdot \left( {\kappa - s_{i, t}^e} \right)} + X \cdot \sum\limits_{i \in {\boldsymbol{U}}} {s_{i, t}^e \cdot {c_i} \cdot {\beta _e}} \tag{24a}$

$ {\rm{s}}.{\rm{t}}. \; s_{i, t}^e \leqslant {b_{i, t}}\tag{24b} $

$s_{i, t}^e \in \left\{ {0, 1} \right\}\tag{24c} $

3.2 基于CMAB的调度优化问题求解

本文改进基于多臂赌博机(multi-armed bandit, MAB)的强化学习方法^[26,29-32]来求解调度排序问题. MAB通常用于在不确定的环境下处理在线优化问题. 一个基本的MAB模型包括一个具有多个相互独立摇臂的开槽机, 每拉动一个摇臂会反馈相应的奖励, 奖励的分布函数未知. 赌徒在每一轮中根据规则拉动一个或多个摇臂, 使得累积奖励最大. 我们将任务排序建模为一个组合多臂赌博机(CMAB)问题.

定义1 (CMAB模型). 令每个设备的索引作为一个摇臂, 即 ${\phi _{i,t}} = \left\langle i \right\rangle$ , 表示通过调度排序, 设备 $ i $ 所卸载的任务可以成功执行. 在决策时隙 $ t $ , 调度单元通过调度策略 $ {{{{\boldsymbol N}}}_t} $ 使得 $ \left| {{\boldsymbol{S}}_t^e} \right| $ 个设备卸载的任务得以成功执行, 即 $ \left| {{\boldsymbol{S}}_t^e} \right| $ 个摇臂按一定顺序被拉动并组成超臂 ${{\boldsymbol{\varPhi }}_t} = \left\{ {{\phi _{i,t}}|s_{i, t}^e = 1} \right\}$ . 如果超臂 ${{\boldsymbol{\varPhi }}_t}$ 被拉动, 那么对于所有 ${\phi _{i,t}} \in {{\boldsymbol{\varPhi }}_t}$ , 更新相应的奖励期望. 由于标准的CMAB算法解决的是最大化问题, 于是本文将P3-SUB2的目标方程转化为最大化问题并导出每个摇臂的奖励方程.

定义2 (奖励函数). 在第 $ t $ 个时隙, 对于所选超臂 ${{\boldsymbol{\varPhi }}_t}$ 中包含的每个摇臂 ${\phi _i} \in {{\boldsymbol{\varPhi }}_t}$ , 奖励函数定义为:

$ {r_{i, t}} = {Y_{i, t}} \cdot s_{i, t}^e - X \cdot s_{i, t}^e \cdot {c_i} \cdot {\beta _e} $

(25)

根据CUCB对于奖励期望的定义, 在时隙s结束摇臂 $ {\phi _i} $ 的奖励经验平均为:

$ { \hat \mu _i} = \left( {\sum\limits_{t = 1}^s {{r_{i, t}}} } \right)/{T_{i, s}} $

(26)

超臂奖励期望的计算则是采用线性加和的方式, 即超臂的奖励是超臂内所包含所有摇臂的奖励之和. 因此, 超臂 $ {{\boldsymbol{\varPhi }}_t} $ 的奖励期望表示为:

$ {r_t} = \sum\limits_{{\phi _i} \in {{\boldsymbol{\varPhi }}_t}} {{r_{i, t}}} $

(27)

基于以上定义, 算法1中展示了调度顺序生成算法. 对于卸载任务的设备所对应摇臂, 首先根据 ${\overline \mu _{i,t}}$ 值进行降序排列(第2行)作为任务的调度顺序, ${\overline \mu _{i,t}}$ 值大的任务具有更高的调度优先级(第3–9行). 其中, $ \bar{\;\mu} _{i,t} $ 的计算在算法2中第5行给出. 然后返回卸载任务的调度排序(第10行).

算法1. 调度顺序生成算法.

输入: ${\boldsymbol{U}}, \; X, \; {\beta _e}, \; \kappa , \; t, \; \left\{ {{{\bar \mu }_i}|i \in {{\boldsymbol{O}}_{{t}}}} \right\}, \; {{\boldsymbol{O}}_t} ;$

输出: ${{\boldsymbol{\varPhi }}_t}, \; r, \; {{{{\boldsymbol N}}}_t} .$

1.　初始化: $r \leftarrow 0; \; \left\{ {Y_{i, t}\leftarrow 0| i \in \boldsymbol{O}_t} \right\}; \; {\phi _i} \leftarrow 0, \; \forall i \in {\boldsymbol{U}}$

2.　使用 $ {\mathbb{D}_t} $ 存储 $\left\{ {{\phi _{i,t}}|{b_{i, t}} = 1} \right\}$ , 按 $\;{\bar \mu _{i,t}}$ 以降序方式排列

3.　初始化一个键值对空集合 $ {{{{\boldsymbol N}}}_t} $

4.　令位次索引 $ m \leftarrow 0 $

5.　for $ n \in {\mathbb{D}_t} $ do

6.　　 ${{{{\boldsymbol N}}}_t} \leftarrow {{{{\boldsymbol N}}}_t} \cup \left\{ {\left\langle {m, {\psi _{j,t}}} \right\rangle } \right\}$ , 其中 ${\psi _{j,t}}$ 是位次为n的摇臂对应的任务

7.　　 $ m \leftarrow m + 1 $

8.　　if $ n = \left| {{{\boldsymbol{O}}_t}} \right| $ then

9.　　　中止循环

10.　根据 $ {{{{\boldsymbol N}}}_t} $ 计算奖赏r得到每个摇臂的 $ s_{i, t}^e $ 值, 并导出调度排序 $ {{{{\boldsymbol N}}}_t} $

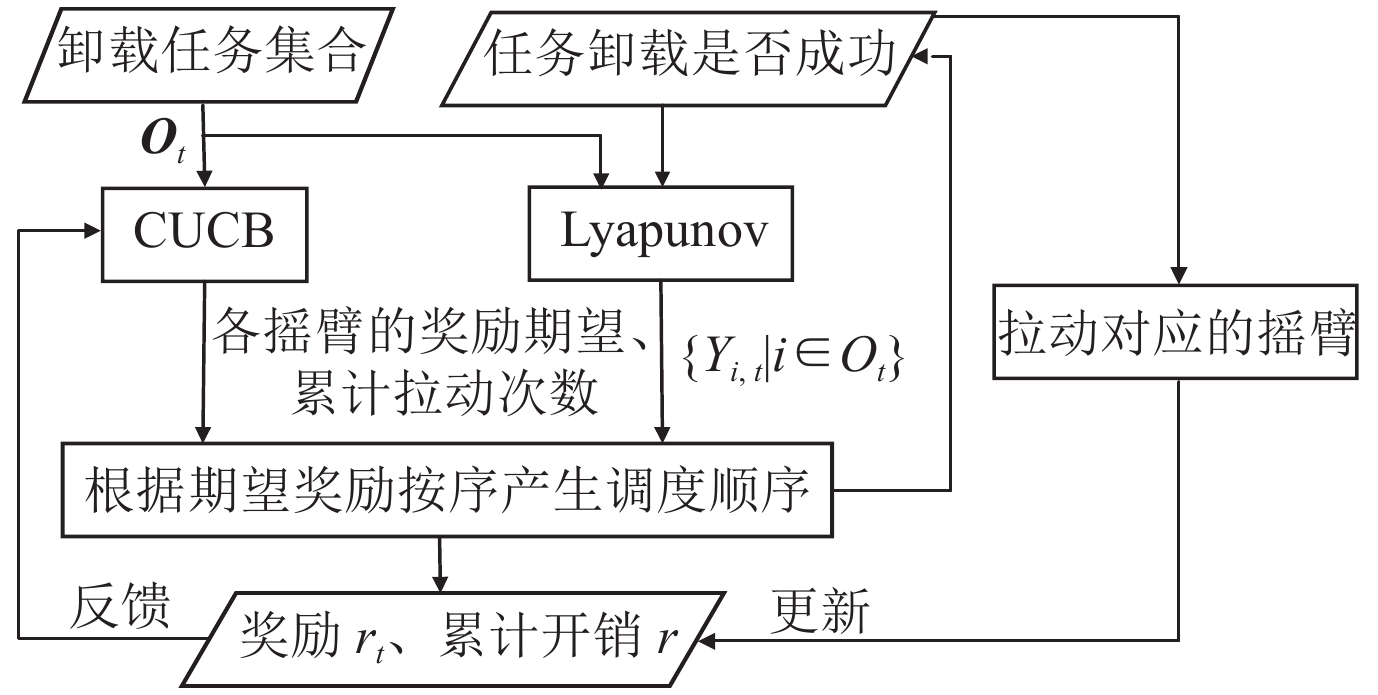
算法2展示了基于CMAB的任务调度流程, 即在执行实际的任务调度的同时不断优化摇臂分布. 算法2中, 首先将每个摇臂的 ${Y_{i,t}}$ 值、被选择的次数 $ {T_{i, t}} $ 、每个摇臂的奖励 $ {r_i} $ 初始化为0 (第1行). 然后对于每个摇臂 $ {\phi _i} $ , 随机选取一个包含该摇臂的超臂, 并更新摇臂的期望 $ \;{ \hat \mu _{i,t}} $ , 同时令所有摇臂的选取次数 $ {T_{i, t}} = 1 $ (第2行). 在调度的迭代阶段, 首先通过计算得到每一个摇臂的真实期望向量 $ \;{{\bar \mu _{i,t}}} $ (第5行). 在使用算法1得到任务的执行顺序之后, 任务按顺序执行并且得到每一个任务是否成功执行的结果 $ s_{i, t}^e $ (第6, 7行). 然后通过调度单元估算任务的执行时间, 确定在时隙 $ t $ 最终选取的摇臂集合为 $ {{\boldsymbol{\varPhi }}_t} = \left\{ {{\phi _i}|s_{i, t}^e = 1} \right\} $ , 即在时隙t如果 $ s_{i, t}^e = 1 $ , 那么摇臂 $ {\phi _{i,t}} $ 就被选入超臂表示的摇臂集合中(第8行). 之后更新超臂相关的 $ {r_t} $ 和 $ \;{ \hat \mu _{i,t}} $ 值(第9行). 对于执行了任务卸载的设备, $ {Y_{i, t}} $ 的值会随着任务执行的失败或者成功产生演化 (第10行). 通过公式(25)和公式(27)的计算, 可以得到超臂的实际奖励 $ {r_t} $ (第11行), 并累加得到第t个时隙的累计奖励(第12行). 在时隙t的调度流程图如图2所示.

算法2. 基于CMAB的任务调度机制.

输入: ${\boldsymbol{U}}, \; X, \; {\beta _e}, \; \kappa ;$

输出: ${\boldsymbol{\varPhi } _t}, \; r .$

1.　初始化: ${Y_{i,t}} \leftarrow 0, \; {r_{i,t}} \leftarrow 0; \; \forall i \in {\boldsymbol{U}}$

2.　对于每个摇臂 ${\phi _{i,t}}$ , 随机选择一个超臂 ${\boldsymbol{\varPhi }}$ 使得 ${\phi _{i,t}} \in {\boldsymbol{\varPhi }}$ , 根据公式(25)和公式(26)得到摇臂 ${\phi _{i,t}}$ 的输出 ${r_{i,t}}$ 和 $\;{\hat \mu _{i,t}}$ . 每个摇臂的选取次数 $ {T_{i, t}} $ 设为1.

3.　 $r \leftarrow 0; \; t \leftarrow 1$

4.　for $t = 1, 2, \ldots, T$ do//任务调度阶段

5.　　对于每个摇臂 ${\phi _{i,t}}$ , 令 $\;{\bar \mu _{i,t}} \leftarrow {\hat \mu _{i,t}} + \sqrt {\left( {3 \cdot \ln t} \right)/\left( {2 \cdot {T_{i, t}}} \right)}$

6.　　使用算法1得到任务的调度顺序

7.　　依据调度顺序执行任务, 并得到每一个任务是否成功执行的信息 $ \left\{ {s_{i, t}^e|{b_{i, t}} = 1} \right\} $

8.　　所有满足 $ s_{i, t}^e = 1 $ 的摇臂 ${\phi _{i,t}}$ 组成超臂 $ {{\boldsymbol{\varPhi }}_t} $

9.　　根据公式(26)更新 $ {{\boldsymbol{\varPhi }}_t} $ 中所有的 $\; {\hat \mu _{{i}}} $ , $ {T_{i, t}} \leftarrow {T_{i, t}} + 1 $

10.　 根据公式(14)更新本轮执行任务卸载对应设备的 $ {Y_{i, t}} $

11.　 根据公式(25)和公式(27)得到超臂的奖励 $ {r_t} $

12.　 ${r} \leftarrow {r} + r_t$

13.　 $ t \leftarrow t + 1 $

3.3 计算卸载的MDP模型

本节介绍如何改进基于DQN的强化学习方法来求解任务卸载问题. DQN算法基于值函数近似, 是深度强化学习的基本算法之一. 本节首先将任务卸载决策建模为一个MDP模型^[33]. 一个典型的MDP模型包含5个元素, 即 $ \left\langle {{{\mathbb{S}}}, {{\mathbb{A}}}, {{\mathbb{P}}}, {R} , \gamma } \right\rangle $ , $ {{\mathbb{S}}} $ 表示状态空间, $ {{\mathbb{A}}} $ 表示有限的动作空间, $ {{\mathbb{P}}} $ 表示转移矩阵, $ R $ 表示回报函数, $ \gamma \in \left[ {0, 1} \right] $ 表示折扣因子. 为减少动作空间, 我们采用多个agent的强化学习方法, 每个设备为一个agent, 这些agent在每个时隙同时做出决策. 对于设备 $ i $ , 状态 $ {S_{i, t}} \in {{\mathbb{S}}} $ 包含了3部分, 包括设备上的队列长度 $ {q_{i, t}} $ , 边缘服务器的队列长度 $ {q_{e, t}} $ , 基站的信道功率增益 $ {g_{i, e}} $ . 因此状态可表示为 $ {S_{i, t}} = \left( {{q_{i, t}}, {q_{e, t}}, {g_{i, e}}} \right) $ . 每个动作 $ {A_{i,t}} \in {{\mathbb{A}}} $ 包含执行位置 $ {b_{i, t}} $ 和所用信道 $ {a_{i, t}} $ 两部分, 如果任务在本机执行 $ {b_{i, t}} = 0 $ , 则 $ {a_{i, t}} = - 1 $ , 表示任务不需经由信道传输. 因此动作表示为 $ {A_{i, t}} = \left( {{b_{i, t}}, {a_{i, t}}} \right) $ . $ {{\mathbb{P}}} $ 是转移概率 $ P\left( {{S_{i, t}}, {S_{i, t + 1}}} \right) $ 的矩阵, 在无模型的强化学习场景中agent无法获知 $ \mathbb{P} $ 的具体信息. 假设在第t个时隙, 生成的任务集合为 $ \left\{ {{\varPsi _{i, t}}|i \in {{\boldsymbol{U}}} } \right\} $ , 其中对应所需的CPU周期和传输数据量为 $ {{{\mathbb{C}}}_t} = \left\{ {\left( {{c_{i, t}}, {v_{i, t}}} \right)|i \in {{\boldsymbol{U}}} } \right\} $ . 根据SUB1-P1中的目标, 回报函数表示为:

$ {R_{i, t}} = - \left( {\left( {1 - {b_{i, t}}} \right) \cdot C_{i, t}^l + {b_{i, t}} \cdot C_{i, t}^e} \right) $

(28)

由于卸载任务是否在截止期限以前完成与调度顺序有关, 所以边缘服务器上任务的调度顺序会影响到强化学习agent获得的回报. 例如, 考虑4个标号为1, 2, 3, 4设备的任务卸载场景. 对于设备4, 时隙t和时隙k $ \text{} $ 具有相同的系统状态 $ {S_{4, t}} = {S_{4, k}} $ , 以及做出同样的任务卸载动作 $ {A_{i, t}} = {A_{i, k}} $ . 在时隙t和时隙k, 卸载到服务器的任务集合均为 $ \left\{ {{\varPsi _1}, {\varPsi _2}, {\varPsi _3}, {\varPsi _4}} \right\} $ . t时的调度顺序为 $ \left\langle {{\varPsi _1}, {\varPsi _2}, {\varPsi _3}, {\varPsi _4}} \right\rangle $ , 此时 $ {\varPsi _4} $ 无法在截止期限内完成, 产生了惩罚因子; 而时隙k $ \text{} $ 的调度顺序为 $ \left\langle {{\varPsi _4}, {\varPsi _2}, {\varPsi _3}, {\varPsi _1}} \right\rangle $ , 所有任务都在截止期限内完成. 所以对于同样的 $ \left( {{S_{i, t}}, {A_{i, t}}} \right) $ , 强化学习agent可能观测到不同的回报, 即 $ {R_{i, t}} = R\left( {{S_{i, t}}, {A_{i, t}}} \right) $ 和 ${R_{i, k}} = \tilde R\left( {{S_{i, t}}, {A_{i, t}}} \right)$ , 并且 $R\left( {{S_{i, t}}, {A_{i, t}}} \right) \ne \tilde R\left( {{S_{i, t}}, {A_{i, t}}} \right)$ . 我们称 $ \tilde R\left( {{S_{i, t}}, {A_{i, t}}} \right) $ 为扰动的回报. 扰动回报的存在会影响卸载决策的有效性^{[34, 35]}.

因为任务调度顺序不断动态调整, 扰动回报出现的概率较大, 因此需要对扰动回报进行修正. 假设任务的计算负载取值范围是 $ \left[ {{c_{\min }}, {c_{\max }}} \right] $ , 传输数据量的取值范围是 $ \left[ {{v_{\min }}, {v_{\max }}} \right] $ . 假设把计算负载和传输数据的取值划分为 $ m $ 个区间, 每个区间的中值作为该区间的取值. 则在执行成功的情况下, $ {R_{i, t}} $ 共有最多 $ \Omega = m + {m^2} \cdot U $ 种可能的取值, 其中任务在本地执行共有 $ m $ 种可能取值, 在服务器上执行共有 $ {m^2} \cdot U $ 种可能的取值, 均包含执行失败的情况. 因此 $ {R_{i, t}} $ 的取值范围是 ${\boldsymbol{R}} = \left\{ {{R_0}, {R_1}, \ldots , {R_\Omega }} \right\}$ , 当执行失败时, $ {R_{i, t}} = {R_0} $ . 混淆矩阵 $ {{{\mathbb{F}}}_{\left( {\Omega + 1} \right) \times \left( {\Omega + 1} \right)}} $ 表示 $ \tilde R $ 的观测概率, 矩阵中元素 $ {f_{j, k}} $ 表示观测到扰动回报的翻转概率: ${f_{j, k}} = P\left( {{{\tilde R}_{i, t}} = {R_k}|{R_{i, t}} = {R_j}} \right)$ .

基于文献 [36] 中的引理2, 本文采用替代回报 $ \hat R\left( {{S_{i, t}}, {A_{i, t}}} \right) $ 来更新值函数. 为了给出替代回报的定义, 本文引入矩阵 $ \hat {{\mathbb{R}}} $ , 并且有 $\hat {{\mathbb{R}}}: = \left[ {\hat R\left( {\tilde R = {R_0}} \right), \ldots , \hat R\left( {\tilde R = {R_\Omega }} \right)} \right]$ , 其中 $\hat R\left( {\tilde R = {R_k}} \right)$ 表示当观测到的扰动回报值为 $ {R_k} $ 时的替代回报值. 同时令 ${{\mathbb{R}}} = \left[ {{R_0};{R_1}; \ldots ;{R_\Omega }} \right]$ 为有界回报值的矩阵. 定义3给出 ${\hat R_{i, t}}$ (即 $\hat R\left( {{S_{i, t}}, {A_{i, t}}} \right)$ )的计算方程.

定义3 (替代回报). 假设矩阵 $ {{\mathbb{F}}} $ 可逆. 通过定义:

$ {\hat {\mathbb{R}}} = {\mathbb{F}^{ - 1}} \cdot \mathbb{R} $

(29)

使得 ${{\boldsymbol{E}}_{\tilde R|R}}\left[ {\hat R\left( {{S_{i, t}}, {A_{i, t}}} \right)} \right] = R\left( {{S_{i, t}}, {A_{i, t}}} \right)$ . 即 $\hat R$ 是 $ R $ 的无偏估计.

3.4 带替代回报估计的任务卸载策略

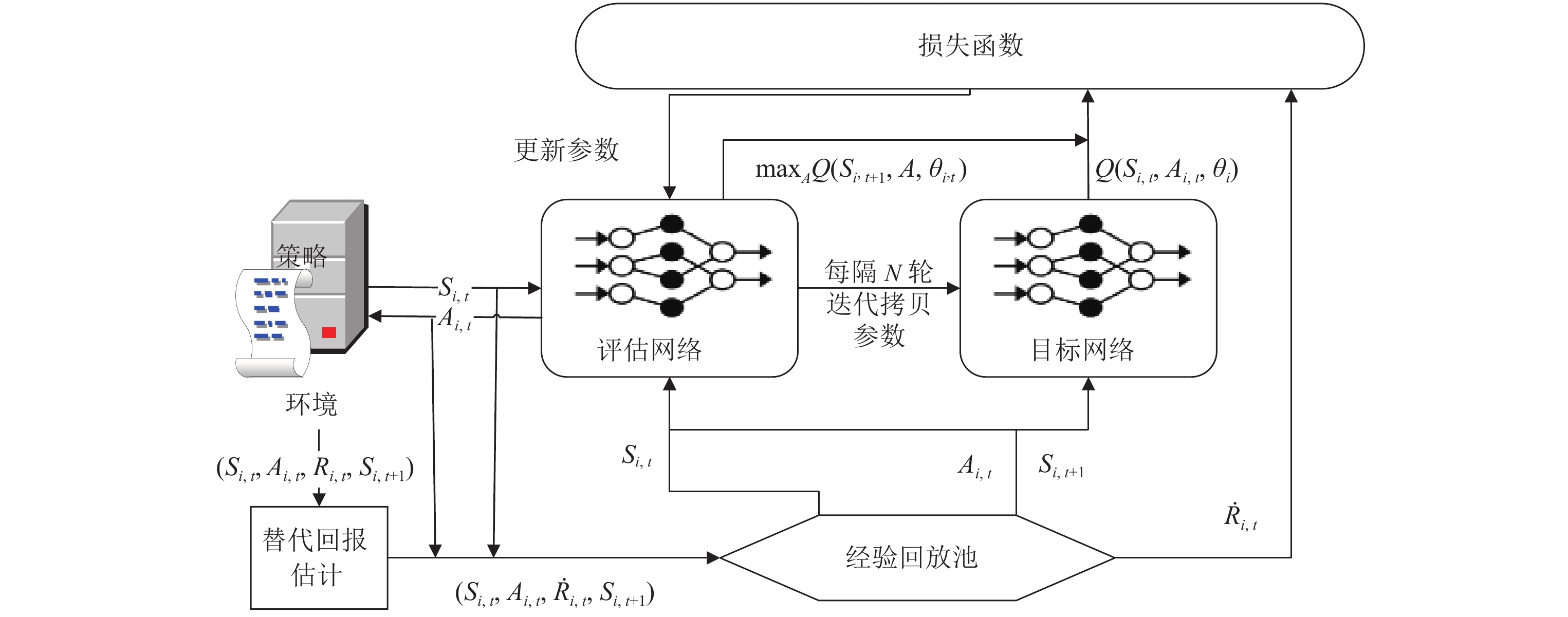
本文采用带有替代回报的DQN算法进行卸载决策. 在状态 $ {S_{i,t}} $ , agent做出动作 $ {A_{i, t}} $ 之后可以观测到下一个状态 $ {S_{i,{t + 1}}} $ 并获得回报 $ {R_{i, t}} = R\left( {{S_{i, t}}, {A_{i, t}}, {S_{i, t + 1}}} \right) \in \mathbb{R} $ . 所以在每个时隙和环境交互之后, agent可以得到一个经验元组 $ \left( {{S_{i, t}}, {A_{i, t}}, {R_{i, t}}, {S_{i, t + 1}}} \right) $ , 并将元组存储到回放池里用于参数更新. Agent的学习目标是学习到一个优化策略, 即一个条件分布来 $ \pi \left( {A|S} \right) $ 最大化状态的值函数. 图3给出了带替代回报的DQN算法运行结构. 经验回放池用于存放探索环境得到的数据, 然后随机采样样本更新评估网络参数. 每隔N轮迭代, 评估网络 $ {\theta _{i,t}} $ 的参数就拷贝到目标网络 $ \theta _{i,t}^ - $ 中. 在每个时隙t, agent选择一个动作 $ {A_{i, t}} $ , 进入一个新的状态 $ {S_{i, t + 1}} $ 和进行Q值更新. DQN算法的核心是值函数迭代过程:

$ Q\left( {{S_{i, t}}, {A_{i, t}}} \right) \leftarrow Q\left( {{S_{i, t}}, {A_{i, t}}} \right) + \alpha \cdot \left[ {{R_{i, t}} + \gamma \cdot {{\max }_\pi }Q\left( {{S_{i, t + 1}}, {A_{i, t + 1}}} \right) - Q\left( {{S_{i, t}}, {A_{i, t}}} \right)} \right] $

(30)

其中, $ \alpha $ 是学习率, $ \gamma $ 是折扣因子. 评估网络参数的调试是通过梯度下降法最小化损失函数:

$ {L_{i, t}}\left( {{\theta _i}} \right) = {\boldsymbol{E}}\left[ {{{\left( {{R_{i, t}} + \gamma \cdot {{\max }_a}A\left( {{S_{i, t + 1}}, a, \theta _{i,t}^ - } \right) - Q\left( {{S_{i, t}}, {A_{i, t}}, {\theta _{i,t}}} \right)} \right)}^2}} \right] $

(31)

如图3所示, 从环境反馈的回报值需要转化为估计的替代回报 $ {\dot R_{{{i, t}}}} $ 才能存储到经验池中. 根据定义6计算 $ \hat R $ 需要所有 $ {f_{j, k}} $ 已知. 然而这一信息在实际场景中无法直接获取, 因此需要在训练MDP模型时对此进行估计. 替代回报估计的核心思路是动态地根据收集到的回报值不断修正错误率估计 $ {\tilde f_{j, k}} $ . 在每个训练轮次, 对于每个属于 $ \mathbb{S} \times \mathbb{A} $ 的状态动作对, agent收集关于该状态动作对的所观测到的回报, 然后使用平均法或是投票法来预测真实的回报. 最后, 基于预测的真实回报以及状态动作对, 回报值错误率 $\tilde {\mathbb{F}}$ 的估算方式如下:

$ \bar R \left( {S, A} \right) = \arg {\max _{{R_i} \in {\boldsymbol{R}}}} \bot \left[ {\bar R \left( {S, A} \right) = {R_i}} \right] $

(32)

$ {\tilde f_{j, k}} = \frac{{\displaystyle\sum\nolimits_{\left( {S, A} \right) \in {{\mathbb{S}}} \times {{\mathbb{A}}}} { \bot \left[ {\tilde R\left( {S, A} \right) = {R_k}|\bar R \left( {S, A} \right) = {R_j}} \right]} }}{{\displaystyle\sum\nolimits_{\left( {S, A} \right) \in {{\mathbb{S}}} \times {{\mathbb{A}}}} { \bot \left[ {\bar R \left( {S, A} \right) = {R_j}} \right]} }} $

(33)

其中, $\perp [ \cdot ]$ 表示在观测到的回报 $ \tilde R\left( {S, A} \right) $ 集合内满足条件 $[\cdot ]$ 的状态动作对的数量. $ \bar R\left( {S, A} \right) $ 和 $ \tilde R\left( {S, A} \right) $ 分别表示在状态动作对为 $ \left( {S, A} \right) $ 时预测的真实回报值和观测回报值. 算法3给出替代回报的估计算法.

在DQN训练阶段, 本文利用分布式的模型训练方式^[37]: 每个agent维护相应的DQN模型参数 $ {\theta _{i, t}} $ 和 $ \theta _{i, t}^ - $ , 在每个训练时隙将所有agent的模型参数以模型平均方式聚合并返回每个agent:

$ {\theta _{t + 1}} \leftarrow \frac{1}{M}\sum\limits_{i = 1}^M {{\theta _{i, t}}} $

(34)

算法3. 替代函数估计策略.

输入: $\tilde R \left( {S, A} \right), \; \eta , \; \tilde {\mathbb{F}} ;$

输出: 替代回报 $\dot R\left( {S, A} \right) .$

1.　if 对 $ \mathbb{S} \times \mathbb{A} $ 空间内的状态动作对收集了足量 $ \tilde R $ then

2.　　根据公式(32)得到预测的真实回报 $ \bar R\left( {S, A} \right) $

3.　　根据公式(33)基于 $ \tilde R $ 和 $ \bar R $ 重新估计 $ \tilde {\mathbb{F}} $

4.　根据公式(31)得到估计的替代回报 $ \dot R\left( {S, A} \right) $

算法4展示具体的计算卸载策略. 其中所有的agent共同更新同一个错误率估计矩阵 $ \tilde {\mathbb{F}} $ . $ \tilde {\mathbb{F}} $ 收集所有agent所产生的回报值并进行统计(算法3第3行), 估计的替代回报表示为 $ \dot R\left( {S{}_{i, t}, {A_{i, t}}} \right) $ . 由于模型聚合可以加快Q网络的收敛, 为了收集足够多的任务状态对来更新矩阵 $ \tilde {\mathbb{F}} $ , 所以在训练深度Q网络之前, 先对 $ \tilde {\mathbb{F}} $ 进行估计(第2–7行), 并在训练阶段继续更新 $ \tilde {\mathbb{F}} $ (第13行).

算法4. 基于替代函数估计的计算卸载策略.

输入: $\tilde {\mathbb{R}}\left( {S, A} \right), \; \varepsilon , \; \gamma ;$

输出: $ Q\left( {S, A} \right) $ $ \text{} $ 和 $\pi \left( S \right) .$

1.　初始化: 随机初始化值函数 $ Q\left( {S, A} \right) $ , 经验回放池 $ \left\{ {{\mathbb{G}_i} =\varnothing |i \in {\boldsymbol{U}}} \right\} $ 将 $\tilde {\mathbb{F}}$ 中所有元素初始化为0

2.　for $t = 1, 2, \ldots, {T_{{\rm{trial}}}}$ do

3.　　初始化状态 $ {\boldsymbol{S}} = \left\{ {S{}_{i, t}|i \in {\boldsymbol{U}}} \right\} $

4.　　while S 不是终止状态 do

5.　　　每个agent随机选择一个动作 $ {A_{i, t}} $

6.　　　每个agent 执行相应动作 $ {A_{i, t}} $ 观察 $ {S_{i, t + 1}} $ 和带有噪声的回报 $ {\tilde R_{i, t}} $

7.　　　每个agent使用算法3得到相应的估计回报 $ \dot R\left( {{S_{i, t}}, {A_{i, t}}} \right) $ 并更新 $ \tilde {\mathbb{F}} $

8.　for $t = 1, 2, \ldots , {T_{{\rm{train}}}}$ do

9.　　初始化状态 $ {\boldsymbol{S}} = \left\{ {S{}_{i, t}|i \in {\boldsymbol{U}}} \right\} $

10.　　while S 不是终止状态 do

11.　　　每个agent采用概率 $ \varepsilon $ 随机选择一个动作 $ {A_{i, t}} $

12.　　　否则 $ {A_{i, t}} = {\text{argma}}{{\text{x}}_A}Q\left( {{S_{i, t}}, {A_{i, t}};\theta _{i,t}^- } \right) $

13.　　　每个agent使用算法3得到估计的回报 $ \dot R\left( {{S_{i, t}}, {A_{i, t}}, {S_{i, t + 1}}} \right) $ 并更新 $ \tilde {\mathbb{F}} $

14.　　　每个agent将 $ \left( {{S_{i, t}}, {A_{i, t}}, {{\dot R}_{i, t}}, {S_{i, t + 1}}} \right) $ 存储到 $ {\mathbb{G}_i} $ 中

15.　　　每个agent从 $ {\mathbb{G}_i} $ 中随机采样一个小批量的 $ \left( {{S_{i, k}}, {A_{i, k}}, {{\dot R}_{i, k}}, {S_{i, k + 1}}} \right) $

16.　　　每隔N轮迭代将模型参数 $ {\theta _{i, t}} $ 拷贝到 $ \theta _{i, t + 1}^ - $

17.　　　每个agent关于 $ {\theta _{i, t}} $ 和 $ \theta _{i, t + 1}^ - $ 执行一步梯度下降

18.　　　采用公式(34)的模型聚合方法得到模型参数 $ {\theta _{t + 1}} $ 并广播到每个agent

19.　返回 $ Q\left( {S, A} \right) $ $ \text{} $ 和 $ \pi \left( S \right) $

3.5 性能分析

本节给出任务卸载以及调度策略的性能评估. 根据所采用的算法, 本文对调度算法和卸载策略分别选取不同的性能评估指标. 对基于CMAB的任务调度策略, 本文采用遗憾界限(regret bound)来衡量算法的性能; 对带有替代回报的任务卸载策略, 本文讨论回报函数的方差和模型训练过程中的采样复杂度. 下面分别从任务调度和任务卸载两方面进行详细分析.

首先给出调度算法的收敛性证明. 根据CMAB收敛性分析^[27], 定理3给出了任务调度算法的后悔度上界.

定理3. 令 $ \alpha = 2/3 $ , 那么在时隙 $ t $ 的遗憾界限为:

$ {\left( {{{\frac{{2 \cdot \ln t \cdot \left( {\displaystyle\sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {t \cdot \kappa } } \right)}}{{3 \cdot {U^2}}}}^3} + {{\frac{{2 \cdot \ln t \cdot \left( {\displaystyle\sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {{Y_{i, t}} + X \cdot \displaystyle\sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {{c_i} \cdot {\beta _e}} } } \right)}}{{{U^2}}}}^3}} \right) + \left( {\frac{\pi }{3} + 1} \right)} \cdot \left| {{{\boldsymbol{O}}_t}} \right| \cdot \left( {\sum\limits_U {t \cdot \kappa } } \right) $

(35)

证明: 假设时隙 $ t $ 优化的调度决策序列为 ${\boldsymbol{\varPhi }}^*$ , 对于一个给定的摇臂 $ {\phi _i} $ 则有:

$ \Delta _{\min }^i = \min \left\{ {\left\{ {{v_t}\left( {\boldsymbol{\varPhi }} \right)|{\boldsymbol{\varPhi }} \in {{\boldsymbol{\varPhi }}_B}} \right\} - {v_{{t}}}\left( {{{\boldsymbol{\varPhi }}^*}} \right)} \right\} $

(36)

$ \Delta _{\max }^i = \max \left\{ {\left\{ {{v_t}\left( {\boldsymbol{\varPhi }} \right)|{\boldsymbol{\varPhi }} \in {{\boldsymbol{\varPhi }}_B}} \right\} - {v_{{t}}}\left( {{{\boldsymbol{\varPhi }}^*}} \right)} \right\} $

(37)

其中, ${v_t}\left( {{\boldsymbol{\varPhi }}^*} \right)$ 是采用最优策略 ${\boldsymbol{\varPhi }}^*$ 所获得在时隙t获得的奖赏. ${{\boldsymbol{\varPhi }}_B} = \left\{ {{\boldsymbol{\varPhi }}|{v_t}\left( {\boldsymbol{\varPhi }} \right) < \left( {2/3} \right) \cdot {v_t}\left( {{\boldsymbol{\varPhi }}^*} \right)} \right\}$ . 进一步定义 $ {\Delta _{{\text{max}}}} = {\text{ma}}{{\text{x}}_i}\Delta _{\max }^i $ 和 $ {\Delta _{{\text{min}}}} = {\text{mi}}{{\text{n}}_i}\Delta _{{\text{min}}}^i $ .令 ${c_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right) = - \displaystyle\sum\nolimits_{i \in {\boldsymbol{U}}} {s_{i, t}^e} \cdot {c_i} \cdot {\beta _e}$ , ${d_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right) = \displaystyle\sum\nolimits_{i \in {\boldsymbol{U}}} {{Y_{i, t}} \cdot s_{i, t}^e}$ .

因此可得:

$ $

$ {v_t}\left( {{{\boldsymbol{\varPhi }}^*}} \right) - {v_t}\left( {\boldsymbol{\varPhi }} \right) = X \cdot \left( {{c_t}\left( {{\boldsymbol{S}}_t^{e*}, {{\boldsymbol{\varPhi }}^*}} \right) - {c_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right)} \right) + \left( {{d_t}\left( {{\boldsymbol{S}}_t^{e*}, {{\boldsymbol{\varPhi }}^*}} \right) - {d_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right)} \right) $

(38)

假设时隙t卸载到服务器的任务集合为 $ {{\boldsymbol{O}}_t} $ . 基于调度策略 $ {\boldsymbol{\varPhi }} $ , 可得:

$ - \sum\limits_{i \in {{\boldsymbol{O}}_t}} {{c_i} \cdot {\beta _e}} \leqslant {c_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right) \leqslant 0 $

(39)

当所有卸载的任务都在截止期限内完成取最小值, 所有任务都超时取最大值.

对于 ${d_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right)$ , 则有:

$ 0 \leqslant {d_t}\left( {{\boldsymbol{S}}_t^e, {\boldsymbol{\varPhi }}} \right) \leqslant \sum\limits_{i \in {{\boldsymbol{O}}_t}} {{Y_{i, t}}} \leqslant \sum\limits_{i \in {{\boldsymbol{O}}_t}} {t \cdot \kappa } $

(40)

因此有 ${v_t}\left( {{\boldsymbol{\varPhi }}^*} \right) < \displaystyle\sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {{Y_{i, t}}}$ , ${\Delta _{\max }} < \displaystyle \sum\nolimits_{i \in {\boldsymbol{U}}} {{Y_{i, t}} + X \cdot \sum\nolimits_{i \in {\boldsymbol{U}}} {{c_i} \cdot {\beta _e}} }$ . 令有界光滑函数 $ g\left( x \right) = U \cdot x $ , 则反函数为 $ {g^{ - 1}}\left( x \right) = U/x $ . 因此时隙t ( $ t \geqslant 1 $ )的后悔度约束为:

$ \sum\limits_{i \in {\boldsymbol{S}}_t^e} {\left( {\frac{{6 \cdot \ln t \cdot {{\left( {\Delta _{\min }^i} \right)}^3}}}{{{U^2}}} + \int_{\Delta _{\min }^i}^{\Delta _{\max }^i} {\frac{{6 \cdot \ln t \cdot {x^2}}}{{{U^2}}}dx} } \right)} + \left( {\frac{\pi }{3} + 1} \right) \cdot \left| {{\boldsymbol{S}}_t^e} \right| \cdot {\Delta _{\max }} $

$ \begin{aligned}[b] &< \sum\limits_{i \in {{{\boldsymbol{O}}_t}} } {\left( {\frac{{6 \cdot \ln t \cdot {{\left( {\Delta _{\min }^i} \right)}^3}}}{{{U^2}}} + \frac{{2 \cdot \ln t \cdot {{\left( {\Delta _{\max }^i} \right)}^3}}}{{{U^2}}}} \right)} + \left( {\frac{\pi }{3} + 1} \right) \cdot \left| {{{\boldsymbol{O}}_t}} \right| \cdot {\Delta _{\max }}\\ &< {\left( {\frac{{2 \cdot \ln t \cdot {{\left( {\displaystyle\sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {t \cdot \kappa } } \right)}^3}}}{{3 \cdot {U^2}}} + \frac{{2 \cdot \ln t \cdot {{\left( {\displaystyle\sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {{Y_{i, t}}} + X \cdot \sum\nolimits_{i \in {{\boldsymbol{O}}_t}} {{c_i} \cdot {\beta _e}} } \right)}^3}}}{{{U^2}}}} \right)} + \left( {\frac{\pi }{3} + 1} \right) \cdot \left| {{{\boldsymbol{O}}_t}} \right| \cdot \left( {\sum\limits_{i \in {\boldsymbol{U}}} {t \cdot \kappa } } \right) \end{aligned} $

(41)

由此可得公式(35)成立. 证毕.

该定理是为了说明文中所提出的在线决策算法与最优策略 ${\boldsymbol{\varPhi }}^*$ 之间的差距是有界的, 也就是文中对于CMAB算法的改进能够保证收敛.

关于任务卸载算法, 性能分析如定理4所示.

定理4. ${R_{i, t}} \in \left\{ {{R_0}, {R_1}, \ldots, {R_\Omega }} \right\}$ 为有界回报函数. 替代回报具有如下性质.

1) 替代回报的方差界为:

$ {\boldsymbol{Var}}\left( R \right) \leqslant {\boldsymbol{Var}}\left( {\hat R} \right) \leqslant \frac{{{{\left( {\Omega + 1} \right)}^2}}}{{\det {{\left( \mathbb{F} \right)}^2}}} \cdot R_0^2 $

(42)

$ k = O\left( {\frac{{T \cdot \left( {{q_{e,\max }} \cdot q_{\max}} \right) \cdot \left( {M + 1} \right)}}{{{\varepsilon ^2} \cdot {{\left( {1 - \gamma } \right)}^2} \cdot \det {{\left( \mathbb{F} \right)}^2}}}\log \frac{{T \cdot \left( {{q_{e,\max }} \cdot {q_{\max }}} \right) \cdot \left( {M + 1} \right)}}{\delta }} \right) $

(43)

其中, 错误率 $ 0 < \delta < 1 $ .

证明: 首先给出方差界的证明.

$ \mathbb{F} $ 的行列式为 $ \det \left( \mathbb{F} \right) $ . 根据罚数的定义, 得到 $ \left| {{R_0}} \right| > \left| {{R_k}} \right| $ .

根据文献[34]中定理3可得:

$ {\boldsymbol{Var}}\left( R \right) \leqslant {\boldsymbol{Var}}\left( {\hat R} \right) \leqslant \frac{{{{\left( {\Omega + 1} \right)}^2}}}{{\det \left( \mathbb{F} \right)}} \cdot R_0^2, \;{R \in {\boldsymbol{R}}} $

(44)

又因为:

$ \frac{{{{\left( {\Omega + 1} \right)}^2}}}{{\det \left( \mathbb{F} \right)}} \cdot R_0^2 \leqslant \frac{{{{\left( {\Omega + 1} \right)}^2}}}{{\det {{\left( \mathbb{F} \right)}^2}}} \cdot R_0^2 $

(45)

综合公式(44)和公式(45), 公式(42)得证.

对于每个agent, 状态空间大小为 $q_{e,\max}\cdot q_{\max}$ , 动作空间大小为 $ \left( {M + 1} \right) $ .根据文献[27]中定理2, 公式(43)得证. 证毕.

又因为 $ \Omega = m + {m^2} \cdot U $ , 所以方差的上界可表示为 $ {\left( {m + {m^2} \cdot U + 1} \right)^2}/\det {\left( \mathbb{F} \right)^2} \cdot R_0^2 $ . 由此可见, 当m值增大, 使用替代回报可以有效降低回报函数的偏差, 但是会增加回报值的方差. 当 $ \det \left( \mathbb{F} \right) \to 0 $ , 回报值的方差界限失效.

从系统开销角度分析, 相比于文献[13, 21, 24]等基于一般强化学习方法的卸载方案, 该方法增加的额外开销主要包括训练时产生的通信和计算开销 ${\rm{O}}\left( {{T_{{\rm{trial}}}}} \right)$ , 对应于替代回报矩阵估计过程; 以及在执行卸载时每个设备存储替代回报估计矩阵的空间复杂度 ${\rm{O}}\left( {{m^2}} \right)$ .

4 仿真实验与结果分析

本节对计算卸载和任务调度策略的性能进行仿真实验, 旨在于评估任务调度算法对于任务超时问题的优化程度、任务卸载策略对于环境扰动的鲁棒性以及二者的整体性能. 仿真实验采用实验室服务器, CPU为7核的Intel(R) Xeon(R) CPU E5-2678, 主频为2.5 GHz, 内存大小为32 GB. 操作系统为Red Hat 4.8.5-44. GPU为RTX 2080 Ti. 本节首先探究环境参数(包括设备数目和服务器最大队列长度)对于算法性能的影响, 然后分别对任务调度和卸载策略分别进行性能分析. 和文献[2, 19]一致, 本节使用人脸识别应用的历史日志作为任务参数来模拟带有时延约束的计算密集型任务, 日志中包含用户id信息. 其中输入数据量和CPU周期的取值范围分别是 [471, 6583] KB和 [49, 1123] MHz. 任务截止期限为1000, 执行超时罚数为2000. 其余环境参数定义如表1所示.

为测试各个改进部分(约束优化目标设计、任务调度策略和带替代回报的卸载策略)的性能, 本文实现了本文所提出的算法(RLSR-CMAB)和以下几个基线算法.

• RL-CMAB: 采用带有一般回报函数的深度Q学习方法进行计算卸载决策, 以及采用基于CMAB的算法产生调度顺序.

• RANDOM-CMAB: 随机决定任务本地处理或者卸载处理, 在本机或者边缘服务器. 以及采用基于CMAB的算法产生调度顺序.

• RLSR-FCFS: 在每个决策时隙采用带有扰动回报的深度Q学习方法进行卸载决策, 任务调度采用先到先服务的策略.

• RLSR-GREEDY: 在每个决策时隙采用带有扰动回报的深度Q学习方法进行计算卸载决策, 在调度方面采用相同的优化目标和约束条件, 并采用贪心算法每次产生使目标函数(公式(24a))最小的调度顺序.

此外, 还将本文算法与相关的已有工作^{[3, 21, 24]}进行对比: 1) 对于时延敏感任务, 以最小化能耗为目标, 采用基于Q学习的卸载策略(QECO)^[24]; 2)以最小化用户计算开销为目标, 采用基于DQN的分布式卸载策略(DRLDCO)^[3]; 3) 对于时延敏感任务, 以最小化能耗为目标, 采用基于DDQN (double deep neural network)的卸载决策(DRLECO)^[21]. 所有开销的计算均基于本文的系统模型.

根据实验目的和本文算法的优化目标, 在实验中设置了如下性能指标.

• 累计系统开销:运行一个epoch所有设备的累计开销之和.

• 卸载率: 在测试数据集上运行一个epoch所有设备的累计卸载次数之和与累计任务数之和比率.

• 最小卸载成功率: 在测试数据集上运行一个epoch所有设备中最小的累计卸载任务执行成功率.

其中卸载成功率指单个设备卸载到服务器并在截止期限前完成的累计任务数与卸载到服务器执行的累计任务数之比. 由于本文是以最小卸载成功率来约束公平性, 对应于该公平性约束, 所以比较的是最小卸载成功率. 任务调度算法是在卸载决策的基础上优化边缘服务器端的任务调度机制, 仅涉及卸载到边缘服务器端的任务, 并且不改变卸载策略, 所以不会导致所有任务整体截止期限满足率的下降. 另外, 在带有扰动回报的深度Q学习算法中, 折扣因子 $ \gamma = 0.9 $ , 探索概率 $ \varepsilon = 0.9 $ , 经验回放池大小 $ \left| \mathbb{G} _i \right| = 1000 $ , 小批量的大小为32. Q网络由两个全连接层构成. 每个训练epoch含有50轮迭代, 目标网络的更新周期是80个epoch. 训练完毕后在测试数据集上运行100轮迭代. 在基于CMAB的调度算法中, $ X = 0.1 $ , $ \kappa = 0.9 $ 对于带有替代回报的任务卸载方法, 本文令 ${T_{{\rm{trial}}}} = 10$ . 实验中默认不同任务由不同用户提交.

4.1 设备数目影响

本组实验研究设备数量对不同卸载和调度策略的影响, 即算法的扩展性能. 参数配置为: 边缘服务器组包含有16个处理器, 每个移动设备装载双核CPU. 实验中不考虑队列长度的限制.

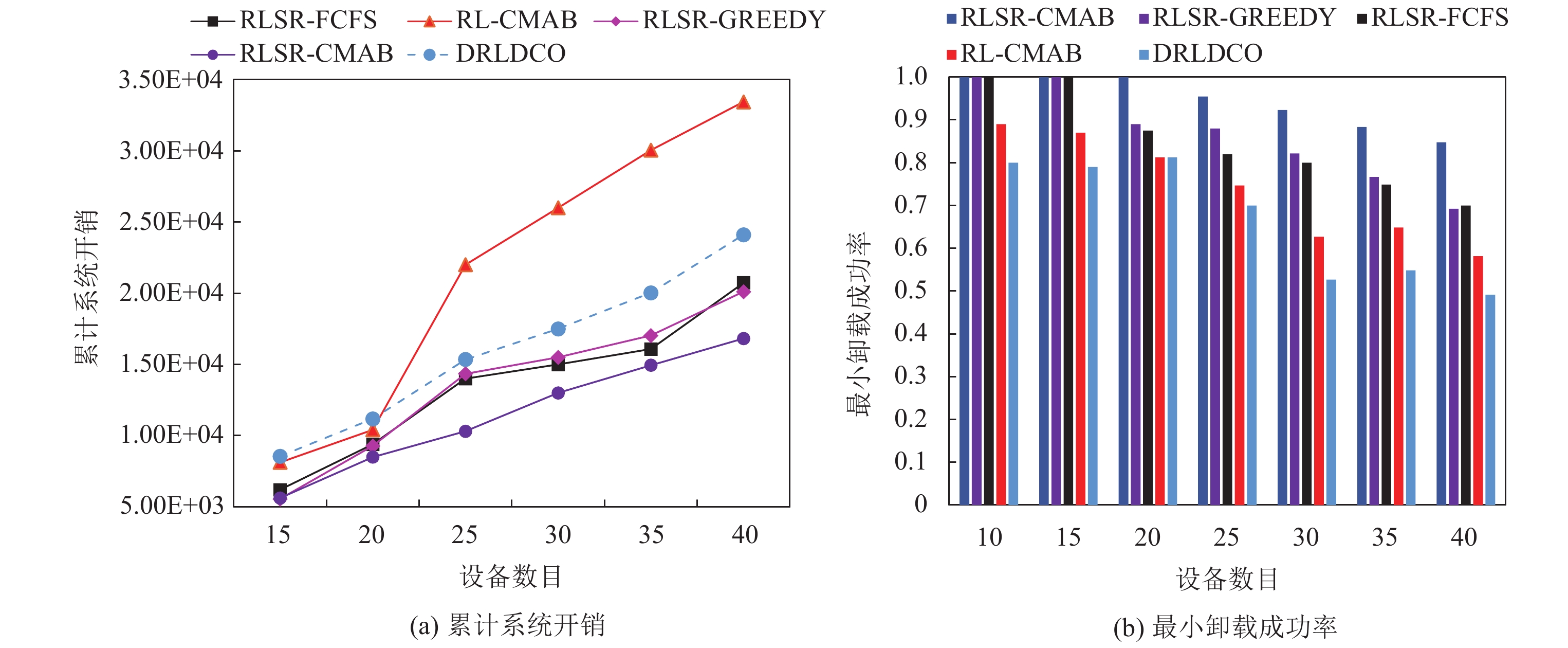
从图4(a)和图4(b)可知: 随着设备数目增加, RLSR-CMAB、RLSR-FCFS、RLSR-GREEDY和RL-CMAB策略的系统总开销都会明显提高, 同时卸载任务的执行成功率也逐渐下降, 主要是随着设备数目增加, 每个时隙产生的待处理任务数增加, 对处理器的竞争加剧, 边缘服务器无法提供足够的资源同时处理多个设备的请求. 在服务器提供资源不足的情况下, 采用替代回报的方案(RLSR-CMAB、RLSR-FCFS、RLSR-GREEDY)倾向于将任务放在本地执行, 所以资源不足的影响相对较小, 卸载任务执行成功率较高. 其中RLSR-FCFS策略和RLSR-GREEDY策略相比, 两者的性能相近, 说明采用贪心策略进行调度优化程度有限. 而RLSR-CMAB算法系统开销和任务执行成功率均较优. 而相比于可针对大规模设备的分布式卸载策略DRLDCO, RLSR-CMAB在累计系统开销和小卸载成功率方面均具有更优的性能. 从表2可以看出, 在设备数较少的情况下, 表明服务器和基站资源充足, 采用替代回报的方案RLSR-CMAB具有较高的卸载率; 随着设备数增加, 卸载到服务器的任务可能出现失效, 并且通信开销因数据传输速率降低而增大, 这时RLSR-CMAB具有明显较低的卸载率, 任务更多地放在设备执行; 而带有普通回报函数的卸载策略无法针对服务器资源是否充裕做出相应的卸载决策, 在设备数目较小的情况下反而具有更低的卸载率, 在服务器资源不充裕的情况下更多将任务放至服务器执行, 从而导致了性能的下降.

4.2 队列长度限制的影响

本组实验研究服务器队列长度限制对不同卸载和调度策略的影响. 参数配置为: 边缘服务器组包含有16个处理器, 每个移动设备装载双核CPU.

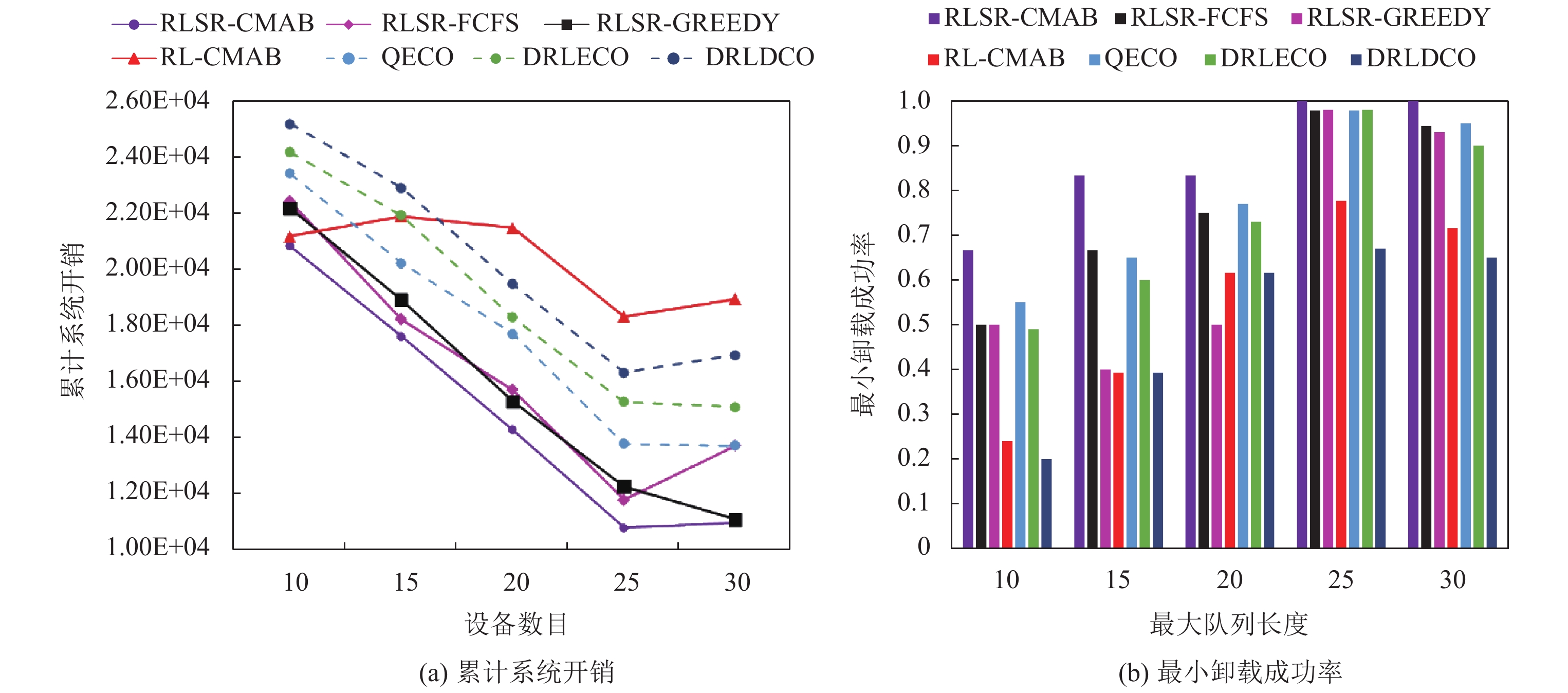
从图5(a)和图5(b)可知: RLSR-CMAB、RLSR-GREEDY、RLSR-FCFS和RL-CMAB的任务执行成功率都与最大队列长度呈正相关. 在队列长度过短会引起卸载任务直接失效的情况下, 带有替代回报的策略RLSR-CMAB相比于其他基线算法具有明显更小的系统总开销和卸载任务执行成功率. 这是因为带有替代回报的卸载策略倾向于通过将任务置于本地执行来缓解服务器资源的紧张, 缩短了任务在边缘服务器的平均等待时间; 而基于CMAB策略的任务调度方案则会折中卸载成功率以及系统开销两个目标来优化系统的整体性能. 此外, RLSR-CMAB相比于已有算法在系统开销和最小卸载成功率方面均有更好的性能. 从后文表3可以看出, 在最大队列长度远小于设备数的情况下, 表明服务器资源不足, 卸载到服务器的任务可能出现失效, 采用替代回报的方案具有较低的卸载率; 随着队列长度限制放宽, 带有替代回报的方案卸载率逐渐增加, 因为此时服务器端相比于终端产生的开销较小, RLSR-CMAB考虑向边缘服务器提交更多的卸载请求; 而RL-CMAB策略无法对服务器资源是否充裕进行正确的观测, 因为回报值存在较大偏差, 所以在不同队列长度限制的情况下卸载率相差不大, 从而导致了性能的下降. RLSR-CMAB相对于已有的3个算法具有更好的性能. 这是因为QECO和DRLECO无法通过动态调整调度顺序以保证截止期限满足率, 而DRLDCO算法未设置截止期限约束, 因此对于时延敏感任务卸载的性能较差.

在本组实验中, 仅将RLSR-CMAB与同为分布式设计的已有算法DRLDCO进行比较. 而QECO和DRLECO均为集中式算法. 在边缘计算中, 用户使用免授权多址方案将其任务数据传输到基站, 然后基站检测卸载用户并解码任务数据. 如果是集中式计算卸载, 可能会出现漏检情况, 并且漏检概率随着卸载用户总数的增加而增加. 此外, 基于强化学习的集中式计算卸载方案的训练复杂度更高, 并且随着用户数的增多, 状态以及动作空间将急剧增加. 因此, 分布式的卸载策略对于较大规模用户具有更好的适应性.

4.3 调度策略的性能评估

本组实验研究在卸载策略相同的情况下, 不同参数对于调度策略的影响. 参数配置为: 边缘服务器组包含有16个处理器, 设备数目为20, 每个移动设备装载双核CPU.

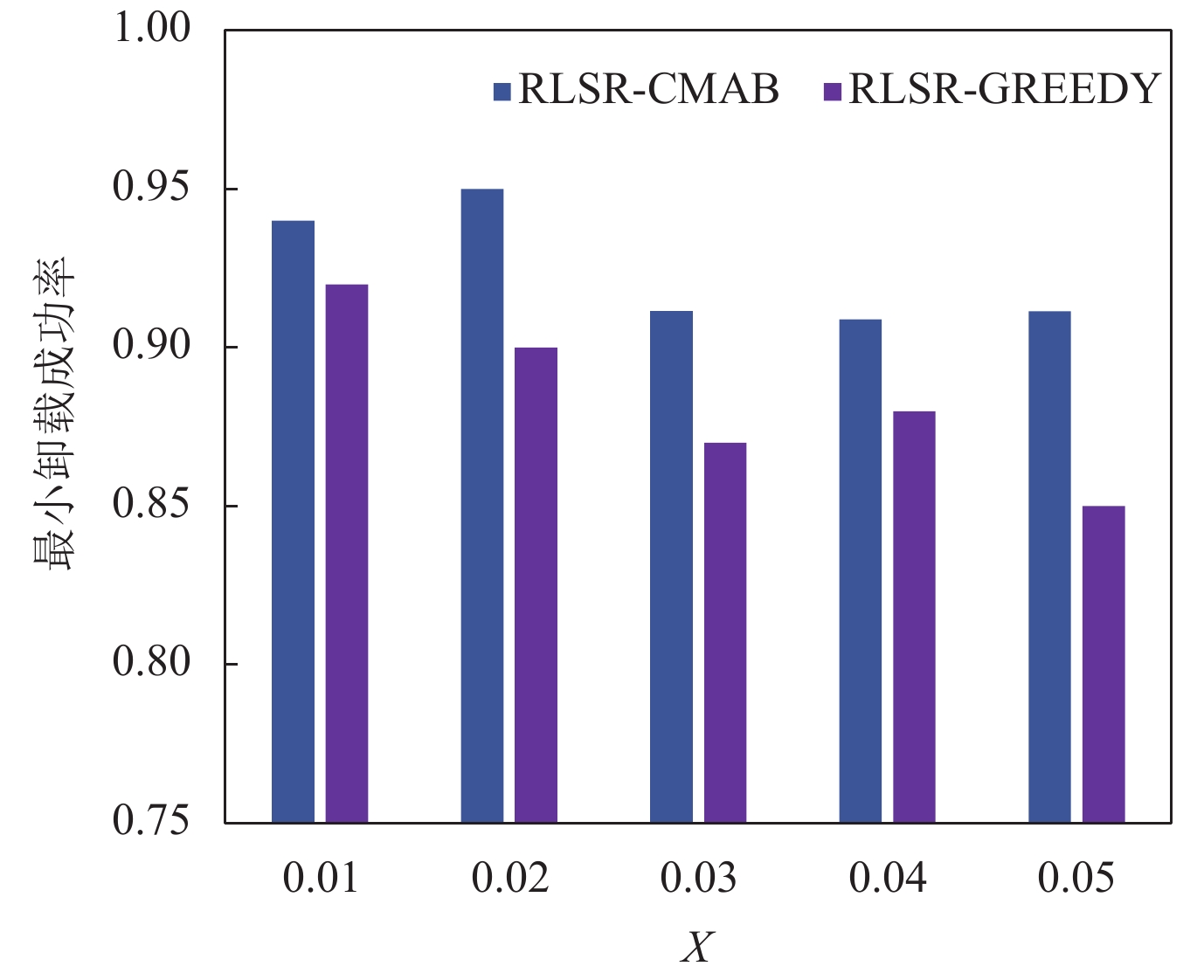
首先固定X 值为0.03, 研究 $ \kappa $ 值对于任务执行成功率的影响. 从表4中可得, 随着 $ \kappa $ 值的提高, 对于执行成功率的约束变得松弛, 成功率也随之下降, 但是不会低于 $ \kappa $ 值的约束. 从图6可以看出, 随着X值的增加, 调度算法对于服务器开销的优化比重增加, 而对于任务执行成功率的比重随之减小. RLSR-CMAB策略和RLSR-GREEDY策略的任务执行成功率都随着X值增加而下降, 但是RLSR-CMAB的最小执行成功率均大于0.9, 而RLSR-GREEDY算法在 $ X \geqslant 0.03 $ 时执行成功率均小于 $ \kappa $ 值. 这说明基于CMAB的调度算法相比于贪心算法能更好地优化长线任务调度目标.

4.4 卸载策略的性能评估

本组实验研究在训练过程中, 不同m值对卸载策略的影响. 参数配置为: 边缘服务器组包含有16个处理器, 设备数目为25, 每个移动设备装载双核CPU. 实验中没有设置最大队列长度.

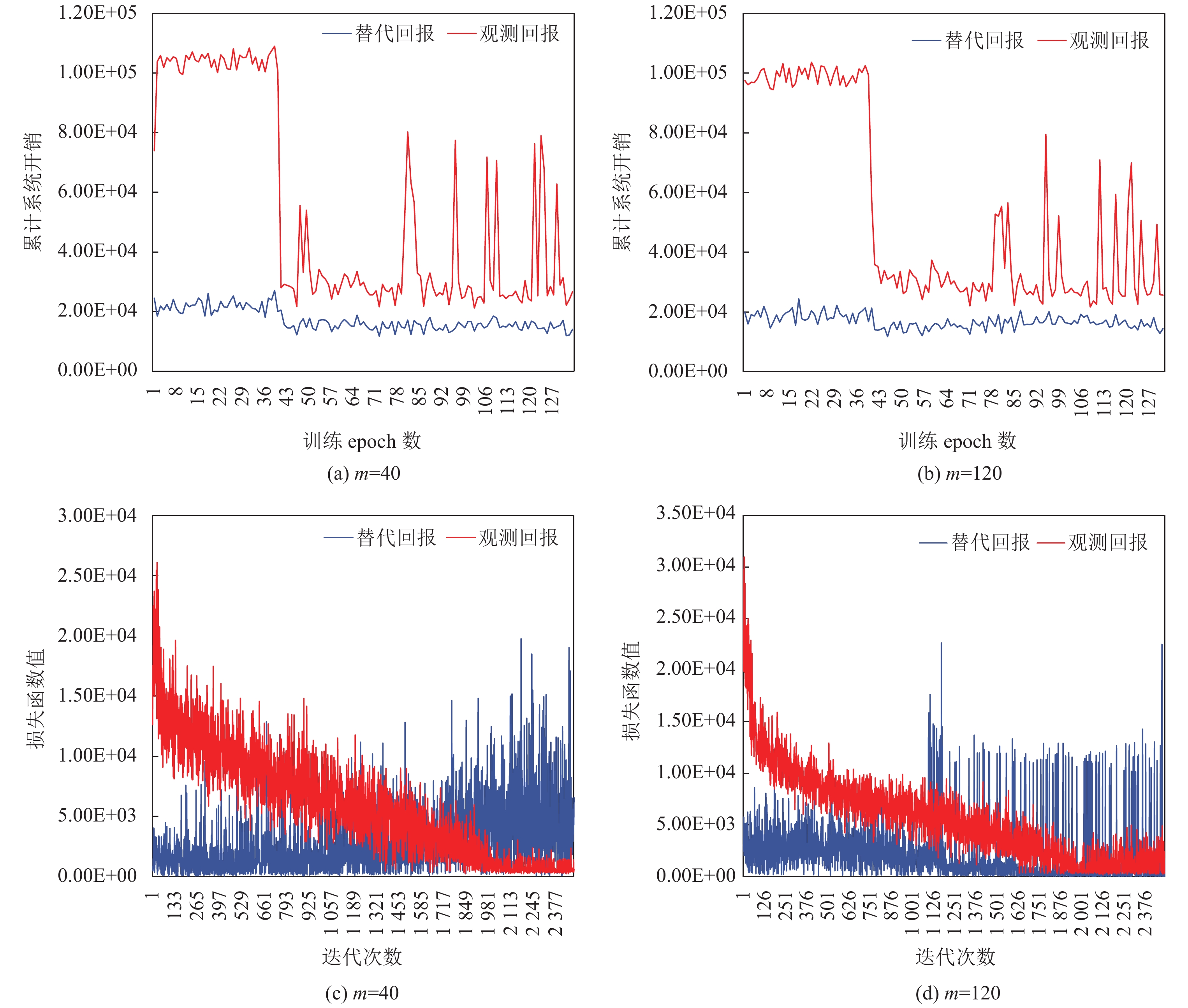
从图7(a)和图7(b)可以看出, m=40和m=120时算法具有相似的曲线, 并且带有替代回报的方法具有更低的累计系统开销. 并且从第1个epoch开始, 带有替代回报的策略累计回报即相对更低, 这是因为在训练DQN之前就已经对替代回报估计参数进行了20轮epoch的拟合. 从图7(c)和图7(d)可以看出, 当m取值增大, 二者训练过程更加稳定, 并且损失函数方差减小. 这是因为当m值增大时, 强化学习agent观测到的回报值更接近于连续回报值, 而m值较小时则偏差较大. 实验结果表明相比于直接使用观测的回报函数, 使用替代回报可以使得任务卸载收敛到一个较优策略. 这是因为替代回报相比于观测回报具有更小的偏差. 通过这一实验可以分析得到, 对于采用替代回报的DQN算法, 虽然回报函数输出值数量的增多可能使得方差增大, 但是这一劣势因回报值的截断误差减小而抵消, 因此能够在训练稳定性和累计回报上取得较好性能. 从表5中可以看出, 在测试数据集上采用替代回报的方案能够得到更低的系统开销. 此外, RLSR-CMAB的卸载策略是离线策略, 而调度顺序的计算时间可以忽略不计( $ \leqslant 500{\text{ ms}} $ ).

5 总结和展望

本文针对边缘服务器资源受限的问题, 提出了一种面向多用户时延敏感任务的任务调度和卸载的联合优化策略. 该策略动态调整服务器的调度顺序以兼顾多用户的优化目标, 同时降低系统总开销, 并采用带替代回报估计的任务卸载策略来消除不同任务排序带来的扰动. 通过对所提出方案的一系列实验测评, 实验结果表明: 本文所提出的任务调度和卸载策略在资源受限的场景下, 在系统总开销和任务执行成功率方面优于基线算法. 其中替代回报估计方法可以使得模型收敛到一个较优策略. 本文任务调度方案通过约束任务的长期失效率来兼顾所有用户的性能目标. 对于基站资源的公平性, 本文令所有的用户同时观测环境并做出系统决策, 没有考虑用户执行动作对于其他用户环境观测的干扰. 为了进一步优化系统性能, 可以结合multi-agent的方法开展研究工作. 此外, 当前工作在卸载方法的鲁棒性方面, 随着设备数量增加, 混淆矩阵的规模也会随之增大, 因此制约了系统的扩展性. 因而可以考虑利用混淆矩阵的稀疏性, 消除替代回报估计的计算与存储的性能瓶颈.