2. 东北大学 信息科学与工程学院, 辽宁 沈阳 110819;
3. 医学影像智能计算教育部重点实验室 (东北大学), 辽宁 沈阳 110819
2. College of Information Science and Engineering, Northeastern University, Shenyang 110819, China;
3. Key Laboratory of Intelligent Computing in Medical Image, Ministry of Education (Northeastern University), Shenyang 110819, China
时间序列分割属于数据挖掘领域的一个重要研究课题, 随着物联网行业的蓬勃发展和数据挖掘技术的日益增进, 该课题在近年来取得了大量的研究成果. 学术界相关的研究集中于提高分割位置的准确率, 加快分割的速度, 实现分割处理的便捷性, 以及将数据分割作为预处理和其他领域相结合, 例如探测研究[1,2]和语音识别[3,4]等. 工业界则是基于时间序列分割技术研发出相应产品, 应用于人体活动分析[5]、异常检测[6]、轨迹预测[7]和交通流预测等.
时间序列分割方法分为两大类, 即基于序列统计学特征和基于时间序列形状模式的变化点边界分割. 基于统计学特征分割通常用于处理单个动作, 统计特征分割以变化点检测方法为主, 有监督方法包括决策树、最近邻、隐马尔科夫和高斯混合模型等[8-13], 如利用决策树快速找出分割点[14]、利用文本挖掘中主题模型提取行为模式[15]和利用隐马尔科夫中时间序列内部状态转变识别活动变化[16]等. 基于变化点检测活动分割模型目标是发现时间序列数据背后的显著变化, 能够有效避免人工反馈[17-19]活动起止点标记冗余工作. 其中, 文献[20]提出基于相对皮尔逊散度估计的变化点检测算法, 实现准确有效地估计. 文献[21]提出一种基于内核的Hilbert-Schmidt独立性准则的检测度量以检测变化点. 文献[22]实现传感器数据实时划分为非重叠活动. 文献[23]利用关键点压缩方法表示时间序列, 基于动态时间规整距离完成分割. 此外, 基于递归神经网络[24]和时序数据符号化[25]也可判别活动起止时刻. 在无监督方法中, 文献[26]提出一种基于信息增益的人体活动时间序列分割算法. 另一个方向是基于序列形状的特征分割, 形状是用于时间序列分段的另一个独特属性, 利用时间序列形状的模式变化点作为分段的边界. 文献[27]提出了基于稀有时间模式的分割模型. 文献[28]用序列重点组成的直线段近似描述时间序列, 又提出一种新的基于重要点分割方法[29]. 基于矩阵轮廓[30,31]的分割算法在相似性重复模式下, 针对连续的动作进行划分, 在此基础上又提出了链式数据形状表示[32,33]. 目前, 基于矩阵轮廓算法及其衍生算法具有处理流式数据、参数少、准确性高等特性, 在处理状态监测等问题上具有无可比拟的优势, 该算法已成为时序分割领域研究热点.
我们针对基于矩阵轮廓的分割方法展开研究, 发现该方法主要存在以下两个问题, 第1个问题是基于矩阵轮廓的快速低代价语义分割算法(fast low-cost semantic segmentation, FLOSS)在对每个位置的子序列搜索最近邻时, 若时间序列中存在非连续的重复状态时容易出现子序列跨越其他状态去匹配相似子序列的现象, 这时通过MP的状态边界来进行划分会产生较大偏差, 从而增大实验结果与真实结果之间的分割偏差. 然而, 非连续性的重复活动状态在不同应用场景下的时间序列中都普遍存在, 也有一些学者把这种活动状态作为模式进行研究[15-17], 常见的如人体日常行为活动, 运动员的训练活动, 病人的康复训练, 驾驶员的行为活动以及一些简单的舞蹈活动等, 而现有的FLOSS算法几乎完全无法应对这一类普遍存在的活动模式. 第2个问题是原提取分割点算法(extract regimes, ER)与最后所形成的纠正弧跨越(corrected arc crossings, CAC)序列密切相关, 算法ER使用窗口提取的最小值作为分割边界值, 然而该算法容易得到局部最优值, 导致提取出的分割结果与真实结果会出现较大的误差.
针对上述研究现状和现有方案存在的问题, 本文提出基于矩阵轮廓的时间序列改进分割算法(LAC-FLOSS)和基于CAC序列的提取分割点改进算法(IER). 本文的主要贡献如下.
(1) LAC-FLOSS: 改进的基于矩阵轮廓的时间序列分割算法
本文对现有的基于矩阵轮廓的时间序列分割算法FLOSS进行研究, 提出了改进的分割算法LAC-FLOSS, 该算法利用给弧添加权重形成一种带权弧, 然后通过设置匹配距离阈值来解决弧的跨状态子序列误匹配问题. 本文首先使用非重复状态数据集进行实验, 并与其他算法进行对比验证LAC-FLOSS算法的有效性, 其次在含重复非连续状态数据集上进行实验, 将LAC-FLOSS与FLOSS进行对比, 验证改进后的LAC-FLOSS算法在分割含重复非连续状态序列的有效性.
(2) IER: 针对基于CAC序列提取分割点算法的改进研究
分割算法处理原始时间序列得到CAC序列, 直观上容易发现分割点, 而使用算法进行提取分割点的过程并非如此. 本文利用CAC序列的形状特征, 从波谷中提取极小值, 进而提出改进的提取分割点算法IER. 该算法能够避免原分割点提取算法使用窗口在非拐点处取到分割点, 提升提取分割结果的准确性. 本文通过与ER算法进行对比, 验证了IER提取分割点的效果要优于ER.
本文将根据上述提出的主要研究内容进行展开论述. 第1节主要介绍时间序列数据划分/分割所涉及的预备知识. 第2节提出基于矩阵轮廓的快速时序分割算法. 第3节提出基于CAC的搜索分割点算法. 第4节进行详尽的实验与分析, 与最新的文献和一些经典方法进行实验对比. 第5节总结与展望, 对本文的工作进行总结概述, 并对未来进一步深入研究进行展望.
1 预备知识 1.1 矩阵轮廓介绍矩阵轮廓(matrix profile, MP)是一种时间序列原语, 能够用于模式挖掘、检测异常、分割、聚类、分类以及相似性度量等领域[34]. 在实际应用过程中, 可以将MP看作是描述时间序列的一种子序列最相似匹配的序列结构, 它能够反映一条时间序列中是否存在相同的模式或者异常. 计算一条给定时间序列的MP, 可以简单概括为两个步骤, 第1步根据给定的时间序列先求出对应的距离轮廓(distance profile, DP), DP是由多个向量堆叠组成的向量矩阵; 第2步, 通过选取DP每个向量中最小值及其对应索引, 得到矩阵轮廓和矩阵轮廓索引(matrix profile index, MPI).
矩阵轮廓的相关定义如下.
时间序列
| $ D[i] = \sqrt {2m\left(1 - \frac{{QT[i] - m{\mu _Q}{m_T}[i]}}{{m{\sigma _Q}\displaystyle\sum\nolimits_T {[i]} }}\right)} $ | (1) |
其中, D[i]是标准化后的欧几里得距离,
当子序列Q匹配到自身时, 计算结果会是0, 导致最终的MP始终是0, 这种自匹配的部分称为平凡匹配. 通过忽略子序列Q位置之前和之后m/2长的部分来避免平凡匹配, 最后得到D的长度如公式(2)所示.
| $ \left| D \right| = \left| T \right| - \left| Q \right| + 1 $ | (2) |
其中, A是时间序列T的一个所有可能的子序列集合, 它是有序的, 包含在T上面所有可能的子序列, 通过在T上滑动一个长度为m的窗口获得.
矩阵轮廓索引表示MP中每个子序列匹配的索引集合,
基于矩阵轮廓的时序分割技术主要包含快速低代价语义分割和分割点提取算法. 与大多处理时间序列分割的方法不同, 它是领域独立的, 不会限制在特定的领域使用, 并且能够轻松处理流式数据, 具备随时即用的特性, 即能够直接处理给定的时间序列, 不需要提前进行复杂的数据处理.
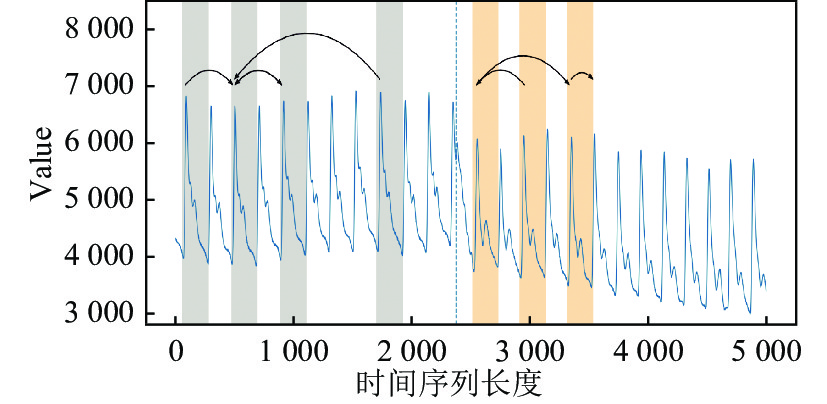
基本思想是: 给定待分割时间序列, 首先计算出该序列对应的矩阵轮廓和矩阵轮廓索引, 矩阵轮廓索引中记录每一个子序列的最相似子序列(也称最近邻)索引, 即匹配过程中当前子序列弧指向的索引. 由于是最相似匹配, 那么具有最相似形状的子序列会匹配到一起, 如图1所示. 图中每一个子序列都会去匹配和自己最相似的子序列, 图中弧即表示两个子序列的匹配.
|
图 1 子序列相似性匹配 |
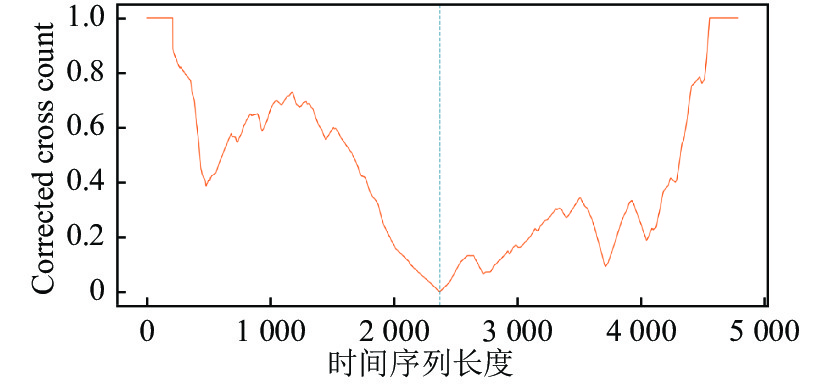
矩阵轮廓索引记录了子序列指向另一个最相似子序列的索引, 这里的弧表示两个子序列进行最相似匹配, 然后使用 FLOSS 算法统计穿过每个索引位置上的弧数. 弧会穿过至少一个索引, 一条弧也可能会被统计到多个索引上, 最后得到每个索引位置上穿过的弧数量集合, 形成弧跨越数(arc curve, AC)序列. 每个索引上都有统计得到的数据, 在活动状态转变的边缘处这个数量相较于状态内部会低很多, 在形状上面的表现则是会形成波谷, 这样最终得到的数据称作AC序列, 可以看出AC序列的两端同样是趋近于0, 为了防止AC序列两端的影响, 对AC序列进行了纠正处理形成纠正弧跨越(CAC)序列, 如图2所示.
|
图 2 在 CAC 序列上的分割结果示意图 |
给定一条时间序列T, 首先使用STAMP算法处理时间序列T, 获取对应的MP和MPI, 然后FLOSS使用MPI统计每一个索引位置上面的弧数得到一条CAC序列, 也就是对整个MP每个子序列上弧跨越数的统计数据, CAC序列实际上是对弧跨越数AC序列使用公式(3)进行了纠正处理.
| $ L^{\rm CAC}_i = \min \left( {\frac{L^{\rm AC}_i}{L^{\rm IAC}_i}, 1} \right) $ | (3) |
其中,
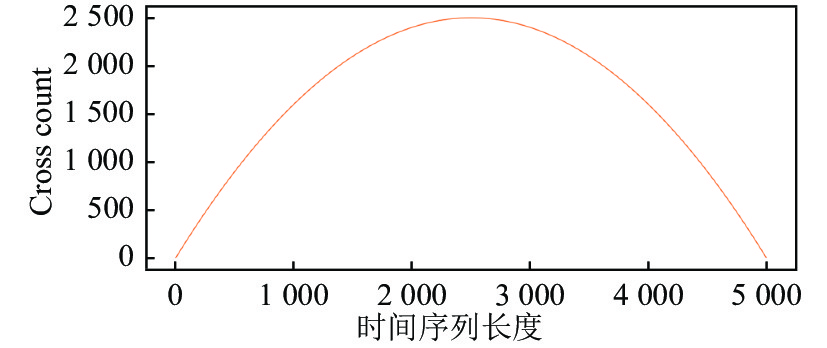
|
图 3 理想化AC序列的示意图[31] |
图3是使用 FLOSS 算法得到的CAC 序列, 最后在 CAC 序列上使用 ER 算法提取分割点, 这些分割点即表示分割原始数据的分割边界, 然后根据该序列结合子序列长度设置一个排除域, 每次从该序列中提取最小值, 然后利用排除域将该值周围附近的值排除在下一次的分割点搜索范围外, 提取到R – 1个分割点停止, R表示状态数.
以上技术仍存在不足之处, 首先, FLOSS算法在计算MP时, 子序列互相匹配的过程中出现弧跨越不同状态去匹配相同状态弧的问题, 导致得到的CAC序列丢失大量可以用于提取分割点的特征, 所以分割效果不好. 其次, ER算法提取的局部最小值, 不一定是我们需要的最优局部最小值, 所以提取效果不佳. 因此, 本文提出改进的基于矩阵轮廓的限制弧跨越的时间序列分割算法LAC-FLOSS和改进的提取分割点算法IER.
2 基于矩阵轮廓的快速低代价语义分割算法的改进研究LAC-FLOSS在计算MP的过程中匹配的弧越长, 表示子序列匹配的距离就越远, 弧的权值也就越小. 它根据弧匹配的距离给弧添加权重形成带权弧, 利用带权弧结合匹配距离阈值来选择最适合的子序列匹配. 由于不同状态的子序列相隔距离相对较远, 因此根据距离进行处理之后即使出现两个重复非连续状态, 也不会受到彼此过多影响. 经过以上处理之后得到新的MP和MPI, 然后使用MPI生成 CAC 序列, 最后再利用分割点提取算法ER在此序列上提取分割点用于确定分割边界.
2.1 基本原理给定一条时间序列
| $ {\mathit{WAC}_i} = \frac{D^{\rm DP}_i}{{\left| {{\mathit{Idx}_{\rm cur}} - i} \right|}},\; i \in [0, n - 1] $ | (4) |
其中,
设定阈值threshold, 如公式(5)所示.
| $ threshold = \frac{{\left| T \right|}}{R} $ | (5) |
其中, R表示状态的数目, |T|表示时间序列的长度, threshold表示平均分割状态长度. Q序列的WAC集合会根据每个对应弧的权重重新排序, T中的所有子序列都有对应的WAC集合. threshold的作用就是判断当前MP对应索引i的子序列是否需要重算弧指向, 如果需要重算则选取当前子序列对应的WAC集合中弧权值不大于给定阈值的最大权值弧作为最优弧. 由于时间序列数据中包含多个活动状态, 每一个状态并非是单独的动作, 因此每一段子序列在进行匹配的过程中, 弧平均的匹配长度往往不会超过整个平均状态长度范围, 使用带权弧重算弧指向之后, 再使用平均状态长度作为阈值便可以限制绝大多数弧的跨越其他状态匹配.
错误匹配的弧经过修正之后指向新的子序列, 形成一个新的MP, 接着使用该MP计算CAC序列, 便可在该序列上提取分割点.
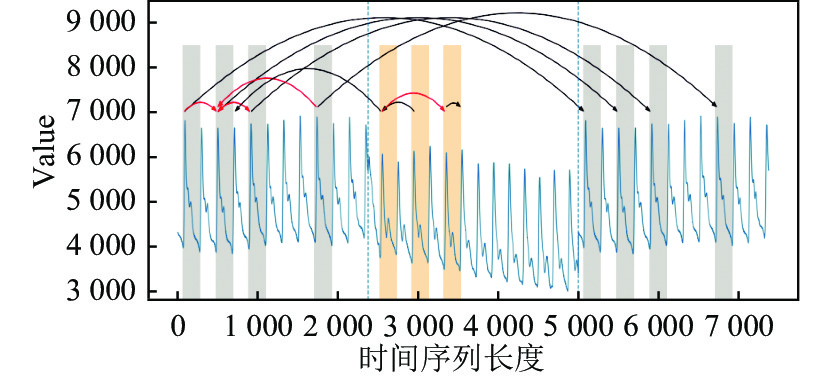
如图4所示, LAC-FLOSS对图中跨状态的弧进行了纠正, 其中部分黑色弧是跨状态的错误匹配, 红色弧为修正后的匹配, 经过修正之后很多索引位置上面对应这些弧的统计数也会减少, 同时也会减少CAC序列特征信息的丢失.
|
图 4 纠正后子序列弧匹配结果示意图 |
如图5所示, 弧在重新指向新的子序列后, 对每个索引位置上统计的弧数也会更新, 重新计算的CAC序列包含了更多易于提取分割点的信息.

|
图 5 CAC序列上的分割结果 |
2.2 算 法
本文已经对目前FLOSS分割算法存在的问题进行了分析, 之后在第2.1节中介绍了本文提出的改进分割算法LAC-FLOSS及其基本原理. 在给出LAC-FLOSS算法之前仍有一些概念需要更加详细地说明, 关于本文中限制弧跨越其他状态的匹配. 正如前文所述, 时间序列的子序列在进行匹配的过程中出现子序列所对应的弧会跨越其他状态去匹配最相似子序列的问题, 这些跨越其他状态的弧即是错误的匹配, 需要避免这样的弧出现, 最理想的状态就是所有弧都会在当前状态下进行匹配, 然而实际情况并非如此. 因此, 本文中的限制弧跨状态匹配即是指避免子序列匹配过程中出现大量的弧跨越其他状态进行匹配相似子序列的情况, 将其限制在当前自身所处的状态下进行匹配子序列. 下面给出LAC-FLOSS算法, 如算法1所示.
算法1. 限制弧跨越的快速低代价语义分割(limit arc curve cross-fast lw-cost semantic segmentation, LAC-FLOSS).
输入: 时间序列T, 查询子序列Q, 状态数R;
输出: 纠正后的弧跨越数序列LCAC.
BEGIN
1.
2.
3.
4.
5.
6.
7. fori=1 ton do
8. if
9. for j=1 to n do
10.
11. endfor
12.
13.
14.
15.
16. endif
17. endfor
18.
19. return
END
LAC-FLOSS算法的过程如算法1所示. 算法第1–2行使用MASS算法计算时间序列T对应的DP. 第3行使用STAMP算法计算MP和MPI. 第4–17行根据带权弧和阈值进行更新MP和MPI, 第4–6行做初始化准备, 第8行首先判断当前子序列的弧是否需要更新, 第9–10行根据每个子序列的DP计算当前子序列所有匹配弧的权重, T中每一个子序列都会和T中除自身外的所有子序列进行计算欧几里得距离, 在这个过程中, 根据所有相似匹配子序列的距离为弧添加权重, 第12–15行根据带权弧重新排序, 将第1个不大于threshold的弧作为新的匹配弧, 并将弧指向的子序列索引记录在当前子序列的MPI中. 第18行在获得重新计算后的MP和MPI后, 使用FLOSS算法根据MPI计算时间序列所对应的CAC序列.
3 基于CAC的搜索分割点算法的改进研究FLOSS算法处理原始时间序列得到CAC序列, 然后可以从该序列中提取分割结果. 目前从CAC序列中提取出分割点这一过程并没有得到足够的关注, 然而, 针对CAC序列提取分割点也同样重要, 这需要提取方法根据设定的规则在CAC序列中搜索得到R – 1个最可能的分割点, R表示状态数, 这些分割点则直接会影响最后划分序列数据的准确性. 本文在相关工作部分介绍了现有的提取分割点算法ER, 该算法结合子序列长度L设定了一个排除域作为提取窗口, 通过该窗口搜索并提取CAC序列的最小值, 每搜索到一个符合的值就将该值周围ERE×L的范围进行排除, 即相当于将该范围的值排除在了后面的搜索范围外, 提取到R – 1个分割点停止.
如图6所示, 这种使用窗口进行提取分割点的方法会出现在非拐点处提取到最小值的问题, 如图中的d点, 其中虚线表示真实的分割结果, 图中字母表示实验结果, 可以看到实验结果中的分割点d与真实结果偏差较大. 图7是对图6中的序列使用ER算法迭代提取分割点的过程, 图6中的d点对应图7(d). 如果调整排除域, 将排除域调大, 由于排除域同时限制着两端需要排除的范围, 容易丢失最两端的分割结果; 将排除域调小, 则分割位置容易发生更大的偏移, 同时会影响到其他分割点, 进而导致更差的分割结果, 并不能解决以上问题.

|
图 6 实验分割结果和真实分割结果对比 |

|
图 7 ER算法提取分割结果的过程 |
ER算法使用排除域窗口提取CAC序列最小值时, 当窗口处在一条斜率不断变大或者不断变小的曲线处, 就无法保证取到的最小值是分割点的位置. 使用算法处理活动状态序列数据得到CAC序列之后, 在该序列上使用窗口提取到的局部分割点并不一定是可用的分割点. 这是因为提取分割点算法与最后形成的CAC序列所包含的分割点特征信息密切相关, 然而现有的算法ER并没有更好地挖掘出这些相关信息. 提取分割点的算法是在CAC序列中提取出能够分割状态边界的局部极小值, 这些值就是最终的状态分割点. 理想情况下, 在没有任何弧跨越的情况下, CAC序列的局部极小值集合完全与真实分割点集合重合. 如果从窗口划分的角度去考虑, 采用变化的长度窗口, 需要迭代多次, 容易陷入得到局部最优的结果, 导致最终得到的分割结果并不理想.
本文针对以上问题从活动序列整体形状的角度出发, 提出改进的提取分割点算法(improved extract regimes, IER), 该算法首先对CAC序列进行平滑处理, 如图8所示, 降低噪声带来的影响, 然后利用CAC序列形状的特性, 提取序列中波谷的极小值, 之后再去下一个波谷中寻找对应的极值, 搜寻完整个CAC序列之后得到极小值集合, 最后根据值排序并选取前R – 1个结果, 即得到分割点集合.

|
图 8 CAC序列和对应的平滑曲线 |
如图8所示是CAC序列形成的有波谷特性的曲线和降噪拟合曲线, 其中波谷趋势变换的位置是CAC中表示活动状态发生变化的地方, 利用这一特性能够更加准确地提取分割点. 在改进的搜索算法IER中, 需要搜索CAC序列中波谷的极值, 根据当前的极值是否在拐点处来判断能否选取. 但是, 由于CAC序列中并不是所有的波谷极小值都是分割点所在的位置, 而且时间序列中的状态分割边界本身具有一定的距离, 因此可以设定距离选取符合的值. 如果两个波谷值的距离小于该限定距离, 表示两个分割点距离较近, 选择值较小的点作为分割点.
图9是使用IER算法得到的分割效果示意图, 图中的虚线为真实结果, 可以看到图中的真实结果都是在波谷位置. IER能够利用CAC序列的形状特性, 从中提取更多有利于分割的信息, 避免在非拐点处取到分割点.

|
图 9 IER分割效果示意图 |
下面给出本文提出的改进的分割点提取算法IER, 如算法2所示. 算法中第1–4行进行数据的准备工作, 第1行初始化活动状态数目n, 第2行初始化分割结果locRegimes. 第3–6行从CAC序列中提取分割点, 第3行对CAC序列使用S-G平滑滤波技术进行降噪处理. 第4行计算波谷的选取阈值. 第5–6行获取序列cac_smooth中波谷的极小值和其对应的索引. 第7–10行将索引和值对应组合, 根据值取其对应的索引, 得到分割点集合.
算法2. 改进的提取分割点(imporoved extract regimes, IER).
输入: 纠正后的弧跨越数LCAC, 时间序列T, 活动状态数numRegimes;
输出: 分割点集合locRegimes.
BEGIN
1.
2.
3.
4.
5.
6.
7.
8. for i = 1 to numRegimes– 1 do
9.
10. endfor
11. return locRegimes
END
4 实验与分析 4.1 实验说明 4.1.1 实验数据集分割算法对比实验共使用两个数据集. 第1个数据集使用的数据是由Gharghabi等人[30,31]提供, 该数据集共包含32条数据, 这些数据并非全部是人体活动相关数据集, 它们来自不同的领域, 包括从人体、鸟类、兔子以及昆虫身上等采集到的数据, 因此这些数据的采集频率也不完全相同, 不过数据集中已经给出每条数据建议使用的窗口大小. 第2个数据集来自Vavoulas团队采集的公开数据集MobiAct数据集[34], 该数据集主要用于研究活动识别、活动分割以及模式挖掘等领域. 由于该实验需要使用的不是含有单一动作的时间序列数据, 而是具有连续多个动作的人体活动时间序列数据, 因此需要使用的是带有注释的人体活动时间序列数据集, 该实验使用12个带标签数据集中的50条含重复状态的数据.
分割点提取算法对比实验使用的数据集为MobiAct数据集中带注释的连续时间序列数据集, 该实验为保证实验数据的全面性和实验结果的可信性, 随机选择14个活动方式, 共34条数据集, 其中使用的数据既有含重复状态数据序列也有非重复状态数据序列.
4.1.2 评价指标目前常用的评价标准是使用召回率(recall)和精确度(precision), 然而Lin等人[35]指出在评价变化点问题时是存在问题的, 假如真实值是10700, 实验值是10701或10759, 是否认为实验值是可行的. 基于上述问题, 为了降低这种影响, 他们提出了时间容忍度(temporal tolerance)的概念, 即给出一个范围, 比如10700±100, 超出范围的进行惩罚, 范围内的进行奖励.
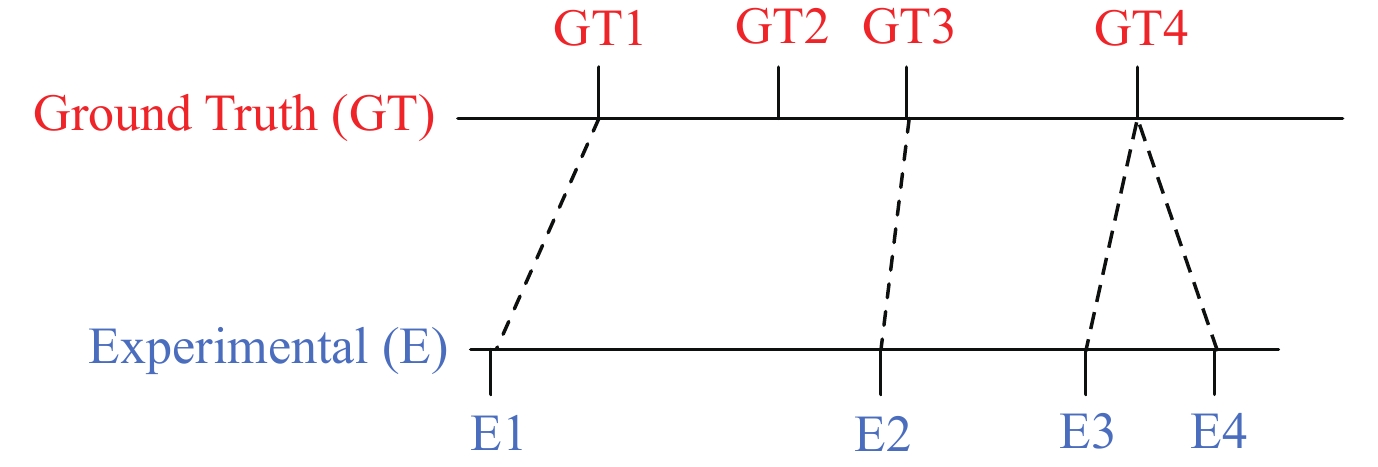
在面对多个分割边界问题时, 实验结果中会出现多个结果映射到一个真实结果上的情况, 如图10所示, 实验分割点E3和E4映射到真实分割点GT4. 如果按照顺序进行映射, 对于部分真实值就会施加过度的惩罚, 这会严重影响对于实验效果的评价.
|
图 10 真实值和实验值映射示例[31] |
Gharghabi等人提出了一个分割结果评价标准, 该算法针对每一个分割点都是去寻找与自身最接近的真实值作为对照点, 这样能够避免对一些分割点过度惩罚, 通过比较实验结果与真实结果之间的偏差score, 可以判断实验结果的分割效果, score越小表明偏差越小, 分割效果也就越好[31]. 我们采用该评价标准来判断实验的分割效果.
下面给出该评价算法, 如算法3所示.
算法3. 计算分割结果得分(score regimes, SR).
输入: 实验分割点集合locRegimes, 真实分割点集合gtRegimes, 时间序列长度ts_length;
输出: 得分score. // [0, 1] 0为最优得分
BEGIN
1.
2.
3. for i = 1 to numRegimes do // 根据真实分割值进行映射最相近的实验值
4.
5.
6.
7. endfor
8.
9. return score
END
SR算法的过程如算法3所示, 算法中第1–2行进行准备工作, 第1行初始化偏差和sumDiff, 第2行计算真实分割结果的数目numRegimes. 第3–7行计算真实值与实验值的偏差和, 第4行计算每一个真实值和其映射实验值的索引, 第5行计算两者之间的差值绝对值, 即偏差, 第6行计算累计偏差和. 第8行计算平均偏差score.
4.1.3 实验平台本文采用Windows Professional 10下PyCharm作为实验平台, CPU为Intel(R) Core(TM) i5-4590M@3.30 GHz, 内存为8 GB.
4.2 实验结果 4.2.1 分割算法对比实验(1) 第1组实验, LAC-FLOSS算法在包含非重复状态数据集上的实验结果
第1组实验中AutoPlait, HOG, Random和Best human方法的实现与文献[31]的保持一致. 实验所用数据集如表1所示. 实验结果展示的是LAC-FLOSS与其他方法进行比较的结果, 如表2所示. 其LAC-FLOSS的表现优于其他方法, 其中LAC-FLOSS与FLOSS算法分割结果相比有10条数据优于FLOSS, 2条差于FLOSS, 20条结果一致. 实验结果表明, 本文提出改进的LAC-FLOSS算法在分割非重复状态数据序列上面的表现是优于其他方法的, 验证了LAC-FLOSS算法的有效性.
| 表 1 数据集信息 |
| 表 2 LAC-FLOSS与6个方法的对比表现 |
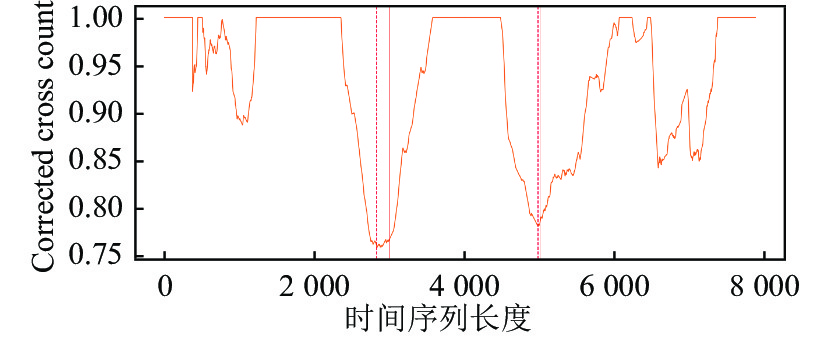
本实验中的数据基本都是非重复状态数据, FLOSS能够很好应对这种数据. 根据以上实验结果分析, 针对子序列进行弧的匹配, 由于部分弧的进行匹配会超出分割点的边界, 会导致分隔位置发生偏移. 图11–图13为第1组实验的一次实验效果对比, 图11是原始数据的真实分割结果, 图12是使用FLOSS算法的分割结果, 分割实验结果与真实结果相比偏差为0.023, 图13是LAC-FLOSS算法的分割结果, 偏差则为0.004. 从以上实验结果可以看出, 使用算法LAC-FLOSS进行分割的效果要优于使用FLOSS算法的分割效果, LAC-FLOSS限制了弧的匹配距离, 相比于FLOSS的分割结果LAC-FLOSS阻止了部分子序列中弧的长距离错误匹配, 进而降低分割边界的偏差, 提升分割结果的准确性.

|
图 11 原始数据的真实分割结果 |
|
图 12 FLOSS的分割结果 |

|
图 13 LAC-FLOSS的分割结果 |
(2) 第2组实验, LAC-FLOSS算法在包含重复非连续状态数据集上的实验结果
本组实验所用数据如表3所示. 表4是LAC-FLOSS与其他方法的对比结果, 根据在第4.1.2节中的评价标准所提出的评价标准算法, 最后通过评价标准算法计算得到的结果表示实验值与真实值的偏差score, 该值越小说明分割的效果越好. 可以看到, LAC-FLOSS与
| 表 3 含重复状态的数据集信息 |
| 表 4 LAC-FLOSS与4个方法的对比表现 |
图14是LAC-FLOSS,

|
图 14 3种算法分割结果对比 |
4.2.2 分割点提取算法对比实验
本部分将对ER和IER算法的对比结果进行展示, 实验数据如表5所示. 使用
| 表 5 数据集信息 |
图15是ER算法和IER算法分别在

|
图 15 分割结果平均score对比 |
从图16–图18可以看出,

|
图 16 |

|
图 17 |

|
图 18 LAC-FLOSS结合两种搜索算法的结果对比 |
4.3 实验总结
本文实验部分总共进行2组实验数据, 分别验证改进的基于矩阵轮廓的时间序列分割算法LAC-FLOSS、改进的基于CAC序列的提取分割点算法的实验效果.
本文主要针对基于矩阵轮廓的时间序列分割技术进行改进研究. 首先是针对基于矩阵轮廓的快速低代价分割算法FLOSS进行改进研究, 提出改进后的算法LAC-FLOSS, 利用AutoPlait算法,
改进的基于矩阵轮廓的LAC-FLOSS分割算法在处理非重复和重复状态序列的分割效果, 优于传统的基于矩阵轮廓的FLOSS分割算法和现有的改进版FLOSS分割算法的, 验证LAC-FLOSS算法的有效性.
改进的提取分割点算法IER在结合LAC-FLOSS,
本文针对以上问题进行研究, 提出限制弧跨越的改进的基于矩阵轮廓的分割算法LAC-FLOSS, 基于CAC序列形状进行改进的分割点提取算法IER, 并在公开数据集datasets_seg和MobiAct上通过充分的对比实验验证这些算法的有效性.
(1) 针对基于矩阵轮廓的FLOSS算法存在的问题, 本文在第2节提出改进的分割算法LAC-FLOSS, 在子序列的匹配过程中限制弧跨越其他状态进行匹配, 并结合改进后的提取分割点算法, 提升分割的准确性, 并通过在公开数据集datasets_seg和MobiAct上进行对比验证, 证明所提出算法的有效性.
(2) 针对基于CAC的搜索分割点算法存在的问题, 本文在第3节提出改进的提取分割点算法IER, 并在公开数据集MobiAct进行了对比实验, 验证了该算法的有效性.
相对于目前的基于矩阵轮廓的分割技术研究成果, 本文提出的算法取得了一定的研究成果. 针对目前国内外分割问题的研究现状, 在本文进行相关研究的基础之上, 仍然有很多地方值得做更进一步的研究: 第1点是本文提出的分割算法LAC-FLOSS虽然在分割准确性上面有很大的提升, 但是在速度上面却仍然需要进一步的改进工作. 第2点是对于多维时间序列的组合方法, 本文未考虑使用不均等加权处理, 比如给不同维度的数据分配不同的权重大小.
| [1] |
Keković G, Sekulić S. Detection of change points in time series with moving average filters and wavelet transform: Application to EEG signals. Neurophysiology, 2019, 51(1): 2-8.
[doi:10.1007/s11062-019-09783-y] |
| [2] |
Chandola V, Vatsavai RR. A Gaussian process based online change detection algorithm for monitoring periodic time series. In: Proc.of the 2011 SIAM Int’l Conf. on Data Mining (SDM). Mesa: SIAM, 2011. 95–106.
|
| [3] |
Chowdhury MFR, Selouani SA, O'Shaughnessy D. Bayesian on-line spectral change point detection: A soft computing approach for on-line ASR. Int’l Journal of Speech Technology, 2012, 15(1): 5-23.
[doi:10.1007/s10772-011-9116-2] |
| [4] |
Lau HF, Yamamoto S. Bayesian online changepoint detection to improve transparency in human-machine interaction systems. In: Proc. of the 49th IEEE Conf. on Decision and Control (CDC). Atlanta: IEEE, 2011. 3572–3577.
|
| [5] |
Aminikhanghahi S, Cook DJ. Using change point detection to automate daily activity segmentation. In: Proc. of the 2017 IEEE Int’l Conf. on Pervasive Computing and Communications Workshops. Kona: IEEE, 2017. 260–267.
|
| [6] |
Rajagopalan V, Ray A. Symbolic time series analysis via wavelet-based partitioning. Signal Processing, 2006, 86(11): 3309-3320.
[doi:10.1016/j.sigpro.2006.01.014] |
| [7] |
Sadri A, Salim FD, Ren Y, Shao W, Krumm JC, Mascolo C. What will you do for the rest of the day? An approach to continuous trajectory prediction. Proc. of the ACM on Interactive, Mobile, Wearable and Ubiquitous Technologies, 2018, 2(4): 186.
[doi:10.1145/3287064] |
| [8] |
Reddy S, Mun M, Burke J, Estrin D, Hansen M, Srivastava M. Using mobile phones to determine transportation modes. ACM Trans. on Sensor Networks, 2010, 6(2): 13.
[doi:10.1145/1689239.1689243] |
| [9] |
Zheng Y, Liu LK, Wang LH, Xie X. Learning transportation mode from raw GPS data for geographic applications on the Web. In: Proc. of the 17th Int’l Conf. on World Wide Web. Beijing: ACM, 2008. 247–256.
|
| [10] |
Cleland I, Han M, Nugent C, Lee H, McClean S, Zhang S, Lee S. Evaluation of prompted annotation of activity data recorded from a smart phone. Sensors, 2014, 14(9): 15861-15879.
[doi:10.3390/s140915861] |
| [11] |
Han M, Vinh LT, Lee YK, Lee S. Comprehensive context recognizer based on multimodal sensors in a smartphone. Sensors, 2012, 12(9): 12588-12605.
[doi:10.3390/s120912588] |
| [12] |
Cho H, Fryzlewicz P. Multiple-change-point detection for high dimensional time series via sparsified binary segmentation. Journal of the Royal Statistical Society Series B-statistical Methodology, 2015, 77(2): 475-507.
[doi:10.1111/rssb.12079] |
| [13] |
Shi MY, Wang P, Wang W. Algorithm of supervised time series segmentation and state recognition. Computer Engineering, 2020, 46(5): 131-138(in Chinese with English abstract).
[doi:10.19678/j.issn.1000-3428.0056243] |
| [14] |
Noor MHM, Salcic Z, Wang KIK. Adaptive sliding window segmentation for physical activity recognition using a single tri-axial accelerometer. Pervasive and Mobile Computing, 2017, 38: 41-59.
[doi:10.1016/j.pmcj.2016.09.009] |
| [15] |
Huynh T, Fritz M, Schiele B. Discovery of activity patterns using topic models. In: Proc. of the 10th Int’l Conf. on Ubiquitous Computing. Seoul: ACM, 2008. 10–19.
|
| [16] |
Matsubara Y, Sakurai Y, Faloutsos C. AutoPlait: Automatic mining of co-evolving time sequences. In: Proc. of the 2014 ACM SIGMOD Int’l Conf. on Management of Data. Snowbird: ACM, 2014. 193–204.
|
| [17] |
Dernbach S, Das B, Krishnan NC, Thomas BL, Cook DJ. Simple and complex activity recognition through smart phones. In: Proc. of the 8th Int’l Conf. on Intelligent Environments. Guanajuato: IEEE, 2012. 214–221.
|
| [18] |
Lester J, Choudhury T, Borriello G. A practical approach to recognizing physical activities. In: Proc. of the 4th Int’l Conf. on Pervasive Computing. Dublin: Springer, 2006. 1–16.
|
| [19] |
He ZY, Jin LW. Activity recognition from acceleration data based on discrete consine transform and SVM. In: Proc. of the 2009 IEEE Int’l Conf. on Systems, Man and Cybernetics. San Antonio: IEEE, 2009. 5041–5044.
|
| [20] |
Liu S, Yamada M, Collier N, Sugiyama M. Change-point detection in time-series data by relative density-ratio estimation. In: Proc. of the 2012 Joint IAPR Int’l Workshops on Statistical Techniques in Pattern Recognition (SPR) and Structural and Syntactic Pattern Recognition. Hiroshima: Springer, 2012. 363–372.
|
| [21] |
Yamada M, Kimura A, Naya F, Sawada H. Change-point detection with feature selection in high-dimensional time-series data. In: Proc. of the 23rd Int’l Joint Conf. on Artificial Intelligence. Beijing: AAAI Press, 2013. 1827–1833.
|
| [22] |
Aminikhanghahi S, Cook DJ. Enhancing activity recognition using CPD-based activity segmentation. Pervasive and Mobile Computing, 2019, 53: 75-89.
[doi:10.1016/j.pmcj.2019.01.004] |
| [23] |
Cao WP, Luo Y, Xiong QJ, Ning B. Algorithm of time series segmentation based on quadratic regression. Computer CD Software and Applications, 2012(18), 157, 159(in Chinese with English abstract).
|
| [24] |
Cho M, Kim Y, Lee Y. Contextual relationship-based activity segmentation on an event stream in the IoT environment with multi-user activities. In: Proc. of the 3rd Workshop on Middleware for Context-aware Applications in the IoT. Trento: ACM, 2016. 7–12.
|
| [25] |
Zhao JP, Itti L. Decomposing time series with application to temporal segmentation. In: Proc. of the 2016 IEEE Winter Conf. on Applications of Computer Vision (WACV). Lake Placid: IEEE, 2016. 1–9.
|
| [26] |
Sadri A, Ren YL, Salim FD. Information gain-based metric for recognizing transitions in human activities. Pervasive and Mobile Computing, 2017, 38: 92-109.
[doi:10.1016/j.pmcj.2017.01.003] |
| [27] |
Huang DTJ, Koh YS, Dobbie G, Pears R. Detecting changes in rare patterns from data streams. In: Proc. of the 18th Pacific-Asia Conf. on Knowledge Discovery and Data Mining. Springer, 2014. 437–448.
|
| [28] |
Zhou DZ, Li MQ. Time series segmentation based on series importance point. Computer Engineering, 2008, 34(23): 14-16(in Chinese with English abstract).
[doi:10.3969/j.issn.1000-3428.2008.23.006] |
| [29] |
Liao J, Zhou ZL, Kou YX, Luo H. Method for time series segment based on important point. Computer Engineering and Applications, 2011, 47(24): 166-170(in Chinese with English abstract).
[doi:10.3778/j.issn.1002-8331.2011.24.047] |
| [30] |
Gharghabi S, Ding YF, Yeh CCM, Kamgar K, Ulanova L, Keogh E. Matrix profile VIII: Domain agnostic online semantic segmentation at superhuman performance levels. In: Proc. of the 2017 IEEE Int’l Conf. on Data Mining (ICDM). New Orleans: IEEE, 2017. 117–126.
|
| [31] |
Gharghabi S, Yeh CCM, Ding YF, Ding W, Hibbing P, LaMunion S, Kaplan A, Crouter SE, Keogh E. Domain agnostic online semantic segmentation for multi-dimensional time series. Data Mining and Knowledge Discovery, 2019, 33(1): 96-130.
[doi:10.1007/s10618-018-0589-3] |
| [32] |
Zhu Y, Imamura M, Nikovski D, Keogh E. Matrix profile VII: Time series chains: A new primitive for time series data mining (best student paper award). In: Proc. of the 2017 IEEE Int’l Conf. on Data Mining (ICDM). New Orleans: IEEE, 2017. 695–704.
|
| [33] |
Yeh CCM, Zhu Y, Ulanova L, Begum N, Ding YF, Dau HA, Silva DF, Mueen A, Keogh E. Matrix profile I: All pairs similarity joins for time series: A unifying view that includes motifs, discords and shapelets. In: Proc. of the 16th IEEE Int’l Conf. on Data Mining (ICDM). Barcelona: IEEE, 2016. 1317–1322.
|
| [34] |
Vavoulas G, Chatzaki C, Malliotakis T, Pediaditis M, Tsiknakis M. The MobiAct dataset: Recognition of activities of daily living using smartphones. In: Proc. of the 2nd Int’l Conf. on Information and Communication Technologies for Ageing Well and e-Health. Rome: SCITEPRESS, 2016. 143–151.
|
| [35] |
Lin JFS, Karg M, Kulić D. Movement primitive segmentation for human motion modeling: A framework for analysis. IEEE Trans. on Human-machine Systems, 2016, 46(3): 325-339.
[doi:10.1109/THMS.2015.2493536] |
| [13] |
史明阳, 王鹏, 汪卫. 有监督时间序列分割与状态识别算法. 计算机工程, 2020, 46(5): 131-138.
[doi:10.19678/j.issn.1000-3428.0056243] |
| [23] |
曹文平, 罗颖, 熊启军, 宁彬. 基于二次回归的时间序列分割算法. 计算机光盘软件与应用, 2012(18), 157, 159.
|
| [28] |
周大镯, 李敏强. 基于序列重要点的时间序列分割. 计算机工程, 2008, 34(23): 14-16.
[doi:10.3969/j.issn.1000-3428.2008.23.006] |
| [29] |
廖俊, 周中良, 寇英信, 罗寰. 一种基于重要点的时间序列分割方法. 计算机工程与应用, 2011, 47(24): 166-170.
[doi:10.3778/j.issn.1002-8331.2011.24.047] |
 2023, Vol. 34
2023, Vol. 34


