对于一些安全性至关重要的系统, 例如航空航天系统, 微小的设计错误就可能会导致严重的后果. 因此, 保证系统的正确性是完全必要的. 然而, 随着系统规模的日益扩大, 可能出现的错误也呈指数级增长, 导致传统的检测手段无法胜任如此繁重的工作. 因此, 对系统设计者来说, 寻找一种逻辑上精确验证系统正确性的方法是很有必要的, 例如各种形式化方法^[1−3]. 模型检测^{[4, 5]}作为一种完全自动化的形式化方法得到了深入的研究, 已成功应用于一些实时系统的正确性验证^[6−8]. 模型检测采用一种形式化语言来模拟各种软硬件系统, 例如Petri网^{[9, 10]}、反应式模块^[11]、解释系统编程语言(ISPL)^[12]等, 使用一种逻辑公式来描述这些系统的设计需求, 例如线性时态逻辑(LTL)^{[13, 14]}、计算树逻辑(CTL)^[15]、交替时态逻辑(ATL)^[16]等, 从而把验证一个系统是否满足它的设计需求的问题等价为验证相应的模型是否满足相应的逻辑公式的问题, 而验证模型是否满足逻辑公式则可以完全通过各种模型检测器自动化完成.

Petri网作为一种形式化语言, 广泛应用于建模和分析各种软硬件系统, 例如柔性制造系统^[17]、业务过程管理系统^[18]、并发程序形式化验证^[19]等. 时间Petri网^{[20, 21]}是一种包含时间因素的高级Petri网, 适用于实时系统的建模和分析^{[22, 23]}. 对于一个时间Petri网, 每个变迁伴随着一个静态发生区间, 它表示该变迁从获得发生权到发生所需要的最短等待时间和最长等待时间, 而变迁本身发生不需要时间. 计算树逻辑(CTL)^[15]作为模型检测技术最常用的逻辑公式之一, 用来描述系统常见的一些设计需求, 例如无死锁、安全性、活性和公平性等. 时间计算树逻辑(TCTL)^{[24, 25]}则是在CTL的基础之上添加了具体的时间约束, 通过量化CTL的时态算子来描述系统与时间相关的一些设计需求, 例如一个任务一旦启动就必须在某个限定的时间内执行完毕. 基于时间Petri网的TCTL模型检测已成功应用于一些实时系统的正确性验证^[26−28].

对于时间Petri网, 如果在一个状态下多个变迁均具有发生权, 且彼此之间不存在时间冲突(在一个状态下两个具有发生权的变迁存在时间冲突, 即一个变迁发生所需要的最短等待时间大于另一个变迁发生所需要的最长等待时间), 则按变迁发生规则, 可随机发生其中一个变迁. 然而这种情况并不适用于一些涉及优先级的实时系统, 因为这里不仅需要考虑任务之间的时间约束, 还要考虑任务执行的优先级. 对于一些更为紧要的任务, 系统通常会给它们更高的优先级, 使得它们在与低优先级的任务竞争资源时优先获得资源执行. 因此, Berthomieu^{[29, 30]}等人提出了优先级时间Petri网, 它是在时间Petri网的基础之上添加了变迁发生的优先级, 即一个变迁在一个状态下是可发生的当且仅当它满足以下3个条件: (1) 在当前状态的标识下, 该变迁具有发生权; (2) 在当前状态下, 该变迁的已等待时间在它的静态发生区间内; (3) 在当前状态下, 所有满足条件(1)和条件(2)变迁的优先级不会高于该变迁. 优先级时间Petri网显然增强了时间Petri网的建模能力, 使得时间Petri网在实时系统中得到了更广泛的应用, 例如一些涉及线程调度、仲裁和同步的实时系统, 均可以通过优先级时间Petri网来建模和分析.

Berthomieu等人提出的优先级时间Petri网虽然可以模拟一些涉及优先级的实时系统, 但是并不能满足所有涉及优先级的实时系统的建模需求, 我们可以通过一个简单的例子来说明这种优先级时间Petri网的局限性. 通常, 用优先级时间Petri网来模拟一个实时系统时, 一些变迁是代表任务的, 称为任务型变迁. 一个任务型变迁t_i代表一个任务Task_i, 伴随t_i的静态时间区间代表任务Task_i执行完毕所需要的最短和最长时间, 变迁t_i已等待的时间代表任务Task_i已执行的时间, 变迁t_i发生代表任务Task_i执行完毕. 在一个状态下, 结构上是并发关系的任务型变迁t₁和t₂同时获得发生权且彼此之间无时间冲突, 经过τ个时间后t₁发生, 则t₁发生后t₂的已等待时间为τ, 即任务Task₂已执行时间为τ. 这时, t₁发生后产生的新状态导致变迁t₃可发生, 它的优先级高于t₂且彼此之间无时间冲突, 则t₃会先于t₂发生, 假设t₂和t₃在结构上是冲突关系, 则t₃的发生会导致t₂失去发生权. 即使t₂后来重新获得发生权, 但它的已等待时间已从0开始计时. 这意味着任务Task₂在占有资源且已执行一段时间的情况下, 被另一个更高优先级的任务Task₃抢占资源而中断, 而后再次获得资源却不会从中断的地方恢复而是从头开始执行, 这显然不符合一些实时系统的抢占式调度机制. 例如多核多任务实时系统, 即高优先级的任务可抢占低优先级的任务所占用的资源导致后者被中断, 前者执行完毕后释放资源, 后者获得资源从中断的地方恢复, 继续执行剩余的一段时间而不是从头开始执行. 这意味着Berthomieu等人提出的优先级时间Petri网不能模拟支持抢占式调度机制的实时系统.

针对传统的优先级时间Petri网对实时系统建模能力的不足, 我们提出了另一种类型的优先级时间Petri网, 它不仅考虑了任务执行的优先级, 还考虑了任务之间的抢占式调度需求. 由于一些多核多任务实时系统的任务执行时间不是一个不确定的区间而是一个确定的值, 因此我们考虑时间Petri网这样的一类子网, 即伴随每个变迁的静态发生区间为点区间, 我们称为点区间时间Petri网. 因此, 本文定义的这种优先级时间Petri网被称为点区间优先级时间Petri网. 这意味着每个变迁从获得发生权到发生所需要的最短和最长等待时间是相同的, 这种变迁从获得发生权到发生的等待时间完全确定的时间Petri网, 减少了所生成的状态图中的状态数, 降低了TCTL模型检测算法的时间和空间复杂度, 提高了对实时系统的验证效率. 除了变迁的静态发生区间不同外, 我们定义的点区间优先级时间Petri网与Berthomieu等人提出的优先级时间Petri网从网的结构、状态的定义到变迁的发生规则等方面也是不同的, 本文将在第2节详细介绍它们的区别. 我们通过点区间优先级时间Petri网来模拟多核多任务实时系统, 使用TCTL来描述它们的设计需求, 设计了相应的TCTL模型检测算法, 并开发了相应的模型检测器, 实现了对多核多任务实时系统的正确性验证.

本文第1节介绍一些基本知识, 包括Petri网、时间Petri网以及相关概念. 第2节介绍我们提出的点区间优先级时间Petri网及它的状态图. 第3节介绍TCTL的语法和语义. 第4节介绍我们的模型检测算法和模型检测器. 第5节通过一个实例来说明模型和方法的有效性. 第6节回顾一些相关的工作. 第7节对全文进行总结并阐述下一步的工作.

1 预备知识

本节简单介绍Petri网、时间Petri网及其相关概念, 有关Petri网的详情见文献[31], 有关时间Petri网的详情见文献[20, 21]. 假设$\mathbb{N} $是自然数集, R是实数集, R⁺是非负实数集. 定义实数闭区间I={x∈R|a≤x≤b}, 记为I=[a, b]. 这里, a, b∈R且a≤b. 用IR和IR⁺分别表示所有实数闭区间和非负实数闭区间的集合. 若a=b, 则I=[a, a]称为点区间. 设I∈IR且I=[a, b], 定义↓I=a, ↑I=b.

1.1 Petri网

一个网定义为三元组N=(P, T, F), 其中, P为库所集, T为变迁集, P∩T=∅, F⊂(P×T)∪(T×P)为P与T之间的流关系. 从形式上看, 一个网就是一个没有孤立结点的有向二分图, 一般用小圆圈表示库所, 小矩形表示变迁. 给定一个节点x∈P∪T, 节点x的前集定义为^•x={y∈P∪T|F(y, x)=1}, 后集定义为x^•={y∈P∪T|F(x, y)=1}. 网的标识是一个映射函数M: P→$\mathbb{N} $, M(p)表示库所p里的token数. 一个标识通常表示为库所上的一个多重集, 例如在标识M下, p₁里有3个token, p₃里有1个token, 而其他库所均无token, 则M表示为{3p₁, p₃}或者3p₁+p₃.

一个带有初始标识M₀的网N被称作为一个Petri网, 记作Σ=(N, M₀). 如果对∀p∈P, 满足F(p, t)≤M(p), 则称变迁t在标识M下具有发生权. t的发生, 使系统进入一个新的标识M′, 记作M[t〉M′, 即: 对$ \forall p \in P: M^{\prime}(p)=M(\tilde{p}) F(p, t)+F(t, p)$. 标识M_k从M出发是可达的当且仅当M_k=M, 或者存在一个可发生序列σ=t₁t₂…t_n−1t_k, 使得M₀[t₁〉M₁[t₂〉…M_k−1[t_k〉M_k成立. 上式也可以表示为M₀[σ〉M_k. 从M出发的所有可达标识记作R(N, M), 则Petri网的所有可达标识即为R(N, M₀). 如果在一个标识下没有变迁具有发生权, 则称该标识为Petri网的一个死锁(deadlock). 如果对∀M∈R(N, M₀)和∀p∈P, 满足M(p)≤1, 则称此Petri网是安全的. 本文只考虑安全的Petri网. 为了保证安全性, 首先要求在初始标识M₀里的每一个库所最多含有1个token; 其次, Petri网的变迁发生规则稍作修改, 即, 如果M[t〉M′, 则M′满足对∀p∈P: M′(p)=min{M(p)−F(p, t)+F(t, p), 1}. 也就是说, 如果一个库所在一个标识下含有一个token, 此后变迁发生又有新token进入该库所, 但它仍然保持为一个token而不是两个token. 本文后面所提到的Petri网均为这种类型的Petri网, 因此下文所提到的每一个标识, 实际上表示为库所上的一个集合而不是多重集.

1.2 时间Petri网

一个时间Petri网可以定义为五元组(P, T, F, M₀, SI), 其中, (P, T, F, M₀)为一个Petri网, SI: T→IR⁺为一个映射函数. SI(t)表示变迁t的静态发生区间, ↓SI(t)为t获得发生权到发生所需要的最短等待时间, ↑SI(t)为t获得发生权到发生所需要的最长等待时间. En(M)表示在标识M下所有具有发生权的变迁, (M, h)表示时间Petri网的一个状态, 其中, h: En(M)→R⁺是一个时钟函数. h(t)表示在标识M下具有发生权的变迁t的已等待时间. 变迁t在状态(M, h)下是可发生的当且仅当它满足以下两个条件: (1) t∈En(M); (2) h(t)∈SI(t). 也就是说, 一个变迁在一个状态下是可发生的当且仅当该变迁在当前状态的标识下具有发生权, 且该变迁的已等待时间在它的静态发生区间内.

时间Petri网的初始状态为S₀=(M₀, h₀), 其中, M₀为初始标识, 对∀t∈En(M₀): h₀(t)=0. 假设S=(M, h)和S′=(M′, h′)为时间Petri网的两个状态, 则时间Petri网中存在着两种状态迁移规则.

1. $ S\xrightarrow{\tau }S' $当且仅当状态S′从状态S经过τ个时间后可达, 即:

(1) M=M′;

(2) ∀t∈En(M): h′(t)=h(t)+τ≤SI(t);

2. $ S\xrightarrow{\tau }S' $当且仅当状态S′从状态S经过变迁t发生后可达, 即:

(1) t∈En(M);

(2) h(t)∈SI(t);

(3) M[t〉M′;

(4) ∀t′∈En(M′): 如果t′∈En(M)且t′≠t, 则h′(t′)=h(t′); 否则, h′(t′)=0.

第1种状态迁移为时间流逝导致的, 即标识不变但每个具有发生权的变迁的已等待时间增加. 第2种状态迁移为变迁发生导致的, 即新标识产生, 如果在变迁发生前后, 一些变迁(非发生变迁)一直具有发生权, 则在变迁发生后, 这些变迁的已等待时间保持不变; 如果之前没有发生权的变迁在变迁发生后获得发生权或者发生变迁本身在变迁发生后再次具有发生权, 则在变迁发生后, 这些变迁的已等待时间为0.

如果一个时间Petri网(P, T, F, M₀, SI)满足对∀t∈T: ↓SI(t)=↑SI(t), 则称它为点区间时间Petri网. 对于点区间时间Petri网, 每个变迁的静态发生区间为点区间, 即, 每个变迁从获得发生权到发生所需要的等待时间是确定的.

2 点区间优先级时间Petri网 2.1 点区间优先级时间Petri网

定义1(点区间优先级时间Petri网). 一个点区间优先级时间Petri网(time-point-interval prioritized time Petri nets)可以定义为七元组Z=(P, T₁, T₂, F, M₀, SI, Pr), 其中, (P, T₁∪T₂, F, M₀, SI)为一个点区间时间Petri网, T₁为不可挂起变迁集, T₂为可挂起变迁集; Pr⊂(T₁∪T₂)×(T₁∪T₂)为变迁之间的优先级关系.

(t, t′)∈Pr表示变迁t发生的优先级高于变迁t′. Pr满足非自反性、非对称性和传递性. En(M)表示在标识M下所有具有发生权的变迁, Pend(M)表示在标识M下所有已挂起的可挂起变迁, (M, h, H)表示Z的一个状态, 其中, M是一个标识; h: En(M)→R⁺是一个时钟函数, h(t)表示在标识M下具有发生权的变迁t的已等待时间; H: Pend(M)→R⁺是一个时钟函数, H(t)表示在标识M下已挂起变迁t的中断时间. 变迁t在Z的一个状态(M, h, H)下是可发生的当且仅当它满足以下3个条件.

(1) t∈En(M);

(2) h(t)∈SI(t);

(3) 对∀t′∈T₁∪T₂: 如果t′∈En(M)且h(t′)∈SI(t′), 则(t′, t)∉Pr.

也就是说, 一个变迁在一个状态下是可发生的当且仅当该变迁在当前状态的标识下具有发生权, 且它的已等待时间在它的静态发生区间内, 同时不存在满足同样条件的其他变迁优先级高于该变迁.

点区间优先级时间Petri网Z的初始状态为S₀=(M₀, h₀, H₀), 其中, M₀为初始标识, 对∀t∈En(M₀): h₀(t)=0. 由于Pend(M₀)=∅, 故H₀=∅. 假设S=(M, h, H)和S′=(M′, h′, H′)为Z的两个状态, 则Z中存在着两种状态迁移规则.

1. $ S\xrightarrow{\tau }S' $当且仅当状态S′从状态S经过τ个时间后可达, 即:

(1) M=M′;

(2) ∀t∈En(M): h′(t)=h(t)+τ≤SI(t);

(3) ∀t∈Pend(M): H′(t)=H(t);

2. $ S\xrightarrow{\tau }S' $当且仅当状态S′从状态S经过变迁t发生后可达, 即:

(1) t∈En(M);

(2) h(t)∈SI(t);

(3) 对∀t′∈T₁∪T₂: 如果t′∈En(M)且h(t′)∈SI(t′), 则(t′, t)∉Pr;

(4) M[t〉M′;

(5) ∀t′∈En(M′): 如果t′∈En(M)且t′≠t, 则h′(t′)=h(t′); 否则, h′(t′)=0;

(6) ∀t′∈Pend(M): 如果t′∈En(M′), 则t′∉Pend(M′)且h′(t′)=H(t′); 否则, H′(t′)=H(t′);

(7) ∀t′∈En(M)∩T₂且t′≠t: 如果t′∉En(M′), 则t′∈Pend(M)且H′(t′)=h(t′).

第1种状态迁移为时间流逝导致的, 即标识不变, 每个已挂起变迁的中断时间不变, 但每个具有发生权的变迁的已等待时间增加. 第2种状态迁移为可发生变迁发生导致的, 即新标识产生, 如果在变迁发生前后, 一些变迁(非发生变迁)一直具有发生权, 则在变迁发生后, 这些变迁的已等待时间保持不变; 如果之前没有发生权的变迁在变迁发生后获得发生权或者发生变迁本身再次具有发生权, 则在变迁发生后, 这些变迁的已等待时间为0. 如果可挂起变迁在变迁发生后失去发生权(非发生变迁), 则它在变迁发生后被挂起且它的中断时间记为它在变迁发生前的已等待时间. 如果已挂起变迁在变迁发生后获得发起权, 则它在变迁发生后恢复为具有发生权的变迁, 且它的已等待时间恢复为它挂起时的中断时间; 否则, 已挂起变迁在变迁发生后, 保持它之前的中断时间不变.

注意, 我们定义的点区间优先级时间Petri网与Berthomieu等人定义的优先级时间Petri网是完全不同的, 主要区别在于以下4点.

(1) 在结构上, 我们把变迁集分为可挂起变迁集和不可挂起变迁集两种类型; 而Berth-omieu等人定义的变迁集没有分类;

(2) 在变迁的静态发生区间上, 我们定义的Petri网是基于点区间时间Petri网而扩展的; 而Berthomieu等人定义的Petri网是基于一般的时间Petri网而扩展的;

(3) 在状态的定义上, 我们定义的状态包含3个参数, 即标识、该标识下每个具有发生权的变迁的已等待时间以及该标识下每个已挂起变迁的中断时间; 而Berthomieu等人定义的状态只包含两个参数, 即标识和该标识下每个具有发生权的变迁的已等待时间;

(4) 在变迁发生规则上, 我们定义: 如果一个可挂起变迁由于别的变迁发生而失去发生权, 则它会被挂起, 它的中断时间会被保存; 反之, 如果一个已挂起变迁由于别的变迁发生而再次具有发生权, 则它会被恢复为具有发生权的变迁, 且它的已等待时间恢复为它挂起时的中断时间. 而Berthomieu等人的定义与时间Petri的定义一样, 即: 如果一个变迁由于别的变迁发生而失去发生权, 则它的已等待时间会被清空, 而该变迁以后再次具有发生权时, 它的已等待时间会从0开始计时.

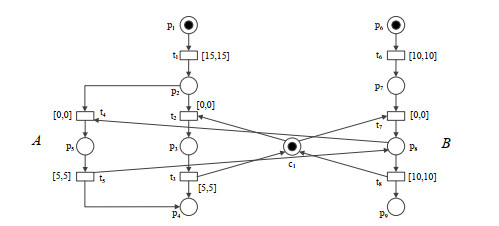
我们通过一个简单的例子来解释本文的相关概念. 图 1为一个点区间优先级时间Petri网, 其中, (t₂, t₇)∈ Pr, 可挂起变迁集T₂={t₈}, 其余变迁构成不可挂起变迁集T₁. 它描述了一个单核双任务实时系统. 该系统有两个任务A和B, 它们共用一个处理器c₁. 任务A在15ms后启动(t₁), 任务B在10ms后启动(t₆). 每个任务均需要先获得处理器c₁, 然后才能执行(t₂, t₇). 任务A需要5ms执行完毕(t₃), 任务B需要10ms执行完毕(t₈). 由于任务A的优先级高于任务B, 所以任务A可抢占任务B所占用的处理器c₁(t₄), 任务A执行完毕后释放处理器c₁(t₅), 之后, 任务B获得处理器c₁从中断的地方恢复, 继续执行剩余的一段时间(t₈). 因此, t₈是唯一的可挂起变迁, 即T₂={t₈}. (t₂, t₇)∈Pr意味着任务A, B同时竞争处理器c₁时, 任务A的高优先级使得任务A优先获得处理器c₁执行.

2.2 状态图

对于时间Petri网来说, 一个变迁从获得发生权到发生一般要经历两个阶段: 一是从获得发生权到可发生, 即它从获得发生权一直等待到它的已等待时间在它的静态发生区间内; 二是该变迁从可发生到发生. 因此, 时间Petri网的两种状态迁移规则完全可以合并到一起, 即$ S\xrightarrow{\tau }S'\xrightarrow{t}S'' $等价为$ S\xrightarrow{{(\tau , t)}}S'' $, 它表示状态S在等待τ个时间后发生变迁t到达状态S″. 我们称变迁t在状态S下是可调度的(schedulable). 对于时间Petri网的状态图, 每一步的状态迁移均为时间流逝+变迁发生导致的. 同理, 我们定义的点区间优先级时间Petri网的两种状态迁移规则也可以合并到一起. 基于此, 我们给出了点区间优先级时间Petri网的状态图的定义.

定义2(状态图). 点区间优先级时间Petri网Z的状态图可以定义为五元组Δ=(Ω, S₀, →, L, time), 其中, Ω是Z中所有的可达状态; S₀=(M₀, h₀, H₀)是Z的初始状态; →⊂Ω×Ω表示状态之间的迁移关系; L为迁移关系上的一个标签函数: (S, S′)→T₁∪T₂, L(S, S′)表示从状态S迁移到状态S′所发生的变迁; time为迁移关系上的一个时钟函数: (S, S′)→R⁺, time(S, S′)表示从状态S迁移到状态S′所等待的时间. 即: 如果∃τ∈R⁺和∃t∈T₁∪T₂使得$ S\xrightarrow{{(\tau , t)}}S' $, 则称S→S′, L(S, S′)=t, time(S, S′)=τ.

注意, 状态图中并非包含了所有的可达状态. 在状态图中, 除了初始状态S₀, 其他所有的状态均是变迁发生后产生的新状态. 对于时间流逝导致的状态迁移, 它所产生的新状态并不会出现在状态图中. 例如在图 1中时间流逝导致的一个状态迁移(p₁+p₆+c₁, h(t₁)=h(t₆)=0)$ \xrightarrow{5} $(p₁+p₆+c₁, h(t₁)=h(t₆)=5), 它所产生的新状态(p₁+p₆+c₁, h(t₁)=h(t₆)=5)并不会出现在状态图中. 然而对于状态图中未出现的状态, 我们可以很容易地由状态图中的已知状态通过时间流逝得到.

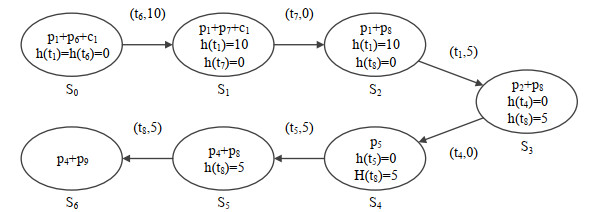
对于点区间优先级时间Petri网, 由于它是安全Petri网且每个变迁发生前的等待时间是确定的, 因此它的状态图中的状态数必然是有限的. 图 2为图 1点区间优先级时间Petri网的状态图, 图中共有7个状态, 除了初始状态S₀外, 其他状态均是变迁发生后产生的新状态.

● 首先, 在状态S₀下, 只有变迁t₁和t₆具有发生权且它们的已等待时间为0. t₁发生所需要的时间为15而t₆发生所需要的时间为10, 因此只有t₆可调度. 在等待10个时间单元后, t₆发生到达状态S₁;

● 在状态S₁下, t₁仍然具有发生权, 因此它的已等待时间为10. t₇刚获得发生权, 因此它的已等待时间为0. t₁发生所需要的时间为5而t₇发生所需要的时间为0, 因此t₇发生到达状态S₂;

● 在状态S₂下, t₁仍然具有发生权, 因此它的已等待时间为10. t₈刚获得发生权, 因此它的已等待时间为0. t₁发生所需要的时间为5而t₈发生所需要的时间为10, 因此只有t₁可调度. 在等待5个时间单元后, t₁发生到达状态S₃;

● 在状态S₃下, t₈仍然具有发生权, 因此它的已等待时间为5. t₄刚获得发生权, 因此它的已等待时间为0. 由于t₈发生所需要的时间为5而t₄发生所需要的时间为0, 因此t₄发生到达状态S₄;

● 在状态S₄下, t₅刚获得发生权, 因此它的已等待时间为0. 由于可挂起变迁t₈失去发生权, 因此t₈被挂起, 且挂起时的中断时间为挂起前的已等待时间, 即H(t₈)=5. t₅发生所需要的时间为5, 因此在等待5个时间后, t₅发生到达状态S₅;

● 在状态S₅下, 已挂起变迁t₈重新获得发生权, 因此由已挂起变迁恢复为具有发生权的变迁, 且它的已等待时间恢复为挂起时的中断时间, 即h(t₈)=5. t₈发生所需要的时间为5, 因此在等待5个时间单元后, t₈发生到达终点状态S₆.

注意: 虽然图 1的点区间优先级时间Petri网定义了优先级关系(t₂, t₇), 但由于任务A和B的启动时间不一致和任务的非周期性执行等原因, 在生成状态图的过程中并没有出现t₂和t₇同时可发生的情况. 然而对于后面要提到的多核多任务实时系统, 模拟它的点区间优先级时间Petri网中的优先级关系, 就会起到两个变迁同时可发生时, 让高优先级的变迁先发生的作用.

3 TCTL

本文使用时间计算树逻辑(TCTL)^{[24, 25]}来描述实时系统的设计需求. 首先, TCTL的语法基于点区间优先级时间Petri网来定义; 然后, TCTL的语义通过它的状态图来解释.

定义3(TCTL的语法). 基于一个点区间优先级时间Petri网Z=(P, T₁, T₂, F, M₀, SI, Pr), TCTL定义如下:

$ \phi::=\mathbf{true}|p| \neg \phi\left|\phi_{1} \wedge \phi_{2}\right| E X \phi|A X \phi| E G \phi|A G \phi| E\left(\phi_{1} U_{\bowtie} \phi_{2}\right) \mid A\left(\phi_{1} U_{\bowtie c} \phi_{2}\right), $

其中, p∈P, ⋈∊{ <, ≤, >, ≥}, c∈R⁺.

TCTL中的其他算子可以由以上的算子推导出: deadlock=¬EXtrue, ϕ₁∨ϕ₂=¬(¬ϕ₁∧¬ϕ₂), ϕ₁→ϕ₂=¬ϕ₁∨ϕ₂, EF_⋈cϕ=E(true U_⋈cϕ), AF_⋈cϕ=A(true U_⋈cϕ).

给定一个状态图Δ和它的一个状态S, 我们定义在Δ中从S出发的一个计算(computation)是一个最大状态序列, 即ω=(S⁰, S¹, …), 其中, S⁰=S. 一个计算可能是无限的也可能是有限的(遇到死锁): 对于一个有限的计算ω=(S⁰, S¹, …, Sⁿ, …), 假设Sⁿ是一个死锁, 则对∀i∈{0, 1, …, n}: (Sⁱ, Sⁱ⁺¹)∈→且ω(i)=Sⁱ, 当i > n, 则ω(i)=∅; 对于一个无限的计算ω=(S⁰, S¹, …), 对∀i∈∞: (Sⁱ, Sⁱ⁺¹)∈→且ω(i)=Sⁱ.℧(S)表示在Δ中所有从S出发的计算.

定义4(TCTL的语义). 给定一个点区间优先级时间Petri网的状态图Δ=(Ω, S₀, →, L, time), 一个状态S∈Ω和一个TCTL公式ϕ, (Δ, S)$ \models$ϕ意味着公式ϕ在状态图Δ的状态S下为真. 换句话说, 状态图Δ中的状态S满足公式ϕ. 如果没有歧义的话, Δ可省略, 满足关系$ \models$归纳定义如下.

● S$ \models$true;

● S$ \models$p当且仅当S的标识M满足M(p)=1;

● S$ \models$¬ϕ当且仅当S $ \models$ ϕ不成立;

● S$ \models$ϕ₁∧ϕ₂当且仅当S$ \models$ϕ₁且S$ \models$ϕ₂;

● S$ \models$EXϕ当且仅当∃S′∈Ω, 满足S→S′且S′$ \models$ϕ;

● S$ \models$AXϕ当且仅当对∀S′∈Ω: 如果S→S′, 则S′$ \models$ϕ;

● S$ \models$EGϕ当且仅当∃ω∈℧(S): 对∀i∈$\mathbb{N} $: ω(i)$ \models$ϕ;

● S$ \models$AGϕ当且仅当对∀ω∈℧(S): 对∀i∈$\mathbb{N} $: ω(i)$ \models$ϕ;

● S$ \models$E(ϕ₁U_⋈cϕ₂)当且仅当∃ω∈℧(S)满足这样的条件: (1) ∃i∈$\mathbb{N} $, 满足ω(i)$ \models$ϕ₂; (2) 对∀j∊{0, 1, …, i−1}, 满足ω(j)$ \models$ϕ₁; (3) time(ω(0), ω(1))+time(ω(1), ω(2))+…+time(ω(i−1), ω(i))⋈c;

● S$ \models$A(ϕ₁U_⋈cϕ₂)当且仅当∀ω∈℧(S)满足这样的条件: (1) ∃i∈$\mathbb{N} $, 满足ω(i)$ \models$ϕ₂; (2) 对∀j∈{0, 1, …, i−1}, 满足ω(j)$ \models$ϕ₁; (3) time(ω(0), ω(1))+time(ω(1), ω(2))+…+time(ω(i−1), ω(i))⋈c.

定义5(有效性). 一个TCTL公式ϕ在点区间优先级时间Petri网Z上是有效的(记作Z$ \models$ϕ)当且仅当Z的状态图Δ满足(Δ, S₀)$ \models$ϕ, 即状态图Δ中的初始状态S₀满足ϕ.

TCTL是在CTL的基础之上添加了具体的时间约束, 通过量化CTL的时态算子来描述实时系统与时间相关的一些设计需求. 例如: 对于图 1中的实时系统, 我们可要求任务B在执行过程中不会被中断, 即任务B一旦启动就必须在10ms内执行完毕, 这样的设计需求可通过TCTL公式ϕ₁=AG(p₇→AF_≤10p₉)来描述, 其中, p₇意味着任务B启动, p₉意味着任务B执行完毕. 后面我们开发的模型检测器可验证ϕ₁在图 1上是无效的.

4 算法和工具

给定一个点区间优先级时间Petri网Z和一个TCTL公式ϕ, 验证Z$ \models$ϕ是否成立主要包含以下3个步骤.

(1) 由点区间优先级时间Petri网Z生成它的状态图Δ;

(2) 在状态图Δ上递归寻找所有满足ϕ的状态(记作Sat(ϕ));

(3) Z$ \models$ϕ当且仅当S₀∊Sat(ϕ).

由点区间优先级时间Petri网生成其状态图的伪代码见算法1.

算法1.

Input: A time-point-interval prioritized time Petri nets Z=(P, T₁, T₂, F, M₀, SI, Pr);

Output: The state graph Δ of Z.

Ω: =From: =S₀: =(M₀, h₀, H₀);

repeat

 To: =∅;

 for each S∈From

  for each t∈T₁∪T₂

   if t is schedulable at S then

    ∃τ∈R⁺ such that $ S\xrightarrow{{(\tau , t)}}S' $; To: =To+S′; Add (S, S′) to →; L(S, S′): =t; time(S, S′): =τ;

   endif

  endfor

 endfor

 New: =To−Ω; From: =New; Ω : =Ω+New;

until New=∅;

return (Ω, S₀, →, L, time).

基于生成的状态图Δ可计算Sat(ϕ). 根据TCTL的语义, 计算Sat(ϕ)的伪代码见算法2.

算法2.

Input: A state graph Δ=(Ω, S₀, →, L, time) and a TCTL formula ϕ;

Output: {S∈Ω|S$ \models$ϕ}.

if ϕ is true then return Ω; endif

if ϕ is p then return {S∈Ω|M(p)=1}; endif

if ϕ is ¬ϕ then return ΩSat(ϕ); endif

if ϕ is ϕ₁∧ϕ₂ then return Sat(ϕ₁)∩Sat(ϕ₂); endif

if ϕ is EXϕ then return Sat_EX(ϕ); endif

if ϕ is AXϕ then return Sat_AX(ϕ); endif

if ϕ is EGϕ then return Sat_EG(ϕ); endif

if ϕ is AGϕ then return Sat_AG(ϕ); endif

if ϕ is E(ϕ₁U_⋈cϕ₂) then return Sat_EU(ϕ₁, ϕ₂, ⋈, c); endif

if ϕ is A(ϕ₁U_⋈cϕ₂) then return Sat_AU(ϕ₁, ϕ₂, ⋈, c); endif

由于在TCTL的定义中, 除了最后两个算子外其他均是常见的CTL算子, 因此本文只给出关于算子

E(ϕ₁U_⋈cϕ₂)和A(ϕ₁U_⋈cϕ₂)的计算Sat(ϕ)的算法, 即Sat_EU(ϕ₁, ϕ₂, ⋈, c)和Sat_AU(ϕ₁, ϕ₂, ⋈, c). 关于其他算子的计算Sat(ϕ)的算法可参考文献[4, 15]. 计算Sat_EU(ϕ₁, ϕ₂, ⋈, c)的伪代码见算法3.

算法3.

X: =∅; Y: =Sat(ϕ₂); Z: =Sat(ϕ₁);

for each S∈Ω min(S): =max(S): =−1; endfor

for each S∈Y min(S): =max(S): =0; endfor

if Y=∅ then return ∅; end if

repeat

 X: =Y;

 for each S∈Z

  flag1: =0; flag2: =0;

  for each S′∈Y

   if (S, S′)∈→ then

    if min(S)=−1 then

     min(S): =min(S′)+time(S, S′); max(S): =max(S′)+time(S, S′); flag2: =1;

    else if min(S)!=0

     if min(S) > min(S′)+time(S, S′) then

      min(S): =min(S′)+time(S, S′); flag2: =1;

     endif

     if max(S) < max(S′)+time(S, S′) then

      max(S): =max(S′)+time(S, S′); flag2: =1;

     endif

    endif

    if flag1=0 then Y: =Y+S; flag1: =1; endif

   endif

  endfor

 endfor

until X=Y & & flag2=0;

Z=∅;

if ⋈=$ \models$ < ’||⋈=$ \models$≤’ then

 for each S∈X

  if min(S)⋈c then Z: =Z+S; endif

 endfor

endif

if ⋈=' > ’||⋈='≥’ then

 for each S∈X

  if max(S)⋈c then Z: =Z+S; endif

 endfor

endif

return Z.

在计算Sat_EU(ϕ₁, ϕ₂, ⋈, c)的过程中, 首先寻找所有满足E(ϕ₁Uϕ₂)的状态, 同时对找到的每一个这样的状态

设置两个时间函数, 即min和max, 它们根据每次添加的新的满足E(ϕ₁Uϕ₂)的状态动态调整其数值. 若用x表示存在一个从状态S出发的计算满足ϕ₁U_=xϕ₂, 则min(S)和max(S)分别表示x的最小值和最大值. 在找到所有

满足E(ϕ₁Uϕ₂)的状态后, 且它们的min值和max值均不再改变, 基于min和max可从中筛选出满足E(ϕ₁U_⋈cϕ₂)的状态. 这里分为两种情况: 一是当⋈为 < 或≤时, 只需保证S的min值< 或≤c, 即可保证存在一个从S出发的计算满足ϕ₁U_⋈cϕ₂; 二是当⋈为 > 或≥时, 只需保证S的max值> 或≥c, 即可保证存在一个从S出发的计算满足ϕ₁U_⋈cϕ₂.

计算Sat_AU(ϕ₁, ϕ₂, ⋈, c)的伪代码见算法4.

算法4.

X=∅; Y=Sat(ϕ₂); Z=Sat(ϕ₁);

for each S∈Ω min(S): =max(S): =−1; endfor

for each S∈Y min(S): =max(S): =0; endfor

while X≠Y

 X: =Y;

  for each S∈Z

   flag: =0;

   for each S′∈Ω such that (S, S′)∈→

    if S′∉Y then flag: =1; break; endif

   endfor

  if flag=0

   Y: =Y+S;

   for each S′∈Ω such that (S, S′)∈→

    if min(S)=−1 then min(S): =min(S′)+time(S, S′); max(S): =max(S′)+time(S, S′);

    else

     if min(S) > min(S′)+time(S, S′) then min(S): =min(S′)+time(S, S′); endif

     if max(S) < max(S′)+time(S, S′) then max(S): =max(S′)+time(S, S′); endif

    endif

   endfor

  endif

 endfor

endwhile

Z: =∅;

if ⋈=‘ < ’||⋈=‘≤’ then

 for each S∈X

  if max(S)⋈c then Z: =Z+S; endif

 endfor

endif

if ⋈=$ \models$ > ’||⋈=$ \models$≥’ then

 for each S∈X

  if min(S)⋈c then Z: =Z+S; endif

 endfor

endif

return Z.

在计算Sat_AU(ϕ₁, ϕ₂, ⋈, c)的过程中, 首先寻找所有满足A(ϕ₁Uϕ₂)的状态, 同时对找到的每一个这样的状态同样设置min和max时间函数. 与计算Sat_EU(ϕ₁, ϕ₂, ⋈, c)的不同之处在于, 所有满足A(ϕ₁Uϕ₂)的状态的min值和max值被设置后就不再调整了. 在找到所有满足A(ϕ₁Uϕ₂)的状态后, 基于min和max可从中筛选出满足A(ϕ₁U_⋈cϕ₂)的状态. 这里分为两种情况: 一是当⋈为 < 或≤时, 只需保证S的max值< 或≤c, 即可保证从S出发的所有计算满足ϕ₁U_⋈cϕ₂; 二是当⋈为 > 或≥时, 只需保证S的min值> 或≥c, 即可保证从S出发的所有计算满足ϕ₁U_⋈cϕ₂.

基于Sat(ϕ), 我们可验证ϕ的有效性. 如果S₀∈Sat(ϕ), 则ϕ在Z上有效; 否则, ϕ在Z上无效.

我们的模型检测算法的复杂度分为两个部分.

● 首先是由点区间优先级时间Petri网生成它的状态图. 由于本文所涉及的Petri网均是安全的, 因此状态图中的最大标识数不会超过2^|P|. 对∀t₁∈T₁∪T₂和∀t₂∈T₂, 我们假设h(t₁)=−1表示t₁在一个标识下不具有发生权, H(t₂)=−1表示t₂在一个标识下未挂起, SI_max表示变迁的所有静态发生点区间中的最大值, 即max{SI(t)|t∈T₁∪T₂}. 在一个状态下, 一个变迁具有发生权就不会是已挂起变迁, 是已挂起变迁就不会具有发生权. 本文只考虑每个变迁的静态发生点区间为整数的点区间优先级时间Petri网, 因此状态图的最大状态数不会超过2^|P|⋅(SI_max+2)⋅(|T₁∪T₂|+|T₂|), 最大状态迁移关系不会超过2^|P|+1⋅(SI_max+ 2)⋅(|T₁∪T₂|+|T₂|). 因此, 由点区间优先级时间Petri网生成状态图的算法复杂度为O(2^|P|⋅SI_max⋅|T₁∪T₂|).

● 然后, 基于生成的状态图验证TCTL公式ϕ的有效性. 该过程主要在于计算Sat(ϕ). 对于一个包含n个状态和k个状态迁移关系的状态图, 计算Sat(ϕ)算法的复杂度为O((n+k)⋅|ϕ|), 其中, |ϕ|为ϕ中库所和算子的总数量. 因此综合来说, 我们的模型检测算法的复杂度为O(2^|P|⋅SI_max⋅|T₁∪T₂|⋅|ϕ|).

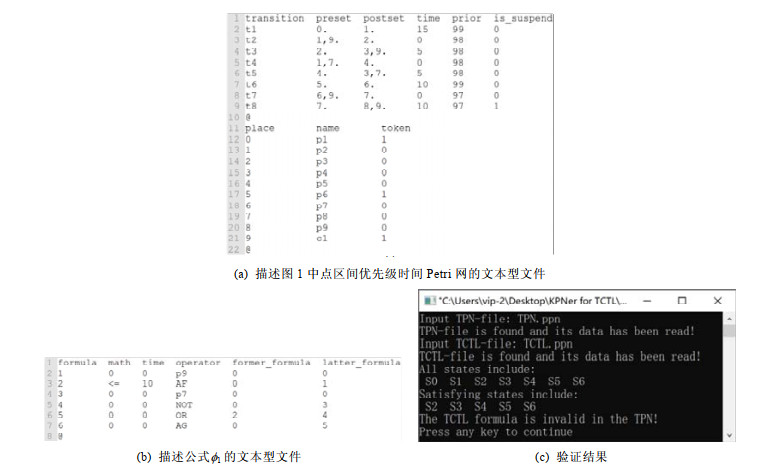
基于以上算法, 我们开发了一个用C++语言编写的TCTL模型检测器. 它在输入一个描述点区间优先级时间Petri网的文本型文件和一个描述TCTL公式的文本型文件后, 会自动输出验证结果. 图 3(a)展示了描述图 1中的点区间优先级时间Petri网的文本型文件, 图 3(b)展示了描述TCTL公式ϕ₁=AG(p₇→AF_≤10p₉)的文本型文件(图中实际上描述的是它的等价形式AG(¬p₇∨AF_≤10p₉)), 图 3(c)为验证结果. 结果显示, ϕ₁无效. 这意味着任务B在执行过程中被中断. 事实上, 任务B从启动到执行完毕需要15ms: 首先, 任务B启动后获得处理器c₁开始执行, 但在执行5ms时被更高优先级的任务A抢占处理器c₁而被迫中断; 接着, 任务A在5ms后执行完毕, 释放处理器c₁; 最后, 任务B获得处理器c₁从中断的地方恢复, 继续执行剩余的5ms后结束. 如果我们把ϕ₁改成AG(p₇→AF_≤15p₉), 则结果显示ϕ₁有效.

5 应用

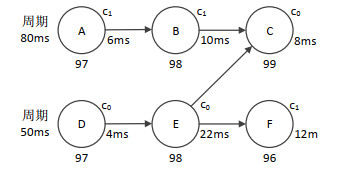
本节通过一个多核多任务实时系统的案例, 来说明本文的模型和方法的有效性. 有这样一个多核多任务实时系统, 它有6个任务(即A, B, C, D, E和F)和两个处理器(即c₀和c₁), 其中, 任务A, B和F共用处理器c₁, 任务C, D和E共用处理器c₀. 任务之间存在依赖关系, 即一个任务的执行结束作为下一个任务的启动. 整个系统的任务依赖图如图 4所示. 任务A和D作为起始任务被周期性驱动, 任务A每过80 ms被驱动一次, 任务D每过50 ms被驱动一次. 任务A获得处理器c₁后执行6 ms, 任务D获得处理器c₀后执行4 ms. 任务A执行完毕驱动任务B, 任务D执行完毕驱动任务E. 任务B获得处理器c₁后执行10 ms, 任务E获得处理器c₀后执行22 ms. 任务B和E执行完毕驱动任务C, 同时, 任务E执行完毕驱动任务F. 任务C获得处理器c₀后执行8 ms, 任务F获得处理器c₁后执行12 ms. 在图 4中, 各个任务之间除了依赖关系, 还存在执行的优先级关系, 这里用优先级值表示. 一个任务的优先级值越大, 代表它的优先级越高. 例如: 任务A, B和F的优先级值分别为97, 98, 96, 因此任务A, B和F获得处理器c₁执行的优先级为B > A > F; 任务C, D和E的优先级值分别为99, 97, 98, 因此任务C, D和E获得处理器c₀执行的优先级为C > E > D. 同时, 引入优先级带来了抢占式调度的需求.例如: 任务A, B和F的优先级为B > A > F, 因此任务A可抢占任务F所占用的处理器, 任务B可抢占任务A和F所占用的处理器; 任务C, D和E的优先级为C > E > D, 因此任务E可抢占任务D所占用的处理器, 任务C可抢占任务D和E所占用的处理器. 注意一般的抢占式调度机制要求: 首先, 高优先级任务可剥夺低优先级任务的资源, 导致后者被中断; 然后, 前者执行完毕后释放资源; 最后, 后者再次获得资源从中断的地方恢复, 继续执行剩余的一段时间.

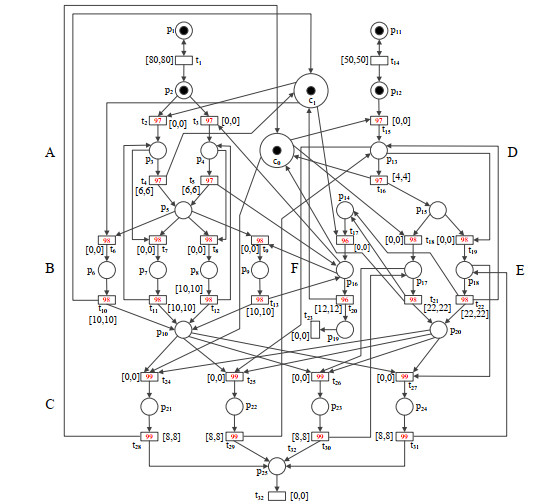
这样的一个多核多任务实时系统可通过我们定义的点区间优先级时间Petri网来模拟, 如图 5所示. 由于这里所涉及的优先级关系众多, 因此我们同样给每一个变迁设置一个优先级值, 值越大, 意味着优先级越高.例如, t₂的优先级值为97, t₆的优先级值为98, 这意味着存在一个优先级关系(t₆, t₂)∈Pr. 此外, 我们定义可挂起变迁集T₂={t₄, t₅, t₁₆, t₂₀, t₂₁, t₂₂}, 其余变迁构成不可挂起变迁集T₁.

在图 5中, 任务A和D通过变迁t₁和t₁₄周期性驱动, 任务A通过变迁t₂和t₄表示获得处理器c₁然后执行6 ms, 任务D通过变迁t₁₅和t₁₆表示获得处理器c₀然后执行4 ms, 任务A执行完毕通过库所p₅驱动任务B, 任务D执行完毕通过库所p₁₅驱动任务E, 任务B通过变迁t₆和t₁₀表示获得处理器c₁然后执行10 ms, 任务E通过变迁t₁₈和t₂₁表示获得处理器c₀然后执行22 ms, 任务B和E执行完毕通过库所p₁₀和p₂₀驱动任务C, 同时, 任务E执行完毕通过库所p₁₄驱动任务F, 任务C通过变迁t₂₄和t₂₈表示获得处理器c₁然后执行8 ms, 任务F通过变迁t₁₇和t₂₀表示获得处理器c₀然后执行12 ms.

对于共用处理器c₁的任务A, B和F, 它们的优先级关系为B > A > F.

● 任务A抢占任务F的过程通过变迁t₃和t₅表示;

● 任务B抢占任务F的过程通过变迁t₉和t₁₃表示;

● 任务B抢占任务A的过程分为两种情况: 一是抢占通过与任务F竞争获得处理器c₁执行的任务A, 这种情况通过变迁t₇和t₁₁表示; 二是抢占通过抢占任务F获得处理器c₁执行的任务A, 这种情况通过变迁t₈和t₁₂表示.

对于共用处理器c₀的任务C, D和E, 它们的优先级关系为C > E > D.

● 任务E抢占任务D的过程通过变迁t₁₉和t₂₂表示;

● 任务C抢占任务D的过程通过变迁t₂₅和t₂₉表示;

● 任务C抢占任务E的过程同样分为两种情况: 一是抢占通过与任务D竞争获得处理器c₀执行的任务E, 这种情况通过变迁t₂₆和t₃₀表示; 二是抢占通过抢占任务D获得处理器c₀执行的任务E, 这种情况通过变迁t₂₇和t₃₁表示.

代表任务C和F执行结束的库所(p₁₉和p₂₅)获得token后会被清空(t₂₃和t₃₂), 这意味着整个系统的所有任务执行完一次后不会结束而是周期性执行.

对于这样一个多核多任务实时系统, 我们可验证它与时间相关的一些设计需求, 例如要求任务D到任务C的延迟不得超过84 ms. 我们可以使用TCTL公式ϕ₂=AG(p₁₂→AF_≤84p₂₅)来表示, 其中, p₁₂意味着任务D启动, p₂₅意味着任务C执行完毕. ϕ₂有效意味着从任务D启动到任务C执行完毕的最长延迟时间不会超过84 ms. 首先, 我们用两个文本型文件分别描述图 5中的点区间优先级时间Petri网和公式ϕ₂; 然后, 把这两个文件输入到我们的模型检测器; 最后, 我们的模型检测器自动输出验证结果(生成的状态图包含138个状态, 由于空间限制, 这里不再展示). 结果显示ϕ₂无效. 实际上, 当我们把公式ϕ₂中的84改为任意大于等于94的整数时, ϕ₂就变得有效了. 然而, 把公式ϕ₂中的84改为任意小于94的整数时, ϕ₂仍然无效. 由于图 5中变迁的所有静态发生点区间值均为整型变量, 因此我们可以断定: 在系统周期性执行的过程中, 任务D到C的最长延迟即为94 ms.

6 相关工作

除了本文提出的时间Petri网外, 据我们所知, 目前还有4种时间Petri网可模拟实时系统的抢占式调度机制, 即调度扩展时间Petri网(scheduling extended time Petri nets)^{[32, 33]}、抢占式时间Petri网(preemptive time Petri nets)^{[34, 35]}、带有抑制超弧的时间Petri网(time Petri nets with inhibitor hyperarcs)^[36]和带有计时器的时间Petri网(time Petri nets with stopwatches)^[37]. 调度扩展时间Petri网是在时间Petri网的库所上添加了资源和优先级, 由此从标识中区分出活跃的标识, 即一个标识对应一个活跃(active)标识. 一个变迁在一个标识下具有发生权但在其活跃标识下不具有发生权, 则意味着该变迁被挂起, 一个已挂起的变迁在一个活跃标识下具有发生权, 则意味着该变迁从挂起状态恢复到它挂起前的状态. 抢占式时间Petri网与之类似, 它在时间Petri网的变迁上添加了资源和优先级, 在一个标识下一个变迁具有发生权但同时和它共享某个资源且优先级更高的变迁也具有发生权, 则意味着该变迁被挂起, 一个已挂起的变迁在一个标识下不存在和它共享某个资源且优先级更高的变迁具有发生权, 则意味着该变迁从挂起状态恢复到它挂起前的状态. 带有抑制超弧的时间Petri网是在时间Petri网上添加了抑制超弧, 这些抑制超弧蕴含着资源的分配以及任务的优先级, 一个变迁在一个标识下具有发生权但同时存在一个抑制超弧抑制它的发生, 则意味着该变迁被挂起, 一个已挂起的变迁在一个标识下不存在一个抑制超弧抑制它的发生, 则意味着该变迁从挂起状态恢复到它挂起前的状态. 带有计时器的时间Petri网是在时间Petri网上添加了计时器弧, 这些计时器弧蕴含着资源的分配以及任务的优先级, 一个变迁在一个标识下具有发生权但同时存在着一个和它相关的计时器弧的前集库所为空, 则意味着该变迁被挂起, 一个已挂起的变迁在一个标识下所有和它相关的计时器弧的前集库所非空, 则意味着该变迁从挂起状态恢复到它挂起前的状态.

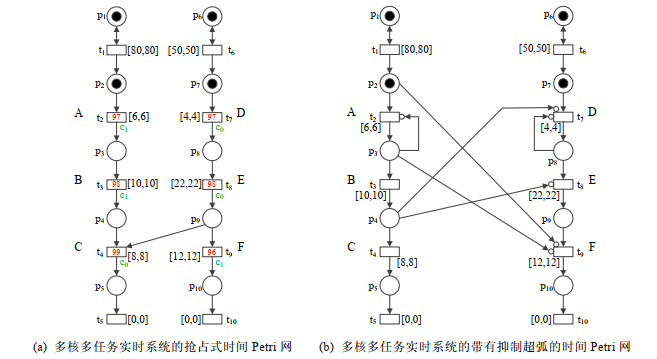
由于调度扩展时间Petri网和抢占式时间Petri网之间的相似性以及带有抑制超弧的时间Petri网和带有计时器的时间Petri网之间的相似性, 本文只选取抢占式时间Petri网和带有抑制超弧的时间Petri网来与本文定义的点区间优先级时间Petri网做对比. 如图 6所示: 对于图 4中的多核多任务实时系统, 图 6(a)用抢占式时间Petri网来模拟它, 图 6(b)用带有抑制超弧的时间Petri网来模拟它. 显然, 抢占式时间Petri网和带有抑制超弧的时间Petri网均无法显式地刻画资源的占用和释放过程, 因此它们自然不能作为模型来验证一些与资源相关的时间限制需求, 例如一个资源一旦被占用就必须在一个限定的时间内得到释放. 此外, 对于抢占式时间Petri网, 由于它在变迁上引入了资源和优先级两个参数, 导致变迁可发生的判定过程要比之前复杂, 从而影响了状态图的生成效率. 对于带有抑制超弧的时间Petri网, 它隐藏了资源分配和任务的优先级等信息, 这些参数需要建模者综合考虑, 然后在建模的时候通过抑制超弧隐式地反映出来. 例如在图 4中, 任务A和B共用处理器c₁且任务B的优先级高于任务A, 则在图 6(b)中, p₃与t₂之间需要一个抑制超弧以实现t₃具有发生权时立即挂起t₂的目的. 由于t₂代表任务A, t₃代表任务B, 这意味着任务A和B共享着某个资源且任务B的优先级高于任务A. 显然, 这样给建模者带来了很大的不便, 即使仅仅修改一个任务的优先级值, 就有可能需要重新定义抑制超弧.

对于我们定义的点区间优先级时间Petri网, 首先, 它可以显式地刻画资源的占用和释放过程, 因此完全可以用来验证一些与资源相关的时间限制需求; 其次, 它在变迁上引入了优先级这一个参数, 使得变迁可发生的判定过程不会太复杂; 最后, 它通过直接给出优先级关系或优先级值来显式地反应变迁发生的优先级, 使得建模的工作量不至于过大. 注意: 我们定义的点区间优先级时间Petri网与以上4种时间Petri网相比有一个很明显的缺点, 即建模时出现的变迁数爆炸问题, 这也是图 5中的网结构没有图 6中的两个网结构简洁的主要原因. 例如在图 4中, 对于共用处理器c₁的任务A, B和F, 优先关系为B > A > F, 因此在图 5中表示任务F需要1个变迁, 表示任务A需要2个变迁, 表示任务B需要4个变迁. 以此类推, 对于共享资源的、具有不同优先级的多个任务, 表示它们需要的变迁数呈指数级增长. 对于以上4种时间Petri网来说, 任务和变迁通常是一一对应的. 这是由于抢占式调度机制会导致中断嵌套, 而点区间优先级时间Petri网精确模拟了这些中断嵌套过程, 因此才会有这样的结果.

7 结论

本文基于传统的优先级时间Petri网对多核多任务实时系统建模能力的不足, 提出了点区间优先级时间Petri网来模拟多核多任务实时系统. 结合TCTL模型检测, 设计了相应的算法并开发了相应的工具, 实现了对多核多任务实时系统的正确性验证. 我们下一步的工作主要从以下4个方面展开: (1) 优化我们定义的点区间优先级时间Petri网, 避免它建模时出现的变迁数爆炸问题; (2) 实现由多核多任务实时系统的任务依赖图自动生成它的点区间优先级时间Petri网; (3) 参考基于Petri网对CTL公式的简化方法^[38], 思考基于点区间优先级时间Petri网对TCTL公式的简化方法; (4) 基于已知的结构化方法如虹吸和陷阱, 以及符号化方法如OBDD, 来缓解点区间优先级时间Petri网的状态爆炸问题.

致谢 本文中的应用实例参考了华为公司的孔辉老师所提供的一个多核多任务实时系统的真实案例, 但考虑其系统安全问题, 本文进行了修改, 并省略了相应任务的具体描述. 在此对孔辉老师表示感谢.