2. 综合业务网理论及关键技术国家重点实验室(西安电子科技大学), 陕西 西安 710071
2. State Key Laboratory of Integrated Service Networks (Xidian University), Xi'an 710071, China
程序合成(program synthesis)的概念最早由美国数学家、逻辑学家Alonzo Church于1957年提出[1], 一直以来都是计算机科学领域的难解问题. 简单地说, 程序合成是一种针对用户意图构造出相关程序的软件开发活动, 而用户意图可以采用形式化或半形式化规约, 甚至是自然语言来描述. 如果意图表达为线性时序逻辑(linear temporal logic, LTL)公式, 则称此类问题为LTL合成(LTL synthesis), 通常看作程序合成的一种子类. 一般来说, 可以将LTL合成定义为二人博弈(two-player game)问题, 博弈的双方是环境(environment)和控制器(controller). 控制器的行为被智能体(agent)操控, 根据环境变化做出反应, 但智能体无法干涉环境的行为. LTL合成的解(称为合成策略)是使得控制器能够获胜的策略, 目的是令环境和控制器的所有交互行为序列满足给定的LTL公式. 1989年, Pnueli和Rosner证明了LTL合成的计算复杂度为2EXPTIME-complete[2]. 由于复杂度较高, 学者们通过研究LTL子集的合成来获得较低的复杂度, 进而提高合成效率. 其中, 针对一类子集GR(1) (generalized reactivity(1)), 学者们提出了复杂度为多项式级别(
近期涌现出许多工作, 通过借鉴高效的符号化技术求解LTL合成问题. 文献[8]致力于研究安全LTL(不含until操作符的LTL公式)合成, 并提出一种构建符号化安全自动机(deterministic safety automata)的方法, 从而利用基于传统的BDD (binary decision diagram)技术直接求解. Bohy等人提出了一种基于反链符号化增量算法求解安全博弈问题, 而安全博弈问题刚好可以由LTL合成问题归约而来[4]. 在求解过程中, LTL公式尽可能地被转换为确定Büchi自动机(deterministic Büchi automata). 该方法的优势在于可以获得更紧凑的策略, 并可对规模较大的LTL合取公式进行组合求解; 而缺点在于不是所有LTL公式都存在对应的确定Büchi自动机, 因此存在一定的局限性.
LTLf是LTL的一个变种, 二者的区别在于, 前者的语义模型限制为有穷[9]. 目前也存在一部分研究工作聚焦LTLf合成问题. Giacomo和Vardi从理论的角度证明了一个重要结论, 即LTLf合成的计算复杂度与LTL合成相同, 前者并没有因为有穷模型而使得复杂度降低[10]. Zhu等人提出了一种基于符号化的框架, 将LTLf合成问题归约为DFA (deterministic finite automata)博弈, 并进一步表示为布尔公式, 然后利用布尔分析生成策略[11]. LTLf合成还在机器人领域得到实际应用. 文献[12]提出了一种基于BDD的组合方法, 将LTLf合成应用于有限视野任务, 能够合成UR5机器人的任务策略. 文献[13]在资源有限条件下研究如何生成机器人策略, 采用LTLf描述有限任务, 并通过将LTLf合成归约为定量博弈的技术路线进行求解. 此外, 最新的工作着重在不同假设的前提下研究LTLf合成问题, 如公平性和稳定性[14]、LTL条件[15]等.
近年来, 有研究成果表明, 智能规划(automated planning)[16]与LTL合成有着紧密的联系, 从而开辟了一种LTL合成的新途径. 具体而言, LTL合成与智能规划的一类子问题, 即非确定规划(non-deterministic planning)存在很多相似之处. Camacho等人将LTLf合成问题转换为非确定规划问题, 融合了动态状态抽象和惰性自动机确定化技术, 不仅能够给出合成策略, 在合成不可实现(unrealizable)的情况下, 还能够给出相应证明[17]. 文献[18]将目标为LTL公式的非确定规划描述为二人博弈, 基于此构建起LTL合成和非确定规划的关系, 使得二者可以很容易地进行相互转换. 本文借鉴了文献[19]提出的转换方法, 并对其进行改进. 关键的区别在于: 本文提出的方法在规划过程中仅模拟自动机的一条路径, 而文献[19]则同时保留多条路径. 两种方法的详细比较将在后续实验章节阐述. 与前述工作不同, D’Ippolito等人从相反的思路研究非确定规划与LTL合成的关系, 将非确定规划编码为LTL合成问题, 并利用合成技术进行规划求解[20]; Bonet等人将广义规划(generalized planning)问题规约为LTL合成问题[21]. 此外, 还有工作研究其他类型时序逻辑的合成问题, 如采用STL (signal temporal logic)描述合成意图[22]. 其中, STL能够表达实值信号的时序性质, 一般可用于分析混成系统或混合信号电路.
本文提出了一种新的基于智能规划技术的LTL合成方法, 其核心思想是: 在二人博弈定义的前提下, 将LTL合成转换为非确定规划模型. 博弈双方的行为均由规划动作模拟. 在此过程中, 需要将LTL公式转换为非确定Büchi自动机. 相比其他求解方法, 本文提出的方法可以直接利用现有高效规划器, 并且获得的合成策略更为紧凑, 具备一定的实际应用价值.
本文第1节简要介绍LTL、LTL合成以及非确定规划的基本概念. 第2节详细给出从LTL合成到非确定规划模型的具体转换方法, 将LTL合成过程变为规划求解过程, 这也是本文的主要贡献. 第3节通过实验对比, 证明本文所提方法的可行性和有效性. 最后总结全文, 并对未来可能的研究方向进行初步探讨.
1 技术背景 1.1 线性时序逻辑LTLLTL是一种模态逻辑, 在命题逻辑的基础上引入时序操作符next(○)和until(U), 用于描述线性时间性质.令P表示原子命题集合, LTL公式ϕ的语法定义如下(其中, p∈P):
| $ \phi::=p|\neg \phi| \phi_{1} \wedge \phi_{2}|\bigcirc \phi| \phi_{1} {\bf{U}} \phi_{2} . $ |
LTL的语义模型定义为无限状态序列σ=s0, s1, …, 其中, 任意si为P的一个子集. true, false和其他命题逻辑操作符∨, →, ↔可以由ϕ中定义的基本操作符导出. LTL公式的可满足性定义如下:
σ, i|p iff p∈P;
σ, i|¬ϕ iff not σ, i|ϕ;
σ, i|ϕ1∧ϕ2 iff σ, i|ϕ1 and σ, i|ϕ2;
σ, i|ϕ1Uϕ2 iff ∃j≥i such that σ, j|ϕ2, and σ, k|ϕ1 for each i≤k≤j−1.
我们称σ满足ϕ, 表示为σ|ϕ, 当且仅当σ, 0|ϕ. 简单地说, ○ϕ描述ϕ将在下一状态成立; ϕ1Uϕ2的含义是直到ϕ2成立之前, ϕ1一直成立. 其他时序操作符, 如eventually(◊)和always(□)定义为: ◊ϕ
定义1. 非确定Büchi自动机(non-deterministic Büchi automata, NBA)是一个五元组: B=(Q, Σ, δ, q0, F), 其中, Q是自动机的状态集合, Σ是字母表, δ⊆Q×Σ×Q是迁移关系, q0是初始状态, F⊆Q是接受状态集合.
P的字集合表示为Lits(P)=P∪{¬p|p∈P}. 一般地, 可令Σ=2Lits(P). B路径γ=q0, q1, …是一个无限状态序列, 定义在字序列σ=s0, s1, …之上, 满足对于任意i≥0, 有(qi, si, qi+1)∈δ. 如果一条路径中出现无限多个接受状态, 则称该路径是可接受的. 如果存在B的一条可接受路径定义在σ之上, 则称B接受σ. 给定LTL公式ϕ, 我们可以构造NBA Bϕ, 使得Bϕ接受σ当且仅当σ|ϕ. 在最坏情况下, 构造Bϕ的时间复杂度随着ϕ大小的增加(公式的大小由其包含的操作符和变量的数量决定)呈指数级增长[23].
例1: 图 1展示了LTL公式□(x↔◊y)和◊□(x↔y)对应的NBA. 自动机的状态表示为圆(双环圆是接受状态), 迁移表示为箭头. 需要注意的是, 这里用“∨”操作符简化了迁移的描述. 例如, 迁移(q0, ¬x∨y, q0)可以看作由两条迁移(q0, ¬x, q0)和(q0, y, q0)组合而成.
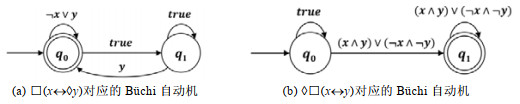
|
图 1 NBA示例 |
1.2 LTL合成
LTL合成的定义最早由Pnueli和Rosner给出[2], 他们将LTL合成描述为二人博弈, 博弈的双方分别为环境和控制器. 博弈过程包括一个无限的回合序列, 每个回合首先由环境执行一个动作, 然后智能体为控制器选择另一个动作应对(控制器也可先于环境执行). 动作的任务是对一些变量赋值. 无论环境如何选择动作, 如果环境和控制器交互产生的状态序列满足给定的LTL公式, 则称控制器存在获胜策略. LTL合成的形式化定义如下:
定义2. LTL合成问题是一个三元组
直观地说, LTL合成要求无论环境如何选择(序列X1, X2, …), 控制器都能找到相应的策略(f), 保证此博弈模型满足ϕ. 实际上, LTL合成问题就对应求解函数f. 若存在f, 称LTL合成问题为可实现的; 否则, 称其为不可实现的.
例2: 令
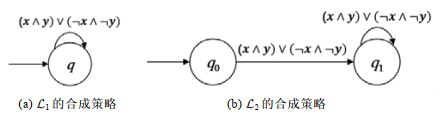
|
图 2 合成策略示例 |
1.3 非确定规划
定义3. 完全可观测的非确定规划(fully observable non-deterministic planning, FOND)问题是一个四元组:
每个动作a∈A包含两个元素(pre(a), eff(a)), 其中, pre(a)⊆Lists(P)是a的前置条件, eff(a)是a的效果. 需要强调的是: eff(a)是非确定的, 即可能存在多个互斥的子效果. 每个子效果e∈eff(a)是一个条件效果集合, 形如C > l, 其中, C⊆Lits(P)并且l∈Lits(P). 给定状态s⊆P和事实p∈P, s满足p当且仅当p∈s, s满足¬p当且仅当p∉s.此外, s满足字集合L当且仅当s满足任意l∈L. 下面将举例说明非确定效果的含义. 在经典的规划问题Tireworld中, 汽车在两点之间移动采用一个动作模拟, 该动作包含两个非确定子效果: 一个是到达目的地后轮胎气充足, 另一个是到达目的地后轮胎亏气. 在求解时, 需要同时考虑两个子效果出现的情况, 即: 若轮胎气充足时继续行驶, 若轮胎亏气时则补气后再行驶.
如果状态s满足pre(a), 则称动作a在s下是可执行的. s′是a在s下执行的结果, 且s′=s\{p|(C > ¬p)∈e, s满足C}∪{p|(C > p)∈e, s满足C}. 策略
如果有限执行π的最终状态s满足字集合L, 则称π达到L. 如果存在无限执行π的某个状态s在π中出现无限多次, 且s满足L, 则称π达到L. 无限执行π是公平的(fair)当且仅当如果s, a在π中出现无限多次, 则s, a, s′也在π中出现无限多次, 其中, s′是a在s下的任意执行结果. 在这种定义下, 意味着有限执行是公平的. 策略
LTL合成是否可实现, 与FOND问题是否存在强循环解有着紧密的联系. 本节主要介绍一种转换方法, 将LTL合成的二人博弈定义转换为FOND模型.
2.1 从LTL合成到非确定规划的转换给定一个LTL合成问题
这里重点阐述
下面将详细说明转换的技术细节. 转换后P的定义如下.
● 事实集合P
P={prev_q, q|q∈Q}∪{env_mode, aut_mode, record_mode}∪{turni|1≤i≤|X|}∪{vx, v¬x|x∈X∪Y}∪{goal}.
自动机的状态是否成立, 由其前序状态以及两状态之间的迁移条件决定. 因此, 针对每个自动机状态q∈Q, 引入两个事实变量prev_q和q与之对应, 分别表示自动机状态q在上一状态是否成立以及在当前状态是否成立. 事实变量env_mode, aut_mode和record_mode用于标记规划所处的模式: 分别表示环境模式、自动机模式和记录模式. 记录模式主要为后续规划记录此时成立或激活的自动机状态. 3个模式依次交替变换. 事实变量turni的作用将在介绍动作集合时给出. 对于每个变量x∈X∪Y, 采用两个事实变量vx, v¬x分别显式描述将x赋值为真或假(值得注意的是, 根据等价关系x≡¬¬x, 可以得出vx≡¬v¬x). goal用于标记规划目标.
● 动作集合A
| $ A={assign_{x}|x∈X}∪{trans_{t}|t∈δ}∪{record_{q}|q∈Q}. $ |
(1) 环境模式下可执行的动作集合为{assignx|x∈X}. 由于环境的行为是智能体不可控的, 环境有可能任意改变变量的值, 因此采用一系列非确定动作来模拟这种不确定性. 假设X={x1, x2, …, x|X|), 其中每个变量xi∈X对应一个非确定动作
| $ \begin{array}{l} pre(assig{n_{{x_i}}}) = \{ env{\text{_}}mode, tur{n_i}\} \hfill \\ eff(assig{n_{{x_i}}}) = oneof(\{ {v_{{x_i}}}, \neg {v_{\neg {x_i}}}\} , \{ \neg {v_{{x_i}}}, {v_{\neg {x_i}}}\} ) \cup \left\{ {\begin{array}{*{20}{l}} {\{ tur{n_{i + 1}}, \neg tur{n_i}\} , {\text{ if }}i < |X|} \\ {\{ aut{\text{_}}mode, \neg env{\text{_}}mode, \neg tur{n_i}\} , {\text{ if }}i = |X|} \end{array}} \right. \hfill \\ \end{array} $ |
所有变量按照一定顺序依次被赋值. turni在
还有其他环境模式的动作定义方法, 只需定义一个动作assignX, 其效果中包含2|X|个非确定子效果. 然而, 这种定义可能会导致效果数量爆炸, 只适用于|X|较小的情况.
| $ \begin{array}{l} pre(assig{n_X}) = \{ env{\text{_}}mode\} \hfill \\ eff(assig{n_X}) = \{ aut{\text{_}}mode, \neg env{\text{_}}mode\} \cup oneof(\{ {v_{{x_1}}}, \neg {v_{\neg {x_1}}}, {v_{{x_2}}}, \neg {v_{\neg {x_2}}}, ..., {v_{{x_{|X|}}}}, \neg {v_{\neg {x_{|X|}}}}\} , \{ {v_{{x_1}}}, \neg {v_{\neg {x_1}}}, {v_{{x_2}}}, \neg {v_{\neg {x_2}}}, ..., \hfill \\ {\text{ }}\neg {v_{{x_{|X|}}}}, {v_{\neg {x_{|X|}}}}\} , ..., \{ \neg {v_{{x_1}}}, {v_{\neg {x_1}}}, \neg {v_{{x_2}}}, {v_{\neg {x_2}}}, ..., \neg {v_{{x_{|X|}}}}, {v_{\neg {x_{|X|}}}}\} ) \hfill \\ \end{array} $ |
(2) 自动机模式下的动作模拟Y中变量赋值以及自动机迁移. 每次更新自动机的迁移, 可以看作智能体观察X中变量赋值后所做出的反应(对Y中变量进行赋值). 智能体决定选择执行哪个迁移动作, 并确保不违反激活迁移的条件. 针对每个迁移t=(qi, guard(t), qj)∈δ, guard(t)∈2Lits(P), 定义一个规划动作transt:
| $ \begin{array}{l} pre(tran{s_t}) = \{ aut{\text{_}}mode, prev{\text{_}}{q_i}\} \cup \{ \neg {v_{\neg l}}|l \in guard(t)\} \hfill \\ eff(tran{s_t}) = \{ record{\text{_}}mode, \neg aut{\text{_}}mode\} \cup \{ {q_j}, \neg prev{\text{_}}{q_i}\} \cup \{ {v_l}|l \in guard(t)\} \hfill \\ \end{array} $ |
当前序状态下qi成立, 即prev_qi成立, 且transt的前置条件不违反t的迁移条件{¬v¬l|l∈guard(t)}, transt才存在执行的可能性. transt的效果包括设置qj为真, 并设置guard(t)的所有事实变量条件成立. 注意, 在每个状态下只保持一个活动的自动机状态. 也就是说, 只模拟记录自动机的一条路径. 在此模式下执行一个动作后, 切换至记录模式.
(3) 每个自动机状态q∈Q对应记录模式下的一个动作recordq, 其前置条件要求q成立. 执行某一recordq动作后, 重新切换至环境模式. recordq的效果重置所有x∈X∪Y, 并为后续规划记录q为活动状态(prev_q置为真). 当q为接受状态时, 此时效果包含两个不确定子效果, 其中: 一个子效果包含目标goal和prev_q; 另一个子效果与q为非接受状态时相同, 即prev_q. 将goal加入非确定效果的做法, 使得求解时必须多次执行recordq才能使得经过所有子效果的路径到达目标, 从而模拟Bϕ的无限可接受路径:
| $ \begin{array}{l} pre(recor{d_q}) = \{ record{\text{_}}mode, q\} \hfill \\ eff(recor{d_q}) = \{ env{\text{_}}mode, \neg record{\text{_}}mode, tur{n_1}, \neg q\} \cup \{ \neg {v_x}, \neg {v_{\neg x}}|x \in X \cup Y\} \cup \hfill \\ {\text{ }}\left\{ {\begin{array}{*{20}{l}} {prev{\text{_}}q, {\text{ if }}q \notin F} \\ {oneof(\{ prev{\text{_}}q\} , \{ goal, prev{\text{_}}q\} ), {\text{ if }}q \in F} \end{array}} \right. \hfill \\ \end{array} $ |
初始状态I和目标G: 初始状态设置模式为环境模式, 且令turn1成立, 并令Bϕ的初始状态成立, 即I={env_mode, turn1, prev_q0}. 将goal设为规划目标, 即G={goal}.
例3: 令
环境模式只包含一个动作assignx:
| $ \begin{array}{l} pre(assig{n_x}) = \{ env{\text{_}}mode, tur{n_i}\} \hfill \\ eff(assig{n_x}) = \{ aut{\text{_}}mode, \neg env{\text{_}}mode, \neg tur{n_1}\} \cup oneof(\{ {v_{{x_i}}}, \neg {v_{\neg {x_i}}}\} , \{ \neg {v_{{x_i}}}, {v_{\neg {x_i}}}\} ) \hfill \\ \end{array} $ |
自动机模式共有5个迁移, 分别为t1=(q0, ¬x, q0), t2=(q0, y, q0), t3=(q0, true, q1), t4=(q1, y, q0), t5=(q1, true, q1), 对应以下5个动作:
| $ \begin{array}{l} pre(tran{s_{{t_1}}}) = \{ aut{\text{_}}mode, prev{\text{_}}{q_0}, \neg {v_x}\} , {\text{ }}eff(tran{s_{{t_1}}}) = \{ record{\text{_}}mode, \neg aut{\text{_}}mode, {q_0}, \neg prev{\text{_}}{q_0}, {v_{\neg x}}\} ; \hfill \\ pre(tran{s_{{t_2}}}) = \{ aut{\text{_}}mode, prev{\text{_}}{q_0}, \neg {v_{\neg y}}\} , {\text{ }}eff(tran{s_{{t_2}}}) = \{ record{\text{_}}mode, \neg aut{\text{_}}mode, {q_0}, \neg prev{\text{_}}{q_0}, {v_y}\} ; \hfill \\ pre(tran{s_{{t_3}}}) = \{ aut{\text{_}}mode, prev{\text{_}}{q_0}\} , {\text{ }}eff(tran{s_{{t_3}}}) = \{ record{\text{_}}mode, \neg aut{\text{_}}mode, {q_1}, \neg prev{\text{_}}{q_0}\} ; \hfill \\ pre(tran{s_{{t_4}}}) = \{ aut{\text{_}}mode, prev{\text{_}}{q_1}, \neg {v_{\neg y}}\} , {\text{ }}eff(tran{s_{{t_4}}}) = \{ record{\text{_}}mode, \neg aut{\text{_}}mode, {q_0}, \neg prev{\text{_}}{q_1}, {v_y}\} ; \hfill \\ pre(tran{s_{{t_5}}}) = \{ aut{\text{_}}mode, prev{\text{_}}{q_1}\} , {\text{ }}eff(tran{s_{{t_5}}}) = \{ record{\text{_}}mode, \neg aut{\text{_}}mode, {q_1}, \neg prev{\text{_}}{q_1}\} . \hfill \\ \end{array} $ |
记录模式有两个动作
| $ \begin{array}{l} pre(recor{d_{{q_0}}}) = \{ record{\text{_}}mode, {q_0}\} , eff(recor{d_{{q_0}}}) = \{ aut{\text{_}}mode, \neg record{\text{_}}mode, \neg {q_0}, oneof(\{ prev{\text{_}}{q_0}\} , \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\{ goal, prev{\text{_}}{q_0}\} ), \neg {v_x}, \neg {v_{\neg x}}, \neg {v_y}, \neg {v_{\neg y}}\} ; \hfill \\ pre(recor{d_{{q_1}}}) = \{ record{\text{_}}mode, {q_1}\} , eff(recor{d_{{q_1}}}) = \{ aut{\text{_}}mode, \neg record{\text{_}}mode, \neg {q_1}, prev{\text{_}}{q_0}, \neg {v_x}, \neg {v_{\neg x}}, \neg {v_y}, \neg {v_{\neg y}}\} . \hfill \\ \end{array} $ |
根据上述FOND模型获得的解, 可以表示为图 3所示的图形. 这里, 有效的迁移为assignx和
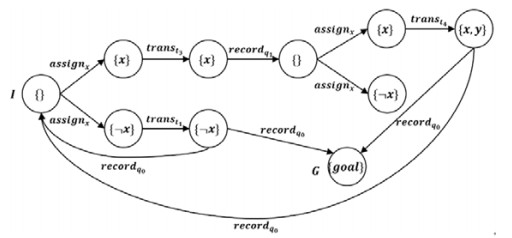
|
图 3 |
2.2 理论证明
定理1. 若|X|+|Y| ≪ |Bϕ|, 则
证明: 按照传统的定义, |Bϕ|=|Q|+|δ|. 令LTL合成问题
● 事实集合转换复杂度: |{prev_q, q|q∈Q}|+|{env_mode, aut_mode, record_mode}|+|{turni|1≤i≤|X|}|+|{vx, v¬x|x∈X∪Y}|+|{goal}|=2|Q|+3|X|+2|Y|+4;
● 动作集合转换复杂度: 第1类环境模式动作转换的时间复杂度为|{assignx|x∈X}|=9|X|, 第2类自动机模式动作转换的时间复杂度为{transt|t∈δ}=(6+2|X|+2|Y|)|δ|, 第3类记录模式动作转换的时间复杂度为|{recordq|q∈Q}|=(9+|X|+|Y|)|Q|.
● 初始状态和目标转换复杂度: 该转换的时间复杂度为常量.
已知|X|+|Y| ≪ |Bϕ|, 因此定理的结论成立.
定理2(正确性). 若
证明: 假设
定理结论得证.
定理3(完备性). 若
证明: 假设
(1) 将Xi和f(X1, X2, …, Xi)分解为一系列动作
(2) 在τi后增加动作
定理结论得证.
2.3 方法对比本节提出的
● 事实集合P
| $ P=\left\{q, q^{5}, q^{t}, q^{5 t} \mid q \in Q\right\} \cup\left\{e n v_{-} {mode,aut\_mode,can\_switch,can\_accept }\right\} \cup\left\{t u r n_{i}|1 \leqslant i \leqslant| X \mid\right\} \cup\left\{v_{x}, v_{\neg {x}} \mid x \in X \cup Y\right\} \cup\{g o a l\} \text {. }$ |
针对每个自动机状态q, 有4个事实变量与之对应, 主要目的在于, 需要同时记录NBA的多条路径. q与qs, qt与qst的关系类似于
● 动作集合A
| $ A={assign_{x}|x∈X}∪{trans_{t}|t∈δ}∪{switch2aut, switch2env, accept}. $ |
(1) 环境模式下的动作与
| $ \begin{array}{l} pre(assig{n_{{x_{X|}}}}) = \{ env{\text{_}}mode, tur{n_{|X|}}\} \hfill \\ eff(assig{n_{{x_{|X|}}}}) = oneof(\{ {v_{{x_{|X|}}}}, \neg {v_{\neg {x_{|X|}}}}\} , \{ \neg {v_{{x_{|X|}}}}, {v_{\neg {x_{|X|}}}}\} ) \cup \{ can\_switch, \neg tur{n_{|X|}}\} \hfill \\ pre(switch2aut) = \{ env{\text{_}}mode, can{\text{_}}switch\} \hfill \\ eff(switch2aut) = \{ aut{\text{_}}mode, \neg env{\text{_}}mode, \neg can{\text{_}}switch\} \cup \{ q \triangleright \{ {q^s}, \neg q\} , {q^t} \triangleright \{ {q^{st}}, \neg {q^t}\} |q \in Q\} \hfill \\ \end{array} $ |
(2) 虽然仍是每个迁移对应一个动作, 自动机模式下的动作与
| $ \begin{array}{l} pre(tran{s_t}) = \{ aut{\text{_}}mode, q_i^s\} \cup \{ \neg {v_{\neg l}}|l \in guard(t)\} \hfill \\ eff(tran{s_t}) = \{ {q_j}\} \cup \{ {v_l}|l \in guard(t)\} \cup \left\{ {\begin{array}{*{20}{l}} {\{ q_i^{st} \triangleright q_j^t\} , {\text{ if }}{q_j} \notin F} \\ {\{ can\_accept\} , {\text{ if }}{q_j} \in F} \end{array}} \right. \hfill \\ \end{array} $ |
从自动机模式切换到环境模式, 可以通过两个动作switch2env和accept. switch2env将所有条件(除了自动机状态变量)置为初值. accept的效果有对自动机状态变量的处理, 并有非确定子效果goal, 使得可以找到访问无限多次接受状态的无限执行. accept也存在效果过多的潜在问题. 更为详细的解释可参考文献[19]:
| $ \begin{array}{l} pre(switch2env) = \{ aut{\text{_}}mode\} \hfill \\ eff(switch2env) = \{ env{\text{_}}mode, \neg aut{\text{_}}mode\} \cup \{ tur{n_1}\} \cup \{ \neg {q^s}, \neg {q^{st}}|q \in Q\} \cup \{ \neg {v_x}, \neg {v_{\neg x}}|x \in X \cup Y\} \hfill \\ pre(accept) = \{ aut{\text{_}}mode, can{\text{_}}accept\} \hfill \\ eff(accept) = oneof(\{ goal\} , \{ tur{n_1}\} \cup \{ env{\text{_}}mode, \neg aut{\text{_}}mode, \neg can{\text{_}}accept\} \cup \{ {q^s} \triangleright \neg {q^s}, {q^{st}} \triangleright \neg {q^{st}}|q \in Q\} ) \cup \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\{ q \wedge {q^t} \triangleright \{ \neg q, \neg {q^t}\} |q \in (Q\backslash F)\} \cup \{ q \wedge \neg {q^t} \triangleright {q^t}|q \in Q\} \cup \{ \neg {v_x}, \neg {v_{\neg x}}|x \in X \cup Y\} \hfill \\ \end{array} $ |
由于
例4: 根据
● 事实集合:
| $ \begin{array}{l} P = \{ {q_0}, q_0^s, q_0^t, q_0^{st}, {q_1}, q_1^s, q_1^t, q_1^{st}|q \in Q\} \cup \{ env{\text{_}}mode, aut{\text{_}}mode, can{\text{_}}switch, can{\text{_}}accept\} \cup \hfill \\ \;\;\;\;\;\;\;\;\{ tur{n_1}\} \cup \{ {v_x}, {v_{\neg x}}, {v_y}, {v_{\neg y}}\} \cup \{ goal\} \hfill \\ \end{array} $ |
● 动作集合定义如下:
环境模式有动作assignx和动作switch2aut:
| $ \begin{array}{l} pre(assig{n_x}) = \{ env{\text{_}}mode, tur{n_1}\} , \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;eff(assig{n_x}) = \{ can{\text{_}}switch, \neg tur{n_1}\} \cup oneof(\{ {v_{{x_i}}}, \neg {v_{\neg {x_i}}}\} , \{ \neg {v_{{x_i}}}, {v_{\neg {x_i}}}\} ); \hfill \\ pre(switch2aut) = \{ env{\text{_}}mode, can{\text{_}}switch\} , \;\;\;\;\;\;\;\;eff(switch2aut) = \{ aut{\text{_}}mode, \neg env{\text{_}}mode, \neg can{\text{_}}switch\} \cup \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\{ {q_0} \triangleright \{ q_0^s, \neg {q_0}\} , q_0^t \triangleright \{ q_0^{st}, \neg q_0^t\} , {q_1} \triangleright \{ q_1^s, \neg {q_1}\} , q_1^t \triangleright \{ q_1^{st}, \neg q_1^t\} \} . \hfill \\ \end{array} $ |
自动机模式共有7个迁移, 包括5个迁移t1=(q0, ¬x, q0), t2=(q0, y, q0), t3=(q0, true, q1), t4=(q1, y, q0), t5=(q1, true, q1)对应的动作以及switch2env和accept:
| $ \begin{array}{l} pre(tran{s_{{t_1}}}) = \{ aut{\text{_}}mode, q_0^s, \neg {v_x}\} , \;\;\;\;\;\;\;\;\;\;\;\;eff(tran{s_{{t_1}}}) = \{ {q_0}, can{\text{_}}accept, {v_{\neg x}}\} ; \hfill \\ pre(tran{s_{{t_2}}}) = \{ aut{\text{_}}mode, q_0^s, \neg {v_{\neg y}}\} , \;\;\;\;\;\;\;\;\;eff(tran{s_{{t_2}}}) = \{ {q_0}, can{\text{_}}accept, {v_y}\} ; \hfill \\ pre(tran{s_{{t_3}}}) = \{ aut{\text{_}}mode, q_0^s\} , \;\;\;\;\;\;\;\;\;\;\;\;\;\;eff(tran{s_{{t_3}}}) = \{ {q_1}, q_0^{st} \triangleright q_1^t\} ; \hfill \\ pre(tran{s_{{t_4}}}) = \{ aut{\text{_}}mode, q_1^s, \neg {v_{\neg y}}\} , \;\;\;\;\;\;\;\;\;eff(tran{s_{{t_4}}}) = \{ {q_0}, can{\text{_}}accept, {v_y}\} ; \hfill \\ pre(tran{s_{{t_5}}}) = \{ aut{\text{_}}mode, q_1^s\} , \;\;\;\;\;\;\;\;\;\;\;\;\;\;eff(tran{s_{{t_5}}}) = \{ {q_1}, q_1^{st} \triangleright q_1^t\} ; \hfill \\ pre(switch2env) = \{ aut{\text{_}}mode\} , {\text{ }}eff(switch2env) = \{ env{\text{_}}mode, \neg aut{\text{_}}mode, can{\text{_}}accept, tur{n_1}, \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\neg q_0^s, \neg q_0^{st}, \neg q_1^s, \neg q_0^{st}, \neg {v_x}, \neg {v_{\neg x}}, \neg {v_y}, \neg {v_{\neg y}}\} ; \hfill \\ pre(accept) = \{ aut{\text{_}}mode, can{\text{_}}accept\} , {\text{ }}eff(accept) = oneof(\{ goal\} , \{ env{\text{_}}mode, \neg aut{\text{_}}mode, \neg can{\text{_}}accept, tur{n_1}, \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\neg q_0^s \triangleright \neg q_0^s, \neg q_1^s \triangleright \neg q_1^s, \neg q_0^{st} \triangleright \neg q_0^{st}, \neg q_1^{st} \triangleright \neg q_1^{st}, \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{q_0} \wedge q_0^t \triangleright \{ \neg {q_0}, \neg q_0^t\} , {q_0} \wedge \neg q_0^t \triangleright q_0^t, {q_1} \wedge \neg q_1^t \triangleright q_1^t, \neg {v_x}, \neg {v_{\neg x}}, \neg {v_y}, \neg {v_{\neg y}}\} ). \hfill \\ \end{array} $ |
假设每个变量的空间复杂度为1, 下面将分析
本节主要通过实验比较本文所提方法与其他方法的优劣, 选取的基准测试集来自最近一届国际合成竞赛SYNTCOMP20 (http://www.syntcomp.org/syntcomp-2020-results/). 实验选取的对比合成工具ltlsynt[7]是参赛工具之一, ltlsynt将输入的LTL公式转换为确定奇偶自动机(deterministic parityautomata), 而后者等价于奇偶博弈(parity game), 并采用Zielonka提出的递归算法求解[25]. 对于其他合成工具, 如Acacia+[4], Lily[5], SynKit[6]等, 它们的求解效率远低于ltlsynt, 本文仅将SynKit作为另一个现有合成工具进行实验对比. SynKit将LTL合成规约为安全博弈问题, 并建立了该问题与多种自动机(universal k-coBüchiWord (UkCW) automata and non- deterministic k-Büchi word (NkBW) automata)之间的关系. 实验采用的FOND规划器为非确定规划的著名工具PRP[26]. LTL公式转换为NBA的过程利用LTL2BA[27]实现. 我们开发了
主要从两个方面对实验结果进行分析: 一是求解时间, 二是策略的规模. 求解时间说明工具的求解效率, 策略的规模说明解的质量. 策略规模越小, 质量越高, 即说明该策略更加具备实用性. 第1个实验采用的测试集均为不可实现(unrealizable)的LTL合成问题, 即问题无解. 表 1列出了相应的实验结果. 每个问题包含多个实例, 复杂度由低到高, 每个实例的求解时间限制在1小时以内. 由于问题不可实现, 所以不存在合成策略, 表 1仅对比求解时间. 列“SYN”表示ltlsynt的求解时间.
| 表 1 不可实现的基准测试集运行结果 |
第2个实验采用的测试集均为可实现的LTL合成问题, 实例的NBA规模普遍比第1个实验大很多. 表 2给出了实验结果. 列“
| 表 2 可实现的基准测试集运行结果 |
4 结论
当前, LTL合成仍然是非常重要且具有挑战性的研究问题. 智能规划涌现出了很多有效的方法和工具, 且与LTL合成有着一定的相似性. 基于此, 本文提出了一种基于非确定规划的LTL合成方法, 试图通过利用非确定规划的高效工具求解LTL合成问题. 本文的主要创新点在于: 提出了一种从LTL合成的二人博弈定义到非确定规划模型的转换方法, 且转换的复杂度与LTL公式的NBA大小线性相关, 并证明了方法的正确性和完备性. 选取国际合成竞赛的基准测试集进行实验, 结果证明: 本文提出的方法在规划解的质量方面具有较大优势, 能够获得更为紧凑的合成策略. 未来的工作将着眼于在保证规划解质量的前提下提高合成效率, 研究在非确定规划工具中设计适合LTL合成过程的启发式算法.
| [1] |
Church A. Applications of recursive arithmetic to the problem of circuit synthesis. Journal of Symbolic Logic, 1963, 28(4): 289-290.
[doi:10.2307/2271310] |
| [2] |
Pnueli A, Rosner R. On the synthesis of a reactive module. In: Proc. of the 16th Annual ACM Symp. on Principles of Programming Languages (POPL'89). ACM, 1989. 179-190. [doi: 10.1145/75277.75293]
|
| [3] |
Piterman N, Pnueli A, Sa'ar Y. Synthesis of reactive (1) designs. In: Emerson EA, Namjoshi KS, eds. Proc. of the 7th Int'l Conf. on Verification, Model Checking, and Abstract Interpretation (VMCAI 2006). Springer, 2006. 364-380. [doi: 10.1007/11609773_24]
|
| [4] |
Bohy A, Bruyère V, Filiot E, et al. Acacia+: Atool for LTLsynthesis. In: Madhusudan P, Seshia SA, eds. Proc. of the 24th Int'l Conf. on Computer Aided Verification (CAV 2012). Springer, 2012. 652-657. [doi: 10.1007/978-3-642-31424-7_45]
|
| [5] |
Jobstmann B, Bloem R. Optimizations for LTL synthesis. In: Proc. of the 6th Int'l Conf. on Formal Methods in Computer-Aided Design (FMCAD 2006). IEEE Computer Society, 2006. 117-124. [doi: 10.1109/FMCAD.2006.22]
|
| [6] |
Camacho A, Muise C, Baier JA, et al. LTL realizability via safety and reachability games. In: Lang J, ed. Proc. of the 27th Int'l Joint Conf. on Artificial Intelligence (IJCAI 2018). 2018. 4683-4691. [doi: 10.24963/ijcai.2018/651]
|
| [7] |
Michaud T, Colange M. Reactive synthesis from LTL specification with Spot. In: Proc. of the 7th Workshop on Synthesis (SYNT 2018). 2018.
|
| [8] |
Zhu SF, Tabajara LM, Li JW, et al. A symbolic approach to safety LTLsynthesis. In: Strichman O, Tzoref- Brill R, eds. Proc. of the 13th Int'l Haifa Verification Conf. (HVC 2017). Springer, 2017. 147-162. [doi: 10.1007/978-3-319-70389-3_10]
|
| [9] |
Li JW, Zhang LJ, Pu GG, et al. LTLf satisfiability checking. In: Schaub T, Friedrich G, O'Sullivan B, eds. Proc. of the 21st European Conf. on Artificial Intelligence (ECAI 2014). IOS, 2014. 513-518. [doi: 10.3233/978-1-61499-419-0-513]
|
| [10] |
Giacomo GD, Vardi MY. Synthesis for LTL and LDL on finite traces. In: Yang Q, Wooldridge MJ, eds. Proc. of the 24th Int'l Joint Conf. on Artificial Intelligence (IJCAI 2015). AAAI, 2015. 1558-1564.
|
| [11] |
Zhu SF, Tabajara LM, Li JW, et al. Symbolic LTLf synthesis. In: Sierra C, ed. Proc. of the 26th Int'l Joint Conf. on Artificial Intelligence (IJCAI 2017). 2017. 1362-1369. [doi: 10.24963/ijcai.2017/189]
|
| [12] |
He KL, Wells AM, Kavraki LE, et al. Efficient symbolic reactive synthesis for finite-horizon tasks. In: Proc. of the Int'l Conf. on Robotics and Automation (ICRA 2019). IEEE, 2019. 8993-8999. [doi: 10.1109/ICRA.2019.8794170]
|
| [13] |
He KL, Lahijanian M, Kavraki LE, et al. Reactive synthesis for finite tasks under resource constraints. In: Proc. of the 2017 IEEE/RSJ Int'l Conf. on Intelligent Robots and Systems (IROS 2017). IEEE, 2017. 5326-5332. [doi: 10.1109/IROS.2017.8206426]
|
| [14] |
Zhu SF, Giacomo GD, Pu GG, et al. LTLf synthesis with fairness and stability assumptions. In: Proc. of the 34th AAAI Conf. on Artificial Intelligence (AAAI 2020). AAAI, 2020. 3088-3095. [doi: 10.1609/aaai.v34i03.5704]
|
| [15] |
Giacomo GD, Stasio AD, Vardi MY, et al. Two-stage technique for LTLf synthesis under LTL assumptions. In: Calvanese D, Erdem E, Thielscher M, eds. Proc. of the 17th Int'l Conf. on Principles of Knowledge Representation and Reasoning (KR 2020). 2020. 304-314. [doi: 10.24963/kr.2020/31]
|
| [16] |
Ghallab M, Nau D, Traverso P. Automated Planning—Theory and Practice. Elsevier, 2004. 1-635.
|
| [17] |
Camacho A, Baier JA, Muise C, et al. Finite LTL synthesis as planning. In: de Weerdt M, Koenig S, Röger G, Spaan MTJ, eds. Proc. of the 28th Int'l Conf. on Automated Planning and Scheduling (ICAPS 2018). AAAI, 2018. 29-38.
|
| [18] |
Camacho A, Bienvenu M, McIlraith SA. Towards a unified view of AI planning and reactive synthesis. In: Benton J, Lipovetzky N, Onaindia E, Smith DE, Srivastava S, eds. Proc. of the 29th Int'l Conf. on Automated Planning and Scheduling (ICAPS 2019). AAAI, 2019. 58-67.
|
| [19] |
Camacho A, Baier JA, Muise C, et al. Bridging the gap between LTL synthesis and automated planning. In: Proc. of the Workshop Generalized Planning. 2017. 1-10.
|
| [20] |
D'Ippolito N, Rodriguez N, Sardina S. Fully observable non-deterministic planning as assumption-based reactive synthesis. Journal of Artificial Intelligence Research, 2018, 61: 593-621.
[doi:10.1613/jair.5562] |
| [21] |
Blai B, Giuseppe DG, Hector G, et al. High-level programming via generalized planning and LTL synthesis. In: Calvanese D, Erdem E, Thielscher M, eds. Proc. of the 17th Int'l Conf. on Principles of Knowledge Representation and Reasoning (KR 2020). 2020. 152-161. [doi: 10.24963/kr.2020/16]
|
| [22] |
Raman V, Donze A, Sadigh D, et al. Reactive synthesis from signal temporal logic specifications. In: Girard A, Sankaranarayanan S, eds. Proc. of the 18th Int'l Conf. on Hybrid Systems: Computation and Control (HSCC 2015). ACM, 2015. 239-248. [doi: 10.1145/2728606.2728628]
|
| [23] |
Vardi MY, Wolper P. Reasoning about infinite computations. Information and Computation, 1994, 115(1): 1-37.
[doi:10.1006/inco.1994.1092] |
| [24] |
Geffner H, Bonet B. A concise introduction to models and methods for automated planning. In: Proc. of the Synthesis Lectures on Artificial Intelligence and Machine Learning. Morgan & Claypool Publishers, 2013. 1-141. [doi: 10.2200/S00513ED1V01Y201306AIM022]
|
| [25] |
Zielonka W. Infinite games on finitely coloured graphs with applications to automata on infinite trees. Theoretical Computer Science, 1998, 200(1-2): 135-183. [doi: 10.1016/S0304-3975(98)00009-7]
|
| [26] |
Muise C, McIlraith SA, Beck JC. Improved non-deterministic planning by exploiting state relevance. In: McCluskey L, Williams BC, Silva JR, Bonet B, eds. Proc. of the 22nd Int'l Conf. on Automated Planning and Scheduling (ICAPS 2012). AAAI, 2012. 172-180.
|
| [27] |
Gastin P, Oddoux D. Fast LTL to Büchi automata translation. In: Berry G, Comon H, Finkel A, eds. Proc. of the 13th Int'l Conf. on Computer Aided Verification (CAV 2001). Springer, 2001. 53-65. [doi: 10.1007/3-540-44585-4_6]
|
 2022, Vol. 33
2022, Vol. 33


