近年来, 深度神经网络凭借其能够用较短时间以较高的准确性解决多种复杂问题的优势, 在物体检测[1]、图像分类[2]、自然语言处理[3]、语音识别[4, 5]等众多领域上取得了优异的成绩. 然而, Szegedy等人[6]发现了深度神经网络的一个致命性弱点——通过施加人眼无法察觉的微小扰动, 诱使深度神经网络分类器错误地分类. 这些有意制作的能够诱导深度神经网络分类器分类错误的输入样本被称为对抗样本, 施加在其上的扰动被称为对抗扰动. 这个致命性弱点使得深度神经网络非常容易受到攻击(即对抗攻击), 尤其在图像方面的网络. 此外, 相同的图像扰动可以欺骗多个分类器(本文中也称为模型). 这种由一个模型生成的对抗样本能够以一定的概率欺骗另一个不同模型的性质, 称为对抗样本的可迁移性. 可迁移性使得对抗扰动可以跨模型甚至跨任务[7]转移, 更进一步地影响深度神经网络的安全性. 这些发现大大影响了深度神经网络在商业领域, 尤其是在安全攸关重要的领域的应用, 比如自动驾驶[8]、网络安全[9]等方面.
对抗样本对深度神经网络的威胁不仅激发了研究者对构建更具鲁棒性的深度神经网络的兴趣, 而且促发了如何构建有效健壮的对抗攻击的研究[10]. 这两者之间不断博弈且互相促进. 现有的对抗攻击工作大多数使用基于梯度的方法来生成对抗样本, 比如迭代梯度下降法[11]、投影梯度下降[12]、动量迭代快速梯度符号法[13]等. 在白盒设置下, 利用现有模型的知识(例如网络结构和网络参数), 这些攻击方法可以获得较高的成功率. 然而在黑盒设置下, 由于无法获得模型的内部信息, 这些攻击方法的成功率往往较低. 特别地, 在对经过对抗训练[14]或输入变换(例如图像变形[15]/去噪[16])的防御模型进行攻击时, 这些攻击方法的成功率被进一步降低.
基于迁移的攻击(transfer-based attack)[17, 18]就是一种致力于提高黑盒攻击成功率的方法, 该方法先在替代模型(源模型)上使用白盒攻击生成对抗样本, 再用生成的对抗样本去攻击未知的目标模型. 已有的基于迁移的对抗攻击通常使用基于梯度的方法来构造对抗样本, 从目前的研究进展而言, 仍然有较大的进度空间. 本文旨在设计一种新的能够提高对抗样本可迁移性的算法, 换句话说, 构造一个健壮的基于迁移的攻击算法.
本文把对抗样本的生成过程视为神经网络的训练过程, 把在替代模型上生成对抗样本的过程视为神经网络在训练数据上训练模型, 把用生成的对抗样本攻击目标模型的黑盒过程视为神经网络在测试数据上测试模型性能, 那么对抗样本的迁移能力就可以看成是神经网络的泛化能力. 因此, 本文主要从3个方面提高对抗样本的迁移能力: (1) 优化基于梯度的白盒攻击方法; (2) 对替代模型进行数据扩充; (3) 集成(ensemble)方法. 第1点, 本文通过改进优化算法避免其陷入较差的局部最优, 尽可能使算法搜索到更优的对抗样本, 更优的对抗样本往往具有更强的迁移性能; 第2点, 从本文使用提高泛化能力的角度看, 通过数据增强对图像进行几何变换, 丰富同类数据的表现形式, 这能够防止对抗样本对替代模型过拟合, 提高对抗样本在目标模型上的迁移成功率; 第3点, ensemble方法利用多个模型的信息, 即所谓“群体的智慧”, 能够很好地提高的模型泛化能力. 另一方面, 从集成攻击[19]的角度看, 攻击算法从只攻击一个源模型变成同时攻击源模型和扩充模型, 生成的对抗样本也从只能欺骗一个模型变成能够欺骗多个模型, 直觉和经验结果都表明, 能够同时欺骗多个模型的对抗样本更有可能成功迁移到其他的黑盒模型.
受MI-FGSM, NI-FGSM[20]的启发, 优化算法的选择能够影响对抗样本的生成及其可迁移性, 因此本文采用了自适应矩估计优化算法Adam的变体Rectified Adam (RAdam)算法, 并结合迭代快速符号下降法和利用目标函数(对抗样本生成对应的优化问题, 具体见第1.1节)的二阶导信息来生成对抗样本. 该方法能够有效地避免其陷入较差的局部最优, 提高对抗样本的可迁移性.
另一种能够提高对抗样本的可迁移性的方法是模型扩充. 现有的数据扩充方法大致可以分为3类: 空间变换[21]、颜色变换[22]和信息丢弃[23]. 在空间变换方面, DIM[17], TIM[18], SIM[20]等工作通过对输入图像的空间变换, 提高了对抗样本的可迁移性; 在信息丢弃方面, Xie等人[24]提出了基于输入的dropout方法; 而在颜色变换方面, 就作者所知, 在对抗攻击中尚未有充分完整的研究内容. 因此, 本文还应用颜色变换方法来进一步提高对抗样本的可迁移性.
本文的主要贡献如下:
(1) 提出了基于RAdam优化算法的对抗攻击方法RLI-FGSM. 该方法将RAdam优化算法与迭代快速符号下降法相结合, 并利用目标函数的二阶导信息来生成对抗样本.
(2) 提出了基于颜色变换的对抗攻击方法CIM. 该方法应用了颜色变换进行数据扩充, 填补并完善了颜色变换在对抗攻击的应用.
(3) 通过在ILSVRC 2012验证集的一些实验验证了本文方法的有效性, 且结果显示, 本文方法不仅在正常训练的模型上产生更高的成功率, 而且还打破了其他强大的对抗网络的防御机制.
本文第1节定义所用符号并介绍相关工作. 第2节对本文提出的对抗样本生成算法进行详细描述. 第3节为实验设置以及结果的分析讨论. 第4节总结全文.
1 符号定义和相关工作 1.1 定义表 1列举了本文所需了解的相关术语和其解释.
| 表 1 术语和符号定义 |
根据表 1, 对抗样本有两个条件: (i) 在原图像的微小抖动; (ii) 分类器分类错误. 本文使用L∞范数表示这个微小抖动. 因此, 这两个条件可以表示为
| $ \left. \begin{array}{l} \mathop {\min }\limits_\eta ||\eta |{|_\infty } = \mathop {\min }\limits_{{x^{adv}}} ||{x^{adv}} - x|{|_\infty } \hfill \\ {\text{s}}{\text{.t}}{\text{. }}f({x^{adv}}) = y,{\text{ }}f(x) = {y^{{\text{true}}}},{\text{ }}y \ne {y^{{\text{true}}}} \hfill \\ \end{array} \right\} $ | (1) |
通过形式化定义可以发现: 对抗样本的生成过程是一个优化问题, 即寻找导致错误分类的模型输入的最小扰动. 对于上述约束优化问题, 由于其求解的困难性, 通常引入模型训练中使用的损失函数J来间接解决, 其中, J通常为交叉熵损失函数(cross entropy loss). 对于无目标攻击(untargeted attack), 即只要求y≠ytrue的攻击而不指定输出标签目标y的类别, 因此要求输出标签y与真实标签ytrue的距离越大越好. 从深度神经网络的角度来看, 这可以等价要求损失函数J(xadv, ytrue)越大越好. 因此, 公式(1)可以转换成如下形式:
| $ \begin{array}{l}\underset{{x}^{adv}}{\mathrm{arg}\;\mathrm{max}}J({x}^{adv},{y}^{\text{true}}),\text{ s}\text{.t}\text{. }\left|\right|{x}^{adv}-x|{|}_{\infty }\le \varepsilon 或\\ \underset{\eta }{\mathrm{arg}\;\mathrm{max}}J(x+\eta ,{y}^{\text{true}}),\text{ s}\text{.t}\text{. }\left|\right|\eta |{|}_{\infty }\le \varepsilon \end{array}\} $ | (2) |
公式(2)中的约束项可以通过Clip函数对x进行剪切来控制x上的扰动大小而消除, 消除后的公式就是一个易于求解的无约束优化问题. 对于公式(2), 本文采用RAdam优化算法和目标函数的二阶导信息进行求解.
1.2 对抗攻击(1) FGSM (fast gradient sign method)
Goodfellow等人提出了快速梯度符号法(FGSM)[25], 在梯度方向上, 通过一大步更新生成使损失函数最大化的扰动, 更新规则如下:
| $ \left. \begin{array}{l} \eta = \varepsilon \cdot sign({\nabla _x}J(\theta ,x,{y^{{\text{true}}}})) \hfill \\ {x^{adv}} = x + \eta \hfill \\ \end{array} \right\} $ | (3) |
其中, ∇xJ是x的损失函数的梯度, θ是模型的参数.
(2) I-FGSM (iterative fast gradient sign method)
由于FGSM算法只涉及1次梯度更新, 有时1次更新不足以成功攻击且1次更新容易陷入局部最优值, Kurakin等人[11]提出了基于FGSM的迭代快速梯度符号法(I-FGSM), 采用小步长α多次迭代:
| $ x_{t + 1}^{adv} = x_t^{adv} + \alpha \cdot sign({\nabla _x}J({x^{adv}},{y^{{\text{true}}}})) $ | (4) |
(3) PGD (projected gradient descent)
Madry等人[12]提出了投影梯度下降(PGD), 这是一种比I-FGSM和FGSM更强大的梯度攻击. 它在允许的标准球内的随机点初始化搜索对抗样本, 然后运行I-FGSM方法多次迭代:
| $ x_{t + 1}^{adv} = Clip_x^\varepsilon \{ x_t^{adv} + \alpha \cdot sign({\nabla _x}J({x^{adv}},{y^{{\text{true}}}}))\} $ | (5) |
其中,
(4) MI-FGSM (momentum iterative fast gradient sign method)
Dong等人[13]提出了动量迭代快速梯度符号法(MI-FGSM), 动量法参数的更新过程中使用的是累积梯度gt, 其中, t表示在迭代次数. 对于当前梯度与上一步梯度指向相同方向的维度, gt+1增加; 而对于当前梯度与上一步梯度指向不同方向的维度, gt+1减少:
| $ \left. \begin{array}{l} {g_{t + 1}} = \mu \cdot {g_t} + \frac{{{\nabla _x}J(x_t^{adv},{y^{{\text{true}}}})}}{{||{\nabla _x}J(x_t^{adv},{y^{{\text{true}}}})|{|_1}}} \hfill \\ x_{t + 1}^{adv} = Clip_x^\varepsilon \{ x_t^{adv} + \alpha \cdot sign({g_{t + 1}})\} \hfill \\ \end{array} \right\} $ | (6) |
动量法得到了更快的收敛和减少振荡. 因为用I-FGSM生成对抗样本时仍然容易陷入较差的局部最大值和过拟合模型, 这样生成的对抗样本是不太可能在模型之间转移的. MI-FGSM将动量集成到迭代攻击中, 可以稳定更新方向, 有助于摆脱较差的局部极值, 减轻过拟合的影响. 因此, MI-FGSM能够提高对抗样本的可迁移性.
(5) NI-FGSM (Nesterov iterative fast gradient sign method)
Lin等人[20]提出了Nesterov迭代快速梯度符号法(NI-FGSM), 将Nesterov加速梯度引入迭代攻击中; 在MI-FGSM的基础上, NI-FGSM还利用了目标函数的二阶导信息, 使得攻击能够有效地向前看, 能够更容易、更快地摆脱局部极值差, 从而提高可迁移性:
| $ \begin{array}{l} x_t^{nes} = x_t^{adv} + \alpha \cdot \mu \cdot {g_t} \\ {g_{t + 1}} = \mu \cdot {g_t} + \frac{{{\nabla _x}J(x_t^{nes},{y^{{\text{true}}}})}}{{||{\nabla _x}J(x_t^{nes},{y^{{\text{true}}}})|{|_1}}} \\ x_{t + 1}^{adv} = Clip_x^\varepsilon \{ x_t^{adv} + \alpha \cdot sign({g_{t + 1}})\} \\ \end{array} $ | (7) |
(6) DIM (diverse inputs method)
Xie等人[17]提出了一种多样化输入方法DIM来改进对抗样本的可迁移性. DIM随机应用一组保持标签的变换(例如调整大小、裁剪和旋转)来训练图像, 并将变换后的图像输入分类器进行梯度计算:
| $ x_{t + 1}^{adv} = Clip_x^\varepsilon \{ x_t^{adv} + \alpha \cdot sign({\nabla _x}J(T({x^{adv}};p),{y^{{\text{true}}}};\theta ))\} $ | (8) |
其中, T(⋅)表示图像变换, p表示进行变换的概率.
(7) TIM (translation-invariant attack method)
Dong等人[18]提出了一种平移不变(TIM)攻击方法, 通过使用一组平移后的图像对对抗样本进行优化, 使对抗样本对被攻击的白盒模型的区分区域不那么敏感, 从而提高了对抗样本的可移动性. TIM证明了对图像进行平移操作后求梯度等价于将梯度与平移矩阵的所有权值组成的核进行卷积:
| $ x_{t + 1}^{adv} = x_t^{adv} + \alpha \cdot sign(W \cdot {\nabla _x}J({x^{adv}},{y^{{\text{true}}}})) $ | (9) |
其中, W表示平移矩阵.
(8) SIM (scale-invariant attack method)
Lin等人[20]还提出了另一种提高对抗样本可迁移性的方法SIM. SIM利用模型的尺度不变特性实现模型扩展, 提高对抗样本的可迁移性:
| $ \mathop {\arg\;\max }\limits_{{x^{adv}}} \frac{1}{m}\sum\limits_{i = 0}^m {J({S_i}({x^{adv}}),{y^{{\text{true}}}})} ,{\text{ s}}{\text{.t}}{\text{. }}||{x^{adv}} - x|{|_\infty } \leqslant \varepsilon $ | (10) |
其中, Si(x)=x/2i表示输入图像x的缩放副本, 缩放因子为1/2i; m表示缩放副本的数量.
(9) RD-DE-RF-IFGSM (resized-diverse-inputs, diversity-ensemble and region fitting method)
Zou等人[26]发现: 在不同输入的梯度中有许多垂直和水平条纹, 可以用来缓解TIM造成的梯度信息的丢失. 他们提出不同输入大小的方法(RDIM), 可以与TIM相结合来发挥更好的攻击性能. 此外, 他们还提出了多样性集成方法(DEM), 即RDIM的多尺度版本, 以进一步提高对抗样本的可移植性. 在前两个步骤之后, 再通过迭代将值拟合转化为区域拟合. RDIM和区域拟合不需要额外的运行时间, 这3个步骤可以很好地集成到其他攻击中.
(10) UAP (universal adversarial perturbations)
通用对抗扰动[27]指的是仅用一个小的图像扰动就能以高概率欺骗深度神经网络分类器, 使分类器对大部分图像分类错误. 换句话说, 就是需要找到一个对抗扰动η, 这个扰动可以加到所有的样本点上, 而且会以1−δ的概率让对抗样本被分类错误:
| $ \mathop P\limits_{x \sim \mu } (f(x + \eta ) \ne f(x)) \geqslant 1 - \delta ,{\text{ s}}{\text{.t}}{\text{. }}||\eta |{|_\infty } \leqslant \varepsilon . $ |
本节将详细描述本文的攻击算法RLI-CI-FGSM. 第2.1节先简单介绍了Adam和RAdam算法, 第2.2节介绍了基于RAdam的攻击方法RLI-FGSM, 第2.3节介绍了基于颜色变换不变的攻击方法CIM. 最后, 第2.4节给出了这两者的合成攻击算法RLI-CI-FGSM.
2.1 Adam和RAdam算法本文所采用的Rectified Adam优化算法是Adam算法的一种变体, 因此在介绍RAdam算法之前, 先对Adam算法进行简单的说明. Adam (adaptive moment estimation)[28]是一种只需要一阶梯度和很少的内存需求的有效的随机优化方法, 该方法根据梯度的一阶和二阶矩估计计算不同参数下的个体自适应学习速率, 可以表示为
| $ m_{t}=\beta_{1} \cdot m_{t−1}+(1−\beta_{1}) \cdot g_{t} $ | (11) |
| $ {v_t} = {\beta _2} \cdot {v_{t - 1}} + (1 - {\beta _2}) \cdot g_t^2 $ | (12) |
其中, mt和vt分别表示梯度的一阶矩(表示梯度均值)和二阶矩(表示方差), β1, β2表示衰减率, gt表示在迭代次数为t时的累加梯度. 用平均移动(moving average)来对一阶矩和二阶矩进行估计时, 因为mt和vt被初始化为0向量, 导致矩估计偏向于0, 所以, Adam使用偏差校正解决初始化偏差对移动平均的影响:
| $ {\hat m_t} = \frac{{{m_t}}}{{1 - \beta _1^t}} $ | (13) |
| $ {\hat v_t} = \frac{{{v_t}}}{{1 - \beta _2^t}} $ | (14) |
接着, 使用上述公式更新Adam的参数:
| $ {\theta _{t + 1}} = {\theta _t} - \frac{\eta }{{\sqrt {{{\hat v}_t}} + \varepsilon '}}{\hat m_t} $ | (15) |
其中,
Liu等人[29]发现: 由于训练早期样本的缺乏, 自适应学习率vt的方差过大, 导致陷入较差的局部最优. 因此, Liu等人提出了RAdam算法, 引入了修正项rt来修正其自适应学习率, 稳定其早期无边界的方差. 同时, 实验表明, RAdam算法也能加速收敛和改进泛化性能. RAdam算法更新规则如下:
| $ {\rho _\infty } = \frac{2}{{1 - {\beta _2}}} - 1 $ | (16) |
| $ {\rho _t} = {\rho _\infty } - 2t \cdot \beta _2^t/(1 - \beta _2^t) $ | (17) |
其中, mt, vt和
当方差易处理时, 如ρt > 4:
| $ {l_t} = \sqrt {(1 - \beta _2^t)/{v_t}} $ | (18) |
| $ {r_t} = \sqrt {\frac{{({\rho _t} - 4)({\rho _t} - 2){\rho _\infty }}}{{({\rho _\infty } - 4)({\rho _\infty } - 2){\rho _t}}}} $ | (19) |
| $ {\theta _t} = {\theta _{t - 1}} - {\alpha _t}{r_t}{\hat m_t}{l_t} $ | (20) |
当方差不易处理时, 如ρt≤4:
| $ {\theta _t} = {\theta _{t - 1}} - {\alpha _t}{\hat m_t} $ | (21) |
其中, ρ∞表示近似SMA (simple moving average)的最大长度, ρt表示近似SMA的长度, αt表示步长, lt表示RAdam中的自适应学习率, rt表示方差校正项, θt表示结果参数.
具体来说, 在训练初期, 自适应学习率vt的方差过大甚至可以趋于无穷大, 这时, Adam的更新方法将不再可靠, 所以RAdam在初期退化成带动量的SGD (随机梯度下降), 即如公式(21)所示, 不再使用自适应学习率. RAdam使用了只与t有关的参数ρt控制算法是否退化. 当β2=0.999 (Adam推荐的参数值), 在t=1−4时(即ρt≤4), 方差过大不易处理, 方差校正项rt会出现一定的震荡, 甚至会出现对负数开根号的情况; 而在t > 4时(即ρt > 4), 方差不再有趋于无穷大的风险易于处理, rt的更新趋于稳定. 因此, RAdam设置ρt≤4时, 算法退化成带动量的SGD; 设置ρt > 4, 算法不退化, 使用方差校正项rt进一步稳定算法.
2.2 RI-FGSM和RLI-FGSM方法本文首先将RAdam算法集成到基于梯度的迭代攻击中, 构建一个健壮的对抗攻击, 称为RI-FGSM. 从g0=0开始, RI-FGSM的更新过程形式化如下:
| $ {g_t} = \mu \cdot {g_{t - 1}} + \frac{{{\nabla _x}J(x_{t - 1}^{adv},{y^{{\text{true}}}})}}{{||{\nabla _x}J(x_{t - 1}^{adv},{y^{{\text{true}}}})|{|_1}}} $ | (22) |
αt, rt,
当方差易处理时, 如ρt > 4:
| $ x_t^{adv} = Clip_x^\varepsilon \{ x_{t - 1}^{adv} + {\alpha _t}{r_t} \cdot sign({\hat m_t} \cdot {l_t})\} $ | (23) |
当方差不易处理时, 如ρt≤4:
| $ x_t^{adv} = Clip_x^\varepsilon \{ x_{t - 1}^{adv} + {\alpha _t} \cdot sign({\hat m_t})\} $ | (24) |
其中, gt表示在迭代次数为t时的累加梯度, μ是gt的衰减因子, sign是符号函数.
受Nesterov加速梯度的启发, 本文在RI-FGSM的基础上再利用目标函数的二阶导信息, 使得攻击能够有效地向前看(look ahead), 构造了RLI-FGSM算法. 具体而言, RLI-FGSM中的梯度不是根据当前参数位置
(1) 计算新参数近似位置
当方差易处理时, 如ρt > 4:
| $ x_t^{lookahead} = x_t^{adv} + {\alpha _t}{r_t} \cdot sign({\hat m_t} \cdot {l_t}) $ | (25) |
当方差不易处理时, 如ρt≤4:
| $ x_t^{lookahead} = x_t^{adv} + {\alpha _t} \cdot sign({\hat m_t}) $ | (26) |
(2) 根据新参数近似位置更新梯度:
| $ {g_{t + 1}} = \mu \cdot {g_t} + \frac{{{\nabla _x}J(x_t^{lookahead},{y^{true}})}}{{||{\nabla _x}J(x_t^{lookahead},{y^{true}})|{|_1}}} $ | (27) |
(3) 更新
当方差易处理时, 如ρt > 4:
| $ x_{t + 1}^{adv} = x_t^{adv} + {\alpha _{t + 1}}{r_{t + 1}} \cdot sign({\hat m_{t + 1}} \cdot {l_{t + 1}}) $ | (28) |
当方差不易处理时, 如ρt≤4:
| $ x_{t + 1}^{adv} = x_t^{adv} + {\alpha _{t + 1}} \cdot sign({\hat m_{t + 1}}) $ | (29) |
除了为对抗攻击考虑一个更好的优化算法外, 本文还考虑通过模型扩充来提高对抗样本的可迁移性. 在同一模型上, 若原始图像和经变换后的图像的损失值是相似的, 则称这种变换为保损变换. 通过保损变换, 本文可以从原模型推导出一个模型集合, 实现模型扩充.
为了得到保损变换, 本文发现深度神经网络具有颜色变换不变性并进行了实验验证, 即适量地改变深度神经网络的颜色特性, 若变化前后网络的损失值可以忽略不计. 因此, 颜色变换可以作为一种模型扩充方法. 在上述分析的驱动下, 本文提出了一种颜色变换不变方法CIM. CIM通过对模型的颜色扩充, 包含亮度、色相、对比度、饱和度这4个特征, 优化了对输入图像的对抗扰动.
令Ci(x)表示颜色变换不变性, CIM方法描述如下:
| $ \left. \begin{array}{l} \mathop {\arg\;\max }\limits_{{x^{adv}}} J({C_i}({x^{adv}}),{y^{{\text{true}}}}),{\text{ }}C = \{ {C_1},{C_2},{C_{3,}}{C_4}\} \hfill \\ ||{x^{adv}} - x|{|_\infty } \leqslant \varepsilon \hfill \\ \end{array} \right\} $ | (30) |
其中, C1, C2, C3, C4分别表示亮度、色相、对比度、饱和度的抖动变化函数.
(1) 对于亮度特征, 本文改变整张RGB图片的亮度, 即在图片x上每一个像素值上添加一个范围在[−max delta, max delta)之间的调整因子δ1, 调整亮度后的图像为
| $ C_{1}(x)=x+δ_{1} $ | (31) |
(2) 对于色相特征, 本文先把图片
| $ C_{2}(x)=RGB(HSV(x)+_{H}δ_{2})$ | (32) |
(3) 对于对比度特征, 本文对RGB图片的每个通道都计算通道中图像像素的均值, 然后根据均值调整每个像素的每个分量, 如下所示:
| $ C_{3}(x_{i})=(x_{i}−mean)×δ_{3}+mean $ | (33) |
其中, δ3为对比度调整因子.
(4) 对于饱和度特征, 本文先把图片x从RGB颜色空间转换成HSV颜色空间, 并将饱和度(S)通道乘以饱和度因子δ4和剪切来调整图像饱和度, 最后再将图像转换回RGB. 饱和度特征调整函数如下所示:
| $ C_{4}(x)=RGB(Clip(HSV(x)×_{S}δ_{4})) $ | (34) |
具体的调整因子的选择在后文第3.2节中给出. 利用CIM, 本文不需训练一组模型来攻击, 而是通过模型扩充来有效地实现对多个模型的集成攻击. 更重要的是, 它可以帮助避免对被攻击的白盒模型的过拟合, 并生成更多可迁移的对抗样本.
2.4 攻击算法本文提出的RLI-CI-FGSM攻击算法是将基于优化算法的攻击方法RLI-FGSM和基于模型扩充的方法CIM结合起来的一个更强大的攻击方法, 具体伪代码如算法1所示.
算法1. RLI-CI-FGSM.
输入: 干净的样本x及其对应的真实标签ytrue, 分类器f, 损失函数J; 最大扰动ε, 最大迭代次数T, 衰减系数μ, 颜色变换扩充的模型数量i.
输出: 对抗样本xadv.
1. α0=ε //初始步长
2. g0=0;
3. for t=0 to T−1 do
4. g=0
5. calculate
6. for i=0 to 4 do //i=0表示未经颜色变换, i=1, 2, 3, 4表示经亮度不变性、色相不变性、对比度不变性、饱和度不变性这4种子方法变换
7. calculate the gradients:
8. sum the gradients:
9. calculate average gradients:
10. update
11. update
12. Return xadv
3 实验本节将介绍实验结果, 以验证本文所提方法的有效性. 第3.1节介绍了实验设置, 包括数据集、模型和超参数的设置. 第3.2节验证了深度神经网络的颜色变换不变特性. 第3.3节研究了初始步长对攻击成功率的影响, 挑选出了合适的初始步长. 第3.4节在单一模型下, 分别将本文方法与基于优化的方法和基于模型扩充的方法进行了比较. 第3.5节在多模型集合的环境下, 将本文方法与基线方法进行集成和比较.
3.1 实验设置(1) 数据集
本文从ILSVRC 2012验证集的1 000个类别中随机选择了1 000张图片, 这些图片几乎被所有测试模型正确分类. ILSVRC 2012是ImageNet Large Scale Visual Recognition Challenge 2012竞赛的数据集, 是图像分类数据集中最常用的测试数据集和预训练数据集之一.
(2) 模型
在正常训练的模型方面, 本文考虑了Inception-v3 (Inc-v3)[30], Inception-v4 (Inc-v4)[31], Inception-Resnet-v2 (IncRes-v2)[31]和Resnet-v2-101 (Res-101)[32].
在对抗训练的模型方面, 本文考虑Inc-v3ens3, Inc-v3ens4和IncRes-v2ens[32].
(3) 超参数设置
本文设置最大扰动ε=16, 迭代次数T=10, RLI-FGSM的步长α=ε, 其余方法的步长α=ε∕T. 对于MI-FGSM, 本文采用默认的衰减因子μ=1.0; 对于DIM, 变换概率设为0.5; 对于TIM, 本文采用大小为7×7的高斯核. 对于CIM, 亮度调整因子δ1∈[−0.9, 0.9], 色相调整因子δ2=0.1, 对比度调整因子δ3=0.2, 饱和度调整因子δ4=0.6.
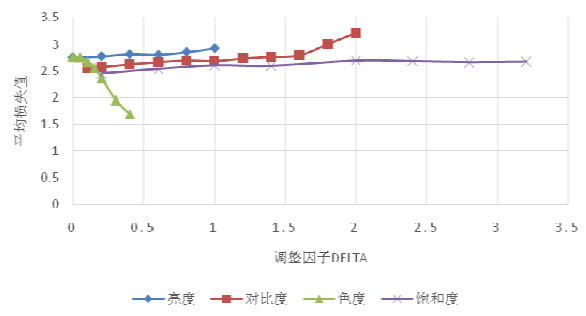
3.2 颜色变换不变特性为了验证深度神经网络的尺度不变特性, 本文从ImageNet数据集中随机选取1 000幅原始图像, 对图像的亮度、色相、对比度、饱和度这4个颜色特征分别进行调整. 然后将原始图像和进行了4种调整后的图像输入测试模型Inc-v3中, 每张输入图像的损失值由模型给出, 图 1给出了不同输入下的1 000张图片的平均损失值.
|
图 1 Inc-v3模型在亮度、色相、对比度、饱和度这4个颜色特征影响下, 在1 000张图片上的平均损失值 |
如图 1所示, 4个颜色特征的调整因子取值范围都不同, 根据观察, 取值范围的选择综合考虑了模型损失值和攻击目标模型的成功率. 本文中, 对于亮度特征, 将调整因子大小保持在[0.1, 0.9]间时, 原始图像和变换图像的损失值相差不大, 因此, 我们假设深度模型在此范围内有颜色变换不变属性; 对于对比度特征, 将调整因子大小保持在[0.2, 1.5]间时, 原始图像和变换图像的损失值相差不大, 因此, 我们假设深度模型在此范围内有对比度变换不变属性; 对于色相特征, 将调整因子大小保持在[0, 0.1]间时, 原始图像和变换图像的损失值相差不大, 因此, 我们假设深度模型在此范围内有色相变换不变属性; 对于饱和度特征, 将调整因子大小保持在[0.6, 3.2]间时, 原始图像和变换图像的损失值相差不大, 因此, 我们假设深度模型在此范围内有饱和度变换不变属性.
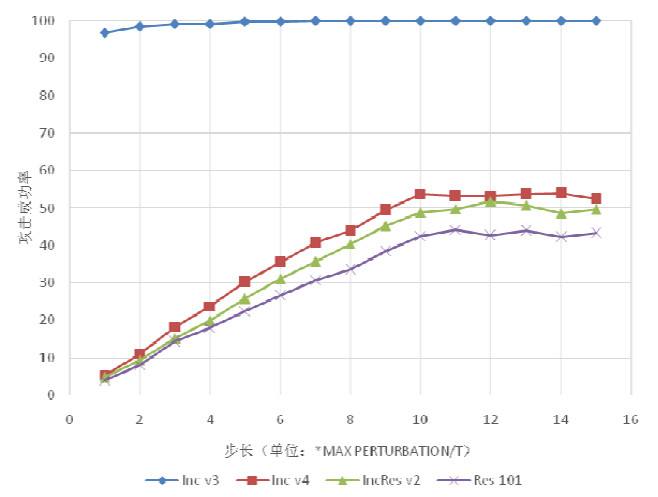
3.3 步长接下来研究初始步长对攻击成功率的影响, 本节在不同步长下, 以Inc-v3为源模型生成对抗样本攻击Inc-v3, Inc-v4, IncRes-v2, Res-101模型, 结果如图 2所示. 不同于前文提到的其他基于梯度的攻击, RLI-FGSM的步长是自适应变化的, 因此, RLI-FGSM需要通过实验选择一个合适的初始步长. 本节中, 初始步长的选择范围是ε/T−15×ε/T, 间隔为ε/T. 如图 2所示, 可以很容易地观察到, 白盒攻击在初始步长α=3×ε/T时, 攻击成功率已经接近100%. 而3条黑盒攻击的曲线在初始步长α=10×ε/T到α=12×ε/T时具有最高的攻击成功率, 在α > 12×ε/T时攻击成功率不再继续增加. 因此, 本文选择α=10×ε/T作为初始步长, 又因迭代次数T=10, 最后α=ε.
|
图 2 不同初始步长设置下, 以Inc-v3为源模型攻击Inc-v3, Inc-v4, IncRes-v2, Res-101模型的攻击成功率 |
3.4 攻击单个模型
本节介绍在单个模型上的对抗攻击实验. 本文只在Inc-v3, Inc-v4, IncRes-v2, Res-101模型上生成对抗样本, 并在正常训练和对抗训练的7个模型上测试它们. 表 2给出了Inc-v3, Inc-v4, IncRes-v2, Res-101这4个模型生成的对抗样本对所有7个模型的攻击成功率, 其中, *表示白盒攻击, 无*则表示黑盒攻击.
| 表 2 在单模型设置下, 不同攻击方法在Inc-v3, Inc-v4, IncRes-v2, Res-101模型生成的对抗样本对7种模型的对抗攻击成功率(%), *表示白盒攻击 |
从表 2可以看出, 本文提出的方法RLI-FGSM能够有效生成迁移性较高的对抗样本. RLI-FGSM应用在Inc-v3, Inc-v4, IncRes-v2, Res-101这4个模型生成的对抗样本在正常训练的4个模型的平均攻击成功率分别为62.4%, 65.2%, 66.2%, 67.9%, 在对抗训练的3个模型的平均攻击成功率分别为11.1%, 13.4%, 16.0%, 19.0%. 而且与已有的基于优化方法(即I-FGSM, MI-FGSM和NI-FGSM)比较, RLI-FGSM具有更高的攻击成功率. 具体地说, RLI-FGSM在本实验中的平均攻击成功率分别比I-FGSM, UAP, MI-FGSM和NI-FGSM高22.7%, 11.6%, 6.1%, 1.1%. 此外, 本文的集成攻击方法RLI-CI-FGSM在正常训练的模型上比RLI-FGSM提升了10%− 20%的成功率, 在对抗训练的模型上比RLI-FGSM提升了0%−20%的成功率.
本文还将RLI-CI-FGSM分别与TIM和DIM集成在一起, 并将集成后的方法RLI-CI-TIM和RLI-CI-DIM分别与TIM和DIM进行比较. 比较结果见表 3和表 4.
| 表 3 在单模型设置下, 针对7种模型进行对抗攻击的成功率(%), 对抗样本分别使用TIM和RLI-CI-TIM在Inc-v3, Inc-v4, IncRes-v2模型上制作, *表示白盒攻击 |
| 表 4 在单模型设置下, 针对7种模型进行对抗攻击的成功率(%), 对抗样本分别使用DIM和RLI-CI-DIM在Inc-v3, Inc-v4, IncRes-v2, Res-101模型上制作, *表示白盒攻击 |
由表 3和表 4可知, RLI-CI-FGSM的集成对攻击成功率的提升效果显著. 具体地说, 在Inc-v3, Inc-v4, IncRes-v2, Res-101模型上, RLI-CI-TIM生成的对抗样本比TIM分别提升了平均20.6%, 19.1%, 16.6%, 15.6%的成功率. RLI-CI-DIM生成的对抗样本比DIM分别提升了平均29.0%, 32.2%, 29.9%, 22.8%的成功率.
由以上可知, RLI-CI-FGSM能够有效地提高对抗样本的可迁移性.
3.5 攻击模型集合虽然表 2的结果表明RLI-FGSM和颜色变换方法CIM可以显著提高对抗样本的可迁移性, 但黑盒设置下, 在攻击对抗训练网络时, 它们仍然相对较弱. 因此, 本节考虑同时攻击多个模型来提高所有方法的攻击成功率, 进一步展示我们方法的性能. 攻击模型集合能提高成功率的原因是——一个样本是多个模型的对抗样本, 比是单个模型的对抗样本更困难, 对样本的要求更高, 那么它成功转移到另一个黑盒模型上的概率就越高.
本节使用TIM, RLI-CI-TIM, DIM, RLI-CI-DIM, TI-DIM和RLI-CI-TI-DIM来攻击正常训练模型Inc-v3, Inc-v4, IncRes-v2, Res-101的集合. 如表 5所示, 本文提出的方法提高了所有基线攻击的攻击成功率, RLI-CI- TI-DIM攻击能够以平均95.6%的成功率欺骗正常训练模型, 能够以平均72.0%的成功率欺骗对抗训练模型.
| 表 5 在多模型设置下, 针对7种模型进行对抗攻击的成功率(%), 对抗样本分别使用RLI-FGSM, RLI-CI-FGSM, TIM, RLI-CI-TIM, DIM, RLI-CI-DIM, TI-DIM, RLI-CI-TI-DIM在Inc-v3, Inc-v4, IncRes-v2, Res-101模型的集成模型上制作, *表示白盒攻击 |
4 总结
本文提出了一种新的基于转移的对抗攻击方法RLI-CI-FGSM. RLI-CI-FGSM由基于RAdam迭代快速梯度符号法(RLI-FGSM)和颜色变换不变攻击法(CIM)共同组成. RLI-FGSM的目标是在基于梯度的攻击中采用RAdam优化算法, 并利用目标函数的二阶导信息, 与迭代快速梯度符号法相结合. CIM的目标是利用模型的颜色变换不变特性实现模型扩充. 本文利用上述算法提高了对抗样本的可迁移性. 此外, RLI-CI-FGSM通过与TIM和DIM攻击的集成, 可以进一步构造一个更强大的基于转移的攻击, 提高对抗样本的可迁移性. 实验结果表明, 本文的方法不仅在正常训练的模型上产生更高的成功率, 而且还打破了其他强大的对抗网络的防御机制.
| [1] |
Redmon J, Farhadi A. Yolov3: An incremental improvement. arXiv: 1804.02767, 2018.
|
| [2] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv: 1409.1556, 2014.
|
| [3] |
Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. In: Zoubin G, ed. Advances in Neural Information Processing Systems 27 (NIPS 2014). 2014. 3104-3112.
|
| [4] |
Xiong W, Droppo J, Huang X, Seide F, Seltzer M, Stolcke A, Yu D, Zweig G. Achieving human parity in conversational speech recognition. arXiv: 1610.05256, 2016.
|
| [5] |
Zhang Z, Geiger J, Pohjalainen J, Mousa AED, Jin W, Schuller B. Deep learning for environmentally robust speech recognition: An overview of recent developments. ACM Trans. on Intelligent Systems and Technology (TIST), 2018, 9(5): Article No.49.
[doi:10.1145/3178115] |
| [6] |
Szegedy C, Zaremba W, Sutskever I, Bruna J, Erhan D, Goodfellow I, Fergus R. Intriguing properties of neural networks. arXiv: 1312.6199, 2013.
|
| [7] |
Lu, Y, et al. Enhancing cross-task black-box transferability of adversarial examples with dispersion reduction. In: Proc. of the 2020 IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR 2020). 2020. 940-949.
|
| [8] |
Ren K, Wang Q, Wang C, Qin Z, Lin X. The security of autonomous driving: Threats, defenses, and future directions. Proc. of the IEEE, 2019, 108(2): 357-372.
|
| [9] |
Ibitoye O, Abou-Khamis R, Matrawy A, Shafiq MO. The threat of adversarial attacks on machine learning in network security—A survey. arXiv: 1911.02621, 2019.
|
| [10] |
Pan WW, Wang XY, Song ML, Chen C. Survey on generating adversarial examples. Ruan Jian Xue Bao/Journal of Software, 2020, 31(1): 67-81(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5884.htm [doi:10.13328/j.cnki.jos.005884] |
| [11] |
Kurakin A, Goodfellow IJ, Bengio S. Adversarial examples in the physical world. In: Artificial Intelligence Safety and Security. Chapman and Hall/CRC, 2018. 99-112.
|
| [12] |
Madry A, Makelov A, Schmidt L, Tsipras D, Vladu A. Towards deep learning models resistant to adversarial attacks. arXiv: 1706.06083, 2017.
|
| [13] |
Dong YP, Liao FZ, Pang TY, Su H, Zhu J, Hu XL, Li JG. Boosting adversarial attacks with momentum. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 9185-9193.
|
| [14] |
Tramer F, Kurakin A, Papernot N, Boneh D, McDaniel P. Ensemble adversarial training: Attacks and defenses. arXiv: 1705.07204, 2017.
|
| [15] |
Xie CH, Wang JY, Zhang ZS, Ren Z, Yuille A. Mitigating adversarial effects through randomization. arXiv: 1711.01991, 2017.
|
| [16] |
Liao FZ, Liang M, Dong YP, Pang TY, Hu XL, Zhu J. Defense against adversarial attacks using high-level representation guided denoiser. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 1778-1787.
|
| [17] |
Xie CH, Zhang ZS, Zhou YY, Bai S, Wang JY, Ren Z, Yuille AY. Improving transferability of adversarial examples with input diversity. In: Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition. 2019. 2730-2739.
|
| [18] |
Dong YP, Pang TY, Su H, Zhu J. Evading defenses to transferable adversarial examples by translation-invariant attacks. In: Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition. 2019. 4312-4321.
|
| [19] |
Hang J, Han K, Chen H, et al. Ensemble adversarial black-box attacks against deep learning system. Pattern Recognition, 2020, 101: Article No. 107184.
|
| [20] |
Lin JD, Song CB, He K, Wang LW, Hopcroft JE. Nesterov accelerated gradient and scale invariance for adversarial attacks. arXiv: 1908.06281, 2019.
|
| [21] |
Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural net-works. In: Bartlett PL, ed. Proc. of the 26th Annual Conf. on Neural Information Processing Systems. Lake Tahoe, 2012. 1106-1114.
|
| [22] |
Howard AG. Some improvements on deep convolutional neural network based image classification. arXiv: 1312.5402, 2013.
|
| [23] |
Chen PG, Liu S, Zhao HS, Jia JY. GriMask data augmentation. arXiv: 2001.04086, 2020.
|
| [24] |
Xie PF, Wang LY, Qin RX, Qiao K, Shi SH, Hu G, Yan B. Improving the transferability of adversarial examples with new iteration framework and input dropout. arXiv: 2106.01617, 2021.
|
| [25] |
Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. arXiv: 1412.6572, 2014.
|
| [26] |
Zou J, Pan Z, Qiu J, Liu X, Rui T, Li W. Improving the transferability of adversarial examples with resized-diverse-inputs, diversity-ensemble and region fitting. In: Proc. of the European Conf. on Computer Vision. Springer, 2020. 563-579.
|
| [27] |
Moosavi-Dezfooli SM, Fawzi A, Fawzi O, Frossard P. Universal adversarial perturbations. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 1765-1773.
|
| [28] |
Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv: 1412.6980, 2014.
|
| [29] |
Liu LY, Jiang HM, He PC, Chen WZ, Liu XD, Gao JF, Han JW. On the variance of the adaptive learning rate and beyond. arXiv: 1908.03265, 2019.
|
| [30] |
Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z. Rethinking the inception architecture for computer vision. In: Proc. of the 2016 IEEE Conf. on Computer Vision and Pattern Recognition. Las Vegas: IEEE Computer Society, 2016. 2818-2826.
|
| [31] |
Szegedy C, Ioffe S, Vanhoucke V, Alemi AA. Inception-v4, inception-ResNet and the impact of residual connections on learning. In: Singh SP, ed. Proc. of the 31st AAAI Conf. on Artificial Intelligence. San Francisco: AAAI, 2017. 4278-4284.
|
| [32] |
He K, Zhang X, Ren S, Sun J. Identity mappings in deep residual networks. In: Leibe B, ed. Proc. of the 14th European Conf. Amsterdam: Springer, 2016. 630-645.
|
| [10] |
潘文雯, 王新宇, 宋明黎, 陈纯. 对抗样本生成技术综述. 软件学报, 2020, 31(1): 67-81.
http://www.jos.org.cn/1000-9825/5884.htm [doi:10.13328/j.cnki.jos.005884] |
 2022, Vol. 33
2022, Vol. 33


