聚类分析旨在从无标签数据中准确有效地发现样本类簇, 其具有重要的科学意义与实际价值. 大数据时代的到来和新媒体的发展, 催生出了大规模的数据样本, 但为其标记类别标签无疑需要耗费大量人力物力. 聚类技术的发展, 为这些数据的特征提取与潜在结构发现提供了强有力的帮助[1].
目前, 主流的机器学习研究框架大多关注样本数据的某一种形式, 我们称其为单视图学习, 其中, 文本和图片等某种形式被称为视图[2], 不同的文本表示或不同的图片增广均可被视为不同视图. 如: 同一条新闻经由不同媒体报道可能有不同的文字描述, 由此可生成不同的文本表示, 这样的不同表示通常被视为多视图数据. 对人类而言, 我们的大脑往往可以同时处理多种视图的信息, 提取不同视图间的互补信息和一致信息并融合, 从而做出更准确、客观的决策. 如: 我们可以对不同媒体报道的同一新闻在大脑中进行整合和提取, 从而推论出新闻事件的较全面的细节. 换言之, 多个视图的信息输入, 使得我们人类可以更全面、客观、多样化地看待问题. 真实世界中的多视图数据各种各样, 不同视图可能有相同的表达形式, 也可能不尽相同. 例如, 上述提到的同样新闻可以被不同的新闻媒体报道, 因此产生了来自不同视图的文本特征; 同样的情感极性既可以通过不同图片来表达, 如微笑、大笑等不同表情图片均可表示开心的情绪, 也可以直接用文字表达, 由此产生了具有不同特征表示形式的视图数据. 当视图之间具有不同表达形式时, 通常被称为多模态数据. 本篇工作主要关注具有相同表达形式的多视图数据. 但不可否认的是, 无论视图特征的形式如何变化, 他们都只是同一样本对象的不同表示. 因而, 不同视图之间必然存在着某种程度的联系[3]. 为了探索不同视图的相关性, 同时挖掘多个视图的特征, 发现其一致性与差异性知识, 使得机器学习算法进一步接近人类智能, 面向多视图学习的研究应运而生.
多视图聚类学习旨在从多个视图中探索并利用互补信息和一致信息, 从而生成一个相比单视图聚类更准确、更鲁棒的数据划分结果[4]. 谱聚类方法由于其对数据结构没有太多假设要求且学习性能优秀, 一直是无监督数据分析中的极受欢迎的技术之一[5]. 多视图谱聚类方法首先从所有视图的邻接矩阵中学习一个融合图, 然后对融合图进行聚类, 得到最后的划分结果. 近年来, 多视图谱聚类算法已经取得了较好的性能, 但是仍存在一些不足: 首先, 其面向复杂数据分布时的时间效率以及性能均不理想; 其次, 大多数方法是基于传统机器学习或者只着眼于浅层模型, 无法充分挖掘样本数据的深层特征, 因此所构建的邻接图的知识表示能力有限[6]. 为进一步提高多视图谱聚类算法解决真实场景问题的能力, 同时考虑尽可能完善上述不足, 众多学者考虑利用深度学习框架提升多视图谱聚类算法的深层特征学习能力. 而多视图谱聚类算法与深度神经网络结合的关键性难点在于谱聚类损失函数与神经网络的联合优化问题. 具体来说, 谱聚类要求解决矩阵分解问题使得联合优化异常困难, 因为矩阵分解的梯度无法被后向传播以达到优化神经网络的目的. 谱网络(spectral clustering using deep neural networks, SpectralNet)[7]采用约束随机优化技术训练神经网络, 同时优化谱聚类损失, 有效解决了联合优化问题. 但是SpectralNet仅考虑了单视图场景, 忽略了多视图之间的互补信息和关联知识. 多视图谱聚类网络(multi-view spectral clustering network, MvSCN)[6]将其拓展到多视图场景, 挖掘视图内一致性与视图间差异性特征, 大大提升了算法性能. 与MvSCN类似, 本篇工作同样关注深度多视图谱聚类网络, 但与之不同的是: 本文主要考虑多视图数据之间既存在单视图局部不变性, 也隐含多视图全局一致性, 因此分别针对单视图和多视图引入局部学习层与全局学习层以获得特有嵌入和共享嵌入, 保证多视图特征的特有性和一致性, 增强算法鲁棒性.
解决深度多视图谱聚类任务的关键挑战主要有以下两点.
1) 如何建立有效的多视图框架并获得包含足够丰富特征的一致性谱嵌入? 与传统多视图谱聚类算法类似, 深度多视图谱聚类利用神经网络层(如全连接层)学习原始数据样本的低秩表示, 并对多视图谱嵌入进行融合;
2) 如何构建样本对间的近邻关系? 邻接矩阵对谱聚类算法有重要影响, 其不仅需要包含丰富的近邻关系, 还需要体现样本对间的隐含关联.
为解决上述挑战, 本文提出了一种知识迁移下的深度一致性多视图谱聚类网络(knowledge transferring based deep consensus network for multi-view spectral clustering, CMvSC), 利用深度学习框架学习多视图数据的谱嵌入, 同时采用结合对比损失的孪生网络构建样本对间的近邻关系. 首先, 为挖掘每个视图的局部不变性, 局部学习层被提出用于获得单视图的特有嵌入, 挖掘单视图内的隐含关联; 同时, 为进一步学习多视图间的全局一致性, 全局学习层被设计以挖掘多视图的共享嵌入; 最后, 我们借鉴传统多视图谱聚类算法中的正交约束, 在CMvSC的顶层引入了正交约束层, 以避免“无效解”问题.
本文工作的主要贡献包括以下5个方面.
1) 设计了一种局部学习层, 用于挖掘单视图特有嵌入. 针对多视图数据中每个视图内具有局部不变性, 我们设计局部学习层深入挖掘单视图有效特征, 同时保证学习到的特有嵌入仍然保持原始相似结构;
2) 设计了一种全局学习层, 用于学习多视图共享嵌入. 考虑多视图数据是同一样本的不同特征表示, 不同视图间具有一定的全局一致性, 我们构建了一种全局学习层, 挖掘不同视图间的一致性特征;
3) 设计了一种基于对比学习的近邻学习框架. 为了同时考虑正负样本的相似性影响, 挖掘样本对间的隐含关联, 我们设计了一种孪生网络, 用于实现自适应的近邻学习, 结合基于距离的对比损失, 可获得具有更鲁棒的特征表征能力的邻接矩阵;
4) 引入了一种正交约束层, 对特征嵌入进行正交约束. 为避免特征嵌入出现“无效解”, 我们在一致性多视图谱聚类网络顶层引入了一种正交约束层, 保证谱嵌入的正交性;
5) 不同数据集上的实验结果表明, 我们提出的CMvSC可以有效解决多视图聚类问题.
1 相关工作在本节中, 我们将讨论与所提出的CMvSC相关的工作, 主要包括多视图聚类和深度聚类.
1.1 多视图聚类近年来, 多视图聚类方法被广泛研究. 多视图聚类旨在整合多个视图的特征, 学习一致性特征表示, 从而将样本划分为多个类簇. 传统的多视图聚类算法可以分为4类.
1) 基于协同训练的方法[4, 8]: 该方法利用一个视图的先验知识或习得的知识来强化另一个视图的聚类性能, 迭代发现与所有视图都足够相近的一致性视图;
2) 多核学习[9, 10]: 该方法根据不同视图定义不同的核函数, 然后线性或非线性地结合所有核以提升聚类性能;
3) 基于子空间的方法[11, 12]: 该方法结合非负矩阵分解挖掘多视图样本之间的关系, 学习一个公共的低维特征表示作为一致性子空间用于聚类任务;
4) 基于图的方法[13, 14]: 该方法旨在所有视图中寻找一个表示样本之间关联性的融合图, 然后利用谱聚类的方法对图进行划分, 从而获得最终聚类结果.
基于子空间的方法和基于图的方法由于其充分学习多视图数据间的补充信息和共享信息, 在数据划分任务上获得了较好的性能. Cao等人提出了一种多样性诱导的多视图子空间聚类模型(diversity-induced multi- view subspace clustering, DiMSC), 其利用希尔伯特-施密特独立性指标(Hilbert-Schmidt independence criterion, HSIC)作为多样性项探索多视图数据间的潜在互补关联[15]. 进一步地, Zhang等人提出了一种潜在多视图子空间聚类方法(latent multi-view subspace clustering, LMSC), 其学习多视图数据的潜在特征, 并且直接生成一个公共子空间表达[16]. 尽管基于子空间学习的方法在聚类等任务中已经获得了较好的性能, 但是其通常受原始数据的质量影响较大[16]. 基于图的方法由于对数据结构和数据类型没有太多限制, 受到了众多研究者的关注.基于图的方法的主要代表是谱聚类算法, 其关键在于如何从数据中发现恰当的邻接矩阵. Kumar等人利用协同训练技术迭代地优化邻接图[17, 18]. Zhou和Burges线性结合多个正则化的伴随矩阵[19]. Nie等人将一个数据样本属于另一个样本的邻居集的概率作为两个样本间的相似性度量, 通过自适应邻居集构造邻接矩阵[20]. 进一步地, 假设所有邻接矩阵共享一个特征向量, Nie等人提出了一种无参多视图聚类算法[21]. 然而, 该算法将邻接矩阵构建和谱聚类分为两个独立过程, 因此无法联合优化. 为解决上述问题, Nie等人设计了一个同时实现邻接矩阵构建与多视图谱聚类的统一框架, 基于自适应邻居集学习一个公共邻接矩阵[22]. 为了提升邻接矩阵的特征表达能力和保留数据中隐含知识, Kang等人提出了一种多图融合的多视图谱聚类算法, 使得融合后的邻接矩阵尽可能接近每个视图的原始邻接矩阵, 但增强了类簇结构[23]. Nie等人提出了一种自加权的多视图聚类算法(self-weighted multiview clustering, SwMC), 利用Laplacian秩约束图, 近似地作为不同视图的图心. 该算法的优势在于一旦获得目标邻接图, 可以直接获得数据划分结果, 而不需要任何传统算法(如K-means)进行后处理[24]. Zhang等人关注二进制多视图数据(如图像数据), 提出了一种二进制多视图聚类框架, 其联合优化紧实的协同离散表示学习过程与二元聚类结构学习过程[25]. 尽管传统的多视图谱聚类算法已经取得了较多成果和进展, 但由于传统算法的限制性, 大多现存的多视图谱聚类算法无法处理大规模复杂场景下的数据, 且无法挖掘数据分布中的深层隐含特征. 因此, 本文考虑结合深度学习的非线性特征处理能力, 通过构建神经网络实现多视图谱聚类, 进一步提升多视图谱聚类算法的泛化能力与聚类性能.
1.2 深度聚类现存的聚类算法虽然已经实现了较好的性能, 但面向复杂数据分布场景时的数据划分能力还亟待提高. 为克服现有工作的缺陷, 结合深度学习的非线性特征处理能力来提升聚类算法的特征挖掘性能不失为一个好的解决方案[26, 27]. Yang等人设计了一种迭代学习数据表达和类簇划分的深度层次聚类模型(joint unsupervised learning of deep representations and image clusters, JULE), 有效抓住了精细的图像类簇信息和可判别的特征表达[28]. 类似地, Caron等人提出了一种深度聚类框架(DeepCluster), 首先采用K-means聚集特征, 然后根据类簇划分更新网络参数, 迭代优化获得最佳聚类性能[29]. Shaham等人引入深度学习方法到谱聚类算法中, 提出了一种深度谱网络(spectral clustering using deep neural networks, SpectralNet)[7], 其旨在通过约束随机优化近似谱聚类算法, 从而学习一个具有更多隐含知识的谱嵌入.
面向多视图学习场景的深度聚类算法也被研究者们争相探讨. 在深度多视图聚类学习中, 首先备受关注的是深度自动编码器, 其旨在挖掘一个可重建出多视图输入的统一表达. 详细来说, 深度自动编码器采用共享编码器提取所有视图的统一特征表示, 然后使用不同的解码器单独重建每一个视图. Andrew等人提出了一种基于典型相关分析(canonical correlation analysis, CCA)的深度神经网络版本(deep canonical correlation analysis, DCCA)来学习两个视图的共享表达[30]. DCCA利用两个子网络分别提取两个视图的非线性特征, 同时最大化学到的特征的相关性以提高模型性能. 进一步地, Wang等人同时优化了所提取的多视图特征之间的线性相关分析以及自动编码器的重建误差, 从而提出了一种深度线性相关自动编码器(deep canonically correlated auto encoders, DCCAE)[31]. Zhao等人利用深度矩阵分解技术学习多视图样本的深层特征, 提出了一种多视图深度矩阵分解方法(multi-view clustering via deep matrix factorization, MvDMF)[32]. Huang等人拓展了谱聚类算法到深度学习版本, 提出了一种多视图谱聚类网络(multi-view spectral clustering network, MvSCN)[6].由上述可知: 深度多视图聚类学习方面的研究尚为较少, 还需深入探索深度神经网络与传统聚类算法之间的关联性, 进一步提升多视图聚类算法在时间与性能上的效率.
2 多视图谱聚类算法本节主要介绍传统的多视图谱聚类算法的基本原理. 正如前面提到的, 多视图谱聚类旨在融合多个邻接图以获得一致性指示矩阵, 从而得到数据划分结果. 假设X={X1, X2, …, XV}是一个包含V个视图的数据集,
| $ {S}_{ij}^{v}=\left\{\begin{array}{l}\mathrm{exp}\left(-\frac{\left|\right|{x}_{i}^{v}-{x}_{j}^{v}|{|}_{2}^{2}}{2{\delta }^{2}}\right),\text{ }{x}_{i}^{v},\text{ }{x}_{j}^{v}互为邻居\hfill \\ 0,\text{ }其他\hfill \end{array}\right. $ | (1) |
其中,
计算得到每个视图的邻接矩阵后, 多视图谱聚类的目标函数可定义如下:
| $ \left. \begin{gathered} \mathop {\arg \min }\limits_{Y,{a^v}} \sum\limits_{v = 1}^V {{{({a^v})}^r}tr({Y^T}{L^v}Y)} \hfill \\ {\text{s}}{\text{.t}}{\text{. }}{Y^T}Y = I,{\text{ }}\sum\limits_{v = 1}^V {{a^v}} = 1,{\text{ }}{a^v} > 0 \hfill \\ \end{gathered} \right\} $ | (2) |
其中, Y∈RN×c是聚类指示矩阵, 也可视为最终的谱嵌入, c是类簇数目; Lv是第v个视图的拉普拉斯矩阵, 定义为Lv=Dv−Sv; Dv=diag(Sv)是对角矩阵; av是反映每个视图贡献度的参数; r是控制每个视图不同权重分布的尺度. 详细细节见文献[16].
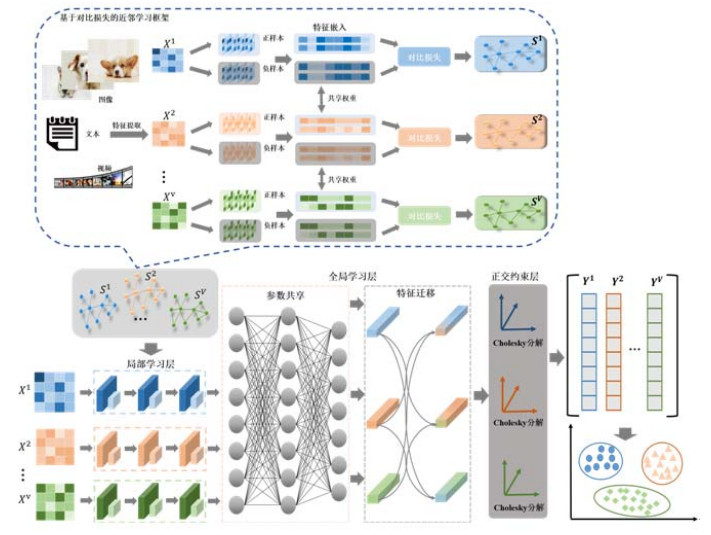
3 知识迁移下的深度一致性多视图谱聚类网络本节将详细介绍提出的知识迁移下的深度一致性多视图谱聚类网络, 整体网络框架包含两部分(如图 1所示): (1) 基于对比损失的近邻学习; (2) 基于知识迁移的谱嵌入学习.
|
图 1 知识迁移下的深度一致性多视图谱聚类框架图 |
由于谱聚类算法需要引入样本对间的近邻关联, 在近邻学习部分, 不同于传统谱聚类中采用的距离度量, CMvSC设计了一个具有对比损失的孪生网络用于同时判别正负样本对, 自适应地学习包含样本隐含关联的近邻矩阵. 在谱嵌入学习部分, CMvSC设计了一个深度学习框架用于多视图数据处理, 首先对每个视图设计网络分支, 将单视图数据输入到局部学习层以获得单视图特有嵌入; 其次考虑全局一致性, 结合知识迁移设计全局学习层, 其中分别包括参数共享与特征迁移, 通过动态融合获得一致性多视图谱嵌入; 最后, 采用K-Means算法得到最终的多视图数据划分结果.
3.1 基于对比损失的近邻学习邻接矩阵对谱聚类算法的性能影响极大, 因此选择一个较好的近邻度量标准能够大大提升聚类效果. 尽管基于距离度量的近邻学习在一定程度上有效定义了样本关系, 但是其在应对数据分布较复杂的场景时效果不佳. 在本文中, CMvSC引入了一种基于对比损失的近邻学习方式, 采用神经网络挖掘样本的非线性特征, 自适应地为每个视图学习邻接矩阵.
与直接采用样本邻居集或距离度量构造邻接矩阵的方法不同, 基于对比损失的近邻学习以孪生神经网络为框架, 引入对比学习原理, 同时考虑了正样本与负样本的影响, 使得最终输出的邻接矩阵既捕获了正样本之间的相似性, 也学习了负样本之间的差异性. 所提出的近邻学习的网络损失可表示为
| $ L_a^v = P||{g_\theta }(x_i^v) - {g_\theta }(x_j^v)||_2^2 + (1 - P)\max (\gamma - ||{g_\theta }(x_i^v) - {g_\theta }(x_j^v)||_2^2,0) $ | (3) |
其中,
● P∈{0, 1}表示判别标签, 即: P=1时表示
● gθ(⋅)表示孪生网络中的映射函数, 用于嵌入样本数据到潜在空间中. 在我们的工作中, 其是指全连接层和ReLu函数组成的嵌入单元;
● γ是指距离边界(通常定义为1).
通过分析公式(3)中的两项, 不难看出, 其很好表达了成对样本的匹配程度. 当样本相似时(即P=1), 损失只保留第1项, 即原本相似的样本经过映射后仍然相似; 当样本不相似时, 损失只剩第2项, 即样本不相似的样本经过映射后仍然不相似.
如何构建正负样本集合, 是基于对比损失的近邻学习的关键. 对于监督学习来说, 我们通常直接采用样本的类别标签来判断样本是否互为正/负样本: 若标签相同/不同, 则为正/负样本. 然而, 对于无监督学习来说, 我们无法得知样本标签, 这种情况下无法直接判断样本是否互为正/负样本. 为解决这个问题, 我们参考基于样本邻居集构造邻接矩阵的方法, 仍然采用最近k近邻法(k-nearest neighbor, kNN)构建每个样本的邻居集, 然后根据邻居集划分正/负样本. 换而言之, 当
构造好所有样本对应的正负样本集合后, 我们结合对比损失来构造具有相同网络分支的孪生网络进行近邻学习, 将样本数据进行映射, 最小化对比损失(如公式(3)所示), 并采用高斯核函数来计算最终的邻接矩阵, 如下:
| $ {S}_{ij}^{v}=\left\{\begin{array}{l}\mathrm{exp}\left(-\frac{\left|\right|{g}_{\theta }({x}_{i}^{v})-{g}_{\theta }({x}_{j}^{v})|{|}_{2}^{2}}{2{\delta }^{2}}\right),\text{ }{x}_{i}^{v},\text{ }{x}_{j}^{v}互为邻居\hfill \\ 0,\text{ }其他\hfill \end{array}\right. $ | (4) |
其中, δ是高斯核函数中的宽度参数, 通常取值大于0. 在本文工作中, 我们设置δ为所有样本点与它们邻居集中最远邻居之间距离的中位数. 高斯核函数将数据映射到高维特征空间, 再计算样本间距离. 因上述孪生网络旨在最小化正样本间的距离而最大化负样本间的距离, 可能造成映射后的正样本对线性不可分, 高斯核函数的引入, 有利于避免线性不可分的问题. 最后, 将计算得到的邻接矩阵[S1, S2, …, SV]用于基于知识迁移的谱嵌入学习(见第3.2节)中, 有效提升最终的特征表达效果, 从而提升聚类性能.
3.2 基于知识迁移的谱嵌入学习尽管传统的多视图谱聚类算法已取得较好性能, 但其仍存在一些限制: (1) 谱嵌入的可扩展性有限, 无法应对大规模数据的场景, 这也是大多传统浅层模型的问题之一; (2) 泛化能力不足, 无法适应复杂数据分布, 隐含特征学习能力有限. 因此, 本文设计了一个基于深度神经网络的参数模型, 挖掘多视图数据的潜在分布结构, 学习单视图的局部不变性和多视图的全局一致性, 结合知识迁移将原始多视图数据映射为一致性谱嵌入, 其数学表达式为
| $ {f_\theta }({X^{N \times {d_v}}}) \to {Y^{N \times c}} $ | (5) |
其中, fθ(⋅)表示CMvSC的网络参数模型;
如何挖掘多视图数据的特有特征和共享特征以获得蕴含丰富信息的一致性谱嵌入, 是CMvSC的一个关键性任务. 考虑到每个视图的数据特征结构不尽相同, 但每个独立视图存在局部不变性, 即同一视图中的不同数据样本满足相同数据分布, 因此, 我们首先设计局部学习层分别学习每个视图的特有嵌入; 其次, 由于不同视图都是相同数据对象的不同特征表示, 因此多视图在潜在分布上存在全局一致性, 同时, 不同视图之间存在重叠、互补的特征, 因而我们提出一种全局学习层, 用于同时挖掘多个视图中的隐含共享知识, 该层先采用参数共享学习多视图间的潜在分布一致性, 再利用特征迁移动态融合不同视图间的互补特征, 以输出一致性多视图谱嵌入.
此外, 传统谱聚类算法中引入了正交约束YTY=I, 因此CMvSC设计一种正交约束层来对网络输出进行限制, 保证多视图谱嵌入矩阵的正交性. 最后得到经网络映射后的多视图一致性特征表示YN×c, 再采用传统的聚类算法(如K-means)获得最终的多视图聚类结果. 以下我们将详细介绍CMvSC中的局部学习层和全局学习层, 以及网络中的其他关键部分.
3.2.1 局部学习层不同视图之间往往存在尺度差异性和特征差异性, 但每个视图内部的所有数据样本却具有分布一致性, 我们称其具有局部不变性. 因此, 我们首先考虑独立学习每个视图的特有嵌入, 以挖掘单视图特有特征. 本节提出了一种局部学习层, 采用全连接层(dense)以及ReLu函数学习每个视图的特有嵌入, 以获得新的单视图特征表示.
新的单视图隐含特征表示需要保证与原始数据结构具有一定一致性, 即: 原始空间中距离较近的样本经过特征映射后, 在新的特征表示空间中距离仍然较近. 因此, 所设计的局部学习层需要尽可能地挖掘原始数据样本的有效特征, 去除冗余特征, 同时不丢失原始数据的隐含结构. 与传统的特征流型学习不同, 全连接层利用每一个网络节点对原始单视图数据进行特征嵌入, 能够更充分地抓住原始数据结构与潜在分布特征, 因此全连接层可以被视为分类器用于融合不同维度的特征; 同时, 当数据样本为图像等形式时, 可以采用卷积层等预处理方式将原始数据(维度为w×h)转换为d维数据, 再使用全连接层; 此外, 当前一层网络层为全连接层时, 此时使用全连接层等价于卷积核为1×1的一维卷积层. 最后, 我们结合ReLu函数引入非线性因素, 将每个网络节点的映射进行非线性输出, 以获得具有更佳特征表示能力的表达.
经过局部学习层后, 我们获得新的单视图特有嵌入. 综上可知, 局部学习层的目标是保证每个视图中相似度较高的数据样本在特征嵌入后仍然相似, 因此局部学习层的损失可表示为
| $ L_1^v = \frac{1}{{{N^2}}}\sum\limits_{i,j}^n {S_{ij}^v||h_{l,i}^v - h_{l,j}^v||_2^2} $ | (6) |
其中,
多视图数据是对相同数据样本的不同特征表示, 不同视图具有相同的簇标签, 因此可以认为多视图间往往存在一定的分布一致性, 即不同视图的数据划分应该是相同的, 我们称其为全局一致性. 同时, 不同视图的特征空间通常具有重叠性和互补性, 因此, 有效融合多视图特征能够在一定程度上强化特征的表达能力, 从而提升最终的聚类性能. 本节提出了一种全局学习层挖掘多视图一致性特征, 采用参数共享与特征迁移分别实现共享知识挖掘与特征动态融合, 从而获得融合多个视图信息的一致性谱嵌入.
全局学习层与局部学习层类似, 同样采用全连接层(dense)对数据表达进行非线性变换, 但为了得到具有分布一致性与特征互补性的一致性多视图谱嵌入, 其借鉴了迁移学习技术, 首先采用参数共享的网络层挖掘所有视图的一致性特征, 然后设计视图特有的网络层从一致性特征中进行知识迁移, 有效融合其他视图信息与当前视图特有信息. 两种学习方式如下.
● 参数共享
神经网络中的参数空间往往是决定最终特征表达的关键因素, 换而言之, 每个视图的参数空间隐含了数据样本的分布特征与潜在结构. 考虑到多视图间存在分布一致性, 本节采用参数共享的全连接层对多个视图进行特征嵌入, 即级联所有视图的局部学习层输出, 再采用全连接层进行学习, 从而挖掘出多个视图共享的分布特征, 其数学表达式如下:
| $ {H_p} = \Theta (concat[H_l^1;...;H_l^v;...;H_l^V]) $ | (7) |
其中, Θ表示一致性网络层的参数空间, concat表示级联操作,
● 特征迁移
众所周知, 多视图数据是同一样本集的多源/多通道特征表示. 因此, 不同视图之间的特征可能存在重叠、互补等特性. 本节考虑多视图特征表示之间的互补原则, 融合其他视图信息能够有效增强当前视图的特征表达能力. 由此, 我们采用视图特有的权重对包含不同视图特征的一致性特征表达进行映射, 通过非线性映射对不同视图信息进行迁移, 并与当前视图的局部信息进行融合, 以实现不同视图间的特征迁移, 形成新的视图表示, 其数学表达式如下:
| $ {Y^v} = W_p^v \circ {H_p} + H_l^v $ | (8) |
其中, ο表示Hadamard积, 即逐元素乘积;
全局学习层旨在最小化不同视图之间的差异性, 以获得多视图共享的特征嵌入. 因此, 多视图全局学习层的目标函数可表示为
| $ {L_2} = \frac{1}{{N{V^2}}}\sum\limits_{v,v'}^V {\sum\limits_i^N {||y_i^v - y_i^{v'}||_2^2} } $ | (9) |
其中, v和v′分别指代不同视图.
3.2.3 正交约束层传统谱聚类算法中为避免出现“无效解”(trivial solution), 通常会引入正交约束. “无效解”是指为了最小化谱聚类的目标损失函数, 模型将所有数据输入在潜在空间中映射为同一表示, 以使得目标损失函数值最小. 但这样的结果对于聚类任务来说是无效的, 我们希望得到包含足够丰富信息的特征嵌入, 才能获得较好的数据划分结果. 在CMvSC中, 同样为了避免出现“无效解”, 我们设计了正交约束层用于引入正交约束, 使得:
| $ {\left( {{Y^v}} \right)^T}{Y^v} = {I_{N \times N}} $ | (10) |
其中, Yv表示模型输出的第v个视图的谱嵌入, I是单位矩阵.
正交约束层的目的与传统谱聚类算法中的正交约束作用一致, 正交化每一列特征嵌入, 以保证最终输出结果的有效性. 在本文中, 我们采用Cholesky分解实现正交约束, 并将正交约束层搭建在网络最顶层, 严格保证最终输出的有效性.
3.2.4 目标函数综上所述, CMvSC主要考虑同时挖掘单视图的局部特有信息与多视图间的全局共享知识, 因此, 网络的目标函数可分为局部学习损失与全局学习损失两部分, 如下所示:
| $ {L_c} = (1 - \lambda )\sum\limits_{v = 1}^V {L_1^v} + \lambda {L_2} $ | (11) |
其中, L1表示局部学习层的损失, L2表示全局学习层的损失, λ是调整两种损失的平衡参数. L1主要用于控制单个视图内的损失, 最小化类内差异, 同时最大化类间差异, 使得原始空间中较相似的样本的隐含表示仍然相似, 保证局部不变性. L2的目的是控制不同视图间的学习损失, 使得不同视图间的对应样本的隐含表示尽可能一致, 保证多视图全局一致性. λ用于平衡局部学习层与全局学习层的损失在目标函数中的重要性, 当λ为0时, 表示只考虑单视图内的损失; λ取1时, 网络只考虑多视图间的损失.
4 网络训练与优化 4.1 网络训练基于知识迁移的谱嵌入学习和基于对比损失的近邻学习是两个独立过程, 因此其训练过程也是相互独立的. 另外, 由于所提出的CMvSC适用于深度聚类任务, 谱嵌入学习与近邻学习的网络训练过程均为无监督, 不需要构建训练集与测试集, 可直接输入样本数据获得最终数据划分结果. 值得注意的是: 谱嵌入学习网络的输出维度为c(类簇数目), 以获得聚类指示矩阵.
4.2 基于代码空间的训练就多视图数据而言, 通常每个视图具有不同的特征分布. 此时, 如果直接进行多视图间的特征提取和知识迁移, 可能会因为度量差异和特征结构差异的影响得到冗余信息, 无法获得有效的一致性谱嵌入. 因此, CMvSC采用基于代码空间(code space)的训练方法. 基于代码空间的表达是指原始数据经过预训练好的模型转换后的低维数据表达, 其通常包含更少的冗余信息和更丰富的有效特征. 部分学者直接采用自动编码器用于网络初始化[33−35], 但是这样的网络初始化往往会在训练过程中改变代码空间的低维数据表达. 因此, 在本篇工作中, 我们借鉴SpectralNet[7]和MvSCN[6]中直接采用基于代码空间的表达作为输入数据的训练方式, 然后应用CMvSC进行处理. 在实验部分, 我们采用文献[34]中的深度嵌入聚类模型(deep embedded clustering, DEC)对原始数据进行处理, 获得的低维表达作为基于代码空间的表达用于CMvSC的输入.
5 实验本节将评估CMvSC与11个对比算法在4个数据集上性能. 此外, 我们将给出网络详细结构设计与实验过程中的详细参数设置.
5.1 数据集实验部分, 我们选择了4个多视图数据集用于性能评估, 包括:
● Noisy MNIST: 我们采用原始数据集作为视图 1, 然后随机选择类内样本添加噪声来构造视图 2. 由此, 我们得到一个包含70 000个样本的双视图数据集(下载链接: http://ttic.uchicago.edu/∼wwang5/dccae.html, createMNIST.m);
|
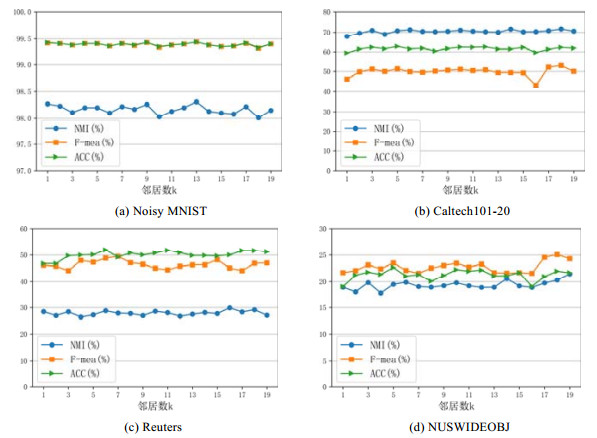
图 2 参数k的影响比较 |
● Caltech101-20: 我们提取6种手工特征作为6个视图, 包括Gabor特征、Wavelet Moments特征、CENTRIST特征、HOG特征、GIST特征和LBP特征, 其包含了20个类别, 共2 386张图片(下载链接: http://www.vision.caltech.edu/ImageDatasets/Caltech101/);
● Reuters: 我们使用Reuters数据库中的英语版本和4种翻译版本(包括法语、德语、西班牙语和意大利语)来构造多视图数据集, 其包含了6个类别, 共18 758个样本(下载链接: https://archive.ics.uci.edu/ml/datasets.html);
● NUSWIDEOBJ: 我们选择NUS提供的5种特征(包括Color Histogram, Color Moments, Color Correlation, Edge Distribution和Wavelet texture)构建多视图数据集, 其包含了31个类别, 共30 000张图片(下载链接: http://lms.comp.nus.edu.sg/research/NUS-WIDE.htm).
大多数对比算法是基于传统机器学习方法, 面对大规模数据场景往往会有内存溢出、矩阵分解失败等问题, 因此, 对于Noisy MNIST, Reuters和NUSWIDEOBJ数据集, 我们随机选择10k数据进行实验. 所有实验数据集的详细信息见表 1.
| 表 1 数据集详细信息 |
5.2 对比算法
本文工作选择了11个算法与我们的CMvSC进行比较, 其中包含3个单视图聚类算法和8个多视图聚类算法.
● 单视图聚类算法: (1) Spectral clustering(SC)[36]; (2) Low rank representation(LRR)[12]; (3) Spectral clustering using deep neural networks (SpectralNet)[7];
● 多视图聚类算法: (1) Deep canonical correlation analysis (DCCA)[30]; (2) Deep canonically correlated autoencoders (DCCAE)[31]; (3) Diversity-induced multi-view subspace clustering (DiMSC)[15]; (4) Latent multi-view subspace clustering (LMSC)[16]; (5) Multi-view clustering via deep matrix factorization (MvDMF)[32]; (6) Self-weighted multiview clustering with multiple graphs (SwMC)[24]、(7) Binary multi- view clustering (BMVC)[25]; (8) Multi-view spectral clustering network (MvSCN)[6].
为采用多视图数据集评估单视图聚类算法, 我们均分别在每个视图上进行实验, 然后选择性能最佳的视图结果作为最终评估结果. 此外, DCCA和DCCAE只适用于两个视图的数据集, 因此我们选择性能最佳的两个视图作为最终的评估结果.
对于所有的对比算法和CMvSC, 我们均使用基于代码空间的低维表达作为数据输入. 所有实验在标准Ubuntu-16.04操作系统中实现, 利用Keras和TensorFlow进行模型搭建, 采用1块NVIDIA 1080Ti GPU加速.值得一提的是: CMvSC采用K-means算法对网络输出的特征表达进行数据划分, 为尽可能降低K-means算法因随机初始化对聚类结果产生较大影响, 在实验过程中, 我们对网络输出进行10次K-means聚类, 且每次选择不同的初始化种子(seed), 最终选择最好的结果作为数据划分结果.
5.3 性能评价指标本篇工作采用准确率(ACC)、F-measure(F-mea)和标准化互信息值(NMI)这3个评价指标评估所提出的CMvSC与所有对比算法的性能, 以上3种指标均为值越大, 表明聚类效果越好.
ACC表示聚类结果的准确率, 正确的结果越多, ACC值越大, 其计算方法如下:
| $ ACC = \frac{{\sum\nolimits_{i = 1}^N {\delta (map({{\tilde y}_i}),{y_i})} }}{N} $ | (12) |
其中, N是样本总数,
F-mea是通过计算查全率和查准率来评估聚类性能的指标, 查全率(R)与查准率(P)的定义如下:
| $ R = \frac{{TP}}{{TP + FN}} $ | (13) |
| $ P = \frac{{TP}}{{TP + FP}} $ | (14) |
其中, TP表示真实标签为同类的样本被聚为同一类簇, FN是真实标签为同类的样本被聚为不同类簇, FP表示真实标签为不同类的样本被聚为同一类簇.
F-mea综合考虑查全率与查准率, 其定义如下:
| $ F{\text{ - }}mea = \frac{{2 \times P \times R}}{{P + R}} $ | (15) |
NMI是一种利用信息论中的信息熵来计算聚类结果与真实标签间的相似程度的指标, 其计算公式如下:
| $ NMI = 2 \times \frac{{I(\tilde Y,Y)}}{{H(\tilde Y) \times H(Y)}} $ | (16) |
其中,
| $ I(\tilde Y,Y) = \sum\nolimits_{i = 1}^c {\sum\nolimits_{j = 1}^c {\frac{{{m_{ij}}}}{N}\log \left({\frac{{{m_{ij}}}}{{|{{\tilde Y}_i}| \times |{Y_j}|}}} \right)} } $ | (17) |
| $ H(Y) = - \sum\nolimits_{i = 1}^C {\frac{{|{Y_i}|}}{N}} \log \left({\frac{{|{Y_i}|}}{N}} \right) $ | (18) |
其中, mij表示网络输出为第i类而真实标签为第j类的样本数, N是样本总数, c是类簇数.
5.4 参数设置及网络结构设计CMvSC中的关键参数主要包括近邻学习中的邻居数k和谱嵌入学习中控制损失函数的平衡参数λ. 因此, 本节主要讨论以上两个参数的影响. 如图 2所示, 我们在4个数据集上探讨了邻居数k的影响.
不难看出, CMvSC对于邻居数k的设置并不算敏感, 整体性能相对稳定. 在实际实验中, 相较于Noisy MNIST, 其他3个数据集的邻居数k取值范围更大. 原因在于: 邻居数越少, 邻接矩阵会更稀疏. 而其他3个数据集的视图数较多, 当数据经过全局学习层处理后, 所获得的特征嵌入可能包含较多极小值, 如果此时邻接矩阵同样太稀疏, 后续的正交约束层将无法完成正交分解.
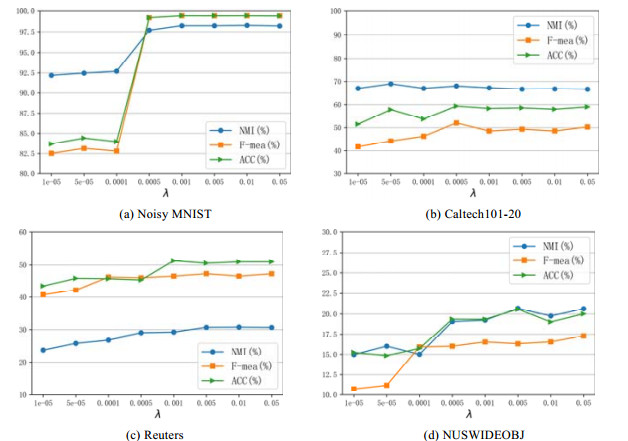
如图 3所示, 我们在4个数据集上讨论了不同平衡参数λ下的性能变化, 可以得出, 不同数据集在参数λ大于0.0005时性能均趋于稳定.
|
图 3 参数λ的影响比较 |
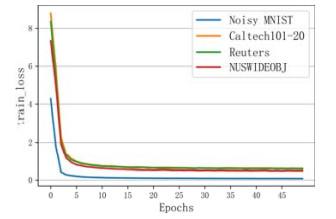
此外, 我们给出了4个数据集的谱嵌入学习的训练损失变化曲线图, 如图 4所示. 可以看出, 所有数据集均在前20次Epochs中迅速收敛.
|
图 4 4个数据集上的训练损失变化曲线 |
最后, 为保证实验结果的可复现性, 我们给出了所有必要参数的设置以及网络结构的设置, 分别见表 2和表 3.
| 表 2 参数设置详细信息 |
| 表 3 网络结构详细信息 |
5.5 性能评估
我们评估了CMvSC和11个对比算法的性能, 性能比较结果见表 4, 最优结果已加粗表示.
| 表 4 对比算法与CMvSC的性能对比(ACC, F-mea, NMI) |
从表 4可以看出:
● 在所有数据集上, 多视图聚类算法整体优于单视图聚类算法, 说明了相较于单视图, 多视图具有更强的特征表示能力, 蕴含更丰富的有效信息;
● 极个别多视图聚类算法在某些数据集上性能弱于单视图聚类算法, 如: DCCA和DCCAE在多个数据集上的NMI值低于SpectralNet, 由此说明不同视图的特征融合可能会产生负面影响, 需要仔细斟酌融合方式与融合时机;
● 与多视图聚类算法相比, 可以看出CMvSC取得了较好的结果, 由此说明了CMVSC通过同时挖掘单视图特有特征和多视图共享知识, 能够学习到更准确有效的特征表达;
● 值得一提的是: SpectralNet和MvSCN与本文提出的CMvSC均采用自适应的邻接图矩阵, 与其他采用传统的邻接图矩阵构造方法的模型(如SC和SwMC)相比, SpectralNet在单视图聚类算法中具有明显的优越性, MvSCN与CMvSC在多视图聚类算法中同样表现优秀, 由此说明了自适应邻接图更能抓住数据的潜在关联;
● CMvSC相较于MvSCN的主要不同在于引入了全局学习层, 从而进行参数共享和特征迁移. 从对比结果中可知, CMvSC具有较优的性能. 证明了多视图间的知识迁移, 能进一步提升特征嵌入的表达能力.
5.6 消融实验为了证明CMvSC网络中各个部分的有效性, 我们设计了不同的变体方法进行消融实验, 评估结果如表 5所示. 变体设计如下.
| 表 5 变体算法与CMvSC的性能对比(ACC, F-mea, NMI) |
● CMvSC-nc: 不使用基于代码空间的低维输入, 直接采用原始数据作为输入;
● CMvSC-na: 不使用基于对比损失的近邻学习, 直接采用公式(4)的方法构造邻接矩阵;
● CMvSC-nl: 不使用局部学习层, 直接将基于代码空间的多视图低维输入级联, 再作为全局学习层的输入;
● CMvSC-np: 不使用参数共享, 直接将局部学习层的输出作为特征迁移的输入;
● CMvSC-nf: 不使用特征迁移, 直接将参数共享的输出作为正交约束层的输入.
如表 5所示, 可以得出以下5点结论.
● CMvSC在不同数据集上的性能远远优于CMvSC-nc, 由此说明了基于代码空间的低秩表达相比原始数据样本包含更少的冗余信息、更多的有效知识. 因此, 采用基于代码空间的训练方法, 模型能够迅速挖掘数据中的隐含关联, 从而提高数据划分性能;
● 与CMvSC-na相比, CMvSC有更好的聚类性能, 证明了基于对比损失的近邻学习比传统的邻接矩阵构造方法更能抓住数据间的深层关联. 此外, 由于基于对比损失的近邻学习同时考虑了正样本与负样本的影响, 这也为性能提升提供了帮助;
● 当不使用局部学习层时, CMvSC-nl与CMvSC相比的聚类效果有所降低, 说明局部学习层抓住了每个视图的特有性质, 对于学习单视图局部不变性具有一定优势, 在一定程度上提升了聚类效果;
● CMvSC-np在各个数据集上的性能都稍逊于CMvSC, 由此证明了参数共享能够有效发现多视图间的共享特征, 学习多视图分布一致性, 增强谱嵌入的表达能力, 从而提高聚类性能;
● CMvSC与CMvSC-nf相比具有更好的聚类性能, 表明了特征迁移能够发现多视图特征表示之间的互补性质, 进一步强化谱嵌入表征能力, 在一定程度上提升聚类性能.
6 结论与展望本文提出了一种知识迁移下的深度一致性多视图谱聚类网络(CMvSC), 利用多视图学习挖掘数据样本的多样性特征, 同时结合深度学习框架提升算法的特征学习能力与可扩展能力. 针对每个视图的局部不变形, CMvSC引入局部学习层挖掘单视图特有嵌入; 考虑到多视图在数据划分上的全局一致性, CMvSC构建全局学习层进行知识迁移, 从而学习多视图共享嵌入; 此外, 为深入发现数据样本中的隐含关联, CMvSC引入孪生网络和对比损失用于近邻学习, 得到同时考虑正负样本影响的邻接矩阵; 最后, 在4个数据集上的实验结果有效证明了CMvSC的优越性.
然而, CMvSC的不足在于其近邻学习与谱嵌入学习是两个独立的过程. 因此在未来工作中, 我们考虑设计一个端到端的模型, 同时进行邻接图构建与多视图聚类.
| [1] |
Kang Z, Zhao XJ, Peng C, et al. Partition level multiview subspace clustering. Neural Networks, 2020: 279−288.
|
| [2] |
Yang Y, Wang H. Multi-view clustering: A survey. Bia Data Mining and Analytics, 2018, 1(2): 83-107.
[doi:10.26599/BDMA.2018.9020003] |
| [3] |
Zhang YP, Zhou J, Deng ZH, et al. Multi-view fuzzy clustering approach based on medoid invariant constraint. Ruan Jian Xue Bao/Journal of Software, 2019, 30(2): 282-301(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5625.htm [doi:10.13328/j.cnki.jos.005625] |
| [4] |
Bickel S, Scheffer T. Multi-view clustering. In: Proc. of the 4th IEEE Int'l Conf. on Data Mining. 2004. 19−26.
|
| [5] |
Xie JY, Ding LJ, Wang MZ. Spectral clustering based unsupervised feature selection algorithms. Ruan Jian Xue Bao/Journal of Software, 2020, 57(9): 1928-1938(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5927.htm [doi:10.13328/j.cnki.jos.005927] |
| [6] |
Huang ZY, Zhou TJ, Peng X, et al. Multi-view spectral clustering network. In: Proc. of of the 28th Int'l Joint Conf. on Artificial Intelligence. 2019. 2563−2569.
|
| [7] |
Shaham U, Stanton K, Li H, et al. SpectralNet: Spectral clustering using deep neural networks. In: Proc. of the 6th Int'l Conf. on Learning Representations. arXiv: 1801.01587, 2018.
|
| [8] |
Appice A, Malerba D. A co-training strategy for multiple view clustering in process mining. IEEE Trans. on Services Computing, 2016, 9(6): 832-845.
[doi:10.1109/TSC.2015.2430327] |
| [9] |
Du L, Zhou P, Shi L, et al. Robust multiple kernel k-means using l2, 1-norm. In: Proc. of the 24th Int'l Joint Conf. on Artificial Intelligence. 2015. 3476−3482.
|
| [10] |
Lu YT, Wang LT, Lu JF, et al. Multiple kernel clustering based on centered kernel alignment. Pattern Recognition, 2014, 47(11): 3656-3664.
[doi:10.1016/j.patcog.2014.05.005] |
| [11] |
Luo SR, Zhang CQ, Zhang W, et al. Consistent and specific multi-view subspace clustering. In: Proc. of the AAAI Conf. on Artificial Intelligence. 2018. 3730−3737.
|
| [12] |
Liu GC, Lin ZC, Yan SC, et al. Robust recovery of subspace structures by low-rank representation. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2013, 35(1): 171-184.
[doi:10.1109/TPAMI.2012.88] |
| [13] |
Hou CP, Nie FP, Tao H, et al. Multi-view unsupervised feature selection with adaptive similarity and view weight. IEEE Trans. on Knowledge and Data Engineering, 2017, 29(9): 1998-2011.
[doi:10.1109/TKDE.2017.2681670] |
| [14] |
Wang H, Yang Y, Liu B. GMC: Graph-based multi-view clustering. IEEE Trans. on Knowledge and Data Engineering, 2019, 32(6): 1116-1129.
|
| [15] |
Cao XC, Zhang CQ, Fu HZ, et al. Diversity-induced multi-view subspace clustering. In: Proc. of the 2015 IEEE Conf. on Computer Vision and Pattern Recognition. 2015. 586−594.
|
| [16] |
Zhang CQ, Hu QH, Fu HZ, et al. Latent multi-view subspace clustering. In: Proc. of IEEE Conf. on Computer Vision and Pattern Recognition. 2017. 4279−4287.
|
| [17] |
Kumar A, Daumé H. A co-training approach for multi-view spectral clustering. In: Proc. of the 28th Int'l Conf. on Machine Learning. 2011. 393−400.
|
| [18] |
Kumar A, Rai P, Daumé H. Co-regularized multi-view spectral clustering. In: Proc. of the 24th Int'l Conf. on Neural Information Processing Systems. 2011. 1413−1421.
|
| [19] |
Zhou DY, Burges CJ. Spectral clustering and transductive learning with multiple views. In: Proc. of the 24th Int'l Conf. on Machine Learning. 2007. 1159−1166.
|
| [20] |
Nie FP, Wang XQ, Huang H. Clustering and projected clustering with adaptive neighbors. In: Proc. of the 20th ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. 2014. 977−986.
|
| [21] |
Nie FP, Li J, Li XL. Parameter-free auto-weighted multiple graph learning: A framework for multiview clustering and semi- supervised classification. In: Proc. the 25th Int'l Joint Conf. on Artificial Intelligence. 2016. 1881−1887.
|
| [22] |
Nie FP, Cai GH, Li XL. Multi-view clustering and semi-supervised classification with adaptive neighbours. In: Proc. of the 31st AAAI Conf. on Artificial Intelligence. 2017. 2408−2414.
|
| [23] |
Kang Z, Shi GX, Huang SD, et al. Multi-graph fusion for multi-view spectral clustering. Knowledge-Based Systems, 2020, 189: 105102.
[doi:10.1016/j.knosys.2019.105102] |
| [24] |
Nie FP, Li J, Li XL. Self-weighted multiview clustering with multiple graphs. In: Proc. of of the 26th Int'l Joint Conf. on Artificial Intelligence. 2017. 2564−2570.
|
| [25] |
Zhang Z, Liu L, Shen FM, et al. Binary multi-view clustering. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2019, 41(7): 1774-1782.
[doi:10.1109/TPAMI.2018.2847335] |
| [26] |
Li XL, Zhang R, Wang Q, et al. Autoencoder constrained clustering with adaptive neighbors. IEEE Trans. on Neural Networks and Learning Systems, 2021, 32(1): 443-449.
[doi:10.1109/TNNLS.2020.2978389] |
| [27] |
Xie JY, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis. In: Proc. of the 33rd Int'l Conf. on Machine Learning, Vol. 48. 2016. 478−487.
|
| [28] |
Yang JW, Parikh D, Batra D. Joint unsupervised learning of deep representations and image clusters. In: Proc. of the 2016 IEEE Conf. on Computer Vision and Pattern Recognition. 2016. 1063−6919.
|
| [29] |
Caron M, Bojanowski P, Joulin A, et al. Deep clustering for unsupervised learning of visual features. In: Proc. of the European Conf. on Computer Vision. 2018. 132−149.
|
| [30] |
Andrew G, Arora R, Bilmes J, et al. Deep canonical correlation analysis. In: Proc. of the 30th Int'l Conf. on Machine Learning. 2013. 1247−1255.
|
| [31] |
Wang WR, Arora R, Livescu K, et al. On deep multi-view representation learning: Objectives and optimization. In: Proc. of the 32rd Int'l Conf. on Machine Learning. 2015. 1083−1092.
|
| [32] |
Zhao HD, Ding ZM, Fu Y. Multi-view clustering via deep matrix factorization. In: Proc. of the 31st AAAI Conf. on Artificial Intelligence. 2017. 2921−2927.
|
| [33] |
Yang B, Fu X, Sidiropoulos ND, et al. Towards k-means-friendly spaces: Simultaneous deep learning and clustering. In: Proc. of the 34th Int'l Conf. on Machine Learning. 2017. 3861−3870.
|
| [34] |
Xie JY, Girshick R, Farhadi A. Unsupervised deep embedding for clustering analysis. In: Proc. of the 33rd Int'l Conf. on Machine Learning. 2016. 478−487.
|
| [35] |
Jiang ZX, Zheng Y, Tan HC, et al. Variational deep embedding: An unsupervised and generative approach to clustering. In: Proc. of the 26th Int'l Joint Conf. on Artificial Intelligence. 2017. 1965−1972.
|
| [36] |
Ng A, Jordan M, Weiss Y. On spectral clustering: Analysis and an algorithm. In: Proc. of the 15th Int'l Conf. on Neural
Information Processing Systems. 2002. 849−856.
|
| [3] |
张远鹏, 周洁, 邓赵红, 等. 代表点一致性约束的多视角模糊聚类算法. 软件学报, 2019, 30(2): 282-301.
http://www.jos.org.cn/1000-9825/5625.htm [doi:10.13328/j.cnki.jos.005625] |
| [5] |
谢娟英, 丁丽娟, 王明钊. 基于谱聚类的无监督特征选择算法. 软件学报, 2020, 57(9): 1928-1938.
http://www.jos.org.cn/1000-9825/5927.htm [doi:10.13328/j.cnki.jos.005927] |
 2022, Vol. 33
2022, Vol. 33


