软件学报  2022, Vol. 33 Issue (12): 4504-4516   PDF    
引用本文
钱亚冠, 马骏, 何念念, 王滨, 顾钊铨, 凌祥, Wassim Swaileh. 面向边缘智能的两阶段对抗知识迁移方法[J]. 软件学报, 2022, 33(12): 4504-4516. http://www.jos.org.cn/1000-9825/6352.htm   
Qian YG, Ma J, He NN, Wang B, Gu ZQ, Ling X, Wassim S. Two-stage Adversarial Knowledge Transfer for Edge Intelligence[J]. Journal of Software, 2022, 33(12): 4504-4516(in Chinese). http://www.jos.org.cn/1000-9825/6352.htm  
面向边缘智能的两阶段对抗知识迁移方法
钱亚冠1 , 马骏1 , 何念念1 , 王滨2 , 顾钊铨3 , 凌祥4 , Wassim Swaileh5     
1. 浙江科技学院 大数据学院, 浙江 杭州 310023;
2. 杭州海康威视网络与信息安全实验室, 浙江 杭州 310052;
3. 广州大学 网络空间先进技术研究院, 广东 广州 510006;
4. 浙江大学 计算机科学与技术学院, 浙江 杭州 310058;
5. CY Cergy Paris University, ETIS Research Laboratory, Paris 95032
收稿时间: 2020-03-06; 修改时间: 2021-03-08; 采用时间: 2021-04-13
基金项目: 浙江省自然科学基金(LY17F020011); 国家重点研发计划(2018YFB2100400); 国家自然科学基金(61902082)
作者简介: 钱亚冠(1976－), 男, 博士, 教授, CCF专业会员, 主要研究领域为深度学习, 人工智能安全, 大数据处理;
马骏(1994－), 男, 硕士生, 主要研究领域为深度学习, 人工智能安全, 大数据处理;
何念念(1994－), 女, 硕士生, 主要研究领域为深度学习, 人工智能安全, 大数据处理;
王滨(1977－), 男, 博士, 研究员, 博士生导师, CCF专业会员, 主要研究领域为物联网, 网络与信息安全, 网络体系机构;
顾钊铨(1989－), 男, 博士, 教授, CCF专业会员, 主要研究领域为无线网络, 分布式计算, 大数据分析, 人工智能安全;
凌祥(1992－), 男, 博士生, 主要研究领域为人工智能安全, 数据驱动的安全;
Wassim Swaileh (1979－), 男, 博士, 副教授, 主要研究领域为机器学习, 模式识别, 自然语言处理.
通讯作者: 王滨, E-mail: wbin2006@gmail.com.
摘要: 对抗样本的出现, 对深度学习的鲁棒性提出了挑战. 随着边缘智能的兴起, 如何在计算资源有限的边缘设备上部署鲁棒的精简深度学习模型, 是一个有待解决的问题. 由于精简模型无法通过常规的对抗训练获得良好的鲁棒性, 提出两阶段对抗知识迁移的方法, 先将对抗知识从数据向模型迁移, 然后将复杂模型获得的对抗知识向精简模型迁移. 对抗知识以对抗样本的数据形式蕴含, 或以模型决策边界的形式蕴含. 具体而言, 利用云平台上的GPU集群对复杂模型进行对抗训练, 实现对抗知识从数据向模型迁移; 利用改进的蒸馏技术将对抗知识进一步从复杂模型向精简模型的迁移, 最后提升边缘设备上精简模型的鲁棒性. 在MNIST, CIFAR-10和CIFAR-100这3个数据集上进行验证, 实验结果表明: 提出的这种两阶段对抗知识迁移方法可以有效地提升精简模型的性能和鲁棒性, 同时加快训练过程的收敛性.
关键词: 对抗样本    对抗训练    知识迁移    知识蒸馏    
Two-stage Adversarial Knowledge Transfer for Edge Intelligence
QIAN Ya-Guan1 , MA Jun1 , HE Nian-Nian1 , WANG Bin2 , GU Zhao-Quan3 , LING Xiang4 , Wassim Swaileh5     
1. School of Big Data Science, Zhejiang University of Science and Technology, Hangzhou 310023, China;
2. Network and Information Security Laboratory of Hangzhou Hikvision Digital Technology Co. Ltd., Hangzhou 310052, China;
3. Cyberspace Institute of Advanced Technology (CIAT), Guangzhou University, Guangzhou 510006, China;
4. College of Computer Science and Technology, Zhejiang University, Hangzhou 310058, China;
5. CY Cergy Paris University, ETIS Research Laboratory, Paris 95032, France
Abstract: The emergence of adversarial examples brings challenges to the robustness of deep learning. With the development of edge intelligence, how to train a robust and compact deep learning mode on edge devices with limited computing resources is also a challenging problem. Since compact models cannot obtain sufficient robustness through conventional adversarial training, a method called two-stage adversarial knowledge transfer is proposed. The method transfers adversarial knowledge from data to models and complex models to compact models. The so-called adversarial knowledge has two forms, one is contained in data with the form of adversarial examples, and the other is contained in models with the form of decision boundary. The GPU clusters of cloud center is first leveraged to train the complex model with adversarial examples to realize the transfer of adversarial knowledge from data to models, and then an improved distillation approach is leveraged to realize the further transfer of adversarial knowledge from complex models to compact models on edge nodes. The experiments over MNIST and CIFAR-10 show that this two-stage adversarial knowledge transfers can efficiently improve the robustness and convergence of compact models.
Key words: adversarial examples    adversarial training    knowledge transfer    knowledge distillation    

近年来, 深度学习被广泛应用到图像识别[1, 2]和自然语言处理[3, 4]等领域. 尤其在机器视觉应用中, 深度学习模型的层数可达数百层, 涉及大量参数. 通常, 训练阶段数据对内存的需求占主导地位, 而推理阶段模型对内存的需求占主导地位[5]. 这些模型的计算需求达到$ {\cal{O}}$(giga-FLOPS), 存储需求达到$ {\cal{O}}$(mega-bytes)[6]. 随着边缘计算和边缘智能的兴起, 深度学习模型被部署到网络边缘的设备上(如监控系统的智能摄像头), 以保证目标识别、异常检测等应用的实时性. 但是这些边缘设备由于资源(内存、计算和功耗)的严重受限, 很难承载大型的深度学习模型, 这已成为一个挑战性的问题[7]. 由于模型参数存在巨大冗余, 因此, 模型压缩成为一种有效的解决方法[8]. 目前提出了各种模型压缩方法, 如剪枝[9]、参数量化[10]和知识蒸馏[11]等, 解决边缘设备部署深度学习模型的问题.

同时, 研究表明, 深度学习模型自身具有内在的脆弱性. 如果在输入数据上添加一些精心设计的微小扰动, 可导致深度学习模型错误预测. 这种被添加恶意扰动的样本称为对抗样本[12]. 对抗样本的出现, 限制了深度学习模型在安全敏感领域的应用. 为了防御对抗样本的攻击, 研究人员展开了大量研究, 其中, 对抗训练被认为是目前最为有效的防御方法之一[13−15]. 新的研究表明: 模型层数越多, 抵御对抗样本的能力越强[16]. 因此, 利用云平台上的计算和内存资源对这些大型深度学习模型进行对抗训练, 是获得鲁棒性的有效途径. 但对边缘设备上的压缩模型而言, 其对抗训练的效果远不及云平台上的大型模型. 我们希望边缘设备上的精简模型仍可获得与大型深度学习模型同样的精度和鲁棒性.

为此, 我们提出两阶段对抗知识迁移方法[17]. 从知识工程的角度看, 模型的鲁棒性不足是由于对抗知识的欠缺引起的. 对抗知识的两种表现形式是: (1) 复杂模型中的鲁棒决策边界; (2) 数据中的对抗样本. 文献[16]认为: 模型复杂度越高, 模型的鲁棒性越好. 由VC维理论可知[18], 复杂模型可以更好地容纳对抗知识. 因此, 第1阶段在云平台上对复杂模型进行对抗训练, 把对抗样本中的对抗知识迁移到模型中, 形成鲁棒决策边界; 第2阶段, 利用对抗蒸馏技术, 把复杂模型的对抗知识迁移到边缘设备的精简模型中, 从而增强边缘设备的防御能力.

考虑到黑盒攻击更符合实际的攻击场景, 本文方法主要针对黑盒攻击进行防御. 为此, 我们需要在云平台上构建代理模型, 模拟我们要攻击的目标模型, 原理与文献[19]相似. 但不同的是: 我们会训练多个代理模型, 增大这些模型在对抗子空间上的差异性, 生成多样性对抗样本, 利用这些对抗样本再训练复杂模型, 以提高对抗知识从数据向模型的迁移率. 在复杂模型向精简模型迁移对抗知识的过程中, 我们借鉴了Hinton提出的模型蒸馏思想[11], 提出了对抗蒸馏技术. 原始的蒸馏技术只是利用正常样本的软标签(输出的概率向量)来迁移正常样本的分类知识, 而本文迁移的是对抗知识, 因此重新定义新的损失函数, 并采用对抗样本在复杂模型(已完成对抗训练)上输出的软标签进行训练, 以便更好地迁移鲁棒决策边界.

我们在Nvidia Jetson Nano和Raspberry Pi嵌入式评估板上分别用MNIST, CIFAR-10和CIFAR-100这3个数据集进行了实验, 对比了: (1) 只使用正常样本训练的精简模型; (2) 直接利用对抗训练迁移对抗知识的精简模型; (3) 集成多钟对抗样本训练的精简模型; (4) 直接用正常样本蒸馏的精简模型及(5) 我们提出的两阶段对抗知识迁移方法. 实验结果表明: 对于边缘计算条件下的精简模型, 我们的方法比其他方法可以获得更好的鲁棒性, 同时加快训练过程的收敛性.

1 预备知识 1.1 对抗样本与威胁模型

图像、语音、文本等数据均可产生对抗样本[20], 本文主要针对图像对抗样本. 图像对抗样本是一种在自然图像上添加精心设计的扰动, 用以欺骗深度学习模型的非自然图像:

定义1(对抗样本[12]). 设x为自然图像样本, y为x的正确分类标签, f(·)为深度学习模型, F(·)为人眼感知分类器. 存在扰动δ, 使得f(x+δ)≠y, 而F(x+δ)=y, 那么我们称x′=x+δ为对抗样本.

利用对抗样本欺骗深度学习模型的攻击称为对抗攻击, 通常建模为如下的优化问题[12]:

$ \begin{array}{l} \min ||\delta |{|_p} \\ {\text{s}}{\text{.t}}{\text{. }}f(x + \delta ) \ne y \\ \;\;\;\;||\delta |{|_p} \leqslant \varepsilon \end{array} $ (1)

这里, ||·||p表示Lp范数(p=1, 2, ∞), ε是对扰动的约束. 对抗攻击又分为有目标攻击和无目标攻击: 有目标攻击是指攻击方希望对抗样本被错误的分类到yadv, 即f(x+δ)=yadv, yadv≠y; 无目标攻击只要求x′=x+δ被错误分类, 即f(x+δ)≠y, 没有特别要求误分类到哪个类.

攻击能力和攻击目标的组合构成威胁模型[19]. 攻击能力是指攻击方了解目标模型的程度, 可分为白盒攻击和黑盒攻击. 如果攻击者知道模型的全部信息, 包括模型的结构、参数和训练数据等, 则称为白盒攻击. 如果攻击方几乎完全不知道目标模型的内部信息, 则称为黑盒攻击. 白盒攻击因为知道模型的全部信息, 攻击能力很强, 但要求知道模型内部信息, 这在现实中较难实现; 而黑盒攻击更易在现实条件下实施. 因此, 本文主要针对深度学习模型的黑盒攻击进行防御.

1.2 生成对抗样本的方法

● FGSM

由于求解模型(1)的计算开销非常大, Goodfellow等人[13]提出一种无目标对抗样本快速生成方法FGSM (fast gradient sign method):

$ {{x}^{\prime }}=x+\varepsilon \cdot {sign}\left( {{{\mathit{\nabla}} }_{x}}J(f(x;\theta ), y) \right) $ (2)

其中, J是损失函数, f是深度学习模型, θ是模型参数, ε是对梯度符号方向sign(·)上的扰动约束. FGSM的基本思想是, 在损失函数对样本的梯度∇xJ的符号方向加扰动. 与L-BFGS[12]相比, FGSM具有快速产生大量对抗样本的优点.

● Step-LL

Kurakin等人[14]提出了基于FGSM的有目标攻击方法Step-LL(single-step least-likely class method), 最大化攻击目标类yadv的后验概率Pr(yadv|x):

$ x^{\prime}=x-\varepsilon \cdot {sign}\left({\mathit{\nabla}}_x J(f(x ; \theta), y)\right) $ (3)

公式(3)与公式(2)不同的是: 损失函数中的正确类别y变为攻击目标类yadv, 由于是有目标攻击, 因此它希望对抗样本x′的预测与目标类yadv越接近越好; 而公式(2)是无目标攻击, 它希望对抗样本x′的预测与正确类y越不接近越好. 因此, 这两个目标函数在ε前的符号正好相反.

● FGSM

Kurakin等人[14]进一步提出了多步无目标攻击I-FGSM:

$ {x'_0} = x, \;\;{x'_{N + 1}} = Cli{p_{x, \varepsilon }}\{ {x'_N} + \alpha \cdot sign({\mathit{\nabla} _x}J(f({x'_N};\theta ), y))\} $ (4)

这里的Clipx, ε(·)是将超出约束的扰动钳制在ε. I-FGSM采用多步迭代寻优, 其攻击成功率比FGSM大, 但计算量也随之增加.

● Iter-LL

Kurakin等人[14]提出了多步迭代的有目标攻击Iter-LL, 可达到99%以上的攻击成功率, 但计算量也大幅提升:

$ {x'_0} = x, \;\; {x'_{N + 1}} = Cli{p_{x, \varepsilon }}\{ {x'_N} - \alpha \cdot sign({\mathit{\nabla} _x}J(f({x'_N};\theta ), {y_{adv}}))\} $ (5)

这里, α前的符号与公式(4)相反是由于前者是有目标攻击, 后者是无目标攻击.

1.3 知识蒸馏

Hinton等人[11]提出了知识蒸馏的迁移学习方法, 实现了分类知识从复杂模型向精简模型的迁移, 前者称为教师模型, 后者称为学生模型. Hinton认为, 教师模型的softmax输出分布蕴含着分类目标的结构信息, 将其作为目标标签(称为软标签)去训练学生模型, 可有效地实现知识迁移. Heo等人[21]认为, 复杂模型的决策边界更接近真实的决策边界, 而知识蒸馏可有效地实现决策边界的迁移, 从而使提升学生模型性能.

Hinton在softmax函数中引入一个称为蒸馏温度的参数T, 将类概率qi表示为

$ {q_i} = {{\exp \left( {\frac{{{z_i}}}{T}} \right)} \mathord{\left/ {\vphantom {{\exp \left( {\frac{{{z_i}}}{T}} \right)} {\sum\limits_j^n {\exp \left( {\frac{{{z_j}}}{T}} \right)} }}} \right. } {\sum\limits_j^n {\exp \left( {\frac{{{z_j}}}{T}} \right)} }} $ (6)

其中, zi表示第i类的logit值, n为分类数. 我们把传统上的独热编码称为硬标签, 而由公式(6)得到的类概率向量ysoft=(q1, q2, …, qn)称为软标签. 知识蒸馏利用教师模型上得到的软标签对学生模型进行训练, 从而实现知识迁移. 训练的损失函数定义为

$ \left.J_{ {student }}=\alpha J(f(x ; \theta), y)+(1-\alpha) J\left(f(x ; \theta), y^{ {soft }}\right) T^2\right) $ (7)

其中, α取值范围为[0, 1], 调节两种损失函数的权重. 由于对抗损失J(·, ysoft)产生的梯度为损失J(·, y)的1/T2, 需要对ysoft为标签的损失函数乘上T2, 保证硬目标与软目标对梯度计算的贡献保持大致相同[11].

2 对抗知识迁移

机器学习是通过模型表示从数据中获取的知识. 正常情况下, 训练数据是自然产生的. 但对抗样本的出现表明模型仅从自然样本中学习分类知识是不够的, 需要进一步从对抗样本学习知识, 来增强模型的鲁棒性.

定义2(对抗知识). 能够防御对抗样本, 增强模型鲁棒性的知识. 它有多种可能的蕴含形式, 可以对抗样本硬标签对(x′, y)和软标签对(x′, ysoft)的形式存在于数据中, 也可以鲁棒模型f(x)的决策边界的形式存在于模型中. 需指出的是: 这里的软标签是指对抗样本经过鲁棒模型后输出的概率向量, 并不是一般模型的输出.

对抗训练可以实现将对抗知识迁移在数据向模型迁移的目的. 研究表明: 模型越复杂, 对抗训练的迁移效果越好[16]. 一个重要的原因是, 复杂模型具有更大的容量(capacity)或VC维来容纳对抗知识. 考虑到边缘智能系统的模型更精简, 模型的容量就更小, 直接进行对抗训练来迁移数据中的对抗知识效率不高, 我们提出了对抗蒸馏技术, 实现对抗知识从复杂教师模型向精简学生模型高效迁移的思路, 称之为二阶段对抗知识迁移. 两阶段对抗知识迁移的流程如图 1所示.

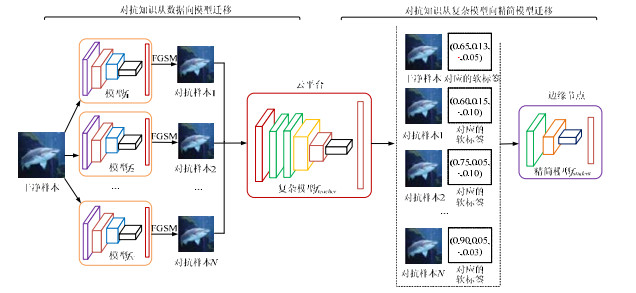
图 1 两阶段对抗知识的迁移流程

首先, 在本地模型上生成用于训练复杂模型的对抗样本. 由于模型结构(深度、宽度、卷积核尺寸等)的差异, 可产生差异性(攻击成功率、可转移性等)较大的对抗样本[15], 我们采用多个模型结构差异较大的本地模型生成对抗样本. 考虑到FGSM是无目标攻击, 具有生成速度快、生成的对抗样本转移性强等优点[19], 因此, 我们选择FGSM生成训练用的对抗样本, 其他方法用于生成测试用的对抗样本. 然后, 将这些对抗样本与正常样本一起训练教师模型, 实现对抗知识从数据到模型的迁移. 最后, 将带软标签的对抗样本和正常样本一起训练学生模型, 实现对抗知识在模型间的迁移. 上述过程可以概括为两个阶段: (1) 对抗知识从数据向复杂模型迁移; (2) 再从复杂模型向精简模型迁移.

2.1 对抗知识从数据向模型迁移

Szegedy等人[12]首次提出利用对抗样本和正常样本同时训练模型, 实践证明是一种增强模型鲁棒性的有效方法. Fawzi等人[22]认为: 模型的鲁棒性不足是因为的决策边界与某些样本之间的距离过小, 使得微小的扰动就可以让这些样本越过决策边界. 利用对抗样本进行训练, 可使决策边界增大与这些样本的距离. 从图 2可以看出: 对抗训练后, 决策边界与邻近样本的间距变大[23]. 这与支持向量机的最大间隔学习获得鲁棒性的原理是一致的. 因此, 我们认为对抗训练是实现对抗知识从数据向模型迁移的有效途径. Aleksander等人[16]从优化的观点出发, 认为对抗训练是一个关于鞍点的优化问题, 他们把传统的经验风险最小(ERM)推广到存在对抗样本条件下的经验风险最小.

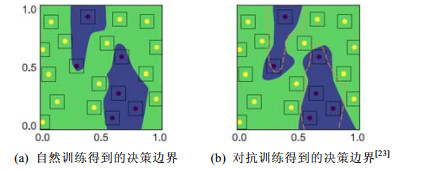
图 2 自然训练和对抗训练得到的决策边界

定义3(对抗训练[16]). 假设(x, ytrue)∈D为原始训练数据, x对应的对抗样本为x′=x+δ, ||δ||p≤ε, 采用当前模型损失最大化的对抗样本对模型进行训练, 在最小化经验风险准则下获得最有参数:

$ {\theta ^*} = \mathop {\arg \min }\limits_{\theta \in \mathit{\Theta} } {\mathbb{E}_{(x, {y_{{\text{true}}}}) \in D}}\left[ {\mathop {\max }\limits_{||{x^{adv}} - x|{|_\infty } \leqslant \varepsilon } J(f(x';\theta ), y)} \right] $ (8)

这里: J(·)为损失函数, θ为模型参数. 由此可见, 对抗训练企图在模型分类准确率和鲁棒性之间取得最佳折中[24], 是内部最大化和外部最小化问题的鞍点问题. 内部最大化问题是在当前模型参数下找到最强的对抗样本. 外部最小化问题是在存在最强对抗样本的条件下, 寻找损失最小的模型参数.

事实上, 通过获得最优对抗样本来求解公式(8)的计算复杂度很高[12]. 由Hoeffding不等式可知, 训练数据的数量决定学习效率. 因此, 我们采用能近似最有对抗样本的FGSM方法生成对抗样本, 可以快速产生大量对抗样本, 得到模型(8)的近似优化模型:

$ {\theta ^*} = \mathop {\arg \min }\limits_{\theta \in \mathit{\Theta} } {\mathbb{E}_{(x, y) \in D}}[J(f({x'_{FGSM}};\theta ), y)] $ (9)

由公式(2)可知, FGSM对抗样本还依赖于生成对抗样本的模型. 受集成学习[25]的启发, 差异性越大的对抗样本可训练得到更加复杂的决策边界, 为此, 我们通过多个结构不同的生成模型, 获得差异性对抗样本. 与Tramèr等人[15]提出的集成对抗训练方法不同, 我们从集成学习理论出发, 通过Bagging方法[26]训练得到N个生成模型f1, f2, …, fN. 给定一个正常样本x, 可获得N个对抗样本: ${x'_i} = x + \varepsilon sign({\mathit{\nabla} _x}J({f_i}(x), y)), \;\; i = 1, ..., N.$假设正常样本集合Dc={(x1, y1), …, (xM, yM)}, 由上述方法获得的对抗样本为

$ {D_a} = \{ ({x'_{11}}, {y_1}), ..., ({x'_{1N}}, {y_1}), ({x'_{21}}, {y_2}), ..., ({x'_{2N}}, {y_2}), ..., ({x'_{MN}}, {y_M})\} . $

当N足够大时, Da就能获得充分的对抗知识. 为实现对抗知识从数据集Da向教师模型fteacher的迁移, 定义如下损失函数:

$ L(\theta ) = \frac{1}{{(M + 1)N}}\left( {\lambda \sum\limits_{(x, y) \in {D_c}} {J({f_{teacher}}(x;\theta ), y)} + (1 - \lambda )\sum\limits_{({x^{adv}}, y) \in {D_a}} {J({f_{teacher}}(x';\theta ), y)} } \right) $ (10)

其中, J是交叉熵损失, λ控制对抗损失的比重.

算法1. 对抗知识从数据向模型迁移.

Input: 正常样本Dc={(x1, y1), …, (xM, yM)};

    生成对抗样本的模型F={f1, f2, …, fN};

Output: 复杂模型fteacher.

1:   初始化fteacher参数

2:   在多个模型上生成对抗样本Da

3:   repeat

4:     for ∀(x, y)∈Dc∨∀(x′, y)∈Da do

5:       使用公式(10)损失函数L(θ)训练fteacher

6:     end for

7:   until 满足结束条件

8:   return fteacher

2.2 对抗知识从复杂模型向精简模型迁移

在完成对抗知识从数据向复杂模型迁移后, 我们继续将复杂模型获得对抗知识向精简模型迁移. 受知识蒸馏的启发, 我们提出了对抗蒸馏的技术, 实现对抗知识在模型间的迁移. 数据向模型迁移采用对抗样本的硬标签(x′, y), 而对抗蒸馏采用对抗样本的软标签(x′, ysoft). 这是因为软标签是经过复杂模型后, 蕴含了复杂模型决策边界的对抗知识, 同时也蕴含着更多关于类分布的结构信息.

定义4(对抗蒸馏). 假设复杂模型fteacher已蕴含了从数据中迁移得到的对抗知识. 对抗样本x′经过fteacher输出的软标签为ysoft, 利用(x′, ysoft)对精简模型fstudent进行训练, 实现对抗知识在模型间的迁移称为对抗蒸馏.

从定义4可知: 区别于Hitton提出知识蒸馏, 对抗蒸馏采用的是对抗样本的软标签, 而不是正常样本的软标签; 同时区别于一般的对抗训练, 我们采用的软标签是对抗样本在复杂模型上的软标签. 由图 1所示, 我们已从前一阶段获得对抗样本Da. 利用第1.3节的公式(6), 选择合适的温度T, 获得带软标签的对抗样本训练集$ D_a^{soft} = \{ ({x'_{11}}, y_{11}^{soft}), ..., ({x'_{1N}}, y_{1N}^{soft}), ({x'_{21}}, y_{21}^{soft}), ..., ({x'_{2N}}, y_{2N}^{soft}), ..., ({x'_{MN}}, y_{MN}^{soft})\} $. 同时, 正常样本带软标签的训练集为$D_c^{soft}$. 考虑到正常样本和对抗样本对于决策边界的影响不同, 我们采用不同的蒸馏温度. 为此, 定义如下的损失函数对精简模型进行训练:

$ \begin{array}{l} L(\theta ) = \lambda (\alpha J({f_{student}}(x;\theta ), y) + (1 - \alpha )J({f_{student}}(x;\theta ), y_c^{soft})T_1^2) + \\ \;\;\;\;(1 - \lambda )(\alpha J({f_{student}}(x';\theta ), y) + (1 - \alpha )J({f_{student}}(x';\theta ), y_a^{soft})T_2^2) \end{array} $ (11)

其中, J是交叉熵函数, λ控制正常样本和对抗样本的比例, α控制硬标签和软标签的比例, $ y_c^{soft} $表示正常样本的软标签, $ y_a^{soft} $表示对抗样本的软标签, T1和T2是蒸馏温度.

算法2. 对抗知识从复杂模型向精简模型迁移.

Input: 正常样本集合Dc={(x1, y1), …, (xM, yM)};

    对抗样本集合$ {D_a} = \{ ({x'_{11}}, {y_1}), ..., ({x'_{1N}}, {y_1}), ({x'_{21}}, {y_2}), ..., ({x'_{2N}}, {y_2}), ..., ({x'_{MN}}, {y_M})\} $;

复杂模型fteacher;

Output: 精简模型fstudent.

1:   初始化fstudent参数

2:   $\forall (x, y) \in {D_c}, \;\; y_c^{soft} \leftarrow {{\exp \left( {\frac{{{f_{teacher}}{{(x)}_j}}}{{{T_1}}}} \right)} \mathord{\left/ {\vphantom {{\exp \left( {\frac{{{f_{teacher}}{{(x)}_j}}}{{{T_1}}}} \right)} {\sum\limits_j^n {\exp \left( {\frac{{{f_{teacher}}{{(x)}_j}}}{{{T_1}}}} \right)} }}} \right. } {\sum\limits_j^n {\exp \left( {\frac{{{f_{teacher}}{{(x)}_j}}}{{{T_1}}}} \right)} }}$, 得到集合$D_c^{soft}$

3:   $\forall (x', y) \in {D_a}, \;\; y_a^{soft} \leftarrow {{\exp \left( {\frac{{{f_{teacher}}{{(x')}_j}}}{{{T_2}}}} \right)} \mathord{\left/ {\vphantom {{\exp \left( {\frac{{{f_{teacher}}{{(x')}_j}}}{{{T_2}}}} \right)} {\sum\limits_j^n {\exp \left( {\frac{{{f_{teacher}}{{(x')}_j}}}{{{T_2}}}} \right)} }}} \right. } {\sum\limits_j^n {\exp \left( {\frac{{{f_{teacher}}{{(x')}_j}}}{{{T_2}}}} \right)} }}$, 得到集合$D_a^{soft}$

4:   repeat

5:     for $\forall (x, y) \in {D_c} \vee \forall (x', y) \in {D_a} \vee \forall (x, y_c^{soft}) \in D_c^{soft} \vee \forall (x', y_a^{soft}) \in D_a^{soft}$ do

6:       使用公式(11)的损失函数L(θ)训练fstudent, 实现对抗知识的迁移

7:     end for

8:   until stop condition satisfied

9:   return fstudent

3 实验评估 3.1 数据集和模型设置

本文采用MNIST, CIFAR-10和CIFAR-100这3个数据集进行实验评估. MNIST是一个手写体数据集, 共包含10个类别, 分别为数字0−9. 每个图像为28×28的灰度图像, 其中5万张用于训练, 1万张用于测试. CIFAR-10数据集是带有复杂背景的RGB图像数据集, 共包含10个类别. 使用随机裁剪和随机水平翻转进行数据增强, 并根据数据集的平均值和方差对输入图像进行归一化. 每个图像大小为32×32, 其中5万张用于训练, 1万张用于测试. CIFAR-100与CIFAR-10的区别是包含更多的类别(100个类).

实验采用的模型为不同层数的ResNet[1], 教师模型为Res26, 学生模型为Res8, 通道大小设置为16, 32和64. 使用SGD算法训练模型, mini-batch大小置为256. 在MNIST上训练20epochs, 在CIFAR-10训练80epochs.学习率从0.1开始, 迭代到最大epoch的1/2时下降到0.01, 迭代到最大epoch的3/4时下降到0.001. 实验中使用的动量为0.9, 权重衰减为0.000 1. 在CIFAR-100上权重衰减为0.000 5, 其余的与CIFAR-10设置相同. 对抗训练时, 对抗样本和正常样本的数量各占mini-batch的一半. Res26, Res20, Res14和Res8用于生成FGSM对抗样本, 对抗样本强度ε=16/256. 在相同条件下进行重复5次实验, 取它们的平均值作为结果. 我们用模型和训练集的组合来描述实验配置, 如Res8(cln)表示用正常样本训练得到的Res8, Res8 (dist-cln)表示从正常样本训练的Res26中知识蒸馏得到Res8, Res8(adv)表示对抗训练得到的Res8, Res8 (dist-adv)表示从对抗训练过的Res26中知识蒸馏得到Res8.

我们使用1台Geforce RTX 2080Tis服务器训练复杂模型, 操作系统为Ubuntu16.04.6LTS, Pytorch1.2实现算法. 采用Nvidia Jetson Nano和Raspberry Pi嵌入式评估板作为边缘设备, 评估复杂模型与精简模型对计算资源的存储消耗与计算消耗(测试图像大小为32×32, 计算消耗为分类一张图片所耗时间). Nvidia Jetson Nano安装的SDK为JetPack4.4, 测试过程不使用TensorRT加速. Raspberry Pi型号为三代B型, 无外接GPU. 表 1给出了复杂模型ResNet26与精简模型Res8(dist-adv)的资源消耗对比, 可以发现, 经过我们提出的对抗蒸馏后的精简模型比复杂模型更适合部署到边缘设备. 本文所有实验基于上述平台进行验证.

表 1 复杂模型与精简模型在边缘设备上的资源消耗对比

3.2 对抗知识迁移的有效性

为实现两阶段对抗知识迁移, 我们采用公式(11)对Res8 (adv-trans)进行对抗训练(T1=3, T2=5, α=0.1, λ=0.5). 与Res8 (dist-adv)不同的是, Res8 (adv-trans)的知识蒸馏包含对抗样本的软标签. 最后, 实验在另一个用干净图像预训练的Res26模型上生成的FGSM, I-FGSM, Step-LL, Iter-LL对抗样本(对抗样本强度ε=16/256), 并对以上模型进行黑盒攻击. 各个模型在MNIST数据集上, 正常样本和对抗样本上的分类准确率见表 2. 我们同样在CIFAR-10和CIFAR-100数据集上重复进行上述实验, 结果见表 3和表 4.

表 2 MNIST数据集分类准确率(%)

表 3 CIFAR-10数据集的分类准确率(%)

表 4 CIFAR-100数据集的分类准确率(%)

(1) 模型Res26(cln)和Res8(cln)没有经过对抗训练, Res26 (adv), Res8 (adv)经过对抗训练, 通过比较可以发现, 对抗训练显著地增强模型的鲁棒性. 以CIFAR-100上的FGSM对抗样本为例, Res26 (cln)的分类准确率从87.05%下降到15.29%, 而Res26(adv)只从81.81%下降到75.20%. 由此可见, 对抗训练都可以从数据向模型迁移对抗知识;

(2) Res8 (dist-adv)是从教师模型Res26 (adv)知识蒸馏得到的. 比较发现: Res8 (dist-adv)对对抗样本的分类准确率显著高于正常样本训练的Res8(cln), 也高于一般知识蒸馏的Res8 (dist-cln). 尽管Res8 (dist-adv)没有通过对抗训练从数据中获取对抗知识, 但利用一般的知识蒸馏也能一定程度上从教师模型迁移获得对抗知识;

(3) 比较Res8 (adv)和Res8 (adv-trans), 以在CIFAR-100上的FGSM对抗样本为例, Res8 (adv-trans)的准确率高于Res8 (adv). 比较CIFAR-100上的I-FGSM, Step-LL和Iter-LL对抗样本, Res8 (adv-trans)也同样高于Res8 (adv). 但在MNIST数据集上, I-FGSM和Iter-LL对抗样本在Res8 (adv-trans)的准确率反而略低于Res8 (adv), 可能MNIST数据集相对比较简单, 导致Res26和Res8之间的差异性不是很大;

(4) 进一步比较Res8 (dist-adv)和Res8 (adv-trans). FGSM对抗样本在Res8 (adv-trans)上的准确率可达75.77%, 而Res8 (dist-adv)仅为35.44%. I-FGSM, Step-LL和Iter-LL对抗样本在Res8 (adv-trans)上的准确率同样明显高于Res8 (dist-adv). 可见: 对于精简模型而言, 两阶段对抗知识迁移比一般的知识蒸馏可获得更多的对抗知识.

综上所述, 无论是直接对精简模型进行对抗训练, 还是直接从教师模型进行知识蒸馏, 两阶段对抗知识迁移与它们相比, 可以获得更多的对抗知识.

3.3 模型的鲁棒性评估

为了比较一般的对抗训练与两阶段对抗知识迁移在精简模型的鲁棒提升效果, 我们分别训练了4类不同的精简模型. 其中, 精简模型Res8(cln)作为比较的基准模型, 仅用正常样本训练; Res8 (self-adv)是用FGSM在自身模型上生成对抗样本进行对抗训练; Res8 (adv)是用FGSM在多个不同模型上生成对抗样本进行对抗训练; Res8 (adv-trans)是两阶段对抗知识迁移获得的精简模型. 我们用Res26, Res20, Res16及Res8模型上生成的FGSM对抗样本(分别表示为FGSMRes26, FGSMRes20, FGSMRes16和FGSMRes8), 验证精简模型的鲁棒性. 表 5−表 7记录了这4类对抗样本在不同精简模型上的分类准确率.

表 5 MNIST数据集上不同模型的分类准确率(%)

表 6 CIFAR-10数据集上不同模型的分类准确率(%)

表 7 CIFAR-100数据集上不同模型的分类准确率(%)

从实验结果中可以明显发现, 没有对抗知识防御的Res8 (cln)鲁棒性最差. Res8 (self-adv)由于采用模型自身产生的对抗样本进行训练, 其鲁棒性远低于Res8 (adv)和Res8 (adv-trans). 这与文献[15]的结论一致, 表明对抗知识过于单一, 不能有效增强模型的鲁棒性. 而Res8 (adv)由于采用多个模型生成的对抗样本进行训练, 获得的对抗知识更加丰富, 因此鲁棒性的提升超过Res8 (self-adv). 模型Res8 (self-adv)不但与Res8 (adv)一样可以从数据中获得对抗知识, 并进一步获得复杂模型中的对抗知识, 因此鲁棒性比Res8 (adv)又有了提升.

我们进一步分析了不同类型的对抗样本(FGSM, step-LL, I-FGSM和Iter-LL)对模型的影响. 表 8−表 10给出了4个精简模型的分类准确率. 这些对抗样本均在Res26模型上生成, 其中, 对抗样本强度设置为ε=16/256, I-FGSM和Iter-LL迭代次数k=5, 步长大小d=ε/5.

表 8 不同类型MNIST对抗样本的分类准确率(%)

表 9 不同类型CIFAR-10对抗样本的分类准确率(%)

表 10 不同类型CIFAR-100对抗样本的分类准确率(%)

从上述表中可发现, Res8 (adv-trans)的分类准确率均高于Res8 (adv)和Res8 (self-adv). 由此可以看出, 两阶段迁移的模型具有更好的鲁棒性. 值得注意的是: 我们测试用的对抗样本是在Res26模型上生成, 而实际的分类模型是Res8模型, 可以认为是黑盒攻击测试. Szegedy等人[12]首先发现了对抗样本的可转移性, 即在一个模型上生成的对抗样本, 可以成功攻击其他模型. 但从实验结果看: 经过对抗训练的模型, 无论针对多步, 还是单步生成的对抗样本都具有较好的鲁棒性, 从另一方面也说明, 对抗训练可以很好地抑制对抗样本的可转移性.

3.4 训练过程的收敛性分析

通过实验可以发现, 我们提出的方法比集成对抗训练具有更好的训练收敛性. 我们采用同样的正常样本和对抗样本, 用不同的方法训练Res8模型. 每经过1个epoch, 就用同一测试集进行测试, 记录其分类准确率.以正常样本训练的Res8模型为比较基准, 并标注为正常训练, 集成对抗训练和我们的方法采用各50%的正常样本和对抗样本, 并分别标注为集成对抗训练和改进算法. 优化过程采用SGD算法, 具体训练设置参见第3.1节. 图 3为CIFAR-10正常样本的测试结果, 图 4为Res26生成的CIFAR-10对抗样本的测试结果, 其中, CIFAR-100与CIFAR-10的趋势相似.

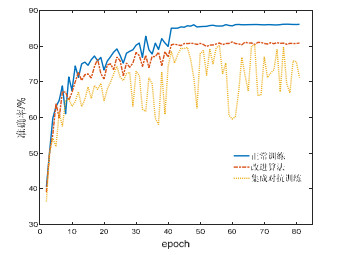
图 3 SGD算法下CIFAR-10正常样本的分类准确率

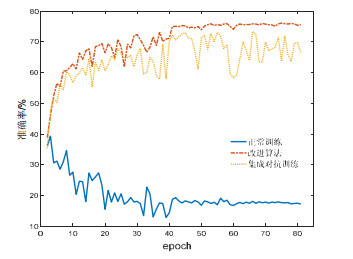
图 4 SGD算法下CIFAR-10对抗样本的分类准确率

由图 3可以看出: 从第42个epoch开始, 正常训练和基于对抗蒸馏的改进算法已收敛到一个较稳定的状态; 而集成对抗训练则始终处于随机抖动状态, 这对于模型的可用性是不利的. 从文献[15]可知: 由于集成对抗训练采用多个不同模型生成的对抗样本, 增加了误差曲面的复杂性, 使得训练过程无法稳定在某个局部最优点, 从而发生逃逸, 进入一个性能更差的区域, 在图像上就呈现出上下抖动的不稳定现象. 改进算法则采用软标签进行对抗蒸馏. Hinton等人[11]指出: 知识蒸馏具有更好的正则化效果, 可使对抗训练在一个更光滑的误差曲面上进行, 从而实现更好的收敛稳定性. 从图 3也看出: 对于正常样本的分类准确率, 正常训练要高于集成对抗训练和改进算法, 所以鲁棒性的增强也是以牺牲分类准确率为代价的.

图 4用对抗样本测试训练过程. 可以发现: 随着训练迭代的进行, 集成对抗训练与改进算法都能提高精简模型的鲁棒性; 但改进算法能实现更稳定的收敛, 且分类准确率高于集成对抗训练. 采用正常样本训练的精简模型随着训练迭代次数的增加也逐步趋于收敛稳定状态, 但对抗样本的分类准确率反而降低. 由此可以得出, 改进算法和正常训练都具有良好的收敛性. 另外, 从图 3和图 4也发现了一个重要规律: 用正常样本训练得越好的模型, 其鲁棒性反而越差.

4 相关工作

深度学习技术和边缘计算系统的成熟, 促进了边缘智能的发展和实现[27, 28]. 但最近的研究表明, 深度学习的鲁棒性和安全性存在严重隐患. 目前, 大量的对抗样本攻击采用基于梯度的方法, 可轻易地欺骗深度神经网络[15]. 为防御对抗攻击, 增强深度神经网络的鲁棒性, 基于梯度掩蔽的防御方法[15]、注入随机噪声[29]、防御性蒸馏[30, 31]、特征压缩[32]及其他多种防御方法[24, 33, 34]被提出. 有研究证明, 这些防御可以被轻易攻破[35]. 目前也提出了基于理论的防御方法, 但实践证明, 防御效果并不显著. 对抗训练[13]是目前在实践中证明最有效的防御方法. 上述提高DNN鲁棒性的方法都针对云平台上的复杂模型, 没有考虑到边缘智能环境下, 模型压缩后的情况.

Madry等人[16]认为: 更大的模型容量具有更好的鲁棒性, 且可以更好地取得准确率和鲁棒性之间的平衡[36]. 由于边缘智能系统的计算和存储资源有限, 人们采取各种模型压缩方法, 如剪枝[9]、参数量化[10]和知识蒸馏[11]来降低模型的容量, 这使得模型的鲁棒性也随之降低[37]. 因此, 研究边缘智能精简模型的鲁棒性变得非常重要. 文献[38, 39]从理论上讨论了剪枝后的权重稀疏性和对抗鲁棒性之间的关系, 但并没有给出具体的防御方法. Ye等人[40]提出了一种并行对抗训练和权值剪枝的框架, 既能压缩模型, 又能保持对抗的鲁棒性, 解决对抗训练的困境. Gui等人[41]提出了一种新的对抗训练模型压缩(ATMC)框架. ATMC构造了一个统一的约束优化公式, 把现有的压缩手段(修剪、因式分解、量化)都集成到约束中, 同时实现准确率与鲁棒性的平衡. Xie等人[42]提出了一种名为盲对抗剪枝(BAP)的方法, 它将盲对抗训练的思想引入渐进剪枝过程, 确保在每个剪枝步骤中, 对抗样本的强度动态地位于合理范围内, 最终提高剪枝模型的整体鲁棒性、准确性和高效性.上述方法都是基于剪枝算法, 本文提出的方法是从迁移学习的角度出发, 往一个成熟的精简模型上迁移对抗知识, 以增强其鲁棒性.

最近, 网络架构搜索(NAS)成为获得轻量级鲁棒DNN一个新的途径[43]. Cubuk等人[43]研究了网络架构对对抗性敏感性的影响, 并提出了使用带有强化学习的NAS在CIFAR 10上寻找具有对抗鲁棒性的架构. Chen等人[44]提出基于去噪块、权值操作、Gabor滤波器和卷积的综合搜索方法, 结合一种新的基于置信下界和置信上界(LCB和UCB)的操作评估方法和搜索过程, 获得鲁棒架构. Yue等人[45]通过考虑性能、鲁棒性和资源约束, 提出了一种高效、鲁棒的神经网络结构搜索(E2RNAS)方法. 尽管利用NAS来搜索鲁棒性的精简网络是一种很有前途的方法, 但是由于搜索空间过大, 目前的NAS方法需要很高的计算资源支持. 因此, 本文倾向于利用已有网络获得的对抗知识进行迁移.

5 结论

精简模型由于容量的限制, 直接对其进行一般的对抗训练很难提升其鲁棒性. 我们提出两阶段对抗知识迁移策略, 实现对抗知识从数据到复杂模型, 再从复杂模型到精简模型的迁移. 在具体实现过程中, 采用了多源对抗样本, 增强了对抗知识的多样性, 有效提高了从数据向模型迁移对抗知识的效果; 同时提出了对抗蒸馏技术, 有效地提高了复杂模型向精简模型迁移对抗知识的效率. 通过两阶段的对抗知识迁移, 使精简模型的鲁棒性大幅提高, 有助于边缘智能系统的部署实现. 本文在Nvidia Jetson Nano和Raspberry Pi嵌入式评估设备上全面分析了对抗知识迁移的有效性、模型的鲁棒性和训练过程的收敛性, 实验结果显示, 我们提出的方法在边缘智能应用中具有更好的优势和实际的应用价值.

参考文献
[1]
He K, Zhang X, Ren S, et al. Deep residual learning for image recognition. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2016. 770−778.
[2]
Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Communications of the ACM, 2017, 60(6): 84-90. [doi:10.1145/3065386]
[3]
Sutskever I, Vinyals O, Le QV. Sequence to sequence learning with neural networks. Advances in Neural Information Processing Systems, 2014, 27: 3104-3112. [doi:10.48550/arXiv.1409.3215]
[4]
He D, Xia Y, Qin T, et al. Dual learning for machine translation. Advances in Neural Information Processing Systems, 2016, 29: 820-828.
[5]
Mishra A, Nurvitadhi E, Cook JJ, et al. WRPN: Wide reduced-precision networks. arXiv: 1709.01134v1, 2017.
[6]
Canziani A, Paszke A, Culurciello E. An analysis of deep neural network models for practical applications. arXiv: 1605.07678v4, 2016.
[7]
Chen J, Ran X. Deep learning with edge computing: A review. Proc. of the IEEE, 2019, 107(8): 1655-1674. [doi:10.1109/JPROC.2019.2921977]
[8]
Denil M, Shakibi B, Dinh L, et al. Predicting parameters in deep learning. Advances in Neural Information Processing Systems, 2013, 26: 2148-2156.
[9]
Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural network. Advances in Neural Information Processing Systems, 2015, 28: 1135-1143. [doi:10.48550/arXiv.1506.02626]
[10]
Wu J, Leng C, Wang Y, et al. Quantized convolutional neural networks for mobile devices. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2016. 4820−4828.
[11]
Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network. arXiv: 1503.02531v1, 2015.
[12]
Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks. In: Proc. of the Int'l Conf. on Learning Representations. 2014.
[13]
Goodfellow IJ, Shlens J, Szegedy C. Explaining and harnessing adversarial examples. Computer Science, 2014.
[14]
Kurakin A, Goodfellow I, Bengio S. Adversarial machine learning at scale. arXiv: 611.01236v2, 2016.
[15]
Tramèr F, Kurakin A, Papernot N, et al. Ensemble adversarial training: Attacks and defenses. arXiv: 1705.07204v5, 2017.
[16]
Madry A, Makelov A, Schmidt L, et al. Towards deep learning models resistant to adversarial attacks. arXiv: 1706.06083v4, 2017.
[17]
Ma J. Research on application of knowledge distillation in deep learning adversarial examples [Ph. D. Thesis]. Hangzhou: Zhejiang University of Science and Technology, 2020. 24−31 (in Chinese with English abstract).
[18]
Vapnik VN. An overview of statistical learning theory. IEEE Trans. on Neural Networks, 1999, 10(5): 988-999. [doi:10.1109/72.788640]
[19]
Papernot N, McDaniel P, Goodfellow I, et al. Practical black-box attacks against machine learning. In: Proc. of the 2017 ACM on Asia Conf. on Computer and Communications Security. 2017. 506−519.
[20]
Zhang SS, Zuo X, Liu JW. The problem of adversarial examples in deep learning. Chinese Journal of Computers, 2019, 41: 15(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201908015.htm
[21]
Heo B, Lee M, Yun S, et al. Knowledge transfer via distillation of activation boundaries formed by hidden neurons. In: Proc. of the AAAI Conference on Artificial Intelligence. 2019. 3779-3787.
[22]
Fawzi A, Moosavi-Dezfooli SM, Frossard P. The robustness of deep networks: A geometrical perspective. IEEE Signal Processing Magazine, 2017, 34(6): 50-62. [doi:10.1109/MSP.2017.2740965]
[23]
Zhang H, Yu Y, Jiao J, et al. Theoretically principled trade-off between robustness and accuracy. In: Proc. of the Int'l Conf. on Machine Learning. 2019. 7472−7482.
[24]
Meng D, Chen H. Magnet: A two-pronged defense against adversarial examples. In: Proc. of the 2017 ACM SIGSAC Conf. on Computer and Communications Security. 2017. 135−147.
[25]
Polikar R. Ensemble Learning. Ensemble Machine Learning. Boston: Springer, 2012. 1−34.
[26]
Breiman L. Bagging predictors. Machine Learning, 1996, 24(2): 123-140.
[27]
Ding Y, Liu C, Zhou X, Liu Z, Tang Z. A code-oriented partitioning computation offloading strategy for multiple users and multiple mobile edge computing servers. IEEE Trans. on Industrial Informatics, 2019, 99: 1. https://d.wanfangdata.com.cn/periodical/5e2638ff70e9200878a1a4e7f6245217
[28]
Li KL, Liu CB. Edge intelligence: Current situation and prospects. Big Data Research, 2019, 5(3): 69-75(in Chinese with English abstract). https://www.cnki.com.cn/Article/CJFDTOTAL-DSJU201903007.htm
[29]
Dhillon GS, Azizzadenesheli K, Lipton ZC, et al. Stochastic activation pruning for robust adversarial defense. arXiv: 1803.01442v1, 2018.
[30]
Papernot N, McDaniel P. Extending defensive distillation. arXiv: 1705.05264v1, 2017.
[31]
Papernot N, McDaniel P, Wu X, et al. Distillation as a defense to adversarial perturbations against deep neural networks. In: Proc. of the 2016 IEEE Symp. on Security and Privacy (SP). IEEE, 2016. 582−597.
[32]
Xu W, Evans D, Qi Y. Feature squeezing: Detecting adversarial examples in deep neural networks. In: Proc. of the Network and Distributed System Security Symp. 2017.
[33]
Hosseini H, Chen Y, Kannan S, et al. Blocking transferability of adversarial examples in black-box learning systems. arXiv: 1703.04318v1, 2017.
[34]
Liao F, Liang M, Dong Y, et al. Defense against adversarial attacks using high-level representation guided denoiser. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition. 2018. 1778−1787.
[35]
Athalye A, Carlini N, Wagner D. Obfuscated gradients give a false sense of security: Circumventing defenses to adversarial examples. arXiv: 1802.00420, 2018.
[36]
Tsipras D, Santurkar S, Engstrom L, et al. Robustness may be at odds with accuracy. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
[37]
Wang L, Ding GW, Huang R, et al. Adversarial robustness of pruned neural networks. 2018.
[38]
Guo Y, Zhang C, Zhang C, et al. Sparse dnns with improved adversarial robustness. Advances in Neural Information Processing Systems, 2018, 31: 242-251. [doi:10.48550/arXiv.1810.09619]
[39]
Xiao KY, Tjeng V, Shafiullah NM, et al. Training for faster adversarial robustness verification via inducing relu stability. In: Proc. of the Int'l Conf. on Learning Representations. 2019.
[40]
Ye S, Xu K, Liu S, et al. Adversarial robustness vs. model compression, or both? In: Proc. of the IEEE/CVF Int'l Conf. on Computer Vision. 2019. 111−120.
[41]
Gui S, Wang HN, Yang H, et al. Model compression with adversarial robustness: A unified optimization framework. In: Proc. of the Advances in Neural Information Processing Systems. 2019. 1285−1296.
[42]
Xie H, Xiang X, Liu N, et al. Blind adversarial training: Balance accuracy and robustness. arXiv: 2004.05914, 2020.
[43]
Cubuk ED, Zoph B, Schoenholz SS, et al. Intriguing properties of adversarial examples. arXiv: 1711.02846v1, 2017.
[44]
Chen H, Zhang B, Xue S, et al. Anti-Bandit neural architecture search for model defense. In: Proc. of the European Conf. on Computer Vision. Cham: Springer, 2020. 70−85.
[45]
Yue Z, Lin B, Huang X, et al. Effective, efficient and robust neural architecture search. arXiv: 2011.09820v1, 2020.
[17]
马骏. 知识蒸馏在深度学习对抗样本中的应用研究[博士学位论文]. 杭州: 浙江科技学院, 2020. 24−31.
[20]
张思思, 左信, 刘建伟. 深度学习中的对抗样本问题. 计算机学报, 2019, 41(8): 15-36. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJX201908015.htm
[28]
李肯立, 刘楚波. 边缘智能: 现状和展望. 大数据, 2019, 5(3): 69-75. https://www.cnki.com.cn/Article/CJFDTOTAL-DSJU201903007.htm