2. 贵州大学计算机科学与技术学院, 贵州 贵阳 550025;
3. 宁夏医科大学 理学院, 宁夏 银川 750004
2. School of Computer Science and Technology, Guizhou University, Guiyang 550025, China;
3. School of Science, Ningxia Medical University, Yinchuan 750004, China
一个子句C是若干个文字的析取(即C=L1∨L2∨…∨Ln), 子句C可以视为文字的集合(即C={L1, L2, …, Ln}).一个合取范式(conjunctive normal form, 简称CNF)公式(以下简称公式)F是若干个子句的合取(即F=C1∧C2∧…∧ Cm), 公式F可以视为子句的集合(即F={C1, C2, …, Cm}).可满足性问题(satisfiability, 简称SAT)是指: 给定一个公式F, 判定是否存在一组指派使得F为真[1].SAT问题是计算机科学中最为著名的NP-完全问题, 其理论及其应用研究是计算机与数理逻辑界众多学者共同关注的一个重大问题.人工智能中的大多数难解问题, 通过编码技术都可转化为SAT问题.SAT问题的NP-完全性表明: 在P≠NP条件下, 不太可能存在多项式时间算法求解该问题.近年来, 随着人工智能的迅速发展, 特别是大数据和物联网的发展, 对SAT问题原有的求解算法需要重新审视和设计, 这为研究SAT问题提供了新的机遇和突破口.
目前, 对于SAT问题的研究主要集中在两个方面: 实例产生模型和求解算法.在实例产生模型研究中, 获取了一些影响实例可满足性的控制参数, 如子句数目m和变元数目n之比值α=m/n.在G(n, 3, m)模型中, 随机实例的可满足与不可满足之间似乎存在一个阈值αd.当α的值小于αd时, 实例高概率满足; 反之, 高概率不可满足.该阈值αd称为满足与不可满足的相变点, 当α的值接近αd时实例往往是难解的[2, 3].目前, 尚无得到αd的精确值, 但αd的下界为3.52[4], 上界为4.489 8[5].许可等人的研究基于B模型和D模型, 针对经典CSP实例产生模型的平凡无解性问题, 提出了具有精确相变点的实例产生模型, 分别为RB和RD模型[6-8], 该模型被广泛应用于国际算法竞赛测试.
基于实例的不可满足性是否能够给出完备性证明, SAT算法分为完备算法和不完备算法.不完备算法相对于完备算法而言, 能够在短时间内求出问题的解, 而完备算法的时间成本较大.因此, 不完备算法得到了更为广泛的应用.DPLL算法是一种典型的完备求解算法, 主要是利用单字句规则和分裂规则对公式进行化简, 其执行过程是一棵二叉搜索树[9], 增加了算法的执行时间.为此, 人们提出了各种各样的策略, 进而出现了许多其他有效的算法, 如, 基于VSIDS策略的ZChaff算法[10]、BerkMin算法[11]、MiniSat算法[12]、SATO算法[13]、GRASP算法[14]、GSAT算法[15]和WALKSAT算法[16]等等.
信息传播算法起源于统计物理领域[17].该算法是一种高效的边缘概率计算方法, 在许多领域得到了广泛应用[18-29].文献[30]中根据不同的随机SAT问题分别提出了3种基于因子图的信息传播算法, 即警示传播(warning propagation, 简称WP)算法、信念传播(belief propagation, 简称BP)算法和调查传播(survey propagation, 简称SP)算法.在3-SAT随机实例中, 该算法被验证非常有效, 特别是SP算法与局部搜索算法相结合, 几乎能够有效求解难解可满足性实例[30-33].信息传播算法这种优秀的性能, 引起了众多学者的关注, 主要集中在两个方面: (1) 信息传播算法的收敛性; (2) 信息传播算法的有效性.
所谓收敛性是指: 信息传播算法两次信息迭代得到的值不变; 有效性是指: 信息传播算法能够有效求解问题.目前, 对信息传播算法的性能分析已取得一些重要的研究成果.文献[34-40]分析了信息传播算法的收敛性和有效性, 并给出了算法收敛的充分条件.文献[41, 42]基于具体的实例产生模型分析了信息传播算法的收敛性, 并给出了算法收敛的概率条件.文献[43]利用压缩函数的相关性质给出了算法收敛的充分条件, 该判定条件由于受消息取值的限制(消息只能取0或1), 导致其应用范围较窄.在此基础上, 文献[44]分析了调查传播算法的消息取值在[0, 1]区间上的收敛性, 并给出算法收敛的一个充分条件.在高斯图模型中, 信息传播算法常被用于计算均值和方差.文献[45]基于高斯线性模型给出了信息传播算法收敛的充分必要条件, 但局限于相邻变量不能共享同一个因子.文献[46]基于信息矩阵分析了信息传播算法的收敛性, 给出了一个充分必要条件, 但局限于消息的信息矩阵为正半定矩阵, 并且主要用于判定高斯BP算法的收敛性.文献[47]得到了信息传播算法的一个收敛条件, 但该条件的证明需要基于双因素线性高斯模型, 而该条件在一般问题上并不适用.文献[48]主要分析了求解高斯模型中方差的信息传播算法的收敛性, 但要求用一个半定规划来检查收敛性, 检查效率较低且非常困难.文献[49]分析了求解均值的信息传播算法的收敛性, 要求估计有限尺度矩阵的谱半径, 在实际应用中可行性不高.文献[50]分析了求解线性规划问题的信息传播算法的收敛性, 给出算法收敛到线性规划问题最优解的一个标准框架.文献[51]分析了求解块内插问题(block interpolation problem)的信息传播算法的有效性, 当因子图是一个N×N的网格图时, 算法能够正确收敛.在附加噪音的高斯图模型网络线性系统中, 利用WLS(weighted least squares)标准进行状态估计, 文献[52]基于协方差分析了信息传播算法收敛的动态行为.特别是在文献[53]中, 利用赋范空间中函数的压缩映射原理, 给出了信念传播算法收敛的一个统一框架.然而, 对于具体的SAT问题, 该条件验证复杂, 可判定的范围有限, 在大多数SAT实例上判定条件失效.不难看出: 上述关于信息传播算法的收敛性分析都是基于某个具体模型, 或者使用范围窄, 或者判定条件验证复杂等.因此, 对信息传播算法的收敛性分析仍然不完善.
综上, 本文针对BP算法在求解SAT问题中的信息传播策略, 对该算法的性能表现进行了系统的理论分析, 将信息迭代方程的取值由(0, 1)扩大到整个实数空间, 得出了验证BP算法收敛的一个有效条件, 检查该条件相对简单.最终, 通过实验分析了该条件的有效性.至此, 我们系统分析了3种求解SAT问题的信息传播算法的收敛性, 这对于基于信息传播算法的求解器设计以及信息传播算法的广泛应用具有重要意义.
1 信念传播算法 1.1 因子图一个CNF公式F={C1, C2, …, Cm}, 公式由变元x1, x2, …, xn构成, 为了方便表示, 将xi简记i.则CNF公式能够表示为一个二部网络G=(C∪X, E), 该二部网络称为因子图.图中包含两类结点, 分别为由所有变元构成的变元结点集, 记为X={1, 2, …, n}, 以及由变元的析取构成的子句结点集, 记为C={C1, C2, …, Cm}.图中的虚边和实边包含原CNF公式中两种不同的信息:
● 实边: (Ci, j)∈E⇔子句Ci含正文字xj;
● 虚边: (Ci, j)∈E⇔子句Ci含负文字¬xj.
为了方便在后文进行表示, 本文用a, b, …表示子句C1, C2, ….
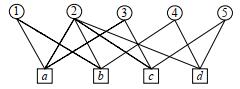
例1:公式F={(x1∨¬x2∨¬x3), (¬x1∨x2∨¬x4), (¬x2∨x3∨x5), (¬x2∨x4∨x5)}={a, b, c, d}的因子图G=(C∪X, E)如图 1所示.
|
Fig. 1 Factor graph 图 1 因子图 |
● V(a): 子句a所包含的所有变元的集合, V(a)=V+(a)∪V-(a).其中,
➢ V+(a): 在子句a中正出现的变元集合;
➢ V-(a): 在子句a中负出现的变元集合;
➢ V(a)\i表示集合V(a)中剔除结点i.
在图 1中, V(a)={x1, x2, x3}, V+(a)={x1}, V-(a)={x2, x3}.
● V(j): 包含变元xj的子句的集合, V(j)=V+(j)∪V-(j).其中,
➢ V+(j): 表示变元xj正出现的子句集合;
➢ V-(j): 表示变元xj负出现的子句集合;
➢ V(j)\a=V(j)-{a}.
在图 1中, V(2)={a, b, c, d}, V+(2)={b}, V-(2)={a, c, d}.
定义两个一致性集合Vau(j)和Vas(j):
● 如果xj∈V+(a), 那么
● 如果xj∈V-(a), 那么
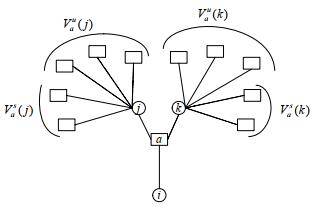
集合Vau(j)和Vas(j)如图 2所示.
|
Fig. 2 Part of factor graph 图 2 局部因子图 |
1.2 信念传播算法
基于消息传递而设计的信念传播算法, 求解可满足性问题时有良好的有效性.文献[30]给出了求解可满足性问题的BP算法, 其特征是基于因子图的消息传递过程.具体地讲, 在因子图的每条边(a, i)上定义消息δa→i∈ [0, 1], 消息更新方程为
| $ {\delta _{a \to i}} = \prod\nolimits_{j \in V(a)\backslash i} {\left( {\frac{{P_{j \to a}^u}}{{P_{j \to a}^u + P_{j \to a}^s}}} \right)} $ | (1) |
其中,
| $ P_{j \to a}^u = \prod\nolimits_{b \in V_a^s(j)} {(1 - {\delta _{b \to j}})} $ | (2) |
| $ P_{j \to a}^s = \prod\nolimits_{b \in V_a^u(j)} {(1 - {\delta _{b \to j}})} $ | (3) |
求解CNF公式的BP算法如算法1所示.
算法1. BP algorithm.
Input: factor graph G, max step tmax, precision ε.
Output: fix message δa→i*.
1. t=0, initialize δa→i(t=0)∈[0, 1] for random order;
2. For t=1 to t=tmax:
2.1. call BP-UPDATE to generating new message δa→i(t);
2.2. If |δa→i(t)-δa→i(t-1)| < ε, setδa→i*,
go to Step 3;
3. If t=tmax
return UN-CONVERGENCE.
Else if t < tmax
return δa→i*=δa→i(t);
算法2. BP-UPDATE.
Input: variable node j∈V(a)\i.
Output: δa→i.
1. compute
If
2. return δa→i by formula (1);
在信息传播算法中, 因子图上的信息δa→i定义为: 子句结点向变元结点发送的一个概率值, 即变元的取值使子句不可满足的概率信息.若BP算法进行若干次迭代后能够收敛, 则可以利用全局信息引导可满足指派的搜索过程, 这种方法被证明是非常有效的[30].然而, 对于因子图含有回路的SAT实例, BP算法有时候表现为不收敛, 因此无法返回SAT实例的可满足性结果.是什么原因导致BP算法不收敛, 目前还未给出理论解释.因此, 仍然有必要对BP算法的收敛性从理论上做更为深入的研究.
2 主要结论及证明设(V, ||·||)为一个有限维实向量空间,
| $ ||x|{|_1} = \sum\nolimits_{i = 1}^N {|{x_i}|} $ | (4) |
| $ \|x\|_{\infty}=\max _{i \in\{1, 2, \ldots, N\}}\left|x_{i}\right| $ | (5) |
向量空间V上的范数可诱导一个V上的度量d(v, w)=||v-w||, v, w∈V.显然, 度量空间(V, d)是完备的.
设函数f: V→V, 当0≤K < 1, 任意v, w∈V, 都有d(f(v)-f(w))≤Kd(v, w), 那么f为压缩函数.函数的压缩原理是指: 如果函数f: V→V是完备度量空间(V, d)中的压缩函数, 对于∀x∈V, f收敛到唯一点x∞.设(V, ||·||)是一个赋范空间, 映射A: V→V的矩阵范数:
| $ \|A\|=\sup _{v \in V}\|A v\| $ | (6) |
| $ ||A|{|_1} = {\max _{j \in \{ 1, 2, ..., N\} }}\sum\nolimits_{i = 1}^N {|{A_{ij}}|} $ | (7) |
| $ ||A|{|_\infty } = {\max _{i \in \{ 1, 2, ..., N\} }}\sum\nolimits_{j = 1}^N {|{A_{ij}}|} $ | (8) |
引理1[54]. 设(V, ||·||)是赋范空间, 函数f: V→V可微, 那么对于任意的x, y∈V, 则可以得到
| $ \|f(x)-f(y)\| \leqslant\|x-y\| \cdot \sup _{z \in V}\left|f^{\prime}(z)\right| $ | (9) |
由上述引理以及函数压缩映射可以知道, 若supz∈V|f'(z)| < 1, 则函数f能够收敛到x∞.如果函数f: V→V是可微的, 那么通过函数f的雅可比矩阵f'(z)来构造矩阵范数A.
为了分析方便, 假设δa→i∈(0, 1).更进一步, 为了利用实向量空间中的压缩映射原理, 我们将(0, 1)扩展为(-∞, +∞), 利用双曲正切函数进行参数化,
| $ \tanh {\lambda _{a \to i}} = 2\prod\nolimits_{j \in V(a)\backslash i} {\left( {\frac{{P_{j \to a}^u}}{{P_{j \to a}^u + P_{j \to a}^s}}} \right) - 1} $ | (10) |
其中,
| $ P_{j \to a}^u = \prod\nolimits_{b \in V_a^s(j)} {\frac{1}{2}(1 - \tanh {\lambda _{b \to j}})} $ | (11) |
| $ P_{j \to a}^s = \prod\nolimits_{b \in V_a^u(j)} {\frac{1}{2}(1 - \tanh {\lambda _{b \to j}})} $ | (12) |
为了书写方便, 假设
| $ {x_j} = \prod\nolimits_{b \in V_a^s(j)} {\frac{1}{2}(1 - \tanh {\lambda _{b \to j}})} , {y_j} = \prod\nolimits_{b \in V_a^u(j)} {\frac{1}{2}(1 - \tanh {\lambda _{b \to j}})} $ |
因此,
| $ \tanh {\lambda _{a \to i}} = 2\prod\nolimits_{j \in V(a)\backslash i} {\left( {\frac{{{x_j}}}{{{x_j} + {y_j}}}} \right) - 1} $ | (13) |
将CNF公式对应的因子图的消息边进行随机排序, 构造序列集合D={a→i: (a, i)∈E}, 定义函数f:
进行讨论.
● 情形1:设
| $ \begin{array}{l} f'({\lambda _{a \to i, b \to j}}) = \frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 2{\left( {\frac{{{x_j}}}{{{x_j} + {x_j}}}} \right)^\prime }\frac{1}{{1 - {{\tanh }^2}{\lambda _{a \to i}}}}\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\rm{ }} = 2\frac{{ - {x_j}{{y'}_j}}}{{{{({x_j} + {y_j})}^2}(1 - {{\tanh }^2}{\lambda _{a \to i}})}}\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} {\rm{.}} \end{array} $ |
由于
| $ {y'_j} = - \frac{1}{2}(1 - {\tanh ^2}{\lambda _{b \to j}})\prod\nolimits_{c \in V_a^u(j)\backslash b} {\frac{1}{2}(1 - \tanh {\lambda _{c \to j}})} = - (1 + \tanh {\lambda _{b \to j}}){y_j}{\rm{, }} $ |
所以,
| $ \begin{array}{l} \frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}} = 2\frac{{{x_j}{y_j}(1 + \tanh {\lambda _{b \to j}})}}{{{{({x_j} + {y_j})}^2}(1 - {{\tanh }^2}{\lambda _{a \to i}})}}\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} \\ \ \ \ \ \ \ \ \ \ = \frac{{{y_j}(1 + \tanh {\lambda _{b \to j}})(1 + \tanh {\lambda _{a \to i}})}}{{({x_j} + {y_j})(1 - {{\tanh }^2}{\lambda _{a \to i}})}}\\ \ \ \ \ \ \ \ \ \ = \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \tanh {\lambda _{a \to i}}}}{\rm{.}} \end{array} $ |
由公式(13)可知:
| $ \tanh {\lambda _{a \to i}} = 2\prod\nolimits_{j \in V(a)\backslash i} {\left( {\frac{{{x_j}}}{{{x_j} + {y_j}}}} \right) - 1} = 2\left( {\frac{{{x_j}}}{{{x_j} + {y_j}}}} \right)\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} - 1{\rm{, }} $ |
其中,
| $ 0 \le \prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} \le 1{\rm{, }} $ |
所以,
| $ \tanh {\lambda _{a \to i}} \le 2\left( {\frac{{{x_j}}}{{{x_j} + {y_j}}}} \right) - 1. $ |
进一步有:
| $ \frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}} = \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \tanh {\lambda _{a \to i}}}} \le \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \left( {2\frac{{{x_j}}}{{{x_j} + {y_j}}} - 1} \right)}} = \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{2\frac{{{y_j}}}{{{x_j} + {y_j}}}}} = \frac{1}{2}(1 + \tanh {\lambda _{b \to j}}) < 1{\rm{, }} $ |
因此,
| $ \left| {\frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}} \right| < 1. $ |
● 情形2:设
| $ \begin{array}{l} f'({\lambda _{a \to i, b \to j}}) = \frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = 2{\left( {\frac{{{x_j}}}{{{x_j} + {x_j}}}} \right)^\prime }\frac{1}{{1 - {{\tanh }^2}{\lambda _{a \to i}}}}\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\rm{ }} = 2\frac{{{{x'}_j}{y_j}}}{{{{({x_j} + {y_j})}^2}(1 - {{\tanh }^2}{\lambda _{a \to i}})}}\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} {\rm{.}} \end{array} $ |
由于
| $ {x'_j} = - \frac{1}{2}(1 - {\tanh ^2}{\lambda _{b \to j}})\prod\nolimits_{c \in V_a^s(j)\backslash b} {\frac{1}{2}(1 - \tanh {\lambda _{c \to j}})} = - (1 + \tanh {\lambda _{b \to j}}){x_j}{\rm{, }} $ |
所以,
| $ \begin{array}{l} \frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}} = - 2\frac{{{x_j}{y_j}(1 + \tanh {\lambda _{b \to j}})}}{{{{({x_j} + {y_j})}^2}(1 - {{\tanh }^2}{\lambda _{a \to i}})}}\prod\nolimits_{k \in V(a)\backslash i, j} {\left( {\frac{{{x_k}}}{{{x_k} + {y_k}}}} \right)} \\ \quad \quad \;\;\, = - \frac{{{y_j}(1 + \tanh {\lambda _{b \to j}})(1 + \tanh {\lambda _{a \to i}})}}{{({x_j} + {y_j})(1 - {{\tanh }^2}{\lambda _{a \to i}})}}\\ \quad \quad \;\;\, = - \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \tanh {\lambda _{a \to i}}}}{\rm{, }} \end{array} $ |
因此,
| $ \begin{array}{l} \left| {\frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}} \right| = \left| { - \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \tanh {\lambda _{a \to i}}}}} \right|\\ \quad \quad \;\;\, = \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \tanh {\lambda _{a \to i}}}}\\ \quad \quad \;\;\, \le \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{1 - \left( {2\frac{{{x_j}}}{{{x_j} + {y_j}}} - 1} \right)}}{\rm{(}}0 < {x_j}, {y_j} < 1{\rm{)}}\\ \quad \quad \;\;\, = \frac{{{y_j}}}{{{x_j} + {y_j}}}\frac{{1 + \tanh {\lambda _{b \to j}}}}{{2\frac{{{y_j}}}{{{x_j} + {y_j}}}}}\\ \quad \quad \;\;\, = \frac{1}{2}(1 + \tanh {\lambda _{b \to j}}) < 1. \end{array} $ |
关于情形1和情形2, 公式(21)和公式(25)表明: 对于∀λb→j∈(-∞, +∞), 都有:
| $ \left| {\frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}} \right| < 1{\rm{, }} $ |
所以,
| $ {\sup _{\lambda \in V}}\left| {\frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}} \right| < 1. $ |
注意: λa→i和λb→j是λ的分量.
利用函数f的雅可比矩阵构造矩阵范数A, 也即A中的元素为
定理1. 对于A1-范数, 如果
证明: 根据公式(6)、公式(7)和公式(9), 有:
| $ ||A|{|_1} = ||f'(\lambda )|{|_1} = {\max _{b \to j}}\sum\nolimits_{a \to i} {\left| {\frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}} \right|} \le {\max _{b \to j}}\sum\nolimits_{a \to i} {{\tau _{a \to i, b \to j}}} . $ |
由压缩映射原理和引理1可知: 如果
同理可得以下定理.
定理2.
对于A∞-范数, 如果
证明: 根据公式(6)、公式(8)和公式(9), 有:
| $ ||A|{|_\infty } = ||f'(\lambda )|{|_\infty } = {\max _{a \to i}}\sum\nolimits_{b \to j} {\left| {\frac{{\partial {\lambda _{a \to i}}}}{{\partial {\lambda _{b \to j}}}}} \right|} \le {\max _{a \to i}}\sum\nolimits_{b \to j} {{\tau _{a \to i, b \to j}}} . $ |
由压缩映射原理和引理1可知: 如果
为了书写方便, 不妨设f2(x)=f(f(x)), f3(x)=(f(f(x))), ….有如下引理成立.
引理2[44]. 设函数f: V→V, d是V上的度量.对于某个N∈
设γ1, γ2, …, γn是方阵M的特征值, 构成M的谱γ(M)={γ1, γ2, …, γn}, M的谱半径为ρ(M)=sup{|γi|: γi∈γ(M)}.假设τ=maxa→i, b→j{τa→i, b→j}, 一个|D|×|D|的方阵M中的元素定义为Ma→i, b→j=1V(j)\a(b)1V(a)\i(j)τ.若x∈X, 则1X(x)=1;若x∉X, 则1X(x)=0.
定理3. 如果方阵M的谱半径ρ(M) < 1, 那么BP算法一定能达到收敛点, 并且收敛过程不依赖于初始条件.
证明: 文献[44]中的定理4表明: 对于任意的x∈
固定点x∞, 也即x, f(x), f2(x), …, x∞.由前文中关于函数f的构造及情形1和情形2的推导可知, |f'(x)|≤M.因此, BP算法能够有效收敛, 收敛过程不依赖于初始条件.
例2:设命题公式为F1={(x1∨x2), (x2∨x3), (x3∨x4), …, (xn-1∨xn), (xn∨x1)}, 该公式的对应因子图中包含一个环路结构.所以, 由上文中所提构造方阵M的过程可知, 方阵中任意行中除了一个值可能不是0的元素之外, 所有元素的值都是0, 将该可能值为非0的元素设为τ.通过圆盘定理可以知道: |λ|≤τ, 其中λ为M的特征值.则利用上文中的证明可知: |λ|≤τ < 1.因此, 有ρ(M) < 1.又由定理3可得, 在公式F1中, BP算法能够迭代至收敛状态.同理, 在 F2={(¬x1∨¬x2), (¬x2∨¬x3), (¬x3∨¬x4), …, (¬xn-1∨¬xn), (¬xn∨¬x1)}中, BP算法同样能够到达收敛的状态.
注意到: 定理1和定理2分别是针对范数||A||1和||A||∞得出的结论, 不同的范数对应的收敛条件不同.然而, 目前还不清楚是否存在一个最优范数, 使得BP算法收敛的判定条件更加有效.
3 数值实验及分析数值实验中用到的数据由模型G(n, k, m)产生, n表示变元个数, m表示子句个数, k表示每个子句的长度.实验中, BP算法的最大迭代次数tmax=103, ε=0.001.
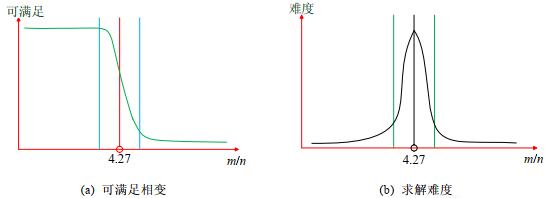
当k=3时, G(n, k, m)模型被用于产生随机3-SAT实例.研究结果表明: 对于随机3-SAT实例, 存在可满足性相变现象.如图 3(a)所示, 当子句个数与变元个数的比值m/n小于3.5时, 随机3-SAT实例高概率可满足[4]; 当子句个数与变元个数的比值m/n大于4.5时, 随机3-SAT实例高概率不可满足[5]; 对于子句个数与变元个数的比值m/n介于3.5与4.5之间的随机3-SAT实例, 其可满足性不能从概率上给出较为确切的回答.同时, 子句个数与变元个数的比值m/n介于3.5与4.5之间的随机3-SAT实例, 其求解难度也较大, 大多数求解算法在该区域的实例集上效果不明显, 称该区域为随机3-SAT实例的难解区域, 如图 3(b)所示.在α=4.27附近, 求解难度最大.因此, 常被国际竞赛用于构造难解实例来测试算法的性能.
|
Fig. 3 Properties change of random 3-SAT instance with parameter m/n 图 3 随机3-SAT实例的特征随参数m/n的变化情况 |
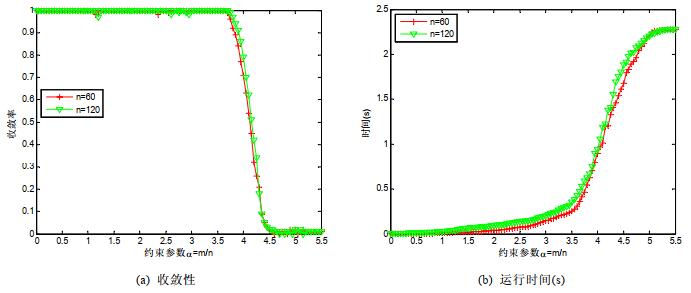
在实验中, 我们选取了两组规模不同的随机3-SAT实例, 分别为n=60和n=120, 每次利用随机实例产生模型生成100个随机实例作为一组数据, 并统计每组数据的实验结果, 作为图中的每个数据点.相关研究表明: 随机实例的难解程度与α的值密切相关.信息传播算法是基于消息迭代的近似算法, 收敛性直接影响算法的性能.图 4(a)是BP算法在随机3-SAT实例集上的收敛情况, 纵坐标是统计了所有实例中, 收敛实例所占的比值, 即实例能够达到收敛状态的所占的概率; 横坐标为α的变化情况.从图中可以看出: 大约α < 3.8时, BP算法高概率收敛; 大约α > 3.8时, BP算法的收敛性开始下降; 大约α > 4.5时, BP算法高概率不收敛.这也表明BP算法主要用于求解可满足性实例, 在求解不可满足的实例时, 算法常常会失效.图 4(b)是BP算法的运行时间随约束参数α的变化情况, 纵坐标表示运行时间(单位: s).当α > 3.52时, 算法的运行时间急剧增大; 随着α的增大, 实例的因子图的结构变得复杂, 导致BP算法的计算时间增加.
|
Fig. 4 Properties change of convergence and time of BP with parameter m/n 图 4 BP算法的收敛性和运行时间随参数m/n的变化情况 |
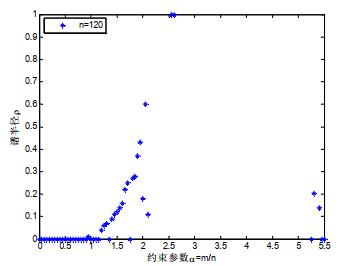
定理3中, 要求计算矩阵的谱半径.图 5为随机3-SAT实例的约束参数α与对应矩阵的谱半径之间的关系.参数ρ随着约束参数α的变化情况, 纵坐标表示谱半径ρ, 横坐标表示约束参数α.当α < 2.0时, 实例的谱半径小于0.7, 由定理3可知, BP算法能够到达收敛状态.当约束参数α > 2.0时, 谱半径ρ几乎不小于1, 定理3失效, 无法判定BP算法的收敛性.直观上, α越小, 因子图的结构就越简单, 对应的方阵M越稀疏, 谱半径ρ越接近0;相反, α越大, 因子图的结构就越复杂, 谱半径ρ也越大, 可能导致定理3中的判定条件失效.
|
Fig. 5 Properties change of spectral radius ρ with parameter m/n 图 5 谱半径ρ随参数m/n的变化情况 |
本文与文献[53]类似, 都可用于约束可满足性问题的收敛性判定.其他文献主要用于其他问题, 与本文没有可比性.所以, 我们把本文结论与文献[53]中的结论做了比较, 见表 1.由于可满足性问题实例的求解难度与问题的规模无关, 实验中取n=120.结合图 3(a)和图 4, 选取约束参数α的值分别为1.0, 2.0, 3.0, 4.0, 5.0进行比较, 每个数据点随机生成100个实例.表 1中的数据表示能够判定BP算法收敛的实例数占总实例数的比例, 可以看出: 当α < 2.0时, 本文结论优于文献[53]中的结论; 当α=3.0和α=4.0时, 本文结论比文献[53]结论略差.然而, 通过实验发现, 验证文献[53]中判定条件远比本文条件复杂, 在实际应用中可操作性不高.
| Table 1 Comparison with other methods 表 1 与其他方法比较 |
4 结束语
本文针对用于求解SAT问题的BP算法的收敛性进行了分析, 在BP算法中, 通过将算法的消息迭代方程取双曲正切, 并且将信息迭代方程的标准化函数的取值由(0, 1)扩展为(-∞, +∞), 得到了BP收敛的一个充分条件, 该判定条件相对简单, 并通过实验验证了该条件的有效性.至此, 本文基于一般条件, 完整分析了求解SAT问题的信息传播算法的收敛性, 该结果对于理论研究或者实际应用提供了很大的参考价值.BP算法求解SAT问题的不收敛现象大致有两种: 算法通过迭代无法收敛于一个固定点或者算法达到了预定的迭代次数上限.由于本文的理论基础均建立在算法能够有效收敛的前提下.因此, 下一步工作需要考虑是否存在收敛的唯一固定点、固定点的分布等问题、从而更为深入地对信息传播算法性能开展相关研究.
| [1] |
Biere A, Heule M, Maaren H. van Walsh T. Handbook of Satisfiability. IOS Press, 2009.
|
| [2] |
Kirkpatrick S, Selman B. Critical behavior in the satisfiability of random Boolean formulae. Science, 1994, 264(5163): 1297-1301.
[doi:10.1126/science.264.5163.1297] |
| [3] |
Mertens S, Mezard M, Zecchina R. Threshold values of random k-SAT from the cavity method. Random Structure Algorithms, 2006, 28(3): 340-373.
[doi:10.1002/rsa.20090] |
| [4] |
Kaporis A, Kirousis L, Lalas E. The probabilistic analysis of a greedy satisfiability algorithm. Random Structures & Algorithms, 2006, 28(4): 444-480.
|
| [5] |
Josep D, Kirousis L, Dieter M, Xavier PG. On the satisfiability threshold of formulas with three literals per clause. Theoretical Computer Science, 2009, 410(30): 2920-2934.
http://dl.acm.org/citation.cfm?id=1568788.1568938 |
| [6] |
Xu K, Li W. Exact phase transitions in random constraint satisfaction problems. Journal of Artificial Intelligence Research, 2000, 12(1): 93-103.
http://www.ams.org/mathscinet-getitem?mr=1752409 |
| [7] |
Xu K, Li W. Many hard examples in exact phase transitions. Theoretical Computer Science, 2006, 355(3): 291-302.
[doi:10.1016/j.tcs.2006.01.001] |
| [8] |
Xu K, Boussemart F, Hemery F. Random constraint satisfaction: Easy generation of hard satisfiable instances. Artificial Intelligence, 2007, 171(8): 514-534.
|
| [9] |
Davis M, Logemann G, Lovelan D. A machine program f or theorem proving. Communications of the ACM, 1962, 5(7): 394-397.
[doi:10.1145/368273.368557] |
| [10] |
Moskewicz MW, Madigan CF, Zhao Y. Chaff: Engineering an efficient SAT solver. In: Proc. of the 38th Design Automation. 2001.530-535.
|
| [11] |
Goldberg E, Novikov Y. BerkMin: A fast and robust SAT-solver. In: Proc. of the Design Automation and Test in Europe. 2002.142-149.
|
| [12] |
Eén N, Sörensson N. An Extensible SAT-solver: Theory and Applications of Satisfiability. Berlin: Springer-Verlag, 2004: 502-518.
|
| [13] |
Zhang H. SATO: An efficient propositional prover. In: Proc. of the Int'l Conf. on Automated Deduction. 1997.272-275.
|
| [14] |
Silva JP, Sakallah KA. GRASP: A search algorithm for propositional satisfiability. IEEE Trans. on Computers, 1999, 48(5): 506-521.
|
| [15] |
Selman B, Kautz H, Cohen B. Noise strategies for improving local search. In: Proc. of the AAAI. 1994.337-343.
|
| [16] |
Selman B, Levesque HJ, Mitchell D. A new method for solving hard satisfiability problem. In: Proc. of the AAAI. 1992.440-446.
|
| [17] |
Pearl J. Probabilistic Reasoning in Intelligent Systems. Morgan Kaufman Publishers, 1988.
|
| [18] |
Zhao CY, Zheng ZM. A belief-propagation algorithm based on variable entropy for constraint satisfaction problems. SCIENTIA SINICA Informationis, 2012, 42(9): 1170-1180(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201209010.htm |
| [19] |
Yin MH, Zhou JP, Sun JG, Gu WX. Heuristic survey propagation algorithm for solving QBF problem. Ruan Jian Xue Bao/Journal of Software, 2011, 22(7): 1538-1550(in Chinese with English abstract).
[doi:10.3724/SP.J.1001.2011.03859] |
| [20] |
Ravanbakhsh S, Greiner R. Perturbed message passing for constraint satisfaction problems. Artificial Intelligence, arXiv Preprint arXiv: 1401.6686, 2014.
|
| [21] |
Chieu HL, Lee WS. Relaxed survey propagation for the weighted maximum satisfiability problem. Journal of Artificial Intelligence Research, 2009, 36(1): 229-266.
http://www.jair.org/media/2808/live-2808-4698-jair.ps.gz |
| [22] |
Bayati M, Shah D, Sharma M. Max product for maximum weight matching: Convergence, correctness, and LP duality. IEEE Trans. on Information Theory, 2007, 54(3): 1241-1251.
http://bioinformatics.oxfordjournals.org/external-ref?access_num=10.1109/TIT.2007.915695&link_type=DOI |
| [23] |
Coja-Oghlan A, Mossel E, Vilenchik D. A spectral approach to analyzing belief propagation for 3-colouring. Combinatorics, Probability and Computing, 2009, 18(6): 881-912.
[doi:10.1017/S096354830900981X] |
| [24] |
Gamarnik D, Shah D, Wei Y. Belief propagation for min-cost network flow: Convergence and correctness. Operations Research, 2012, 60(2): 410-428.
[doi:10.1287/opre.1110.1025] |
| [25] |
Sanghavi S, Malioutov DM, Willsky AS. Belief propagation and LP relaxation for weighted matching in general graphs. IEEE Trans. on Information Theory, 2011, 57(4): 2203-2212.
[doi:10.1109/TIT.2011.2110170] |
| [26] |
Sanghavi S, Shah D, Willsky AS. Message passing for maximum weight independent set. IEEE Trans. on Information Theory, 2009, 55(11): 4822-4834.
[doi:10.1109/TIT.2009.2030448] |
| [27] |
Hetterich S. Analysing survey propagation guided decimation on random formulas. arXiv Preprint arXiv: 1602.08519, 2016.
|
| [28] |
Amin CO. On belief propagation guided decimation for random k-SAT. In: Proc. of the 22nd Annual ACMSIAM Symp. on Discrete Algorithms. San Francisco, 2016.957-966.
|
| [29] |
Marino R, et al. The backtracking survey propagation algorithm for solving random K-SAT problems. Nature Communications, 2016, 7: Article No. 12996. [doi: 10.1038/ncomms12996(2016)]
|
| [30] |
Braunstein A, Mezard M, Zecchina R. Survey propagation: An algorithm for satisfiability. Random Structures and Algorithms, 2005, 27(2): 201-226.
[doi:10.1002/rsa.20057] |
| [31] |
Maneva E, Mossel E, Wainwright M. A new look at survey propagation and its generalizations. Journal of the ACM, 2007, 54(4): 1089-1098.
|
| [32] |
Yedidia JS, Freeman WT, Weiss Y. Understanding belief propagation and its generalizations. Artificial Intelligence, 2003, 8(1): 239-269.
http://www.scienceopen.com/document/vid/1c2da320-18e6-4fec-b099-9ce584b7fb1a |
| [33] |
Braunstein A, Zecchina R. Survey and belief propagation on random k-SAT. LNCS, 2004, 2919(1): 519-528.
http://link.springer.com/chapter/10.1007/978-3-540-24605-3_38 |
| [34] |
Weiss Y. Correctness of local probability propagation in graphical models with loops. Neural Computation, 2000, 12(1): 1-41.
[doi:10.1162/089976600300015880] |
| [35] |
Weiss Y, Freeman WT. Correctness of belief propagation in gaussian graphical models of arbitrary topology. Neural Computation, 2001, 13(10): 2173-2200.
[doi:10.1162/089976601750541769] |
| [36] |
Tatikonda S, Jordan MI. Loopy belief propagation and Gibbs measure. In: Proc. of the 18th Annual Conf. on Uncertainty in Artificial Intelligence. 2002.493-500.
|
| [37] |
Heskes T. On the uniqueness of loopy belief propagation fixed points. Neural Computation, 2004, 16(11): 2379-2413.
[doi:10.1162/0899766041941943] |
| [38] |
Ihler AT, Lii JWF, Willsky AS. Loopy belief propagation: Convergence and effects of message errors. Machine Learning Research, 2005, 6(1): 905-936.
http://dl.acm.org/citation.cfm?id=1088703 |
| [39] |
Shi XQ, Schonfeld D, Tuninetti D. Message error analysis of loopy belief propagation for the sum-product algorithm. Computer and Information Science, 2010, 1009: 1-30.
|
| [40] |
Feige U, Mossel E, Vilenchik D. Complete convergence of message passing algorithms for some satisfiability problems. Theory of Computing, 2013, 9(19): 617-651.
http://www.ams.org/mathscinet-getitem?mr=3070855 |
| [41] |
Wang XF, Xu DY, Wei L. Convergence of warning propagation algorithms for random satisfiable instances. Ruan Jian Xue Bao/Journal of Software, 2013, 24(1): 1-11(in Chinese with English abstract).
[doi:10.3724/SP.J.1001.2013.04213] |
| [42] |
Wang XF, Xu DY. Convergence of the belief propagation algorithm for RB model instances. Ruan Jian Xue Bao/Journal of Software, 2016, 27(11): 2712-2724(in Chinese with English abstract).
[doi:10.13328/j.cnki.jos.004877] |
| [43] |
Wang XF, Xu DY. Sufficient conditions for convergence of the warning propagation algorithm. Ruan Jian Xue Bao/Journal of Software, 2016, 27(12): 3003-3013(in Chinese with English abstract).
[doi:10.13328/j.cnki.jos.004940] |
| [44] |
Wang XF, Xu DY, Jiang JL, Tang YH. A sufficient condition for survey propagation convergence. SCIENTIA SINICA Informationis, 2017, 47(12): 1646-1661(in Chinese with English abstract).
https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201712003.htm |
| [45] |
Du J, Ma S, Wu YC, Kar S, Moura JMF. Convergence analysis of distributed inference with vector valued Gaussian belief propagation. Journal of Machine Learning Research, 2018, 18(172): 1-38.
http://dl.acm.org/doi/10.5555/3122009.3242029 |
| [46] |
Du J, Ma S, Wu YC, Kar S, Moura JMF. Convergence analysis of the information matrix in Gaussian belief propagation. In: Proc. of the IEEE Int'l Conf. on Acoustics, Speech and Signal Processing. 2017.4074-4078.
|
| [47] |
Du J, Ma S, Wu YC, Kar S, Moura JMF. Convergence analysis of belief propagation for pairwise linear Gaussian models. In: Proc. of the IEEE Global Conf. on Signal and Information Processing. 2017.548-552.
|
| [48] |
Su Q, Wu YC. Convergence analysis of the variance in Gaussian belief propagation. IEEE Trans. on Signal Processing, 2014, 62(19): 5119-5131.
[doi:10.1109/TSP.2014.2345635] |
| [49] |
Su Q, Wu YC. On convergence conditions of Gaussian belief propagation. IEEE Trans. on Signal Processing, 2015, 63(5): 1144-1155.
[doi:10.1109/TSP.2015.2389755] |
| [50] |
Park S, Shin J. Convergence and correctness of max-product belief propagation for linear programming. Siam Journal on Discrete Mathematics, 2017, 31(3): 2228-2246.
[doi:10.1137/15M1042565] |
| [51] |
Wang Y, Reyes MG, Neuhoff DL. Correct convergence of min-sum loopy belief propagation in a block interpolation problem. arXiv Preprint arXiv: 1702.06391, 2017.
|
| [52] |
Sui T, Marelli D, Fu M. Convergence analysis for guassian belief propagation: Dynamic behaviour of marginal covariances. In: Proc. of the IEEE Int'l Conf. on Acoustics, Speech and Signal Processing. 2016.2599-2602.
|
| [53] |
Mooij JM, Kappen HJ. Sufficient conditions for convergence of the sum-product algorithm. IEEE Trans. on Information Theory, 2007, 53(12): 4422-4437.
[doi:10.1109/TIT.2007.909166] |
| [54] |
Dieudonne J. Foundations of Modern Analysis. New York: Academic Press, 1960.
|
| [18] |
赵春艳, 郑志明. 一种基于变量熵求解约束满足问题的置信传播算法. 中国科学: 信息科学, 2012, 42(9): 1170-1180.
https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201209010.htm |
| [19] |
殷明浩, 周俊萍, 孙吉贵, 谷文祥. 求解QBF问题的启发式调查传播算法. 软件学报, 2011, 22(7): 1538-1550.
[doi:10.3724/SP.J.1001.2011.03859] |
| [41] |
王晓峰, 许道云, 韦立. 随机实例集上警示传播算法的收敛性. 软件学报, 2013, 24(1): 1-11.
[doi:10.3724/SP.J.1001.2013.04213] |
| [42] |
王晓峰, 许道云. RB模型实例集上置信传播算法的收敛性. 软件学报, 2016, 27(11): 2712-2724.
[doi:10.13328/j.cnki.jos.004877] |
| [43] |
王晓峰, 许道云. 警示传播算法收敛的充分条件. 软件学报, 2016, 27(12): 3003-3013.
[doi:10.13328/j.cnki.jos.004940] |
| [44] |
王晓峰, 许道云, 姜久雷, 唐延辉. 调查传播算法收敛的一个充分条件. 中国科学: 信息科学, 2017, 47(12): 1646-1661.
https://www.cnki.com.cn/Article/CJFDTOTAL-PZKX201712003.htm |
 2021, Vol. 32
2021, Vol. 32


