2. 河池学院 大数据与计算机学院, 广西 河池 546300
2. School of Big Data and Computer Science, Hechi University, Hechi 546300, China
随着当今世界进入大数据时代, 各类工程优化问题、科学计算问题等越来越复杂化, 各个领域中的复杂优化计算也越发地成为社会急需解决的问题, 如电力系统无功优化、物流中最优配送、大数据虚拟资源调度及化工过程最优控制等众多实际问题.传统的优化算法在解决这些大规模、高难度和不确定性的复杂实际工程优化问题时, 在收敛精度、鲁棒性和收敛速度等方面都难以获得令人满意的结果.受自然界中各种演化规律及其生物种群行为的启发, 众多国内外学者提出了一系列群智能优化算法, 如粒子群算法[1]、蜂群优化算法[2]、差分进化算法[3]及教与学优化算法[4]等, 并且成功地用于求解上述大量的工程问题.
受显花植物花授粉过程的启发, 学者Yang[5]构建了一种新的优化算法——花授粉算法(flower pollination algorithm, 简称FPA).FPA算法是模拟自然界显花植物授粉繁殖后代的不同方式, 它是一种基于种群集体搜索行为的启发式智能算法, 与其他群智能算法相比, 由于其概念简单、容易实现、寻优效率较高, 并通过参数p较好地解决了探测和开采之间的平衡问题等优点, 一经提出就引起国内外众多学者的广泛关注.目前, FPA算法在多目标优化、无线传感器网络生命周期优化、神经网络优化、桁架结构优化、数据挖掘及能源[6-11]等众多领域中得到了广泛应用.然而FPA算法在解决众多工程问题时, 存在后期收敛速度慢、收敛精度低和易陷入局部极小等不足, 尤其是对于具有多局部极值点、高维较复杂的优化问题.为了提高FPA算法在实际应用中的优化能力, 国内外众多学者对该算法进行了一系列研究和改进.从目前已出版的有关文献梳理结果来看, 当前国内外学者对其研究主要从以下几个方面展开.
(1) 对算法的关键参数p值的设置及其动态调整策略进行了研究[12].
从算法的仿生原理可知: 控制算法性能的参数较少, 但关键参数p对该算法的优化能力具有较大的影响.
Madasu等人[13]对p在[0.1, 1]的取值进行了实验仿真分析, 实验结果表明: 当p在[0.5, 0.6]之间取值时, FPA算法的性能较好.且Madasu等人在文献[13]中指出: p=0.55时, 算法的优化性能最好.Draa[14]对关键参数p值的设置进行了定量仿真实验分析, 仿真结果显示: 当p取0.2时, FPA算法的优化能力表现最优.
Mahdad等人[15]根据迭代次数把转换概率p进行分阶段的动态自适应调整, 同时将分区搜索机制引入到FPA算法中, 然后利用改进的FPA算法求解带安全约束的优化功率流问题, 在IEEE 30-Bus和IEEE 57-Bus电力测试系统上对燃料成本、功率损耗和电压偏差这3个不同目标进行优化, 并与其他方法进行比较, 实验结果表明: 其优化效果要优于对比方法, 同时, 其鲁棒性也得到了较好的提升.
(2) 将其他优秀的算子引入到FPA算法中.
这类改进研究是根据著名的“无免费午餐定理”.每种元启发式算法都会存在各自的优点和缺点, 故国内外众多学者对算法进行改进时, 都把多种算子融合到一起, 构成超大型智能优化算法, 使其优势互补, 提高算法的整体性能.
Zhou等人[16]首先运用精英反向学习策略对FPA算法的全局授粉部分进行改进, 提高其种群个体的多样性, 从而有利于扩展其搜索领域; 其次, 他们还把自适应贪婪机制融入到局部搜索, 改善其探索能力; 最后, 参数p采用动态调整策略.实验结果显示, FPA算法的优化能力获得了较大提升.
肖辉辉等人[17]针对花授粉算法种群个体之间缺乏信息交流, 容易导致算法陷入早熟的问题; 同时, 为了将进化中的最差个体变为较好个体, 改善解的质量, 构建了基于复合形法的花授粉算法模型.测试结果验证了改进方法的有效性.
Chakraborty等人[18]在FPA算法中融入差分进化思想: 先运用差分进化算法来改善FPA算法初始解的质量; 然后, 为了消除p对FPA算法优化性能的不利影响, 增强FPA算法的鲁棒性, 受粒子群优化算法设计思想的启发, 通过引入两个动态参数, 把FPA算法的两个搜索方程合二为一.测试结果表明, 改进策略提高了FPA算法的收敛能力.
Wang等人[19]针对k-means算法在求解聚类问题时容易陷入局部最优且解的质量高度依赖初始解等问题, 提出了用改进的FPA算法求解聚类问题.该算法首先在FPA算法的全局搜索部分引入人工蜂群算法中的丢弃解操作, 该策略有利于个体跳出局部最优; 其次, 再将基于精英的变异算子和交叉算子融入到FPA算法的局部搜索中, 分别用来提高算法的开采能力和增加种群的多样性.
Draa[14]将反向学习方法融入到FPA算法中, 实验结果显示, 该措施能够有效提升算法的优化性能.
肖辉辉[20]构建了一种基于引力搜索机制的花授粉算法, 对全局寻优部分进行改进: 采用花朵个体间的万有引力和算法本身的莱维飞行共同实现个体位置的更新, 使花朵个体受莱维飞行和个体间引力的双重影响.在进化中, 种群个体利用万有引力的相互作用实现优化信息的共享及向质量大(最优位置)的个体靠近, 且个体间的万有引力也牵制莱维飞行的随机游走; 同时又运用莱维飞行的跳跃及不均匀性步长, 避免个体陷入局部极值, 从而提高算法的寻优能力.实验结果表明, 改进方法能够有效提升FPA算法的性能.
以上文献中的改进方法均能有效提升FPA算法的寻优性能, 但都没有从FPA算法的搜索策略所存在的固有缺陷这个角度对其进行改进, 也没有考虑在进化中劣解对FPA算法寻优能力的影响; 同时, 上述改进算法在求解高维多峰的复杂优化问题时, 其优化性能还不够理想, 并且有些改进算法修改了FPA算法的演化思路, 另一些改进算法与FPA算法相比, 其时间复杂度较高.
针对上述存在的问题, 本文构建了一种改进的基于多策略的花授粉算法(an improved flower pollination algorithm based on multi-strategy, 简称MIFPA).该算法在全局搜索部分引入两组随机个体差异矢量以增强算法的扰动性, 提高个体在进化后期逃离局部极值的概率; 将精英变异策略融入到局部授粉, 并通过一个线性递减概率规则与基本FPA算法的变异机制构成新的局部搜索策略, 在较好地保持算法种群多样性的同时, 加速了算法的收敛速度; 利用余弦函数搜索因子方法对进化中的劣解进行改进, 以提高算法解的质量.上述改进方法的有机融合, 构成了MIFPA算法的主要框架, 这些方法在算法的不同进程中执行, 并相互协调地提升FPA算法的整体性能.新算法中的参数实施自适应调整策略, 增强了算法的灵活性.其实现非常简单, 且既不会大幅增加FPA算法的时间复杂度, 也未改变FPA算法的基本演化思想.实验结果表明, MIFPA算法简单且高效、求精能力强、收敛速度快和鲁棒性好, 在单模态高维函数、多模态高维函数、多模态低维函数、带旋转的多模态高维函数和变换旋转的复杂函数上的优化能力与已有典型的改进FPA算法和其他知名改进算法相比, 显示出其良好的竞争力; 同时, 在求解实际的复杂工程问题时, 与其他对比算法相比, MIFPA算法的优势也表现突出.
1 基本花授粉算法FPA算法概念简单、容易实现及寻优效率较高, 且通过参数p实现了其异花授粉和自花授粉之间的相互切换, 平衡了算法的探索和开发能力.同时, FPA算法利用了莱维飞行策略来实现对个体位置的更新, 扩展其开采领域, 从而达到提高算法的优化能力.
为了更好地利用FPA算法解决实际优化问题, Yang[5]在算法中假定每株显花植物只开一朵花, 每朵花只有一个花粉配子, 一个配子对应于求解问题的一个解.此外, 还需假定以下4条规定.
(1) 显花植物的异花授粉对应于算法的勘探行为, 全局授粉是由蜜蜂等传播者携带花粉并采用莱维飞行来实现;
(2) 非生物自花授粉对应于算法的开采行为, 局部授粉是通过同种植物的不同花朵之间传粉来实现;
(3) 繁衍概率对应于花的常性, 进化中两个个体(花朵)之间的相似性与其值大小具有一定的比例关系;
(4) 参数p∈[0, 1]对FPA算法的勘探(全局授粉)和开采(局部授粉)之间的相互转换进行调节, 且因受花朵个体之间所处位置的邻近性和风等其他自然因素影响, 使得授粉更偏重于自花授粉[21].
从上述可知, 异花授粉(全局授粉)和自花授粉(局部授粉)是FPA算法的核心, 算法的全局授粉(优化)通过公式(1)实现, 局部授粉(优化)通过公式(5)实现.
全局授粉(优化)的进化公式如下:
| $x_i^{t + 1} = x_i^t + \gamma L(\lambda )(x_i^t - {x_{best}})$ | (1) |
其中,
| $L(\lambda )\sim \frac{{\lambda G(\lambda )\sin (\pi \lambda /2)}}{\pi }\frac{1}{{{s^{1 + \lambda }}}}(s > > {s_0} > 0)$ | (2) |
其中, λ=3/2, G(λ)是标准伽马函数, s由公式(3)得到:
| $s = \frac{\mu }{{|\nu {|^{1/\lambda }}}}$ | (3) |
其中, μ~N(0, σ2), ν~N(0, 1), σ2由公式(4)计算获得:
| ${\sigma ^2} = {\left\{ {\frac{{G(1 + \lambda )}}{{\lambda G[(1 + \lambda )/2]}} \cdot \frac{{\sin (\pi \lambda /2)}}{{{2^{(\lambda - 1)/2}}}}} \right\}^{1/\lambda }}$ | (4) |
花朵个体的局部授粉(优化)可通过公式(5)进行局部搜索:
| $x_i^{t + 1} = x_i^t + \varepsilon (x_j^t - x_k^t)$ | (5) |
其中,
依据基本FPA算法的仿生原理可知: 其是由全局搜索和局部搜索通过参数p进行融合组成的, 并利用公式(1)和公式(5)实现了数学模型化, 为其解决一系列复杂的优化问题奠定了理论基础.而对基本FPA算法的搜索机制进行定性分析显示: 基本FPA算法的搜索策略存在的不足制约着算法的收敛效果, 包括存在收敛速度慢和易陷入局部最优等缺点.对于这些影响算法性能的不利因素, 本文对FPA算法进行了多策略改进.
2.1 新全局搜索策略从技术角度来说, FPA算法在全局授粉时, 莱维飞行和最优个体(xbest)对种群中的个体同时施加影响.由于受全局最优个体xbest的吸引, FPA算法在优化简单问题时具有较快的收敛速度; 但在解决复杂的优化问题时, 若种群中的个体xbest陷入到探索领域中的某些局部极小位置, 则其他个体受xbest的影响, 也快速移动到xbest所在的位置, 使得(
| $x_i^{t + 1} = x_i^t + \gamma L(\lambda )(x_i^t - {x_{best}} + x_{{i_1}}^t - x_{{i_2}}^t + x_{{i_3}}^t - x_{{i_4}}^t)$ | (6) |
其中, i、i1、i2、i3、i4分别是从当前群体中随机选取的5个不同个体的下标, 其余变量的含义同公式(1).
从公式(6)可以看出: 在莱维飞行机制的基础上, 引入了两组差异矢量, 增加了种群个体之间的差异性, 提高了算法在多维空间的探索能力, 有利于抑制算法早熟收敛, 提升算法的性能.
2.2 引入精英变异策略的局部搜索策略在基本花授粉算法的局部搜索部分, 利用公式(5)的变异操作产生一个新个体.从公式(5)可知: 新个体是在父代个体的基础上加上一个扰动项, 其值是一个随机数和两个个体差分矢量的乘积.于是, 新个体的产生具有较大的随机性, 这使得种群个体的多样性能够较好地得到维持, 从而使算法能够保持良好的持续优化能力.但是由于个体缺乏对种群中最优个体良好经验的继承和学习机制, 个体的进化方向具有很强的盲目性, 这导致了对搜索全局最优解的计算量增大, 降低了算法的收敛速度.
为了解决上述存在的这个问题, 基于差分进化算法的思想和FPA算法的特性, 本文把差分进化算法中的经典变异算子DE/best/2的思路融入到局部授粉中, 提出一种新的复合型局部搜索机制: 如果rand < ζ, 则按式(7)进行处理; 否则按式(8)进行处理.
| ${v_i} = {x_i} + \delta ({x_{{r_2}}} - {x_{{r_3}}})$ | (7) |
| ${v_i} = {x_{best}} + \alpha ({x_{{r_1}}} - {x_{{r_2}}} + {x_{{r_3}}} - {x_{{r_4}}})$ | (8) |
其中, rand是[0, 1]上服从均匀分布的随机数; ζ=1-t/Max_iter, t是当前迭代次数, Max_iter为最大迭代次数; 参数δ、α是服从高斯分布且均值和标准偏差分别为0.5、0.1, 其作用是用于控制算法的演化速度; n为种群数, i∈(1, 2, …, n)为当前个体的下标, r1、r2、r3、r4为4个不同的随机个体的下标, xbest为当前种群中最优个体.
从上述改进的局部授粉策略可知: 公式(7)采用变异策略增加种群个体的差异性, 从而达到提升算法的全局优化能力, 但算法的搜索速度比较慢; 对于公式(8)运用的变异机制, 是通过精英个体对其他个体的演化方向进行引导, 同时利用精英个体的信息有利于开发其周围领域, 提高FPA算法的搜索效率, 从而提升了算法的收敛速度和开采能力, 但这一策略也容易导致FPA算法陷入局部极小问题.为了能够使这两种方法优势互补, 提高FPA算法的寻优能力, 本文通过一个线性递减概率规则融合这两种变异机制, 构建MIFPA算法的新局部搜索策略.
同时, 从上述新的局部搜索策略可以看出: 在进化过程中, 通过线性递减概率规则“rand < ζ”对两种变异策略进行调节, 如果rand产生的随机数小于ζ, 则个体执行公式(7)的变异机制; 否则, 执行公式(8)的变异策略.
依据ζ=1-t/Max_iter可知: 在算法进化初期, 选择公式(7)的变异策略的概率要比选择公式(8)的变异机制的概率大, 这有利于种群个体在演化初期扩大搜索空间.因为从公式(7)可以发现: 在算法进化初期, 由于个体之间的差异性比较大, 则
在基本花授粉算法中, 总是以贪婪式演化策略选择较优个体来保证群体向前进化, 即: 经过全局搜索或局部搜索后, 产生一个新个体, 只有当子代的适应度值优于父代才能演化.然而, 依据FPA算法的具体流程可知: 如果子代劣于父代, 则父代直接保留到下一代, 并没有对其作任何改进措施, 算法直接进入下一次进化, 这使得本次迭代的计算资源严重浪费, 增加了对全局最优解的搜索计算量, 降低了算法的收敛速度, 且容易造成算法收敛精度不高.
针对基本花授粉算法存在的这一不足, 在算法进入下次迭代之前, 如果父代没有得到改善, 则利用公式(9)重新产生一个新个体, 若新解优于原始解, 则用新解代替原始解:
| ${x^{new{\rm{ }}}} = 2 \times \cos ((\pi \times t)/(2 \times {\rm{Max\_}}iter)) \times \varphi \times {x_t}(r) $ | (9) |
其中, φ是[-1, 1]上服从均匀分布的随机数, 其作用是使种群个体实现随机游走; Max_iter为最大迭代次数, xt(r)是迭代次数为t时种群中的一个随机个体; xnew为产生的新个体, t=1, 2, …, Max_iter.
由上述可以看出: 原始解的质量获得提升的概率得到提高, 从而达到提高FPA算法解的质量.下面就公式(9)可改善算法解的质量、提高算法优化能力的原因进行分析.
(1) 公式(9)能够有效避免随机产生的新个体(解)的质量太差(新个体远离全局最优个体xbest)而影响算法的搜索速度.从公式(9)中可以看出: 新个体的产生是以xt(r)为中心, 充分利用原有个体的信息引导新个体在其四周产生, 使其产生的新个体的位置距全局最优个体xbest更近, 避免了由于产生的新个体质量差而导致算法的收敛速度慢.
(2) 依据上述新的全局搜索方程(6)和新的局部搜索方程(8)可以发现: 在新构建的搜索策略中都采用了最优个体(xbest)策略, 这增加了算法陷入局部最优的风险.为了有效防止FPA算法早熟, 本文利用公式(9)来产生一个新个体以替换没有得到改善的父代个体.从公式(9)可以发现: 新个体的产生利用了余弦函数因子, 使得算法有利于跳出局部最优.这是因为, 余弦函数因子与线性递减因子相比, 余弦函数因子具有振荡性.
本文通过融入余弦函数搜索因子, 利用其振荡特点使得种群个体位置具有振荡性, 扩展个体的搜索范围, 有效引导个体跳出局部最优, 提高解的质量.
图 1是余弦函数在x不同取值范围内的曲线图, 从图 1可知: 随着x取值的不断扩大, 余弦函数的峰值个数增多, 这说明余弦函数的振荡性更加剧烈.但是, 如果算法的振荡性太强, 不利于算法快速收敛, 甚至造成算法找不到全局最优解.鉴于此, 本文把余弦函数的x取值设为π×t/(2×Max_iter)∈(0, π/2), 以减缓个体的振荡性, 使算法获得更优质量的解.
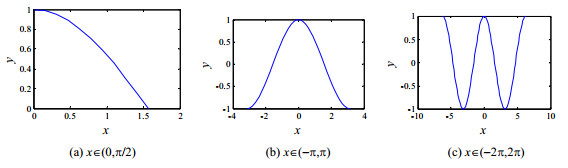
|
Fig. 1 Curve graph of cosine functions within the range of different values of x 图 1 余弦函数在x不同取值范围内的曲线图 |
(3) 同时, 利用公式(9)中的余弦函数搜索因子, 其作用是对产生的新个体半径范围进行调节.其思想是: 在算法进化初期, cos(π×t/(2×Max_iter))值较大, 则以原有个体xt(r)为中心的搜索半径较大, 使得算法具有良好的全局搜索能力; 而随着演化的不断深入, 其搜索半径越来越小, 因此到进化的后期, 新个体更侧重于局部精细化开采.由此可知: 通过利用余弦函数因子, 可使算法具有良好的全局搜索和局部搜索平衡性, 提高了算法的全局优化能力, 并找到最优解.
2.4 MIFPA算法的流程根据第2.1节~第2.3节描述的算法改进思想, 本节给出MIFPA算法流程, 如算法1所示.其中, n为花朵的个数, xbest是全局最优解, fmin是xbest对应的最优值.
Aglorithm 1. MIFPA.
1. Randomly produce n flowers {xi|i=1, 2, …, n};
2. Compute the fitness fun(xi);
3. fmin=min(fun(xi));
4. Find the best individual xbest in the initial population;
5. FEs=n;
6. while FEs≤Max_FEs do
7. for i=1: n do
8. Generate a new p according to Eq.(11);
9. if p > rand(0, 1) //global optimization
10. Randomly produce four flowers (solutions);
11. produce a new candidate
12. else // local optimization
13. Randomly generate four flowers (solutions);
14. if rand(0, 1) < ζ
15. Generate a new candidate
16. else
17. Generate a new candidate
18. endif
19. endif
20. Evaluate the newly generated solution
21. FEs=FEs+1;
22.
if
23. replace
24. else
25. Generate a new candidate
26. Evaluate the newly generated solution
27. FEs=FEs+1;
28.
if
29. replace
30. endif
31. endif
32. endfor
33. Update the current best solution xbest;
34. endwhile
MIFPA算法与基本FPA算法的框架基本类似, 但其中主要有4个不同之处: ①转换概率p采用自适应调整策略, 详见第8行; ②增加了两组随机个体的差异矢量到全局搜索(全局授粉)中, 详见第10行、第11行; ③采用一个线性递减概率规则融合两种变异机制进行局部搜索(局部授粉), 详见第14行~第18行; ④利用余弦函数搜索因子对算法中的劣解进行改进, 详见第25行.
2.5 MIFPA算法的复杂度分析衡量改进算法的有效性和可行性, 一是算法的寻优性能要有较大的提高, 二是算法的时间复杂度也不能比原算法高太多.在群智能优化算法中, 时间复杂度是指通过优化算法求解优化问题的最优解或次优解所需要的进化次数.下面对MIFPA算法的复杂度进行分析.
假设目标函数设为f(x), 算法的种群规模设为n, 求解问题的维数设为D, f(D)为计算给定解的目标函数的执行时间与求解问题维数D有关的函数, 则依据算法的描述和符号O(时间复杂度符号)的计算规则为:
● 在初始化种群并计算得到最优值和最优解阶段的时间复杂度为O(n(r1D+f(D)))=O(D+f(D)), 其中, r1为产生均匀分布随机数的执行时间;
● 全局优化部分的时间复杂度为O(n(r2D))=O(D), 其中, r2为式(1)生成新解时一维变量的执行时间;
● 局部优化部分的时间复杂度为O(n(r3D))=O(D), 其中, r3为式(5)生成新解时一维变量的执行时间;
● 更新全局最优值和全局最优解部分的时间复杂度为O(n(r4+r5D+f(D)))=O(D+f(D)), 其中, r4、r5分别为比较新解与旧解和替换一维旧解变量的执行时间.
所以, FPA算法的时间复杂度[20]表示为T(FPA)=2O(D+f(D))+2O(D)=O(D+f(D)).从第2.4节的算法流程可知: 公式(6)~公式(9)是改进算法修改之处, 即包括新的全局搜索策略、新的局部搜索策略和对质量不好的解的改进方法.依据上述对算法公式的描述和符号O的计算规则, 可推导出MIFPA的时间复杂度为
T(MIFPA)=T(FPA)+T(公式(6))+T(公式(7))+T(公式(8))+T(公式(9))
=O(D+f(D))+O(n(r6D))+O(n(r7D))+O(n(r8D))+O(n(r9D))
=O(D+f(D))+4O(n(D))
=O(D+f(D)),
其中, r6~r9分别为公式(6)~公式(9)中生成新解时一维变量的执行时间.因此, MIFPA算法的时间复杂度与FPA算法的时间复杂度属于同一数量级, 也就是说, 改进算法的复杂度并未比FPA算法提高太多.
根据上述对MIFPA算法的时间复杂度的理论分析(定性分析)可知, MIFPA算法的时间复杂度与基本FPA算法属于同一数量级.因为FPA的迭代次数为Max_Gf=Max_FEs/n, 其中, n为种群数, MIFPA算法的最大迭代次数为Max_FEs/(2×n) < Max_Gc < Max_FEs/n, 故Max_Gc < Max_Gf.从上述分析可知: 在相同的最大函数评估次数Max_FEs=10000×D(其中, D为函数的维数)下, MIFPA算法并没有增加算法的时间复杂度.
3 实验仿真及分析 3.1 实验测试函数及参数设置为了检验MIFPA算法的有效性, 本节选用19个经典的标准测试函数(包含CEC测试函数)进行实验, 测试函数的函数名称、搜索空间、维数及理论最优值的描述见表 1[22, 23].按其特性, 可将测试函数分为五大类: f1~f4是单模态高维函数; f5~f9是非旋转的多模态高维函数; f10~f13是多模态低维函数; f14~f16是带旋转的多模态高维函数; f17~f19是变换旋转高维函数.本文中所用的所有函数都是求解最小值.
| Table 1 Experimental test functions in the paper 表 1 本文使用的实验测试函数 |
3.2 余弦函数搜索因子对算法性能的影响分析
为了更直观地进一步说明本文引入余弦函数搜索因子能够提高算法解的质量这一点, 本节对带余弦函数搜索因子的花授粉算法(flower pollination algorithm with cosine function factor, 简称CFPA)与基本花授粉算法(FPA)进行定量分析.本节利用表 1中经典的标准测试函数(包含CEC测试函数)进行实验测试, 其实验参数设置为: 种群个数n=50;函数维数D=30或4;最大函数评估次数Max_FEs=10000×D, 独立运行30次.其中, Mean_ error(平均值误差)通过公式(10)计算:
| $ { Mean\_error }=f(x)-f\left(x^{*}\right) $ | (10) |
其中, x为算法当前获得的解, x*为算法当前求解到的全局最优解.
由公式(10)可知: Mean_error越小, 则算法解的质量越好.
实验结果见表 2, 其中, 加粗的数值表示该算法在该测试函数上取得的最优计算结果.
| Table 2 Mean_error of the two algorithms (D=30, 4) 表 2 两种算法的Mean_error(D=30, 4) |
从表 2可知: CFPA算法在19个测试函数上取得了15个最优值, 而FPA算法取得8个最优值.这表明, 本文把余弦函数搜索因子融入到算法中, 能够提高算法解的质量.
为了更好地阐述带余弦函数搜索因子的花授粉算法与基本花授粉算法之间的不同, 本文利用这两种不同的算法来优化二维的Griewank函数, 该函数是非线性多模态函数, 具有众多局部最小值和一个全局最优值.
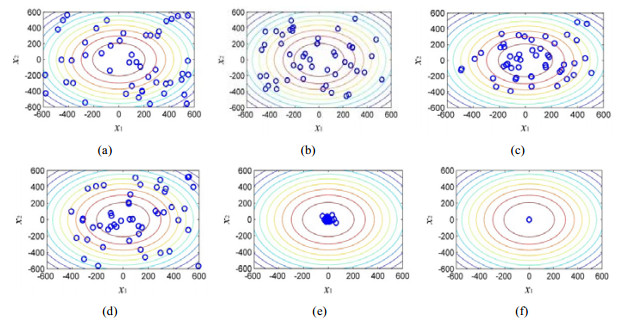
基本FPA算法和带余弦函数搜索因子的FPA算法分别在第1次、第10次、第20次迭代后的种群分布结果如图 2所示, 其中, 图 2(a)~图 2(c)是基本FPA算法的种群分布图, 图 2(d)~图 2(f)是带余弦函数搜索因子的FPA算法的种群分布图.
|
Fig. 2 Population distribution of the 2 algorithms after first, 10th and 20th iterations respectively 图 2 两种算法分别在第1次、第10次、第20次迭代后种群的分布 |
从图 2可以看出: 两种算法在开始进化时(第1次迭代后), 种群几乎覆盖了整个搜索空间; 但是随着进化的不断深入, 改进的FPA算法的收敛性能显著地优于基本FPA算法.这说明, 通过引入余弦函数搜索因子来提高算法解的质量, 能够帮助FPA算法快速地收敛到全局最优解.
3.3 p对算法性能的影响分析及动态调整策略p是FPA算法的重要参数, 而依据基本FPA算法提供的参数可知: 对每个优化问题, p都设置为固定的值0.8.受其他智能算法参数研究经验的启发, 转换概率参数p的取值应该是依赖于不同优化问题, 其取值对解决不同的优化问题应该是敏感的.为了研究上述结论是否成立, 本节利用基本FPA算法对两个经典函数Sphere(单模态函数)及Ackley(多模态函数)进行优化, 研究p的取值对FPA性能的影响是否具有敏感性.实验参数设置: p取值范围[0.001:0.001:0.01, 0.02:0.01:0.1, 0.2:0.1:1], 每个函数的问题维数设置为D=30, 种群数设置为n=50, 最大评估次数设置为10000×D; 为了减小实验误差, 对p的每个值, 算法都独立执行30次, 求其平均值的误差.实验结果如图 3所示, 图中的Fsph和Fack分别表示函数Sphere和Ackley.
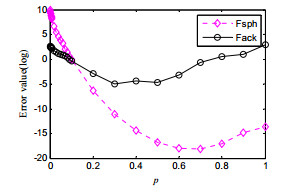
|
Fig. 3 Performances of FPA with different p values 图 3 p取不同值时, FPA的性能 |
从图 3可以看出:
(1) 对于函数Ackley, p=0.3时, FPA的性能最好; 对于函数Sphere, p=0.7时, FPA获得的性能最优;
(2) 如果p的取值太大或太小, FPA的性能都较差;
(3) FPA在求解不同的优化问题时, 其性能依赖于p的取值.
从上述实验可知: 如果转换概率p取固定的值, 不利于FPA找到全局最优解.为了解决这一不足, 本文采用公式(11)对p进行自适应调整, 提高FPA算法的性能和灵活性:
| $ \left.p=p_{\min }+\left(p_{\max }-p_{\min }\right) \times( { (Max\_iter-t) }) / { Max\_iter }\right) $ | (11) |
其中, pmax、pmin分别是p的最大值(本文取0.9)和最小值(本文取0.2), Max_iter是最大迭代次数, t是当前迭代次数.
根据上述公式(11)和改进算法的流程可知: 在算法的进化初期, 变量t的值较小, 则转化概率p的取值较大, 算法更偏向于异花授粉(全局搜索); 当算法进入演化后期, 变量t的值越来越大, 转换概率p的值越来越小, 则算法更倾向于自花授粉(局部搜索).综上所述, 通过p的自适应调整策略, 能够更有效地解决算法的全局搜索和局部搜索之间的平衡问题, 从而更有利于提高算法的全局优化能力.
3.4 MIFPA算法的有效性分析为了验证本文算法的可行性和正确性等性能, 本文在5类共19个测试函数上, 从如下几个方面进行实验对比与分析.
(1) 解的质量对比分析;
(2) 算法的维度扩展性分析;
(3) 算法的鲁棒性和收敛速度分析;
(4) Friedman与Wilcoxon检验;
(5) 运行时间比较分析.
为了检验MIFPA算法在性能上是否具有较大的提升, 本节除了与基本FPA算法对比外, 还将其与异构综合学习PSO(heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation, 简称HCLPSO)算法[24]、基于多种群变异策略集成的差分进化算法(differential evolution with multi- population based ensemble of mutation strategies, 简称MPEDE)[25]、融入精英反向学习策略的FPA算法(elite opposition-based flower pollination algorithm, 简称EOFPA)[16]、引入广义反向学习机制的FPA算法(modified generalised oppsition-based flower pollination algorithm, 简称MGOFPA)[14]分别从上述几个方面进行比较分析.
3.4.1 解的质量对比分析为了验证本文算法的有效性, 并能较好地防止算法陷入局部最优, 佐证其解的质量的优越性, 同时为了减少实验误差, 本文对每种比较算法在每个测试函数上都分别独立执行30次, 计算其Mean_error(平均值误差)、Std.Dev(标准方差).实验的其他参数设置为: 种群个数n=50;函数维数D=30或4;最大评估次数为10000×D; 转换概率p=0.8[5, 26-29].
为了对所有算法的优化能力做出公平公正的评估, 本文对所有测试函数的测试结果分别利用Wilcoxon(威尔科克森)秩和检验(а=0.05)进行实验分析, 测试结果见表 3.其中, 符号“†”“≈”“‡”分别表示MIFPA算法解的质量好于、相当于或差于对比算法, 符号“w/t/l”分别表示MIFPA算法解的质量有w个函数优于对比算法、t个函数与对比算法相当、l个函数差于对比算法.
| Table 3 Optimal mean error values and standard deviations of the six algorithms (D=30, 4) 表 3 6种算法的优化均值误差和标准差(D=30, 4) |
表 3中给出了6种对比算法的优化均值误差及标准差, 其中, 加粗的数值表示该算法在该测试函数上取得的最优计算结果.从表 3可知: 在相同种群数和评估次数的计算条件下, MIFPA算法在19个测试函数上获得了12个最优计算结果, 其中, MIFPA算法在7个函数上取得了全局最优解, 在2个函数上获得了次优结果.表 3最后一行的Wilcoxon秩和检验结果可以直观地显示: 在所有对比算法中, MIFPA算法的优化性能最好且优势非常明显.具体分析如下.
(1) 对于单模态高维的第1类函数, MIFPA算法与对比算法相比显著地提高了解的质量, 4个函数中有2个函数取得了全局最优解, 其收敛精度高; 尤其是对于非凸病态且非常难以找到全局最优值的经典高维单模态测试函数f3, 除MIFPA算法外的其余算法都易收敛到局部极小, 求解结果不太理想, 而MIFPA算法的收敛精度达到10-4, 无限接近最优解, 其收敛性能远远优于对比算法, 尤其是基本FPA算法几乎寻优失败.这充分说明改进策略能够有效地提高基本FPA算法的优化能力;
(2) 在具有大量局部极值点的非旋转多模态高维的第2类函数上, MIFPA算法与HCLPSO、EOFPA、MGOFPA及FPA算法相比, 解的质量优于对比算法; 与MPEDE比较, 两者解的质量相当; 尤其是对于基本FPA算法而言, 在此类函数上的优化能力不太理想.这充分表明了本文提出的改进方法能够显著地提高基本FPA算法的求解精度;
(3) 对于多模态低维的第3类函数, MIFPA算法与EOFPA算法相比显著地提高了解的质量, 在4个函数上, 都优于对比算法; 对HCLPSO、MPEDE和FPA算法而言, 只有在函数f10上比HCLPSO算法略有逊色, 剩余函数解的质量要优于或者相当于比较算法; 与MGOFPA比较, MIFPA解的质量要稍差一些;
(4) 在第4类带旋转的多模态高维函数上, MIFPA算法与HCLPSO、FPA算法相比优势非常明显, 解的质量要好于对比算法, 尤其是在函数f15和f16上, MIFPA算法能够找到理论最优解, 而对比算法近乎寻优受挫; 与其余3种算法对比, MIFPA算法的优化性能也要优于或相当于对比算法.MIFPA算法之所以能够在绝大部分函数上提高了解的质量, 这是因为新方法能够有效地改进基本FPA算法在搜索策略和解的质量方面存在的不足, 从而改善算法的全局优化能力;
(5) 在第5类变换旋转的高维函数上, 在函数f17和f18上, MIFPA算法与其他对比算法相比, MIFPA算法解的质量明显优于或相当于对比算法, 尤其是对于函数f18, MIFPA算法的优势更为突出, 它能找到全局最优解, 而其他5种对比算法无法获得全局最优解; 6种对比算法在优化函数f19时, MIFPA获得解的质量与MPEDE、MGOFPA和FPA算法相当, 但差于其他两种算法.由上述可知: MIFPA算法与其余算法对比, 更适合求解此类问题.
为了更深入、直观地表明MIFPA算法的优化性能好于其对比算法, 图 4展示了6种算法在部分测试函数上的全局最优值方差分析结果.
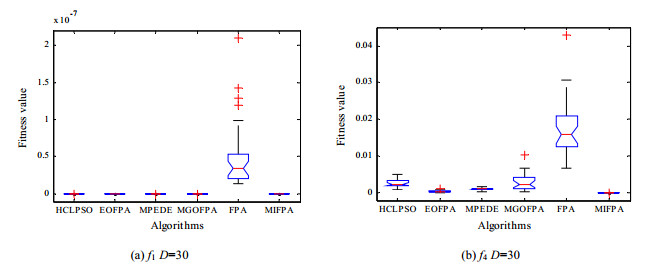
|
Fig. 4 Anova analyses of global minimum for six algorithms on test functions 图 4 6种算法在测试函数上的全局最优值方差分析 |
由图 4可知: MIFPA算法在两个函数上的收敛精度取得了两个最优结果; 只有在函数f1上的收敛精度与基本EOFPA算法相当, 但MIFPA算法在该函数上的求解精度显著地优于其余对比算法.尤其是对于函数f4, MIFPA算法找到的解无限接近于最优解, 其解的精度要比其余的5种对比算法更优.这表明, MIFPA算法具有很好的收敛性能, 也验证了表 3中的实验结果.
通过对上述5类不同的测试函数进行对比实验, 实验结果表明: MIFPA算法具有很好的收敛能力, 显著地提高了FPA算法解的质量, 不仅适合解决低维问题, 而且也适用于优化高维复杂问题.
3.4.2 算法的维度扩展性分析对于演化算法而言, 算法的优化性能会随着问题维度的增加而降低.为了验证MIFPA算法在高维上同样具有良好的寻优能力, 不会陷入“维灾难”, 本节将测试函数的维度由D=30扩展到D=50和D=100;所有算法的其他参数设置与上节相同, 最大评估次数为10000×D, 在所有函数上每种算法都独立运行30次.因为是扩展高维函数的维度, 故不对第3类函数进行测试.
表 4列出了6种算法在D=50时的优化结果, 为了客观、公平地对算法性能进行对比, 对实验结果从数学角度进行了统计分析.
| Table 4 Optimal mean error values and standard deviations of the six algorithms (D=50) 表 4 6种算法的优化均值误差和标准差(D=50) |
对表 4进行分析可知:
(1) 在15个高维函数上, MIFPA、HCLPSO、MPEDE、EOFPA、MGOFPA和FPA算法分别取得9个、4个、5个、8个、3个和0个最优结果, 且MIFPA算法有7个函数获得全局最优解, 2个函数获得次优解;
(2) 从表 4最后一行可以直观地看出: 在15个函数上, MIFPA算法分别有8个、8个和13个函数的实验结果分别优于HCLPSO、MPEDE和FPA算法, 有2个、3个和1个函数的实验结果与HCLPSO、MPEDE和FPA算法相当, 有5个、4个和1个函数的实验结果逊色于HCLPSO、MPEDE和FPA算法; MIFPA算法分别有7个、10个函数的实验结果好于EOFPA和MGOFPA算法, 有1个、1个函数分别稍差于EOFPA和MGOFPA算法, 有7个、4个函数的实验结果与EOFPA和MGOFPA算法相当.
为了进一步检验MIFPA算法在更高维数上也同样具有良好的优化能力, 此次实验选择在100维上对MIFPA算法的优化性能进行验证.由于篇幅所限, 此次实验只选择f1~f9共9个函数进行测试, 其实验结果见表 5.
| Table 5 Optimal mean error values and standard deviations of the six algorithms (D=100) 表 5 6种算法的优化均值误差和标准差(D=100) |
从表 5最后一行可以看出: MIFPA算法的收敛能力在100维上与对比算法相比, 其优势同样也很突出.尤其是MIFPA算法与FPA算法相比, 其全局优化能力的优势非常显著, 只有在函数f9上稍差于FPA算法, 而在其余8个函数上, 无论是优化均值误差还是标准差, 都明显好于FPA算法, 说明MIFPA算法获得的解的质量和鲁棒性都优于FPA算法.同时从表 4和表 5可知: MIPFA在100维上的优化能力与在50维上相比较, 其优化均值误差和标准差变化较小.这表明, MIFPA算法不会陷入“维灾难”问题.
因此, 在D=50, 100上, 无论是在单模态高维函数上, 还是在复杂高维多模态函数上, MIFPA算法都优于对比算法, 并且取得了非常不错的优化效果.说明改进算法在高维函数上同样具有较好的优化能力, 与对比算法相比具有良好的竞争力.
3.4.3 鲁棒性和收敛速度对比分析为了检验MIFPA算法的鲁棒性和收敛速度的优越性, 对其鲁棒性和收敛速度进行对比分析.在实验中, 对所有测试函数分别设定一个计算精度阈值, 若算法的运行评估次数高于10000×D次时还没有达到设定的收敛精度阈值, 则认定本次寻优不成功; 其余实验参数设置与第3.4.1节相同, 在所有函数上每种算法都独立运行30次; 执行成功率SR=找到精度阈值的次数/总的运行次数, Mean_FEs为平均评估次数, 其中, “NA”表示寻优失利, 最优结果用加粗凸显.实验结果见表 6.
| Table 6 Algorithms' results of mean number of FEs and success rate of optimization under predefined precision 表 6 在固定精度下算法的函数评估次数平均值及寻优成功率 |
从表 6可知:
(1) 在第1类4个单模态多维函数上, 对于优化成功率, MIFPA、HCLPSO、MPEDE、EOFPA、MGOFPA和FPA算法分别获得了4个、2个、4个、4个、3个和1个最优结果, 这表明, MIFPA算法的鲁棒性强于HCLPSO、MGOFPA和FPA算法, 与MPEDE、EOFPA算法相当, 但MIFPA的平均评估次数优于MPEDE、EOFPA算法; 对于平均评估次数, MIFPA算法获得了3个最优结果, MPEDE算法只取得1个最优结果, 其余算法没有取得最优结果.因此, 在第1类函数上, 本文算法的收敛速度最快, 也进一步验证了本文的改进措施能够有效地提高FPA算法的收敛速度;
(2) 对于第2类高维多模态函数, MIFPA算法在所有函数上都运行成功, 且寻优成功率优于其他对比算法; 同时, MIFPA算法的平均评估次数也好于其他对比算法.因此, 本文算法在此类函数上的鲁棒性和搜索速度都有一定的优势;
(3) 对于第3类的4个低维多峰函数, MIFPA算法的寻优成功率与基本FPA算法相当, 但优于其他4种对比算法; 对于平均评估次数, MIFPA算法好于MGOFPA、FPA算法, 与MPEDE算法平分秋色, 但稍差于其他两种算法.因此, 在第3类函数上, 本文算法的鲁棒性整体要比对比算法更优, 且收敛速度要快于MGOFPA、FPA算法, 与MPEDE相当, 但要逊色于其他两种算法;
(4) 对于第4类带旋转的多模态高维函数, MIFPA算法的平均评估次数和寻优成功率都优于EOFPA、MGOFPA和FPA对比算法; 与HCLPSO和MPEDE算法相比, MIFPA算法在函数f15和f16上的平均评估次数显著地好于HCLPSO和MPEDE算法, 同时, 3种算法在这两个函数上的寻优成功率相当, 对于函数f14, MIFPA算法的平均评估次数和寻优成功率都稍逊色于HCLPSO和MPEDE算法.因此, 在第4类函数上, 本文算法的鲁棒性和收敛速度与对比算法相比具有一定的竞争力;
(5) 对于第5类变换旋转的高维函数, MIFPA算法的平均评估次数和寻优成功率都优于MGOFPA和FPA对比算法; 与EOFPA算法相比, 两者的寻优成功率相当, 但本文算法的平均评估次数要差于对比算法; 与其余两种算法相比, MIFPA算法的平均评估次数和寻优成功率都稍逊色于对比算法.
从表 6倒数第2行可以看出: 基本FPA算法的平均寻优成功率只有62.28%;但通过对基本FPA算法的搜索策略、劣解和转换概率进行改进后, MIFPA的收敛成功率达到96.32%, 这是基本FPA算法成功率的1.54倍; 与其他4种算法相比, 寻优成功率至少高出0.36个百分点.因此, MIFPA算法的鲁棒性最强.同时, 在总的平均评估次数上, MIFPA算法的实验结果也是最优的, 尤其是对基本FPA算法而言, MIFPA算法总的平均评估次数提高了将近1个数量级, 这证实了MIFPA算法的收敛速度是所有算法中最快的.同时, 从表 6最后一行可知, 本文算法的收敛速度和鲁棒性排名第1, 表明其鲁棒性和搜索速度表现突出.
MIFPA算法之所以能够提高搜索速度, 原因是: 在算法的演化后期, 随着整个种群搜索范围的不断缩小, 算法主要侧重于开采; 而基本FPA算法通过公式(5)随机产生一个新的个体, 该策略具有较大的盲目性, 产生的新个体有可能处于搜索范围之外, 导致无效的搜索次数增加, 从而降低了算法的收敛速度.对于MIFPA算法而言, 在局部搜索部分利用了最优个体搜索策略, 使种群中其他个体受最优个体引导作用, 快速地向最优解靠近, 从而起到了提高算法搜索速度的效果.
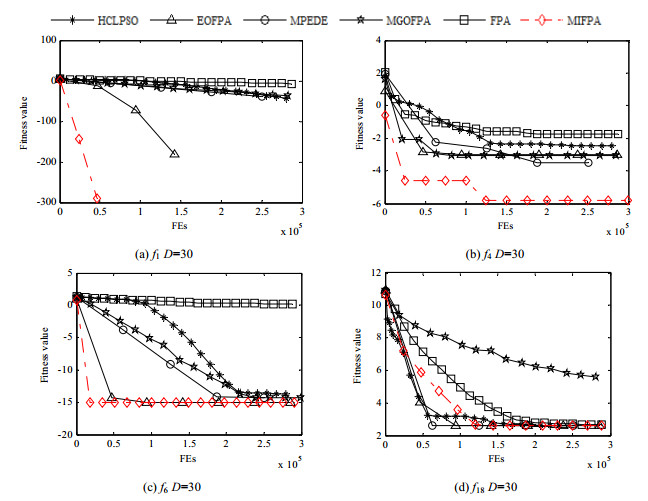
为了更深入、直观地显示MIFPA算法的稳定性及收敛速度好于其对比算法, 图 5给出了部分函数的收敛曲线图.为了便于分析算法的收敛趋势, 这里对测试函数的适应度值取了以10为底的对数.
|
Fig. 5 Convergence curve of fitness value for six algorithms on partial functions 图 5 6种算法在部分函数上的适应度值收敛曲线 |
从图 5可以看出, MIFPA算法在4个函数上的收敛速度都显著地快于基本FPA等对比算法; 对于函数f18, MIFPA算法在进化初期搜索速度要慢于HCLPSO、MPEDE和EOFPA算法, 但求精能力要优于HCLPSO、MPEDE和EOFPA算法, 从而考证了表 3的结果.而与其余算法相比, MIFPA算法在函数f18上的收敛速度明显要快; 在另外3个函数上, MIFPA算法的搜索速度都要快于其他对比算法.同时, 从图 5可知, 其收敛精度也好于对比算法, 因此, 进一步佐证了表 3的实验结果.
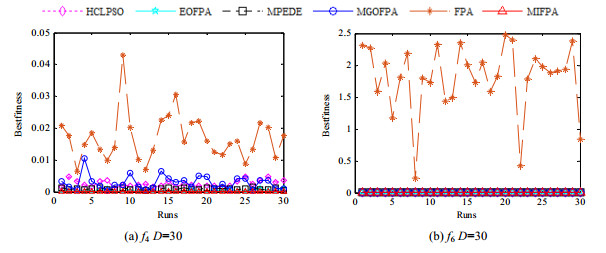
图 6是每种算法分别在两个测试函数上都独立运行30次的最优值对比分析图.由图 6可以看出: MIFPA算法均未出现波动现象, 而其他对比算法都出现了不同程度的波动性.因此, 进一步表明MIFPA算法的鲁棒性是所有对比算法中最强的, 也更深入地验证了本文提出的改进策略是行之有效的.
|
Fig. 6 Comparison of optimal fitness value for six algorithms on partial functions 图 6 6种算法在部分函数上的最优适应度值比较图 |
3.4.4 Friedman及Wilcoxon检验方法
为了对算法的寻优性能做出更客观的评价, 本文运用两种数学统计方法对算法收敛能力进行整体对比分析.表 7和表 8是所有算法分别在19个函数(维数D=30或4, 函数f10~f13为低维函数)和15个函数(维数D=50)上的Friedman的检验结果.Rankings的值越小, 则算法的优化性能越优, 排名越靠前.从表 7和表 8可以看出: MIFPA算法的秩均值(rankings)分别是2.62和2.45, 是所有算法中最小的, 比FPA算法的秩均值分别小2.52和3.02.这表明, MIFPA算法非常有效地提高了FPA算法的性能.对于其他4种算法而言, MIFPA算法的秩均值分别至少要少0.35和0.30.因此, MIFPA算法无论是在低维还是高维函数上, 总体性能都是最好的, 与对比算法相比, MIFPA算法具有较好的竞争力, 这进一步证明了本文提出的改进策略是卓有成效的.
| Table 7 Average rankings achieved by Friedman test for the six algorithms (D=30, 4) 表 7 6种算法的Friedman秩均值检验(D=30, 4) |
| Table 8 Average rankings achieved by Friedman test for the six algorithms (D=50) 表 8 6种算法的Friedman秩均值检验(D=50) |
为了判断算法之间的差异性是否显著, 本文通过Wilcoxon检验对实验结果进行统计分析.表 9和表 10分别是6种算法在19个函数(维数D=30或4, 函数f10~f13为低维函数)和15个函数(维数D=50)上的Wilcoxon检验结果.由表 9和表 10可知: 在显著性水平а=0.05时, 虽然MIFPA与MPEDE、EOFPA算法的显著性差异小于а, 但MIFPA算法的秩均值排序要好于MPEDE、EOFPA算法; 对于其他3种算法而言, 与MIFPA算法的显著性差异较为明显.这进一步证明了MIFPA算法的收敛性能优于对比算法, 也验证了通过对原有FPA算法的搜索策略、转换概率和劣解进行改进, 能够有效提高FPA算法的寻优能力.
| Table 9 Wilcoxon test between MIFPA 表 9 MIFPA与其他5种算法的Wilcoxon检验(D=30, 4) |
| Table 10 Wilcoxon test between MIFPA and other five algorithms (D=50) and other five algorithms (D=30, 4) 表 10 MIFPA与其他5种算法的Wilcoxon检验(D=50) |
3.4.5 算法的运行时间比较分析
为了更直观地验证第2.5节中的理论分析结果, 本节从实验角度对MIFPA算法的时间复杂度进行验证, 其实验参数的设置与第3.4.1节相同.实验结果见表 11, 表中MT是每种算法在所有测试函数上CPU运行时间总的平均值.从表 11的最后一行可以看出: ① FPA算法的MT值比MIFPA算法多1.37s, 验证了上述理论剖析的正确性, 也说明与FPA算法对比, MIFPA算法性能更好; ② MIFPA算法的MT值要比其余对比算法稍大一些, 即CPU运行的时间要长一些, 但仍在可承受的范围内.这是因为, 在最大函数评估次数相同的情况下, 其他4种对比算法的迭代次数要比MIFPA算法少.从上述实验结果可以看出, 上述的理论分析是正确的.
| Table 11 Average CPU run time of six algorithms on functions 表 11 6种算法在函数上的平均CPU运行时间 |
3.5 不同策略的FPA算法优化性能分析
MIFPA算法对FPA算法进行了4个方面的改进: 在全局授粉部分增加了两组随机个体的差异矢量; 通过一个线性递减概率规则, 融合两种变异机制对局部授粉部分进行改进; 自适应地调整转换概率; 引入余弦函数搜索因子对劣解进行改善.为了验证这些改进策略分别对基本FPA算法的性能提升的效果, 我们分别把这些策略融入到基本FPA算法中, 并比较这些不同策略对基本FPA算法的性能改进效果, 从而达到证明这些策略的效用.利用不同方法改进的FPA算法如下.
● IGFPA: 在基本FPA算法的全局搜索部分增加了两组随机个体的差异矢量改进后的算法;
● ILFPA: 对基本FPA算法的局部搜索部分改进后的算法;
● IPFPA: 采用自适应调整转换概率的FPA算法;
● CFPA: 融入余弦函数搜索因子的FPA算法;
● MIFPA: 引进上述所有改进策略的FPA算法.
在实验中, 所有算法都采用第3.4.1节相同的参数设置.实验结果见表 12, 如果两种算法的优化均值误差相等, 则标准差好的算法, 其性能更优.
| Table 12 Optimal mean error values and standard deviations with different strategies 表 12 不同策略的优化均值误差和标准差 |
从表 12中倒数第2行可知: 基本FPA算法取得的Average_rank(排名平均数)值为4.0, 是所有算法中最大的, 这说明本文提出的所有改进措施都能改善FPA算法的优化性能; 在5种改进算法中, MIFPA算法获得的Average_rank值为1.26, 是5种改进算法中最小的.同时, 从表 12最后一行可以看出, MIFPA算法的Total_rank(表示所有算法性能的排名)的值为1.这即证明, 本文提出的改进策略能够很好地相互协调, 并最终提高FPA算法的全局优化能力.
4 新算法求解UCAV工程优化问题随着现代战争环境的日趋复杂, 如何在现代战争中利用高科技降低战争风险, 是现代军事领域面临的一个重要课题.而从近年来的几场典型战役(伊拉克、反恐等)可知, 无人机的高效使用是规避现代战争中巨大风险的非常有效的手段之一.因为无人机无需人员驾驶, 在现代战争和反恐中, 可以通过无人机深入敌方危险区域进行情报收集或者攻击, 而无需担忧人员伤亡, 降低了战争或反恐的代价.同时, 无人机的造价也相对比较低廉, 所以无人机在战争环境日益复杂的现代战争和反恐中得到广泛使用.但是随着现代技术的日新月异, 威胁无人机的不利因素(导弹、雷达等)日益增多, 给无人机的作战、监视、侦查和其他方面的任务带来巨大的挑战.如何获取无人机的最优或次优航线路径, 是提高其战斗力的关键问题.
为了进一步验证新算法对复杂的实际工程优化问题的优化能力, 本文利用MIFPA算法来解决无人作战飞行器(unmanned combat air vehicle, 简称UCAV)的航线规划问题.首先阐述该优化问题的数学模型, 再利用本文提出的改进算法求解该优化问题, 并进行实验仿真与实验结果分析.
4.1 无人机航线优化问题的数学模型无人机航线路径规划问题是在满足一定的约束条件下, 找到一条从出发点到终点之间的代价最小的最优或者次优的航线路径.最优航线路径是指无人机在避开所有潜在威胁区域且能耗少时所经过的一条从起始点到目的地的最短路径.从上述定义可知, 其优化模型的性能评估指标包括威胁代价和能耗代价, 故无人机航线路径规划问题的数学模型定义如公式(12):
| $ \min J=\vartheta J_{t}+(1-\vartheta) J_{f} $ | (12) |
其中, ∈[0, 1]是能耗性能与安全性能之间的平衡系数; Jf和Jt分别表示能耗最小的性能评估指标和威胁最小的性能评估指标, 其值分别通过公式(13)和公式(14)获得:
| $\min {J_t} = \int_0^L {{w_t}{\rm{d}}l} $ | (13) |
| $\min {J_f} = \int_0^L {{w_f}{\rm{d}}l} $ | (14) |
其中, wt和wf分别表示航线路径上每个点的威胁代价和能耗代价, L表示路径长度.在本文实验中, wf1.
当无人机沿着路径Lij飞行时, 其总的威胁代价通过公式(15)计算取得:
| ${w_{t, {L_{ij}}}} = \frac{{L_{ij}^5}}{5}\sum\limits_{k = 1}^{{N_t}} {{t_k}\left( {\frac{1}{{d_{0.1, k}^4}} + \frac{1}{{d_{0.3, k}^4}} + \frac{1}{{d_{0.5, k}^4}} + \frac{1}{{d_{0.7, k}^4}} + \frac{1}{{d_{0.9, k}^4}}} \right)} $ | (15) |
其中, Lij表示节点i和节点j之间的长度, 是L的子段; Nt是无人机飞行过程中所要面临的威胁领域的个数; tk表示第k个威胁领域的威胁度; d0.1, k表示子段Lij上1/10处的分割点到第k个威胁领域的距离.
4.2 实验结果与分析 4.2.1 测试参数与测试问题为了验证本文改进算法对UCAV航线规划问题的求解是否行之有效, 采用表 13、表 14的两个测试实例1和实例2进行实验仿真, 并与FPA、EOFPA[16]、MGOFPA[14]、HCLPSO[24]和MPEDE[25]算法进行实验对比分析.实验参数设置为: 种群数和迭代次数分别为30和200, 6种对比算法的其他参数设置同第3.4.1节.
| Table 13 Details of test case 1 表 13 测试实例1的详细信息 |
| Table 14 Details of test case 2 表 14 测试实例2的详细信息 |
4.2.2 实验结果与分析
为了比较算法的优化能力, 采用最优值(best)、平均值(mean)和最差值(worst)这3个性能指标对算法的优化能力进行度量.各种问题维度下的实验仿真结果见表 15, 最优结果用加粗凸显.
| Table 15 Comparison of experimental results of eight algorithms on two test cases 表 15 8种算法在两个测试实例上的实验结果对比 |
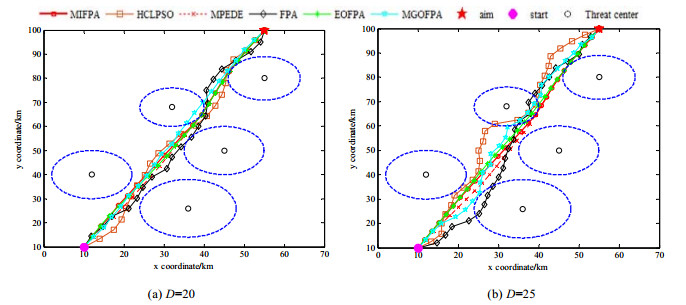
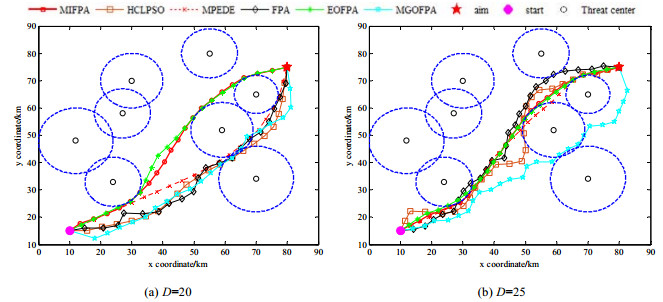
为了减少实验误差, 每种算法在每种维数上独立运行30次.为了更直观地表达MIFPA算法的优化性能, 本文给出了6种对比算法在测试实例1和测试实例2上部分不同维度上的最优飞行航线图, 分别如图 7、图 8所示.
|
Fig. 7 Optimal flight route charts of six algorithms D=20 and D=25 on example 1 图 7 6种算法在实例1上D=20和D=25的最优飞行航线图 |
|
Fig. 8 Optimal flight route charts of six algorithms D=20 and D=25 on example 2 图 8 6种算法在实例2上D=20和D=25的最优飞行航线图 |
从图 7可知:
● 在D=20上, 除FPA和MGOFPA算法不能解决UCAV问题外, 其余算法都能较好地解决UCAV航线规划问题, 可以使无人机有效地避开危险区域;
● 对于D=25而言, MIFPA和MPEDE算法可获得良好的寻优结果, 能够使无人机有效地避开危险区域; 而其余对比算法都不能使无人机有效地避开威胁区域, 寻优失败.
从图 8可以看出: MIFPA算法都能较好地解决UCAV航线规划问题, 可以使无人机有效地避开威胁区域.且从表 15可知, MIFPA算法的寻优性能都要好于其余对比算法.
从表 15可以看出:
(1) 在测试实例1上: 当D=5, 10, 15时, MIFPA算法的优化能力显著优于5种对比算法; 当D=20时, MIFPA算法的优化性能要逊色于EOFPA算法, 但从图 7可以看出, MIFPA算法也可以较好地使无人机有效地避开危险区域, MIFPA算法的寻优性能要优于其余4种对比算法; 当D=25时, MIFPA算法的寻优能力要稍差于MPEDE算法, 但从图 7可以看出, MIFPA算法也可以较好地使无人机有效地避开危险区域, MIFPA算法的寻优性能要优于其余4种对比算法.这表明, 本文算法在解决UCAV航线规划问题时总体上要优于对比算法;
(2) 在测试实例2上: MIFPA算法的优化能力表现得更为突出, MIFPA算法的寻优能力都要优于对比算法.这说明, MIFPA算法解决UCAV问题的能力更强.
综上所述, 本文提出的新算法在求解UCAV工程优化问题时, 其优化能力同样具有很好的竞争力.
5 结束语一方面, 花授粉算法是一种新型元启发式优化算法, 由于该算法实现过程简单且具有较好的全局探索和局部开采平衡能力等优点, 使其在函数优化与工程优化等领域取得了成功应用.但又因其搜索方程、进化策略和参数设置方面存在一些不足, 导致其收敛精度低、收敛速度慢和易早熟等问题, 进而造成其应用范围受到一定程度的限制.另一方面, 当前已有的研究没有考虑FPA算法的搜索方程存在的不足对算法性能的影响, 也没有考虑FPA算法采用贪婪式进化机制中的劣解对算法性能的影响, 以及转换概率p采用固定值对算法性能的影响, 同时, 也没有对全局搜索方程中运用最优个体策略对算法性能带来的问题进行探索, 并且现有的改进FPA算法寻优能力还有待提升, 其时间复杂度也较高.
本文对基本FPA算法的搜索策略进行了定性分析, 发现其存在着多方面的不足, 制约着该算法的全局优化能力.为了提高算法的收敛能力, 本文提出了一种改进的基于多策略的花授粉算法MIFPA: 首先, 在全局搜索方程中加入两组差异矢量来增加种群多样性, 有利于防止算法早熟, 进而提高算法的寻优性能; 其次, 将精英变异策略和线性递减概率规则引入到局部搜索方程, 与原有的搜索方程构建一种新的复合型局部搜索方程, 以有效提升算法的收敛能力; 最后, 利用余弦函数搜索因子对进化中产生的劣解进行改进, 从而达到改善解的质量、提高算法优化能力的目的.
为了检验新算法的优越性和可行性, 首先, 在经典测试函数上进行测试, 实验结果显示, MIFPA算法与知名的HCLPSO和MPEDE算法、典型的EOFPA和MGOFPA算法以及基本的FPA算法相比, 其解的质量、鲁棒性和收敛速度、时间复杂度等方面总体上都要优于对比算法; 其次, 利用新算法对UCAV问题进行求解, 实验结果表明, 新算法在求解复杂的实际工程优化问题时, 其优化能力表现更优.
实验结果表明: 本文提出的MIFPA算法与对比算法相比, 其全局优化能力获得较大的提高; 但从表 6中的函数f14和f19的优化结果可以看出, 其鲁棒性还具有提升的空间.这是因为, 本文的参数p虽然采用了自适应调整策略, 但算法在寻优过程中还是依据p的值与一个大于0的随机小数进行比较, 以随机选择全局搜索或者局部搜索, 这导致算法在寻优过程中具有振荡性, 从而影响了算法的鲁棒性.因此, 在今后的工作中, 如何消除参数p对算法寻优能力的影响, 以及运用新算法来解决更多的实际工程优化问题, 推广其应用领域, 是我们今后所要研究的内容.
| [1] |
Kennedy J, Eberhart R. Particle swarm optimization. In: Proc. of the IEEE Int'l Conf. on Neural Networks. Piscataway: IEEE, 1995.942-948. [doi: 10.1109/ICNN.1995.488968]
|
| [2] |
Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. Journal of Global Optimization, 2007, 39: 459-471.
[doi:10.1007/s10898-007-9149-x] |
| [3] |
Storn R, Price K. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 1997, 11: 341-359.
[doi:10.1023/A:1008202821328] |
| [4] |
Rao RV, Savsani VJ, Vakharia DP. Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems. Computer-aided Design, 2011, 43(3): 303-315.
[doi:10.1016/j.cad.2010.12.015] |
| [5] |
Yang XS. Flower pollination algorithm for global optimization. In: Proc. of the 11th Int'l Conf. on Unconventional Computation and Natural Computation. LNCS 7445, 2012.240-249. [doi: 10.1007/978-3-642-32894-7_27]
|
| [6] |
Yang XS, Karamanoglu M, He XS. Multi-objective flower algorithm for optimization. Procedia Computer Science, 2013, 18: 861-868.
[doi:10.1016/j.procs.2013.05.251] |
| [7] |
Sharawi M, Emary E, Saroit IA, El-Mahdy H. Flower pollination optimization algorithm for wireless sensor network lifetime global optimization. Int'l Journal of Soft Computing and Engineering, 2014, 4(3): 54-59.
http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=53BEC478805C399BBB560EC5A6881B22?doi=10.1.1.458.7082&rep=rep1&type=pdf |
| [8] |
Chiroma H, Khan A, Abubakar AI, Saadi Y, Hamza MF, Shuib L, Gital AY, Herawan T. A new approach for forecasting OPEC petroleum consumption based on neural network train by using flower pollination algorithm. Applied Soft Computing, 2016, 48: 50-58.
[doi:10.1016/j.asoc.2016.06.038] |
| [9] |
Bekdaş G, Nigdeli SM, Yang XS. Sizing optimization of truss structures using flower pollination algorithm. Applied Soft Computing, 2015, 37: 322-331.
[doi:10.1016/j.asoc.2015.08.037] |
| [10] |
Majidpour H, Gharehchopogh FS. An improved flower pollination algorithm with Adaboost algorithm for feature selection in text documents classification. Journal of Advances in Computer Research, 2018, 9(1): 29-40.
http://jacr.iausari.ac.ir/index.php/jsw/article/view/data/jacr/coversheet/article_24937_e31d7e3163df2a22faf6465036a4b07b.pdf |
| [11] |
Peesapati R, Yadav VK, Kumar N. Flower pollination algorithm based multi-objective congestion management considering optimal capacities of distributed generations. Energy, 2018, 147: 980-994.
[doi:10.1016/j.energy.2018.01.077] |
| [12] |
Łukasik S, Kowalski PA. Study of flower pollination algorithm for continuous optimization. Advances in Intelligent Systems and Computing, 2015, 322: 451-459.
[doi:10.1007/978-3-319-11313-5_40] |
| [13] |
Madasu SD, Kumar MLSS, Singh AK. A flower pollination algorithm based automatic generation control of interconnected power system. Ain Shams Engineering Journal, 2018, 9(4): 1215-1224.
[doi:10.1016/j.asej.2016.06.003] |
| [14] |
Draa A. On the performances of the flower pollination algorithm-Qualitative and quantitative analyses. Applied Soft Computing, 2015, 34: 349-371.
[doi:10.1016/j.asoc.2015.05.015] |
| [15] |
Mahdad B, Srairi K. Security constrained optimal power flow solution using new adaptive partitioning flower pollination algorithm. Applied Soft Computing, 2016, 46: 501-522.
[doi:10.1016/j.asoc.2016.05.027] |
| [16] |
Zhou YQ, Wang R, Luo QF. Elite opposition-based flower pollination algorithm. Neurocomputing, 2015, 188: 294-310.
[doi:10.1016/j.neucom.2015.01.110] |
| [17] |
Xiao HH, Wan CX, Duan YM. Flower pollination algorithm based on complex method. Journal of Chinese Computer Systems, 2015, 36(6): 1373-1378(in Chinese with English abstract).
[doi:10.3969/j.issn.1000-1220.2015.06.042] |
| [18] |
Chakraborty D, Saha S, Dutta O. DE-FPA: A hybrid differential evolution-flower pollination algorithm for function minimization. In: Proc. of the Int'l Conf. on High Performance Computing and Applications. Bhubaneswar, 2014.1-6. [doi: 10.1109/ICHPCA.2014.7045350]
|
| [19] |
Wang R, Zhou YQ, Qiao SL, Huang K. Flower pollination algorithm with bee pollinator for cluster analysis. Information Processing Letters, 2016, 116: 1-14.
[doi:10.1016/j.ipl.2015.08.007] |
| [20] |
Xiao HH, Wan CX, Duan YM, Tan QL. Flower pollination algorithm based on gravity search mechanism. Acta Automatica Sinica, 2017, 43(4): 576-594(in Chinese with English abstract).
[doi:10.16383/j.aas.2017.c160146] |
| [21] |
He XS, Yang XS, Karamanoglu M, Zhao YX. Global convergence analysis of the flower pollination algorithm: A discrete-time markov chain approach. Procedia Computer Science, 2017, 108: 1354-1364.
[doi:10.1016/j.procs.2017.05.020] |
| [22] |
Nasir M, Das S, Maity D, Sengupta S, Halder U, Suganthan PN. A dynamic neighborhood learning based particle swarm optimizer for global numerical optimization. Information Sciences, 2012, 209: 16-36.
[doi:10.1016/j.ins.2012.04.028] |
| [23] |
Karaboga D, Akay B. A comparative study of artificial bee colony algorithm. Applied Mathematics and Computation, 2009, 214(1): 108-132.
[doi:10.1016/j.amc.2009.03.090] |
| [24] |
Lynn N, Suganthan PN. Heterogeneous comprehensive learning particle swarm optimization with enhanced exploration and exploitation. Swarm & Evolutionary Computation, 2015, 24: 11-24.
[doi:10.1016/j.swevo.2015.05.002] |
| [25] |
Wu GH, Mallipeddi R, Suganthan PN, Wang R, Chen HK. Differential evolution with multi-population based ensemble of mutation strategies. Information Sciences, 2016, 329: 329-345.
[doi:10.1016/j.ins.2015.09.009] |
| [26] |
Nabil E. A modified flower pollination algorithm for global optimization. Expert Systems with Applications, 2016, 57: 192-203.
[doi:10.1016/j.eswa.2016.03.047] |
| [27] |
Ouadfel S, Taleb-Ahmed A. Social spiders optimization and flower pollination algorithm for multilevel image thresholding: A performance study. Expert Systems with Applications, 2016, 55: 566-584.
[doi:10.1016/j.eswa.2016.02.024] |
| [28] |
Sayed SA, Nabil E, Badr A. A binary clonal flower pollination algorithm for feature selection. Pattern Recognition Letters, 2016, 77: 21-27.
[doi:10.1016/j.patrec.2016.03.014] |
| [29] |
Dubey HM, Pandit M, Panigrahi BK. A biologically inspired modified flower pollination algorithm for solving economic dispatch problems in modern power systems. Cognitive Computation, 2015, 7(5): 594-608.
[doi:10.1007/s12559-015-9324-1] |
| [17] |
肖辉辉, 万常选, 段艳明. 一种基于复合形法的花朵授粉算法. 小型微型计算机系统, 2015, 36(6): 1373-1378.
[doi:10.3969/j.issn.1000-1220.2015.06.042] |
| [20] |
肖辉辉, 万常选, 段艳明, 谭黔林. 基于引力搜索机制的花朵授粉算法. 自动化学报, 2017, 43(4): 576-594.
[doi:10.16383/j.aas.2017.c160146] |
 2021, Vol. 32
2021, Vol. 32


