2. 泰州学院 计算机科学与技术学院, 江苏 泰州 225300;
3. 复旦大学 计算机科学技术学院, 上海 200433
2. School of Computer Science and Technology, Taizhou University, Taizhou 225300, China;
3. School of Computer Science, Fudan University, Shanghai 200433, China
随着物联网、云计算和大数据等新一代信息技术的发展, 在数字图书、城市交通、工业制造、通信服务、网络安全、金融证券、生命科学、医疗健康等众多领域产生了由若干值对(事件类型, 发生时间)组成的事件序列.事件序列中蕴藏着丰富的语义模式, 作为最常见的语义模式, 频繁情节揭示了事件序列中用户或系统的行为规律, 因此, 频繁情节挖掘有着广阔的应用前景, 典型场景如文献推荐阅读、城市智慧交通、工业智能制造、通信故障诊断、网络入侵检测、股市态势预测、基因序列分析、疾病预防控制等.
自Manilla等人[1]引入事件序列上的频繁情节挖掘问题以来, 众多学者对此展开了研究, 提出了许多具有代表性的频繁情节挖掘算法, 见表 1.
| Table 1 Existing algorithms for frequent episode discovery 表 1 现有的频繁情节挖掘算法 |
从表 1可以看出, 支持度定义是挖掘频繁情节时必须考虑的一个尺度.一方面, 支持度定义决定着挖掘的结果, 针对同一事件序列根据不同支持度定义挖掘的频繁情节不尽相同; 另一方面, 支持度定义影响着挖掘的过程, 有些支持度定义满足单调性, 有些则不然, 而单调性是加快频繁情节搜索的重要依据.
上述算法在各自支持度定义下具有较好的挖掘效果, 但在支持度定义发生变化时却很难甚至无法直接挖掘频繁情节.为此, Achar等人[19]提出了基于Apriori思想逐层发现频繁情节的统一算法.该算法采用广度优先搜索策略, 首先由k(k > 0)层的频繁情节产生k+1层的候选频繁情节, 然后通过扫描事件序列来跟踪各个候选频繁情节状态机的状态变化, 跟踪过程由参数TRANSIT、COPY、JOIN、INCREMENT和RETIRE来分别控制当前状态机是否发生状态转移、当前状态机转移至下一状态前是否要复制一个副本、两个状态机转移至同一状态时是否要删除较早的状态机、当前状态机转移至终止状态时情节发生次数是否增1、情节发生次数增1后是否删除该情节的所有状态机, 从而计算每个候选频繁情节在不同支持度定义下的发生次数, 进而发现k+1层的频繁情节.该算法虽然兼顾了多种支持度定义, 但挖掘过程中需要多遍扫描事件序列, 且每遍扫描前都要存储大量的候选频繁情节, 这势必导致较为昂贵的时间和空间代价.
如何在单遍扫描事件序列和不产生候选频繁情节的前提下, 融合多种支持度定义来挖掘频繁情节, 即为本文的研究动机.
1 预备知识 1.1 基本概念定义1(事件, 事件序列).给定事件类型集ε={E1, E2, …, En}, 一个事件就是一个二元组(E, t), 其中, E∈ε, t表示该事件的发生时间.定义在ε上的一个事件序列ES是按发生时间先后排列的若干事件, 表示为ES=〈(E1, t1), (E2, t2), …, (Em, tm)〉, 其中, ti < tj(1≤i < j≤m).为讨论方便, 本文假设在每个时间点上至多只发生一个事件.
例如, ES1=〈(A, 1), (A, 2), (A, 4), (B, 5), (A, 6), (A, 7), (C, 8), (B, 9), (D, 11), (C, 12), (A, 13), (B, 14), (C, 15), (D, 16), (A, 17)〉就是一个事件序列.如图 1所示.

|
Fig. 1 A sequence of events 图 1 事件序列示例 |
定义2(情节, 子情节).情节α是ε中由若干事件类型组成的序列, 记为α=〈E1E2…Ek〉, 其中, Ei(1≤i≤k)∈ε且对于所有的i和j(1≤i < j≤k)满足Ei排列在Ej之前.情节α中事件类型的个数称为α的长度(记为|α|), 长度为k的情节称为k-情节.若情节β中的事件类型均来自情节α, 且与α中这些事件类型的先后顺序一致, 则称β是α的子情节, 记作β⊆α.
例如, 〈ABC〉是一个3-情节, 〈AB〉是〈ABC〉的子情节, 而〈BA〉不是.
定义3(窗口).给定事件序列ES=〈(E1, t1), (E2, t2), …, (Em, tm)〉, 设t1≤ts≤te≤tm, 则[ts, te]是ES上的一个窗口, 该窗口包含了ts到te的所有事件, te–ts称为该窗口的宽度, ts和te分别称为该窗口的起始和终止时间.
例如, [2,8]是事件序列ES1上一个宽度为6的窗口, 其起始时间为2, 终止时间为8.
定义4(前缀, 后缀, 串接).给定情节α=〈E1E2…Ek〉, 则〈E1E2…Ek–1〉称为α的前缀, 记为prefix(α); 〈E2…Ek〉称为α的后缀, 记为suffix(α).给定情节α=〈E1E2…En〉和
例如, 〈AB〉和〈BC〉分别是情节〈ABC〉的前缀和后缀, concat(〈AB〉, 〈BC〉)=〈ABBC〉.
定义5(发生, 最早转移发生).给定事件序列ES和情节α=〈E1E2…Ek〉, 若〈(E1, t1), (E2, t2), …, (Ek, tk)〉是从ES中删除若干事件后得到, 其中, ti < ti+1(1≤i≤k–1), 则称[t1, t2, …, tk]为α在ES上的一次发生, [t1, tk]为发生区间, tk–t1为区间长度.若[t1, t2, …, tk]是情节α=〈E1E2…Ek〉在事件序列ES上的一次发生, 且ti(2≤i≤k)是继ti-1之后事件类型Ei的首次发生时间, 则称[t1, t2, …, tk]是α在ES上的一次最早转移发生, 情节α在ES上所有最早转移发生组成的集合记为eto(α).
例如, 在事件序列ES1上, [4,9,12]是情节〈ABC〉的一次发生(但不是最早转移发生), 该发生区间为[4,12], 区间长度为8,eto(〈ABC〉)={[1,5,8], [2,5,8], [4,5,8], [6,9,12], [7,9,12], [13,14,15]}.
性质1(单调性).若β是α的任一子情节, 则β的发生次数不小于α的发生次数.
性质2(前缀单调性). prefix(α)的发生次数不小于α的发生次数.显然, 性质2是性质1的一种情形.
性质3(后缀单调性). suffix(α)的发生次数不小于α的发生次数.显然, 性质3也是性质1的一种情形.
定义6(基于窗口发生的支持度).给定事件序列ES=〈(E1, t1), (E2, t2), …, (En, tn)〉和窗口宽度w, 则ES上共包含(tn–t1+w+1)个宽度为w的窗口, 其中, 第1个窗口仅包含事件(E1, t1), 最后一个窗口仅包含事件(En, tn).宽度为w且至少包含情节α一次发生的窗口的集合记为wo(α), 集合wo(α)的基数|wo(α)|称为情节α基于窗口发生的支持度.基于窗口发生的支持度定义满足性质1.
例如, 设窗口宽度w=6,情节α=〈ABC〉, 则在事件序列ES1上, wo(α)={[2,8], [3,9], [4,10], [6,12], [7,13], [9,15], [10,16], [11,17], [12,18], [13,19]}, |wo(α)|=10.
定义7(基于最小发生的支持度).设[t1, t2, …, tk]是情节α=〈E1E2…Ek〉在事件序列ES上的一次发生, 若ES上不存在α的另一次发生
情节α在ES上所有最小发生组成的集合记为mo(α), 集合mo(α)的基数|mo(α)|称为情节α基于最小发生的支持度.
例如, 设情节α=〈ABC〉, β=〈AC〉, 则在事件序列ES1上mo(α)={[4,5,8], [7,9,12], [13,14,15]}, |mo(α)|=3,mo(β) ={[7,8], [13,15]}, |mo(β)|=2.因β是α的子情节, 且|mo(β)| < |mo(α)|, 所以基于最小发生的支持度定义不满足性质1,但满足性质2和性质3.
定义8(基于头发生的支持度).给定事件序列ES=〈(E1, t1), (E2, t2), …, (En, tn)〉和窗口宽度w, 若宽度为w的窗口[ts, te]至少包含了情节α=〈E1E2…Ek〉的一次发生, 且ts正好是E1的发生时间, 则称[ts, te]是α的一次头发生.情节α在ES上所有头发生组成的集合记为ho(α), 集合ho(α)的基数|ho(α)|称为情节α基于头发生的支持度.
例如, 设窗口宽度w=6,情节α=〈ABC〉, β=〈BC〉, 则在事件序列ES1上, ho(α)={[2,8], [4,10], [6,12], [7,13], [13,19]}, |ho(α)|=5,ho(β)={[5,11], [9,15], [14,20]}, |ho(β)|=3.因为β是α的后缀, 且|ho(β)| < |ho(α)|, 所以基于头发生的支持度定义不满足性质1和性质3,但满足性质2.
定义9(基于总发生的支持度).设β是α的一个子情节, 若不存在α的另一个子情节γ, 使得|ho(γ)| < |ho(β)|, 则称|ho(β)|为情节α基于总发生的支持度, 记为|to(α)|.基于总发生的支持度定义满足性质1.
例如, 设窗口宽度w=6,在事件序列ES1上, ho(〈AC〉)={[2,8], [4,10], [6,12], [7,13], [13,19]}, ho(〈AB〉)={[1,7], [2,8], [4,10], [6,12], [7,13], [13,19]}, ho(〈BC〉)={[5,11], [9,15], [14,20]}, 所以, |to(〈ABC〉)|=|ho(〈BC〉)|=3.
定义10(基于非交错发生的支持度).设[t1, t2, …, tk]和
例如, 设情节α=〈ABC〉, β=〈AC〉, 在事件序列ES1上ni(α)={[1,5,8], [6,9,12], [13,14,15]}, |ni(α)|=3,ni(β)= {[1,8], [13,15]}, |ni(β)|=2.因为β是α的子情节, 且|ni(β)| < |ni(α)|, 所以基于非交错发生的支持度定义不满足性质1,但满足性质2和性质3.
定义11(基于非重叠发生的支持度).设[t1, t2, …, tk]和
例如, 在事件序列ES1上, no(〈ABC〉)={[1,5,8], [13,14,15]}, |no(ABC〉)|=2.
定义12(基于最小且非重叠发生的支持度).设[t1, t2, …, tk]和
例如, 在事件序列ES1上, mn(〈ABC〉)={[4,5,8], [13,14,15]}, |mn(ABC〉)|=2.
定义13(频繁情节).给定支持度阈值min_sup, 若情节α的支持度不小于min_sup, 则称α是一个频繁情节.
1.2 问题描述给定事件序列ES、窗口宽度w、支持度阈值min_sup和支持度定义def_sup, 则问题描述为:设计一个能够挖掘ES上所有频繁情节的算法, 要求:(1)单遍扫描ES; (2)挖掘过程中不产生候选频繁情节; (3)融合基于窗口发生、最小发生、头发生、总发生、非交错发生、非重叠发生、最小且非重叠发生的支持度定义.
2 频繁情节挖掘算法FEM-DFS 2.1 算法思想因为许多频繁情节具有相同的前缀或后缀, 所以采用共享前/后缀树来存储发现的频繁情节, 可以节省存储空间[4,12,16].共享前/后缀树是一棵有向根树, 除根节点外, 树中的每个节点是一个三元组(Name, Occ, Child), 其中, Name表示该节点对应的情节, Occ表示该节点对应情节的发生集, Child表示该节点的孩子指针集.树中父节点的Name, 要么是子节点Name的前缀, 要么是子节点Name的后缀, 故取名共享前/后缀树.
为了在频繁情节发现过程中只扫描事件序列1遍, 且不产生候选频繁情节, 本文采用深度优先搜索方式来发现频繁情节, 并利用性质1、性质2或性质3来压缩频繁情节的搜索空间.共享前/后缀树的构建过程如下.
第1步, 生成一个只有根节点的树T.
第2步, 扫描事件序列ES一遍, 依据支持度定义和支持度阈值, 发现所有的频繁1-情节并按字典序排列.
第3步, 对于每个频繁1-情节α, 在树T中生成根节点的孩子节点Nα.
第4步, 分别对每个频繁1-情节α, 进行如下递归处理.
依次取出每个频繁1-情节β对α进行情节增长, 令增长后的情节为γ=concat(α, β)或γ=concat(β, α), 即γ是以α为前缀或后缀进行增长, 每次增长后依据支持度定义计算γ的发生集, 若γ是频繁情节, 则在树T中添加Nα的孩子节点Nγ, 并对γ进行类似于α的情节增长处理, 如此不断迭代, 直至没有发现更长的频繁情节为止.
显然, 构建共享前/后缀树时需要解决两个关键问题:一是存储策略, 即每个节点存储情节的何种发生集才能保证不丢失情节支持度的计算依据; 二是增长策略, 即情节增长时是选择前缀增长还是后缀增长才能保证挖掘过程不会丢失频繁情节.为此, 需要依据不同的支持度定义作如下处理.
情形1.窗口发生.
若节点Nα存储情节α的窗口发生集wo(α), 则无法计算α增长后情节的窗口发生集, 这是因为wo(α)的每个窗口并未记载α中各事件类型的发生时间.为此, 节点Nα需要存储情节α的最早转移发生集eto(α), 这样既可以计算情节α的窗口发生集wo(α), 也便于与其他支持度定义采取同一存储策略.例如, 设窗口宽度w=6,情节α=〈ABC〉, 则在事件序列ES1上, eto(α)={[1,5,8], [2,5,8], [4,5,8], [6,9,12], [7,9,12], [13,14,15]}, 由eto(α)中每个区间长度≤w的发生[t1, t2, …, tk], 可以得到w–(tk–t1)+1个宽度为w的连续窗口.从以上窗口集中删除重复的窗口后, 得到wo(α)={[2,8], [3,9], [4,10], [6,12], [7,13], [9,15], [10,16], [11,17], [12,18], [13,19]}.
该支持度定义满足性质1,情节增长时可以选用前缀增长或后缀增长.
情形2.最小发生.
最小发生不受窗口宽度的约束.若节点Nα存储情节α的最早转移发生集eto(α), 则可以由此计算情节α的最小发生集mo(α).例如, 设情节α=〈ABC〉, 则事件序列ES1上, eto(α)={[1,5,8], [2,5,8], [4,5,8], [6,9,12], [7,9,12], [13,14,15]}, 对于eto(α)中相邻的两个发生, 若结束时间相同, 则前者一定不是最小发生, 所以mo(α)={[4,5,8], [7,9,12], [13,14,15]}.
该支持度定义满足性质2和性质3,情节增长时可以选用前缀增长或后缀增长.
情形3.头发生.
头发生是一种窗口发生, 也受窗口宽度的约束.若节点Nα存储情节α的最早转移发生集eto(α), 则可以由此计算情节α的头发生集ho(α).例如, 设窗口宽度w=6,情节α=〈ABC〉, 则在事件序列ES1上, eto(α)={[1,5,8], [2,5,8], [4,5,8], [6,9,12], [7,9,12], [13,14,15]}, 由eto(α)中每个区间长度≤w的发生[t1, t2, …, tk], 可以得到1个长度为w的窗口[t1, t1+w], 所有这些窗口组成的集合即为ho(α)={[2,8], [4,10], [6,12], [7,13], [13,19]}.
该支持度定义只满足性质2,情节增长时只能进行前缀增长, 否则会丢失频繁情节.
情形4.总发生.
总发生是一种头发生, 同样受窗口宽度的约束.若节点Nα存储情节α的最早转移发生集eto(α), 则可以由此计算情节α的总发生集to(α).由定义9可知, 只有知道α的所有子情节基于头发生的支持度, 才能计算α基于总发生的支持度.然而, 在共享前/后缀树构建过程中若α由其前缀增长得到, 则此时α的部分子情节支持度可能是未知的.
文献[11]提出了另一种基于总发生的支持度计算方法|to(α)|=min(|ho(α)|, |to(suffix(α))|), 这说明情节增长时只能采用后缀增长.设增长后情节为α, 增长前|to(suffix(α))|已知, 增长后|ho(α)|可由eto(α)计算得到.例如, 设窗口宽度w=6,情节α=〈ABC〉, 则在事件序列ES1上, eto(α)={[1,5,8], [2,5,8], [4,5,8], [6,9,12], [7,9,12], [13,14,15]}, |to (suffix(α))|=|to(〈BC〉)|=3,故有|ho(α)|=|{[2,8], [4,10], [6,12], [7,13], [13,19]}|, |to(α)|=min(|ho(α)|, |to(suffix(α))|)=min(5,3)=3.
情形5.非交错发生.
非交错发生也不受窗口宽度的约束.若节点Nα存储情节α的最早转移发生集eto(α), 则可以由此计算情节α的非交错发生集ni(α).例如, 设情节α=〈ABC〉, 则在事件序列ES1上, eto(α)={[1,5,8], [2,5,8], [4,5,8], [6,9,12], [7,9,12], [13,14,15]}.初始令ni(α)={[1,5,8]}, 然后将eto(α)中首先与[1,5,8]非交错的发生[6,9,12]添加至ni(α)中, 再将eto(α)中首先与[6,9,12]非交错的发生[13,14,15]添加至ni(α)中, 最后有ni(α)={[1,5,8], [6,9,12], [13,14,15]}.
该支持度定义满足性质2和性质3,情节增长时可以选用前缀增长或后缀增长.
情形6.非重叠发生.
非重叠发生(未必是最小发生)也不受窗口宽度的约束.若节点Nα存储α的非重叠发生集no(α), 则深度优先搜索时可能会丢失频繁情节.例如, 在事件序列ES1上, no(〈AAB〉)={[1,2,5], [6,7,9]}, no(〈A〉)={[1,1], [2,2], [4,4], [6,6], [7,7], [13,13], [17,17]}, 从而有no(〈AABA〉)={[1,2,5,6]}.若支持度阈值min_sup=2,则认为〈AABA〉是非频繁的.事实上, 〈AABA〉在ES1上有非重叠发生[1,2,5,6]和[7,13,14,17], 〈AABA〉是频繁情节.
若节点Nα存储情节α的最早转移发生集eto(α), 则不仅可以计算情节α的非重叠发生集no(α), 而且也保证挖掘过程中不会丢失频繁情节.例如, 在事件序列ES1上, eto(〈AAB〉)={[1,2,5], [2,4,5], [4,6,9], [6,7,9], [7,13,14]}.初始令no(〈AAB〉)={[1,2,5]}, 然后将eto(〈AAB〉)中首先与[1,2,5]非重叠的发生[6,7,9]添加至no(〈AAB〉)中, 从而有no(〈AAB〉)={[1,2,5], [6,7,9]}.因eto(〈A〉)={[1,1], [2,2], [4,4], [6,6], [7,7], [13,13], [17,17]}, 故eto(〈AABA〉)= {[1,2,5,6], [2,4,5,6], [4,6,9,13], [6,7,9,13], [7,13,14,17]}, 从而有no(〈AABA〉)={[1,2,5,6], [7,13,14,17]}.
该支持度定义满足性质1,情节增长时可以选用前缀增长或后缀增长.
情形7.最小且非重叠发生.
最小且非重叠发生也不受窗口宽度的约束.若节点Nα存储α的最小且非重叠发生集mn(α), 则深度优先搜索时也可能会丢失频繁情节.例如, 在事件序列ES1上, mn(〈AAB〉)={[2,4,5], [6,7,9]}, mn(〈A〉)={[1,1], [2,2], [4,4], [6,6], [7,7], [13,13], [17,17]}, 从而有mn(〈AABA〉)={[2,4,5,6]}.若支持度阈值min_sup=2,则认为〈AABA〉是非频繁的.事实上, 〈AABA〉在ES1上有最小且非重叠发生[2,4,5,6]和[7,13,14,17], 〈AABA〉是频繁情节.
若节点Nα存储情节α的最早转移发生集eto(α), 则不仅可以计算情节α的最小且非重叠发生集mn(α), 而且也保证挖掘过程中不会丢失频繁情节.例如, 在事件序列ES1上, eto(〈AAB〉)={[1,2,5], [2,4,5], [4,6,9], [6,7,9], [7,13,14]}, mo(〈AAB〉)={[2,4,5], [6,7,9], [7,13,14]}.初始令mn(〈AAB〉)={[2,4,5]}, 然后将mo(〈AAB〉)中首先与[2,4,5]非重叠的发生[6,7,9]添加至mn(〈AAB〉)中, 从而有mn(〈AAB〉)={[2,4,5], [6,7,9]}.由eto(〈AABA〉)={[1,2,5,6], [2,4,5,6], [4,6,9,13], [6,7,9,13], [7,13,14,17]}可得mo(〈AABA〉)={[2,4,5,6], [6,7,9,13], [7,13,14,17]}, 从而有mn(〈AABA〉)={[2,4,5,6], [7,13,14,17]}.
该支持度定义满足性质1,情节增长时可以选用前缀增长或后缀增长.
2.2 算法描述基于上述思想, 我们设计了一种融合多种支持度定义的频繁情节挖掘算法FEM-DFS(frequent episode mining-depth first search).该算法在进行情节增长时, 基于窗口发生、头发生、最小发生、非交错发生、非重叠发生、最小且非重叠发生的支持度定义都采用前缀增长, 而基于总发生的支持度定义采用后缀增长.
算法FEM-DFS的伪代码如下.
Algorithm FEM-DFS(ES, w, min_sup, def_sup).
Input: ES: an event sequence=〈(E1, t1), (E2, t2), ..., (En, tn)〉;
w: a window width;
min_sup: a support threshold;
def_sup: one of support definitions. wo, mo, ho, to, ni, no, mn stand for window occurrence-based, minimal occurrence-based, head occurrence-based, total occurrence-based, non-interleaved occurrence- based, non-overlapped occurrence-based, minimal and non-overlapped occurrence-based respectively.
Output: T: a tree which stores all frequent episodes found from ES
1. Create a tree T with simply a root node
2. Scan ES once to find all frequent 1-episodes and sort them in lexicographical order
3. FOR each frequent 1-episode α do
4. Create node Nα as a child of the root
5. FOR each frequent 1-episode α do
6. EpisodeGrow(α)
7. Return T
Procedure EpisodeGrow(α).
Input: α: an episode to be grown
Objective: grow the existing frequent episode α
1. FOR each frequent 1-episode β do
2. IF def_sup≠‘to’
3. Let γ=concat(α, β)
4. ELSE
5. Let γ=concat(β, α)
6. Let eto(γ)=ComputeETO(eto(α), eto(β), def_sup)
7. Let sup(γ)=ComputeSUP(eto(γ), def_sup)
8. IF sup(γ)≥min_sup
9. Create node Nγ as a child of node Nα
10. EpisodeGrow(γ)
Procedure ComputeETO(eto(α), eto(β), def_sup).
Input: eto(α): the earliest transiting occurrences of α listed in increasing order of start time;
eto(β): the earliest transiting occurrences of β listed in increasing order of start time;
def_sup: one of support definitions
Output: eto(γ): the earliest transiting occurrences of concat(α, β)
1. Let eto(γ)=Ø
2. IF def_sup≠‘to’
3. FOR i=1 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
4. FOR j=1 to |eto(β)| do //j points to the jth occurrence [tj, tj] of eto(β)
5. IF tj > ti|α|
6. Add [ti1, ti2, …, ti|α|, tj] to eto(γ)
7. break
8. ELSE
9. FOR j=1 to |eto(β)| do //j points to the jth occurrence [tj, tj] of eto(β)
10. FOR i=1 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
11. IF ti1 > tj
12. Add [tj, ti1, ti2, …, ti|α|] to eto(γ)
13. break
14. RETURN eto(γ)
Procedure ComputeSUP(eto(α), def_sup).
Input: eto(α): the earliest transiting occurrences of α listed in increasing order of start time;
def_sup: one of support definitions
Output: sup(α): the support of α
1. switch(def_sup)
2. case ‘wo’:
3. Let wo(α)=Ø
4. FOR i=1 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
5. IF ti|α|–ti1≤w
6. FOR j=0 to w–(ti|α|–t1) do
7. IF [ti|α|–w+j, ti|α|+j]∉wo(α)
8. Add [ti|α|–w+j, ti|α|+j] to wo(α)
9. RETURN |wo(α)|
10. case ‘mo’:
11. Let mo(α)=Ø
12. FOR i=1 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
13. IF ti|α| < t(i+1)|α|
14. Add [ti1, ti2, …, t|α|] to mo(α)
15. RETURN |mo(α)|
16. case ‘ho’:
17. Let ho(α)=Ø
18. FOR i=1 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
19. IF ti|α|–ti1≤w
20. Add [ti1, ti1+w] to ho(α)
21. RETURN |ho(α)|
22. case ‘to’:
23. IF |α|=1
24. RETURN |eto(α)|
25. ELSE
26. RETURN min(|eto(α)|, ComputeSUP(eto(suffix(α)), ‘to’))
27. case ‘ni’:
28. Let ni(α)={[t11, t12, …, t1|α|]} //Add the first occurrence of eto(α) to ni(α)
29. Let j=1 //j points to the jth occurrence [tj1, tj2, …, tj|α|] of ni(α)
30. FOR i=2 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
31. FOR k=1 to |α|–1 do
32. IF tik < tj(k+1)
33. break
34. IF k > |α|–1
35. Add [ti1, ti2, …, ti|α|] to ni(α)
36. j=j+1
37. RETURN |ni(α)|
38. case ‘no’:
39. Let no(α)={[t11, t12, …, t1|α|]} //Add the first occurrence of eto(α) to no(α)
40. Let j=1 //j points to the jth occurrence [tj1, tj2, …, tj|α|] of no(α)
41. FOR i=2 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
42. IF ti1 > tj|α|
43. Add [ti1, ti2, …, ti|α|] to no(α)
44. j=j+1
45. RETURN |no(α)|
46. case ‘mn’:
47. Let mn(α)=Ø
48. FOR i=1 to |eto(α)| do //i points to the ith occurrence [ti1, ti2, …, ti|α|] of eto(α)
49. IF ti|α|≠t(i+1)|α|∧ti|α| < t(i+1)1
50. Add [ti1, ti2, …, ti|α|] to mn(α)
51. RETURN |mn(α)|
2.3 算法正确性证明算法FEM_DFS的关键步骤是以发现的频繁情节为前缀或后缀进行情节增长, 并由过程ComputeETO和ComputeSUP来分别计算增长后情节的最早转移发生集和支持度.为此, 需要证明过程ComputeETO和ComputeSUP的正确性.不失一般性, 对于过程ComputeETO而言, 只证明前缀增长情形下的正确性.
定理1.给定频繁情节α和频繁1-情节β的最早转移发生集eto(α)和eto(β), 过程ComputeETO计算得到的是情节γ=concat(α, β)的最早转移发生集eto(γ).
证明:
(1) 证明eto(γ)中的每个发生都是情节γ=concat(α, β)的最早转移发生.
设[t1, t2, …, t|α|, tβ]是由[t1, t2, …, t|α|]∈eto(α)和[tβ, tβ]∈eto(β)根据时序关系连接得到(记为条件1), 这表示[t1, t2, …, t|α|]是tβ前α的最近一次最早转移发生, tβ是t|α|后β的最早发生时间.
若[t1, t2, …, t|α|, tβ]不是γ的一次最早转移发生, 则必然存在γ的一次最早转移发生[t1, t2, …, t|α|, tβ'], 此时, tβ'有两种可能:tβ' < t|α|或t|α| < tβ' < tβ.若tβ’ < t|α|, 说明[t1, t2, …, t|α|]不是α的一次最早转移发生, 这与条件1矛盾; 若t|α| < tβ' < tβ, 说明tβ不是t|α|后β的最早发生时间, 这也与条件1矛盾.
(2) 证明eto(γ)包含了情节γ=concat(α, β)的所有最早转移发生.
γ的任何一次最早转移发生[t1, t2, …, t|α|, tβ]都蕴含着[t1, t2, …, t|α|]是tβ前α的最近一次最早转移发生, tβ是t|α|后β的最早发生时间.根据时序关系, 算法ComputeETO都能将[t1, t2, …, t|α|]和[tβ, tβ]连接成[t1, t2, …, t|α|, tβ]作为γ的一次最早转移发生.
综合上述(1)和(2), 定理1得证.
性质4.设h是情节α的一次最早转移发生, h'是情节α的一次发生, 若h(t1)≤h'(t1), 则h(ti)≤h'(ti), 其中, 1≤i≤|α|, h(ti)和h'(ti)分别表示h和h'中α的第i个事件类型发生的时间.
推论1.记hi是情节α的第i次最早转移发生.若hi(t1) < hj(t1), 则hi(tk)≤hj(tk), 其中, i < j, 2≤k≤|α|.
推论2.设hi是情节α的第i次最早转移发生, 当且仅当hi(t|α|)=hi+1(t|α|)时, hi不是情节α的一次最小发生.
证明:
(a) 证明充分性
因为hi(t|α|)=hi+1(t|α|), 且由推论1可知hi(t1) < hi+1(t1), 所以hi不是情节α的一次最小发生, 充分性得证.
(b) 证明必要性
假设hi=[hi(t1), hi(t2), …, hi(t|α|)]不是α的一次最小发生, 则窗口[hi(t1), hi(t|α|)]中必然包含α的另一次发生h=[h(t1), h(t2), …, h(t|α|)], 此时有两种可能:h(t1)=hi(t1)或h(t1) > hi(t1).若h(t1)=hi(t1), 则h(t|α|) < hi(t|α|), 然而, 由于hi是α的最早转移发生, 任何由hi(t1)开始的α的发生不可能在h(t|α|)之前结束, 所以, h(t|α|) < hi(t|α|)是不可能的, 这表示h(t1)=hi(t1)也是不可能的.若h(t1) > hi(t1), 则根据性质4, 有hi(t|α|)≤h(t|α|).因为h是窗口[hi(t1), hi(t|α|)]中的一次发生, 所以hi(t|α|)=h(t|α|).由于hi+1是继hi之后α的最近最早转移发生, 且存在由h(t1)开始的α的发生h, 所以hi+1(t1)≤h(t1), hi+1(t|α|)≤h(t|α|).再由性质4, 有hi(t|α|)≤hi+1(t|α|).综合hi(t|α|)=h(t|α|), hi+1(t|α|)≤h(t|α|)和hi(t|α|)≤hi+1(t|α|), 有hi(t|α|)= hi+1(t|α|), 必要性得证.
综合上述(a)和(b), 推论2得证.
推论3.由推论2可知, 设hi是情节α的第i次最早转移发生, 若hi(t|α|) < hi+1(t|α|), 则hi是情节α的一次最小发生, 反之亦然.为此, 要计算情节α的最小发生集mo(α), 可以从情节α的最早转移发生集eto(α)中, 选择满足hi(t|α|) < hi+1(t|α|)的最早发生hi.
性质5. no(α)中h1是情节α的第1次最早转移发生, hi+1是hi(t|α|)之后与hi首次非重叠的发生, hn(t|α|)之后不存在与hn非重叠的发生.
推论4.情节α至多存在|no(α)|=n个非重叠的发生.
证明:设no'(α)={h1', h2', …, hm'}是α的任一非重叠发生集, 并令k=min(m, n).现用归纳法证明hi(t|α|)≤hi'(t|α|), 其中, 1≤i≤k.证明过程如下.
当i=1时, 假设h1'(t|α|) < h1(t|α|), 则存在α的一个开始于h'(t1)的最早转移发生g.由性质4, 有g(t|α|)≤h1'(t|α|), 这表示找到α的一个比h1还早的最早转移发生, 这与性质5矛盾.因此, h1(t|α|)≤h1'(t|α|)成立.
当1≤i < k时, 假设hi(t|α|)≤hi'(t|α|)成立, 需要证明hi+1(t|α|)≤hi+1'(t|α|)也成立.假设hi+1'(t|α|) < hi+1(t|α|), 则与i=1时类似, 在hi(t|α|)之后可以找到一个比hi+1还早且与hi非重叠的发生, 这与性质5矛盾.因此, hi+1(t|α|)≤hi+1'(t|α|)成立.
综上, hi(t|α|)≤hi'(t|α|), 其中, 1≤i≤k, 从而有m≤n.因为hn(t|α|)之后不存在与hn非重叠的发生(性质5), 所以情节α至多存在|no(α)|=n个非重叠的发生.推论4得证.
定理2.给定情节α的最早转移发生集eto(α)和支持度定义, 过程ComputeSUP计算得到的是α的支持度.
证明:给定事件序列和窗口宽度, 则有如下事实:情节α的窗口发生集wo(α)、头发生集ho(α)和最小发生集mo(α)都是唯一的; 由α的所有子情节的头发生集可以计算α的总发生支持度|to(α)|; 情节α的非重叠发生集no(α)、非交错发生集ni(α)、最小且非重叠发生集mn(α)可能是不唯一的.以下分情形证明定理2的正确性.
(1) 窗口发生、头发生和总发生
对于窗口发生, 过程ComputeSUP依据定义6, 首先计算情节α的窗口发生集wo(α), 然后求得α的支持度|wo(α)|; 对于头发生, 过程ComputeSUP依据定义8, 首先计算情节α的头发生集ho(α), 然后求得α的支持度|ho(α)|; 对于总发生, 过程ComputeSUP依据文献[11]提出的总发生支持度计算方法, 首先计算情节α的|ho(α)|, 然后由min(|ho(α)|, |to(suffic(α))|)求得情节α的支持度|to(α)|.
(2) 最小发生
依据推论3, 过程ComputeSUP首先计算情节α的头发生集mo(α), 然后求得α的支持度|mo(α)|.
(3) 非重叠发生
过程ComputeSUP依据定义11, 首先计算情节α的非重叠发生集no(α)={h1, h2, …, hn}, 其中, 每个hi都是α的最早转移发生, 然后求得α的支持度|no(α)|.依据推论4, no(α)是α的一个非重叠发生最大集.
(4) 非交错发生、最小且非重叠发生
过程ComputeSUP首先依据定义10和定义12, 分别计算情节α的非交错发生集ni(α)、最小且非重叠发生集mn(α), 然后分别求得α的支持度|ni(α)|、|mn(α)|.ni(α)和mn(α)是最大集的证明同no(α).
综合上述(1)~(4), 定理2得证.
2.4 算法复杂度分析设|ES|为事件序列ES的长度, ε为ES上的事件类型集, FE为ES上的频繁情节集, 则有:
定理3. FEM-DFS的时间复杂度为O(|FE|·|ε|·|ES|).
证明:FEM-DFS的时间代价主要在情节增长处理.设待增长的频繁情节为α, 与之串接的频繁1-情节为β, 增长后的情节为γ, 完成一次情节增长, 需要扫描eto(α)和eto(β)以计算eto(γ)和sup(γ), 其时间复杂度为O(|ES|). FEM-DFS需以FE中的每个情节为前缀或后缀进行情节增长, 增长次数至多为频繁1-情节的个数(上界为|ε|).因此, FEM-DFS的时间复杂度为O(|FE|·|ε|·|ES|).
定理4. FEM-DFS的空间复杂度为O(|FE|·|ES|).
证明:FEM-DFS需要维护所有的频繁情节, 每个频繁情节需要存储其最早转移发生集, 至多需要空间|ES|, 所以FEM-DFS的空间复杂度为O(|FE|·|ES|).
3 各种支持度比较定理5.情节α在给定事件序列上的支持度满足:|wo(α)|≥|ho(α)|≥|to(α)|, |ni(α)|≥|mo(α)|≥|no(α)|=|mn(α)|.
证明:
(1) 证明|wo(α)|≥|ho(α)|≥|to(α)|.
由定义6、定义8、定义9得证.
(2) 证明|ni(α)|≥|mo(α)|≥|mn(α)|=|no(α)|.
首先证明|ni(α)|≥|mo(α)|, 即证明:对于情节α相邻的最早转移发生hi和hi+1, 若hi是最小发生, 则hi和hi+1一定是非交错发生.我们使用反证法证明.因为hi是最小发生, 所以有hi(tk) < hi+1(tk), 其中, 1≤k≤|α|.假设hi和hi+1不是非交错发生, 则必然存在一个小于|α|的k, 使得hi+1(tk) < hi(tk+1), 则有hi(tk) < hi+1(tk) < hi(tk+1) < hi+1(tk+1).因hi(tk) < hi+1(tk) < hi(tk+1), 且hi和hi+1是相邻的最早转移发生, 所以有hi(tk+1)=hi+1(tk+1), 这与hi(tk+1) < hi+1(tk+1)矛盾, 说明若hi是最小发生, 则hi和hi+1一定是非交错发生, 从而证明了|ni(α)|≥|mo(α)|.
其次证明|mn(α)|=|no(α)|.对于no(α)中的任何一个发生h, 若h是最小发生, 则h∈mn(α), 否则, 根据推论2, 一定存在一个发生h', 满足h'(t|α|)=h(t|α|).显然, h'与no(α)中的其他发生都是非重叠的.这表明, 最小且非重叠发生的次数至少等于非重叠发生的次数, 即|mn(α)|≥|no(α)|.假设|mn(α)| > |no(α)|, 则说明no(α)不是α的非重叠发生的最大集, 这与推论4矛盾.因此, |mn(α)|=|no(α)|.
最后证明|mo(α)|≥|mn(α)|.因为mn(α)中的发生都是最小发生, 所以mn(α)⊆mo(α), 即|mo(α)|≥|mn(α)|.
4 实验评估我们使用文献[20, 21]的合成数据集与真实数据集来进行实验评估.对于合成数据集, 首先使用IBM合成数据生成器Quest Market-Basket的修改版生成了每个交易为单个项的交易序列, 通过设置D=0.001, C=300000, N=20, S=300000, 其中, 参数D表示交易序列的个数(单位为1 000), C表示每个交易序列中交易的平均个数, N表示所有交易项的类型种数(单位为1 000), S为最长交易序列中交易的平均个数, 这样就得到了一个20 000种交易项类型上的由300 000个交易组成的交易序列.然后, 为该交易序列中的每个交易依次赋上一个连续的正整数以作为每个交易发生的时间戳, 这样, 就构造了一个20K种事件类型上的由300K个事件组成的事件序列.
对于真实数据集, 考虑到作为国内最具影响力的知识传播与数字化学习平台, 中国知网为全社会提供了最丰富、最全面的文献资源, 为了能够发现中国知网相关文献之间的引用关系, 并为广大学者展开相关研究提供个性化的推荐服务, 我们选用了中国知网的一个Web服务器上从2010年11月1日~2010年11月30日的日志数据, 该日志数据包括了相关读者对132 885种不同文献的211 665个阅读序列.
通过7组实验对比算法FEM-DFS和文献[19]提出的算法(为描述方便, 简称为FEM-BFS)的时空性能, 并分析FEM-DFS在不同支持度定义下的挖掘结果.实验的硬件环境为3.6GHz Intel(R) Core(TM) i7-4790 CPU, 内存为8GB, 操作系统为Windows 8, 程序采用Java实现.
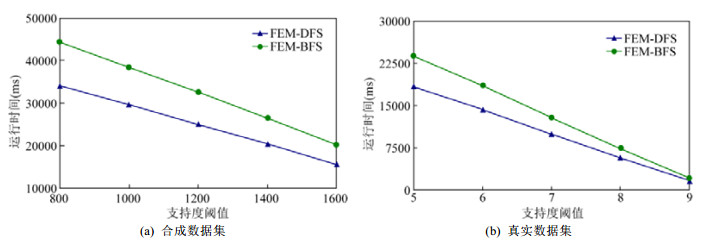
实验1.运行时间vs.支持度阈值.合成数据集和真实数据集的窗口宽度分别设定为200和5天, 通过改变支持度阈值, 得到如图 2所示的两种算法各自在7个支持度定义下的平均运行时间.
|
Fig. 2 Average runtime vs. support threshold 图 2 运行时间vs.支持度阈值 |
可以看出, 随着支持度阈值的增加, 两种算法的运行时间都在线性减少, 且FEM-DFS要优于FEM-BFS, 主要原因是:支持度阈值越大, 频繁情节越少; FEM-BFS采用广度优先搜索策略, 需要多遍扫描事件序列, 而FEM-DFS采用深度优先搜索策略, 只需单遍扫描事件序列.
尽管算法FEM-DFS和FEM-BFS在运行时间上存在差异, 但它们的挖掘结果相同.例如, 〈基于隐马尔可夫模型的多步攻击预测研究, 面向分布数据安全的误用检测算法和入侵检测系统的研究, 隐马尔可夫模型在入侵检测中的应用, 基于入侵响应的入侵警报关联性的攻击预测算法, 基于因果网络的攻击计划认别与预测, 面向网络安全的基于入侵事件的早期预警方法〉是两种算法在真实数据集上都能挖掘得到的一个频繁6-情节, 该情节刻画了一种行为模式:读者们旨在研究一个基于隐马尔可夫模型的攻击预测方法(见第1篇阅读文档), 他们首先研究了两种常用的入侵检测模型, 即误用检测模型(见第2篇阅读文档)和异常检测模型(见第3篇阅读文档),然后分析了现有攻击方法的不足(见后3篇阅读文档).算法FEM-DFS和FEM-BFS的挖掘结果有助于CNKI向读者提供个性化的文献阅读推荐服务.
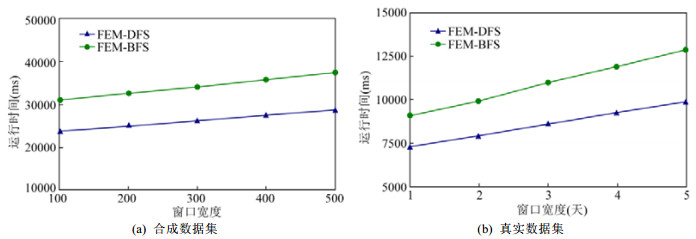
实验2.运行时间vs.窗口宽度.合成数据集和真实数据集的支持度阈值分别设定为1 200和7, 通过改变窗口宽度, 得到如图 3所示的两种算法各自在窗口发生、头发生和总发生支持度定义下的平均运行时间.
|
Fig. 3 Average runtime vs. window width 图 3 运行时间vs.窗口宽度 |
可以看出, 随着窗口宽度的增加, 两种算法的运行时间也在线性增加, 这是因为窗口宽度越大, 频繁情节越多.另外, FEM-DFS要优于FEM-BFS, 这是因为两者采用了不同的搜索策略.
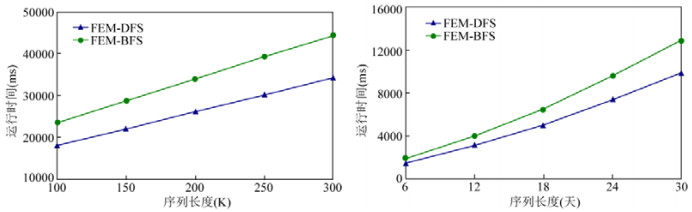
实验3.运行时间vs.序列长度.设定合成数据集的支持度阈值和窗口宽度分别为800和200, 真实数据集的支持度阈值和窗口宽度分别为7和5天, 并选择前100K、前150K、前200K、前250K个和所有300K个合成数据作为5个合成子序列, 选择前6天、前12天、前18天、前24天和所有30天真实数据作为5个真实子序列, 通过改变序列长度, 得到如图 4所示的两种算法各自在7个支持度定义下的平均运行时间.
|
Fig. 4 Average runtime vs. sequence length 图 4 运行时间vs.序列长度 |
可以看出, 两种算法的运行时间都随着序列长度的增加而线性增加, 这是因为序列长度越大, 频繁情节越多.另外, FEM-DFS优于FEM-BFS, 这也源于两者不同的搜索策略.
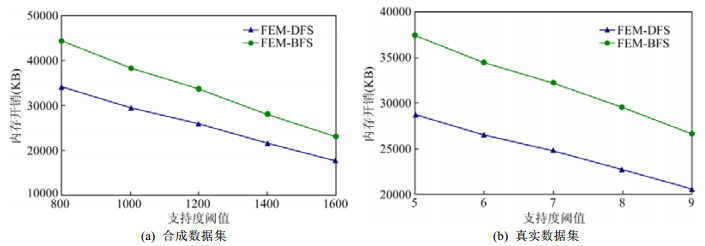
实验4.内存开销vs.支持度阈值.与实验1的设置相同, 通过改变支持度阈值, 得到如图 5所示的两种算法各自在7个支持度定义下的平均内存开销.
|
Fig. 5 Average memory vs. support threshold 图 5 内存开销vs.支持度阈值 |
可以看出, 随着支持度阈值的增加, 两种算法的内存开销都在线性减少, 且FEM-DFS要优于FEM-BFS, 原因与实验1相同.
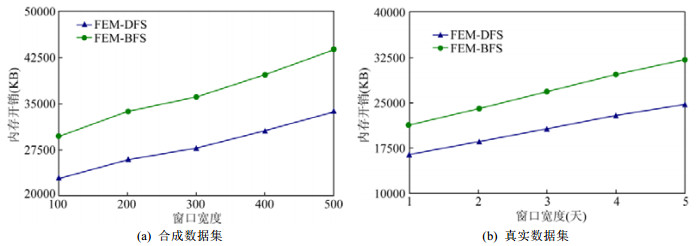
实验5.内存开销vs.窗口宽度.与实验2的设置相同, 通过改变窗口宽度, 得到如图 6所示的两种算法各自在窗口发生、头发生和总发生支持度定义下的平均内存开销.
|
Fig. 6 Average memory vs. window width 图 6 内存开销vs.窗口宽度 |
可以看出, 随着窗口宽度的增加, 两种算法的内存开销都在线性增加, 但FEM-DFS要优于FEM-BFS, 原因与实验2相同.
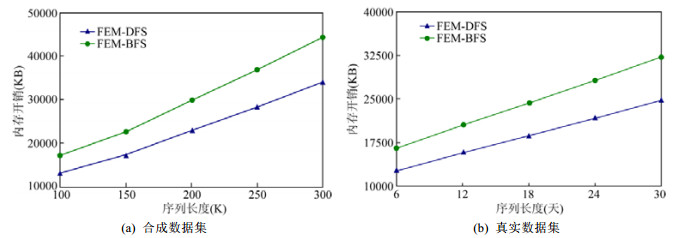
实验6.内存开销vs.序列长度.与实验3的设置相同, 通过改变序列长度, 得到如图 7所示的两种算法各自在7个支持度定义下的平均内存开销.
|
Fig. 7 Average memory vs. sequence length 图 7 内存开销vs.序列长度 |
可以看出, 两种算法的内存开销都随着序列长度的增加而呈线性增加, 但FEM-DFS要优于FEM-BFS, 原因与实验3相同.
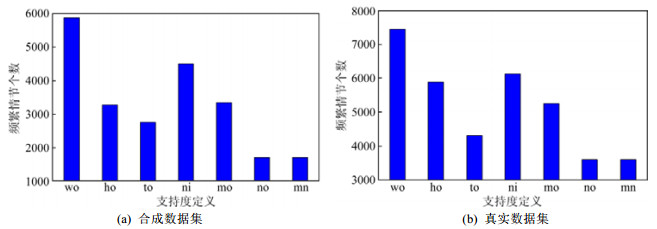
实验7.频繁情节个数vs.支持度定义.选择300K合成数据集和30天真实数据集, 两个数据集的支持度阈值分别设定为800和7, 窗口宽度分别设定为200和5天, 通过改变支持度定义, 得到如图 8所示的算法FEM-DFS在不同支持度定义下的频繁情节个数.
|
Fig. 8 Episode number vs. support definition 图 8 频繁情节个数vs.支持度定义 |
可以看出, 基于窗口发生、头发生、总发生的3种支持度定义, 发现的频繁情节个数依次递减; 基于非交错发生、最小发生、非重叠发生的3种支持度定义, 发现的频繁情节个数也在依次递减; 基于非重叠发生、最小且非重叠发生的两种支持度定义, 发现的频繁情节个数相同.主要原因:同一情节的发生次数在不同支持度定义下有着固定的比较关系, 这与定理5一致.
5 总结与展望针对现有频繁情节挖掘算法存在的不足, 本文提出了一个采用深度优先搜索方式和共享前/后缀树存储结构的频繁情节挖掘算法FEM-DFS, 满足了实际情况下用户多变的支持度定义需求, 实验评估证实了算法FEM-DFS能够有效地发现事件序列上的频繁情节.
未来将基于事件流环境, 研究一种能够融合多种支持度定义的频繁情节挖掘算法.
| [1] |
Mannila H, Toivonen H, Verkamo AI. Discovery of frequent episodes in event sequences. Data Mining and Knowledge Discovery, 1997, 1(3): 259-289.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1205.4477 |
| [2] |
Méger N, Rigotti C. Constraint-based mining of episode rules and optimal window sizes. In: Proc. of PKDD. 2004. 313-324.
|
| [3] |
Lin YF, Huang CF, Tseng VS. A novel methodology for stock investment using high utility episode mining and genetic algorithm. Applied Soft Computing, 2017, 59: 303-315.
[doi:10.1016/j.asoc.2017.05.032] |
| [4] |
Ma X, Pang HH, Tan KL. Finding constrained frequent episodes using minimal occurrences. In: Proc. of the ICDM. 2004. 471-474.
|
| [5] |
Zhou WZ, Liu HY, Cheng H. Mining closed episodes from event sequences efficiently. In: Proc. of the PAKDD. 2010. 310-318.
|
| [6] |
Wu JJ, Wan L, Xu ZR. Algorithms to discover complete frequent episodes in sequences. In: Proc. of the PAKDD. 2011. 267-278.
|
| [7] |
Wu CW, Lin YF, Yu PS, Tseng VS. Mining high utility episodes in complex event sequences. In: Proc. of the SIGKDD. 2013. 536-544.
|
| [8] |
Lin SK, Qiao JZ. An episode mining method based on episode matrix and frequent episode tree. Control and Decision, 2013, 28(3): 339-344(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/kzyjc201303003 |
| [9] |
Ao X, Luo P, Li CK, Zhuang FZ, He Q, Shi ZZ. Discovering and learning sensational episodes of news events. In: Proc. of the WWW. 2014. 217-218.
|
| [10] |
Huang KY, Chang CH. Efficient mining of frequent episodes from complex sequences. Information Systems, 2008, 33(1): 96-114.
http://dl.acm.org/citation.cfm?id=1316258 |
| [11] |
Iwanuma K, Ishihara R, Takano Y, Nabeshima H. Extracting frequent subsequences from a single long data sequence. In: Proc. of the ICDM. 2005. 186-193.
|
| [12] |
Avinash A, Ibrahim A, Sastry PS. Pattern-growth based frequent serial episode discovery. Data & Knowledge Engineering, 2013, 87: 91-108.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0231774865/ |
| [13] |
Laxman S. Discovering frequent episodes: Fast algorithms, connections with HMMs and generalizations[Ph.D. Thesis]. Bangalore, 2006.
|
| [14] |
Laxman S, Sastry PS, Unnikrishnan K. Discovering frequent episodes and learning hidden Markov models:A formal connection. IEEE Trans. on Knowledge and Data Engineering, 2005, 17(11): 1505-1517.
[doi:10.1109/TKDE.2005.181] |
| [15] |
Laxman S, Sastry PS, Unnikrishnan KP. A fast algorithm for finding frequent episodes in event streams. In: Proc. of the SIGKDD. 2007. 410-419.
|
| [16] |
Zhu HS, Wang P, He XM, Li YJ, Wang W, Shi BL. Effcient episode mining with minimal and non-overlapping occurrences. In: Proc. of the ICDM. 2010. 1211-1216.
|
| [17] |
Zhu HS, Wang P, Wang W, Shi BL. Discovering frequent closed episodes from an event sequence. In: Proc. of the IJCNN. 2012. 2292-2299.
|
| [18] |
Liao GQ, Yang XT, Xie S, Yu PS, Wan CX. Two phase mining for frequent closed episodes. In: Proc. of the WAIM. 2016. 55-66.
|
| [19] |
Avinash A, Laxman S, Sastry PS. A unified view of the apriori-based algorithms for frequent episode discovery. Knowledge and Information Systems, 2012, 31: 223-250.
[doi:10.1007/s10115-011-0408-2] |
| [20] |
Zhu HS, Wang W, Shi BL. Extracting non-redundant episode rules based on frequent closed episodes and their generators. Chinese Journal of Computers, 2012, 35(1): 53-64(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/jsjxb201201006 |
| [21] |
Zhu HS. Research on stream prediction based on episode rule matching[Ph.D. Thesis]. Shanghai: Fudan University, 2011(in Chinese with English abstract).
|
| [8] |
林树宽, 乔建忠. 一种基于情节矩阵和频繁情节树的情节挖掘方法. 控制与决策, 2013, 28(3): 339-344.
http://d.old.wanfangdata.com.cn/Periodical/kzyjc201303003 |
| [20] |
朱辉生, 汪卫, 施伯乐. 基于频繁闭情节及其生成子的无冗余情节规则抽取. 计算机学报, 2012, 35(1): 53-64.
http://d.old.wanfangdata.com.cn/Periodical/jsjxb201201006 |
| [21] |
朱辉生.基于情节规则匹配的数据流预测研究[博士学位论文].上海: 复旦大学, 2011.
|
 2020, Vol. 31
2020, Vol. 31


