2. 广东省信息安全技术重点实验室(中山大学), 广东 广州 510006
2. Guangdong Key Laboratory of Information Security Technology(Sun Yat-Sen University), Guangzhou 510006, China
可信第三方(trusted third party, 简称TTP)在安全协议中往往是功能较强大的一个设计模块[1], 如证书颁发机构(certificate authority, 简称CA)是一种中心化TTP, 可以证明身份和公钥之间的绑定关系.计票系统中的计票机构(tally agent, 简称TA)是另一种中心化TTP, 负责诚实地统计选票.中心化TTP通常知道一些敏感信息或者具备一些特殊的能力, 例如TA知道计票信息, 可以权威地公布计票结果.这些信息和能力往往会引起外部攻击者的兴趣, 增加了这些TTP的安全风险.例如, 敌手可以尝试攻击TA, 在TA公布选票前修改投票结果.此外, 中心化TTP也可能遭受内部攻击, 例如内部工作人员因为抵抗不住诱惑而拿敏感信息换取经济利益.此外, 中心化TTP自身的硬件和软件也可能出现故障, 使得服务中断, 威胁信息系统的可用性.另外, 如果中心化TTP的硬件和软件跟不上业务的规模, 中心化TTP会成为整个安全协议的性能瓶颈.最后, 中心化TTP的业务范围有限, 往往只能服务一个区域, 一般做不了全球的可信中心.总之, 中心化的TTP往往具有较低的可靠性和较高的安全风险.
区块链技术为人们提供了一种基于点对点网络的无中心的TTP, 可以诚实地记录交易和执行脚本.粗略地看, 区块链网络中的节点通过某种共识机制产生一个新区块, 由创建了新区块的节点记录最近的交易并执行相关脚本.创建了新区块的节点也可以从交易中收取交易费, 甚至获得奖励.基于理性经济人假设, 区块链网络中的节点行为是可预期的.以比特币为例, 比特币网络的节点通过工作量证明的共识机制生成新的区块, 创建新区块的节点可以获得比特币奖励和交易费.比特币系统自2009年出现后, 到目前为止运行良好.这在一定程度上说明无中心TTP是可行的.以太坊[2]是比特币系统的升级版, 提供了图灵完备的脚本语言, 支持智能合约.
这种无中心TTP所存储的数据都是公开的, 所以对以获取秘密为目标的外部攻击者而言没有吸引力.另外, 无中心TTP的节点是动态加入、动态退出的, 实现内部攻击需要对共识算法进行颠覆才有可能, 需要的代价非常大.同时, 节点的动态性保证了单个节点的故障对全网影响不大.比较而言, 区块链这种无中心TTP具有较高的可靠性和较低的安全风险[1].
无中心TTP的优点自然吸引了不少协议设计者在区块链中设计协议.目前, 在以太坊平台上有100多个可部署的应用, 包括投票、合同签署、拍卖等应用[3].然而并不存在保护隐私的应用, 例如投票协议中投票人的投票是公开的.Zhao等人[4]提出了比特币投票协议, 通过比特币交易来执行投票过程, 并且保护了投票人的隐私.他们通过秘密分享、承诺、零知识证明[5]等技术生成秘密且可验证的二选一的投票, 之后, 分别使用“索赔或退款”[6]和“联合交易”[7]这两种公平交换的模式给出了两个投票过程.特别的, 为了解决比特币交易的延展性问题[7], 他们使用了门限签名体制, 需要较多的交互次数和较高的计算代价.
本文汲取并扩展了Zhao等人[4]的投票生成技术, 支持生成对m个候选人的一般化投票; 进而采用了智能合约来实现投票和资助过程, 避免了采用门限签名体制带来的问题; 最后, 在模型检测工具中对合约的主要逻辑进行了验证.
1 相关工作Zhao等人[4]提出了比特币投票的概念.n个投票人从2个候选人中选择1个进行资助.要求每个候选人的投票是隐私的, 并且是可验证的.当投票结果揭晓后, 获胜者可以获得所有投票人的资助.例如, 每个投票人资助1比特币, 那么获胜者可以获得n比特币.任何投票人不能因为不喜欢获胜者而撤回资助.
与比特币投票密切相关的工作之一自然是电子投票.“n个投票人从2个候选人中选择1个”是一种典型的“赞成与否”的投票方式.这种投票可以一般化为“n个投票人从m个候选人中至少选择kmin个、至多选择kmax个候选人”[8].此外还有其他的一些投票方式, 例如在m个候选人中分配一些选票, 每个候选人获得选票的数量有上限等.在选票的秘密性和可验证性方面, 电子投票也积累了丰富的实践经验.通常采用的技术包括同态加密、秘密分享、混合网络、零知识证明等[8, 9], 这些设计方法在比特币投票协议中显然是可以借鉴的.
在Zhao等人[4]的协议中使用了zkSNARK[10]这一特殊的零知识证明技术.该技术用于ZCash[10]中.与一般的零知识证明相比, zkSNARK可以把哈希函数的原像或者对称加密算法的明文作为输入, 给出原像或者明文具有某种可判别关系的证明.例如, 给定两个哈希值及其原像值, 使用zkSNARK可以给出一个证明, 使得验证人在仅有两个哈希值及证明的情况下, 验证这两个哈希值的原像是是否相等.
与比特币投票密切相关的另外一类工作就是区块链中的协议设计方法.例如, Zhao等人[4]使用“索赔或退款”[6]和“联合交易”[7]这两种公平交换的模式来完成投票.其中, “索赔或退款”模式是Barder等人[6]在设计公平的比特币混合器时提出的, 这一模式由Bentov等人[11]在全局可组合模型中进行了定义.进一步地, Kiayias等人[12]利用这一模式构建了一般的公平多方计算协议.Andrychowic等人[13]指出“索赔或退款”模式容易受比特币交易的延展性攻击, 进而提出“时间承诺”模式来设计公平的协议.进一步, Andrychowic等人[7]进一步给出了“同步时间承诺”模式来提供双方公平的安全协议.比特币交易的延展性攻击可以让攻击者改变交易的唯一标识, 却保持不变的语义.Decker和Wattenhofer认为, 该问题是导致原比特币交易市场MtGox倒闭的原因[14].但是在最近的比特币发展中, 采用了隔离认证的方式, 该方式通过区分交易内容和签名字段也克服了可延展问题, 这使得原来的“抵押-赔偿”协议设计的方式重新成为一个可选项.
本文设计的是以太币投票协议, 基于以太坊平台[2].以太坊平台提供了完备图灵机的能力和高级编程语言, 同时具有以太币, 可以完成支付.以太坊中的智能合约是一种由事件驱动、具有状态、运行在可复制的共享区块链数据账本上的计算机程序[15].该程序本身也部署在区块链上, 记入区块链的特定区块中.用户通过调用智能合约实现智能合约的运行, 以改变智能合约的状态, 生成新的交易, 或者返回用户希望的数据.
本文对合约的验证使用了模型检测工具.模型检测通过模型状态搜索的方法来验证系统是否具有某些性质[16].给定描述合约逻辑的程序和规约条件, 模型检测工具生成对应的合约模型, 并验证规约条件在合约模型中是否成立.如果经过模型状态搜索没有发现违背规约条件的状态, 就证明合约满足规约条件; 如果发现了违背规约条件的状态, 则进行反向逆推, 给出反例出现的路径, 以找到合约设计的缺陷.本文中使用进程元语言(process meta language, 简称Promela)[17]描述合约逻辑, 用Spin模型检测[18]工具进行验证, 用线性时态逻辑(linear temporal logic, 简称LTL)[19, 20]描述规约条件.
进一步地, 本文用CCS 2016[21]中Luu等人给出的一个专门针对以太坊智能合约的分析工具对合约进行了安全性测试.该工具旨在检查可执行的分布式代码合约(executable distributed code contract, 简称EDCC)的缺陷, 并且与任何基于以太坊的EDCC语言兼容, 包括Soldity, Serpent和LLL.其检测的智能合约的安全问题包括交易顺序依赖、时间戳依赖、异常处理不当、可重入攻击等.使用该工具时, 需要输入智能合约的代码和以太坊的全局状态, 经过分析之后, 该工具可以给出关于上述攻击的安全性结论.经该工具检测, 仅提示本文的智能合约存在交易顺序依赖问题.但是经过我们对合约逻辑的分析, 本文的智能合约在规定的时间内只能执行符合约定条件的交易, 并不存在交易顺序依赖的问题.
我们注意到, 在金融密码会2017中, 出现了基于智能合约的投票协议[22].该协议需要在智能合约中直接运行较为复杂的密码运算, 导致合约代码较为复杂.它需要较多的燃料(gas)才能执行, 是一种把复杂性放在以太坊区块链上的技术选择.本文采取了Zhao等人[4]的思路, 使用了zkSNARK技术, 合约代码相对简单, 只需要目前以太坊支持的一些操作即可, 是一种把复杂性放在客户端的技术选择.另外, 有文献提出采用Zcash进行投票[23], 属于Zcash框架的简单应用, 还需要较多的探索.
1.1 主要贡献总体上, 本文提供了一种以太币投票智能合约, 通过该智能合约, 投票发起人可以让n个投票人出资并对m个候选人进行投票, 可以要求每个投票人至少选择kmin个候选人、至多选择kmax个候选人.投票阶段结束后, 通过智能合约可以完成计票, 揭示每个候选人的得票数, 并择优资助.
具体来看, 在选票生成阶段, 本文把Zhao等人[4]生成选票的协议进行了扩展, 平凡推广到m个候选人的情况, 并增加了零知识证明确保投票的合法性.在投票阶段, 本文通过智能合约完成了“联合交易”的逻辑和“时间承诺”的逻辑, 实现了计票、资助等功能.此外, 我们发现Zhao等人的协议设计存在资金黑洞, 即投票失败时所有投票者的资助金会被锁住, 我们的投票协议成功地避免了此类问题.并且通过模型检测工具, 本文对合约的主要业务逻辑进行了检验, 确认了合约的正确性.
2 以太币投票协议类似于比特币投票协议, 本文的协议也分为选票生成和投票两个阶段.
2.1 选票生成本文的选票生成协议把Zhao等人[4]的选票生成协议作为子程序来调用.该子程序称为VCi(Oi), 表示投票人pi对一个候选人的投票Oi做出的可验证的承诺投票, 其中, Oi∈{0, 1}, 0表示不赞成, 1表示赞成.pi执行VCi(Oi)的过程如下.
1. 生成随机数:pi生成n个零和的随机数rij∈
2. 验证承诺的零和属性:pi收到每个其他投票人的n个承诺和1个zkSNARK证明后, 验证其正确性.
3. 分发打开承诺的密钥:当pi收到所有其他投票人正确的承诺后, 对所有j∈{1, …, n}\{i}, pi发送kij给pj.
4. 生成选票:对所有的j∈{1, …, n}\{i}, pi等待pj发送的kji, 并验证rji=open(cji, kji)≠⊥.当pi收到所有其他投票人打开承诺的密钥, 并验证非空后, 计算
(a)
(b)
5. 广播选票及其零知识证明:pi广播承诺Ci,
6. 验证选票:pi接收每个投票人的承诺值, 并与该投票人第1次广播的承诺值一起作为zkSNARK的输入, 验证其选票的正确性.
需要注意的是, 第3步分发打开承诺的密钥时, pi需要与其他投票人建立安全通道, 安全地递交密钥.另外, 对每个投票人pi, 其VCi(Oi)的运行需要n-1次安全的单播和2次广播, 同时需要3次zkSNARK证明和3(n-1)次验证.
基于以上的VCi(Oi)子程序, 我们设计一般的选票生成协议如下.
设m个候选人{1, …, m}.投票人pi对每一个候选人c∈{1, …, m}调用
| $ \sum\limits_c {O_i^c} \in [{k_{\min }}, {k_{\max }}] $ | (1) |
注意到pi有所有承诺
通过上述过程, 每个投票人都可以从m个候选人中选择至少kmin个、至多kmax个候选人, 形成有效的选票.其中, pi的选票是
投票阶段采用智能合约完成, 该智能合约对应的业务逻辑如下.
1. 合约的创建者初始化m个候选人n个投票人的账户地址.
2. 投票人pi计算所有投票人的选票的哈希值Hi=H(V0, …, Vn), 其中, H是一个公用的哈希算法, 例如SHA- 256;然后, pi把自己的选票Vi、哈希值Hi、以太币保证金和以太币资助金发送到智能合约.
3. 如果所有投票人不能在30个区块时间内把自己的选票、哈希值、以太币保证金和以太币资助金全部发送到智能合约, 则此次投票失败.每个已经发送了选票的投票人都可以把以太币保证金和资助金取回.
4. 当所有投票人发送了自己的选票、哈希值、以太币保证金和以太币资助金之后, 投票人pi可以打开自己选票中的承诺, 取回自己的保证金.
5. 当所有投票人都打开选票中的承诺后, 智能合约统计所有的投票, 确定候选人各自的得票数, 确定获胜者, 并由获胜者获得所有投票人的资助金.当获胜者有多人时, 平分所有投票人的资助金.
6. 如果在20个区块时间内, 有投票人没有打开选票中的承诺, 则这些投票人的保证金由m个候选人平分, 同时把所有的资助金返还给各个投票人, 投票失败.
3 投票阶段智能合约的实现和测试 3.1 投票阶段智能合约的实现我们在以太坊中使用Solidity语言实现了投票阶段智能合约.简单起见, 合约包含1个合约创建者、2个候选人和2个投票人.多个投票人和候选人的情况可以类推.合约代码的命名主要参考了Solidity官网中电子投票的智能合约[24], 然后根据我们的以太币投票协议完善了投票功能.
首先, 我们定义投票人和候选人的结构体.投票人结构体如下.
struct Voter {
address id;
bool rights;
bool voted;
bool claimed;
bytes32 commitA;
bytes32 commitB;
bytes32 commits;
bytes32 openkeyA;
bytes32 openkeyB;
}
其中, id代表投票人的地址, rights代表是否被合约部署人授予投票权, voted指是否承诺并投票, claimed指是否打开承诺取回押金, commitA、commitB和commits分别代表投票人对候选人proposalA和proposalB的承诺值以及所有投票人选票的哈希值, openkeyA和openkeyB分别代表投票人对候选人proposalA和proposalB打开承诺的值.
候选人结构体中, id代表候选人地址, index是候选人对应的一个数标, voteCount统计该候选人的所有选票.
struct Proposal {
address id;
int index;
int voteCount;
}
接下来, 对应投票阶段的6个业务逻辑, 依次实现了Ballot、Commits、stopVoting、Claims、winningProposal和Prize、proposalClaim这6组功能函数.
1.合约创建者chairperson部署智能投票合约到区块链, 并指定候选人proposalA和proposalB, 投票人voter1和voter2的地址.初始化候选人结构体, 设置候选人地址, 初始化proposalA对应的index为1, proposalB对应的index为2.初始化投票人结构体, 设置投票人地址, 并赋予投票人具有参与投票的权利, 其他参数默认为false或者0.
function Ballot(address_proposalA, address_proposalB, address_voter1, address_voter2) {
chairperson=msg.sender;
proposalA=_proposalA;
proposalB=_proposalB;
proposals[proposalA]=Proposal(proposalA, 1, 0);
proposals[proposalB]=Proposal(proposalB, 2, 0);
voter1=_voter1;
voter2=_voter2;
voters[voter1]=Voter(voter1, true, false, false, 0, 0, 0, 0, 0);
voters[voter2]=Voter(voter2, true, false, false, 0, 0, 0, 0, 0);
}
2.投票人对两个候选人的选票表示为_commitA和_commitB, 对所有投票人选票的哈希值表示为_commits.每个投票人通过交易, 调用智能合约的Commits函数发送自己的选票、哈希值, 同时提交保证金和资助金.本实例中, 把保证金deposit设为10以太币, 资助金fund设为1以太币, 每个投票人需要一定时间内提交amounts大小为11以太币.智能合约会判断投票人交易中的amounts, 确认保证金和资助金恰好是11以太币, 若多了则返回, 若不够则退回投票人要求重新提交.另外, 该函数还会统计提交选票的人数, 且记录第1个选票提交时的区块高度, 以配合其他函数完成“时间承诺”的功能.与普通的“时间承诺”相比, 我们规定了提交选票操作的允许时间段, 开始时间为第1个投票人提交选票的区块时间, 最多持续30个区块时间后结束.计时结束后不能再提交选票, 只能取回提交的保证金并停止此次投票.另外, 该函数会判断每个人所提交的各自的_commits是否一致, 并且在所有投票人提交选票后判断每个人提交的_commits是否与智能合约按照每个人的选票计算的哈希值一致.这一步骤主要是为了判断所有投票人是否就选票达成了一致, 具有比特币投票协议中“联合交易”的特点.
下面给出该函数的部分核心代码, 其中, msg.sender表示合约接口的调用者, msg.value表示调用该合约接口交易发送给合约的交易金额.
function Commits(bytes32_commitA, bytes32_commitB, bytes32_commits) public payable {
if (voters[msg.sender].rights!=true) throw;
if (msg.value > =amounts){
if (msg.sender==voter2 & & voters[voter2].commits!=voters[voter1].commits){
msg.sender.transfer(msg.value);
throw;
}
msg.sender.transfer(msg.value-amounts);
if (votersNum==0) firstFundTime=block.number;
voters[msg.sender]=Voter(msg.sender, false, true, false, _commitA, _commitB, _commits, 0, 0);
votersNum+=1;
…
}
else {
msg.sender.transfer(msg.value);
throw;
}
if (votersNum==2) {
bytes32 cohash=sha256(voters[voter1].commitA|voters[voter1].commitB|
voters[voter2].commitA|voters[voter2].commitB);
if (cohash!=voters[voter2].commits){
voter1.transfer(amounts);
voter2.transfer(amounts);
votersNum=0;
voters[voter1]=Voter(voter1, true, false, false, 0, 0, 0, 0, 0);
voters[voter2]=Voter(voter2, true, false, false, 0, 0, 0, 0, 0);
throw;
}
}
}
3.注意到, 在智能合约的Commits函数中, 第1个投票人调用时, 合约会记录下区块高度.在30个区块之后, 每个投票人都可以在投票失败的情况下调用stopVoting函数来终止投票, 取回保证金和资助金.该函数执行时, 会首先根据当前区块判断时间是否已经超过了30个区块, 如果确实超过了30个区块, 并且所有的投票人确实没有全部参与该次投票, 而且该函数的调用方确实参与了投票, 就可以把该参与方的保证金和资助金退回.如果以上条件不满足, 则不会执行任何操作.
function stopVoting(·)public {
if (voters[msg.sender].voted!=true) throw;
if (votersNum==2) throw;
uint time=block.number;
uint t=time-firstFundTime;
if (t > 30){
msg.sender.transfer(amounts);
voters[msg.sender].voted=false;
}
}
4.如果所有投票人都发送了自己的选票、哈希值、保证金和资助金, 每个投票人就可以通过调用Claims函数, 打开自己选票的承诺值以取回自己的保证金.该函数的输入包括每个选票中的承诺的打开密钥, 在本实例中, 选票的承诺值就是哈希值, 所以相应的承诺打开密钥就是哈希值的原像, 对一个候选人而言, 就是选票生成阶段的
同时, 该函数还会记录第1次有投票人打开承诺时的区块高度, 投票人只能在第1次打开承诺后20个区块内打开承诺取回保证金, 否则会被候选人平分.
下面给出该函数的部分核心代码.
function Claims(bytes32_openkeyA, bytes32_openkeyB){
if (voters[msg.sender].claimed==true||votersNum < 2) throw;
if (backNum==0) firstClaimTime=block.number;
uint time=block.number;
timer=time-firstClaimTime;
if (timer > 20) throw;
if (sha256(_openkeyA)==voters[msg.sender].commitA & & sha256(_openkeyB)==voters[msg.sender].commitB{
msg.sender.transfer(deposit);
backNum++;
voters[msg.sender].claimed=true;
voters[msg.sender].openkeyA=_openkeyA;
voters[msg.sender].openkeyB=_openkeyB;
…
}
}
5.当所有投票人都打开选票中的承诺后, 智能合约统计所有的投票, 确定候选人各自的得票数, 确定获胜者.所有人都可以通过winningProposal函数查看获胜者.获胜者可以通过Prize函数获得所有投票人的资助金.当获胜者有多人时, 获胜者中的任意一人调用Prize函数, 智能合约平分所有投票人的资助金给所有获胜者.
function winningProposal(·) public returns(uint) {
if (backNum==2) {
proposals[proposalA].voteCount=int(voters[voter1].openkeyA)+int(voters[voter2].openkeyA);
proposals[proposalB].voteCount=int(voters[voter1].openkeyB)+int(voters[voter2].openkeyB);
if (proposals[proposalA].voteCount > proposals[proposalB].voteCount) index=1;
if (proposals[proposalA].voteCount < proposals[proposalB].voteCount) index=2;
if (proposals[proposalA].voteCount==proposals[proposalB].voteCount) index=3;
return (index);
}
}
function Prize(·) {
uint winnerprize=votersNum*fund;
if (index==1){
if (msg.sender!=proposalA) throw;
proposalA.transfer(winnerprize);
}
if (index==2){
if (msg.sender!=proposalB) throw;
proposalB.transfer(winnerprize);
}
if (index==3){
if (msg.sender==proposalA||msg.sender==proposalB){
proposalA.transfer(winnerprize/2);
proposalB.transfer(winnerprize/2);
}
}
}
6.如果在第1次打开承诺后, 有20个新区块生成还有投票人没有打开承诺, 则投票失败, 由候选人平分所有没有取回的保证金, 同时把投票人交的资助金返还.只有候选人才能调用proposalClaim函数.该函数首先判断是否所有承诺者打开了承诺.若是, 则退出合约.否则, 继续判断在第1次打开承诺后是否已有20个新区块生成:若是, 则统计所有没取回的保证金, 由候选人平分, 同时把资助金返还给投票人; 否则, 退出合约.
function proposalClaim(·) public returns(string){
if (backNum==2) throw;
if (msg.sender!=proposalA & & msg.sender!=proposalB) throw;
uint time=block.number;
timer=time-firstvoteTime;
if (timer > 20){
uint depositPrizeNum=2-backNum;
uint prize=deposit*depositPrizeNum;
proposalA.transfer(prize/2);
proposalB.transfer(prize/2);
voter1.transfer(fund);
voter2.transfer(fund);
return (“Vote Fail Fine”);
}
}
3.2 投票阶段智能合约的测试我们使用基于智能合约浏览器的开发环境browser-solidity进行了仿真测试, 验证了上述代码的正确性.
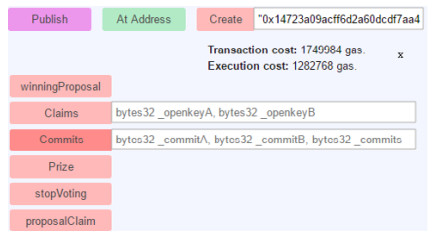
1. Ballot函数:Ballot函数是智能合约的构造函数, 当合约创建者在区块链中部署合约时会触发该函数.在browser-solidity开发环境中, 通过点击“Create”按钮, 即可完成智能合约的部署.如果合约部署成功, 则开发环境中会给出智能合约的函数运行接口和对应的参数输入框, 如图 1所示.
|
Fig. 1 Costs and smart contract interfaces returned by the development environment after a successful deployment 图 1 部署智能合约成功后开发环境返回的合约函数接口和相关开销 |
合约创建者在部署智能合约时需要在对应的参数输入框传入4个地址, 前两个是候选人地址, 后两个是投票人地址:
● “0x14723a09acff6d2a60dcdf7aa4aff308fddc160c”;
● “0x4b0897b0513fdc7c541b6d9d7e929c4e5364d2db”;
● “0x583031d1113ad414f02576bd6afabfb302140225”;
● “0xdd870fa1b7c4700f2bd7f44238821c26f7392148”.
当合约部署成功后, 开发环境会返回交易的相关开销.图 1中, “Execution cost”是存储全局变量和方法调用运行时间的所有开销, “Transaction cost”是由编译合约的开销加上“Execution cost”的开销得到的.如果合约部署失败会提示相应的错误.
2. Commits函数:两个投票人提交保证金、奖金和选票和哈希值.注意到, 选票是在选票生成阶段得到的, 采用的是哈希函数, 投票人voter1的选票是:
● “0x8d17b2536d3905e4b709f53152aaa15327030c1cc96e6828c41c63f558aba405”;
● “0xb7eecb2394b8fd348adecb8bffd0f75e45e5054a3386f36b2da11ca733bfe517”.
投票人voter1使用在选票生成阶段获得的voter2的选票, 计算包括双方选票的哈希值:
“0x5976d7670c2bc6cdabaa57021cce5758d85b5e6036206500e27ab65c4a6cd708”.
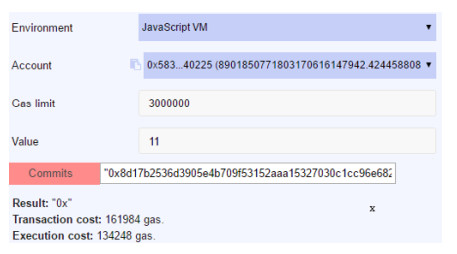
之后, voter1在browser-solidity开发环境中触发Commits函数, 输入上述选票和哈希值, 设置运行环境、账户、交易金额等信息, 然后执行该函数.图 2给出了该函数执行的参数和结果信息, 其中, “Environment”指明运行环境是JavaScript VM, 为本地虚拟调试模式; “Account”即voter1的账户地址信息; “Gas limit”指明交易费的上限; “Value”即交易金额, 包括保证金和奖金.该函数成功执行后, 会返回默认结果“0X”; 同时, 开发环境显示此次函数执行的相关开销.
|
Fig. 2 Parameters and results of the Commits function executed by the voter1 图 2 voter1执行Commits函数的参数及结果 |
投票人voter2类似地把自己的选票、哈希值、保证金、奖金通过交易发布到以太坊中, 其中, voter2的选票是:
● “0x0c7c173185d95a8187b90977b78f7dd9724c64d64dad4fe82f8f479b65a61376”;
● “0x6e0b3b51af1129b42809b2c993c6d3d6a8a38da95e5ef95c24ea3654662d2dc1”.
其计算的哈希值包括选票生成阶段获得的voter1的选票信息:
“0x5976d7670c2bc6cdabaa57021cce5758d85b5e6036206500e27ab65c4a6cd708”.
如我们所期望的, 两个选票人的哈希值应当是一致的.
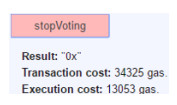
3. stopVoting函数:投票人可以随时触发该函数, 但是根据该函数的实现逻辑, 只有某些投票人不在30个区块时间内提交选票时, 已提交过选票的投票人触发该函数才是有意义的.这些提交过选票的投票人可以通过该函数要回自己的保证金和奖金.此时该轮投票已经失败, 需要合约创建者重新触发Ballot函数, 才能发起一轮新的投票.图 3是在voter1投票完成、voter2没有投票时, 由voter1触发的函数执行结果, 执行成功返回的是默认结果“0X”.
|
Fig. 3 A voter gets back their deposits and rewards, and stops the voting 图 3 投票人取回保证金和奖金并结束投票 |
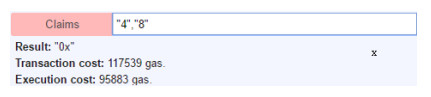
4. Claims函数:投票人提交选票对应的承诺值, 取回保证金.在本测试例中, 选票生成阶段voter1的真实投票是(“1”, “1”), 即对两个候选人投投了赞成票.选票生成阶段, voter1用于混淆真实投票的随机数是(“3”, “7”), 所以voter1选票对应的承诺值是(“4”, “8”).
在browser-solidity开发环境中, voter1提交(“4”, “8”), 取回保证金, 如图 4所示.
|
Fig. 4 voter1 submits the commitment value of their ballot and gets back their deposit 图 4 voter1提交选票的承诺值, 取回保证金 |
类似地, voter2的真实投票是(“0”, “1”), 对应的随机数为(“-3”, “-7”), 承诺值是(“-3”, “-6”).在browser-solidity开发环境中, voter2提交(“-3”, “-6”), 取回保证金.
5. winningProposal函数和Prize函数:在所有投票人提交承诺值之后, 任何实体都可以调用winningProposal函数查看获胜者.图 5展示了触发winningProposal后得到的返回结果.可以看到, 返回的结果是2, 表明获胜者是proposalB.

|
Fig. 5 Trigger the winningProposal function and get the returned value 图 5 触发winningProposal函数获得返回值 |
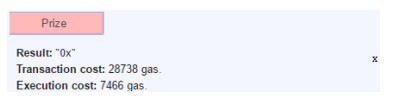
此时, 获胜者proposalB可以触发Prize函数, 获得奖金, 图 6展示了该函数的执行结果.
|
Fig. 6 Execution status after a winner triggers the Prize function 图 6 获胜者触发Prize函数后的执行情况 |
6. proposalClaim函数:如果有投票人在第1个投票人公布承诺值之后的20个区块时间内不公布自己的承诺值, 其保证金作为罚金由候选人平分.在测试例中, voter1提交了承诺值, voter2没有提交承诺值, 此时, 任意候选人都可以调用该函数, 由候选人平分保证金.该函数会返回“Vote Fail Fine”提示, 如图 7所示.
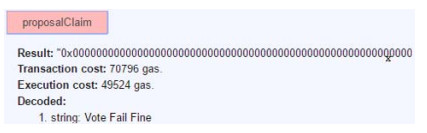
|
Fig. 7 Execution status of sharing deposits after a candidate triggers the proposalClaim function 图 7 候选人触发proposalClaim函数平分保证金的执行情况 |
上述智能合约的测试表明:在两个投票人、两个候选人、一个合约创建者的情况下, 可以通过智能合约完成电子投票.当投票人和候选人的数量增加后, 可以通过适应性的修改代码, 完成投票.在本测试例中, proposalB得到了2票, 因为只有两个投票人, 可以无异议地推断出每个投票人对于proposalB的真实投票, 这种信息泄露自然是允许的.对于proposalA, 通过查询可以知道其获得的投票是1票, 那么通过“4”和“-3”无法推断出这一票到底是谁投的, 投票人具有隐私性.
4 投票阶段智能合约的逻辑验证 4.1 投票阶段智能合约的模型我们采用了模型检验工具来验证投票阶段智能合约的内在逻辑, 主要验证了步骤2~步骤6以太币流通的内在逻辑, 包括:
(1) 投票人根据步骤2的合约内容提交保证金和资助金, 如果在规定时间内有的投票人没有提交保证金和资助金, 则步骤3的合约内容能够顺利执行, 即已经提交以太币的投票人能够顺利地取回自己的保证金和资助金.
(2) 投票人根据步骤4的合约内容提交选票后, 可以顺利取回保证金.
(3) 候选人根据步骤5的合约内容, 获胜者可以顺利领到奖金.
(4) 候选人根据步骤6的合约内容, 如果在规定时间内有的投票人没有取回保证金, 则能够平分没有取回的保证金.
由于上述验证的智能合约只涉及以太币的流通情况, 我们把原智能合约中步骤2提交选票和步骤4提交选票承诺值的过程简化为在步骤4直接提交真实选票.这当然意味着我们的验证逻辑不涉及隐私性的验证.但是这样简化之后, 对以太币的流通情况并没有任何的修改, 所以验证的结果对于原智能合约的以太币流通情况是有效的.事实上, 通过逻辑验证, 我们确认了Zhao等人的比特币投票协议[4]并没有完备地考虑比特币的流通.例如, 当诚实的投票人公开承诺值, 取回保证金之后, 如果有不诚实的投票人没有公开承诺值, 则所有投票人的资助金不能被候选人领取, 也不能退还投票人.这形成了事实上的资助金“黑洞”.由于矿工可以把交易的输入输出差额作为自己的收入, 这在事实上鼓励了矿工不诚实的执行协议, 以形成资助金黑洞, 获得比特币.本文使用了Spin模型, 给出1个时间进程、5个投票人进程和2个候选人进程来验证以太币的流通情况.
1.时间进程
时间进程用于模拟智能合约中投票人和候选人在不同的时间段内执行不同操作的行为.我们根据进程的执行时间, 保守地选取了2s作为一个时间段.具体来说, 投票人需要在程序开始执行后2s以内完成保证金和奖金的提交, 2s~4s内完成选票的提交, 超过4s停止计时.注意到, 在智能合约的实现上, Commits、Claims、proposalClaim等函数都有计时器的功能, 与该时间进程对应.使用Promela描述, 时间进程核心代码如下.
do
::time < =4- >
time=time+1;
:: else- > break;
od
2.投票人进程
投票人进程是投票人允许的所有操作.根据时间进程的不同, 投票人在0~2s、2s~4s这样两个时间段可以执行3个不同的原子操作.原子操作在Spin中用关键字atomic标识, 标识范围内的代码执行时不可分割.我们设置了5个投票人, 每个投票人用其进程号减去1的值(pid-1)来标识, 可以看作不同投票人的编号.对每一个投票人, 我们设置了usrmoney来表示该投票人的账户余额, 初始化每个账户为11, 设置了Contractmoney代表智能合约的余额.注意, 在在智能合约中, 投票人的对手方是智能合约.与投票协议相关的变量包括rights、voted和votersNum, 其中, rights表示用户有一次的投票权, voted表示投票者是否提交了保证金和资助金到智能合约, 而votersNum则统计了提交保证金和资助金到智能合约的人数, 分别与智能合约的状态变量一一对应.
在0~2s, 投票人的原子操作如下所示, 对应实现了智能合约步骤2的资金流向和投票状态的改变.
::(timer < =2 & & rights[_pid-1]==1 & & userMoney[_pid-1] > =11)- > atomic{
contractmoney=contractmoney+11;
userMoney[_pid-1]=userMoney[_pid-1]-11;
rights[_pid-1]=0;
voted[_pid-1]=1;
votersNum=votersNum+1;
}
在2s后, 投票人的原子操作分两种情况:一种是Commits顺利执行的情况, 对应Claims函数; 一种是Commits阶段有投票人没有参与的情况, 对应stopVoting函数.这两种情况涵盖了智能合约步骤3和步骤4的资金流向和投票状态的改变.
在有投票人没有参与Commits函数时, votersNum小于投票人的总数, 执行下面的操作, 实现了stopVoting相同功能.
::(timer > 2 & & votersNum < 5 & & voted[_pid-1]==1)- > atomic{
contractmoney=contractmoney-11;
userMoney[_pid-1]=userMoney[_pid-1]+11;
voted[_pid-1]==0;
}
同样在2s~4s, 当所有投票人都参与了Commits函数时, 投票人可以执行Claims函数.该函数对应的操作如下.
::(timer > 2 & & timer < =4 & & votersNum==5 & & claimed[_pid-1]==0)- > atomic{
if
::voteId=0;
::voteId=1;
fi
count[voteId]=count[voteId]+1;
contractmoney=contractmoney-10;
userMoney[_pid-1]=userMoney[_pid-1]+10;
claimed[_pid-1]=1;
backNum=backNum+1;
break;
}
其中, voteId代表随机选择的候选人, count[voteId]用来统计候选人的投票总数, 这两个状态量表示了简化的投票过程; claimed标记是否已参与Commits函数, 用backNum统计取回保证金的人数, 与Claims函数的backNum对应.
3.候选人进程
候选人进程对应候选人可以运行的所有操作.从时间进程上看, 候选人的操作时间有两个起点:一个是2s~ 4s内投票人完成投票后, 候选人可以开始确认胜利者和获得奖金; 一个是4s后依旧有投票人没有投票, 候选人从4s开始可以平分投票人的保证金.第1种情况使用backNum这个记录返回保证金的状态量来标识, 投票人在2s~4s内完成投票取回保证金, 那么这个状态量是5;第2种情况使用了时间和backNum状态量以及votersNum状态量来标识, 其中, votersNum表示Commits阶段成功执行了, 是候选人平分保证金的前提条件.
投票人完成投票时, 候选人的操作如下所示, 对应winningProposal函数和Prize函数.
::backNum==5- > atomic{
contractmoney=contractmoney-5;
if
::(count[0] > count[1])- >
moneyA=moneyA+5;
:: else- >
moneyB=moneyB+5;
fi
break;
}
其中, count是在投票操作时记录的投票.在测试例中, 每个投票人要么选0要么选1, 不存在平票的情况.奖金的流向也是要么给候选人A的账户moneyA, 要么给候选人B的账户moneyB.
如果投票人完成了承诺却没有完成投票, 时间也大于4s了, 候选人就可以平分投票人的保证金.对应proposalClaim函数, 其中, getDepositA和getDepositB表明候选人取得了保证金.
::(votersNum==5 & & timer > 4)- > atomic{
if
::backNum < 5
for (i:0, ..., 4){
contractmoney=contractmoney-1;
userMoney[i]=userMoney[i]+1;
if
::claimed[i]==0
contractmoney=contractmoney-10;
moneyA=moneyA+5;
moneyB=moneyB+5;
:: else- > skip;
fi
}
getDepositA=true;
getDepositB=true;
break;
:: else- > break;
fi
}
4.逻辑验证
前面我们定义了投票人、候选人、时间进程, 这些进程运行之后模拟智能合约投票阶段的运行, 运行的结果可以反映资金的可能流向.我们使用LTL描述期望的运行结果, 如果实际的运行结果与期望的运行结果相同, 则表明资金的流向满足我们的期望; 否则, 表明资金流向存在问题.鉴于投票人进程运行的代码是完全一致的, 我们在验证资金流向时, 仅选取了一个下标为0的投票人, 即第1个投票人的进程.
我们期望验证的4个资金流向逻辑描述如下.
● ltl backMoney{[·]((votersNum < 5 & & voted[0]==1)- > < > (userMoney[0]==11))}
该逻辑定义为backMoney.投票人根据步骤2的合约内容提交保证金和资助金.如果在规定时间内有的投票人没有提交保证金和资助金, 根据投票人的定义, 即votersNum < 5.此时, 已经提交保证金和资助金的投票人根据投票人的定义, voted[0]为1.那么, 这样的投票人应该可以取回保证金和资助金, 即可以期望userMoney[0]为11.
● ltl IfrightsThenbackDeposit{[·](claimed[0]==1- > < > (userMoney[0]==10))}
该逻辑定义为IfVotedThenbackDeposit.根据投票人的定义, 如果投票人完成了投票, 那么claimed[0]应该为1.此时, 投票人应该同时取回了保证金, 所以期望账户余额userMoney应该是10.对应智能合约的Claims函数的资金流向.
● ltl IfSuccessThenOneGetPrize{[·](backNum==5- > < > (moneyA==5 & & moneyB==5))}
该逻辑定义为IfSuccessThenOneGetPrize.根据候选人的定义, 如果backNum==5即投票成功了.此时, 可以期望候选人获得了奖金, 则此时获胜者账户余额应该为5.
● ltl IfFaildThenGetDeposit{[·]((votersNum==5 & & backNum < 5)- > < > (getDepositA==1 & & getDepositB== 1))}
该逻辑定义为IfFaildThenGetDeposit.根据候选人的定义, 若所有投票人交了保证金和资助金(votersNum== 5), 但是有投票人没有取回保证金(backNum < 5), 那么可以期望候选人A和B平分投票人没有取回的保证金, 即getDepositA和getDepositB都是1.
5.逻辑验证结果
我们把第3节的各种进程的定义和第4节的逻辑验证形成了4个ballotContract.pml文件, 每个文件中包含完整的进程定义和1个单独的逻辑验证条件.对于每一个逻辑验证条件, 在Windows平台的命令行界面下运行6.4.3版本的Spin程序, 执行spin -a ballotContract.pml, 生成c语言的模型检测程序pan.c, 并在命令行中显示该代码所检测的逻辑验证条件.然后执行gcc -o pan pan.c命令编译, 生成可执行程序pan.该pan程序运行时间进程、投票人进程、候选人进程, 尝试所有可能的状态, 以判断投票人进程和候选人进程能否满足其逻辑验证条件.
如图 8所示, 4个逻辑验证条件的运行结果是类似的, 只有相关状态和运行序列的不同, 而遍历的状态总数是确定的, 结论也是相同的, 即满足逻辑验证条件(errors=0).
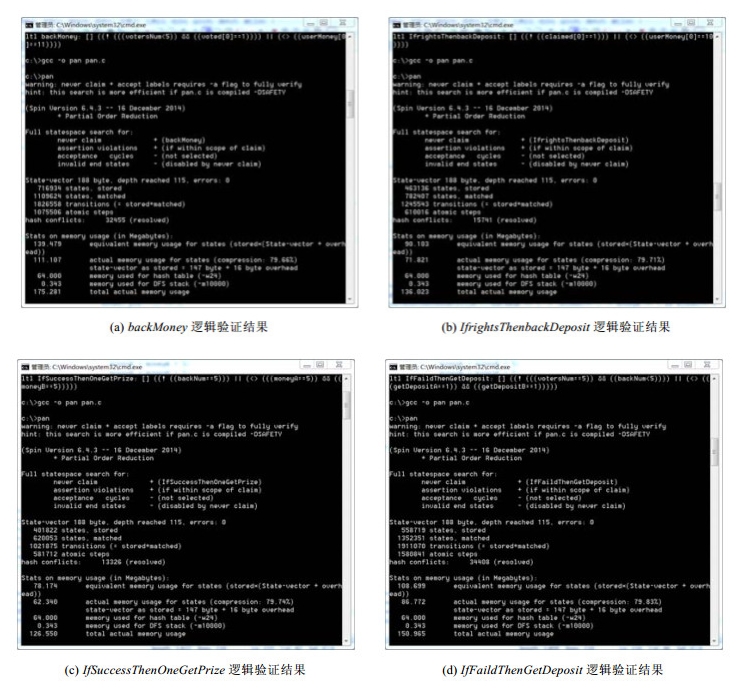
|
Fig. 8 Logic verification result of the smart contracts 图 8 智能合约逻辑验证结果 |
5 结论
本文给出了一个保持隐私的以太币投票协议, 特别是其投票阶段的智能合约.我们给出了在以太坊中智能合约的详细实现过程, 并给出了测试结果.进一步地, 我们对智能合约和实现的代码进行了逻辑验证, 确保智能合约的资金流向是符合预期的.我们同时指出了Zhao等人给出的比特币投票协议因为缺乏逻辑验证的过程, 存在资金流向黑洞的问题.
| [1] |
Tian HB, He JJ, Fu LQ. A privacy preserving fair contract signing protocol based on block chains. Journal of Cryptography, 2017, 4(2): 187-198(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/mmxb201702009 |
| [2] |
Wood DG. Ethereum: A secure decentralised generalised transaction ledger homestead. 2014. http://gavwood.com/paper.pdf
|
| [3] |
EtherCasts. A curated collection of decentralized apps. 2017. http://dapps.ethercasts.com
|
| [4] |
Zhao Z, Chan TH. How to vote privately using bitcoin. In: Qing S, Okamoto E, Kim K, Liu D, eds. Proc. of the 17th Int'l Conf. on Information and Communications Security (ICICS 2015). Beijing: Springer Int'l Publishing, 2015.
|
| [5] |
Sasson EB, Chiesa A, Garman C, Green M, Miers I, Tromer E, Virza M. Zerocash:Decentralized anonymous payments from bitcoin. In:Proc. of the 2014 IEEE Symp. on Security and Privacy. IEEE, 2014, 459-474.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0235299446/ |
| [6] |
Barber S, Boyen X, Shi E, Uzun E. Bitter to better-How to make Bitcoin a better currency. In: Keromytis AD, ed. Proc. of the 16th Int'l Conf. on Financial Cryptography and Data Security (FC 2012). Berlin, Heidelberg: Springer-Verlag, 2012.399-414. https://link.springer.com/chapter/10.1007%2F978-3-642-32946-3_29
|
| [7] |
Andrychowicz M, Dziembowski S, Malinowski D, Mazurek L. Fair two-party computations via Bitcoin deposits. In: Böhme R, Brenner M, Moore T, Smith M, eds. Proc. of the Workshops on Financial Cryptography and Data Security (FC 2014), BITCOIN and WAHC 2014. LNCS 8438, Berlin, Heidelberg: Springer-Verlag, 2014.105-121. https://link.springer.com/chapter/10.1007%2F978-3-662-44774-1_8
|
| [8] |
Kulyk O, Volkamer M. Efficiency comparison of various approaches in E-voting protocols. In: Clark J, et al. eds. Proc. of the FC 2016 Workshops. LNCS 9604, Berlin, Heidelberg: Springer-Verlag, 2016.209-223. https://link.springer.com/chapter/10.1007%2F978-3-662-53357-4_14
|
| [9] |
Shahandashti SF, Hao F. DRE-ip: A verifiable E-voting scheme without tallying authorities. In: Proc. of the ESORICS. LNCS 9879, Springer-Verlag, 2016.223-240. https://link.springer.com/chapter/10.1007/978-3-319-45741-3_12
|
| [10] |
Sasson EB, Chiesa A, Garman C, Green M, Miers I, Tromer E, Virza M. Zerocash: Decentralized anonymous payments from bitcoin. In: Proc. of the 2014 IEEE Symp. on Security and Privacy. IEEE, 2014.459-474. https://www.researchgate.net/publication/286668243_Zerocash_Decentralized_Anonymous_Payments_from_Bitcoin
|
| [11] |
Bentov I, Kumaresan R. How to Use Bitcoin to Design Fair Protocols. Berlin, Heidelberg: Springer-Verlag, 2014: 421-439.
|
| [12] |
Kiayias A, Zhou HS, Zikas V. Fair and robust multi-party computation using a global transaction ledger. In: Fischlin M, Coron JS, eds. Proc. of the Advances in Cryptology 35th Annual Int'l Conf. on the Theory and Applications of Cryptographic Techniques (EUROCRYPT 2016). Berlin, Heidelberg: Springer-Verlag, 2016.705-734.
|
| [13] |
Andrychowicz M, Dziembowski S, Malinowski D, Mazurek L. Secure multiparty computationson Bitcoin. In: Proc. of the 2014 IEEE Symp. on Security and Privacy. IEEE, 2014.443-458.
|
| [14] |
Decker C, Wattenhofer R. Bitcoin Transaction Malleability and MtGox. Cham: Springer Int'l Publishing, 2014: 313-326.
|
| [15] |
Buterin V. Ethereum: A next-generation smart contract and decentralized application platform. 2014. https://github.com/ethereum/wiki/wiki/%5BEnglish%5D-White-Paper
|
| [16] |
Lin HM, Zhang WH. Model checking:Theories, techniques and applications. Acta Electronica Sinica, 2002, 30(12A): 1907-1912(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/dianzixb2002z1002 |
| [17] |
Hu K, Bai XM, Gao LH, Dong AQ. Formal verification method of smart contract. Ruan Jian Xue Bao/Journal of Software, 2008, 19(7): 1565-1580(in Chinese with English abstract). http://www.jos.org.cn/1000-9825/19/1565.htm[doi:10.3724/SP.J.1001.2008.01565]
|
| [18] |
Barnat J, Brim L, Stříbrná J. Distributed LTL model-checking in SPIN. In: Dwyer M, ed. Proc. of the SPIN 2001. LNCS 2057, Heidelberg: Springer-Verlag, 2001.200-216. https://www.researchgate.net/publication/221105729_Distributed_LTL_model-checking_in_SPIN
|
| [19] |
Liu J. Research and design of electronic voting protocol based on Internet[Ph.D. Thesis]. Fuzhou: Guangxi University, 2001(in Chinese with English abstract).
|
| [20] |
He ZH, Ceng QK. Research on LTL attribute decomposition method based on SPIN. Computer Applications and Software, 2014, 31(7): 43-46(in Chinese with English abstract).
[doi:10.3969/j.issn.1000-386x.2014.07.012] |
| [21] |
Luu L, Chu DH, Olickel H, Saxena P, Hobor A. Making smart contracts smarter. In: Proc. of the 2016 ACM CCS. ACM, 2016.254-269.
|
| [22] |
McCorry SSP, Hao F. A smart contract for boardroom voting with maximum voter privacy. In: Kiayias A, ed. Proc. of the Financial Cryptography and Data Security 2017. LNCS 10322, Springer-Verlag, 2017.357-375. https://link.springer.com/chapter/10.1007%2F978-3-319-70972-7_20
|
| [23] |
Tarasov P, Tewari H. Internet voting using zcash. 2017. https://eprint.iacr.org/2017/585
|
| [24] | |
| [1] |
田海博, 何杰杰, 付利青. 基于公开区块链的隐私保护公平合同签署协议. 密码学报, 2017, 4(2): 187-198.
http://d.old.wanfangdata.com.cn/Periodical/mmxb201702009 |
| [16] |
林惠民, 张文辉. 模型检测理论、方法与应用. 电子学报, 2002, 30(12A): 1907-1912.
http://d.old.wanfangdata.com.cn/Periodical/dianzixb2002z1002 |
| [17] |
胡凯, 白晓敏, 高灵超, 董爱强.智能合约的形式化验证方法.软件学报, 2008, 19(7): 1565-1580. http://www.jos.org.cn/1000-9825/19/1565.htm[doi:10.3724/SP.J.1001.2008.01565]
|
| [19] |
刘峻.基于Internet的电子投票协议的研究与设计[博士学位论文].福州: 广西大学, 2001.
|
| [20] |
贺志宏, 曾庆凯. 基于SPIN的LTL属性分解方法研究. 计算机应用与软件, 2014, 31(7): 43-46.
[doi:10.3969/j.issn.1000-386x.2014.07.012] |
 2019, Vol. 30
2019, Vol. 30


