2. 武汉大学 信息管理学院, 湖北 武汉 430072;
3. 武汉大学 深圳研究院, 广东 深圳 518000
2. School of Information Management, Wuhan University, Wuhan 430072, China;
3. Shenzhen Research Institute of Wuhan University, Shenzhen 518000, China
近年来出现的许多网络, 如社会网络[1]、语义网络[2]、通信网络以及生物网络[3], 大部分都可以自然地建模成图数据库(graph databases).图数据库越来越广泛地成为一种建模和查询图数据的重要工具.在各种图操作中, 子图匹配(subgraph match), 亦称子图查询(subgraph query)[2-6]是最基本的操作:给定一个由实际网络建模成的图数据库G(称为数据图)和用户指定的查询图Q, 找出G中所有精确匹配Q的子图, 这些子图不仅结构与Q相同, 且对应节点的标签也完全相同[3].然而在实际的图数据库中, 每个节点可能包含很多表示该节点特征的元素.在查询时, 一方面, 用户可能只关心部分节点元素是否匹配, 而对其他元素是否匹配并不关心, 即, 用户对不同元素的关心程度不同; 另一方面, 用户可能无法知道图数据库中节点的所有元素, 因此难以给出精确匹配的条件, 导致精确图匹配无法进行.
基于上述观察, 本文提出子图匹配的一个变种——基于动态权重包含度[7]的子图匹配(subgraph match with inclusion degree, 简称SMID).在SMID查询中, 每个图节点拥有一个元素集合, 而不是一个标签, 且每个元素对应一个动态权重, 元素的权重由用户在查询时指定.具体而言, 给定拥有n个节点{u1, u2, …, un}的查询图Q, SMID查询能够找出图数据库G中所有包含n个节点{v1, v2, …, vn}的子图X, 满足:(1) S(ui)和S(vj)的加权包含度大于用户指定的阈值, 其中, ui与vj对应, S(ui)与S(vj)分别表示ui与vj的元素集合, i, j∈{1, 2, 3, …, n}; (2) X与Q结构上同构.
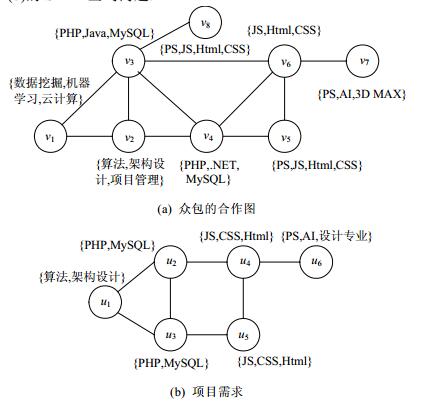
例1:众包(crowdsourcing).
众包是互联网带来的新的生产组织形式, 企业利用互联网分配工作、发现创意或解决技术问题.图 1(a)是某众包社区中用户的合作关系图, 其中:每个节点代表一个用户, 节点旁的集合表示用户的技能, 节点之间的连线表示用户的合作关系.设想某企业拟从中选择5位用户为其开发项目, 其要求如图 1(b)所示.于是, 该问题便转换成了在图 1(a)中完成图 1(b)的SMID查询问题.
|
Fig. 1 An example of crowdsourcing 图 1 众包的例子 |
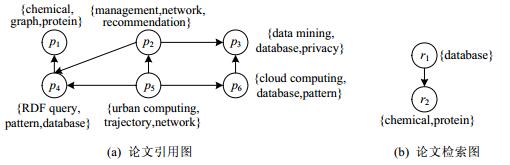
例2:论文检索[8].
图 2(a)表示部分论文的引用图, 其中, 每个节点表示一篇论文, 节点旁的单词表示该论文的关键字集合, 边表示论文之间的引用关系.例如, 论文p4引用了论文p1.如果需要找到引用了“生物蛋白质”论文的“数据库”论文, 那么该检索就转化成了图 2(b)在图 2(a)上的SMID查询.
|
Fig. 2 An example of paper search 图 2 论文检索的例子 |
实际上, 若将图 1(a)的节点看成社交网络的用户, 节点旁的集合表示对应用户的兴趣集合, 边表示用户之间的好友关系, 那么社区发现[9]也可以转化为SMID查询问题.可见, SMID在很多应用中都非常有用.然而, 目前关于结构同构和节点元素包含度子图匹配问题的研究并不多.由于对子图匹配定义不同, 此前精确子图匹配或模糊子图匹配的相关技术[2-5, 10, 11]不能直接用于SMID.
有两种直接修改现有算法的方法来解答SMID问题.
● 第1种方法首先利用现有子图同构算法[10, 12]找出查询图的所有同构子图, 然后验证对应节点的包含度, 过滤掉那些不满足条件的同构子图;
● 第2种方法顺序相反:首先找出每个查询图节点的候选节点, 这些候选节点满足包含度限制; 然后, 从这些候选节点验证结构是否同构.
然而, 这两种方法通常会产生很高的查询代价, 对大图数据库而言更是如此.因为在第1步的过程中, 第1种方法忽略了包含度的限制, 而第2种方法没有考虑到图结构信息.
由于现有方法在效率上存在问题, 本文提出一种更为高效的SMID方法:首先为图数据库节点签名, 并将节点签名组织成动态签名树(dynamic signature tree, 简称DS-Tree), 在查询过程中同时考虑了查询图的拓扑结构和图节点加权包含度的限制, 减少了搜索空间.此外, 本文还提出了支配子图(dominating subgraph)查询算法, 进一步加快SMID.
本文主要贡献总结如下:
(1) 提出了一种新的子图查询问题SMID.与传统子图查询不同的是, SMID要求图结构同构, 且对应节点的加权包含度大于用户给定阈值.这种问题在现实生活中非常普遍;
(2) 设计了一种利用DS-Tree进行SMID查询的策略, DS-Tree是一种动态平衡签名树.首先, 分别针对数据图和查询图设计了两种签名机制, 并将数据图节点签名组织成DS-Tree.注意, 这两种签名均包含了节点元素信息和图结构信息.然后, 利用DS-Tree找出每个查询图节点的候选节点集合.最后, 根据候选节点集合确定同构子图;
(3) 为减少DS-Tree占用的内存空间, 设计了一种DS-Tree的压缩方法, 在对查询效率影响不大的情况下, 减少了内存空间占用;
(4) 为进一步提高SMID的查询效率, 提出了支配子图查询算法.首先找到查询图的最小支配子图, 然后利用签名树找到支配子图每个节点(称为查询图的支配节点)的候选节点集合.根据距离保留定理, 利用支配节点的候选节点找到非支配节点的候选节点集合, 最后确定查询图的同构子图;
(5) 通过人工数据和真实数据的实验结果表明, 本文提出的SMID查询方法具有较好的效率和扩展性.
1 预备知识本节首先总结子图匹配的相关工作, 然后形式化定义SMID查询, 最后给出SMID查询的基本算法框架.
1.1 相关工作子图匹配问题可以大致分为两类:精确子图匹配和模糊子图匹配.
精确子图匹配要求所有的节点和边都完全匹配.Ullmann提出的子图同构算法[12]和VF2算法[10]没有利用任何索引结构, 因此对于大图数据库来说代价通常很高.Zou等人[2]提出了一种新的签名索引和过滤规则来解决语义子图查询问题.Zhao等人[4]研究的SPath算法利用节点周围的最短路径作为索引单元.Shang等人[13]提出的QuickSI算法主要解决子图同构的检查, 它基于图的一些静态信息确定搜索顺序, 从而减少了搜索空间.近年来, Han等人[14]提出的Turboiso算法在效率和扩展性两个方面都优于之前子图同构算法.Ma等人[15]结合传统的关系型数据库技术设计了一种高效图查询引擎, 能够处理精确子图匹配问题.然而, 现有精确子图匹配没有考虑节点元素的相似性, 在候选节点很多的情况下, 查找同构子图的代价很高.
模糊子图匹配允许一些节点或边不匹配, Closure-Tree[16]是第一个同时支持精确子图匹配和模糊子图匹配的图索引.TALE[3]模糊查询算法是一种基于索引技术的算法, 它允许某些节点不匹配和某些边缺失.SAPPER[5]算法提出了一种基于混合网络单元的新型索引结构来解决模糊子图查询, 它允许一些边缺失.文献[17]提出了复杂生物分子网络中基于半Markov随机游走的迭代加权子图查询算法, 综合考虑了节点相似性及结构相似性, 但其主要目标是提高生物分子的匹配准确率, 并未建立有效的索引机制.Ye等人[18]在集群上实现了网页图结构的近似子图匹配.本文要研究的问题与这些模糊子图查询问题不同, 并不允许任何边和节点缺失, 但只要求对应匹配节点元素集合的加权包含度大于一给定值.
社交网络中的组队问题[19, 20]与SMID查询问题也不同.
● 首先, 组队问题不需要指定查询图的结构, 只需给出技能集合; 而SMID需要用户给定查询图的结构以及每个查询节点的元素集合;
● 其次, 二者的匹配条件不同:组队问题要求在社交网络中找出满足给定条件(如包含所有技能、地理位置相近、任务分配均匀等)的节点, 而SMID查询需要从数据库中找到所有与查询图结构同构, 并且对应节点的包含度大于给定阈值的所有子图;
● 最后, 组队问题不考虑边的连接条件, 也不要求查询结果中的节点连接; 而SMID查询要求查询结果与给定查询图同构.
近年来, 研究人员提出了一些新的近似子图查询问题.NeMa[21]集中于满足下列两个条件的子图查询问题:(1)多对一的子图匹配; (2)节点的元素相似.S4系统[1]能够找出那些与查询图结构完全相同并且语义相似的子图.与它们不同的是, SMID考虑的是一对一的结构同构, 并且节点元素加权包含度满足一定限制.Zou[22]提出了top-k子图匹配问题, 这种方法考虑了两个匹配实体间的相似性, 但它假定节点间的相似性已经给定, 也没有利用集合相似的过滤技术来优化匹配性能.Peng等人[23]提出了一个查询RDF图的分布式处理框架.文献[24, 25]分别提出了两种基于图编辑距离的RDF近似查询问题.Lian[26]针对RDF图可能不一致提出了一种基于概率的近似匹配问题, 但是RDF图节点通常只有一个标签, 这与SMID查询不同.Liang等人[27]提出的SMS2查询问题首次考虑了图节点拥有多个元素, 它要求图结构同构, 并且对应节点元素的集合相似度大于给定阈值.然而, 集合相似度不能较好地对很多现实问题进行建模, 例如, 用户通常不知道图数据库节点的所有元素, 因此无法完整给出SMS2的查询条件.本文提出的SMID查询, 只需要用户给出关心的部分元素及其权重即可.
1.2 问题定义一个网络可以建模成图G=〈V(G), E(G)〉, 称为数据图, 其中, V(G)表示顶点集合, E(G)⊆V(G)×V(G)是边集合, 每个顶点v∈V(G)拥有一些元素, 记为S(v), 所有节点的元素全集记为Σ(G).
类似地, 查询图也可以表示成Q=〈V(Q), E(Q)〉.本文讨论无向简单图中的SMID查询, 不失一般性, 我们的算法能够扩展到有向简单图中.
包含度(inclusion degree)是模糊集理论中的概念, 是一种描述不确定性关系的有效度量方法[7], 其定义为:
定义1(包含度). 设(L, ≤)为偏序集.若对于任意x, y∈L, 有数字ID(y/x)与之对应, 且满足:
(1) 0≤ID(y/x)≤1;
(2) 若x≤y, ID(y/x)=1;
(3) 若x≤y≤z, ID(x/z)≤ID(x/y);
(4) 若x≤y, 对于任意的z∈L, 有ID(x/z)≤ID(y/z).
则ID称为偏序集(L, ≤)上的包含度.
定义2(集合包含度(set inclusion degree)). 对于集合X和Y, X为非空集合, SID(Y/X)定义为
| $SID(Y/X) = \frac{{|Y \cap X|}}{{|X|}}$ | (1) |
其中, |*|表示集合内的元素个数, ∩表示集合交运算.
容易验证, SID满足:
(1) 0≤SID(Y/X)≤1;
(2) 若X⊆Y, SID(Y/X)=1;
(3) 若X⊆Y⊆Z, SID(X/Z)≤SID(X/Y);
(4) 若X⊆Y, 对于任意的非空集合Z, 有SID(X/Z)≤SID(Y/Z).
称SID为集合包含度.
定义3(动态加权集合包含度(dynamic weighted set inclusion degree)). 对于集合X和Y, a是X或Y内的元素, W(a)表示元素a的权重, 由用户在每次查询前指定, 其中, 0≤W(a)≤1.
WID(Y/X)定义为
| $WID(Y/X)\frac{{\sum\nolimits_{a \in Y \cap X} {W(a)} }}{{\sum\nolimits_{a \in X} {W(a)} }}$ | (2) |
称WID为动态加权集合包含度.为简单起见, 若无特殊说明, 下文中的包含度均指动态加权集合包含度.
定义4(基于包含度的子图匹配(subgraph match with inclusion degree, 简称SMID)). 给定数据图G, V(G)= {v1, …, vm}, 查询图Q, V(Q)={u1, …, un}, 用户指定的各元素权重以及包含度阈值τ, 当且仅当满足下面3个条件, 我们说Q与G的子图X, V(X)={v1, …, vn}基于包含度的子图匹配:
(1) 存在双射函数f, 对每个ui∈V(Q)和vj∈V(X), 均有f(ui)=vj.其中, 1≤i, j≤n;
(2) WID(S(ui), S(vj))≥τ, 其中, S(ui)和S(vj)分别表示ui和vj的元素集合, WID(S(ui), S(vj))表示S(ui)和S(vj)的加权包含度;
(3) 对于任意边(ui, uk)∈E(Q), 均有(f(ui), f(uk))∈E(X), 其中, 1≤k≤n.
由于SMID与边是否有向无关, 因此, 我们的方法同时适应于有向图和无向图的情况.
本文利用加权包含度作为节点是否匹配的计量方法有以下两个原因.
(1) 包含度能够较好地建模很多实际问题, 例如, 用户往往无法知道数据图中节点特征集合的所有元素, 通常只需要给出用户关心的部分元素;
(2) 给每个元素赋予不同的权重, 真实反映了用户对每个元素关注程度不一样.实际应用中, 由用户指定查询图和每个元素的权重.例1中, 关于设计人员是否为设计专业的要求有时并不重要, 只需要精通PS和AI设计, 因此可以为设计专业元素指定一个较低权重.
1.3 方法概览子图查询问题非常困难, 因为子图同构验证问题是NP完全问题[28].而实际应用中的网络非常巨大, 为保证在短时间内完成子图查询, 需要设计良好的索引技术和查询优化技术来解决子图查询问题.
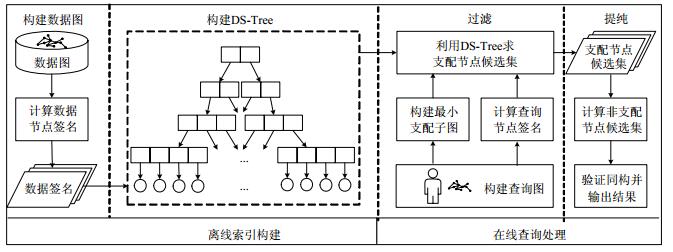
图 3所示的是SMID查询算法的基本框架.SMID查询算法包含离线索引构建过程和在线查询处理过程两部分.
|
Fig. 3 Framework of SMID 图 3 SMID的基本框架 |
● 离线索引构建是为数据图建立索引的过程:首先为数据图节点签名, 该签名同时包含节点元素信息和数据图的结构信息; 然后, 将数据签名组织成动态签名树;
● 在线查询处理过程中, 首先获得查询图节点签名, 同样, 此签名也包含了数据图节点元素和结构信息.为进一步加快查询效率, 本文提出了支配子图查询算法, 选择查询图的最小支配子图; 然后, 利用DS-Tree找出每个支配节点的候选节点集, 再利用距离保留定理找出非支配节点的候选集; 最后找出所有与查询图匹配的图.
SMID查询算法与SMS2算法的不同点在于以下3个方面.首先, 子图匹配的定义不同.SMS2要求对应节点元素的集合相似度大于给定阈值, 而SMID要求它们的动态加权包含度满足一定条件; 其次, 索引结构不同.SMS2在离线处理阶段为数据图创建了倒排模式格(inverted pattern lattice)和签名桶(signature buckets)索引, 而SMID提出了针对动态权重集合包含度特点的DS-Tree索引; 最后, 查询处理过程不同.SMS2采用了多种剪枝技术加快在线查询处理过程, 而SMID使用了支配子图以加快查询.
2 离线索引构建本节详细介绍离线索引构建过程.
● 首先, 针对数据图和查询图分别设计一种签名机制:数据签名和查询签名.这两种签名既保留了数据(查询)节点元素信息, 也保留了数据(查询)图的部分结构信息;
● 然后, 将数据签名组织成DS-Tree, 作为数据图的索引;
● 最后, 还针对索引空间较大的问题探讨了DS-Tree的空间压缩算法.
2.1 数据签名为查询节点u和数据节点v定义了两种不同的签名, 分别称为查询签名Sig(u)(query signature)和数据签名Sig(v)(data signature).利用这两种签名, 我们能快速过滤掉一些不满足条件的数据节点.
定义5(位向量). 数据图G中所有节点的元素并集为Σ(G), Σ(G)中元素按指定顺序排序, 对于某个节点u, 其包含的元素集S(u)对应的位向量BV(u)是一个长度为|Σ(G)|的二进制串, 若元素e∈S(u), 那么e在BV(u)对应的位设为1, 否则为0.
定义6(查询签名). 给定查询图中的节点u, 设u有m个相邻节点ui(i=1, …, m), 则查询节点u的签名Sig(u)= {〈BV(u), BV(u1)〉, …, 〈BV(u), BV(um)〉}, 其中, BV(u)和BV(ui)分别是S(u)和S(ui)元素集合对应的位向量.
例1中, 若指定所有元素的顺序为〈.NET, 3D MAX, AI, CSS, Html, Java, JS, MySQL, PHP, PS, 云计算, 数据挖掘, 机器学习, 架构设计, 算法, 设计专业, 项目管理〉, Sig(u5)={〈00011010 00000000 0, 00011010 00000000 0〉, 〈00011010 00000000 0, 00000001 10000000 0〉}.
定义7(数据签名). 给定数据图中的节点v, 设v有n个相邻节点vi(i=1, …, n), 则数据节点v的签名:
Sig(v)=〈BV(v), ∨i=1nBV(vi) 〉,
其中, BV(v)是S(v)的位向量, ∨是按位或操作, ∨i=1nBV(vi)称为合并位向量(union bit vector), 记为BV∪(v), 其值等于v所有相邻节点的S(vi)的位向量按位或.
由于数据节点非常多, 数据签名中采用相邻节点的合并位向量既能保留部分图结构信息, 又不会让图索引太大.例1中, Sig(v5)={〈00011010 01000000 0, 10011011 10000000 0〉}.而查询图通常不会太大, 因此查询签名保留所有的邻居节点信息, 方便后续的过滤.
文献[2]提出的gStore也为查询图和数据图设计了签名以加快SPARQL查询过程.与之不同的是:
● 首先, 本文处理的是边无标签的图查询, 在编码时不考虑边的标签, 而gStore需要考虑边的标签;
● 其次, 在哈希函数的选择上, 本文使用了位向量, gStore针对边标签和节点值选用了不同的哈希函数;
● 最后, gStore对数据签名和查询签名均采用了类似合并位向量的策略, 而本文为提升过滤效果, 查询签名中保留了所有的邻居节点信息.
定义8(签名面积). 给定一个签名sig, 定义其面积为sig中1的个数, 记为Area(sig).为简单起见, 节点v的签名面积记为Area(v).
定义9(签名增量面积). 签名sigj相对于签名sigi的增量面积由公式(3)给出:
| $ \mathit{\Delta }Area(si{g_i}, si{g_j}) = Area((\neg si{g_i}) \wedge si{g_j}) $ | (3) |
先将sigi按位取反, 然后与sigj对应位做与运算, 得到的结果签名面积.其含义为:sigj对应的集合加入到sigi对应的集合中产生的新集合的签名相对于sigi的增长面积.注意, 签名增量不满足交换律, 即, 一般地:
ΔArea(sigi, sigj)≠ΔArea(sigj, sigi).
2.2 构建DS-Tree为更好地利用签名信息, 我们将数据签名组织成动态签名树.本节介绍如何构建数据图的DS-Tree; 下一节我们将会看到, DS-Tree能够很好地帮助我们完成SMID.
DS-Tree是S-Tree[29-31]的变形.S-Tree是一种形如B+树的动态平衡树.S-Tree中, 每个节点包含若干个形如〈sig, ptr〉的条目.在叶子节点中, sig是一个数据节点的签名, ptr是指向该数据节点的指针.对于非叶子节点, ptr指向该条目对应的子树根节点, sig是对应子树根节点所有条目签名的按位或称为该子树根节点的节点签名.节点node内可允许的最大条目数称为该节点的容量, 记为Cap(node).图 4是例1对应的S-Tree(灰色背景是树节点签名, 白色背景是条目签名), 对于所有的node, Cap(node)=3.

|
Fig. 4 An example of S-Tree 图 4 S-Tree示例 |
图 4中, 灰色背景的签名表示树节点签名, 在实现时不会存储, 可通过父节点的条目获得.
在S-Tree中, 每层的节点容量都相同, 这样会导致一个问题:在构造S-Tree的过程中, 越底层的节点越容易装满, 而高层节点的条目一般比较少.若统一将容量设为较大的值, 一个树节点内将包含很多条目, 这会导致S-Tree的过滤性能低下.若将容量设为较小的值, 在构建过程中, 树节点不断地分裂, 导致构建过程非常慢.这是因为上一层节点的一个条目对应了下一层单个节点的所有条目.因此, 本文提出一种基于S-Tree的动态DS-Tree索引.DS-Tree采用动态容量策略.容量的选定与DS-Tree节点的层数、数据节点数目和数据节点元素的总数有关.直观上看, DS-Tree节点所在的层数越高, 其容量应该越小; 数据节点数目越多或者数据节点元素总数|Σ(G)|越少, 数据节点分配到同一个DS-Tree节点的数目就越多, DS-Tree节点容量应该越大.因此, Cap(node)的计算可采用公式(4):
| $ Cap(node) = \max \left\{ {3, \left\lfloor {s' \times \frac{{|V(G)|/|\mathit{\Sigma }(G)|}}{{{e^{r' \times l}}}}} \right\rfloor } \right\} $ | (4) |
其中, |V(G)|, |Σ(G)|分别表示数据图G节点和元素的个数, l表示DS-Tree节点所在的层数, e为自然对数的底数.我们取叶子节点所在层为第0层.r', s'是正实数, r'表示容量随层数的增加而递减的速度, s'决定每一层容量的大小.取3为下限是防止无限分裂.给定一个数据集, 其节点数目和元素总数固定, 因此, 树节点node的容量仅取决于s', r'和l.故, 公式(4)可以简写成公式(5):
| $ Cap(node) = \max \{ 3, \left\lfloor {s \times {e^{r \times l}}} \right\rfloor \} $ | (5) |
其中, s, r为正实数.
为DS-Tree的不同层节点设置不同的容量, 一方面控制了不同层树节点的分裂时机, 加快了树的构建过程; 另一方面, 也能加快查询过程.高层(靠近根节点)的DS-Tree节点具有更粗粒度的过滤效果, 而低层(靠近叶子节点)具有更细的过滤效果.若高层节点的容量较大, 节点签名面积将更大, 即签名中1的数目将会更多, 过滤效果往往不好; 若低层叶子节点容量设置较小, 会导致DS-Tree的高度过大, 减慢了查询过程.
算法1是DS-Tree的构建算法, 主要包括两个步骤——InsertDSTree和Split.
● InsertDSTree方法为条目e自顶向下选择合适的路径插入到DS-Tree的一个叶节点中;
● Split方法自底向上分裂那些超过最大容量的DS-Tree节点.
稍后我们将看到, DS-Tree过滤效果的好坏与相似数据节点的聚集程度相关.因此, InsertDSTree与Split有一个共同目标:对于同层的DS-Tree节点, 节点内的数据节点尽可能相似, 节点间的数据节点尽可能不同.这取决于算法1中的第11步和第20步.
算法1. DS-Tree Construction.
输入:数据图G;
输出:DS-Tree.
方法:
/*DS-Tree构建的主方法*/
(1) function DSTreeBuild (DataGraph G) {
(2) DSNode root; //DS-Tree的根节点
(3) foreach data vertices v in G {
(4) Entry e=〈Sig(v), v.ID〉; //获得对应的条目
(5) InsertDSTree(root, e); //将条目插入DS-Tree中
(6) }
(7) return root;
(8) }
/*将e插入到DS-Tree中*/
(9) function InsertDSTree (DSNode node, Entry e) {
(10) while (node is not a leaf) {
(11) node=ChooseSubtree(node, e); //选择某个子树
(12) }
(13) Insert e into node;
(14) if (node overflows) { //若超过了最大容量, 则分裂
(15) Split(node);
(16) }
(17) }
/*DS-Tree节点分裂*/
(18) function Split (DSNode node) {
(19) while (node overflows) {
(20) Split node into two nodes; //将node分裂
(21) node=node.parent; //向上传递分裂
(22) }
(23) }
第11步的ChooseSubtree方法选择使节点node内面积增量最小的条目对应的子树.条目增长的面积可以通过公式(3)算出, 将node中每个条目的签名取反后与e的签名按位与运算.也就是说, 对于node内的每一个条目ei, 选出使得ΔArea(ei, e)最小的条目.若存在多个这样的条目, 为使DS-Tree更平衡, 选择对应子树根节点条目最少的条目.
第20步将DS-Tree节点node分裂成两个节点.有多种分裂方法可供选择[29, 30], 根据文献[30]的实验结果, 采用基于层次合并聚类(agglomerative hierarchical clustering, 简称AHC)算法, 将node内的条目聚成两类, 分别放入两个新节点中, 并删除原来的节点node.
具体实现为:最开始, 将node内的每个条目分别视为一个簇, 簇的签名为其内所有条目的签名按位或运算; 然后, 将两个Jaccard相似度最大的簇合并成一个簇.如此反复, 直到剩下两个簇为止.为使分裂后DS-Tree平衡, 当其中一个簇的条目数大于原DS-Node容量的一半时, 直接将其他簇合并成一个簇; 接着, 将剩下的两个簇中的条目放入到两个DS-Tree新节点中, 同时更改相应的父子关系, 最后删除node.由于分裂使父节点的条目数增加了, 因此验证父节点是否溢出:若溢出, 分裂父节点.如此递归下去.
图 1(a)的数据图中, |V(G)|=8, |Σ(G)|=17.假设公式(4)中s'=10, r'=0.45, 那么最底层的DS-Tree节点的容量为4, 第1层的DS-Tree节点的容量为3.最开始, DS-Tree只有一个空节点, 如图 5(a)所示(灰色背景是DS-Node签名, 白色背景是条目签名).逐一插入数据图节点到DS-Tree中, 并更新相应的DS-Tree节点签名.前4个数据节点插入后的状态如图 5(b)所示.

|
Fig. 5 Construction of DS-Tree 图 5 DS-Tree的构建过程 |
继续插入数据节点v5, 此时, 该DS-Tree节点的条目数为5, 超过了最大容量, 将其分裂成两个节点.分裂过程如图 5(c)所示:开始, 每个条目单独形成一个簇, 找到最相似的两个簇C3, C4合并成一个新簇C3, 4; 继续找最相似的两个簇C3, 4, C2合并成C2, 3, 4, 此时, C2, 3, 4中的条目数大于原DS-Tree节点容量的一半, 直接将其他的簇合并成一个簇; 将最后两个簇的条目放入两个新的DS-Tree节点中, 并为两个新的DS-Tree创建一个父节点, 父节点的两个条目分别指向两个新的DS-Tree节点; 最后, 删除原来的DS-Tree节点, 此时, DS-Tree如图 5(d)所示.
当插入v6时, 自顶向下找到一条插入路径.首先找到使图 5(d)根节点中条目签名增量面积最小的条目, 指向左子树的条目增量面积为3, 指向右子树的条目增量面积为5, 选择左子树节点插入v6, 同时更改根节点和左子树节点的节点签名.同样办法插入v7, v8.最后, DS-Tree如图 5(e)所示.注意:除根节点外, 每个DS-Tree节点的签名对应其父节点的一个条目, 因此在实现中只保存根节点的签名.
2.3 DS-Tree压缩存储许多应用中, 数据签名都非常稀疏, 即, 单个数据节点包含的元素很少.也就是说, 元素的种类很多, 单个节点的签名面积非常小.因此, 按位存储签名会浪费很多空间.为解决这个问题, 可以采用一种压缩技术:只记录位向量中为1的位置.例如, 数据图节点v5的压缩签名为Sig(v5)压缩={3, 4, 6, 9, 17, 20, 21, 23, 24, 25}.
另一方面, 可以利用DS-Tree的特点对DS-Tree进行压缩.文献[32]指出:根据DS-Tree的特点, 若父节点中某一位为0, 其对应子树内所有条目签名的该位均为0, 因此, 只需记录父节点的0, 所有子节点条目签名对应位的0均可删除.此外, 利用DS-Tree同一树节点内的签名相似度高的特点, 首先将DS-Tree每个树节点内的条目重新排序, 使得相邻条目签名更接近, 这样, 相邻条目签名异或操作将会得到一个稀疏签名; 然后, 利用上述稀疏签名的压缩方法对DS-Tree进行压缩.
由于在查询过程中, 上述提到的方法均需要解压缩, 因此降低了查询效率.本文提出了一种新的压缩策略.同一个数据集中不同元素的出现次数一般不同, 甚至相差很大.基于上述观察, 区别对待不同频率的元素, 只对低频元素进行压缩, 如图 6所示.首先统计数据集中每个元素的出现次数.然后按出现次数对元素进行降序排列, 对应的节点签名按降序进行编码.然后, 将元素及其对应的编码分别分成高频低频两部分, 如图 6(a)所示.对于低频部分, 进行折叠压缩.设低频部分的编码下标为0, 1, …, n-1, 将第0编码与第n-1编码按位或, 得到的结果放入压缩结果的第0位, 将第1位编码与第n-2位编码按位或的结果放入压缩结果的第1位, 以此类推, 直到每个低频编码都参与了压缩运算(n为偶数), 或者只剩下一个低频编码(n为奇数), 直接将剩下的编码加入压缩结果.最后将压缩结果替换低频部分的编码.注意数据节点v自身签名BV(v)及其邻居签名BV∪(v)分别执行上述压缩操作, 最终得到图 6(b)的压缩结果.查询时, 查询节点编码也采用相同的压缩方法, 查询策略不变.压缩后, DS-Tree的过滤效果会下降, 因此得到的候选节点会增多.

|
Fig. 6 An example of compressing DS-Tree 图 6 DS-Tree压缩示例 |
因为低频元素对应的编码比较稀疏, 因此我们只对这些编码进行压缩, 压缩后对过滤效果影响不大.折叠压缩的原因是尽量让折叠后的编码比较均匀.由于在查询时无需进行解压操作, 因此在查询效率影响不大的情况下, 减少了DS-Tree占用的空间(见第4节).
3 查询处理 3.1 利用DS-Tree查询根据SMID查询的定义, 给定数据节点v和查询节点u, 若u与v的加权包含度小于τ, 那么v节点可以被过滤掉.与加权包含度对应, 我们定义位向量之间的加权包含度.
定义10(位向量加权包含度). 给定查询图节点u和数据图节点v, 位向量BV(u)和BV(v)的加权包含度为
| $VID(BV(v)/BV(u)) = \frac{{\sum\nolimits_{a \in BV(v) \wedge BV(u)} {W(a)} }}{{\sum\nolimits_{a \in BV(u)} {W(a)} }}$ | (6) |
其中, ∧是按位与操作符, a∈BV(u)∧BV(v)表示位向量中对应的位为1;W(a)是元素a对应的权重.
SMID查询转化为:对于查询图每个节点的位向量BV(ui), 需要在数据图中找到一个节点的位向量BV(vj), 使得VID(BV(vj)/BV(ui))≥τ.这里定义合并包含度上限.
定义11(合并位向量加权包含度上限). 给定位向量BV(ui)和BV∪(v), 其中, ui是目标查询图节点u的某个邻居节点, 则它们的合并加权包含度上限为
| $ UID(B{V_ \cup }(v)/BV({u_i})) = \frac{{\sum\nolimits_{a \in B{V_ \cup }(v) \wedge BV({u_i})} {W(a)} }}{{\sum\nolimits_{a \in BV({u_i})} {W(a)} }} $ | (7) |
基于定义10和定义11, 我们有如下聚集定理:
定理1(聚合定理). 给定查询节点u和数据节点v, ui是u的某个邻居节点.如果UID(BV∪(v)/BV(ui)) < τ, 那么对于v的所有直接邻居vj, 均有VID(BV(vj)/BV(ui)) < τ.
证明:
基于聚合定理, 有如下推论.
推论1.给定查询签名Sig(u)和数据签名Sig(v), 如果VID(BV(v)/BV(u)) < τ, 或者存在一个u的邻居节点ui, 使得UID(BV∪(v)/BV(ui)) < τ, 那么v不会与u匹配.
推论2.给定查询签名Sig(u)和DS-Tree节点node的签名Sig(node), 如果VID(BV(node)/BV(u)) < τ, 或者存在u的一个邻居节点ui, 使得UID(BV∪(node)/BV(ui)) < τ, 那么v不会与以node为根节点的子树内所有的数据节点匹配.
因此, 利用DS-Tree过滤方法如下:给定查询图Q和包含度阈值τ, 对于每一个ui∈V(Q), 从DS-Tree的根节点开始深度遍历(depth first search, 简称DFS).若DS-Tree的节点node不满足推论2, 则以node为根节点的子树无需继续遍历.逐一验证所有满足推论2的DS-Tree叶子节点对应的数据节点, 那些满足包含度上限的数据节点构成的集合即为ui的候选节点集, 记为C(ui).最后, 通过算法2验证ui对应的每个候选节点能否构成Q的同构图.
基于文献[13], 本文提出了一种启发式子图同构验证算法(算法2).其他的子图同构算法(如文献[12])也可直接应用于SMID查询.算法2首先将查询节点按照候选集合元素个数从小到大排序, 这样能够减少递归调用次数, 然后调用DFSCheckMatch函数.DFSCheckMatch函数用哈希表记录所有已经匹配的结果, 开始时循环遍历当前查询节点的所有候选节点, 若当前候选节点未匹配其他查询节点, 并且对应的边也匹配(第10行), 那么将此候选节点放入结果集中(第11行).若所有的查询节点都找到了匹配节点, 则输出结果, 否则继续递归调用DFSCheckMatch函数.最后删除当前候选节点(第17行), 以便验证当前查询节点的其他候选节点, 找出所有匹配的子图.
算法2. Check Isomorphic.
输入:数据图G、查询图Q、Q的每个节点ui的候选集C(ui);
输出:Q的所有同构子图.
方法:
(1) function CheckIsomorphic(DataGraph G, QueryGraph Q, CandidatesMap C) {
(2) Map matchedNode=∅; //已经用作匹配的数据节点集
(3) Sort C by candidates’ number in ascending order; //将C按候选节点数升序排序
(4) DFSCheckMatch (G, Q, C.begin(), matchedNode);
(5) }
(6) function DFSCheckMatch(DataGraph G, QueryGraph Q,
CandidatesMapIterator it, Map matchedNode) {
(7) QueryNode node=it→key;
(8) CandidatesSet candidates=it→value;
(9) foreach candidate in candidates {
(10) if (candidate not exist in matchedNode //该候选点未被使用
and all edges of node match) { //所有已匹配节点的边匹配
(11) Add 〈node, candidate〉 to matchedNode;
(12) if (matchedNode.size==Q.size) {
(13) output matchedNode as a matched graph;
(14) } else {
(15) DFSCheckMatch (G, Q, it.next(), matchedNode);
(16) }
(17) Remove 〈node, candidate〉 from matchedNode;
(18) }
(19) }
(20) }
例如, 利用图 5(e)的DS-Tree来查询图 1(b)中u4节点的候选节点.若指定元素权重为:W(“设计专业”)=0.2, 其他均为0.9, τ=0.8.Sig(u4)={〈BV(u4), BV(u2)〉, 〈BV(u4), BV(u5)〉, 〈BV(u4), BV(u6)〉}, 分成3部分, 验证每部分与DS-Tree节点的条目是否满足推论2.首先与DS-Tree根节点签名比较, 包含度为{〈1, 1〉, 〈1, 1〉, 〈1, 1〉}, 满足条件, 进一步验证根节点中每个条目.由于与第1、第2个条目的包含度分别为{〈0, 1〉, 〈0, 1〉, 〈0, 0〉}和{〈0, 1〉, 〈0, 1〉, 〈0, 1〉}, 不满足推论2, 过滤其子树对应的所有数据节点; 与第3个条目的包含度上限为{〈1, 1〉, 〈1, 1〉, 〈1, 1〉}, 因此继续比较第3个条目对应的子树.用上述同样的方法验证该节点的每个条目.只有指向v6节点的条目满足条件, 因此C(u4)={v6}.注意, 这里自动过滤了元素包含度大于0.8但结构不满足条件的v8, v5.
3.2 支配子图我们发现:对于查询节点ui, 其候选节点集为C(ui).设uj为ui的邻居节点, 那么uj的匹配节点一定包含在C(ui)的邻居节点集中.基于上述观察, 我们提出基于支配子图(dominating subgraph)的SMID算法, 当DS-Tree较大时, 能减少遍历DS-Tree的次数, 进一步提高查询效率.
支配子图的定义基于支配集[33-35], 因此我们先看支配集的定义.
定义12(支配集(dominating set)). 给定图Q, 称集合DS(Q)是V(Q)的支配集, 当且仅当DS(Q)⊆V(Q), 且Q的每个节点u要么u∈DS(Q), 要么u与DS(Q)的某些节点相邻.
定理2(支配集定理). 给定节点u∈DS(Q), 若|DS(Q)|≥2, 则至少存在一个节点u'∈DS(Q), 使得Hop(u, u')≤3.其中, Hop(·, ·)表示Q中两个节点之间最少边的数目.支配节点u'称为u的相邻支配节点(neighboring dominating vertex).
证明:假定不存在u'∈DS(Q)使得Hop(u, u')≤3, 那么u与任何其他支配节点u'之间至少存在3个节点.此时至少有一个非支配节点与u或者u'均不相邻, 与定义12矛盾.
定义13(一阶邻居和二阶邻居). 给定图Q, u∈V(Q), u的一阶邻居集N1(u)和二阶邻居集N2(u)定义如下:
● N1(u)={u'|u'∈V(Q), 且u'和u之间至少存在一条长度为1的路径};
● N2(u)={u'|u'∈V(Q), 且u'和u之间至少存在一条长度为2的路径}.
图 7所示两个相邻支配节点ui和uj之间可能的拓扑结构.图 7(a)表示ui和uj直接相邻, 图 7(b)表示ui和uj有共同的一阶邻居, 图 7(c)表示ui的二阶邻居中存在一个节点是uj的一阶邻居, 图 7(d)表示ui的一阶邻居中存在一个节点是uj的二阶邻居.实际上, 图 7(c)和图 7(d)的情况等价.

|
Fig. 7 Possible topologies between two dominant vertexes 图 7 两个支配点之间可能的拓扑结构 |
基于支配集和支配集定理, 我们定义支配子图:
定义14(支配子图(dominating subgraph, 简称DS-graph)). 给定图Q的支配集DS(Q), 图Q的支配子图QD= 〈V(QD), E(QD), Θ〉, 其中, V(QD)=DS(Q), Θ是映射函数:V(QD)×V(QD)→E(QD), 边(ui, uj)∈E(QD)当且仅当下面至少一个条件满足:
(1) ui与uj在Q中相邻(对应图 7(a));
(2) |N1(ui)∩N1(uj)| > 0(对应图 7(b));
(3) |N2(ui)∩N1(uj)| > 0(对应图 7(c));
(4) |N1(ui)∩N2(uj)| > 0(对应图 7(d)).
对于情形(1), 边(ui, uj)的距离为1(即ui~uj至少有一条长度为1的路径); 对于情形(2), 边(ui, uj)的距离为2;情形(3)和情形(4), 边(ui, uj)的距离均为3.
将查询图Q转化成支配子图, 首先找到Q的支配节点, 然后对于DS(Q)的每一对节点ui和uj, 确定它们之间是否有边及距离.对于同一个查询图Q, 可能存在多个支配子图.图 8(a)~图 8(c)的灰色节点为例1查询图支配节点的3种情况.为减少遍历DS-Tree的次数、加快查询效率, 我们选择最小支配子图.

|
Fig. 8 Dominant vertexes of example 1 图 8 例1查询图的支配节点 |
定义15(最小支配子图(minimum dominating subgraph, 简称Min DS-graph)). 图Q的所有支配子图中, 节点数目|V(QD)|最少的支配子图称为Q的最小支配子图, 记为QminD
对于同一个查询图Q, 可能存在多个最小支配子图.例如, 图 8(b)和图 8(c)对应的支配子图都是例1查询图的最小支配子图.文献[33]证明:对于含有n个节点的任意图Q, 其最小支配子图数目的下限和上限分别是1.5704n和1.7159n.而找最小支配子图是一个NP难问题, 当前已知最快的精确查找最小支配子图的算法时间复杂度为O(1.4957n)[35].综合考虑, 本文提出一种贪心算法找出近似最小支配子图.
算法开始时, 初始化集合DS=∅, 不断加入节点到DS中, 直到DS集合是支配集.为便于描述, 我们将Q中的节点分成两类:一类是DS中的节点及其相邻节点, 称为标记节点, 记为集合M; 另一类称为未标记节点, 与未标记节点u相邻的所有未标记节点的数目记为D(u).直观上看, 为使最终|DS|最小, 每次加入到DS中的未标记节点u的D(u)应该最大.基于上述观察, 贪心查找近似最小支配子图见算法3.
算法3. Find Min DS-graph.
输入:查询图Q;
输出:近似最小支配子图QminD*.
方法:
(1) function FindMinDSGraph(QueryGraph Q) {
(2) Set DS=∅;
(3) while (∃unmarked nodes){
(4) Choose u∈{x|D(x)=maxv∈(V(Q)-M){D(v)}};
(5) DS=DS∪{u};
(6) M=M∪{u and u’s neighbors};
(7) }
(8) Find E(QminD*) based on DS;
(9) return QminD*;
(10) }
按照算法3的近似支配子图QminD*, 任何两个支配节点都不可能相邻, 因为每次都会标记当前支配节点u及其邻居(第6行).例1查找图的近似最小支配子图过程是:最开始, DS=∅, M=∅, V(Q
定理3(距离保留定理(distance preservation principle, 简称DP-Principle)). 假设X是Q在G中的一个子图匹配, XD是与QD对应的支配子图匹配.QD和XD分别有n个节点u1, …, un和v1, …, vn.对于QD中任意边(ui, uj), 均有:
(1) 如果距离是1, 那么vi与vj相邻;
(2) 如果距离是2, 那么|N1(vi)∩N1(vj)| > 0;
(3) 如果距离是3, 那么|N1(vi)∩N2(vj)| > 0或者|N2(vi)∩N1(vj)| > 0.
根据SMID和支配子图的定义, 容易证明定理3的正确性.因此, 对于那些非支配节点, 我们可以通过支配节点的候选集找到非支配节点的候选集.例1中查询图利用DS-Tree找到支配节点u3, u4的候选集, C(u3)={v3, v4}, C(u4)={v6}.查询图的非支配节点u5的候选节点集C(u5)⊆N1(v6)∩(N1(v3)∪N1(v4))={v3, v4, v5}, 因此, C(u5)={v5}.同样办法确定其他非支配节点的候选集C(u6)={v7}, C(u2)={v3, v4}, C(u1)={v2}.
3.3 SMID算法首先, 调用算法1建立数据图G的DS-Tree, 这一步是离线过程, 只需执行一次, 把结果存入数据库或文件,在查询时只需加载即可.然后, 调用算法3建立查询图Q的近似最小支配子图QminD*.对于每个支配节点u, 利用DS-Tree找到其候选集C(u), 对于非支配节点u', 利用距离保留定理找到其候选集C(u').最后, 调用算法2检查子图同构并输出结果.
算法4. SMID.
输入:查询图Q, 数据图G, 包含度阈值τ, 各元素权重集W;
输出:Q的所有同构子图.
方法:
(1) Call Algorithm 1 to build G’s DS-Tree;
(2) Call Algorithm 3 to build QminD*;
(3) foreach u∈V(QminD*){
(4) Using DS-Tree to find C(u);
(5) }
(6) foreach u'∈V(Q)-V(QminD*){
(7) Using DP-Principle to find C(u );
(8) }
(9) Call Algorithm 2 to check isomorphic and output result.
4 实验首先介绍本文实验用到的数据集和实验环境, 然后介绍对比方法的基本思想, 最后对本文提出的SMID方法与对比方法的离线性能和在线性能进行分析比较.
4.1 数据集和实验环境本文采用表 1描述的数据集验证基于DS-Tree索引的SMID算法性能, 其中包括Freebase和DBpedia两个真实数据集以及3个人工数据集.实验代码采用C++语言编写, 运行在主频2.40GHz、内存16G的64位Windows 8.1操作系统上.
| Table 1 Details of datasets 表 1 数据集详细信息 |
(1) Freebase(http://www.freebase.com/)是一个知识数据库, 其中包含很多实体(演员、电影等).可以将实体看成图节点, 每个实体拥有的特征描述构成节点的元素集, 实体之间的关联关系看成边.因此, Freebase可以构成一个无向图, 记为FB.实验时, 元素权重随机指定, 并标准化在[0, 1]范围之间;
(2) DBpedia(http://wiki.dbpedia.org/)抽取了维基百科(https://www.wikipedia.org/)的结构信息.在DBpedia数据集(记为DBP)中, 每个节点对应一篇维基百科的文章, 采用特征抽取方法[36]从文章中选取TF/IDF最高的200个单词作为该节点的元素, 元素权重即为对应的TF/IDF, 并标准化在[0, 1]之间;
(3) 文献[37]的图产生器能够产生节点度满足幂律分布的连接无向图.实验中使用3个不同大小的图数据集S1M, S5M和S10M, 其节点数目分别为1 000 000, 5 000 000, 10 000 000.每个节点随机赋予2个~20个元素, 每个元素的权重随机赋值, 并标准化在[0, 1]之间.
4.2 对比方法近年来, Liang等人提出的SMS2查询问题[27]考虑了节点元素集合.与SMID不同的是, SMS2要求图结构同构, 且对应节点元素的集合相似度大于给定阈值.在离线处理过程中, SMS2为数据图创建了倒排模式格和签名桶索引.在线处理阶段, 首先利用横向剪枝、纵向剪枝、反单调性剪枝等多种剪枝技术找出查询图每个节点的候选节点集, 然后进行子图同构验证.本文以SMS2算法作为其中一个对比方法, 同时为公平起见, 修改SMS2算法的相似度为加权包含度.
DS-Tree是S-Tree的变形, 不同的是, DS-Tree的节点容量随着层数的增加而减少, 而S-Tree中每层节点容量相同.为证明DS-Tree的有效性, 我们比较基于S-Tree索引的SMID查询性能, 记为SMIDS.为便于区分, 基于DS-Tree索引的SMID查询记为SMIDDS.
为验证本文提出的DS-Tree压缩算法的有效性, 我们比较DS-Tree压缩前后的索引大小及查询时间.基于压缩算法的SMID查询记为SMIDCDS.SMIDCDS将数据图中的元素按频次倒序排序后, 取前50%作为高频, 后50%作为低频, 然后对低频元素对应的签名进行折叠压缩.在实际应用中, 可以根据实际情况调整高频和低频的范围, 高频所占比例越少, 压缩率越高.
同时, 为验证支配子图查询算法能够加快查询效率, 我们还比较基于DS-Tree索引并使用支配子图的查询方法, 记为SMIDDSD.
4.3 离线处理性能离线处理主要开销为DS-Tree索引的建立, 而DS-Tree索引大小和索引时间与公式(5)中的s, r参数有关.图 9所示在S1M数据集上, 使用压缩的方法SMIDCDS与不使用压缩的方法SMIDDS的索引大小和索引时间随s的变化情况.

|
Fig. 9 Impact of s on offline performance in dataset S1M 图 9 参数s对S1M数据集离线性能的影响 |
由图 9可知:随着s的增长, SMIDCDS与SMIDDS索引文件均变小, 但索引时间均变大.因为当s增大时, 表明每一层的相对容量变大, DS-Tree的层数就越少, 产生的DS-Tree就越小.但由于节点分裂采用原生聚类算法, 节点容量越大时聚类时间越长, 因此索引时间也在增长.整体而言, SMIDCDS的索引空间约为SMIDDS索引空间的76%~80%, 因为压缩的DS-Tree对应的节点签名长度是未压缩的75%, 因此整体所占用的空间更小.SMIDCDS在索引建立的过程中需要进行折叠压缩操作, 因此索引所需要的时间更长.一个有趣的现象是:当s过小(等于30), 索引文件大小和索引时间急剧上升, 因为此时DS-Tree节点不断溢出和分裂.当s=30时, SMIDDS索引时间为1 000s, 索引文件达到2G(为了使图更清楚, 当s=30时的索引空间情况未在图中体现).因此, s不能太小.
图 10所示S1M数据集的索引大小和索引时间随r的变化情况.由图可知:随着r的增长, SMIDDS与SMIDCSD索引空间和索引时间都呈上升趋势.因为r决定每一层容量的递减速度, r越大, 高层的节点容量就越小, 产生的DS-Tree索引越大.当r大于一定值时, 索引空间和索引时间上升得更快, 因为此时高层节点不断分裂.同样, SMIDCDS索引空间约为SMIDDS的80%左右, 因为对应的签名长度为75%.由于压缩需要时间, 因此SMIDCDS需要更多的时间.

|
Fig. 10 Impact of r on offline performance in dataset S1M 图 10 参数r对S1M数据集离线性能的影响 |
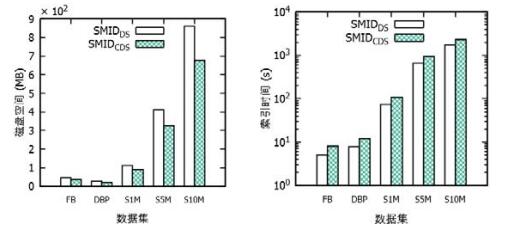
根据多组实验, 我们对各数据集的r, s选择见表 2.图 11显示了各数据集的索引空间和索引时间情况.
| Table 2 Default value of r/s in each dataset 表 2 各数据集的默认参数设置 |
|
Fig. 11 Index space and index time of different datasets 图 11 不同数据集的索引空间和索引时间 |
由图可知, 索引空间和索引时间随着数据集的大小呈指数级增长.但即使对于1000 000 000节点的数据集, SMIDDS方法的索引空间约为800M, 索引时间不到30分钟, 单机性能仍可接受.对于每个数据集, 基于以上同样的原因, SMIDCDS方法的索引空间要小, 而索引时间稍高.
4.4 在线处理性能在线处理阶段, 我们比较SMIDDS, SMIDS, SMIDCDS和SMS2的查询响应时间.对于每组实验, 从数据图中随机抽取100个特定大小的子图作为查询图.
图 12(a)表示包含度上限τ=0.8、查询图大小n=5时, 不同数据集上的平均查询时间.当数据量较小时, SMIDCDS, SMIDDS, SMIDS和SMS2算法性能相差不大, 但SMIDCDS和SMIDDS算法最佳, SMIDS次之, SMS2较差.随着数据量增大, SMIDDS优势愈发明显, 表明DS-Tree索引的扩展性较好.SMIDCDS比SMIDDS所需查询时间稍长, 因为SMIDCDS过滤的数据节点较少, 产生的候选集较多, 在验证同构时所需的时间更长.在小数据集上, SMIDDSD查询时间比SMIDDS稍长, 当数据集较大时, SMIDDSD算法略优.因为在小数据集上, 验证子图同构的时间占主导地位.而大数据集对应的DS-Tree大, 查询DS-Tree所需的时间更长.
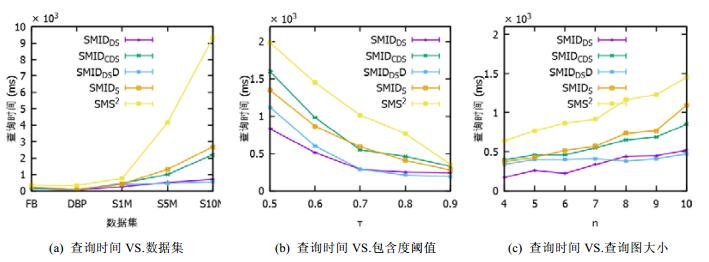
|
Fig. 12 Query time of different methods 图 12 不同方法的查询时间 |
图 12(b)显示的是在S1M数据集上, 当n=5时, 不同方法随着包含度阈值τ的变化情况.τ越小, 每个节点的候选节点就越多, 验证子图同构所需的时间就越多, 因此查询时间越久.随着τ的增大, 过滤的节点数就越多, 因此总查询时间越少.对于SMIDDSD方法, 当τ≥0.8时, 所需时间比SMIDDS方法少, 因为当包含度阈值越大, 查到的候选节点少, 由支配节点扩展找到非支配节点的候选节点也越少.此时, 查找DS-Tree的时间占主要部分.随着包含度阈值增大, SMIDDSD查找时间少于SMIDDS时间.
图 12(c)比较了不同方法的查询时间随查询图大小的变化情况, 此时选择数据集为S1M, τ=0.8.对于各方法, 容易理解:当查询图越小时, 验证子图同构的时间越少, 查询就越快.可以发现一个有趣的现象, SMIDDSD方法随着查询图增大所需的查询时间变化不大.因为查询图变大时, 支配子图的大小变化不大.因此, SMIDDSD适合查询图较大的情况.
上述实验结果表明:在大数据图、高包含度阈值、查询图节点较多的情况下, 基于支撑节点的SMIDDSD方法要优于SMIDDS方法.此外, 本文提出的DS-Tree压缩方法能够在对查询时间影响不大的情况下, 缩小DS-Tree的内存空间, 这对数据图较大的情况非常有用.最后, SMIDDS优于基于S-Tree索引的查询方法SMIDS.原因是:对于DS-Tree, 每层节点的容量是不同的, 越往高层的容量越小.这符合DS-Tree的增长规律, 即, 越往高层的节点越难装满.同时, SMIDDS方法优于SMS2方法, 因为DS-Tree相对于SMS2中的签名桶具有以下优势.
(1) 更好的适应性.签名桶基于局部敏感哈希(locality sensitive hashing, 简称LSH)[38], 但LSH与特定应用相关, 找到一个合适的哈希函数并不容易.而DS-Tree无需特定其他函数, 能够适用不同应用的需求;
(2) 更大的灵活性.签名桶的层数需要事先指定, 而层数的多少取决于数据图的大小, 在创建之前难以预估.而DS-Tree动态增长, 无需实现指定层数;
(3) 更好的扩展性.同一个数据节点可能存在于多个签名桶中, 这会造成存储空间浪费.当数据量大的时候, 造成索引文件非常大.而对于DS-Tree, 一个数据节点只会存在于一个DS-Tree的叶节点中.
5 结论本文提出了一种应用广泛的子图查询问题, 即基于包含度的子图匹配SMID.在SMID查询中, 图结构必须同构, 且对应节点的加权包含度大于用户给定阈值.此外, 给出了一种基于DS-Tree和最小支配子图的SMID查询算法.最小支配子图算法在数据图较大、包含度阈值较高和查询图较大的情况下, 能够加快查询效率.针对DS-Tree占用内存空间高的问题, 提出了一种DS-Tree的压缩算法, 在对查询效率影响不大的情况下, 缩小了内存空间.通过实验证明, 本文给出的SMID算法在单机上具有较高的查询效率和较好的扩展性.下一步工作, 将集中精力在计算机集群中实现SMID查询.
| [1] |
Yu X, Sun Y, Zhao P, Han J. Query-Driven discovery of semantically similar substructures in heterogeneous networks. In: Proc. of the ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. New York: ACM Press, 2012. 1500-1503. [doi:10.1145/2339530.2339765] |
| [2] |
Zou L, Mo J, Chen L, Özsu MT, Zhao D. gStore:Answering SPARQL queries via subgraph matching. Proc. of the VLDB Endowment, 2011, 4(8): 482–493.
[doi:10.14778/2002974.2002976] |
| [3] |
Tian Y, Patel JM. TALE: A tool for approximate large graph matching. In: Proc. of the 2008 IEEE 24th Int'l Conf. on Data Engineering. IEEE Computer Society, 2008. 963-972. [doi:10.1109/ICDE.2008.4497505] |
| [4] |
Zhao P, Han J. On graph query optimization in large networks. Proc. of the VLDB Endowment, 2010, 3(1-2): 340–351.
[doi:10.14778/1920841.1920887] |
| [5] |
Zhang S, Yang J, Jin W. Sapper:Subgraph indexing and approximate matching in large graphs. Proc. of the VLDB Endowment, 2010, 3(1-2): 1185–1194.
[doi:10.14778/1920841.1920988] |
| [6] |
Sun Z, Wang H, Wang H, Shao B, Li J. Efficient subgraph matching on billion node graphs. Proc. of the VLDB Endowment, 2012, 5(9): 788–799.
[doi:10.14778/2311906.2311907] |
| [7] |
Qu KS, Zhai YH. Posets, inclusion degree theory and FCA. Chinese Journal of Computers, 2006, 29(2): 219–226(in Chinese with English abstract).
[doi:10.3321/j.issn:0254-4164.2006.02.004] |
| [8] |
Ren X, Liu J, Yu X, Khandelwal U, Wang L, Han J. Cluscite: Effective citation recommendation by information network-based clustering. In: Proc. of the 20th ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. ACM Press, 2014. 821-830. [doi:10.1145/2623330.2623630] |
| [9] |
Duan L, Street WN, Liu Y, Lu H. Community detection in graphs through correlation. In: Proc. of the 20th ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. ACM Press, 2014. 1376-1385. [doi:10.1145/2623330.2623629] |
| [10] |
Cordella LP, Foggia P, Sansone C, Vento M. A (sub) graph isomorphism algorithm for matching large graphs. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2004, 26(10): 1367–1372.
[doi:10.1109/TPAMI.2004.75] |
| [11] |
Zhao X, Xiao C, Lin X, Wang W, Ishikawa Y. Efficient processing of graph similarity queries with edit distance constraints. VLDB Journal, 2013, 22(6): 727–752.
[doi:10.1007/s00778-013-0306-1] |
| [12] |
Ullmann JR. An algorithm for subgraph isomorphism. Journal of the ACM, 1976, 23(23): 31–42.
[doi:10.1145/321921.321925] |
| [13] |
Shang H, Zhang Y, Lin X, Yu J. Taming verification hardness:An efficient algorithm for testing subgraph isomorphism. Proc. of the VLDB Endowment, 2008, 1(1): 364–375.
[doi:10.14778/1453856.1453899] |
| [14] |
Han WS, Lee J, Lee JH. Turbo iso: Towards ultrafast and robust subgraph isomorphism search in large graph databases. In: Proc. of the ACM SIGMOD Int'l Conf. on Management of Data. 2013. 337-348. [doi:10.1145/2463676.2465300] |
| [15] |
Ma H, Shao B, Xiao Y, Chen LJ, Wang H. G-SQL:Fast query processing via graph exploration. Proc. of the VLDB Endowment, 2016, 9(12): 900–911.
[doi:10.14778/2994509.2994510] |
| [16] |
He H, Singh AK. Closure-Tree: An index structure for graph queries. In: Proc. of the 22nd Int'l Conf. on Data Engineering (ICDE 2006). IEEE, 2006. 38-38. [doi:10.1109/ICDE.2006.37] |
| [17] |
Zhang XC, Yu H, Gong XJ. A random walk based iterative weighted algorithm for sub-graph query. Journal of Computer Research and Development, 2015, 52(12): 2824–2833(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.2015.20140801] |
| [18] |
Yuan Y, Wang G, Xu JY, Chen L. Efficient distributed subgraph similarity matching. The VLDB Journal, 2015, 24(3): 369–394.
[doi:10.1007/s00778-015-0381-6] |
| [19] |
Gupta M, Gao J, Yan X, Cam H, Han J. Top-k interesting subgraph discovery in information networks. In: Proc. of the 2014 IEEE 30th Int'l Conf. on Data Engineering. IEEE, 2014. 820-831. [doi:10.1109/ICDE.2014.6816703] |
| [20] |
Rangapuram SS, Bühler T, Hein M. Towards realistic team formation in social networks based on densest subgraphs. In: Proc. of the 22nd Int'l Conf. on World Wide Web. ACM Press, 2013. 1077-1088. [doi:10.1145/2488388.2488482] |
| [21] |
Khan A, Wu Y, Aggarwal CC, Yan X. Nema:Fast graph search with label similarity. Proc. of the VLDB Endowment, 2013, 6(3): 181–192.
[doi:10.14778/2535569.2448952] |
| [22] |
Zou L, Chen L, Lu Y. Top-k subgraph matching query in a large graph. In: Proc. of the ACM First Ph. D. Workshop in CIKM. ACM Press, 2007. 139-146. [doi:10.1145/1316874.1316897] |
| [23] |
Peng P, Zou L, Özsu MT, Chen L. Processing SPARQL queries over distributed RDF graphs. Computer Science, 2016, 25(2): 1–26.
[doi:10.1007/s00778-015-0415-0] |
| [24] |
Zheng W, Zou L, Lian X, Wang D, Zhao D. Efficient graph similarity search over large graph databases. IEEE Trans. on Knowledge and Data Engineering, 2015, 27(4): 964–978.
[doi:10.1109/TKDE.2014.2349924] |
| [25] |
Zheng W, Zou L, Peng W, Yan X, Song S, Zhao D. Semantic SPARQL similarity search over RDF knowledge graphs. Proc. of the VLDB Endowment, 2016, 9(11): 840–851.
[doi:10.14778/2983200.2983201] |
| [26] |
Lian X, Chen L, Wang G. Quality-Aware subgraph matching over inconsistent probabilistic graph databases. IEEE Trans. on Knowledge and Data Engineering, 2016, 28(6): 1560–1574.
[doi:10.1109/TKDE.2016.2518683] |
| [27] |
Hong L, Zou L, Lian X, Philip SY. Subgraph matching with set similarity in a large graph database. IEEE Trans. on Knowledge & Data Engineering, 2015, 27(9): 2507–2521.
[doi:10.1109/TKDE.2015.2391125] |
| [28] |
Garey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. W. H. Freeman and Company, 1979. |
| [29] |
Deppisch U. S-Tree: A dynamic balanced signature index for office retrieval. In: Proc. of the 9th Annual Int'l ACM SIGIR Conf. on Research and Development in Information Retrieval. ACM Press, 1986. 77-87. [doi:10.1145/253168.253189] |
| [30] |
Mamoulis N, Cheung DW, Lian W. Similarity search in sets and categorical data using the signature tree. In: Proc. of the 19th Int'l Conf. on Data Engineering. IEEE, 2003. 75-86. [doi:10.1109/ICDE.2003.1260783] |
| [31] |
Chen Y, Chen Y. On the signature tree construction and analysis. IEEE Trans. on Knowledge and Data Engineering, 2006, 18(9): 1207–1224.
[doi:10.1109/TKDE.2006.146] |
| [32] |
Kontaki M, Manolopoulos Y, Nanopoulos A. Compressing large signature trees. Lecture Notes in Computer Science, 2003, 2798: 163–177.
[doi:10.1007/978-3-540-39403-7_14] |
| [33] |
Fomin FV, Grandoni F, Pyatkin AV, Stepanov AA. Combinatorial bounds via measure and conquer:Bounding minimal dominating sets and applications. ACM Trans. on Algorithms, 2008, 5(1): 596–600.
[doi:10.1145/1435375.1435384] |
| [34] |
Couturier JF, Heggernes P, van't Hof P, Krastsch D. Minimal dominating sets in graph classes:Combinatorial bounds and enumeration. Theoretical Computer Science, 2013, 487: 82–94.
[doi:10.1016/j.tcs.2013.03.026] |
| [35] |
Rooij JMMV. Exact Exponential-Time Algorithms for Domination Problems in Graphs. Boxpress, 2011. |
| [36] |
Yang Y, Pedersen JO. A comparative study on feature selection in text categorization. In: Proc. of the 14th Int'l Conf. on Machine Learning. Morgan Kaufmann Publishers Inc., 1998. 412-420.http://dl.acm.org/citation.cfm?id=657137 |
| [37] |
Viger F, Latapy M. Efficient and simple generation of random simple connected graphs with prescribed degree sequence. 2005, 3595: 440-449. [doi:10.1007/11533719_45] |
| [38] |
Chakrabarti A, Parthasarathy S. Sequential hypothesis tests for adaptive locality sensitive hashing. Computer Science, 2014. [doi:10.1145/2736277.2741665] |
| [7] |
曲开社, 翟岩慧. 偏序集、包含度与形式概念分析. 计算机学报, 2006, 29(2): 219–226.
[doi:10.3321/j.issn:0254-4164.2006.02.004]
|
| [17] |
张小驰, 于华, 宫秀军. 一种基于随机游走的迭代加权子图查询算法. 计算机研究与发展, 2015, 52(12): 2824–2833.
[doi:10.7544/issn1000-1239.2015.20140801]
|
 2018, Vol. 29
2018, Vol. 29


