2. 东北大学 计算机科学与工程学院, 辽宁 沈阳 110819 ;
3. 信息安全国家重点实验室(中国科学院 信息工程研究所), 北京 100093 ;
4. 肇庆学院 计算机学院, 广东 肇庆 526061
2. 东北大学 计算机科学与工程学院, 辽宁 沈阳 110819 ;
3. 信息安全国家重点实验室(中国科学院 信息工程研究所), 北京 100093 ;
4. School of Computer Science, Zhaoqing University, Zhaoqing 526061, China
云存储[1, 2]是分布式存储技术与虚拟化技术相结合的产物,其通过集群、网格和分布式文件系统等技术,将网络中各种不同类型的存储设备通过软件集合起来协同工作,共同对外提供数据存储和业务访问功能的一种新兴的存储模式.云存储是信息存储发展的重要趋势,可为用户带来如下好处:(1) 无需购置初始耗资较大的服务器,也免去了专业的服务器及数据管理人员,避免过大的投资;(2) 实现任意地点、任意时间以及任意数据访问;(3) 提供可用性、可维护性与扩展性保障;(4) 保障法规遵从的需求;(5) 实现数据的长期保存.
随着云存储及其相关技术的深入发展,越来越多的企业开始搭建属于自己的云存储平台,并通过一些特定的接口为企业或个人提供存储服务.Amazon是最早提供云存储服务的公司之一,其基于云计算平台提供了简单存储服务S3,使得用户可以将数据存储到云服务器上,通过网络来管理和访问自己的数据.Google也于2012年4月正式推出在线云存储服务Google Drive.Google Drive可以协作、存储文件到云端,并支持云端搜索.Azure是Microsoft公司推出的云计算操作系统平台,可以为开发者提供按需定制的计算服务和基于微软数据中心的Web应用程序.此后,Microsoft又推出了Sky Drive.Sky Drive改进了同步文件上传和存储的能力,同时增加了对Windows平台外的终端支持.
尽管云存储有着价格低廉、部署方便等优点,但其推广过程却相对缓慢.究其原因,主要是近年来,云存储系统的安全隐患不断出现.例如,2009年,谷歌的Gmail服务和News服务连续出现中断事故,部分Gmail用户的邮件被无故删除;2010年,由于数据备份中心发生故障,导致Google App Engine宕机,同样给谷歌用户造成了严重的影响;2012年,国内云服务提供商盛大云因机房物理服务器的故障,导致客户部分数据丢失.层出不穷的用户数据泄露和丢失事件,使得用户对于使用云存储系统的信心严重不足.从Twin Strata公司2012年最新的云存储应用调查来看:只有20%的人愿意将自己的私有数据放在云存储中;仅有50%的人愿意使用云存储来进行数据备份、归档存储以及灾难恢复等作业.由此可见,数据安全问题是云存储推广的重大障碍之一,并已经严重地制约了云存储的快速发展[3, 4].
数据的机密性和容错性是云存储中数据安全的两个重要属性,也是用户最为关心的云存储安全问题.数据机密性是指无论存储还是传输过程中,只有数据拥有者和授权用户才能够访问数据明文,其他任何用户或云存储服务提供商都无法得到数据明文,从理论上杜绝一切数据泄漏的可能.数据的容错性是指云端在发生意外(如硬盘损坏、IDC失火、网络故障等)时,用户的数据能够在何种程度上可用.目前,对于数据机密性和容错性的研究成果较多,但是将二者综合起来,全面考虑的研究方案则比较少见.
1 相关工作云存储在给人们带来规模经济、高可用性等多种好处的同时,其核心技术特点(虚拟化、分布式、资源共享等)也决定了其在安全性方面存在着天然隐患.例如,当数据存储在物理位置不确定的云端,数据安全与隐私安全就面临着严峻的威胁和挑战.而云存储服务器的任何故障,如硬盘损坏、失火、网络故障等都有可能导致用户数据的部分甚至全部损坏.因此,云存储中的数据安全问题已成为云安全研究中最为重要的研究课题之一,特别是云存储中的数据机密性和容错性问题,已受到越来越多的关注.
(1) 数据机密性方面
为保证数据的机密性,数据在云存储系统中应该以密文形式存放,但是加密的方式又带来了运算上的开销,因此要以尽可能小的计算开销带来实现可靠的数据机密性[5, 6].代理重加密[7]、广播加密[8]以及基于属性的加密[9]是目前云存储中的主流数据机密性保护方法.同时,在考虑用户隐私的情况下,通过完全同态加密[10],服务器在密文上的任何操作都能够直接对应到明文上的相应操作.支持搜索的加密方法也是云存储中的一个重要应用需求.文献[11]提出了一种基于双线性对函数的单关键字可搜索公钥加密方案.在此之后,又有很多学者提出了支持搜索的加密方法,包括文献[12]提出一种加密数据的模糊搜索方案;文献[13]提出了一个高效的支持返回结果排序的加密数据搜索方案;文献[14]提出的支持多关键字搜索并能够对返回结果进行排序的加密搜索方案;文献[15]中提出的一个授权关键字搜索方案,该方案能够实现多维的多关键字简单范围搜索,同时能够保护用户隐私.
(2) 数据容错性方面
数据容错是实现云存储系统可靠性的关键.通常的数据容错机制包括两类:一类是完全的数据备份机制,即镜像方法(mirrired method),另一类是基于纠删码(erasure code)的方法.镜像方法又称完全副本方法,就是把数据拷贝多个副本分别存储,以实现冗余备份.镜像方法是最简单的抵抗任意服务器失效、维持系统弹性的方法.但是,镜像方法的存储利用率极低,存储成本过高.纠删码技术是一类源于信道传输的编码技术,因为能够容忍多个数据帧的丢失,被引入到分布式存储领域.在分布式存储系统中,纠删码将数据编码成数据块和校验块,分别存储在不同的节点中.当系统中部分节点失效或者部分数据块损坏时,存储系统仍能根据剩余的数据块来恢复原文件,从而保障数据的可靠性.基于纠删码的容错技术,以其较强的容错能力,较高的空间利用率,成为能够容忍多个数据块同时失效的、最常用的容错技术.在相同容错能力的前提下,基于纠删码的容错技术存储开销更低,已经应用于许多大规模存储系统.
当前,基于副本的容错技术[16]是云存储中的主流容错技术,也是最简单的抵抗任意服务器失效、维持系统弹性的方法.但是,该方法的存储利用率较低,存储成本过高.文献[17]指出在存储容量和存储代价方面,基于纠删码的容错技术比基于副本的容错技术更加具备优势.因此,在云存储的数据容错性问题中,多数学者选择了基于纠删码的容错性保护技术.例如,文献[16]提出了一种安全编码——SRCS编码,以保证在云存储这种高度开放的环境下,存储系统容错过程中数据的安全性;文献[18]提出了一种副本复制和纠删码融合的云存储文件系统容错方法,为云存储文件系统设计了双重保险的容错机制.
综上所述,关于数据机密性和容错性的独立研究成果较多,但是将二者综合起来,全面考虑的研究方案则比较少见.为此,本文将门限公钥加密与指数纠删码融合,构造了一种同时具有机密性与容错性的安全云存储模型SCSM-DCF.SCSM-DCF的安全性主要体现在数据和密钥两个方面:对于数据来说,都是以加密、编码后的形式进行存储,既能保证云存储系统中的数据机密性,又能抵抗服务器失效故障;对于系统中的密钥采用分层管理机制,主密钥通过秘密共享方案交给一系列可信的密钥服务器进行维护,会话密钥使用主密钥进行加密,同时使用EC-E技术进行编码,而后存储到云端,存储服务器无法拥有解密的密钥,访问权管理完全由用户控制.文中给出了SCSM-DCF的形式化定义、安全性定义以及实体间通信协议;之后,对SCSM-DCF的安全性以及相关代价进行了分析;最后通过相关实验,分析了引入了加密机制和容错机制后对系统的性能影响情况.
本文第2节给出SCSM-DCF的形式化定义、安全性定义以及实体间通信协议.第3节对SCSM-DCF的安全性进行分析.第4节从计算代价、存储代价等方面对SCSM-DCF进行性能分析.最后对全文进行总结.
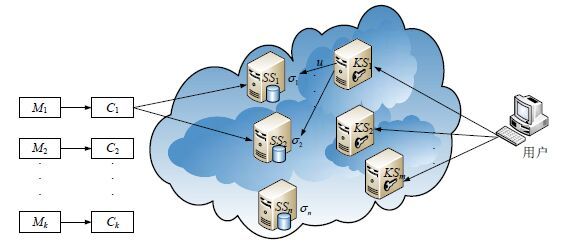
2 SCSM-DCF设计 2.1 模型描述及形式化定义SCSM-DCF包括客户端与服务器.客户端是云存储用户,即数据的拥有者.服务器分为两种:存储服务器和密钥服务器.存储服务器的数量较多,计算性能较低,安全性相对较弱;密钥服务器数量相对较少,但计算性能高,安全性较高.SCSM-DCF架构如图 1所示,其包括n台存储服务器(storage server,简称SS)SS1,SS2,…,SSn和m台密钥服务器(key server,简称KS)KS1,KS2,…,KSm.存储服务器提供数据和会话密钥的存储服务,密钥服务器提供主密钥管理服务.加密后的数据和会话密钥在存储服务器中随机分配存储.存储服务器对接收到的密文执行编码操作,只存储密文编码后的结果以及选取的系数向量.
|
Fig. 1 System model of SCSM-DCF 图 1 SCSM-DCF 架构 |
在SCSM-DCF中,云存储用户想要将私人数据存储到云端服务器,首先需要为数据生成对应的会话密钥,会话密钥可以直接用于对数据进行加密.数据的加密操作由客户端负责完成,加密后的数据被上传至云端存储服务器,使用指数纠删码进行编码存储.编码工作由服务器执行.为了减少用户的密钥管理代价,会话密钥同样需要放置到云端存储服务器进行存储.客户端为会话密钥生成相应的主密钥,主密钥负责对会话密钥进行加密,加密操作同样由客户端负责完成.加密后的会话密钥被发送至云端存储服务器,服务器负责对密钥文件进行冗余编码.而主密钥则交由可信的密钥服务器,使用秘密共享方案进行存储,以保证密钥的安全,防止因密钥丢失而导致的文件不可读.主密钥的分片过程由客户端负责执行.
当用户想要从云端获取相应数据时,需要根据文件名,找到相对应的会话密钥,根据会话密钥,查找相应的主密钥,将主密钥进行重组,对会话密钥进行部分解密操作,部分解密操作由密钥服务器负责执行.然后密钥服务器将解密分片发送给用户,用户对密钥文件进行解密,获取相应的会话密钥.在得到会话密钥之后,获取云端文件,使用会话密钥对文件进行解密,得到原始的用户数据.
SCSM-DCF主要包括3个处理过程:初始化、数据存储以及数据获取.
(1) 初始化
服务器端选择并计算公共参数.用户A拥有自己的存储空间、公钥PKA及私钥SKA.用户A将自己的公钥发布,然后将其私钥与一系列密钥服务器共享,服务器数量需要达到一个最小临界值(阈值)t.因此,每台被选中的密钥服务器KSi(1≤i≤m)拥有用户私钥SKA的一个密钥分片SKA,i.
(2) 数据存储
用户A将文件F分成k块(M1,M2,…,Mk)(1≤i≤k),并生成一个会话密钥K.用户使用K对文件分块Mi进行加密,得到密文Ci=E(K,Mi).然后,将密文发送给n台存储服务器SSi(1≤i≤n),SSi使用EC-C对密文进行编码.对于会话密钥K,首先将其分成k块(K1,K2,…,Kk),并使用用户的公钥PKA对Ki(1≤i≤k)进行门限公钥加密.将会话密钥的密文分块发送至v台存储服务器,这些存储服务器是随机挑选的,并使用EC-C将接收到的密文分块进行编码,形成最终的存储数据si.
(3) 数据获取
如果要获取k块数据,用户A首先根据文件加密内容,获取文件与主密钥的对应关系,确定文件对应的主密钥.然后用户对m台密钥服务器下达指令.接收到数据获取指令后,每台密钥服务器从u台存储服务器中获取所存储的会话密钥,然后对获取的数据执行部分解密.之后,用户A从密钥服务器处收集部分解密的结果,即解密份,用户A将这些部分解密的结果结合起来,恢复原始的会话密钥K.
当成功获取会话密钥后,用户向存储服务器下达数据获取指令,获取存储服务器上存储的文件,并使用K对数据进行解密,获取原始的用户数据.
定义1 是对SCSM-DCF的形式化描述.
定义1. 具有机密性与容错性的安全云存储模型(secure cloud storage model with data confidentiality and fault-tolerant,简称SCSM-DCF).该模型可以由以下元组表示:
| $SCSM-DCF\left\{ C,SS,KS,DFM-EC-E,TPKE \right\}$ |
其中包括客户端C、存储服务器SS和密钥服务器KS以及基于指数纠删码的数据容错方法(data fault-tolerant method based on erasure codes over exponents,简称DFM-ECE)和门限公钥加密方案(key management scheme based on threshold public key encryption,简称TPKE).
2.2 安全性定义SCSM-DCF的安全性依赖于密钥加密方案的安全性.定义2对SCSM-DCF的安全性进行了描述.
定义2. SCSM-DCF的安全性.如果SCSM-DCF是安全的,那么其密钥加密方案就应该可以抵抗选择明文攻击(chosen plaintext attack,简称CPA).
在SCSM-DCF的威胁模型中,考虑这样的一个敌手A,他想要破坏某目标用户密钥的机密性,并且劫持所有的存储服务器以及不超过t-1个的密钥服务器.假定,攻击者不会篡改存储数据,但是他将试图推断数据内容.本文用标准的CPA来模拟这种攻击,这里的CPA是与门限公钥加密方案(详见第2.3.2节)相关的.
为适应本文所采用的门限公钥加密方案,本文对标准的CPA安全游戏进行扩展.门限CPA安全游戏包含挑战者C和敌手A.
(1) 初始化(setup)
挑战者C完成以下工作:
① 运行Setup(λ),得到$u=(p,{{G}_{1}},{{G}_{2}},\widetilde{e},g).$
② 运行KeyGen(u),得到密钥对(PK,SK),对(SK,t,n)执行ShareKeyGen(),得到SKi(1≤i≤n),t和n是随机选取的.
③ 发送(u,PK,t,n)给A.
(2) 密钥共享查询(key share query)
A从C处查询(t-1)个密钥分片:
| $S{{K}_{{{q}_{1}}}},S{{K}_{{{q}_{2}}}},...,S{{K}_{{{q}_{t-1}}}},{{q}_{1}},{{q}_{2}},...,{{q}_{t-1}}\in [1,n].$ |
(3) 挑战(challenge)
A选择两条信息M0和M1(M0≠M1),并将它们发送给挑战者C.C将Mb(b从{0,1}中随机选取)加密后返回给A.
(4) 输出(output)
A输出一个比特值b'来猜测b的值.
A的优势定义为$Ad{{v}_{A}}=|\Pr [{b}'=b]-{1}/{2}\;|.$门限公钥加密方案是CPA安全的,指的是当且仅当对于任意不确定的多项式时间算法A,AdvA在l中是可以忽略不计的.
若门限公钥加密方案是CPA安全的,则SCSM-DCF是安全的.
2.3 关键技术 2.3.1 基于EC-E的数据容错方法EC-E属于随机线性码的一种变体.令G为p阶循环乘法群,消息$\overset{\to }{\mathop{I}}\,=({{m}_{1}},{{m}_{2}},...,{{m}_{k}}),$生成矩阵$G=$${{[{{g}_{i,j}}]}_{1\le i\le k,1\le j\le n}},$码字$\overset{\to }{\mathop{O}}\,=({{w}_{1}},{{w}_{2}},...,{{w}_{k}}).$$\overset{\to }{\mathop{I}}\,$和$\overset{\to }{\mathop{O}}\,$的元素都是定义在有限域Fp上的.生成矩阵G的矩阵条目则从有限域Zp中随机选取.
EC-E的生成矩阵G同样由编码器按如下方式生成.首先,对每行来说,编码器随机选取一个条目,标记为1,重复执行这个置换过程anlnk/k次(一个条目可以被标记多次),此处,a为常数.然后,编码器随机为每个标记过的条目设定一个有限域Zp内的值.
编码过程可以表示为
| $[{{w}_{1}},{{w}_{2}},...,{{w}_{n}}]=[{{m}_{1}},{{m}_{2}},...,{{m}_{k}}]\left[ \begin{matrix} {{g}_{1,1}} & {{g}_{1,2}} & ... & {{g}_{1,n}} \\ {{g}_{2,1}} & {{g}_{2,2}} & ... & {{g}_{2,n}} \\ ... & ... & ... & \cdots \\ {{g}_{k,1}} & {{g}_{k,2}} & ... & {{g}_{k,n}} \\ \end{matrix} \right]({{w}_{1}},{{w}_{2}},...,{{w}_{n}}\in G,{{w}_{i}}=m_{1}^{{{g}_{1,i}}},m_{2}^{{{g}_{2,i}}},...,m_{k}^{{{g}_{k,i}}}).$ |
解码时,解码器随机获取生成矩阵G的k列数据j1,j2,…,jk及相应的码字元素${{w}_{{{j}_{1}}}},{{w}_{{{j}_{2}}}},...,{{w}_{{{j}_{k}}}}.$利用所获得的k列矩阵数据构造kxk矩阵K,计算矩阵K的逆,令${{K}^{-1}}={{[{{d}_{i,j}}]}_{1\le i,j\le k}},$解码过程按如下方式进行:
| $[{{m}_{1}},{{m}_{2}},...{{m}_{k}}]=[{{w}_{{{j}_{1}}}},{{w}_{{{j}_{2}}}},...{{w}_{{{j}_{k}}}}]\left[ \begin{matrix} {{d}_{1,{{j}_{1}}}} & {{d}_{1,{{j}_{2}}}} & ... & {{d}_{1,{{j}_{k}}}} \\ {{d}_{2,{{j}_{1}}}} & {{d}_{2,{{j}_{2}}}} & ... & {{d}_{2,{{j}_{k}}}} \\ ... & ... & ... & ... \\ {{d}_{k,{{j}_{1}}}} & {{d}_{k,{{j}_{2}}}} & ... & {{d}_{k,{{j}_{k}}}} \\ \end{matrix} \right].$ |
解码的过程即为计算${{m}_{i}}=w_{{{j}_{1}}}^{{{d}_{1,i}}},w_{{{j}_{2}}}^{{{d}_{2,i}}},...,w_{{{j}_{k}}}^{{{d}_{k,i}}}$的过程.成功解码的概率即为选取的kxk子阵可逆的概率,类似于分布式纠删码,成功解码的概率至少为1-k/p-O(1).
下面给出SCSM-DCF应用EC-E的实例.
设有两条消息(M1,M2)存储到3台服务器(SS1,SS2,SS3)中,消息M1和M2随机分配给存储服务器SS1,SS2和SS3,存储服务器为接收到的消息随机选取系数g1,1,并以同样的方式为接收到的数据选取系数,计算最后的码字后,存储最后的编码结果及系数向量.
由于解码器只需要矩阵G的k列数据以及它们相应的码字元素来解码,因此能够抵抗(n-k)个删除错误,而且每个码字元素wi都可以由不同的存储服务器独立产生.
SCSM-DCF按如下方式使用随机纠删码:若数据拥有者存储k条信息Mi(1≤i≤k).对每个Mi,数据拥有者随机选取v台存储服务器(可重复),然后发送Mi的副本给每台被选中的服务器.每台存储服务器为每个接收到的信息随机选取一个系数,然后将所有接收到的消息线性结合.这些服务器随机选取的系数形成了矩阵的一列,线性结合的结果是一个码字.由于共有n台服务器,则一个kxn的生成矩阵以及n个码字就形成了,并且每台服务器可以独立地执行这种计算.
2.3.2 门限公钥加密方案本文使用的门限公钥加密方案TPKE由6种算法构成:SetUp,KeyGen,ShareKeyGen,Enc,ShareDec,Combine.下面分别对这些算法进行描述.
(1) SetUp算法:生成系统参数u.
| $u=(p,{{G}_{1}},{{G}_{2}},\widetilde{e},g).$ |
(2) KeyGen算法:为每位用户生成一对密钥,包括公钥PK和私钥SK.
| $PK={{g}^{x}},SK=x,x\in {}_{R}{{Z}_{p}}.$ |
(3) ShareKeyGen算法:用户通过该算法将其私钥SK分割为m个密钥分片,其中任意t个分片便可以恢复得到SK.
(4) Enc算法:使用公钥PK对给定消息进行加密,输出密文;
(5) ShareDec算法:使用密钥分片对给定的密文执行部分解密,输出解密分片;
(6) Combine算法:算法的输入为一组解密分片,当且仅当至少有t个解密分片存在时,算法可以正确运算,输出原始消息.
下面给出门限公钥加密方案TPKE的执行过程.
Step 1. 运行SetUp(1λ)算法,生成系统参数u,$u=(p,{{G}_{1}},{{G}_{2}},\widetilde{e},g).$
Step 2. 运行KeyGen(u)算法,为用户生成公/私钥对:
| $PK={{g}^{x}},SK=x,x\in {}_{R}{{Z}_{p}}.$ |
Step 3. 运行ShareKeyGen(SK,t,m)算法.密钥分片由多项式f(z)计算而得:
| $f(z)=SK+{{a}_{1}}z+{{a}_{2}}{{z}^{2}}+...+{{a}_{t-1}}{{z}^{t-1}}(mod~\text{ }p),{{a}_{1}},{{a}_{2}},...{{a}_{t-1}}{{\in }_{R}}{{Z}_{p}}.$ |
Step 4. 运行Enc(PK,M)算法,对消息M$\in $G2进行加密得到密文C,其中,C按如下方式计算得到:
| $C=(\alpha ,\beta ,\gamma )=({{g}^{r}},h,M\widetilde{e}({{g}^{x}},{{h}^{r}})),r\in {}_{R}{{Z}_{p}},h\in {}_{R}{{G}_{1}}.$ |
Step 5. 运行ShareDec(SKi,C)算法,使用密钥分片对给定的密钥文件执行部分解密,输出解密分片.令C=(a,b,g),通过使用密钥分片SKi,密文C的解密分片Vi可以通过如下方式获得:
| ${{\varsigma }_{i}}=({{\alpha }_{i}},{{\beta }_{i}},{{{\beta }'}_{i}},{{\gamma }_{i}})=(\alpha ,\beta ,{{\beta }^{S{{K}_{i}}}},\gamma ).$ |
Step 6. 运行$\operatorname{Combine}({{\varsigma }_{{{i}_{1}}}},{{\varsigma }_{{{i}_{2}}}},...,{{\varsigma }_{{{i}_{t}}}})$算法,结合t个解密分片的值$({{{\beta }'}_{{{i}_{1}}}},{{{\beta }'}_{{{i}_{2}}}},...,{{{\beta }'}_{{{i}_{t}}}}),$通过对指数位置运用拉格朗日插值算法,计算得到${{\beta }^{SK}}={{\beta }^{f(0)}}:$
| ${{\beta }^{SK}}=\prod\limits_{i\in S}{\left( {{({{{{\beta }'}}_{i}})}^{\prod\nolimits_{r\in S,r\ne i}{\frac{-r}{i-r}}}} \right)},S=\{{{i}_{1}},{{i}_{2}},...,{{i}_{t}}\}.$ |
对于任意1≤j≤t,都有${{\varsigma }_{{{i}_{j}}}}=({{\alpha }_{{{i}_{j}}}},\beta ,{{(\beta {)}'}_{{{i}_{j}}}},{{\gamma }_{{{i}_{j}}}}).$
最终输出为$M={\gamma }/{\widetilde{e}(\alpha ,{{\beta }^{f(0)}})}\;.$
h值相同的同一组密文,具有乘法同态的性质,即,给定M1和M2的密文,可以在不知道私钥x,M1和M2的条件下计算得到M1xM2的密文.令${{C}_{1}}=Enc(PK,{{M}_{1}}),{{C}_{2}}=Enc(PK,{{M}_{2}}),$这里,${{C}_{1}}=({{g}^{{{r}_{1}}}},h,{{M}_{1}}\widetilde{e}({{g}^{x}},{{h}^{{{r}_{1}}}})).$在公钥PK已知的条件下计算得到M1xM2的密文C.
| $C=({{g}^{{{r}_{1}}}}{{g}^{{{r}_{2}}}},h,{{M}_{1}}\widetilde{e}({{g}^{x}},{{h}^{{{r}_{1}}}}){{M}_{2}}\widetilde{e}({{g}^{x}},{{h}^{{{r}_{2}}}}))=({{g}^{{{r}_{1}}+{{r}_{2}}}},h,{{M}_{1}}{{M}_{2}}\widetilde{e}({{g}^{x}},{{h}^{{{r}_{1}}+{{r}_{2}}}})).$ |
SCSM-DCF的实体间通信协议包括数据存储协议和数据获取协议.
2.4.1 数据存储协议在SCSM-DCF中,存储k条消息的过程如下.
Step1. 数据加密.用户通过门限公钥加密方案TPKE对hID相同的k条消息进行加密,这里,
| ${{h}_{ID}}=H({{M}_{1}}||{{M}_{2}}||...||{{M}_{k}}),$ |
是一组消息M1,M2,…,Mk的标识符.消息Mi的密文为
| ${{C}_{i}}=({{\alpha }_{i}},\beta ,{{\gamma }_{i}})=({{g}^{{{r}_{i}}}},{{h}_{ID}},{{M}_{i}}\widetilde{e}({{g}^{x}},h_{ID}^{r})),{{r}_{i}}\in {}_{R}{{Z}_{p}},1\le i\le k.$ |
Step 2. 密文分发.对于每个Ci,用户随机选取v台存储服务器,并将Ci的副本发送给所选服务器.
Step 3. 编码.存储服务器SSj将接收到的所有具有相同hID的密文分组为Nj.存储服务器SSj为每条密文Ci$\in $Nj从Zp中随机选取系数gi,j,对于Ci$\notin $Nj,设定gi,j=0.最终形成指数纠删码的生成矩阵$G={{[{{g}_{i,j}}]}_{1\le i\le k,1\le j\le n}}.$
每台存储服务器计算(Aj,Bj),并存储数据sj.
| ${{A}_{j}}=\prod\limits_{{{C}_{i}}\in {{N}_{j}}}{\alpha _{i}^{{{g}_{i,j}}}},{{B}_{j}}=\prod\limits_{{{C}_{i}}\in {{N}_{j}}}{\gamma _{i}^{{{g}_{i,j}}}},{{\sigma }_{j}}=({{A}_{j}},{{h}_{ID}},{{B}_{j}},({{g}_{1,j}},{{g}_{2,j}},...,{{g}_{k,j}})).$ |
$({{A}_{j}},{{h}_{ID}},{{B}_{j}})$是$\prod\nolimits_{1\le i\le k}{M_{i}^{{{g}_{i,j}}}}$的密文,这是因为:
| $\begin{align} & ({{A}_{j}},{{h}_{ID}},{{B}_{j}})=\left( {{\prod\limits_{{{C}_{i}}\in {{N}_{j}}}{({{g}^{{{r}_{i}}}})}}^{{{g}_{i,j}}}},{{h}_{ID}},{{\prod\limits_{{{C}_{i}}\in {{N}_{j}}}{({{M}_{i}}\widetilde{e}({{g}^{x}},h_{ID}^{{{r}_{i}}}))}}^{{{g}_{i,j}}}} \right) \\ & \text{ }=\left( {{g}^{\prod\nolimits_{{{C}_{i}}\in {{N}_{j}}}{^{{{r}_{i}}{{g}_{i,j}}}}}},{{h}_{ID}},\left( \prod\limits_{{{C}_{i}}\in {{N}_{j}}}{M_{i}^{{{g}_{i,j}}}} \right)\left( \widetilde{e}\left( {{g}^{x}},h_{ID}^{\prod\nolimits_{{{C}_{i}}\in {{N}_{j}}}{^{{{r}_{i}}{{g}_{i,j}}}}} \right) \right) \right) \\ & \text{ }=\left( {{g}^{\widetilde{r}}},{{h}_{ID}},\left( \prod\limits_{{{C}_{i}}\in {{N}_{j}}}{M_{i}^{{{g}_{i,j}}}} \right)\widetilde{e}({{g}^{x}},h_{ID}^{\widetilde{r}}) \right),\widetilde{r}=\prod\nolimits_{{{C}_{i}}\in {{N}_{j}}}{{{r}_{i}}{{g}_{i,j}}}. \\ \end{align}$ |
信息加密后,被分布到存储服务器.每台存储服务器将所有接收到的密文所结合,存储最后的结果及所选系数.
2.4.2 数据获取协议Step 1. 获取指令.数据拥有者向m台密钥服务器下达数据获取指令,并将信息标识符hID发送给密钥服务器.
Step 2. 部分解密.每台密钥服务器KSi随机查询u台存储服务器,查询其中标识符为hID的数据,最终从存储服务器处获得至多u份存储数据sj.然后,密钥服务器KSi利用其密钥分片SKi对每条接收到的密文执行算法ShareDec,以获得密文的解密分片.假设密钥服务器KSi接收到储数据sj.KSi将密文(Aj,hID,Bj)解密为解密分片$({{A}_{j}},{{h}_{ID}},h_{ID}^{S{{K}_{i}}}{{B}_{j}}),$然后将数据发送给用户:${{\widetilde{\varsigma }}_{i,j}}=({{A}_{j}},{{h}_{ID}},h_{ID}^{S{{K}_{i}}},{{B}_{j}},({{g}_{1,j}},{{g}_{2,j}},...,{{g}_{k,j}})).$
Step 3. 结合和解码.用户从所有接收数据${{\widetilde{\varsigma }}_{i,j}}$中选取${{\widetilde{\varsigma }}_{{{i}_{1}},{{j}_{1}}}},{{\widetilde{\varsigma }}_{{{i}_{2}},{{j}_{2}}}},...,{{\widetilde{\varsigma }}_{{{i}_{t}},{{j}_{t}}}},$对指数项使用拉格朗日插值,计算:
| $h_{ID}^{SK}=h_{ID}^{f(0)}=h_{ID}^{x},{{i}_{1}}\ne {{i}_{2}}\ne ...\ne {{i}_{t}},S=\{{{i}_{1}},{{i}_{2}},...,{{i}_{t}}\},h_{ID}^{x}=\prod\limits_{i\in S}{{{(h_{ID}^{S{{K}_{i}}})}^{\prod\nolimits_{r\in S,r\ne i}{\frac{-i}{r-i}}}}}.$ |
如果接收到的${{\widetilde{\varsigma }}_{i,j}}$的数量大于t,用户随机选取其中的t份.如果数量小于t,则数据获取失败.得到$h_{ID}^{x}$之后,用户查找接收到的所有数据,选取${{\widetilde{\varsigma }}_{{{i}_{1}},{{j}_{1}}}},{{\widetilde{\varsigma }}_{{{i}_{2}},{{j}_{2}}}},...,{{\widetilde{\varsigma }}_{{{i}_{k}},{{j}_{k}}}},{{j}_{1}}\ne {{j}_{2}}\ne ...\ne {{j}_{k}}.$通过使用$h_{ID}^{x}$,用户将${{\widetilde{\varsigma }}_{i,j}}$解密为wj((i,j)$\in $ {(i1,j1),(i2,j2),…,(ik,jk)}):
| ${{w}_{j}}=\frac{{{B}_{j}}}{\widetilde{e}({{A}_{j}},h_{ID}^{x})}=\prod\limits_{{{c}_{l}}\in {{N}_{j}}}{M_{l}^{{{g}_{l,j}}}}.$ |
这里,$K={{[{{g}_{i,j}}]}_{1\le i\le k,j\in \{{{j}_{1}},{{j}_{2}},...,{{j}_{k}}\}}}.$如果K不可逆,则数据获取过程失败.否则,用户通过以下计算成功获取Mi(1≤i≤k):
| $w_{{{j}_{1}}}^{{{d}_{1,i}}}w_{{{j}_{2}}}^{{{d}_{2,i}}}...w_{{{j}_{k}}}^{{{d}_{k,i}}}=M_{1}^{\sum\nolimits_{l=1}^{k}{g_{1,{{j}_{l}}}^{{{d}_{l,i}}}}}M_{2}^{\sum\nolimits_{l=1}^{k}{g_{2,{{j}_{l}}}^{{{d}_{l,i}}}}}...M_{k}^{\sum\nolimits_{l=1}^{k}{g_{k,{{j}_{l}}}^{{{d}_{l,i}}}}}=M_{1}^{{{T}_{1}}}M_{2}^{{{T}_{2}}}...M_{k}^{{{T}_{k}}}={{M}_{i}},$ |
其中,如果r=i,则${{T}_{r}}=\sum\nolimits_{l=1}^{k}{g_{r,{{j}_{l}}}^{{{d}_{l,i}}}}=1;$否则,Tr=0.
下面举例对上述过程进行描述.在密文分布的过程中,密文C1被分布到存储服务器SS1,SS2和SS3.密文C2被分布到服务器SS2和SS3.在接收到${{\widetilde{\varsigma }}_{1,1}},$${{\widetilde{\varsigma }}_{1,2}},$${{\widetilde{\varsigma }}_{2,2}}$和${{\widetilde{\varsigma }}_{2,3}}$后,用户由${{\widetilde{\varsigma }}_{1,1}}$和${{\widetilde{\varsigma }}_{2,2}}$计算得到$h_{ID}^{x}.$通过使用$h_{ID}^{x}.$用户计算编码后的信息$M_{1}^{{{g}_{1,2}}}M_{2}^{{{g}_{2,2}}}$和$M_{1}^{{{g}_{1,3}}}M_{2}^{{{g}_{2,3}}},$然后将它们解码,获得最终的M1和M2.
3 安全性分析SCSM-DCF的安全性依赖于密钥的加密方案.下面通过定理1证明本文提出的门限公钥加密方案TPKE是安全的.
定理1. 门限公钥加密方案TPKE在标准模型下基于判定性双线性Diffie-Hellman假设是选择明文安全的.
证明:通过反证法进行证明.假定存在算法A能够以2e的优势破解门限公钥加密方案TPKE,赢得CPA安全游戏.则可以构造算法A'以e的优势解决判定性双线性Diffie-Hellman问题.
(1) 初始化(setup)
算法A的输入为(g,gx,gy,gz,Q)以及公共参数$(\widetilde{e},{{G}_{1}},{{G}_{2}},p).$然后A'将(u,PK,t,n)发送给A,这里,$u=(p,{{G}_{1}},$${{G}_{2}},\widetilde{e},g),$PK=gx,t为门限值,n为私钥密钥分片的数量.在这里隐含着SK=x.
(2) 密钥共享查询(key share query)
为应答A针对(t-1)个密钥分片的查询${{q}_{1}},{{q}_{2}},...,{{q}_{t-1}},$A'设置$S{{K}_{{{q}_{1}}}},S{{K}_{{{q}_{2}}}},...,S{{K}_{{{q}_{t-1}}}}$为随机值,并发送给A.为不失一般性,这里假定${{q}_{1}},{{q}_{2}},...,{{q}_{t-1}}$互不相同.
(3) 挑战(challenge)
A给定两条信息M0和M1.A'随机选取b$\in ${0,1},计算加密后的Mb:
| $C=Enc(PK,{{M}_{b}})=({{g}^{y}},{{g}^{z}},{{M}_{b}}Q).$ |
(4) 输出(output)
A'将C发送给A,获取A的输出b'.如果b'=b,那么,A'猜测$Q={{Q}_{0}}=\widetilde{e}{{(g,g)}^{xyz}},$输出0.如果b'≠b,那么A'猜测$Q={{Q}_{1}}=\widetilde{e}{{(g,g)}^{r}},$输出1.
当$Q={{Q}_{0}}=\widetilde{e}{{(g,g)}^{xyz}}$时,C是Mb的密文;因此,A有2ε的优势赢得游戏,即,$\Pr [{b}'=b\text{ }\!\!|\!\!\text{ }Q=\widetilde{e}{{(g,g)}^{xyz}}]={1}/{2}\;+2\varepsilon ,$对于任意值r,当$Q={{Q}_{1}}=\widetilde{e}{{(g,g)}^{r}}$时,$({{g}^{y}},{{g}^{z}},{{M}_{0}}Q)$和$({{g}^{y}},{{g}^{z}},{{M}_{1}}Q)$是不可区分的,因为对于任意r,存在r'使得${{M}_{0}}\widetilde{e}{{(g,g)}^{r}}={{M}_{1}}\widetilde{e}{{(g,g)}^{{{r}'}}}.$因此,有$\Pr [{b}'=b\text{ }\!\!|\!\!\text{ }Q=\widetilde{e}{{(g,g)}^{r}}]={1}/{2}\;.$
A'的优势为
| $|\Pr [{A}'\to 0|Q={{Q}_{0}}]\Pr [Q={{Q}_{0}}]+\Pr [{A}'\to 1|Q={{Q}_{1}}]\Pr [Q={{Q}_{1}}]-{1}/{2}\;|=|({1}/{2}\;+2\varepsilon )\times {1}/{2}\;+{1}/{2}\;\times {1}/{2}\;-{1}/{2}\;|=\varepsilon .$ |
通过上面证明,可知本文提出的门限公钥加密方案是安全的,因此SCSM-DCF也是安全的.
4 代价与性能分析 4.1 代价分析在进行代价分析前,首先给出相关符号描述,见表 1.
| Table 1 Symbols 表 1 符号表 |
4.1.1 计算代价
下面通过G1和G2群中的对数运算、模指数运算,G1和G2群中的模乘运算,以及GF(p)域上的算术运算数量来分析SCSM-DCF的计算代价.分别用Pairing,Exp1,Exp2,Mult1,Mult2以及Fp来代表这些运算操作.这是因为数据存储和获取过程都是针对包含k条消息的一组数据的,因此以k条信息为单位,研究其计算代价.事实上,Fp代价远比Mult1和Mult2要低.平均来讲(通过使用最快的平方和乘法算法),Exp1约等同于1.5(log2p)Mult1.同样,Exp2约等同于1.5(log2p)Mult2.
由于在实际操作过程中系数可以从一个较小的集合中选取,Exp1和Exp2计算代价的衡量是高于实际情况的.Pairing的计算代价远比Exp要高.然而,为提高对数运算的速度,学者们已经提出了改进的算法.
SCSM-DCF的计算代价见表 2.
| Table 2 Computation cost of SCSM-DCF 表 2 SCSM-DCF的计算代价 |
数据存储过程中,对于每条加密的信息,产生∂i需要一次Exp1;产生γi需要一次Exp1、一次Pairing和一次Mult2.因此,在k条信息的加密过程中,计算代价为(kPairing+2kExp1+kMult2).在密文分发阶段,没有计算代价产生.编码阶段,每台SSi对所有接收到的密文进行编码.在这里做最坏的估计,即每台SSi接收到k条密文.为计算Ai,SSi需要kExp1和(k-1)Mult1,为计算Bi,计算代价为kExp2和(k-1)Mult2.
部分解密阶段,每台KSi执行一次Exp1以获取$h_{ID}^{S{{K}_{i}}}.$对于一次成功的数据获取,至少需要t台密钥服务器.因此,这一过程考虑t台密钥服务器的整体代价,即tExp1.对于结合和解码阶段,将它分为两步:结合子步骤和解码子步骤.结合的过程包括计算$h_{ID}^{x}$和由解密分片${{\widetilde{\varsigma }}_{i,j}}$计算码字元素wj.$h_{ID}^{x}$的计算是通过使用G1中的拉格朗日插值算法,需要$O({{t}^{2}})F(p)$、tExp1以及(t-1)Mult1.由Aj、Bj和$h_{ID}^{x}$计算wj需要一次Pairing、一次模除法;一次模除法运算需要两次Mult2.解码过程包括矩阵求逆和由码字元素wj计算消息Mi.矩阵求逆消耗GF(p)域上的O(k3)次算术运算,每条信息解码需要kExp2和(k-1)Mult2.
4.1.2 存储代价下面对SCSM-DCF的存储代价进行分析.
某特定用户在密钥服务器的存储代价为log2p,因为密钥服务器只需要存储私钥的密钥分片.主要的存储开销在于存储服务器.
用比特值作为单位来衡量存储服务器的平均存储开销.若存储k条信息,每台存储服务器SSi需要存储Aj,hID,Bj(Aj,hID$\in $G1;Bj$\in $G2)以及系数向量(g1,j,g2,j,…,gk,j).存储服务器的总代价为
| $2{{l}_{1}}+{{l}_{2}}+k\left( lo{{g}_{2}}p \right)$ |
因此,每条消息的平均存储代价为(2l1+l2+k(log2p))/kl2比特,对于足够大的k,这个值取决于log2p/l2.
4.2 性能分析通过相关实验对本文提出的模型进行性能分析.在进行实验测试之前首先介绍实验环境.模型中的客户端和服务器端分别运行在两台配置一样的主机上,主机装载了Windows 7旗舰版64位操作系统,CPU为Pentium E5800,内存为4G.测试的每一组数据均是程序在单独线程中运行结果的记录,而且每一个数据均是10次运行结果的平均值,其中排除了明显错误的数据.
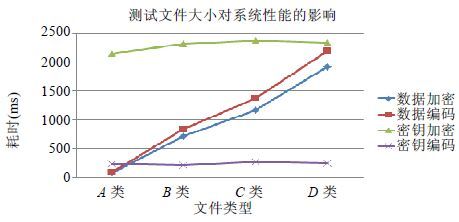
实验1.测试文件大小对系统性能的影响.实验数据分为4组,第1组为1KB~10KB大小的文件,记为A类文件,第2组为100KB~200KB的文件,记为B类文件,第3组为300KB~400KB的文件,记为C类文件,第4组为1000KB~2000KB之间的文件,记为D类文件.每类文件数量均为10个.利用上述文件进行存储测试,得到加密(采用AES加密)和编码操作的时间开销,结果如图 2所示.
|
Fig. 2 Effects of file size on system performance 图 2 文件大小对系统性能的影响 |
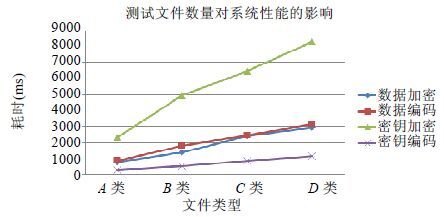
实验2.测试文件数量对系统性能的影响.实验数据分为5组,第1组为10个文件,第1组为20个文件,依次到第5组为50个文件,每组文件的大小均在100KB~200KB之间,实验结果如图 3所示.
|
Fig. 3 Effects of the number of files on system performance 图 3 文件数量对系统性能的影响 |
从图 2中可以看出,随着文件体积的逐渐增大,数据加密和编码操作的耗时呈现递增趋势.这是由于AES加密属于分组加密,随着文件体积的增长,分组数量增多,处理时间相应增长,EC-E编码同样是分组进行读取的,当文件大小超过缓冲区设置,则编码耗费时间随着文件体积的增长而增加.密钥加密和编码的操作随着文件体积的增大均呈现水平趋势,这是因为密钥的大小是固定的,而密钥的数量与文件的数量相关,在文件数量相同的条件下,文件的体积对密钥的相关操作并无影响.
由图 3可知,随着文件集合的不断增大,数据加密和编码操作耗时不断递增.密钥加密和编码的耗时同样呈现递增趋势.由此可知,随着文件数量的不断增大,无论是对文件还是密钥的操作,耗时逐渐增加.
本文所提出的SCSM-DCF与传统的云存储系统相比,由于引入机密性和容错性机制,因此在时间和空间上的消耗有一定增加.首先来分析时间代价.由于传统的云存储服务不需要对文件进行处理,直接进行上传,所以其时间代价主要存在于数据传输阶段.而SCSM-DCF上传阶段需要对文件进行加密处理,这部分的时间代价包括主密钥生成、会话密钥生成、主密钥分片、会话密钥加密和文件加密,以20K的文件为例,总计耗时约为3.38ms(多次计算取平均值).文件上传到服务器后,服务器端需要对文件和密钥进行冗余编码,总计耗时约为1.05ms(多次计算取平均值).与传统云存储服务相比,虽然SCSM-DCF在时间代价上有所增加,但仍是可接受的;同时,系统的安全性有较大幅度提升.下面分析SCSM-DCF在空间上的代价开销.SCSM-DCF需要额外的空间来存储编码结构,包括数据编码结果,会话密钥编码结果以及主密钥分片后的子密钥.但是在相同容错概率的前提下,使用指数纠删码比备份机制更能提高空间利用率.以数据编码为例,系统将数据分为8块,编码结果12块,即系统提供的数据容错率为75%,若每个编码结果大小为10K,若想使用副本技术提供相同的容错率,系统需要为所有的8块源数据存储2份完整的副本,共需要16份10K大小的空间,而SCSM-DCF使用的指数纠删码技术只需要使用4份10K大小的存储空间,存储空间的利用率提高了75%.
5 结束语针对现有云存储中的数据安全问题,提出了一种同时满足机密性与容错性要求的安全储模型,既能解决云存储系统中的数据机密性问题,又能抵抗服务器失效故障等问题.在模型中,数据都是以加密、编码后的形式进行存储,存储服务器无法拥有解码密钥,访问权管理完全由用户控制,即使所有服务器同时被敌手控制,数据的机密性也能得到充分保障.由于,融合基于指数的纠删码技术,系统同时具有容错能力,即使系统数据遭到破坏,仍能在允许的范围内得到有效恢复.因此,本模型的提出对于当前的云存储中的数据安全问题有一定理论意义和实际应用价值.
| [1] | Li H, Sun WH, Li FH, Wang BY. Secure and privacy-preserving data storage service in public cloud. Journal of Computer Research and Development, 2014, 51 (7) :1397–1409 . |
| [2] | Fu YX, Luo SM, Shu JW. Survey of secure cloud storage system and key technologies. Journal of Computer Research and Development, 2013, 50 (1) :136–145 . |
| [3] | Feng DG, Zhang M, Zhang Y, Xu Z. Study on cloud computing security. Ruan Jian Xue Bao/Journal of Software, 2011, 22 (1) :71–83 . [doi:10.3724/SP.J.1001.2011.03958] |
| [4] | Julisch K, Hall M. Security and control in the cloud. Information Security Journal: A Global Perspective, 2010, 19 (6) :299–309 . [doi:10.1080/19393555.2010.514654] |
| [5] | Yu NH, Hao Z, Xu JJ, Zhang WM, Zhang C. Review of cloud computing security. Acta Electronica Sinica, 2013, 41 (2) :371–381 . |
| [6] | Padilha R, Pedone F. Confidentiality in the cloud. IEEE Security & Privacy, 2015, 13 (1) :57–60 . [doi:10.1109/MSP.2015.4] |
| [7] | Wang HB, Cao ZF, Wang LC. Multi-Use and unidirectional identity-based proxy re-encryption. Information Sciences, 2010, 180 (20) :4042–4059 . [doi:10.1016/j.ins.2010.06.029] |
| [8] | Zhu WT. Towards secure and communication-efficient broadcast encryption systems. Journal of Network and Computer Applications, 2013, 36 (1) :178–186 . [doi:10.1016/j.jnca.2012.09.007] |
| [9] | Wei HJ, Liu WF, Hu XX. Forward-Secure ciphertext-policy attribute-based encryption scheme. Journal on Communications, 2014, 35 (7) :38–45 . |
| [10] | Gentry C. Fully homomorphic encryption using ideal lattices. In: Proc. of the STOC 2009. Bethesda: ACM Press, 2009. 169-178. [doi: 10.1145/1536414.1536440] |
| [11] | Boneh D, Crescenzo GD, Ostrovsky R, Persiano G. Public key encryption with keyword search. In: Proc. of the EUROCRYPT 2004. Interlaken: Springer-Verlag, 2004. 506-522. [doi: 10.1007/978-3-540-24676-3_30] |
| [12] | Li J, Wang Q, Wang C, Cao N, Ren K , Lou WJ. Fuzzy key word search over encrypted data in cloud computing. In: Proc. of the INFOCOM 2010. San Diego: IEEE Press, 2010. 441-445. [doi: 10.1109/INFCOM.2010.5462196] |
| [13] | Wang C, Cao N, Li J, Ren K, Lou WJ. Secure ranked keyword search over encrypted cloud data. In: Proc. of the ICDCS 2010. Genova: IEEE Computer Society, 2010. 253-262. [doi: 10.1109/ICDCS.2010.34] |
| [14] | Cao N, Wang C, Li M, Ren K, Lou WJ. Privacy-Preserving multi-keyword ranked search over encrypted cloud data. In: Proc. of the INFOCOM. Shanghai: IEEE Computer Society, 2011. 829-837. [doi: 10.1109/INFCOM.2011.5935306] |
| [15] | Li M, Yu SC, Cao N, Lou WJ. Authorized private keyword search over encrypted data in cloud computing. In: Proc. of the ICDCS 2011. Minneapolis: IEEE Computer Society, 2011. 383-392. [doi: 10.1109/ICDCS.2011.55] |
| [16] | Tan PX, Chen Y, Lan JL, Jia HY. Secure fault-tolerant code for cloud storage. Journal on Communications, 2014, 35 (3) :109–115 . |
| [17] | Weatherspoon H, Kubiatowicz JD. Erasure coding vs. replication: A quantitative comparison. In: Proc. of the 1st Int´l Workshop on Peer to Peer Systems. Cambridge: Springer-Verlag, 2002. 328-337. [doi: 10.1007/3-540-45748-8_31] |
| [18] | Yang DR, Wang Y, Liu P. Fault-Tolerant mechanism combined with replication and error correcting code for cloud file systems. Journal of Tshinghua University (Sci. & Technol.), 2014, 54 (1) :137–144 . |
| [1] | 李晖, 孙文海, 李凤华, 王博洋. 公共云存储服务数据安全及隐私保护技术综述. 计算机研究与发展, 2014,51 (7) :1397–1409. |
| [2] | 傅颖勋, 罗圣美, 舒继武. 安全云存储系统与关键技术综述. 计算机研究与发展, 2013,50 (1) :136–145. |
| [3] | 冯登国, 张敏, 张妍, 徐震. 云计算安全研究. 软件学报, 2011,22 (1) :71–83. [doi:10.3724/SP.J.1001.2011.03958] |
| [5] | 俞能海, 郝卓, 徐甲甲, 张卫明, 张驰. 云安全研究进展综述. 电子学报, 2013,41 (2) :371–381. |
| [9] | 魏江宏, 刘文芬, 胡学先. 前向安全的密文策略基于属性加密方案. 通信学报, 2014,35 (7) :38–45. |
| [16] | 谭鹏许, 陈越, 兰巨龙, 贾洪勇. 用于云存储的安全容错编码. 通信学报, 2014,35 (3) :109–115. |
| [18] | 杨东日, 王颖, 刘鹏. 一种副本复制和纠错码融合的云存储文件系统容错机制. 清华大学学报(自然科学版), 2014,54 (1) :137–144. |
 2016, Vol. 27
2016, Vol. 27


