2 广西大学 计算机与电子信息学院, 广西 南宁 530004
2 School of Computer, Electronics and Information, Guangxi University, Nanning 530004, China
云计算作为一种新型的网络计算模式,以一种比传统IT更经济的方式向用户提供按需的IT服务(计算、存储和应用等).由于云计算的发展理念符合当前低碳经济与绿色计算的总体趋势,它得到了世界各国政府和企业的大力倡导与推动,正带来计算领域和商业领域的巨大变革.
但在已经实现的云计算服务中,隐私安全问题一直令人担忧,并已经成为阻碍云计算发展和推广的主要因素之一.用户的隐私数据包括可用来识别或定位个人的信息(例如电话号码、地址和信用卡号等)、敏感的信息(例如个人的健康状况、财务信息、公司的重要文件等).云计算的隐私安全问题源于云计算的数据外包和服务租赁的特点.用户数据存储到云环境中,人们失去了对数据的直接控制力,可能会导致个人隐私数据的泄露和滥用.而近年来发生的Google,MediaMax和Salesforce.com等云服务商泄露或丢失用户数据的事实证实了人们的担心[1].加密是一种常用的保护用户隐私数据的方法,但目前的大多数加密方案都不支持对密文的运算,如对加密的数据进行检索、对加密的公司财务信息进行排序等统计分析,因而严重妨碍了云服务商为用户提供更进一步的数据管理和运算服务,从而削弱了云计算的优势.针对上述问题,本文提出一种基于随机树的保序加密算法OPEART(order-preserving encryption algorithm based on random tree).OPEART通过树状结构组织数据,同时,通过随机地为树中节点分配大小不同的区域实现对数据的加密.该算法支持对加密数据的任何关系运算(==,>,<,<=,>=等),特别适用于云计算环境中的大型数据库,方便建立索引和快速检索.
本文第1节回顾相关研究的进展情况.第2节建立支持隐私保护的网络计算模型和攻击模型.第3节定义OPEART并介绍其具体实现.第4节和第5节分别就OPEART的安全性和性能进行评估.第6节做出总结.
1 相关工作对于加密数据的关系运算问题,目前已有一些研究成果,可以大致分为以下几类:(1) 支持精确匹配的加密算法;(2) 保序的最小完美哈希函数;(3) 保序的加密算法;(4) 不保序的加密算法;(5) 借助索引的方法.
(1) 支持精确匹配的加密算法
Song等人[2]提出了基于对称加密和数据异或运算的加密关键字检索算法;Boneh等人[3]提出了基于双线性映射的加密关键字检索算法PEKS;Ohtaki等人[4]使用BloomFilter来存储关键字的各种布尔组合信息,从而实现了支持逻辑运算的密文检索;Liu等人[5]提出了基于双线性映射的加密关键字检索算法EPPKS,它是在PEKS的基础上增加了对外包数据(而不仅仅是外包数据的关键字)的加密部分,并让服务提供者参与了一部分解密工作,减轻了用户的计算负载.以上算法都只支持关系运算中的“==”比较,功能较为单一,不能完全解决云计算环境中对密文数据的关系运算问题.
(2) 保序的最小完美哈希函数
假设一个集合S有m个关键字,一个有n个桶的哈希函数h是保序的最小完美哈希函数需满足:
i) h:S®n是单射函数;
ii) m=n;
iii) 如果x<y,那么h(x)<h(y).
Belazzougui等人[6]通过建立相关分级树和前缀匹配的方法实现了一个单调变化的最小完美哈希函数,该函数没有隐藏原数据的值,而是把该数据映射到与该值相近的桶中.Czech等人[7,8]通过以两个任意函数的函数值作为顶点构造带权无环图实现了一个保序的最小完美哈希函数,该函数能够很好地隐藏原数据的值,但是要构造一个无环图可能需要多次尝试.以上的哈希函数都是针对静态数据域的,计算复杂度随着数据域中元素个数的增加而增长,当数据域很大或者动态变化时,保序的最小完美哈希函数的方法是不适用的.另外,要用哈希函数来实现对数据的加解密运算,需要保存一份映射表,这无疑增加了数据拥有者的存储负载.
(3) 保序的加密算法
Agrawal等人[9]基于桶划分和分布概率映射的思想提出了一种保序对称加密算法OPES,支持对加密数值数据的各种关系运算,其不足是:当定义域较大时,桶划分的计算负载较大;而且面对已知明文的攻击时,当输入分布的桶与对应的输出分布的桶中点的个数足够多时,可以通过解方程的方式破解.Boldyreva等人[10,11]提出了一种基于折半查找和超几何概率分布的保序对称加密算法OPSE,支持对加密数据的各种关系运算,但由于在计算超几何概率时需要进行多次组合运算,其计算负载较大.以上两种保序的加密方法的优点是保序性,即,密文反映了明文的大小关系,从而方便服务提供者对密文数据建立索引,加快查找速度,并易于实现各种关系运算;不足是,它们都不能同时满足高效性和安全性的要求.
(4) 不保序的加密算法
Wong等人[12]设计了一个基于向量标量积的对称加密方案,该方案支持对加密数据库进行KNN(k-nearest neighbor)计算,具有IND-CCA安全性,其不足是:
i) 只能对对象之间的距离进行比较,并不支持两对象本身的比较;
ii) 由于该算法是IND-CCA安全的,数据加密后具有不确定性和不保序性,因此要找到满足条件的数据,
必须搜索整个数据库,这对于大型数据库来说是不现实的.
Boneh等人[13,14]基于双线性映射理论实现了支持关系运算检索的加密方案,它们的优点是具有IND-CCA安全性,缺点是:
i) 计算复杂度高;
ii) 数据加密后具有不确定性和不保序性,服务提供者必须对表中的所有数据进行遍历才能找到符合条
件的数据,效率很低.
Shi等人[15]提出了一个Interval tree的概念,并基于双线性映射原理实现了支持关系运算检索的加密方案.该方案的优点是IND-CCA安全的,缺点是:
i) Interval tree只能定义在静态数据域上;
ii) 计算复杂度高;
iii) SP必须对表中的所有数据进行遍历才能找到符合条件的数据.
通过以上分析可知,不保序的加密算法的优点是安全性高(IND-CCA),缺点是:
i) 计算负载大;
ii) 要对整个表进行遍历才能找到满足要求的所有数据,这对于大型数据库来说是不现实的.
(5) 借助索引的方法
Wang等人[16]针对XML数据库提出了一个安全的加密方案:
i) 采用任意一种确定的对称加密算法加密外包数据;
ii) 为了快速定位,构建可用于结构检索的结构索引和可用于数值比较的值索引.
该方案的不足是:
i) 需要服务提供者开辟额外的存储空间存放索引,且当数据发生变化时,数据拥有者要重新建立索引;
ii) 在建立值索引时采用了保序的加密算法,因此具有这类算法的不足.
Hacıgümüş等人[17]将关系数据库中表的属性分为5类,并采用不同的加密方式:
i) 对于需要进行聚合型运算(SUM,AVG)的属性,采用隐私同态方案[18]加密;
ii) 对于需要进行精确匹配的属性,采用确定的对称加密算法来加密;
iii) 对于需要进行关系运算的属性,建立一个粗粒度的索引,将整个数据域分为若干段,每一段给一个编
号,用编号来代替实际的属性值;
iv) 对于不会被单独访问的属性,对整个对象进行加密.
该方案中采用的粗粒度索引不能真正实现关系运算.
Wang等人[19]通过建立索引实现了查找与关键字最相关(例如出现频率)的k个文件的功能,其索引主要包括用哈希函数加密的关键字和用任意一种对称加密算法加密的,包含该关键的文件编号和相关度,其中,为了隐藏真实的相关度,先用改进的OPSE对相关度进行了加密.该方法有以下不足:
i) 建立索引时需要对包含某个关键字的文件进行扫描,从而得到与该关键字相关的信息,例如出现频
率,这增加了用户的计算负担;
ii) 索引占用了服务提供者额外的存储空间;
iii) 当增加或删除与某个关键字相关的文件时,用户必须重新设置并加密索引,这是非常麻烦的事.
以上方法都是借助索引来实现支持关系运算的检索,需要数据拥有者自己建立并维护索引,这增加了数据拥有者的负担,同时也占有了服务提供者额外的存储空间.
针对云计算环境中的大型数据库系统,我们权衡了以上加密算法的利弊,就已有的保序加密算法不能同时满足高效性和安全性的要求,设计了一种随机数据结构——随机树,并构建了基于随机树的保序加密算法OPEART(order-preserving encryption based on random tree),能够满足:
(1) 具有保序性,从而支持大规模数据库的快速检索,并支持各种关系运算;
(2) 安全性介于已有的保序加密算法和不保序的加密算法之间,即IND-DNCPA安全性;
(3) 不需要事先建立额外的索引,减轻Owner的计算和存储负担;
(4) 负载不会随着数据域的变化而变化.
2 问题描述 2.1 支持隐私保护的云计算模型如图 1所示,支持隐私保护的云计算模型反映了数据拥有者(owner)、用户(user)和服务提供者(service provider,简称SP)之间的交互,具体过程如下:
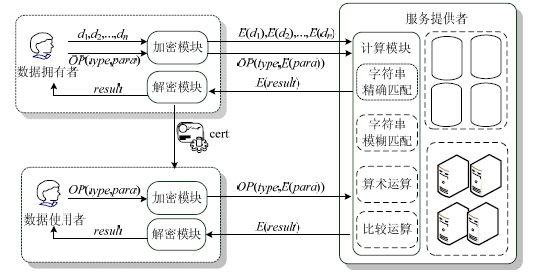 | Fig. 1 Privacy-Preserving calculation model of cloud图 1 支持隐私保护的云计算模型 |
(1) Owner用加密算法E对敏感数据di(iÎ[1,n],n≥1)加密,得到E(di),然后存储到SP的服务器上;
(2) User获得Owner的授权后,对敏感计算参数(para)加密,得到E(para),并将E(para)和计算要求(type)提交给SP;
(3) SP验证User的权限,然后根据User的计算要求,对其权限范围的E(di)和计算参数E(para)进行计算,得到计算结果E(result),并将E(result)返回给User;
(4) User对E(result)进行解密,得到结果的明文result.
在这个过程中,由于Owner和User分别对敏感的外包数据和计算参数进行了加密处理,使得Owner和User的隐私得到了很好的保护.但同时也带来了一个新的问题:SP如何对加密的数据进行计算呢?如果这个问题不能得到有效的解决,Owner和User就不能利用云计算中的计算资源对敏感数据进行处理,从而削弱了云计算的优势.因此,本文提出的支持关系运算的加密算法是解决这一矛盾的关键技术之一.
2.2 威胁模型根据图 1可知,在用户交换的过程中可能存在以下几种隐私攻击:
(1) 数据从Owner传递到SP的过程中,外部攻击者可以通过窃听等方式盗取数据;
(2) 外部攻击者可以通过无授权的访问、木马和钓鱼软件来攻击SP从而获取数据;
(3) Owner和User将数据提交给SP进行存储和运算,SP(内部攻击者)能够获得数据,因此,SP要发起攻击(例如盗取、泄露数据、私自分析和统计数据等)更为容易.
在以上的3种攻击中,第(1)种和第(2)种是传统网络安全中涉及的问题;第(3)种是在云计算模式下出现的新的攻击形式,也是破坏性最大的一种隐私威胁.因此,我们设计的加密算法主要针对第3类攻击,同时能够有效地防御前两种攻击.
3 基于随机树的保序的加密算法OPEART(order-preserving encryption algorithm based on random tree) 3.1 OPEART定义本节将构造一种基于随机树的保序加密算法OPEART.OPEART在确保Owner和User数据安全的前提下,支持对加密数据进行任何关系运算.
定义1(保序的加密算法). 假设加密算法E的定义域为D,E是保序的加密算法,满足:如果x1>x2(x1,x2ÎD),那么E(x1)>E(x2).
定义2(随机树). 随机树(random tree,简称RT)是一棵多叉树,树中每个节点都对应定义域中的一点,并占据值域中的一段区间;树中的子节点区间是对父节点区间的一种随机划分,如图 2所示.RT的定义域为D=[0,4x1012],值域为V且V的大小|V|Î[1016,264](264为long类型的取值范围大小),RT=(Gen,Div)由以下两种算法组成:
(1) RT生成算法Gen:{min,max,level,num}¬Gen(|V|,key),其中,key表示用户的密钥;|V|表示值域的大小; min和max定义了RT的针对key的值域V=[min,max],且min=|V|x(-1)(key mod 2)xrandom(key),max= min+|V|,其中,random(key)Î(0,1);level表示树的高度;num定义了每个节点的子节点的数量,满足:
numlevel≥|D|;
(2) 区间划分算法(iÎZ且iÎ[1,num])}¬Div(nodex,key,i),其中,
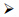 nodex是当前待划分区间的节点,它的4个属性分别是:nodex.value表示该节点对应的明文值,nodex.level表示该节点处于RT中的层数,nodex.min和nodex.max分别表示其区间的最小值和最大值;
nodex是当前待划分区间的节点,它的4个属性分别是:nodex.value表示该节点对应的明文值,nodex.level表示该节点处于RT中的层数,nodex.min和nodex.max分别表示其区间的最小值和最大值;
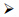 i是待求子节点的编号,即,是nodex的第i个子节点.
i是待求子节点的编号,即,是nodex的第i个子节点.
如图 2所示,随机树首先将整个值域V=[min,max]根据密钥key分为值域vf0和间隔域gf0两部分,然后对vf0按照子节点的个数平均分为num份,再根据key将gf0分为大小不等的m(mÎZ且m≤num)份,并分给随机选择的m个子节点,每一层按照以上原理依次往下分裂.除L=0层外,以下各层分配的值域、间隔域大小以及间隔域的分裂份数和选择哪些子节点由key和该节点本身代表的值共同决定.
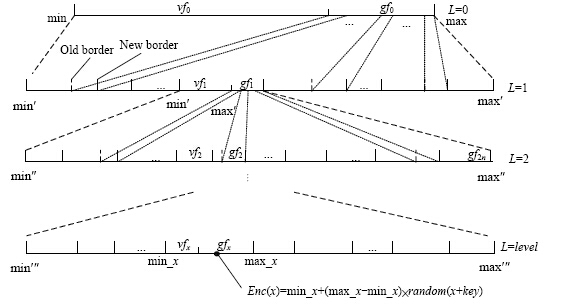 | Fig. 2 Schematic of RT图 2 随机树原理的示例图 |
定义3(OPEART). 设OPEART的定义域为D,值域为V,OPEART=(Gen_RT,Enc,Dec)由以下3种算法组成:
(1) RT生成算法Gen_RT:RT¬Gen(|V|,key),其中,key表示用户的密钥;
(2) 确定的加密算法Enc:"mÎD,c¬Enc(RT,key,m)且cÎV;
(3) 确定的解密算法Dec:对于密文c,m/^¬Dec(RT,key,c),^表示无解.
定义4(IND-DNCPA). 一种加密算法E是IND-DNCPA(indistinguishability under distinct and neighbouring chosen plaintext attack)安全的,如果攻击者A发起以下攻击:
(1) A选择一组明文M={x1,x2,…,xk}(xiÎD,xi¹xj且i,jÎ[1,k])向E进行加密询问,E将加密的结果C={c1,c2,…,ck}返回给A,A不能通过(xi,ci)(iÎ[1,k])解出其他密文c(cÏC)对应的明文;
(2) A选择两个数据m0,m1发给E,其中m1=m0+1,且m0ÏM,m1ÏM;
(3) E随机加密其中一个数据mb(bÎ{0,1}),并将产生的密文cb返回给A;
(4) A输出b¢作为对b的猜测.
A的优势概率定义为
Adv(A)=|Pr[b¢=b]-0.5|=e.
如果e足够小,可忽略不计,则E是IND-DNCPA安全的.
定义5(随机性强度).OPEART基于随机树和用户的密钥为定义域中的每个点分配了大小不等的密文区间,从而实现了对数据的加密,其随机性强度通过以下两个参数来衡量:
(1) 值参数(parameter of value,简称pv):
假设任取连续的k个点{x1,x2,…,xk}(xiÎD,iÎ[1,k],k≥2),定义平均距离d=(Enc(xk)-Enc(x1))/(k-1),点x的参照值可以通过函数f(x)=Enc(& lt; i>x1)+(x-x1)xd计算得到,则有:
| $pv = \frac{k}{{\sum\limits_{i = 1}^k {\sqrt {|Enc{{({x_i})}^2} - f{{({x_i})}^2}|} } }}$ | (1) |
pv反映了OPEART产生的密文与参考值的差距大小,变化越大,pv的值越小,攻击者通过密文猜测明文就越困难.
(2) 值变化参数(parameter of value change,简称pvc):
假设任取连续的k个点{x1,x2,…,xk}(xiÎD,iÎ[1,k],k≥2),平均距离为d=(Enc(xk)-Enc(x1))/(k-1),用d¢= (Enc(xi)-Enc(xi-1))(iÎ[2,k])来表示相邻两点间密文值的差距.假设OPEAT的值域为V,其中共有n个点,则d¢Î[1,V-n].下面将d¢的取值范围[1,V-n]分为5个区间,每个区间赋予一个权值:(0,d/2)的权值为1,(d/2,d)的权值为2,(d,dx3/2)的权值为3,(dx3/2,2xd)的权值为4,(2xd,V-n)的权值为5.假设在以上的k个点对应的密文值的差距中,在以上5个区间中的比例分别为(p1,p2,p3,p4,p5),下面定义值变化参数pvc如下:当pi¹0(iÎ[1,5])时,
| pvc=p1+p2x2+p3x3+p4x4+p5x5 | (2) |
由于平均距离为d,所以平均值变化参数pvcavg为
| pvcavg=2 | (3) |
最大值变化参数pvcmax可通过下面的方程组求出:
| $\left\{ {\begin{array}{*{20}{l}} {p{}_1 + {p_2} + {p_3} + {p_4} + {p_5} = 1}\\ {{p_1} \times \left( {\frac{{0 + \frac{d}{2}}}{2}} \right) + {p_2} \times \left( {\frac{{\frac{d}{2} + d}}{2}} \right) + {p_3} \times \left( {\frac{{d + \frac{{3d}}{2}}}{2}} \right) + {p_4} \times \left( {\frac{{\frac{{3d}}{2} + 2d}}{2}} \right) + {p_5} \times \left( {\frac{{2d + \frac{{5d}}{2}}}{2}} \right) = d} \end{array}} \right.$ | (4) |
解方程(4)可得:
| pvcmax=2.5 | (5) |
因此,当pvc=pvcmax时,密文值之间的差距变化最大.注意,为了方便计算,方程(4)假设第5区间的范围为(2xd,5xd/2],因此pvcmax=2.5;当实际的连续密文距离超过5xd/2时,pvcmax>2.5.这对安全性分析没有影响.
3.2 算法描述本节先对RT的区域划分算法Div(×)进行描述,再对OPEART的加密算法Enc(×)和解密算法Dec(×)进行描述.
1) Div(×)算法用于求出nodex的第i个子节点的区间范围.其原理是:将节点nodex的区间[nodex.min,nodex.max]随机地分为值域vf和间隔域gf两部分,其中,vf部分被均匀的划分为num份;而gf部分则使用密钥key和本节点对应的值作为随机运算的种子,随机地划分为m(mÎZ且m≤num)份并分给随机选择的m个子节点,第j份表示为gfj,其中的第j个子节点的区间大小(nodex.max-nodex.min)/num+gfj.
算法1. RT的区域划分算法Div(×).
输入:待划分区域的节点nodex、密钥key、待求子节点的编号i.
1: min=nodex.min; max=nodex.max;
2: If nodex.level==0 then
3: ran_root=key; //产生随机数的种子
4: Else
5: ran_root=key+nodex.value;
6: End If
7: 根据ran_root分割数据域(min,max)产生值域vf和间隔域gf;
8: d=|vf|/num;
9: 根据ran_root产生间隔域gf的分裂份数m和选择m个子节点:
$Node = \{ nod{e'_{{x_1}}},...,nod{e'_{{x_m}}}\} ,$满足:
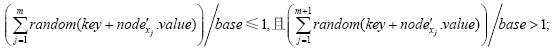
//base为间隔域的分割基数(见第3.3.4节),可调整值参数pv和值间隔参数pvc;
10: For j=0 to ido
11: If $nod{e_{{x_j}}} \in Node$then
12: $nod{e_{{x_j}}}.\min = \min ;$
13: $nod{e_{{x_j}}}.\max = \min + d + |gf| \times random(key + nod{e_{{x_j}}}.value);$
14: Else
15: $nod{e_{{x_j}}}.\min = \min ;$
16: $nod{e_{{x_j}}}.\max = \min + d;$
17: End If
18: $\min = nod{e_{{x_j}}}.\max + 1;$
19: End For
20:$nod{e_{{x_i}}}.value$=nodex.valuenum+i;
21: $nod{e_{{x_i}}}.level$=nodex.level+1;
2) 加密算法Enc(×)对数据进行加密,即,要寻找一条从随机树的根节点到加密数据对应的叶子节点的路径.
算法2. OPEART的加密算法Enc(×).
输入:值域V=[min,max]、随机树RT、密钥key、待加密数据x.
1: 在x的前面补0,使得补位后的x¢满足|x¢|=|max-1|;将x¢分解为RT.level段,第i段的值用x[i]表示;
2: node=noderoot,其中,noderoot.min=min,noderoot.max=max,noderoot.level=0,noderoot.value=0,
3: For L=0 to RT.level do
4: For j=0 to RT.num do //判断x[L]对应node的哪个子节点
5: nodej.value=node.valuexnum+j; //nodej表示node的第j个子节点
5: If x[L]==nodej.value then
6: i=j; break;
7: End If
8: End For
9: node=RT.Div(node,key,i);
10: If L==RT.level then
11: ciphertext=node.min+(node.max-node.min)xrandom(key+x[L]);
12: End If
13: End For
14: return ciphertext;
3) 解密算法Dec(×)也是要寻找一条从随机树的根节点到加密数据对应的叶子节点的路径.
算法3. OPEART的解密算法Dec(×).
输入:值域V=[min,max]、随机树RT、密钥key、待解密数据val.
1: node=noderoot,其中,noderoot.min=min,noderoot.max=max,noderoot.level=0,noderoot.value=0,
2: For L=0 to RT.level do
3: For j=0 to RT.num do //判断val属于node的哪个子节点的区间
4: nodej =RT.Div(node,key,j);
5: If valÎ[nodej.min,nodej.max] then
6: i=j; break;
7: End If
8: End For
9: node= nodej;
10: plaintext=plaintext+node.value; //字符串连接
11: End For
3.3 关键问题 3.3.1 密钥的值域和字符串的基本长度OPEART的密钥key的值域用Vkey来表示.字符串的基本长度len定义了OPEART一次能处理的最长字符串长度.当一个字符串S的长度|S|>len时,在S后补充最少的随机字符得到S¢,满足:|S¢| mod len==0.然后,将S¢分割成(S¢/len)段,每一段字符串作为一个基本字符串进行处理.
密钥的值域和字符串的基本长度直接影响到OPEART算法的安全性强度,分析如下:
攻击者A可能会发起以下两种袭击:
(1) 当A得到一对明密文对(x,c)时,可通过遍历法求出key.假设OPEART加密一次基本字符串所需要的时间为t,则A攻破密钥的平均时间T为
| $T = {\left( {t \times \frac{{|x'|}}{{len}}} \right)^{|{V_{key}}|}}$ | (6) |
其中,x¢是在x后补充随机字符后得到的字符串.根据公式(6)可知,指数越大,T值越大,A攻破密钥的难度就越大.
(2) 当A知道基本字符串长度len后,可以通过密文c的长度lenc判断出明文x的长度lenx;然后,通过分析密文的出现频率和长度为lenx的明文字符的各种组合的使用频率来推断明文x.假设明文字符的集合为Dx,长度为len的字符串加密后的密文长度为lenb,则A要完成以上分析的计算复杂度Oc为
| ${O_c} = O\left( {|{D_x}{|^{\left( {len \times \frac{{le{n_c}}}{{le{n_b}}}} \right)}}} \right)$ | (7) |
根据公式(7)可见,Oc的最小值为O(Dx|len).因此,len越长,A推断明文的难度就越大.
OPEART采用long类型作为密钥key的类型,即:keyÎ[-9223372036854775808,9223372036854775807],|Vkey|=264,字符串的基本长度len=12(由RT的定义域可知).通过实验得出:当RT.level=7,RT.num=100时,OPEART加密一次基本字符串所需要的时间t=0.088ms.假设已知一个长度为len的明密文对,则根据公式(6),A要破解密钥需要2.9亿年;根据公式(7),假设明文字符都是数字,A要进行统计分析,其计算复杂度为O(1012).因此,OPEART采用long类型作为密钥key的类型,字符串的基本长度len=12能够有效抵御以上两种攻击.
3.3.2 RT的高度和宽度的平衡RT的高度指树的层数RT.level,宽度表示每一个节点的子节点数RT.num,假设RT的定义域为D,则:
| |D|=RT.num(RT.level-1) | (8) |
满足公式(8)的RT.num和RT.level的值并不是唯一的,例如,当|D|=1012时,(RT.num,RT.level)可以取以下几种值:v1=(10,13),v2=(100,7),v3=(1000,5),v4=(10000,4).图 3反映了以上几种值对对OPEART加解密性能的影响,其中,length为明文的长度,“Enc_v& lt; /i>1”表示在v1的情况下的加密时间,其他符号以此类推.如图 3所示,(RT.num,RT.level)的取值对加密和解密时间都有影响,对解密时间影响最大.其原因是,根据算法Div(×)的第10步,要判断
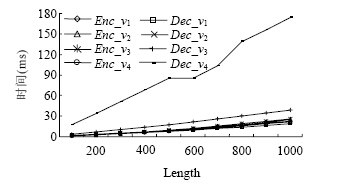 | Fig. 3 Effects of the height and width of RT on OPEART performance图 3 RT的高度和宽度对OPEART性能的影响 |
一个子节点是否属于Node,这是一个遍历的过程,对于加密操作,从根节点找到对应的叶子节点的计算复
杂度为O(RT.numxRT.level);对于解密操作,从根节点找到对应的叶子节点的计算复杂度为O(RT.numxRT.numx RT.level).因此在实现RT的时候,要根据RT的定义域,选择合适的高度和宽度,从而获得较好的效率.
3.3.3 随机数的选取在RT中,划分节点nodex的区间Dx=[nodex.min,nodex.max]时,以密钥key和nodex.value作为选取随机数的根,从而生成随机数ranx(ranxÎR且ranxÎ(0,1 )),然后根据ranx将Dx分为值域vf和间隔域gf两部分.假设nodex的直接子节点和间接子节点的个数为Sumx,为使vf能够容纳下所有子节点且能够保持随机性,ranx应满足如下要求:
(1) 当Sumx/Dx≤0.3时,ranxÎ(0.3,0.7);
(2) 当Sumx/DxÎ(0.3,0.7)时,ranxÎ(Sumx/Dx,0.7);
(3) 当Sumx/Dx≥0.7时,ranxÎ(Sumx/Dx,1).
3.3.4 间隔域的分割基数间隔域的分割基数base(baseÎ[1,RT.num])限定了分割间隔域的最小份数.根据算法1,将间隔域gf根据
ran_root随机分裂为大小不等的m份,再根据ran_root随机选择m个子节点满足:
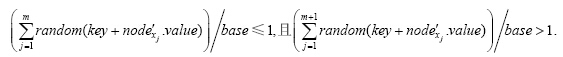
Node中的子节点$nod{e'_{{x_i}}}$可分配得到大小为$|gf| \times random(key + nod{e'_{{x_i}}}.value)$的子间隔,因此,间隔域分裂时产
生的子间隔大小是随机的,分裂份数m是不确定的,但m≥base.间隔域主要用于实现对数据分布的干扰,一方面,m越大,受干扰的子节点就越多;另一方面,如果m太大,那么,虽然受干扰的子节点个数多,但对每个节点的干扰不大.因此,选择合适的分裂基数将直接影响到RT的随机性.
图 4反映了间隔域分裂基数base对RT随机性的影响,其中,
RT1.level=7,RT1.num=100;RT2.level=5,RT2.num=1000.
如图 4(a)和图 4(b)所示,对于RT1来说:
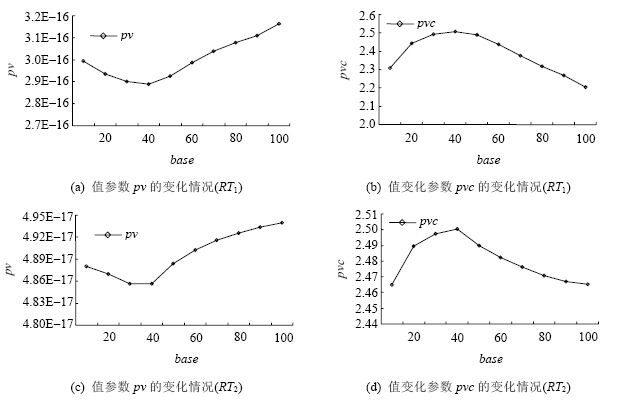 | Fig. 4 Effects of segmentation base on RT randomness图 4 分割基数base对RT随机性的影响 |
· 当base=40时,pv的值最小,pvc的值最大.由RT的随机性强度定义可知,这时,RT1的随机性最好;
· 当base<40时,受干扰的子节点个数不够多,因此随机性不够强;
· 当base>40时,每个节点的干扰区域太小,因此随机性也不够强.
根据图 4(c)和图 4(d)所示,对于RT2来说:当base=400时,pv的值最小,pvc的值最大.这时,RT2的随机性最好.
通过以上分析可知,间隔域分割基数对RT的随机性是有直接影响的,当base=RT.numx40%时,RT的随机性最好.
3.3.5 拐 点在RT的Div(×)算法中,对于nodex节点,根据密钥key和nodex.value随机地将nodex的区域Dx分为值域vf和间隔域gf两部分,然后再以key和nodex.value为根,随机地将间隔域gf分裂成m份,并随机地选择m个子节
点构成子节点集合满足:
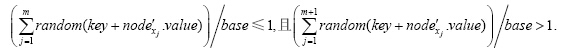
因此,在进行加解密时,当判断某一子节点是否属于Node时,平均需要进行(m/2)次取随机数运算和
加法运算.当间隔域的分割基数为RT.numx40%,OPEART的随机性最好,则m≥RT.numx40%.因此,加解密一个基本字符串S时,除最底层以外的各层都要进行上述判断,其平均计算复杂度Or为
${O_r} = O\left( {\frac{{RT.num}}{5} \times (RT.level - 1)} \right)$例如,当RT.num=1000,RT.level=5时,一共需要进行800次随机运算和加法运算,这是一个较大的计算负载.因此,OPEART引入了拐点的概念.
引入拐点的目的是对间隔域gf=[gmin,gmax]进行粗粒度的划分,得到多个大小不等的桶,每个桶的边界即为拐点.生成拐点的步骤如下:采用二叉树结构,在二叉树的第1层,根据key和nodex.value取随机值i(iÎR,且iÎ(0.3,0.7)),拐点为x=gmin+é(gmax-gmin)xiù,其中,限定iÎ(0.3,0.7)是为了尽可能平均分割gf.于是,拐点x将gf分割成[gmin,x]和(x,gmax)两个桶.接下来,递归的对两部分进行划分,直至产生足够的拐点.假设有n个拐点,则gf被分成了(n+1)个桶.
判断某一子节点是否属于Node时,首先按照拐点生成的方法寻找一条从树根到叶子节点的路径,确定对应的桶,然后再对桶内的子节点逐一比较,判断它是否在桶内即可.实际上,拐点实现了对Node中的
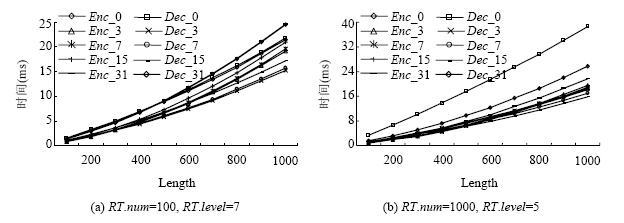
m个子节点的近似折半查找.合适的拐点个数n要依据RT.level和RT.num来确定.图 5反映了拐点个数对OPEART加解密性能的影响,其中,length为明文的长度,“Enc_0”表示在拐点个数n .
 | Fig. 5 Effects of number of RT inflexion on OPEART performance图 5 RT拐点个数对OPEART性能的影响 |
如图 5(a)所示,在RT.num=100,RT.level=7的情况下,当拐点个数n=3时,OPEART的加解密效率最高;其次是n=7的情况;当n=32时,与n=0的情况相似,OPEART的加解密效率最低.如图 5(b)所示,在RT.num=1000,RT.level=5的情况下,当拐点个数n=7时,OPEART的加解密效率最高;其次是n=15的情况;当n=0的时,即,没有拐点的情况下,OPEART的加解密效率最低.
根据以上分析可知,拐点可以提高OPEART的加解密效率,但合适的拐点个数要依据RT.level和RT.num来确定.
4 OPEART的正确性和安全性定理1. OPEART=(Gen_RT,Enc,Dec)是正确的,如果满足以下条件:
(1) "mÎD,$Dec(RT,key,Enc(RT,key,m))=m;
(2) 如果x1>x2(x1,x2ÎD),那么Enc(x1)>Enc(x2).
证明:
(1) 根据RT的结构,每个节点对应定义域中的一个点,每个子节点的值域是对父节点值域的任意划分且没有交集,因此保证了任何密文值只能属于一个叶子节点的值域空间.另外,如算法2和算法3所示,加密和解密的过程都是寻找一条从RT的根节点到明文值对应的叶子节点的路径.不同的是,在加密时,由于知道明文x,因此只需调用RT.Div(×)算法一次,根据由密钥key和x构成的ran_root直接求出分裂份数m和选择m个子节点集合Node;在解密时,由于不知道x,因此要逐一检查节点nodex的每个子节点,根据由key和构成的ran_root产生的值域,然后判断密文val是否属于该子节点的值域,从而找到对应的明文,也就是说,要多次调用RT.Div(×)算法.因此,只要加密和解密的过程中使用相同的密钥key,就能找到相同的一条路径.
因此,"mÎD,$Dec(RT,key,Enc(RT,key,m))=m.
(2) 根据RT的结构,每个子节点的值域是对父节点值域的任意划分且没有交集,假设nodex的两个相邻的
子节点为$nod{e_{{x_j}}}$和$nod{e_{{x_{j + 1}}}},$其中$nod{e_{{x_{j + 1}}}}.value = nod{e_{{x_j}}}.value + 1$,则有$nod{e_{{x_{j + 1}}}}.\min = nod{e_{{x_j}}}.\max + 1$.
因为$Enc(nod{e_{{x_j}}}.value) = nod{e_{{x_j}}}.\min + Random(key + nod{e_{{x_j}}}.value) \times (nod{e_{{x_j}}}.\max - nod{e_{{x_j}}}.\min ),$
$Enc(nod{e_{{x_{j + 1}}}}.value) = nod{e_{{x_{j + 1}}}}.\min + Random(key + nod{e_{{x_{j + 1}}}}.value) \times (nod{e_{{x_{j + 1}}}}.\max - nod{e_{{x_{j + 1}}}}.\min ),$
所以,$Enc(nod{e_{{x_j}}}.value) < Enc(nod{e_{{x_{j + 1}}}}.value)$.
所以,OPEART是保序的.
综上所述,OPEART是正确的. □
定理2. OPEART是IND-DNCPA安全的.
证明:假设攻击者A发起以下攻击:
(i) 选择一组明文M={x1,x2,…,xk}(xiÎD,xi¹xj且i,jÎ[1,k])向OPEART进行加密询问,OPEART将加密的结果C={c1,c2,…,ck}返回给A,A试图通过解方程的方式解出其他密文c(cÏC)对应的明文;
(ii) A选择两个数据m0,m1发给OPEART,其中,m1=m0+1,且m0ÏM,m1ÏM;
(iii) OPEART随机加密其中一个数据mb(bÎ{0,1}),并将产生的密文cb返回给A;
(vi) A输出b¢作为对b的猜测.
(1) OPEART通过以下操作产生了随机性,从而使得从明文到密文的映射关系是无法通过解方程的方式来破解的:
(i) 对于非叶子节点xi,以密钥key和xi来决定该点的值域和间隔域的大小,使得不同的点具有不同的值域和间隔域大小;
(ii) 对于非树根节点xj,以key和xj作为随机数的根,将父节点的间隔域随机地分成大小不等的mj份,并分配任选的mj个子节点;
(iii) 对于叶子节点xk,以key和xk产生随机数在(mink,maxk)之间选择一点作为xk的密文.
(2) 由于OPEART具有保序性,A可能通过分析M中密文的差距以及与m0或m1最近的点的密文来推断b.M中密文的差距受OPEART的随机性的影响:
(i) 当A通过求出平均距离d=(Enc(xk)-Enc(x1))/(k-1)来猜测x的值时,由于pv®0,说明由于OPEART的
随机性,使得密文与参照函数f(x)=Enc(x1)+(x-x1)xd相差很大,因此,A无法从密文直接猜测出对应的明文;
(ii) 当A通过分析密文之间的距离d¢来推测密文的值域时,由于pvc>pvcavg,说明相邻点密文之间的变化
超过了d,尤其是pi¹0(iÎ[1,5])且pvc®pvcmax时,处于5个变化区间的百分比达到了最大值,d¢的波动
最大,即,d¢Î[1,V-n],使得A要判断值域的大小变得很困难.因此,A的优势概率为
Adv(A)=|Pr[b¢=b]-0.5|=|(0.5+e)-0.5|=e,
其中,e是一个足够小可忽略不计的数.
综上所述,OPEART是IND-DACPA安全的. □
5 OPEART的性能本节将通过测试OPEART的随机性能判断其是否能够达到IND-DACPA安全性的要求;通过对比OPEART和OPES的性能来分析OPEART的效率,性能指标包括加、解密性能,关系运算性能以及存储/通信负载等.实验部署在由本研究小组自行研发的青云实验平台3.0上,该平台是一个基于Web的面向校园的云计算环境,以KVM和Hadoop的HDFS为底层支撑技术,并部署在由12台服务器构成的集群上.
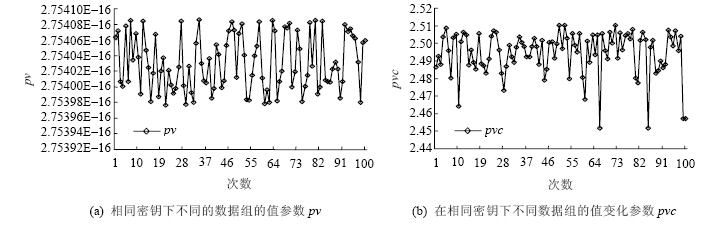
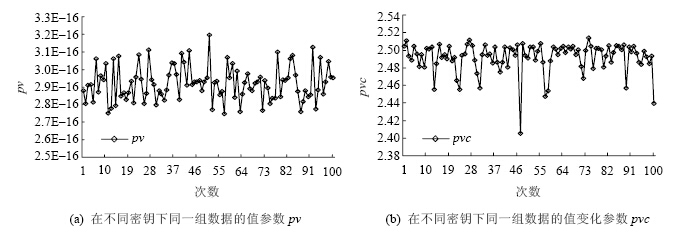
5.1 随机性能实验1测量OPEART在相同密钥下不同数据组的pv值和pvc值,每次随机抽取10 000个连续的数进行加密,重复100次,如图 6所示.实验2测量OPEART在不同密钥下同一组数据的pv值和pvc值,每次随机生成密钥,对同一组由10 000个连续的数组成的数据组进行加密,重复100次,如图 7所示.在测试pvc值时,当出现pi=0 (iÎ[1,5])时,pvc=0.
 | Fig. 6 Randomness of OPEART under the same keys图 6 OPEART在相同密钥下的随机性 |
 | Fig. 7 Randomness of OPEART under the different keys图 7 OPEART在不同密钥下的随机性 |
如图 6(a)和图 7(a)所示,pv值均小于10-15,是一个足够小的数,因此满足pv®0的随机性要求;如图 6(b)和图 7(b)所示,pvc值均大于2.4,满足pi¹0(iÎ[1,5]),pvc>pvcavg且pvc®pvcmax的要求.在某些点的pvc值大于2.5,那是因为处于第五区间[(2xd,V-n)]的连续密文之间的差距的平均距离大于9xd/4.实验1和实验2表明:OPEART具有很好的随机性能,能够满足IND-DACPA的安全性要求.
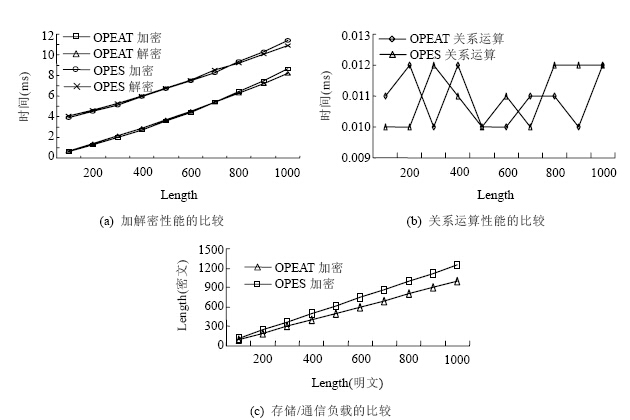
5.2 OPEART的效率实验3比较了OPEART与OPES在加解密、关系运算以及存储/通信负载这3个方面的性能,其中,OPEART的level=7,num=100;OPES具有和OPEART相同的数据域和值域,输入分布函数和输出函数的分桶数分别为100和150.结果如图 8所示.
 | Fig. 8 Efficiency of OPEART图 8 OPEART的效率 |
如图 8(a)所示,OPEART的加密和解密负载几乎是一样的,而且均比OPES的加解密负载低;在进行关系运算时,OPEART与OPES的运算负载相差不大,基本上是在0.01ms~0.013ms之间;对于相同长度的明文,OPEART的密文长度小于OPES.总的说来,OPEART比OPES具有更好的运行效率.
6 结束语针对云计算中的隐私保护问题,本文提出了支持隐私保护的云计算模型,并设计了一种支持隐私保护的加密方案OPEART.OPEART是一种保序的、确定的对称加密方案,支持对加密数据的任何一种关系运算(=,>,<等).安全分析和性能评估证实:OPEART具有IND-DNCPA安全性,并且具有很好的运行效率.
下一步,我们将从提高安全性的角度对OPEART进行改进,同时也计划研究新的加密技术来实现安全的密文计算.
| [1] | Jessica EV. Google discloses privacy glitch (2009). 2011. http://blogs.wsj.com/ digits/2009/03/08/1214/ |
| [2] | Song DX, Wagner P, Perrig P. Practical techniques for searches on encrypted data. In: Proc. of the 2000 IEEE Symp. on Security and Privacy. 2000. 44-55. [doi: 10.1109/SECPRI.2000.848445] |
| [3] | Bonech D, Crescenzo GD, Ostrovsky R, Persiano G. Public-Key encryption with keyword search. In: Proc. of the Eurocrypt 2004. 2004.506-522. |
| [4] | Ohtaki Y. Partial disclosure of searchable encrypted data with support for boolean queries. In: Proc. of the 3th Int'l Conf. on Availability, Reliability and Security (ARES 2008). 2008. 1083-1090. [doi: 10.1109/ARES.2008.80] |
| [5] | Liu Q, Wang GJ, Wu J. An efficient privacy preserving keyword search scheme in cloud computing. In: Proc. of the 2009 Int'l Conf. on Computational Science and Engineering. IEEE, 2009. 715-720. [doi: 10.1109/CSE.2009.66] |
| [6] | Boldyreva A, Chenette N, Lee Y, O'Neill A. Order-Preserving symmetric encryption. In: Proc. of the 28th Annual Int'l Conf. on Advances in Cryptology (Eurocrypt 2009). 2009. 224-241. [doi: 10.1007/978-3-642-01001-9_13] |
| [7] | Belazzougui D, Boldi P, Pagh R, Vigna S. Monotone minimal perfect hashing. In: Proc. of the 20th Annual ACM-SIAM Symp. on Discrete Algorithms. 2009. 785-794. |
| [8] | Fox EA, Chen QF, Daoud AM, Heath LS. Order-Preserving minimal perfect hash functions and information retrieval. ACM Trans. on Information Systems, 1991,9(3):281-308. |
| [9] | Czech ZJ, Havas G, Majewski B. An optimal algorithm for generating minimal perfect hash functions. Information Processing Letters, 1992,43(5):257-264. [doi: 10.1016/0020-0190(92)90220-P] |
| [10] | Agrawal R, Kiernan J, Srikant R, Xu YR. Order-Preserving encryptiion for numeric data. In: Proc. of the 2004 ACM SIGMOD Int'l Conf. on Management of Data (SIGMOD 2004). 2004. 563-574. [doi: 10.1145/1007568.1007632] |
| [11] | Boldyreva A, Chenette N, O'Neil A. Order-Preserving encryption revisited: Improved security analysis and alternative solutions. .In: Proc. of the 31st Annual Conf. on Advances in Cryptology. 2011 578-595. |
| [12] | Wong WK, Cheung DW, Kao B, Mamoulis N. Secure kNN computation on encrypted databases. In: Proc. of the 35th SIGMOD Int'l Conf. on Management of Data (SIGMOD 2009). 2009. 139-152. [doi: 10.1145/1559845.1559862] |
| [13] | Boneh D, Sahai A, Waters B. Fully collusion resistant traitor tracing with short ciphertexts and private keys. In: Proc. of the Eurocrypt 2006. LNCS 4004, 2006. 573-592. [doi: 10.1007/11761679_34] |
| [14] | Boneh D, Waters B. Conjunctive, subset, and range queries on encrypted data. In: Proc. of the TCC 2007. LNCS 4392, 2007. 535-554. [doi: 10.1007/978-3-540-70936-7_29] |
| [15] | Shi E, Bethencourt J, Chan THH, Song D, Perrig A. Multi-Dimensional range query over encrypted data. In: Proc. of the 2007 IEEE Symp. on Security and Privacy. 2007. 350-364. [doi: 10.1109/SP.2007.29] |
| [16] | Wang PH, Lakshmanan LVS. Efficient secure query evaluation over encrypted XML databases. In: Proc. of the 32nd Int'l Conf. on Very Large Databases. 2006. 127-138. |
| [17] | Hacıgümüş H, Iyer B, Mehrotra S. Efficient execution of aggregation queries over encrypted relational databases. In: Proc. of the 9th Int'l Conf. on Database Systems for Advanced Applications (DASFAA 2004). 2004. 633-650. [doi: 10.1007/978-3-540-24571- 1_10] |
| [18] | Hacıgümüş H. Privacy in database-as-a-service model [Ph.D. Thesis]. Irivne: Department of Information and Computer Science, University of California, 2003. |
| [19] | Wang C, Cao N, Li J, Ren K, Lou WJ. Secure ranked keyword search over encrypted cloud data. In: Proc. of the 30th Int'l Conf. on Distributed Computing Systems (ICDCS 2010). 2010. 253-262. [doi: 10.1109/ICDCS.2010.34] |
 2015, Vol. 26
2015, Vol. 26


