2003年,Al-Riyami等人^[1]首次提出无证书密码体制.该体制不但成功地解决了密钥托管问题,而且不涉及公钥证书.这使它成为近期一个研究热点,似雨后春笋般地涌出众多满足不同需求的无证书签名方案^[2,3,4,5,6],如无证书代理签名方案^[3]、无证书群签名方案^[4]、无证书聚合签名方案^[5,6,7,8,9].

聚合签名^[10]是把来自n个不同签名者对n条不同消息的签名通过一种有效的算法压缩成单个签名.持有聚合签名的验证人可通过确定的验证算法检验其有效性,以此判定n个签名人对这n条消息的分别认可.故而,聚合签名可以有效地减少签名验证的计算代价和通信开销.

近年来,各具特色的无证书聚合签名方案^[5,6,7,8,9]陆续被提出来,其中,文献^[6,9]中方案的聚合签名验证计算量和聚合签名的长度均与聚合人数无关,但前者每次都要协商新的状态信息,后者完成个体签名时需要用户之间互相传递必须的数据,这些都会引起额外的通信开销致使方案低效.另外,上述除文献^[8]以外的无证书聚合签名方案所给出的安全模型中的攻击者^[1]能力相对较弱.虽然文献^[8]中的攻击者能力得以加强,使之成为超级攻击者^[2],但是签名验证计算量很大.本文提出一个在聚合签名验证阶段只需4个双线性运算的无证书聚合签名方案.它在保证较高效率的基础上,实现了在最强安全模型(即,赋予攻击者最强的攻击能力)下是可证安全的.受文献^[6]的启发,我们的方案也选择使用一个共同的状态信息,以实现强安全性的聚合签名方案的设计.与文献^[9]中方案的显著区别是,在我们的方案中,参与聚合的用户之间独立地完成个体签名,无需交换彼此的数据.因此,我们的聚合方案可方便地实现系统内的用户动态地加入完成聚合签名.

本文第1节给出无证书聚合签名的概念和安全模型.第2节提出一个无证书聚合签名方案.第3节分析方案的安全性和效率.最后总结全文.

无证书聚合签名方案包含了n个用户、一个密钥生成中心(KGC)和一个聚合者,它由系统参数生成、部分私钥提取、设置公/私钥、个体签名、聚合和聚合签名验证等6个算法组成.各算法的定义参见文献^[5].

无证书聚合签名中存在两类攻击者,即第一类攻击者A_I和第二类攻击者A_II.文献^[1]最初赋予攻击者的能力为“A_I不能获知系统主密钥,但可在公钥空间随意取值以替代任何用户的公钥;A_II可获知系统主密钥,但不能替换任何用户的公钥.”后来,文献^[2]不仅对A_II能力作了增强——“可获知系统主私钥,可替换除了目标用户之外的任何用户的公钥”,而且对安全模型中所定义的签名预言器按能力强弱分为正常、强和超级这3种签名预言器.进而,每种类型的攻击者依据被允许访问签名预言器的类型进一步分为正常、强和超级攻击者.具体细节见表 1和表 2.

表 1(Table 1)

Table 1Types of attackers 表 1 攻击者类型 类型 第一类 第二类 正常攻击者 强攻击者 超级攻击者 正常攻击者 强攻击者 超级攻击者 能力 不能获知系统主密钥,但可以替换系统 中任何用户的公钥 可以获知系统主密钥,可以替换系统中除了 目标身份以外的任何用户的公钥 配置的签名预言器 O1 O2 O3 O1 O2 O3

Table 1 Types of attackers 表 1 攻击者类型

表 2(Table 2)

Table 2 Types of oracles 表 2 签名预言器类型 正常签名 预言器O1 输入:身份ID,消息m;O1输出有效签名s.这里的签名要使用身份ID在“用户生成算法中产生的秘密 值和部分私钥”来生成;验证签名s有效性要使用“用户生成算法中产生的公钥”完成. 强签名 预言器O2 输入:身份ID,消息m,秘密值x;O2输出有效签名s.若攻击者没有提供秘密值x,则O2的签名使用身份 ID在“用户生成算法中产生的秘密值和部分私钥”来生成;验证签名s有效性使用“用户生成算法中 产生的公钥”完成.若攻击者提供了秘密值x,则O2的签名使用身份ID在“用户生成算法中产生的部 分私钥和攻击者所提供的秘密值x”来生成;验证签名s有效性使用“该秘密值所对应的公钥”完成. 超级签名 预言器O3 输入:身份ID,消息m;O3输出有效签名s.验证签名s有效性使用“该用户当前的公钥”完成.这里, “当前的公钥”是指用户公钥列表上的最新记录.换句话说,若该用户的公钥截止当前已被替换了 k≥0次,则使用第k次替换的公钥去验证签名.特殊地,k=0表示公钥没有被替换.

Table 2 Types of oracles 表 2 签名预言器类型

为了方便下面方案之间安全性的比较,本文把具有文献^[1]所赋予的攻击能力并且只允许访问正常签名预言器的攻击者称为弱正常攻击者.

无证书聚合签名的不可伪造性是通过一个解决困难问题的挑战者Q和一个攻击者AÎ{A_I,A_II}之间的游戏来定义.本文考虑的攻击者为超级攻击者,对其他类型攻击者,只需相应地修改签名询问过程.

· 设置系统参数:Q初始化系统,以安全参数l作为输入,输出参数列表List.若A是A_I,则Q把List给A;

否则,Q把ListÈ{系统主密钥}给A.

· 攻击:A被允许受限次地访问受控于Q的预言器(和可能存在的hash函数预言器).另外,Q要维护和A交互过程中涉及到的数据所形成的一些列表,这些列表初始均为空表:

生成用户询问:输入List,一个身份ID,它输出该用户的公钥P_ID和身份ID的哈希值Q_ID.

部分私钥询问(仅对A_I有效):输入List和一个用户的身份ID,它输出其部分私钥D_ID.

公钥替换询问:输入List,一个用户的身份ID和新公钥,它把身份ID的公钥置为

秘密值询问:输入List,一个用户的身份ID,它输出其秘密值x_ID.

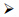个体签名询问:输入List、消息m、状态信息D、签名者的身份ID和公钥P_ID,它输出有效的个体签名d.若公钥已被替换,攻击者不必提供相应的秘密值.

· 伪造:攻击者A输出在相同状态信息Δ*下,公钥集是 $L_{PK}^* = \{ P_1^*,P_2^*,...,P_n^*\} $、身份集是 $L_{{\rm{ID}}}^* = \{ ID_1^*,ID_2^*,...,$ $ID_n^*\} $的n个用户对消息 $m_1^*,m_2^*,...,m_n^*$的聚合签名 ${\sigma ^*} = (R_1^*,R_2^*,...,R_n^*,{K^*})$作为伪造A在游戏中获胜,当且仅当同时满足如下两个条件:

$1 \leftarrow verify(List,{\Delta ^*},m_1^*,...,m_n^*,L_{PK}^*,L_{{\rm{ID}}}^*,{\sigma ^*}).$

(2) 至少存在一个身份 $ID_j^* \in L_{{\rm{ID}}}^*$未对 $({\Delta ^*},m_j^*,ID_j^*,P_j^*)$做个体签名询问.同时,当A是A_I时,则未曾做 $ID_j^*$的部分私钥询问;否则,未曾做$ID_j^*$的秘密值询问,也未曾做$ID_j^*$公钥替换询问.

在游戏中,若任何多项式有界的攻击者AÎ{A_I,A_II}获胜的概率是可忽视的,则称此无证书聚合签名方案是自适应选择消息和身份攻击存在不可伪造的.

另外,因攻击者获得个体签名后可以自己生成聚合签名,故我们的安全模型无需进行聚合签名询问.

受文献^[6]的启发,我们在构造聚合签名方案时也引入了状态信息,为了增强方案的安全性以抵抗超级攻击者的攻击.聚合者在个体签名前随机选取并广播状态信息,这里状态信息可选择随机长度的比特串.

· 系统参数的生成:设安全参数为l,素数(G₁,+)和(G₂,×)是循环群,其阶均为q.双线性映射e:G₁x G₁®G₂.是5个抗碰撞的哈希函数.P是G₁的一个生成元,KGC设置系统主密钥 $s{ \in _R}_q^*,$>系统公钥为P₀=sP,消息空间M={0,1},公开参数:

List={G₁,G₂,e,q,P,P₀,H₁,H₂,H₃,H₄,H₅}.

· 部分私钥提取:KGC对用户所提交的身份ID_iÎ{0,1}认证后,为其计算部分私钥D_i=sQ_i=sH₁(ID_i),并安全地传D_i给该用户.

· 设置公/私钥:用户ID_i选计算P_i=x_iP.这里,P_i为公钥,(x_i,D_i)为私钥,x_i作为其秘密值.

· 个体签名:聚合者随机选择一个状态信息D并广播.公钥和身份分别为P_i与ID_i的用户,用其私钥(x_i,D_i),按如下步骤对消息m_i签名,其中,i=1,2,…,n:

① 任选计算R_i=r_iP,h_i=H₄(m_i||D||R_i||ID_i)和g_i=H₅(m_i||D||R_i||P_i);

② 计算W_i=g_iD_i+x_ih_iU+r_iV,其中,U=H₂(D||P),V=H₃(D||P₀);

③ 输出s_i=(R_i,W_i)为个体签名.

· 聚合:设L_ID={ID₁,ID₂,…,ID_n}是参与聚合的n个用户的身份集,公钥集是L_PK={P₁,P₂,…,P_n}.当收齐这n个用户在相同状态信息D下的消息-签名对(m₁,s₁),(m₂,s₂),...,(m_n,s_n)后,聚合者计算W=W₁+W₂+… +W_n并输出聚合签名s=(R₁,R₂,…,R_n,W).

· 聚合签名验证:在状态信息D下,欲验证身份集是L_ID={ID₁,ID₂,…,ID_n},公钥集是L_PK={P₁,P₂,…,P_n}的n个用户对消息m₁,m₂,...& lt; /span>,m_n的聚合签名s=(R₁,R₂,…,R_n,W),验证者按如下步骤进行检验:

① 计算U=H₂(D||P),V=H₃(D||P₀),h_i=H₄(m_i||D||R_i||ID_i),g_i=H₅(m_i||D||R_i||P_i),Q_i=H₁(ID_i),i=1,2,…,n;

② 验证$e(W,P) = e\left( {\sum\nolimits_{i = 1}^n {{g_i}{Q_i}} ,{P_0}} \right)e\left( {\sum\nolimits_{i = 1}^n {{h_i}{P_i}} ,U} \right)e\left( {\sum\nolimits_{i = 1}^n {{R_i}} ,V} \right)$是否为真:若真,则接受s;否则,拒绝s.

下面证明方案是正确的.

符号 $Query_A^t({x_1},{x_2},{x_3},{x_4},{x_5},{x_6},{x_7},{x_8},{x_9})$表示在时间t内,攻击者A被允许至多做x₁次生成用户询问、x₂次

H₂询问、x₃次H₃询问、x₄次H₄询问、x₅次H₅询问、x₆次部分私钥询问、x₇次公钥替换询问、x₈次秘密值询问、x₉次个体签名询问.上述9种询问中,每种询问一次的耗时依次记为t₁,t₂,t₃,t₄,t₅,t₆,t₇,t₈和t₉.符号A(n,m)表示从m个不同事物中选出n个物体的排列数,其中n≤m且n,mÎ¥.用(t,e)-CDH表示给定的CDH问题可在t时间内以概率e解决.

定理1. 在随机预言模型下,如果A_I是第一类超级攻击者,做自适应选择消息和身份攻击询问 q₃,q₄,q₅,q₆,q₇,q₈,q₉)后,以不可忽略的概率攻破所提出的方案,那么存在一个(t¢,e¢)-CDH算法Q,其中, $t' \le 2t + 2\sum\nolimits_{i = 1}^9 {{q_i}{t_i}} ,\varepsilon ' \ge {[66 \cdot A(n,{q_5})]^{ - 1}} \cdot q_1^{ - 2}{(1 - q_1^{ - 1})^{{q_6}}} \cdot {\varepsilon ^2}{\rm{.}}$

证明:若有(G₁,+)上的CDH问题的一个随机实例(P,P₁=aP,P₂=bP),该困难问题的解决者是Q,则其目标是算出abP.下证凭借A_I的能力,Q是一个(t¢,e¢)-CDH的挑战者.

· 设置系统参数:Q置P₀=P₁=aP并把List={G₁,G₂,e,q,P,P₀,H₁,H₂,H₃,H₄,H₅}给A_I.

· 攻击:抗碰撞的哈希函数H₁~H₅受控于Q,它们被作为随机预言器.为简单,假设A_I的询问都是不同的. Q维护H₁~H₅和L等列表,它们初始都为空.这些列表中每项的格式依次为

(ID_i,Q_i,P_i,D_i,a_i,x_i),(D_i,U_i,b_i),(D_i,V_i,l_i),(m_i,D_i,R_i,ID_i,h_i),(m_i,D_i,R_i,P_i,g_i),(m_i,D_i,ID_i,P_i,R_i,r_i,h_i,g_i,W_i).

· 生成用户询问:Q随机选择kÎ{1,2,…,q₁}.当A_I询问Create(ID_i)时,Q选择满足(*,*,*,*,a_i,*)

以前未出现在H₁列表.当i=k时,置Q_k=a_kP+P₂,D_k=^(符号^表示该值未知,下同),P_k=x_kP;当i¹k时,置Q_i=a_iP,P_i=x_iP,D_i=a_iP₁.Q将(ID_i,Q_i,P_i,D_i,a_i,x_i)添加到H₁列表,并把P_i,Q_i返给A_I. 不失一般性,下面A_I询问所涉及的ID_i均已生成.

· 部分私钥询问:当A_I询问PPKey(ID_i)时,Q执行:当i=k时,终止协议;否则,检查H₁列表寻找元组(ID_i,Q_i,P_i,D_i,a_i,x_i),将D_i返给A_I.

· 公钥替换询问:当A_I询问时,Q据ID_i检查H₁列表,把元组(ID_i,Q_i,P_i,D_i,a_i,x_i)替换为 $(I{D_i},{Q_i},{P'_i},{D_i},{\alpha _i},\bot )$

· 秘密值询问:当A_I询问Value(ID_i)时,Q据ID_i检查H₁列表:若x_i¹^,则返回x_i给A_I;否则,输出^.

· H₂哈希询问:当A_I询问H₂(D||P)时,Q选择满足(*,*,b_i)未出现在H₂列表,将U_i=b_iP返给A_I并把(D_i,U_i,b_i)添入H₂列表.

· H₃哈希询问:当A_I询问H₃(D_i||P₀)时,Q选择满足(*,*,l_i)未出现在H₃列表,将V_i=l_iP-P₁返给A_I并添(D_i,V_i,l_i)到H₃列表.

· H₄哈希询问:当A_I询问H₄(m_i||D||R_i||ID_i)时,Q选择满足(*,*,*,*,h_i)未出现在H₄列表,将h_i返给A_I并添(m_i,D_i,R_i,ID_i,h_i)到H₄列表.

· H₅哈希询问:当A_I询问H₅(m_i||D||R_i||P_i)时,Q选择满足(*,*,*,*,g_i)未出现在H₅列表,将g_i返给A_I,并把(m_i,D_i,R_i,P_i,g_i)添入H₅列表.

· 个体签名询问:当A_I询问Sign(m_i,D_i,ID_i,P_i)时,Q查询H₂,H₃列表以分别获得U_i=b_iP和V_i=l_iP-P₁.

Q执行如下步骤:

(1) 任选满足(*,*,*,*,h_i)和(*,*,*,*,g_i)分别未出现在H₄和H₅列表.

(2) 计算R_i=r_iP+g_iQ_i,并置H₄(m_i||D||R_i||ID_i)=h_i和H₅(m_i||D||R& lt; sub>i||P_i)=g_i.

(3) 计算W_i=h_ib_iP_i+l_ig_iQ_i+l_ir_iP-r_iP₁.

Q把(m_i,D_i,ID_i,P_i,R_i,r_i,h_i,g_i,W_i)添入L列表并以R_i,W_i作答.由设定P₀=P₁和个体签名验证算法可知,该返回值(R_i,W_i)是关于(m_i,D_i,ID_i,P_i)的一个有效签名,;因为 $\begin{array}{c} e({g_i}{Q_i},{P_0})e({h_i}{P_i},U)e({R_i},V) = e({g_i}{Q_i},{P_1})e({h_i}{P_i},{\beta _i}P)e({r_i}P + {g_i}{Q_i},{\lambda _i}P - {P_1})\\ = e({h_i}{\beta _i}{P_i} + {\lambda _i}{g_i}{Q_i} + {r_i}{\lambda _i}P - {r_i}{P_1},P)\\ = e({W_i},P). \end{array}$

· 伪造:A_I输出公钥集是 $L_{PK}^* = \{ P_1^*,P_2^*,...,P_n^*\} $、身份集是 $L_{ID}^* = \{ ID_1^*,ID_2^*,...,ID_n^*\} $的n个用户在相同状态信息D下对消息 $m_1^*,m_2^*,...,m_n^*$的聚合签名 ${\sigma ^*} = (R_1^*,R_2^*,...,R_n^*,{W^*})$,且同时满足如下条件:

$e({W^*},P) = e\left( {\sum\nolimits_{i = 1}^n {g_i^*Q_i^*} ,{P_0}} \right)e\left( {\sum\nolimits_{i = 1}^n {h_i^*P_i^*} ,{U^*}} \right)e\left( {\sum\nolimits_{i = 1}^n {R_i^*} ,{V^*}} \right){\rm{.}}$

(2) 至少存在一个身份 $ID_j^* \in L_{ID}^*,$既未对它做部分私钥询问,也未对做个体签名询问. Q只把哈希函数H₅替换为 $({\Delta ^*},m_j^*,ID_j^*,P_j^*)$其余保持不变.重复上述交互过程.由Forking lemma^[11]可知:在不大于2t时间内,借助A_I的能力以不低于e²×[66×A(n,q₅)]^-1的概率,获得一个新的有效的伪造元组% ${\sigma ^*}^\prime = (R_1^*,R_2^*,...,R_n^*,{W^*}^\prime ),$其中存在sÎ{1,2,…,n},当iÎ{1,2,…,n}\{s}时,总有 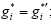但当i=s时,有:

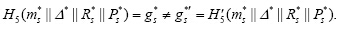
于是,Q得到方程组:

$\left\{ {\begin{array}{*{20}{l}} {e\left( {\sum\nolimits_{i = 1}^n {g_i^*Q_i^*} ,{P_0}} \right)e\left( {\sum\nolimits_{i = 1}^n {h_i^*P_i^*} ,{U^*}} \right)e\left( {\sum\nolimits_{i = 1}^n {R_i^*} ,{V^*}} \right) = e({W^*},P)}\\ {e\left( {\sum\nolimits_{i = 1}^n {g{{_i^*}^\prime }Q_i^*} ,{P_0}} \right)e\left( {\sum\nolimits_{i = 1}^n {h_i^*P_i^*} ,{U^*}} \right)e\left( {\sum\nolimits_{i = 1}^n {R_i^*} ,{V^*}} \right) = e({W^*}^\prime ,P)} \end{array}} \right.{\rm{.}}$

两式相除,得到:

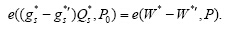
若 $ID_j^* = I{D_k} = ID_s^*{\rm{,}}$ 则$Q_s^* = {Q_k} = {\alpha _k}P + {P_2}{\rm{,}}$解出

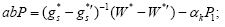
否则,Q终止协议.

· 成功概率:Q成功解决给定的CDH问题可转化为以下3个事件的发生:

S₁:协议未终止于部分私钥询问.

S₂:聚合签名被A_I成功地伪造且Forking Lemma应用成功.

S₃:满足 $ID_j^* = I{D_k} = ID_s^*.$

Q解决CDH问题的概率是P(S₁ÇS₂ÇS₃)=P(S₁)P(S₂|S₁)P(S₃|S₁ÇS₂),其中, $P({S_1}) \ge {(1 - 1/{q_1})^{{q_6}}},$P(S₂|S₁)≥e²×[66×A(n,q₅)]^-1且 $P({S_3}|{S_1} \cap {S_2}) \ge q_1^{ - 2},$即, □

定理2. 在随机预言模型下,如果A_II是第二类超级攻击者,做自适应选择消息和身份攻击询问 q₂,q₃,q₄,q₅,q₆,q₇,q₈,q₉)后,以不可忽略的概率攻破提出的方案,那么存在一种(t¢,e¢)-CDH算法Q,其中, $\varepsilon ' \ge {[66 \cdot A(n,{q_5})]^{ - 1}} \cdot q_1^{ - 2}{(1 - q_1^{ - 1})^{{q_6}}} \cdot {\varepsilon ^2}{\rm{.}}$

证明:Q选择系统主密钥计算P₀=sP,把{G₁,G₂,e,q,P,P₀,H₁,H₂,H₃,H₄,H₅}È{s}给A_II.Q仍然将H₁~H₅ 作为随机预言器,维护H₁~H₅和L等列表,Q的目标是由(P,P₁=aP,P₂=bP)计算出abP.

· 生成用户询问:Q随机选择kÎ{1,2,…,q₁}.当A_II询问Create(ID_i)时,Q选择 ${x_i},{\alpha _i}{ \in _R}_q^*$满足(*,*,*,a_i,*)以前未出现在H₁列表.当i¹k时,置Q_i=a_iP,P_i=x_iP;当i=k时,置Q_k=a_kP,P_k=x_kP+P₂.Q把(ID_i,Q_i,P_i,a_i,x_i)添入到H₁列表,并把Pi&l t;/ i>和Q_i返给A_II.

· 公钥替换询问:当A_II询问$Replace(I{D_i},{P'_i})$时,Q执行:当i=k时,终止协议;当i¹k时,Q检查H₁列表,把元组(ID_i,Q_i,P_i,a_i,x_i)更新为 $(I{D_i},{Q_i},{P'_i},{\alpha _i},\bot ).$

· 秘密值询问:当A_II询问Value(ID_i)时,Q遍历H₁列表.当i=k时,终止协议.当i¹k& lt; span style='font-family:宋体;color:black'>且x_i¹^时,则为A_II输出x_i;否则,返回^.

· H₂哈希询问:当A_II询问H₂(D||P)时,Q选择满足(*,*,b_i)未出现在H₂列表,把U_i=b_iP+P₁返给A_II并添(D_i,U_i,b_i)到H₂列表.

H₃,H₄和H₅哈希询问与定理1的证明过程相同.

· 个体签名询问:当A_II询问Sign(m_i,D_i,ID_i,P_i)时,Q查询H₂,H₃列表以分别获得U_i=b_iP+P₁和V_i=l_iP-P₁.Q执行如下步骤:

(1) 任选满足(*,*,*,*,h_i)和(*,*,*,*,g_i)分别未出现在H₄和H₅列表;

(2) 计算R_i=r_iP+h_iP_i并置H₄(m_i||D||R_i||ID_i)=h_i和H₅(m_i||D||R_i||P_i)=g_i;

(3) 计算W_i=h_i(b_i+l_i)P_i+sg_iQ_i+l_ir_iP-r_iP₁. Q把(m_i,D_i,ID_i,P_i,R_i,r_i,h_i,g_i,W_i)添入L列表并以R_i,W_i作答.根据P₀=sP和个体签名验证算法知:该返回值(R_i,W_i)是关于(m_i,D_i,ID_i,P_i)的一个有效签名,因为

$\begin{array}{c} e({g_i}{Q_i},{P_0})e({h_i}{P_i},U)e({R_i},V) = e({g_i}{Q_i},sP)e({h_i}{P_i},{\beta _i}P + {P_1})e({r_i}P + {h_i}{P_i},{\lambda _i}P - {P_1})\\ = e(s{g_i}{Q_i},P)e({h_i}{\beta _i}{P_i},P)e({h_i}{P_i},{P_1})e({\lambda _i}{r_i}P + {\lambda _i}{h_i}{P_i},P)e( - {r_i}{P_1},P)e({h_i}{P_i},- {P_1})\\ = e({h_i}{\beta _i}{P_i} + {\lambda _i}{h_i}{P_i} + s{g_i}{Q_i} + {\lambda _i}{r_i}P - {r_i}{P_1},P)\\ = e({W_i},P). \end{array}$

· 伪造:类似与定理1相应过程,只是Q选择不同的哈希函数并应用Forking lemma^[11],进而构造出

一个方程组:

$\left\{ {\begin{array}{*{20}{l}} {e\left( {\sum\nolimits_{i = 1}^n {g_i^*Q_i^*} ,{P_0}} \right)e\left( {\sum\nolimits_{i = 1}^n {h_i^*P_i^*} ,{U^*}} \right)e\left( {\sum\nolimits_{i = 1}^n {R_i^*} ,{V^*}} \right) = e({W^*},P)}\\ {e\left( {\sum\nolimits_{i = 1}^n {g_i^*Q_i^*} ,{P_0}} \right)e\left( {\sum\nolimits_{i = 1}^n {h{{_i^*}^\prime }P_i^*} ,{U^*}} \right)e\left( {\sum\nolimits_{i = 1}^n {R_i^*} ,{V^*}} \right) = e({W^*}^\prime ,P)} \end{array}} \right..$

两式相除,得出:

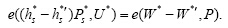
若 $ID_j^* = I{D_k} = ID_s^*$,则U=b_kP+P₁, $P_s^* = {P_k} = {x_k}P + {P_2}$.Q可以解出:

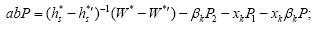
否则,Q终止协议.

· 成功概率:类似于定理1中相应的部分. □

表 3列举了几个在随机预言模型下可证安全的无证书聚合签名方案.数据显示,只有文献^[8]和本文的方案给出了能够抵抗两类超级攻击者形式化的证明,而文献^[5,6,7,9]中的方案给出了只能抵抗弱正常攻击者A_II的 证明.

表 3(Table 3)

Table 3 Comparison of certificateless aggregate signature schemes 表 3 无证书聚合签名方案比较 方案 个体签名 聚合验证 聚合签名长度 安全性 文献[5] 3SM+2H (n+3)BP+(2n+1)H (n+1)L 抗超级AI和弱正常AII 文献[6] 5SM+3H 5BP+2nSM+(2n+3)H 2L 抗超级AI和弱正常AII 文献[7]-1 2SM+1H (2n+1)BP+2nH (n+1)L 抗强AI和弱正常AII 文献[7]-2 3SM+1H (n+2)BP+nSM+2nH 2L 抗强AI和弱正常AII 文献[9] 4SM+1H 4BP+nSM+(n+1)H 2L 抗正常AI和弱正常AII 文献[8] 3SM (n+1)BP+2nSM+nH (n+1)L 抗超级AI和超级AII 本文 4SM+2H 4BP+2nSM+(n+2)H (n+1)L 抗超级AI和超级AII

Table 3 Comparison of certificateless aggregate signature schemes 表 3 无证书聚合签名方案比较

方案的效率从两个方面考察:计算和通信代价.为了方便,用L表示群G₁中元素的比特长度,pairing运算用

BP表示,上的hash运算记为H,群G₁中标量乘运算为SM.这3种运算代价较大,尤其是BP.故比较

时只考虑它们.文献^[7]包含两个聚合签名方案,我们用^[7]-1和^[7]-2加以区别.表 3数据显示:本文方案的聚合验证运算量明显小于文献^[5,6,7,8],稍大于文献^[9].虽然我们的聚合签名长度比文献^[9]大,但是文献^[9]中每个个体签名时必须所有参与成员互相传递数据后才能完成,最后再聚合产生聚合签名.因需要成员间交互信息而加大了通信代价,这必将极大地降低方案的效率,故在通信代价上,文献^[9]并不比我们的方案占优势.另外,由于文献^[9]涉及交换数据,所以在个体签名之前需要确定参与的成员.而我们的方案却没有这种限制,故它可以方便地实现系统中成员动态地加入每次的聚合签名.

本文利用双线性映射提出一个无证书聚合签名方案.该方案具有效率高、安全性强等优点.另外,方案中用户个体签名只使用公共信息和用户自己的信息,阻断了用户间的耦合性,可以方便实现系统中用户动态加入聚合签名,这使得方案具有应用的灵活性.鉴于该方案安全、高效和无证书管理的优点,它可应用于多对一的通信系统中对消息的认证.