2. 上海寻梦信息技术有限公司, 上海 200051
2. Shanghai Xun-Meng Information Technology Co., Ltd., Shanghai 200051, China
矩阵是工程领域中常用的一种数据结构, 比如: 飞行控制系统中, 使用矩阵实现坐标转换和动力学方程计算; 在深度学习领域, 矩阵乘法是神经网络训练中的核心关键计算.但是, 传统命令式语言中的矩阵运算程序容易产生各种错误, 比如下标越界, 这些错误会引起非法存储访问从而导致程序崩溃.深度学习的引入, 使得矩阵计算进一步复杂化, 也增加了矩阵计算错误的可能性.深度学习中的超大规模矩阵计算往往超出传统CPU的能力, 为了提高矩阵计算的速度, 往往需要采用GPU、超级计算机或者专用的硬件加速器, 这些特殊的硬件计算装置通过引入并行计算来大幅度减少矩阵计算的时间.实现矩阵并行计算的一个核心技巧就是把矩阵分解成分块矩阵, 把原本顺序执行的矩阵计算转变成并行执行的分块矩阵计算; 然后把这些并行计算任务分配到相应的硬件资源上, 通过硬件并行计算, 大幅度提高矩阵计算速度.然而, 分块矩阵的计算进一步提升了矩阵算法的复杂性和可理解性, 也使得矩阵计算代码更容易出现错误.
传统的程序测试方法并不能全面地挖掘矩阵程序中的所有错误.形式化方法[1]为提高软件可靠性提供了更有力的技术.从原理上讲, 软件的形式化方法就是用数学方法证明软件在任何情况下都满足所期望的性质.形式化方法分成很多种类, 一些方法(比如模型检查)通过自动证明工具验证软件满足某些性质, 但是这种方法通常不能保证软件满足所有期待的性质.本文采用基于高阶定理证明器的形式化验证方法, 这种方法使用通用的定理证明工具, 在高阶逻辑系统中全面验证软件性质.基于定理证明[2]的验证方法的工作原理同数学定理证明的过程类似, 它需要首先证明一组中间引理, 然后在这些中间结果的基础上证明最后的定理.这一方法同数学研究一样, 需要逐步证明和积累数学定理.因此, 为了矩阵计算软件的验证, 我们一方面需要在定理证明器中描述矩阵计算的各种函数, 另一方面需要证明这些函数所需满足的各种数学性质.在矩阵软件形式化的过程中, 我们需要首先证明矩阵的各种数学性质, 比如矩阵加法的结合律交换律、乘法结合律、加法和乘法的分配律、加法和乘法同0元和单位元作用的有关性质等等.这样一个过程, 我们称为矩阵的形式化.
分块矩阵在神经网络的计算中起到特别重要的作用.神经网络的训练是一种非常耗时的计算工作, 主要的计算量用于超大规模的矩阵的加法和乘法.为了减少计算时间, 人们引入了各种硬件计算进行矩阵运算加速, 这些技术包括多核计算、高性能计算、GPU、TPU及各种专用的硬件加速器、FPGA等等.这些硬件提速的核心原理就是把矩阵运算并行化, 而并行化的基本技术之一就是采用分块矩阵.分块矩阵的实现代码比普通矩阵代码要复杂的多, 更难以理解, 因此也更需要通过形式化方法进行软件验证.
本文的主要贡献是: 在对基于Coq记录的矩阵形式化方法[3]的整理和完善的基础上, 进一步实现了分块矩阵运算的形式化; 接着, 详细分析了在矩阵形式化的证明过程中所遇到的难点, 总结了归纳证明的经验; 最后形成了矩阵与分块矩阵的基础库, 并利用Coq代码抽取机制将矩阵及分块矩阵运算函数转换为可执行的OCaml代码.在文献[3]中, 构建的理论是模块化的, 矩阵理论是一个函子, 当它作用到一个关于元素类型的模块之后, 可以产生对应于这类元素的具体的矩阵理论.用这种方法, 我们可以获得自然数、整数、实数和复数的矩阵理论, 对于矩阵函子中证明的加法和乘法性质在实例化的理论中依然有效, 避免了大量的重复性证明.但是, 上述这个方法并不能应用于分块矩阵, 原因如下: 一是普通矩阵的等价判断函数不适用于分块矩阵; 二是矩阵函子所形成的分块矩阵模块中的乘法与转置函数不能产生正确结果; 三是矩阵函子要求输入的用于描述矩阵元素的模块中的加法和乘法都满足交换律, 分块矩阵是元素为矩阵的矩阵, 而矩阵的乘法并不满足交换律, 因此无法通过函子作用直接获得分块矩阵的主要性质.所以在本文中, 我们对分块矩阵的形式化进行了专门的研究.
在Coq中定义的矩阵函数是函数式风格的函数.函数式编程可靠性高但计算效率低, 因此函数式矩阵运算本身并不适合直接在硬件中实现.不过, 深度学习软件的发展趋势是把算法的高层描述同算法的底层优化分离开来, 一个有代表性的做法就是亚马逊公司开发的TVM框架, 它定义了两种语言: 一种是面向用户的高层算法描述语言, 另一种是面向实现的用于描述优化策略的策略语言.在这种工作方式之下, 高层算法的描述并不一定需要采用命令式语言, 只要是任何一种便于编译优化的语言即可.文献[4]即采用了基于函数式语言的高层算法描述方法, 并且提出了比TVM更为简洁有效的策略优化技术.这一工作也说明: 基于函数式语言的深度学习算法高层描述不但具有可行性, 而且具有便于代码优化的良好特性.本文不但描述了基于函数式语言的分块矩阵计算基本函数, 并且通过形式化方法验证了它们的重要特性, 保障了这些函数的可靠实现.因此, 这项工作为深度学习算法的并行实现及形式验证提供了基础性的支撑.
本文第1节介绍Coq定理证明器[5]并且总结分析了矩阵形式化的相关工作.第2节介绍并完善基于Coq记录的矩阵形式化方法.第3节提出基于Coq记录的分块矩阵形式化方法.第4节对矩阵与分块矩阵形式化证明中所遇到的困难进行总结和分析.最后总结全文.
1 背景知识 1.1 Coq定理证明器Coq定理证明器是基于高阶带类型λ演算的交互式高阶逻辑定理证明器, 它不但表达能力强, 而且具备多个具有实用价值的证明机制, 比如可扩充的重写机制、基于模块的形式化理论构建机制以及程序抽取机制等等.这些优秀的特点, 使得这一证明工具在学术界越来越受欢迎, 成为当今最为流行的定理证明工具之一.
Coq基于归纳构造演算, 有着强大的数学模型基础和很好的扩展性.Coq中的归纳类型扩展了传统设计语言中有关类型定义的概念, 这与大多函数式程序设计语言中的递归类型定义相似.基于模式匹配和递归, 每个归纳类型对应一个计算结构, 对于含有递归类型参数(如自然数、表等)的目标证明通常采用归纳证明方法, 归纳证明的过程取决于该递归类型的归纳定义.每个归纳声明定义了一组数据值, 这些值可以用声明过的构造子来构造.例如: 布尔值可以用true和false来构造, 自然数可以用0或S应用到另一个自然数上来构造, 而列表可以用nil或者将cons应用到一个自然数和另一个列表上来构造.对于归纳类型进行归纳证明原理与数学归纳法类似, 以表类型为例证明步骤: 1) 首先, 证明当表list1为nil时P list1成立; 2) 然后, 证明当表list1为cons n list1'时P list成立.其中, n是列表头元素, list1'是某个更小的列表, 假设P list1'成立.利用归纳证明所证明的引理能够保证该引理内存在的情况都满足引理内容.
与许多其他编程语言(C, Java, Pascal等)相似, 我们可以在Coq中定义块机制, 在块(section)内部, 我们可以声明或定义局部变量, 并控制他们的作用域.在Coq系统中, 各个Section都有相应作用范围, 系统分别使用“Section id”和“End id”表示Section的开始和结束.Section可以嵌套, 在其内部我们可以使用关键字“Parameter”和“Variable”来进行全局声明和局部声明; 在Section结束之后, 局部变量会从当前上下文中消失.而在Section内部, 使用到这些变量的定义以及引理, 都会增加局部变量类型作为参数.
Coq提供了程序抽取功能, 可以将经过认证的程序提取为Ocaml, Haskell或者Scheme之类的语言.在程序抽取时, 可将Coq中指定类型按一定规则映射到指定语言如Ocaml含有的类型之上.
1.2 相关工作定理证明技术已成为当今软件工程领域中一种非常重要的形式化技术, 该技术已经广泛应用于数学定理证明、协议验证以及硬软件的安全特性验证, 是人们解决软件系统正确性、可靠性的重要方法.
在基于定理证明器的矩阵形式化研究中, 已存在部分相关工作: 在Isabelle/HOL和Coq中, 已有向量的形式化[6-8]; Mizar中描述了向量空间以及线性变换特征值[9, 10]; Harrison则在HOL Light中对欧几里德空间实向量以及矩阵正交变换进行了较完整的形式化[11].在首都师范大学施智平团队中也开展了部分有关矩阵形式化的工作: 刘振科等人提出了函数矩阵理论在HOL4中的形式化[12]; 康西楠在HOL4中已有的矩阵基本性质的基础上给出矩阵变换形式化理论[13]; 杨秀梅等人在HOL4中对向量和函数矩阵进行形式化, 并对其连续性、微分以及积分性质进行验证[14]; 马振威提出了基于Coq记录的矩阵形式化方法[3].
在矩阵形式化的研究中, 首先要解决的一个关键问题是矩阵在定理证明器中的表示方法.一种是把矩阵定义成从下标集合到元素集合的函数映射, 基于Isabelle/HOL系统的研究工作主要采用了这种方法.这种方法的优点在于比较容易证明矩阵的各种性质.在Coq的ssreflect库中包含的矩阵库也使用该方法的思路定义二维矩阵[15], 将矩阵定义为由自然数矩阵生成实数的函数.但该实现比较复杂, 并且不易理解以及使用.这类利用函数来实现矩阵形式化的方法有一个缺点, 即没有很好的对应计算机软件中的矩阵计算函数, 也就是说, 这些方法从数学上证明了各种矩阵性质, 却没有很好的验证软件中的矩阵函数的性质.
在基于Lambda演算的定理证明器中(比如HOL/ISABELLE, Coq), 可以用表list来表示矩阵, 并在表的基础上定义矩阵操作函数, 并进行矩阵性质的证明.但是表本身没有长度限制, 表类型也没有反映出指定长度或大小的向量和矩阵.在基于依赖类型的定理证明器中, 可通过依赖类型定义出可设定长度的表. Magaud基于依赖类型定义了带有长度的向量类型, 其定义如下:
Inductive vect (A: Set): nat
|vnil: vect A 0
|vcons: forall n: nat, A
该定义与表类型list相似, 不同在于其增加了一个表示列表长度的参数(类型为自然数).然而, 这一技术在操作和证明上都十分繁琐, 不仅无法利用表结构上的各种已知函数, 而且当处理更为复杂的二维矩阵问题时, 将面临较大的困难.
在Coq的Coquelicot库中也有一种矩阵形式化方法[16], 该方法与上述方法都基于依赖类型实现了定长向量, 其利用对pair函数的递归实现向量, 矩阵由向量的嵌套实现.该方法的相比于上述方法构造更加巧妙、易于理解、矩阵函数的实现简单, 但后续函数性质的证明较少.
马振威提出一种基于Coq记录类型的方法来实现矩阵的形式化[3], 该方法用包含3个分量的记录来表示二维矩阵, 其中一个分量是实现矩阵的二维表, 另外两个分量分别是对矩阵的长度和宽度满足指定长宽的两个证明.这种方式易于理解, 能够让我们定义出具有指定长宽的矩阵类型, 并且我们能够在向量类型和矩阵类型上定义基本的矩阵操作函数(矩阵加法、转置、乘法等).文献[3]证明了一组矩阵操作的基本性质.这种实现矩阵形式化方法的好处在于易于理解并且方便使用, 利用该方法构建的函数可直接通过程序抽取得到可执行的OCaml代码.但是, 在文献[3]中有一个问题没有得到很好的解决, 它就是矩阵的相等性问题.对于两个基于记录的矩阵, 传统等号并不能准确表达它们的相等性, 因为两个记录相等当且仅当这两个记录的所有分量相等.但对于两个列表相同的矩阵记录, 它们所包含的关于长度和宽度的证明是不必要求相等的.
目前, 我们还未看到有关于分块矩阵运算的形式化研究工作.
本文期望在解决基于Coq记录类型的方法存在问题的基础上, 对更多矩阵函数性质进行补充证明, 并且利用该技术对分块矩阵及其运算形式化, 最后不仅能够构建多个不同类型的矩阵形式化的基础库供后续研究人员使用, 还能为从事该研究方向的人员提供一些经验上的参考.
2 矩阵形式化本次工作所采用的矩阵形式化方法是对文献[3]中的矩阵形式化方法的完善, 其中包括矩阵等价定义、部分矩阵函数修改以及矩阵函数性质的补充证明.本节介绍基于Coq记录的矩阵形式化方法, 其中矩阵类型定义、矩阵函数定义方法以及矩阵函数性质证明思路.
2.1 矩阵类型定义Record类型是一个允许定义记录的宏, 使用Record可以定义出一种数据结构.该数据结构中具有一些数据, 而这些数据满足某种性质, 如下即为利用Record定义的矩阵类型.
Record Mat (A: Set)(m n: nat): Set: =mkMat
{
mat: list (list A);
mat_height: height mat=m;
mat_width: width mat n
}.
其中, A表示矩阵内部元素类型, m表示矩阵行数, n表示矩阵列数, height函数用于返回二维表的高度, width函数用于判别输入二维表的宽度是否等于输入参数, mat用于存储矩阵内部数据即二维表, mat_height为二维表的高度的等价证明, mat_width为二维表的宽度的等价证明.因此, 在创建一个大小为m×n的矩阵时, 需要提供一个二维表、该二维表的高度性质证明以及该二维表的宽度性质证明.以下是构建一个3×3的矩阵Tm1的例子.
Definition tm1:=[[1;2;3];[2;3;4];[3;4;5]].
Lemma tm1_cond1:height tm1=3.
Lemma tm1_cond2:width tm1 3.
Definition Tm1:=mkMat nat 3 3 tm1 tm1_cond1 tm1_cond2.
由于构建一个矩阵所需要写的代码过多, 因此我们可以将固定尺寸的矩阵构造封装成函数, 后期构造时只需输入矩阵内部元素即可得到所构造的矩阵, 如构建3×3矩阵函数mkMat_3_3.
Definition mkMat_3_3' (a11 a12 a13 a21 a22 a23 a31 a32 a33: A): =
[[a11;a12;a13]; [a21;a22;a23]; [a31;a32;a33]].
Definition cond2_mkMat_3_3': forall a11 a12 a13 a21 a22 a23 a31 a32 a33,
width(mkMat_3_3' a11 a12 a13 a21 a22 a23 a31 a32 a33) 3%nat.
Definition mkMat_3_3 (a11 a12 a13 a21 a22 a23 a31 a32 a33:A): =
mkMat A 3 3 (mkMat_3_3' a11 a12 a13 a21 a22 a23 a31 a32 a33)
eq_refl(cond2_mkMat_3_3' a11 a12 a13 a21 a22 a23 a31 a32 a33).
其中, eq_refl是自定义的一个证明目标, 其能够自动证明二维表的高度.在此基础上, Tm1的构建代码大大减少, 如下.
Definition Tm1:=mkMat_3_3 1 2 3 2 3 4 3 4 5.
2.2 矩阵类型等价性质在文献[3]中, 对矩阵类型的等价判断是采用Coq中的eq函数表示, 其采用公理Meq作为二维表(即矩阵内部数据)相等与矩阵相等的转换理论, 如下:
| $ \text { Axiom } ~~{Meq}: \text { forall }(A: S e t)(m ~n: n a t)(m 1~ m 2: {Mat} A m n), { mat } ~A~ m~ n~ m 1={mat}~ A~ m ~n ~m 2 \leftrightarrow m 1=m 2 . $ |
其中: A为矩阵元素类型; m和n分别为矩阵的高度以及宽度; m1和m2为元素类型为A、大小为m×n的矩阵; mat是获取矩阵内部二维表的函数, 其参数分别为元素类型、矩阵高度、矩阵宽度以及矩阵.由于eq函数对于Record类型相等要求的特性, 即要求Record类型中每一条记录相等, 而当两个矩阵相等时(即内部数据相等), 不要求其关于该数据的高度以及宽度证明相等, 因此该公理存在部分错误, 即, 由二维表相等无法推导出矩阵相等.
为了解决该公理存在的问题, 我们提出了新的矩阵等价判断函数M_eq, 定义如下:
| $ \text { Definition } M_{-} e q\{A: { Set }\}\{m ~n: n a t\}(m 1 m 2: { Mat } A ~m ~n):=m a t ~A ~m ~n ~m 1=m a t~ A~ m~ n ~m 2 . $ |
其实现原理如图 1所示.

|
Fig. 1 Implementation principle of M_eq function 图 1 M_eq函数实现原理 |
该函数用于判断两个矩阵类型中的二维表(即矩阵内部数据)是否相等.该判断方法有效避免了关于Record类型使用eq函数进行等价判断所存在的问题, 也消除其使用错误公理而产生的漏洞.该函数具有自反性、对称性以及传递性, 因此, 我们借助Coq中的重写扩张机制构建重写性质, 使其成为一个重写可用的二元关系.下面使用“===”标记表示M_eq函数.下面是M_eq的自反性、对称性和传递性的引理表示.
Lemma M_eq_ref: forall {A: Set} {m n: nat} (m0:Mat A m n), m0===m0.
Lemma M_eq_sym: forall {A: Set} {m n: nat} (m0 m1:Mat A m n),
m0===m1
Lemma M_eq_trans: forall {A: Set} {m n: nat} (m0 m1 m2:Mat A m n),
m0===m1
关于矩阵类型的运算操作函数主要分为矩阵取负运算函数、加减运算函数、矩阵数乘运算函数、矩阵乘法运算函数以及矩阵转置函数.矩阵处理函数的构造主要分为3个步骤: 一是构建对二维表处理操作函数, 二是完成该函数输出二维表的高度和宽度等价证明, 三是利用前两者构建处理矩阵并且生成矩阵的函数(封装).采用该方法构造的矩阵处理函数使得矩阵的高度与宽度证明贯穿于函数处理过程中, 能够真正地保证输入与输出矩阵高度与宽度固定, 因此无法产生矩阵越界错误.以矩阵乘法函数为例, 矩阵乘法的原理如下.
若A为m×n矩阵, B为n×p矩阵, 则其两者的乘积AB会是一个m×p矩阵:
| ${(AB)_{ij}} = \sum\limits_{r = 1}^n {{a_{ir}}{b_{rj}}} .$ |
矩阵乘法函数的构造需依次构造多个递归函数, 其分别为product', l_mul_dl, dl_mul_dl, mat_mul_mat.其中,
● product'函数为表的内积函数, 其接受两个表作为输入参数并返回其内积结果;
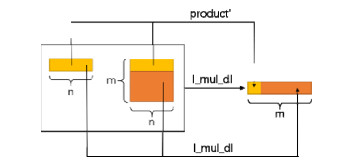
● l_mul_dl函数是表与二维表相乘函数, 其利用递归将l与m中每个表分别进行内积, 将其结果以表类型输出.在完成该函数的构造后, 还需对其输出结果(表)的长度进行证明, 如图 2所示;
|
Fig. 2 Implementation principle of l_mul_dl function 图 2 l_mul_dl函数实现原理 |
● dl_mul_dl为二维表与二维表的相乘函数, 其基于l_mul_dl函数利用递归实现两个二维表中的表依次内积, 并以二维表类型输出.在完成该函数的构造后, 还需对其输出结果(二维表)的高度与宽度进行证明, 如图 3所示;

|
Fig. 3 Implementation principle of dl_mul_dl function 图 3 dl_mul_dl函数实现原理 |
● mat_mul_mat以两个矩阵类型作为输入参数, 由于矩阵乘法原理要求乘号左边的矩阵的每一行乘上与乘号右边的矩阵的每一列作内积, 根据dl_mul_dl函数的实现原理, 需要将第二个矩阵进行转置后再进行运算.在完成该函数的构造后, 还需对其输出结果(二维表)的高度与宽度进行证明, 如图 4所示.

|
Fig. 4 Implementation principle of mat_mul_mat function 图 4 mat_mul_mat函数实现原理 |
根据以上函数以及有关函数输出结果高度与宽度证明性质构造矩阵乘法函数matrix_mul, 其定义如下.
Definition matrix_mul {m n p: nat}(left: Mat A m n)(rightMat A n p): =
let ll: =mat_mul_mat left right in
mkMat A m p ll(height_mat_mul_mat left right)(width_mat_mul_mat left right).
该函数是将mat_mul_mat函数以及该函数输出结果的高度与宽度等价性质这3部分封装成一个输入为矩阵类型、输出为矩阵类型函数.
2.4 矩阵函数性质证明Coq采用反向推理的方法构造证明, 即: 在证明一条引理时会产生一个证明目标, 需要通过使用一组引理以及证明命令来产生保证该目标的成立的子目标.当所有子目标已知或为公理时, 则完成证明; 反之, 则需要继续对子目标进行证明, 直到所有的目标都得到证明.对于矩阵函数性质的证明, 需要根据矩阵函数内部定义来选择归纳目标, 从而产生符合预期的子目标.此类有关于矩阵的性质证明难点之一在于证明思路的构建, 证明思路决定了变量是否需要归纳以及变量归纳证明的顺序.证明思路需要根据函数内部定义而建立, 下面以矩阵乘法右分配律为例.
矩阵乘法右分配律形式为A×(B+C)=A×B+A×C, 如图 5所示.

|
Fig. 5 Right distributive law of matrix multiplication function and matrix addition function 图 5 矩阵乘法函数与矩阵加法函数的右分配律 |
在证明该定理时, 需要将变量进行归纳, 该定理中的变量有m, n, A, B, C, 在第2.3节中介绍矩阵乘法函数(matrix_mul)定义的实现是由表与表之间的内积函数、表与二维表的乘法函数、二维表与二维表的乘法函数到矩阵以及矩阵乘法函数(返回二维表)的顺序实现的, 如图 6所示.

|
Fig. 6 Structure of the definition of matrix multiplication 图 6 矩阵乘法函数定义结构 |
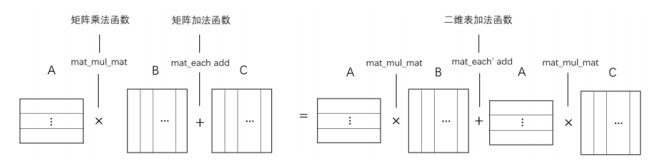
由于matrix_mul为非递归函数, 其与矩阵加法函数的右分配律性质展开后形成的证明目标将作为一条新待证引理(mat_mul_mat函数同理), 完成该待证引理的证明即可完成该性质的证明.图 7为matrix_mul函数展开后需要证明的子目标, 即mat_mul_mat函数与二维表加法函数的右分配律.
|
Fig. 7 Right distributive law of mat_mul_mat function and two-dimensional list addition function 图 7 mat_mul_mat函数与二维表加法函数的右分配律 |
由于mat_mul_mat是一个非递归函数, 其是在dl_mul_dl函数的基础之上定义的, 主要功能是分别取出两个输入矩阵中的二维表, 并对第2个二维表进行转置, 再利用dl_mul_dl函数对两个二维表进行乘法函数操作, 将mat_mul_mat函数展开化简后得到需要证明的两个子目标, 分别是二维表转置函数与二维表加法性质((A+B)T= AT+BT)和dl_mul_dl函数与二维表加法右分配律性质.
二维表转置函数与二维表加法性质的证明在这部分不详细介绍, dl_mul_dl函数与二维表加法右分配律如下, 此处以及下文代码部分采用Section机制A, m和n为局部变量(A: Set; m n: nat).
Lemma dl_mul_dl_distr_r: forall m n (a b c: list(list A)),
width a n
dl_mul_dl a (mat_each' A add b c)=mat_each' A add (dl_mul_dl a b)(dl_mul_dl a c).
由于dl_mul_dl函数定义在l_mul_dl函数之上, 利用数学归纳法对二维表变量a(图 8)进行归纳展开时, 当a的形式为a: : a0时, 会取出其二维表中的第1个子表, 并拆分成含有l_mul_dl的形式, 如下所示.

|
Fig. 8 Right distributive law of two-dimensional list multiplication and two-dimensional list addition 图 8 dl_mul_dl函数与二维表加法的右分配律 |
l_mul_dl a (mat_each' A add b c): : dl_mul_dl a0 (mat_each' A add b c)=
list_each A add (l_mul_dl a b) (l_mul_dl a c)
: : mat_each' A add (dl_mul_dl a0 b) (dl_mul_dl a0 c)
这提示二维表乘法与二维表加法的右分配律定理的证明需要一个新定理的证明支持, 即表与二维表乘法函数l_mul_dl与二维表加法的右分配律.
Lemma l_mul_dl_distr_r: forall m n (a: list A) (b c: list(list A)),
length a=n
l_mul_dl a (mat_each' A add b c)
=list_each A add (l_mul_dl a b) (l_mul_dl a c).
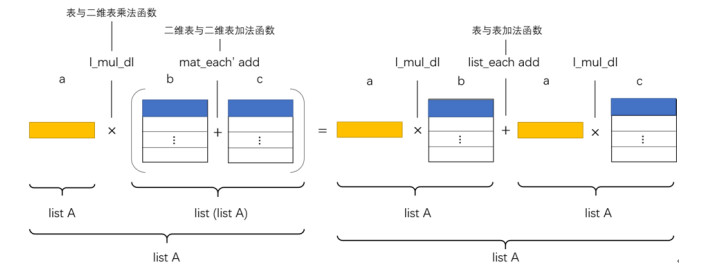
由于l_mul_dl函数定义在product'函数之上, 再次利用数学归纳法对二维表变量b和c(图 9)进行归纳展开时, 当b的形式为a3:: b且c的形式为a4:: c时, 会取出其二维表中的第一个子表, 并拆分成含有product'的形式, 如下所示.
|
Fig. 9 Right distributive law of list and two-dimensional list multiplication and two-dimensional list addition 图 9 表与二维表乘法与二维表加法的右分配律 |
product' A Zero add mul a0 (list_each A add a3 a4)=
add (product' A Zero add mul a0 a3) (product' A Zero add mul a0 a4)
这提示表与二维表乘法和二维表加法的右分配律定理的证明需要一个新定理的证明支持, 即表内积函数product'与加法add的右分配律.
Lemma product_distr_r: forall n (a b c: list A),
length a=n
product' A Zero add mul a (list_each A add b c)
=add (product' A Zero add mul a b) (product' A Zero add mul a c).
由于product'函数定义在mul函数之上, 利用数学归纳法对a, b和c(图 10)进行归纳展开时, 当a的形式为a0:: a, b的形式为a1:: b且c的形式为a2:: c时, 利用化简拆分成含有mul的形式, 如下所示.

|
Fig. 10 Right distributive law of inner product function and addition 图 10 product函数与加法的右分配律 |
add (mul a (add a1 a2)) (product' A Zero add mul a0 (list_each A add b c))=
add (add (mul a a1) (product' A Zero add mul a0 b))
(add (mul a a2) (product' A Zero add mul a0 c))
这提示表内积函数与加法的右分配律定理的证明需要一个新定理的证明支持, 即乘法mul与加法add的右分配律: a*(b+c)=a*b+a*c, 其表示如图 11所示.

|
Fig. 11 Right distributive law of multiplication and addition 图 11 乘法与加法的右分配律 |
大部分的乘法与加法都具有右分配律性质, 因此, 只要在证明中添加该定理作为前提, 即可通过反向推导证明矩阵乘法与矩阵加法具有右分配性质.
上述依次需要证明的定理整理见表 1.
| Table 1 Lemmas needed to prove the right distributive law of matrix multiplication 表 1 矩阵乘法右分配律证明所需引理 |
在利用数学归纳法进行归纳证明, 尤其当证明的性质中含有多个变量时, 不建议在证明开始时盲目地对所有变量进行统一归纳展开.
● 一是因为在有些变量展开后证明中的前提条件产生假命题.在这种情况下, 可以直接跳过该目标证明.若在该情况下继续进行对其他变量进行归纳展开, 会增加许多重复代码与不必要的证明工作;
● 二是对于变量是否进行归纳展开主要依据在于证明思路, 如在图 8中含有3个变量: a, b和c, 选择a作为主要归纳对象的原因在于dl_mul_dl函数在运算过程中首先对左侧变量进行模式匹配, 当a归纳为不同结构时, 可进行化简并且能够进一步产生与l_mul_dl函数相关引理的形式.若先对b或c进行归纳, 不仅不能进一步化简, 还会使得证明目标变得更加繁琐.
但对于一些更为复杂的引理, 如乘法结合律以及单位矩阵乘矩阵性质, 没有明确的证明思路时, 需要构造特殊的函数以及引理来支持其每一个归纳证明目标的证明, 这使得这些引理的证明更加复杂并且难以理解, 具体的部分我们将在第4节详细讨论.
本次工作在已有引理基础上对未完成的引理进行补充以及证明, 其内容见表 2、表 3.
| Table 2 Existing matrix lemma 表 2 现有矩阵引理 |
| Table 3 Supplemental matrix lemma 表 3 补充矩阵引理 |
对于一些相似的性质, 我们无需一一证明, 可以通过已有的矩阵函数性质推导得到, 这样可以大幅度减少工作量, 如单位矩阵右乘性质:
| $\begin{gathered} A \times I = A{\rm{ }}(apply~meq\_teq) \\ {(A \times I)^T} = {A^T}~(apply~teq\_mul) \\ {I^T} \times {A^T} = {A^T}{\rm{ }}(apply~trans\_MI) \\ I \times {A^T} = {A^T}{\rm{ }}(apply~matrix\_mul\_unit\_l) \\ \end{gathered} $ |
本文定义的矩阵以及矩阵函数是多态类型, 其能够使得矩阵向各个域扩展, 因此在所有性质证明完成后, 使用Module对其进行封装, 当输入实数模块参数时, 获得实数矩阵模块, 其中包括所有的矩阵类型、函数定义以及相关性质.本次矩阵形式化工作中提出了整数矩阵、实数矩阵、复数矩阵以及函数矩阵的基础库.
坐标系转换矩阵构成了飞行控制系统的基本组成部分, 其可靠性对飞行安全有重要影响.飞行控制系统设计中使用了5种坐标系, 它们之间存在20种转换矩阵, 其中, 许多转换矩阵相当复杂, 利用人工计算难免会产生错误.在本次研究工作中, 我们利用矩阵形式化基础库对飞行控制系统中坐标系之间的转换矩阵做了验证, 下面我们利用实数矩阵库来验证其中一个简单的例子, 即飞行控制系统中气流坐标系与稳定坐标系的旋转矩阵.
验证内容:
| $\left( {\begin{array}{*{20}{c}} {\cos \alpha }&0&{ - \sin \alpha } \\ 0&1&0 \\ {\sin \alpha }&0&{\cos \alpha } \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {\cos \beta }&{ - \sin \beta }&0 \\ {\sin \beta }&{\cos \beta }&0 \\ 0&0&1 \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\cos \alpha *\cos \beta }&{ - \cos \alpha *\sin \beta }&{ - \sin \beta } \\ {\sin \beta }&{\cos \beta }&0 \\ {\sin \alpha *\cos \beta }&{ - \sin \alpha *\sin \beta }&{\cos \alpha } \end{array}} \right)$ |
图 12为对该转换矩阵验证的代码部分.

|
Fig. 12 Verification of rotation matrix of airflow coordinate system and stable coordinate system 图 12 气流坐标系与稳定坐标系的旋转矩阵的验证 |
3 分块矩阵形式化
本节将介绍利用第2节中的矩阵形式化方法所构建的分块矩阵形式化方法.由于在第2节中的矩阵形式化方法中所定义的类型、函数以及证明的函数性质都是带多态参数的, 因此我们可以利用该多态性构造同样具有多态性的分块矩阵类型、分块矩阵函数以及证明分块矩阵函数所满足的性质.但我们无法通过函子将矩阵作为元素类型输入到矩阵模块之中, 原因在于: 矩阵使用的等价判断函数M_eq不适用于分块矩阵; 矩阵乘法不具有乘法交换律, 其无法形成一个满足矩阵模块要求的输入元素模块.因此在本节中, 我们提出新的分块矩阵的等价性判别函数、分块矩阵运算函数, 并且对分块矩阵函数的性质采用了一种新的方式进行证明.
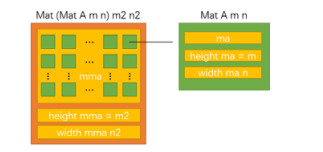
3.1 分块矩阵类型定义在分块矩阵类型定义中, 我们使用矩阵类型定义的双层嵌套来表示分块矩阵类型定义.根据第2.1节中矩阵类型的定义, 当矩阵元素类型为A且其高度和宽度分别为m和n时, 其类型表示为Mat A m n, 以该矩阵的类型作为矩阵内部元素的类型即可构造出一个内部分块大小为m×n分块矩阵.图 13为高度和宽度分别为m2和n2、内部元素为m×n矩阵的分块矩阵的内部结构.
|
Fig. 13 Type definition of block matrix 图 13 分块矩阵类型定义 |
3.2 分块矩阵类型等价性质
在第2.2节中, 我们提出了一个新的函数M_eq来判别矩阵相等, 但该函数不适用于分块矩阵, 当使用M_eq来判别分块矩阵相等时, 会出现图 14的情况:

|
Fig. 14 Problems caused by M_eq discriminating the equality of block matrices 图 14 由M_eq判别分块矩阵相等引起的问题 |
M_eq函数的作用是: 提取出矩阵类型中的二维表后, 用eq函数判别是否相等.由图 14可以看出: 使用M_eq判别分块矩阵时, 需要用eq函数判别两个二维表相等.这要求二维表中所有元素相等(使用eq函数作为判别函数), 但该分块矩阵中的二维表内元素为用Record表示的矩阵类型, 在第2.2节中我们说明了矩阵类型不能使用eq函数来判别矩阵类型相等的问题, 因此我们提出了针对分块矩阵的等价判别函数MM_eq.该函数是一个递归函数, 其依赖于两个递归函数list_Meq和dlist_Meq.为了代码的简洁性, 在分块矩阵形式化的代码部分我们也采用了Section机制, 在下文的代码中, A, m, n, m2和n2都为局部变量, 其类型为(A: Set)(m n m2 n2:nat).
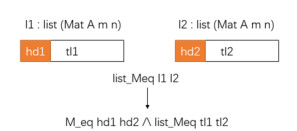
list_Meq主要对由矩阵构成的表进行相等判断, 该函数对表中的每个相应的矩阵利用M_eq函数进行相等判断, 最后返回的是所有矩阵相等的与命题, 其实质是利用M_eq来判别两个表内所有相应矩阵相等.下面是list_Meq函数的定义以及图示(如图 15所示).
|
Fig. 15 Implementation principle of the list_Meq function 图 15 list_Meq函数的实现原理 |
Fixpoint list_Meq(l1 l2:list(Mat A m n)): =
match l1, l2 with
|hd1:: tl1, hd2:: tl2
|nil, nil
|_, _
end.
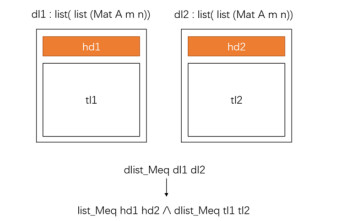
dlist_Meq函数主要用于对由矩阵构成的二维表进行相等判断, 对二维表中每个矩阵的表利用list_Meq函数进行相等判断, 最后返回的是所有由矩阵构成的表相等的与命题, 其实质就是利用M_eq来判别两个二维表内所有相应矩阵相等.下面是dlist_Meq函数的定义以及图示(如图 16所示).
|
Fig. 16 Implementation principle of the dlist_Meq function 图 16 dlist_Meq函数的实现原理 |
Fixpoint dlist_Meq(dl1 dl2:list(list(Mat A m n))): =
match dl1, dl2 with
|hd1:: tl1, hd2:: tl2
|nil, nil
|_, _
end.
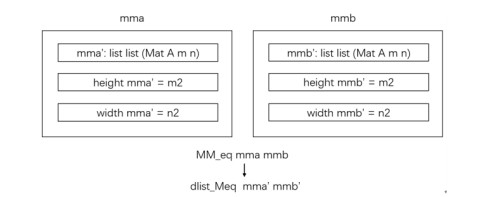
在这上述两个函数的基础之上, 我们定义了分块矩阵(即矩阵的矩阵)相等判断函数MM_eq, 具体定义以及图示如下(如图 17所示).
|
Fig. 17 Implementation principle of the MM_eq function 图 17 MM_eq函数的实现原理 |
Definition MM_eq{A: Set} {m n m2 n2:nat} (ma mb: Mat (Mat A m n) m2 n2): =
dlist_Meq (mat (Mat A m n) m2 n2 ma) (mat (Mat A m n) m2 n2 mb).
该函数的定义解决了分块矩阵相等判别问题, 后续我们对该函数的自反性、对称性以及传递性进行了证明, 并利用Coq中的重写扩展机制实现了该函数的重写.在此基础上, 我们可以对分块矩阵函数性质进行验证.
3.3 分块矩阵函数定义本节主要介绍了分块矩阵函数的定义, 由于第2.3节中定义的矩阵运算函数具有多态性, 分块矩阵的函数可以利用其多态性进行构造.但并不是所有的分块矩阵运算函数都可以通过该方法定义, 例如分块矩阵的乘法函数以及转置函数.在下面部分, 我们将讨论为什么无法通过上述方式构造以及我们的解决方法.
分块矩阵的加减法实现原理如下:
| $\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{...}&{{A_{1n}}} \\ \vdots & \ddots & \vdots \\ {{A_{m1}}}&{...}&{{A_{mn}}} \end{array}} \right) \pm \left( {\begin{array}{*{20}{c}} {{B_{11}}}&{...}&{{B_{1n}}} \\ \vdots & \ddots & \vdots \\ {{B_{m1}}}&{...}&{{B_{mn}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{A_{11}} \pm {B_{11}}}&{...}&{{A_{1n}} \pm {B_{1n}}} \\ \vdots & \ddots & \vdots \\ {{A_{m1}} \pm {B_{m1}}}&{...}&{{A_{mn}} \pm {B_{mn}}} \end{array}} \right)$ |
分块矩阵加减法的实现, 可以利用矩阵函数matrix_each的多态性直接实现.matrix_each函数具有6个参数, 分别是元素类型、元素运算函数、矩阵高度、矩阵宽度以及两个相同大小的矩阵.该函数的主要功能是将两个矩阵中相应位置的元素一一代入提供的运算函数, 从而生成一个新的矩阵.当我们构造分块矩阵加法或减法时, 可以通过输入矩阵类型、矩阵加法即可生成一个分块矩阵加/减法函数.具体分块矩阵加法函数定义如下:
Definition MMadd: =@matrix_each (Mat A m n) (@matrix_each A add m n).
同理, 分块矩阵取负函数可由矩阵函数matrix_map的多态性直接实现, 具体定义如下:
Definition MMopp m n: =@matrix_map (Mat A m n) (matrix_map A opp).
分块矩阵转置原理是将分块矩阵以矩阵为元素进行转置后再对内部元素一一转置, 具体如下:
| ${\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{...}&{{A_{1n}}} \\ \vdots & \ddots & \vdots \\ {{A_{m1}}}&{...}&{{A_{mn}}} \end{array}} \right)^T} = \left( {\begin{array}{*{20}{c}} {{A_{11}}^T}&{...}&{{A_{m1}}^T} \\ \vdots & \ddots & \vdots \\ {{A_{1n}}^T}&{...}&{{A_{mn}}^T} \end{array}} \right)$ |
在矩阵形式化部分, 我们所定义的矩阵转置函数trans具有的5个参数分别是元素类型、缺省值、矩阵高度、矩阵宽度以及输入矩阵, 该函数主要作用是将矩阵进行转置.但如果我们直接使用该函数作为分块矩阵的转置函数, 会出现由于缺少内部矩阵转置操作而产生错误结果的现象, 具体函数定义如下:
Definition MMtrans: =trans (Mat A m n) (MO A m n).
利用该函数对分块矩阵操作后产生结果如下:
MMtrans:
| $\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{...}&{{A_{1n}}} \\ \vdots & \ddots & \vdots \\ {{A_{m1}}}&{...}&{{A_{mn}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{A_{11}}}&{...}&{{A_{m1}}} \\ \vdots & \ddots & \vdots \\ {{A_{1n}}}&{...}&{{A_{mn}}} \end{array}} \right) \ne \left( {\begin{array}{*{20}{c}} {{A_{11}}^T}&{...}&{{A_{m1}}^T} \\ \vdots & \ddots & \vdots \\ {{A_{1n}}^T}&{...}&{{A_{mn}}^T} \end{array}} \right)$ |
因此, 该MMtrans所产生的转置结果不等于分块矩阵转置的结果, 原因在于其内部分块没有转置.面对这个问题, 我们构造新的转置函数mmtrans, 在实现对分块矩阵整体转置的同时, 对其内部分块进行转置.我们提出了一个新的递归函数mhead, 该函数与List库中head函数相似, 不同之处在于: 其对由矩阵类型构成的表取头元素时, 会同时对该元素进行转置操作.该函数定义如下.
Definition mhead (l: list(Mat A m n)): =
match l with
|[]
|x: : _
end.
然后, 我们基于mhead函数提出了一个提取由矩阵类型构成的二维表第1列的函数mheadcolumn, 该函数在取出第1列的同时, 会对该列内的每一个矩阵元素进行一个转置; 接着, 我们提出了一个对由矩阵类型构成的二维表进行转置的函数mgettrans; 最后完成对上述函数输出的二维表的长宽证明, 并封装成一个分块矩阵转置函数mmtrans.上述3个函数的定义同普通矩阵转置函数类似.
同样, 矩阵形式化中提出的矩阵乘法函数也无法适用于分块矩阵乘法函数, 原因在于矩阵乘法函数matrix_ mul需要提供的参数中有一个为元素相乘函数, 对于A类型元素构成的矩阵则需要提供一个A
| $\left( {\begin{array}{*{20}{c}} {{A_{11}}}&{...}&{{A_{1n}}} \\ \vdots & \ddots & \vdots \\ {{A_{m1}}}&{...}&{{A_{mn}}} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {{B_{11}}}&{...}&{{B_{1p}}} \\ \vdots & \ddots & \vdots \\ {{B_{n1}}}&{...}&{{B_{np}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{A_{11}} \times {B_{11}} + ... + {A_{1n}} \times {B_{n1}}}&{...}&{{A_{1n}} \times {B_{1p}} + ... + {A_{1n}} \times {B_{np}}} \\ \vdots & \ddots & \vdots \\ {{A_{m1}} \times {B_{11}} + ... + {A_{mn}} \times {B_{n1}}}&{...}&{{A_{m1}} \times {B_{1p}} + ... + {A_{mn}} \times {B_{np}}} \end{array}} \right)$ |
矩阵乘法中, 相乘的两个矩阵必须满足第1个矩阵的列数与第2个矩阵的行数相等(如m×n和n×p).因此, 实现分块矩阵的乘法对分块矩阵内部分块大小有要求: 若第1个分块矩阵内部分块为m×n, 则要求第2个分块矩阵内部分块需要为n×p, 并且要求两个分块矩阵大小为m2×n2和n2×p2.其构造方法如下:
首先是两个元素为矩阵的表的“内积”函数product, 其实现原理同矩阵乘法函数定义中使用到的product'函数类似, 区别在于输入元素加法与乘法函数由普通加法与乘法变为矩阵的加法与乘法函数, 并且其缺省值类型为一个矩阵.其定义如下.
Fixpoint product(l1:list (Mat A m n))(l2:list (Mat A n p)): =
match l1, l2 with
|h1:: t1, h2:: t2
|_, _
end.
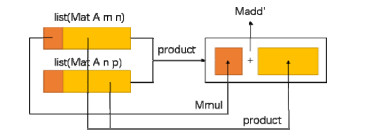
其中, Madd'表示为矩阵加法函数, Mmul表示为矩阵乘法函数, mZero为零矩阵.其实现原理如图 18所示.
|
Fig. 18 Implementation principle of the product function 图 18 product函数的实现原理 |
在该函数的基础之上, 我们继续实现了元素为矩阵的表与二维表相乘函数ml_mul_dl、元素为矩阵的二维表与二维表相乘函数mdl_mul_dl以及分块矩阵相乘函数(输出类型为元素为矩阵的二维表)mmat_mul_mat和(输出类型为分块矩阵的)mmatrix_mul.上述函数的实现方法同第2.3节中矩阵乘法函数的定义类似.但我们在分块矩阵的乘法函数(输出类型为元素为矩阵的二维表)mmat_mul_mat之中使用的转置函数为普通矩阵转置函数, 而非分块矩阵转置函数.具体如下.
Definition mmat_mul_mat {m2 n2 p2:nat} (left: Mat (Mat A m n) m2 n2) (right: Mat (Mat A n p) n2 p2): =
let l1:=mat (Mat A m n) m2 n2 left in
let right': =trans (Mat A n p) (MO A Zero n p) right in
let l2:=mat (Mat A n p) p2 n2 right' in
mdl_mul_dl l1 l2.
此处使用普通矩阵转置函数的原因在于: 我们在每个内部分块做矩阵相乘时会进行对第2个矩阵进行转置操作, 而当我们使用分块矩阵的转置函数, 则会使得其内部分块也进行转置, 这两个操作在对内部分块的转置操作重复.对于一个分块矩阵内部分块大小为m×n, 则要求其相乘分块矩阵内部分块为n×p, 若使用分块矩阵转置函数, 则会使得分块矩阵内部分块大小分别为m×n和p×n, 这不符合矩阵元素乘法函数的参数要求.
下面是利用定义好的函数进行计算验证的例子.
验证

|
Fig. 19 Verification example of block matrix multiplication function 图 19 分块矩阵乘法函数验证例子 |
3.4 分块矩阵函数与普通矩阵函数等价性证明
分块矩阵函数与普通矩阵函数的等价性证明成为分块矩阵形式化工作中的重要内容之一的原因有两个: 1) 保证分块矩阵运算函数的正确性; 2) 将普通矩阵运算函数的性质利用该等价性移植于分块矩阵运算函数之上, 能够大大减少证明过程.分块矩阵能够使得矩阵运算并行化, 但分块矩阵的函数相比于普通矩阵函数更加复杂且容易出错.因此, 为了保证利用分块矩阵技术对矩阵进行运算后得到的结果仍然等于其原结果, 我们需要对分块矩阵函数与普通矩阵函数进行等价性证明.
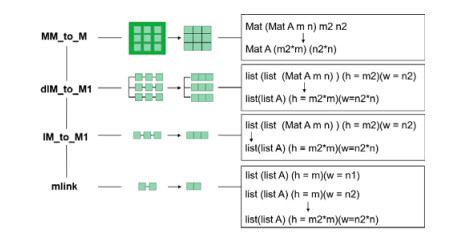
为了证明分块矩阵函数的等价性, 我们构造了一个将分块矩阵转换为矩阵的函数MM_to_M(如图 20所示), 该函数的作用是将一个分块矩阵类型转换成普通矩阵.该函数的定义思路如下: 分块矩阵中不同分块的合并涉及到二维表的横向合并以及二维表的竖向合并, 二维表的竖向合并可使用app函数实现, 二维表的横向合并有多种设计方法, 对于方法的选择以及原因将在第4.2节中详细说明.
|
Fig. 20 Implementation principle of the MM_to_M function 图 20 MM_to_M函数的实现原理 |
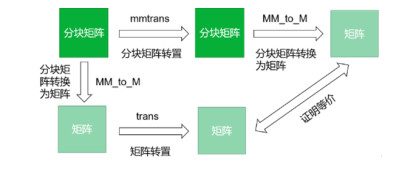
以分块矩阵转置函数和普通矩阵转置函数为例, 首先, 利用定义好的分块矩阵转置函数对分块矩阵进行转置; 然后将其结果通过分块矩阵与矩阵的转换函数转换为矩阵, 证明其等价于先转换为矩阵再进行矩阵转置得到的结果.其内容如图 21所示.
|
Fig. 21 Proof of the equivalence of transposed function of block matrix 图 21 分块矩阵转置函数等价性证明思路 |
分块矩阵转置函数等价引理表示如下:
Lemma MMtrans_eq_Mtrans: forall (me: Mat (Mat A m n) m2 n2)
MM_to_M(mmtrans A Zero m n me)===trans A Zero (MM_to_M me).
该引理的证明依赖于一个重要的基础引理, 即二维表的横向连接函数和二维表转置函数的关系, 若完成该引理的证明, 即可完成上述分块转置函数等价引理的证明.其表示如下.
forall (A: Set) (Zero: A) (h1 h2 w: nat) (ma mb: list (list A)),
height ma=h1
gettrans A Zero (ma++mb) w=mlink A (gettrans A Zero ma w) (gettrans A Zero mb w).
其中, gettrans是对二维表的转置, “++”代表app函数表示表的连接, mlink表示二维表的左右连接.该引理用数学的方法表示为
在分块矩阵函数等价性证明部分, 我们成功证明了以下3个分块矩阵函数等价性引理, 具体如下.
1) 分块矩阵加减运算函数等价引理.
Lemma MMf_eq_Mf: forall (me mf: Mat (Mat A m n) m2 n2),
MM_to_M (matrix_each (Mat A m n) (matrix_each A f) me mf)
===matrix_each A f (MM_to_M me) (MM_to_M mf).
2) 分块矩阵取负运算函数等价引理.
Lemma MMm_eq_Mm: forall (me: Mat (Mat A m n) m2 n2),
MM_to_M (matrix_map (Mat A m n) (matrix_map A f1) me)===matrix_map A f1 (MM_to_M me).
3) 分块矩阵转置函数等价引理.
Lemma MMtrans_eq_Mtrans: forall (me: Mat (Mat A m n) m2 n2)
MM_to_M(mmtrans A Zero m n me)===trans A Zero (MM_to_M me).
4) 分块矩阵乘法函数等价引理.
Lemma MMmul_eq_Mmul: forall (me: Mat (Mat A m n) m2 n2) (mf: Mat (Mat A n p) n2 p2)
MM_to_M (mmatrix_mul A Zero add mul m n p me mf)
===matrix_mul A Zero add mul(MM_to_M me)(MM_to_M mf).
利用以上引理, 可直接将普通矩阵函数所具有的性质移植到分块矩阵的函数之上, 无需对分块矩阵函数所满足的性质一一证明, 加快了证明效率.对于证明较为简单的分块矩阵加法交换律, 利用归纳证明其证明步骤如图 22所示.

|
Fig. 22 Ordinary inductive proof process of addition distributive law of block matrix 图 22 分块矩阵加法分配律的普通归纳证明过程 |
对于使用分块矩阵函数与普通矩阵函数的等价性的分块矩阵加法交换律证明如图 23所示.

|
Fig. 23 Proof process of addition distributive law of block matrix using the above equivalence 图 23 分块矩阵加法分配律利用等价性的证明过程 |
从该例子的证明中我们可以明显发现证明的简化, 并且该简化对于难度更大的引理证明仍然适用.因此, 我们在证明分块矩阵函数与矩阵函数等价性, 不仅能够保证分块矩阵运算函数的正确性, 还能够在很大程度上简化分块矩阵函数性质证明过程, 减少重复证明工作.
目前已成功证明的分块矩阵函数性质引理见表 4.
| Table 4 Lemma of the properties of the block matrix function 表 4 分块矩阵函数性质引理 |
4 矩阵与分块矩阵形式化证明总结与分析
本节主要对本次研究工作中的证明部分的经验进行总结, 并利用具体例子对几个难点进行了详细的分析.
4.1 证明总结本次有关矩阵函数性质证明的研究工作是在文献[3]的基础上进行的, 对其缺少的引理进行了补充证明, 在数量上增加了10余条矩阵函数性质, 并且部分性质证明难度较高.函数性质证明难度的高低取决于其涉及到的函数的定义的复杂性, 例如矩阵乘法结合律以及矩阵与单位矩阵相乘性质.由于引理证明难度的增加, 导致其需要的辅助引理的数量也大大增加.文献[3]中提供的代码量在2 000行左右, 本次矩阵与分块矩阵形式化研究工作在其基础上进行扩充, 最后统计有关于矩阵与分块矩阵形式化的代码部分在10 000行左右.
无论是在矩阵形式化还是在分块矩阵形式化的研究工作中, 都有大量有关函数性质的证明, 我们在进行对函数性质的证明时, 主要采用归纳证明的方式进行证明.引理的证明与个人的证明经验挂钩, 在证明中有许多的策略, 证明经验能够帮助我们针对不同情况选择不同的证明策略.在对函数性质的证明过程中, 我们可以发现一些函数的潜在问题, 然后根据这些问题对函数进行一定调整与修改, 并重新对该函数性质进行证明.因此, 函数的构造与函数性质的证明并不是一蹴而就的, 而是一个反复的过程.在函数性质证明中发现的函数定义存在问题, 则需要在函数中进行相应调整, 在调整后需要对调整后的函数的性质进行重新证明.采用这种方法所产生的函数能够在很大程度上修正函数定义中存在的问题.当函数定义存在一些难以察觉的问题时, 即产生结果正确却在证明时与引理产生一定冲突和矛盾, 此时我们需要重新修改函数的定义.对于部分引理利用当前已有函数和引理无法完成证明的情况, 我们需要构造新的辅助函数并且提出新的辅助引理, 辅助函数构造方式的选择也成为证明途中一个阻碍.在引理的归纳证明中, 需要对引理中的变量进行归纳.如何选择归纳变量以及确定变量归纳的顺序, 对于引理的证明来说非常重要, 正确的选择能够使得引理更快地得到证明.
下面是我们对本次研究工作中归纳证明时的经验的总结.
● 对必要的变量进行归纳证明.每条引理中存在多个变量, 当引理较为复杂时, 其中变量的数量也较多, 若对每个变量都进行归纳, 会加大证明的困难程度.因此, 对于一些不必要变量可以不用归纳, 归纳变量的选择由该引理中的函数定义结构决定.在对一个变量进行归纳证明时, 重复同样证明操作即表示该变量有可能存在不必要的归纳;
● 归纳变量顺序可变动(根据经验以及具体例子而定).归纳变量顺序不同, 所依赖的证明思路也有所不同.在本次工作中, 主要采用由高度-宽度-二维表的归纳顺序进行归纳证明.对于一些涉及特殊函数的引理, 需要观察其函数内部定义结构, 从而选择有利于进一步化简的变量进行归纳;
● 根据归纳变量所产生的归纳条件进行化简拆分, 得到归纳条件中的形式, 再进行重写证明.遇到无法证明的引理, 存在两种情况: 1) 引理本身存在矛盾, 这可能由引理本身描述错误或函数定义存在问题导致引理中产生冲突或无法证明的情况; 2) 当前函数以及引理无法满足其证明化简的要求.对于第2)种情况, 则需要考虑构造新的函数以及引出新引理进行化简证明.在下一小节中, 将详细分析这两种情况;
● 引理的等价变换和泛化, 在引理的证明中起到一个重要的作用.当我们证明一个引理时, 可能会产生多个子目标, 若当前子目标则需要新的化简后才可证明, 则需要将该化简泛化为一个引理.同样, 我们对于一个引理的证明中也可以依据该引理涉及到的函数性质对函数做一些等价转换, 以达到在一定程度上简化证明步骤的目的.
4.2 难点分析对于上一小节中我们所提及的引理证明存在的两种情况, 将在下面以例子详细解释.
1) 由函数定义引起引理无法证明的情况
引理本身存在矛盾这种情况可能由两种原因导致: 一种是引理本身描述错误, 这可以通过检查发现错误的原因并且对其进行修改; 第2种是引理内部涉及的函数定义不合理而导致引理产生矛盾或者是无法证明的情况, 这需要对函数定义进行修改.下面以单位矩阵左乘性质为例分析第2种原因.
文献[3]中采用的单位矩阵生成函数MI由以下几个函数构成.
list_i函数的作用是产生一个长度为n的表, 其中, 第i个元素为1, 其余元素为0, 如list_i 4 3=[0;0;1;0].其定义如下.
Fixpoint list_i n i: =
match n, i with
|O, _
|S n', O
|S n', S O
|S n', S i'
end.
dlist_i函数的作用是产生一个类型为二维表的单位矩阵, 其中, 参数n表示产生单位矩阵的阶数, dlist_i 3=
[[1;0;0];[0;1;0];[0;0;1]].其定义如下.
Fixpoint dlist_i' n i: =
match i with
|O
|S i'
end.
Definition dlist_i n: =List.rev (dlist_i' n n).
单位矩阵生成函数MI定义如下:
Definition MI n: =let m: =dlist_i n in mkMat A n n m (dlist_i_length n) (all_len_n_dlist_i n).
该定义从结果上显示是正确的, 即对于任意参数n, 都可产生n阶单位矩阵.但其定义中所使用的rev函数却在后期证明中成为证明的一大阻碍, rev函数的作用是将一个表内元素进行逆向排放, 下面以单位矩阵左乘性质引理为例具体说明.
对于需要证明的单位矩阵左乘性质引理如下:
| $\begin{gathered} {\rm{Lemma }}~~matrix\_mul~~unit~~l:{\rm{ forall }}\{ m~n:nat\} ~~(ma:Mat~A~m~n), \\ {\rm{ }}matrix\_mul~(MI~m)~ma = = ma. \\ \end{gathered} $ | (1) |
其中, matrix_mul为矩阵乘法函数, MI为单位矩阵生成函数(MI m代表m阶单位矩阵), ma代表m×n的矩阵.该引理所表示的性质为: 单位矩阵与矩阵相乘结果等于矩阵本身.
在证明matrix_mul_unit_l引理时, 首先对已封装的处理矩阵的函数(matrix_mul, MI)以及矩阵相等判断函数(M_eq)展开, 并进行一些变换操作化简成有关于二维表类型的引理, 引理整理后如下:
| $\begin{gathered} {\rm{Lemma }}~dlist\_mul\_unit\_l':{\rm{ forall }}~m~n~(ma:list(list~A)), ~height~ma = m \to width~ma~n \to \\ {\rm{ }}dl\_mul\_dl~A~Zero~add~{\rm{ }}mul~(rev~(dlist\_i'~A~Zero~One~m~m))~(gettrans~A~Zero~ma~n) = ma. \\ \end{gathered} $ | (2) |
其中, gettrans是对二维表的转置函数, 其带有4个参数, 分别为二维表内元素类型A、A类型中零的表示、二维表以及二维表的宽度.引理(2)等号左侧的结构看起来非常复杂, 为了简化引理, 我们证明了dl_mul_dl函数与rev函数的关系, 具体如图 24所示.

|
Fig. 24 Relationship between dl_mul_dl function and rev function 图 24 dl_mul_dl函数与rev函数的关系 |
接着, 使用该引理对引理(2)进行化简并为新的证明目标, 如下:
| $\begin{gathered} {\rm{Lemma }}~dlist\_mul\_unit\_l':{\rm{ forall }}~m~n~(ma:list(list~A)), ~height~ma = m \to width~ma~n \to \\ rev(dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~m~m)~(gettrans~A~Zero~ma~n)) = ma. \\ \end{gathered} $ | (3) |
由于rev函数对一个参数使用两次后的结果等于其本身, 我们将等式两边都使用rev函数以消除左侧的rev函数, 并对等式左侧ma的转置项(gettrans A Zero ma n)替换为普通二维表.该化简的目的是为了减少引理等号左侧的复杂性, 并将其转移至引理等号右侧.最终需要进行归纳证明的引理如下:
| $\begin{gathered} {\rm{Lemma }}~dlist\_mul\_unit\_l':{\rm{ forall }}~m~n~(ma:list(list~A)), ~height~ma = m \to width~ma~n \to \\ dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~n~n)~ma = rev(gettrans~A~Zero~ma~n). \\ \end{gathered} $ | (4) |
在该引理的归纳证明中, 我们需要对n和ma两个变量进行归纳, 在n=S n和ma=a: : ma时, 化简后得到如下形式子目标:
| $\begin{gathered} l\_mul\_dl~A~Zero~add{\rm{ }}~mul~(list\_i~A~Zero~One~(S~n)(S~n))~(a::ma) \\ ::dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~(S~n)~n)~(a::ma) = \\ rev(gettrans~A~Zero~{\rm{ (}}tl~a::tailcolumn~A~ma)~n) + + (hd~Zero~a::headcolumn~A~Zero~ma)::nil \\ \end{gathered} $ | (5) |
该子目标看起来较为复杂, 但其整体形式为a: : A=B++(b: : nil), 如图 25所示.

|
Fig. 25 Proof problem caused by rev function 图 25 rev函数引起的证明问题 |
该问题产生的原因在于rev函数, rev函数将a: : ma形式的参数转变为ma++(a: : nil)形式, 其中, ++为app函数用于连接两个表.而我们通常对该类问题进行证明时, 采用一定方法将子目标化简为a: : A=b: : B形式, 再利用f_ equal策略使该目标转化为两部分各自相等的子目标.若对其内部继续进行归纳化简, 证明会变得更加复杂繁琐.因此面对该问题时, 我们分析了问题出现的原因并且发现重新思考与rev函数相关的函数定义, 在该例子中即为单位矩阵生成函数的定义.
因此, 我们不采用文献[3]中所定义的单位矩阵生成函数.虽然该函数产生结果满足我们的要求, 但其内部构造不利于有关单位矩阵的性质证明.因此, 我们对其单位矩阵生成函数进行了修改.对于list_i函数, 我们不决定修改, 原因在于该函数满足我们的要求, 并且没有在证明过程中产生阻碍.我们对单位矩阵的二维表的生成函数做了以下修改.
Fixpoint dlist_i' m n i: =
match m with
|O
|S m'
end.
dlist_i'函数的作用是产生一个行数为m、每行长度为n的二维表, dlist_i' n n 0即为n阶单位矩阵(二维表类型).在完成函数的构造后, 对该函数输出结果(二维表)的高度以及宽度进行等价性证明.下面是对该函数进行的测试部分, 如图 26所示.

|
Fig. 26 Test result of dlist_i' fucntion 图 26 dlist_i'函数测试结果 |
Compute (dlist_i' nat 0 1 3 3 0) (构建3阶单位矩阵):
| $\begin{gathered} = [~[1;~0;~0];~[0;~1;~0];~[0;~0;~1]~] \\ ~:list~(list~nat) \\ \end{gathered} $ |
经过测试, 我们可以看到, 该函数所产生的二维表满足单位矩阵的特性.利用上述函数以及性质, 将dlist_i'封装成单位矩阵生成函数MI, 如下:
Definition MI n: =let ma: =dlist_i' n n 0 in mkMat A n n ma (height_dlist_i' n n 0) (width_dlist_i' n n 0).
在上述无rev函数定义的单位矩阵生成函数定义下, 对引理(1)进行展开化简, 得到如下引理:
| $\begin{gathered} {\rm{Lemma }}~dlist\_mul\_unit\_l':{\rm{ forall }}~m~n~(ma:list(list~A)), ~height~ma = m \to width~ma~n \to \\ {\rm{ }}dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~m~m~0)~gettrans~A~Zero~ma~n = ma. \\ \end{gathered} $ | (6) |
为了使证明更加简单, 我们利用转置函数的特性对该引理进行化简, 如下:
| $\begin{gathered} {\rm{Lemma }}~dlist\_mul\_unit\_l':{\rm{ forall }}~m~n~(ma:list(list~A)), ~height~ma = m \to width~ma~n \to \\ {\rm{ }}dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~n~n~0)~ma = gettrans~A~Zero~ma~n. \\ \end{gathered} $ | (7) |
下面对该引理进行归纳证明.对变量n进行归纳证明时, 得到一个子目标如下:
| $\begin{gathered} dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~n~(S~n)~1)~ma = \\ dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~n~n~0)~(tailcolumn~A~ma) \\ \end{gathered} $ | (8) |
观察该子目标发现, 需要将dlist_i' A Zero One n (S n)进行化简.但利用已有函数无法进行化简, 因此需要构造新的函数link1来辅助该化简证明.该函数的作用是将一个表左接于一个二维表, 其实现原理如图 27所示.

|
Fig. 27 Implementation principle of link1 function 图 27 link1函数实现原理 |
对于子目标(8)中的dlist_i' A Zero One n (S n) 1部分, 我们需要利用link1函数进行化简, 其化简引理如下:
| $\begin{gathered} {\rm{Lemma }}~dlist\_i'\_link1:{\rm{ forall }}~m~n~i, \\ dlist\_i'~A~Zero~One~m~(S~n)~(S~i) = link1~(list\_o~A~Zero~m)~(dlist\_i'~A~Zero~One~m~n~i). \\ \end{gathered} $ | (9) |
利用该性质将子目标(8)进行化简, 得到:
| $\begin{gathered} dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(link1~(list\_o~A~Zero~n)~(dlist\_i'~A~Zero~One~n~n~0))~ma = \\ dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~n~n~0)~(tailcolumn~A~ma) \\ \end{gathered} $ | (10) |
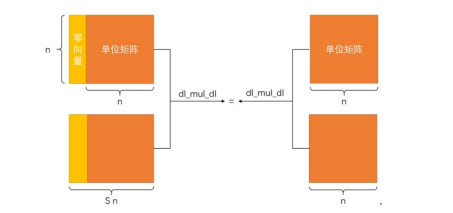
观察该子目标, 需要证明dl_mul_dl函数与link1(list_o A Zero n)函数之间的关系, 其原理如图 28所示.
|
Fig. 28 Relationship between dl_mul_dl function and link1 function 图 28 dl_mul_dl函数与link1函数的关系 |
为了使该引理更易证明, 将其泛化成以下形式:
| $\begin{gathered} {\rm{Lemma }}~dlist\_mul\_unit\_l:{\rm{ forall }}~m~n~i~ma, ~width~ma~(S~n) \to \\ {\rm{ }}dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(link1~(list\_o~A~Zero~m)~(dlist\_i'~A~Zero~One~m~n~i))~ma \\ = dl\_mul\_dl~A~Zero~add{\rm{ }}~mul~(dlist\_i'~A~Zero~One~m~n~i)~(tailcolumn~A~ma) \\ \end{gathered} $ | (11) |
完成该引理的证明后, 加上一些辅助引理的证明即可完成单位矩阵左乘性质的证明.
整体的证明框架如图 29所示.

|
Fig. 29 A proof framework for the property of left multiplication of identity matrix 图 29 单位矩阵左乘性质证明框架 |
由图 29可知: 该单位矩阵左乘性质的证明依赖于17个引理的证明, 并且每个引理都需要有策略地对多个变量按一定顺序进行归纳证明, 部分引理依赖于其他引理.一个矩阵函数性质的证明过程较为复杂以及繁琐, 对如第2.4节中分析的乘法右分配律性质, 可以在证明过程中产生较为清晰的证明思路; 但对于一些证明思路并不明显的性质, 如本节例子的单位矩阵左乘性质, 证明过程中产生的一些引理主要是根据其归纳证明过程中子目标需要的化简步骤以及子目标的泛化而产生的, 这些引理专门为这一个性质而服务, 以支持该性质的证明.
2) 辅助函数有多种构造方式的情况
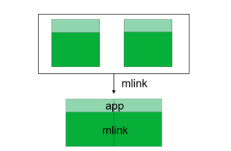
在分块矩阵函数与矩阵函数等价性证明中, 我们需要一个辅助函数——将分块矩阵转化为矩阵的函数MM_to_M.然而, 该函数的定义依赖于一个二维表的横向合并函数mlink, 该函数可以由多种实现方法, 构造方式的选择还需通过后续的证明决定.以下是两种不同的实现方法(如图 30、图 31所示).

|
Fig. 30 Implementation principle of the first mlink definition 图 30 第1种mlink定义实现原理 |
|
Fig. 31 Implementation principle of the second mlink definition 图 31 第2种mlink定义实现原理 |
Fixpoint mlink ma mb n: =
match n with
|O
|S n'
(mlink (tailcolumn A ma) mb n')
Fixpoint mlink(ma mb: list (list A)): =
match ma with
|nil
|x: : x'
|nil
|y: : y'
end
end.
这两种定义所产生的操作结果经过测试都满足我们的要求, 即横向合并两个二维表, 根据这两种定义可以构造出两种分块矩阵到矩阵的转换函数.虽然两种定义的函数产生的结果相同, 但由于定义的不同, 在证明过程中, 前一种定义方法会产生矛盾以及无法证明的问题.
第1种mlink的定义使用文献[3]中的link函数作为辅助函数, 但在归纳变量化简后, 中会出现过于复杂而导致无法继续证明的情况, 具体如图 32所示.

|
Fig. 32 Problems caused by mlink constructed using link function 图 32 使用link函数构造的mlink所产生的问题 |
其原因在于, mlink利用第1个二维表的宽度作为递归参数, 利用headcolumn以及tailcolumn函数将二维表按列分割, 跟二维表的归纳方式不同(按行分割), 因此不利于后续归纳证明.在该情况下, 即使对所有涉及到的变量进行多次归纳仍难以化简, 并且给证明制造了更多的困难.因此, 虽然该函数的定义所产生的结果满足我们的需求, 但由于无法证明后续引理, 我们选择了第2种定义.
第2种定义主要使用辅助函数app来辅助mlink的构造, 该定义较第1种定义更为简单, 无需提供输入参数中第1个二维表的宽度, 并且后续的一系列有关于该函数的引理都可以顺利证明.
在后续的证明中, 仍需要构造新的辅助函数以及大量辅助引理以支撑证明.在分块矩阵函数等价性证明中, 还需要构造两个辅助函数, 分别是headcolumn_n以及tailcolumn_n.这两个函数的作用分别是取二维表前n列、取二维表除前n列以外剩余的列数, 这两个函数主要起过渡作用, 用于建立部分函数之间的关系.
在矩阵和分块矩阵形式化研究工作中, 通常函数定义无法一步到位, 一个函数的实现有多种方式, 一开始定义的函数看起来正确, 但是具有一些潜在问题难以发现, 在后期性质证明时产生冲突或无法证明, 则要思考是否需要修改函数定义; 性质证明无法一步到位, 在证明一个引理时往往需要多个引理以支撑.这些性质可以分为辅助引理与关键引理, 当目前无引理可帮助化简证明时, 需要构造过渡函数以创建新的引理进行进一步化简证明, 如link1函数、headcolumn_n函数以及tailcolumn_n函数.此时, 辅助引理的构造方式也需要在后续证明中选择; 定义与证明同时进行时, 遇到证明失败时难以确定是函数定义问题还是证明策略问题, 需要在不断的尝试中进一步理解问题所在.
5 总结利用Coq定理证明器中的Record类型所实现的矩阵形式化方法与其他矩阵实现方法相比, 其实现更加简洁且更容易理解, 使用起来也更加方便, 并且可以使用代码抽取机制将经过验证的函数抽取为可执行的OCaml代码.我们在完善了矩阵形式化方法的基础上, 为矩阵函数的引理进行了补充证明, 并且建立了基于不同类型的矩阵基础库, 具体包括实数矩阵库、整数矩阵库、复数矩阵库以及函数矩阵库.后续在矩阵形式化方法的基础上实现分块矩阵形式化方法, 其能够实现将高阶矩阵运算转换为多个低阶矩阵运算.在后续有关于分块矩阵形式化证明工作中, 我们不仅证明了分块矩阵运算的正确性, 并将矩阵形式化中已证明的函数移植于分块矩阵形式化库中.最后, 我们建立了基于不同类型的分块矩阵基础库.目前, 我们已经实现用函数式语言描述矩阵, 在未来的工作中, 我们考虑定义一组重写优化规则并进行代码优化, 将该矩阵运算以及分块矩阵运算函数转换为高效率并行C代码, 并验证该重写优化的等价性, 从而构建一个深度学习代码优化系统, 并完成深度学习矩阵运算的形式化验证.
本次研究工作的代码地址: https://gitee.com/yingyingma/Matrix.
致谢 感谢石正璞对本次工作提出的问题和建议以及在编译方面的支持工作, 感谢沈楠、邓昊对本文存在的语病和问题的检查和纠正, 感谢张正、崔敏以及讨论班的同学对本次研究工作的热心讨论和研究.
| [1] |
Almeida JB, Frade MJ, Pinto JS, Sousa SMD. An overview of formal methods tools and techniques. In: Proc. of the Rigorous Software Development. London: Springer-Verlag, 2011. 15-44.
|
| [2] |
Formalizing the safety of Java, the Java virtual machine, and Java card. ACM Computing Surveys (CSUR), 2001, 33(4).
|
| [3] |
Ma ZW, Chen G. Matrix formalization based on Coq record. Computer Science, 2019, 46(7): 139-145(in Chinese with English abstract).
[doi:10.11896/j.issn.1002-137X.2019.07.022] |
| [4] |
Hagedorn B, Lenfers J, Koehler T, Qin XY, Gorlatch S, Steuwer M. Achieving high-performance the functional way—A functional pearl on expressing high-performance optimizations as rewrite strategies. In: Proc. of the ACM SIGPLAN Int'l Conf. on Functional Programming (ICFP 2020). 2020. [doi: 10.1145/3408974]
|
| [5] |
Bertot Y, Casteran P. Interactive theorem proving and program development. In: Proc. of the Coq'Art: The Calculus of Inductive Constructions. Springer, 2004.
|
| [6] |
Obua S. Proving bounds for real linear programs in Isabelle/HOL. In: Proc. of the Theorem Proving in Higher Order Logics. 2005. 227-244.
|
| [7] |
Paşca I. Formal proofs for theoretical properties of Newton's method. Mathematical Structures in Computer Science, 2011, 21(4).
[doi:10.1017/S0960129511000077] |
| [8] |
Paşca I. Formally verified conditions for regularity of interval matrices[Ph. D. Thesis]. Intelligent Computer Mathematics, 2010.
|
| [9] |
Alama J. The rank-nullity theorem. Formalized Mathematics, 2007, 15(3).
|
| [10] |
Karol PK. Eigenvalues of a linear transformation. Formalized Mathematics, 2008, 16(4): 289-295.
[doi:10.2478/v10037-008-0035-x] |
| [11] |
Solovay RM, Arthan RD, Harrison J. Some new results on decidability for elementary algebra and geometry. Annals of Pure and Applied Logic, 2012, 163(12).
[doi:10.1016/j.apal.2012.04.003] |
| [12] |
Shi ZP, Liu ZK, Guan Y, Ye SW, Zhang J, Wei HX, Luo GM. Formalization of function matrix theory in HOL. Journal of Applied Mathematics, 2013, 34(3): 654-658 (in Chinese with English abstract). [doi: 10.1155/2014/201214]
|
| [13] |
Kang XN, Shi ZP, Ye SW, Guan Y. Formalization of matrix transformation theory in HOL4. Computer Simulation, 2014, 31(3): 289-294(in Chinese with English abstract).
[doi:10.1080/19443994.2014.944221] |
| [14] |
Yang XM, Guan Y, Shi ZP, Wu AX, Zhang QY, Zhang J. Higher-Order logic formalization of function matrix and its calculus. Computer Science, 2016, 43(11): 24-29 (in Chinese with English abstract). [doi: 10.11896/j.issn.1002-137X.2016.11.005]
|
| [15] | |
| [16] |
Boldo S, Lelay C, Melquiond G. Coquelicot: A user-friendly library of real analysis for Coq. Mathematics in Computer ence, 2015, 9(1): 41-62.
[doi:10.1007/s11786-014-0181-1] |
| [3] |
马振威, 陈钢. 基于Coq记录的矩阵形式化方法. 计算机科学, 2019, 46(7): 139-145.
[doi:10.11896/j.issn.1002-137X.2019.07.022] |
| [12] |
刘振科, 施智平, 关永, 等. 函数矩阵理论在HOL4中的形式化. 小型微型计算机系统, 2013, 34(3): 654-658. [doi: 10.1155/2014/201214]
|
| [13] |
康西楠, 施智平, 叶世伟, 关永. 矩阵变换理论在HOL4中的形式化. 计算机仿真, 2014, 31(3): 289-294.
[doi:10.1080/19443994.2014.944221] |
| [14] |
杨秀梅, 关永, 施智平, 等. 函数矩阵及其微积分的高阶逻辑形式化. 计算机科学, 2016, 43(11): 24-29. [doi: 10.11896/j.issn.1002-137X.2016.11.005]
|
 2021, Vol. 32
2021, Vol. 32


