Petri网作为一种分布式并发系统的建模和分析工具, 在柔性制造系统^{[1, 2,]}、业务过程管理系统^{[3, 4]}、并发程序形式化验证^{[5, 6]}等方面得到了广泛使用.然而, 状态爆炸问题妨碍了Petri网在大规模并发系统分析中的应用.为此, McMillan^[7]首次提出利用网的展开描述系统行为, 并通过分支进程^[8]与偏序技术构造展开网的有限完备前缀, 有效缓解了Petri网性质分析中的状态爆炸问题, 由此受到了研究者们的广泛关注.

Esparza等人^[9]指出, McMillan定义的偏序关系在某些情况下会导致有限完备前缀的规模呈指数级增长, 并针对安全Petri网提出了一种全序关系, 最小化有限完备前缀的规模.Khomenko等人^[10]规范了展开的定义, 并对展开进行参数化配置.Heljanko等人^[11]将展开技术并行化, 提高了展开的效率.Benito等人^[12]将展开技术扩展到时间Petri网.Schwarick等人^[13]将展开技术扩展到于颜色Petri网.在Petri网展开技术的应用方面, Lu等人^[5]针对网系统的死锁检测提出一种无界Petri网的有限展开技术.Xiang等人^[6]基于展开技术对并发系统中的数据不一致问题进行检测.Dong等人^[14]基于Petri网的可达图对CTL进行验证.Liu等人^[15]借助分支进程技术检测工作流的健壮性.在Petri网的性质分析方面, Chatain等人^[16]针对Petri网的可覆盖性问题设计了一种目标导向的展开技术, 通过分析内部因果关系对冗余变迁进行剪枝.Bonet等人^[17]结合启发式技术提出了一种semi-adequate ordering, 提升了展开技术在Petri网可覆盖性分析上的效率, 并在后续的论文^[18]中证明扩展顺序可以与截断事件的偏序分离, 拓宽了启发式展开技术在Petri网性质分析中的应用.

网的展开通过分支进程与偏序技术可在一定程度上缓解Petri网性质分析中的状态爆炸问题.但展开网中仍然包含了系统的所有状态信息.某些应用问题仅需对系统特定状态标识的可覆盖性进行判定, 以此为目标有望对网系统的展开进行化简.为此, 本文针对安全Petri网的可覆盖性判定问题提出了一种目标导向的反向展开算法.反向展开从需要做出可覆盖性判定的目标标识出发, 仅刻画与可覆盖性判定相关的系统状态, 并结合启发式技术缩减展开的规模, 以此提高目标标识可覆盖判定的效率.进而, 将反向展开算法应用于并发程序的形式化验证, 将并发程序的数据竞争检测问题转换为Petri网特定标识的可覆盖性判定问题.实验对比了启发式反向展开与directed unfolding^[17](一种同样采用了启发式技术的正向展开)在Petri网可覆盖性问题上的效率, 结果表明: 在415组测试数据中, 反向展开的规模在85组数据上优于directed unfolding, 在26组数据上与directed unfolding持平.最后, 本文对影响反向展开效率的关键因素做了分析与总结.

本文第1节围绕Petri网的可覆盖性判定问题, 分别分析正向展开与反向展开的适用场景, 并结合实例说明反向展开相比正向展开的优势.第2节介绍Petri网的反向展开算法, 包括相关概念的形式化定义、算法流程以及启发式优化策略.第3节将反向展开应用于并发程序的数据竞争检测.第4节结合实验评估正向展开与反向展开在Petri网可覆盖性判定问题上的效率.第5节对本文所做的工作进行总结与展望.

1 实例与动机分析

本节首先在Petri网的可覆盖性判定问题上分别论述正向展开与反向展开的适用场景.之后, 将通过一个实例说明反向展开相比正向展开的优势.

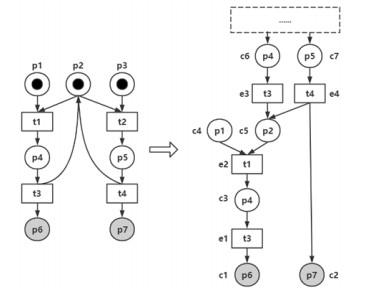
先来看两个简单的例子.图 1(a)中Petri网的初始标识为{ps}, 需验证目标标识{pt}的可覆盖性.为了便于表述, 将图 1(a)左侧的路径称为path1, 右侧的路径称为path2.在这个例子中, 正向展开从初始标识{ps}出发, 难以在path1与path2间做出选择, 若不慎选择了path2, 将会做很多冗余的扩展.与正向展开不同, 反向展开从目标标识{pt}出发, 仅需要沿着path1反向扩展, 很容易找到与初始标识{ps}间的可达路径.

图 1(b)可以看作图 1(a)的“倒置”.在这个例子中, 反向展开从目标标识{pt}出发, 难以在path1与path2间做出选择.而正向展开从初始标识{ps}出发, 很容易沿着path1到达目标标识{pt}.

从上述两个例子中可观察到: 当Petri网的正向分支较多时, 反向展开往往更加适用; 当Petri网的反向分支较多时, 正向展开往往更加适用.具体而言, 正向展开从Petri网的初始标识出发刻画系统, 隐含了系统完整行为; 而反向展开从需要做出可覆盖性判定的目标标识出发, 仅刻画与可覆盖性判定相关的系统状态.本文正是从这个角度出发设计并实现了反向展开算法.

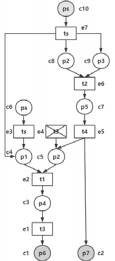
接下来, 将结合一个实例进一步说明反向展开相比正向展开的优势.图 2(a)中, Petri网的初始标识为{p1}, 需验证目标标识{p10}的可覆盖性.图 2(b)是Petri网的正向展开^[9].图 2(c)是Petri网的反向展开.二者都采用基于广度优先策略的adequate order作为扩展顺序, 一旦验证目标标识的可覆盖性就终止扩展.在这个例子中, 正向展开共产生19个节点、20条流关系, 反向展开总共产生14个节点、14条流关系, 反向展开的规模优于正向展开.这是因为变迁{t1, t3, t4, t7}对于{p10}可覆盖性的贡献是冗余的(即“左侧”的路径是冗余的).正向展开隐含了系统的完整行为, 难以避免对{t1, t3, t4, t7}的冗余行为分析.而反向展开仅刻画与可覆盖性判定相关的系统状态, 避免了对{t3, t7}的冗余刻画.尽管反向展开中仍有冗余, 但总体规模优于正向展开.

本节论述了正向展开与反向展开各自的优势.值得一提的是: 这种相互之间的优势是由算法的性质决定的, 具备一定的一般性.像goal-driven unfolding^[16], directed unfolding^[17]等正向展开, 尽管它们会使用内部因果关系进行剪枝、亦或是使用启发式技术优化算法效率, 但在正向分支过多的情况下, 还是难以避免对系统冗余行为的分析.同样, 即使反向展开配备了启发式技术, 在反向分支过多时, 也难以保证算法的效率.在这个前提下, 本节进而通过实例表明, 反向展开在某些情况下优于正向展开.接下来将详细介绍反向展开算法.

2 Petri网的反向展开 2.1 反向展开的概念 2.1.1 Petri网

一个网可以定义为一个三元组(P, T, F), P为库所集, T为变迁集, F为P与T间的流关系, F⊂(P×T)∪(T×P).节点x的前集定义为x^·={y∈P∪T|F(y, x)=1}, 节点x的后集定义为x^·={y∈P∪T|F(x, y)=1}.网(P, T, F)的标识是建立在P上的一个多重集.在图形化表示时, 网的标识通过在各个库所中添加相应数量的token来表示.

一个网系统可以定义为一个四元组(P, T, F, M₀), 其中, M₀是网(P, T, F)的初始标识.如果∀p∈P: F(p, t)≤M(p), 则标识M下变迁t使能, 使能的变迁可以执行.t的执行使系统进入一个新的标识M', 记作M $ \xrightarrow{t}$M', 即: 对每个库所p, M'(p)=M(p)-F(p, t)+F(t, p).一个变迁序列σ=t₁t₂…t_n称之为触发序列, 当且仅当存在标识M₁, M₂, …, M_n-1, M_n, 使得$ {M_0}\xrightarrow{{{t_1}}}{M_1}\xrightarrow{{{t_2}}} \ldots \xrightarrow{{{t_{n - 1}}}}{M_{n - 1}}\xrightarrow{{{t_n}}}{M_n}$成立.上式也可以表示为$ {M_0}\xrightarrow{\sigma }{M_n}$, 称M_n是触发序列σ下的可达标识.

对于标识M_f, 若有标识M, M'和触发序列σ, 使得$ M\xrightarrow{\sigma }M' \wedge {M_f} \subseteq M'$, 则称M_f可被M覆盖, 记为M↦M_f.

若可达标识M满足∀p: M(p)≤n, 则称M是n-safe的.一个网系统是n-safe的, 当且仅当其所有可达标识都是n-safe的.特别地, 将1-safe网系统称为安全网系统.本文只考虑安全Petri网的可覆盖性问题, 并记可覆盖性判定的目标标识为M_f, 即验证M₀↦M_f是否成立.

2.1.2 反向出现网

定义1(反向出现网). 反向出现网是出现网的子类, 用以判定一个Petri网中目标标识M_f的可覆盖性, 对应一个四元组RON=(C, E, F', CM_f).其中, C为条件集, 每个条件对应Petri网库所中的一个token; E为事件集, 每个事件对应Petri网中某变迁的一次执行; F'为C与E间的流关系, 对应Petri网的流关系; CM_f为Petri网目标标识M_f在RON中对应的条件集合, 满足∀c∈CM_f: c^·=Ø.

以图 3(a)中的Petri网与目标标识M_f={p4}为例, 它对应的反向出现网见图 3(b), 其中, CM_f={c1}.

RON上的两个节点x₁, x₂有以下3种关系.

(1)   反向因果: 若从x₁出发的某条路径可到达x₂, 则记x₂≤x₁.特别的, 对于任意节点x, 有x=x.图 3(b)中, 有c1≤c5, e2≤e3;

(2)   反向冲突: 若存在两个不同的事件e₁, e₂∈E, e₁^·∩e₂^·≠Ø∧e₁≤x₁∧e₂≤x₂, 则称x₁与x₂反向冲突, 记为x₁#x₂.图 3(b)中, c2与c3反向冲突, 这是因为e1≤c2, e2≤c3, 且e1^·∩e2^·={c1}≠Ø.同理, c2与c4反向冲突、e1与e2反向冲突;

(3)   反向并发: 若¬(x₁≤x₂∨x₂≤x₁∨x₁#x₂), 则称x₁与x₂反向并发, 记为x₁‖x₂.图 3(b)中, c3与c4反向并发.

RON满足以下3个性质.

(1)   ∀c∈C: |c^·|≤1;

(2)   RON中没有反向自我冲突, 即: 不存在事件e∈E, 使得e#e;

(3)   F'是无环的, 即F'的反自反传递闭包是一个偏序.

定义2(反向配置). RON中的反向配置Cfg为若干个事件的集合, 满足以下两个性质.

(1)   若事件e∈Cfg, 则∀e' < e: e'∈Cfg;

(2)   Cfg中不存在反向冲突的事件, 即∀e, e'∈Cfg: ¬(e#e').

定义3(反向局部配置). 特别地, 将{e'|e'∈E∧e' < e}定义为事件e的反向局部配置, 记作[e].

图 3(b)中, [e1]={e1}, [e3]={e2, e3}.

定义4(反向切). 对于配置Cfg, 定义其反向切为Cut(Cfg)=(CM_f∪^·Cfg)\Cfg^·.另外, 对于一个条件集合, 若其各元素之间两两反向并发, 则称其为一个co-set.不难发现, Cut(Cfg)是一个co-set.

图 3(b)中, Cut([e2])={c3, c4}, Cut([e3])={c5}.

反向配置、反向切会在第2.1.3节中用于建立反向出现网标识与Petri网标识间的映射关系.

2.1.3 反向展开

对于给定的Petri网∑=(P, T, F, M₀), 需验证目标标识M_f的可覆盖性.定义∑和RON=(C, E, F', CM_f)各节点间的映射关系μ: C∪E→P∪T如下.

(1)   若c∈C, 则μ(c)∈P; 若e∈E, 则μ(e)∈T;

(2)   ∀e∈E, ^·e到^·μ(e)在μ的约束下满足双射关系, e^·到μ(e)^·在μ的约束下满足单射关系.这里与正向展开不同, 在反向展开中, e^·到μ(e)^·可以不满足满射关系;

(3)   CM_f与M_f在μ的约束下满足双射关系.

定义5(反向标识). 定义Mark(Cfg)=μ(Cut(Cfg))为配置Cfg的反向标识.Mark(Cfg)可看作RON的一个中间标识, M_f的可覆盖性判定可转化为Mark(Cfg)的可覆盖性判定^[19].

图 3(b)中, Mark([e2])=μ({c3, c4})={p2, p3}, Mark([e3])=μ({c5})={p1}.

定义6(反向展开). 在上述概念的基础上, Petri网∑中目标标识M_f的反向展开定义为一个二元组RUnf(RON, μ), 满足以下性质:

(1)   RUnf是完备的: 记∑的初始标识M₀, 若M₀aM_f, 则在RUnf存在一个反向配置Cfg, 使得Mark(Cfg)⊆M₀.这里只需要保证M_f的可覆盖性不被破坏即可, 不必获取全部触发序列;

(2)   RUnf是有限的, 即RUnf中包含有限的条件与事件.

2.2 反向展开算法

给定Petri网∑=(P, T, F, M₀)和需要进行可覆盖性判定的目标标识M_f, 反向展开算法的基本思想如下: 首先, 针对M_f中每个库所, 在RUnf中添加一个相应的条件, 即创建CM_f; 之后, 从CM_f出发逐步反向扩展, 添加能生成这些条件的事件以及这些事件使能所需的条件, 并对冗余的事件进行截断.如此重复, 直到一个反向标识能被∑的初始标识所覆盖, 或者能证明目标标识不可覆盖.

接下来将结合图 4所示的实例, 给出反向扩展与反向截断事件的准确定义, 并介绍目标标识可覆盖性的判定方法.假设图 4中需进行可覆盖性判定的目标标识为{p6, p7}.

2.2.1 反向扩展

定义7(反向扩展). 反向扩展为一个二元组rext=(t, C), 其中, C是一个co-set, μ(C)⊆t^·, 记反向扩展组成的集合为RExt.

对每一个从RExt中选中并用以扩充RUnf的反向扩展rext=(t, C)而言, 一方面需要向RUnf中添加一个事件e=(t, C); 同时, 需要为^·t中的每个库所添加一个条件至RUnf中.之后重新计算RExt, 记此过程为NE(RUnf, e).

NE(RUnf, e)计算候选扩展集的过程如下: ^·e的加入会为RUnf添加新的co-set, 对每个新增的co-set C, 若有变迁t满足μ(C)⊆t^·, 则添加一个新的候选扩展rext=(t, C)到RExt中.

按照上述定义, RExt中会存在大量冗余扩展.例如, 假设{c1, c2, c3}是一个co-set, 那么按照co-set的定义, {c1, c2}, {c1, c3}, {c2, c3}, {c1}, {c2}, {c3}都是co-set.若有反向扩展(t, {c1, c2, c3}), 那么同样会有反向扩展(t, {c1, c2}), (t, {c1, c3}), (t, {c2, c3}), (t, {c1}), (t, {c2}), (t, {c3}).可见: 不加额外限制的话, RExt的规模将会非常大.因此, 为RExt添加如下两个条件.

(1)   对于RUnf中任意事件e, RExt中不存在反向扩展rext=(t, C), 使得μ(e)=t∧e^·=C;

(2)   对于RExt内任意两不同的反向扩展rext₁=(t₁, C₁), rext₂=(t₂, C₂), 若t₁=t₂∧C₁⊂C₂∧Mark([rext₁])≥ Mark([rext₂]), 则将扩展rext₁从RExt中删除.这里假设e为rext在RUnf中对应的事件, [rext]可视为[e].

条件(2)中, Mark([rext₁])≥Mark([rext₂])看上去有些多余.实际上, Parosh早在文献[19]中就提出过反向展开的概念, 且仅用到了条件(2)中t₁=t₂∧C₁⊂C₂这个限制.遗憾的是, 这样做会破坏反向展开的完备性, 致使Parosh的反向展开算法在某些情况下出错, 附录B给出了相关反例的分析.为此, 本文添加了Mark([rext₁])≥Mark([rext₂])这个限制, 大量实践表明, 这个限制是有效的.

图 5中, 生成事件e2时用到了反向扩展rext=(t1, {c3}), 同时生成了e2的前驱条件{c4, c5}.{c4, c5}的加入, 产生了新的co-set, 并产生了相应的反向扩展(t3, {c5}), (t4, {c5}), (t4, {c2, c5}).其中, 对于rext₁=(t4, {c5}), rext₂=(t4, {c2, c5}), 有Mark([rext₁])={p1, p5, p7}≥{p1, p7}=Mark([rext₂]), 由RExt的条件(2)删除rext₁.故最终:

$ NE\left( {RUnf, e} \right) = \left\{ {\left( {t3, \{ c5\} } \right), \left( {t4, \{ c2, c5\} } \right)} \right\}. $

2.2.2 反向截断事件

前述反向扩展规则能确保RUnf的完备性, 但无法保证其有限性.为此, 下文将给出反向截断事件的识别规则, 据此保证反向展开过程的可终止性.

定义8(反向截断事件). 事件e为反向截断事件, 当且仅当RUnf中存在事件e', 满足以下两个条件.

(1)   Mark([e'])≤Mark([e]);

(2)   [e'] [e].

其中, 是定义在配置上的偏序, 称为adequate order, 满足以下3个条件.

(1)   是良基的;

(2)   是⊂的精炼, Cfg₁⊂Cfg₂意味着Cfg₁Cfg₂;

(3)    若Mark(Cfg₁)≤Mark(Cfg₂), Cfg₁Cfg₂, 则对Cfg₂的任意前缀E₂, 有E₁满足Mark(Cfg₁⊕E₁)≤ Mark(Cfg₂⊕E₂), 且Cfg₁⊕E₁Cfg₂⊕E₂.其中: 对于一个配置Cfg, Cfg⊕E表示存在事件集E, 使得Cfg∩E=Ø, 且Cfg∪E也是一个配置.E也叫作Cfg的前缀.

本文使用_r作为adequate order, 相关证明可参考附录A中的定理1.Cfg_1rCfg₂定义为:

(1)   |Cfg₁| < |Cfg₂|;

(2)   |Cfg₁|=|Cfg₂|∧Lex(μ(Cfg₁)) < Lex(μ(Cfg₂)).其中, μ(Cfg)是配置Cfg₂映射到∑上的变迁集合, 这个变迁集合是一个多重集.Lex(μ(Cfg))将μ(Cfg)中的变迁按照ID从小到大排序.可以理解为: 当两个配置大小相同时, 比较其对应的变迁集合的字典序.

图 5中的事件e3将因事件e1而截断, 如图 6所示.这是因为|[e1]| < |[e3]|, 即[e1] _r[e3], 且:

$ Mark\left( {\left[ {e1} \right]} \right) = \left\{ {p4, p7} \right\} \leqslant \left\{ {p1, p4, p7} \right\} = Mark\left( {\left[ {e3} \right]} \right). $

反向扩展和反向截断事件保证了RUnf的完备性与有限性, 相关证明见附录A中的定理2与定理3.

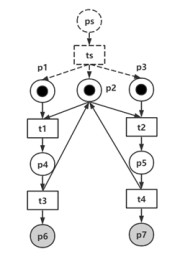
2.2.3 反向展开的可覆盖性判定

本文只考虑安全Petri网, 可以在Petri网上添加源库所ps、源变迁ts、流关系(ps, ts), 并对∀p∈M₀添加流关系(ts, p), 从而将求解M₀aM_f转化为求解{p_s}aM_f.这样仅需判断RUnf中是否存在一个配置Cfg, 使得Mark(Cfg)={ps}, 即可验证M_f的可覆盖性.以图 4中的Petri网为例, 添加源节点后的Petri网如图 7所示.

2.2.4 反向展开算法与可覆盖性判定实例

反向展开可覆盖性判定的流程可以总结为: 初始时, RUnf中只有与M_f相对应的条件集合CM_f, 算法会基于CM_f计算初始扩展集Rext.随后, 只要RExt不为空, 则算法将持续进行反向扩展.每次扩展都会从RExt中随机取出一个rext=(t, C), 并在RUnf中创建相应的事件e=(t, C).若e不为反向截断事件, 则对^·t中的每个库所p在RUnf中创建相关的条件c=(p, e).之后, 通过计算RExt=RExt∪NE(RUnf, e)更新RExt.若存在一个事件e, 使得Mark([e])= {ps}, 则说明M_f可覆盖, 终止算法.若最终RExt为空, 且没有事件e满足Mark([e])={ps}, 则说明M_f不可覆盖.反向展开算法的伪代码如下.

Petri网的反向展开与目标标识可覆盖性判定算法.

Input: A net system ∑=(P, T, F, {p_s}), with target M_f={p₁, p₂, …, p_n};

Output: The coverability of M_f.

RUnf={(p₁, Ø), (p₂, Ø), …, (p_n, Ø)}

RExt=NE(RUnf, Ø)

while RExt≠Ø do

  poll an extension rext=(t, C) from RExt randomly

  create an event e=(t, C) in RUnf

   if e is not a reverse cut-off event then

     for ∀p∈^·t, append a condition c=(p, e) to RUnf

     if Mark([e])={ps} then

       return true

     endif

    RExt=RExt∪NE(RUnf, e)

   endif

endwhile

return false

下面结合图 7的Petri网实例, 展示反向展开判定目标标识{p6, p7}可覆盖性的完整流程, 见表 1.

以上就是整个反向展开算法的流程, 然而算法目前并没有规定扩展顺序, 仅采用随机扩展.实际上, 扩展顺序对反向展开算法的效率有着决定性的影响.接下来将使用启发式技术对反向展开做优化.

2.3 反向展开算法的启发式优化

扩展顺序对目标标识可覆盖性验证的效率有着关键影响, 为此, 本文基于实践总结并参考文献[17]提出了3种启发式技术:

(1)   block策略.

在反向扩展rext=(t, C)中, C到t^·可以不满足满射关系.然而实践表明: C到t^·不满足满射时往往意味着rext产生得过早, 相应的条件还没来得及产生, 此时由其引导的扩展都将会是冗余扩展.为了尽可能避免这种情况发生, 将不满足满射关系的rext加入阻塞队列, 优先选择满足满射关系的反向扩展.仅当所有反向扩展都不满足满射关系时, 才会在阻塞队列中选择一个rext激活.实践中, block策略通常会配合其他启发式策略共同使用.

(2)   hmax策略.

hmax策略是Bonet在文献[17]中提出的一种基于距离的启发式策略.定义d(M, M')为标识M到M'间的距离.hmax将M到变迁t的距离定义为$ {\max _{p{ \in ^ \cdot }t}}d\left( {M\left\{ p \right\}} \right)$, 将M到库所p的距离定义为$ {\min _{t{ \in ^ \cdot }p}}d\left( {M{, ^ \cdot }t} \right)$如此递推.计算d(M, M')时, 只需求M到M'中每个库所的最大距离, 即计算max_p∈M'd(M, {p}).

上述过程可总结为

$ d(M,M') = \left\{ {\begin{array}{*{20}{l}} {0,{\text{ }}M' \subseteq M} \\ {1 + {{\min }_{t{ \in ^ \cdot }p}}d(M{,^ \cdot }t),{\text{ }}M' = \{ p\} } \\ {{{\max }_{p \in M'}}d(M,\{ p\} ),{\text{ otherwise}}} \end{array}} \right.. $

(3)   hsum策略.

hsum与hmax十分相似, 不同的是: hsum将M到变迁t的距离定义为∑_p∈^·td(M, {P})与之对应, 计算d(M, M')时, 统计M到M'中每个库所的距离总和, 即计算∑_p∈^·M'd(M, {P})

上述过程可总结为

$ d(M, M') = \left\{ {\begin{array}{*{20}{l}} {0, {\text{ }}M' \subseteq M} \\ {1 + {{\min }_{t{ \in ^ \cdot }p}}d(M{, ^ \cdot }t), {\text{ }}M' = \{ p\} } \\ {\sum\nolimits_{p{ \in ^ \cdot }t} {d(M, \{ p\} )} , {\text{ otherwise}}} \end{array}} \right.. $

hmax策略与hsum策略在使用时会结合配置大小.具体而言: 对于两个反向扩展rext₁=(t₁, C₁), rext₂=(t₂, C₂), 若有|[rext₁]|+d(M₀, Mark([rext₁])) < |[rext₂]|+d(M₀, Mark([rext₂])), 则优先选择rext₁进行扩展.

3 基于反向展开的数据竞争检测

由于线程调度的不确定性, 多线程程序往往伴随着数据竞争.数据竞争是指在非线程安全的情况下, 多个线程对同一内存地址空间进行访问.数据竞争会影响程序的运行结果, 甚至会导致系统崩溃.由于数据竞争通常只在一些特定的线程轨迹中出现, 这给开发人员检测数据竞争带来了极大的挑战.历史上几起严重的事故, 如Therac-25放射治疗设备事故^[20]、2003年北美的大规模停电^[21]以及纳斯达克的FaceBook故障^[22]都与数据竞争有关.数据竞争检测主要分为静态检测^[23-25]与动态检测^[26-28]两类.本节将基于Petri网的反向展开对Java并发程序中的数据竞争进行静态检测.

3.1 程序Petri网模型的构建

Krishna^[29]针对C-Pthread程序提出了其同步原语、流程控制语句的Petri网模型构建方法.本文将这些建模方法应用到Java并发程序上, 主要考虑以下4种语句的模型构建.

(1)   线程启动与合并: Java中, 线程t的启动与合并分别对应t.start(·), t.join(·).调用t.start(·)后, 线程t的状态变为Runnable, 在得到CPU调度后, 变为Running状态正式运行.调用t.join(·)后, 当前线程的状态变为Blocked, 直到线程t执行完毕后才会变为Runnable状态, 重新等待CPU调度.线程的启动与合并对应的Petri网模型如图 8(a)所示;

(2)   锁的申请与释放: Java中使用synchronized语句实现线程的互斥, 包括同步方法和同步代码块, 二者本质上是相同的.当线程t1与线程t2同时访问同步代码块时, 只有一个线程可获取访问权限.锁的申请与释放对应的Petri网模型如图 8(b)所示;

(3)   分支: Java程序中的分支在逻辑上都等价于if, if-else型分支.对应的Petri网模型如图 8(c)所示;

(4)   循环: Java程序中的循环分为for/while型循环和do-while型循环, 二者的结构相似, 都由一个控制条件和一个循环体构成.对应的Petri网模型如图 8(d)所示.

图 9给出了一个Java多线程程序的实例以及由上述规则构造所得的程序Petri网模型, 其中, 带星号的变迁对应程序语句, 其余变迁仅用于表达程序结构.具体而言:

(1)   程序语句方面, t1代表创建线程t1, t6代表创建线程t2, t14代表将线程t1合并到主线程.t7, t8代表申请锁lock, t15, t16代表释放锁lock.t9对应语句x=2, t10对应语句x=1, t11对应语句System.out.println(x);

(2)   程序结构方面, t2, t4代表进入if结构, t13, t17代表退出if结构.t3代表一轮循环的开始, t5代表一轮循环的结束, t12代表退出循环.

3.2 基于可覆盖性判定的数据竞争检测

程序中关于同一个共享变量的两条读/写或者写/写操作, 如果它们在执行顺序上存在先后依赖关系, 则不会产生数据竞争; 反之, 若他们之间存在并发关系, 则会导致数据竞争.由此一来, 可以对程序的Petri网模型进行分析, 判别两个操作对应的变迁是否在某些状态下具有并发关系.实际上, 对于任意的两个变迁t和t', 我们只需要判定是否存在一个可达标识M, 使得M≥^·t+^·t', 即判定标识^·t+^·t'的可覆盖性.

考虑图 9所示的例子, 其中, 读共享变量System.out.println(x)与写共享变量x=2之间未加同一把锁, 会发生数据竞争.共享变量x的写操作x=2对应变迁t9, 读操作System.out.println(x)对应变迁t11, 判定数据竞争只需验证目标标识{p8, p11}的可覆盖性.

程序Petri网模型的反向展开流程见表 2.

不难发现, Mark([e9])={ps}, 故目标标识{p8, p11}是可覆盖的, 两个读写操作对应的变迁可以并发, 程序存在潜在的数据竞争.

本节构建了Java并发程序的Petri网模型, 将数据竞争检测转化为验证相关变迁的可覆盖性, 并结合实例展示了反向展开算法在数据竞争检测上的应用.然而, 本文仅给出了Java多线程程序的Petri网建模方法, 并没有设计实际的建模工具.在实际应用中, 可以考虑使用Soot^[30]对Java并发程序自动化建模.Soot是一款Java字节码分析优化框架, 可以将Java源码转换为Jimple中间代码进行分析.比如: 可以借助JInvokeStmt分析线程的启动与合并, 以及各种函数调用; 借助JEnterMonitorStmt与JExitMonitorStmt分析锁的申请与释放; 借助JIfStmt与JGotoStmt分析程序中的分支与循环.篇幅所限, 我们将在后续工作对此展开研究.

4 实验评估

本节将通过实验对比启发式反向展开与directed unfolding^[17](一种同样采用了启发式技术的正向展开)在Petri网可覆盖性问题上的效率.本文将通过事件总数及运行时间评估算法效率.实验所用的基准库包含415组测试用例, 包含directed unfolding的358组用例以及我们自己构造的57组用例, 且所有用例均可覆盖.其中, Petri网的变迁数量从6~9462不等, 共计261694个变迁.实验环境为AMD Ryzen 7 4800U, 16GB RAM.源码及测试用例可通过文献[31]获取.

4.1 无启发式策略时反向展开与正向展开的对比

由于启发式策略对算法效率有很大影响, 不利于直观地体现反向展开在性质上的优势.因此, 本文首先采用基础的广度优先和深度优先策略对比两种算法(正向展开参考文献[18]).实验所用的用例集randomtree随机构建了37个树状结构的Petri网, 树中每个节点都是类似图 8(d)的循环模型, 并随机选择叶节点中的标识进行可覆盖性判定.规定算法的最大扩展次数为10 000次, 最大运行时间为35s.实验结果见表 3.

结果表明: 在randomtree上, 基于深度优先策略的反向展开效果最佳, 在全部37组用例上, |E|的规模均最优; 同时, 无论采用深度优先策略还是广度优先策略, 反向展开的效率均优于正向展开.这是因为randomtree具备树状结构.正向展开隐含刻画了系统的完整行为, 涵盖了树结构的每个分支.而反向展开仅刻画与可覆盖性判定相关的系统状态, 只涵盖树的一条分支.

4.2 含启发式策略时反向展开与正向展开的对比

本节将对比启发式反向展开与directed unfolding在Petri网可覆盖性问题上的效率.在实现directed unfolding时, 本文采用了文献[17]中的启发式策略hmax, hsum以及文献[18]中扩展顺序可以与截断事件的偏序分离这一性质; 在实现反向展开时, 本文采用了第2.3节中的启发式策略block, hmax, hsum, 并在实现细节上尽可能保证二者一致.为便于比较, 每组实验仅选择directed unfolding与反向展开中最优的启发式策略进行对比.相关实验如下.

(1) randomtree

第4.1节中仅对比了无启发式策略下正向展开与反向展开的效率, 这里为二者配备启发式技术进行比较.规定算法的最大扩展次数为10 000次, 最大运行时间为35s.实验结果如表 4与图 10(a)所示.

结果表明: 在randomtree上, 基于block+深度优先策略的反向展开效果最佳, 在全部37组用例上, |E|的规模均最优.值得注意的是: 在正向展开, hmax策略相比无启发式策略有明显的效率提升.这在一定程度上说明了, 启发式技术可以弥补算法在性质上的不足.

(2)   threadlock

用例集threadlock按照如下规则模拟了一类线程-锁模型: 假设有x个线程y把锁, x个线程依次申请锁1, 锁2, ..., 锁y, 接着依次释放锁y, 锁y-1, ..., 锁1.目标标识由每个线程的终止库所组成.规定算法的最大扩展次数为10 000次, 最大运行时间为70秒.实验结果如表 5与图 10(b)所示.

结果表明: 基于深度优先策略的正向展开在threadlock上效果最佳, 其|E|的规模在20组用例中有15次最优, 有5次同基于block+深度优先策略的反向展开持平; 且随着用例规模的增大, 正向展开的运行时间明显优于反向展开.然而threadlock中, Petri网的正向分支与反向分支数量相差不大, 理论上正向展开与反向展开的效率也应该相近, 这与实验结果相违背.分析可知: 随着用例规模的增大, RExt中的冗余扩展数量迅速增加, 导致反向展开的运行速度缓慢; 另外, 庞大的扩展集也不利于启发式技术做出正确的选择.可见: 如何有效减少冗余扩展的数量, 是提升反向展开效率的关键因素.

(3)   directed unfolding基准库

directed unfolding使用了dartes, random, airport, openstacks这4个用例集, 本文分别与之进行比较.4个用例集上的最大扩展次数均设为10 000次, 最大运行时间设为35s.

dartes用例集的实验结果如图 10(c)所示.正向展开中, hsum策略效果最好, 总共验证了256/257组用例的可覆盖性.反向展开中, hmax策略效果最好, 总共验证了257/257组用例的可覆盖性.进一步, 反向展开|E|的规模在48组用例上最优, 在2组用例上与正向展开持平.在这个用例集上, 正向展开与反向展开都发挥了各自的优势.

在random用例集上: 正向展开中, hsum策略效果最好, 总共验证了33/45组用例的可覆盖性; 反向展开中, block+hsum策略效果最好, 总共验证了26/45组用例的可覆盖性.进一步, 正向展开|E|的规模在33组用例上最优, 在12组用例上与反向展开持平.在接下来对airport, openstacks的测试中, 正向展开结合hsum策略分别能验证19/26, 30/30组用例的可覆盖性, 而反向展开无法验证任何用例的可覆盖性.在这些用例上的低效甚至失效说明了反向展开并不能适用于所有场景, 这也是其性质决定的.然而, 启发式技术往往能够弥补算法在性质上的不足.因此, 针对反向展开低效或失效的情况, 应设计更有效的启发式技术加以优化.

本节对比了启发式反向展开与directed unfolding在Petri网可覆盖性上的效率.结果表明: 415组测试数据中, 反向展开的规模在85组数据上优于正向展开, 在26组数据上与正向展开持平.实验验证了反向展开在部分用例上的有效性, 在Petri网的正向分支较多时, 反向展开可以从目标标识出发, 仅刻画与可覆盖性判定相关的系统状态, 从而提升目标标识可覆盖性判定的效率.然而, 目前反向展开在多数用例中仍效率低下, 主要原因分为以下两个方面: 一是冗余扩展的数量, 冗余扩展数量过多会导致算法运行缓慢, 且不利于启发式技术做出正确的选择; 二是由算法的特性决定的, 在Petri网的反向分支较多时, 反向展开的效率往往低于正向展开.不过, 启发式技术往往能够弥补算法在性质上的不足.因此, 针对反向展开低效或失效的情况, 应考虑设计更有效的启发式技术加以优化.

5 总结与展望

本文针对安全Petri网的可覆盖性判定问题, 提出了一种目标导向的反向展开算法.反向展开从需要做出可覆盖性判定的目标标识出发, 仅刻画与可覆盖性判定相关的系统状态, 并结合block, hmax, hsum等启发式技术缩减展开的规模, 以此提高目标标识可覆盖判定的效率.进而, 将反向展开算法应用于并发程序的形式化验证, 将并发程序的数据竞争检测问题转换为Petri网特定标识的可覆盖性判定问题.实验对比了启发式反向展开与directed unfolding在Petri网可覆盖性上的效率, 验证了反向展开在Petri网的正向分支较多时可提高可覆盖性判定效率.

然而, 本文尚有很多不足.在算法效率上, 一方面需要进一步减少冗余扩展的数量, 并设计更加高效的启发式技术; 另一方面, 可以尝试将正向展开与反向展开相结合, 综合二者的优势.在数据竞争检测上, 可以考虑使用其他静态检测算法初步确定可能发生数据竞争的语句位置, 在此基础上, 再结合反向展开算法进行验证.此外, 文献[32]中基于展开技术探讨一般化的并发系统的健壮性、兼容性与死锁检测等问题, 后续拟围绕反向展开技术在这些领域的应用展开研究.

附录A

首先给出adequate order的定义.偏序关系是一个adequate order, 如果它满足:

(1)    是良基的;

(2)   是⊂的精炼, Cfg₁⊂Cfg₂意味着Cfg₁Cfg₂;

(3)   若Mark(Cfg₁)≤Mark(Cfg₂), Cfg₁Cfg₂, 则对Cfg₂的任意前缀E₂, 有E₁满足:

Mark(Cfg₁⊕E₁)≤Mark(Cfg₂⊕E₂), 且Cfg₁⊕E₁Cfg₂⊕E₂.

定理1. _r是adequate order.

证明: 易得_r满足adequate order的条件(1)、条件(2).只需证明_r满足条件(3)即可.即证明: 当Mark(Cfg₁)≤ Mark(Cfg₂)∧Cfg_1rCfg₂时, 对Cfg₂的任意前缀E₂, 有E₁满足Mark(Cfg₁⊕E₁)≤Mark(Cfg₂⊕E₂), 且Cfg₁⊕E_1rCfg₂⊕E₂.

定义Ek为配置Cfg的一个大小为k前缀, Cfg^k=Cfg⊕E^k.接下来按|E₂|的大小进行归纳证明.|E₂|=0时, 结论显然成立.|E₂|=k时, 由归纳假设有$Mark(Cfg_1^k) \leqslant Mark(Cfg_2^k)$, 且$Cfg_1^k{ \prec _r}Cfg_2^k$.|E₂|=k+1时, 对任意变迁t.

●  设e₂=(t, C₂), $\mu ({C_2}) \subseteq {t^ \cdot } \wedge {C_2} \subseteq Cut(Cfg_2^k)$, 有$Cfg_2^{k + 1} = Cfg_2^k \cup \{ {e_2}\} $;

●  设e₁=(t, C₁), $\mu ({C_1}) \subseteq {t^ \cdot } \wedge {C_1} \subseteq Cut(Cfg_1^k)$, 有$Cfg_1^{k + 1} = Cfg_1^k \cup \{ {e_1}\} $.要求μ(C₁)≤μ(C₂)且C₁尽可能大(C₁可以为Ø).

接下来只需证明$Mark(Cfg_1^{k + 1}) \leqslant Mark(Cfg_2^{k + 1})$, 且$Cfg_1^{k + 1}{ \prec _r}Cfg_2^{k + 1}$, 有以下两种情况.

(1)   C₁=Ø: $Cfg_1^k = Cfg_1^{k + 1}$.由于要求了C₁尽可能大, 可知: ∀p∈μ(C₂), $p \notin Mark(Cfg_1^k)$, 易得$ Mark(Cfg_1^{k + 1}) = Mark(Cfg_1^k) \leqslant Mark(Cfg_2^k) - \mu ({C_2}) + {}^ \cdot t = Mark(Cfg_2^{k + 1})$.又因为$ |Cfg_2^k| ＜ |Cfg_2^{k + 1}|$, 由_r的定义(1), 有$Cfg_2^k \prec Cfg_2^{k + 1}$, 进而有$ Cfg_1^{k + 1} = Cfg_1^k{ \prec _r}Cfg_2^k{ \prec _r}Cfg_2^{k + 1}$.C₁=Ø时结论成立;

(2)   C₁≠Ø: 由于要求了C₁尽可能大, 且μ(C₁)≤μ(C₂), 可知: ∀p∈μ(C₂), $ p \in \mu ({C_1}) \vee p \notin Mark(Cfg_1^k)$, 易得$ Mark(Cfg_1^{k + 1}) = Mark(Cfg_1^k) - \mu ({C_1}) + {}^ \cdot t \leqslant Mark(Cfg_2^k) - \mu ({C_2}) + {}^ \cdot t = Mark(Cfg_2^{k + 1})$.当$ |Cfg_1^k| ＜ |Cfg_2^k|$时, 有$ |Cfg_1^{k + 1}| = |Cfg_1^k| + 1 ＜ |Cfg_2^k| + 1 = |Cfg_2^{k + 1}|, Cfg_1^{k + 1}{ \prec _r}Cfg_2^{k + 1}$.当$|Cfg_1^k| = |Cfg_2^k|$, 且$ Lex(\mu (Cfg_1^k)) ＜ Lex(\mu (Cfg_2^k))$时, 有$ |Cfg_1^{k + 1}| = |Cfg_1^k| + 1 ＜ |Cfg_2^k| + 1 = |Cfg_2^{k + 1}|$.两个长度相同的有序串添加一个相同元素并重新排序后, 二者间的字典序大小关系不会发生改变, 因此$ Lex(\mu (Cfg_1^{k + 1})){\text{ ＜ }}Lex(\mu (Cfg_2^{k + 1})),Cfg_1^{k + 1}{ \prec _r}Cfg_2^{k + 1}$ .C₁≠Ø时结论成立.

综上, 有Mark(Cfg₁⊕E₁)≤Mark(Cfg₂⊕E₂), 且Cfg₁⊕E_{1 r}Cfg₂⊕E₂.因此, _r是adequate order.

定理2. 反向截断事件不会破坏RUnf的完备性.

证明: 对于满足M↦M_f的任意可达标识M, 应存在配置Cfg满足Mark(Cfg)⊆M.假设Cfg不存在于RUnf中, 则Cfg中一定包含反向截断事件e, 且RUnf中存在事件e', 使得Mark([e'])≤Mark([e])∧[e'][e].

由adequate order的条件(3)可知: 对于Cfg=[e]⊕E, 存在Cfg'=[e']⊕E', 使得Mark(Cfg')≤Mark(Cfg)≤M∧Cfg' Cfg.由于是良基的, 上述过程最终会找到一个存在于RUnf中的极小配置, 这与假设不符.故反向截断事件不会破坏RUnf的完备性.

定理3. RUnf是有限的.

证明: 对于RUnf内的任意事件e, 可以得到一条最长链e₁ < e₂ < … < e, 设其长度为d(e), 有以下3个结论.

(1)   对于任意条件c, ^·c与c^·是有限的; 对于任意事件e, ^·e与e^·是有限的;

(2)    设安全Petri网的可达标识总数为n, 有d(e)≤n+1.长度为n+1的链e₁ < e₂ < … < e_n+1必然存在两个事件e_i, e_j, i < j, 使得Mark([e_i])≤Mark([e_j]).又因为[e_i]⊂[e_j], 由adequate order的条件(2)可知[e_i]p[e_j], e_j为反向截断事件.由此可知, 链中不存在e使得e_j < e, 即链长不可能大于n+1;

(3)   对于任意k(k≥0), RUnf中仅包含有限多的事件e, 使得d(e)≤k.

可以进行归纳证明: k=0时, 结论显然成立.设E_k为d(e)≤k的事件集合, 由归纳假设可知, E_k是有限的.E_k+1为d(e)≤k+1的事件集合.由E_k+1^·⊆^·E_k∪CM_f以及结论(1)可知, E_k+1是有限的.

由结论(2)、结论(3)可知, RUnf包含有限多的事件; 再由结论(1)可知, RUnf包含有限多的条件, 故RUnf是有限的.

附录B

首先回顾一下RExt的两个条件.

(1)   对于RUnf中任意事件e, RExt中不存在反向扩展rext=(t, C), 使得μ(e)=t∧e^·=C;

(2)   对于RExt内任意两不同的反向扩展rext₁=(t₁, C₁), rext₂=(t₂, C₂), 若t₁=t₂∧C₁⊂C₂∧Mark([rext₁])≥ Mark([rext₂]), 则将扩展rext₁从RExt中删除.

Parosh在文献[19]中首次提出了反向展开的思想, 但未在扩展规则中加入Mark([rext₁])≥Mark([rext₂])这个限制, 由此导致其反向展开不满足完备性.这里分析其反例.

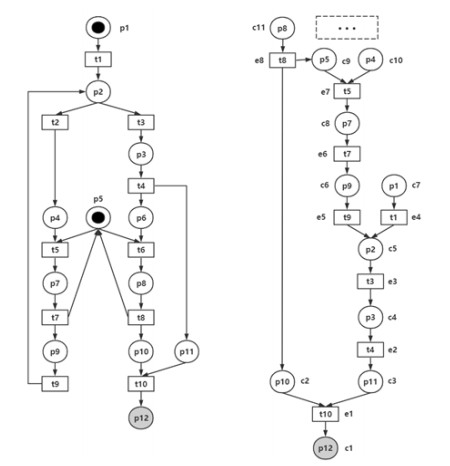
考虑图 11所示的Petri网及其反向展开.左图是原Petri网, 目标标识为{p12}, 不难发现, 目标标识是可覆盖的.右图是未加限制条件Mark([rext₁])≥Mark([rext₂])时的反向展开.反向展开算法在生成事件e8时对应的反向扩展为rext1=(t8, {c2, c9}), 根据Parosh的规则会丢弃rext2=(t8, {c2}).然而, 分析原Petri网会发现: rext1对应的反向标识{p4, p8}是不可覆盖的, 而rext2对应的反向标识{p8, p11}是可覆盖的.进一步, rext2对应的反向标识对判断{p12}的可覆盖性来说是必要的, 此时无论后续如何扩展都无法验证目标标识的可覆盖性, RUnf的完备性已被破坏.