近年来, 以Internet为代表的信息技术的发展, 已使我们处于由无处不在的网络构成的世界中.此外, 网络结构数据分布在各种相关领域数据中, 包括分子结构网络、生物蛋白质交互网络、推荐系统、社交网络、引文网络等等.这些数据结构都可以通过网络来描述实体及实体之间的交互关系, 网络结构数据是我们生产、生活中常见的一种数据形式.其中, 复杂网络是一类具有幂率度分布、强聚类、小世界特性的网络.对复杂网络的分析有利于网络数据结构的潜在信息挖掘, 这将促进一系列应用, 如节点分类、社区发现、链路预测等^[1-6].例如, 可以通过“推特、微博”用户关注所形成的社交网络进行“朋友推荐”, 通过生物蛋白质代谢网络发现潜在的蛋白质功能.

复杂网络的分析具有极强的现实意义, 但直接对大规模、稀疏的邻接矩阵进行分析需要较高的时间复杂度和空间复杂度, 难以进行并行计算^[2].另一方面, 在机器学习浪潮下, 复杂网络学科与机器学习的结合成为当下热点研究问题, 很多机器学习算法试图将网络结构数据引入作为特征输入.该输入数据一般可以被表示为包含特征信息的向量形式, 传统方法使用网络的统计参数、核函数或通过精心设计的特征来描述邻居结构信息, 但这些设计代价昂贵且不能自适应学习过程^[6].

为了解决这些困难和挑战, 大量研究使用表征学习来编码网络结构信息.网络表征学习通过假设网络节点位于低维空间, 在该空间中学习网络节点的低维向量表示, 低维向量将进一步用于处理后续任务.表征学习的目标是通过优化网络节点的向量表示来实现保留网络结构信息的降维表达, 向量空间中节点的位置和节点间距离可以表征网络的高阶拓扑信息.如图 1所示, GCN^[7]是一种用于网络结构数据的神经网络架构, 随机初始化的3层GCN也可以生成网络中节点的邻近特征表征.

大部分的网络表征学习针对的是图数据, 通过图计算形式实现降维表达.而复杂网络的表征学习针对具有幂率度分布、强聚类、小世界特性的网络, 其研究有利于降低网络数据维度, 使网络数据可以与机器学习相结合, 更好地分析网络节点间联系, 为各种后续实际应用提供解决方案.近年来, 在网络表征学习领域涌现出大量的研究成果, 其中一些研究表明, 双曲空间可以很好地描述具有近似树状层次结构的复杂网络.双曲空间具有负常数曲率, 是树状图的连续近似空间, 无限树在双曲空间中也有近乎等距的嵌入^[8].复杂网络的双曲几何模型嵌入理论将复杂网络几何化, 同时又不损失复杂网络中的无标度、小世界等特性, 是一种可以解释复杂网络拓扑特征和生长机制的新型模型.为了更好地分析与应用该类模型, 本文围绕复杂网络的双曲空间表征学习方法展开系统性介绍和总结, 以供后续研究参考.

本文第1节对网络表征学习及其分类进行总结, 将网络表征学习分为矩阵分解、随机游走、深度自编码机和图神经网络的方法.第2节在介绍双曲空间的基础上, 对已有的复杂网络双曲空间生成模型和嵌入方法进行总结.第3节从复杂网络双曲空间表征学习的应用出发, 结合双曲空间特征, 概括了其主要应用场景.第4节给出不同的双曲空间表征学习方法性能评估结果.第5节总结全文, 指出复杂网络的双曲空间表征学习的特征优势, 并对未来研究方向做出展望.

1 网络表征学习 1.1 网络表征学习定义

网络表征学习是一个降维表达的过程, 将高维的网络结构数据转换为低维的节点向量表示, 向量可作为节点特征用于后续网络应用.表 1给出了本文所用符号的含义, 网络表征学习的目标是:对网络G中每个节点v_i, 学习一个实值向量表示$ {{z}_{i}}\in {{\mathbb{R}}^{d}}\left( d\ll \left| V \right| \right) $.部分方法会用到节点属性或连边属性, 如m维节点属性可通过$ X\in {{\mathbb{R}}^{\left| V \right|\times m}} $的实值矩阵来表示.通过网络表征学习形成保留网络结构信息的低维实值向量, 可以用于重构出原网络、有效支撑网络推断和提高后续应用算法执行效率.

1.2 网络表征学习分类及特征

网络表征学习方法众多, 按照不同的分类标准, 可得到不同的结果.本文根据不同方法的技术特点, 把网络表征学习分为基于矩阵分解、随机游走、深度自编码机、图神经网络的方法:矩阵分解的方法将网络信息使用矩阵表示, 然后通过分解该矩阵获取节点向量表示^[9-11]; 随机游走方法将网络信息通过采样一系列随机游走的路径表示, 然后将深度学习方法应用到采样路径中进行图嵌入, 以保持路径所携带的图属性^{[1, 12]}; 深度自编码机将网络信息编码到表征空间, 然后译码重构, 使得重构误差最小化; 图神经网络通过在图上定义近似卷积等操作, 将神经网络应用于图信息处理.表 2对每种方法的特征及适用性进行描述^[13-28].

基于矩阵分解、随机游走、深度自编码机和图神经网络的网络表征学习方法的相关研究层出不穷, 它们一般都是通过某种策略将实体对象嵌入到低维欧氏向量空间中, 该策略的目标是捕获语义信息, 如节点近似度或节点间最短路径等信息.但是, 欧几里德对称模型不能很好地反映复杂的数据模式, 比如分类数据中潜在的层次结构^[29].为了解决这一问题, 非欧几里德流形表示学习成为新的发展趋势.实际上, 许多复杂网络都呈现出幂率度分布和潜在的树状结构, 该结构的存在通常可以追溯到层次结构.为了利用这种结构特性来学习更有效的表示, 许多研究建议不在欧几里德空间中计算嵌入, 而是在双曲空间中计算嵌入^[30-32], 即曲率为负常数的空间.

关于网络表征学习, 已有大量综述文献^{[1-6, 9, 11, 12]}, 但描述的方法大多以网络特征提取和表示为目标, 将网络嵌入到低维欧氏空间中.本文主要聚焦于双曲空间中的复杂网络表征学习, 亦属于网络表征学习中的一类, 但该类方法来源于对复杂网络形成过程和规律的研究, 所表征的节点向量具有独特的物理含义.该类方法认为:双曲空间是复杂网络潜在的几何度量空间, 将双曲空间几何性质与复杂网络的特征相结合, 形成复杂网络的生成模型, 而相应的表征学习则是对原始坐标的逆向推断.下一节将介绍双曲空间基本性质、双曲空间适合表达近似树状结构的复杂网络的原因、从双曲空间到实际网络的生成过程以及从实际网络到双曲空间的嵌入方法.

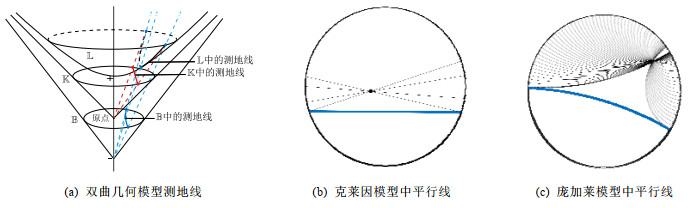
2 复杂网络的双曲空间表征学习 2.1 双曲空间概述

非欧几何的诞生, 源自于对欧几里德第五公设的讨论与研究.双曲几何是非欧几何的一种特例, 在双曲几何中, 前4条公设保留, 第5公设修改为“过已知直线外一点至少可以作两条直线与已知直线平行”.双曲空间由于具有负常数的曲率, 无法等度量地嵌入到欧氏空间中, 难以直观表达.有研究学者为此建立了很多等价模型, 这里我们介绍常用的3种模型:双曲面模型、克莱因模型和庞加莱球模型.图 2(b)和图 2(c)所示为克莱因模型和庞加莱圆盘模型(二维庞加莱球模型)中的过给定点的平行线.

2.1.1 双曲空间表达模型

(1) 双曲面模型

双曲面模型将n维双曲空间视为n+1维闵可夫斯基空间中的伪球面, n+1维闵可夫斯基空间是内积为公式(1)的实值空间:

${\langle \boldsymbol{u}, \boldsymbol{v}\rangle _{n:1}} = \sum\nolimits_{i = 1}^n {{u_i}{v_i}} - {u_{n + 1}}{v_{n + 1}}$

(1)

n维双曲面模型中的点可由n+1维闵可夫斯基空间中的点表示, 如公式(2)所示:

$ {{\mathbb{L}}^{n}}=\left\{ \boldsymbol{u}\in {{\mathbb{R}}^{n:1}}{{\left\langle \boldsymbol{u}, \boldsymbol{u} \right\rangle }_{n:1}}=-1, {{x}_{n+1}}>0 \right\} $

(2)

如图 2(a)所示, 双曲面模型中的每一条测地线都是$ {{\mathbb{L}}^{n}} $和过原点的平面的交线, 两点间的测地距离如公式(3)所示:

${d_{{\mathbb{L}^n}}}(\boldsymbol{u}, \boldsymbol{v}) = \arccos {\rm{h}}( - {\langle {\boldsymbol{u}, \boldsymbol{v}}\rangle _{n:1}}),{\boldsymbol{u}, \boldsymbol{v}} \in {\mathbb{L}^n}$

(3)

(2) 克莱因模型

如图 2(a)所示, 将$ {{\mathbb{L}}^{n}} $中的每个点通过原点发散出的射线映射到x_n+1=1的超平面上, 可得克莱因模型:

$ {{\mathbb{K}}^{n}}=\left\{ \boldsymbol{x}\in {{\mathbb{R}}^{n}}\left| \left\| \boldsymbol{x} \right\|<1 \right. \right\} $

(4)

即:该过原点的平面与$ {{\mathbb{L}}^{n}} $相交形成双曲面模型中的测地线, 与x_n+1=1的超平面相交形成克莱因模型中的测地线.克莱因模型和双曲面模型互为映射:

${\rho _{\mathbb{L} \to \mathbb{K}}}{(\boldsymbol{x})_i} = \frac{{{x_i}}}{{{x_{n + 1}}}}, {\rho _{\mathbb{K} \to \mathbb{L}}}(\boldsymbol{x}) = \frac{1}{{\sqrt {1 - ||\boldsymbol{x}||} }}(\boldsymbol{x}, 1)$

(5)

克莱因模型中的测地线距离为

${d_\mathbb{K}}(\boldsymbol{u}, \boldsymbol{v}) = {d_\mathbb{L}}({\rho _{\mathbb{K} \to \mathbb{L}}}(\boldsymbol{u}), {\rho _{\mathbb{K} \to \mathbb{L}}}(\boldsymbol{v}))$

(6)

(3) 庞加莱球模型

如图 2(a)所示, 将$ {{\mathbb{L}}^{n}} $中的每个点通过(0, 0, …, 0, -1)发散出的射线映射到x_n+1=0的超平面上, 可得到庞加莱球模型:

$ {{\mathbb{B}}^{n}}=\left\{ \boldsymbol{x}\in {{\mathbb{R}}^{n}}\left| \left\| \boldsymbol{x} \right\|<1 \right. \right\} $

(7)

同样, 双曲面模型与庞加莱球模型互为映射:

${\rho _{\mathbb{L} \to \mathbb{B}}}{(\boldsymbol{x})_i} = \frac{{{x_i}}}{{{x_{n + 1}} + 1}}, {\rho _{\mathbb{B} \to \mathbb{L}}}(\boldsymbol{x}) = \frac{2}{{1 - ||\boldsymbol{x}|{|^2}}}\left( {{x_1}, ..., {x_n}, \frac{{1 + ||\boldsymbol{x}|{|^2}}}{2}} \right)$

(8)

庞加莱球模型中的测地线距离为

${d_{{\mathbb{B}^n}}}\left( {\boldsymbol{u}, \boldsymbol{v}} \right) = \arccos \rm{h}\left( {1 + 2\frac{{||\boldsymbol{u} - \boldsymbol{v}|{|^2}}}{{(1 - ||\boldsymbol{u}|{|^2})(1 - ||\boldsymbol{v}|{|^2})}}} \right)$

(9)

庞加莱圆盘模型为庞加莱球模型在二维下的具体体现.庞加莱圆盘模型具有保角性, 即模型中双曲线之间的欧几里德角与其双曲值相等; 庞加莱圆盘模型中的距离与欧氏空间中的不同, 从圆盘中心出发的双曲距离r_h与欧氏距离r_e之间具有如下关系:

${r_e} = \tan \rm{h}\left( {\frac{{{r_h}}}{2}} \right)$

(10)

然而, 在扩展的庞加莱圆盘中, 径坐标r使用双曲距离表示, 即:

$ r\equiv {{r}_{h}}={{r}_{e}} $

(11)

在曲率为$ K=-{{\zeta }^{2}}<0, \zeta >0 $的扩展庞加莱圆盘中, (r_i, θ_i)和(r_j, θ_j)之间的测地线距离d_ij通过双曲余弦定理表示为

$ \cosh \left( \zeta {{d}_{ij}} \right)=\cosh \left( \zeta {{r}_{i}} \right)\cdot \cosh \left( \zeta {{r}_{j}} \right)-\sinh \left( \zeta {{r}_{i}} \right)\cdot \sinh \left( \zeta {{r}_{j}} \right)\cdot \cos \left( \Delta {{\theta }_{ij}} \right) $

(12)

其中, $ \Delta {\theta _{ij}} = {\rm{\pi - }}\left| {{\rm{\pi }} - } \right|\left. {{\theta _i} - {\theta _j}} \right\| $.若ζr_i和ζr_j足够大, 满足$\Delta {\theta _{ij}} > 2\sqrt {{{\rm{e}}^{ - 2\zeta {r_i}}} + {{\rm{e}}^{ - 2\zeta {r_j}}}} , $则测地线距离可通过下式近似计算:

${d_{ij}} = {r_i} + {r_j} + \frac{2}{\zeta }\ln \left[ {\sin \left( {\frac{{\Delta {\theta _{ij}}}}{2}} \right)} \right] \approx {r_i} + {r_j} + \frac{2}{\zeta }\ln \left( {\frac{{\Delta {\theta _{ij}}}}{2}} \right).$

复杂网络的双曲几何模型多采用扩展的庞加莱圆盘模型表征双曲空间, 该模型直观, 可视化效果好, 二维表达下更容易分析几何空间中潜在的物理含义.若非特别说明, 本文所提及的庞加莱圆盘或双曲圆盘均指扩展的庞加莱圆盘模型.

2.1.2 双曲空间基本属性

双曲空间具有负常数的曲率, 其指数扩张速度远大于欧氏空间的多项式扩张.

如表 3所示, 在曲率为K=-ζ² < 0, ζ > 0的庞加莱圆盘中, 圆周长L和面积S均随半径r以e^ζr增长.

除了上述固有属性外, 双曲空间中还有一系列几何定理, 这些属性和定理可供复杂网络的双曲空间模型使用.下面给出几个常见定理.

定理1.   在非欧几何中, 三角形ΔABC的面积S与量π-(∠A+∠B+∠C)成正比:S=M[π-(∠A+∠B+∠C)].特别地, 任意三角形的面积是有界的:S < Mπ.

定理2.   在双曲空间的三角形ΔABC中, a, b, c分别为∠A, ∠B, ∠C所对的边长, 则有:

●  双曲正弦定理:$\frac{{\sinh (a)}}{{\sin (\angle A)}} = \frac{{\sinh (b)}}{{\sin (\angle B)}} = \frac{{\sinh (c)}}{{\sin (\angle C)}}$

●  双曲余弦定理:cosh(c)=cosh(a)·cosh(b)-sinh(a)·sinh(b)·cos(∠C).

定理3.   设a为D_R={z||z| < R}内一点, 分式线性变换$ {{f}_{a, \theta }}(z)={{\text{e}}^{i\theta }}\frac{{{R}^{2}}(z-a)}{{{R}^{2}}-\bar{a}z} $是庞加莱模型的非欧几何中的刚体运动, 其中, θ是任意实数.

定理4.   如图 3所示:设l是一条给定的非欧直线, 记d(z, l)是点z到l的非欧距离, d > 0是任意给定的正数.集合D={z∈U:d(z, l) < d}为关于l的一个超圆域(图中阴影部分), 超圆域的边界是两条欧氏圆弧, 如图中HC所示, 称为超圆周.它们关于给定的非欧直线对称, 并且与该非欧直线在单位圆周上有共同端点.

2.1.3 双曲空间与复杂网络的联系

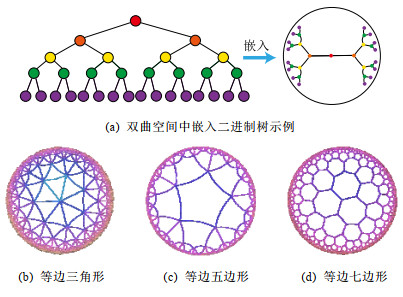
双曲空间适合嵌入具有幂率度分布的复杂网络, 与双曲空间的特性关系密切.幂率度分布的复杂网络具有近似树状的层次结构, 而双曲空间是树网络的连续版本, 对于n进制的树, 圆盘周长和面积可分别类比于距离根节点r跳的节点数(n+1)n^r-1和不超过r跳的所有节点总数[(n+1)n^r-2]/(n-1).如果令圆盘所表示的双曲空间曲率满足$\zeta = \sqrt {|K|} = \ln (n), $则双曲空间圆周和圆面积以e^ζr增长, 与n进制树增长速率n^r保持一致.故树状结构可视为离散的双曲空间.例如, 双曲空间的任何镶嵌细分(如图 4所示)自然定义了由多边形边的某些子集形成的一类树的等距嵌入^[31].已有研究表明:任何有限树都可以通过任意低失真嵌入到有限双曲空间中, 而欧氏空间以多项式速率扩张, 无限维的欧氏空间也无法满足任意低失真嵌入有限树^{[33, 34]}.

由于复杂网络的无标度性质和近似树状结构与双曲空间的负曲率和指数扩张高度贴合, 基于双曲空间生成模型的嵌入方法作为一类基于几何模型的网络表征学习方法诞生.该模型通过将复杂网络嵌入到双曲空间的庞加莱圆盘模型中, 通过圆盘的径向坐标表示节点流行性, 角坐标间距离表示节点间相似性, 将网络的生长解释为流行性和相似性的竞争, 可以很好地解释复杂网络中无标度、小世界、强聚类等拓扑特征^[32].本文首先描述复杂网络双曲空间的生成模型, 然后介绍基于该模型的嵌入方法及无模型的嵌入方法, 最后引入嵌入后的应用、性能对比及研究展望.

2.2 复杂网络双曲空间的生成模型

对复杂网络的拓扑结构和动态演化过程的刻画, 是复杂网络研究领域内的基础性问题之一, 由此引发的复杂网络生成模型的研究具有很长一段历史.起初, 关于复杂网络结构的假设形成规则网络和随机网络两个极端, 较著名的研究是ER随机图模型^[35], 该模型假设网络中每条连边独立且连接概率相同, 可以生成稀疏、存在巨片、平均距离较短的网络, 但该模型无法解释实际网络中出现的聚类特性和度分布非均匀性; 规则的最近邻网络和ER随机图模型都不能解释许多实际网络同时具有的强聚类、小世界特征, WS小世界模型^[36]作为一种完全规则网络向完全随机网络的过渡模型诞生, 该模型通过在规则网络中引入少量随机性产生具有小世界特征的网络, 包括较短的平均距离和高聚类系数; 文献[37]中指出, ER随机图模型和WS小世界模型忽略了实际网络中的增长特性和优先连接特性, 提出了BA无标度网络模型, 该模型生成的网络具有幂率度分布和较短的平均距离, 但无法解释很多现实网络中的强聚类效应.在上述这些网络模型中, 连边关系都是独立的, 而现实网络并非如此.例如社交网络中, 如果两个人具有共同好友, 则他们将比陌生人更容易产生联系.当网络引入几何模型时, 这些拓扑特征就很容易得到解释.最近, 复杂网络的双曲空间生成模型被提了出来, 该模型假设复杂网络处于双曲几何空间中, 节点间连接概率受空间中的距离影响, 几何空间中的三角不等式可以解释现实网络的强聚类效应.通过调整模型参数, 可转化为随机网络、BA网络模型等^{[32, 38]}.本节首先介绍复杂网络几何空间生成模型的基本思想, 然后对复杂网络双曲空间的各类生成模型展开介绍.

2.2.1 复杂网络几何空间的生成模型基本思想

复杂网络几何空间的生成模型一般认为网络存在潜在的几何空间, 网络由节点和连边组成, 在几何空间中布点, 然后根据一定的概率进行连边即可生成不同拓扑结构的网络.不同的生成模型在几何空间的选择、节点间连接概率的设计和网络生成过程这3方面有所不同.一般认为, 连接概率受到几何空间中的距离和节点的内在固有属性两方面的影响, 节点固有属性通过设计节点来隐藏变量表现.根据网络生成过程, 可以将生成模型分为静态模型和动态模型:静态模型中, 节点和连边一次性生成, 不随时间变化; 动态模型中, 网络中的节点会增加或删减, 连边在节点加入或移除时发生变化.

2.2.2 多种双曲空间生成模型

(1) $ {{\mathbb{S}}^{1}} $生成模型

$ {{\mathbb{S}}^{1}} $生成模型是一种简单的复杂网络几何生成模型^[39], 由Krioukov等人在文献[40]中提出.该文认为, 复杂网络存在隐藏的几何度量空间.提出了$ {{\mathbb{S}}^{1}} $生成模型, 通过模型参数控制生成网络的度分布、聚类系数, 并且生成的网络可具有无标度、强聚类、自相似、小世界特性.

$ {{\mathbb{S}}^{1}} $生成模型中, 假设节点均匀分布在半径为|V|/2π的圆环上, 每个节点对(v_i, v_j)之间的连接概率受到几何空间中的距离d_ij和节点拓扑相关固有属性d_c(i, j)的影响, 表现为p(d_ij/d_c(i, j)).令κ为与节点度相关的隐藏变量, 则d_c(i, j)∝κ_iκ_j.该式保证节点平均度$\bar k(\kappa ) = \kappa , $连接概率的具体形式可见后文表 5.为了生成符合幂率度分布的网络, 可令满足概率分布$P(\kappa ) = (\gamma - 1)\kappa _0^{\gamma - 1}{\kappa ^{ - \gamma }}, \kappa > {\kappa _0} \equiv (\gamma - 2)\bar k/(\gamma - 1).$

(2) $ {{\mathbb{H}}^{2}} $生成模型

由于双曲空间是指数扩张的, 空间本身就是一个连续版本的“树”, 这与复杂网络的树状结构高度吻合.Krioukov等人在文献[30]中提出了$ {{\mathbb{H}}^{2}} $生成模型, 该模型是$ {{\mathbb{S}}^{1}} $生成模型的等价模型.该文认为, 无标度复杂网络的节点分布在二维有界的双曲圆盘上.将节点连边表示能量为隐藏双曲距离的非相互作用费米子, 使用费米狄拉克统计解释双曲距离与连接概率的关系, 如公式(13)所示:

$ {p_{ij}} = \frac{1}{{1 + {{\rm{e}}^{\frac{{\beta \zeta }}{2}\left( {{d_{ij}} - {R_{{\mathbb{H}^2}}}} \right)}}}}$

(13)

其中, β=1/T, T为温度系数, 影响生成网络的聚类系数.T→0时, 公式(13)转化为${p_{ij}} = \Theta \left( {{R_{{\mathbb{H}^2}}} - {d_{ij}}} \right), $此时聚类系数最大化; 随着T的增大聚类系数降低, T→1时, 聚类系数趋近于0;T→∞时, 图为经典随机图.该模型生成网络的度分布满足公式(14), 由此可生成具有任意幂率指数度分布、聚类系数的复杂网络:

$P(k)\sim{k^{ - \gamma }}, \gamma = \left\{ {\begin{array}{*{20}{l}} {\frac{{2\alpha }}{\zeta } + 1, \;\;\;{\rm{ if }}\frac{\alpha }{\zeta } \geqslant \frac{1}{2}\;{\rm{ and }}\; T \leqslant 1} \\ {\frac{{2\alpha }}{\zeta }T + 1, \;{\rm{ if }}\frac{\alpha }{\zeta } \geqslant \frac{1}{2}\;{\rm{ and }}\; T > 1} \\ {2, \;\;\;\;\;\;\;\;\;\;\;{\rm{otherwise}}} \end{array}} \right.$

(14)

(3) 双曲空间的随机几何图生成模型

基于$ {{\mathbb{S}}^{1}} $和$ {{\mathbb{H}}^{2}} $生成模型, 文献[31]进一步提出研究复杂网络的几何框架, 该文假设复杂网络是一种嵌入在双曲空间中的随机几何图, 从而非常容易解释网络异质性(无标度分布现象)和高聚集性.

如图 5所示, 与经典的随机几何图类似, 双曲空间中的随机几何图首先需要在半径为R的双曲圆盘上撒N个点, 然后以每个点P为圆心、以r=R为半径作双曲圆, 落在圆内的点均与P点相连接形成网络, 连接概率可表示为公式(15), 通过该模型生成的网络则同时可具备无标度和高聚集性:

$ {{p}_{ij}}=\mathit{\Theta} \left( R-{{d}_{ij}} \right) $

(15)

在该模型中, 只有距离小于R的节点对才产生连接, 距离较远则无连接.Krioukov等人进一步提出软化连接模型, 任意两点的连接概率与$ {{\mathbb{H}}^{2}} $模型相同, 当β趋近于无穷大时, 该模型退化为标准的双曲空间随机几何图模型.一般情形下, 节点间连接概率随着彼此双曲距离的增大而减小, R为阈值; 当双曲距离超过R时, 连接概率减小速率加快.文献[38]对双曲空间的随机几何图模型进行了详细分析, 证明该模型可扩展为6种不同的模型, 见表 4.

(4) PSO动态生长模型

前面提到的模型都是静态模型, 网络中的节点和连接都是一次建立, 不随时间变化的.文献[32]提出了一个在双曲空间下的动态生长模型(popularity-similarity-optimization model, 简称PSO).

如图 6所示, PSO生长模型建立在扩展的庞加莱圆盘上, 生成网络过程如下:(1) t=0时刻, 网络为空; (2) t≥0时刻, 坐标为(r_t, θ_t)的新节点t加入, 其中, r_t=ln(t), θ_t为[0, 2π]的随机值; (3) t≤m时, 新节点t连接到所有已存在的节点; (4) t > m时, 新节点连接到m个双曲距离最近的节点, 可转化为求解m个sΔθ_st最小的节点, 其中, $m = \bar k/2$是控制网络平均节点度的参数, s < t是s时刻生成的节点, Δθ_st是节点s和节点t的角距离.

该模型中, 网络的生长过程表现为流行性和相似性的竞争, 每个节点径坐标为ln(s), s为诞生时间, 代表流行性特征, s越小, 节点诞生越早, 新节点连接它的概率越大; Δθ为相似性特征, Δθ越小, 节点越相似, 连接概率越大.在上述模型中, 流行性与相似性对节点连接具有同样的影响力, 可引入流行性与相似性的权重调节参数λ∈[0, 1], 使得新节点连接时最小化s^λΔθ_st.改进后的模型即为流行性的衰减模型, 在t时刻, 新节点加入时, 对于已存在的节点s < t, 增大它的径坐标至r_s(t)=λr_s+(1-λ)r_t, 其中, λ=1/(λ-1)∈[0, 1], 故λ可控制流行性衰减的速度.另一方面, 该模型新节点每次严格与最近的m个节点相连, 与静态的随机几何图模型一样, 考虑软化连接模型, 新节点t与s以一定概率产生连接:

$ p\left( x \right) = \frac{1}{{1 + {{\rm{e}}^{\left( {{d_{ij}} - {R_t}} \right)/T}}}} $

(16)

其中, R_t是t时刻双曲圆盘半径.

相比于静态的双曲空间随机几何图模型, 该动态模型具有一些优点.

(a)   动态模型中节点根据时间逐个加入网络, 可以模拟实际网络动态生长情况;

(b)   动态模型将双曲坐标赋予了实际含义, 径坐标表示的是节点的流行性, 角坐标相对差值表示节点间的相似性, 节点间的连接产生则表现为实际网络中流行性与相似性的竞争;

(c)   该模型可以扩展为偏好依附网络模型、适应度网络模型等.

PSO模型存在进一步变体GPA(geometric preferential attachment)模型和nPSO(nonuniform PSO)模型, 以便产生具有软社区^[41]或所需社区结构^[42]的双曲合成网络.

(5) GPA模型

由于PSO模型及前述双曲空间中的静态模型均假设节点角坐标均匀分布在0~2π范围内, 节点间连接概率随双曲距离的增大而减小, 故没有角区域包含空间上紧密相连的节点集群以形成明确的社区结构.文献[41]提出了GPA生成模型, 通过使双曲圆盘中不同角域具有不同的吸引力来形成社区.该模型仅修改了PSO模型中的角坐标生成机制, 在每个节点加入网络中时, 先根据均匀分布选取角坐标的候选位置φ₁, φ₂, …, φ_i, 对每个候选点计算其引力大小, 然后根据公式(17)的概率选取角坐标:

${p_i}({\varphi _j}) = \frac{{{A_i}({\varphi _j}) + \mathit{\Lambda} }}{{\sum\nolimits_{k = 1}^i {{A_i}({\varphi _k})} + \mathit{\Lambda} }}$

(17)

其中, 引力A_i(φ_j)为离候选点(r_i, φ_j)距离小于r_i的已存在节点个数; Λ≥0为模型参数, 代表初始引力, 节点角度分布的异质性是其减函数.

(6) nPSO模型

GPA模型通过调整PSO模型中角坐标的分布来形成社区结构, 但该模型不能明确控制社区的个数和规模.文献[42]提出了nPSO模型, 通过高斯混合分布生成角坐标, 可调整社区数量和规模, 高效地生成高聚类网络.

表 5总结了上述几种几何生成模型的设计特点.

2.3 复杂网络双曲空间的嵌入方法 2.3.1 基于生成模型的嵌入方法

复杂网络的双曲空间生成模型能够构建跨越多种拓扑结构和动态特性的类似于真实网络的合成网络, 我们是否可以逆转这种合成, 并给定一个真实网络, 将网络映射(嵌入)到双曲空间中, 在某种程度上与生成模型保持一致?这种嵌入是否存在高效的后续应用?这些问题成为当下的研究热点, 引出了大量研究成果.其中, 基于生成模型的嵌入方法假设网络由给定的生成模型产生, 逆向推断最可能生成该网络的生成模型参数, 主要可分为基于最大似然估计的嵌入方法、基于流形学习的嵌入方法和两者结合的嵌入方法.

一般来说, 复杂网络双曲空间的嵌入方法要求输入为连通图G=(V, E), 因为与网络中巨片不连通的部分没有相应的邻接信息, 可以被嵌入到双曲空间中的任意位置.由于生成模型中径坐标与节点度高度相关, 不同的嵌入方法对于径坐标一般均根据模型采用直接推断方法来估计.

对于静态随机几何图模型, 一般采用公式(18)来估计双曲圆盘最大半径, 用公式(19)来估计每个节点的径坐标:

$R = 2\ln \left[ {\frac{{|V{|^2}{{(\gamma - 1)}^2}T}}{{|E|\sin (\pi T){{(\gamma - 2)}^2}}}} \right]$

(18)

${r_i} = \min \left\{ {R, 2\ln \left( {\frac{{2|V|(\gamma - 1)T}}{{{k_i}\sin (\pi T)(\gamma - 2)}}} \right)} \right\}$

(19)

对于动态PSO模型, 一般重现其生长过程, 根据r_i=2λln(i)+2(1-λ)ln(N)指定径坐标, 其中, i={1, 2, …, N}为按节点度降序排列的节点编号, λ=1/(γ-1), γ为度分布幂指数.

上述基于生成模型的嵌入方法由此转变为一个角坐标参数估计问题.基于最大似然估计的嵌入方法根据似然函数推断每个节点在隐藏的几何空间中的坐标, 该问题为NP-Hard问题^[39], 只能通过启发式方法获取可能的近似解, 该类方法的计算复杂度和嵌入精确度依赖于选择的启发式方法和生成模型.基于流形学习的嵌入方法具有一些快速算法, 但其中使用矩阵分解的一类方法在应用于大规模网络嵌入时仍然具有$ \mathcal{O}\left( {{N}^{2}} \right) $)的复杂度.另外, 基于流行学习的嵌入方法一般在欧氏空间中计算, 只能通过庞加莱圆盘的保角性完成角坐标的近似推断, 径坐标推断则需要使用上述方法来计算得出.将流行学习与最大似然估计结合所形成的嵌入方法一般先通过流行学习方法近似估计嵌入坐标初值, 然后通过最大似然估计法提高嵌入精度.本节将对不同的嵌入方法展开介绍.

(1) 基于最大似然估计的嵌入方法

最大似然估计的目标是找到生成模型与观测网络的最佳匹配, 实际是在根据观测网络解析参数估计问题.在贝叶斯准则下, 该估计问题的后验概率为

$Prob(\{ {r_i}, {\theta _i}\} |A;Model) = \frac{{Prob(A, \{ {r_i}, {\theta _i}\} ;Model)}}{{Prob(A;Model)}} = \frac{{Prob(\{ {r_i}, {\theta _i}\} ;Model) \times Prob(A|\{ {r_i}, {\theta _i}\} ;Model)}}{{Prob(A;Model)}}$

(20)

其中, Prob(A, {r_i, θ_i}; Model)表示Model生成坐标{r_i, θ_i}和观测网络邻接矩阵A的联合概率, Prob(A; Model)表示Model生成观测网络邻接矩阵A的先验概率.公式(21)表示Model生成坐标{r_i, θ_i}的先验概率, 公式(22)表示Model在坐标{r_i, θ_i}下生成邻接矩阵A的条件概率:

$Prob(\{ {r_i}, {\theta _i}\} ;Model) = \prod\nolimits_{i = 1}^N {p({r_i}, {\theta _i})} $

(21)

$Prob(A|\{ {r_i}, {\theta _i}\} ;Model) = \prod\nolimits_{i < j} {p_{ij}^{{a_{ij}}}{{(1 - {p_{ij}})}^{1 - {a_{ij}}}}} $

(22)

如果公式(21)的先验概率已知, 则可使用贝叶斯估计最大化公式(20)来获得最佳估计.然而, 在大部分情况下先验信息未知, 一般通过最大化似然函数公式(22), 或其对数形式公式(23)来推断嵌入坐标:

$\ln [Prob(A|\{ {r_i}, {\theta _i}\} ;Model)] = \sum\nolimits_{i < j} {[{a_{ij}}\ln ({p_{ij}}) + (1 - {a_{ij}})\ln (1 - {p_{ij}})]} $

(23)

基于最大似然估计的嵌入方法通过不同的策略最大化该似然函数来推断角坐标.

●  HyperMap

HyperMap^[43]是一种基于最大似然估计的双曲空间无权网络嵌入方法, 通过重现PSO模型生长过程完成角坐标的推断.具体过程如下.

1)   节点按照度从大到小重整为i=1, 2, …, N;

2)   节点i=1诞生, 随机角坐标θ₁∈[0, 2π];

3)   节点i=2, 3, …, N的角坐标通过最大化${\mathcal{L}_i} = \prod\nolimits_{1 \leqslant j < i} {p_{ij}^{{a_{ij}}}{{(1 - {p_{ij}})}^{1 - {a_{ij}}}}} $来获取.

●  HyperMap-CN

在HyperMap中, 度大的节点先生成, 且在生成时仅考虑与度更大的节点是否存在连接对其在双曲空间中坐标的影响, 导致度大的节点嵌入的角坐标并不精确.HyperMap-CN^[44]通过修改HyperMap中的似然函数, 引入共同邻居信息来推断节点嵌入坐标.经过调整后, 节点坐标推断更加精确, 但计算复杂度由HyperMap的(N³)增大到(N⁴).为了减小计算量, Papadopoulos等人进一步提出混合模型, 仅对度大的节点i(k_i≤k_speedup)使用修改后的似然优化, 并且可采用加速的启发式方法估计角坐标.对于度大的节点i, 先仅考虑i的邻居节点j(j < i)来估计角坐标初值$\theta _i^{init}, $然后对$\theta _i^{init}$使用局部搜索确定最终角坐标.通过该方法, 在降低计算复杂度至$ \mathcal{O}\left( {{N}^{2}} \right) $的同时保持了嵌入精确度.

●  EE

在HyperMap和HyperMap-CN的基础上, 文献[45]提出一种可应用于大规模网络的双曲空间静态随机几何图模型高效嵌入方法, 该方法具有拟线性的时间复杂度.与HyperMap相似, 该方法采用贪婪策略完成嵌入.与对网络全局的嵌入结果同时优化相比, 采用贪婪策略, 每次最优化一个节点的嵌入坐标相对容易.在得到模型的全局参数估计后, 该方法先嵌入网络的核心部分, 即度较大的节点.通过引入共同邻居信息, 优化随机几何图阶跃模型的似然来获取节点对的角度差, 然后借助弹性嵌入方法完成网络核心部分嵌入.对于其他度较小的节点, 先根据已嵌入的邻居节点估计角坐标初值, 然后在初值附近随机采样多个坐标点, 选取似然最优值作为最终结果.

(2) 基于流行学习的嵌入方法

基于流行学习的嵌入方法以Laplace特征映射为代表, 原始用于高维数据的降维.该类方法一般针对高维情形下的数据稀疏、难以计算等“维数灾难”问题, 通过某种策略将原始高维空间转换为低维子空间, 在子空间中, 数据密度提高, 结构简化, 便于后续应用计算.但这类方法降维的子空间一般为欧氏空间, 双曲嵌入只能通过该相似子空间推断角坐标, 而径坐标及其他参数的推断则根据具体模型计算得出.

●  LaBNE

基于网络中互相连接的节点在双曲空间中彼此靠近的基本思想, 针对无向、无权、单一组成成分的网络, Alanis-Lobato等人提出了基于Laplace谱分解的庞加莱圆盘嵌入方法LaBNE(Laplacian-based network embedding)^[46].定义由节点度组成的对角阵D, 网络的邻接矩阵A, 则网络的Laplace矩阵为L=D-A; Y=[y₁, y₂]为N×2矩阵, 该矩阵的第i行为节点嵌入欧氏圆盘坐标.最小化$\frac{1}{2}\sum\nolimits_{i, j} {{a_{ij}}||{Y_i} - {Y_j}|{|^2}} = tr({Y^T}LY), $使彼此连接的节点坐标靠近, 同时加入约束条件Y^TDY=I来避免节点聚集(I为单位阵).最终, Y的求解可以转换为求解广义特征值问题.基于庞加莱圆盘模型的保角性, 角坐标可以通过θ=arctan(y₂/y₁)计算得到.

●  Coalescent embedding

基于LaBNE, 文献[47]衍生出一类基于流行学习的双曲空间嵌入方法.该类方法通过节点度、共同邻居和节点间最短路径等局部拓扑信息定义了RA(repulsion-attraction)规则和EBC(edge betweenness centrality)规则.首先, 基于该规则对无权网络加权; 然后, 使用流行学习方法, 如Isomap、拉普拉斯特征映射获取近似角坐标; 最后, 引入角度均匀化调整, 使角坐标满足生成模型关于节点分布的基本假设.通过此流程, 提高了LaBNE嵌入的精确性, 并提供了一系列嵌入方法.

(3) 流行学习与最大似然估计结合的嵌入方法

●  LaBNE+HM

HyperMap方法基于搜索求解最大似然估计来完成双曲空间嵌入, 该方法嵌入精度高, 但是计算量大, 对于大规模的网络则只能通过启发式方法求解; LaBNE方法基于Laplace谱分解, 计算速度相对较快, 但却高度依赖于拓扑信息, 仅考虑使有连接的节点彼此靠近, 无法保证无连接的节点彼此远离, 在网络平均度高、聚类系数高时才能获得较为精确的嵌入结果.LaBNE+HM^[48]将两者的优势相结合, 先使用LaBNE近似估计嵌入初值, 再根据网络特征调整搜索范围, 采用HyperMap精确求解, 在保证嵌入精度的前提下, 缩短了HyperMap求解时间.

●  Mercator

Mercator^[39]将流行学习与最大似然相结合, 在观测网络和$ {{\mathbb{S}}^{1}} $模型间求解最佳匹配.该方法不仅推断节点角坐标次序及具体值, 还推断节点隐藏期望度和模型全局参数, 并且可以将任意度分布网络嵌入到$ {{\mathbb{S}}^{1}} $模型中. Mercator提供两种模式:在快速模式下, 首先根据$ {{\mathbb{S}}^{1}} $模型统计分析推断得到全局参数β、μ和每个节点i的隐藏期望度变量κ_i, 然后使用拉普拉斯特征映射估计角坐标θ_i, 基于推断的β、μ、κ_i以及节点间有无连边进一步调整角坐标; 精确模式将快速模式嵌入结果作为初值, 基于最大似然估计理论, 使用洋葱分解^[49]从中心节点开始, 在节点邻居角坐标均值处局部搜索优化角坐标, 最后根据优化后的角坐标更新隐藏期望度.

(4) 其他嵌入方法

●  LPCS

与前述流行学习或最大似然估计的嵌入方法有所不同, LPCS^[50]是一种基于社区结构的双曲空间嵌入方法, 通过将社区结构信息引入, 使不同社区的节点具有一定的相对角度, 相同社区的节点彼此靠近以完成嵌入.该方法基于EPSO^[43]生成模型, 具有线性时间复杂度, 适用于具有一定社区结构的幂率度分布网络, 具体按照如下步骤完成嵌入.

1)   检测层次性社区;

2)   从节点数量最多的社区开始, 利用社区亲密度指数对顶层社区进行排序, 该指数考虑了社区内部和社区之间的连边比例;

3)   根据高层社区的顺序, 递归地对低层社区进行排序, 直至到达层次结构的底层;

4)   为每一个底层社区分配一个与社区节点大小成比例的角度范围, 以不重叠的角度范围覆盖整个社区.在相关底层社区的角度范围内, 随机均匀采样节点的角坐标.

CHM^[51]采用与LPCS类似的方法得到双曲空间嵌入初值, 然后使用最大似然估计优化初值, 提高精确度.

●  MCA

具有稀疏、强聚类、小世界、异质性的复杂网络通常可以通过最小生成树实现高效导航.MCA^[52]方法定义相似性依附机制, 通过不断生长的最小生成树满足最低弯曲度策略, 有效地近似双曲圆盘中节点角坐标, 完成双曲空间嵌入.该方法具有近似线性复杂度, 同时, 嵌入精度超过HyperMap-CN, 低于Coalescent Embedding.具体过程如下.

1)   定义RA规则$x_{ij}^{RA1} = \frac{{1 + {e_i} + {e_j}}}{{1 + C{N_{ij}}}}$和$x_{ij}^{RA2} = \frac{{1 + {e_i} + {e_j} + {e_i}{e_j}}}{{1 + C{N_{ij}}}}$, 其中, CN_ij表示i和j的共同邻居, e_i表示i的外部邻居节点数目(不与CN_ij相连也不与v_j相连);

2)   通过$x_{ij}^{RA1}$或$x_{ij}^{RA2}$规则将无权网络赋予权值;

3)   基于Prim最小生成树构造方法依次排列最低排斥度节点, 将节点序列通过角度等距调整或斥力-引力等距调整使角坐标分布在[0, 2π].

表 6对上述几种复杂网络双曲空间嵌入方法的时间复杂度进行了简单总结.

2.3.2 无生成模型的嵌入方法

由于表达信息的能力是学习和泛化的先决条件, 因此提高嵌入方法的表示能力非常重要, 这样它就可以用于各种实际数据的复杂模式之中.尽管欧氏空间嵌入取得了成功, 但最近的研究结果表明, 来自多个领域(如生物学、网络科学、计算机图形学或计算机视觉)的许多类型的复杂数据(例如图数据)都显示出高度非欧几里德潜在结构^[53].在这种情况下, 欧几里德空间没有提供最强大或最有意义的几何表示.为了更好地学习数据的层次结构和复杂模式, 近期涌现了许多无生成模型的双曲空间嵌入方法^{[8, 29, 34, 54-59]}.这些方法一般通过双曲距离刻画数据间相似度来将其嵌入到双曲空间中, 利用双曲空间对数据的表达能力, 在贪婪路由、层级表示学习、知识问答、链路预测、最短路径长度预测、机器翻译等应用上取得性能上的提升.

3 复杂网络双曲空间模型的应用

通过将复杂网络嵌入到双曲空间中, 高维稀疏的网络结构信息转化为低维稠密的实值向量, 具有一般嵌入方法降低计算复杂度的特点.另外, 每个节点被表示为潜在几何空间中确定位置的坐标, 几何空间中的距离度量决定节点间存在连接的可能性, 因此可将几何工具和方法论应用到网络研究中, 以有效解释现实网络中的物理现象.例如, 几何空间中的三角不等式给出了现实网络中聚类效应的合理解释^[60].

由于复杂网络双曲空间模型的物理含义和低维向量表示便于进行高效计算, 基于该模型的嵌入将有益于很多图分析的应用.本节将围绕基于复杂网络双曲空间模型嵌入后的各类应用展开介绍.

3.1 基于双曲径坐标的层次结构发现

近年来, 因双曲空间嵌入对潜在层次结构的有效捕获, 将数据嵌入双曲空间表示受到越来越多的关注^{[8, 34, 56-58]}.这种层次结构捕获的能力可能与双曲空间的关键特性密切相关, 即:空间容量随径向呈指数增长, 而在非欧氏空间中呈缓慢的多项式增长.树状结构数据几何形状的增长方式与双曲空间保持一致, 因此可以通过双曲空间精确捕捉树状的层次结构.如图 7所示:文献[56, 57]将WordNet等网络嵌入到低维双曲空间中, 学习其层次结构, 与高维欧氏空间相比具有更优的重构误差和链路预测能力; 文献[58]将问答系统嵌入到双曲空间中, 发现其潜在的层次结构, 对问答系统进行快速而高效的排序检索; 文献[61]将单词和句子嵌入到双曲空间中, 保留了单词的共现频率信息和句子短语选区信息.

3.2 基于双曲角坐标划分的社区发现

在复杂网络的庞加莱圆盘嵌入结果中, 双曲距离较近的节点存在较大的连接概率.双曲空间随圆盘半径呈指数增长, 位于庞加莱圆盘中心附近的节点有大量的连接, 而外围的节点只靠近角坐标相近的节点.文献[62-64]研究表明:真实网络在庞加莱圆盘中嵌入的节点角坐标不是均匀分布的; 相反, 它们以一种异构的方式分布, 节点在某些角坐标附近的集群化揭示了节点之间存在大量连接的区域, 该区域组成一个社区^{[32, 41, 42, 65-68]}.另外, 文献[69]的研究也说明, 具有强模块化的网络嵌入到双曲圆盘中表现出同一社区内节点角度的高度一致性.基于这种思想, 根据双曲模型嵌入结果的聚类^[70]或角坐标划分^[64]可以设计快速而高效的社区发现算法, 如图 8所示, 相同颜色的节点组成一个社区.基于复杂网络双曲圆盘嵌入的社区划分操作简单、高效, 划分结果直观、明确.

3.3 基于双曲距离度量的路径搜索

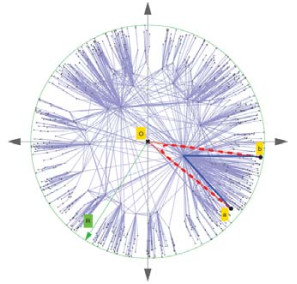
从脑神经网络到社交网络、互联网和交通网络, 信息或能量的传递是许多复杂系统的关键功能.已有研究结果表明:即使不具备系统的全局知识, 网络中的节点仍能执行有效的信息路由.双曲嵌入为网络中每个节点提供了几何空间坐标, 故可以借助坐标进行高效的贪婪路由.在信息转发时, 不需要提前计算路由, 每个节点只需知道目的节点坐标和邻居节点坐标, 通过计算双曲距离, 每次选取最接近目的节点的邻居节点作为下一跳转发节点, 该应用说明, 双曲模型具有可导航性^{[54, 62, 71, 72]}.如图 9所示:由于双曲空间庞加莱圆盘模型中的测地线(红色虚线)为弧形, 故贪婪路由的中继转发节点更偏向于靠近圆盘中心的枢纽节点(蓝色实线为转发路径).大规模图中, 计算最短路径较为困难^[73], 贪婪路由仅需要嵌入后的少量局部信息计算双曲距离, 就可以获取接近最短的转发路径, 是一种高效的路由方法.

由于复杂网络具有路径多样性, 结合双曲嵌入, 大量不相交路径分布于双曲空间通过源目的节点的测地线附近^[62], 类似于贪婪路由的单路径搜索亦可扩展到多路径搜索.

3.4 基于双曲距离度量的关键节点发现

复杂网络的异构性导致每个节点的结构和功能有所不同, 精确估计网络中的关键节点在网络优化、药物研发、舆情控制等方面具有广泛的应用前景.网络的介数中心性这一经典的关键节点排序指标需要计算所有节点对的最短路径, 在无权网络中, 用布兰德斯的算法计算介数中心性具有$ \mathcal{O}\left( \left| V \right|\left| E \right| \right) $的时间复杂度.而在双曲空间中, 通过贪婪路由近似最短路径, 只需要计算所有节点对的双曲距离即可估算出介数中心性, 具有$ \mathcal{O}\left( {{\left| V \right|}^{2}} \right) $的时间复杂度^[73].类似的研究工作包括文献[74]提出的双曲空间中快速计算接近度中心性方法和文献[75]提出的双曲流量负载中心性(hyperbolic traffic load centrality)方法.

3.5 基于双曲距离度量的链路预测

链路预测是指通过已知的各种信息, 预测给定网络中尚不存在连边的两个节点之间产生连接的可能性.链路预测模型可以帮助我们理解网络结构, 并且具有很多实际的应用价值, 比如指导蛋白质交互实验、建立推荐系统等^[50].很多链路预测方法基于节点相似性, 其基本假设是:相似性越大的节点之间, 存在链接的可能性越大.复杂网络的双曲空间模型中明确定义了与双曲距离密切相关的连接概率, 仅仅只需要根据嵌入坐标计算节点对的双曲距离, 就可以进行链路预测.该思想操作简单, 并且可以获得高精度预测结果, 在部分网络上性能甚至优于Common-neighbors(CN)和Katz index(Katz)等经典链路预测方法^{[32, 43, 44, 50, 67, 76]}.

3.6 基于双曲坐标的网络演化分析

本文所述研究大多都是静态网络的双曲空间嵌入, 但是现实网络一般都具有复杂的动态演变过程, 比如社交网络中不断有新用户加入和用户交友行为产生.随着网络的演化, 网络的表征也需要随之更新.已有的双曲空间中网络演化的分析方法将动态网络视为由多个静态网络快照组成, 分时段对静态快照嵌入双曲空间来研究网络演化规律^[64].但这类方法将静态网络嵌入算法直接应用到动态演化网络上会遇到一系列问题, 比如:由于缺乏增量嵌入方法, 即使网络变化很小也必须重新嵌入; 由于一些随机噪声的存在, 不同时段的嵌入结果可能不够稳定、前后差异较大等.因此, 双曲空间中的网络演化分析仍然是未来研究的重要课题之一.

3.7 基于双曲坐标的多层网络关联性及鲁棒性分析

关系的多重性是现实网络的共同特征, 比如社交网络中, 人与人之间的关系多种多样.现实的多层网络往往不是单层网络的随机组合, 分析不同网络层次之间的关联性, 对于理解现实网络具有重大意义.通过将每一层网络嵌入到双曲空间中, 节点层与层之间的坐标会表现出显著的相关性, 这些相关性揭示了多层网络隐藏的几何关联, 可以应用于层间链路预测、贪婪路由、社区发现^[67].另外, 在相互作用的多层网络中, 部分节点的失效会导致与之依赖的节点失效, 从而产生级联失效现象, 这种级联失效往往会导致整个相互依赖系统的崩溃.在网络科学研究中, 渗流理论是研究复杂网络鲁棒性与网络团簇演变的一个重要手段.已有研究结果表明:当层间角坐标的相关性较高时, 渗流变换平滑, 网络鲁棒性较强; 当相关性较低时, 渗流变换易发生突变, 网络鲁棒性较弱^{[69, 77]}.多层网络的双曲空间嵌入, 可以对层间关联性及鲁棒性进行分析, 有助于设计网络保护策略和更健壮、更可控的相互依赖系统.

3.8 基于双曲坐标的复杂网络几何重整化

许多复杂的网络, 如Internet、社交和生物网络, 往往具有节点的异构度分布.这些分布可以用幂律衰减来描述:它们在度变量重新标度的情况下保持不变.这表明可能存在对网络结构的某种变换, 使其统计特性保持不变^[78].重整化变换按照一定的规则将网络中的数个节点合并为超级节点, 抓取网络中的部分属性.通过重整化变换, 可将复杂结构简单化, 便于分析网络结构特征.例如, 该变换揭示了某些网络具有自相似嵌套的层次结构^[79].已有研究结果表明:通过对复杂网络双曲空间嵌入的结果进行重整化, 使相同径坐标下角坐标彼此靠近的节点合并, 可实现网络规模缩小和多尺度贪婪路由^[80].

3.9 基于双曲空间表达模型的可视化

图的二维可视化问题研究遍布网络科学、数据挖掘、生物科学等各个领域.复杂网络双曲空间的表征学习为可视化提供了极大的便利, 将每个节点通过二维实值向量表示, 研究者们可以很容易地获得高维数据的可视化表达.并且, 利用复杂网络双曲空间模型的物理含义, 该可视化表达对社区发现、层次结构提取、流行性相似性分析以及其他潜在网络结构发现都具有重大意义.

3.10 双曲空间结合机器学习

基于双曲空间对树状结构数据的精确表示和高效捕获层次结构的能力, 双曲空间的嵌入已经应用到各类领域中, 包括自然语言处理^{[34, 56, 61]}和网络科学^{[43, 44, 46]}等.相比于高维的欧氏空间, 这些方法仅只需要低维的双曲空间, 便能够在各自的后续任务中取得更佳性能^{[81, 82]}.例如, 文献[81]将支持向量机(support vector machine, 简称SVM)与双曲空间相结合, 提出了双曲支持向量机, 通过双曲面模型进行超平面划分, 在合成网络与现实网络的节点多分类任务上取得性能上的提升.文献[29, 59, 82]将双曲空间与神经网络相结合, 分别引入双曲神经网络、双曲注意力网络、双曲图卷积网络, 在机器翻译、图分析、可视化问答等任务上取得性能上的提升.

4 复杂网络双曲空间表征学习方法的性能评估

本文介绍了多种复杂网络双曲空间的表征学习方法, 不同方法在坐标推断精确度、后续任务性能以及算法执行时间上存在一定的差异.通过将各种方法应用于合成网络和真实网络, 来给出其性能对比结果.其中, 合成网络通过PSO模型生成, 节点数均为1 000, 幂律度分布幂指数γ=2.5, 平均度$\bar k = 4, 8, 12$, 温度系数T=0.1, 0.3, 0.5, 0.7, 0.9, 每组参数合成5个网络.图 10给出了实验结果, a、b、c组分别对应平均度为4、8、12的合成网络.C-score衡量角坐标正确排序的节点对比例; HD-correlation为所有节点对真实和推断的双曲距离之间的皮尔逊相关系数; GR-score衡量嵌入后贪婪路由的性能, 当GR-score为1时, 所有节点对贪婪路由均可成功且为最短路径; Time为嵌入算法执行时间.各指标的详细定义参见文献[47].

除了合成网络, 本文还将不同的表征学习方法应用于真实网络, 表 7给出了不同真实网络数据的相关特征和来源, 所有的真实网络均经过去除自环、重边、取最大连通片的处理过程.

由于真实网络数据无法获知双曲空间原始坐标, 只能根据推断坐标分析其性能差异, 故无法计算C-score和HD-correlation指标, 这里使用连接概率和对数似然替代分析.图 11给出了真实网络双曲嵌入的性能对比结果.

5 结论及展望

本文介绍了现有的复杂网络的双曲几何模型、嵌入方法以及应用任务.相对于其他网络模型, 双曲几何模型具有以下优势:(1)双曲空间的指数扩张使得空间容量大、易于表达树状层次结构数据; (2)双曲几何模型能够近似网络的树状分支, 产生具有幂率度分布和自相似性的网络; (3)双曲几何空间中的三角不等式说明与某节点A相连的两个节点B和C之间容易产生连接, 可以解释现实网络中出现的强聚类效应; (4)复杂网络的双曲空间模型将网络映射到双曲几何空间中, 通过双曲距离编码节点间连接概率, 使得模型参数可以反映节点的流行性和相似性; (5)复杂网络的双曲空间嵌入是一个网络降维过程, 便于后续应用的高效计算, 其嵌入坐标可以作为机器学习算法输入; (6)该模型提供了一种新的强有力的网络可视化方法, 社区结构可以通过角区域集聚性来加以表征.

相对于欧氏空间的多项式扩张, 指数扩张的双曲空间具有更大的容量, 更适合表达树状结构、层次结构的数据.通过将数据嵌入到双曲空间, 可以近似捕获其潜在的层次结构.径坐标与节点度高度相关, 可用于发现度相关结构、网络自相似结构、快速比较和分析节点流行性、快速层级划分等任务; 角坐标间距离与节点相似性相关, 可用于快速社区划分、相似节点融合、多层网络关联性及鲁棒性分析、链路预测等任务.双曲几何模型在具有较强可解释性的同时, 还能通过几何工具和方法研究数据结构.其强大的层次结构表达能力使得双曲几何的嵌入不仅能够应用于传统的复杂网络图分析任务, 还为表征学习及其后续应用开辟了新的方向.如图 12(a)所示:可以将双曲空间嵌入应用于监督学习, 对象可以是具有层次结构的文本符号数据或图像数据, 研究其分类、层次表达等相关问题; 类似地, 对于无监督学习, 可以构建相似矩阵完成双曲嵌入, 如图 12(b)所示.

虽然复杂网络的双曲几何模型已经取得了丰富的研究成果, 但是仍在以下几个方面面临着巨大挑战.

(1)   动态变化网络的生成.现实生活中, 大量网络的结构具有动态性, 现有的双曲几何模型主要是静态的, 虽然PSO模型能够刻画一类网络的动态生成过程, 但仍存在许多现实网络无法通过PSO模型动态重现.因此, 如何在双曲几何模型的框架下模拟现实网络的动态变化过程, 是亟待解决的问题;

(2)   多层次、多关系网络的生成.在已有的研究中, 复杂网络的双曲几何模型成功地描述了从生物系统到信息系统和社会系统等各种复杂系统的形成过程, 然而目前的研究对象大多是单一层次的网络, 仅有少数多层网络双曲空间的生成模型^[67], 许多现实网络具有多层次、多关系的网络结构.这些网络的不同层之间一般不是随机连接的, 如何挖掘层间关联关系, 形成多层次、多关系网络的双曲几何模型, 是复杂网络双曲空间表征学习面临的重要挑战;

(3)   高维双曲空间的嵌入.目前, 基于生成模型的双曲空间嵌入方法大多将复杂网络嵌入到二维的双曲空间中, 现实数据中, 实体之间的关系往往更加复杂, 难以在二维双曲空间中精确表示.提升双曲空间的嵌入维度, 可以增强模型的表达能力和适应性, 高维双曲空间嵌入方法的研究, 是未来的一个重要方向;

(4)   更大规模、更高速率的嵌入方法.已有的双曲空间嵌入方法仅仅能够应用于小规模网络, 而实际场景中的网络动辄上亿节点, 因此, 克服大规模网络嵌入面临的存储、计算复杂度等困难, 推广双曲空间嵌入方法到大规模网络中, 将开辟更加广泛的应用领域;

(5)   与神经网络、机器学习相结合, 将适合使用双曲空间表示的数据、距离, 转移到双曲空间中.双曲空间相较于欧氏空间具有更强的树状结构表达能力, 如何调整神经网络、机器学习的模型, 充分发掘双曲空间的表达能力, 是未来的一个开放性研究问题.