2. 数学工程与先进计算国家重点实验室, 河南 郑州 450001
2. State Key Laboratory of Mathematical Engineering and Advanced Computing, Zhengzhou 450001, China
布尔函数作为流密码和分组密码的重要组件, 广泛应用于对称密码算法的设计中.一方面, 可以作为流密码算法的非线性组合部分, 产生性质好的密钥流序列; 另一方面, 可以作为描述分组密码非线性组件S盒的工具, 实现算法的混淆作用.因此, 布尔函数密码学性质的好坏直接关系到密码算法的安全性.随着诸多攻击算法的相继提出, 密码学中的布尔函数理论得到了一系列重要的结果.目前, 布尔函数的密码学指标主要有非线性度、相关免疫度、平衡性、雪崩准则和扩散准则、代数次数和代数免疫度等.文献[1-3]解决了具有最优代数免疫对称布尔函数的构造问题; 文献[4, 5]基于有限域构造了具有最优代数免疫度、最优代数次数和高非线性度等各种良好密码学性质的布尔函数; 文献[6]通过设计良好的算法利用计算机搜索得到兼具多种良好密码学性质的弹性布尔函数.
在布尔函数所有的密码学指标中, 代数次数是一个重要的指标.任何一个加密算法理论上均可写成关于输入的布尔函数, 若一个加密算法的布尔函数表达式或其代数次数可知, 密码分析者便可利用这一条件进行区分攻击或密钥恢复攻击.目前, 在对称密码的分析中已经出现了很多直接或间接地利用布尔函数表达式及其代数次数的攻击方法, 如代数攻击[7]、高阶差分攻击[8]、Cube攻击[9]和积分攻击[10]等.可见, 对布尔函数代数次数的研究在密码学中具有非常重要的意义.
最直接确定布尔函数代数次数的方法是通过真值表求解布尔函数的代数正规型, 但通常情况下, 得到一个密码算法确切的布尔函数代数正规型并不是一件容易的事.事实上, 求解代数次数并不需要知道布尔函数所有的单项式分布, Climent等人[11]根据布尔函数的support集推导出其代数正规型的一些性质, 提出了计算布尔函数代数次数的算法.但由于时间复杂度和存储复杂度的限制, 无法广泛适用于一般密码算法代数次数的求解.后来, 随着密码分析方法的发展, 相继提出了一些代数次数上界的理论估计工具.Boura等人[12]利用Walsh谱和高阶差分性质, 给出了适用于迭代密码Feistel和SPN型算法代数次数上界的估计.在欧密会2015上, Todo[13]提出了一种基于分离特性构造积分区分器的方法.随后, Todo和Morii[14]将分离特性应用于分组密码算法SIMON, 并指出分离特性与布尔函数的推导之间存在着一定的对应关系, 所以由分离特性导出指标集的性质在一定程度上可以反映布尔函数代数次数的上界.在美密会2017上, Liu[15]提出了数值映射的方法, 用来估计非线性反馈密码算法的代数次数, 并成功应用于Trivium等密码算法.本文主要研究布尔函数代数次数的求解算法及其在分组密码SIMON-like算法中的应用.
● 首先, 在利用真值表求解代数正规型算法的基础上, 建立了基于CUDA的并行求解架构.我们利用GPU加速求解并存储密码算法的真值表, 利用CPU多核并行技术和快速莫比乌斯变换求解算法的代数正规型.作为应用, 在较短的时间内求解了SIMON32, SIMECK32算法任意轮数的代数正规型和代数次数.
● 其次, 在Cube攻击理论的基础上, 根据代数次数和超多项式取值之间的关系.我们将代数次数的估计问题转化为超多项式值的求解, 设计了估计代数次数的概率算法, 估计了一般SIMON-like算法轮函数布尔函数的代数次数.
● 最后, 考虑到SIMON设计者并未给出轮函数循环移位常数(a, b, c)的选取依据, 我们从布尔函数代数次数的角度出发, 对SIMON-like算法循环移位常数的选取进行分析, 给出参数选择的依据.通过测试其他参数, 发现SIMON算法在原始参数下, 达到最大代数次数所需的轮数最短, 进而说明原始参数具有更高的安全性.
本文第1节描述论文的预备基础知识.第2节给出基于CUDA并行架构的代数次数的求解模型及其在分组为32比特的密码算法中的应用.第3节给出Cube攻击的理论基础和利用Cube变元估计代数次数的概率算法.第4节从布尔函数代数次数的角度出发, 对SIMON-like算法轮函数循环移位参数的选取进行分析.最后总结全文.
1 预备知识 1.1 基本概念设F2代表二元有限域;
布尔函数f(x1, x2, …, xn)可以唯一的表示为F2上的多元多项式, 即
| $ f({x_1}, {x_2}, ..., {x_n}) = {a_0} \oplus \sum\limits_{1 \le i \le n} {{a_i}{x_i}} \oplus \sum\limits_{1 \le i < j \le n} {{a_{ij}}{x_i}{x_j}} \oplus ... \oplus {a_{12 \cdots n}}{x_1}{x_2}...{x_n} $ | (1) |
其中, 系数a0, ai, aij, a12…n属于{0, 1}.称公式(1)为布尔函数f的代数正规型(简称ANF).布尔函数的代数次数deg(f)为布尔函数f代数正规型表示中, 系数不为0单项式中最大的变量个数.
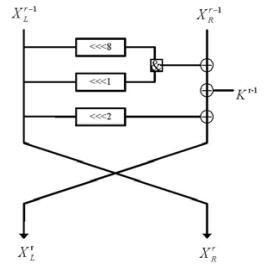
1.2 SIMON-like算法2013年, 美国国家安全局提出了硬件优势明显的轻量级密码算法SIMON[16].SIMON算法是典型的Feistel结构, 轮函数采用异或、循环移位运算和按位与运算, 建议的分组规模为2n(n=16, 24, 32, 48, 64), 密钥规模为mn, 根据不同的主密钥规模, m取2, 3或4, 记为SIMON 2n/mn.SIMON算法的结构如图 1所示.
|
Fig. 1 r-round structure of SIMON 图 1 SIMON第r轮结构 |
其中,
| $ f\left( x \right) = \left( {\left( {x < < < 8} \right)\& \left( {x < < < 1} \right)} \right) \oplus \left( {x < < < 2} \right). $ |
SIMON算法第r轮状态值可以如下表示.
| $ \left\{ {\begin{array}{*{20}{l}} {X_L^r = f(X_L^{r - 1}) \oplus X_R^{r - 1} \oplus {k^{r - 1}}}\\ {X_R^r = X_L^{r - 1}} \end{array}} \right. $ |
定义采用SIMON算法结构, 仅轮函数循环移位参数选取不同的算法为SIMON-like算法, 其轮函数的表示如下.
| $ {f_a}_{, b, c}\left( x \right) = \left( {\left( {x < < < a} \right)\& \left( {x < < < b} \right)} \right) \oplus \left( {x < < < c} \right). $ |
一种典型的算法是Yang等人[17]在CHES2015提出的SIMECK算法, SIMECK算法与SIMON结构相同, 但循环移位常数(a, b, c)取值为(5, 0, 1).
2 基于CUDA并行架构的代数次数求解最直接的确定布尔函数代数次数的方法是计算布尔函数的代数正规型, 进而得到布尔函数的代数次数.如果已知布尔函数的真值表, 可以基于莫比乌斯变换计算布尔函数的代数正规型.
对于一个n变量的布尔函数f(x), f(x)的真值表存储在长度为2n的数组v中, 则可以利用算法1[18]求解布尔函数的代数正规型.算法1使用了两个长度为2n-1的辅助数组t和u, ||表示连接运算.
算法 1.利用真值表计算代数正规型.
输入:真值表数组v.
输出:f的代数正规型.
for i=1, 2, …, n
for j=1, 2, …, 2n-1
tj=v2j-1
uj=v2j-1⊕v2j
end for
v=t||u
end for
遍历算法1得到代数正规型的系数数组, 即可知道布尔函数的代数次数.算法1的时间复杂度O(n2n), 空间复杂度O(2n), 运行时间和所需空间随着分组长度的增加呈指数级增长.在计算资源有限的情况下, 求解得到的代数次数有限.为了提高算法的运行效率, 充分利用计算资源实现算法的并行处理, 我们构建了基于CUDA并行架构的代数次数的求解模型, 协同利用GPU和CPU同时进行数据计算, 极大地降低了代数次数的求解时间.
2.1 GPU与CUDA架构GPU(graphic processing unit)最早的设计是用来对大量的图形图像数据进行并行处理, 以减轻CPU的工作负担.随着GPU设计理念的不断完善与制作工艺的飞速发展, GPU的内存带宽与浮点运算能力已远远超过了同时代的CPU性能.用GPU做通用计算已经成为研究的热点, 相比于CPU的更适合对复杂的运算指令、多路的分支与判断的逻辑控制程序的处理, GPU则更适合处理具有大数据量、高并行性、低耦合性、高计算密度的数据计算程序.
在GPU基础上发展起来的CUDA(compute unified device architecture)[19]并行计算架构, 在高性能计算方面得到广泛应用.NVIDIA公司为CUDA应用程序开发人员提供了一整套程序开发与调试环境组件, 包括NVCC编译器、GDB调试器、CUDA库函数、CUDA运行时库(CUDA runtime API)以及CUDA驱动程序(CUDA driver API).在上述的CUDA编程的软件体系中, 其核心部分是CUDA C语言, 它实质上是标准C语言的一个极小扩展集和一个运行时库, 源文件可以通过NVCC编译器编译得到调用这些扩展和运行时库的目标程序; 使用NVCC编译器得到的目标程序只是在GPU设备上运行的代码, 而要管理GPU的计算资源, 就需要借助CUDA运行时库和CUDA驱动程序来实现.与传统的GPU相比, CUDA编程模型[20]中属于同一个线程块内的线程之间不仅能够相对独立的执行并行程序, 而且还可以通过共享存储器和线程同步技术实现同一个线程块内不同的线程间相互通信.考虑到CUDA并行架构的高效性和便捷性, 我们构建了基于CUDA架构的代数次数的求解模型.
2.2 基于CUDA架构代数次数的求解利用CUDA实现高性能计算, 实质上是通过CPU与GPU的分工合作、并行运行来完成的.CUDA编程模型可以分为Host端(主机端)和Device端(设备端):Host端为CPU部分, 主要在计算机内存中执行, 负责处理逻辑性较强的任务和执行串行部分的计算; Device端为GPU部分, 主要在计算机显卡内存中执行, 负责处理高度线程化的并行任务, 又称为核函数(kernel).CUDA程序是由许多Device端内核函数并行执行步骤和许多Host端串行执行步骤共同完成的, 从而提高了程序的整体运行性能.
对于分组密码算法, 轮函数可以表示为关于该轮输入的布尔函数.利用真值表求解布尔函数的代数次数时, 首先需要求解密码算法的真值表, 其次利用真值表求解布尔函数的代数正规型, 进而得到对应轮数的代数次数.对于分组长度为n的算法, 一方面, 求解真值表需要遍历2n个全部的输入状态, 可以并行化执行; 另一方面, 真值表的求解过程不需要做复杂的运算和逻辑判断, 因而将求解真值表的部分指定为设备端程序_device_, 由GPU调用运行.然而, 对于利用快速莫比乌斯变换求解代数正规型的过程, 由于涉及多路的分支与复杂的逻辑判断, 不适用于GPU计算, 因而将实现快速莫比乌斯变换的过程指定为主机端程序_host_, 由CPU运行.此外, 为了缩短CPU的运行时间, 我们利用Antoine Joux[21]提出的求解代数正规型的并行优化算法, 采用CPU多核并行技术, 做到多个比特同时运算, 从而实现了算法加速.
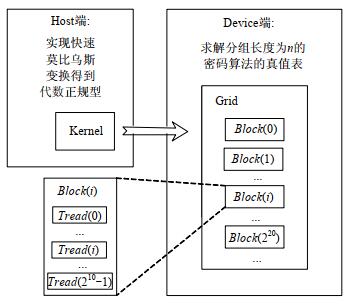
整个CUDA程序的实现模型是串行和并行任务的交互完成.当有并行任务时, Host端调用kernel函数, 将执行算法真值表求解的任务交给Device端解决.当kernel函数映射到GPU上后, 分配到网格(grid)上, 网格中的线程又被细分为一维的线程块(block), 每个线程块分解为多个线性(tread), 在同一个多处理器上运行, 提高了数据处理的效率, 极大地降低了密码算法真值表的生成时间.基于CUDA架构实现密码算法代数次数求解的模型如图 2所示.
|
Fig. 2 Model of algebraic degree estimate based on CUDA 图 2 基于CUDA代数次数的求解模型 |
2.3 代数次数的求解结果
基于CUDA架构计算密码算法的代数次数虽然可以极大地缩短运行时间, 提高求解效率, 但是当计算和存储资源有限时, 仍然无法准确求解分组长度较大的密码算法的代数次数.作为应用, 我们在个人PC机上(Intel(R) Core(TM) i7-7700HQ CPU@2.8GHz 16.00GB, NVIDIA GeForce GTX1060)配置了VS 2012和CUDA 9.1.85的环境, 编写了相关的程序, 在较短的时间内求解了轻量级分组密码算法SIMON32和SIMECK32全轮布尔函数的代数次数, 结果分别见表 1和表 2.
| Table 1 Algebraic degree of SIMON32 表 1 SIMON32的代数次数 |
| Table 2 Algebraic degree of SIMECK32 表 2 SIMECK32的代数次数 |
我们从算法第1轮开始算起, 多次运行程序求解平均值, 给出了计算布尔函数代数正规型和代数次数的时间.由表 1可知, 对于SIMON32来说, 轮函数的代数次数增长比较缓慢, 并没有达到算法迭代所期望的代数次数, 从第13轮开始, SIMON32代数次数达到上界31.我们利用CUDA架构可以在不到两分钟内求解任意轮SIMON 32算法的代数正规型, 且代数正规型的求解时间随轮数的增长没有特别明显的增大.此外, 计算代数次数由于需要遍历代数正规型的单项得到最大值, 因而求解代数次数的时间比代数正规型大, 且随代数正规型的复杂程度而变化.
由表 2可知, SIMECK算法代数次数随轮数的变化与SIMON算法相同, 从第13轮开始, SIMON32代数次数达到上界31.此外, 由于SIMECK算法结构与SIMON相同, 计算真值表的时间花销与SIMON相同, 因而SIMECK32代数次数的计算时间与表 1大致相同, 同样可以在不到两分钟内求解任意轮SIMECK 32算法的代数正规型, 在6分钟内给出全轮SIMECK32算法的代数次数.
本节在利用真值表求解代数正规型算法的基础上构造了基于CUDA架构的代数次数的求解模型.随后, 作为应用, 求解了对分组长度较小的算法SIMON和SIMECK任意轮数的代数次数.对于已知体制和结构的密码算法, 基于CUDA架构的代数次数求解模型的关键是利用GPU遍历求解算法的真值表.在此基础上, 协同利用CPU求解代数正规型.与传统算法实现相比, 有效分配了计算资源, 极大地提高了求解代数正规型算法的运行效率, 缩短了计算代数次数的时间.但是对于分组长度较大的算法, 由于计算和存储资源有限, 无法准确求解密码算法的代数次数, 但仍然可以给出密码算法代数次数上界的估计.下面, 我们利用Cube攻击理论与代数次数之间的关系, 设计估算代数次数上界的概率算法.
3 基于Cube理论的代数次数的估计Cube攻击是由Dinur和Shamir[9]在2009年欧密会上提出的一种基于代数思想的新型攻击方法, 其攻击的主要原理是:将密码算法的输出可以描述为有限域GF(2)上关于密钥k和公开变量v(明文比特或者IV比特)的多项式f(v, k), 攻击者通过选择部分公开变量组成Cube, 并询问密码系统获得输出值, 从而得到关于密钥k的低次方程组, 通过求解方程恢复一定数目的密钥k.Cube攻击在序列密码、分组密码和Hash函数的分析中具有广泛的应用.本节在Cube攻击理论的基础上分析了Cube攻击中超多项式的取值和代数次数之间的关系, 设计了代数次数的估计算法.
3.1 Cube理论基础对于任意n元布尔函数f(x1, x2, …, xn), 对任意指标集I={i1, i2, …, ik}⊆{1, 2, …, n}, 记
| $ f\left( {{x_1}, {x_2}, \ldots , {x_n}} \right) = {f_S}_{(I)} \times {t_I} \oplus q\left( {{x_1}, {x_2}, \ldots , {x_n}} \right) $ | (2) |
其中, fS(I)不含tI中的变量, q(x1, x2, …, xn)中不含能被tI整除的项.
称
遍历CI所有的取值, 对公式(2)求和可得:
| $ \sum\limits_{{C_I}} {f({x_1}, {x_2}, ..., {x_n})} = \sum\limits_{{C_I}} {{t_I}{f_{S(I)}}} \oplus \sum\limits_{{C_I}} {q({x_1}, {x_2}, ..., {x_n})} $ | (3) |
由于q(x1, x2, …, xn)中的项成对出现和为0, 故有下面的等式成立.
| $ {f_{S(I)}} = \sum\limits_{{C_I}} {f({x_1}, {x_2}, ..., {x_n})} {\rm{mod}}{\kern 1pt} 2 $ | (4) |
由公式(4)可知, 超多项式fS(I)的取值为布尔函数f(x1, x2, …, xn)在k维Cube CI上的异或和.超多项式的取值与布尔函数的代数次数之间具有以下关系.
引理 1. 对于任意n元布尔函数f(x1, x2, …, xn), 若对{1, 2, …, n}的任意d元子集I, fS(I)取值都为常数, 则f(x1, x2, …, xn)的代数次数至多为d次.
证明:若函数f(x1, x2, …, xn)的代数次数大于d, 设其次数为s≥d+1, 不妨设
引理 2. 对于任意n元布尔函数f(x1, x2, …, xn), 若存在{1, 2, …, n}的某个d元子集I, 其对应的超多项式fS(I)不是常数, 则f(x1, x2, …, xn)的代数次数至少为d+1次.
证明:对于布尔函数f(x1, x2, …, xn), 由公式(2)可知,
| $ f\left( {{x_1}, {x_2}, \ldots , {x_n}} \right) = {f_S}_{(I)} \times {t_I} \oplus q\left( {{x_1}, {x_2}, \ldots , {x_n}} \right). $ |
其中, tI为d次单项式, fS(I)不是常数, fS(I)·tI次数至少为d+1, 而q(x1, x2, …, xn)中单项式不是tI的倍式, 因而不会和fS(I)·tI中的项抵消, 所以f(x1, x2, …, xn)代数次数至少为d+1.
利用引理1和引理2, 通过测试某些Cube集合对应的超多项式fS(I)的取值是否为常数, 可以得到f(x1, x2, …, xn)代数次数的上界和下界.下面我们给出定理1, 给出计算布尔函数代数次数的充要条件.
定理 1. 布尔函数f(x1, x2, …, xn)的代数次数为d次, 当且仅当对{1, 2, …, n}的任意d元子集I, 都有fS(I)都为常数, 并且存在{1, 2, …, n}的某个d-1元子集I', 其对应的超多项式fS(I')不是常数.
证明:充分性的证明由引理1和引理2可得, 只需要证明必要性.若布尔函数f(x1, x2, …, xn)的代数次数为d次, 则由超多项式的定义和性质可知, 对{1, 2, …, n}的任意d元子集I, fS(I)都为常数.另一方面, 不妨设
根据定理1可知, 利用Cube方法所找到的临界值d, 就是布尔函数f(x1, x2, …, xn)的代数次数.定理1需要计算d元子集I对应的超多项式fS(I)的取值, 为了计算方便, 可以利用性质1进行计算.
性质 1[9]. 对于布尔函数f(x1, x2, …, xn), 选择{1, 2, …, n}中的任意d元子集I={i1, i2, …, id}, 记L[α1, α2, …, αd]是一组基α1, α2, …, αd生成的线性空间, 其中,
| $ {f_{S(I)}} = \sum\limits_{v \in {C_I}} {f{|_v}} = \sum\limits_{\beta \in L[{\alpha _1}, {\alpha _2}, ..., {\alpha _d}]} {f(x \oplus \beta )} . $ |
对于分组密码算法, 轮函数可以表示为关于该轮输入的布尔函数.当分组长度2n较大, 选取的Cube变元较多时, 需要遍历所有的Cube变元集合, 计算超多项式的值, 计算量太大.我们采用随机选取Cube点的方法, 设计了概率算法进行次数估计.算法的基本思路是:从低到高依次检测布尔函数代数次数是否为d次(1 < d < n), 而在检测代数次数是否是d时, 根据定理1, 随机选择不同的输入点进行测试, 利用性质1计算不同测试点的超多项式的值, 判断取值是否相等, 进而估计代数次数, 具体算法如算法2所示.
算法 2. 利用Cube理论估计代数次数.
输入:待估计次数的分组密码算法E, 最大检测次数max.
输出:代数次数d.
1. 设置d=1, count=0;
2. While (d < n)
{
3. 选择d个线性无关的n维向量{α1, α2, …, αd};
4. 随机选择输入x, 计算
5. While (count < max)
{
6. 随机选择y≠x, 计算
7. if sum≠tmp break;
8. count=count+1;
}
9. if count=max输出代数次数d;
10. else d=d+1;
}
只要测试次数max的取值比较大, 则可以较大的正确性保证估计结果是对的.算法2的时间复杂度为O(n2d), 空间复杂度为O(1), 可以忽略不计.算法2的前提是随机选取d维Cube变元, 遍历所有Cube变元的集合后, 在现有有限的计算资源下, 可以计算对应超多项式的值, 因而特别适合于分组密码算法输入变元个数比较大而实际轮函数布尔函数的代数次数比较小的情况.
3.3 在SIMON-like算法中的应用我们利用算法2针对循环移位常数(a, b, c)取值为全为奇数和全为偶数的Simon-like算法的代数次数进行估计, 以SIMON[1,7,3]为例, 不同分组长度的求解结果具体见表 3.
由表 3可知, 分组长度为2n的Simon-like算法在参数选择(1, 7, 3)时, 不同轮代数次数增长缓慢, 且达不到代数次数的上界2n-1.分组长度为32比特的算法从第9轮开始代数次数保持15不变, 分组长度为48比特的算法从第11轮开始代数次数保持23不变, 分组长度为64比特的算法从第13轮开始代数次数保持31不变, 代数次数的上确界为n-1.事实上, 对于参数选择全是奇数或者偶数的SIMON-like算法, 都有以下定理成立.
| Table 3 Algebraic degree estimation of SIMON[1,7,3] 表 3 SIMON[1,7,3]代数次数的估计 |
定理 2. 对于分组长度为2n的SIMON-like[a, b, c]算法, 布尔函数
记为deg(f), 若循环移位参数(a, b, c)同为奇数或同为偶数, 则对任意的轮数r, 都有deg(f)≤n-1.
证明:以分组长度为32的SIMON-like为例, 不妨假设循环移位参数(a, b, c)同为奇数.首先利用数学归纳法证明:迭代r轮输出的每一比特的值至多只由初始输入的n比特决定.
记SIMON-like 32第1轮的输入为x0, x1, …, x15, x16, …, x31, 输出为y0, y1, …, y15, y16, …, y31, 第3轮的输入为z0, z1, …, z15, z16, …, z31, 迭代轮数为r轮.根据算法结构, 第1轮的输出按比特表示成输入比特的布尔函数为
| $ \left\{ {\begin{array}{*{20}{l}} {{y_i} = {x_{(i + a)\bmod 16}} \cdot {x_{(i + b)\bmod 16}} \oplus {x_{(i + c)\bmod 16}} \oplus {x_{15 + i}}, {\rm{ }}0 \le i \le 15}\\ {{y_i} = {x_{i - 16}}, {\rm{ }}16 \le i \le 31} \end{array}} \right.. $ |
因为(a, b, c)同为奇数, 所以yi(i=1, 3, …, 15, 16, …, 30)能够表示成输入比特集合(x0, x2, …, x14, x17, …, x31)的布尔函数, yi(i=0, 2, …, 14, 17, …, 31)能够表示成输入比特集合(x1, x3, …, x15, x16, …, x30)的布尔函数.
对于第2轮的输出, 表示为第2轮输入的布尔函数为
| $ \left\{ {\begin{array}{*{20}{l}} {{z_i} = {y_{(i + a)\bmod 16}} \cdot {y_{(i + b)\bmod 16}} \oplus {y_{(i + c)\bmod 16}} \oplus {y_{15 + i}}, {\rm{ }}0 \le i \le 15}\\ {{z_i} = {y_{i - 16}}, {\rm{ }}16 \le i \le 31} \end{array}} \right.. $ |
因为(a, b, c)同为奇数, 所以zi(i=1, 3, …, 15, 16, …, 30)能够表示成输入比特集合(y0, y2, …, y14, y17, …, y31)的布尔函数, zi(i=0, 2, …, 14, 17, …, 31)能够表示成输入比特集合(y1, y3, …, y15, y16, …, y30)的布尔函数.综合两轮的结果可知, zi (i=1, 3, …, 15, 16, …, 30)能够表示成输入比特集合(x1, x3, …, x15, x16, …, x30)的布尔函数, zi(i=0, 2, …, 14, 17, …, 31)能够表示成输入比特集合(x0, x2, …, x14, x17, …, x31)的布尔函数.
假设对于任意的r≤k∈N, SIMON-like 32输出的每一比特至多只由初始输入的n比特决定(第1, 3, …, 15, 16, …, 30比特或第0, 2, …, 14, 17, …, 31比特), 则当r=k时, 不妨设SIMON-like 32算法的第k-1轮的输出分别为(w0, w1, …, w15, w16, …, w31), 第k轮的输出分别为(v0, v1, …, v15, v16, …, v31).若k为偶数, k-1为奇数, 第k轮的输出表示为第k轮输入的布尔函数为
| $ \left\{ {\begin{array}{*{20}{l}} {{v_i} = {w_{(i + a)\bmod 16}} \cdot {w_{(i + b)\bmod 16}} \oplus {w_{(i + c)\bmod 16}} \oplus {w_{15 + i}}, {\rm{ }}0 \le i \le 15}\\ {{v_i} = {w_{i - 16}}, {\rm{ }}16 \le i \le 31} \end{array}} \right.. $ |
因为(a, b, c)同为奇数, 所以vi(i=1, 3, …, 15, 16, …, 30)能够表示成输入比特集合(w0, w2, …, w14, w17, …, w31)的布尔函数, vi(i=0, 2, …, 14, 17, …, 31)能够表示成输入比特集合(w1, w3, …, w15, w16, …, w30)的布尔函数.由归纳假设可知, vi (i=1, 3, …, 15, 16, …, 30)能够表示成输入比特集合(x1, x3, …, x15, x16, …, x30)的布尔函数, 不存在的项即系数为0;vi(i=0, 2, …, 14, 17, …, 31)能够表示成输入比特集合(x0, x2, …, x14, x17, …, x31)的布尔函数, 不存在的项即系数为0.若k为奇数, 同理可以证明.因而当循环移位参数(a, b, c)同为奇数时, 对任意的r轮的SIMON-like 32算法, 输出的每一比特的值至多只由初始输入的n比特决定.所以输出比特表示成输入比特的布尔函数f时, 代数次数deg(f)至多为n-1次.循环移位参数同为偶数时证明类似.定理2得证.
本节在Cube攻击理论基础上, 研究了代数次数和超多项式取值之间的关系, 将代数次数的估计问题转化为超多项式值的求解.在此基础上, 设计了概率算法估计一般SIMON-like算法的代数次数.作为应用, 求解了参数选取全为奇数或者全为偶数的SIMON-like算法任意轮数的代数次数, 并从理论上证明了参数选择全为奇数和偶数的SIMON-like算法代数次数的上确界.下面, 我们从布尔函数代数次数的角度出发, 进一步讨论循环移位参数的选择对SIMON-like算法的影响, 给出算法设计时参数的选择依据.
4 SIMON-like算法循环移位参数选取分析目前, 很多不同结构的分组密码算法, 不管是密钥扩展算法还是算法运行的轮函数, 都会采用循环移位参数防止对密钥进行逐段破译以及隐蔽明文的统计特性, 选择不好的循环移位参数会对算法的安全性产生致命的影响.目前公开的算法, 设计者大多没有给出循环移位参数的选择依据和设计标准.对于非线性部件简单的SIMON-like算法, 选择不好的循环参数会导致算法分解为几个独立的简单算法, 从而减少算法分析过程需要的复杂度.由定理2的证明过程可知, 分组长度为2n的Simon-like算法, 当循环移位参数(a, b, c)全为奇数或者全为偶数时, 算法可以分解为两个分组长度为n的小算法, 无法保证原算法的安全强度, 算法攻击的难度大幅减少.因而为了安全起见, SIMON-like算法在选择循环移位参数时, 应该避免参数选择全为奇数或者全为偶数.
SIMON和SIMECK算法循环移位参数的选择既有奇数也有偶数, 但设计者并没有给出其他的选取依据. Kölbl等人[22]在CRYPTO 2015上, 从抵抗差分和线性攻击的角度对循环移位常数的选取进行了分析, 通过研究SIMON循环移位常数对其扩散性的影响, 证明了SIMON算法的原始参数并不具有最强的抗差分和线性的能力.此外, 文献[22]根据相关的评判准则, 从所有可能的移位常数(a, b, c)中选择了3个优于原参数(8, 1, 2)的参数SIMON[12,5,7], SIMON[7,0,2], SIMON[1,0,2].随后, Kondo等人[23]从抵抗不可能差分攻击和积分攻击的能力评判了参数选择的优劣, 发现参数SIMON[12,5,7]总体的安全性比原始参数高.我们从布尔函数代数次数的角度出发, 对SIMON-like型算法轮函数循环移位参数的选取进行分析.利用第2节和第3节的算法, 对Kölbl等人选出的表现优良的SIMON[1,0,2], SIMON[12,5,7], SIMON[7,0,2]算法的代数次数进行求解, 以分组长度为32的算法为例, 求解结果见表 4~表 6.
| Table 4 Algebraic degree of SIMON[1,0,2] 表 4 SIMON[1,0,2]的代数次数 |
| Table 5 Algebraic degree of SIMON[12,5,7] 表 5 SIMON[12,5,7]的代数次数 |
| Table 6 Algebraic degree of SIMON[7,0,2] 表 6 SIMON[7,0,2]的代数次数 |
由表 4可知, 与SIMON算法相比, SIMON[1,0,2]轮函数的代数次数增长缓慢.从第16轮开始, SIMON[1,0,2]代数次数才达到上界31.从积分攻击的角度来看, 如果代数次数增长缓慢, 达到上界所需的轮数越大, 则可以找到更长轮数的积分区分器, 进而攻击更长轮数的算法.因此, 与原参数相比, SIMON[1,0,2]算法抵抗积分攻击的能力明显较弱.
由表 5可知, 与SIMON算法相比, SIMON[12,5,7]轮函数的代数次数增长缓慢.从第14轮开始, SIMON[1,0,2]代数次数达到上界31.从积分攻击的角度来看, SIMON[12,5,7]可以找到至少比SIMON多1轮的积分区分器.因此, 从抵抗积分攻击的角度来看, SIMON[12,5,7]算法没有原始参数安全.
由表 6可知, 虽然SIMON[7,0,2]与SIMON算法轮函数的代数次数都是从第13轮开始上界31, 但是SIMON[7,0,2]每一轮布尔函数的代数次数没有对应轮SIMON算法的大, 从算法攻击所需的复杂度来看, 攻击原始参数的SIMON算法难度更大, 需要的复杂度也更大.因而原始参数具有更高的安全性.
5 总结本文主要给出了两种布尔函数代数次数的求解模型:一种在利用真值表求解代数正规型算法的基础上建立了基于CUDA的并行求解架构, 协同利用CPU和GPU的计算资源, 极大地缩短了求解代数次数的时间, 在较短的时间内求解了SIMON32, SIMECK32算法任意轮数的代数正规型和代数次数; 另一种求解模型根据代数次数和Cube攻击中超多项式取值之间的关系设计了概率算法, 估计了一般SIMON-like型算法的代数次数.作为应用, 从布尔函数代数次数的角度出发, 给出了SIMON-like算法轮函数在选择不同循环移位参数时, 代数次数变化的差异性, 进而给出循环移位参数的选取依据.实验结果表明, 与其他循环移位参数相比, SIMON算法在原始参数下达到最大代数次数所需的轮数最短, 说明原始参数具有更高的安全性.下一步将研究代数次数的求解模型在其他类型算法设计与分析中的应用.
| [1] |
Li N, Qi W. Symmetric Boolean functions depending on an ODD number of variables with maximum algebraic immunity. IEEE Trans. on Information Theory, 2006, 52(5): 2271-2273.
[doi:10.1109/TIT.2006.872977] |
| [2] |
Peng J, Wu Q, Kan H. On symmetric Boolean functions with high algebraic immunity on even number of variables. IEEE Trans. on Information Theory, 2011, 57(10): 7205-7220.
[doi:10.1109/TIT.2011.2132113] |
| [3] |
Wang H, Peng J, Li Y, Kan H. On 2k-variable symmetric Boolean functions with maximum algebraic immunity k. IEEE Trans. on Information Theory, 2012, 58(8): 5612-5624.
[doi:10.1109/TIT.2012.2201350] |
| [4] |
Wang Q, Peng J, Kan H, Xue X. Constructions of cryptographically significant Boolean functions using primitive polynomials. IEEE Trans. on Information Theory, 2010, 56(6): 3048-3053.
[doi:10.1109/TIT.2010.2046195] |
| [5] |
Carlet C, Feng K. An infinite class of balanced functions with optimal algebraic immunity, good immunity to fast algebraic attack and good nonlinearity. In: Proc. of the ASIACRYPT 2008. LNCS 5350, Berlin: Springer-Verlag, 2008. 425-440.
|
| [6] |
Yang J, Zhang W. Generating highly nonlinear resilient Boolean functions resistance against algebraic and fast algebraic attacks. Security and Communication Networks, 2015, 8(7): 1256-1264.
[doi:10.1002/sec.1078] |
| [7] |
Courtois N, Meier W. Algebraic attacks on stream ciphers with linear feedback. In: Proc. of the EUROCRYPT 2003. LNCS 2656, Berlin: Springer-Verlag, 2003. 345-359.
|
| [8] |
Lai X. Higher order derivatives and differential cryptanalysis. In: Proc. of the Communications and Cryptography. Kluwer Academic Press, 1994. 227-233.
|
| [9] |
Dinur I, Shamir A. Cube attacks on tweakable black box polynomials. In: Proc. of the EUROCRYPT 2009. LNCS 5479, Berlin: Springer-Verlag, 2009. 278-299.
|
| [10] |
Knudsen L, Wagner D. Integral cryptanalysis. In: Proc. of the FSE 2002. LNCS 2365, Berlin: Springer-Verlag, 2002. 112-127.
|
| [11] |
Climent H, Garca F, Requena V. Computing the degree of a Boolean function from its support. In: Proc. of the ISITA 2010. IEEE, 2010. 123-128. https://www.researchgate.net/publication/220961162_Computing_the_degree_of_a_Boolean_function_from_its_support
|
| [12] |
Canteaut A, Videau M. Degree of composition of highly nonlinear functions and applications to higher order differential cryptanalysis. In: Proc. of the EUROCRYPT 2002. LNCS 2332, Berlin: Springer-Verlag, 2002. 518-533.
|
| [13] |
Todo Y. Structural evaluation by generalized integral property. In: Proc. of the EUROCRYPT 2015. LNCS 9056, Berlin: Springer-Verlag, 2015. 287-314.
|
| [14] |
Todo Y, Morii M. Bit-based division property and application to Simon family. In: Proc. of the FSE 2016. LNCS 9783, Berlin: Springer-Verlag, 2016. 357-377.
|
| [15] |
Liu M. Degree evaluation of NFSR-based cryptosystems. In: Proc. of the CRYPTO 2017. LNCS 10403, Berlin: Springer-Verlag, 2017. 227-249.
|
| [16] |
Beaulieu R, Shors D, Smith J, et al. The SIMON and SPECK families of lightweight block ciphers. IACR Cryptology ePrint Archive, Report, 2013/404, 2013. http://eprint.iacr.org/2013/404
|
| [17] |
Yang G, Zhu B, Suder V, Aagaard MD, Gong G. The Simeck family of lightweight block ciphers. In: Proc. of the CHES 2015. LNCS 9293, Berlin: Springer-Verlag, 2015. 307-329.
|
| [18] |
Johansson T. A framework for chosen IV statistical analysis of stream ciphers. In: Proc. of the INDOCRYPT 2007. LNCS 4859, Berlin: Springer-Verlag, 2007. 268-281.
|
| [19] |
John C, Max G, Ty M. Professional CUDA C Programming. Indianapolis: Wrox, 2014.
|
| [20] |
Cook S. CUDA Programming:A developer's Guide to Parallel Computing with GPUs. Newnes, 2012.
https://www.worldcat.org/title/cuda-programming-a-developers-guide-to-parallel-computing-with-gpus/oclc/842439171 |
| [21] |
Joux A. Algotithmic Cryptanalysis. Chapman & Hall/CRC, 2009.
https://dl.acm.org/doi/book/10.5555/1642719 |
| [22] |
Köbl S, Leander G, Tiessen T. Observations on the SIMON block cipher family. In: Proc. of the CRYPTO 2015. LNCS 9215, Berlin: Springer-Verlag, 2015. 161-185.
|
| [23] |
Kondo K, Yu S, Iwata T. On the design rationale of Simon block cipher: Integral attacks and impossible differential attacks against Simon variants. In: Proc. of the ACNS 2016. LNCS 9696, Berlin: Springer-Verlag, 2016. 518-536. https://link.springer.com/chapter/10.1007%2F978-3-319-39555-5_28
|
 2020, Vol. 31
2020, Vol. 31


