稀疏表示因其具有鲁棒性, 在数字图像处理和模式识别领域中有着广泛的应用.它使用字典中原子的线性组合来重构样本[1-4], 对于一个过完备字典, 每一个测试样本有一个稀疏系数.基于稀疏表示的样本分类方法将样本的分类问题转化为基于稀疏系数的多个线性回归模型的分类问题, 且已有的稀疏表示及字典学习的方法大多作用于向量空间[4, 5].本文则是将基于稀疏表示的分类方法用于解决黎曼空间中样本的分类任务.
在数字图像处理和模式识别领域中, 样本的描述方法是否具有鲁棒性和判别性, 对最后的实验结果起到至关重要的作用.其中, 最为简单的就是先将图像进行灰度化处理, 然后将图像矩阵展开为列向量.但是该方法会对导致向量的维度过高, 且忽略了样本中像素点的几何信息, 影响了判别性.最近, 协方差描述因其具有较强的鲁棒性, 在计算机视觉领域得到了广泛的关注[6-8].
| $ C = \frac{1}{{r - 1}}\sum\limits_{i = 1}^r {({f_i} - \bar f){{({f_i} - \bar f)}^T}} $ | (1) |
若是对单幅图像进行描述, 公式(1)中的fi为图像中第i个像素点的特征向量, 这些特征可能是灰度值、梯度值或者Gabor滤波值等.r是该图像中像素点的个数, f是所有像素点特征向量的平均向量.若是对图像集进行描述, 公式(1)中fi为图像集中第i幅图像的灰度值, r是该图像集中图像的个数, f是所有的图像灰度值的平均向量.协方差描述融合了多种特征, 且通过协方差描述得到的矩阵为对称正定(symmetric positive definite, 简称SPD)矩阵, 该SPD矩阵的维度只与特征向量fi的维度有关, 与图像中像素点的个数和图像集中的图像的个数都无关.由于协方差描述在建模时有平均化操作, 所以协方差描述可以减少样本中的噪声带来的干扰.该描述方法已经被广泛地应用于弥散张量成像(diffusion tensor imaging, 简称DTI)、行人检测[9]、人脸识别[1-3]和纹理识别[10].由SPD矩阵所张成的空间是一个SPD流形, 即非线性的黎曼空间.如果将欧氏空间的度量方法和分类方法直接应用于SPD矩阵, 则忽略了黎曼空间的黎曼度量和破坏了SPD流形的黎曼几何结构, 将无法得到较好的分类效果.通过以上分析, 若将欧氏空间中基于稀疏表示的分类方法用于解决SPD流形[6, 7, 10]中样本的分类任务, 则将面临如下几个方面的挑战.
(1) 在SPD流形这个非线性的黎曼空间中, 如何用字典中的原子(SPD矩阵)去表达一个测试样本(SPD矩阵), 将面临着巨大的挑战.
(2) 在欧氏空间中, 样本多以向量的形式描述, 通过l2范数度量原样本和重构样本之间的误差.而对于SPD矩阵, l2范数将不再适合.
(3) 字典中的原子也是SPD矩阵, 所以在字典的更新过程中, 将会涉及在SPD流形上的约束优化问题.
SPD流形存在于一个非线性的黎曼空间中, 阻碍了将欧氏空间的稀疏表示和字典学习的方法直接应用于SPD矩阵.综合考虑以上几个方面的困难和SPD流形的特性, 有如下的几组策略可以将基于稀疏表示的分类方法应用于SPD矩阵, 以实现SPD流形上样本的分类任务.
(1) 用统计度量计算重构误差
该策略主要是更换度量方法计算原样本和重构样本之间的误差, 虽并没充分考虑SPD流形的几何特性, 但是解决了重构误差的计算问题.在样本的重构过程中, 将SPD矩阵视为欧氏空间的样本, 用字典中原子的线性组合表示原样本, 忽略了SPD流形的几何特性.在误差估计误差时, 不是用l2范数来度量原样本和重构样本, 而是用一些经典的统计度量计算它们之间的误差, 如LogDet散度(log-determinant divergence)[11-14]和Stein散度(Stein divergence)[6, 7]等.文献[11, 12]提出一种张量稀疏表示(tensor sparse representation, 简称TSR)方法, 用字典中原子的线性组合重构样本, 且用LogDet散度度量原样本和重构样本之间的误差.基于此框架, 文献[13, 14]提出了张量字典的更新方法(tensor dictionary learning, 简称TDL), 文献[15]提出一种在线字典学习(generalized dictionary learning, 简称GDL)方法, 在样本的重构过程中, 用秩为1的矩阵的线性组合重构样本, 用矩阵的F范数(Frobenius norm)计算重构样本与原样本之间的误差.以上两种方法——TSR和GDL, 将稀疏表示方法与SPD流形相结合, 实现了SPD流形上样本的分类任务.但在稀疏表示和字典学习的过程中, 都是将SPD矩阵视为欧氏空间的样本, 忽略了SPD流形的几何特性.在误差度量时, 使用的并不是SPD流形上的黎曼度量, 忽略了SPD流形的黎曼度量.文献[16]提出的黎曼稀疏表示(Riemannian sparse representation, 简称Rie_SR)方法考虑了SPD流形的黎曼度量.虽然也是用字典中原子的线性组合来重构样本, 忽略了黎曼几何特性, 但是在误差估计时, 使用仿射不变黎曼度量(affine invariant Riemannian metric, 简称AIRM)[6, 7, 17, 18]计算原样本和重构样本之间的误差.基于这一框架, 文献[17]利用黎曼共轭梯度的方法实现了黎曼字典的更新(Riemannian dictionary learning, 简称Rie_DL).
(2) 考虑SPD流形的几何的特性
在SPD流形上, 度量SPD流形两点之间的测地距离, 除了仿射不变黎曼度, 还有很多其他的黎曼度量方法, 其中, LEM(log-Euclidean metric)[8, 10, 19, 20]是一个用于SPD流形的简洁有效的黎曼度量.该度量充分考虑SPD流形的几何特性, 通过矩阵的对数映射(logarithm mapping), 将SPD样本矩阵映射到其切空间中, 切空间中的样本与原SPD流形上的样本是一一对应的关系.由于切空间是一个平面, 可以视为欧氏空间, 该度量用样本在切空间中的欧氏距离作为原SPD矩阵之间的测地距离.其中, 对数映射是该度量方法的特别之处, 文献[21, 22]提出的方法就是首先将SPD矩阵映射到切空间中, 对切空间中的样本进行字典学习和稀疏表示, 然后通过切空间中字典原子的线性组合重构样本, 用欧氏度量去计算重构误差.我们称这种方法为LE_SR+LE_DL.该策略考虑了SPD流形的黎曼几何特性, 将基于SPD流形上样本的分类问题转化为了基于切空间中样本的分类问题.
(3) 黎曼核稀疏表示
该策略与对数映射类似, 首先将SPD矩阵映射到一个线性空间.但是该策略是通过核函数将样本映射到再生核希尔伯特空间(reproducing kernel Hilbert space, 简称RKHS), 通过核空间字典原子的线性组合重构样本.文献[23]第一次提出将SPD矩阵映射到核空间以解决黎曼空间的稀疏表示问题, 并提出了基于Stein散度[6, 7, 24-26]的黎曼核, 其中, Stein散度为dS=log|(1/2)(X+Y)|-(1/2)log|XY|.我们称这种核空间稀疏表示的方法为Ker_SR, 并将基于这个框架的字典更新方法[23, 26]称为Ker_DL.与该方法类似, 文献[26, 27]分别提出了基于Jeffrey核和Log- Euclidean核的核空间稀疏表示分类方法.
本文提出的方法与黎曼核稀疏表示方法类似, 首先将SPD流形嵌入到RKHS中.但原黎曼核稀疏表示方法中字典原子的类别信息是预定义, 所以我们在核空间的字典学习过程中嵌入潜在矩阵[28], 提出了核空间潜在稀疏表示分类算法, 灵活地联系核空间中字典原子与类别信息, 增加了核空间中字典的判别性, 并最终实现了SPD流形上样本的分类任务.但由于核空间中样本没有具体的表示形式, 给核空间中潜在字典和潜在向量的学习带来了不便.本文使用Nyström方法[29, 30]得到训练样本在核空间的向量表示, 通过核空间样本的近似表示更新潜在字典和潜在向量.表 1给出了以上方法在SPD流形上的稀疏表示和字典学习的对比.
| Table 1 Comparisons of various methods on sparse representation and dictionary learning on SPD manifold 表 1 各方法在SPD流形上稀疏表示和字典学习的对比 |
本文第1节介绍与我们方法相关的工作:LEM黎曼度量以及Log-Euclidean黎曼核、Nyström方法和潜在矩阵.第2节介绍核空间潜在稀疏表示模型, 并研究核空间的潜在字典和潜在矩阵学习方法.第3节给出各种算法在5个数据集上的实验对比及实验分析.第4节进行总结与展望.
1 相关工作本节将简单介绍LEM黎曼度量以及相关的黎曼核、Nyström方法和潜在矩阵.本文将使用以下的符号:Sn+表示由SPD矩阵所张成的空间(SPD流形), 且每个SPD矩阵的维度是n×n; Sn是由维度为n×n的对称矩阵所张成的空间, 是在单位矩阵In∈Rn×n处的切平面; 核映射φ:Sn+→H表示将SPD流形嵌入到RKHS中.
1.1 黎曼度量和黎曼核在SPD流形上, 较为常用的黎曼度量有AIRM[6, 7, 17, 18]、Stein散度[6, 7, 24-26, 31]、Jeffrey散度[6, 7, 26, 31]和LEM度量[8, 10, 19, 20, 27].其中, LEM度量是一种简洁有效的黎曼度量方法, 对于任意给定的两个SPD矩阵Spi, Spj, 通过LEM度量得到的距离dLEM为
| $ {d_{LEM}}(S{p_i}, S{p_j}) = ||log(S{p_i}) - log(S{p_j})|{|_F} $ | (2) |
公式(2)中的log(·)为矩阵的对数操作, ||·||F为矩阵的F范数.其中, 矩阵的对数操作是将SPD矩阵映射到其所在SPD流形的切空间.
| $ {\varphi _{\log }} = S_n^ + \to {S_n}, Sp \to \log (Sp), {\rm{ }}Sp \in S_n^ + $ | (3) |
由SPD流形的这一几何特性, 在SPD流形上, Log-Euclidean核[8]可以通过切空间中样本的内积来表示.对于任意给定的两个SPD矩阵Spi, Spj:
| $ {{k}_{LogE}}(S{{p}_{i}},S{{p}_{j}})={{\left\langle S{{p}_{i}},S{{p}_{j}} \right\rangle }_{LogE}}=tr(log(S{{p}_{i}})log(S{{p}_{j}})) $ | (4) |
其中, tr表示矩阵的迹.文献[5]证明了Log-Euclidean核满足Mercer定理.
1.2 Nyström方法Nyström方法[29, 30, 32, 33]可通过采样的方式构建一个低秩矩阵, 去近似表示原核矩阵:K∈Rn×n, 降低核矩阵在计算中的运算代价; 同时, 也可以得到核空间中样本的向量表示.
● 首先, 通过采样得到含有m个样本的集合
● 然后, 构建一个低秩矩阵
● 最后, 对采样矩阵进行SVD分解:
| $ {z_n}(x) = \hat D_r^{ - 1/2}\hat V_r^T{(k(x, {\hat x_1}), k(x, {\hat x_2}), ..., k(x, {\hat x_m}))^T} $ | (5) |
其中,
由于本文处理的样本为SPD矩阵, 我们需用公式(4)中Log-Euclidean核来计算核矩阵, 然后用上述介绍的方法得到SPD矩阵的向量表示.
1.3 潜在矩阵基于潜在字典的稀疏表示分类算法[28], 在字典学习的过程学习一个潜在矩阵, 该潜在矩阵描述的是潜在字典中原子与不同类别之间的关系.对于M类样本的分类问题, 字典D=[d1, d2, …, dN], 潜在矩阵W是一个N×M的矩阵:W=[Wr1, Wr2, …, WrN]或W=[Wc1, Wc2, …, WcM].其中, Wri=[Wi, 1, Wi, 2, …, Wi, M]是潜在矩阵W的第i行, 表示字典中第i个原子与M个类样本之间的关系(如图 1所示); Wcj=[W1, j, W2, j, …, WN, j]是潜在矩阵W的第j列, 表示第j类样本与N个字典原子之间的关系(如图 2所示).与共享字典和类别相关字典不同, 潜在字典不需要对字典中原子的类别信息预定义, 而是通过潜在矩阵中的潜在向量去灵活的联系字典中原子和类别之间的关系.通过学习得到的字典具有较小的类内散度, 且属于同类样本的潜在稀疏系数也更加的相似[28].
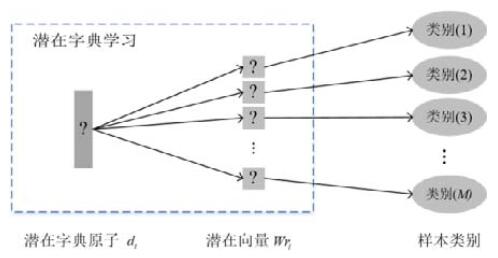
|
Fig. 1 Relationship between the i-th dictionary atom and the sample categories 图 1 第i个字典原子和样本类别之间的关系 |

|
Fig. 2 Relationship between the samples of j_th class and dictionary atoms 图 2 第j类样本和字典原子之间的关系 |
2 基于SPD流形潜在稀疏表示分类算法
本节将介绍基于SPD流形潜在稀疏表示分类算法.首先, 将SPD矩阵映射到RKHS中, 提出了核空间潜在稀疏表示模型及潜在分类模型; 然后, 使用Nyström方法得到SPD矩阵在RKHS中的近似表示来学习核空间中的潜在字典和潜在矩阵.
2.1 核空间潜在稀疏表示模型本小节介绍核空间潜在稀疏表示模型及潜在分类模型.现有M类样本, 测试样本Y∈Sn+和潜在字典:D={d1, d2, …, dN}, di∈Sn+.该字典在核空间中的表示形式可以被写为:ψ(D)=[φ(d1), φ(d2), …, φ(dN)], 潜在矩阵[28]:W∈RN×M.核空间的潜在稀疏表示模型如下:
| $ {\tilde v_j} = \mathop {\arg \min }\limits_{{v_j} \in {R^N}} (||\varphi (Y) - \psi (D)diag(W{c_j}){v_j}||_2^2 + \lambda ||{v_j}|{|_1}) $ | (6) |
| $ Er{r_j} = ||\varphi (Y) - \psi (D)diag(W{c_j}){\tilde v_j}||_2^2 $ | (7) |
通过公式(7), 可以求得测试样本对于每一个类样本的重构误差, 那么我们可以根据重构误差的大小来给测试样本进行分类, 及将测试样本划分到重构误差最小的一类:
| $ identity(Y) = \mathop {\arg \min }\limits_j (Er{r_j}), j = 1, 2, ..., M $ | (8) |
由于核映射φ没有具体的表达形式, 所以公式(6)的第1项和公式(7)都需要利用核技巧改写.其中, 公式(6)中的第1项可以改写为
| $ \left. \begin{array}{l} ||\varphi (Y) - \psi (D)diag(W{c_j}){v_j}||_2^2 = ||\varphi (Y) - \sum\limits_{i = 1}^N {W{c_{j, i}}{v_{j, i}}\varphi ({d_i})} ||_2^2\\ {\rm{ }} = k(Y, Y) - 2v_j^Tdiag(W{c_j})K(Y, D) + v_j^Tdiag(W{c_j})K(D, D)diag(W{c_j}){v_j} \end{array} \right\} $ | (9) |
公式(9)中的K(Y, D)=[k(Y, d1), k(Y, d2), …, k(Y, dN)]T, K=[ki, j]N×N; ki, j=k(di, dj).其中, 经过改写后的公式(6)的优化问题是核化Lasso问题[23, 26, 27, 34], 也可以用CVX工具包[23, 35]进行优化求解.同理, 公式(7)也可以通过利用核技巧改写求得重构误差.由公式(9)可知, 核空间潜在稀疏表示分类方法无须知道核映射φ的具体形式, 只需要知道测试样本与字典原子通过核函数所得到的向量K和字典原子之间通过黎曼核函数得到的核矩阵K, 就可以得到测试样本Y的稀疏系数及对于每一个类样本的重构误差, 然后根据重构误差的大小将测试样本分类.
2.2 核空间潜在字典学习模型核空间的潜在字典和潜在矩阵[28]在我们提出的分类算法中起着至关重要的作用, 但是核映射φ没有明确的形式, 阻碍了核空间中潜在字典和潜在矩阵的更新.为了能够得到核空间的潜在字典和潜在矩阵, 我们使用Nyström方法得到训练样本在核空间的近似表示, 通过样本的近似表示去学习核空间的潜在字典和潜在矩阵[28].
现有M类样本, 训练样本集为:X={X1, X2, …, XM}, 其中, Xj={Xj, 1, Xj, 2, …, Xj, m}为第j类样本的子集, 该子集中的每个样本都是SPD矩阵且样本的个数为m.对于该训练集合, 可以使用第1.2节中的Nyström方法得到训练样本在RKHS中的近似表示:Z(X)=[Z(X1), Z(X2), …, Z(XM)], 其中, Z(Xj)为第j类的m个训练样本集合Xj的核空间近似表示集合.在核空间的潜在字典学习模型中, 需要被学习的有潜在字典:D=[d1, d2, …, dN]和潜在矩阵W= [Wc1, Wc2, …, WcM], 其中, N是字典中原子的个数, W中的第j列Wcj表示核空间中的第j类样本与字典D中原子的关系.稀疏系数矩阵A=[A1, A2, …, AM], 其中, Aj为第j类样本子集的近似表示Z(Xj)在字典D上的稀疏系数矩阵.对于第j类样本, 学习到的字典D和第j类潜在向量Wcj可以很好地表示第j类的训练样本Z(Xj), 即Z(Xj)≌Ddiag(Wcj)Aj.核空间的潜在字典学习模型[28]为
| $ \left. \begin{array}{l} \mathop {\min }\limits_{A, D, {\cal W}} \sum\limits_{j = 1}^M {||Z({X_j}) - Ddiag({\cal W}{c_j}){A_j}||_2^2 + {\lambda _1}||{A_j}|{|_1} + {\lambda _2}||{A_j} - {M_j}||_F^2} + {\lambda _3}\sum\limits_{j = 1}^M {\sum\limits_{l \ne j} {\sum\limits_{n = 1}^N {\sum\limits_{r \ne n} {{\cal W}{c_{j, r}}{{(d_r^T, {d_n})}^2}{\cal W}{c_{l, n}}} } } } \\ {\rm{s}}{\rm{.t}}{\rm{. }}{\cal W}{c_{j, r}} \ge 0, \forall j, r;\sum\nolimits_r {{\cal W}{c_{j, r}}} = \delta , \forall r \end{array} \right\} $ | (10) |
公式(10)里的δ是一个常量, 为了平衡不同类的潜在向量Wcj表达数据的能力.对于不同类的潜在向量, 潜在向量中值的和应该相等, 即
在公式(10)的目标函数中, 需要学习的有潜在字典、潜在向量和训练样本在潜在字典上的稀疏系数.对于该优化问题, 使用ADMM(alternating direction method of multipliers)算法, 首先固定潜在向量, 学习潜在字典和潜在稀疏系数, 公式(10)的潜在字典学习模型可以重新写为
| $ \mathop {\min }\limits_{A, D} \sum\limits_{j = 1}^M {||Z({X_j}) - Ddiag({\cal W}{c_j}){A_j}||_2^2 + {\lambda _1}||{A_j}|{|_1} + {\lambda _2}||{A_j} - {M_j}||_F^2} + {\lambda _3}\sum\limits_{j = 1}^M {\sum\limits_{l \ne j} {\sum\limits_{n = 1}^N {\sum\limits_{r \ne n} {{\cal W}{c_{j, r}}{{(d_r^T, {d_n})}^2}{\cal W}{c_{l, n}}} } } } $ | (11) |
对于该优化问题, 使用ADMM算法对公式(11)中的字典D和稀疏系数A进行迭代更新.当字典D固定时, 逐类求解稀疏系数, 第j类样本稀疏系数的优化问题为
| $ \mathop {\min }\limits_{{A_j}} ||Z({X_j}) - Ddiag({\cal W}{c_j}){A_j}||_2^2 + {\lambda _1}||{A_j}|{|_1} + {\lambda _2}||{A_j} - {M_j}||_F^2 $ | (12) |
公式(12)的优化问题可以像文献[28]中那样使用IPM(iterative projection method)[28, 36]求解.当稀疏系数固定时, 我们重新定义潜在稀疏系数L=[L1, L2, …, LM], 其中, Lj=diag(Wcj)Aj.字典更新模型为
| $ \mathop {\min }\limits_D ||Z(X) - DL||_F^2 + {\rm{ }}{\lambda _3}\sum\limits_{j = 1}^M {\sum\limits_{l \ne j} {\sum\limits_{n = 1}^N {\sum\limits_{r \ne n} {{\cal W}{c_{j, r}}{{(d_r^T, {d_n})}^2}{\cal W}{c_{l, n}}} } } } $ | (13) |
公式(13)是为了更新核空间中的潜在字典D.令Γ=LLT, Λ=Z(X)LT, 若要更新核空间潜在字典D中的第n个原子, 公式(13)可以重写为[28]
| $ \mathop {\min }\limits_{{d_n}} ||{D^T}D\Gamma - 2{D^T}\Lambda ||_F^2 + 2{\lambda _3}\sum\limits_{r \ne n} {{{(d_r^T{d_n})}^2}} \sum\limits_{j = 1}^M {\sum\limits_{l \ne j} {{\cal W}{c_{j, r}}{\cal W}{c_{l, n}}} } $ | (14) |
该问题是一个收敛问题.基于文献[37]提出的字典更新方法, 公式(14)的解为
| $ u={{({{\Gamma }_{n}}{{_{,}}_{n}}I+2{{\lambda }_{3}}{{I}_{Q}})}^{-1}}({{\Lambda }_{n}}-D{{\Gamma }_{n}}-2{{\lambda }_{3}}Q{{D}_{n}}) $ | (15) |
| $ {d_n} = u/||u|{|_2} $ | (16) |
公式(15)中的I为单位矩阵,
对于公式(10)中核空间潜在向量的优化问题[28], 使用ADMM方法, 固定潜在字典和潜在稀疏系数, 更新潜在向量.潜在矩阵中, 每一类的潜在向量都有约束条件, 第j类的潜在向量的约束为
| $ \left. \begin{array}{l} \mathop {\min }\limits_{{\cal W}{c_j}} \sum\limits_{j = 1}^M {||Z({X_j}) - Ddiag({\cal W}{c_j}){A_j}||_2^2 + 2{\lambda _3}\sum\limits_{n = 1}^N {{\cal W}{c_{j, n}}} \sum\nolimits_{r \ne n} {{{(d_r^T, {d_n})}^2}} \sum\limits_{l \ne j}^M {{\cal W}{c_{l, r}}} } \\ {\rm{s}}{\rm{.t}}{\rm{. }}{\cal W}{c_{j, r}} \ge 0, \forall j, r;\sum\nolimits_r {{\cal W}{c_{j, r}}} = \delta , \forall r \end{array} \right\} $ | (17) |
公式(17)是一个受限二次规划问题.令Aj(n)表示稀疏系数矩阵Aj的第n行; B=[B1, B2, …, BN]T, 其中,
| $ \left. \begin{array}{l} \mathop {\min }\limits_{{\cal W}{c_j}} ||a - R{\rm{ }}{\cal W}{c_j}||_F^2 + 2{\lambda _3}{B^T}{\cal W}{c_j}\\ {\rm{s}}{\rm{.t}}{\rm{. }}{\cal W}{c_{j, r}} \ge 0, \forall j, r;\sum\nolimits_r {{\cal W}{c_{j, r}}} = \delta , \forall r \end{array} \right\} $ | (18) |
基于IPM[28, 36]框架, 公式(18)的优化问题可以通过迭代更新求解.其中, 第j类的潜在向量的第t+1次迭代的结果Wcjt+1为[28, 36]
| $ {T_0} = {\cal W}c_j^t - ({R^T}(R{\cal W}c_j^t - a) + {\lambda _3}B)/\sigma $ | (19) |
| $ {{T}_{1}}={{T}_{0}}-{\left( \sum\limits_{n}{{{T}_{0,n}}}-\delta \right)}/{N}\; $ | (20) |
| $ {T_2} = max({T_1}, 0) $ | (21) |
| $ \mathcal{W}c_{j}^{t+1}={{{T}_{2}}}/{\sum\nolimits_{n}{{{T}_{2,n}}}\cdot \delta }\; $ | (22) |
公式(19)中的σ为IPM算法[28, 36]的步长, max为取大操作, 且当T1为负数时, T2=0.公式(22)得到了第t+1次迭代的第j类潜在向量.算法1是核空间潜在字典和潜在矩阵学习的详细步骤.
算法1.核空间潜在字典和潜在矩阵学习.
输入:
● 初始化的潜在矩阵W, 字典学习时的迭代次数;
● 训练样本集X={X1, X2, …, XM}, 其中, Xj={Xj, 1, Xj, 2, …, Xj, m}为第j类样本的子集.
输出:
● 更新后的潜在矩阵;
● 核空间的潜在字典.
1) 使用Nyström方法求得样本在核空间的近似表示;
2) 学习潜在字典(循环至收敛):
使用公式(12)逐类更新稀疏系数;
使用公式(13)更新潜在字典;
3) 使用公式(17)逐类更新潜在矩阵中的潜在向量;
4) 如果公式(10)中目标函数的值足够小或者迭代次数达到, 输出潜在字典和潜在矩阵; 否则返回第2)步.
通过核空间训练样本的近似表示, 我们学习到了核空间的潜在字典和潜在矩阵.在核空间潜在稀疏表示模型中, 核映射φ没有具体的形式, 为了得到解析解, 将公式(6)和公式(7)中带φ的项通过核技巧转换成公式(9)中核内积K(Y, D)和K(D, D)的形式, 以求得对于不同类潜在向量的稀疏系数及重构误差.在我们的方法中, 由于使用核空间的近似表示求得了字典D和潜在矩阵W, 且核空间是高维的线性空间, 所以可用测试样本的近似表示Z(Y)和学习到的字典D的内积去近似的表示公式(9)中的K, 即K(Y, D)≌DTZ(Y), 用学习到的字典D中原子的内积去近似表示公式(9)中的K, 即K(D, D)≌DTD.算法2给出了基于SPD流形潜在稀疏表示分类算法的详细步骤.
算法2.基于SPD流形潜在稀疏表示分类算法.
输入:
● 训练样本集X={X1, X2, …, XM}, 其中, Xj={Xj, 1, Xj, 2, …, Xj, m}为第j类样本的子集;
● 测试样本Y∈Sn+.
输出:测试样本Y∈Sn+的类别.
1) 利用算法1学习核空间的潜在字典和潜在矩阵;
2) 使用公式(6)和公式(9)计算测试样本在不同类潜在向量条件下的稀疏系数;
3) 使用公式(7)和公式(9)计算测试样本对于不同类样本的重构误差;
4) 将样本归为重构误差最小的一类.
3 实验结果与分析为了验证我们的方法的有效性, 我们在5个基准数据集上进行测试, 他们分别应用于纹理识别、病毒细胞识别、材质识别、人脸识别和对象分类.这5个数据集分别是Brodatz纹理数据集[16, 17]、Virus病毒细胞基准数据集[28]、UIUCM基准数据集[38]、YouTube Celebrities(YTC)基准数据集[8]和ETH-80基准数据集[39], 其中, 后两个数据集常被用于基于图像集的分类任务中.在每个数据集上, 我们分别做了10次迭代实验, 取10次实验识别率的平均值和标准差作为最终的结果.
在5个数据集上, 我们与已有的一些在SPD流形上使用稀疏表示的分类算法作对比, 例如Rie_SR+Rie_ DL[17], LE_SR+LE_DL[21]和Ker_DLSR(LogEK)[27].同时, 在这5个数据集上, 我们共同对比了以下几种方法.
(1) Frob_SR+Frob_DL[17]:将SPD矩阵视为欧氏空间的点, 用字典原子的线性组合来重构样本, 并用矩阵的F范数[15]来度量重构样本的误差.
(2) CDL-LDA(covariance discriminant learning)[8]:该方法是通过黎曼核将SPD矩阵映射到核空间, 然后利用LDA(linear discriminant analysis)方法进行学习和分类.
对于Brodatz, Virus和UIUCM这3个数据集, 我们还与文献[40]中给出的3种纹理识别的方法做对比, 它们分别是:
1) COV-SVM:该方法将对象建模成SPD矩阵, 并用SVM分类器进行分类.
2) Gau-SVM:该方法将对象建模成高斯模型, 并用SVM分类器进行分类.
3) RoG-SVM:RoG是文献[40]提出一种样本描述模型, 该方法将样本建模成RoG模型[40], 并用SVM分类器进行分类.
对于上述的SVM方法, 我们使用LIBSVM工具包[41]实现“one vs all”分类器, 该工具包中的参数“-c -p”与文献[40]中一致, 分别设为4和10-5, 其余参数保持工具包种的默认设置.
对于YTC和ETH-80这两个图像集的数据集, 我们与一些经典的基于图像集的分类算法进行对比, 它们是:
1) PML(projection metric learning)[42]:该算法首先将图像集建模为Grassmann流形上的点, 然后通过学习得到一个正交的投影矩阵, 使得投影空间的样本具有较大的类间散度和较小的类内散度.
2) GDA(Grassmann discriminant analysis)[43]:该算法与PML一样首先将图像集建模为Grassmann流形上的点, 然后将Grassmann流形嵌入到一个高维的希尔伯特空间, 再通过Fisher判别准则去学习一个映射, 从而使得原始的流形被映射到一个维度较低同时鉴别性更好的空间.
3) SPDML(SPD manifold leaning)[6, 7]:该方法首先将样本建模为SPD矩阵, 然后通过学习得到一个投影矩阵, 使得原始的SPD流形被投影到一个维度更低且更具有判别性的空间.
如第2.1节所述, 潜在矩阵W=[Wr1, Wr2, …, WrN], 潜在向量Wri表示第i个字典原子与样本类别之间的关系.在潜在字典的初始化过程中, 我们通过直接从训练样本中抽取样本作为字典的原子, 假设潜在向量中只有一个非0元素(例如等于1)来初始化潜在向量Wri, 若Wri, j=1, 那么字典中的第i个原子应用第j类样本中随机抽取来初始化潜在字典.在所有的实验中, 通过交叉验证来确定公式(10)中的λ1, λ2和λ3的值.由于本文的实验和文献[27]的方法都是基于Log-Euclidean黎曼核, 为了实验数据具有公正性, 本文给出的这两个方法的实验数据, 都是基于LEM度量的指数核[27]所得出的实验结果.根据文献[33]中的描述, Nyström方法的算法复杂度为O(rmn), 这里的r为矩阵的秩, m为采样样本的数量.潜在字典学习和潜在向量的复杂度为O(jn2), j为字典学习时的迭代次数; 潜在稀疏表示模型的算法复杂度为O(n2), 因此, 算法的整体复杂度为O((j+1)n2).
3.1 图像分类Brodatz是一个纹理数据库[16, 17], 在该数据集中包含112张纹理图片, 选择前20张纹理图片作为该实验的样本集.在实验中, 将每张图片的尺寸调整为500x500, 并将每张图片分成大小相等的25个方块, 每个块的尺寸为100x100, 其中每张图片中, 任意选择10块用作训练样本, 剩下的15块用做测试样本.为了使得每个块可以用协方差描述表示, 对块中的每个像素点的提取一个5维的特征描述.
| $ {F_{Brodatz}}(x, y) = [x, y, I, abs({I_x}), abs({I_y})] $ | (23) |
公式(23)中, 前2维的特征是该像素点在该图片块中的横、纵坐标, 后面3维的特征分别是该像素点的灰度值、x轴和y轴方向的梯度.最后, 每个图像块被描述为一个5×5的协方差矩阵.在该数据集上, 通过交叉验证得: λ1=0.05, λ2=0.5和λ3=0.05.表 2给出了各个算法在Brodatz数据集上的平均结果.
| Table 2 Average results of algorithms on Brodatz, Virus and UIUCM datasets 表 2 各算法在Brodatz, Virus和UIUCM数据集上的平均结果 |
Virus病毒数据集[33]包含15个类别的病毒细胞图片, 每个类别包含100张图片, 每张图片的尺寸为41x41, 共1 500张图片.在每一类样本中, 我们将100张样本随机分成10份, 从每份中随机选择8张图片作为训练样本, 剩下的2张作为测试样本.为了可以使用协方差矩阵描述图片样本, 我们用Gabor滤波[23, 27]为每个像素点提取特征值.
| $ {F_{Virus}}(x, y) = [{G_{0, 0}}(x, y), \ldots , {G_{0, 7}}(x, y), \ldots , {G_{4, 7}}(x, y)] $ | (24) |
公式(24)为每个像素点提取了40维(5尺度, 8方向)的特征值, 最后得到的协方差矩阵的维度是40x40.在该数据集上, 通过交叉验证得:λ1=0.05, λ2=0.01和λ3=0.01.表 2给出了各个算法在Virus数据集上的平均结果.
UIUCM数据集包含18个类别的材质图片, 每个类包含12张样本图片, 每张图片的尺寸大小不唯一.在每类样本中, 我们随机抽取6张样本用于训练, 剩余的6张样本用测试.为了使得每个样本可以用协方差描述表示, 先将彩色图片转换为灰度图, 对其中每个像素点提取45维的特征描述.
| $ {F_{UIUCM}}(x, y) = [x, y, I, abs({I_x}), abs({I_y}), {G_{0, 0}}(x, y), \ldots , {G_{0, 7}}(x, y), \ldots , {G_{4, 7}}(x, y)] $ | (25) |
公式(25)中的特征为公式(23)和公式(24)特征的组合, 最后得到的协防差矩阵维度为45x45.在该数据集上, 通过交叉验证得:λ1=0.005, λ2=0.5和λ3=0.5.表 2给出了各种算法在UIUCM数据集上的平均结果.
3.2 图像集分类相比于单幅图像, 图像集包含了更多的有效信息, 例如光照、姿态和遮挡等.最近, 基于图像集的分类问题在计算机视觉和模式识别领域获得了广泛的关注.所以, 为了验证我们方法的泛化性, 本文也将我们的方法应用于图像集的分类任务, 分别在ETH-80和YTC两个数据集上与一些经典的基于图像集的分类算法作对比.
ETH-80数据集[36]中含有8个类别, 每个类别有10个图像集, 每个图像集中有41张从不同角度拍摄的照片.我们把每个图片的尺寸调整为20x20, 并且在每一类图像集中, 任意选5个图像集用作训练, 剩下的用作测试.在该数据集上, 通过交叉验证得:λ1=0.05, λ2=0.001和λ3=0.001.表 3为各算法在ETH-80上的平均结果.
| Table 3 Average results of algorithms on ETH-80 dataset 表 3 各算法在ETH-80数据集上的平均结果 |
YouTube Celebrities(YTC)数据集[8]包含47个类, 由于每一类的对象所包含的图像集的个数不一样, 所以我们从每一类图像中随机抽取图像制作成9个图像集, 任选3个图像集作训练, 剩下的6个图像集用作测试, 图像集中每个图片的尺寸调整为20x20.在该数据集上, 通过交叉验证得:λ1=0.05, λ2=0.05和λ3=0.005.表 4为各算法在YTC上的平均结果.
| Table 4 Average results of algorithms on YTC dataset 表 4 各算法在YTC数据集上的平均结果 |
3.3 实验分析
上述表中的实验结果通过我们在每个数据集上经过10次迭代实验获得, 其中, 有个别稀疏表示方法中的字典原子是从样本中随机抽取得到的, 而不是通过学习得到, 我们称这种字典为Random_DL.通过所得10次实验结果的均值和标准差作为最终的结果, 从这3个表中的数据来看, 在5个基准数据集上, 我们提出的方法在分类正确率上都是最好的.在已有的将稀疏表示应用于SPD流行上样本的分类算法中, 方法LE_SR+LE_DL[21]和Ker_SR+Random_DL[27]也可以获得相对较好的效果.这两种方法都不是直接在SPD流形上进行分类的任务, 而是通过映射函数分别将SPD流形嵌入到切空间和核空间中, 然后再进行稀疏表示和样本分类.文献[37]中的3种方法——COV-SVM, Gau-SVM和RoG-SVM之间的识别率的差距并不大, 但由于Gau-SVM方法在对样本建模时考虑了平均值信息, 所以Gau-SVM的识别率要比COV-SVM高出一点.方法RoG-SVM在对样本建模时使用了更加鲁棒的描述方法, 所以RoG-SVM的识别率要比Gau-SVM高出一点.综上, 在这3个方法中, 方法RoG- SVM可以得到较高的识别率.在表 2的实验数据中, 确实是RoG-SVM的识别率高于Gau-SVM, Gau-SVM的识别率高于COV-SVM.在Brodatz数据集上, 除了方法Ker_SR+Random_DL以外[27], 我们的方法的优势非常明显, 识别率可以达到90.22%, 同时具有最小的标准差1.07.这说明在该数据集上, 我们的方法不仅具有较好的识别效果, 还具有很强的鲁棒性.在Virus数据集上, 我们的方法具有最高的识别率62.67%, 但是我们的方法的标准差并不是最小的, 但7.83的标准差在所有的方法中也是相对较小的, 说明我们的方法在该数据上的鲁棒性仍然可以得到保证.在UIUCM数据集, 所有方法的识别率普遍偏低, 但是我们的方法获得了最好的识别率, 且标准差较小.在ETH-80数据集上, 我们的方法标准差为3.75, 仅次于PML[38].但是我们方法的识别率为96.00%, 远高于PML的90.00%.其中, 方法LE_SR+LE_DL[21]和Ker_SR+Random_DL[27]的识别率和标准差都仅次于我们的方法.在YTC数据集上, 除了方法Ker_SR+Random_DL[27]和Ker_SR+Random_DL[27], 我们的方法的优势非常明显, 识别率可以达到78.12%, 同时具有最小的标准差2.56.综上, 我们的方法在5个数据集上具有最好的识别率以及相对较好的鲁棒性.
4 总结与展望用SPD矩阵描述图像或者图像集具有较强的鲁棒性, 且由SPD矩阵所张成的SPD流形是一个非线性的黎曼空间.本文充分考虑SPD流形的黎曼度量和几何性质, 提出了基于SPD流形潜在稀疏表示分类算法.首先, 将SPD流形嵌入到核空间, 且在核空间字典学习过程中学习一个潜在矩阵, 灵活联系核空间中字典原子和类别之间的信息, 提出了核空间潜在稀疏表示分类模型.但核空间的样本没有明确的形式, 给核空间的字典的更新带来了不便, 我们使用Nyström方法获得核空间训练样本的向量表示去学习更新核空间的潜在字典和潜在矩阵.至此, 我们将欧氏空间分类算法与黎曼流形结合起来, 实现SPD流形上样本的分类任务.接下来, 如何在SPD流形上更新字典, 将是我们下一步的研究重点.
| [1] |
Wright J, Yang AY, Ganesh A, Sastry SS, Ma Y. Robust face recognition via sparse representation. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227.
[doi:10.1109/TPAMI.2008.79] |
| [2] |
Zhang L, Yang M, Feng X. Sparse representation or collaborative representation:Which helps face recognition? In:Proc. of the 2011 IEEE Int'l Conf. on Computer Vision (ICCV). IEEE, 2011, 471-478.
[doi:10.1109/ICCV.2011.6126277] |
| [3] |
Yang M, Zhang L. Gabor feature based sparse representation for face recognition with Gabor occlusion dictionary. In:Proc. of the European Conf. on Computer Vision. Berlin, Heidelberg:Springer-Verlag, 2010, 448-461.
[doi:10.1007/978-3-642-15567-3_33] |
| [4] |
Chen Z, Wu XJ, Yin HF, Kittler J. Robust low-rank recovery with a distance-measure structure for face recognition. In:Proc. of the Pacific Rim Int'l Conf. on Artificial Intelligence. Cham:Springer-Verlag, 2018, 464-472.
[doi:10.1007/978-3-319-97310-4_53] |
| [5] |
Aharon M, Elad M, Bruckstein A. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Trans. on Signal Processing, 2006, 54(11): 4311-4322.
[doi:10.1109/TSP.2006.881199] |
| [6] |
Harandi MT, Salzmann M, Hartley R. From manifold to manifold:Geometry-aware dimensionality reduction for SPD matrices. In:Proc. of the European Conf. on Computer Vision. Cham:Springer-Verlag, 2014, 17-32.
[doi:10.1007/978-3-319-10605-2_2] |
| [7] |
Harandi M, Salzmann M, Hartley R. Dimensionality reduction on SPD manifolds:The emergence of geometry-aware methods. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2018, 40(1): 48-62.
[doi:10.1109/TPAMI.2017.2655048] |
| [8] |
Wang R, Guo H, Davis LS, Dai Q. Covariance discriminative learning:A natural and efficient approach to image set classification. In:Proc. of the 2012 IEEE Conf. on Computer Vision and Pattern Recognition (CVPR). IEEE, 2012, 2496-2503.
[doi:10.1109/CVPR.2012.6247965] |
| [9] |
Feng F, Wu XJ, Xu T. Object tracking with kernel correlation filters based on mean shift. In:Proc. of the 2017 Int'l Smart Cities Conf. (ISC2). IEEE, 2017, 1-7.
[doi:10.1109/ISC2.2017.8090863] |
| [10] |
Ren J, Wu X. Sparse coding for symmetric positive definite matrices with application to image set classification. In:Proc. of the Int'l Conf. on Intelligent Science and Big Data Engineering. Cham:Springer-Verlag, 2015, 637-646.
[doi:10.1007/978-3-319-23989-7_64] |
| [11] |
Sivalingam R, Boley D, Morellas V, Papanikolopoulos N. Tensor sparse coding for region covariances. In:Proc. of the European Conf. on Computer Vision. Berlin, Heidelberg:Springer-Verlag, 2010, 722-735.
[doi:10.1007/978-3-642-15561-1_52] |
| [12] |
Sivalingam R, Boley D, Morellas V, Papanikolopoulos N. Tensor sparse coding for positive definite matrices. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2014, 36(3): 592-605.
[doi:10.1109/TPAMI.2013.143] |
| [13] |
Sivalingam R, Boley D, Morellas V, Papanikolopoulos N. Positive definite dictionary learning for region covariances. In:Proc. of the 2011 IEEE Int'l Conf. on Computer Vision (ICCV). IEEE, 2011, 1013-1019.
[doi:10.1109/ICCV.2011.6126346] |
| [14] |
Sivalingam R, Boley D, Morellas V, Papanikolopoulos N. Tensor dictionary learning for positive definite matrices. IEEE Trans. on Image Processing, 2015, 24(11): 4592-4601.
[doi:10.1109/TIP.2015.2440766] |
| [15] |
Sra S, Cherian A. Generalized dictionary learning for symmetric positive definite matrices with application to nearest neighbor retrieval. In:Proc. of the Machine Learning and Knowledge Discovery in Databases., 2011, 318-332.
[doi:10.1007/978-3-642-23808-6_21] |
| [16] |
Cherian A, Sra S. Riemannian sparse coding for positive definite matrices. In:Proc. of the European Conf. on Computer Vision. Cham:Springer-Verlag, 2014, 299-314.
[doi:10.1007/978-3-319-10578-9_20] |
| [17] |
Cherian A, Sra S. Riemannian dictionary learning and sparse coding for positive definite matrices. IEEE Trans. on Neural Networks and Learning Systems, 2017, 28(12): 2859-2871.
[doi:10.1109/TNNLS.2016.2601307] |
| [18] |
Pennec X, Fillard P, Ayache N. A Riemannian framework for tensor computing. Int'l Journal of Computer Vision, 2006, 66(1): 41-66.
[doi:10.1007/s11263-005-3222-z] |
| [19] |
Quang MH, San Biagio M, Murino V. Log-Hilbert-Schmidt metric between positive definite operators on Hilbert spaces. In:Proc. of the Advances in Neural Information Processing Systems., 2014, 388-396.
https://www.researchgate.net/publication/271834194_Log-Hilbert-Schmidt_metric_between_positive_definite_operators_on_Hilbert_spaces |
| [20] |
Faraki M, Harandi MT, Porikli F. Image set classification by symmetric positive semi-definite matrices. In:Proc. of the 2016 IEEE Winter Conf. on Applications of Computer Vision (WACV). IEEE, 2016, 1-8.
[doi:10.1109/WACV.2016.7477621] |
| [21] |
Guo K, Ishwar P, Konrad J. Action recognition using sparse representation on covariance manifolds of optical flow. In:Proc. of the 20107th IEEE Int'l Conf. on Advanced Video and Signal Based Surveillance (AVSS). IEEE, 2010, 188-195.
[doi:10.1109/AVSS.2010.71] |
| [22] |
Arsigny V, Fillard P, Pennec X, et al. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magnetic Resonance in Medicine, 2006, 56(2): 411-421.
[doi:10.1002/mrm.20965] |
| [23] |
Harandi MT, Sanderson C, Hartley R, et al. Sparse coding and dictionary learning for symmetric positive definite matrices:A kernel approach. In:Proc. of the Computer Vision (ECCV 2012). Berlin, Heidelberg:Springer-Verlag, 2012, 216-229.
[doi:10.1007/978-3-642-33709-3_16] |
| [24] |
Sra S. Positive definite matrices and the S-divergence. Proc. of the American Mathematical Society, 2016, 144(7): 2787-2797.
[doi:10.1090/proc/12953] |
| [25] |
Cichocki A, Cruces S, Amari S. Log-determinant divergences revisited:Alpha-beta and gamma log-det divergences. Entropy, 2015, 17(5): 2988-3034.
[doi:10.3390/e17052988] |
| [26] |
Harandi MT, Hartley R, Lovell B, Sanderson C. Sparse coding on symmetric positive definite manifolds using Bregman divergences. IEEE Trans. on Neural Networks and Learning Systems, 2016, 27(6): 1294-1306.
[doi:10.1109/TNNLS.2014.2387383] |
| [27] |
Li P, Wang Q, Zuo W, Zhang L. Log-Euclidean kernels for sparse representation and dictionary learning. In:Proc. of the IEEE Int'l Conf. on Computer Vision., 2013, 1601-1608.
[doi:10.1109/ICCV.2013.202] |
| [28] |
Yang M, Dai D, Shen L, et al. Latent dictionary learning for sparse representation based classification. In:Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition., 2014, 4138-4145.
[doi:10.1109/CVPR.2014.527] |
| [29] |
Ren JY, Wu XJ. Vectorial approximations of infinite-dimensional covariance descriptors for image classification. Computational Visual Media, 2017, 3(4): 379-385.
[doi:10.1007/s41095-017-0094-4] |
| [30] |
Faraki M, Harandi MT, Porikli F. Approximate infinite-dimensional region covariance descriptors for image classification. In:Proc. of the 2015 IEEE Int'l Conf. on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2015, 1364-1368.
[doi:10.1109/ICASSP.2015.7178193] |
| [31] |
Harandi M, Salzmann M. Riemannian coding and dictionary learning:Kernels to the rescue. In:Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition., 2015, 3926-3935.
[doi:10.1109/CVPR.2015.7299018] |
| [32] |
Yang T, Li Y F, Mahdavi M, Jin R, Zhou ZH. Nyström method vs random Fourier features:A theoretical and empirical comparison. In:Proc. of the Advances in Neural Information Processing Systems., 2012, 476-484.
http://dl.acm.org/citation.cfm?id=2999188 |
| [33] |
Kumar S, Mohri M, Talwalkar A. Sampling methods for the Nyström method. The Journal of Machine Learning Research, 2012, 13(1): 981-1006.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1080/10618600.2014.995799 |
| [34] |
Elad M. Sparse and redundant representation modeling-What next?. IEEE Signal Processing Letters, 2012, 19(12): 922-928.
[doi:10.1109/LSP.2012.2224655] |
| [35] | |
| [36] |
Rosasco L, Verri A, Santoro M, et al. Iterative projection methods for structured sparsity regularization. Technical Report, MIT-CSAIL-TR-2009-050CBCL-282, 2009.
http://hdl.handle.net/1721.1/49428 |
| [37] |
Mairal J, Bach F, Ponce J, et al. Online learning for matrix factorization and sparse coding. Journal of Machine Learning Research, 2010, 11(1): 19-60.
[doi:10.1145/1756006.1756008] |
| [38] |
Liao Z, Rock J, Wang Y, Forsyth D. Non-parametric filtering for geometric detail extraction and material representation. In:Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition., 2013, 963-970.
[doi:10.1109/CVPR.2013.129] |
| [39] |
Huang Z, Wang R, Shan S, Li X, Chen X. Log-Euclidean metric learning on symmetric positive definite manifold with application to image set classification. In:Proc. of the Int'l Conf. on Machine Learning., 2015, 720-729.
http://jmlr.csail.mit.edu/proceedings/papers/v37/huanga15.html |
| [40] |
Wang Q, Li P, Zuo W, Zhang L. RAID-G:Robust estimation of approximate infinite dimensional Gaussian with application to material recognition. In:Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition., 2016, 4433-4441.
[doi:10.1109/CVPR.2016.480] |
| [41] |
Chang CC, Lin CJ. LIBSVM:A library for support vector machines. ACM Trans. on Intelligent Systems and Technology (TIST), 2011, 2(3): 1-27.
[doi:10.1145/1961189.1961199] |
| [42] |
Huang Z, Wang R, Shan S, Chen X. Projection metric learning on Grassmann manifold with application to video based face recognition. In:Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition., 2015, 140-149.
[doi:10.1109/CVPR.2015.7298609] |
| [43] |
Hamm J, Lee DD. Grassmann discriminant analysis:A unifying view on subspace-based learning. In:Proc. of the 25th Int'l Conf. on Machine Learning. ACM, 2008, 376-383.
[doi:10.1145/1390156.1390204] |
 2020, Vol. 31
2020, Vol. 31


