受益于地图服务和移动终端的普及和发展, 游客在规划旅游路线时不仅将路径长度作为考量, 同时会综合考虑其他方面的因素[1-5].其中, 路径长度、路径开销和路径所覆盖兴趣点是游客普遍关注的3个最优路径选择因素[4].关键词覆盖最优路径查询(keyword-aware optimal route query, 简称KOR)[4, 5]就是综合考虑这些因素规划路线的一类查询, KOR可以描述为:游客希望从某个给定出发点开始, 寻找一条可以包含所有计划去的兴趣点(如名胜古迹、娱乐美食), 最终到达指定目的地的最优路线.同时, 这一最优路线应当满足游客的行程预算, 并且在总开销上越少越好.
KOR本身是一个NP-hard问题[4], 查询时间随关键词个数呈指数型增长.现有查询算法[4-7]的思路都是寻求近似最优解.其中, OSScalling算法[4]提供了一套高效的算法框架.该框架把地图顶点与路径抽象成路网图, 在预处理阶段, 通过Floyd算法[8]得到每对顶点间的代价值和目标值数组, 用以查询过程中判别剪枝和拓展路径; 在路径拓展阶段, 利用路径标签在拓展路径的同时剪除不满足阈值的中间结果以加快拓展, 从可行解中选择目标值最小的路径作为最优解.
随着路网图规模的不断扩大, 越来越多的兴趣点也被添加到路网图中[9, 10].截至2006年, 西欧地区路网图已拥有18M个顶点[11].现有算法的预处理数组占用内存随顶点数量增加呈多项式级别增长.在顶点数量为1K时, 内存占用约为20M;但当顶点数量达到10M时, 内存占用为2PB.这显然是大多数设备无法承受的.在路网图局部更新后, 现有算法预处理必须全局更新数组, 而大多数顶点间最小目标(代价)值的计算并不会受到新加入的顶点的影响, 因此, 更新过程会产生大量无用的计算.此外, 在每轮路径拓展中, 会有更多的待拓展顶点加入拓展中, 严重影响了查询速度.
针对以上问题, 本文提出一种大规模路网图下关键词覆盖最优路径查询算法KORL(keyword-aware optimal route on large-scale road networks), 分别从预处理存储方法和路径拓展策略上对现有算法进行改进.对于预处理中现有算法保存大规模路网图信息时占用海量内存的问题, 本文采用分治思想, 将路网图进行分割, 并构建相应的树形索引结构, 仅保存子图内路径和子图之间路径的信息, 将预处理空间复杂度由O(n2)降低至O(n), 极大节省了内存.对于路径拓展中存在大量无效拓展(拓展后路径代价超出阈值, 从而路径被剪枝)的问题, 本文通过对路网图结构的分析, 发现从某一顶点到另一不同子图顶点必然经过两子图间的关联路径.基于此, 提出最小代价剪枝策略.该策略利用最小中间路径代价值来快速剪枝所有完整路径, 快速筛除大量无效待拓展顶点.
本文的创新点总结如下:
(1) 本文提出了分治存储的预处理方法.采用PUNCH算法[12]划分路网图, 根据划分构建树形索引结构, 在树形索引的叶节点上保存子图内部顶点间的信息, 在根节点上保存各子图边界点间的信息, 极大地减少预处理的内存占用.
(2) 本文提出了一种快速筛除无效待拓展顶点的策略——最小代价剪枝策略.在路径拓展前, 首先计算有效待拓展子图(与拓展顶点所在子图间最小代价值不超过剩余代价阈值的子图), 若待拓展顶点不属于有效待拓展子图, 则不予拓展, 避免大量无效拓展.
(3) 本文综合运用最小代价剪枝、近似支配剪枝、全局优先拓展和关键词顶点拓展等策略, 加快了查询速度.
本文第1节介绍KOR相关研究.第2节介绍KOR的形式化定义与查询算法框架.第3节给出大规模路网图下关键词覆盖最优路径查询算法KORL.第4节通过实验验证KORL算法良好的可扩展性.第5节总结全文.
1 相关工作目前, 多约束最优路径查询问题已得到广泛关注[4-7, 13-16], KOR[4-7]是典型的一类多约束最优路径查询问题.在求解多约束最优路径查询问题时, 关键是如何处理多约束之间的关系.Li等人[13]通过平衡路径代价与长度所得的得分函数来寻找最优路径, 但KOR旨在寻求一定代价阈值下目标最小的路径, 不能简单使用得分函数来实现.张金增等人[14]利用区域子网划分技术和贪婪算法实现了路网环境下访问序列受限的多标签最优路径查询, 但贪婪策略返回结果无法保证精度, 无法适用于KOR.鲍金玲等人[15]提出一种支持约束关系的高效的行程规划算法, 其问题定义中路网图中的顶点具有游览代价和游览分数, 边具有游览代价.由于问题定义与KOR不同, 因此不适用于KOR.在此基础上, 他们解决多约束的方法是认为顶点的目标值与代价值存在正比关系[16], 通过降低约束维度来加快查询速度, 而在现实中无法准确找到这种比例关系, 因此不适用于KOR.
Cao等人[4]定义了KOR并给出了3个求解算法:OSScalling、BucketBound和Greedy.金鹏飞等人[6]提出KSRG算法, 在OSScalling算法基础上加入关键词顶点拓展策略, 并在后续工作[7]中引入Skyline路径集合, 将路径拓展剪枝过程放在预处理中进行, 进一步加快查询速度.这些算法求解过程中都需要产生大量拓展操作, 而拓展操作的本质就是更新拓展路径的目标值、代价值(下文统称权值).为了避免在路径拓展阶段产生大量这样的计算而影响查询速度, 需要预先将所有路径的权值计算并保存以便调用.
在预处理阶段, OSScalling是通过Floyd算法计算路网图每对顶点间的最小权值并保存在数组中, 但该方法空间复杂度为O(n2).在大规模路网下, 大多数设备都无法承受这样急剧膨胀的内存开销.此外, 在路网图局部更新时, 该方法必须对数组进行全局更新, 造成大量时空开销.由于现有其他研究都是对路径拓展阶段进行改进, 并未解决甚至加重(需要在预处理中生成所有顶点间skyline路径集合)预处理时空开销, 因此本文采用一种分治存储的方法, 将路网划分后仅保存子图内路径和子图之间路径的权值, 极大减少了内存开销.
为了实现分治存储, 本文采用划分路网图的方法以分块保存, 因此需要选择合适的路网图划分算法.常见的划分算法有METIS[17]、DiBaP[18]和PUNCH[12]等.METIS和DiBaP虽然能将路网图划分成大小平均的区域, 但METIS丢失了很多密集区域顶点间的联系, DiBaP划分路网图需要切割大量的边.PUNCH算法仅切割了自然连接处少量的边, 较好地保存了路网图的整体结构, 更适合用于路网图划分.
在路径拓展方面, OSScalling为后续研究提供了一套算法框架.BucketBound在此基础上优化了拓展顺序. Greedy采用贪婪策略, 精度无法保证.KSRG引入近似支配剪枝、关键词顶点拓展等策略, 但这些算法均未解决拓展是否有效必须经过完整拓展后才能判别的问题.因此, 本文在综合运用除Greedy外所有改进策略的基础上, 提出最小代价剪枝, 仅通过局部拓展结果判别拓展是否有效, 极大加快了拓展速度.
2 KORKOR的本质是三重约束下的路径拓展问题.约束条件分别为关键词全覆盖最优路径必须覆盖所有关键词、满足代价阈值(最优路径总代价不超过代价阈值)和目标最优化(最优路径为所有满足前两个约束下的目标值最优的路径).
本节给出KOR的形式化定义(第2.1节)并介绍KOR查询算法框架(第2.2节), 作为后续讨论的基础.
2.1 问题定义KOR查询使用的路网图G由实际地图的顶点和边抽象所得, 如图 1所示.为方便筛出包含特定关键词的顶点, 根据路网图中的关键词与顶点的对应关系构建出关键词倒排列表, 如图 2所示.

|
Fig. 1 Road network structure 图 1 路网图结构 |

|
Fig. 2 Keyword inverted list 图 2 关键词倒排列表 |
定义 1(路网图). G(V, E)由一个无向路网图的顶点集V和边集E构成, 其中, 任意顶点v∈V表示路网图中的一个兴趣点.兴趣点的本质是一个空间文本对象, 既包含空间经纬度, 表示为v.loc; 又包含对该兴趣点的文本描述关键词集合<v.kw1, v.kw2, …>, 表示为v.ψ.任意边e∈E表示两个邻接顶点vi, vj之间的路径, 记为(vi, vj).每条边包含两个属性值:目标值OS和代价值BS.对于一条边e, 目标值表示其路径费用OS(e), 在图中表示为括号外的数值; 代价值表示其路径长度, 记为BS(e), 在图中表示为括号内的数值.
定义 2(路径).路径p=(v0, v1, v2, …, vn)表示由v0出发, 顺序经过v1, v2, …直到vn的一条路径.对于该路径, 目标值
定义 3(KOR).在给定路网图G下, KOR查询可表示为Q=(vs, vt, ψ, Δ), 其中, vs表示查询起点, vt表示查询终点, ψ是关键词集合, Δ是代价值阈值.假定Ps, t表示从vs到vt的所有路径的集合, 满足关键词覆盖和代价阈值的路径集合为
OSScalling算法是一个高效的KOR查询算法, 被后续研究沿用为算法框架.该算法为加快拓展速度, 在预处理时计算所有顶点间的权值并保存在内存中, 方便拓展时大量相加运算的快速调用.为更好地表示路径拓展中间结果并实现拓展操作, 该算法设计了一种数据结构:路径标签, 将路径拓展转化为标签内关键词集合的并运算和权值的相加运算.为减少无效拓展, 在拓展时进行代价阈值剪枝(当前路径代价值超过代价阈值)、可行解目标值剪枝(当前路径目标值超过当前最优可行解的目标值)和支配剪枝.为将问题时间复杂度限制在多项式级别, 采用目标修正策略剪去很多目标值相近的路径.为快速拓展出可行解, 该算法在每轮拓展时首先计算所有待拓展顶点的优先级, 然后选择其中最有可能成为可行解的路径拓展下去, 既避免了盲目拓展, 又加快了拓展速度.该算法步骤如下.
● 预处理阶段
(1) 修正路网图中各边目标值[19].
(2) 通过Floyd算法[8]计算路网图每对顶点间权值数组.
● 路径拓展阶段
(1) 为图中每个顶点维护一个标签列表存放该顶点上的标签, 维护一个全局队列用来存放待拓展的路径标签.在起点建立一个路径标签, 加入队列;
(2) 开始循环拓展.取出队列中局部优先度最高的标签, 计算该标签所有邻边待拓展顶点中优先级最高的顶点, 并拓展至该顶点, 生成新标签.判别新标签是否满足剪枝条件, 若满足, 则用该标签剪枝该顶点上与其起点相同的标签;
(3) 循环拓展直至某一标签已覆盖所有关键词, 直接拓展至终点并判别是否满足剪枝条件, 若满足, 则保留为可行解并更新可行解目标值.重复此过程, 直到循环结束.
定义 4(路径标签).对每条从vs到vi的路径pik, 在vi处构建一个路径标签
定义 5(标签操作).当顶点vi向另一个顶点vj拓展时, 会根据Lik和两顶点间路径的OS, BS创建一个新的标签Ljl, 其属性如下.
(1)
(2)
(3)
(4)
定义 6(局部优先度).假设Lik, Ljl是路径标签, 则两者的局部优先度可以定义为:(1)若两者中有一个标签已经拓展到终点, 则优先度更高, 即
定义 7(支配).若两条起终点相同的路径p1, p2满足
支配剪枝策略通过剪除被支配的路径以避免大量无效后续拓展.为进一步提高查询速度, 采用完全多项式时间近似策略(fully polynomial-time approximation scheme)[20, 21]对目标值相近的路径进行目标修正后, 结合支配剪枝策略, 进一步减少中间路径的数量.
定义 8(目标修正).给定代价阈值Δ, 图边最小代价值bmin, 最小目标值omin, 最大目标值omax和介于(0, 1)的参数ε, 修正比例
定理 1.使用目标修正策略所得最优解与实际最优解在一定误差范围内:
大规模路网图下, 现有KOR查询算法会遇到两个问题:预处理内存开销过大、无效拓展路径过多.本文对其改进之处分别体现在预处理和路径拓展两个方面:改进预处理的关键问题是如何节省内存开销, 改进拓展策略的关键问题是如何进一步剔除无效路径.
3.1 改进思路现有算法无法解决大规模路网下KOR的根本原因是预处理索引结构不具有良好的可扩展性, 其预处理采用单一数组保存所有顶点间权值, 而数组大小会随顶点数增加呈多项式级别增长.大规模路网下, 大多数机器无法承受该索引所需内存开销.因此, 解决该问题的重点在于选择合适的索引结构, 大幅减少内存占用且不丢失路网信息.
减少数组内存占用, 必然要压缩路网信息, 需要保证信息的可恢复性.这实质上是一个无损压缩问题.该问题的关键是确定可丢弃数据及其还原策略.我们注意到:计算大部分顶点间的权值需经过很多顶点, 造成大量时间开销, 保存这些顶点间权值又造成大量空间开销.这提示我们:把路网图划分成顶点数较少、相对更集中的子图, 并将各子图间之间的关联关系体现在一张关联图中.在预处理阶段划分路网图, 仅保存各子图和关联图的信息, 丢弃大量不同子图顶点间权值信息, 从而大幅减少内存占用; 在路径拓展时, 如果需要不同子图内顶点间权值信息, 可以通过组合各子图与关联图上的路径实现复原.
因为预处理过程策略导致路径拓展时需要不断地做还原计算, 所以查询算法必须避免大量的拓展操作产生.避免拓展主要体现在加强剪枝能力、优化拓展顺序和筛除无效待拓展顶点.在剪枝能力方面, 我们采用近似支配策略剔除同源同终的目标值相近路径; 在拓展顺序方面, 我们优先选择导致目标值最小的待拓展顶点拓展; 在筛除无效拓展顶点方面, 我们仅向尚未覆盖的关键词对应的顶点拓展, 同时, 为了解决拓展顶点与待拓展顶点间存在多条拓展路径的问题, 在预处理时计算顶点间的精简skyline路径集合, 在拓展时仅沿这些路径拓展.
关键词顶点拓展策略还会导致一种现象:在向所有包含未拓展关键词的待拓展顶点拓展时, 大部分路径都因不满足代价阈值剪枝条件而被剔除.在大规模路网下, 关键词对应顶点个数也会大幅增加, 这种现象更加明显.导致该现象的根本原因是:所有路径只有拓展到待拓展顶点后才能进行代价阈值剪枝, 而拓展的过程涉及大量还原计算, 造成大量时间开销.因此, 该问题的关键是如何避免还原计算并筛除大量不满足代价阈值的待拓展顶点.我们观察到:还原路径权值的过程是将分段的路径组合并消去支配现象的过程, 其中权值最大的一段路径大多是关联图上两子图间的路径, 因此可以利用该部分路径权值来剪枝其他路径.为在拓展中快速调用两子图间的权值, 需要在预处理中通过关联图的精简skyline路径集合与路网图的划分结果计算出所有子图间的最小权值数组.在每轮拓展前, 通过子图间最小代价值判断有效待拓展子图, 从而批量筛去大量无效待拓展顶点.
3.2 预处理KORL算法预处理阶段采用划分路网图, 在此基础上构建树形索引的方法来组织路网信息.路网图划分对构建树形索引有重要作用, 优秀的路网图划分不仅需要保持子图大小近似一致, 还需要尽量减少边界点数量.本文采用PUNCH算法[12]将路网划分, 在划分的结果上构建该路网图的关联图[22].
定义 9(关联图).给定一个图G(V, E), 对其进行一种子图划分T={G1, G2, …, G|T|}, 其中, Gi=(Vi, Ei).划分后:(1)
假定对图 1路网图进行一种划分T={G1, G2, G3}, 相对应的关联图及3个划分子图如图 3所示.

|
Fig. 3 Subgraphs and correlation graph of the road network 图 3 路网图的子图及关联图 |
根据划分结果, 可以将原路网图视为根节点, 将各子图视为叶节点, 构建树形索引结构来保存路网信息.假定对路网图进行了图 3所示的划分, 则可以构建图 4所示的树形索引结构RN-tree.

|
Fig. 4 Tree index of road network 图 4 路网图树形索引 |
通过将路网图压缩成各个子图和关联图, 可以很好地减少预处理时空开销.在非叶节点(如图中G)上, 只保存边界点间的权值数组; 在叶节点(G1, G2, G3)上, 保存所有内部顶点间的权值数组.由于顶点间非支配路径有很多条, 所以每个数组单元可能保存多个权值, 具体计算方法将在第3.3.4节给出, 节点信息如图 5所示.

|
Fig. 5 Information on tree nodes 图 5 树形结构节点包含信息 |
3.3 现有加速策略
在路径拓展阶段, 本文综合运用了各现有算法对OSScalling的加速策略:近似支配剪枝策略、全局优先拓展策略和关键词顶点拓展策略.以下3个小节分别介绍这些策略.
3.3.1 近似支配剪枝策略近似支配剪枝策略在支配剪枝基础上引入一个近似参数, 并保证所求解与实际最优解在一定误差范围内.
定义 10(近似支配).在图G下, 给定一个略大于1的参数α(假定α=1.1), 若两条起终点相同的路径p1, p2满足BS(p1)≤BS(p2)∧SOS(p1)≤αSOS(p2), 则称p1近似支配p2.
定理 2.近似支配最优解与目标修正最优解在一定误差范围内:OS(pdom)≤αOS(pOS)[7].
定理 3.近似支配目标修正最优解与实际最优解误差不超过α/(1-ε), 即OS(pdom)≤α/(1-ε)OS(popt).
证明:由定理2可知, OS(pdom)≤αOS(pOS), 联立定理1可得OS(pdom)≤αOS(pOS)≤α/(1-ε)OS(popt).
3.3.2 全局优先拓展策略全局优先拓展策略是在选取拓展标签时考虑局部优先度的基础上, 引入全局优先度来保证所求解在一定误差范围内是一个最优解.全局优先度的基础是BucketBound思想.
定义 11(BucketBound).一个存放部分标签的队列称为一个桶(bucket), 每个桶对应一个目标值范围.给定一个参数β(1 <β <2), 假设第i个桶Bi对应一个区间[βiOS(τs, t), βi+1OS(τs, t)), τs, t代表起终点间最小目标值路径, 目标值落在该范围的路径标签存在这个桶内.不同的桶按照目标值由小到大的顺序排列, 每轮拓展从最小目标值的桶内选一个标签拓展至该桶为空, 第1个可行路径目标值近似最小, 此时可近似视为最优解而放弃后续拓展.
定理 4. BucketBound所求解与实际最优解在同一个桶内, βi+1OS(τs, t)≤OS(pdom)≤OS(p)≤βi+2OS(τs, t)[4].
BucketBound策略主要考察拓展是否会使当前路径越来越偏离最小目标路径, 偏离最小的可行解即为最优解.这种偏离程度可以表示为全局优先度.
定义 12(全局优先度).给定参数β, 标签Lik全局优先度
全局优先度代表了路径标签分到哪个桶中, 序号越小的桶, 存储的路径标签遍历优先级越高.
3.3.3 关键词顶点拓展策略关键词顶点拓展策略是在初始化时仅维护关键词顶点路径标签列表, 在拓展时仅向尚未覆盖的关键词的顶点拓展, 可有效减少查询时空开销.关键词顶点间存在多条拓展路径, 因此在预处理中采用SHARK算法[23]计算出各子图与关联图内所有顶点间的精简skyline路径集合.
定义 13(关键词顶点).对给定查询Q=(vs, vt, ψ, Δ)和kwi∈Q.ψ.若存在vm满足kwi∈vm.ψ, 则称vm是关键词kwi的一个关键词顶点.所有对应于kwi的关键词顶点集记为Vkwi, 关键词对应顶点的个数∣Vkwi∣称为该关键词顶点稠密度.
定义 14(精简skyline路径集合).以给定两顶点vs, vt为起终点的路径中, 不能被其余路径近似支配的所有路径的总集, 符号表示为SP(s, t).
求出各图精简skyline路径集合后, 按照目标值从小到大的顺序排序, 并在树形索引中相应子节点上维护集合信息.将vi, vj两顶点间最小OS(p)的路径记为τi, j, 最小BS(p)(即最大OS(p))的路径记为σi, j.
3.4 最小代价剪枝策略由于预处理阶段仅保存了各子图和关联图的精简skyline路径集合, 在路径拓展阶段调用不同子图顶点间权值时需要实时计算, 在此提出不同子图顶点间精简skyline路径的计算方式.
假定查询起点vs, 起点所在子图边界点v's∈V's, 终点vt, 终点所在子图边界点集为v't∈V't.任一起终点间路径可划分为3段:起点至某一起点所在子图边界点(vs, v's)、该起点所在子图边界点至某一终点所在子图边界点(v's, v't)、该终点所在子图边界点至终点(vt, v't).不同子图顶点间精简skyline路径是由相应的3个精简skyline路径集合中路径组成的不被其他路径支配的路径集合:
| $ \begin{array}{l} S{P_{cand}}({v_s}, {v_t}) = \{ p|p = ({p_1}, {p_2}, {p_3}) \wedge {p_1} \in SP({v_s}, {{v'}_s}), {p_2} \in SP({{v'}_s}, {{v'}_t}), {p_3} \in SP({{v'}_t}, {v_t}) \wedge ({{v'}_s}, {{v'}_t}) \in ({{V'}_s}, {{V'}_t})\} , \\ SP({v_s}, {v_t}) = \{ p|\forall p' \in S{P_{cand}}({v_s}, {v_t}), \not \exists SOS(p') <SOS(p) \wedge BS(p') <BS(p)\} . \end{array} $ |
定理 5.不同子图顶点间所有精简skyline路径都由起点至起点所在子图边界点集、终点至终点所在子图边界点集、起终点边界点集间的精简skyline路径组合构成.
证明:由于起终点不在同一子图中, 所以起终点间的路径必定经过起点所在子图边界点集V's和终点所在子图边界点集V't.不妨假设
通过对实际路网图的观察与分析, 可以认为关联图中所有顶点间权值往往大于各子图内部的权值, 这种现象在大规模路网下尤为明显[24].利用路网图这种特性, 可以加快不同子图顶点间精简skyline路径集合的计算速度.首先, 在预处理过程中寻找到任意两子图Gi, Gj所包的含边界点间最小目标值OS(τGi, Gj)和最小代价值BS(σGi, Gj), 构建子图最小目标矩阵O(τG)和最小代价矩阵B(σG), 存放在RN-tree根节点上.在查询阶段, 若计算的是vi, vj(vi∈Gi, vj∈Gj)间精简skyline路径集合, 首先找出
为解决关键词顶点稠密度增加导致大量不符合代价阈值的顶点被拓展到的问题, 本文在上述对路网图观察和分析的基础上, 提出最小代价剪枝策略.在每轮拓展前计算剩余代价, 与B(σG)对比后得到当前子图所对应的所有有效待拓展子图.在拓展时, 若待拓展顶点不属于这些子图对应的节点, 则不予拓展.
3.5 算法详述综合上文, 第3.5.1节给出KORL算法步骤和运行示例, 第3.5.2节对KORL时间、空间复杂度和近似度作出分析.
3.5.1 算法步骤算法1. KORL.
Input:RN-tree, Q=(vs, vt, ψ, Δ), β.
Output:Lopt.
1: set B0=null, Lopt=null, Found=false, get Vkw where kw∈Q.ψ-vt.ψ
2: create
3: while Found=false do
4: get the first non-empty queue Br
5: if all queues are empty then
6: return no feasible route
7: dequeue Lik which has the highest local priority
8: if Lik covers all keywords then
9: for each sp∈SP(i, t) do
10:
11: if Ltl.BS≤Δ then
12: enqueue Ltl on Bgp where
13: else delete Ltl
14: if Bgp doesn’t exists then
15: create Bgp and enqueue Ltl on Bgp
16: if Bgp=Br then
17: Found=true, Lopt=Ltl
18: else
19: for each vj∈Vkw,
20: for each sp∈SP(i, j) do
21: create
22: if Ljl isn’t dominated by other labels on vj and
23: enqueue Ljl on Bgp where
24: else delete Ljl
25: if Bgp doesn't exists then
26: create Bgp and enqueue Ljl on Bgp
27: for each L on vj do
28: if L is dominated by Ljl then
29: delete L
算法第1行、第2行给出了各变量初始化结果, 计算出算法中经常使用的一些定量.第3行~第6行表示从第1个非空队列中取出局部优先度最高的标签.若所有队列为空, 表示无可行解.第7行~第17行表示路径标签覆盖所有关键词后如何拓展至终点并近似求得最优路径, 其中, 第7行~第10行代表沿着标签所在顶点到终点的不同精简skyline路径拓展新标签; 第11行~第15行表示若新标签满足剪枝条件, 则将其放入对应队列; 第16行、第17行表示若新标签所入队列与当前队列一致, 则近似输出最优结果.第18行~第29行介绍路径标签未覆盖全部关键词时的相应操作, 其中, 第18行~第21行表示从拓展时满足剪枝条件的子图中, 取出尚未拓展的关键词对应的顶点, 沿着不同的精简skyline路径拓展, 创建新标签; 第22行~第26行判别新标签是否满足剪枝条件, 满足则将其放入对应队列; 第27行~第29行利用新标签剪裁标签所处顶点中原有标签.
算法运行示例:以图 1路网图、图 2关键词倒排列表、图 3的划分为例.查询Q=(v1, v10, <kw1, kw2>, 11), 修正参数ε=0.5, 修正相当于将目标值放大22倍, 近似支配参数α=1.1, 全局优先度参数β=1.1.
经计算τs, t=(v1, v3, v7, v10), 初始化队列B0, 起点处初始化路径标签L11=(ϕ, 0, 0, 0)并放入B0, 从B0中取出L11, 向未覆盖关键词、并不在距起点所在子图目标值代价值超标的子图中的关键词顶点拓展, 待拓展顶点有v3, v7, v8, v9.对每一个顶点进行拓展过程中, 沿着不同的精简skyline路径, 得到的新的标签:
从B0中按局部优先度取出(B0目前只包含一个标签)L31, 按照拓展规则向v8, v9拓展.得到新标签
由于B0中已无其他标签, 故从B2中取出局部优先级最高的标签L82, 对其进行拓展.由于所有关键词已包含, 故直接向终点拓展, 产生两个新标签
● 时间复杂度
由于KORL算法是一种近似算法, 查询时间存在着很大的随机性, 所以需按照算法最坏情况来计算时间复杂度, 即:忽略掉全局优先策略, 按照无剪枝效果的OSScalling算法来计算时间复杂度.
根据第3.4节的描述, 顶点间所有精简skyline路径是由被分割的3段skyline路径组合并剪枝所得.在子图或关联图中, 顶点间精简skyline路径集合最大元素个数
根据定义8, 每个关键词顶点最多拥有
最坏情况下, 向队列中取标签的复杂度为O(lg(|ψ|VmaxLmax)), 判别新标签与顶点中其他标签是否支配复杂度为O(Lmax), 故总时间复杂度为
● 空间复杂度
KORL算法空间消耗主要是顶点列表和队列中存储的路径标签, 由于最坏情况下需要遍历所有关键词顶点, 加上起终点会产生路径标签, 队列最多存储|ψ|VmaxLmax个路径标签, 所以空间复杂度为O((2|ψ|Vmax+2)·Lmax).
● 近似度分析
假定最终解为p, OSScalling算法(只采用近似支配和目标修正策略)所求解为pdom, 实际最优解为popt.若P对应队列为Bi, 根据定理4可知, OS(pdom)≥βiOS(τs, t), OS(p)≤βi+1OS(τs, t), 结合定理3, 可得:
| $ \frac{{OS(p)}}{{OS({p_{opt}})}} = \frac{{OS(p)}}{{OS({p_{dom}})}}\frac{{OS({p_{dom}})}}{{OS({p_{opt}})}} <\frac{{\alpha {\beta ^{i + 1}}OS({\tau _{s, t}})}}{{(1 - \varepsilon ){\beta ^i}OS({\tau _{s, t}})}} = \frac{{\alpha \beta }}{{1 - \varepsilon }}. $ |
故最终解近似度为
本节通过实验对KORL算法进行相关验证与分析.第4.1节介绍实验数据集与环境.第4.2节介绍实验的设计思路.第4.3节对比KORL算法与现有算法预处理阶段的性能表现.第4.4节分析KORL算法在不同查询因素下的查询效率.
4.1 数据集与环境本文所有实验运行在Intel(R) Xeon(R) CPU E5-2609 v4@1.70GHz×8的服务器上, 内存大小为16G.所有算法均在Java上实现.
本文实验采用9th DIMACS Implementation Challenge[11]所提供的路网图数据, 路网图边集具有路径长度和路径耗时两个属性.本实验采用不同规模的4个查询图, 其中, G1~G3是通过程序从纽约市路网图中截取3个子图, 将路径长度视为KOR中的代价值, 路径耗时视为目标值, 并采用1 000个关键词随机为查询图中各顶点生成关键词描述[7]; G4是在完整的纽约市路网图上采用10 000个关键词随机生成的查询图.数据集具体信息见表 1.
| Table 1 Query graph 表 1 查询图 |
4.2 实验设计
为验证KORL算法非常适用于大规模路网图, 需要分别验证其在预处理和查询阶段的性能.为了验证KORL算法在预处理阶段具有良好的可扩展性, 我们设置了实验1.由于现有算法无法运行在大规模查询图上, 因此我们仅验证不同查询因素对算法效率的影响.针对3个查询因素:查询图规模、关键词个数和代价阈值, 我们设置了实验2~实验4, 并且为了验证KORL算法在查询阶段拥有不错的表现, 我们在实验2中, 现有算法可运行的查询图上加入与现有算法的对比.
● 实验1:预处理时空开销实验
为了验证KORL算法在预处理表现上的优越性, 需要对比KORL算法与现有算法在预处理上的时空开销.由于现有算法预处理方法大致相同, 因此选取最近提出的算法KSRG[7]作为对比.实验运行在本机环境(16G内存)下, 采用G1~G4作为查询图, 评价标准是两种算法在预处理阶段的内存占用空间和预处理计算时间.
● 实验2:查询图规模影响实验
为了判断查询图规模对算法效率的影响, 需要控制关键词个数与代价阈值相同的前提下改变查询图规模, 评价标准是平均查询时间.实验设定关键词个数为6, 代价阈值为60km, 分别采用G1~G4作为查询图.为了验证KORL算法具有不错的查询表现, 需要和现有算法作对比.实验采用OSScalling[4], KSRG[7]和KORL算法, 随机提交10个查询并对查询时间取平均.
● 实验3:关键词个数影响实验
为了判断关键词个数对算法效率的影响, 需要控制数据集与代价阈值相同的前提下改变关键词个数, 评价标准是平均查询时间.实验采用G2~G4作为查询图, 代价阈值设定为60km, 关键词个数分别取2, 4, 6, 8.实验采用KORL算法, 随机提交10个查询并对查询时间取平均.
● 实验4:代价阈值影响实验
为了判断代价阈值对算法效率的影响, 需要控制数据集与关键词个数相同的前提下改变查询代价阈值, 评价标准是平均查询时间.实验采用G2~G4作为查询图, 关键词个数设定为6, 代价阈值分别取20, 40, 60, 80km.实验采用KORL算法, 随机提交10个查询并对查询时间取平均.
4.3 预处理开销对比实验1的预处理空间开销如图 6所示, 时间开销如图 7所示.

|
Fig. 6 Preprocessing space overhead 图 6 预处理空间开销 |

|
Fig. 7 Preprocessing time overhead 图 7 预处理时间开销 |
从图 6中可以看到, 当查询图为G2(顶点数为25 000)时, KSRG算法内存开销已经接近16GB.对于G3, G4而言, 内存开销已远远超出16GB, 故不在图中标明.而KORL算法处理G4仅需5GB左右的内存, 对比可见, KORL算法预处理空间开销远小于以往算法.
在时间开销方面, KSRG算法对G2的预处理已经超过50h, 后续查询图因时间太长不再标明.而KORL算法对G4的预处理仅需1h.由此体现出KORL算法预处理在大规模路网图下性能远超以往.
4.4 不同查询因素对算法效率的影响本小节分别给出实验2~实验4的结果并进行分析.
4.4.1 查询图规模对算法效率的影响实验2结果如图 8所示.从图 8中可以看出, 当查询图规模扩大时, 查询时间增长会变缓.这是因为查询图规模越大, 代价阈值的剪枝能力就相对越强.若在很小的图中, 最优路径的代价值还未达到代价阈值, 需要遍历整个解空间才能得到最优解; 而当图的规模越大时, 越多的顶点会被最小代价剪枝策略筛去, 增长速度也会放缓.这种放缓趋势会延续下去, 直到查询图大到很多顶点间的代价值已超过代价阈值时, 此时在第1轮拓展中就会把无关顶点筛去, 导致查询时间基本不会变化.

|
Fig. 8 Querying time on different scales of query graph 图 8 不同查询图规模下的查询时间 |
在本实验中, 同样观察了两种以往算法在大规模路网图上的表现.由于以往算法对G3, G4的预处理内存开销超过本实验环境, 故仅标出其在G1, G2上的查询时间.对比3个算法在查询阶段的表现, KORL算法查询时间介于OSScalling与KSRG算法之间.虽然KORL算法需要在路径拓展中动态计算拓展路径, 但由于多种加速策略的使用, 导致其查询时间并未显著增加.通过预处理阶段和查询阶段的良好表现, 验证了KORL算法良好的可扩展性.
4.4.2 关键词个数对算法效率影响实验3的结果如图 9所示.从图 9中G2~G4这3个查询图上查询时间随关键词个数别的变化可以看出, 当关键词达到6个以上时, 查询时间会显著上升.这是由于关键词增多时, 遍历的深度也会大幅上升, 即使采用了关键词顶点拓展策略, 也会产生大量中间结果, 导致查询时间的显著上升.
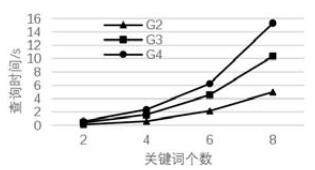
|
Fig. 9 Querying time on different numbers of keywords 图 9 不同关键词个数下的查询时间 |
当图的规模增大时, 查询时间随关键词个数增加而增加的速度会上升.这是因为在更大规模的图中, 关键词个数增加会导致最优路径更难被拓展出来, BucketBound算法筛去后续拓展的效率变慢.因此在越大的图中, 关键词个数的增加会造成查询时间显著增加.
4.4.3 代价阈值对算法效率影响实验4结果如图 10所示.从图 10中G2~G4这3条曲线的共同变化趋势可以看出, 查询时间呈先增长后平稳的趋势.这是由于在代价阈值很小的时候, 很多待拓展顶点会被最小代价剪枝手段筛去; 当代价阈值增大到实际最小目标路径的代价值时, BucketBound近似策略会使KORL算法尽快地返回近似最优解, 不再进行后续拓展; 当代价阈值继续增大时, 实际最优解不会发生改变, 故查询时间不再有显著变化.

|
Fig. 10 Querying time on different cost threshold 图 10 不同代价阈值下的查询时间 |
当图的规模增大时, 查询时间随代价阈值增加而增加的速度会上升.因为在越大规模的查询图中, 相对越小的代价阈值对查询算法的剪枝能力就越弱, 查询时间增长的增长速度就会上升.
5 总结与展望本文针对以往KOR算法预处理无法适用于大规模路网的问题, 提出一种利用划分路网和构建树形索引的预处理方法来组织路网信息, 在此基础上提出相应的查询算法KORL并做出改进.通过大规模查询图上的实验证明KORL算法良好的可扩展性.对KOR查询的优化一方面要继续寻找更好的剪枝策略, 另一方面探索利用执行过的KOR查询的子路径也是一个重要方向.
| [1] |
Gao YJ, Qin X, Zheng BH. Efficient reverse top-k Boolean spatial keyword queries on road networks. IEEE Trans. on Knowledge and Data Engineering, 2015, 27(5): 1205-1218.
[doi:10.1109/TKDE.2014.2365820] |
| [2] |
Cao X, Cong G, Jensen CS, Beng CO. Collective spatial keyword querying. In:Proc. of the ACM SIGMOD Int'l Conf. on Management of Data (SIGMOD 2011)., 2011, 373-384.
[doi:10.1145/1989323.1989363] |
| [3] |
Choudhury FM, Culpepper JS, Sellis T, Cao X. Maximizing bichromatic reverse spatial and textual k nearest neighbor queries. Proc. of the VLDB Endowment, 2016, 9(6): 456-467.
[doi:10.14778/2904121.2904122] |
| [4] |
Cao X, Chen LS, Cong G, Xiao XK. Keyword-aware optimal route search. Proc. of the VLDB Endowment, 2012, 5(11): 1136-1147.
[doi:10.14778/2350229.2350234] |
| [5] |
Cao X, Chen LS, Cong G, Guan JH, Phan NT, Xiao XK. KORS:Keyword-aware optimal route search system. In:Proc. of the ICDE 2013., 2013, 1340-1343.
[doi:10.1109/ICDE.2013.6544939] |
| [6] |
Jin PF, Niu BN, Zhang XZ. KSRG:An efficient optimal route query algorithm for multi-keyword coverage. Journal of Computer Applications, 2017, 37(2): 352-359(in Chinese with English abstract).
[doi:10.11772/j.issn.1001-9081.2017.02.0352] |
| [7] |
Jin PF. Research on efficient keyword-aware optimal route query processing method[MS. Thesis].. Jinzhong: Taiyuan University of Technology, 2017.
|
| [8] |
Floyd RW. Algorithm 97:Shortest path. Communications of the ACM, 1962, 5(6): 345-346.
[doi:10.1145/367766.368168] |
| [9] |
Xiao XY, Luo Q, Li ZS, Xie X, Ma WY. A large-scale study on map search logs. ACM Trans. on the Web (TWEB), 2010, 4(3): 8-9.
[doi:10.1145/1806916.1806917] |
| [10] |
Zhong RC, Li GL, Tan KL, Zhou LZ, Gong ZG. G-tree:An efficient and scalable index for spatial search on road networks. IEEE Trans. on Knowledge and Data Engineering, 2015, 27(8): 2175-2189.
[doi:10.1109/TKDE.2015.2399306] |
| [11] | |
| [12] |
Delling D, Goldberg AV, Razenshteyn I, Werneck RF. Graph partitioning with natural cuts. In:Proc. of the IEEE Int'l Conf. on Parallel and Distributed Processing Symp. (IPDPS)., 2011, 1135-1146.
[doi:10.1109/IPDPS.2011.108] |
| [13] |
Li RH, Qin L, Yu JX, Mao R. Optimal multi-meeting-point route search. IEEE Trans. on Knowledge and Data Engineering, 2016, 28(3): 770-784.
[doi:10.1109/TKDE.2015.2492554] |
| [14] |
Zhang JZ, Wen J, Meng XF. Multi-tag route query based on order constraints in road networks. Chinese Journal of Computers, 2012, 35(11): 2317-2326(in Chinese with English abstract).
[doi:10.3724/SP.J.1016.2012.02317] |
| [15] |
Bao JL, Yang XC, Wang B, Wang JY. An efficient trip planning algorithm under constraints. Journal of Chinese Computer Systems, 2013, 34(12): 429-434(in Chinese with English abstract).
[doi:10.1109/WISA.2013.87] |
| [16] |
Bao JL, Wang B, Yan SC, Yang XC. Multi-constrained optimal path search algorithms. In:Proc. of the 16th Asia-Pacific Web Conf. Springer-Verlag, 2014, 355-366.
[doi:10.1007/978-3-319-11116-2_31] |
| [17] |
Karypis G, Kumar V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM Journal on Scientific Computing, 1998, 20(1): 359-392.
[doi:10.1137/S1064827595287997] |
| [18] |
Meyerhenke H, Monien B, Sauerwald T. A new diffusion-based multilevel algorithm for computing graph partitions. Journal of Parallel and Distributed Computing, 2009, 69(9): 750-761.
[doi:10.1016/j.jpdc.2009.04.005] |
| [19] |
Tsaggouris G, Zaroliagis C. Multiobjective optimization:Improved FPTAS for shortest paths and non-linear objectives with applications. Theory of Computing Systems, 2009, 45(1): 162-186.
[doi:10.1007/s00224-007-9096-4] |
| [20] |
Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to Algorithms. 3rd ed. London:MIT Press, 2009, 1048-1128.
[doi:10.1002/9783527649846.ch17] |
| [21] |
Dumitrescu I, Boland N. Improved preprocessing, labeling and scaling algorithms for the weight-constrained shortest path problem. Networks, 2003, 42(3): 135-153.
[doi:10.1002/net.10090] |
| [22] |
Wang SB, Xiao XK, Yang Y, Lin WQ. Effective indexing for approximate constrained shortest path queries on large road networks. Proc. of the VLDB Endowment, 2016, 10(2): 61-72.
[doi:10.14778/3015274.3015277] |
| [23] |
Delling D, Wagner D. Pareto paths with SHARC.In:Proc. of the Int'l Symp. on Experimental Algorithms. Springer, 2009, 125-136.
[doi:10.1007/978-3-642-02011-7_13] |
| [24] |
Abeywickrama T, Cheema MA, Taniar D. K-nearest neighbors on road networks:A journey in experimentation and in-memory implementation. Proc. of the VLDB Endowment, 2016, 9(6): 492-503.
[doi:10.14778/2904121.2904125] |
| [6] |
金鹏飞, 牛保宁, 张兴忠. 高效的多关键词匹配最优路径查询算法KSRG. 计算机应用, 2017, 37(2): 352-359.
[doi:10.11772/j.issn.1001-9081.2017.02.0352] |
| [7] |
金鹏飞. 基于关键词的最优路径查询高效处理方法的研究[硕士学位论文]. 晋中: 太原理工大学, 2017.
|
| [14] |
张金增, 文洁, 孟小峰. 路网环境下访问序列受限的多标签路线查询算法. 计算机学报, 2012, 35(11): 2317-2326.
[doi:10.3724/SP.J.1016.2012.02317] |
| [15] |
鲍金玲, 杨晓春, 王斌, 王佳英. 一种支持约束关系的高效的行程规划算法. 小型微型计算机系统, 2013, 34(12): 2702-2707.
[doi:10.1109/WISA.2013.87] |
 2020, Vol. 31
2020, Vol. 31


