高维数据包含大量冗余信息, 直接处理十分耗时.随着数据维数的增加, 更会产生“维度灾难”^[1]问题.通过维度约简将高维数据映射到低维空间中, 不仅可以有效地去除冗余特征^[2], 而且减少了计算量.目前, 维度约简在图像聚类^[3]、数据挖掘^[4]、机器学习^{[5, 6]}等领域发挥着重要作用.

流形学习^[7]是一种有效的维度约简方法, 近年来流形学习得到迅猛发展, 许多经典算法被提了出来, 包括等距特征映射(isometric feature mapping, 简称ISOMAP)^[8]、局部线性嵌入(local linear embedding, 简称LLE)^[9]、拉普拉斯特征映射(Laplacian eigenmaps, 简称LE)^[10]、局部保持投影(locality preserving projection, 简称LPP)^[11]、谱回归(spectral regression, 简称SR)^[12]、无监督大规模图嵌入(unsupervised large graph embedding, 简称ULGE)^[13]等等.

流形学习假设原始数据存在嵌入高维空间的低维流形^[14], 这里, 低维流形维度即为本征维度^[15].研究发现, 约简维度的选择会影响流形学习方法的性能.当约简维度大于本征维度时, 得到的低维数据中包含过多的冗余信息; 当约简维度小于本征维度时, 又会造成数据点在低维空间中重叠, 不利于研究其内在性质.如果能够找到高维数据的本征维度, 就能轻易地探索数据的内部结构.然而, 探究数据的本征维度十分困难.

为了避免本征维度对流形学习方法的影响, 本文提出了一种无监督相似流形学习方法, 即基于选择聚类集成的相似流形学习(similar manifold learning based on selective cluster ensemble, 简称SML-SCE)算法.SML-SCE将高维数据映射到不同的低维空间中, 获得多个相似流形.不同低维嵌入的多样性更有利于集成学习^[16].因此, 在SML-SCE中采用基于权重的选择聚类集成方法^[17]对相似低维流形嵌入的聚类结果进行融合.首先采用K- means方法对这些相似的低维嵌入进行聚类得到子聚类结果, 然后计算子聚类之间的归一化互信息(normalized nutual information, 简称NMI)^[18]作为衡量权重的标准.最后, 舍弃权重较低的子聚类, 采用基于权重的选择性投票方案来获得最终的聚类结果.通过对多个不同维度下相似流形的融合, SML-SCE避免了对本征维度的估计, 同时性能得到提升.

此外, 本文还提出了一种新的锚点生成方法——改进的层次平衡K-means(modified balanced k-means based hierarchical K-means, 简称MBKHK)方法, MBKHK克服了层次平衡K-means(balanced K-means based hierarchical K-means, 简称BKHK)^[19]方法要求锚点个数必须是2的整数次幂的缺点, 并选出具有代表性的锚点.

本文的创新点总结如下.

(1) 提出MBKHK方法.MBKHK可生成具有代表性的锚点, 并且对锚点个数没有限制.

(2) 提出SML-SCE算法.SML-SCE采用选择聚类集成方法将不同维度下的相似低维流形嵌入的聚类结果进行融合, 避免了对本征维度的估计.

本文第1节介绍相关工作, 包括相似流形的定义、经典流形学习算法, 并介绍拉普拉斯特征映射算法.第2节详细介绍SML-SCE算法, 包括锚点生成方法MBKHK、低维嵌入学习方法以及相似流形结合策略.第3节给出SML-SCE和其他对比方法的实验结果.第4节进行总结和展望.

1 相关工作 1.1 相似流形学习

在介绍相似流形学习之前, 首先给出相似流形的定义.

定义1(相似流形).设M和N是两个光滑流形, f:M→R^d和g:N→R^d为两个不同的光滑嵌入映射, 若对于高维样本集X={x₁, x₂, …, x_n}, x_i∈R^d, 可由低维空间的样本集合Y_M(Y_M⊂M)和Y_N(Y_N⊂N)分别通过f和g得到, 那么M和N是相似流形.

在相似流形定义中, f和g表示两个不同的映射, 这里的不同可以是由计算方式带来的, 也可以是由低维空间维度不同带来的.而相似流形学习则是在相似流形的基础上, 通过对多个低维相似流形进行研究, 来探究高维数据的内在性质.

1.2 经典流形学习算法

2000年, Tenenbaum在保持流形全局结构的基础上, 提出了ISOMAP算法, ISOMAP在计算样本点之间的距离时, 采用测地线距离来取代欧氏距离, 随后应用经典的多维尺度分析(multidimensional scaling, 简称MDS)^[20]算法, 保持数据点之间的几何结构不变, 最终得到嵌入在高维空间的低维流形.Roweis和Saul考虑保持流形的局部线性结构, 提出了局部线性嵌入LLE算法, LLE假设样本点可由局部邻域内的点加权平均重建, 并且可以在低维空间内保持样本点的邻域权值不变, 从而找出低维流形结构.2001年, Belkin和Niyogi提出了LE算法, LE利用拉普拉斯-贝尔特拉米算子(Laplacian-Beltrami operator)的特性, 求解拉普拉斯Beltrami算子的特征函数, 得到流形的最优嵌入.2003年, He等人在LE的基础上, 提出了LPP算法, LPP假设高维空间与低维空间之间存在线性投影关系, 随后采用与LE类似的原理求解, 最终得到映射关系, 因此, LPP也被称为LE的线性扩展.2007年, Cai等人提出了SR算法, SR解决了LPP在求解时需要对稠密矩阵进行特征分解的问题, 大大减少了计算量.2017年, Nie等人提出了ULGE算法, ULGE结合基于锚点策略^[21]和无参近邻策略^[22], 构造了一个对称、双随机、半正定、秩为约简维度的相似度矩阵, 随后采用回归方程计算得到投影矩阵, ULGE降低了计算复杂度且可应用于大规模数据.

1.3 拉普拉斯特征映射(LE)

拉普拉斯特征映射LE是一种无监督局部流形学习算法.LE假设在高维空间距离较近的点映射到低维空间后, 仍保持其距离相近, LE通过保持近邻关系来发现低维流形.对于高维样本点X={x₁, x₂, …, x_n}^T∈R^n×d, n为样本个数, d为每个样本点维度.LE的具体算法步骤如下.

(1) 构造近邻图:LE通过εNN或者kNN确定近邻点.在εNN方法中, 若||x_i–x_j||≤ε, 则x_i与x_j存在边相连; 在kNN方法中, 若样本点x_j是x_i的k最近邻点, 则x_i与x_j相连.在此基础上, 构造近邻图.

(2) 构造相似度矩阵:常见方法有两种, 一种是0-1法, 即若样本点x_i和x_j之间存在边相连, 相似度a_ij=1, 否则为0;另一种为热核法, 即若边存在, 相似度${{a}_{ij}}=\exp \left( {-\left\| {{x}_{i}}-{{x}_{j}} \right\|_{2}^{2}}/{2{{\sigma }^{2}}}\; \right)$(σ为热核参数), 否则, a_ij=0.

(3) 获得低维嵌入:LE通过保持近邻关系来获得低维嵌入, 其优化的目标函数如下^[10]:

$ \underset{Y}{\mathop{\min }}\, {{Y}^{T}}LY\text{ s}\text{.t }{{Y}^{T}}DY=I $

(1)

其中, Y∈R^n×p表示p维度下的低维嵌入, p为约简维度.L∈R^n×n是拉普拉斯矩阵, L=D–A.度矩阵D∈R^n×n是一个对角矩阵, 对角元素定义为${{d}_{ii}}=\sum\nolimits_{j=1}^{n}{{{a}_{ij}}}.$公式(1)的最优解Y可以转化为广义特征矩阵的特征分解问题.Y由前p个最小非零特征值对应的特征向量组成.

$ LY = \lambda DY $

(2)

2 基于选择聚类集成的相似流形学习算法 2.1 锚点生成

传统方法通常直接构造样本点间的相似度矩阵.然而, 当数据规模较大时, 这种方法的计算复杂度极高.为了解决这一问题, 可采用基于锚点的图构造方法, 从而降低计算成本.

基于锚点的方法需要生成锚点并计算样本点和锚点之间的相似度矩阵, 其中最重要的一步就是锚点的选择.常见方法有随机选择方法和K-means方法.随机选择方法计算简单, 但不能保证锚点的代表性, 性能较差.K-means方法可以选出具有代表性的锚点, 但计算复杂度较高.在数据集规模较大时, 性能会受到很大影响.为了解决以上问题, Zhu等人提出了层次平衡K-means(BKHK)方法.BKHK采用平衡二叉树结构, 计算复杂度小于K-means方法.但是, BHKH也存在缺点, 即BKHK要求锚点个数必须是2的整数次幂.

本文提出了一种改进的层次平衡K-means(MBKHK)方法, 可避免上述缺点.本质上, MBKHK是多次运用了两类平衡K-means方法.

下面首先介绍两类平衡K-means方法.在聚类中, 平衡K-means方法要保持簇集内部的点到其中心点的距离尽可能地小, 因此得到其目标函数为

$ \mathop {\min }\limits_R \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^2 {\left\| {{x_i} - {c_j}} \right\|_2^2{r_{ij}}} } $

(3)

其中, C=[c₁, c₂]∈R^d×2为中心点矩阵, c₁和c₂分别为两类的聚类中心点.初始中心点为随机选取.R∈R^n×2为所求的样本点类别矩阵.若x_i属于c₁类, r_i1=1且r_i2=0;若x_i属于c₂类, r_i2=1且r_i1=0.因此, r_i1+r_i2=1.

令α和β分别是两类样本点个数, 则α+β=n.在平衡K-means方法中, 为了能够在两类间迭代地执行平衡K- means方法, 需保持这两类样本点个数基本相等, 设$\alpha =\left\lfloor \frac{n}{2} \right\rfloor $(如果n为奇数, 则$\alpha =\frac{n-1}{2}$), β=n–α.

为了方便起见, 定义样本点X到中心点C的距离为H∈R^n×2且${{h}_{ij}}=||{{x}_{i}}-{{c}_{j}}||_{2}^{2}.$因为r_i1+r_i2=1, 所以r_i2可以被表示为(1–r_i1).那么, 对公式(3)进行化简, 可得:

$ \left. \begin{array}{l} \mathop {\min }\limits_R \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^2 {\left\| {{x_i} - {c_j}} \right\|_2^2{r_{ij}} = \mathop {\min }\limits_R \sum\limits_{i = 1}^n {(\left\| {{x_i} - {c_1}} \right\|_2^2{r_{i1}} + \left\| {{x_i} - {c_2}} \right\|_2^2{r_{i2}})} } } \\ {\rm{ }} = \mathop {\min }\limits_R \sum\limits_{i = 1}^n {({h_{i1}}{r_{i1}} + {h_{i2}}{r_{i2}})} \\ {\rm{ }} = \mathop {\min }\limits_R \sum\limits_{i = 1}^n {({h_{i1}}{r_{i1}} + {h_{i2}}(1 - {r_{i1}}))} \\ {\rm{ }} = \mathop {\min }\limits_R \sum\limits_{i = 1}^n {({r_{i1}}({h_{i1}} - {h_{i2}}) + {h_{i2}})} \\ {\rm{ }} \Rightarrow \mathop {\min }\limits_R \sum\limits_{i = 1}^n {({r_{i1}}({h_{i1}} - {h_{i2}}))} \\ {\rm{ }} = \mathop {\min }\limits_R r_1^T({h_1} - {h_2}) \end{array} \right\} $

(4)

其中, r₁表示矩阵R的第1列.h₁和h₂分别为矩阵H的第1列和第2列.

r₁中仅包含0和1两个元素, 即r₁∈{0, 1}ⁿ.从公式(4)可以得到:

$ \mathop {\min }\limits_R r_1^T({h_1} - {h_2}){\rm{ s}}{\rm{.t}}{\rm{. }}{r_1} \in {\{ 0, 1\} ^n}, \sum\limits_{i = 1}^n {{r_{i1}} = \alpha } $

(5)

问题(5)的答案很明显.当(h₁–h₂)的第i个元素是所有元素的前α个最小值时, 令r_i1=1, 除此之外的r_i1设为0, r_i1=1–r_i1, 此时满足r₁^T(h₁-h₂)取得最小值.在得到每个样本点的类别后, 计算每一个点到其中心点的距离, 取平均值更新两类中心点, 重复以上步骤, 直到中心点不再变化, 此时得到两类的最终聚类结果.

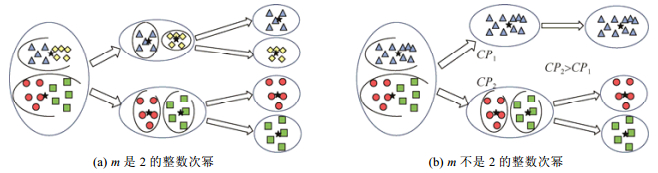
MBKHK在这两类聚类上分别执行平衡K-means方法, MBKHK示意图如图 1所示.锚点的个数为m (m < < n).下面就m的取值分两种情况进行讨论.

(1) 当m是2的整数次幂时, 层次执行logm次平衡K-means方法, 获得m个锚点.在这种情况下所产生的锚点的示意图如图 1(a)所示.

(2) 当m不是2的整数次幂时, 首先层次执行$\left\lfloor \log m \right\rfloor $次平衡K-means方法, 获得2^{$\left\lfloor \log m \right\rfloor $}个锚点.每一个锚点都是聚类中心点, o_i即是簇集Ω_l(i=1, …, 2^{$\left\lfloor \log m \right\rfloor $})的中心点.每个簇集的样本点到中心点的平均距离可以衡量这个簇集的紧凑性.第i个簇集的平均距离CP_i表示如下:

$ \mathop {\min }\limits_R r_1^T({h_1} - {h_2}){\rm{ s}}{\rm{.t}}{\rm{. }}{r_1} \in {\{ 0, 1\} ^n}, \sum\limits_{i = 1}^n {{r_{i1}} = \alpha } $

(6)

其中, |Ω_l|表示簇集Ω_l的元素个数.CP_i值越高, 说明簇集Ω_l越松散.因此, 从2^{$\left\lfloor \log m \right\rfloor $}个簇集中选出前(m–2^{$\left\lfloor \log m \right\rfloor $})个CP_i值最大的簇集执行平衡K-means方法, 最终得到m个锚点.当m不是2的整数次幂时, 示意图显示如图 1(b)所示.

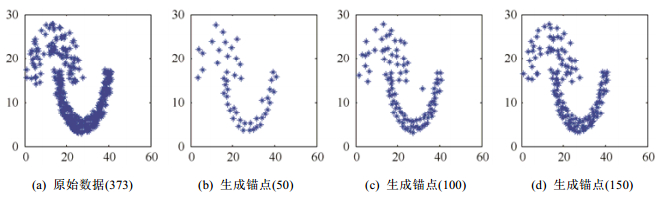
为了验证MBKHK方法的性能, MBKHK在二维数据集Jain^[23]上进行实验.图 2显示了Jain原始数据和选出的不同数量锚点的分布情况.图 2(a)所示为有373个样本点的原始数据情况, 图 2(b)~图 2(d)分别为生成的50、100和150个锚点的分布图.从图中可以明显看出, MBKHK选出的锚点具有代表性, 可以很好地反映原始数据的分布状况.

2.2 低维嵌入学习

获得锚点之后, 使用基于锚点的策略构建相似度矩阵.U∈R^m×d表示锚点矩阵.第i个样本点和该样本点的第j个最近邻锚点之间的距离用${{d}_{ij}}=\left\| {{x}_{i}}-{{u}_{j}} \right\|_{2}^{2}$表示.很明显, 有${{d}_{i1}}\le {{d}_{i2}}\le \cdots \le {{d}_{im}}.$通过以下公式计算可得到样本点与锚点之间的相似度矩阵Z∈R^n×m[13]:

$ {z_{ij}} = \left\{ \begin{array}{l} \frac{{{d_{i(k + 1)}} - {d_{ij}}}}{{k{d_{i(k + 1)}} - \sum\nolimits_{j'{\rm{ = }}1}^k {{d_{ij'}}} }}, {\rm{ if }}{u_j} \in \Gamma ({x_i})\\ 0, {\rm{ otherwise}} \end{array} \right. $

(7)

其中, Γ(x_i)是样本点x_i的k近邻锚点集合.

根据相似度矩阵Z, 样本点之间的相似度矩阵A∈R^n×n可通过以下公式计算得到^[21]:

$ A = Z{{\bf{\Delta }}^{ - 1}}{Z^T} $

(8)

其中, Δ∈R^m×m是对角矩阵, 对角上元素${{\Delta }_{jj}}=\sum\nolimits_{i=1}^{n}{{{z}_{ij}}}.$

由文献[21]可知, 相似度矩阵A是对称、半正定和双随机的.双随机意味着矩阵A的各行之和等于1, 各列之和也等于1, 即$\sum\nolimits_{i=1}^{n}{{{a}_{ij}}}=\sum\nolimits_{j=1}^{n}{{{a}_{ij}}}=1.$度矩阵D对角上元素定义为${{d}_{ii}}=\sum\nolimits_{j=1}^{n}{{{a}_{ij}}}.$根据\[\sum\nolimits_{j=1}^{n}{{{a}_{ij}}}=1, \]度矩阵的对角元素值等于1, 此时, D=I, I∈R^n×n为单位矩阵.L=D–A=I–A, L=I–A将带入LE的目标函数(1), 可得:

$ \mathop {\min }\limits_Y {Y^T}(I - A)Y{\rm{ s}}{\rm{.t }}{Y^T}IY = I $

(9)

公式(9)可以化简为

$ \mathop {\max }\limits_Y {Y^T}AY{\rm{ s}}{\rm{.t }}{Y^T}Y = I $

(10)

公式(10)的最优解Y可以转化为特征矩阵AY=λY的特征分解问题.Y由矩阵A的前p个最大特征值对应的特征向量组成.

重复以上步骤, 可以获得不同维度下的低维流形嵌入, 维度范围记为$[\kappa , \iota ]$.

2.3 相似流形结合

对于高维数据, 可以通过约简维度进行研究.在本征维度下, 数据的内部性质更容易被探究.然而, 本征维度的研究十分耗时.SML-SCE通过将高维数据映射到不同低维空间, 然后采用选择聚类集成方法将这些相似的低维嵌入进行结合.SML-SCE避免了对本征维度的寻找, 且取得了良好的效果.

采用K-means方法对t个相似低维嵌入进行聚类, t=ι–κ+1, 获得多个聚类结果.但是, K-means方法得到的聚类结果是混乱的.例如, 对于聚类标签向量[1,1,1,2,2,3,]^T和[2,2,2,3,3,1]^T, 两者有着不同的呈现, 但却表达了同一种聚类结果.为了结合这些聚类结果, 首先需要对聚类标签向量进行校正.一般而言, 有较强对应关系的聚类标记覆盖相同对象的个数应该是最大的.例如, 标签向量[1,1,1,2,2,3,]^T中的标记{1}和标签向量[2,2,2,3,3,1]^T中的标记{2}.将第2个聚类标签向量向第1个聚类标签向量匹配, 找到具有最大相同覆盖对象的对应标记, 使得第2个聚类标签向量中的该标记等于第1个聚类标签向量中的对应标记, 并记入新标签向量中.随后, 在两个标签向量中分别移除已匹配的标记.重复以上过程, 直到第2个聚类标签向量中的所有标记均在第1个聚类标签向量中找到对应的标记.该校正方法被称为bestMap方法.bestMap方法举例见表 1.

对于多个聚类标签向量, 从中随机选择一个作为参考标签向量, 并将剩下的标签向量与参考标签向量相匹配, 得到校正后的聚类标签向量.

随后, 采用基于权重的选择聚类集成方法来结合这些聚类结果.聚类标签向量之间的归一化互信息NMI在一定程度上可以描述聚类之间的紧密性.因此, 在本算法中, NMI被用作聚类间衡量权重的标准.

由K-means方法得到的聚类标签向量${{\eta }_{a}}\in {{\mathbb{R}}^{n}}$和${{\eta }_{b}}\in {{\mathbb{R}}^{n}}, $其聚类标记分别为$\{C_{a}^{1}, C_{a}^{2}, ..., C_{a}^{K}\}$和$\{C_{b}^{1}, C_{b}^{2}, ..., C_{b}^{K}\}.$假设聚类标记C_aⁱ和C_b^j分别包含n_i和n_j个元素, 那么很明显$\sum\nolimits_{i=1}^{K}{{{n}_{i}}=}\sum\nolimits_{j=1}^{K}{{{n}_{j}}=}n.$将在C_aⁱ和C_b^j中共同含有的元素个数记为n_ij.两类之间的NMI定义为

$ {\Phi ^{NMI}}({\eta _a}, {\eta _b}) = \frac{2}{n}\sum\limits_{i = 1}^K {\sum\limits_{j = 1}^K {{n_{ij}}} {{\log }_{{K^2}}}\frac{{{n_{ij}}n}}{{{n_i}{n_j}}}} $

(11)

聚类标签向量${{\eta }_{i}}(i=1, 2, ..., t)$的平均NMI可通过公式(12)计算得到:

$ {\gamma _i} = \frac{1}{{t - 1}}\sum\limits_{j = 1, j \ne i}^t {{\Phi ^{NMI}}({\eta _i}, {\eta _j})} $

(12)

γ_i的值越高, 聚类η_i中包含的信息越多.因此, η_i的权重可通过以下公式计算得到:

$ {w_i} = \frac{{{\gamma _i}}}{{\sum\nolimits_{j = 1}^t {{\gamma _j}} }} $

(13)

很明显, 各聚类的权重之和等于1, 即$\sum\nolimits_{i=1}^{t}{{{w}_{i}}}=1.$

当聚类结果的权重过低时, 则意味着这个聚类结果对集成学习有负面影响, 因此需要将其舍弃.换言之, 将该聚类的权重置为0.在本算法中, 按照百分比来选择权重, 舍弃率标记为dr.最终, 采用基于权重的选择性投票方案, 得到最终的聚类结果.

$ FC({x_i}) = \mathop {\arg \max }\limits_{q \in \{ 1, 2, \ldots , K\} } \sum\limits_{j = 1}^t {{w_j}I(\eta _j^i = q)} $

(14)

其中, K是样本数据集X的类别数, η_jⁱ表示聚类η_j的第i个元素.I(·)是一个指示矩阵, 当“$\cdot $”为真时, I(·)=1, 反之, 当“$\cdot $”为假时, I(·)等于0.

SML-SCE方法的具体流程见算法1.

算法 1.基于选择聚类集成的相似流形学习算法(SML-SCE).

输入:样本数据集X∈R^n×d, 低维嵌入维度范围[κ, ι], 锚点个数m, 权重舍弃率dr.

输出:最终聚类结果.

1.获得t=ι–κ+1个相似低维流形嵌入子聚类:

For i=κ, …, ι Do

(a) 执行MBKHK, 获得m个锚点;

(b) 根据公式(7)和公式(8)计算相似度矩阵A;

(c) 对矩阵A进行特征分解, 得到i维度下的低维嵌入Y_i;

(d) 对低维嵌入Y_i进行K-means聚类, 得到子聚类结果;

End For

2.采用bestMap方法对t个聚类结果进行校正;

3.根据公式(12)和公式(13)计算聚类之间的NMI并得到权重;

4.将聚类中权重较低的dr舍弃, 这些舍弃聚类的权重置为0;

5.根据公式(14)采用基于权重的选择投票策略来获得最终聚类结果.

3 实验结果与分析

为了验证SML-SCE算法的性能, 将其与多种方法进行对比, 包括主成分分析(principal component analysis, 简称PCA)^[24]、LPP、SR、ULGE、图嵌入集成学习(graph embedding-based ensemble learning, 简称GEEL)^[25]算法、基于图嵌入的无监督集成学习(unsupervised ensemble learning based on graph ebedding, 简称UEL-GE)^[26]算法.其中, PCA、LPP、SR、ULGE是流形学习算法, GEEL和UEL-GE是集成学习算法.此外, K-means方法直接在高维数据进行聚类, 作为一种Baseline方法.

3.1 数据集介绍

实验分别在3个图像数据集上进行, 分别为DBRHD^[27]、COIL20^[28]和ETH^[29].DBRHD是手写体数字数据集, 包含0~9这10个数字, 一共10个类别.COIL20是哥伦比亚大学图像库数据集, 包含20个物品, 每个物品拥有72张不同角度的图片.ETH是物品聚类和识别数据集, 包含80个物品, 一共归属为8个类别.这3个数据集的详细信息见表 2.

3.2 参数设置

为了验证SML-SCE和对比方法的性能, 在不同的低维空间进行实验.SML-SCE结合多个相似低维嵌入, 令低维嵌入的维度范围为1~15, 即, κ=1, ι=15.在构建图时, LPP、SR中的近邻样本点数和ULGE、GEEL、UEL-GE、SML-SCE中的近邻锚点数相同, 都等于5^[13].LPP和SR中的高斯核参数设置为1.在SR、ULGE和UEL-GE的正则化参数等于0.01^[13].GEEL和UEL-GE中的个体学习器的个数为7^[25].ULGE、GEEL、UEL-GE和SML-SCE都有关于锚点个数的参数.在4种方法中, 锚点个数都等于数据集样本点个数的35%.在SML-SCE中, 权重的丢弃率dr设置为70%.

3.3 评价指标

为了比较各种算法之间的性能, 采用K-means方法对低维嵌入进行聚类.聚类结果可通过聚类准确率(accuracy, 简称ACC)和归一化互信息(NMI)来衡量, ACC和NMI的值越高, 表示聚类效果越好.将聚类结果和真实标签进行比较, 分别计算ACC和NMI.为了保证实验结果的准确性, 每种方法运行20次, 并记录平均值.

所有实验代码均采用MATLAB编写.实验硬件环境为3.19GHz, Intel(R) Core(TM) i5-6500 CPU, 8GB内存, 系统为Windows 10.

3.4 结果分析

图 3是在不同约简维度下所有方法的ACC曲线.图 3(a)~图 3(c)分别为在DBRHD、COIL20和ETH数据集上的实验结果.因为SML-SCE结合了从1维到15维的相似低维嵌入, 所以在图中显示为一条直线.从图中可以发现, SML-SCE在3个数据集上的性能均优于所有对比方法.无论降到多少维度, SML-SCE均表现出明显的优越性.

DBRHD数据集共含有10类, 从中随机选取2/4/6/8/10类作为新数据集进行实验, 实验结果呈现在表 3中.相似地, 从COIL20中随机选取5/10/15/20类, 从ETH中随机选取2/4/6/8类作为新数据集进行实验, 将SML-SCE与其他方法进行对比.在实验中, 对比算法的约简维度设置为数据集类别数.表 3~表 5分别记录了在DBRHD、COIL20和ETH数据集上的平均ACC和NMI.在同一数据集下表现最好方法的实验结果加粗显示.由表格可知, 在3个数据集的不同类别下, SML-SCE均表现最优, 这表明SML-SCE算法明显优于其他对比算法.

3.5 参数分析

这一节讨论对算法性能产生影响的两个参数, 即锚点个数m和权重的舍弃率dr.图 4(a)展示了3个数据集上不同锚点个数下的ACC曲线.设锚点取值范围为样本点总数的10%~90%.从图中可以观察到, 当m取值为35%时, 在3个数据集上ACC均取得最大值.并且, 大量的锚点对于最终性能来说是无用的, 甚至会使得ACC值有所下降.因此, 在SML-SCE中, 锚点取值为样本点总数的35%.

图 4(b)是在3个数据集上不同权重舍弃率dr下的ACC曲线.观察图像可知, 在不同舍弃率dr下ACC的变化并不明显, 但是, 当舍弃率取值为70%时, SML-SCE在3个数据集上均表现最好.基于此, 实验中舍弃率dr取值为70%.

4 总结与展望

本文提出了一种新型的锚点生成方法, 名为改进的层次平衡K-means(MBKHK)方法.MBKHK生成了具有代表性的锚点, 且对锚点的个数没有限制.此外, 文中提出了相似流形的概念, 并提出基于选择聚类集成的相似流形学习(SML-SCE)算法.SML-SCE利用MBKHK生成锚点, 构造相似度矩阵, 直接得到低维嵌入, 并采用选择聚类集成融合多个不同维度的相似低维流形, 得到最终聚类结果.SML-SCE避免了对约简维度的选择和对本征维度的估计, 并取得了优异的性能.在3个图像数据集上的实验结果也表明了SML-SCE算法的优越性.

SML-SCE是一种无监督的相似流形算法, 但在现实生活中, 大多数数据并不全都是无标签的未知数据, 因此, 未来可以结合部分有标签数据和大多数无标签数据, 对本文算法进行改进, 将其拓展到半监督领域.