整数规划(integer programming, 简称IP)是20世纪60年代发展起来的规划论中的一个分支[1], 是一个NP难问题[2], 长期以来一直是受到应用数学、运筹学、管理科学、决策科学、系统科学、经济学等学科关注的前沿课题[3], 研究整数规划问题对社会的发展有着重大的研究意义.但是, 尽管众多学者投身于对整数规划问题的研究, 由于求解整数规划问题的难度远比求解一般规划问题要大, 因而至今仍缺乏有效的通用算法.
目前, 用于求解整数规划问题的方法[4]除了传统的分支定界法[5]、填充函数法[6]等和经典的群智能优化算法(如遗传算法(genetic algorithm, 简称GA)[7]、粒子群优化(particle swarm optimization, 简称PSO)算法[8]、蚁群优化(ant colony optimization, 简称ACO)算法[9]等)之外, 近几年来涌现出了大量的新算法.如在2013年, 吴炅等人[10]采用截断取整的方法, 将基本布谷鸟搜索算法用于求解整数规划问题; 魏林等人[11]采用和声搜索更新种群策略和个体扰动策略改善了蚁群算法过早收敛的问题, 提出了用和声蚁群耦合算法求解整数规划问题; 在2014年, Fahim等人[12]以变邻域搜索为核心, 提出了用混合分散搜索算法求解整数规划问题; 在2015年, Wu等人[13]采用新的人口初始化技术和动态非线性比例因子提高算法的优化能力, 提出了用改进的差分进化算法求解整数规划问题; 谢瑜等人[14]采用截断取整的方法, 将花授粉算法扩展到求解整数规划问题; 在2016年, Mohamed等人[15]将社会蜘蛛算法与Nelder Mead方法结合起来, 提出了用单纯形社会蜘蛛算法求解整数规划问题; 在2018年, 石礼堂等人[16]将滤子方法融合于填充函数法中, 提出了用滤子填充函数算法求解整数规划问题等等.这些算法都经过数值仿真实验证明了对求解整规划问题的性能, 但它们仍然存在自身的缺陷.如文献[10]中的算法虽然具备跳出局部最优的能力, 但其需要很大的迭代次数才能实现.文献[11]中的算法虽然改善了和声搜索算法过早收敛的缺点, 但还是没有克服鲁棒性差的特点.因此, 研究整数规划问题仍然是一个需要继续探索的工作.
传统的群智能演化算法有着共同的缺点, 即未能解决种群内部个体或者种群之间的探索与开采、竞争与协作的矛盾.在2018年, 谈庆在其硕士学位论文[17]中提出了一种基于金字塔结构的群智能演化策略(swarm intelligence evolution strategy based on pyramid structure, 简称PES), 通过理论分析以及实验仿真, 验证了该算法能够很好地解决上述两大矛盾.但该算法在内部合作上, 新产生的个体仅考虑了与旧个体之间的协作关系, 而未考虑与当前种群最优个体以及全局最优个体之间的协作关系, 使得算法在收敛速度上较慢.因此, 本文提出了基于择优协作模型的PES算法, 通过改变算法的内部协作方式来提高算法的收敛速度.此外, PES算法是针对连续性函数优化提出的一种群智能算法, 当所研究的问题的决策变量是离散型时, 该算法就不能直接被用于求解.因此, 本文设计了基于择优协作策略的PES算法去求解整数规划问题, 拓展了PES算法的应用领域.
本文第1节给出研究的相关工作, 介绍了标准的PES算法, 对算法的机理作了深入分析.第2节介绍基于择优协作策略的PES算法.第3节介绍该算法求解整数规划问题的实现过程.第4节对所提出的算法进行探索实现和对比实验, 通过实验结果分析算法对求解整数规划的性能.第5节总结全文并进行展望.
1 相关工作 1.1 标准的PES算法标准的PES算法是针对函数优化提出的一种群智能演化算法, 在文献[17]中, 它主要由以下几个公式完成对全局最优解的探索.
| $ {\left[ {{F^\prime },I} \right] = {\mathop{\rm sort}\nolimits} (F)} $ | (1) |
| $ {{X^\prime } = X[I] = \left[ {{X_4},{X_3},{X_2},{X_1}} \right]} $ | (2) |
| $ {\sum_{i = 1}^4 {length} \left( {{X_i}} \right) = length(X)} $ | (3) |
| $ {length\left( {{X_i}} \right) < length\left( {{X_{i + 1}}} \right),i = 1,2,3} $ | (4) |
| $ {x_i^{k + 1} = x_i^k + R_i^k \times \sigma } $ | (5) |
| $ {R_i^k \le R_{i + 1}^k,i = 1,2,3} $ | (6) |
| $ {R_i^{k + 1} = R_i^0 \times {\alpha ^k}} $ | (7) |
| $ {x = x_i^{k + 1} + \lambda \left( {x_i^{k + 1} - x_i^k} \right)} $ | (8) |
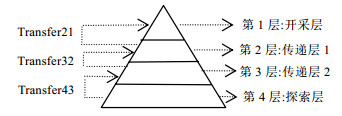
公式(1)是依据种群X的适应度值F的大小进行升序排序, 得到排序后的适应度值F'以及索引I.把排序后的群体X'按公式(2)与公式(3)将种群划分为4个部分, 每一部分的个体数目满足公式(4), 即由优秀个体组成的群体X1的数目最少, 由最劣个体组成的群体X4的数目最多.标准的PES算法将群体X1称为开采层, X2与X3称为传递层, X4称为探索层.每一层的个体
从第1.1节的寻优过程可以发现, 如图 1所示, 从开采层至探索层, 它们的数量、搜索邻域的大小、种群适应度值的大小自上而下地呈现金字塔形状, 每一层内的个体之间通过相互竞争来获得向上一层传递的机会, 依据层与层之间的传递来达到群与群之间的协作交流.整个金字塔模型与一个国家的组成架构非常相似, 少数的优秀个体视为国家的领导层, 部分个体视为管理层, 大多数个体视为基层.在国家的发展中, 个体所处的位置不同, 赋予的职能也就不同:领导层负责宏观调控, 做出一些大型决策; 管理层负责接收命令以及传递命令; 基层负责进行实现.层与层之间通过信息交互、互相协作来促进国家的发展, 层内个体之间一方面通过相互竞争来获取晋升的目的, 另一方面通过相互协作来完成上级的任务.随着国家的逐步发展, 个体的特性会因社会环境以及以往的经验与学习得以改变, 社会分工也会因之改变.如果个体业绩优秀, 他将成为同层之中的佼佼者, 拥有极大的上升的机会; 反之, 则有可能不适应所处环境而被淘汰.因此, 依据个体的特性, PES将种群划分为开采层、传递层1、传递层2、探索层这4个层次, 对不同层的个体赋予不同的职能:开采层主要负责深入挖掘已存在的优秀个体所在区域; 传输层一方面兼并开采与探索的工作, 另一方面通过传递操作构建开采层与探索层之间的桥梁; 探索层负责探索发现新的潜在优秀个体所存在的区域.PES算法通过这种明确的分工解决了开采与探索的矛盾.
对于传统的群智能算法, 它们大都忽略了种群个体以及群体之间的竞争与协作的矛盾, 如遗传算法的个体通过杂交将父代优秀基因传递给子代进行更新; 粒子群算法的个体依靠全局极值与当局部极值个体对该个体产生的驱动力进行更新; 蚁群算法的个体通过群体产生的信息素来进行分工协作进行更新.这些算法只涉及到极少个体之间的协作, 忽略了群体之间的协作, 缺乏信息交换传递.PES算法运用了层内竞争与层间协作策略解决了上述矛盾.对于层内竞争而言, 层内个体不仅因适者生存的压力不断的改善自身, 也会因个体间的晋升机制而相互竞争, 通过单精英轮盘赌策略以及与父代个体的协作完成各层的更新, 这种更新策略为算法的收敛性提供了理论基础.除了内部协作之外, PES算法还通过层与层之间个体的传递来完成群体间的交流, 这种层内竞争、层间协作的策略大大提升了算法探寻全局最优的能力.
2 基于择优协作策略的PES算法标准的PES算法包含两种协作:一种是层与层之间的群体协作, 加强了种群间的交流; 一种是层内个体与父代个体之间的协作, 虽然父代个体对子代产生新个体有一定的引导作用, 但它对产生优秀个体的指导性不强, 会造成算法的收敛速度缓慢, 影响算法应用的运行效率.粒子群算法通过与个体极值与全局极值来完成种群的更新, 具有收敛速度快的优点[18], 而这种更新规则恰好弥补了PES算法的个体间协作的不足.本文把这种思想融于标准的PES算法之中, 将通过选择与当前代层内种群的最优个体与整个种群的最优个体的协作来完成每一层个体的更新, 提出了一种基于择优协作策略的PES算法, 每一层个体的更新规则如下.
| $x_i^{k + 1} = x_i^k + rand \times R_i^k \times [w(pBest_i^k - x_i^k) + (1 - w)(gBes{t^k} - x_i^k)]$ | (9) |
其中,
基于择优协作的策略, 可以让父代个体沿着个体极值与全局极值协同产生的合力方向进行搜寻探索, 不仅加强了层内个体间的相互协作, 而且建立了各层内的个体与全局最优的个体之间的联系, 在层与层之间的协作、个体间的择优协作的策略之下, 加快了PES算法的收敛的速度, 提高了算法的寻优效率.
因此, 基于择优协作策略的PES算法不仅继承了标准PES算法跳出局部最优的特点[17], 还提高了算法收敛速度.基于择优策略的PES算法的操作流程见算法1.
算法1. 基于择优协作策略的PES算法.
Step 1. 初始化参数, 设置最大迭代次数M, 种群规模N, 各层初始搜索半径
Step 2. 随机产生种群规模为N的初始种群X0, 并置迭代次数k=0.
Step 3. 计算种群Xk的适应度值, 依据适应度值F(Xk)的大小将种群分为4个子种群
Step 4. 按公式(9)为第i(i=1, 2, 3, 4)层的个体
Step 5. 将更新后的每一层群体
Step 6. 判断停机条件.当迭代次数达到最大迭代次数M时, 则输出gBestk, 算法停止; 否则, 置k=k+1, 并更新各层搜索半径
整数规划的一般形式[19]可展开为
| $\left. \begin{gathered} \min {\;}f(x) \\ {\rm{s}}{\rm{.t}}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{g_i}(x) \leqslant 0,{\rm{ }}i = 1,...,m} \\ {{h_i}(x) = 0,{\rm{ }}i = m + 1,...,n} \\ {l \leqslant x \leqslant u} \\ {x = ({x_1},...,{x_n}),{\;}{x_i} \in Z,i = 1,...,n} \\ {l = ({l_1},...,{l_n}),{\rm{ }}u = ({u_1},...,{u_n})} \end{array}} \right. \\ \end{gathered} \right\}$ | (10) |
其中, gi(x)与hi(x)所在的不等式称为性能约束条件; l与u是变量的上下界, 所在不等式称为边界约束.如果要求的是目标函数f(x)的最大值, 只需在相同的约束条件下, 求-f(x)的最小值即可.
标准的PES算法优化的函数的决策变量是连续型的, 因而它不能直接用于求解整数规划问题.本文将提出的基于择优策略的PES算法扩展应用到求解整数规划问题上, 其设计如下:
3.1 适应度值函数首先利用罚函数的方法处理约束条件, 定义一族罚函数[20]{pi(x)}.
| ${p_i}(x) = \left\{ {\begin{array}{*{20}{l}} {\max \{ 0,{g_i}(x)\} ,{\;}1 \leqslant i \leqslant m} \\ {|{h_i}(x)|,{\rm{ }}1 + m \leqslant i \leqslant n} \end{array}} \right.$ | (11) |
| $viol(x) = \sum\limits_{i = 1}^n {{p_i}(x)} ,i = 1,...,n$ | (12) |
viol(x)反映了个体x偏离可行解的程度.以此偏离程度作为惩罚的大小, 适应度函数F(x)的定义如下.
| $F(x) = \left\{ {\begin{array}{*{20}{l}} { - f(x),{\rm{ if }}x \in D} \\ {F(gBest) - viol(x),{\rm{ if }}x \in \bar D} \end{array}} \right.$ | (13) |
其中, gBest是上代群体中最佳个体, D是可行解区域,
从以上定义可知:如果x∈D, 则偏离程度为0, 不对它进行惩罚, 以目标函数值的相反数作为它的适应度值;如果
标准的PES算法所求解问题的决策变量是连续型的, 它不能直接应用于求解整数规划问题.因此, 本文应用基于择优策略的PES算法在边界约束条件内产生规模为N的初始种群X0的规则如下.
| $ {X_0} = l + randint(0,u - l) $ | (14) |
其中, randint(0, u-l)是在指在区间[0, u-l]内产生含有n个随机整数的向量.
3.3 更新种群设
首先, 将公式(9)的决策变量转化成整数, 则每层个体的探索规则如下.
| $x_i^{k + 1} = x_i^k + round\{ rand \times R_i^k \times [w(pBest_i^k - x_i^k) + (1 - w)(gBes{t^k} - x_i^k)]\} $ | (15) |
其中, round{·}是一个取整操作.
然后, 从上一层的群体中选取一定比例的个体向下一层进行传递, 这里按照联赛规模为2的随机联赛的规则选取每一个被传递的个体.
接着, 将每一层产生的所有新个体、传递个体和父代个体, 按适应度值从大到小所整合在一起, 从该群体中选择相应层数的个数的个体作为该层的个体, 每个个体按照保留精英策略的轮盘赌规则进行选择.
最后, 将更新后的每层个体整合在一起作为新种群.由于新种群中可能出现相同的个体, 为了更好地体现种群多样性以及更有效率的寻优, 这里只保留所有相同个体中的一个, 其他个体用公式(14)随机产生的个体进行替代.找出当前种群中的全局最优个体gBest以及所对应的目标函数值f(gBest).
4 仿真实验实验工具:Matlab R2016a.实验环境:Windows 10操作系统, Intel处理器1.80GHz, 8GB内存.
4.1 PES探索实验此实验的目的是通过附录中的仿真问题[21]作为实验算例, 来验证基于择优协作策略的PES算法有着跳出局部最优、探寻到全局最优的特点.该算例的全局最优解为(0, 0), 最优函数值为0.该算例中的目标函数是一个不可分离的多峰函数, 图 2是它的三维图形, 从图中可以发现, 由于全局最优与最好的局部最优相距很远, 因此搜索算法往往朝着错误的方向进行收敛, 该函数带有一定的欺骗性.用PES求解该问题的参数设置为:最大迭代次数为1 000, 种群规模为40, 加速步长为0.5, 传递的个体比例各为0.2, 0.4, 0.6, 各层个体数目比例分别为0.1, 0.2, 0.3, 0.4.对于各层搜索半径分别为1, 2, 6, 8, 偏向权重设为0.5.其实验结果为图 3与图 4.

|
Fig. 2 3-D chart 图 2 三维图 |
|
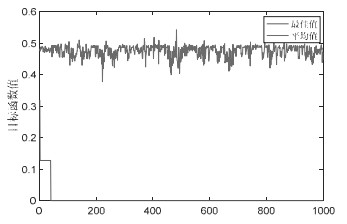
Fig. 3 Evolutionary curve 图 3 进化曲线 |

|
Fig. 4 Exploration process 图 4 探索过程 |
从图 3中可知, 在迭代40次后, 算法寻求到全局最优点, 各代种群平均适应度值平稳浮动.可见, 基于择优协作策略的PES算法有着可观的收敛速度.图 4是算法探索最优点的探索过程, 用不同的颜色区别不同层的个体.从图中可以发现, 初始时, 由于随机性产生初始种群, 因而种群分布比较分散; 但随着迭代的进行, 从第2代开始, 对每一个个体来说, 一方面受到层内竞争的压力以及上层对优秀个体的吸引力, 另一方面受到择优协作的指导, 在这种混合驱动的压力下, 使得优秀个体在PES算法的结构框架中能够更好地流动, 保留下来并孵化出新的优秀个体, 逐步探寻到全局最优点.由此可见, 在择优协作的策略下, PES能够很好地运用在求解整数规划问题上.
4.2 对比实验为进一步测试基于择优策略的PES算法在求解整数规划问题上的寻优性能, 对文献[22]中的5个经典整数规划问题以及文献[23]的3个整数规划问题进行了测试, 将结果与文献[22]中的遗传算法(GA)、模拟退火算法(SA)、遗传模拟退火算法(GSA)、混合遗传算法(HGA)和文献[23]中的混沌搜索的混合粒子群算法(CLSPSO)以及将粒子群优化算法与混沌搜索相结合的其他6种混合算法(CLSPSO、CLSPSO1、CLSPSO2、CLSPSO3、CLSPSO4、CLSPSO5)作了对比.
本实验所选择的测试问题包含多种类别:前两个问题是仅含边界约束的测试算例, 后6个测试算例含有性能约束条件.从峰值点的角度来看, 这些测试算例的目标函数均含有多个峰值点, 其中, 问题1、问题2、问题6、问题7具有多个局部最优点, 但仅含一个全局最优点.对于其他问题, 均存在多个局部最优点, 这些局部最优点的存在很容易“欺骗”算法陷入局部最优, 从而这些算例对测试算法跳出局部最优的性能具有重要的参考意义.
4.2.1 参数设置基于择优策略的PES算法对实验的8个实验算例均将最大迭代次数设置为1 000, 种群规模50, 分层比例设为0.1, 0.2, 0.3, 0.4, 由上至下层与层之间的传递比例设为0.2, 0.4, 0.6, 收缩因子α设为1, 偏向权重w设为0.5.由于问题规模不同, 故初始各问题的各层搜索邻域半径不同.其中, 问题1设为[1, 2, 4, 6], 问题2与问题3设为[1, 2, 3, 4], 问题4设为[1, 2, 3, 6], 其他问题均设为[1, 2, 4, 8].问题2~问题6给定的初始全局最优个体分别设为(0, 0, 0, 0, 0, 0, 0), (1, 1, 1, 1, 1, 1, 1, 1, 1, 1), (0, 0, 0, 0, 0, 0, 0, 0, 0, 0), (20, 20, 20, 20, 20), 问题7的前20个元素为10, 后20个元素为20;问题8的初始全局最优个体为原点.
4.2.2 实验结果与分析以下各表中, Pb表示问题的编号, min, max分别指求问题的最小与最大值.为了更好地与文献中的其他算法做出对比, 表 1中基于择优策略的PES所对应最佳值也是独立算得5次取最好所得到的结果, 消费时间是指5次运行消耗的总时间.
| Table 1 Comparison results of five algorithms 表 1 5种算法比较结果 |
从表 1中可以发现:
● 在最优值这个指标上, 对于问题1与问题2, 本文算法与HGA所得结果相同, 它们均找到了全局最优点, 而GA、SA、GSA都陷入了局部最优; 对于问题3~问题5, 本文算法比其他4种算法所得到的结果要好, 说明本文算法比其他算法跳出局部最优的能力要强.
● 在运行时间这个指标上, 除了问题3以外, 其他算法运行5次的所消耗的总时间都至少比本文算法出高出1倍.
| Table 2 Experimental results of seven algorithms on three testing functions over 50 trials 表 2 7种算法对3个测试函数50次实验的实验结果 |
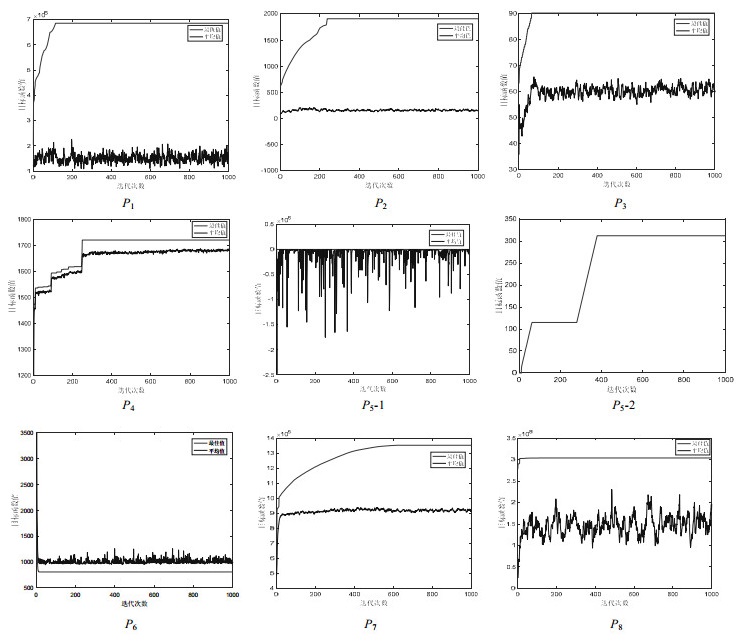
图 5是基本文算法对各问题求解中的进化曲线.其中, 对于P5, 由于公式(13)的设立, 各代种群平均值与最佳值的相差较大(P5-1), 为了明显地看到最佳值的进化过程, 单独作了种群平均值的进化曲线图P5-2.
|
Fig. 5 Evolution curves of various problems (Continued) 图 5 各问题的进化曲线 |
在图 5中可以看到, 大多数问题在200代便能找到最佳函数值, 并且在前几代进化速度非常快.这是种群之间的分工合作的结果, 个体的更新受到个体极值与全局极值的指引, 在各自的职能范围内完成寻优过程.
由以上各分析可知, 基于择优策略的PES算法继承了标准PES算法善于寻找全局最优的特点, 并且通过运用择优协作的策略, 提高了算法的收敛速度; 相对所对比的算法, 本文算法能够很好地求解具有多峰特点的整数规划问题.
5 总结与展望本文深入分析了标准的PES算法的机理, 针对PES算法的群内协作的不足, 提出了基于择优策略的PES算法, 并将它应用到求解整数规划问题上.通过数值仿真实验, 说明了所提出的算法在求解具有多峰特点的整数规划问题上有着良好的性能.除了本文对PES算法的拓展之外, 还有很多方面值得探讨, 如在理论上对PES算法的性能加以分析; 给出算法的收敛性、稳定性、全局最优性的理论支持.这是下一步的重点研究工作.
| [1] |
Moeini A. Identification of unidentified equality constraints for integer programming problems. European Journal of Operational Research, 2017, 260(2): 460-467.
[doi:10.1016/j.ejor.2016.12.040] |
| [2] |
Huang ZC, Wu FC, Hu XL. An evolutionary algorithm to integer programming problem based on pheromone. Computer Application Research, 2001, 18(7): 27-29(in Chinese with English abstract).
[doi:10.3969/j.issn.1001-3695.2001.07.010] |
| [3] |
Li T, Wang CF, Wang WB, Su WL. A bionic global optimization algorithm for solving integer programming-Plant growth simulation algorithm. System Engineering Theory and Practice, 2015, 25(1): 76-85(in Chinese with English abstract).
[doi:10.3321/j.issn:1000-6788.2005.01.012] |
| [4] |
Yang F, Wang PX, Zhang YZ, Zheng LT, Lu JC. Survey of swarm intelligence optimization algorithms. In:Proc. of the 2017 IEEE Int'l Conf. on Unmanned Systems (ICUS). IEEE, 2017, 558-563.
[doi:10.1109/ICUS.2017.8278405] |
| [5] |
Chiang HD, Wang T. A novel trust-tech guided branch-and-bound method for nonlinear integer programming. IEEE Trans. on Systems Man Cybernetics-Systems, 2015, 45(10): 1361-1372.
[doi:10.1109/TSMC.2015.2399475] |
| [6] |
Li MM, Zhang LS, Liang YM. A filled function method with one parameter for integer programming. Chinese Journal of Computers, 2008, 12(2): 73-83.
[doi:10.1007/BF02842060] |
| [7] |
Yang CR, Qian Q, Wang F, Sun MH. Application of improved adaptive genetic algorithm in function optimization. Computer Application and Research, 2018, 35(4): 1042-1045(in Chinese with English abstract).
[doi:10.3321/j.issn:1000-6788.2005.01.012] |
| [8] |
Bera A, Sychel D. Hybrids of two-subpopulation PSO algorithm with local search methods for continuous optimization. Artificial Intelligence and Soft Computing, 2015, 9119: 307-318.
[doi:10.1007/978-3-319-19324-3_28] |
| [9] |
Zhao YP, Dong ZZ, Li Z. Improved ant colony algorithm for integer programming. Journal of Xi'an Petroleum University (Natural Science Edition), 2013, 28(3): 100-103(in Chinese with English abstract).
[doi:10.3969/j.issn.1673-064X.2013.03.022] |
| [10] |
Wu J, Zhou JY. Cuckoo search algorithm for solving integer programming. Mathematical Theory and Application, 2013, 33(3): 99-106(in Chinese with English abstract).
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sxllyyy201303015 |
| [11] |
Wei L, Fu H, Yin YP. Application of harmony ant colony algorithm to integer programming. Computer Engineering and Applications, 2013, 49(20): 5-8(in Chinese with English abstract).
[doi:10.3778/j.issn.1002-8331.1304-0332] |
| [12] |
Fahim A, Hedar AR. Hybrid scatter search for integer programming problems. In: Proc. of the 9th Int'l Conf. on Informatics and Systems. IEEE, 2015.[doi: 10.1109/INFOS.2014.7036698]
|
| [13] |
Wu J, Gao YL, Yan LN. An improved differential evolution algorithm for mixed integer programming problems. In:Proc. of the 9th Int'l Conf. on Computational Intelligence and Security. IEEE, 2013, 31-35.
[doi:10.1109/CIS.2013.14] |
| [14] |
Xie Y, Gao XZ. Flower polling algorithm for integer programming. Techniques and Methods, 2015, 34(3): 82-85(in Chinese with English abstract).
[doi:10.19358/j.issn.1674-7720.2015.03.026] |
| [15] |
Mohamed AT, Ahmed FA. Simplex particle swarm optimization with arithmetical crossover for solving global optimization problems. OPSEARCH, 2016, 53(4): 705-740.
[doi:10.1007/s12597-016-0256-7] |
| [16] |
Shi LT, Chen W. Filter filled function algorithm for integer programming problems. Journal of Applied Mathematics and Computational Mathematics, 2018, 32(2): 331-342(in Chinese with English abstract).
[doi:10.3969/j.issn.1006-6330.2018.02.013] |
| [17] |
Tan Q. Swarm intelligence evolution strategy based on pyramid[MS. Thesis]. Wuhan: Wuhan University of Technology, 2018(in Chinese with English abstract).
|
| [18] |
Cai XJ, Cui ZH, Zeng JC, Tan Y. Dispersed particle swarm optimization. Information Processing Letters, 2008, 1005(6): 231-235.
[doi:10.1016/j.ipl.2007.09.001] |
| [19] |
Yang LF, Jin BJ, Wang YY, Dong ZZ. Projected mixed integer programming formulations for unit commitment problem. Int'l Journal of Electrical Power & Energy Systems, 2015, 68: 195-202.
[doi:10.1016/j.ijepes.2014.12.054] |
| [20] |
Deep K, Singh KP, Kansal ML, Mohan C. A real coded genetic algorithm for solving integer and mixed integer optimization problems. Applied Mathematics and Computation, 2009, 212(2): 505-518.
[doi:10.1016/j.amc.2009.02.044] |
| [21] |
Yang RH, Liu JH. Quantum particle swarm optimization algorithm for integer programming. Science Technology and Engineering, 2011, 11(13): 1671-1815(in Chinese with English abstract).
[doi:10.3969/j.issn.1671-1815.2011.33.021] |
| [22] |
Huang S, Ma L. Improved harmony search algorithm for solving general integer programming problems. Computer Engineering and Applications, 2014, 50(3): 250-255(in Chinese with English abstract).
[doi:10.3778/j.issn.1002-8331.1203-0483] |
| [23] |
Tan Y, Tan GZ, Deng SG. Hybrid particle swarm optimization with chaotic search for solving integer and mixed integer programming problems. Journal of Central South University, 2014, 21(7): 2731-2742.
[doi:10.1007/s11771-014-2235-6] |
| [2] |
黄樟灿, 吴方才, 胡晓林. 基于信息素的整数规划的演化求解. 计算机应用研究, 2001, 18(7): 27-29.
[doi:10.3969/j.issn.1001-3695.2001.07.010] |
| [3] |
李彤, 王春峰, 王文波, 宿伟玲. 求解整数规划的一种仿生类全局优化算法——模拟植物生长算法. 系统工程理论与实践, 2015, 25(1): 76-85.
[doi:10.3321/j.issn:1000-6788.2005.01.012] |
| [7] |
杨从锐, 钱谦, 王锋, 孙铭会. 改进的自适应遗传算法在函数优化中的应用. 计算机应用研究, 2018, 35(4): 1042-1045.
[doi:10.3321/j.issn:1000-6788.2005.01.012] |
| [9] |
赵元鹏, 董张卓, 李哲. 改进的求解整数规划的蚁群算法. 西安石油大学学报(自然科学版), 2013, 28(3): 100-103.
[doi:10.3969/j.issn.1673-064X.2013.03.022] |
| [10] |
吴炅, 周健勇. 整数规划的布谷鸟算法. 数学理论与应用, 2013, 33(3): 99-106.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=sxllyyy201303015 |
| [11] |
魏林, 付华, 尹玉萍. 和声蚁群耦合算法求解整数规划的应用研究. 计算机工程与应用, 2013, 49(20): 5-8.
[doi:10.3778/j.issn.1002-8331.1304-0332] |
| [14] |
谢瑜, 高晓智. 整数规划的花授粉算法. 技术与方法, 2015, 34(3): 82-85.
[doi:10.19358/j.issn.1674-7720.2015.03.026] |
| [16] |
石礼堂, 陈伟. 整数规划问题的滤子填充函数算法. 应用数学与计算数学学报, 2018, 32(2): 331-342.
[doi:10.3969/j.issn.1006-6330.2018.02.013] |
| [17] |
谈庆.基于金字塔结构的群智能演化策略[硕士学位论文].武汉: 武汉理工大学, 2018.
|
| [21] |
杨荣华, 刘建华. 量子粒子群算法求解整数规划的方法. 科学技术与工程, 2011, 11(13): 1671-1815.
[doi:10.3969/j.issn.1671-1815.2011.33.021] |
| [22] |
黄帅, 马良. 改进和声搜索算法求解一般整数规划问题. 计算机工程与应, 2014, 50(3): 250-255.
[doi:10.3778/j.issn.1002-8331.1203-0483] |
 2020, Vol. 31
2020, Vol. 31