2. 武汉大学 计算机学院, 湖北 武汉 430072
2. School of Computer Science, Wuhan University, Wuhan 430072, China
计算机已经渗透到社会生产和人类生活的方方面面, 与计算机相关的各种故障足以造成巨大的经济损失. 2017年, 全球爆发的勒索病毒(WannaCry)源于Windows操作系统的漏洞(MS17-010);早在1994年, 奔腾处理器的浮点除运算错误使得英特尔公司不得不召回成百上千万芯片, 损失约4.5亿.更为严格的研发方法, 能够避免许多这样的错误.在这些方法中, 机械化定理证明是被学术界广泛认可的形式验证技术[1], 并在工业界获得了越来越多的成功应用.
机械化定理证明是指使用计算机, 以定理证明的方式对数学定理或计算机软、硬件系统进行形式验证, 是人工智能(artificial intelligence, 简称AI)的一种体现.Leibniz早在17世纪时就形成了由机器证明定理的思想, 然而直到19世纪末现代逻辑的创立和发展, 以及20世纪40年代计算机的出现, 才使得这一设想的实现具有了现实可能性[2].
始于20世纪50年代和60年代, 机械化定理证明围绕计算机如何高度自动化地完成证明而展开.受当时倡导的人工智能潜能的影响, 自动定理证明(automated theorem proving, 简称ATP)技术的研究经历了一段炽热的研发期, 也取得了许多具有影响力的成果; 但是随着新问题、新技术和新思想的到来, 完全自动定理证明的研究渐入停滞期, 对于大多数有意义的数学定理或计算机系统的正确性, 交互式地进行证明可能是唯一可行的工作方式[3].
交互式定理证明(interactive theorem proving, 简称ITP)在20世纪60年代开始呈现, 交互式定理证明工具也称为证明助手(proof assistant).交互式意味着用户能够引导证明过程, 在这个过程中, 用户使用某种语言编写证明纲要(outline); 证明助手自动填充证明的细节, 并检查证明, 最终机器完成整个形式证明.这种证明纲要的思想最初体现在Wang于1960年的著作中[4].McCarthy在1961年也指出:相比完全手工的数学证明, 由计算机检查的证明(纲要)可能更为简短和易于编写; 在证明(纲要)的引导下, 计算机能够生成大量证明细节, 并检查每步证明的正确性; 这些大量的、机械性的证明工作对于实际定理的证明来讲, 人工是很难胜任的[5].
自动定理证明最初旨在证明数学定理.不过, McCarthy同时指出:计算机能够检查的不仅仅是数学证明, 而且还包括复杂工程系统以及计算机程序是否符合它们的规范.事实正是如此, 从20世纪60年代晚期开始, 人们认识到许多其他问题, 譬如程序属性、专家系统和集成电路设计相关的许多问题等, 都可以表示为定理, 而由自动定理证明工具予以解决[6].并且, 对于程序的机械化验证而言, 交互式方式比完全自动化更为适用, 也促进了许多研究从完全自动化转换到交互式方式.
机械化定理证明的研究发展至今, 已经产生了比较成熟的证明助手, 如Isabelle/HOL(http://isabelle.in.tum.de/)、Coq(https://coq.inria.fr/)、HOL4(https://hol-theorem-prover.org/)、ACL2(http://www.cs.utexas.edu/users/ moore/acl2/)等.经过许多年的努力, 分别在Coq和Isabelle/HOL的支持下, 出现了首个验证的C优化编译器, 称为CompCert[7—9], 以及第一个验证的操作系统微内核seL4[10—12], 已应用于安全攸关的工业开发中.这一领域的研究已经催生了每年举办的交互式定理证明(interactive theorem proving, 简称ITP)国际会议, 全世界范围的研究者们在这一会议上分享自己的研究成果.许多有关数据结构和算法分析、深度学习算法以及文件比较算法等研究成果也正在被机器验证[13—16].
这些研究结果究竟是如何取得的?19世纪末, 德国哲学家、逻辑学家及数学家Frege试图证明“所有数学都可归为逻辑”, 结果创立了谓词逻辑; 20世纪, 德国数学家Hilbert试图证明数学是没有矛盾的, 他创建了现代证明理论; 荷兰数学家和哲学家Brouwer同样为了研究数学基础而开创了直觉主义的数学哲学[17].建立在这些基础之上, 许多数学家、逻辑学家和计算机科学家在进一步研究的过程中提出了新的理论, 在实践中不断发现新问题, 并给出有意义的解决方案.机械化定理证明的理论基石和支撑技术就来自这些交织进行的研究发展, 并在长达约60多年的持续研究过程中稳步向前推进.本文重点关注了对机械化定理证明具有重要影响力的理论和技术、相应的实现以及它们的应用.
本文第1节阐述与机械化定理证明紧密相关的概念和理论、主流或具有持续影响力的技术, 并剖析它们之间的联系以及变迁发展.第2节分析、比较各类证明助手的特点、开发和实现.第3节讨论它们在数学和计算机领域的应用现状, 并对编译器验证和操作系统微内核验证进行了详细分析.最后对机械化定理证明进行总结, 并提出面临的挑战和未来研究方向.
1 逻辑基础和关键技术分析本节从一阶逻辑(first-order logic)和基于消解(resolution-based)的证明技术开始论述, 这是机械化定理证明研究得最久并仍然活跃的自动定理证明领域.然后, 论述将自然演绎和类型理论关联起来的Curry-Howard同构(correspondence), 它是当前以类型论为基础的证明助手的理论基石.接下来, 针对被广泛研究的程序的机械化验证, 讨论该领域主要使用的3种编程逻辑(logics of programming)和相关的编程语言语义(semantics).之后, 阐述在当时相当激进但却获得成功的基于高阶逻辑(higher-order logic)的硬件验证.最后讨论了程序构造(program construction)和求精(refinement)的方法.
1.1 一阶逻辑和基于消解的证明技术自动定理证明要解决的主要问题是:
1) 知识如何展现?即用什么语言表述定理;
2) 如何由已有知识推导得到新的知识?即研究由已有定理(或公理)推出新定理的推理规则;
3) 如何找到证明, 即控制推理规则的使用.
自动定理证明最初使用相对简单的命题逻辑语言, 但是命题逻辑所能表述的定理太具限制性.相比而言, 一阶谓词逻辑(简称一阶逻辑)具有更强的表述力, 并具有理论上的完备性, 自动定理证明转而采用一阶逻辑.
第2)和第3)两个问题的解决相对更困难一些:数学家们或者人类在证明定理时, 人脑存储了许多已有知识.通常, 经验、洞察力、甚至直觉对完成定理的证明也起了很大作用; 开发自动定理证明工具需要找到适合机器推理的方法.Prawitz首次提出了通过计算进行合一(unification)的置换方法[18], 许多后来的合一算法都使用了类似的计算方式.Davis和Putnam于1960年提出了反驳法(refutation)和单文字子句(one-literal clauses)的消除规则, 称为单元消解法(unit resolution)[19].在这些研究成果的推动下, Robinson重新发现了合一和消解规则[20], 并以优雅的方式将这两个强大的技术实现在了IBM 704机器上[21], 称为基于消解的技术.
基于消解的证明技术迅速成为了广被研究的主题.大量研究开始深入探索启发式策略, 用来控制消解, 以减少证明搜索空间.许多启发式策略是领域特定的, 譬如适合平面几何的策略并不适合群理论.一些研究赞成更为通用的启发式策略, 将策略实现为作用在证明机制上的限制[22], 并研究施加了限制之后的一阶系统是否仍然是完备的, 能否证明所有一阶定理(不计时间和内存空间限制).到20世纪60年代晚期, 大量研究提出了一系列技术, 产生了丰硕的研究成果.然而, 接之而来的研究实验结果表明:随着待证明定理复杂性的递增, 自动定理证明工具所花费的时间甚至远远超出了人的寿命.在当时, 这种灾难性的结果因为Gödel的不完备性定理而被理解, 因为“在一致的、定义了算术的一阶逻辑系统中, 总存在既不能证明又不能证否的定理”.从20世纪70年代开始, 自动定理证明的重心开始转向有效性方面, 并在程序验证、专家系统、电路设计验证等领域发挥作用.
Davis和Putnam也定义了可满足的(satisfiable)命题逻辑公式, 即布尔可满足性问题(Boolean satisfiability problem), 也称为SAT, 并受到广泛关注.针对这个问题, Davis和Putnam以及Logemann和Loveland提出了著名的DPLL算法[19, 23], 成为当前许多SAT求解器的基础算法.在SAT的基础之上, SMT(satisfiability modulo theories)处理了具有相等的一阶逻辑(first-order logic with equality)公式.许多SMT求解器的开发相当成功, 如微软公司开发的Z3是一个强大的自动定理证明工具(https://github.com/Z3Prover/z3), 用于验证软件及电路设计.Liu等人开发了NuTL2PFG工具, 用来判定线性μ演算(vTL)公式的可满足性[24].当前, 开发SMT求解器的研究仍然活跃, 可满足性理论及其应用大会每年承办SMT-COMP竞赛, 评估众多SMT求解器(http://smtcomp.sourceforge.net/2018).
一阶逻辑自动定理证明本身的研究是非常具有意义的, 基于消解技术的具大影响力也一直持续到现在. Vampire被认为是当前相当成功的一阶逻辑自动定理证明工具(http://vprover.org), 它的研究始于1994年, 已连续多年获得由自动推理大会承办的自动定理证明工具竞赛的FOF(first-order formulas)组和CNF(first-order problems in conjunctive normal form)/MIX组的冠军.
值得指出的是, 早在20世纪60年代初, McCarthy就将语言设计作为他的优先研究领域:良好设计的语言能够很大程度地减轻编写证明助手的工作量; 他在1962年设计和实现了被广泛使用的人工智能语言Lisp.事实证明了McCarthy的正确:当前主流证明助手ACL2、Nuprl(http://www.nuprl.org)和PVS(http://pvs.csl.sri.com)等的实现语言就是Lisp方言Common Lisp.
1.2 自然演绎和Curry-Howard同构基于消解的证明技术使用的是反驳法, 譬如, 如果要证明“由P→Q和P可以推出Q”, 其过程是:首先, 用逻辑与操作将待证明结论Q的否¬Q和所有前提联结, 形成(P→Q)∧P∧(¬Q), 再转换成合取范式(¬P∨Q)∧P∧(¬Q), 所有合取分量形成子句集{(¬P∨Q), P, (¬Q)}; 于是, 可在前两个子句上运用消解规则, 消除互补公式¬P和P, 得到结果子句集{Q, (¬Q)}; 同理, 在剩余的一对子句上再次运用消解规则, 结果产生空子句, 因此初始推测就是定理.若不能继续运用消解规则, 而未产生空子句, 表示前提推不出结论.因此, 初始推测并不是定理.事实上, 上述证明的定理是肯定前件式(modus ponens), 它本身可以视为一个特殊的消解规则.
自然演绎系统通常并不否定待证明定理, 它力图自然地、像人类思考那样进行推理.自然演绎系统具有许多推理规则, 它们和简单类型理论的类型规则之间存在着对应关系.Curry-Howard同构的发现以及扩展, 使得逻辑学家和计算机科学家基于证明和程序之间的对应关系而开发出了强大的类型理论以及相应的证明助手.
1.2.1 自然演绎Hilbert于1920年启动了称为“Hilbert’s program”的研究计划, 目标是证明数学是一致的(consistent):所有数学都可由正确选择的一套公理系统而推得.然而, Gödel的不完备性定理被广泛认为宣告了Hilbert研究计划的失败.尽管如此, Hilbert创立了现代证明理论.在他的演绎推理系统中, 公理定义了大多数逻辑操作符的语法, 而仅有一条称为肯定前件式的推理规则, 这使得有些公理看起来令人生畏, 譬如((P→(q→r))→((P→q)→(P→ r))).Łukasiewicz在1926年提出了改进Hilbert的公理系统, 他建议在推理规则的前提和结论中包括假定(assumptions), 允许由假定推得结论.响应于他的倡导, Gentzen于1934年设计了这样的系统[25].
Hilbert公理系统中的命题形如⊦A, 而在Gentzen设计的系统中形如B1, …, Bn⊦A, 表示“假定B1, …, Bn都成立的条件下, A是真的”; 将大写希腊字母Γ表示一系列命题B1, …, Bn, 则形如Γ⊦A.一个Gentzen风格的命题逻辑自然演绎系统如图 1所示.从图 1可以看出:为了更接近于真实的推理, 除了相等(identity)规则外, Gentzen为每个逻辑操作定义了一对规则:引入(introduction)和消除(elimination)[26]规则.

|
Fig. 1 A natural deduction system of Gentzen style (propositional logic) 图 1 一个根岑风格的自然演绎系统(命题逻辑) |
Gentzen的初始动机是为了证明数论的一致性.为实现这个目标, 他提出了称为“子公式属性(subformula property)”的概念, 即“任何形如Γ⊦A定理的证明都可以简化, 使得出现在简化证明中的定理只可能是A, 或者来自Γ, 或者来自A和Γ”.Gentzen设计了“sequent calculi”作为技术手段, 阐明他的思想.在这个演算中, 定理形如B1, …, Bn⊦A1, …, Am, 称为sequent.Gentzen定义了一个cut规则, 如公式(2.1)所示:
| $\frac{{\mathit{\Gamma } \vdash A, \mathit{\Delta }\quad \mathit{\Pi }, A \vdash \mathit{\Lambda }}}{{\mathit{\Gamma }, \mathit{\Pi } \vdash \mathit{\Delta }, \mathit{\Lambda }}}$ | (2.1) |
即“cut”掉了A的出现.然后, 他证明了“cut elimination定理”:任何使用了cut规则而得到证明的sequent, 都可以不使用该规则而得到证明.从这个意义上讲, 不使用cut规则的定理证明具有子公式属性.
这种简化的证明更易于机器推理.sequent推理演算系统事实上提供了一个方便的工具, 用于设计证明搜索算法, 该算法应用推理规则, 后向证明定理.Gentzen证明了一阶经典逻辑和直觉主义逻辑的sequent推理演算满足子公式属性, 并证明了具有一个无限归纳规则的算术公理系统的一致性.但是, 他不能证明形如Γ⊦A的自然演绎系统具有子公式属性.
自然演绎系统具有大量的推理规则, 控制这些规则的使用, 是实现机械化推理的重要手段.譬如, 对于A, B⊦A∧B, 即从假定A和B推出A∧B这样一个简单的定理, 机器可能会以一种相当繁琐的方式进行, 如图 2所示:通过推得(B∧A→A∧B)和B∧A, 再利用肯定前件式推理规则完成证明.

|
Fig. 2 A roundabout mechanical proof of A, B⊦A∧B 图 2 机器证明A, B⊦A∧B可能的一个繁琐过程 |
从图 2的证明过程可以看出:除了待证明定理A, B⊦A∧B中出现的公式A, B和A∧B以外, 还出现了B∧A.但是, 一个直接且简单的证明只应用两次相等规则和一次与引入规则就可以完成证明, 如图 3所示.与图 2的证明过程相比, 没有出现B∧A.事实上, 简化自然演绎的关键技术已经发表, 即Church的λ演算, 接下来我们对此加以分析.

|
Fig. 3 A simple mechanical proof of A, B⊦A∧B 图 3 A, B⊦A∧B简单证明过程 |
1.2.2 类型化的λ演算
Church于1940年提出类型化的λ演算[27], 称为简单类型理论(simple theory of types).“简单”一词可追溯到类型论的早期历史.Russell和Whitehead为解决朴素集合论中的悖论问题而系统性地论述了分支类型论(the ramified type theory)[28].分支类型一层来源于分支的分层(ramified hierarchy)这个概念, 即对类型进一步分阶(orders).在类型分层中, 个体具有的类型处于最低层, 高层类型的数学对象基于低层所构建, 构建的对象具有固定的类型.当形成集合时, 集合中的元素必须具有相同的类型, 设为τ, 而该集合的类型是τ set, 因此, 不可能构造出R∈R这样的命题:如果R的类型是τ, 它的类型不可能同时又是τ set.类型分层的引入, 避免了著名的Russell悖论[29].阶分层是为了避免“说谎者(liar)”这种悖论.然而, 阶分层出现了新的问题, 为此, Russell引入了可归约公理(reducibility axiom).最终, Russell的学生宣布:阶分层和可归约公理在“逻辑”悖论中是多余的, 该观点得到了Russell的认可.之后, Chwistek和Ramsey提出了去除可归约公理, 保留类型分层, 从而得到简化了的类型理论, 即简单类型理论.
最具有影响力的简单类型理论就是Church的类型化λ演算.在这个演算中, Church准确地形式化了包括量词的语法, 解决了原始λ演算中的不一致, 这项技术成为当前证明助手的标准[30].
λ演算的设计初衷是为了使用函数, 而不是使用集合来研究数学基础, 因此, Church设计了这种非常紧凑的函数书写形式.通常, 函数f的定义形式是f(x)=t, 其中, t是包含了x的项.在λ演算中, 书写为λx.t, 称为λ抽象.x取某个特定值u而产生一个函数返回值f(u), 对应的λ项书写为(λx.t)(u), 称为应用(application).t[u/x]也是一个λ项, 表达置换(substitution), 即t中x的每个出现都置换为u.于是, 计算是项的归约.应用的归约规则如公式(2.2)所示:
| $ \begin{equation} (\lambda x, t)(u) \Rightarrow t[u / x] \end{equation} $ | (2.2) |
其中, 符号⇒的意思是“归约为”.
为使得λ演算支持更多的数据结构, 进一步添加λ项:元组⟨t, u⟩, ⟨t, u⟩.fst和⟨t, u⟩.snd, 后两项分别表示取得元组的首元素和第2个元素, 相应的归约规则是公式(2.3)和公式(2.4):
| $ \langle t, u\rangle .fst \Rightarrow t $ | (2.3) |
| $ \langle t, u\rangle .snd \Rightarrow u $ | (2.4) |
在λ演算中, 函数可以作为参数, 并可以返回函数.自然数n可以定义为一个λ函数, 该函数以函数作为参数, 应用了n次.
类型化的λ演算是给每个λ项指定一个类型, 以冒号表示.记A→B为函数类型, 表示函数的形参类型是A, 而返回值类型是B.记A∧B为元组的类型, 表示元组中首元素的类型是A, 第2个元素的类型是B.因此, Church的类型化λ演算的片段如图 4所示.

|
Fig. 4 A fragment of Church's typed λ-calculus 图 4 Church类型化λ演算片段 |
类型论并未受到数学家们的欢迎, 但是通过Church的简单类型理论, 它得到了计算机科学家们的推崇:类型化的λ演算特别适合软、硬件系统的规范和验证.许多后来的类型系统都在这个简单类型理论的基础上进行了扩展, 增加了更为丰富的类型, 譬如多态和依赖类型, 因此从这个意义上也可以说, Church的类型化λ演算是简单类型的(simply typed).函数可以作为参数, 也可以返回函数; 量化可以不受限制地应用在所有阶的命题上, 简单类型理论也称为高阶逻辑(higher-order logic)[31].
相比集合论, 类型论在机械化解决许多问题方面更具有优势.譬如, 在集合论中可以书写被类型论视为不合法的各种表达式, 数学家们能从直觉上拒绝它们.但是操纵这些数学表达式的计算机并不具备这样的直觉, 如果不以某种策略方式告诉计算机区分不同类型的数学对象, 计算机的处理是相当低效的.此外, 自动推理系统中的一个基本操作是找到变量的合适置换, 区分不同实体的类型, 避免了大量无用搜索.
近些年来, 普林斯顿高等研究院(Institute for Advanced Study in Princeton)着手探究一种基于依赖类型的更复杂的类型论, 即同伦类型理论(homotopy type theory)[32].该理论使用homotopy这个代数拓扑学的分支来解释类型理论, 将类型视为空间(spaces).这个逻辑允许用相对简单的方式定义和计算代数拓扑里的基本群概念, 对于形式化数学有很大帮助.
1.2.3 Curry-Howard同构和扩展由图 1和图 4可以看出:如果忽略类型化λ演算中的黑体加粗部分, 它和自然演绎规则是完全一样的.这种对应关系最早由Curry发现:组合子(可以视为一种无变量的λ表达式)的类型对应于Hilbert公理系统中的直觉主义命题逻辑公理.
直觉主义指的是Brouwer所代表的数学哲学思想.为解决朴素集合论中的悖论问题, Brouwer提出了与主流数学界完全不同的观点:悖论的存在说明了经典数学本身存在问题, 而不是因为数学家们在证明数学没有矛盾的方法上出了问题, 数学必须重新构建, 因此产生了直觉主义的算术、代数、集合论等等.Brouwer认为, 数学是人的思维活动, 数学由这样的思维活动一个接一个地归纳构造出来, 任何不能构造出来的东西都不属于数学.因此, 数学直觉主义哲学也称为构造主义数学.直觉主义拒绝排中律, 这在当时是一个相当尖锐的观点, 也因此没有得到主流数学的青睐.但是, 其“构造”的思想建立了直觉主义逻辑与计算之间的联系.
Gentzen的自然演绎在1934年发表, 但他不能简化自然演绎的证明; Church类型化的λ演算在1940年发表, 而类型化λ项的归约就对应着证明的简化; 直至1965年, Prawitz给出了自然演绎的全面总结, 他将大部分sequent推理演算工作都转换到了自然演绎框架中, 证明了自然演绎具有子公式属性[33]; 最后在1969年, Howard描述了自然演绎与类型化λ演算之间的对应关系, 称为Curry-Howard同构[34].在这个同构中, 直觉主义逻辑的命题公式对应于简单类型理论的类型, 称为“命题即类型(propositions-as-types)”, 或者“公式即类型(formulae-as-types)”.于是, 证明一个永真式(定理)等同于找到该类型的一个λ项, 因此也称为“证明即项(proofs-as-terms)”或者“证明即程序(proofs-as-programs)”.譬如, 对于图 3中每步证明中的命题逻辑公式, 都可以构建相应的λ项, 如图 5中的黑体加粗项所示.可以看出, 构建出来的λ项是一个元组⟨x, y⟩, 两个分量的类型分别是A和B.
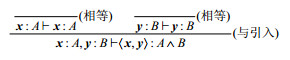
|
Fig. 5 A proof of A, B⊦A∧B with type derivations 图 5 证明A, B⊦A∧B的类型推导 |
进一步考虑, 根据图 2所示的证明过程, 所构建的λ项是(λz.⟨z.snd, z.fst⟩)(⟨y, x⟩), 其中, x是A类型, y是B类型.按照归约规则可以归约为⟨x, y⟩, 如公式(2.5)所示:
| $ (\lambda z.\langle z.snd, z.fst\rangle )(\langle y, x\rangle ) \Rightarrow \langle \langle y, x\rangle .snd, \langle y, x\rangle .fst\rangle \Rightarrow \langle x, y\rangle $ | (2.5) |
因此, 项的归约对应着证明的简化; 并且, 项的归约不会改变类型.
在“命题即类型”下, 定理的证明过程是高度构造的.证明一个定理就是构造出给定类型的项, 证明规范化成了计算, 证明检查对应于类型检查.Curry-Howard同构为许多主流证明助手的开发奠定了理论基础.
对简单类型理论进行扩展, 从而支持更丰富的类型, 可以使得Curry-Howard同构扩展到更丰富的逻辑, 如高阶逻辑, 能够表达更多有意义的定理.在Martin-Lof构造类型论(constructive type theory, 简称CTT)中[35], 依赖积类型对应于全称量词, 依赖和类型对应于存在量词, 支持归纳类型.构造演算(calculus of constructions, 简称CoC)支持多态类型, 将Martin-Lof构造类型论扩展到二阶逻辑[36].归纳构造演算(calculus of inductive constructions, 简称CIC)扩展了CoC而支持归纳类型[37].
1.3 编程逻辑对程序进行推理, 可以使用特定针对程序验证而开发的逻辑, 如Floyd-Hoare逻辑, 或者直接作用在编程语言的语义上.程序视为形式化的数学对象, 程序规范视为数学对象具有的性质, 因此, 程序验证可以理解成形式化的数学证明.下面我们来分析3种具有影响力的编程逻辑.
1.3.1 一阶编程逻辑及变体一阶编程逻辑, 也称为函数式语义(functional semantics), 是指将程序视为由输入状态映射到输出状态的递归函数, 因此, 程序性质可以使用递归归纳(recursion induction)进行验证.这种方法由McCarthy提出, 他也建立了一种新的递归函数理论, 即条件表达式(the theory of conditional expressions)理论来支持该方法[38].基于条件表达式, McCarthy定义了一系列恒等式作为公理, 同时定义一系列推理规则, 譬如分配律规则等, 条件表达式理论形成了一套一阶逻辑形式系统.
McCarthy提出的这种方法将程序推理建立在递归函数上, 带有条件表达式的递归函数表达了程序语义.对程序性质进行推理时, 程序首先转化为递归函数, 递归函数的定义被翻译为逻辑等式.1976年, Cartwright和McCarthy展示了该逻辑能够用来推理递归函数的性质, 并适用于Pascal程序性质的推理[39, 40].深受McCarthy和Bledsoe[41]的影响, Boyer和Moore于1975年基于一阶编程逻辑的限制性变体(restricted variant of first-order programming logic)实现了LISP程序的定理证明工具, 称为“纯粹的Lisp定理证明助手(pure Lisp theorem prover)[42]”.这个开发具有突破性的意义:当时流行的基于消解的技术不能证明诸如串联结的结合律这类更有意义的定理, 为此, Boyer和Moore研究了归纳证明(proof by induction)技术[43].
归纳证明的机械化存在两个主要挑战:机器如何选择归纳变量以及如何找到有用的归纳公理[44].Boyer和Moore设计了显式归纳(explicit induction)技术, 用来生成显式归纳假定; 并且能够泛化(generalize)待证明的定理, 以更好地利用归纳技术.归纳和泛化技术是Boyer和Moore开发的自动定理证明工具的核心技术, 这个自动定理证明工具也包括重写(rewriting)等技术; 在证明定理时, 推荐优先采用诸如重写这类相对简单且更可控的技术, 当这类技术不能完成证明的时候, 才考虑归纳和泛化.
理论上讲, 一阶编程逻辑更适合于如Lisp这类函数式编程语言, 因为这类编程语言避免了将程序转换成递归函数的麻烦.此外, 一阶编程逻辑的表达能力不及高阶逻辑, 也在一定程度上制约了这种逻辑系统的广泛应用.
1.3.2 Floyd-Hoare逻辑Floyd-Hoare逻辑也称为归纳断言(inductive assertions).1967年, Floyd提出了证明程序正确性的基本思想[45]:程序表示为流程图, 断言表示在流程图的边上.1969年, Hoare将流程图方式的断言表示为三元式, 由前置断言、程序和后置断言组成[46].Hoare给出了简单命令式语言成分的公理和推理规则, 称为Hoare公理系统.在这个公理系统中, 公理和命题都是形如{P}S{Q}的三元式, P和Q都是一阶逻辑公式, 三元式表示的意思是:如果程序S执行前P为真, 且执行完后Q成立, 那么这个三元式成立.因此, 若一个命题{P}S{Q}为真, 其表达的意思是:如果P在执行S前为真, 并且S能够终止, 那么Q在S终止时为真.
Hoare公理系统吸引了众多学者对其展开后续研究, 这些研究包括循环不变式的构造、支持并发、指针等语言特性、终止性问题、该公理系统的可靠性和完备性问题等, 产生了很多研究成果.其中, 1975年, Dijstra提出了最弱前置条件(weakest precondition)和谓词转换器(predicate transformer)[47], 成为开发循环不变式的指导思想.
归纳断言系统除了需要自动定理证明工具之外, 验证条件生成器(verification condition generator, 简称VCG)是另一个重要的组成部分, 通过验证条件生成器将断言转换为验证条件, 即一阶公式, 然后再由自动定理证明工具进行证明.早期基于Floyd-Hoare逻辑的大型验证工具是Stanford Verifier和Gypsy Verification Environment(GVE)[48, 49].当前, 许多工业应用的程序验证工具都采用了这种基于验证条件的程序验证方式, 如Why verification platform[50]、the Spec# static program verifier[51]、ESC/Java2[52]、SPARK GNATprove[53]等.其中, Spec#语言是C#的扩展, 其源程序可以包括方法契约(contracts)、不变式、类、成员以及类型的注解(annotations); Spec#的设计代表着编译器验证(compiler verification)的一种方法:编译器在编译源程序的同时也处理注解, 然后验证条件生成器将它们转换成一阶公式, 通常由自动定理证明工具Z3进行证明.
在归纳断言这种方法中, 程序以及加在程序上的注解被转换成大量逻辑公式, 当这些公式未通过证明时, 难以确定究竟是程序出了问题, 还是注解出了问题.而支持封装、继承、多态等面向对象特性编程语言的语义复杂性更加剧了这一问题的严重性.
旨在验证程序正确性的霍尔公理系统也被看成是一种公理语义(axiomatic semantics).公理语义没有操作语义中“状态”的概念, 程序变量的取值反映在断言中, 语义建立在这种断言上:断言是关于程序中变量取值的逻辑公式, 这些值随着程序的执行而发生改变, 但是存在着某种保持不变的关系, 程序执行前的初始断言和执行后的终止断言反映了这些不变式关系, 表示了这段程序代码的语义.从这种意义上讲, 公理语义是一种不直接的语义定义方式.
1.3.3 可计算函数逻辑的方法Milner于1968年实现了一个自动定理证明工具, 尽管他盛赞Robinson基于消解的证明技术, 但是他还是被这个工具所能证明出有意义定理的困难性所击败, Milner对机器辅助(machine-assisted)而不是完全自动的程序证明更感兴趣[54].1969年, Milner在牛津大学聆听了Scott的域理论(domain theory)[55], 他意识到可以运用这个逻辑定义程序语法和语义实现其设想, Milner将这个逻辑称为可计算函数的逻辑(logic for computable functions, 简称LCF).于是, 他于1972年在斯坦福大学开发了一个证明检查器(proof checker), 称为Stanford LCF[56].为方便实现, Milner将类型化的组合子(combinators)转换为λ表达式, 类型解释为Scott域(domains), 逻辑公式是谓词演算公式.在证明机制上, 用户使用证明命令与Stanford LCF进行交互, 将待证明的定理(称为目标)分解为子目标, 子目标通过简化器(simplifier)得到证明, 或者进一步分解为更简单的子目标, 直到这些子目标全部得到证明.在分解子目标时, 代表着形式证明的数据结构被创建, 因此消耗了大量存储空间.
为了能够灵活地添加证明命令而不损害可靠性, 并可节约存储空间, Milner等人于1973年~1978年设计了Edinburg LCF[57].Edinburgh LCF不存储整个证明的数据结构, 只存储证明的结果, 即定理.为了确保定理只能由证明产生, 一个抽象数据类型, 称为thm, 用来表示定理的类型.它的预定义值是公理, 在这个类型上的操作只能是推理规则.推理规则实现为函数, 因此, 严格的类型检查将保证所有thm类型的值只能通过公理, 并使用推理规则而得到, 这种经由推理得到的定理保证了它的可靠性.此外, 这种将定理表示成抽象数据类型的方式使得这个机器证明工具支持了前向证明.
为了方便证明命令的扩展和使用, Edinburg LCF设计了函数式编程语言ML(meta language), ML是严格类型化的, 用来支持抽象类型机制.分解待证明目标的证明命令如推理规则一样, 也实现为函数, 称为策略(tactics).策略是由目标(goal)到子目标(subgoal)的函数.策略能够以不同的方式组合成为新的策略, 组合方式也是一个ML函数, 称为tacticals.策略可以视为推理规则的逆, 支持了后向证明.可编程的Edinburgh LCF为用户提供了更多与机器的交互, 但并不损失可靠性.
Edinburgh LCF为证明助手的开发建立了一个标准框架, 许多后来的证明助手或多或少都采用了其中的核心技术特点.这些证明助手包括对Edinburgh LCF进行了大量改进和完善的Cambridge LCF[58]、始于硬件验证的HOL系列[59]、基于Martin-Lof类型理论的Nuprl[60]、Isabelle和Coq等.
Milner成功地将斯科特的域理论应用在实践中, 而域理论为Strachey.20世纪60年代所提出的指称语义(denotational semantics)奠定了数学基础[61].由于指称语义以数学递归函数定义语义, 具有组合性(compositiona- lity)特点, 使得指称语义直接支持了两个语义等同语言成分的置换.这种组合性建立在其抽象生成规则所产生的语法成分的“结构(structure)”上, 称为语法制导的(syntax-directed).因此, 程序性质可以使用结构化归纳(structural induction)进行推理.但是, 严格的数学特性也导致了指称的困难; 并且, 指称语义在指称并发时相当复杂, 需要引入新的模型.从某种程度上看, 指称语义可能过于“数学化”, 而并不方便编程语言的设计.指称语义在20世纪70年代占据了主导地位, 之后让位于基于规则的操作语义(rule-based operational semantics), 即结构化的操作语义(structural operational semantics, 简称SOS)[62]和自然语义(natural semantics)[63], 它们分别也称为小步(small-step)和大步(big-step)操作语义.
由于指称语义的状态是程序状态, 即程序中各变量的取值, 它纯粹使用数学函数来定义状态的变化, 这使得LCF方法在推理程序的方式上非常不同于上述讨论的一阶编程逻辑和Floyd-Hoare逻辑.一阶编程逻辑和Floyd-Hoare逻辑都将程序语义嵌入在某种算法中:一阶编程逻辑将程序的语义转换为带有条件表达式的递归函数; Floyd-Hoare逻辑将程序语义通过验证条件生成器转换为验证条件; 而在LCF逻辑中, 程序是这个逻辑系统所操纵的对象, 因此程序的语义可以显式定义, 这也称为嵌入(embed)编程语言到证明助手中.事实上, 在Isabelle/HOL和Coq等证明助手中, 可以方便地定义大步操作语义和小步操作语义.程序的许多性质, 譬如程序的相等性、程序变换以及一致性和终止性等, 都能够方便地在证明助手的逻辑系统中得到表达.
从另外一方面来看, 由于Hoare逻辑是一种特定用于程序验证的逻辑, 证明程序的性质会更直接.为了充分利用LCF方法和Hoare逻辑的优势, Gordon、Mehta和Nipkow分别使用证明助手HOL和Isabelle/HOL, 将Hoare逻辑实现为推理出来的规则[64, 65], 保证了Hoare逻辑的可靠性.以这种方式, Hoare逻辑被优雅地嵌入在高阶定理证明助手中, 使得在这些证明助手内可以使用Hoare逻辑进行程序验证.
1.4 基于高阶逻辑的硬件验证技术20世纪70年代, 定理证明工具的设计与实现围绕一阶逻辑而展开, 这在很大程度上是因为一阶逻辑具有很强的理论属性, 如完备性.然而, Gordon指出:这类属性对于验证是不相关的, 而简单类型理论, 即高阶逻辑所具有的额外表述力对于验证而言却是必要的[66].Gordon对高阶逻辑的研究是与硬件验证联系在一起的, 这不同于当时绝大多数的验证研究:出于历史原因, 也可能因为当时的硬件设计并不那么复杂, 除了Wagner于1977年使用FOL初步尝试了硬件验证[67]以外, 几乎所有其他同时代的验证研究在本质上都是以软件为主的.
当Paulson正在剑桥致力于Cambridge LCF的开发时, Gordon也正在剑桥从事着硬件验证的研究, 因此他对Cambridge LCF非常熟悉.Gordon对Milner所开发的通信演算系统(communication calculus system, 简称CCS)留有深刻印象, 他认识到:通过并行组合硬件系统中个体结构的描述, 可以计算推理得到整个硬件系统的行为.于是设计了称为LSM(logic of sequential machine)的符号, 用来表示机器的顺序行为, 并构造了一条类似CCS的Expansion Theorem的规则.接下来, Gordon对Cambridge LCF进行了改进, 使之适合LSM.这个改进的证明助手获得了初步成功, 对Viper处理器进行了规范和正确性证明[68].同时, 在剑桥攻读博士后的Moskowski向Gordon提出LSM中的项可用谓词逻辑进行编码, 使得LSM的Expansion Law可以推理得到, 而不是构造为公理.这种方法既优雅又具有更牢固的逻辑基础, 于是HOL诞生.
高阶逻辑的选择在当时相当激进, 譬如高阶合一在理论上是不可判定的, 不过在实际中, Huet开发的半可判定的高阶合一算法[69]在证明助手中表现得相当可靠[70].Gordon和他的学生继续扩展了这项技术, HOL进化成了HOL4.HOL吸引了许多研究者的兴趣, 他们开发出了不同版本, 形成了HOL系列[71].基于高阶逻辑的硬件验证技术具有很好的递增性, 可以验证单传感器设备, 也可以验证整个计算机, 囊括了大量数字系统, 包括浮点小数硬件、概率算法以及其他许多应用.
1.5 程序构造和求精程序构造(program construction)也称为程序综合(synthesis), 是指由规范(specification)构造出具体程序.一个主要方法是将由规范到实现的过程视为一系列对数据结构和控制结构进行求精(refinement)的程序变换, 因此, 程序构造也常和求精这一术语联系在一起.
逐步求精(step refinement)的程序构造技术最初由Dijstra[72]和Wirth[73]提出.这是一种构造即正确(correct by construction)的方法:如果每步求精都能够谨慎地执行而保持了正确性, 那么最后的程序一定是正确的.但是, 实际算法和数据类型在实现过程中所包含的每步求精并不简单, 直觉远远不能判断其正确性.Gerhart明确提出了程序变换正确性概念[74].Burstall和Darlington提出使用预定义的一套程序变换规则构造每步求精[75], 许多理论研究围绕这种方法而展开, 这些方法大多并不利用定理证明技术, 而是将规则直接应用到规范上.不过, Manna和Waldinger研究了使用定理证明的方法进行程序构造[76].
旨在将逐步求精和程序变换与基于不变式的方法统一起来用于程序构造, 在一系列研究积累之上, Back利用Dijstra最弱前置条件演算, 于1988年提出了求精演算(refinement calculus)[77]:如果语句S的最弱前置条件能够推出语句S'的最弱前置条件, 那么S'是S的正确求精; 证明等同于计算它们的前置条件, 使得表达了这个正确性的一阶逻辑公式为真.李彬等人提出了一个通过抽象程序证明复杂具体程序的框架, 使得满足一致性比较容易得到证明, 并可能自动证明[78].
求精演算会产生大量既冗长又易错的谓词公式, 需要完成的工作非常艰巨.一些研究开始寻求机械化手段来支持求精演算[79, 80], 这些工具通常由验证条件生成器和自动定理证明工具两个独立部分组成.不同于这种方式, Back和Wright使用HOL, 在一个工具中实现了他们所设计的形式系统, 证明了许多求精规则[81].经过机器检查的规则, 避免了预定义程序变换规则可能存在的不一致性问题.Wright进一步利用HOL的窗口推理工具(window inference tool)(该工具支持程序变换风格的推理), 建构了一个用于求精的原型工具[82].
求精的思想也由Abadi和Lamport用来证明分布式程序的低层规范正确实现了高层规范, 称为求精映射(refinement mapping)[83].Lamport进一步将求精映射和时序逻辑(temporal logic)相结合, 提出了行为时序逻辑[84].Jonsson和Lynch等人泛化了求精映射, 称为模拟(simulation)[85, 86].这些方法和技术通常以模型检查(model checking)或者模拟技术而不是以定理证明的方式对并发程序进行验证.不过, Pnueli等人使用时序逻辑, 以定理证明的方式提出了一种对并发程序进行构造的算法[87].
一个获得了工业级应用的逐步求精工具是B方法的工具包Atelier B[88, 89].B方法以一阶公理化ZF (Zermelo-Fraenkel)集合论为基础; 1998年, Atelier用于巴黎城市地铁14号线全自动无人驾驶系统.
基于定理证明方法的求精工具较为少见.就目前我们所知, Isabelle/HOL通过Locales机制支持逐步求精. Cornell大学的PRL团队维护着NuPRL的开发, 其中, PRL代表证明或程序求精逻辑(proof/program refinement logic).从技术发展上看, 求精的概念和应用非常宽泛, 譬如可以应用在编译器验证的研究中.
2 证明助手特点比较和实现已经详细剖析了证明助手的主要理论基础和关键技术, 接下来讨论证明助手的实现和应用.限于篇幅, 仅针对部分主流证明助手的设计特点进行分析比较, 阐述具有代表性的证明助手的开发与实现.
2.1 设计特点比较证明助手的设计与实现并不像传统软件开发那样具有规范化的标准可以遵循, 特别是在早期阶段.从历史发展上看, 它的开发是一个从错误中不断修正、渐趋成熟的过程.不同证明助手之间相互影响, 一些完成了它的历史使命而终止开发或者进化成新的证明助手, 一些仍然活跃.在这个过程中, 逐步形成了开发一个现代证明助手所需要考虑的重要特点.本节先比较这些设计特点, 然后重点阐述几个具有代表性的证明助手的开发和实现.
针对证明助手的可靠性和使用性, 表 1对部分主流证明助手的设计特点进行了比较.
| Table 1 A comparison of features of some mainstream proof assistants 表 1 部分主流证明助手的特点比较 |
各项特点分析如下.
(1) 小核
证明助手用来验证数学、计算机软/硬件的正确性, 它们本身是正确可靠的吗?一方面, 鉴于机器证明的机械刻板性, 即使存在某些缺陷, 它在证明定理时所具有的可靠性量级也远胜人工证明; 另一方面, 通常认为:如果一个证明助手具有相对较小的内核, 所有其他推理规则都是基于小核中的规则来定义的, 那么, 需要信任的就是这个小核[90]; 相对较小的内核更值得信任, 因而更可靠.
在LCF方法的证明助手中, Agda、Coq、Nuprl和PVS是基于类型理论的, 它们通常会生成证明对象, 由一个相对简单的证明检查程序进行检查, 这个小程序可被认为是一个小核, 不过, PVS的设计者并不太关注理论上的可靠性, 而持有相当松散和实际的正确性观点, 本文中标记为“—”; LCF方法的直接后代:HOL4、HOL Light以及Isabelle本身就是基于非常小的可信内核来设计的.
ACL2在设计时注重强大的自动推理能力和使用上的方便; Mizar旨在建立形式化验证的数学知识库.因此, 对这两种证明助手不按小核标准进行比较, 显示为符号“—”.
(2) 声明/过程式证明语言
用户使用证明助手支持的证明语言与证明助手进行交互.证明语言可分为声明式和过程式两种:前者指出证明什么, 后者指明如何进行证明.因此, 声明式的证明可读性较高.
在早期基于LCF方法证明助手的开发中, 策略脚本是传统过程式的, 其晦涩难懂性与Mizar声明式证明语言的相对高可读性形成了巨大反差, 因此, Harrison倡导Mizar声明式证明语言[91].虽然HOL Light支持声明式语言, 但并不常用, 因此标识为过程式.Isabelle于1999年支持了声明式的证明语言Isar[92].Coq的证明语言是过程式的, 不过, Gonthier等人为Coq设计了Ssreflect(small scale reflect language), 能够声明式地用于证明的高层结构中, 但在低层结构中切换到过程式[93], 因此在表中也标识为过程式.Nuprl的证明语言更接近于将声明式和过程式加以综合[94].自动定理证明工具, 如ACL2的证明语言可以视为声明式的:在这样的证明助手中, 仅陈述(声明)待证明的定理, 或书写一些中间定理, 证明助手自动完成证明任务.Agda支持声明式的证明.
(3) 实现语言
大多数证明助手, 譬如Coq、Isabelle等都是以函数式编程语言编写的, 譬如Haskell、Ocaml、Common Lisp、Standard ML以及Scala等.不过, Mizar的实现语言是Free Pascal, Free Pascal是Pascal编译器, 其目标平台包括多种处理器架构, 如Intel x86、AMD64/x86-64、PowerPC、MIPS和JVM等.
(4) 代码生成
许多证明助手支持代码生成, 或称为程序抽取(program extraction).代码生成是指将在证明助手中以证明语言书写的各种定义翻译成可执行的函数式程序, 可以独立运行.譬如, Isabelle/HOL可生成SML、OCaml和Haskell程序, Coq可以生成Ocaml、Haskell和Scheme程序, PVS可以生成Common Lisp程序, ACL2和Agda本身是可执行的.Mizar旨在建立合适的数学语言对数学进行形式定义和证明, 因此对它不考虑代码生成这个特点, 显示为符号“—”.
(5) 用户界面
证明助手建立在函数式编程语言之上, 使用命令行方式与之进行交互.Aspinall于1999年开发了Proof General[95], 许多证明助手的早期版本支持一种称为Emacs模式的图形用户界面:交互依然是基于一系列命令, 但是可以区分未检查的证明和已检查的证明, 用户可以一步步地引导证明, 证明助手返回结果.Emacs界面模式主导了Isabelle和Coq的开发约10年之久.
一种不同的方法是通过证明助手集成开发环境框架(prover IDE framework, 简称PIDE)完成.PIDE非常类似于现代软件集成开发环境, 用户在输入源码时, IDE就检查语法.Coq和Isabelle现已支持这种用户界面, 分别称为GTK-based CoqIDE和the Isabelle/jEdit IDE[96, 97].ACL2团队开发了Eclipse插件, 称为ACL2 Sedan theorem prover(ACL2s), 供用户与ACL2进行交互.Mizar旨在建立数学知识库, 为了更好地进行测试, Cairns为Mizar开发了一个用户界面Alcor, 方便用户与这个知识库进行交互[98].
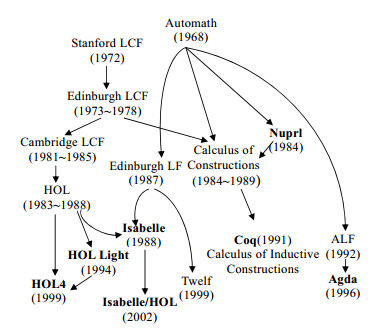
以上分析比较了主流证明助手的设计特点, 为了更好地理解证明助手的设计, 图 6给出了联系比较紧密的证明助手之间的开发进化及影响关系, 黑体标识的是当前仍然活跃的证明助手.一些证明助手, 如ACL2、PVS和Mizar的设计相对独立, 没有包含在图 6中.
|
Fig. 6 Evolvement of proof assistants and influences on each other 图 6 一些证明助手的进化以及之间的相互影响 |
总体上讲, Milner设计的Edinburgh LCF和Bruijn设计的Automath[99]是具有先驱性的两大证明助手, 并且这两大证明助手衍生系统的开发也是交叉影响的.Bruijn基于他自己设计的依赖类型理论而实现了Automath, 可以说, 他独立发现了Curry-Howard同构[3], 以“证明即对象(proofs-as-objects)”的方式体现在Automath的开发中.Automath旨在准确地表达所有数学并进行验证, 尽管Automath几乎没有被广泛使用过, 但是它对许多以类型理论为基础的证明助手的开发都产生了很大影响.接下来, 我们分别阐述几个具有代表性的证明助手的开发和实现.
2.2 主要证明助手的开发和实现 2.2.1 Isabelle/HOLIsabelle/HOL是当前被广泛使用的、LCF方法的证明助手, 它是建立在Isabelle元逻辑(meta-logic)之上的一个目标逻辑(object logic).Isabelle元逻辑也称为Isabelle/Pure.
Paulson于1985年开始Isabelle的开发, 他考虑以元逻辑, 即通用的、适用于多种特定逻辑的证明助手的开发.以Paulson的观点来看:许多特定逻辑证明助手开发的困难性都是类似的, 故开发通用证明助手可以一劳永逸地解决这些难题, 而将特定逻辑要解决的特定问题留给特定逻辑, 由以元逻辑为基础的目标逻辑去处理.
这种观点也体现在Edinburgh逻辑框架(logical framework, 简称LF)中[100].在第1.3.3节所述的Edinburgh LCF完成之后, 在爱丁堡大学的开发重心转移至逻辑框架和构造类型论上, 导致的系统称为Edinburgh LF, 之后进化为Twelf.另一个逻辑框架是ALF(another logical framework), 最后成为Agda.
在这些以逻辑框架为设计思想的证明助手中, Isabelle是唯一得到广泛应用的证明助手, 它可以视为LCF方法和逻辑框架的联合.
Isabelle元逻辑的实现基础是Church的简单类型理论, 是具有蕴含、全称量词和相等的高阶逻辑, 推理规则不是前提到结论的ML函数, 而是前提蕴含结论的公理, 允许目标逻辑以自然演绎风格进行构造.Isabelle/Pure并未利用类型化λ演算与自然演绎之间“证明即程序”的对应关系, 没有显式的计算, 不显式生成独立可检查的证明对象.这种方式称为LCF方法的直接后代, 区别于使用了LCF方法, 但以类型理论为基础而设计的证明助手.
受Huet的启发, Isabelle实现了高阶合一, 在高阶合一的基础上, Isabelle支持许多自动推理工具, 从而具有强大的自动推理功能:高阶重写的简化器Simplifier、结合了Metis证明工具的经典推理器(the classical reasoner)和经典Tableau证明工具; 支持使用外部自动定理证明工具, 如Vampire、SPASS的Sledghammer工具; 支持反例搜索的Quickcheck和Refute.此外, Isabelle使用Locales处理参数化的理论, 支持了模块化的理论开发(modular theory development).
由元逻辑Isabelle/Pure可以构造许多不同种类的目标逻辑(object logics), 譬如经典和直觉的一阶逻辑(Isabelle/FOL)、Martin-Lof构造类型理论(Isabelle/CTT)、一阶ZF集合论(Isabelle/ZF)以及经典的高阶逻辑Isabelle/HOL等, 如图 7所示.

|
Fig. 7 Meta-logic and object logics of Isabelle 图 7 Isabelle元逻辑和目标逻辑 |
Isabelle/HOL是当前使用最多的一个目标逻辑, 在图 7中以黑体标识, 主要由Nipkow于2002年完成[101].从用户的观点看, 该目标逻辑可以理解为函数式编程和逻辑的结合, 供用户用来交互的编程语言类似于Haskell.利用Locales, 在Isabelle/HOL中可以表达由抽象规范到具体数据结构和算法的逐步求精的概念.此外, Isabelle/ HOL能够充分利用多核处理器进行并行证明[102, 103].Isabelle/HOL仍然在不断改进和完善中, 当前的稳定版本是Isabelle 2019.许多有关安全协议、数学、编程语言和系统验证等众多领域的正确性问题都可以在Isabelle/HOL内进行描述并得到验证.
2.2.2 HOL系列Gordon在剑桥大学为研究硬件验证而开发了HOL.历经了数个版本的改进完善之后, 当前最新版本为HOL4.HOL也衍生出了新的证明助手, 这些统称为HOL系列, 如图 8所示, 其中, HOL4、HOL Light、HOL Zero (http://proof-technologies.com/holzero/index.html)以及ProofPower(http://www.lemma-one.com/ProofPower/index/)现仍然在开发和维护中, 它们都是经典的高阶逻辑.HOL light由在Intel公司工作的Harrison于1994年推出.虽然始于硬件验证的动机, HOL系列也可以进行算法和程序验证, 并支持进程代数以及极限理论、微分和积分等经典数学验证.

|
Fig. 8 Evolvement of HOL family 图 8 HOL系列的进化 |
2.2.3 Coq和Nuprl
1984年, 法国国家信息与自动化研究所INRIA的Huet和Coquand决定实现构造演算(calculus of constructions, 简称CoC), 初始版本是一个证明检查器, 紧接着采纳了LCF方法的策略方式, 导致的系统可以视为Automath的Martin-Lof构造类型论的扩展, 综合了依赖类型和多态.之后, Mohring实现了称为Auto的证明搜索策略, 代表着Coq证明助手的诞生.Mohring和Coquand于1988年开始设计归纳构造演算(calculus of inductive constructions, 简称CIC).之后, Coq经历了反复的重设计和实现, 当前, Coq的稳定版本是8.8.0.一个新的扩展是Coq团队开始实现同伦类型理论.
Nuprl是康奈尔大学的PRL(proof/program refinement logic)研究团队的Constable等人于1986年开发的证明助手, 实现的也是Martin-Lof的构造类型论.PRL团队一直致力于开发基于逻辑的编程工具和实现构造主义的数学, 当前的稳定版本是Nuprl 5.2003年, Hickey等人以逻辑框架的思想重新实现了Nuprl, 称为MetaPRL (http://metaprl.org).
Coq与Nuprl都是使用了LCF方法且以类型理论而设计的证明助手.这类证明助手基于非简单的类型理论, 即依赖类型等.利用命题即类型、证明即项的思想, 类型化的λ项既用于表示逻辑定理, 又表示证明, 通过依赖类型, 类型检查执行了大多数推理任务.
2.2.4 ACL2和PVSACL2始于Boyer和Moore于1973年开发的纯粹Lisp定理证明工具, 该工具解决了归纳证明的机械化问题, 如第1.3.1节所述.之后, Boyer和Moore继续对其进行完善.20世纪80年代中期, Kaufmann加入了开发团队.经过多年的持续改进, Boyer和Moore终于实现了他们在1973年设计自动定理证明工具的目标:ACL2(a computational logic for applicative common Lisp)诞生[104], 其效率远远超出了设计之初的纯粹Lisp定理证明工具, 而成为工业可用的工具, 并于2005年集成到Centaur公司的开发流程中.为充分利用多核处理器的功效, ACL2和Isabelle/HOL一样也处理了并行证明的问题[105].当前, ACL2的稳定版本是8.0.
PVS是Prototype Verification System的简称, 由SRI公司于1992年开始研发.PVS和ACL2一样具有强大的自动化证明能力, 但是PVS也意图提供如证明助手所具有的强表述力和逻辑, 提供了类Lisp语言供用户与之进行一定的交互.PVS是经典类型化的高阶逻辑, 但不像Coq和Nuprl那样产生独立可检查的证明对象.PVS当前的稳定版本是6.0.
3 机械化定理证明应用成果分析从第一个定理证明工具至今, 经过约60多年的持续研究, 机械化定理证明在实际应用中产生了丰硕的研究成果, 以下从数学、编译器验证、操作系统微内核验证、电路设计验证等几个具有影响力的研究领域来讨论所取得的应用成果.
3.1 数学定理的证明最早提出“数学机械化”思想, 并做出卓越贡献的是美籍华裔数理学家王浩先生.他于1959年编写了一个计算机程序, 实现了带有相等关系的谓词逻辑, 在很短时间内证明了Russell和Whitehead所著的数学原理中的几百条定理.秉承数学机械化的思想, 针对几何定理的机器证明, 吴文俊在1977年提出了“吴方法”:待证定理由坐标间的代数关系表示, 从而将平面几何问题代数化; 再通过多项式的消元法进行验证[106].这种方法既可以手工完成, 又可方便地以计算机编程进行实现, 这种方法被进一步推广到一类微分几何问题上.1996年, 杨路和张景中等人建立了多项式完全判别系统[107], 使得不等式的机器证明成为现实.1999年, 杨路和夏壁灿等人进一步编制了研究半代数系统(semi-algebraic-system)实解的新软件包DISCOVERER[108].DISCOVEREER现已集成到Maple工具箱, 在自动求解参系数半代数系统实解分类问题上具有优势.
许多数学家们都接受了使用证明助手来证明数学定理.van BJLS使用Automath形式化了由Landau所著的数学教科书中的定理[109].旨在设计具有强表述力的数学语言, Trybulec开发了Mizar[110], Mizar库已经成为当前最大的形式化验证的数学知识库.此外, 形式化数学越来越多地用于验证目的.Hurd使用HOL形式化了概率论, 验证了Miller-Rabin概率素性测试[111].Holzl使用Isabelle/HOL形式化了马尔可夫链[112].
表 2列举了几个具有代表性的机器证明的数学定理.其中, 开普勒猜想和四色定理的证明是两个非常具有说服力的例子.Hales于1998年给出了长达300多页的开普勒猜想证明, 并辅以40 000行的程序代码, 经过长达4年的评审之后, 因其代码的不可信而被拒绝.于是, Hales启动了一个联合项目Flyspeck, 多个研究小组使用不同的证明助手共同完成证明:HOL Ligth提供欧氏几何背景知识; Coq用于非线性的不相等验证, 之后改为使用Isabelle/HOL完成该验证; Isabelle/HOL用于图枚举和线性编程.Flyspeck项目获得了成功, 确定并简化了Hales的证明, 它是迄今为止完成的最大的形式化证明[113, 114].四色定理的机器证明也非常有意义.Appel和Haken于1976年完成了四色定理的证明[115], 他们使用一个计算机程序检查了近2 000个实例, 争议由此产生.虽然争议在Robertson等人于1996进行了优雅的修正后而可能平息, 但是缺陷仍然存在:这两个证明都使用了计算机代码, 而这些代码超出了人工评审的能力, 却又没有经过机器检查.最后, Gonthier使用Coq证明了四色定理[116], 用来检查实例的算法在Coq中进行了验证.
| Table 2 Lists of some representative mathematical theorems which are machined checked 表 2 几个具有代表性的机器证明的数学定理列表 |
数学的机械化证明能够清除疑问, 解决模糊性, 并发现错误.正如Lakatos指出的:数学家们常会出错, 有时甚至连定义都会出错[117].因此, 形式化验证数学的驱动力越来越多地来自数学家们自身.此外, 许多与电路设计正确性相关的验证都需要纯数学定理和数学算法的支持, 数学的机械化证明是非常有意义的研究领域[118]. Isabelle的开发者Paulson正在剑桥大学致力于数学的形式化, 当前, 他正主持一个形式化数学的大型项目Alexandria[119], 它以Isabelle/HOL为基础, 目标是得到一个覆盖所有大学水平数学的形式化数学库.国内施智平等人在数学形式化领域也做出了比较有影响力的工作, 他们在HOL-light中建立了几何代数系统的形式化模型, 在共形几何代数空间中, 给刚体运动问题提供了一种简单、有效的形式化建模与验证方法[120, 121].
3.2 编译器验证编译器是将高级语言编写的程序转换到能在目标平台上运行指令集的重要系统软件.当前, 绝大多数编译器都没有经过形式化验证, 虽然在发布前已经进行了大量测试, 但仍存在许多问题.形式化验证编译器的研究随着第一个高级语言编译器的诞生就开始展开.但是, 表达和证明编译器正确的困难性, 以及不断发展的高级编程语言带来的语义和编译转换过程的复杂性使得这项研究历经几十年而经久不衰.随着关键技术和证明助手的成熟, 编译器验证领域涌现出了大量研究成果.这些成果可以分为“验证的编译器(verified compiler)”和“验证编译器(verifying compiler)”[122].验证的编译器是获得一个正确性得到验证的编译器, 而验证编译器并不获得这样一个编译器, 而是验证编译后的目标程序相对于源程序的正确性, 因此验证的是一次编译(compilation)是否正确.何炎祥等人深入研究了可信软件的构造理论和方法, 并在编译器验证领域开展了有意义的研究工作.为了表述方便, 以下按照何炎祥等人的研究[123], 将这两种验证方式分别称为编译器自身的正确性验证和编译后代码的正确性验证.
3.2.1 编译器自身的正确性验证传统的编译器自身正确性验证的方法原理源自莫里斯(Morris F. L.), 如图 9所示:定义源语言和目标语言的语义, 定义源语言到目标语言的编译, 构造语义等同(homomorphism)定理, 最后采用归纳对定理进行证明[124].在实际应用中, 源语言和目标语言的语义定义方式大多采用了操作语义或者指称语义, 并且需要构造许多辅助定理才能完成一个真实语言编译器的语义等同定理的证明.

|
Fig. 9 Semantics homomorphism diagram 图 9 语义等同示意图 |
伴随编程语言语义的不断发展进化, 表 3列举了部分具有代表性或者影响力的编译器自身正确性验证的研究成果.
| Table 3 Lists of achievements of verified compiler 表 3 编译器自身正确性的机器验证研究成果列表 |
编译器的机器验证最开始针对的是实验性质的语言.20世纪80年代, 两个比较大型的编译器验证分别使用Stanford Verifier和Boyer-Moore定理证明工具完成.前者的源语言类似Pascal, 目标机器类似B6700, 源语言和目标机器指令的指称语义之间的等同性表示为断言(assertions)语言, 这些断言转换为验证条件, 再由Stanford Verifier进行证明[125].后者的源语言是类似Pascal语言的Micro-Gypsy, 目标语言是高级汇编语言Piton, 语义采用操作的方式进行定义, 使用结构化归纳完成证明[126].Moore进一步完成了从Piton汇编语言到寄存器传输级(RTL)的正确性验证[127].
到20世纪90年代, 更多的证明助手被开发出来.使用HOL, Curzon基于指称语义证明了一个结构化的汇编语言Vista到目标Viper微处理器的编译[128].同样基于指称语义, Calvert使用PVS, 对Stepney给出的一个学习案例进行了实现[129], 该案例的源语言Tosca是一个小但并不简单的高级语言, 目标语言是典型的汇编语言.
到20世纪末和21世纪初, 证明助手已渐趋成熟, 联合结构化操作语义和自然语义的出现, 这些为实际编程语言编译器的验证创造了良好条件.最具代表性的两个项目是使用Coq的C编译器CompCert, 以及使用Isabelle/HOL的Java编译器Jinja和JinjaThread, 下面分别予以阐述.
(1) C优化编译器CompCert
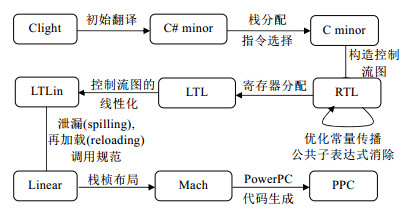
始于2005年, Leroy等人使用Coq定义了C语言子集(Clight)的大步操作语义, 经过多遍翻译变换, 完成了从Clight到PowerPC汇编码的验证, 如图 10所示.CompCert对编译优化也进行了验证, 形式化了静态单赋值的语义, 并验证了基于SSA的全局值计数(global value numbering, 简称GVN)算法.
|
Fig. 10 Compilation passes and intermediate languages of CompCert 图 10 CompCert多遍编译和中间语言 |
严格上讲, 为了对优化算法进行验证, CompCert结合了编译后代码验证, 并辅以手工证明:编译器在编译转换的同时, 也生成安全性规范.对于编译器的每遍翻译, 证明翻译前后的语义等同; 或暂不证明而延迟到后续的某遍翻译中去验证翻译后的程序是否满足安全性规范, 并以注解的形式表示在翻译结果中; 最后对这些注解的一致性进行验证.国内王生原编译器研究组采用Coq实现了一个可信编译器L2C, L2C将同步数据流语言Lustre编译到了Clight, 他们对L2C的核心翻译步骤及其设计与实现进行了论述[130, 131].
建立在CompCert2.0基础之上, Beringer等人证明了在共享内存交互情况下的编译优化[132].Jaroslav等人形式化了一个支持共享内存的并发算法, 并证明了编译这类并发程序的正确性[133].目前, CompCert已成功应用于工业开发中, 它是迄今为止最为成功的C语言验证编译器.
(2) Java编译器Jinja和JinjaThread
Java编译器因其面向对象特性以及内建多线程机制而使得验证更为复杂.Nipkow和Oheimb首先于1998年使用Isabelle/HOL对Java子集进行了形式定义, 并证明了它的类型安全性[134].2002年, Klein对Java虚拟机(Java virtual machine, 简称JVM)字节码验证器的正确性进行了机器验证[135].在这些基础之上, 2006年, Klein和Tobias构建了包括Java、JVM目标机器以及编译器等在内的统一模型, 证明了Java编译到JVM虚拟机的正确性[136], 为Java这样的OO语言编译器验证奠定了良好的研究基础.Jinja源码共涉及1 000多个定理的证明, 所有定义和定理证明包括在BV、Common、Compiler、DFA、J、JVM这6个理论文件夹中, 构成语义等同框架的核心理论如图 11所示(包括类型安全).

|
Fig. 11 Core theories of semantics homomorphism of Jinja (including type safety) 图 11 Jinja语义等同框架(包括类型安全)的核心理论 |
建立在Jinja基础之上, Lochbihler设计了一个能够定义线程的语义框架JinjaThread, 如图 12所示, 将Java内存模型(Java memory model, 简称JMM)规范与运行时操作语义联合在一起进行分析, 机器证明了交错语义和JMM的类型安全、DRF(data race free)保证, 分析了值凭空出现的问题等, 并将编译器的正确性验证扩展到了支持线程, 具有良好的模块性[137, 138].何炎祥和江南等人以Jinja为基础, 研究了Java语言子集编译到Android Dalvik虚拟机字节码的机器验证[139, 140].在他们的形式化中, 用新的Dalvik VM理论文件夹取代了JVM.由于寄存器架构的Dalvik虚拟机不同于栈架构的Java虚拟机, 大量规范描述需要重新定义, 并构造和证明新的定理, 这些修改主要包含在Common、Compiler和BV中.

|
Fig. 12 Semantics stack of JinjaThreads with JMM 图 12 带有内存模型的JinjaThreads语义栈 |
除了传统的语义等同原理方法外, 编译器自身验证的另外一种方法是采用如第1.5节所述的“构造即正确”的方法:定义程序转换规则, 源语言程序按照转换规则被逐步求精到可执行的目标语言程序.转换规则是编译器行为, 规则的可靠性保证编译的正确性.20世纪90年代初期开始的欧洲项目ProCos(provably correct systems)采用了类似方法[141, 142].ProCos项目旨在建立所有开发阶段的正确性, 并包括显式并行和时间约束条件.其中, Buth和Buth等人研究了Occam顺序子集编译到Transputer机器语言的正确性验证[143], 何积丰和Ian等人研究了将Occam子集编译到适合用于现场可编程门阵列(field-programmable gate array, 简称FPGA)硬件的范式(normal form)[144].此外, 作为ProCos项目的一部分, 周巢尘提出了规范和验证实时系统的时段演算(duration calculus)[145], 这项研究获得国际同行的重视[146], 并进一步对时段演算的可判定性和不可判定性进行了研究[147], 在机械化自动证明研究方面取得了很大进展.
在ProCos项目研究的大环境下, Sampaio使用项重写term rewriting系统OBJ3[148], 针对编译器验证的代数方法进行了研究[149], 他的工作建立在Back[76]和Morris[150]的基础之上.Sampaio深入研究了范式方法[151]:范式代表着不可继续归约(reduction)的目标代码, 编译视为一种程序求精, 是程序到范式的归约; 归约包括一系列语义等同的转换, 语义等同的中心概念是程序的排序关系(ordering relation); 代表着代数语义的转换法则用来证明归约定理, 证明了归约定理可以作为重写规则执行编译任务, 自动地完成编译, 也保证了编译转换的语义等同.与Sampaio的方法一致, Duran等人针对类似Java的面向对象语言的编译器进行了正确性构造[152], 但是没有进行机器检测.
虽然从理论上讲, 这种编译器自身正确性验证方法的代数特性使得可以使用项重写工具对证明进行检查, 但是正如Sampaio所指出的:不能保证初始选择的一套代数法则的一致性.但是从Back和Wright的研究[81]中可以获得一些启示:代数法则是在证明助手HOL中推理得到的, 从而能保证其一致性.综合来看, 代数的逐步求精方法在复杂的命令式高级编程语言编译器自身正确性的验证方面, 可能难以得到有效的机械化证明.
编译器自身的正确性验证需要准确定义源语言和目标语言的形式语义.形式语义的研究始于20世纪60年代, 操作语义、指称语义、公理语义以及代数语义构成了编程语言语义的四大主线, 陆汝钤深入剖析了这四大流派的形式语义以及形式语义学的现代应用[153].其中, 操作语义最初指的是基于抽象机的操作语义; 之后, 在20世纪70年代让步于指称语义, 而指称语义在20世纪80年代初又让步于基于规则的操作语义.目前也并无定论什么是定义编程语言语义最好的方法, 复杂的语言特性以及一些编译优化算法也难以得到有效定义并得到相应证明.虽然编译器自身的正确性验证具有高可靠性, 但是语义定义的困难性使得它的开发难度很大.
3.2.2 编译后代码的正确性验证鉴于编译器自身验证的困难性, 一些研究者转而对编译后的程序代码进行验证.一个具有影响力的成果是携带证明的代码(proof-carrying code, 简称PCC)[154], 验证原理如图 13所示.C源程序经Compiler工具翻译成优化的DEC Alpha汇编程序, 同时生成每个函数对应的类型规范以及表示循环不变式的代码注解, 这些作为Certifier工具的输入.Certifier包括3个子系统, 分别是验证条件生成器(VCGen)、证明助手(prover)和证明检查器(proof checker).VCGen使用类型规范和代码注解, 为每个函数生成代表安全属性的谓词公式, 称为安全谓词; Prover工具对安全谓词进行证明, 如果成功, 则输出对应的证明, 否则, 给出反例, 代表汇编程序类型系统的潜在冲突; 最后, 安全谓词和证明都作为输入, 由Proof Checker工具进一步检查.

|
Fig. 13 Framework of certifying compiler 图 13 认证编译器原理图 |
这个出具证明的编译器只需要保证工具VCGen和Proof Checker的正确性, 无关复杂的编译器和证明助手.胡荣贵和陈意云等人通过构造扩展数据流图, 设计实现了从C语言子集源程序到携带类型注解的x86目标代码的认证编译器, 能够处理公共子表达式消除等优化操作[155].
另一个有影响力的成果是Pnueli等人提出了翻译确认(translation validation)[156], 验证原理如图 14所示.源程序经Compiler工具翻译成目标程序; 然后, 源程序和目标程序都作为Analyzer工具的输入, 如果该工具分析出目标程序“正确实现”了源程序, 则生成证明, 并交给Proof Checker作进一步证明检查, 否则, 给出反例, 表示目标程序的行为与源程序行为不同, 代表编译器有误.其中, “正确实现”的概念形式化为一种求精关系(refinement relation).为了表达这种关系, Pnueli等人设计了一个既能够表示源程序, 又能表示目标程序的语义框架, 称为同步变迁系统(synchronous transition system, 简称STS), 源程序和目标程序是STS两个模型.在这个统一框架下, 基于求精映射的思想, 提出时钟化的求精映射(clocked refinement mapping), 归纳证明源程序和目标程序可观察行为之间的语义包含(containment).进一步地, 为了自动化处理整个过程, Pnueli等人采用了Lamport等人对时序逻辑进行模拟求精的思想, 将求精映射表示为语法概念, 使得主要证明部分能够通过计算推得, 因而实现完整的自动化, 这个自动化的工具称为CVT(code validation tool).

|
Fig. 14 Framework of translation validation 图 14 翻译确认示意图 |
Pnueli给出了同步语言Signal到目标C语言的翻译确认.虽然STS是非常通用的, 但是将正确实现定义为模拟求精可能更适合建立Signal同步语言到C之间的正确实现关系.翻译确认的思想是基于模拟的, 而不是严格意义上讲的证明构造的技术.与PCC相比, Pnueli提出的语法上的基于模拟的证明方法保证了验证的完全自动化, 而在PCC中, 正确性证明的关键部分是手工完成的; 此外, 翻译确认的基本思想以不同的实现和证明方式, 运用在了操作系统微内核seL4的源程序到ARM机器码的编译验证中, 接下来对此给出讨论.
3.3 操作系统微内核验证2014年, 第一个验证的操作系统微内核seL4开源发布, 这是一个持续了约20年开发的研究成果.seL4作为L4操作系统验证家族的第三代, 致力于形式化验证可潜在应用于强调安全和关键性任务的操作系统内核程序, 提供了最基本也是最重要的操作系统服务:线程、进程间通信、虚拟内存、中断、授权机制等.整个系统可分为两部分:安全的操作系统内核源程序和该源程序到ARM机器码的翻译确认, 下面分别予以阐述.
(1) 安全的操作系统微内核源程序
工程上, 操作系统开发人员更倾向于从底层细节出发, 通过有效管理硬件而获得高性能, 而形式化方法的实践者更愿意采取一种自顶向下的开发方法, 始于硬件的高度抽象.seL4团队采取了一个折中方法:始于一个由函数式编程语言Haskell编写的可执行规范.sel4的设计过程如图 15所示.

|
Fig. 15 sel4 design process 图 15 seL4设计过程 |
在这个设计中, 首先, 操作系统的需求由人工实现为可执行的Haskell代码, 称为Haskell原型(Haskell prototype).一方面, 该代码可以通过硬件模拟器导出为二进制码, 用于测试; 更为重要的是, 它能够自动导入到Isabelle/HOL中, 成为可执行规范(executable specification).抽象规范(abstract specification)定义了微内核系统各项操作的功能是什么, 并通过嵌入在Isabelle/HOL中的Hoare逻辑对其正确性进行陈述; 大多数定理都是有关不变式的:低层内存不变式、类型不变式、数据结构不变式、算法不变式等.抽象规范与可执行规范之间的求精证明建立了高层(抽象)与低层(具体)之间的对应关系:抽象规范中的所有Hoare逻辑属性对于可执行规范来讲也是成立的.Haskell原型、可执行规范以及抽象规范这3个部分之间的交互不断迭代, 最终达到会聚(convergence), 得到一个安全的Haskell微内核代码.
虽然Haskell原型是可执行的模型, 但是它并不满足高性能的需求.于是, seL4团队使用C编程语言手工重新实现了这个模型, 以允许更多优化, 而成为高性能的C实现(high performance C implementation).因此, 也必须建立高性能的C实现与可执行的规范之间的求精关系, 证明它不会产生比可执行规范更多的行为.
seL4团队于2009年完成了这个操作系统微内核源程序的正确性验证:没有死锁、活锁、空指针使用、缓冲区溢出、算术异常以及未初始化变量的使用, 因此获得了第一个高性能的安全操作系统微内核C源程序.
(2) 微内核源程序到ARM机器码的翻译确认
已经获得了安全的操作系统微内核高性能C源程序, 接下来待解决的问题是如何保证该源程序编译后的二进制代码的安全.seL4团队初始考虑使用在Coq中验证的C编译器CompCert进行编译, 但是效果不太理想: Coq对C语言标准的解释不同于Isabelle/HOL, 而调和这些不同并不容易——Coq的底层逻辑与Isabelle/HOL的底层逻辑不是直接兼容的.因此, seL4团队采用了Pnueli提出的翻译确认的基本思想:将源程序和目标程序转化成统一形式, 即描述控制流图的公共中间语言程序, 其简单的控制流机制和标准的算术操作为C语言、CPU指令集以及SMT的位向量理论(bit-vector theory)所共有, 这非常适合利用SMT求解器进行分析处理和证明检查.seL4的翻译确认原理如图 16所示, 主要包括3个证明系统:Isabelle/HOL、HOL4和seL4团队开发的基于SMT的证明工具.

|
Fig. 16 Artifacts of correctness proof of the sel4 translation validation 图 16 seL4的翻译确认的正确性证明 |
在图 16的左边, 将高性能C源程序作为输入, 利用Norrish开发的C parser工具, 转换为相应的语义(C semantics).C parser工具是一个通用操作语义框架, 在其上定义了Hoare逻辑以及验证条件生成器, 它们的可靠性和相对完备性得到了证明.接下来, C Semantics在Isabelle/HOL内进一步转换成Adjusted C Semantics, 然后由外部工具将语义规则转换为更为简单的控制流图程序C Graph Program, 最后转换为更接近二进制码形式的Compiled C Graph Program.在图 16的右边, 将gcc编译生成的ARM机器码作为输入, 参照由剑桥大学开发的高可信的ARM ISA规范, 获得以HOL 4定义的ARM二进制码语义(ARM binary semantics).该语义非常详尽而庞大, 以致不易于在定理证明助手中进行大规模程序的交互式推理.于是采用Myreen等人开发的自动工具decompiler, 从二进制码中抽取出描述了二进制代码运行效果的函数, 称为(decompiled functions); 同时, decompiler参照剑桥ARM ISA规范, 证明了抽取到的每个函数都是准确的.由于Isabelle/HOL和HOL 4的底层逻辑几乎相同, 这个Decompiled Functions可以容易地导入到Isabelle/HOL中, 成为Decompiled Functions 2.然后, 它也由外部工具转换为更为简单的控制流图程序, 称为Decompiled Graph Program.最后, 既然C源程序和编译后的程序都以控制流图程序表示, 并且它们在转换过程中已经尽可能接近, 则它们之间的求精关系可以使用基于SMT的证明工具器, 如Z3或者SONOLAR进行证明:编译后的二进制码的确是源码的求精.
安全可信的操作系统微内核seL4现在已经应用在了几个安全攸关的工业开发中, 譬如波音公司的无人驾驶小鸟直升机(little bird helicopter)项目.
国内的冯新宇等人在操作系统微内核验证方面也做出了比较有影响力的研究成果[157], 他们使用Coq, 针对抢占式多任务操作系统内核的形式化验证提出了一个实际的验证框架, 将操作系统内核API实现的正确性建模为其抽象规范的上下文求精(contextual refinement), 并成功地应用在嵌入式操作系统uC/OS-Ⅱ关键模块的验证中.
3.4 电路设计验证鉴于大规模集成电路的高额成本以及它们在许多安全攸关领域的应用, 硬件设计验证显得越来越重要.相比软件而言, 硬件设计的特性更益于进行自动验证, 在工业界也得到了许多成功应用.硬件验证传统上采用模拟技术, 不过, 学术界和工业界一直也在研究使用定理证明技术奠定更为可靠的硬件电路设计的正确性.
早期工业级验证由Moore和Lynch等人完成了AMD K5微处理器的浮点小数除法的正确性验证[158], 使用的是自动定理证明工具ACL2.之后, Russinoff对AMD K7的浮点乘、除和开方算法进行了验证[159].ACL2也经常和其他工具结合, 广泛应用于数字电路的验证:Sammane和Schmaltz等人结合符号模拟技术, 设计了TheoSim, 对片上网络体系结构进行了初步验证[160]; Hunt设计了EMOD硬件描述语言, 嵌入在ACL2逻辑中, 对威盛凌珑(VIA Nano™)处理器的设计进行了验证[161]; Sawada和Sandon等人针对结合ACL2与IBM公司的SixthSense模型检查器进行了研究[162].不过, 与模拟技术的结合会损害完整性, 而与模型检查器的给合会影响可伸缩性:在验证大规模集成电路时, 状态转换检查呈指数倍增长.
Gordon开创了使用高阶逻辑进行硬件设计验证的先河.Harrison和Kaivola使用HOL light对Intel处理器浮点小数算法进行了验证[163, 164].Harrison和O’Leary等人一直与Intel公司合作, 从事使用HOL light进行电路设计的正确性验证的研究[165, 166].Tverdyshev等人将Isabelle/HOL用于门级电路控制单元的硬件平台的验证[167].Deng使用PVS定理证明系统对现场可编程门阵列(FPGA)的设计进行了验证[168].Berg和Jacobi对VAMP处理器中的浮点单元进行了验证[169].Braibant等人使用Coq开发了一个理论库, 用于硬件电路的建模和验证[170].Shiraz和Hasan等人使用HOL 4也开发了一个用于硬件验证的通用理论库[171].
与高阶的交互式定理证明相比, 自动定理证明难以处理大型电路设计的验证问题, 这是由于大量变量和中间节点的提升, 计算呈指数倍增长而造成的.具有更高表述力的高阶逻辑能克服这些不足, 但是需要用户的介入, 该用户既应该是电路系统的设计专家, 又需要精通定理证明助手.这种困难性限制了高阶定理证明在工业界的使用, 工程师们宁愿选择更易于使用的工具; 通用理论库的建立应该有助于复杂的电路设计的验证, 在一定程度上能够减轻这种困难性.
4 结束语机械化定理证明是历经60多年、稳步向前推进的研究领域.验证的C优化编译器CompCert以及操作系统微内核sel4在工业界的成功应用也充分说明这是一个有意义且可行的建构可信的软/硬件系统的方式.回到引言部分的问题, 这些成果究竟是如何取得的?
可以说, 这些成果的取得非常来之不易, 它们是无数哲学家、数学家、逻辑学家和计算机科学家智慧的结晶:20世纪上半叶对数学基础的严格辩论, 使得形式系统的表述能力和形式证明系统的推理能力得到了系统而深入的探索.20世纪下半叶, 机械化定理证明技术在计算机上优雅地实现了数理逻辑的严格推理, 并提供了人工完全不可比拟的检查证明的能力.尽管这条研究道路曲折而漫长, 但纵观整个过程, 它一直保持着生机和活力, 并最终成就斐然.机械化定理证明具有:
1) 高可靠性.它以数理逻辑和类型论的经典研究成果为基础, 由计算机自动或半自动地完成并检查证明, 这种机械性证明的可靠性远胜人类的手工证明;
2) 可执行性.除了提供可靠的证明结果, 大多证明助手都支持可执行性, 能够生成可执行代码获得原型工具, 通过运行测例, 确认(validate)所定义的形式规范的合法性;
3) 共享性.具有类似逻辑基础的不同证明助手之间能够共享证明结果, 如Isabelle/HOL和HOL 4以及HOL light之间等[172].这种共享性避免了重复研究, 也推进了机械化定理证明技术在工业界的应用.
因此, 有理由乐观地估计, 机械化定理证明将不再只由少数人所掌握和推崇, 而将广泛成为数学研究、计算机软/硬件系统设计开发的一部分, 确保严格的正确性.一些重要问题和挑战包括:
(1) 并发程序的机械化证明.
并发程序的验证一直是具有挑战性的难题, 而机械化证明的研究成果更为少见.林惠民实现了世界上第一个通用交互式进程代数验证工具PAM[173], 获得国际同行的赞誉.林惠民进一步对PAM加以扩充, 实现了能处理消息传送进程的验证工具VPAM[174].蒋炎岩等人针对并发程序动态分析的访存依赖获取技术, 提出了包含4个评价指标(时性、准确性、高效性和简化性)、两种方法(在线追踪和离线合成)和两类应用(轨迹分析和并发控制)的综述框架[175].
致力于共享内存并发程序执行的安全问题, 许多研究围绕内存模型展开[133, 176—181].Lochbihler将Java内存模型规范与运行时操作语义联合在一起进行分析[137, 138], 能够更为准确地刻画并发行为.他在Isbaelle/HOL中定义了双模拟(bisimulation)和延迟双模拟(delay bisimulation), 并完成了相应的证明.不过, 这些成果距工业应用还有一段距离.
(2) 支持并发的面向对象语言的编译器验证.
虽然出现了一个验证的、支持面向对象特性和线程的Java编译器, 但是并没有考虑字节码到本地二进制码的正确翻译.此外, 并发以及可执行性都是需要进一步解决和完善的问题.
(3) 更加强大的证明助手的开发.
当前存在许多较为成熟的证明助手, 但是不尽完善, 仍然有待支持更强大的自动证明能力[182]、更方便友好的用户交互、更多的数学和算法知识库、更多的不同证明助手之间的共享.一些研究者们正在致力于提高证明效率:Irving等人首次将递归神经网络运用到交互式定理证明问题上[183], Loos等人正在研究联合机器学习和自动推理的技术, 较大地提升了HOL 4的证明搜索效率[184].
(4) 机械化定理证明的开发成本较高, 使用和掌握比较困难, 需要探讨解决方法.
致谢 本文在由何炎祥教授主持的与可信软件和可信编译等相关的项目执行过程中逐步形成.感谢何炎祥教授主持的博士讨论班上各位师生所发表的意见和建议.感谢各位审稿人和编辑提出的修改意见和建议.
| [1] |
Paulson LC. Computational logic:Its origins and applications. Proc. of the Royal Society A Mathematical Physical and Engineering Sciences, 2018, 474(2210): 20170872.
[doi:10.1098/rspa.2017.0872] |
| [2] |
Wu WJ. Mathematics Mechanization. Beijing: Science Press, 2003.
|
| [3] |
Harrison J, Urban J, Wiedijk F. History of interactive theorem proving. Handbook of the History of Logic, 2014, 9(2): 135-214.
[doi:10.1016/B978-0-444-51624-4.50004-6] |
| [4] |
Wang H. Toward mechanical mathematics. IBM Journal of Research and Development, 1960, 4: 2-22.
[doi:10.1147/rd.41.0002] |
| [5] |
McCarthy J. Computer programs for checking mathematical proofs. In:Proc. of the 5th Symp. on Pure Mathematics of the American Mathematical Society, 1961, 219-227.
[doi:10.2307/2270190] |
| [6] |
Wos L, Pereira F, Hong R, Boyer RS, Moore JS, Bledsoe WW, Henschen LJ, Buchanan BG, Wrightson G, Green C. An overview of automated reasoning and related fields. Journal of Automated Reasoning, 1985, 1(1): 5-48.
[doi:10.1007/BF00244288] |
| [7] |
Blazy S, Dargaye Z, Leroy X. Formal verification of a C compiler front-end. In:Proc. of the 14th Int'l Symp. on Formal Methods. Hamilton, 2006, 460-475.
[doi:10.1007/11813040_31] |
| [8] |
Leroy X. A formally verified compiler back-end. Journal of Automated Reasoning, 2009, 43(4): 363-446.
[doi:10.1007/s10817-009-9155-4] |
| [9] |
Demange BD, Pichardie D. A formally verified SSA-based middle-end-Static single assignment meets CompCert. In:Proc. of the 21st European Conf. on Programming Languages and Systems. Tallinn, 2012, 47-66.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0212503125 |
| [10] |
Klein G, Elphinstone K, Heiser G, Andronick J, Cock D, Derrin P, Elkaduwe D, Engelhardt K, Kolanski R, Norrish M, Sewell T, Tuch H, Winwood S. seL4:Formal verification of an OS kernel. In:Proc. of the 22nd Symp. on Operating Systems Principles. Montana, 2009, 207-220.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0223674090/ |
| [11] |
Sewell T, Myreen MO, Klein G. Translation validation for a verified OS kernel. ACM SIGPLAN Notices, 2013, 48(6): 471-482.
[doi:10.1145/2499370.2462183] |
| [12] |
Klein G, Andronick J, Elphinstone K, Murry T, Sewell T, Kolanski R, Heiser G. Comprehensive formal verification of an OS microkernel. ACM Trans. on Computer Systems, 2014, 32(1): 136-156.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=2872bd98f4a3401167763dc5fb749fd3 |
| [13] |
Nipkow T, Brinkop H. Amortized complexity verified. Journal of Automated Reasoning, 2018.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0215076597/ |
| [14] |
Eberl M, Haslbeck MW, Nipkow T. Verified analysis of random binary tree structures. In:Proc. of the ITP, 2018.
https://link.springer.com/chapter/10.1007/978-3-319-94821-8_12 |
| [15] |
Bentkamp A, Blanchette JC, Klakow D. A formal proof of the expressiveness of deep learning. In:Proc. of the 8th Interactive Theorem Proving. Brasília, 2017, 46-64.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/002200277001400206 |
| [16] |
Song LH, Wang HT, Ji XJ, Zhang XY. Verification of file comparison algorithm fcomp in Isabelle/HOL. Ruan Jian Xue Bao/Journal of Software, 2017, 28(2): 203-215(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5098.htm [doi:10.13328/j.cnki.jos.005098] |
| [17] |
Wadler P. Proofs are programs: 19th century logic and 21st century computing. 2000. https://philpapers.org/rec/WADPAP
|
| [18] |
Prawitz D. An improved proof procedure. Theoria, 1960, 26: 102-139.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ027582117/ |
| [19] |
Davis M, Putnam H. A computing procedure for quantification theory. Journal of the ACM, 1960, 7: 201-215.
[doi:10.1145/321033.321034] |
| [20] |
Robinson JA. A machine-oriented logic based on the resolution principle. Journal of the ACM, 1965, 12(1): 23-41.
[doi:10.1145/321250.321253] |
| [21] |
Bibel W. Early history and perspectives of automated deduction. In:Proc. of the 30th German Conf. on Advances in Artificial Intelligence. Osnabrück, 2007, 2-18.
|
| [22] |
Fitting M. First-order Logic and Automated Theorem Proving. 2nd ed., Springer-Verlag, 1996.
|
| [23] |
Davis M, Logemann G, Loveland D. A machine procedure for theorem-proving. Communications of the ACM, 1962, 5(7): 394-397.
[doi:10.1145/368273.368557] |
| [24] |
Liu Y, Duan ZH, Tian C. NuTL2PFG:Checking satisfiability of νTL formulas. Ruan Jian Xue Bao/Journal of Software, 2017, 28(4): 898-906(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5057.htm [doi:10.13328/j.cnki.jos.005057] |
| [25] |
Gentz G. Investigations into logical deduction. 1964. http://www.jstor.org/stable/20009142 [doi:10.2307/20009142]
|
| [26] |
D'Agostino M. Classical natural deduction:We will show them! In:Proc. of the Essays in Honour of Dov Gabbay, 2005, 429-468.
http://d.old.wanfangdata.com.cn/Periodical/hhdxxb200906017 |
| [27] |
Church A. A formulation of the simple theory of types. Journal of Symbolic Logic, 1940, 5(2): 56-68.
[doi:10.2307/2266170] |
| [28] |
Russell B, Whitehead A. Principia Mathematica, Vol.3. Cambridge: Cambridge University Press, 1994.
|
| [29] |
Kamareddine F, Laan T, Nederpelt R. A Modern Perspective on Type Theory. Springer-Verlag, 2005.
|
| [30] |
Andrews PB. An introduction to mathematical logic and type theory:To truth through proof. Applied Logic, 1986, 27(1): 312-314.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/048661348301500107 |
| [31] |
Paulson LC. A Formulation of the Simple Theory of Types (for Isabelle). Berlin. Heidelberg:Springer-Verlag, 1990.
|
| [32] |
Awodey S, Pelayo Á, Warren MA. Voevodsky's univalence axiom in homotopy type theory. Notices of the American Mathematical Society, 2013, 60(8): 1164-1167.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1302.4731 |
| [33] |
Prawitz D, Deduction N. A Proof-theoretical Study. Uppsala:Almqvist & Wilkselll, 1965.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_cs%2f0703018 |
| [34] |
Howard WA. The formulae-as-types notion of construction. In:Proc. of the H.b.Curry Essays on Combinatory Logic Lambda Calculus & Formalism, 1980, 480-490.
|
| [35] |
Martin-Lof P. Intuitionistic type theory. In:Proc. of the Notes by Giovanni Sambin of a Series of Lecturees Give in Padua. Bibliopolis, 1980.
http://d.old.wanfangdata.com.cn/Periodical/kzllyyy201209019 |
| [36] |
Coquand T, Huet G. The calculus of constructions. Information and Computation, 1988, 76(2): 95-120.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_cs%2f0610072 |
| [37] |
Bertot Y, Casteran P. Interactive Theorem Proving and Program Development:Coq'Art:The Calculus of Inductive Constructions. Berlin:Springer-Verlag, 2010.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0218486615/ |
| [38] |
McCarthy J. Towards a mathematical theory of computation. In:Proc. of the Western Joint IRE-AIEE-ACM Computer Conf. New York, 1961, 225-328.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1012.5432 |
| [39] |
Carwright R. Practical formal semantic definition and verification systems for typed lisp. 1976. https://www.researchgate.net/publication/244996781_A_PRACTICAL_FORMAL_SEMANTIC_DE_NITION_AND_VERI_CATION_SYSTEM_FOR_TYPED_LISP
|
| [40] |
Carwright R, McCarthy J. First order programming logic. In:Proc. of the 6th ACM Sigact-Sigplan Symp. on Principles of Programming Languages. New York, 1979, 68-80.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0227164777/ |
| [41] |
Bledsoe WW. Splitting and reduction heuristics in automatic theorem proving. Artificial Intelligence, 1971, 2: 55-77.
[doi:10.1016/0004-3702(71)90004-X] |
| [42] |
Boyer RS, Moore JS. Proving theorems about LISP functions. Journal of the ACM, 1973, 22(1): 486-493.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0210789950/ |
| [43] |
Moore JS, Wirth CP. Automation of mathematical induction as part of the history of logic. Computer Science, arXiv: 13096226.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1309.6226 |
| [44] |
Walther C. Mathematical Induction:Handbook of Logic in Artificial Intelligence and Logic Programming. Oxford: Oxford University Press, 1994.
|
| [45] |
Floyd RW. Assigning meanings to programs. In:Proc. of the American Mathematical Society Symp. on Applied Mathematics, 1967, 19: 19-31.
|
| [46] |
Hoare CAR. An axiomatic basis for computer programming. Communications of the ACM, 1969, 12: 576-580.
[doi:10.1145/363235.363259] |
| [47] |
Edsger W. Dijkstra, guarded commands, nondeterminancy and formal derivation of program. Communications of the ACM, 1975, 18(8): 453-457.
[doi:10.1145/360933.360975] |
| [48] |
Igarashi S, London R, Luckham DC. Automatic program verification Ⅰ: A logical basis and its implementation. Technical Report, ISI/RR-73-11, Information Science Institute, 1973.
|
| [49] |
Good D, Cohen Richard M, Lawrence HW. A report on the development of Gypsy. In:Proc. of the 1978 Annual Conf. ACM Press, 1978, 116-122.
[doi:10.1145/800127.804078] |
| [50] |
Filliâtre JC, Marché C. The why/krakatoa/caduceus platform for deductive program verification. In:Proc. of the 19th Int'l Conf. on Computer Aided Verification. Berlin, 2007, 173-177.
|
| [51] |
Barnett M, Deline R, Jacobs B, Fähndrich M, Leino MRK, Schulte W, Venter H. The Spec# programming system:Challenges and directions. In:Proc. of the Verified Software:Theories, Tools, Experiments. Berlin, Heidelberg:Springer-Verlag, 2008, 144-152.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1004.1142 |
| [52] |
Flanagan C, Leino KRM, Lillibridge M, Nelson KRM, Saxe JB, Stata R. Extended static checking for Java. Technical Report, 159, Compaq Systems Research Center, 1998.
|
| [53] |
Barnes J. High Integrity Software:The SPARK Approach to Safety and Security. Addison Wesley, 2003.
|
| [54] |
Gordon AD, Harper R, Harrison J, Jeffrey A, Sewell P. Robin milner 1934~2010:Verification, languages, and concurrency. In:Proc. of the 43th ACM SIGPLAN-SIGACT Symp. on Principles of Programming Languages. Pittersburg, 2016, 473-474.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=170bc15f24f9c919719f6a5a24f2b735 |
| [55] |
Scott DS. A type-theoretical alternative to ISWIM, CUCH, OWHY. Theoretical Computer Science, 1993, 121(1-2): 411-440.
[doi:10.1016/0304-3975(93)90095-B] |
| [56] |
Milner R. Implementation and applications of Scott's logic for computable functions. In:Proc. of the Conf. on Proving Assertions About Programs. ACM Press, 1972, 1-6.
https://www.researchgate.net/publication/234798280_Implementation_and_applications_of_Scott's_logic_for_computable_functions |
| [57] |
Gordon MJ, Milner AJ, Wadsworth P. A mechanised logic of computation. In:LNCS 78, 1979.
|
| [58] |
Paulson LC. Logic and Computation:Interactive Proof with Cambridge LCF. Cambridge University Press, 1987.
|
| [59] |
Gordon MJ, Melham TF. Introduction to HOL:A Theorem Proving Environment for Higher Order Logic. Cambridge University Press, 1993.
|
| [60] |
Constable RL, Allen SF, Bromley HM, Cleaveland WR, Cremer JF, Harper RW, Howe DJ, Knoblock TB, Mendler NP, Panangaden P, Sasaki J T, Smith SF. Implementing Mathematics with the Nuprl Proof Development System. Prentice-Hall, 1987.
|
| [61] |
Scott DS. Towards a mathematical semantics for computer language. In:Proc. of the Symp. on Computers and Automation, 1971, 19-46.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1207.2300 |
| [62] |
Plotkin G. A structural approach to operational semantics. Journal of Logic & Algebraic Programming, 1981, s 60-61: 17-139.
http://d.old.wanfangdata.com.cn/NSTLQK/10.1016-j.jlap.2004.05.001/ |
| [63] |
Despeyroux J. Proof of translation in natural semantics. In:Proc. of the 1st Symp. on Logic in Computer Science, 1986, 16-18.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/000306517702500404 |
| [64] |
Gordon MJC. Mechanizing programming logics in higher order logic. In:Current Trends in Hardware Verification and Automated Theorem Proving, 1989, 387-439.
|
| [65] |
Mehta F, Nipkow T. Proving pointer programs in higher-order logic. Information and Computation, 2005, 199(1-2): 200-227.
[doi:10.1016/j.ic.2004.10.007] |
| [66] |
Gordon MJ. Why higher-order logic is a good formalism for specifying and verifying hardware. In:Proc. of the Edinburgh Workshop Formal Aspects of VLSI Design. Amsterdam, 1986, 153-177.
|
| [67] |
Wagner TJ. Hardware verification[Ph. D. Thesis]. Stanford University, 1977.
|
| [68] |
Cohn A. A proof of correctness of the Viper microprocessor:The first level. In:Proc. of the VLSI Specification, Verification and Synthesis. Springer US, 1988, 27-71.
https://link.springer.com/chapter/10.1007%2F978-1-4613-2007-4_2 |
| [69] |
Huet GP. A unification algorithm for typed λ-calculus. Theoretical Computer Science, 1975, 1(1): 27-57.
[doi:10.1016/0304-3975(75)90011-0] |
| [70] |
Paulson LC. Isabelle:The next 700 theorem provers. Computer Science, 2000, 310(1): 772-773.
http://d.old.wanfangdata.com.cn/Periodical/jfjlgdxxb200805010 |
| [71] |
Gordon M. From LCF to HOL:A short history. In:Proc. of the Proof, Language, and Interaction, Essays in Honour of Robin Milner. DBLP, 2000, 169-186.
|
| [72] |
Dijkstra EW. A constructive approach to the problem of program correctness. BIT Numerical Mathematics, 1968, 8(3): 174-186.
[doi:10.1007/BF01933419] |
| [73] |
Wirth N. Program development by stepwise refinement. Commmunications of ACM, 1971, 14(4): 221-227.
[doi:10.1145/362575.362577] |
| [74] |
Gerhart SL. Correctness-preserving program transformations. In:Proc. of the 2nd Symp. on Principles of Programming Languages. California, 1975, 54-66.
[doi:10.1145/512976.512983] |
| [75] |
Burstall RM, Darlington J. A transformation system for developing recursive programs. ACM SIGPLAN Notices, 1975, 10(6): 465-472.
[doi:10.1145/390016.808470] |
| [76] |
Manna Z, Waldinger R. A deductive approach to program synthesis. Readings in Artificial Intelligence & Software Engineering, 1980, 2(1): 90-121.
http://d.old.wanfangdata.com.cn/NSTLQK/10.1145-357084.357090/ |
| [77] |
Back RJR. A calculus of refinements for program derivations. Acta Informatica, 1988, 25(6): 593-624.
[doi:10.1007/BF00291051] |
| [78] |
Li B, Tang ZH, Zhai J, Zhao JH. Verification of concrete programs with respect to abstract programs. Ruan Jian Xue Bao/Journal of Software, 2017, 28(4): 786-803(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5195.htm [doi:10.13328/j.cnki.jos.005195] |
| [79] |
Vickers T. An overview of a refinement editor. In:Proc. of the Institution of Radio and Electronic Engineers, 1990.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/106939718802200102 |
| [80] |
Groves L, Nickson R, Utting M. A tactic driven refinement tool. In:Proc. of the 5th Refinement Workshop. London, 1992, 272-297.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=10.1177/03058298010300010901 |
| [81] |
Back RJ, von Wright J. Refinement concepts formalized in higher order logic. Formal Aspects of Computing, 1990, 2(1): 247-272.
[doi:10.1007/BF01888227] |
| [82] |
Wright JV. Program refinement by theorem prover. In:Proc. of the 6th Refinement Workshop. London:Springer-Verlag, 1994, 121-150.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=Doaj000003837336 |
| [83] |
Abadi M, Lamport L. The existence of refinement mapppings. Theorectical Computer Science, 1991, 82(2): 253-384.
[doi:10.1016/0304-3975(91)90224-P] |
| [84] |
Lamport L. The Temporal Logic of Actions. ACM Press, 1994.
http://d.old.wanfangdata.com.cn/NSTLQK/10.1145-177492.177726/ |
| [85] |
Jonsson B. Simulations between specifications of distributed systems. In:Proc. of the 2nd Int'l Conf. on Concurrency Theory. Amsterdam, 1991, 346-360.
|
| [86] |
Lynch NA, Vaandrager FW. Forward and backward simulations for timing-based Systems. In:Proc. of the Real-Time:Theory in Practice, REX Workshop. Berlin, Heidelberg:Springer-Verlag, 1991, 391-446.
http://cn.bing.com/academic/profile?id=c2b2977139605ecc825ca41d15636129&encoded=0&v=paper_preview&mkt=zh-cn |
| [87] |
Pnueli A, Rosner R. On the synthesis of a reactive module. In:Proc. of the 16th Symp. on Principles on Programming Languages. Texas, 1989, 179-190.
http://cn.bing.com/academic/profile?id=d9df6a5ca58f64ee8e2dcb3040f3c9e8&encoded=0&v=paper_preview&mkt=zh-cn |
| [88] |
Abrial JR. The B-book:Assigning Programs to Meanings. Cambridge University Press, 1996.
|
| [89] |
Clearsy. ATELIER B Interactive Prover Reference Manual. 2016.
|
| [90] |
Geuvers H. Proof assistants history, ideas and future. Sadhana, 2009, 24(1): 3-25.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ025080951/ |
| [91] |
Harrison J. A Mizar mode for HOL. In:Proc. of the 9th Int'l Conf. on Theorem Proving in Higher-Order Logics. Turku, 1996, 203-220.
|
| [92] |
Wenzel M. Isar:A generic interpretative approach to readable formal proof documents. In:Proc. of the Int'l Conf. on Theorem Proving in Higher Order Logics. Berlin, Heidelberg:Springer-Verlag, 1999, 167-183.
http://d.old.wanfangdata.com.cn/Periodical/hwyhmb201505006 |
| [93] |
Gonthier G, Mahboubi A, Tassi E. A small scale reflection extension for the Coq system. Research Report, RR-6455, INRIA, 2008.
http://cn.bing.com/academic/profile?id=347c01e08607229e6deda72c19644f2b&encoded=0&v=paper_preview&mkt=zh-cn |
| [94] |
Wiedijk F. A synthesis of the procedural and declarative styles of interactive theorem proving. Logical Methods in Computer Science, 2012, 8(1): 106-108.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1201.3601 |
| [95] |
Aspinall D. Proof general:A generic tool for proof development. In:Proc. of the 6th Int'l Conf. on Tools and Algorithms for the Construction and Analysis of Systems. Berlin, 2000, 38-43.
http://cn.bing.com/academic/profile?id=bdf9270074525c5326e201bb39291319&encoded=0&v=paper_preview&mkt=zh-cn |
| [96] |
Bertot Y, Théry L. A generic approach to building user interfaces for theorem provers. Journal of Symbolic Computation, 1998, 25(2): 161-194.
[doi:10.1006/jsco.1997.0171] |
| [97] |
Wenzel M. Isabelle/jEdit-A prover IDE within the PIDE framework. Computer Science, 2012, 468-471.
|
| [98] |
Cairns P. Alcor:A user interface for Mizar. Mechanized Mathematics & Its Applications, 2008, 4(1): 2005.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0222688202/ |
| [99] |
De Bruijn NG. AUTOMATH:A language for mathematics. In:Automation of Reasoning, 1968, 159-200.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0214745958/ |
| [100] |
Harper R, Honsell F, Plotkin G. A framework for defining logics. In:Proc. of the 8th Symp. on Logic in Computer Science. Montreal, 1993, 143-184.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_cs%2f9703101 |
| [101] |
Nipkow T, Wenzel M, Paulson LC. Isabelle/HOL: A Proof Assistant for Higher-Order Logic. Springer-Verlag, 2002(latest available in 2014).
|
| [102] |
Wenzel M. Shared-memory multiprocessing for interactive theorem proving. In:Proc. of the 4th Interactive Theorem Proving. Rennes, 2013, 418-434.
http://cn.bing.com/academic/profile?id=96fe4bcd668cbf853516ed762ec1a16a&encoded=0&v=paper_preview&mkt=zh-cn |
| [103] |
Wenzel M. Parallel proof checking in Isabelle/Isar. In:Proc. of the ACM SIGSAM Workshop on Programming Languages for Mechanized Mathematics Systems, 2009.
http://cn.bing.com/academic/profile?id=f1d997eab4f6f5b7d1ef33c803154bf3&encoded=0&v=paper_preview&mkt=zh-cn |
| [104] |
Kaufmann M, Manolios P, Moore JS. Computer-aided Reasoning:ACL2 Case Studies. Kluwer Academic Publishers, 2000.
http://d.old.wanfangdata.com.cn/Periodical/cjce200404009 |
| [105] |
Rager DL, Jr WAH, Kaufmann M. A parallelized theorem prover for a logic with parallel execution. In:Proc. of the 4th Int'l Conf. on Interactive Theorem Proving. Rennes, 2013, 435-450.
|
| [106] |
Wu WT. On the decision problem and the mechanization of theorem-proving elementary geometry. Science in China, 1979, 6: 94-102.
[doi:10.1142/9789812791085_0008] |
| [107] |
Yang L, Zhang JZ, Hou XR. The Series in Nonlinear Science:Nonlinear Algebraic Equations and Theorem Proving. Shanghai: Shanghai Education Press, 1996.
|
| [108] |
Yang L, Xia BC. Inequality Proving and Automatic Discovery. Beijing: Science Press, 2008.
|
| [109] |
van Benthem Jutting LS. Checking Landau's "Grundlagen" in the automath system. Studies in Logic and the Foundations of Mathematics, 1994, 133: 701-720.
[doi:10.1016/S0049-237X(08)70222-2] |
| [110] |
Trybulec A. The Mizar-QC/6000 logic information language. ALLC Bulletin, 1978, 6(2).
|
| [111] |
Hurd J. Verification of the Miller-Rabin probabilistic primality test. Journal of Logic & Algebraic Programming, 2001, 56(1): 3-21.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=94ef84d74f6ceaede6564c9842edbc84 |
| [112] |
Hölzl J. Markov chains and Markov decision processes in Isabelle/HOL. Journal of Automated Reasoning, 2017, 59: 345-387.
[doi:10.1007/s10817-016-9401-5] |
| [113] |
Nipkow T, Bauer G, Schultz P. 2006 Flyspeck Ⅰ:Tame graphs. In:Proc. of the 3rd Int'l Joint Conf. Seattle, 2006, 21-35.
|
| [114] |
Hales T, Adams M, Bauer G, Dang DT, Harrison J, Le Hoang T, Kaliszyk C, Magron V, McLaughlin S, Nguyen TT, Nguyen TQ, Nipkow T, Obua S, Pleso J, Rute J, Solovyev A, Ta AHT, Tran TN, Trieu DT, Urban J, Vu KK, Zumkeller R. A formal proof of the Kepler conjecture. Forum of Mathematics, 2017, 5.
|
| [115] |
Appel K, Haken W. Every planar map is four colorable. Bulletin of the American Mathematical Society, 1976, 82: 711-712.
[doi:10.1090/S0002-9904-1976-14122-5] |
| [116] |
Gonthier G. The four color theorem:Engineering of a formal proof. In:Proc. of the Computer Mathematics. Springer-Verlag, 2008, 333.
|
| [117] |
Lakatos I, Worrall J, Zahar E. Proofs and refutations:The logic of mathematical discovery. Mathematical Gazette, 2015, 61(416): xii, 174-146.
|
| [118] |
Avigad J, Harrison J. Formally verified mathematics. Communications of the ACM, 2014, 57(4): 66-75.
[doi:10.1145/2591012] |
| [119] |
Paulson L. ALEXANDRIA: Large-scale formal proof for the working mathematician. 2018. https://www.cl.cam.ac.uk/~lp15/Grants/Alexandria/
|
| [120] |
Ma S, Shi ZP, Shao ZZ, Guan Y, Li L, Li Y. Higher-order logic formalization of conformal geometric algebra and its application in verifying a robotic manipulation algorithm. Advances in Applied Clifford Algebras, 2016, 26(4): 1305-1330.
[doi:10.1007/s00006-016-0650-5] |
| [121] |
Ma S, Shi ZP, Li LM, Guan Y, Zhang J, Song XY. Formalization of geometric algebra theories in higherorder logic. Ruan Jian Xue Bao/Journal of Software, 2016, 27(3): 497-516(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/4977.htm [doi:10.13328/j.cnki.jos.004977] |
| [122] |
Safonov VO. Trustworthy Compilers. John Wiley & Sons, 2010.
http://d.old.wanfangdata.com.cn/Periodical/rjxb201907007 |
| [123] |
He YX, Wu W. Theories and Technologies of Trusted Compiler Construction. Beijing: Science Press, 2013.
|
| [124] |
Morris FL. Advice on structuring compilers and proving them correct. In:Proc. of the 1st Symp. on Principles of Programming Languages. Massachusetts, 1973, 144-152.
|
| [125] |
Polak W. Compiler Specification and Verification. Springer-Verlag, 1981.
http://d.old.wanfangdata.com.cn/Periodical/jsjkx200306049 |
| [126] |
Young WD. Verified compilation in micro-Gypsy. In:Proc. of the 3rd Symp. on Software Testing, Analysis, and Verification. Florida, 1989, 20-26.
[doi:10.1145/75308.75312] |
| [127] |
Moore JS. A mechanically verified language implementation. Journal of Automated Reasoning, 1989, 5(4): 461-492.
|
| [128] |
Curzon P. A verified compiler for a structured assembly language. In:Proc. of the Int'l Workshop on the HOL Theorem Proving System and its Applications, 1991, 253-262.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC026275818 |
| [129] |
Stringer-Calvert DWJ. Mechanical verification of compiler correctness[Ph. D. Thesis]. York University, 1998.
|
| [130] |
Liu Y, Gan YK, Wang SY, Dong Y, Yang F, Shi G, Yan X. Trustworthy translation for eliminating high-order operation of a synchronous dataflow language. Ruan Jian Xue Bao/Journal of Software, 2015, 2(2): 332-347(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/4785.htm [doi:10.13328/j.cnki.jos.004785] |
| [131] |
Shang S, Gan YK, Shi G, Wang SY, Dong Y. Key translations of the trustworthy compiler L2C and its design and implementation. Ruan Jian Xue Bao/Journal of Software, 2017, 28(5): 1233-1246(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5213.htm [doi:10.13328/j.cnki.jos.005213] |
| [132] |
Beringer L, Stewart G, Dockins R, Appel WA. Verified compilation for shared-memory C. In:Proc. of the 23rd European Symp. on Programming Languages and Systems. Grenoble, 2014, 107-127.
|
| [133] |
Sevcik J, Vafeiadis V, Nardelli FZ, Jagannathan S, Sewell P. Relaxed-memory concurrency and verified compilation. ACM SIGPLAN Notices, 2011, 46(1): 43-54.
[doi:10.1145/1925844.1926393] |
| [134] |
Nipkow T, Oheimb DV. Java light is type-safe definitely. In:Proc. of the 3rd Symp. on Principles on Programming Languages. California, 1998, 161-170.
|
| [135] |
Klein G. Verified bytecode verifiers[Ph. D. Thesis]. Technical University of Munich, 2002.
|
| [136] |
Klein G, Nipkow T. A machine-checked model for Java-like language, virtual machine and compiler. In:Proc. of the 33rd European Symp. on Programming Languages and Systems. South Carolina, 2006, 619-695.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f85d14d3f95ddace27438563bece5044 |
| [137] |
Lochbihler A. A machine-checked, type-safe model of Java concurrency:Language, virtual machine, memory model, and verified compiler[Ph. D. Thesis]. Karlsruher Institute Technology, 2012.
|
| [138] |
Lochbihler A. Making the Java memory model safe. ACM Trans. on Programming Languages & Systems, 2014, 35(4): 1-65.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=f937fdba9f85ebb4ae3b3b46b7bd708c |
| [139] |
He YX, Jiang N, Li QA, Zhang J, Shen FF. Machine-checked model for Micro-Dalvik virtual machine. Ruan Jian Xue Bao/Journal of Software, 2015, 26(2): 364-379(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/4787.htm [doi:10.13328/j.cnki.jos.004787] |
| [140] |
Jiang N, He YX, Zhang XT. mJava compiler targeting Micro-Dalvik virtual machine. Acta Electronica Sinica, 2016, 44(7): 1619-1629(in Chinese with English abstract).
[doi:10.3969/j.issn.0372-2112.2016.07.015] |
| [141] |
Mike H, Bowen Jonathan P, Ernst-Rudiger O. Provably Correct Systems. Springer Publishing Company, 2017.
http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0226739936/ |
| [142] |
He J, Hoare CAR, Fränzle M, Muller-Olm M. Provably correct systems. LNCS, 1994, 863: 288-335.
[doi:10.1007/3-540-58468-4_171] |
| [143] |
Buth B, Buth KH, Fränzle M, Karger B, Lakhneche Y, Langmaack H, Muller-Olm M. Provably correct compiler development and implementation. In:Proc. of the Int'l Conf. on Compiler Construction, 1992, 141-155.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC026604804/ |
| [144] |
He J, Page I, Bowen JP. A provably correct hardware implementation of Occam. ESPRIT ProCoS project document[OU HJF 9/5]. Oxford University Computing Laboratory, 1992.
|
| [145] |
Zhou CC, Hoare CAR, Ravn AP. A calculus of durations. Information Processing Letters, 1991, 40(5): 269-276.
[doi:10.1016/0020-0190(91)90122-X] |
| [146] |
Hansen MR, Zhou C. Duration calculus:Logical foundations. Formal Aspects of Computing, 1997, 9(3): 283-330.
[doi:10.1007/BF01211086] |
| [147] |
Zhou CC, Hansen MR, Sestoft P. Decidability and undecidability results for duration calculus. In:Proc. of the 10th Symp. on Theoretical Aspects of Computer Science. Würzburg:Springer-Verlag, 1993, 58-68.
|
| [148] |
Goguen J, Winklerz T, Meseguerz J, Futatsugix K, Jouannaud JP. Introducing OBJ. Technical Report, SRI Int'l, 1993.
http://d.old.wanfangdata.com.cn/Periodical/kjjbydc201505009 |
| [149] |
Sampaio A. An algebraic approach to compiler design[Ph. D. Thesis]. Oxford University, 1993.
|
| [150] |
Morris JM. Laws of data refinement. Acta Informatica, 1989, 26: 287-308.
http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_1360ef60f6c680bdb2600e173c54f81a |
| [151] |
Hoare CAR, He J, Sampaio A. Normal form approach to compiler design. Acta Informatica, 1993, 30(8): 701-739.
[doi:10.1007/BF01191809] |
| [152] |
Duran A, Cavalcanti A, Sampaio A. An Algebraic Approach to the Design of Compilers for Object-Oriented Languages. SpringerVerlag, 2010.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=048c64c3c7df198ba1581232d2773e65 |
| [153] |
Lu RQ. Formal Semantics of Computing Systems. Beijing: Tsinghua University Press, 2017.
|
| [154] |
Necula GC. Proof-carrying code. In:Proc. of the 2nd Symp. on Principles on Programming Languages. San Francisco, 1997, 106-119.
http://d.old.wanfangdata.com.cn/Periodical/jsjkxjsxb-e200703010 |
| [155] |
Hu RG, Chen YY, Guo F, Zhang Y. Design and implementation of a certifying compiler for type-based annotation. Journal of Computer Research and Development, 2004, 41(1): 28-33(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/jsjyjyfz200401005 |
| [156] |
Pnueli A, Siegel M, Singerman E. Translation validation. In:Proc. of the 4th Tools and Algorithms for Construction and Analysis of Systems. Lisbon, 1998, 151-166.
http://d.old.wanfangdata.com.cn/Periodical/hwyjggc200502022 |
| [157] |
Xu FW, Fu M, Feng XY, Zhang X, Zhang H, Li Z. A practical verification framework for preemptive OS kernels. In: Proc. of the Computer Aided Verification. Springer Int'l Publishing, 2016.
|
| [158] |
Moore JS, Lynch T, Kaufmann M. A mechanically checked proof of the correctness of the kernel of the AMD5K86 floating point division algorithm. IEEE Trans. on Computers, 1996, 47: 913-926.
|
| [159] |
Russinoff DM. A mechanically checked proof of IEEE compliance of the floating point multiplication, division and square root algorithms of the AMD-K7TM processor. Journal of Computation & Mathematics, 1998, 1: 148-200.
|
| [160] |
Sammane GA, Schmaltz J, Toma D, Ostier P, Borrione D. TheoSim:Combining symbolic simulation and theorem proving for hardware verification. In:Proc. of the 17th Symp. on Integrated Circuits and System Design. Pernambuco, 2004, 60-65.
[doi:10.1145/1016568.1016591] |
| [161] |
Hunt WA. Verifying VIA NANO microprocessor components. In:Proc. of the 10th Formal Methods in Computer-Aided Design. Lugano, 2010, 3-10.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0210591033/ |
| [162] |
Sawada J, Sandon P, Paruthi V, Baumgartner J. Hybrid verification of a hardware modular reduction engine. In:Proc. of the 11th Int'l Conf. on Formal Methods in Computer-Aided Design. Texas, 2011, 207-214.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0212095996 |
| [163] |
Harrison J. Floating point verification in HOL light:The exponential function. In:Proc. of the 3rd Int'l Conf. on Algebraic Methodology and Software Technology. Sydney, 1997, 246-260.
|
| [164] |
Kaivola R, Kohatsu K. Proof engineering in the large:Formal verification of Pentium®4 floating-point divider. Int'l Journal on Software Tools for Technology Transfer, 2003, 4(3): 323-334.
[doi:10.1007/s10009-002-0081-6] |
| [165] |
Harrison J. Formal verification at Intel. In:Proc. of the Logic in Computer Science. Ottawa, 2003, 45-54.
http://d.old.wanfangdata.com.cn/Periodical/jsjkxjsxb-e201004016 |
| [166] |
O'Leary J, Zhao X, Gerth R, Seger CJ. Formally verifying IEEE compliance of floating-point hardware. Intel Technical Journal, 1999, 69-72.
|
| [167] |
Tverdyshev S. A verified platform for a gate-level electronic control unit. In:Proc. of the 9th Formal Methods in Computer-Aided Design. Austin, 2009, 164-171.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC0210248079 |
| [168] |
Deng H. Formal verification of FPGA based systems[MS. Thesis]. Department of Conmputer and Sofrware, McMaster University, 2011.
|
| [169] |
Berg C, Jacobi C. Formal Verification of the VAMP Floating Point Unit. Berlin. Berlin, Heidelberg:Springer-Verlag, 2001.
|
| [170] |
Braibant T. Coquet: A Coq library for verifying hardware. In: Proc. of the 1st Certified Programs and Proofs, Vol. 7086. Kenting: Springer-Verlag, 2011. 330-345.
|
| [171] |
Shiraz S, Hasan O. A HOL library for hardware verification using theorem proving. IEEE Trans. on Computer-Aided Design of Integrated Circuits and Systems, 2018, PP(99): 1.
[doi:10.1109/TCAD.2017.2705049] |
| [172] |
Mclaughlin S. An interpretation of Isabelle/HOL in HOL light. In:Proc. of the 3rd Int'l Joint Conf. on Automated Reasoning. Springer-Verlag, 2006, 192-204.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC026738881 |
| [173] |
Lin H. PAM:A process algebra manipulator. Formal Methods in System Design, 1995, 7(3): 243-259.
[doi:10.1007/BF01384078] |
| [174] |
Lin H. A verification tool for value-passing process algebras. In:Proc. of the IFIP TransactionsC-16:Protocol Specification, Testing and Verification, 1993, 79-92.
|
| [175] |
Jiang YY, Xu C, Ma XX, Lü J. Approaches to obtaining shared memory dependences for dynamic analysis of concurrent programs:A survey. Ruan Jian Xue Bao/Journal of Software, 2017, 28(4): 747-763(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5193.htm [doi:10.13328/j.cnki.jos.005193] |
| [176] |
Aspinall D, Ševčík J. Formalising Java's Data Race Free Guarantee. Berlin, Heidelberg:Springer-Verlag, 2007, 22-37.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC025178863/ |
| [177] |
Batty M, Owens S, Sarkar S, Sewell P, Weber T. Mathematizing C++ concurrency. In: Proc. of the 38th Symp. on Principles on Programming Languages. Austin, 2011.
|
| [178] |
Ševčík J. Safe optimisations for shared-memory concurrent programs. In: Proc. of the 32nd Conf. on Programming Language Design and Implementation. San Jose, 2011.
|
| [179] |
Pichon-Pharabod J, Sewell P. A concurrency semantics for relaxed atomics that permits optimisation and avoids thin-air executions. In:Proc. of the 43rd Symp. on Principles on Programming Languages. St. Petersburg, 2016, 622-633.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=1f30dd796539a5ff5aa3bfa22e12fe43 |
| [180] |
Liang H, Feng X, Fu M. Rely-guarantee-based simulation for compositional verification of concurrent program transformations. ACM Trans. on Programming Languages & Systems, 2014, 36(1): 1-55.
http://cn.bing.com/academic/profile?id=84b8cb7948360d598e4c44f77224d210&encoded=0&v=paper_preview&mkt=zh-cn |
| [181] |
Liang H, Feng X. A program logic for concurrent objects under fair scheduling. In:Proc. of the 43rd Symp. on Principles on Programming Languages. St. Petersburg, 2016, 385-399.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=d1d91e35d05f6beaa0cf20eea98b4f3b |
| [182] |
Zhang HR, Fu M. Design and implementation of Coq tactics based on Z3. Ruan Jian Xue Bao/Journal of Software, 2017, 28(4): 819-826(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/5196.htm [doi:10.13328/j.cnki.jos.005196] |
| [183] |
Alemi AA, Chollet F, Een N, Irving G, Szegedy C, Urban J. DeepMath-Deep sequence models for premise selection. In: Proc. of the NIPS 2016. 2016.
|
| [184] |
Loos S, Irving G, Szegedy C, Kaliszyk C. Deep network guided proof search. In: Gauthier T, Kaliszyk C, Urban J, eds. Proc. of the TacticToe: Learning to Reason with HOL4 Tactics (LPAR 2017). 2017.
|
| [2] |
吴文俊. 数学机械化. 北京: 科学出版社, 2003.
|
| [16] |
宋丽华, 王海涛, 季晓君, 张兴元. 文件比较算法fcomp在Isabelle/HOL中的验证. 软件学报, 2017, 28(2): 203-215.
http://www.jos.org.cn/1000-9825/5098.htm [doi:10.13328/j.cnki.jos.005098] |
| [24] |
刘尧, 段振华, 田聪. NuTL2PFG:νTL公式的可满足性检查. 软件学报, 2017, 28(4): 898-906.
http://www.jos.org.cn/1000-9825/5057.htm [doi:10.13328/j.cnki.jos.005057] |
| [78] |
李彬, 汤震浩, 翟娟, 赵建华. 通过抽象程序证明复杂具体程序. 软件学报, 2017, 28(4): 786-803.
http://www.jos.org.cn/1000-9825/5195.htm [doi:10.13328/j.cnki.jos.005195] |
| [107] |
杨路, 张景中, 侯晓荣. 非线性科学丛书:非线性代数方程组与定理机器证明. 上海: 上海科技教育出版社, 1996.
|
| [108] |
杨路, 夏壁灿. 数学机械化丛书:不等式机器证明与自动发现. 北京: 科学出版社, 2008.
|
| [121] |
马莎, 施智平, 李黎明, 关永, 张杰, Xiao-Yu SONG. 几何代数的高阶逻辑形式化. 软件学报, 2016, 27(3): 497-516.
http://www.jos.org.cn/1000-9825/4977.htm [doi:10.13328/j.cnki.jos.004977] |
| [123] |
何炎祥, 吴伟. 可信编译构造理论与关键技术. 北京: 科学出版社, 2013.
|
| [130] |
刘洋, 甘元科, 王生原, 董渊, 杨斐, 石刚, 闫鑫. 同步数据流语言高阶运算消去的可信翻译. 软件学报, 2015, 2: 332-347.
http://www.jos.org.cn/1000-9825/4785.htm [doi:10.13328/j.cnki.jos.004785] |
| [131] |
尚书, 甘元科, 石刚, 王生原, 董渊. 可信编译器L2C的核心翻译步骤及其设计与实现. 软件学报, 2017, 28(5): 1233-1246.
http://www.jos.org.cn/1000-9825/5213.htm [doi:10.13328/j.cnki.jos.005213] |
| [139] |
何炎祥, 江南, 李清安, 张军, 沈凡凡. 一个机器检测的Micro-Dalvik虚拟机模型. 软件学报, 2015, 26(2): 364-379.
http://www.jos.org.cn/1000-9825/4787.htm [doi:10.13328/j.cnki.jos.004787] |
| [140] |
江南, 何炎祥, 张晓瞳. mJava到Micro-Dalvik虚拟机的编译验证. 电子学报, 2016, 44(7): 1619-1629.
[doi:10.3969/j.issn.0372-2112.2016.07.015] |
| [153] |
陆汝钤. 计算系统的形式语义(上下). 北京: 清华大学出版社, 2017.
|
| [155] |
胡荣贵, 陈意云, 郭帆, 张昱. 基于类型注解的认证编译器设计与实现. 计算机研究与发展, 2004, 41(1): 28-33.
http://d.old.wanfangdata.com.cn/Periodical/jsjyjyfz200401005 |
| [175] |
蒋炎岩, 许畅, 马晓星, 吕建. 获取访存依赖:并发程序动态分析基础技术综述. 软件学报, 2017, 28(4): 747-763.
http://www.jos.org.cn/1000-9825/5193.htm [doi:10.13328/j.cnki.jos.005193] |
| [182] |
张恒若, 付明. 基于Z3的Coq自动证明策略的设计和实现. 软件学报, 2017, 28(4): 819-826.
http://www.jos.org.cn/1000-9825/5196.htm [doi:10.13328/j.cnki.jos.005196] |
 2020, Vol. 31
2020, Vol. 31


