1 引言

在概率图中, 节点表示变量, 边表示变量的依赖关系.按节点的连接方式, 概率图分为有向图和无向图两类, 有向图可以清晰地表示节点间的条件概率, 适合知识的推理^[1].随着深度学习的兴起, 深度置信网(deep belief nets, 简称DBNs)是最早的结合了深度学习概念的混合图模型^[2].然而, 解释消除(explain-away)现象很大程度上影响了有向图的解释能力^[3], 且有些问题天然地适合使用无向图进行建模.概率无向图又称为马尔可夫网, 还可称为马尔可夫随机场(Markov random fields, 简称MRFs), MRFs的概率分布通过势函数ϕ(v)表示, 其中, v是该无向图最大子图中的节点集合.由此, MRFs的概率分布可以表达为P(s)=Z^–1$\prod\nolimits_i {{w_i}{\phi _i}({v_i})} , $其中, Z为归一化因子, 也被称为配分函数.为了方便表述和计算, MRFs的概率分布可以表示为指数族的形式:P(s)=Z^–1exp$\left( {\sum\nolimits_i {{w_i}{f_i}({v_i})} } \right), $其中, f(v_i)=log(ϕ(v_i)).由因子f(v_i)的不同表示形式可以得到不同的无向图模型^[4-7].玻尔兹曼机是一种特殊的MRFs, 其联合分布可以表示为P(s)=Z^–1e^–E(s), 其中, E(s)称为能量函数, 与MRFs中势的概念对应.从网络拓扑结构上看, 玻尔兹曼机可以分为指数族RBM(exp-RBMs)^[8]、半受限的玻尔兹曼机(SRBMs)^[9]以及全连接的玻尔兹曼机, 其中, 传统的二值RBMs模型是Exp-RBMs模型的特例.以RBMs为基础, 深度玻尔兹曼机(deep Boltzmann machines, 简称DBMs)和深度置信网(deep belief nets, 简称DBNs)等多层网络促进了深度学习的发展^[10-14].其中, DBNs是一种混合的概率图模型, 其顶部的两层是无向的关联记忆, 其余层之间的权值为自上而下的生成连接.DBMs是一种无向图模型, 其结构可以看作层次化的玻尔兹曼机, 整个深度玻尔兹曼机通过一个能量函数来表达.

RBMs、基于RBMs的拓展模型及其应用是本文综述的重点.从目标函数的角度来看, 在基于极大似然估计的RBMs中需要计算由配分函数产生的模型期望, 而配分函数的计算需要对所有节点的状态求和, 其计算复杂度极高, 因此, 基于极大似然估计的精确计算是不可行的.在基于近似计算的训练方法中, 大致可分为采样算法和变分推断(variational inference)两种^{[15, 16]}.采样算法的基础是马尔可夫链, 其目标是极大化似然函数(极小化KL散度), 几种比较有效的采样方法为:持续的马尔可夫链(persistent Markov chain)^[17]、对比散度(contrastive divergence, 简称CD)算法^[15]、持续的对比散度(persistent contrastive divergence, 简称PCD)算法^[18]以及基于快速权值的PCD(fast persistent contrastive divergence with, 简称FPCD)算法^[19]等.为了促进马尔可夫链收敛, 模拟退火和模拟回火算法被应用于采样中^[20-23].当可见层单元的激活不再条件独立时, 可以使用混合的蒙特卡罗算法替代吉布斯采样.RBMs另一种有效的训练算法是变分推断, 在变分推断中, 假设存在一个近似分布q, 其目标是最小化RBMs联合概率分布和近似的后验分布q之间的KL散度, 常用的变分推断方法有平均场算法(mean-field method)等^[24].另一种思路是修改RBMs模型训练的目标函数, 极大似然估计等价于最小化模型分布和数据分布之间的KL散度, KL散度是f散度的一种特殊形式, 可以有效地缩小两个分布之间存在的较大差异, 但是当两个分布之间的差异较小时, KL散度存在过度平滑的问题.因此, 针对RBMs的目标函数的改进, 一种思路是使用Wasserstein距离来替代KL散度^[25], 另一种思路是在原有的似然函数基础上引入对抗损失^[26].

传统的RBMs的节点状态是二值的, 适合处理二值化的数据.对于实值的输入样本, 如自然图像和语音, 二值RBMs表现比较差.为了解决这个问题, 在RBMs的基础上, 学者们提出了多种适用于实值数据的RBMs模型, 包括高斯-二值RBMs(mRBMs)^{[27, 28]}、协方差RBMs(cRBMs)^[29]、期望-协方差RBMs(mcRBMs)^[30]、ReLu-RBMs以及spike-and-slab RBMs(ssRBMs)等^[31-35].以RBM为基础, 组合变分自动编码器(variational autoencoders, 简称VAEs)^[36], 将RBMs作为VAEs的先验, 可以有效地拟合数据中存在的多峰分布.以RBMs为基础的无向图模型在图像识别、图像分割、降噪、视频处理以及图像生成领域都有广泛的应用.下面, 本文针对上述内容详细介绍相关模型以及算法.最后, 本文讨论了RBMs算法存在的问题.

2 玻尔兹曼机 2.1 受限制的玻尔兹曼机

玻尔兹曼机的概念来源于热力学背景.在统计力学中, 玻尔兹曼分布(或吉布斯分布)可以表示为指数族的形式:P(s)∝exp(–E(s)/kT), 其中, s是量子的状态, E(s)是对应的能量函数, P(s)是相应的概率分布, k是玻尔兹曼常量, T是系统温度.令kT=1, 表达式可以简化为P(s)∝exp(–E(s)), 为了方便计算, 分布函数可以写成更加细化的形式:$P({s_i}) \propto {{{{\rm{e}}^{ - E({s_i})}}} \mathord{\left/ {\vphantom {{{{\rm{e}}^{ - E({s_i})}}} {\sum\nolimits_s {{{\rm{e}}^{ - E(s)}}} }}} \right. 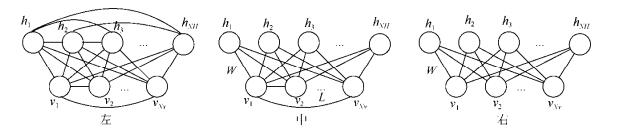} {\sum\nolimits_s {{{\rm{e}}^{ - E(s)}}} }}, $令$Z = \sum\nolimits_s {{{\rm{e}}^{ - E(s)}}} , $那么P(s)=Z^–1e^–E(s), 其中, Z是配分函数.为了方便表示, 概率分布函数还可以写成如下形式P(s|θ)=exp(–E(s)–A(θ)), 其中, A(θ)是正则化项, 对应于配分函数.能量函数E(s)有多种表示形式, 不同的形式对应于不同的模型结构, 由此可以得到不同的玻尔兹曼机模型.在玻尔兹曼机中, 根据马尔可夫独立性, 一个节点的激活只取决于与之直接连接的节点.假设节点有两个状态:激活和灭活, s是可见单元v和隐藏单元h的合集, 本文从拓扑结构上将MRFs分为玻尔兹曼机(Boltzmann machines, 简称BMs)、半受限的玻尔兹曼机(semi restricted Boltzmann machines, 简称SRBMs)^[13]和受限的玻尔兹曼机(restricted Boltzmann machines, 简称RBMs), 模型分别表示为图 1的左中右3幅图像.图 1中的每个模型包含1个可见层和1个隐藏层, 可见层对应于输入数据, 隐藏层表示输入数据的特征表达.在SRBMs中(如图 1中间图像所示), 可见层单元之间是全连接的, 隐藏层节点之间不存在连接, 权值矩阵W位于可见层节点和隐藏层节点之间.在给定可见层节点的条件下, 隐藏层节点的激活条件独立.然而, 在给定隐藏层节点的条件下, 可见层单元相互依赖, 其激活概率需要使用变分推断方法或混合的蒙特卡洛采样近似求解.RBMs与SRBMs不同, 可见层单元间不存在连接(如图 1右图所示), 对于RBMs模型, 其能量函数表示如下:

$E(v, h) = {a^T}v + {b^T}h + {h^T}Wv$

(1)

其中, a和b是RBMs的偏置, v表示可见层向量, h表示隐藏层向量, W是权值矩阵, 基于能量函数E(v, h), 联合分布可以表示为P(v, h)=Z^–1exp(–E(v, h)), 可见层单元和隐藏层单元的激活函数可以表示如下:

$P({h_k} = 1|v) = {\rm{sigmoid}}\left( {{b_k} + \sum\nolimits_{i = 1}^{{N_V}} {{w_{ki}}{v_i}} } \right)$

(2)

$P({v_k} = 1|h) = {\rm{sigmoid}}\left( {{a_k} + \sum\nolimits_{j = 1}^{{N_H}} {{h_j}{w_{kj}}} } \right)$

(3)

其中, k是向量的第k个分量, N_V是可见层向量的维度, N_H是隐藏层向量的维度, RBMs的拓扑结构可以表示为图 1右图的形式.

在RBMs的拓扑结构中, 权值矩阵W连接可见层单元和隐藏层单元.当RBMs的节点为二值单元时, 其激活函数可以表示为sigmoid形式.给定可见层单元时, 隐藏层单元的激活是条件独立的.从图模型的角度看, 目标函数可以表示为似然函数的形式, 似然函数定义为${L_s} = \ln \prod\nolimits_{i = 1}^{{n_V}} {P({v^i})} = \prod\nolimits_{i = 1}^{{n_V}} {\ln P({v^i})} , $令θ=(a, b, W), 根据极大似然估计, 似然函数关于参数的梯度可以表示如下:

$\frac{{\partial \ln P(v)}}{{\partial \theta }} = - \sum\limits_h {P(h|v)} \frac{{\partial E(v, h)}}{{\partial \theta }} + \sum\limits_{v, h} {P(v, h)} \frac{{\partial E(v, h)}}{{\partial \theta }}$

(4)

将公式(4)表示为期望的形式, 可以得到:

$\frac{{\partial {L_s}}}{{\partial \theta }} = {E_{P(v, h)}}\left[ {\frac{{\partial E(v, h)}}{{\partial \theta }}} \right] - {E_{P(h|v)}}\left[ {\frac{{\partial E(v, h)}}{{\partial \theta }}} \right]$

(5)

如公式(5)所示, 等式右边的第1项称为模型期望, 第2项称为数据期望, 两个期望的差值决定了似然函数关于参数的梯度.直观上看, 数据期望给出了参数迭代的起始条件, 模型期望提供了迭代的终止条件, 随迭代进行, 数据期望和模型期望逐渐接近, RBMs的训练随迭代趋于稳定, 此时, RBMs模型建模了输入样本的分布特性.然而在大样本下, 精确地计算这两个期望是非常困难的, 尤其是模型期望.因此, 为了降低RBMs训练的复杂度, 需要对似然函数的梯度做近似, 3种不同思路的近似策略可以表示如下.

(1) 首先从似然函数梯度的角度出发, 尝试使用采样策略, 近似似然函数梯度中的两个期望.采样策略基于马尔可夫链蒙特卡洛方法.采样过程可以看作一个马尔可夫链的状态转移过程, 简单来说, 当马尔可夫链趋于稳定时, 采样得到的样本就可以代表该分布下的期望值.基于这种思想, Persistent Markov Chain方法被引入到RBMs的训练中, 并用于近似计算似然函数的梯度.然而, 这种方法的弊端在于, 我们很难判断马尔可夫链何时达到收敛, 而且从收敛性理论分析的角度看, 为了保证马尔可夫链收敛, 在训练过程中, RBMs的学习速率需小于马尔可夫链的混合率.然而, 马尔可夫链的混合速率很难量化, 为了保证收敛, 训练过程往往使用很小的学习率, 这在很大程度上影响了RBMs的训练时间.为了缓解这个问题, 学者们提出了两种对应的思路.

●  第1种思路针对马尔可夫链的混合过程, 尝试加速马尔可夫链的收敛.典型的方法为模拟退火和模拟回火, 在退火和回火算法的帮助下, 马尔可夫链可以在更大的学习速率下收敛到稳态.然而, 算法的计算复杂度比较高, 很难在大规模样本下训练RBMs模型以解决实际问题, 目前, 退火回火算法多用于马尔可夫链的评估;

●  另一个思路尝试在马尔可夫链的基础上, 对梯度作进一步的近似.在迭代中, 不要求马尔可夫链达到稳态, 而是选择K次迭代后的KL散度作为学习的梯度信号, 该算法称为K步对比散度(K-step contrastive divergence, 简称CD-K)算法.从梯度下降(上升)的角度看, CD算法虽然在迭代的步长上作了进一步的近似, 但在似然函数的梯度方向上, CD算法的偏差很小, 而且CD算法弱化了马尔可夫链的收敛条件, RBMs可以使用一个比较大的学习率.在CD算法的基础上, 为了进一步优化似然函数的梯度, PCD算法、FPCD算法相继提出, 这些算法在CD算法的基础上, 维持数条马尔可夫链, 直到RBMs训练结束, 这样既在一定程度上保证了模型的训练效率, 又从理论上保证了算法的收敛性.

(2) 从似然函数梯度的角度出发, 采用变分推断的思想, 通过构造变分下界, 利用近似后验分布q逼近RBMs的联合分布; 或者使用变分推断的方法近似配分函数.根据这两种思想, 在基于变分推断的RBMs模型中, 大致可以分为基于平均场方法的RBMs模型和基于追踪配分函数的RBMs模型.

●  在基于平均场的方法中, 似然函数可以利用琴生不等式或凸对偶原则进行近似, 通过引入近似分布Q, 得到似然函数的下界.似然函数的下界可以表示为

$\ln P(v) \geqslant \sum\nolimits_{\{ H\} } {Q(H|v)\ln P(H|v) - Q(H|v)\ln Q(H|v)} $

(6)

由公式(6)可以看出, 极大化似然函数与最小化分布Q和P之间的KL散度是等价的.此时, 极大似然估计的计算可以使用EM算法, 平均场算法的优势在于:计算速度相比Gibbs采样为基础的采样算法快得多.然而, 平均场算法在逼近模型期望时效果并不理想, 因为模型期望通常是多模态的(multi-modal), 而平均场算法假设分布是单模态的.为了缓解这个问题, 有学者提出将平均场算法用于近似数据期望, 使用持续的马尔可夫链来近似模型期望; 另外有学者将平均场算法结合CD算法; 还有学者在原平均场算法的基础上, 使用二阶近似; 或者在平均场的基础上, 进一步参数化平均场参数.

●  在基于追踪配分函数的RBMs模型中, RBMs的配分函数是能量函数针对所有状态的和, 可以表示为如下的表达式:

$Z = \int_x {\tilde p(x){\rm{d}}x} = \int_x {\frac{{\tilde p(x)}}{{q(x)}}q(x){\rm{d}}x} $

(7)

其中, $\tilde p(x)$为指数形式的能量函数, 可以表示为e^–E(x), 对于配分函数, 可以使用参数化的变分分布q来近似未积分的能量函数$\tilde p(x), $然后使用q(x)来追踪配分函数.此方法相比于平均场方法的优点在于, 可以相对有效地近似多峰分布, 缺点是计算复杂度较高, 需要多次从近似分布q(x)中采样, 并交替更新$\tilde p(x)$和q(x)才能取得比较理想的近似效果.

(3) 从目标函数的角度出发, 修改RBMs模型训练的目标函数, 传统的RBMs模型采用的目标函数都是基于边缘分布的似然函数, 以KL散度的形式表达, 但是KL散度的特点导致了RBMs模型训练得到的分布相比于样本分布来说过于平滑, 为了解决这个问题, 学者们从目标函数入手, 改变目标函数的形式, 解决KL散度中存在的问题.一种修改的思路是将传统的KL散度替换为Wasserstein距离, 从而使RBMs得到锐利的生成图像; 另一种思路是在原有的似然函数的基础上, 加入对抗损失, 利用对抗生成网络(generative adversarial nets, 简称GANs)的思想来训练RBMs模型, 利用对抗损失缓解RBMs模型过度平滑的问题.

2.2 RBM的训练算法 2.2.1 对比散度算法

似然函数关于参数的梯度可以表示为$\frac{{\partial {L_s}}}{{\partial \theta }} = {E_{P(v, h)}}\left[ {\frac{{\partial E(v, h)}}{{\partial \theta }}} \right] - {E_{P(h|v)}}\left[ {\frac{{\partial E(v, h)}}{{\partial \theta }}} \right].$其中, 第1项为模型期望, 第2项为数据期望.在实际应用中, 数据期望的计算复杂度是可执行的, 但是来自于配分函数Z的模型期望的计算复杂度过高.为了保证算法的时效性, 需要使用近似算法来估计模型期望, 最大化似然函数在效果上等价于最小化RBMs的自由能.与之对应, 最小化自由能是一个P-Hard问题.CD算法基于Gibbs采样.假设初始分布表示为P⁽⁰⁾, 一次状态转移(1步Gibbs采样)后的分布表示为P⁽¹⁾, 马尔可夫链达到稳态时的分布为P^(∞), P⁽⁰⁾和P^(∞)的KL散度表示为KL(P⁽⁰⁾, P^(∞)), P⁽¹⁾和P^(∞)的KL散度表示为KL(P⁽¹⁾, P^(∞)), 在CD算法中, 对比散度的梯度可以表示为

$ - \frac{\partial }{{\partial \theta }}\left( {KL({P^{(0)}}, {P^{(\infty )}}) - KL({P^{(1)}}, {P^{(\infty )}})} \right) = {E_{{P^{(0)}}}}\left[ {\frac{{\partial E(v, h)}}{{\partial \theta }}} \right] - {E_{{P^{(1)}}}}\left[ {\frac{{\partial E(v, h)}}{{\partial \theta }}} \right] + \frac{{\partial {P^{(1)}}}}{{\partial \theta }}\frac{{\partial \left( {KL({P^{(1)}}, {P^{(\infty )}})} \right)}}{{\partial {P^{(1)}}}}$

(8)

根据文献[15], 公式(8)的最后一项可以忽略, 将CD算法应用到RBMs模型中, 首先在给定输入向量v⁽⁰⁾时, 利用W计算隐藏层单元的激活概率和激活状态h⁽⁰⁾, 然后基于W计算v⁽¹⁾和h⁽¹⁾, 得到的(v⁽¹⁾, h⁽¹⁾)作为一步CD算法的状态量, 似然函数的梯度估计可以表示为

$\frac{{\partial \ln P(v)}}{{\partial {W_{ij}}}} \approx P({h_i} = 1|{v^{(0)}}){v^{(0)}} - P({h_i} = 1|{v^{({\rm{1}})}}){v^{({\rm{1}})}}$

(9)

$\frac{{\partial \ln P(v)}}{{\partial {a_i}}} \approx {v_i}^{(0)} - {v_i}^{({\rm{1}})}$

(10)

$\frac{{\partial \ln P(v)}}{{\partial {b_i}}} \approx P({h_i} = 1|{v^{(0)}}) - P({h_i} = 1|{v^{({\rm{1}})}})$

(11)

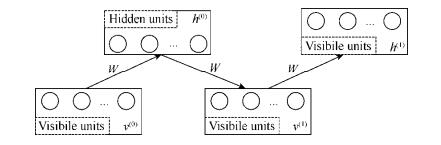
CD算法在很大程度上减小了采样过程的复杂度, 为了直观表示CD算法的计算过程, 本文将算法的示意图绘制如图 2所示.

CD算法被广泛用到RBMs模型的训练中.使用一步CD算法来估计似然函数的梯度, 可使用一个较大的学习率来训练RBMs模型, 然而CD算法是一个非常粗糙的近似, 该算法还可以利用马尔可夫链的思想进行优化.

2.2.2 PCD算法和FPCD算法

虽然CD算法降低了似然函数梯度计算的复杂度, 但是CD算法在迭代步长上作了一个粗糙的近似, 为了更加精确地逼近似然函数的梯度, 并把算法的计算复杂度控制在合理的范围内, PCD算法和FPCD算法被提了出来, 不同于CD算法, PCD算法在训练过程中维持了完整的马尔可夫链, 马尔可夫链的数量等于每一个mini-batch中的样本数, 马尔可夫链的状态转移过程一直维持到训练过程结束.使用PCD算法在计算开销上几乎与CD算法一致, 但是由于维持了完整的马尔可夫链, 算法对似然函数的逼近更加有效.FPCD算法讨论了学习速率和马尔可夫链混合速率之间的关系, 指出权值的更新过程加速了马尔可夫链的混合, 促进马尔可夫链收敛到稳态.因此, FPCD算法引入快速权值来加速马尔可夫链的收敛.

2.2.3 平均场算法

平均场算法是变分推断方法的一种, 变分推断方法通过引入额外的参数来获取似然函数的边界, 通过引入变分分布q(h|x), 参数化后验分布的下边界, 从而逼近后验概率.在RBMs中使用最多的变分推断方法是平均场算法.平均场算法假设每个节点的激活概率用参数u来表示, $u_j^H$表示隐藏层的第j个单元的激活, $u_j^V$表示可见层的第j个单元的激活.此时, 极大似然估计过程可以使用EM算法实现, 当给定似然函数时, 优化u得到的激活函数为sigmoid形式:

$u_i^H = {\rm{sigmoid}}\left( {\sum\nolimits_j {{\theta _{ij}}u_j^V + {\theta _{i0}}} } \right)$

(12)

其中, θ为参数.为了获得极大似然估计, 需要求解似然函数关于参数的梯度:

$\Delta {\theta _{ij}} \propto \left( {u_i^Vu_j^H - {E_{P(v, h)}}\left[ {s_i^Vs_j^H} \right]} \right)$

(13)

公式(12)的第2个期望依然无法直接计算, 可以继续使用平均场方法逼近该期望.然而, 用平均场算法直接估计模型期望是不精确的, 原因在第2.1节中已经给出解释, 为了缓解这个问题, 学者们在平均场方法的基础上提出了如下方法.

第1种借助对比散度算法, 采用基于对比散度思想的平均场算法;

第2种方法利用平均场来近似数据期望, 采用Persistent Markov Chains来近似模型期望, 该方法与PCD算法有些类似;

第3种思路是在原有的平均场算法的基础上, 通过进一步假设平均场参数u是服从高斯分布的随机变量, 引入u的先验分布, 从而缓解传统平均场难以近似多峰分布的问题^[37].

第4种思路是使用二阶平均场近似来代替传统的一阶平均场方法.二阶近似也可以在一定程度上增加平均场方法近似多峰分布的能力.

2.2.4 基于追踪配分函数的变分推断法

传统的变分推断方法使用变分近似分布q(h|x)来近似后验概率p(h|x), 这种方法在RBMs中被简化为平均场方法, 但是传统的平均场理论存在难以近似多峰分布的缺点, 因此, 为了能够更加有效地近似多峰分布, 学者们从变分推断的角度出发, 利用变分推断的思想近似RBMs模型的配分函数, 通过追踪RBMs的配分函数, 达到近似似然函数的目的.不同于传统的变分推断, 变分近似q(x)被用于近似未积分的函数$\tilde p(x), $此时配分函数可以写成如下形式:

$Z = \int_x {\tilde p(x){\rm{d}}x} = \int_x {\frac{{\tilde p(x)}}{{q(x)}}q(x){\rm{d}}x} $

(14)

其中, $\tilde p(x)$是指数形式的能量函数, 在该方法中, 通过近似这个能量函数, 利用期望的形式得到了配分函数的近似, 由于由配分函数得到的期望在梯度更新中是负的, 因此需要求出配分函数的上界, 配分函数Z的上界的一种表达形式如下:

${E_{q(x)}}\left[ {\frac{{\tilde p(x)}}{{q(x)}}} \right] \geqslant {Z^2}$

(15)

将公式代入RBMs模型中, 得到如下似然函数的下界:

$\ln p(x) \geqslant \mathop {\max }\limits_{\theta , q} \frac{1}{n}\sum\nolimits_{i = 1}^n {\theta {x^{(i)}} - \frac{1}{2}\left( {a{E_{x \in q}}\left[ {\frac{{\tilde p{{(x)}^2}}}{{q{{(x)}^2}}}} \right] - \ln a - 1} \right)} $

(16)

其中, a是超参数.该方法虽然能够有效地利用变分推断的方法追踪配分函数, 但仍然存在一些问题, 在训练过程中, 由于需要交替地更新$\tilde p(x)$和q(x), 因此算法的计算复杂度较高.

2.2.5 基于Wasserstein距离的RBMs模型和基于对抗损失的RBMs模型

传统的RBMs模型是基于似然函数的, 似然函数定义为可见层单元的边缘分布形式, 优化似然函数等价于最小化模型分布和数据分布之间的KL散度, KL散度是f散度的一种特殊形式, 基于f散度的RBMs模型在训练中会存在过度平滑化的问题, 从而忽略了数据分布中存在的一些非平滑现象, 为了解决这个问题, 学者们尝试从RBMs的目标函数入手, 创建新的目标函数来优化RBMs模型存在的问题.首先, 度量模型分布和数据分布之间的距离可以使用更加有效的方式来定义.一种基于该思想的改进模型为基于Wasserstein距离的RBMs (WRBMs), 在WRBMs中, 使用Wasserstein距离来度量模型分布和数据分布之间的差异, 这种形式的目标函数不仅能够惩罚两个分布之间差异较大的部分, 也能够惩罚分布之间较小的差异, 缓解RBMs模型存在的过度平滑化的问题.

另一种针对RBMs目标函数的改进是构建基于对抗损失的RBMs模型(GAN-RBMs), 在GAN-RBMs中, 目标函数在似然函数的基础上引入对抗损失函数, 使用RBMs作为对抗网络的生成器, 同时隐层单元的激活作为对抗生成网络的critic函数, 用来判别可见层单元的激活是来自于数据还是来自于RBMs模型的重构, 基于这种思想, 在目标函数中加入对抗损失, 可以使RBMs模型有效地拟合数据分布中存在的多峰分布.这两种方法的缺点在于计算复杂度较高, 而RBMs模型存在的最大问题就是其训练比较困难, 进一步增强RBMs模型的建模能力并降低RBMs训练算法的复杂度仍然是研究的重点问题.

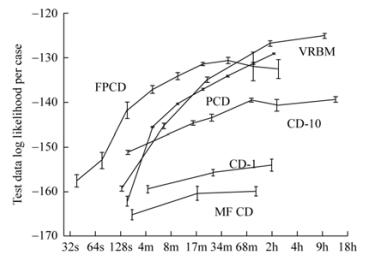
2.2.6 不同训练算法的联系与比较

从极大似然估计的角度来看, PCD算法和FPCD算法是CD算法的扩展, 他们的优势在于, 在CD算法的基础上, 维持了完整的马尔可夫链来近似模型的分布, 相比于CD算法, PCD算法和FPCD算法在付出较少的额外计算开销的前提下, 可以使用较大的学习率、更加精确的逼近似然函数的梯度.平均场算法与这3种算法不同, 是基于变分推断的近似方法, 算法不需要采样过程, 因此速度更快, 但是, 由于存在更强的独立性假设, 算法在近似模型期望的时候效果不好.一般而言, 平均场方法比较适合近似数据期望, 而采样方法比较适合近似模型期望.在DBMs的训练中, 就使用平均场方法和Persistent Markov Chain分别来逼近数据期望和模型期望.无论是变分近似还是采样算法, 都是为了近似模型分布以及模型分布下的期望而提出的方法, 模型期望源于配分函数, 因此, 在2017年, 有学者提出了基于变分方法的近似算法来直接逼近配分函数, 这就是第2.2.4节的内容.直接构建变分边界从而逼近配分函数的优势在于可以获得更有效的极大似然估计.缺点是, 相对于CD以及PCD算法, 该方法的计算复杂度更高, 需要更多的训练时间.以上的方法都是基于极大似然估计的, 对于RBMs而言, 极大似然估计等价于最小化数据分布和模型分布之间的KL散度, 但是, KL散度是不对称的, 最小化数据分布和模型分布之间的KL散度, 在一定程度上会使模型分布和数据分布之间的KL散度增大, 这会导致RBMs模型产生的模型分布过度平滑(over-smoothing), 为了解决这个问题, 有学者将对抗损失引入到RBMs模型中, 构建了(Boltzmann embedded adversary machines, 简称BEAMs)模型, 从另一个角度上看, 将KL散度替换为其他的距离度量方式, 也可以改善RBMs模型分布过度平滑的问题, 基于这个思路, Wassertein距离被引入到RBMs中, 这就是第2.2.5节的内容.为了更加直观地对比各种算法在近似log似然时的精度, 参照FPCD算法中的实验, 我们列举了如下的对比结果.

由于Wasserstein RBMs采用的loss形式不同, 因此未加入对比图.由图 3可知, 虽然基于变分方法的VRBM训练耗时较长, 但是对于测试数据集上的log似然指标, VRBM表现较优.

2.3 实值RBMs模型

传统的RBMs的单元有两种状态:0或1, 这种形式的激活单元适合处理二进制数据, 最初的RBMs也被称为二值RBMs(binary-RBMs).虽然二值的RBMs在MNIST等二值化数据集上的分类和特征提取都取得了令人满意的效果, RBMs也被用来构建深度模型, 成为深度神经网络的重要组成部分, 但是对于实值图像的建模, 二值的RBMs表现得并不理想, 因为在输入数据的二值化过程中, 一些重要信息将会丢失.因此, 如何调整RBMs模型, 使其更适合建模实值数据, 是RBMs研究的另一个重点问题.

2.3.1 指数族RBMs

从概率图的角度看, RBMs是一种无向图模型, 其中, 每一层单元的激活是条件独立的, 传统的二值RBMs模型可以看作指数族RBMs(Exp-RBMs)的特例, 在Exp-RBMs中, 激活概率可以利用Bregman Divergence表示如下:

$P({h_j}|{\eta _j}) = \exp \left( { - {D_f}({\eta _j}||{h_j}) + g({h_j})} \right)$

(17)

$P({v_i}|{\mu _i}) = \exp \left( { - {D_f}({\mu _i}||{v_i}) + g({v_i})} \right)$

(18)

其中, η_j是单元h_j的输入, u_i是单元v_i的输入, g是基础统计量(base measure), D_f是激活函数f的Bregman Divergence, 可以表示为D_f(η_j||h_j)=–η_jh_j+F(η_j)+F^*(h_j), F为f的积分函数, 有:dF(η_j)/dη=f(η_j), F^*是f反函数f^–1的积分函数.假设基础统计量为常量.即g(h_i)=c, 那么, 分布函数P(h_j||η_j)可以使用高斯分布来近似:

$\exp \left( { - {D_f}({\eta _j}||{h_j}) + c} \right) \approx N\left( {{h_j}|f({\eta _j}), {\rm{ }}f'({\eta _j})} \right)$

(19)

基于公式(19), 我们可以看出, 不同形式的激活函数将产生不同形式的高斯近似.并且, 根据激活函数及其积分函数, Exp-RBMs的能量函数可以表示为

$E(v, h) = - {v^T}Wh + \sum\nolimits_i {\left( {{F^ * }({v_i}) + g({v_i})} \right)} + \sum\nolimits_j {\left( {{F^ * }({h_j}) + g({h_j})} \right)} $

(20)

表 1列举了不同形式的激活单元和Exp-RBMs中高斯近似分布之间的对应关系.

在Exp-RBMs中, 给定与节点i直接相连的所有节点时, 节点i与本层内的其他节点是条件独立的.对于不同的激活函数, 利用Exp-RBMs可以得到不同的条件高斯分布.然而, Exp-RBMs同样也存在一些问题:虽然条件高斯分布是实值化的, 但是可见层单元的激活是条件独立的, 在独立性假设下, Exp-RBMs不能表达可见层节点之间的相关性, 而这种相关性在一些实际问题中非常关键.接下来, 本文将综述一些实值RBMs模型, 这些模型尝试利用条件高斯分布建模可见层单元的激活概率和相关关系.

2.3.2 其他形式的实值RBMs

为了建模实值的输入数据, 学者们尝试使用实值单元替换RBMs中的二值单元.基于这一思想, 高斯RBMs (mRBMs)提出.假设给定隐藏层节点时, 可见层单元的激活服从条件高斯分布, mRBMs利用网络中的权值和偏置参数化条件高斯分布的期望, 并假设协方差是一个超参数的对角矩阵, 此时mRBMs的能量函数可以表示如下:

$E(v, h) = - \frac{{{v^T}Wh}}{\sigma } - {b^T}h + \frac{{{{(v - a)}^2}}}{{2{\sigma ^2}}}$

(21)

其中, σ是协方差, a, b是偏置, 激活函数可以表示为如下形式:

$P({v_i}|h) = \frac{1}{{{\sigma _i}\sqrt {2{\rm{ \mathsf{ π} }}} }}\exp \left( { - \frac{1}{{2\sigma _i^2}}\left( {{v_i} - {a_i} - {\sigma _i}\sum\nolimits_j {{w_{ij}}} {h_j}} \right)} \right)$

(22)

$P({h_j} = 1|v) = {\rm{sigmoid}}\left( {\sum\nolimits_i {\frac{{{v_i}}}{{{\sigma _i}}}{W_{ij}} + {b_j}} } \right)$

(23)

从公式(22)可以看出, P(v_i|h)服从高斯分布, 其中, 期望为${a_i} + {\sigma _i}\sum\nolimits_j {{W_{ij}}{h_j}} , $协方差为$\sigma _i^2, $利用CD-K算法, mRBMs的参数更新过程可以表示如下:

$W = W + {\eta _W}{{\left( {\sum\nolimits_{n = 1}^N {\frac{{{v_n}}}{\sigma }h_n^T} - \sum\nolimits_{n = 1}^N {\frac{{v_n^{(K)}}}{\sigma }{{\left( {h_n^{(K)}} \right)}^T}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{n = 1}^N {\frac{{{v_n}}}{\sigma }h_n^T} - \sum\nolimits_{n = 1}^N {\frac{{v_n^{(K)}}}{\sigma }{{\left( {h_n^{(K)}} \right)}^T}} } \right)} N}} \right. } N}$

(24)

$a = a + {\eta _a}{{\left( {\sum\nolimits_{n = 1}^N {\frac{{{v_n}}}{\sigma }} - \sum\nolimits_{n = 1}^N {\frac{{v_n^{(K)}}}{\sigma }} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{n = 1}^N {\frac{{{v_n}}}{\sigma }} - \sum\nolimits_{n = 1}^N {\frac{{v_n^{(K)}}}{\sigma }} } \right)} N}} \right. } N}$

(25)

$b = b + {\eta _b}{{\left( {\sum\nolimits_{n = 1}^N {{h_n}} - \sum\nolimits_{n = 1}^N {h_n^{(K)}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{n = 1}^N {{h_n}} - \sum\nolimits_{n = 1}^N {h_n^{(K)}} } \right)} N}} \right. } N}$

(26)

由于mRBMs的协方差矩阵是一个对角矩阵, 已知隐藏层节点的状态时, 可见层单元的激活是条件独立的.从Exp-RBMs的角度看, mRBMs是一种特殊形式的Exp-RBMs, 尤其是当激活函数为ReLU或Softplus时, Exp-RBMs中可见层和隐藏层单元都是实值化的^{[38, 39]}.然而, 很多实值数据之间是存在相关性的, 例如自然图像, 图像的像素点之间是相关的, 而忽略这种相关性的mRBMs和Exp-RBMs都不能很好地建模实值图像数据.针对这个问题, 学者们提出了一类新的RBMs模型:协方差RBMs(cRBMs)和(spike-and-slab RBMs, 简称ssRBMs).在cRBMs中, 可见层单元服从条件高斯分布, 不同于mRBMs, cRBMs在隐藏层h引入附加因子f用于建模条件高斯分布非对角的协方差矩阵, 其能量函数可以表示如下:

$E(v, h) = - \sum\limits_{f = 1}^F {{{\left( {\sum\limits_{i = 1}^D {{v_i}{C_{if}}} } \right)}^2}\left( {\sum\limits_{j = 1}^J {{h_j}{P_{jf}}} } \right)} - \sum\limits_{j = 1}^J {{b_j}{h_j}} $

(27)

其中, F是附加因子的数量, C=(C_if)∈R^D×F是可见层单元和因子f之间的权值矩阵, P=(P_if)∈R^J×F是隐藏层单元和因子之间的权值矩阵, 激活概率可以表示如下:

$P\left( {h_k^c = 1|v} \right) = {\rm{sigmoid}}\left( {\frac{1}{2}\sum\nolimits_{f = 1}^F {{P_{fk}}{{\left( {\sum\nolimits_{i = 1}^D {{C_{if}}{v_i}} } \right)}^2} + b_k^c} } \right)$

(28)

$P(v|{h^c}) = N\left( {0, {\rm{ }}Cdiag(P{h^c})C'} \right)$

(29)

由于可见层单元的激活函数具有非对角的协方差矩阵, 分块的Gibbs采样不适用于采样可见层单元的状态值.因此, 基于自由能的混合蒙特卡罗算法(hybrid Monte Carlo, 简称HMC)被引入到可见层单元的采样过程中, cRBMs的自由能可以表示如下:

$F(v) = - \sum\nolimits_{j = 1}^J {\log \left( {1 + \exp \left( {\sum\nolimits_{f = 1}^F {{P_{jf}}{{\left( {\sum\limits_{i = 1}^D {{v_i}{C_{if}}} } \right)}^2} + {b_j}} } \right)} \right)} $

(30)

在cRBMs中, 激活函数与自由能成F(v)反比:P(v)∝exp(–F(v)), 其中, 协方差被参数化.然而, 高斯分布的期望在建模图像的过程中也是非常重要的, 为了同时参数化条件高斯分布的期望和协方差, 并且降低采样过程的计算复杂度, ssRBMs被提了出来, ssRBMs的能量函数可以表示如下:

$E(v, s, h) = \frac{1}{2}{v^T}{\bf{\Lambda }}v - \sum\nolimits_{j = 1}^J {\left( {{v^T}{W_j}{s_j}{h_j} + \frac{1}{2}{s_j}{\alpha _j}{s_j} + {b_j}{h_j}} \right)} $

(31)

其中, W_j是权值矩阵的第j列, α和Λ是对角矩阵, ssRBMs的条件激活概率可以表示如下:

$P({h_j} = 1|v) = \sigma \left( {\frac{1}{2}{v^T}{W_j}{\alpha _j}W_j^Tv + b{}_j} \right)$

(32)

$P({s_j}|v, h){\rm{ = }}N\left( {{h_j}\alpha _j^{ - 1}W_j^Tv, \alpha _j^{ - 1}} \right)$

(33)

$P(v|s, h){\rm{ = }}N\left( {{{\bf{\Lambda }}^{ - 1}}\sum\nolimits_{j = 1}^J {{W_j}{s_j}{h_j}} , {{\bf{\Lambda }}^{ - 1}}} \right)$

(34)

在RBMs模型的基础上, 稀疏编码也可以被拓展到ssRBMs中.表 2显示了ssRBMs与其他RBMs算法(mRBMs、cRBMs、mcRBMs)在分类上的对比结果.

RBMs有许多针对特定问题的模型变体, 例如:Mixed-variate RBMs^{[40, 41]}、Cumulative RBMs^[42]、Thurstonian RBMs^[43]、correspondence RBMs^[44]、Relevance RBMs^[45].为了处理异构数据, Tran等人提出了Mixed-variate RBMs模型建模变量, 在此基础上, Tran等人针对向量和矩阵数据类型, 提出了Cumulative RBMs; 在跨模态任务中, Feng等人提出correspondence RBMs模型, Zhao等人提出Relevance RBMs来处理图像视频中的分类问题.与此同时, 许多学者针对RBMs的模型结构和能量函数做出了一些针对性的调整, 例如:Discriminative RBMs^[46]、Boosted Categorical RBMs^[47]、Fuzzy RBMs^[48].其中, Larochelle和Bengio将决策成分(discriminative component)引入到RBMs模型中, 并提出了Discriminative RBMs模型.针对不平衡数据问题, Lee和Yoon在CD算法的基础上提出了Boost CD算法.Chen等人提出了Fuzzy RBMs以提高RBMs的鲁棒性.

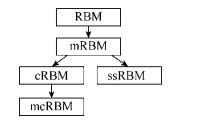
2.3.3 实值RBMs之间的联系和区别

首先需要指明的是, 高斯-二值RBMs(mRBMs)是早期对RBMs的扩展, 其计算复杂度与RBMs相当, 是最常用的实值RBMs模型, 但是由于其建模实值图像的效果不佳, 后期学者们以条件高斯分布为基础, 相继扩展出了cRBMs、mcRBMs、ssRBMs等模型, 这些模型的产生与发展关系可如图 4所示.

具体来说, 在RBMs刚提出的时候, 模型仅适合处理二值数据, 这在很大程度上限制了RBMs模型的使用和推广, 为了缓解这个问题, 学者们开始研究如何将RBMs模型应用到实值数据中.最初, Hinton等人提出, 使用RBMs中节点的激活概率来表示节点状态, 这样, RBMs可以表示区间[0, 1]之间的数据, 但是使用这种近似方法取得的效果并不理想.为了解决这个问题, mRBMs提出, 该模型假设RBMs的可见层节点在给定隐层节点的时候相互独立并服从高斯分布, 通过建模高斯分布的期望来建模条件概率分布.mRBMs是RBMs模型的直接扩展, 是早期最有效的处理实值数据的RBMs模型, 其计算复杂度不高, 至今仍在被广泛地使用在简单的图像识别问题中.然而, mRBMs假设可见层单元是条件独立的, 把基于这种假设构建的后验概率应用到Gibbs采样中, 会导致采样的模型分布也隐含了条件独立性, 从而影响了RBMs建模实值数据的效果, 尤其是实值图像, 因为图像像素点之间往往是存在一定相关性的, 因此, mRBMs建模实值数据的能力还存在提升的空间.在此基础上, 为了建模条件高斯分布的协方差, cRBMs和ssRBMs被提出.在cRBMs的基础上, mcRBMs被提出, mcRBMs用于同时建模条件高斯分布的期望和协方差.然而, cRBMs和mcRBMs训练存在的问题是, 需要使用混合蒙特卡洛采样来计算可见层单元的激活概率.为了能使用分块的Gibbs采样, ssRBMs及其改进模型引入了额外的因子, 从而构建基于对角矩阵的高斯分布.然而, 目前主流的实值RBMs及其训练算法也存在一定的不足.对于无向图模型, 由于需要计算由配分函数产生的模型期望, 因此精确的计算是不可行的, 目前的算法都是以使用不同的近似方法来逼近模型期望的梯度.本节涉及的实值RBM模型都是基于采样算法的, 采样算法的一个问题是需要维持马尔可夫链, 并且计算复杂度较高.如何高效地近似RBM中的模型期望, 一直以来是研究的难点问题.并且, 扩展RBM的层数也是目前研究的热点问题.目前学者们研究的主流方向一方面是结合RBMs和其他模型已完成分类或图像生成等任务, 另一方面, 学者们也在研究如何更加有效地训练RBMs模型.

3 RBMs与神经网络

20世纪80年代, Hinton和LeCun等学者提出了反向传播算法(BP)用来训练多层神经网络.基于梯度下降的思想(gradient descent), BP算法是一种求目标函数梯度的训练算法, 参数的更新与误差函数关于参数的梯度相关: $ {{\theta }_{i}}\leftarrow {{\theta }_{i-1}}-{{\nabla }_{\theta }}Loss$, 根据链式法则, BP算法在计算多层网络每一层的梯度$ {{\nabla }_{\theta }}Loss$时是高效的, 但是, 基于BP算法的神经网络存在一些问题.反向传播算法是通过随机梯度下降的思想来计算的, 这是一个高度非凸问题, 并且非常依靠微调和经验, 且反向传播算法受限于局部最优、过拟合等问题, 只能训练浅层网络.为了解决多层网络的训练问题, 有学者从神经网络的误差曲面和局部最优解的角度分析, 利用正则化等手段, 改变神经网络的初始化权值在误差曲面上生成的位置, 从而使多层神经网络更容易收敛到较好的局部最优解.为了使神经网络得到一个较好的初始权值, 基于Boltzmann分布和马尔可夫随机场理论的玻尔兹曼机被提了出来.玻尔兹曼机利用能量函数来描述神经网络的统计特征.而神经网络可以被描述为一种特殊形式的玻尔兹曼机:RBMs.通过RBMs模型, 神经网络可以在统计力学上获得解释, 基于RBMs的深度置信网(deep belief nets, 简称DBNs), 利用逐层预训练的贪婪算法, 成功地训练了多层的神经网络.随后, 深度学习的概念逐渐出现在公众视野中.可以说, RBMs是深度学习的先驱.在普通的前馈神经网络的基础上, 简单的堆叠RBMs模型可以产生两种不同的深度结构:DBNs和DBMs, 结合卷积网络结构, 卷积深度置信网(convolutional neural networks, 简称CNNs)在处理图像数据时非常有效^[49-55].目前, RBMs模型还被结合到当下常用的变分推断模型(如变分自编码器)以及对抗神经网络中.RBMs和神经网络的结合一方面促进了传统多层感知器的训练, 使网络的层数得以扩展, 进而开辟了深度学习的浪潮.另一方面, 由于RBMs的推理是双向的, 将神经网络和RBMs结合得到的模型既可以用于判别, 也可以用于生成, 而生成模型是目前阶段深度学习研究的另一个热点.

3.1 DBNs和DBMs

DBNs是一种混合的图模型, 顶部为无向的关联记忆, 余下的层满足自上而下的生成连接.DBNs可以由RBMs逐层堆叠来创建, 逐层贪婪地训练RBMs模型, 将前一个RBM的输出作为下一个RBM的输入, 逐层堆叠则得到DBNs.DBNs可以用于初始化神经网络的权值, 以一个简单的3层模型为例, 由DBNs建立的联合概率分布可以表示如下:

$P(v, {h^{(1)}}, {h^{(2)}}, {h^{(3)}}) = P(v|{h^{(1)}})P({h^{(1)}}|{h^{(2)}})P({h^{(2)}}, {h^{(3)}})$

(35)

其中, P(h⁽²⁾, h⁽³⁾)表示RBMs的联合分布, P(v|h⁽¹⁾)和P(h⁽¹⁾|h⁽²⁾)为RBMs的条件分布, 根据RBMs的分布函数, 有:

$P({h^{(i)}}|{h^{(i + 1)}}) = \prod\nolimits_j^{{J^{(i)}}} {P(h_j^{(i)}|{h^{(i + 1)}})} = {\rm{simgoid}}\left( {\sum\nolimits_{k = 1}^{{J^{(i + 1)}}} {h_k^{(i + 1)}W_{jk}^{(i)}} + b_j^{(i)}} \right)$

(36)

其中, b⁽ⁱ⁾表示第i个隐藏层的偏置, W⁽ⁱ⁾表示第i–1层和第i层之间的权值矩阵, 利用逐层训练的方法, 可以有效地初始化一个DBNs模型.DBMs是一种层次化的概率无向图模型, 每一层单元的激活取决于与之直接相连的上下两层的节点.虽然DBMs的计算复杂度高于DBNs, 但是由于DBMs每一层单元的激活组合了更加抽象的特征, DBMs的图像生成能力更加出色.以含有2个隐藏层的DBM模型为例, 其能量函数可以表示如下:

$E\left( {v, {h^{(1)}}, {h^{(2)}}} \right) = - \sum\nolimits_{i = 1}^D {\sum\nolimits_{j = 1}^{{J^{(1)}}} {{v_i}W_{ij}^{(1)}h_j^{(1)}} } - \sum\nolimits_{j = 1}^{{J^{(1)}}} {\sum\nolimits_{j' = 1}^{{J^{(2)}}} {h_j^{(1)}W_{jj'}^{(2)}h_{j'}^{(2)}} } - \sum\nolimits_{j = 1}^{{J^{(1)}}} {b_j^{(1)}h_j^{(1)}} - \sum\nolimits_{j' = 1}^{{J^{(2)}}} {b_{j'}^{(2)}h_{j'}^{(2)}} - \sum\nolimits_{i = 1}^D {{c_i}{v_i}} $

(37)

根据能量函数, DBMs单元的激活概率为

$P\left( {h_j^{(1)} = 1|v, {h^{(2)}}} \right) = {\rm{simgoid}}\left( {\sum\nolimits_i {{v_i}W_{ij}^{(1)}} + \sum\nolimits_{j'} {W_{jj'}^{(2)}h_{j'}^{(2)}} + b_j^{(1)}} \right)$

(38)

$P\left( {h_{j'}^{(2)} = 1|{h^{(1)}}} \right) = {\rm{sigmoid}}\left( {\sum\nolimits_j {h_j^{(1)}W_{jj'}^{(2)}} + b_{j'}^{(2)}} \right)$

(39)

$P({v_i} = 1|{h^{(1)}}) = {\rm{sigmoid}}\left( {\sum\nolimits_j {W_{ij}^{(1)}h_j^{(1)}} + c{}_i} \right)$

(40)

DBNs和DBMs模型都可以看作前馈神经的多层神经网络, 通常, 使用RBMs初始化的DBNs和DBMs是一种无监督模型, 无监督初始化的神经网络若想完成监督学习的任务, 则必须建立特征与标签之间的映射关系.基于训练后的DBNs和DBMs, 综合监督学习的方法, 可以完成模式识别任务, 常用的监督学习方法有:

(1) 基于BP算法的权值微调.

(2) 基于wake-sleep算法的认知生成过程.

(3) 基于Class-RBMs和分类器的组合.

第1种方法是目前最主流的监督学习算法, BP算法基于梯度下降的思想, 其中, 有一个相当粗糙的梯度下降法取得了巨大的成功:随机梯度下降(stochastic gradient descent, 简称SGD), 在基于监督学习的深度网络(deep neural nets, 简称DNNs)中, SGD是梯度下降法中最简单的, 然而, SGD算法在训练DNN时取得了非常好的效果.至于为什么非常粗糙的算法对神经网络这种复杂的优化问题有效, 仍然是一个有待进一步研究的问题.

Wake-sleep算法是一种基于认知科学的算法:在神经网络中, 当训练数据是自上而下生成的时候, 那么被用于自上而下(top-down)生成图像的隐藏层单元的状态就可以用于训练自下而上(bottom-up)的认知权值(reco-weights)^[56].如果我们已经获得了较好的认知连接(reco-connections), 就可以根据前一层的活跃度信息重建下一层的活跃度, 从而学习生成权值.给定生成权值(generative weights), 算法学习得到认知权值(recognition weights); 反之, 给定认知权值, 算法也可以学习生成权值.在清醒阶段(“wake” phase), 认知权值被用于自下而上驱动神经元, 相邻层神经元的状态被用于训练生成权值; 在睡眠阶段(“sleep” pahse), 自上而下地生成连接被用于认知连接的学习, 从而生成数据, 此时相邻层的神经元状态就可用于学习认知连接.

第3种方法是基于Class-RBMs以及分类器的监督学习方法.Class-RBMs是一种基于样本和标签的RBMs模型, Class-RBMs建模输入x和标签y之间的联合概率分布.其能量函数可以表示如下:

$E(x, y, h) = - {h^T}Wx - {b^T}x - {c^T}h - {d^T}{e_y} - {h^T}U{e_y}$

(41)

基于能量函数, 激活函数可以表示为

$P(h|y, x) = {\rm{sigmoid}}\left( {{c_j} + {U_{jy}} + \sum\nolimits_i {{W_{ji}}{x_i}} } \right)$

(42)

$P({x_i} = 1|h) = {\rm{sigmoid}}\left( {{b_i} + \sum\nolimits_j {{W_{ji}}{h_j}} } \right)$

(43)

此时, 可以求得关于标签y和输入x的条件概率:

$P(y|x) = \frac{{\exp ( - F(y, x))}}{{\sum\nolimits_{y \in \left\{ {1, 2, ..., C} \right\}} {\exp ( - F(y, x))} }}$

(44)

其中, F(y, x)为自由能.Class-RBMs建立了输入数据和标签之间的联合分布, 这在一定程度上类似于BP算法, 不同的是, BP算法包含了特征逐层抽象的过程.基于Class-RBMs, 在模型堆叠之后直接使用分类器, 例如支持向量机(support vector machines, 简称SVMs), 也可以获得比较理想的识别效果.

3.2 基于变分自编码和GAN的混合模型

VAEs模型被广泛地应用于半监督学习和图像生成中, VAEs是基于贝叶斯原理的有向图模型, 分为编码器和解码器两部分, 在传统的自编码网络中, 从X→Z→X', X表示输入, Z是自编码器的隐式表达, X'是解码表示.这样的一个过程实现了无监督表征学习.可以学习到隐式表达Z.VAEs不同于普通的自编码网络, 隐式表达Z是概率分布的形式, 模型从边缘分布P(x)出发, 利用KL散度, 获得似然函数的变分下界.在VAEs中, 编码器和解码器可以具有不同的形式, 其中最常用的形式为神经网络, 编码器和解码器都由神经网络组成, 其中假设基于输入x的条件概率q(z|x)表示编码器, 为了引入变分边界, 似然函数可以写为如下形式:

$\ln ({p_\theta }(x)) = KL({q_\phi }(h|x)||{p_\theta }(h|x)) + L(x, \theta , \phi )$

(45)

其中, L为似然函数中剩余的部分, 由于KL散度是大于等于0的, 因此上述的似然函数可以进一步写成如下形式:

$\ln ({p_\theta }(x)) \geqslant L(x, \theta , \phi ) = - KL({q_\phi }(h|x)||{p_\theta }(h)) + {E_{{q_\phi }(h|x)}}\left[ {\ln {p_\theta }(x|h)} \right]$

(46)

其中, p(h)是隐层节点的先验概率, 一般情况下, 假设先验概率为简单的分布形式, 例如均值为0、方差为1的标准正态分布, 由这个正态分布和概率解码器来生成数据x, 但是使用高斯分布来建模输入数据存在一定的不足, 对于图像数据, 深度网络在提取特征的过程中其特征是逐步抽象化的, 仅使用连续的随机变量来建模图像会导致模型分布过度平滑, 为了在抽象特征的基础上实现特征的离散化组合, 基于VAEs和RBMs的混合模型被提了出来, 在VAEs的基础上, 使用RBMs作为先验替换传统的标准正态分布, 多层卷积网络的基础上, 使用RBMs建模离散化的高度抽象化的特征, 并通过参数化手段, 使用BP算法训练模型, 基于这种方法的图像生成模型可以得到更加清晰、锐利的生成图像.

另一种思路是将RBMs和对抗生成网络相结合.GANs是目前非常有效的生成模型, 传统的GANs通过对抗的方式最小化模型分布和数据分布之间的JS散度, WGANs在GANs的基础上进行了改进, 最小化模型分布和数据分布之间的Wasserstein距离, 但是, WGAN的训练还存在一定的问题, 其训练不稳定且有随时崩溃的风险, 且GANs对超参数非常敏感, 往往需要进行大量的调试和人为干预, 才能获得一个比较好的生成模型, 为了获得比较稳定且融合GANs优势的生成模型, 有学者将对抗的思想引入到RBMs中, 同时最小化数据分布和模型分布之间的forword KL散度和模型分布与数据分布之间的reverse KL散度, 综合自编码器结构, GAN-RBMs可以结合VAEs或自动编码器模型, 组成多层的生成模型.

3.3 卷积深度置信网

另一种成功的DNNs模型是卷积神经网络(convolutional neural nets, 简称CNNs), 不同于预训练的机制, CNNs从网络拓扑结构上优化DNNs, 利用卷积和池化操作, 将局部性信息和不变性信息引入到神经网络中, 利用先验信息减少网络参数, 进一步降低了计算复杂度.CNNs在自然图像处理、音频、视频等方面取得了很多研究成果.基于结构的特殊性, CNNs的训练参数比一般的全连接神经网络的要少得多, 为了加速网络的训练, 并减缓梯度扩散现象, CNNs可以使用ReLU作为激活单元, 并在GPU上并行训练.目前在工业界的推广下, 除了各种小的修改(Residual Nets、ReLU、BatchNorm、Adam Optimizer、Dropout、GRU、GAN、LSTMs等)外, 神经网络的主要训练方法又回到30年前的BP算法^[57-73].针对图像处理问题, BP算法将原始的复杂统计问题转化为神经网络的参数调节问题和网络结构的优化问题.这大幅度地降低了DNNs研究的门槛, 吸引了更多的学者追踪DNN的相关研究.同时, GPU的使用提供了训练DNNs的硬件基础.基于GPU的深度学习框架, 如CAFFE、TensorFlow等, 为针对DNNs的程序设计提供了方便、有力的支持.目前, 许多对DNNs的研究贡献都集中在神经网络的梯度流上, 如:传统的网络采用sigmoid函数作为激活函数, 然而sigmoid函数是一种饱和函数, 这会导致梯度扩散问题, 为了缓解这个问题, 线性整流单元(rectified linear unit, 简称ReLU)以及改进的Leaky ReLU被引入到DNNs中; 为了强调梯度和权值分布的稳定性, ELU和SELU激活函数被引入到DNNs中^[62]; 当DNNs的深度过大时, 尽管使用了非饱和的激活函数, DNNs的训练还是会面临梯度消失的问题, 为此, 学者们提出了highway网络和ResNets模型^{[65, 66]}.为了稳定参数的均值和方差, BatchNorm方法被应用到DNN的训练中^[63].为了缓解过拟合, Dropout方法和Weight uncertainty方法被用于DNNs^[67-70].

基于RBMs, 卷积神经网络可以被用于处理图像识别和图像生成任务, Lee等学者组合卷积网络和RBMs, 提出了卷积深度置信网(convolutional deep belief nets, 简称CDBNs), 通过引入卷积和概率最大池化操作, CDBNs实现了图像的识别和生成过程.卷积深度置信网的能量函数可以表示如下:

$E(v, h) = - \sum\limits_{l = 1}^L {\sum\limits_{i, j} {{c^l}v_{i, j}^l} } - \sum\limits_{k = 1}^K {\sum\limits_{m, n} {h_{m, n}^k\left( {\sum\limits_{l = 1}^L {{{({{\tilde W}^{k, l}} \times {v^l})}_{m, n}}} } \right)} } - \sum\limits_{k = 1}^K {\sum\limits_{m, n} {{b^k}h_{m, n}^k} } $

(47)

其中, $\mathbf{v}\in {{R}^{{{N}_{v}}\times }}{{^{{{N}_{v}}\times }}^{L}},h\in {{R}^{{{N}_{h}}\times {{N}_{h}}\times K}},$ N_v×N_v是输入图像的尺寸, L表示输入图像的通道数, K表示滤波器的数目, W^{k, l}∈R^ws×ws为一个ws尺寸的滤波器, $\tilde W$表示矩阵W的翻转矩阵.那么, CDBNs的激活函数可以表示为

$P(h_{m, n}^k = 1|v) = {\rm{sigmoid}}\left( {\sum\limits_{l = 1}^L {{{({{\tilde W}^{k, l}} \times {v^l})}_{m, n}}} + {b^k}} \right)$

(48)

$P(v_{i, j}^l = 1|h) = {\rm{sigmoid}}\left( {\sum\limits_{k = 1}^K {{{({W^{k, l}} \times {h^k})}_{i, j}}} + {c^l}} \right)$

(49)

Lee等人为了实现基于CDBNs的图像重构, 提出了概率最大池化方法(probabilistic max-pooling), 输入图像经过卷积运算, 得到的卷积层的输出为h^k, h^k可以被划分为C×C大小的图像块, 每个图像块α对应一个二值的池化单元$p_\alpha ^k, $那么, 池化层p^k的尺寸可以表示为N_p=N_h/C.从直观上看, 在概率最大池化中, 当池化层单元激活时, 有且仅有一个对应的α中的单元激活, 当池化层单元灭活时, α中所有单元都不激活.基于最大概率池化理论, CDBNs的能量函数可以表示如下:

$\begin{gathered} E(v, h) = - \sum\limits_{l = 1}^L {\sum\limits_{i, j} {{c^l}v_{i, j}^l} } - \sum\limits_{k = 1}^K {\sum\limits_{m, n} {h_{m, n}^k\left( {\sum\limits_{l = 1}^L {{{({{\tilde W}^{k, l}} \times {{\bf{v}}^l})}_{m, n}}} } \right)} } - \sum\limits_{k = 1}^K {\sum\limits_{m, n} {{b^k}h_{m, n}^k} } \\ \text{subject}\ \ \text{to}\sum\limits_{(m, n) \leqslant \alpha } {h_{m, n}^k} \leqslant 1, {\rm{ }}\forall k, \alpha \\ \end{gathered} $

(50)

基于能量函数, CDBNs的条件激活概率可以表示为

$P(h_{m, n}^k = 1|v) = \frac{{\exp \left( {I(h_{mn}^k)} \right)}}{{1 + \sum\nolimits_{(m', n') \in \alpha } {\exp \left( {I(h_{m'n'}^k)} \right)} }}$

(51)

$P(p_\alpha ^k = 0|v) = \frac{1}{{1 + \sum\nolimits_{(m', n') \in \alpha } {\exp \left( {I(h_{m'n'}^k)} \right)} }}$

(52)

其中, $I(h_{mn}^{k})=\sum\nolimits_{l=1}^{L}{{{({{{\tilde{W}}}^{k,l}}\times {{\text{v}}^{l}})}_{m,n}}}+{{b}^{k}}, $可见层单元的激活形式与之前的CDBNs一致, 基于概率最大池化, CDBNs可以有效地利用网络的层次化结构学习图像逐层抽象的特征, 并完成图像的生成工作.

3.4 RBMs与神经网络结合的总结和展望

目前常用的生成模型包括VAEs和GANs等, 常用的判别模型为CNNs等, 将RBMs作为预训练模型应用在CNNs中, 能够使CNNs既可以用于图像识别也可以用于图像生成, 且RBMs可以为CNNs提供更有效的初始化权值, 从而促进CNNs收敛到更加优秀的局部最优解.但是将RBMs作为预训练算法也存在一些问题, 首先, RBMs作为无监督学习算法, 并不能保证其特征表达是有利于分类的, 随着神经网络层数的增加, 使用RBMs作为预训练对分类精度带来的提升会越来越不明显, 且预训练会非常耗时.如何改变RBMs的能量函数和损失函数, 从而使RBMs得到的特征更有利于多层CNNs的分类任务, 是RBMs未来研究的一个重点问题.其次, 作为生成模型, 虽然RBMs可以有效地与VAEs和GANs结合, 但是作为生成模型本身, RBMs难以扩展其深度, 由于RBMs的训练需要采用近似算法, 其计算复杂度很高, 同样深度下, RBMs的训练复杂度要远大于VAEs和GANs.如何改进RBMs的训练算法和RBMs的网络结构, 从而扩展RBMs的深度, 构建更加有效的生成模型也是RBMs研究的重点和难点.

4 总结与展望

本文综述了RBMs和神经网络在理论研究和应用中的进展.在过去十年中, 深度学习逐渐成为人工智能研究的主流方向, 许多学者致力于该领域, 并将概率图模型应用到深度学习中.目前已有大量研究结果证明了RBMs模型的有效性.然而, 仍存在一些值得进一步研究的问题:RBMs模型的算法理论问题需要进一步研究, 如缓解RBMs中过拟合的方法、加快RBMs模型的训练以及提高RBMs模型建模实值数据的能力.Carlson等学者发现, RBMs的目标函数由Shatten-∞范数限定, 并提出了在赋范空间中更新参数的SSD算法.目前常用的缓解过拟合问题的方法有:权值衰减、Dropout方法、DropConnect方法和Weight-uncertainty方法等.如何获得图像处理中有效的抽象化特征也是RBMs研究的重点.已知RBMs的特征表达可以结合CRFs应用到图像分割和标注中.相反地, CRFs中的图像分割和标记结果是否也可用于RBMs的特征提取中, 以提高特征表达的能力?这也是我们今后的研究中关注的问题.目前除了向量神经网络(capsule nets)的训练方式不同外, 神经网络的训练是基于BP算法的, 其特征表示和特征学习仍然是一种黑箱的形式.这个问题也为基于梯度的RBMs算法带来了相同的困扰.如何在RBMs模型中引入新的训练方式也是接下来我们研究的重点.