近年来, 基于Petri网的模型检测技术已经成功地应用于并发程序的验证与分析[1-4]中.Petri网是一种适用于描述并发程序的模型, 德国学者Sistla[5]首次提出了使用Petri网来为程序建模的方法.具体来说, 可以用Petri网模型中的位置(place)表示程序的状态, 用模型中的迁移(transition)表示程序的执行流, 以及每个位置的令牌(token)数表示当前有多少个进程刚好运行到该位置.
并发系统的安全性问题是指系统是否会有可能进入某一错误状态(比如需保证进程互斥的系统发生了多个进程同时运行到某一关键位置), 规约到Petri网的可覆盖性问题为:给定一个Petri网和一个状态M(对应到并发系统中的一个错误状态), 是否会有一些由初始状态M0可达的状态M'覆盖了M.如果存在可达状态覆盖错误状态M, 就表明模型对应的系统不是绝对安全的, 系统在理论上会覆盖这个错误状态.现有的验证Petri网可覆盖性的算法大致分为两类:一类是基于Petri网状态空间的遍历, 通过搜索Petri网的可达状态空间来判断是否覆盖待验证状态M.然而, 由于Petri网的状态空间规模与其位置迁移数是指数级别关系, 所以这类算法在面对规模较大的Petri网时都显得力不从心.比如BFC[4]、MIST、IIC[6]等工具都会有超时的问题存在.第2类是基于约束的, 从Petri网的模型结构以及待验证状态中提取出约束条件, 然后去求解这些约束来验证可覆盖性.然而由于约束的表达能力有限, 不可能完美地表达出Petri网的可达状态空间, 所以这些约束条件只能成为可覆盖性问题的必要而非充分条件.因此, 这类算法在理论上是不完备的, 比如Petrinizer[7]工具只能验证那些安全的测试用例, 对于不安全的测试用例则无法判定.
本文针对非交互式Petri网(communication-free Petri net), 又被称作基本并发进程(basic parallel processes, 简称BPP), 设计并实现了可以高效验证其可覆盖性的工具(communication-free Petri net coverability verifier, 简称CFPCV).BPP在模型上的计算相对简单, 其可覆盖性问题是NP完备问题[8], 同时, 它又能为一类并发程序建模并且进行验证.我们采用基于约束的方法, 从非交互式Petri网的模型结构和待验证状态中提取出约束, 然后将这些约束交给Z3 SMT求解器求解.如果求解器得出无解, 则说明不存在任何可达状态覆盖待验证状态, 即待验证状态不可覆盖.而如果求解器有解(可能有多组解), 并不能说明待验证状态可覆盖, 因为约束条件的表达能力有限, 满足约束条件的状态并不一定是该非交互式Petri网的可达状态, 需要额外增加子网可标记方法去验证该状态是否可达.如果验证通过, 则说明待验证状态可覆盖.如果没有通过, 则需要迭代地去验证其他满足约束条件的状态, 直到最终得出结论, 这样就保证了该工具的算法在理论上是完备的, 不存在无法判定的情况.同时, 只要对我们的约束条件稍加修改, CFPCV就可以很容易地验证BPP的可达性问题.
我们通过一个实例来说明基于约束验证BPP可覆盖性问题的方法, 图 1展现的是包含两个进程的并发程序及其对应的非交互式Petri网.
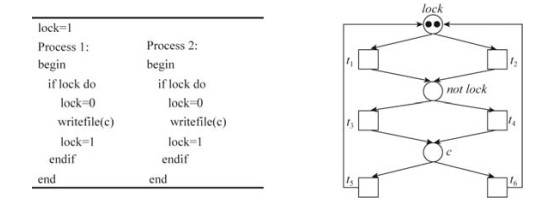
|
Fig. 1 Basic parallel process instance and its corresponding communication-free Petri net 图 1 简单并发进程实例及其对应的非交互式Petri网 |
假定该并发程序需要维护一个写锁, 即同一时刻最多只能有一个进程可以获取锁来写文件, 对应到非交互式Petri网为最多只能有1个进程可以处在位置c, 所以该非交互式Petri网必须满足c≤1(即位置c内的令牌数量不大于1)的性质, 也就是说, 满足c≥2的状态都是错误状态.我们通过基于约束的方法来验证该非交互式Petri网是否会覆盖满足c=2的状态.首先根据BPP的模型要求, 每个位置内的令牌数以及每个迁移的触发次数都必须大于等于0, 可以得到约束集{lock≥0, not lock≥0, c≥0, t1≥0, t2≥0, t3≥0, t4≥0, t5≥0, t6≥0}.然后根据位置和迁移的转移关系得到约束集{lock=2+t5+t6–t1–t2, not lock=0+t1+t2–t3–t4, c=0+t3+t4–t5–t6}.最后加入待验证状态的约束集{c≥2}.将这些约束集合并作为输入交给Z3 SMT求解器求解, 得出一个解{lock=0, not lock=0, c=2, t1=1, t2=1, t3=1, t4=1, t5=0, t6=0}.之后通过子网可标记验证发现这组解确实是合法解, 我们就可以判定该非交互式Petri网可以覆盖满足c=2的状态, 从而说明对应的并发程序是不安全的, 可能会存在两个进程同时得到锁一起写文件的情况.
本文第1节介绍所用到的背景知识, 包括传统Petri网、非交互式Petri网、可达性和可覆盖性问题的数学定义, 以及本文所使用到的Z3 SMT求解器介绍.第2节介绍验证非交互式Petri网可覆盖性的安全性方法以及子网可标记验证技术.第3节介绍CFPCV的总体技术框架以及使用的算法细节.第4节主要介绍实验及实验结果的分析.第5节介绍Petri网可覆盖性研究的一些相关工作.第6节总结全文, 并展望未来的工作.
1 预备知识 1.1 Petri网Petri网可以用一个四元组N=(P, T, F, M0)来表示, 其中, P是Petri网中所有位置的有限集合, T是Petri网中所有迁移的有限集合, F:(P×T)∪(T×F)→{0, 1}称为Petri网的流函数, 它表示位置和迁移之间的连接关系.而M0表示该Petri网的初始状态.对于x∈P∪T,
一个迁移t∈T在状态M下使能(enabled)当且仅当
迁移序列σ=t1t2…tx是一系列迁移的触发序列, 状态Mx由M0经过迁移序列σ可达(记作
Petri网的可达性问题是指给定一个Petri网N=(P, T, F, M0)和一个状态M, 判断M∈R(M0)是否成立, 即判断状态M是否由M0到达; 可覆盖性问题是指给定一个Petri网N=(P, T, F, M0)和一个状态M, 判断是否存在一个状态M'∈R(M0), 满足∀p∈P, M'(p)≥M(p).如果存在, 则称该Petri网覆盖状态M.
1.2 非交互式Petri网非交互式Petri网是指满足
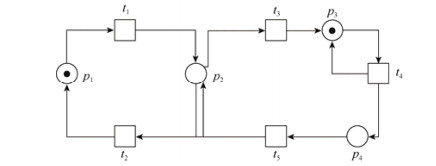
|
Fig. 2 Graphical representation of communication-free Petri net 图 2 一个非交互式Petri网的图形化表示 |
1.3 SMT求解器
SAT问题被证明是第一个NP完备问题.作为SAT问题的扩展, SMT问题[9]处理的对象是一阶逻辑公式, 相比于命题逻辑, 增加了谓词和量词, 很大程度上增强了SMT公式的表达能力.用以求解SMT问题的自动化工具称为SMT求解器.SMT求解技术在有界模型检测、基于符号执行的程序分析、线性规划和调度、测试用例生成以及电路设计和验证等领域有非常广泛的应用.很多科研机构以及公司都在致力研发正确率高、性能优异的SMT求解器, 并且已经成功应用到了具体的领域.目前流行的SMT求解器有:Barcelogic[10]、Beaver[11]、Yices[12]以及Z3[13]等.其中, 由微软公司主导开发的Z3 SMT求解器所支持的理论最多, 性能也最好, 因此本文使用了Z3 SMT求解器作为我们的求解引擎.
2 安全性方法与子网可标记验证本节主要介绍验证非交互式Petri网可覆盖性所用到的安全性方法以及子网可标记验证技术, 在介绍安全性方法之前, 我们首先介绍其核心——状态方程的概念, 最后介绍两个加速剪枝的技巧.
2.1 状态方程对于一个给定的非交互式Petri网N=(P, T, F, M0), 用一个大小为|P|的列向量M表示N的当前状态, 用一个大小为|T|的列向量X代表迁移序列σ中每个迁移触发的次数, 那么状态方程表示为
| $M={{M}_{0}}+CX, $ |
其中, C称作关联矩阵, 它是一个|P|x|T|大小的矩阵, 它的每一项的值按如下方法计算:
| $C(p, t)=F(t, p)-F(p, t).$ |
显然, 关联矩阵记录了该非交互式Petri网中每一个位置与迁移之间的连接关系.而X是迁移序列σ中每个迁移触发的次数.可以用Parikh映射(Parikh mapping)来表示它们之间的关系:
| $X=Parikh(\sigma )=(\omega ({{t}_{1}}), \omega ({{t}_{2}}), ..., \omega ({{t}_{n}})), $ |
其中, ω(ti)代表迁移ti在迁移序列σ触发的次数.
比如对于图 3给定的非交互式Petri网和一个迁移序列σ=t1t2t1t3t2t1, 就可以根据状态方程计算出σ触发后的新状态M=[5, 3, 3, 1, –1]T, 其中,
| $ {{M}_{0}}={{[0, 0, 0, 1, 0]}^{\text{T}}}, X={{[3, 2, 1]}^{\text{T}}}, C=\left[ \begin{matrix} 1 & 1 & 0 \\ 1 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -1 & 1 \\ \end{matrix} \right]. $ |
对于状态方程M=M0+CX中的X, 可能不存在一个在M0下使能的迁移序列σ(
安全性方法(safety method)是验证非交互式Petri网可覆盖性的基本方法, 顾名思义, 其目的就是为了验证非交互式Petri网对应的并发系统是否安全.其基本思想是给定一个非交互式Petri网N和一个性质φ, 如果根据状态方程M=M0+CX得出的所有状态都不会违反
本文只讨论满足如下条件的非交互式Petri网.
1) 在任何合法的状态下, 每个位置的令牌数必须大于等于0.
2) 在任何合法的迁移序列中, 每个迁移的触发次数必须大于等于0.
结合状态方程可以用如下约束条件表示[7]:
| $ C(N):=C(P, T, F, {{M}_{0}}):=\left\{ \begin{align} & M={{M}_{0}}+CX, \ \ \ 状态方程 \\ & M\ge 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 每个位置内的令牌数非负 \\ & X\ge 0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 每个迁移的触发次数非负 \\ \end{align} \right.. $ |
安全性方法用约束条件来表达就是将C(N)约束与待验证性质j的取反结合, 表示为
| $C(P, T, F, {{M}_{0}})\wedge \neg \varphi $ | (1) |
约束(1)可以表示成多元一次等式和不等式的组合, 而SMT求解器可以很快地求解这些等式与不等式的组合.将约束(1)作为输入交给SMT求解器求解, 得出:
1) 无解, 则说明状态方程得出的状态都不会违反性质φ, 即Set(M)|=φ, 又因为R(M0)⊆Set(M), 所以R(M0)|=φ, 继而推出该非交互式Petri网N|=φ.也就说明对应的并发系统是安全的.
2) 有解, 则说明存在某状态M'违反性质φ, 但由于Set(M)⊇R(M0), 所以M'不一定是该非交互式Petri网N的可达状态, 因此无法判定N是否满足性质φ, 这也是安全性方法的局限所在.下一小节提出的子网可标记验证方法, 可以有效地判定候选状态M'是否是N的可达状态, 从而弥补了安全性方法的不足.
2.3 子网可标记验证前文介绍了验证非交互式Petri网可覆盖性的安全性方法, 虽然该算法借助于SMT求解器可以很高效地运行, 但是该算法在理论上却不完备, 只能验证非交互式Petri网N满足性质φ, 却无法得出N不满足性质φ的结论.原因是安全性方法依赖于状态方程, 对于状态方程得出的候选状态M', 我们无法判断M'是否是N的可达状态.
而子网可标记验证可以严谨地判定某个状态M'是否是非交互式Petri网的可达状态, 从而可以弥补安全性方法的不足, 在验证非交互式Petri网可覆盖性时达到理论完备.
在介绍如何使用子网可标记验证判定状态M'是否为非交互式Petri网的可达状态之前, 需要引入如下的定义、引理与定理[8].
定义1. 给定一个Petri网N=(P, T, F)和一个迁移集合T的子集S, 那么由S构成的N的子网NS=(PS, S, FS).其中,
定义1说明, 给定一个迁移触发次数的向量X, 由X构成的子网
定义2. 给定一个Petri网N=(P, T, F, M0)和一个状态M:
●如果存在一个状态M', 使得M'由M可达, 且M'(p) > 0(其中, p∈P), 则称位置p由状态M可标记.
●对于N的子网N'=(P', T', F', M0'), 如果N上的状态M在N'上的投影为M', 且位置p(其中, p∈P')由状态M'可标记, 则称位置p在N'上由M可标记.
引理1. 给定一个非交互式Petri网N和它的一个状态M, 一个位置p由状态M可标记当且仅当N中存在一条从p'到p的路径, 其中, p'满足M(p') > 0.
证明:我们将p'到p路径上的位置依次记为p1, p2, p3, …, px, 迁移依次记为t1, t2, t3, …, tx.因为非交互式Petri网每个迁移的输入位置只有一个, 所以
引理1给出了一个在非交互式Petri网N上, 快速判定位置p是否由状态M可标记的方法, 即如果在M状态下内部令牌数大于0的某个位置p', 存在一条到位置p的路径, 那么就可以说明位置p在N上由M可标记.也就是说, 对于M状态下内部令牌数大于0的位置, 从这些位置经过迁移可以到达的位置都是由状态M可标记的.
例如, 针对图 3所示的Petri网, 给定向量X=[1,0,0]T, 则子网NX如图 4所示, 包含p1, p2, p3, p4这4个位置, t1一个迁移以及它们之间的流关系.在子网NX中, 显然, p1, p2, p3, p4都由状态M0可标记, 因为M0状态下, p4内的令牌数大于0, 且p1, p2, p3都由p4可达.

|
Fig. 3 Communication-free Petri net 图 3 非交互式Petri网 |
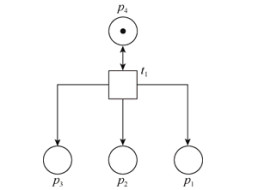
|
Fig. 4 Subnet NX 图 4 子网Nx |
定理1(文献[8]中的定理3.1). 给定一个非交互Petri网N=(P, T, F, M0)和每个迁移触发次数的向量X.存在一个迁移序列σ使得
1)
2) 子网NX内的任一位置都能在NX上由M0可标记.
定理1给出了判定一个迁移触发次数的向量X是否合法的充要条件, 即在向量X的作用下, 该非交互式Petri网的每个位置内的令牌数必须大于等于0, 而且子网NX内的所有位置都必须由M0可标记.结合定义2和引理1, 则定理1的条件2)可以表述为:NX内的所有位置都必须由
对于传统的Petri网, 我们很难判定某个状态是否是可达状态.而对于非交互式Petri网, 结合状态方程与定理1, 可以有效地判定某个状态是否可达.我们可以通过状态方程M'=M0+CX'求得M'对应的解X'(可能有多个解), 然后再去验证X'是否合法, 如果合法, 就可以得出M'可达的结论.而如果不合法, 则可以迭代地去验证其余解, 如果所有的解都不合法, 就可以断定M'不可达.
在安全性方法中, 任何非交互式Petri网N=(P, T, F, M0)都必须满足C(N)约束, 规定了在任何状态下每个位置内的令牌数都必须大于等于0, 所以, 定理1的第1个条件天然满足.至于第2个条件, 在安全性方法中, 如果约束(1)有解(可能有多组解), 即∃M'∈Set(M), φ(M')成立.我们可以通过定理1来判定M'是否可达, 即判定其对应的X'是否合法.这样就可以严格地去验证非交互式Petri网是否覆盖某个错误状态, 使得算法在理论上达到完备.
结合安全性方法与子网可标记验证, 验证非交互式Petri网可覆盖性的方法可以表述如下.
从非交互式Petri网N和待验证性质φ中获取约束条件C(P, T, F, M0)^
1) 无解, 即约束条件不满足, 说明该非交互式Petri网的所有状态都满足性质φ, N不会覆盖满足性质
2) 有解, 即∃M'∈Set(M),
a) 若满足, 说明
b) 若不满足, 说明满足
因为对于SMT求解器的每组解, 我们都需要验证其是否符合定理1的条件2), 为了减少算法的迭代次数, 我们可以增加两种剪枝加速的方法.
1) 在给定的非交互Petri网N=(P, T, F, M0)中, 对于那些满足M0(p) > 0的位置, 它们的输出迁移必须至少有一个触发次数大于0.约束化为Constraints 1.
| $ \left. \begin{gathered} InitPlace = \{ p|p \in P, {M_0}(p) > 0\} \\ InitTransition = \{ t|t \in T, t \in InitPlac{e^ \bullet }\} \\ Constra\operatorname{int} s{\rm{ }}1 = {V_{t \in InitTransition}}t > 0 \\ \end{gathered} \right\} $ | (2) |
因为我们要验证每组解是否符合定理1的条件2), 也就是子网内的每个位置都要由M0可标记.由引理1可知, 该子网内至少有一个位置p满足M0(p) > 0.因此, 如果Constraint 1无法满足, 也就是说, 满足M0(p) > 0的位置p根本没有路径“出去”, 则子网内的其他位置p'都无法由M0可标记.
2) 在给定的非交互Petri网N=(P, T, F, M0)中, 如果存在这样的位置, InitPlace集合中的任意一个位置都不存在一条到它的路径, 那么它的输入和输出迁移发生的次数都为0.约束化为Constraints 2.
| $ \left. \begin{gathered} UnmarkPlace = \{ p|p \in P, {\forall _{pp \in InitPlace}}\neg path(pp, p)\} \\ UnmarkTransition = \{ t|t \in T, t \in {}^ \bullet UnmarkPlace \cup UnmarkPlac{e^ \bullet }\} \\ Constraints2 = {\Lambda _{t \in UnmarkTransition}}t = 0 \\ \end{gathered} \right\} $ | (3) |
因为对于这些无法从InitTransition中的位置到达的位置, 它们在任何状态子网上都是无法由M0可标记的, 如果它们的输入或者输出迁移发生的次数大于0, 那么子网就必须将这些位置包含进去, 那么该子网就不可能满足定理1的条件2).
使用上述两种剪枝技巧, 可以有效地减少算法的迭代次数, 使得验证更加高效、实用.
3 CFPCV工具技术框架我们采用基于约束的方法, 实现了可以高效验证非交互式Petri网可覆盖性的工具CFPCV, 它在安全性方法的基础上, 加上子网可标记验证, 从而使得该算法在理论上完备.本节主要介绍CFPCV工具的技术架构以及使用到的具体算法.
3.1 技术架构本文的技术方案如图 5所示.主要分为约束提取、约束求解、候选解验证、增加约束进行迭代这4个部分.具体内容如下.
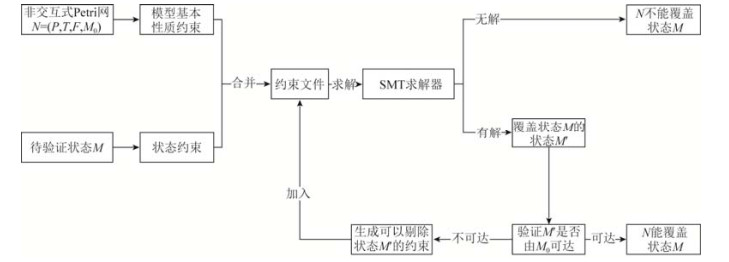
|
Fig. 5 Technology architecture of CFPCV 图 5 CFPCV工具技术架构 |
1) 首先根据给定的非交互Petri网模型N=(P, T, F, M0)得到一些模型的基本约束, 例如每个位置内的令牌数必须大于等于0, 每个迁移发生的次数必须大于等于0, 再根据需要验证的状态M得到状态约束, 例如待验证性质为p1=1 & p2=1, 则约束p1≥1 & p2≥1可以覆盖满足此性质的状态.
2) 将步骤1)得到的约束条件和剪枝技巧合并为约束文件, 作为输入交给SMT求解器求解.
3) 如果无解, 则表明不存在满足这些约束条件的状态, 也就是说, N不能覆盖状态M'; 如果有解并不能代表N覆盖状态M, 只能代表M'满足这些约束条件, 还必须验证M'由M0可达, 即需要将状态M'从状态方程的状态空间压缩到该非交互式Petri网的可达状态空间内.
4) 如果验证出M'状态确实由M0可达, 则可以表明N覆盖M; 如果不可达, 说明SMT求解器求出的这组解(基于约束条件可能有很多组解, 求解器每次只给出一组解)不满足要求.需要将状态M'代表的这一类状态剔除, 即生成新的约束加入到约束文件中, 重复步骤3)和步骤4), 直到程序得到解退出为止.
3.2 算法实现CFPCV工具使用到的核心算法伪代码如下.
关于算法的逻辑, 前文已经解释清楚, 主要分为约束提取、约束求解、候选解验证、增加约束进行迭代这4个部分, 这里不再赘述.其中, 第8行的代码表示提取新约束来剔除子网SN所代表的一系列解.比如, T={t1, t2, t3, t4}, X={1, 0, 3, 1}.那么, SN就是根据t1, t3, t4这3个迁移构成的子网, 如果子网SN不满足定理1的条件2), 则在下一次迭代中, 必须增加约束将SN所代表的一系列解剔除, 即新约束δ为not(t1 > 0 & t2=0 & t3 > 0 & t4 > 0).
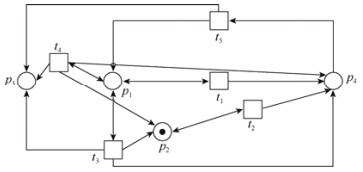
3.3 算法求解示例我们可以通过一个实例再进一步更加直观、清晰地认识这一算法, 对于图 8给定的非交互式Petri网和带验证性质φ(p1+p3 < 3), 安全性约束C(P, T, F, M0)^

|
Fig. 6 Subnet NX1 图 6 子网NX1 |
|
Fig. 7 Subnet NX2 图 7 子网NX2 |
|
Fig. 8 Communication-free Petri net instance 图 8 示例非交互式Petri网 |
p1, p2, p3, p4≥0
t1, t2, t3, t4, t5≥0
p1=0+t5
p2=1+t3+t4
p3=0+t3+t4+t5
p4=0+t1+t2+t3+t4–t5
p1+p3≥3
两种剪枝约束Constraint 1(2)和Constraint 2(3).
t2 > 0
将上述约束作为输入交给SMT求解器求解, 有解, 解Model A1为
p1=0, p2=3, p3=3, p4=4
t1=0, t2=1, t3=0, t4=3, t5=0
所以X1=(0, 1, 0, 3, 0), 构成的子网NX1如图 6所示.
显然, 该子网中只有p2, p4由M0可标记, 因此需要增加新约束δ not(t1=0 & t2 > 0 & t3=0 & t4 > 0 & t5=0), 剔除该子网进行下一次迭代, 下一次迭代的约束即为
p1, p2, p3, p4≥0
t1, t2, t3, t4, t5≥0
p1=0+t5
p2=1+t3+t4
p3=0+t3+t4+t5
p4=0+t1+t2+t3+t4–t5
p1+p3≥3
t2 > 0
not(t1=0 & t2 > 0 & t3=0 & t4 > 0 & t5=0)
将新的约束文件作为输入交给SMT求解器求解, 依然有解, 解Model A2为
p1=1
p2, p2, p3=3
t1, t2, t3, t4, t5=1
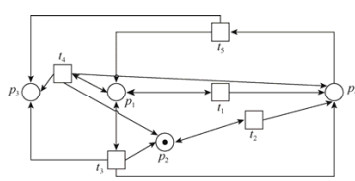
所以X2=(1, 1, 1, 1, 1), 而由NX2构成的子网如图 7所示.
我们可以发现, 子网NX2就是本来的Petri网, 该子网内每个位置都由M0可标记, 所以满足定理1的条件.因此存在一个迁移序列σ满足
由于现有的验证可覆盖性问题的工具都是针对传统Petri网的, 它们所使用到的标准测试集也都是传统Petri网, 所以这些测试集对于CFPCV工具的测试不再适用.因此, 针对非交互式Petri网, 我们随机生成了3组非交互式Petri网的测试用例, 它们的位置和迁移数规模分别是1~10、1~100、1~1000.我们主要从成功率、迭代次数、性能比这3个方面对CFPCV进行了评测.我们主要与Petrinizer、MIST这两个工具进行了比较, Petrinizer工具是通过提取约束并求解的方法来验证传统Petri网的可覆盖性问题, 与CFPCV一样, 它也是采用安全性方法来获得约束.不过, 正如前文所述, 安全性方法在理论上是不完备的, 其只能验证那些覆盖的用例, 对于不覆盖的用例则无能为力.但从文献[7]中的实验结果来看, Petrinizer在应对一些特定的测试集时仍然有不错的成功率.而MIST工具是采用状态空间探索的方法, 其内部集成了多种验证算法, 包括从待验证状态反向探索状态空间的backward[14]算法, 以及先对原Petri网模型进行抽象精化(abstraction refinement)来缩小模型规模, 然后再结合前驱和反向探索状态空间来进行验证的ic4pn[15]算法、tsi[15]算法和eec[16]算法.尽管增加了抽象精化的过程来缩小模型的规模, 但是对于随机模型这个过程的效果甚微, 依然会有状态爆炸(state explosion)的问题存在.
4.1 成功率我们将随机生成的3组测试用例作为输入交给CFPCV、Petrinizer、MIST工具求解, 后两种工具都是验证传统Petri网可覆盖性的工具, 所以它们肯定也可以验证非交互式Petri网的可覆盖性问题.我们分别比较了这3种工具在每组测试用例下的成功率, 见表 1~表 3(注:Positive表示满足性质φ, Negative表示不满足, Timeout表示超时, Don’t know表示无法判定, Success rate表示成功率).
| Table 1 Success rate of the 3 tools in test cases which scales of place and transition are between 1 to 10 表 1 测试用例位置迁移数规模1~10之间3种工具的成功率 |
| Table 2 Success rate of the 3 tools in test cases which scales of place and transition are between 1 to 100 表 2 测试用例位置迁移数规模1~100之间3种工具的成功率 |
| Table 3 Success rate of the 3 tools in test cases which scales of place and transition are between 1 to 1000 表 3 测试用例位置迁移数规模1~1000之间3种工具的成功率 |
从3张表可以发现, Petrinizer工具的成功率最低, 因为Petrinizer使用到的方法也是安全性方法, 但因其针对传统Petri网, 并没有子网可标记验证来保证候选解是正确解, 所以该工具使用到的算法在理论上不完备, 可能存在其无法判定的情况, 所以对于随机生成的测试用例, 有大量的测试用例其无法判定, 因此成功率在3种工具中最低, 在第3组测试用例上只有4.6%的成功率.而MIST工具是基于Petri网可达状态空间的搜索, 由于Petri网的可达状态空间可能很大, 所以该工具经常发生超时情况, 对于规模较大的输入, 超时情况更加严重.所以, 对于随机生成的测试用例, MIST工具超时最多, 而且随着测试用例规模的扩大, 其超时情况变得非常严重, 成功率直接从100%下降到了46.9%.显然, CFPCV工具的成功率最为优异, 对于3组测试用例成功率都在99%以上.
4.2 迭代次数因为CFPCV使用到的算法是基于迭代的, 需要在每次迭代中验证候选解是否是正确解, 如果不是, 则需要增加约束继续迭代求解, 所以算法的迭代次数直接决定了算法的运行效率.如果迭代次数过多, 就可能发生超时的情况.我们记录了每组测试用例算法的迭代次数, 见表 4.
| Table 4 Iteration time of CFPCV 表 4 CFPCV运行迭代次数 |
由表 4可以发现, 对于绝大多数(2587+397)测试用例, 只需要1~2次迭代即可得解, 只有极个别的测试用例需要10次以上的迭代(12次2个, 16次1个, 超时10个).因为只需要很少的迭代次数即可得解, 所以CFPCV工具的运行效率理应很高.
4.3 性能比因为CFPCV和Petrinizer都用到了安全性方法, 且Petrinizer的性能也非常高, 只不过其成功率较低, 所以我们比较了3组测试用例下这两种工具的性能(未比较MIST是因为MIST超时情况严重, 所以其性能自然较低), 性能比如图 9~图 11所示, 单位为s.

|
Fig. 9 Performance ratio of Petrinizer and CFPCV in test cases which scales of place and transition are between 1 to 10 图 9 测试用例位置迁移数规模1~10之间Petrinizer和CFPCV的性能比 |

|
Fig. 10 Performance ratio of Petrinizer and CFPCV in test cases which scales of place and transition are between 1 to 100 图 10 测试用例位置迁移数规模1~100之间Petrinizer和CFPCV的性能比 |
|
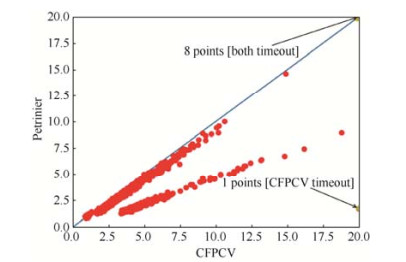
Fig. 11 Performance ratio of Petrinizer and CFPCV in test cases which scales of place and transition are between 1 to 1000 图 11 测试用例位置迁移数规模1~1000之间Petrinizer和CFPCV的性能比 |
由图 9~图 11可知, Petrinizer和CFPCV性能相当, 大部分测试用例两种工具在20s内得解.图中箭头标注的点分为两类, 一类是CFPCV需要的较多的迭代才可得解, 因此这些点代表的测试用例CFPCV运行较慢.另一类是两种工具都超时(图 11右上角的8个点), 原因是因为SMT求解器求解约束超时, 这种情况是合理的, 因为有些约束求解问题(比如SAT问题)就是NP完备问题, 可能存在一些测试用例SMT求解器根本无法求解, 因此两种工具都发生了超时的情况.因为Petrinizer没有验证候选解的迭代过程, 所以Petrinizer的性能理应比CFPCV要好.但是由第4.2节迭代次数的记录来看, 对于绝大多数测试用例, CFPCV只需要一两次迭代即可得解, 因此CFPCV的性能和Petrinizerx相差无几.考虑到第4.1节提到的CFPCV极高的成功率, 这样的性能是非常令人欣慰的.
5 相关工作Petri网的可覆盖性问题虽然已被证明是EXPSPACE完备问题[17, 18], BPP的可达性以及可覆盖性问题也都被证明是NP完备问题[3], 但是近年来学术界依然提出了很多解决该问题的算法, 它们可以大致分为两类:第1类就是基于状态空间的探索.由Karp和Miller(简称KM)提出的Karp and Miller procedure[17]是第一个可以验证Petri网可覆盖性的完备算法, 它的主要思想是从Petri网的初始状态前驱探索(forward exploration)状态空间, 不断加入可以覆盖前一状态的新状态来构造Petri网的覆盖树, 然后判断待验证状态是否在该覆盖树上来进行验证.但是, 由于Petri网的可达状态可以无限制地增长, 导致覆盖树的规模可能非常之大, 所以这个构造过程通常比较低效, 它具有非原始递归最坏情况的复杂度.这项技术已在TINA-KM[19]工具上实现, 可想而知, 该工具在处理状态空间较大的模型时效率很低.另外, 这项技术的一种优化方法就是构造Petri网的最小覆盖集(minimal coverability sets)[20]而非覆盖树, 最小覆盖集已被证明是存在且有限的[21], 而且其规模要远小于覆盖树的规模, 所以其构造效率有了较大的提升, 这项技术已在Pep[22]工具上实现.另外, 还有反向探索(backward exploration)[23]状态空间的算法, 就是从待验证状态反向探索状态空间, 直到到达初始状态为止, 这项技术已在工具IST-BC和PETR-BC[24]上实现, 不过, 反向探索和前驱探索本质上没有太大的区别, 所以算法效率并没有显著的提升.当然, 还有将前驱探索和反向探索结合[25, 26]的算法, 分别从初始状态前驱探索状态空间和从待验证状态反向探索状态空间, 直到两条探索路径触碰为止, 这项技术已在工具BFC上实现, 性能得到了较大的提升.文献[16]中提出的‘Expand, Enlarge and Check’方法通过并发地构造两个Petri网的近似序列来验证可覆盖性, 第1个序列是系统的向下近似, 它可以用来判定覆盖的实例, 另外一个序列是系统的向上近似, 用来判定那些不覆盖的实例.这项技术已在工具MIST上实现.MIST内部集成了多种算法, 不过, 它们的思路大体一致, 都是先对原模型进行一层抽象来缩小模型的规模, 然后对抽象后的模型通过前驱探索和反向探索结合的方法来加以验证.另外一类是基于约束的方法.其主要思想与本文的算法类似, 都是用约束条件来表达Petri网的性质, 通过求解约束来验证可覆盖性.然而, 由于约束的表达能力有限, 不可能准确表述出Petri网的可达状态空间, 所以这些约束条件只能成为可覆盖性问题的必要条件而非充分条件.因此这类算法在理论上是不完备的, 比如Petrinizer[7]工具, 它是通过安全性方法来提取约束并求解来进行验证, 不过, 由于安全性方法在理论上不完备, 所以它只能验证那些不覆盖的测试用例, 对于覆盖的测试用例则无法验证.
除此之外, 并发程序的性质也可以通过基于Petri网的模型检测技术来分析, 使用TCTL(时间计算树逻辑)[27]来描述待验证性质, 通过检测Petri网的迁移发生序列来验证模型是否满足这些性质.其具体思路是先构造包含待验证性质取反语义序列的Büchi自动机, 然后再计算Petri网可达图和自动机的乘积图.若将乘积图看成一个有向图, 则模型检测的问题等价于检测乘积图中是否包含一个从初始状态可达的最大强连通分量, 且在该强连通分量中包含了一个接受状态.对于安全性一类的性质来说, 等价于检测乘积图中是否存在一条从初始节点到接受节点的路径.对于活性一类的性质来说, 等价于检测乘积图中是否存在由初始节点可达的包含接受节点的环.但是, 基于Petri网的模型检测技术也会受到状态爆炸问题的困扰, 因为Petri网模型的状态空间通常非常之大, 甚至无界, 所以Petri网的模型检测问题难度非常之大, 其上的很多逻辑算子都不存在多项式时间算法.比如EG/AF(即我们通常所说的活性)逻辑在Petri网和BPP上都是不可判定的, EF逻辑在Petri网同样不可判定, 在BPP上虽然可判定, 但也拥有PSPACE完备的复杂度[28].所以, 传统的基于Petri网的模型检测技术在验证并发程序的性质时存在较大的局限性.
6 总结及未来的工作本文设计并实现了可以高效验证非交互式Petri网可覆盖性的工具CFPCV, 它在验证传统Petri网可覆盖性使用到的安全性方法的基础上, 增加了只对非交互式Petri网适用的子网可标记验证, 从而保证了其解的正确性, 并且通过实验验证了该工具具有较高的成功率以及不错的性能.
由于业界缺乏针对非交互Petri网可覆盖性验证的标准测试集, 所以本文测试所使用测试集都是随机产生的.未来会使用数量更多以及质量更高的测试集进行测试, 以验证CFPCV的表现是否依然优秀.另外, 其实除了本文所提的剪枝方法以外, 还有一种叫作阱(trap)约束[29]的技巧可以进行加速, 不过我们通过测试发现, 阱约束的表现却不尽人意, 可能和我们测试集的随机性有关.未来业界若有质量较高的测试集公开, 我们会在算法上增加阱约束进行测试, 如果性能得到提升, 则将加以改进.
未来, 我们也会在BPP上做模型检测, 虽然第5节提到BPP上的模型检测问题难度很大, 但是我们如果做有界模型检测, 比如将某个性质在无限的转移序列上都要成立限定为在k(k为大于0的自然数)步转移内成立, 同时也保证这样的性质具有一定的实际意义, 那么问题的复杂度将大幅下降.同样通过提取约束, 使用SMT求解器求解约束的方法, BPP上的有界模型检测问题可能会有很高效的解决方案.
| [1] |
Bouajjani A, Emmi M. Bounded phase analysis of message-passing programs. Int'l Journal on Software Tools for Technology Transfer (STTT), 2014, 16(2): 127-146.
[doi:10.1007/s10009-013-0276-z] |
| [2] |
D'Osualdo E, Kochems J, Ong CHL. Automatic verification of erlang-style concurrency. In: Proc. of the Int'l Static Analysis Symposium. Berlin: Springer-Verlag, 2013. 454-476.
|
| [3] |
Ganty P, Majumdar R. Algorithmic verification of asynchronous programs. ACM Trans. on Programming Languages and Systems, 2012, 34(1): 1-48.
|
| [4] |
Kaiser A, Kroening D, Wahl T. Efficient coverability analysis by proof minimization. In: Proc. of the Int'l Conf. on Concurrency Theory. Berlin: Springer-Verlag, 2012. 500-515.
|
| [5] |
German SM, Sistla AP. Reasoning about systems with many processes. Journal of the ACM (JACM), 1992, 39(3): 675-735.
[doi:10.1145/146637.146681] |
| [6] |
Kloos J, Majumdar R, Niksic F, et al. Incremental, inductive coverability. In: Proc. of the Int'l Conf. on Computer Aided Verification. Berlin: Springer-Verlag, 2013. 158-173.
|
| [7] |
Esparza J, Ledesma-Garza R, Majumdar R, et al. An SMT-based approach to coverability analysis. In: Proc. of the Int'l Conf. on Computer Aided Verification. Cham: Springer-Verlag, 2014. 603-619.
|
| [8] |
Esparza J. Petri nets, commutative context-free grammars, and basic parallel processes. Fundamenta Informaticae, 1997, 31(1): 13-25.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC025753777/ |
| [9] |
Barrett C, Tinelli C. Satisfiability modulo theories. Journal on Satisfiability Boolean Modeling and Computation, 2018, 3(3): 141-224.
http://d.old.wanfangdata.com.cn/Periodical/jsjgcykx201001015 |
| [10] |
Bofill M, Nieuwenhuis R, Oliveras A, et al. The barcelogic SMT solver. In: Proc. of the Int'l Conf. on Computer Aided Verification. Berlin: Springer-Verlag, 2008. 294-298.
|
| [11] |
Jha S, Limaye R, Seshia SA. Beaver: Engineering an efficient SMT solver for bit-vector arithmetic. In: Proc. of the Int'l Conf. on Computer Aided Verification. Berlin: Springer-Verlag, 2009. 668-674.
|
| [12] |
Dutertre B, De Moura L. The YICES SMT solver. 2006. http://yices.csl.sri.com/tool-paper.pdf
|
| [13] |
Moura LD, Bjørner N. Z3: An efficient SMT solver. In: Proc. of the Int'l Conf. on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2008. 337-340.
|
| [14] |
Delzanno G, Raskin JF, Begin LV. Towards the automated verification of multithreaded Java programs. In: Proc. of the Int'l Conf. on Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2002. 173-187.
|
| [15] |
Ganty P, Raskin JF, Begin LV. From many places to few:Automatic abstraction refinement for Petri nets. Fundamenta Informaticae, 2008, 88(3): 275-305.
http://www.springerlink.com/content/wj802m0563152824 |
| [16] |
Geeraerts G, Raskin JF, Van Begin L. Expand, enlarge, and check:New algorithms for the coverability problem of WSTS. Journal of Computer and System Sciences, 2006, 72(1): 180-203.
http://link.springer.com/chapter/10.1007/978-3-540-30538-5_24 |
| [17] |
Karp RM, Miller RE. Parallel program schemata. Journal of Computer and System Sciences, 1969, 3(2): 147-195.
http://d.old.wanfangdata.com.cn/NSTLHY/NSTL_HYCC0213703503/ |
| [18] |
Rackoff C. The covering and boundedness problems for vector addition systems. Theoretical Computer Science, 1978, 6(2): 223-231.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=c320e2ff665391335da201077fd8b7d3 |
| [19] |
Berthomieu B, Ribet PO, Vernadat F. The tool TINA-Construction of abstract state spaces for Petri nets and time Petri nets. Int'l Journal of Production Research, 2004, 42(14): 2741-2756.
[doi:10.1080/00207540412331312688] |
| [20] |
Geeraerts G, Raskin JF, Begin LV. On the efficient computation of the minimal coverability set for Petri net. In: Proc. of the Int'l Symp. on Automated Technology for Verification and Analysis. Berlin: Springer-Verlag, 2007. 98-113.
|
| [21] |
Finkel A. Reduction and covering of infinite reachability trees. Information and Computation, 1990, 89(2): 144-179.
http://www.sciencedirect.com/science/article/pii/0890540190900097 |
| [22] |
Grahlmann B. The PEP tool. In: Proc. of the Int'l Conf. on Computer Aided Verification. Berlin: Springer-Verlag, 1997. 440-443.
|
| [23] |
Abdulla PA, Cerans K, Jonsson B, et al. General decidability theorems for infinite-state systems. In: Proc. of the Logic in Computer Science (LICS'96). IEEE, 1996. 313-321.
|
| [24] |
Meyer R, Strazny T. Petruchio: From dynamic networks to nets. In: Proc. of the Int'l Conf. on Computer Aided Verification. Berlin: Springer-Verlag, 2010. 175-179.
|
| [25] |
Finkel A. Monotonic extensions of Petri nets. Electronic Notes in Theoretical Computer Science, 2003, 68(6): 85-106.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=646dd0ad06f1f3a17aa2ea403e9974c9 |
| [26] |
Ganty P, Raskin JF, Begin LV. A complete abstract interpretation framework for coverability properties of WSTS. In: Proc. of the Int'l Workshop on Verification, Model Checking, and Abstract Interpretation. Berlin: Springer-Verlag, 2006. 49-64.
|
| [27] |
Gerth R, Peled D, Vardi MY, et al. Simple on-the-fly automatic verification of linear temporal logic. In: Protocol Specification, Testing and Verification. Boston: Springer-Verlag, 1995. 3-18.
|
| [28] |
Esparza J. Decidability of model checking for infinite-state concurrent systems. Acta Informatica, 1997, 34(2): 85-107.
http://link.springer.com/article/10.1007/s002360050074 |
| [29] |
Murata T. Petri nets:Properties, analysis and applications. Proc. of the IEEE, 1989, 77(4): 541-580.
[doi:10.1109/5.24143] |
 2019, Vol. 30
2019, Vol. 30


