2. 数字出版技术国家重点实验室, 北京 100871;
3. 天津市认知计算与应用重点实验室, 天津 300354
2. State Key Laboratory of Digital Publishing Technology, Beijing 100871, China;
3. Tianjin Key Laboratory of Cognitive Computing and Application, Tianjin 300354, China
近年来, 随着信息技术和互联网的飞速发展, 图数据作为一种重要的数据模型变得愈加重要.在很多领域, 图数据刻画了不同实体之间的相互关系, 例如社交网络[1, 2]、道路交通网[3]、生物信息网[4]、计算机网络[5]和Web网络[6]等.
其中, 最短路径查询是图数据管理中的一类非常重要的研究问题.在社交网络中, 每个人都构成了图中的一个顶点, 人与人之间的联系则形成了边.社交网络中的最短路径是网络顶点影响力评判的重要因素, 小世界网络中, 直径的计算一般也是通过计算最长最短路径得到的[7]; 在Web网络中, 数据转发时每个路由器使用路由协议和链路状态信息来识别从自己到其他路由器的最短路径, 网络拓扑通常随时间而变化, 因此, 一个高效的最短路径算法在路由计算中显得尤为重要[8]; 在道路交通网中, 经常需要计算两个地点之间的最短路径, 有时因为一些特殊的需求还要计算最小的前k条最短路径[9-11].
在实际应用中, 用户往往需要查询带有约束条件的最短路径.例如, 某游客去一座城市旅行, 他计划首先前往某餐馆就餐, 然后分别参观景点A~景点C, 最后返回酒店.特别地, 该游客计划在参观景点B之前先参观景点A.因此, 如何设计一条满足用户约束且代价最小的观光路径成为一个重要的问题.在该例中, 道路交通网被建模为一张图G(V, E), 则上述问题可形式化描述为:给定起点vs和终点ve, 寻找一条从vs到ve的最短路径, 使得此路径经过用户指定点集Vs⊆V中的所有点, 且某些点的访问要满足一定的先后顺序.在本文中, 该问题被称为基于规则的最短路径查询问题.
目前, 存在少量工作研究了最优路径查询问题optimal route queries(ORQ).ORQ将图G中全部顶点划分为多个不同的类别, 用户查询时, 给出起点vs和一个访问顺序图GQ.这里, GQ是一个有向无环图, GQ中的每个点都对应于G中的一个类别信息, GQ中每条有向边(c, c')表示G中类别c优先于类别c'访问.查询结果是一条以vs为起点且满足GQ的最优路径.例如, 某游客计划去餐馆、酒吧和电影院, 每个类别都有多个具体的地点可供选择, 而且游客希望在去酒吧之前要先去餐馆吃饭, 因此, 他需要制定一条路线使得在满足约束条件的前提下路线的总距离最短.目前, 解决ORQ问题的精确算法的基本思想是:首先计算GQ中所有类别的全排列(每个类别在排列中的顺序代表此类的访问顺序), 并删除访问顺序不满足约束条件的排列; 然后对于每一个排列, 依次从排列的每个类中选择一个点构成一条路径; 最终枚举出满足约束条件的所有路径, 并返回具有最短距离的路径.然而这些方法在面对基于规则的最短路径问题时, 主要存在以下两个缺点:(1)针对基于规则的路径查询问题, 对图G进行划分所得的每个类仅包含一个顶点, 即任意两点对应的类都不相同, 已有的算法求解此类问题相当于枚举出所有满足约束条件的排列, 然而大部分排列对于求解最短路径来说是冗余的; (2)目前已有的解决ORQ问题的算法面向的是空间数据库, 这些算法均通过计算两点之间的欧氏距离加速查询, 然而本文所解决的问题是基于普通的图模型, 两点间的最短距离即为最短路径的长度, 而存储全部顶点对之间的最短距离空间开销过高.因此, 本文设计了一种前向扩展算法来快速求解基于规则的最短路径问题, 其主要思想是, 尽可能早地过滤掉不能构成最短路径的子路径.真实数据集上的实验结果证明了本文提出的算法的效率远远优于传统ORQ算法.
本文的主要贡献如下:
(1) 提出了广义规则树的概念, 设计了生成广义规则树的算法, 并利用广义规则树来判断算法是否找到一条基于规则的最短路径;
(2) 设计了基于最优子路径的前向扩展算法, 该算法可以快速求解基于规则的最短路径问题, 并设计了前向扩展算法的改进算法——基于最短优先策略的前向扩展算法;
(3) 在真实的数据集上设计了大量的实验, 并与已有的性能最好的算法比较, 实验结果验证了本文算法的有效性.
本文第1节给出基于规则的最短路径查询问题的形式化定义, 并证明此类问题是NP-hard问题.第2节介绍广义规则树的概念, 并设计生成广义规则树的算法.第3节介绍一种图数据的预处理技术, 可以用来快速求解两点之间的最短路径.第4节和第5节分别介绍前向扩展算法以及基于最短优先策略的前向扩展算法, 并分别对它们的算法复杂度进行分析.第6节在真实的数据集上验证本文算法的高效性.第7节介绍相关工作.最后一节对全文进行总结.
1 问题定义有向加权图可以表示为G(V, E, w)(简称G), V表示图G中全部顶点的集合, E表示全部边的集合.任意一条有向边e∈E可以表示为e=(vi, vj), 其中, vi, vj∈V, e称为vi的出边或者vj的入边, vj(vi)被称为vi(vj)的出边(入边)邻居.w是一个权重函数, 并且对图G中的每条边都赋予一个非负的权重, 本文使用wi, j来表示有向边(vi, vj)∈E的权重, 即wi, j=w(vi, vj).图G中的路径p是一个顶点序列, 即p=(v1, v2, …vk), 其中, (vi, vi+1)(1≤i≤k-1)是图G中的一条有向边, 路径p的权重用w(p)表示, 表示p中全部有向边的权重之和, 即
本文主要研究基于规则的最短路径查询问题, 首先介绍什么是路径查询规则, 然后给出基于规则的路径定义.本文中, 路径规则用
(ⅰ) I是V的一个顶点子集, 即I⊆V;
(ⅱ)
R是一组偏序关系〈vi, vj〉的集合, 其中, vi, vj∈I.〈vi, vj〉表示vi
需要注意的是:偏序关系集R中不存在环, 即R中不存在一个偏序关系子集{〈v1, v2〉, …, 〈vk-1, vk〉, 〈vk, v1〉}, 其中, 顶点v1, v2, …, vk∈I.下面给出基于规则的路径定义.
定义1.1(基于规则的路径).给定图G(V, E, w), 起点为vs, 终点为ve, 规则
(1) 对每一个顶点vi∈I, 都有vi∈p;
(2) 对每一个偏序关系〈vi, vj〉∈R(或者vi
在定义1.1中, 条件(1)是指:若路径p基于规则
给定图G中的两个顶点vs, ve以及规则
| Table 1 List of notations 表 1 符号列表 |
例1.1:给定有向图G(V, E, w), 如图 1(a)所示, 已知规则
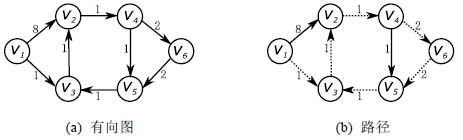
|
Fig. 1 Rule-based shortest path 图 1 基于规则的最短路径 |
定理1.1. 基于规则的最短路径查询问题是一个NP-hard问题.
证明:本文通过将其归约到哈密尔顿路问题(NPC问题)证明.给定一个有向图G, 令vs和ve分别表示起点和终点.G中每条边的权重都设为1, 规则
若p为一条基于规则
定义2.1(广义规则树). 满足规则
(1) 起点vs为根结点、终点ve为唯一叶结点;
(2) 对
广义规则树满足以下两个性质.
性质2.1. 给定起点vs、终点ve和规则
证明:当给定起点vs和终点ve,
性质2.2. R中蕴含的任意一个偏序关系都对应广义规则树中的一对祖先后代结点.
证明:若R中蕴含vi
显然, 在广义规则树中, 起点是所有其他点的祖先结点, 终点是所有其他点的后代结点.规则点vi∈IR的全部父结点集合表示为
例2.1:给定有向图G, 如图 1(a)所示, 其中, 起点为v1, 终点为v3, 规则
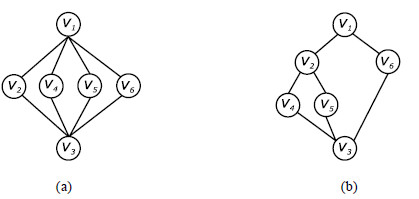
|
Fig. 2 Generalized rule tree 图 2 广义规则树 |
下文中, 规则点vi∈IR的父结点、子结点、祖先结点和后代结点均指广义规则树中对应树结点vi的父结点、子结点、祖先结点和后代结点.例如在图 2(b)中, 规则点v2的父结点集合
算法1展示了构造广义规则树的伪代码.初始阶段, 算法将所有的规则点初始化一棵广义树(第1行), 广义树的根设为起点vs, 唯一叶结点设为终点ve, I中的所有顶点都互为兄弟结点, 且它们的父结点和祖先结点都设为vs, 子结点和后代结点都设为ve, 因此, vs的子结点集合和ve的父结点集合均为I.算法1的主要思想是:依次处理R中的每一对偏序关系, 并逐步构造广义规则树.在每次迭代中, 对每个〈vi, vj〉∈R, 算法判断在
●首先, 对
●然后, 将vi加入vj的父结点集合, 将vj加入vi的子结点集合(第16行);
●最后, 对vj的每个祖先结点vk, 将vk的后代结点集合更新为
算法1. GeneralizedRuleTree(G, vs, ve,
输入:图G, 起点vs, 终点ve, 规则
输出:广义规则树
1.用所有的规则点初始化广义树, 即:广义树的根结点为vs, 叶结点为ve, I中的所有顶点都互为兄弟结点, 并且它们的父结点和祖先结点都设为vs, 子结点和后代结点都设为ve;
2. for each 〈vi, vj〉∈R do
3. if
4. continue;
5. end if
6. for
each
7. if
8.
9. end if
10. end for
11. for
each
12. if
13.
14. end if
15. end for
16.
17. for
each
18.
19. end for
20. for
each
21.
22. end
23. end for
24. return
例2.2:接例1.1, 利用算法1构造其对应的广义规则树.首先, 初始化广义规则树, 结果如图 3(a)所示; 当偏序关系v2

|
Fig. 3 Construction of generalized rule tree 图 3 广义规则树的构造过程 |
广义规则树
定理2.1.路径p为一条从起点vs到终点ve的路径, 若终点ve被路径p合法访问, 则路径p为一条基于规则
证明:由规则点被路径合法访问的定义可知, 集合I中的点都在路径p中.下面证明偏序关系集R中的所有偏序关系均已满足.假设存在一个偏序关系〈vi, vj〉∈R, 使得p不满足此偏序关系, 即p中不存在一条从vi到vj的子路径, 因此, 规则点vj没有被合法访问且vj的所有子结点也没有被合法访问.由于终点ve是所有规则点的后代结点, 可得终点ve没有被路径p合法访问.这与已知条件矛盾.因此, 所有的偏序关系均已满足.综上可得, 路径p为一条基于规则
由定理2.1可知:可以依据一个查询的终点是否被一条路径合法访问, 来判断此路径是否为基于规则的路径.在下文介绍的前向扩展算法中, 本文依据定理2.1来判断是否已找到一条基于规则的路径.
3 分层收缩技术分层收缩(contraction hierarchies, 简称CH)[12]是一种简单有效的图数据预处理技术, 它可以提高最短路径的查询效率.CH本质上是预先存储一些最短路径信息, 从而实现加速最短路径查找的目的.本文采用CH技术进行预处理, 以使算法能更高效地计算两点之间的最短路径.给定图G(V, E, w), CH首先给V中所有顶点分配一个序号, 任意两个顶点的序号都不相同; 然后依据序号的大小, 按照从小到大的顺序对点进行收缩.顶点vi被收缩是指:把vi以及与vi相连的边从G中删除, 并且添加一些新的边到G中.具体地, 对每一对vi的入边(vj, vi)和出边(vi, vk), 如果路径(vj, vi, vk)是连接vj和vk的唯一的最短路径, 则往G中添加边(vj, vk), 并且将边(vj, vk)的权重设为(vj, vi)和(vi, vk)的权重之和.所有顶点收缩完成之后, CH将原图G分为两个新图, 分别为前向图Gu和后向图Gd; 然后, CH利用Gu和Gd计算最短路径.CH技术的具体细节见文献[12].
4 FE算法本节提出前向扩展算法(forward expanding, 简称FE)来求解基于规则
给定有向图G(V, E, w)、规则
(1) 对π中任意点vi, p中都包含点vi;
(2) 若π中点vi的位置在vj之前, 则p中包含一条从vi到vj的子路径;
(3) 路径p的起点和终点分别为v1和vr.
给定路径p|π, 它可以被π中的所有点划分为r-1条子路径v1
在例1.1中, 路径
定义4.1(基于规则的排列).给定图G(V, E, w), 起点为vs, 终点为ve, 规则
由定义4.1可知:若π为一个基于规则
定理4.1.给定图G(V, E, w), 起点为vs, 终点为ve, 规则
证明:给定IR的一个基于规则
由定理4.1可知:对于一个基于规则的排列p, 只有当π所对应的路径p|π中的所有路径片段都为最短路径时, 即p|π为p*|π, 此路径才有可能成为基于规则的最短路径.因此, 本文后续部分所提到的任意排列π所对应的路径都特指p*|π, 即所有的路径片段都为最短路径.
对于点集Vs⊆V, 可以逐步扩展点序列的长度来得到Vs的排列, 其中, 点序列中的每个点都属于Vs, 且点序列中不包含重复的顶点.如果点序列中包含l个顶点, 本文称此点序列为Vs的l-子排列(特别地, 本文规定:规则点集IR的所有子排列均以起点vs作为起始位置的顶点), 记为πl, 其中, 1≤l≤r(r=|Vs|).包含πl中l个顶点的点集合称为子排列πl对应的点集, 记为
定义4.2(子排列满足的规则
利用定义4.2, 可以很容易地给出最优子排列定理.
定理4.2. 给定图G(V, E, w), 起点为vs, 终点为ve, 规则
证明:假设存在一个
给定有向图G(V, E, w)如图 1(a)所示, 已知规则
| $ w(p{{|}_{{{\pi }_{4}}}}) <w(p{{|}_{{{{{\pi }'}}_{4}}}}). $ |
推论4.1. 给定图G(V, E, w), 起点为vs, 终点为ve, 规则
推论4.1的结论是显然的.因此, 对于
本节提出求解基于规则
前向扩展算法的伪代码见算法2.
算法2. FE(G, vs, ve,
输入:图G, 起点vs, 终点ve, 规则
输出:
1.
2.利用NN算法得到路径pg;
3. θ←w(pg);
4. π1←vs;
5.
6. for l=2 to r=|IR| do
7. Rl←Ø;
8. 依据点集
9. for each v∈IR-{vs} do
10. for each划分Rl-1得到的集合
11. R'←Ø;
12. for each
13. if πl-1不包含v且v的所有父结点均已被
14. πl←πl-1⊕v;
15.
16. end if
17. end for
18. 查找R'中具有最小权重的路径, 记为
19. if
20.
21. end if
22. end for
23. end for
24. end for
25.查找Rr中具有最小权重的路径, 记为
26. return
给定图G(V, E, w), 起点为vs, 终点为ve, 规则
FE用Rl来存储IR的l子排列所对应的路径:首先, 将Rl初始化为空集(第7行); 然后, FE对长度为l-1的子排列进行扩展操作, 并利用最优子排列理论过滤不可能成为基于规则的最短路径所对应排列的前缀.依据子排列πl-1对应的点集
FE求得IR的r-子排列所对应的路径之后, 由于IR的r子排列所对应的路径的最后一个顶点为终点ve, 由定理2.1可知, IR的r子排列所对应的路径都为基于规则
例4.1:接例1.1, 利用FE算法求解基于规则
| Table 2 Solving process of FE algorithm 表 2 FE算法的求解过程 |
4.3 复杂度分析 4.3.1 时间复杂度.
FE的时间复杂度主要集中在计算IR的长度为1至r(r=|IR|)的子排列上, 对于长度为l(1≤l≤r)的子排列, 由最优子排列可知, FE至多生成
FE需要利用长度为l-1的子排列来求解长度为l的子排列, 因为FE至多生成
本节提出FE算法的改进算法——基于最短优先策略的前向扩展算法(forward expanding based on best-first searching, 简称FEBF).接下来, 本文首先分析如何对FE算法进行改进; 然后给出基于最短优先策略的前向扩展算法, 并对算法做出详细的介绍; 接着, 对FEBF算法提出了几个优化技术; 最后, 分析了FEBF算法的时间和空间复杂度.
5.1 基于最短优先策略的前向扩展算法从第4.2节可知, FE算法依次扩展规则点集IR的长度为1至长度为r(r=|IR|)的子排列, 最后从长度为r的子排列对应的路径中选择权重最小的路径作为问题的解.在求解长度为l的子排列时, FE必须先求得长度为l-1的所有子排列.事实上, 某些长度为l-1的子排列所对应路径的权重已大于基于规则
FEBF算法本质上也是逐步扩展IR的长度为1的子排列到长度为r的子排列, 它采用最短优先的策略尽可能少地计算IR的子排列, 从而可以尽快找到问题的解.FEBF算法的伪代码见算法3.
算法3. FEBF(G, vs, ve,
输入:图G, 起点vs, 终点ve, 规则
输出:
1.定义一个优先级队列Q, Q中的元素为元组〈π, w(p|π)〉且以w(p|π)的大小进行从小到大排序;
2.
3.利用NN算法得到路径pg;
4. θ←w(pg);
5.将Ω中的每一个元素的值初始化为∞;
6. π1←vs;
7.将
8.弹出Q的队首元素〈π', w(p|π')〉, 令v*为π'末尾位置的点;
9. while v*≠ve do
10. for each v∈IR-{vs} do
11. if π'不包含v且v的所有父结点均已被p|π'合法访问then
12. π←π'⊕v;
13. if
14.
15. 将〈π, w(p|π)〉插入到Q中;
16. end if
17. end if
18. end for
19. 弹出Q的队首元素〈π', w(p|π')〉, 令v*为π'末尾位置的点;
20. end while
21.
22. return
给定图G(V, E, w), 起点为vs, 终点为ve, 规则
在构建IR的1-子排列时, 因为只有π1=vs这一个1子排列满足规则, 因此, FEBF将
例5.1:接例1.1, 利用FEBF算法求解基于规则
FEBF首先生成〈v1, 0〉并把它插入到优先级队列Q中, 接下来的操作是:
从Q中弹出〈v1, 0〉, 利用它扩展得到〈v1v2, 2〉, 〈v1v6, 5〉并分别插入到Q中;
从Q中弹出〈v1v2, 2〉, 利用它扩展得到〈v1v2v4, 3〉, 〈v1v2v5, 4〉, 〈v1v2v6, 5〉并分别插入到Q中;
从Q中弹出〈v1v2v4, 3〉, 利用它扩展得到〈v1v2v4v5, 4〉, 〈v1v2v4v6, 5〉并分别插入到Q中;
从Q中弹出〈v1v2v5, 4〉, 利用它扩展得到〈v1v2v5v4, 7〉, 〈v1v2v5v6, 9〉并分别插入到Q中;
从Q中弹出〈v1v2v4v5, 4〉, 利用它扩展得到〈v1v2v4v5v6, 9〉并插入到Q中;
从Q中弹出〈v1v6, 5〉, 利用它扩展得到〈v1v6v2, 9〉并插入到Q中;
从Q中弹出〈v1v2v6, 5〉, 利用它扩展得到〈v1v2v6v4, 10〉, 〈v1v2v6v5, 7〉并分别插入到Q中;
从Q中弹出〈v1v2v4v6, 5〉, 利用它扩展得到〈v1v2v4v6v5, 7〉并插入到Q中;
从Q中弹出〈v1v2v5v4, 7〉, 利用它扩展得到〈v1v2v5v4v6, 9〉并插入到Q中;
从Q中弹出〈v1v2v6v5, 7〉, 利用它扩展得到〈v1v2v6v5v4, 10〉并插入到Q中;
从Q中弹出〈v1v2v4v6v5, 7〉, 利用它扩展得到〈v1v2v4v6v5v3, 8〉并插入到Q中;
从Q中弹出〈v1v2v4v6v5v3, 8〉且满足路径搜索终止条件, 此时算法终止, FEBF返回(v1, v3, v2, v4, v6, v5, v3)作为问题的解.
在例4.1中, FE算法总共生成24个子排列; 而在例5.1中, FEBF总共生成18个子排列.显然, FEBF能有效减少算法生成的子排列个数.
5.2 优化技术本节提出3个优化技术来提高FEBF算法的效率.
●缓存机制
给定IR的基于规则
●排列过滤
当FE对长度为l-1的子排列πl-1进行扩展操作时, 它首先判断规则点v∈IR是否已在πl-1中, 然后再判断v的所有父结点是否已被路径
定理5.1. 给定长度为l-1的子排列πl-1, v*是πl-1末尾位置的顶点, 已知vi, vj
证明:不失一般性, 设πl-1=v1v2…v*是IR的长度为l-1的子排列, πl-1⊕vj和πl-1⊕vi分别为FE用vj和vi对πl-1进行扩展操作得到的长度为l的子排列, 已知v*到vj的最短路径是v*到vi最短路径的子路径.
设π=v1v2…v*vi…vkvjvx…vr为IR的基于规则
综上可得w(p|π')≤w(p|π).证毕.
在例4.1中, 对于长度为2的子排列v1v2, 可以分别用点v4, v5, v6对v1v2进行扩展操作, 从而得到v1v2v4, v1v2v5, v1v2v6.因为从v2到v4的最短路径(v2, v4)是从v2到v5最短路径(v2, v4, v5)的子路径, 也是从v2到v6最短路径(v2, v4, v6)的子路径, 因此可以过滤掉子排列v1v2v5和v1v2v6.
●权重预估
当FE扩展长度为l-1的子排列得到长度为l的子排列πl时, v*是πl末尾位置的顶点.对于IR的所有基于规则
本文首先分析FEBF的时间复杂度, 对于长度为l(1≤l≤|IR|)的子排列, FEBF至多生成
本节使用不同规模的真实数据集来验证算法的有效性, 并与解决同类问题中已有的最好算法作对比.第6.1节介绍了实验的基本设置, 第6.2节对实验的结果进行分析.
6.1 实验设置本文的所有算法都使用C++语言实现, 并在Linux操作系统环境下进行测试, 硬件的信息为:Intel(R) Core(TM) i7-4770K, 32GB RAM.本文对每组实验重复100次, 并把平均值作为此组实验的结果.如果一个算法在某个数据集上的运行时间超过24h或者超过32GB RAM, 则忽略此算法在这个数据集上的运行结果.
●数据集
本文使用8个真实数据集来验证本文提出的算法, 其中4个为道路交通网数据集(http://www.dis.uniroma1.it/challenge9/index.shtml ), 另外4个为非道路交通网数据集(http://snap.stanford.edu/data/), 数据集的详细信息见表 3, d表示顶点的平均度的大小.对于道路交通网数据集, 本文将两点之间的距离作为边的权重; 对于非道路交通网数据集, 本文给每一条边随机生成一个1~100之间的值作为此边的权重值.
| Table 3 Datasets 表 3 数据集 |
●查询集
对于每个数据集, 本文生成25个查询集Q1~Q25, 它们分别对应不同规模的规则
●对比算法
对每一组实验, 本文将算法FE、FEBF与算法SBS和SFS作对比, SBS[13]和SFS[13]是同类问题的已有算法中性能最好的精确算法.本文不与其他的算法对比的原因是:(1) BBS[13]和BFS[13]分别为SBS和SFS的优化算法, 主要是解决当I中包含的不是点而是类别信息时, 随着每个类中包含顶点的个数增多, 导致搜索空间增大的问题, 当每个类中只包含一个顶点时, 优化前后的算法性能相同; (2) NN[14]是一个启发式算法, 它最终返回的路径是一条接近最优的路径, 而本文的算法返回的是一条最优的路径.
●其他
由于SBS和SFS都为应用于空间数据集上的算法, 在空间数据集上可以直接利用经纬度坐标求得两点之间的欧氏距离, 而本文所设计的算法均应用于普通的图数据, 即, 由点和边构成的数据, 考虑到对比的公平性, 本文对所有的算法均利用CH技术来求解两点之间的最短距离.
6.2 结果分析●查询效率
在查询集Q1~Q5上算法的运行结果如图 4所示.可以看出:对于每一个数据集, SFS的查询时间都大于其他算法的查询时间, FE算法的查询时间明显小于SBS和SFS的查询时间, FEBF算法的查询时间小于其他所有算法, 即使在具有百万个顶点的数据集(FLA)上, FEBF也能在1s左右得到查询的结果.因为查询集Q1~ Q5具有相同个数的偏序关系, 随着规则点集的规模逐渐增大, 规则点集的基于规则
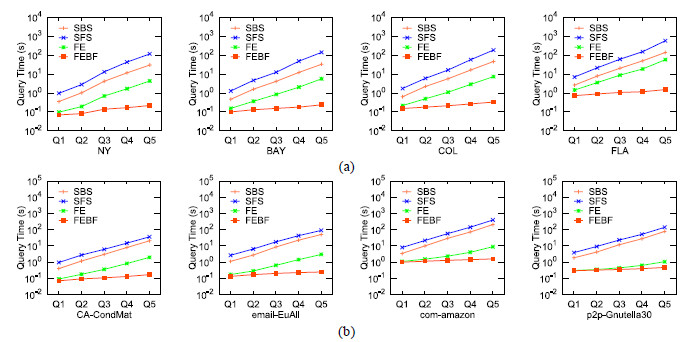
|
Fig. 4 Query efficiency on Q1~Q5 图 4 在Q1~Q5上的查询效率 |
图 5展示了算法在查询集Q6~Q10上的查询结果.对于所有的数据集, SFS具有最大的查询时间, FEBF算法的查询时间小于其他所有算法.因为查询集Q6~Q10具有相同个数的规则点, 随着R中偏序关系的逐渐增多, 规则点集的基于规则
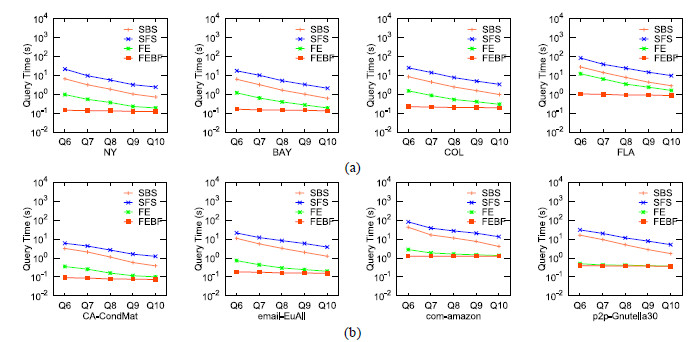
|
Fig. 5 Query efficiency on Q6~Q10 图 5 在Q6~Q10上的查询效率 |
查询集Q11~Q15中包含的偏序关系个数为0, 此问题退化为广义旅行商问题, 算法的查询结果如图 6所示.因为Q11~Q15的偏序关系个数为0, 则规则点集的任意排列都为基于规则
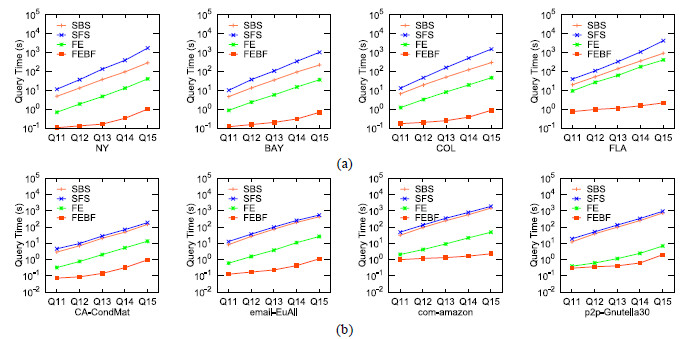
|
Fig. 6 Query efficiency on Q11~Q15 图 6 在Q11~Q15上的查询效率 |
查询集Q16~Q20的偏序集可以构成一个全序集, 即I中顶点的合法访问顺序已确定, 此问题退化为最优序列路径查询问题, 算法的查询结果如图 7所示.由于每个类中仅包含一个顶点, 因此, Q16~Q20本质上为计算|I|+1个最短路径.从图中可知:对于每一个数据集, SBS算法的查询时间都是最短的.这是因为SBS没有利用其他的优化策略来过滤子排列, 而对于Q16~Q20来说, 基于规则

|
Fig. 7 Query efficiency on Q16~Q20 图 7 在Q16~Q20上的查询效率 |
查询集Q21~Q25对应的规则
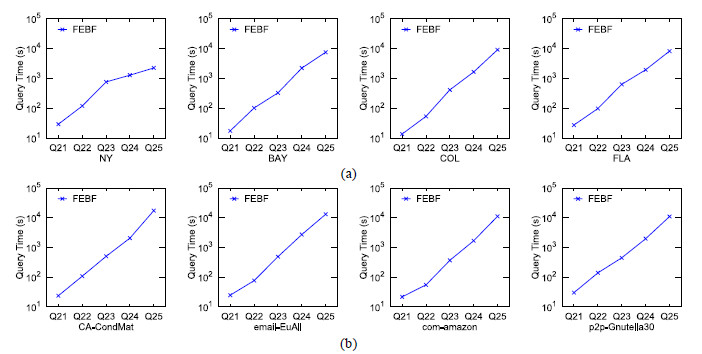
|
Fig. 8 Query efficiency on Q21~Q25 图 8 在Q21~Q25上的查询效率 |
●改进后的算法有效性
FEBF算法是FE算法的改进算法, 图 9展示了FE和FEBF算法在查询集Q11~Q15上的加速比(加速比是指FE算法的查询时间与FEBF算法的查询时间的比值), 结果表明:在每个数据集上, 随着规则点个数的增多, 加速比越来越大.显然, 改进后的FEBF算法的运行效率极大地优于FE算法的运行效率.

|
Fig. 9 Speedup ratio of improved algorithm 图 9 改进后算法的加速比 |
FE和FEBF算法的查询时间主要与生成的子排列个数有关:生成的子排列越多, 查询时间则越长; 反之, 查询时间则越短.因此, 本文用子排列的减少比
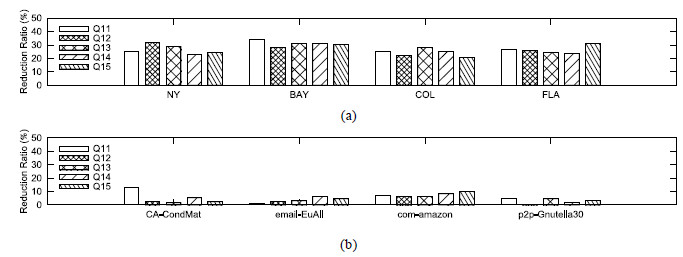
|
Fig. 10 Reduction ratio of sub-permutation 图 10 子排列的减少比 |
●优化技术的有效性
对于FEBF算法, 本文提出了3个优化技术.图 11展示了在查询集Q11~Q15上, FEBF算法在未使用优化技术与使用优化技术两种情况下的加速比(即未使用优化技术的FEBF算法的查询时间与使用优化技术的FEBF算法的查询时间的比值), 结果表明:在每个数据集上, 相对于未使用优化技术的FEBF算法, 使用优化技术的FEBF算法能够有效降低算法的查询时间.
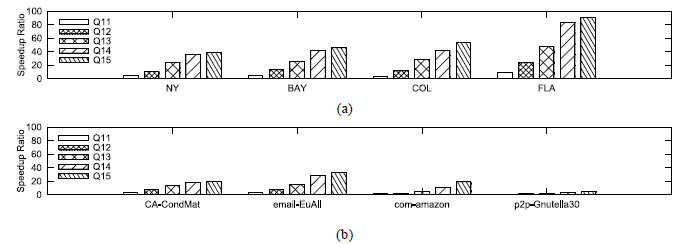
|
Fig. 11 Effectiveness of optimizing techniques 图 11 优化技术的有效性 |
7 相关工作
本节介绍相关的工作, 并把最短路径问题分为传统的最短路径问题和ORQ问题.ORQ问题又细分为如下几类:已指定必须经过类别的访问顺序、未指定必须经过类别的访问顺序、部分指定必须经过类别的访问顺序.下面分类依次介绍相关的工作.
●传统的最短路径问题
传统的最短路径问题具有不同的应用场景.稠密距离图(dense distance graph, 简称DDG)是平面图的分解图, 即:将一个平面图分解为几个区域, 每个区域所包含的顶点个数最多为r, 其中, r < n, n为平面图中包含的顶点个数.Shay等人[15]提出了一种求解稠密距离图上的最短路径的算法, 并从理论上证明了所提的算法优于已有的最优算法.对于一个有向加权图, 如果它的权重存在负值, 称此图为实有向加权图, Fahim等人[16]提出了一种实有向加权图上的单源最短路径算法, 此算法可以快速检测路径中是否包含权值为负的环路, 且性能优于已有的算法.对于规模较大的加权图, Qiu等人[17]提出了一种并行最短路径距离查询框架——ParaPLL, ParaPLL能够快速给出大规模加权图上的最短路径的距离, ParaPLL通过使用共享内存和消息传递来实现最短路径距离的并行计算.给定起点vs和终点ve, 重路由序列是一系列从vs到ve的最短路径序列, 使得在序列中相邻的两个最短路径只有一个顶点不相同.Paul[18]研究了最短路径重路由问题(即:给定图G中从vs到ve的两条最短路径P和Q, 是否存在从P到Q的重路由序列), 并给出了求解最短路径重路由问题的动态规划方法.进化图序列是指一系列静态图序列, 它本质上是随时间变化的时序图, 在每一时刻的图快照都对应于进化图序列中的一张静态图.Ren等人[19]研究了进化图序列上的最短路径查询问题, 并提出了解决方案框架——FVF.Jihye等人[20]提出了基于磁盘的大规模动态图上的最短路径查询算法, 此算法可以有效求解边的插入或删除以及边权重的增加或减少情况下的最短路径查询问题.Hasan[21]提出了针对稀疏图的top-k最短路径查询算法, 该算法较已有的top-k最短路径算法有明显的性能提升.对于有向无环图, Matus等人[22]提出了计算两点之间的近似最短路径算法, 即:给定起点vs和终点ve以及权重阈值L, 该算法返回一条从vs到ve权重不超过L的路径.
●已指定必须经过类别的访问顺序
已知必须经过的类别集合, 若已规定所有类别的访问顺序, 则ORQ问题称为类别全序的最优路径查询问题.R-LORD[23]是一个精确算法, 用来求解空间数据集上类别全序的最优路径查询问题, 假设p*=(vs, v1, v2, …, vr, ve)是上述问题的一个最优路径, 则p*的任意一个后缀p在p中都是最短的, P是满足下面两个条件的路径集合: (1)以p的起点作为起点; (2)与p相同的顺序访问p中的所有类.基于此, R-LORD采用动态规划的方式逐步构建最优后缀表.在构建最优后缀表之前, R-LORD利用贪心算法得到一条满足类别访问顺序的路径, 并用此路径的权重作为阈值来过滤不可能成为最优路径的后缀.在构建最优后缀表时, R-LORD利用椭圆剪枝技术来排除无法构成最优路径的子路径.Michael等人提出了基于动态规划的算法求解类别全序的最优路径查询问题[24], 此算法主要是逐步构建一个实值矩阵X, X是一个r行g列的矩阵, 其中, r表示必须经过的类别个数, g表示规模最大的类中包含的顶点个数.矩阵的每个元素X[i, j]是一个最优子路径的长度, 此路径表示从起点到访问顺序为i的类别中的第j个顶点的最优子路径.此外, Michael还设计了两个优化技术, 分别为图结构优化和问题结构优化, 并通过剪枝策略来解决由于类别规模过大导致算法运行时间过长的问题.由于本文所研究的问题对类别的访问顺序只做了部分的限制, 即, 并未完全指定每个类别的访问顺序, 因此, 上述两个算法都无法用来求解本文所研究的问题.
●未指定必须经过类别的访问顺序
已知必须经过的类别集合, 若没有规定任何类别的访问顺序, 则ORQ问题称为类别无序的最优路径查询问题.对于空间数据集, Li等人提出了几个近似算法来求解类别无序的最优路径查询问题[25].ANN[25]是一个近似算法, 其主要思想是:从单个起点构成的路径p'开始, 反复地从G中选择一个离p'末尾顶点最近的点(记为vc), 且vc对应的类别c尚未被p'访问, 然后将vc添加到p'的末尾构成新的p'.重复上述操作, 直至所有的类别都已被p'访问, 最后将终点添加到p'的末尾, 从而构成一条包含指定所有类别的路径.AMD[25]也是一个近似算法, 它的主要思想是:对于每一个必须访问的类c, 从类c中选择一个顶点vc, 使得vc离起点和终点的距离之和小于其他任意点离起点和终点的距离之和, 从每个类中选择得到的点构成集合VC, 然后调用ANN算法(此处在调用ANN算法时, 将G中的点替换为VC中的点), 从而得到一条包含指定所有类别的路径.LESS[26]是一个求解此类问题的精确算法, 它的本质是将指定的所有类别进行全排列, 每个类别在排列中的位置表示此类别在路径中被访问时所处的位置.对于每一个排列, 按顺序依次从排列的类别中选择一个顶点, 最终构成一条包含指定所有类别的路径. LESS枚举出所有排列对应的所有路径, 然后选择一条长度最小的路径作为问题的最优解.由于本文所研究的问题对类别的访问顺序做了部分的限制, 而上述算法只能解决访问顺序没有限制的情况, 因此, 上述两个算法都无法用来求解本文所研究的问题.
●部分指定必须经过类别的访问顺序
已知必须经过的类别集合, 若已规定部分类别的访问顺序, 则ORQ问题称为类别偏序的最优路径查询问题.NN[14]是求解类别偏序的最优路径查询问题的启发式算法, 它最终返回一条接近最优的路线, 算法的具体流程为:从单个起点构成的路径p'开始, 反复地从G中选择一个离p'末尾顶点最近的点(记为vc), 且vc对应的类别c在图GQ(GQ是查询图且是一个有向无环图, GQ中的每个点都对应于G中的一个类别信息, GQ中每条有向边(c, c')表示G中类别c的点先于类别c'的点访问)中且入度为0, 然后, 从GQ中删除类别c以及与它相连的边, 接着将vc添加到p'的末尾构成新的p'.重复上述操作, 直至GQ中不包含任何点, 最终找到一条满足约束条件的路线.Li等人提出了4个精确算法来求解在空间数据集上的此类问题[13], 它们分别为SBS, BBS, SFS和BFS. SBS利用R-LORD[23]中提出的后缀最优定理, 逐步求解1后缀到r后缀(r为必须经过的类别的个数), 然后, 从r后缀中选择一个路径长度最小的路径作为此问题的最优解.BBS是SBS的优化算法, 对于每一个必须经过的类别, BBS首先将具有相同类别的点进行聚类, 即, 把彼此距离较近的一些点归为同一组, 然后, BBS以每一个组的点为单位, 执行与SBS相同的操作, 当每个类中包含的点的个数较多时, BBS可以很大程度地提高算法的运行效率.SFS本质上是采用分层回溯的方式求解问题的解, 算法运行时所处的层数表示此时已得到的子路径所包含的类别个数.SFS采用NN[14]添加顶点的方式, 每次选择离当前路径末尾顶点最近的一个点, 每往路径中添加一个新的顶点, 则意味着SFS进入到当前层的下一层, 然后再执行相同的添加顶点的操作.当算法到达第r层后, 则表明此算法已找到一条满足约束的路径, 然后算法回溯到r-1层, 将离当前路径末尾顶点次近的点添加到路径的末尾.重复上述回溯操作, 直至得到所有满足约束的路径, 最后返回一条最优的路径.BFS是SFS的优化算法, 与BBS类似, BFS首先将具有相同类别的点进行聚类, 即, 把彼此距离较近的一些点归为同一组, 然后, BFS以每一个组的点为单位, 执行与SFS相同的操作, 最终得到问题的最优解.由于本文所研究的问题是基于普通的图数据而非空间数据, 因此上述4个算法无法直接应用于本文所研究的问题, 而且这些算法较少过滤掉不可能成为最优路径的子路径, 使得算法的运行时间较长.
广义旅行商问题是传统旅行商问题的变种, 带优先级约束的旅行商问题属于广义旅行商问题的一种, 它可以描述为:已知n个城市之间的相互距离, 现有一旅行商计划全部访问这n个城市, 并且每个城市只能访问一次, 在访问这些城市时必须满足一定的约束条件(例如, 必须先访问城市1和城市2, 然后才能访问城市3), 最后, 旅行商返回到出发的城市, 目的是寻找一条旅行商行走的路线, 使得此路线满足上述约束条件且具有最小的距离. Ascheuer等人[27]提出了基于分支切割的算法来解决不对称的有约束条件的旅行商问题.Moon等人[28]和Wang等人[29]分别采用遗传算法和整数规划的方式解决带有约束条件的旅行商问题; 有优先约束的哈密顿路径问题(Hamiltonian path problems with precedence constraints)又称为顺序排序问题(sequential ordering problem), 可描述为寻找由指定的起点前往指定的终点的最短路径查询问题, 途中经过其他所有顶点有且只有一次, 而且顶点之间存在先后顺序约束, Karan等人[30]提出了一个基于分支界限法的算法来解决顺序排序问题.已有的解决广义旅行商问题的精确算法本质上为枚举出每一种可能的路径, 因此这些算法不适用于大规模图上问题的求解, 而本文所提的算法可以很好地应用于大规模图上的查询.
8 总结本文设计了一个基于最优子路径的前向扩展算法, 该算法可以快速求解基于规则的最短路径查询问题, 并设计了前向扩展算法的改进算法——基于最短优先策略的前向扩展算法.从实验的结果来看, 基于最短优先策略的前向扩展算法对原始算法的查询效率有很大程度的提高.本文在真实的数据集上设计了大量的实验, 并与已有的性能最好的算法作比较, 实验结果表明, 本文的算法大幅度优于已有的算法.
| [1] |
Pham TAN, Li X, Cong G, et al. A general graph-based model for recommendation in event-based social networks. In: Proc. of the 2015 IEEE 31st Int'l Conf. on Data Engineering (ICDE). IEEE, 2015. 567-578.
|
| [2] |
Chen X, Lui JCS. Mining graphlet counts in online social networks. In: Proc. of the IEEE Int'l Conf. on Data Mining. IEEE, 2017. 71-80.
|
| [3] |
Salamanis A, Kehagias DD, Filelis-Papadopoulos CK, et al. Managing spatial graph dependencies in large volumes of traffic data for travel-time prediction. IEEE Trans. on Intelligent Transportation Systems, 2016, 17(6): 1678-1687.
[doi:10.1109/TITS.2015.2488593] |
| [4] |
Hartsperger ML, Blöchl F, Stümpflen V, et al. Structuring heterogeneous biological information using fuzzy clustering of k-partite graphs. Bmc Bioinformatics, 2010, 11(1): 1-15.
http://d.old.wanfangdata.com.cn/OAPaper/oai_pubmedcentral.nih.gov_3247861 |
| [5] |
Wang T, Li WS. A fast low-cost shortest path tree algorithm. Ruan Jian Xue Bao/Journal of Software, 2004, 15(5): 660-665(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/rjxb200405004 |
| [6] |
Tang JT, Wang T, Wang J. Shortest path approximate algorithm for complex network analysis. Ruan Jian Xue Bao/Journal of Software, 2011, 22(10): 2279-2290(in Chinese with English abstract).
http://www.jos.org.cn/1000-9825/3924.htm [doi:10.3724/SP.J.1001.2011.03924] |
| [7] |
Maier M, Rattigan M, Jensen D. Indexing network structure with shortest-path trees. ACM Trans. on Knowledge Discovery from Data (TKDD), 2011, 5(3): 15.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ff45d4cf0854abfeecee2b62da707a5e |
| [8] |
Zhang X, Chan FTS, Yang H, et al. An adaptive amoeba algorithm for shortest path tree computation in dynamic graphs. Information Sciences, 2017, 405: 123-140.
[doi:10.1016/j.ins.2017.04.021] |
| [9] |
Zhu CJ, Lam KY, Cheng RCK, et al. On using broadcast index for efficient execution of shortest path continuous queries. Information Systems, 2015, 49: 142-162.
[doi:10.1016/j.is.2014.12.005] |
| [10] |
Wang S, Xiao X, Yang Y, et al. Effective indexing for approximate constrained shortest path queries on large road networks. Proc. of the VLDB Endowment, 2016, 10(2): 61-72.
[doi:10.14778/3015274] |
| [11] |
Liu H, Jin C, Yang B, et al. Finding top-k shortest paths with diversity. IEEE Trans. on Knowledge and Data Engineering, 2018, 30(3): 488-502.
[doi:10.1109/TKDE.2017.2773492] |
| [12] |
Geisberger R, Sanders P, Schultes D, et al. Contraction hierarchies:Faster and simpler hierarchical routing in road networks. In:Proc. of the Int'l Workshop on Experimental and Efficient Algorithms. Berlin, Heidelberg:Springer-Verlag, 2008. 319-333.
|
| [13] |
Li J, Yang YD, Mamoulis N. Optimal route queries with arbitrary order constraints. IEEE Trans. on Knowledge & Data Engineering, 2013, 25(5): 1097-1110.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=aa8a6f35fb702a34d51954611a9703a0 |
| [14] |
Chen H, Ku WS, Sun MT, et al. The multi-rule partial sequenced route query. In: Proc. of the 16th ACM SIGSPATIAL Int'l Conf. on Advances in Geographic Information Systems. ACM Press, 2008. 10.
|
| [15] |
Mozes S, Nussbaum Y, Weimann O. Faster shortest paths in dense distance graphs, with applications. Theoretical Computer Science, 2018, 711: 11-35.
[doi:10.1016/j.tcs.2017.10.034] |
| [16] |
Ahmed F, Anzum F, Islam MN, et al. A new algorithm to compute single source shortest path in a real edge weighted graph to optimize time complexity. In: Proc. of the 2018 IEEE/ACIS 17th Int'l Conf. on Computer and Information Science (ICIS). IEEE, 2018. 185-191.
|
| [17] |
Qiu K, Zhu Y, Yuan J, et al. ParaPLL: Fast parallel shortest-path distance query on large-scale weighted graphs. In: Proc. of the 47th Int'l Conf. on Parallel Processing. ACM Press, 2018. 2.
|
| [18] |
Bonsma P. Rerouting shortest paths in planar graphs. Discrete Applied Mathematics, 2017, 231: 95-112.
[doi:10.1016/j.dam.2016.05.024] |
| [19] |
Ren C, Lo E, Kao B, et al. Efficient processing of shortest path queries in evolving graph sequences. Information Systems, 2017, 70: 18-31.
[doi:10.1016/j.is.2017.05.004] |
| [20] |
Hong J, Park K, Han Y, et al. Disk-based shortest path discovery using distance index over large dynamic graphs. Information Sciences, 2017, 382: 201-215.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=28c1fa4ee44de61ea0d233a5dc497cb7 |
| [21] |
Jamil HM. Efficient top-k shortest path query processing in sparse graph databases. In: Proc. of the 7th Int'l Conf. on Web Intelligence, Mining and Semantics. ACM Press, 2017.
|
| [22] |
Mihalák M, Šrámek R, Widmayer P. Approximately counting approximately-shortest paths in directed acyclic graphs. Theory of Computing Systems, 2016, 58(1): 45-59.
http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1304.6707 |
| [23] |
Sharifzadeh M, Kolahdouzan M, Shahabi C. The optimal sequenced route query. VLDB Journal, 2008, 17(4): 765-787.
[doi:10.1007/s00778-006-0038-6] |
| [24] |
Rice MN, Tsotras VJ. Engineering generalized shortest path queries. In: Proc. of the IEEE Int'l Conf. on Data Engineering. IEEE Computer Society, 2013. 949-960.
|
| [25] |
Li F, Cheng D, Hadjieleftheriou M, et al. On trip planning queries in spatial databases. In: Proc. of the Int'l Symp. on Spatial and Temporal Databases. Berlin, Heidelberg: Springer-Verlag, 2005. 273-290.
|
| [26] |
Rice MN, Tsotras VJ. Exact graph search algorithms for generalized traveling salesman path problems. In:Proc. of the Int'l Symp. on Experimental Algorithms. Berlin, Heidelberg:Springer-Verlag, 2012. 344-355.
|
| [27] |
Ascheuer N, Jünger M, Reinelt G. A branch & cut algorithm for the asymmetric traveling salesman problem with precedence constraints. Computational Optimization & Applications, 2000, 17(1): 61-84.
http://cdmd.cnki.com.cn/Article/CDMD-10766-1015962063.htm |
| [28] |
Moon C, Kim J, Choi G, et al. An efficient genetic algorithm for the traveling salesman problem with precedence constraints. European Journal of Operational Research, 2002, 140(3): 606-617.
[doi:10.1016/S0377-2217(01)00227-2] |
| [29] |
Wang X, Regan AC. The traveling salesman problem with separation requirements. European Journal of Operational Research, 2002, 140(5).
http://dl.acm.org/citation.cfm?id=586933 |
| [30] |
Karan M, Skorin-Kapov N. A branch and bound algorithm for the sequential ordering problem. In:Proc. of the 34th Int'l Convention. IEEE, 2011. 452-457.
|
| [5] |
王涛, 李伟生. 低代价最短路径树的快速算法. 软件学报, 2004, 15(5): 660-665.
http://d.old.wanfangdata.com.cn/Periodical/rjxb200405004 |
| [6] |
唐晋韬, 王挺, 王戟. 适合复杂网络分析的最短路径近似算法. 软件学报, 2011, 22(10): 2279-2290.
http://www.jos.org.cn/1000-9825/3924.htm [doi:10.3724/SP.J.1001.2011.03924] |
 2019, Vol. 30
2019, Vol. 30


