软件学报  2019, Vol. 30 Issue (12): 3579-3589   PDF    
引用本文
张国帅, 许道云. 量子隐形传态的通用线路[J]. 软件学报, 2019, 30(12): 3579-3589. http://www.jos.org.cn/1000-9825/5672.htm   
Zhang GS, Xu DY. Universal Circuits for Quantum Teleportation[J]. Journal of Software, 2019, 30(12): 3579-3589(in Chinese). http://www.jos.org.cn/1000-9825/5672.htm  
量子隐形传态的通用线路
张国帅1 , 许道云2     
1. 贵州大学 数学与统计学院, 贵州 贵阳 550025;
2. 贵州大学 计算机科学与技术学院, 贵州 贵阳 550025
收稿时间: 2018-06-19; 修改时间: 2018-09-21; 采用时间: 2018-10-08; jos在线出版时间: 2019-01-21
基金项目: 国家自然科学基金（61762019，61462001）
作者简介: 张国帅(1993—), 男, 山东潍坊人, 硕士, 主要研究领域为量子计算, 计算复杂性;
许道云(1959—), 男, 博士, 教授, 博士生导师, CCF高级会员, 主要研究领域为可计算分析与计算复杂性, 算法设计与分析.
通讯作者: 许道云, E-mail:dyxu@gzu.edu.cn.
摘要: EPR态作为最基本的量子纠缠态，在量子隐形传态中起着重要作用.研究适应任意类型EPR通道的单量子比特隐形传送通用线路，并推广到任意N比特量子隐形传送通用线路.首先设计出4种EPR态，分别作为量子通道的单比特量子隐形传态，通过分析EPR量子通道与量子操作门之间的关系，设计一种单比特通用线路；然后，设计两比特的标准量子隐形传态线路，并用Mathematica进行仿真验证线路的正确性，再把它推广到N比特量子隐形传送线路；最后，将单量子比特通用线路与N比特量子隐形传送线路进行融合，最终设计出任意N比特量子隐形传送通用线路.N粒子量子比特通用线路通过信息接受者进行带参数的幺正变换，其中，参数由制备出的EPR对类型确定，解决了因EPR制备中心出错导致的信息传送失败问题.
关键词: 量子隐形传态    通用线路    EPR态    纠缠态    量子通道    
Universal Circuits for Quantum Teleportation
ZHANG Guo-Shuai1 , XU Dao-Yun2     
1. College of Mathematics and Statistics, Guizhou University, Guiyang 550025, China;
2. College of Computer Science and Technology, Guizhou University, Guiyang 550025, China
Foundation item: National Natural Science Foundation of China (61762019, 61462001)
Abstract: EPR state as the most basic quantum entangled state plays an important role in quantum teleportation. In this work, the universal single-qubit quantum teleportation adapted to any type of EPR channel is studied and generalized to universal N-qubit quantum teleportation. In the single-bit quantum teleportation mode with four kinds of EPR states as quantum channels respectively, design single-bit universal circuits by analyzing the relationship between the EPR and the quantum gate, then design a two-bit standard quantum teleportation circuit and use Mathematica to verify the correctness of the circuit, and then generalize it to an N-bit quantum teleportation circuit, the next step, the single-qubit universal circuit and the N-qubit quantum teleportation circuit are implemented for fusion, finally any N-bit quantum teleportation universal circuit is designed. The universal circuits for N-particle quantum bits perform unitary transformation with parameters by the recipient of the information, where the parameters are determined by the type of EPR prepared, which solves the problem of information transmission failure due to an error in the EPR preparation center.
Key words: quantum teleportation    universal circuit    EPR state    entangled state    quantum channel    

量子隐形传态是一种传递量子状态的重要通信方式, 是可扩展量子网络和分布式量子计算的基础.从事量子隐形传态实验, 是实现全球量子通信网络的可行性的前提研究.1993年, Bennet首次提出了量子隐形传态的设想[1], 原理是利用量子态纠缠EPR粒子对的远程关联[2], 引起了研究者对量子隐形传态的研究热潮[3-5], 提出了各种形式的量子隐形传送方案[6-8].其中, 方建兴等人[9-13]提出了多种通过N对二粒子纠缠态传送N粒子的方案, 臧鹏等人[14]提出了五粒子团簇态实现四粒子团簇态的概率隐形传态方案, Song[15]给出了利用两个EPR态进行隐形传送双模连续变量量子态的方案, 解光军等人[16]也对量子线路进行了改进, 还有一些其他类型的传送方案[17-21].

在上述文献的所有传送方案中, 信息传送成功的前提是制备出准确的共享量子通道.例如用EPR态作为量子通道实现单比特量子隐形传送, 如果此时EPR制备中心出错, 制备出或者选择其他类型的量子通道, 就只能重新制备EPR态或者重新选择适应此种类型量子通道的传送方案.随着传送信息量的增加, EPR态相应制备的数量也会增加, 制备出不符合预期的量子通道的概率也就相应地增加.

本文从数学分析的角度, 理论上提出一种通用量子线路.通过概述4种EPR态分别作为量子通道的量子隐形传态, 分析这4个线路中EPR态的类型与量子操作门之间的联系, 设计出一种适应任意类型EPR通道的量子线路.这种线路中的量子操作门是带参数的幺正变换, 其中, 参数由EPR态的类型确定.最后把单比特通用线路推广到任意N比特通用线路.本文设计的通用线路适应EPR制备中心制备出的各种类型的EPR态, 信息接受者只需进行带参数的幺正变换, 并根据制备出的EPR态类型输入相应的参数值, 即可实现隐形传送.

1 单粒子量子态的通用隐形传送方案

EPR对的4个Bell态分别为

$|{\beta _{00}}\rangle = \frac{{|00\rangle + |11\rangle }}{{\sqrt 2 }}, {\rm{ }}|{\beta _{01}}\rangle = \frac{{|01\rangle + |10\rangle }}{{\sqrt 2 }}, {\rm{ }}|{\beta _{10}}\rangle = \frac{{|00\rangle - |11\rangle }}{{\sqrt 2 }}, {\rm{ }}|{\beta _{11}}\rangle = \frac{{|01\rangle - |10\rangle }}{{\sqrt 2 }}.$

通过4种Bell态分别作为量子通道, 设计出它们的量子隐形传送线路, 并分析量子通道与量子操作们之间的关系.首先选取|β00〉作为共享量子通道, 假设Alice要传送的未知量子态为|ψ〉=α|0〉+β|1〉.线路在信息传输之前的量子态为

$|{\psi _0}\rangle = |\psi \rangle |{\beta _{00}}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|00\rangle + |11\rangle ) + \beta |1\rangle (|00\rangle + |11\rangle )], $

其中, 前两个量子比特属于Alice, 第3个量子比特属于Bob.

为了实现信息的量子隐形传送, Alice需要将他所拥有的量子比特通过一个受控非门, 其量子态变为

$|{\psi _1}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|00\rangle + |11\rangle ) + \beta |1\rangle (|10\rangle + |01\rangle )].$

然后, Alice再让他的第1个量子比特通过一个Hadamard门, 此时的量子态为

$|{\psi _2}\rangle = \frac{1}{2}[\alpha (|0\rangle + |1\rangle )(|00\rangle + |11\rangle ) + \beta (|0\rangle - |1\rangle )(|10\rangle + |01\rangle )].$

我们把这个量子态进行重新组项, 可重写为如下量子态:

$|{\psi _2}\rangle = \frac{1}{2}[|00\rangle (\alpha |0\rangle + \beta |1\rangle ) + |01\rangle (\alpha |1\rangle + \beta |0\rangle ) + |10\rangle (\alpha |0\rangle - \beta |1\rangle ) + |11\rangle (\alpha |1\rangle - \beta |0\rangle )].$

该表达式共含有4项, 每一项的前两个量子比特属于Alice, 第3个量子比特属于Bob.此时, 如果Alice对前两个量子比特进行投影测量, Bob拥有的量子比特将会塌缩到相应的量子态上.依赖于Alice的测量结果, Bob将会得到4种不同的量子态, Bob再经过一个幺正变换即可恢复出要传送的的量子态α|0〉+β|1〉.具体操作见表 1.

Table 1 Results of quantum measurement and corresponding unitary transformation 表 1 量子测量的结果和相应的幺正变换

其中, $I = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right), X = \left( {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right), Z = \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right)$.其实现线路如图 1所示.

Fig. 1 Quantum teleportation for |β00〉 图 1 关于|β00〉的量子隐形传态

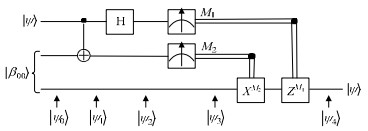
线路图中的M1, M2即为Alice测得的经典信息, Bob只需进行幺正变换${Z^{{M_1}}}{Z^{{M_2}}}$既可恢复出量子态|ψ〉.

考虑|β01〉作为量子通道, 按照第1个方案的操作步骤, 各个阶段的量子态分别如下.

$ \begin{array} [c]{l} |{\psi _0}\rangle = |\psi \rangle |{\beta _{01}}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|01\rangle + |10\rangle ) + \beta |1\rangle (|01\rangle + |10\rangle )], \\ |{\psi _1}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|01\rangle + |10\rangle ) + \beta |1\rangle (|11\rangle + |00\rangle )], \\ |{\psi _2}\rangle = \frac{1}{{\sqrt 2 }}[|00\rangle (\alpha |1\rangle + \beta |0\rangle ) + |01\rangle (\alpha |0\rangle + \beta |1\rangle ) + |10\rangle (\alpha |1\rangle - \beta |0\rangle ) + |11\rangle (\alpha |0\rangle - \beta |1\rangle )]. \end{array} $

Bob根据Alice的测量结果做相应的幺正变换, 具体操作见表 2.

Table 2 Results of quantum measurement and corresponding unitary transformation 表 2 量子测量的结果及相应的幺正变换

其实现线路如图 2所示.

Fig. 2 Quantum teleportation for |β01〉 图 2 关于|β01〉的量子隐形传态

考虑|β10〉作为量子通道, 按照第1个方案的操作步骤, 各个阶段的量子态分别如下.

$ \begin{array} [c]{l} |{\psi _0}\rangle = |\psi \rangle |{\beta _{10}}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|00\rangle - |11\rangle ) + \beta |1\rangle (|00\rangle - |11\rangle )], \\ |{\psi _1}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|00\rangle - |11\rangle ) + \beta |1\rangle (|10\rangle - |01\rangle )], \\ |{\psi _2}\rangle = \frac{1}{{\sqrt 2 }}[|00\rangle (\alpha |0\rangle - \beta |1\rangle ) + |01\rangle ( - \alpha |1\rangle + \beta |0\rangle ) + |10\rangle (\alpha |0\rangle + \beta |1\rangle ) + |11\rangle ( - \alpha |1\rangle - \beta |0\rangle )]. \end{array} $

Bob根据Alice的测量结果做相应的幺正变换, 具体操作见表 3.

Table 3 Results of quantum measurement and corresponding unitary transformation 表 3 量子测量的结果及相应的幺正变换

其中, ${\sigma _{I'}} = \left( {\begin{array}{*{20}{c}} { - 1}&0 \\ 0&{ - 1} \end{array}} \right)$, 其实现线路如图 3所示.

Fig. 3 Quantum teleportation for |β10〉 图 3 关于|β10〉的量子隐形传态

考虑|β11〉作为量子通道, 按照第1个方案的操作步骤, 各个阶段的量子态分别如下.

$\begin{array} [c]{l} |{\psi _0}\rangle = |\psi \rangle |{\beta _{11}}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|01\rangle - |10\rangle ) + \beta |1\rangle (|01\rangle - |10\rangle )], \\ |{\psi _1}\rangle = \frac{1}{{\sqrt 2 }}[\alpha |0\rangle (|01\rangle - |10\rangle ) + \beta |1\rangle (|11\rangle - |00\rangle )], \\ |{\psi _2}\rangle = \frac{1}{{\sqrt 2 }}[|00\rangle (\alpha |1\rangle - \beta |0\rangle ) + |01\rangle ( - \alpha |0\rangle + \beta |1\rangle ) + |10\rangle (\alpha |1\rangle + \beta |0\rangle ) + |11\rangle ( - \alpha |0\rangle - \beta |1\rangle )]. \\ \end{array} $

Bob根据Alice的测量结果做相应的幺正变换, 具体操作见表 4.

Table 4 Results of quantum measurement and corresponding unitary transformation 表 4 量子测量的结果及相应的幺正变换

其实现线路如图 4所示.

Fig. 4 Quantum teleportation for |β11〉 图 4 关于|β11〉的量子隐形传态

通过上述演算和图示, 我们发现了4种不同的EPR态对应线路中量子通道的类型参数与接收者进行的幺正变换之间的对应关系, 并设计出如图 5所示的通用线路.

Fig. 5 Universal circuit for single-qubit quantum teleportation 图 5 单比特量子隐形传态通用线路

从图 5中线路可以看出, 当给定线路中m和n赋值之后, 通用线路就变为4种EPR态作为量子信道的量子隐形传态的其中一种.此线路中, 接收者进行的操作${Z^{{M_1} \oplus m}}{X^{{M_2} \oplus n}}{\sigma _{I'}}^{m{M_2}}$是具有4个参数的矩阵, 参数值由制备出的EPR类型和测量结果决定.观察此线路还可以发现, 无论制备中心制备出哪种类型的EPR态, 只要根据制备出来的EPR类型输入m, n的值, 最后再根据测量结果输入M1, M2的值, 即可完成信息的传送.

2 任意两粒子量子态的隐形传送方案

首先考虑任意两比特量子隐形传态.因为每次传送一比特信息都需要一个EPR态, 并且在测量阶段EPR态会发生塌缩无法再继续使用, 所以需要传送多少比特的信息, 相应地就需要制备多少个EPR态.

假设待传送的未知量子态为

$ \begin{array} [c]{c} |ψ〉=a|00〉_{1, 2}+b|01〉_{1, 2}+c|10〉_{1, 2}+d|11〉_{1, 2}(a^{2}+b^{2}+c^{2}+d^{2}=1). \end{array} $

Alice和Bob共享的量子通道为

$ \begin{array} [c]{c} |{\beta _{00}}{\rangle _{1x, 1y}} = \frac{1}{{\sqrt 2 }}{(|00\rangle _{1x, 1y}} + |11{\rangle _{1x, 1y}}), {\rm{ }}|{\beta _{00}}{\rangle _{2x, 2y}} = \frac{1}{{\sqrt 2 }}{(|00\rangle _{2x, 2y}} + |11{\rangle _{2x, 2y}}), \end{array} $

其中, 粒子1, 2, 1x, 2x归Alice所有, 粒子1y, 2y归Bob所有.此时, 线路的初始状态为

$ \begin{array} [c]{c} |ψ_{0}〉=|ψ〉|β_{00}〉_{1x, 1y}|β_{00}〉_{2x, 2y}. \end{array} $

如果把初始态展开进行重新组项, 我们发现可以将初始态重新表示为

$\begin{array} [c]{c} |{\psi _0}\rangle = |\psi \rangle |{\beta _{00}}{\rangle _{1x, 1y}}|{\beta _{00}}{\rangle _{2x, 2y}} = \frac{1}{4}\sum\limits_{{m_i}, {n_i} \in \{ 0, 1\} } {|{\beta _{{m_1}{n_1}}}{\rangle _{1, 1x}}|{\beta _{{m_2}{n_2}}}{\rangle _{2, 2x}}} {Z^{{m_1}}} \cdot {X^{{n_1}}} \otimes {Z^{{m_2}}} \cdot {X^{{n_2}}}\left( {\begin{array}{*{20}{c}} a \\ b \\ c \\ d \end{array}} \right), \end{array} $

其中, 向量(a, b, c, d)'表示量子态a|00〉1y, 2y+b|01〉1y, 2y+c|10〉1y, 2y+d|11〉1y, 2y.

为了实现信息的量子隐形传态, Alice需要把粒子1, 2, 1x, 2x经过受控非门和Hadamard门, 此时, 系统的量子态变为

$\begin{array} [c]{c} |{\psi _2}\rangle = \frac{1}{4}\sum\limits_{{m_i}, {n_i} \in \{ 0, 1\} } {|{m_1}{n_1}{\rangle _{1, 1x}}|{m_2}{n_2}{\rangle _{2, 2x}}} {Z^{{m_1}}} \cdot {X^{{n_1}}} \otimes {Z^{{m_2}}} \cdot {X^{{n_2}}}\left( {\begin{array}{*{20}{c}} a \\ b \\ c \\ d \end{array}} \right). \end{array} $

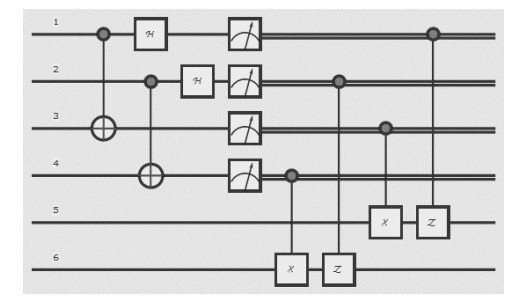
如果Alice的测量结果分别是|10〉1, 1x和|01〉2, 2x, 则粒子1y和2y将会塌缩到量子态b|00〉1y, 2y+a|01〉1y, 2y- d|10〉1y, 2y-c|11〉1y, 2y上, Alice把测量结果告诉Bob, Bob根据Alice的测量结果将粒子1y通过Z门、粒子2y通过X门, 此时, 量子态为:a|00〉1y, 2y+b|01〉1y, 2y+c|10〉1y, 2y+d|11〉1y, 2y.对其他测量结果进行类似操作, 最终会恢复出待传量子信息.通过Mathematica仿真实验得到的线路图如图 6所示.

Fig. 6 Two-qubit quantum teleportation 图 6 两比特量子隐形传态

图 6中的1、2表示待传送量子比特, 3、5分别表示1x比特、1y比特, 4、6分别表示2x比特、2y比特.对这个线路输入任意未知量子态:

$a|{0_{\hat 1}}\rangle \otimes |{0_{\hat 2}}\rangle + b|{0_{\hat 1}}\rangle \otimes |{1_{\hat 2}}\rangle + c|{1_{\hat 1}}\rangle \otimes |{0_{\hat 2}}\rangle + d|{1_{\hat 1}}\rangle \otimes |{1_{\hat 2}}\rangle .$

经过这个线路如果能够恢复出这个量子态, 则证明这个实现线路是正确的, 通过Mathematica进行仿真, 结果见表 5.

Table 5 Results of quantum measurement and corresponding transmission probability 表 5 量子测量的结果及相应的操作概率

通过表 5我们可以发现, Alice共有16种测量结果, 而每一种结果最终都恢复出量子态:

$a|{0_{\hat 5}}\rangle \otimes |{0_{\hat 6}}\rangle + b|{0_{\hat 5}}\rangle \otimes |{1_{\hat 6}}\rangle + c|{1_{\hat 5}}\rangle \otimes |{0_{\hat 6}}\rangle + d|{1_{\hat 5}}\rangle \otimes |{1_{\hat 6}}\rangle .$

其中, $\sqrt {a{a^*} + b{b^*} + c{c^*} + d{d^*}} $为归一化因子, 其值等于1.此表明图 6的量子线路是正确的.

3 任意N粒子量子态的通用量子隐形传送方案

现在, 我们把任意两粒子量子态的隐形传态推广到传送任意N粒子量子态的情形.假设待传送的量子态为

$|\psi \rangle = {a_1}|00...0{\rangle _{1, ..., n}} + {a_2}|00...1{\rangle _{1, ..., n}} + ... + {a_{{2^n}}}|11...1{\rangle _{1, ..., n}}.$

Alice和Bob共享的量子通道为n对EPR纠缠态:

$|{\beta _{00}}{\rangle _{ix, iy}} = \frac{1}{{\sqrt 2 }}{(|00\rangle _{ix, iy}} + |11{\rangle _{ix, iy}}), i \in [1, n].$

此时, 输入线路的初始态为

$ |ψ_{0}〉=|ψ〉|β_{00}〉_{1x, 1y}|β_{00}〉_{2x, 2y}…|β_{00}〉_{nx,ny}. $

我们将初始态展开进行重新组项, 发现初始态可以重新表示为

$|{\psi _0}\rangle = |\psi \rangle |{\beta _{00}}{\rangle _{1x, 1y}}|{\beta _{00}}{\rangle _{2x, 2y}}...|{\beta _{00}}{\rangle _{nx, ny}} = \frac{1}{{{2^n}}}\sum\limits_{{m_i}, {n_i} \in \{ 0, 1\} } { \otimes _{i = 1}^n|{\beta _{{m_i}{n_i}}}{\rangle _{i, ix}}( \otimes _{k = 1}^n{Z^{{m_k}}} \cdot {X^{{n_k}}})\left( {\begin{array}{*{20}{c}} {{a_1}} \\ \vdots \\ {{a_{{2^n}}}} \end{array}} \right)} .$

为了实现信息的量子隐形传送, Alice需要将自己拥有的粒子分别通过n个受控非门和n个Hadamard门, 然后进行投影测量.此时, 系统的量子态变为

$|{\psi _2}\rangle = \frac{1}{{{2^n}}}\sum\limits_{{m_i}, {n_i} \in \{ 0, 1\} } { \otimes _{i = 1}^n|{m_i}{n_i}{\rangle _{i, ix}}( \otimes _{k = 1}^n{Z^{{m_k}}} \cdot {X^{{n_k}}})\left( {\begin{array}{*{20}{c}} {{a_1}} \\ \vdots \\ {{a_{{2^n}}}} \end{array}} \right)} .$

向量$({a_1}, ..., {a_{{2^n}}})'$表示${a_1}|00...0{\rangle _{1y...ny}} + {a_2}|00...1{\rangle _{1y...ny}} + ... + {a_{{2^n}}}|11...1{\rangle _{1y...ny}}.$

如果Alice的测量结果为|11〉1, 1x…|11〉n, nx, 那么粒子1y…ny就会塌缩到量子态(-1)na1|11…1〉1y…ny+${( - 1)^{n - 1}}{a_2}|11...0{\rangle _{1y...ny}} + ... + {a_{{2^n}}}|00...0{\rangle _{1y...ny}}$上, Alice把测量结果告诉Bob, Bob根据Alice的测量结果将粒子1y, …,ny分别都通过X门和Z门.对其他测量结果进行类似操作, 最终会恢复出待传量子态.其实现线路如图 7所示.

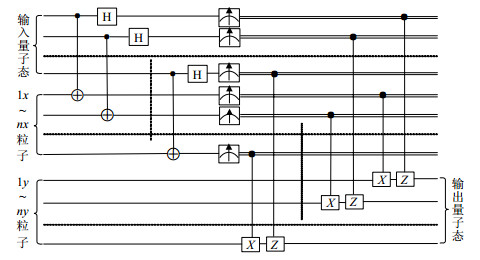
Fig. 7 N-qubit quantum teleportation 图 7 N比特量子隐形传态

如果把这个任意N比特量子隐形传态线路与单比特量子通用线路进行结合, 以随机的EPR态作为量子通道, 我们就可以设计出传送任意N粒子量子比特的通用线路.其实现线路如图 8所示.

Fig. 8 Universal circuit for N-qubit quantum teleportation 图 8 N比特量子隐形传态的通用线路

线路中的量子通道为$|{\beta _{{a_1}{b_1}}}{\rangle _{1x, 1y}}, |{\beta _{{a_2}{b_2}}}{\rangle _{2x, 2y}}, ..., |{\beta _{{a_n}{b_n}}}{\rangle _{nx, ny}}$(其中, ai, bi∈{0, 1}).这种N量子比特的通用线路可以适应各种类型的EPR通道, 不会因为没有制备出预期的EPR类型而导致信息传输失败.

下面通过一个简单的例子进行解释.假设待传送的量子态为

$ |ψ〉=a|00〉_{1, 2}+b|01〉_{1, 2}+c|10〉_{1, 2}+d|11〉_{1, 2}(a^{2}+b^{2}+c^{2}+d^{2}=1). $

首先, 我们先把两比特量子隐形传态的通用线路设计完成(如图 9所示).

Fig. 9 Universal circuit for two-qubit quantum teleportation 图 9 两比特量子隐形传态的通用线路

此线路中有4个参数m1, n1, m2, n2, 此时, 如果我们预期制备两个纠缠态|β00〉作为量子通道, 此时EPR制备中心出错, 假设制备结果为|β10〉1x, 1y和|β10〉2x, 2y, 那么我们只需要根据制备出的结果输入相应的参数即可.这里的m1=0, n1=1, m2=1, n2=0.当我们输入对应的参数值之后, 此时的通用线路也就等价于下面一般情况下的量子隐形传态了(如图 10所示).

Fig. 10 Two-qubit quantum teleportation 图 10 两比特量子隐形传态

此时, Bob只需对手中的量子态进行相应的酉变换, 即可得到最终待传的量子态.

4 结论

本文从数学的角度分析了单比特量子隐形传态EPR信道与接收者量子操作门之间的联系, 理论上提出一种通用线路, 并把它推广到任意N量子比特隐形传送通用线路.此通用线路的优点在于, 它可以避免因EPR制备中心制备出错误的EPR态造成的信息传输失败问题.在N量子比特通用线路中, 接收者对每个比特信息都进行相同的矩阵操作${Z^{{M_1} \oplus m}}{X^{{M_2} \oplus n}}{\sigma _{I'}}^{m{M_2}}, $如果把这个矩阵看作通用门, 那么无论EPR制备中心制备出何种EPR类型,接收者只需根据制备出的EPR类型和测量结果输入相应参数值m, n, M1, M2, 即可完成信息传送.

本文提出的通用线路的意义在于抵制EPR信道制备出错, 可以在EPR制备中心出错的情况下顺利完成信息传输.下一步工作是对其他更多的线路进行改进, 提高线路的纠错及抗干扰能力.

参考文献
[1]
Bennett CH, Brassard G, Crépeau C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Physical Review Letters, 1993, 70(13): 1895-1899. [doi:10.1103/PhysRevLett.70.1895]
[2]
Nielson MA, Chuang IL. Quantum Computation and Quantum Information. Cambridge University Press, 2000: 558-559.
[3]
Jiang WX, Fang JX, Sha JQ. Quantum teleportation and its quantum circuit implementation. Popular Science & Technology, 2006(5): 30-32(in Chinese with English abstract). [doi:10.3969/j.issn.1008-1151.2006.05.019]
[4]
Su XQ, Guo GC. Quantum teleportation. Progress in Physics, 2004, 24(3): 259-273(in Chinese with English abstract). [doi:10.3321/j.issn:1000-0542.2004.03.001]
[5]
Cao ZL, Dong P, Xue ZY. Progress on quantum teleportation. Journal of Anhui University, 2006, 30(3): 48-53(in Chinese with English abstract). [doi:10.3969/j.issn.1000-2162.2006.03.013]
[6]
Zhou XQ, Wu YW. Discussion on building the net of quantum teleportation using three-particle entangled states. Acta Physica Sinica, 2007, 56(4): 1881-1887(in Chinese with English abstract). [doi:10.3321/j.issn:1000-3290.2007.04.008]
[7]
Yang T, Pan JW. Experimentak demonstration of five-photon entangkement and open-destination tekeportation. Bulletin of Chinese Academy of Sciences, 2004, 19(5): 355-358(in Chinese with English abstract). [doi:10.3969/j.issn.1000-3045.2004.05.010]
[8]
Peng JY, Mo ZW. Several teleportation schemes of an arbitrary unknown multi-particle state via different quantum channels. Chinese Physics B, 2013, 22(5): 160-167. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zgwl-e201305022
[9]
Guo ZY, Zhang XH, Fang JX, et al. Probabilistic propagation of arbitrary n-particle entangled states and its quantum logic circuits. Acta Optica Sinica, 2008, 28(2): 387-391(in Chinese with English abstract). [doi:10.3321/j.issn:0253-2239.2008.02.033]
[10]
Xi YJ, Fang JX, Zhu SQ, et al. Teleportation of N-particle quantum entanglement. Acta Sinica Quantum Optica, 2005, 11(1): 25-28(in Chinese with English abstract). [doi:10.3969/j.issn.1007-6654.2005.01.006]
[11]
Sha JQ, Fang JX, Jiang WX, et al. Teleportation of N-particle in Entangled W State. Acta Sinica Quantum Optica, 2007, 13(2): 114-117(in Chinese with English abstract). [doi:10.3969/j.issn.1007-6654.2007.02.007]
[12]
Qian XM, Fang JX, Zhu SQ, et al. Quantum logic networks for probabilistic teleportation of an arbitrary three-particle state. Communications in Theoretical Physics, 2005, 44(10): 611-614. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4fe1533467adf965436109646336d3ad
[13]
Tan X, Zhang X, Fang JX. Perfect Quantum Teleportation by Four-Particle Cluster State. Elsevier North-Holland, Inc., 2016. https://www.researchgate.net/publication/291185675_Perfect_quantum_teleportation_by_four-particle_cluster_state?ev=prf_high
[14]
Zang P, Song RY, Jiang Y, et al. Probabilistic teleportation of four particle cluster state via five particle cluster state. Chinese Journal of Quantum Electronics, 2017, 34(4): 456-461(in Chinese with English abstract). http://d.old.wanfangdata.com.cn/Periodical/lzdzxb201704013
[15]
Song TQ. Teleportation of two-mode quantum state of continuous variables. Theoretical Physics, 2004, 41(3): 362. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_0710.2777
[16]
Zhang XM, Xie GJ, Xiao H. A new quantum teleportation circuit. Chinese Journal of Quantum Electronics, 2007, 24(1): 54-58(in Chinese with English abstract). [doi:10.3969/j.issn.1007-5461.2007.01.011]
[17]
Cao ZL, Song W. Teleportation of a two-particle entangled state via W class states. Physica A Statistical Mechanics & Its Applications, 2005, 347: 177-183. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_quant-ph%2f0401054
[18]
Lu H, Guo GC. Teleportation of a two-particle entangled state via entanglement swapping. Physics Letters A, 2000, 276(5-6): 209-212. [doi:10.1016/S0375-9601(00)00666-6]
[19]
Zheng YZ, Gu YJ. Teleportation of a three-particle entangled W state. Chinese Physics C, 2002, 11(6): 537-542. [doi:10.1088/1009-1963/11/6/304]
[20]
Dai HY, Li CZ, Chen PX. Probabilistic teleportation of an arbitrary three-particle state via a partialentangled four-particle state and a particle entangled pair. Chinese Physics B, 2003, 12(12): 1354-1359. [doi:10.1088/1009-1963/12/12/003]
[21]
Zha XW, Zhang W, Cha XM, et al. Perfect teleportation an arbitrary three-particle state. Acta Photonica Sinica, 2009, 38(4): 979-982. http://d.old.wanfangdata.com.cn/Periodical/gzxb200904048
[3]
姜炜星, 方建兴, 沙金巧. 量子隐形传态及其量子线路实现. 大众科技, 2006(5): 30-32. [doi:10.3969/j.issn.1008-1151.2006.05.019]
[4]
苏晓琴, 郭光灿. 量子隐形传态. 物理学进展, 2004, 24(3): 259-273. [doi:10.3321/j.issn:1000-0542.2004.03.001]
[5]
曹卓良, 董萍, 薛正远. 量子隐形传态的研究进展. 安徽大学学报(自然科学版), 2006, 30(3): 48-53. [doi:10.3969/j.issn.1000-2162.2006.03.013]
[6]
周小清, 邬云文. 利用三粒子纠缠态建立量子隐形传态网络的探讨. 物理学报, 2007, 56(4): 1881-1887. [doi:10.3321/j.issn:1000-3290.2007.04.008]
[7]
杨涛, 潘建伟. 量子信息技术的新进展——五光子纠缠和开放目的的量子隐形传态. 中国科学院院刊, 2004, 19(5): 355-358. [doi:10.3969/j.issn.1000-3045.2004.05.010]
[9]
郭战营, 张新海, 方建兴, 等. 任意n粒子纠缠态的概率传送及其量子逻辑线路. 光学学报, 2008, 28(2): 387-391. [doi:10.3321/j.issn:0253-2239.2008.02.033]
[10]
席拥军, 方建兴, 朱士群, 等. N粒子量子纠缠态的隐形传送. 量子光学学报, 2005, 11(1): 25-28. [doi:10.3969/j.issn.1007-6654.2005.01.006]
[11]
沙金巧, 方建兴, 姜炜星, 等. N粒子W纠缠态的隐形传输. 量子光学学报, 2007, 13(2): 114-117. [doi:10.3969/j.issn.1007-6654.2007.02.007]
[14]
臧鹏, 宋若愚, 蒋跃, 等. 基于五粒子团簇态实现四粒子团簇态的概率隐形传态. 量子电子学报, 2017, 34(4): 456-461. http://d.old.wanfangdata.com.cn/Periodical/lzdzxb201704013
[16]
张晓明, 解光军, 肖晗. 一个改进的量子隐形传态回路. 量子电子学报, 2007, 24(1): 54-58. [doi:10.3969/j.issn.1007-5461.2007.01.011]