近年来, 随着基于位置的服务在移动智能设备上的广泛应用, 保密探测问题已经成为移动、社交网络中保护隐私的一个研究热点.保密近感探测, 是保密探测问题的一个重要分支.保密近感探测问题研究的是移动网络中任意两个用户如何协同计算出他们的实时位置是否彼此临近而不泄漏各方的具体位置.时至今日, 保密近感探测问题已取得了一些可喜的成果^[1-21], 但这些成果中除了Mu等人^[1]取得的以外, 其他协议^[2-21]都是采用格栅分解技术(如果参与方在相同的格栅内, 即同在一个预先设定大小的圆形区域内, 则认为参与各方毗邻)实现保密近感探测的.然而, 这种方法不满足移动或社交网络用户的个性化需求, 如:Alice正在颐和园度周末, 她想知道她的业余划船搭档Bob是否也在颐和园内, 是否可以和Bob一起参加公园里正在举办的双人划船比赛.采用格栅分解技术的近感探测只能探测到Bob是否处在以Alice为中心、预先设定半径值的圆域内.2016年, Mu等人^[1]综合运用安全多方计算、Paillier^[22]和ElGamal^[23]同态加密方案设计了一个保密探测区域为任意凸多边形的协议.该协议满足了用户个性化的需求(用户不再预先设定保密探测区域阈值的大小, 保密探测区域可以是任意的多边形), 非常方便用户表示保密探测区域.

但文献[1]的协议仍然存在以下两个方面的不足.

(1)   文献[1]的协议除了用Paillier加密系统保密计算符号外, 还需要调用K(凸多边形的顶点数)次高计算复杂度的、由ElGamal加密方案实现的保密比较大小运算.

(2)   文献[1]的协议并未彻底解决保密近感探测问题, 只适用于解决用户参与计算区域的临近两点坐标分量差大于0的情形, 当用户参与计算区域的临近两点坐标分量差值小于0时, 该协议会输出错误的结果.原因是文献[1]的协议用Paillier加密方案直接加密负数, 并在加密负数的结果上实施同态运算.

事实上, Paillier加密方案不能直接用于加密负数, 加密负数以及在加密的负数上进行同态操作需要做额外的比特密文同态运算.关于Paillier加密方案不能直接用于加密负数, 并在加密负数的结果上实施同态运算方面的具体阐述如下.

命题1. Paillier加密方案不能直接用于加密负数.

证明:Paillier加密方案的同态实质是${Z_n} \times Z_n^ * $与$Z_{{n^2}}^ * $的同态, 而同态$f:{Z_n} \times Z_n^ * \to Z_{{n^2}}^ * $由f(a, b)=(1+kn)^a·bⁿ(mod n²)给出^[22].从而有结论:在$Z_{{n^2}}^ * $上, $f:{Z_n} \times Z_n^ * \to Z_{{n^2}}^ * $是双射函数.也就是说, 它既是满射又是单射.下面用反证法证明命题1的正确性.

设a∈Z_n, $b \in Z_n^ * $, -a表示负数, 并假定Paillier加密方案能够直接加密一个负数, 则由其加密算法的正确性可知:由加密运算$Enc( - a) = f( - a, b) = ({(1 + kn)^{ - a}}{b^n}(\bmod {\rm{ }}{n^2}) = \frac{{{b^n}(\bmod {\rm{ }}{n^2})}}{{{{(1 + kn)}^a}(\bmod {\rm{ }}{n^2})}}{\rm{ }}\bmod {\rm{ }}{n^2}$生成的密文Enc(-a), 经过解密运算Dec(Enc(-a)), 一定能正确恢复出消息-a.

事实上, 由解密运算:

$ \begin{align} & Dec(Enc(-a))=\frac{L({{f}^{\lambda }}(a,b)\,\bmod \,{{n}^{2}})}{L({{g}^{\lambda }}\,\bmod \,{{n}^{2}})}\ \bmod \ n=\frac{\left( \frac{{{b}^{\lambda n}}(\,\bmod \,{{n}^{2}})}{{{(1+kn)}^{\lambda a}}(\,\bmod \,{{n}^{2}})}-1 \right)\,\bmod \,{{n}^{2}}}{({{(1+kn)}^{\lambda }}-1)\,\bmod \,{{n}^{2}}}\,\bmod \,n \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{\left( \frac{1}{(1+\lambda kan)\ \bmod \ {{n}^{2}}}-1 \right)\,\bmod \,{{n}^{2}}}{\lambda kn\,\bmod \,{{n}^{2}}}\ \bmod \ n=\frac{\frac{-\lambda kan\,\bmod \,{{n}^{2}}}{(1+\lambda kan)\,\bmod \,{{n}^{2}}}}{\lambda kn\,\bmod \,{{n}^{2}}}\,\bmod \,n \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\frac{-a\ \bmod \ {{n}^{2}}}{(1+\lambda kan)\ \bmod \ {{n}^{2}}}\ \bmod \ n \\ \end{align} $

得到消息-a的概率很小, 因为$\frac{{ - a{\rm{ }}\bmod {\rm{ }}{n^2}}}{{(1 + \lambda kan){\rm{ }}\bmod {\rm{ }}{n^2}}}{\rm{ }}\bmod {\rm{ }}n$要等于-a, 则需1≡(1+λkan) mod n²成立.即n|λka因为gcd(λ, n)=1, 所以n|λka则必有n|ka.而为安全起见, 系统参数k是不会取κp或者κq的, 所以只有当a≡0 mod n, 解密算法才能正确恢复出消息-a.因此, Paillier加密算法能够加密负数的假设不成立.

同理, 已知a∈Z_n在Paillier加密体制下的密文c_a=g^arⁿ mod n²a∈Z_n无法直接通过同态计算得到c_-ab=g^-ab(r')ⁿ mod n²a∈Z_n, 其中, b∈Z_n.

用Paillier通过特殊处理可以实现对一个负数的加密, 但难以实现对若干个正、负数对应密文实施若干次同态运算.目前所采用的特殊处理方法大致可以分为3类.

(1)   明文的符号由明文所处的区间隐式地确定, 用这种方法能够加密明文的范围是$\left[ { - \frac{{n + 1}}{2}, \frac{{n - 1}}{2}} \right]$.通常是将整型区间[0, n]划分成两个等长的区间$\left[ {0, \frac{{n - 1}}{2}} \right]$和$\left[ {\frac{{n + 1}}{2}, n} \right]$, 并事先规定哪个区间内的数代表负数.例如, 可以事先规定处在$\left[ {\frac{{n + 1}}{2}, n} \right]$内表示负数, 如果解密结果$m \in \left\{ {\frac{{n + 1}}{2}, \frac{{n + 3}}{2}, ..., n} \right\}$, 则解密方需要在解密的基础上执行额外计算:m'=m-n.

(2)   用加密加法逆元的方法实现对[-n, 0]内整数的加密:用-a表示负数, 则在Z_n群上可将-a视为a的逆元n-a, 进而可以通过加密运算$Enc(n - a) = ({(1 + kn)^{n - a}}r_1^n(\bmod {\rm{ }}{n^2}))$生成的密文Enc(n-a), 经过解密运算Dec(Enc(n-a)), 一定能够正确恢复出消息n-a.而后再做运算(n-a)-n, 可以得到-a.

(3)   明文的符号由加密额外的比特信息标识, 用此种方法能够解决[-n, n]内的问题.通信双方需要事先商定符号的数字标识, 通常规定“0”代表“+”, “1”代表“-”.由运算$Enc(a) = ({(1 + kn)^a}r_1^n(\bmod {\rm{ }}{n^2})), Enc({s_\mu }) = $ $({(1 + kn)^\mu }r_2^n(\bmod {\rm{ }}{n^2})), $μ∈{0, 1}计算出的密文(Enc(a), Enc(s_μ)), 通过解密运算:

$(Dec(Enc(a), Dec(Enc({s_\mu })) = \left\{ {\begin{array}{*{20}{l}} {(a, 0), {\rm{ }}a} \\ {(a, 1), {\rm{ }} - a} \end{array}} \right.$ ,

即可恢复出消息-a.

但是, 上述加密负数的方法在需要对差商对应的密文实施若干次同态运算的环境下将变得异常复杂:一方面, 多次同态运算会导致明文运算结果所处区间的变换, 这会影响多方保密计算结果的准确性; 另一方面, 在保密多方计算中, 各参与方都不想泄露自己的、哪怕是1比特的信息(在涉及坐标运算的保密计算中, 坐标符号的泄露有可能造成相对位置信息的泄露), 又有哪个无私钥的参与方愿意对外透露自己的符号信息呢?

由上述分析可得, 现有的基于位置服务的保密探测方法绝大多数只能解决保密探测区域在预先设定半径阈值的圆形内的情形, 这不能满足用户个性化的需求(用户不再预先设定保密探测区域阈值的大小, 保密探测区域可以是任意的多边形).文献[1]的协议提出了一种解决探测区域为任意凸多边形情形的很好的方法.它虽然能够满足用户个性化的需求(无需将探测区域设定为带阈值的圆形区域), 但是并未彻底解决保密探测计算中保密坐标符号计算问题.因此, 对于涉及到保密计算(正、负)符号的、利用同态加密实现的由多方协同参与的安全/保密几何计算问题以及基于位置服务的移动、社交网络隐私保护问题则需要另辟新径.

如今, 社交网络用户又对保密地探测提出了新的个性化需求:保密社交意愿筹划, 即保密社交意愿探测.保密社交意愿探测已经成为基于位置服务的社交网络用户的一个新的个性化需求.我们将如下一类问题称为保密意愿探测问题:拥有便携智能设备的用户间可以事先保密地探测他们的社交意愿——Alice由她的便携智能设备秘密地获取Bob是否处在自己愿意与Bob约会(如果Bob愿意赴约的话)的“理想区域内”, Bob由自己的便携智能设备保密地表达自己是否愿意赴约的意愿, 但双方都不想泄露各自的位置信息(Alice既不想泄露自己的位置, 也不想泄露自己的“理想区域”; Bob不想泄露自己的位置信息).

保密意愿探测可以视作保密近感探测协议^[1]在移动、社交网络用户个性化需求方面的深度拓展.虽然二者都是基于位置服务的移动、社交网络用户隐私保护问题, 但它们有明显的区别:保密近感探测问题研究的是两个用户如何计算他们的实时位置是否在预先设定的距离阈值内而不泄漏双方各自的具体位置; 保密意愿探测问题研究的则是参与双方如何计算出他们是否可以在某一区域内共事而不泄漏具体的共事区域与双方计划共事的具体位置, 即保密社交筹划.

为了解决移动、社交网络用户在社交筹划方面隐私保护的个性化需求问题, 同时也为了解决基于同态加密方案与安全多方计算的保密近感探测(如文献[1]的协议)中未能彻底解决的问题(当用户参与计算区域的临近两点坐标分量差值小于0时, 文献[1]的协议会输出错误的结果), 本文首先提出了一个基于位置服务的移动、社交网络隐私保护问题:保密社交意愿探测.然后综合采用安全多方几何计算^[24-26]、保密计算分数(一种新的保密比较大小方法)、同态加密以及云外包计算等技术设计了一个高效的社交网络保密意愿探测协议.

本文的主要贡献如下:

(1)   构造了一个由云辅助计算的新型同态加密方案, 该方案在预处理阶段由云服务器提前完成复杂的自模乘运算$(r_x^2{\rm{ }}\bmod {\rm{ }}{n^2}), $加密阶段的另一复杂运算g^m mod n²由等价的简单模乘运算m·(g-1) mod n²代替, 因此只通过几次简单的模乘运算, 就可以实现一次加密.

(2)   提出了一种新的保密符号计算方法, 并利用该方法和新构造的基于云计算的同态加密方案, 设计了一个新的保密意愿探测协议.该协议对于半诚实参与者是安全的.

(3)   提出了一种新的加密思想:由加密一方自主确定一次加密需要执行多少次模乘运算.

1 预备知识 1.1 关于加密方案的安全性定义

定义1(不可区分安全游戏).“加密语义安全”通常利用一个(由敌手和加密系统产生者)两方进行的思维游戏进行刻画.本文将引用文献[27]中对于文献[28]中关于公钥加密方案的选择明文攻击不可区分性(indistinguishability under chosen-plaintext attack, 简称IND-CPA)游戏$PubK_{\mathcal{A}, \mathcal{E}}^{cpa}(k)$的翻译表述(其中, $\mathcal{E}$为任意一个公钥加密方案, $\mathcal{A}$为任意一个概率多项式时间的敌手, $Ad{v_{\mathcal{A}, \mathcal{E}}}(k)$为$\mathcal{A}$在攻击$\mathcal{E}$的不可区分游戏中的成功优势).

(1)   输入系统安全参数1^k, 生成密钥对(K_pub, K_pri).

(2)   $\mathcal{A}$获得公钥K_pub, 并且它能够访问加密谕言机Enc(·), 经过一些加密问询后输出两个相同长度的明文m₀和m₁.

(3)   系统搭建者随机选择b∈{0, 1}, 然后输出一个挑战密文c=Enc(m_b).

(4)   $\mathcal{A}$继续调用Enc(·), 输出一个比特位b'作为对b的猜测结果.

(5)   若b'=b, 则游戏输出$PubK_{\mathcal{A}, \mathcal{E}}^{cpa}(k) = 1;$否则, 输出$PubK_{\mathcal{A}, \mathcal{E}}^{cpa}(k) = 0.$

如果存在一个可忽略的函数δ, 满足:

$Adv_{\mathcal{A}, \mathcal{E}}^{cpa}(k) = \left| {\Pr [PubK_{\mathcal{A}, \mathcal{E}}^{cpa}(k) = 1] - \frac{1}{2}} \right| \leqslant \delta (k)$ ,

则方案$\mathcal{E}$在选择明文攻击下具有不可区分安全性.

1.2 关于安全多方计算的安全性定义^[27]

要证明一个安全多方计算协议的安全性, 需要用到定义:理想保密计算协议、半诚实参与者、协议π可被用于保密计算函数f(a, b).本文将引用文献[27]中对于学者Goldreich关于这3个定义的翻译描述.

定义2(理想保密计算协议)^[27].假设TTP是网络中存在的一个绝对可信的第三方, 作为协议的参与方, Alice与Bob在TTP协助下, 可以按照如下方式协作完成一次安全计算:Alice与Bob各自将他们的秘密信息a和b分别秘密地发送给TTP, 由TTP独立计算完函数f(a, b)后, 再将计算出的函数值分别秘密地发送给Alice和Bob.其中规定函数f满足:已知a与b之一以及函数值f(a, b)时, 不能计算出a与b中的另一个.显然, 网络中这样一个简单的协议是保密程度最高的安全两方计算协议, 除此之外, 再也找不到一个用于计算f(a, b)的实际安全两方计算协议在安全性上可以超越该协议.

定义3(半诚实参与者)^[27].不严格地说, 作为某安全多方计算协议的半诚实参与者, 在其执行协议的过程中绝对会按照协议规定, 执行安全计算协议的每一步, 但其可能会在协议执行过程中记录所有中间结果, 并试图利用这些记录数据去计算安全多方计算协议之外的有关其他参与者的隐私信息.

将计算概率多项式函数f=(f₁, f₂):{0, 1}^*×{0, 1}^*→{0, 1}^*×{0, 1}^*的协议记作π.给π输入(a, b), 在协议执行过程中, Alice和Bob的视图(view)分别记作$view_1^\pi (a, b) = (a, {r_d}, {m_{{d_1}}}, {m_{{d_2}}}, ..., {m_{{d_k}}})$和$view_2^\pi (a, b) = (b, {r_d}, {m_{{d_1}}}, {m_{{d_2}}}, ..., {m_{{d_k}}}).$其中, d∈{1, 2}, r_d是Alice或Bob自己选择的随机数, ${m_{{d_1}}}$是Alice或Bob收到的第i个消息; 将Alice和Bob协同执行完协议得到的结果分别记作$output_1^\pi (a, b)$和$output_2^\pi (a, b).$

定义4(协议π可被用于保密计算函数f(a, b))^[27]. Goldreich如下定义一个安全两方计算协议的安全性:如果存在概率多项式时间模拟算法$\mathcal{S}$₁与$\mathcal{S}$₂, 使得

${\{ ({\mathcal{S}_1}(a, {f_1}(a, b)), {f_2}(a, b))\} _{a, b}}\mathop \equiv \limits^c {\{ (view_1^\pi (a, b), output_2^\pi (a, b))\} _{a, b}}$

(1)

${\{ ({f_1}(a, b), {\mathcal{S}_2}(a, {f_2}(a, b)))\} _{a, b}}\mathop \equiv \limits^c {\{ (output_1^\pi (a, b), view_2^\pi (a, b))\} _{a, b}}$

(2)

成立, 则称协议π可被用于保密计算函数f(a, b).其中, $\mathop \equiv \limits^c $表示计算不可区分.

Goldreich利用比特承诺和零知识证明理论设计了一个编译器.向该编译器输入一个在半诚实参模型下安全计算f的协议π时, 编译器会自动为我们编译输出一个安全协议π', 该协议在有恶意参与者参与协同计算情况下也能安全计算f.考虑到工程实际, 本文规定本文构造协议中的参与者皆为半诚实类型.

1.3 Paillier同态加密方案^[22]

Paillier构造的方案(如图 1所示)可以利用密文的运算在明文空间$Z_n^{}$上实现同态加运算:E(x+y)=E(x)·E(y).该方案具有第1.1节中定义1定义的安全性:将等长的两个消息m₀和m₁加密, 并将它们的密文分别记作C₀与C₁, 对于任何实施选择明文攻击的敌手而言, 计算上无法区分C₀与C₁, 即${C_0}\mathop \equiv \limits^c {C_1}.$

1.4 高阶剩余类判定性问题

定义5(高阶剩余类判定性问题).该问题在文献[11]中被称作“decisional composite residuosity problem”, 简称为DCR).简单地讲, 如果给定两个等长大素数的乘积$n=pq$(其中p与q保密)和一个与$n$互素的整数$z$, 对于敌手而言, 判定事件“是否存在一个y, 满足$z \equiv {y^n}{\rm{ mod }}{n^{\rm{2}}}$”成功的概率可以表述为一个忽略的函数^[11].

文献[27]从可证明安全的需求出发, 将其用形式化语言描述为如下形式:

设D是一种区分任意两个分布${D_{ran}} = \{ (n, {\mathit{\pmb{R}}})|{\mathit{\pmb{R}}}\xleftarrow{R}{Z_{{n^2}}}\} $和${D_\mathcal{E}} = \{ (n, {\mathit{\pmb{R}}})|{\mathit{\pmb{R}}} \leftarrow \{ {r^n}{\rm{ }}\bmod {\rm{ }}{n^2}|r \in {Z_n}\} \} $的算法, 以系统安全参数τ为自变量的函数Adv_D(τ)表示敌手利用区分算法D能够区分出D_ran与${D_\mathcal{E}}$的优势函数.

如果任意选取一个分布$(n, {\mathit{\pmb{R}}}) \in \{ {D_{ran}}, {D_\mathcal{E}}\} $发给敌手进行挑战, 并把敌手里利用D对于(n, R)的区分结果记作D(n, R)=D_ran或${\mathit{\pmb{D}}}(n, {\mathit{\pmb{R}}}) = {D_\mathcal{E}}, $则敌手利用D可以区分(n, R)的优势函数Adv_D(τ)可以形式化表示成:

$Ad{v_{\mathit{\pmb{D}}}}(\tau ) = |\Pr [{\mathit{\pmb{D}}}(n, {\mathit{\pmb{R}}}) = {D_{ran}}] - \Pr [{\mathit{\pmb{D}}}(n, {\mathit{\pmb{R}}}) = {D_\mathcal{E}}]|.$

DCR一直是在现代密码学中一个被公认的难解问题, 关于DCR难解性证明或阐述请参阅Paillier^[22].所以, 对于任意的敌手而言, 利用任意多项式时间的概率算法D区分分布(n, R)的优势函数Adv_D(τ)是一个可忽略的量, 即存在一个关于安全参数τ的可忽略函数δ(τ), 使得Adv_D(τ)满足:

$ Ad{{v}_{\mathit{\pmb{D}}}}(\tau )\le \delta (\tau ). $

2 带云辅助计算的同态加密方案

对于Paillier加密方案而言, 主要的计算开销包括g^m mod n², rⁿ mod n²和c^λ mod n², 其中, g=1+kn, $k \in Z_n^*$.本节基于Paillier加密方案和云外包计算, 并采下述思想1和思想2设计了一个高效的同态加密方案.

思想1.在执行加密算法的过程中, 将运算复杂度高的模指数运算g^m mod n²(或g^λ mod n²)用与之运算结果等价的、运算高效的模乘运算1+m·(g-1)(mod n²)(或1+λ·(g-1)(mod n²))替代, 从而实现快速而正确的加密.

思想2.将计算开销大的模指数运算rⁿ mod n²委托给云服务器.

2.1 具体方案

此同态加密系统由4种随机算法组成:云外包随机数模指数运算算法(COR)、密钥生成算法(KGen)、加密算法(Enc)和解密算法(Dec), 其中, 云外包随机数模指数运算可以在预处理阶段完成, 也可以与密钥生成算法并行执行.在此, 我们将该加密方案记作$\mathcal{E}$=(COR, Kgen, Enc, Dec).

●  COR:云服务器随机选择${{r}_{1}},{{r}_{2}},...,{{r}_{k}}\in Z_{n}^{*}$(其中, k≤n), 计算足够多的${{R}_{i}}=r_{i}^{n}\left( \text{mod }{{n}^{2}} \right)\left( 1\le i\le k \right),$并将它们存储在集合R中.当加密者或者是数据运算者需要$r_{x}^{n}\left( \text{mod }{{n}^{2}} \right)\left( {{r}_{x}}\in Z_{n}^{*} \right)$时, 随时可以从该服务器上下载R, 利用集合R中的某些元素, 通过适量的简单模乘运算, 就可以秘密地得到$r_{x}^{n}\left( \text{mod }{{n}^{2}} \right).$

●  KGen:产生长度相等的两个大素数p, q, 并计算二者的乘积(n=pq)与二者分别减1后的最小公倍数$(\lambda = lcm(p - {\rm{1}}, q - {\rm{1}})), $为加密方案输出公钥(K_pub=(n, 1+kn), 其中, $k \in Z_n^*$)与私钥$({K_{pri}} = \lambda ).$

●  Enc:加密一方按照如下方式执行加密计算:

(1)   从云服务器上下载集合R.

(2)   自由确定适量的自模乘运算次数(θ), 并从R上随机选择$\ell $($\ell $ < < n)个数(记作${R_1}, {R_2}, ..., {R_\ell } \in R$), 随机选择${\chi _1}, {\chi _2}, ..., {\chi _\ell } \in \{ 0, ..., \ell \} $, 其中, 2≤θ≤$\ell $(为了表述简单, 在此约定文中此后的加密运算将以两个数为例:R_i, R_j∈R, i, j∈{0, …, $\ell $}).

(3)   对于m < n, 计算${M_g} = m \cdot (g - 1)(\bmod {\rm{ }}{n^2}), {R_x} = R_i^{{\chi _1}} \cdot R_j^{{\chi _2}}{\rm{ }}\bmod {\rm{ }}{n^2}, $其中,

$ ({{\chi }_{1}}, {{\chi }_{2}}\in \{0, \ldots , \ell \})\wedge ({{\chi }_{1}}+{{\chi }_{2}}\ge 2), c=(1+{{M}_{g}}(\text{mod}\ {{n}^{2}}))\cdot {{R}_{x}}\ \text{mod}\ {{n}^{2}}. $

●  Dec:解密方执行解密运算:

$ m=\frac{L\left( {{c}^{\lambda }}\,\bmod \,{{n}^{2}} \right)}{L\left( (1+\lambda \cdot (g-1))\,\bmod \,{{n}^{2}} \right)}\,\bmod \,n,其中,L(u)=\frac{u-1}{n},u\in Z_{{{n}^{2}}}^{*}. $

2.2 正确性验证 2.2.1 由云服务器计算${{R}_{i}}=r_{i}^{n}\left( \,\bmod \,{{n}^{2}} \right)\left( 1\le i\le k,{{r}_{x}}\in Z_{n}^{*} \right)$的合理性

显然, 云服务器计算${R_i} = r_i^n(\bmod {\rm{ }}{n^2})$是否合理, 就是看其是否满足以下两个条件:(1)加密运算中引入的随机变量可以在解密运算中被成功消除, 即${R_x} = R_i^{{\chi _1}} \cdot R_j^{{\chi _2}}{\rm{ }}\bmod {\rm{ }}{n^2}$(χ₁, χ₂∈{0, …, $\ell $})Λ(χ₁+χ₂≥2)在形式上依然可以表示成${R_x} = r_x^n{\rm{ }}\bmod {\rm{ }}{n^2}, $其中, ${r_x} \in Z_n^ * $; (2)加密运算采用计算${R_x} = R_i^{{\chi _1}} \cdot R_j^{{\chi _2}}{\rm{ }}\bmod {\rm{ }}{n^2}$的方式引入随机变量, 不会削弱方案的安全性.

(1) 加密运算中引入的随机变量可以在解密运算中被成功消除.

如果解密运算能够成功将加密运算中引入的随机变量消除, 则${R_x} = R_i^{{\chi _1}} \cdot R_j^{{\chi _2}}{\rm{ }}\bmod {\rm{ }}{n^2}$必满足$R_x^\lambda {\rm{ }}\bmod {\rm{ }}{n^2} \equiv 1, $即${R_x} = r_x^n{\rm{ }}\bmod {\rm{ }}{n^2}, $其中, ${r_x} \in Z_n^ * $.令${r_i}, {r_j} \in Z_n^ * $, 则r_ir_j可以表示成$r_i^{{\chi _1}}r_j^{{\chi _2}} = {r_x} + \gamma n$, 其中, ${r_x} \in Z_n^ * $(因为${r_i}, {r_j} \in Z_n^ * $, 所以$r_i^{{\chi _1}}r_j^{{\chi _2}}$不能被n整除, 从而可得r_x≠0), 其中, γ∈Z_n-1之间的整数.

因为${R_i} = r_i^n(\bmod {\rm{ }}{n^2})(1 \leqslant i \leqslant k), {R_j} = r_j^n(\bmod {\rm{ }}{n^2})(1 \leqslant j \leqslant k), $所以,

$\begin{align} & {{R}_{x}}=R_{i}^{{{\chi }_{1}}}\cdot R_{j}^{{{\chi }_{2}}}\left( \,\bmod \,{{n}^{2}} \right) \\ & \ \ \ \ \ ={{\left( r_{i}^{n} \right)}^{{{\chi }_{1}}}}\cdot {{\left( r_{j}^{n} \right)}^{{{\chi }_{2}}}}\left( \,\bmod \,{{n}^{2}} \right) \\ & \ \ \ \ \ ={{\left( r_{i}^{{{\chi }_{1}}}r_{j}^{{{\chi }_{2}}} \right)}^{n}}\left( \,\bmod \,{{n}^{2}} \right) \\ & \ \ \ \ \ ={{\left( {{r}_{x}}+\gamma n \right)}^{n}}\left( \,\bmod \,{{n}^{2}} \right) \\ & \ \ \ \ \ =\sum\limits_{k=0}^{n}{\left( \begin{array}{*{35}{l}} n \\ k \\ \end{array} \right)}r_{x}^{n-k}{{(\gamma n)}^{k}}\left( \,\bmod \,{{n}^{2}} \right) \\ & \ \ \ \ \ =r_{x}^{n}\left( \,\bmod \,{{n}^{2}} \right) \\ \end{align}$

(2) 加密运算采用计算${R_x} = R_i^{{\chi _1}} \cdot R_j^{{\chi _2}}{\rm{ }}\bmod {\rm{ }}{n^2}$的方式引入随机变量, 在语义安全层面不会削弱方案的安全性.

R虽然是公开的, 但${R_1}, {R_2}, ..., {R_\ell } \in R$, $\ell $以及${\chi _1}, {\chi _2}, ..., {\chi _\ell } \in \{ 0, ..., \ell \} $都是加密者在加密运算中随机选择的, 因此, 以${R_1}, {R_2}, ..., {R_\ell } \in R$为随机种子, 由随机函数${R_x} = R_1^{{\chi _1}} \cdot R_2^{{\chi _2}} \cdot ... \cdot R_\ell ^{{\chi _\ell }}{\rm{ }}\bmod {\rm{ }}{n^2} = r_x^n{\rm{ }}\bmod {\rm{ }}{n^2}$计算得到的R_x与计算${(1 + kn)^0} \cdot r_{x'}^n{\rm{ }}\bmod {\rm{ }}{n^2}$(其中, ${{r}_{{{x}^{*}}}}\in Z_{n}^{*}$是随机选择的)是等效的, 因此, 任何敌手由R计算R_x的困难性与破解Paillier加密方案的困难性是等价的.

综上所述, 加密方案$\mathcal{E}$将计算${{R}_{i}}=r_{i}^{n}\left( \,\bmod \,{{n}^{2}} \right)\left( 1\le i\le k,{{r}_{i}}\in Z_{n}^{*} \right)$委托给云服务器执行, 在语义安全的安全层面上是合理的.

2.2.2 替换运算的正确性

定理1. 1+m·(g-1)(mod n²)的结果与模指数运算g^m mod n²的结果是等价的, 即

$ 1+m\cdot (g-1)(\text{mod}\ {{n}^{2}})\Leftrightarrow {{g}^{m}}\ \text{mod}\ {{n}^{2}}. $

证明:因为g=1+kn$(k \in Z_n^ + )$, 所以,

$ 1+m\cdot (g-1)(\text{mod}\ {{n}^{2}})=1+m\cdot (1+kn-1)(\text{mod}\ {{n}^{2}})=1+m\cdot kn(\text{mod}\ {{n}^{2}}); $

又由二项式展开定理得:

${g^m}{\rm{ }}\bmod {\rm{ }}{n^2} = {(1 + kn)^m}{\rm{ }}\bmod {\rm{ }}{n^2} = \sum\limits_{\kappa = 0}^m {\left( \begin{gathered} m \\ \kappa \\ \end{gathered} \right)} 1_x^{m - \kappa }{(kn)^\kappa }{\rm{ }}\bmod {\rm{ }}{n^2} = 1 + \left( \begin{gathered} m \\ 1 \\ \end{gathered} \right) \cdot kn{\rm{ }}\bmod {\rm{ }}{n^2} = 1 + m \cdot kn{\rm{ }}\bmod {\rm{ }}{n^2}.$

综上可得:1+m·(g-1)(mod n²)⇔g^m mod n²

2.2.3 解密正确性

因为

$ \begin{align} & c=((1+m\cdot (g-1))(\,\bmod \,{{n}^{2}}))\cdot (({{R}_{i}}\cdot {{R}_{j}}\,\bmod \,{{n}^{2}})\,\bmod \,{{n}^{2}})\,\bmod \,{{n}^{2}} \\ & \ \ \ =(1+m\cdot (1+kn-1)(\,\bmod \,{{n}^{2}}))\cdot (r_{x}^{n}\,\bmod \,{{n}^{2}})\,\bmod \,{{n}^{2}} \\ & \ \ \ =({{(1+kn)}^{m}}\,\bmod \,{{n}^{2}})\cdot (r_{x}^{n}\,\bmod \,{{n}^{2}})\,\bmod \,{{n}^{2}} \\ & \ \ \ ={{g}^{m}}r_{x}^{n}\,\bmod \,{{n}^{2}}, \\ \end{align} $

所以有:

$\frac{{L({c^\lambda }{\rm{ }}\bmod {\rm{ }}{n^2})}}{{L((1 + \lambda \cdot (g - 1)){\rm{ }}\bmod {\rm{ }}{n^2})}}{\rm{ }}\bmod {\rm{ }}n = \frac{{({c^\lambda }{\rm{ }}\bmod {\rm{ }}{n^2}) - 1}}{{((1 + \lambda \cdot kn){\rm{ }}\bmod {\rm{ }}{n^2}) - 1}}{\rm{ }}\bmod {\rm{ }}n = \frac{{(1 + m \cdot kn) - 1}}{{(1 + kn) - 1}}{\rm{ }}\bmod {\rm{ }}n = m.$

2.3 安全性分析

定理2.如果DCR是难解问题, 则$\mathcal{E}$=(COR, Kgen, Enc, Dec)具有第1.1节中定义1所定义的不可区分安全性.

证明:在此先回忆一下DCR问题挑战者的工作方式.

●  在安全时间1^k内, 通过执行算法(1^k)算法产生两个大素数p和q, 以及它们的乘积n.

●  在Z_n上随机选取一个数r, 并从{0, 1}中均匀选取一个数f.

●  若f为0, 则将R置为rⁿ mod n²; 若f为1, 则将R置成R.

设$\mathcal{E}$=(COR, Kgen, Enc, Dec)是2.1节中构造的方案, 将攻击$\mathcal{E}$=(COR, Kgen, Enc, Dec)时, 敌手使用的多项式时间算法记作$\mathcal{A}$, 下面利用算法$\mathcal{A}$构造一个算法$\mathcal{B}$用于解决DCR问题.该算法的具体工作方式如下.

(1)   接收DCR挑战者发来的(n, (n, R));

(2)   令pk=(n, 1+kn);

(3)   将1ⁿ和pk发送给$\mathcal{A}$;

(4)   接收$\mathcal{A}$发来的消息m₀和m₁;

(5)   均匀地选取d∈{0, 1};

(6)   令${C^ * } = (n, y, y, y', y'', {(g')^{{m_d}}} \cdot \mathcal{R}(\bmod {\rm{ }}{n^2})), $并将C^*发送给$\mathcal{A}$;

(7)   用d'表示敌手A对d的猜测结果;

(8)   输出f'(如果d=d', 则置f'=0;如果d≠d', 则置f'=1).

因为算法$\mathcal{B}$只通过调用算法$\mathcal{A}$实现且只调用了3次, 而作为构成算法$\mathcal{B}$的子算法$\mathcal{A}$是在多项式时间内可被完成的算法, 所以通过3次调用算法$\mathcal{A}$而实现的算法$\mathcal{B}$是一种在多项式时间内可被完成的算法.因此, (1^k)也是一种在多项式时间内完成的算法.于是, 构造$\mathcal{B}$在DCR安全游戏中获胜的概率可以表示成贝叶斯公式形式:

$\left. \begin{gathered} \Pr [f = f'] = \Pr [f = 0]\Pr [f = f'|f = 0] + \Pr [f = 1]\Pr [f = f'|f = 1] \\ {\rm{ }} = \frac{1}{2}\Pr [f' = 0|f = 0] + \frac{1}{2}\Pr [f' = 1|f = 1] \\ {\rm{ }} = \frac{1}{2}\Pr [d = d'|f = 0] + \frac{1}{2}\Pr [d \ne d'|f = 1] \\ \end{gathered} \right\}$

(3)

当f=0时, DCR挑战者置R=rⁿ mod n².这样, 由算法$\mathcal{A}$构造的$\mathcal{B}$呈现给掌握算法$\mathcal{A}$的敌手的视图与掌握算法$\mathcal{A}$的敌手在实际攻击$\mathcal{E}$=(COR, Kgen, Enc, Dec)的安全游戏中获取的视图相同.因此, 掌握算法$\mathcal{A}$的敌手在攻击$\mathcal{E}$=(COR, Kgen, Enc, Dec)的安全游戏中获胜的概率等于d=d'在条件f=0下的条件概率, 即

$\Pr [d = d'|f = 0] = \frac{1}{2} + \delta $

(4)

当f=1时, DCR挑战者将$\mathcal{R}$置成R.因为$R \in {Z_{{n^2}}}$是均匀选取的, 所以, 执行运算${(g')^{{m_d}}} \cdot \mathcal{R}(\bmod {\rm{ }}{n^2})$后的结果在群Z/n²Z上是均匀分布的; 又因为3个随机变量m₀, m₁, d相互独立, 因此, pk和C^*没有暴露关于d的任何消息, 这意味着掌握算法$\mathcal{A}$的敌手对于d的猜测结果d'与d相互独立.若在{0, 1}上随机选取d, 则d=0或d=1的概率各为$\frac{1}{2}$, 故有:

$\Pr [d = d'|f = 1] = \frac{1}{2}$

(5)

成立.联立公式(3)~公式(5), 我们可以得到:

$\Pr [f = f'] = \frac{1}{2}\left( {\frac{1}{2} + \delta } \right) + \frac{1}{2} \times \frac{1}{2} = \frac{1}{2} + \frac{1}{2}\delta $

(6)

因此, $\mathcal{B}$在DCR安全游戏中获胜的优势为

$\left| {\Pr [f = f'] - \frac{1}{2}} \right| = \left| {\left( {\frac{1}{2} + \frac{1}{2}\delta } \right) - \frac{1}{2}} \right| = \frac{\delta }{2}$

(7)

由第1.1节中定义1可知, 在DCR安全性游戏中, 利用算法$\mathcal{A}$构造的$\mathcal{B}$获胜的优势是一个可忽略的量, 所以$\frac{\delta }{2}$是一个可忽略的值.这意味δ也是一个可忽略的量.所以利用算法$\mathcal{A}$的敌手在攻击方案$\mathcal{E}$的IND-CPA安全游戏中获胜的优势是一个可忽略的量, 即$\mathcal{E}$=(COR, Kgen, Enc, Dec)具有IND-CPA安全性.

2.4 加密方案的效率分析

因为同态加密方案$\mathcal{E}$中的计算${R_i} = r_i^n{\rm{ }}\bmod {\rm{ }}{n^2}$是在预处理阶段由云服务器完成, 并且加密者可以在加密前的预处理阶段从云服务器下载集合$R = \{ {R_i}|{R_i} = r_i^n{\rm{ }}\bmod {\rm{ }}{n^2}\} , $加密时利用集合中的元素通过执行简单的几次模乘运算(${R_x} = R_i^{{\chi _1}} \cdot R_j^{{\chi _2}}{\rm{ }}\bmod {\rm{ }}{n^2}, $其中, (χ₁, χ₂∈{0, …, l})Λ(χ₁+χ₂≥2))即可秘密地得到$r_x^n{\rm{ }}\bmod {\rm{ }}{n^2}, $无需再做n次复杂的自模乘运算.同时, 加密时运算复杂度高的模指数运算g^m mod n²(解密时g^λ mod n²)是用与之运算结果等价的、运算简单高效的模乘运算1+m·(g-1)(mod n²)(解密时1+λ·(g-1)(mod n²))替代实现的; 若忽略预处理时间, 则用方案$\mathcal{E}$加密一个消息的总计需要花费6+λ次模乘运算.而用Paillier方案加密一个小小的总开销绝不会少于2n次模乘运算.表 1是加密方案$\mathcal{E}$和Paillier方案在加、解密效率方面的对比.

3 保密社交意愿探测协议 3.1 保密社交意愿应用背景描述及其形式化

Alice(需求者)是保险公司的职员, 某天在某一个城市推销保险产品, 她只想约谈现在正好在某个区域内的客户(可能住在该区域, 也可能正在该区域且有空闲时间), 她与不想向不在该区域且不愿约谈的用户透露自己的活动区域, 例如她想约谈客户Bob, 但Bob只想让Alice知道他是否可被约谈而不想透露自己的具体位置.Bob和Alice怎样做才能同时实现他们的各自的目的呢?然而, 安全多方几何计算为解决这种问题提供了一种可行的方法.我们将Bob和Alice采用安全多方几何计算思路实现保密测试社交意愿的问题称为保密社交意愿探测问题, 其形式化描述如下:

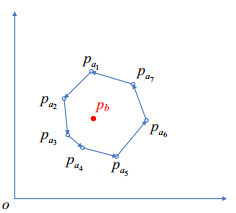
Alice拥有一个有K个顶点${p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}({p_i} = ({a_{{x_i}}}, {a_{{y_i}}}), 1 \leqslant i \leqslant K)$构成的私有凸多边形P, 表示她现在利益最大的活动范围.其中, 该多边形的边是按逆时针方向标注的, 如图 2所示(以K=7为例).

Bob拥有一个私有点p_b=(b_x, b_y), 表示他现在所处的位置.Alice想知道Bob是否处在自己的想活动的范围内, Bob不想透露自己的具体位置.我们设计一个这样的安全多方计算协议要实现对Alice与Bob的隐私保护.

●  协议结束时, Alice只得到一个意愿探测的结果(一个布尔值), 而Bob的具体位置信息对于Alice仍然是一个秘密.

●  协议结束时, 最多只得到Alice多边形的边数K-1(Bob没有得到意愿探测的结果), 而Alice的活动区域的形状、位置与活动区域的大小对于Bob仍然是一个秘密.

3.2 保密社交意愿探测协议 3.2.1 判定凸多边形与一个点位置关系

非保密的近感探测问题实际上就是判定某个凸多边形P(有K个顶点${p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}$)是否包含一个点p_b= (b_x, b_y)的问题.可以通过K次计算有向线段$\overrightarrow {{p_i}{p_{i + 1}}} $与点p_b=(b_x, b_y)的位置关系来实现^{[24-26, 29]}.对于点p_i, p_b, p_i+1构成的有序元组xy p_i, p_b, p_i+1>在平面上可能对应着3种位置关系(如图 3所示).

●  正向:3个点构成的方向角∠p_i, p_b, p_i+1为逆时针走向(如图 3(a)所示).

●  反向:3个点构成的方向角∠p_i, p_b, p_i+1为顺时针走向(如图 3(b)所示).

●  零向:3个点构成的方向角∠p_i, p_b, p_i+1=180°, 即p_i, p_b, p_i+1共线(如图 3(c)所示).

假设点p_i, p_b, p_i+1的坐标分别为${p_i} = ({a_{{x_i}}}, {a_{{y_i}}}), {p_b} = ({b_x}, {b_y}), {p_{i + 1}} = ({a_{{x_{i + 1}}}}, {a_{{y_{i + 1}}}}), $则3点构成的方向角∠p_i, p_b, p_i+1的方向可以通过计算下列行列式来确立:

$ \left. \begin{align} & {{D}_{i}}=\left| \begin{matrix} {{a}_{{{x}_{i}}}}-{{b}_{x}} & \ \ {{a}_{{{y}_{i}}}}-{{b}_{y}} \\ {{a}_{{{x}_{i+1}}}}-{{b}_{x}} & \ \ \ {{a}_{{{y}_{i+1}}}}-{{b}_{y}} \\ \end{matrix} \right| \\ & \ \ \ \ ={{b}_{x}}({{a}_{{{y}_{i+1}}}}-{{a}_{{{y}_{i}}}})+{{b}_{y}}({{a}_{{{x}_{i}}}}-{{a}_{{{x}_{i+1}}}})+({{a}_{{{y}_{i}}}}{{a}_{{{x}_{i+1}}}}-{{a}_{{{x}_{i}}}}{{a}_{{{y}_{i+1}}}}) \\ & \ \ \ \ ={{b}_{x}}{{a}_{{{y}_{i+1}}}}+{{b}_{y}}{{a}_{{{x}_{i}}}}+{{a}_{{{y}_{i}}}}{{a}_{{{x}_{i+1}}}}-({{b}_{x}}{{a}_{{{y}_{i}}}}+{{b}_{y}}{{a}_{{{x}_{i+1}}}}+{{a}_{{{x}_{i}}}}{{a}_{{{y}_{i+1}}}}) \\ \end{align} \right\} $

(8)

其中, D_i > 0, D_i < 0, D_i=0分别对应着图 3(a)~图 3(c).

因此, 下面的算法可以正确计算出近感探测的结果.

凸多边形与点的关系判定算法.

输入:由K个按逆时针顺序访问的顶点${p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}$构成的凸多边形P, 点p_b.

输出:“1”, 如果p_b在P内; “0”, 否则p_b不在P内.

(1)   对于i∈{1, 2, …, K-1}计算点p_b与有向线段$\overrightarrow {{p_i}{p_{i + 1}}} $两个端点所构成的方向角∠p_i, p_b, p_i+1的方向D_i.

(2)   如果对于∀i∈{1, 2, …, K-1}都有D_i≤0, 则返回“1”; 否则, 返回“0”.

3.2.2 保密社交意愿探测协议

利用上述凸多边形与点的位置关系判定方法、第2.1节中设计的带云辅助计算的同态加密方案以及一种新的保密符号计算方法, 设计了一个保密社交意愿探测协议.

保密社交意愿探测协议.

输入:Alice输入由K个按逆时针顺序访问的顶点${p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}$构成的凸多边形P, Bob输入点p_b.

输出:“1”, 如果p_b在P内; “0”, 否则p_b不在P内.

1. COR:云服务器随机选${{r}_{1}},{{r}_{2}},\ldots ,{{r}_{k}}\in Z_{n}^{*}$(其中, k≤n), 计算足够多的${{R}_{i}}=r_{i}^{n}\left( \,\bmod \,{{n}^{2}} \right)(1\le i\le k),$并将它们存储在集合R中.当加密者或者是数据运算者需要$r_{x}^{n}\left( \,\bmod \,{{n}^{2}} \right)$时, 随时可以从该服务器上下载R, 利用集合R中的某些元素通过一些简单的模乘运算就可以秘密地得到$r_{x}^{n}\left( \,\bmod \,{{n}^{2}} \right).$

2. Alice运行加密系统$\mathcal{E}$=(COR, Kgen, Enc, Dec)的密钥生成算法Kgen, 生成公钥K_pub=(n, 1+kn)和私钥K_pri=λ;

3. Alice首先从云服务器上下载集合R并随机选取${R_{{A_{j1}}}}, {R_{{A_{j2}}}}, ..., {R_{{A_{j12}}}} \in R$, 然后按照如下方式操作:

(1) 对于j∈{1, 2, …, K-1}计算(假设Alice将χ₁, χ₂取作χ₁=χ₂=1, 并置l=2):

$\begin{align} & {{E}_{\mathcal{E}}}({{a}_{{{y}_{j+1}}}})\equiv (1+{{a}_{{{y}_{j+1}}}}(g-1))\cdot {{R}_{{{A}_{j1}}}}\cdot {{R}_{{{A}_{j2}}}}\,\bmod \,{{n}^{2}},{{E}_{\mathcal{E}}}({{a}_{{{x}_{j}}}})\equiv (1+{{a}_{{{x}_{j}}}}(g-1))\cdot {{R}_{{{A}_{j3}}}}\cdot {{R}_{{{A}_{j4}}}}\,\bmod \,{{n}^{2}}, \\ & {{E}_{\mathcal{E}}}({{a}_{{{y}_{j}}}}{{a}_{{{x}_{j+1}}}})\equiv (1+{{a}_{{{y}_{j}}}}{{a}_{{{x}_{j+1}}}}(g-1))\cdot {{R}_{{{A}_{j5}}}}\cdot {{R}_{{{A}_{j6}}}}\,\bmod \,{{n}^{2}},{{E}_{\mathcal{E}}}({{a}_{{{y}_{j}}}})\equiv (1+{{a}_{{{y}_{j}}}}(g-1))\cdot {{R}_{{{A}_{j7}}}}\cdot {{R}_{{{A}_{j8}}}}\,\bmod \,{{n}^{2}}, \\ & {{E}_{\mathcal{E}}}({{a}_{{{x}_{j+1}}}})\equiv (1+{{a}_{{{x}_{j+1}}}}(g-1))\cdot {{R}_{{{A}_{j9}}}}\cdot {{R}_{{{A}_{j10}}}}\,\bmod \,{{n}^{2}},{{E}_{\mathcal{E}}}({{a}_{{{x}_{j}}}}{{a}_{{{y}_{j+1}}}})\equiv (1+{{a}_{{{x}_{j}}}}{{a}_{{{y}_{j+1}}}}(g-1))\cdot {{R}_{{{A}_{j11}}}}\cdot {{R}_{{{A}_{j12}}}}\,\bmod \,{{n}^{2}}. \\ \end{align}$

(2) 将密文元组$({E_\mathcal{E}}({a_{{y_{j + 1}}}}), {E_\mathcal{E}}({a_{{x_j}}}), {E_\mathcal{E}}({a_{{y_j}}}{a_{{x_{j + 1}}}}), {E_\mathcal{E}}({a_{{y_j}}}), {E_\mathcal{E}}({a_{{x_{j + 1}}}}), {E_\mathcal{E}}({a_{{x_j}}}{a_{{y_{j + 1}}}}))$记作${E_\mathcal{E}}({A_j}), $其中, j∈{1, 2, …, K-1}, 对所有密文元组${E_\mathcal{E}}({A_1}), {E_\mathcal{E}}({A_2}), ..., {E_\mathcal{E}}({A_{K - 1}})$做随机置换, 并将所有的密文元组$({E_\mathcal{E}}({a_{{y_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}), {E_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), $ ${E_\mathcal{E}}({a_{{y_i}}}), {E_\mathcal{E}}({a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}})) \in \{ {E_\mathcal{E}}({A_1}), {E_{\rm E}}({A_2}), ..., {E_\mathcal{E}}({A_{K - 1}})\} $发给Bob.

4.对于i∈{1, 2, …, K-1}, Bob收到${{E}_{\mathcal{E}}}\left( {{a}_{{{y}_{i+1}}}} \right),{{E}_{\mathcal{E}}}\left( {{a}_{{{x}_{i}}}} \right),{{E}_{\mathcal{E}}}\left( {{a}_{{{y}_{i}}}}{{a}_{{{x}_{i+1}}}} \right),{{E}_{\mathcal{E}}}\left( {{a}_{{{y}_{i}}}} \right),{{E}_{\mathcal{E}}}\left( {{a}_{{{x}_{i+1}}}} \right),{{E}_{\mathcal{E}}}\left( {{a}_{{{x}_{i}}}}{{a}_{{{y}_{i+1}}}} \right)$后, 按照如下方式进行:

(1) 计算:${{E}_{\mathcal{E}}}({{b}_{x}}{{a}_{{{y}_{i+1}}}})\equiv {{({{E}_{\mathcal{E}}}({{a}_{{{y}_{i+1}}}}))}^{{{b}_{x}}}}\, \bmod \, {{n}^{2}}, {{E}_{\mathcal{E}}}({{b}_{y}}{{a}_{{{x}_{i}}}})\equiv {{({{E}_{\mathcal{E}}}({{a}_{{{x}_{i}}}}))}^{{{b}_{y}}}}\, \bmod \, {{n}^{2}}.$

(2) 从云服务器上下载集合R后, 随机选择${k_b}, {r_{{b_1}}} \in {Z_n}, $2l(l≤k)个数:${R_1}, {R_2}, ..., {R_\ell } \in R, {\chi _1}, {\chi _2}, ..., {\chi _\ell }, {\chi '_1}, {\chi '_2}, ..., $ ${\chi '_\ell } \in \{ 0, ..., \ell \} , $其中, l是一个比1大一些的小整数.并计算:

$\begin{align} & {E_\mathcal{E}}({r_{b1}}) = (1 + {r_{b1}} \cdot {k_b} \cdot (g - 1) \cdot R_1^{{\chi _1}} \cdot R_2^{{\chi _2}} \cdot ... \cdot R_\ell ^{{\chi _\ell }}{\rm{ }}\bmod {\rm{ }}{n^2}, \\ & {E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{b1}}) \equiv ({({E_\mathcal{E}}({b_x}{a_{{y_{i + 1}}}}){E_\mathcal{E}}({b_y}{a_{{x_i}}}){E_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}){\rm{ }}\bmod {\rm{ }}{n^2})^{{k_b}}}{\rm{ }}\bmod {\rm{ }}{n^2}){E_\mathcal{E}}({r_{b1}}){\rm{ }}\bmod {\rm{ }}{n^2}, \\ & {E_\mathcal{E}}({b_x}{a_{{y_i}}}) \equiv {({E_\mathcal{E}}({a_{{y_i}}}))^{{b_x}}}{\rm{ }}\bmod {\rm{ }}{n^2}, \\ & {E_\mathcal{E}}({b_y}{a_{{x_{i + 1}}}}) \equiv {({E_\mathcal{E}}({a_{{x_{i + 1}}}}))^{{b_y}}}{\rm{ }}\bmod {\rm{ }}{n^2}. \\ \end{align} $

(3) 随机选择${r_{{b_2}}} \in {Z_n}, $并计算:

$\begin{align} & {E_\mathcal{E}}({r_{{b_2}}}) = (1 + {r_{{b_2}}} \cdot {k_b} \cdot (g - 1) \cdot R_1^{\chi _1^\prime } \cdot R_2^{\chi _2^\prime } \cdot ... \cdot R_\ell ^{\chi _\ell ^\prime }{\rm{ }}\bmod {\rm{ }}{n^2}, \\ & {E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{{b_2}}}) \equiv ({({E_\mathcal{E}}({b_x}{a_{{y_i}}}){E_\mathcal{E}}({b_y}{a_{{x_{i + 1}}}}){E_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}}))^{{k_b}}}{\rm{ }}\bmod {\rm{ }}{n^2}){E_\mathcal{E}}({r_{{b_2}}}){\rm{ }}\bmod {\rm{ }}{n^2}, \\ \end{align} $

并将${E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{{b_1}}}), {E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{{b_2}}})$按随机顺序发给Alice.

5.对于i∈{1, 2, …, K-1}, 收到${{E}_{\mathcal{E}}}\left( {{k}_{b}}\left( {{b}_{x}}\left( {{b}_{x}}{{a}_{{{y}_{i+1}}}}+{{b}_{y}}{{a}_{{{x}_{i}}}}+{{a}_{{{y}_{i}}}}{{a}_{{{x}_{i+1}}}} \right)+{{r}_{{{h}_{1}}}} \right),{{E}_{\varepsilon }}\left( {{k}_{b}}\left( {{b}_{x}}{{a}_{{{y}_{i}}}}+{{b}_{y}}{{a}_{{{x}_{i+1}}}}+{{a}_{{{x}_{i}}}}{{a}_{{{y}_{i+1}}}} \right)+{{r}_{{{b}_{2}}}} \right) \right.$以后, Alice计算:

${\theta _i} = \frac{{\frac{{L({{({E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{b1}}))}^\lambda }{\rm{ }}\bmod {\rm{ }}{n^2})}}{{L({g^\lambda })}}}}{{\frac{{L({{({E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{b2}}))}^\lambda }){\rm{ }}\bmod {\rm{ }}{n^2}}}{{L({g^\lambda })}}}} = \frac{{L{{({E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{b1}}))}^\lambda }{\rm{ }}\bmod {\rm{ }}{n^2})}}{{L({{({E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{b2}}))}^\lambda }{\rm{ }}\bmod {\rm{ }}{n^2})}}.$

6.通过判断θ_i与“1”的关系, 确定D_i的符号:

$Sign({D_i}) = \left\{ {\begin{array}{*{20}{l}} {1, {\rm{ }}{\theta _i} > 1} \\ {0, {\rm{ }}{\theta _i} = 1} \\ { - 1, {\rm{ }}{\theta _i} < 1} \end{array}} \right., $

其中, Sign(·)为符号函数.

7.如果对于∀i∈{1, 2, …, K-1}都有D_i≤0, 则返回“D=1”; 否则, 返回“D=0”.

3.3 保密社交意愿探测协议保密性分析

定理3.保密社交意愿探测协议可以安全地实现Alice, Bob两方的社交意愿探测.

证明:该协议安全与否的关键是协议执行后有没有造成参与者私有信息的泄露.接下来, 我们将证明保密意愿探测协议在安全计算约谈意愿的过程中, Alice(持有凸多边形的活动区域P, 由顶点${p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}$构成)、Bob(持有位置p_b)两方除了得到“是否约谈”外, 都无法获得有关对方私有数据的其他任何信息, 即协议未给Alice、Bob两方造成信息泄露.

●  对于Alice数据的安全性

我们首先构造一个模拟保密探测协议执行的模拟器$\mathcal{S}$_B.该模拟器的输入为:Alice随机选择一个凸的活动区域${p'_{{a_1}}}, {p'_{{a_2}}}, ..., {p'_{{a_K}}}, $Bob的私有位置p_b, 那么由模拟器$\mathcal{S}$_B产生的视图为(${p_b}, {E'_\mathcal{E}}({a_{{y_{i + 1}}}}), {E'_\mathcal{E}}({a_{{x_i}}}), {E'_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E'_\mathcal{E}}({a_{{y_i}}}), $ ${E'_\mathcal{E}}({a_{{x_{i + 1}}}}), {E'_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}})$), 其中, 1≤i≤k; 而保密社交意愿探测协议的实际执行产生的视图为(${p_b}, {E_\mathcal{E}}({a_{{y_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}), $ ${E_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{y_i}}}), {E_\mathcal{E}}({a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}})$), 其中1≤i≤k.因为Alice传输给Bob的信息是用自己的公钥(n, n+1)对自己的私有信息加密后的密文, 又因方案$\mathcal{E}$已被证明在选择明文攻击下具有语义不可区分安全, 所以由加密方案$\mathcal{E}$产生的密文是语义不可区分的, 可得${E'_\mathcal{E}}({a_{{y_{i + 1}}}}), {E'_\mathcal{E}}({a_{{x_i}}}), {E'_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E'_\mathcal{E}}({a_{{y_i}}}), {E'_\mathcal{E}}({a_{{x_{i + 1}}}}), {E'_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}})$与${E_\mathcal{E}}({a_{{y_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}), $ ${E_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{y_i}}}), {E_\mathcal{E}}({a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}})$是不可区分的.从而可得${\mathcal{S}_B}({E'_\mathcal{E}}({a_{{y_{i + 1}}}}), {E'_\mathcal{E}}({a_{{x_i}}}), {E'_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E'_\mathcal{E}}({a_{{y_i}}}), {E'_\mathcal{E}}({a_{{x_{i + 1}}}}), $ ${E'_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}}), {p_b})$与真实视图$view_B^\Pi ({E_\mathcal{E}}({a_{{y_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}), {E_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{y_i}}}), {E_\mathcal{E}}({a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}}), {p_b})$是不可区分的, 也就是说, 满足定义关系式(2).

●  对于Bob位置信息的私密性

我们构造一个Bob, 输入其私有位置信息以及由其随机选择的${k_b}, {r_{{b_1}}}, {r_{{b_2}}} \in {Z_n}, $就能模拟Alice视图的模拟器$\mathcal{S}$_A.于是, 由模拟器$\mathcal{S}$_A产生的视图为

$({p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}, {E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{{b_1}}}), {E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{{b_2}}}), D).$

因密文${E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{{b_1}}}), {E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{{b_2}}})$是Bob由密文${E_\mathcal{E}}({a_{{y_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}), $ ${E_\mathcal{E}}({a_{{y_i}}}{a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{y_i}}}), {E_\mathcal{E}}({a_{{x_{i + 1}}}}), {E_\mathcal{E}}({a_{{x_i}}}{a_{{y_{i + 1}}}})$通过同态运算计算得到的, Alice获得${E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{{b_1}}}), $ ${E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + {a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{{b_2}}})$后, 通过解密运算, 最多只能得到两个各包含5个未知数的方程, 通过联立方程组计算出具体的$({b_x}, {b_y})$是不可行的, 故$({p_{{a_1}}}, {p_{{a_2}}}, ..., {p_{{a_K}}}, {E_\mathcal{E}}({k_b}({b_x}{a_{{y_{i + 1}}}} + {b_y}{a_{{x_i}}} + {a_{{y_i}}}{a_{{x_{i + 1}}}}) + {r_{{b_1}}}), {E_\mathcal{E}}({k_b}({b_x}{a_{{y_i}}} + {b_y}{a_{{x_{i + 1}}}} + $ ${a_{{x_i}}}{a_{{y_{i + 1}}}}) + {r_{{b_2}}}), D)$与实际执行中的视图是计算不可区分的, 即满足安全定义中的等式(1).

综上所述, Alice和Bob的私密性满足安全定义的形式化等式(1)和等式(2).所以, 保密社交意愿探测协议可以安全地实现Alice、Bob两方社交意愿的探测.

4 保密社交意愿探测协议效率分析

不失一般性, 我们假定Alice和Bob为文献[1]的协议和本文协议的参与者, 并假定Bob的坐标为(b_x, b_y), Alice提供的意愿区域为K个顶点构成的凸多边形.为了进行公平比较, 此处将执行协议时花费的总开销统一用一次自模乘运算($r_x^2{\rm{ }}\bmod {\rm{ }}{n^2}$)作为统计的基本单位.

Alice和Bob在执行文献[1]的协议时, 总共至少需要K(8n+b_x+b_y+2λ)次自模乘运算($r_x^2{\rm{ }}\bmod {\rm{ }}{n^2}$).因为基于云外包计算的同态加密方案$\mathcal{E}$中的计算${R_i} = r_i^n{\rm{ }}\bmod {\rm{ }}{n^2}$可以在预处理阶段由云服务器完成, 并且Alice和Bob在预处理阶段可以随时随地地从云服务器下载集合$R = \{ {R_i}|{R_i} = r_i^n{\rm{ }}\bmod {\rm{ }}{n^2}\} $, 所以得到集合$R = \{ {R_i}|{R_i} = r_i^n{\rm{ }}\bmod {\rm{ }}{n^2}\} $的时间可以忽略不计; 又因为Alice和Bob在得到集合$R = \{ {R_i}|{R_i} = r_i^n{\rm{ }}\bmod {\rm{ }}{n^2}\} $后, 利用集合中的元素, 通过执行有限次的模乘运算($r_x^2\, \bmod \, {n^2}$), 即可秘密地得到$r_x^n{\rm{ }}\bmod {\rm{ }}{n^2}, $不再需要做n次自模乘运算($r_x^2{\rm{ }}\bmod {\rm{ }}{n^2}$).因此, 基于同态加密方案$\mathcal{E}$的保密社交意愿探测协议时, Alice和Bob总计需要花费K(18+2b_x+2b_y+2k_b+2(l+2)+2λ)次自模乘运算($r_x^2{\rm{ }}\bmod {\rm{ }}{n^2}$).显然, 本文的协议比文献[1]的协议在运算效率上有了质变性的提升.

基于同态加密方案$\mathcal{E}$的保密社交意愿探测协议可以解决Alice出具的K个顶点相邻顶点坐标差小于0的情形; 而对于文献[1]的协议而言, 当Alice出具的K个顶点相邻顶点坐标差小于0时, 它无法正确运行.此外, 文献[1]的协议只能用于解决实时位置的近感探测问题, 已经不能满足社交网络用户新的个性化需求; 而本协议不仅可以用于彻底解决文献[1]的协议提出的近感探测问题, 还能满足社交网络用户日益增长的个性化需求:保密社交筹划, 即保密社交意愿探测, 解决的是保密探测领域中的新问题.下表是保密社交探测协议和协议在效率(用执行协议时各参与方在加密和解密算法中花费的计算开销总和体现)、解决问题的能力(从能否解决保密探测区域相邻两点坐标差商小于0的情形体现)以及能够解决的问题这3个方面的对比.保密探测协议与文献[1]的协议的对比分析见表 2.

5 结束语

本文对保密意愿探测问题进行了研究.为了高效地解决这一问题, 首先设计了一个带云辅助计算的同态加密方案; 然后, 利用该加密方案设计了一个高效的保密意愿探测协议.分析结果表明, 此协议在效率和安全性方面都优于先前的类似协议, 并且其安全性是在标准的ideal/real模型下实现的.