2. 中原工学院 电子信息学院 河南 郑州 450007
2. School of Electric and Information Engineering, Zhongyuan University of Technology, Zhengzhou 450007, China
随着工程技术的发展和数学模型的完善, 对于复杂问题的优化主要有以下几个方面的难点:(1)决策变量多, 计算量大; (2)优化目标无法用明示的函数表示, 不好测试; (3)至少有两个目标; (4)不确定性, 环境及问题本身有扰动.因此, 简化复杂问题的表达方式十分必要.对于优化问题的复杂度来说, 决策变量的个数是其主要的决定因素.其中, 把决策变量大的问题定义为大规模问题, 许多科学和工程应用问题都可以设计成大规模问题来进行求解.因为大规模问题具有非线性、不可微等特点, 所以不能使用传统的梯度下降的方法求解[1].大规模优化问题的决策变量非常多, 至少为1 000个, 并且这些变量之间相互联系, 增加了计算的复杂度以及求解的难度.虽然近些年来进化算法在实参优化中取得了很大的成功, 但是在面对大规模问题时往往会遭遇“维数灾难”.随着优化问题维数的增加, 算法的性能急剧下降[2].这是因为维数的增加导致搜索空间成指数的形式扩展, 考虑到进化算法生成的样本均匀分布在全局搜索空间中, 算法的停止条件是该算法在最优区域(即, 在全局最优解的周围的小邻域的搜索空间)内产生一个解决方案时, 达到算法的停止条件.在最佳区域中生成样本的概率是最佳区域的大小除以搜索空间的体积, 所以找到最优解的概率和搜索空间的维数有关, 并且这个概率会随着搜索空间的维数的增加而呈指数下降.优化算法在解决高维问题时一般先进行种群的初始化, 即, 在搜索空间中随机产生种群.当搜索空间比较大时, 理论上产生的种群也应该比较大.但是种群规模越大, 在更新种群时算法所花费的代价也越大.因此, 在低维中性能良好的进化算法在高维中的表现并不能令人满意.
解决复杂问题的基本思路有:(l)以复杂问题空间分解为基础, 将问题分解为子系统、子空间, 适用于将复杂大系统划分为子系统然后再优化, 例如用协同进化算法优化问题[3]; (2)以时间为出发点, 开发并行算法, 如并行遗传算法、并行粒子群优化算法; (3)以空间分解和时间并行为基础, 开发分布式并行计算[2].
本文针对大规模问题的高维特性提出了一种有效的分组策略.将大规模复杂问题分解为一个个单维或低维的简单问题来解决, 是近些年的常见策略.根据这个思想, 论文提出了将动态随机分组的协同进化机制嵌入种群分组的动态多种群算法中, 实现维数和种群的双分组, 动态维数分组可以解决决策变量多且变量之间相互关联的问题, 而动态多种群则可以解决多模态和算法收敛过快陷入局部最优的问题.然后, 调节算法中的具体策略并对策略进行测试, 选取最佳策略, 提高算法的性能.最后, 将论文中提出的算法和其他算法在测试平台上进行对比, 测试验证结果的有效性.
1 相关工作自从大规模优化算法成为当前科学和工程领域的研究热点以来, 已经有很多学者提出了解决大规模全局优化问题的几个特定机制.总的来说, 主要有两种方式:一种是问题维数分组的协同进化策略, 另一种是不分组的方法.协同进化策略是受分治(divide-and-conquer)策略启发而来, 主要是将大规模复杂问题的高维分解成低维简单问题分别进行优化求解, 最后分组求解的结果结合成最终的高维解[4]; 而不分组策略是针对大规模问题的特点利用新的进化算法或在原有的算法中加入局部搜索策略、禁忌搜索策略等方式对优化问题的整体求解.
将维数分解的策略是由Potter在1994年提出的策略[5], 他们在遗传算法中加入协同进化策略, 将问题分成单维问题求解, 并在30维的问题上进行了测试, 但是并没有测试更高的维数.但是由于决策变量之间有具有相互关联的特性, 会使分成单维的策略产生“两步向前, 一步向后”的缺点.简单来说, 就是个体的适应度值改进了, 但是粒子的某一方向上的位置距离期望值更远了, 因此, 将维数分组是其中一个比较好的策略.Frans在2004年提出了两个新的协同进化离子群优化算法(cooperative particle swarm optimization, 简称CPSO)的模型, 将该策略和粒子群优化算法结合起来[6].上面两种算法使用的是静态的协同进化策略, 但是在部分可分的测试问题中, 将不可分的决策变量分到两个组中会使得算法一直不能找到最优解, 因此, 动态的分组策略比较可行.Yang等人在2008年提出了动态的协同进化策略(self-adaptive differential evolution with neighbourhood search with cooperative coevolution, 简称DECC-G), 利用自适应权重的方法调节各个决策变量所占的比例[7].Li等人在2009年提出了新的协同进化粒子群优化算法(cooperative coevolving particle swarm optimization, 简称CCPSO), 在算法中加入了随机分组和自适应加权策略, 证明在高维不可分问题中是有效的.将早前提出的只能优化30维的CPSO算法扩展到了1 000维的高维问题中[8].该作者在2012年对CCPSO算法进行了优化, 提高了算法性能, 使其可以解决2 000维的优化问题[9].2016年, Mahdavi提出了基于变量效应的多级优化框架, 在优化所有维数之前先优化最重要决策变量的分组, 这种方法是一种基于学习的协同进化策略[10].前面介绍的算法均是使用协同进化策略将问题分解, 减少问题复杂度的方法.还有不使用维数分组策略的算法, Zhao在2008年将局部搜索策略加入算法中求解大规模问题, 也取得了不错的结果[11].2015年, Cheng等人提出了社会学习粒子群优化算法(social learning particle swarm optimization, 简称SLPSO)[12]和竞争学习算法(competitive swarm optimizer, 简称CSO), 也可以用于求解大规模问题[13].2017年, Omidvar等人提出了DG2算法(differential grouping)用于解决大规模的黑盒问题, 通过估计舍入误差的大小来找到可靠的阈值, 在效率和精度方面, DG2在最新的大型连续优化基准套件上胜过最先进的分解方法.DG2在目标函数中决策变量的贡献不平衡的情况下也能可靠地执行[14].文献[15]也提供了一种分治策略的新思路, 将一个子问题看做是一个计算上昂贵的问题并通过元模型来解决, 提出了一种新颖的方法, 即自我评估演化(self-evaluation evolution, 简称SEE), 并分析其优缺点.文献[16]中提出了一种将协作共同演化方法与各种类型的模拟算法相结合的异构框架, 使用协同进化方法将大问题分解为子问题以提高解决过程的效率, 然后使用各种异构模拟算法来解决子问题.所提出的异构框架为每个解决方案自适应地分配不同的运算符、参数值和本地搜索算法, 以有效地探索和利用给定问题实例的搜索空间.
2 大规模优化问题描述大规模优化问题可以用公式(1)表述:
| $ \begin{gathered} \min /\max F(x) = f({x_1}, {x_2}, ..., {x_D}) \hfill \\ {x_i} \in [{x_{\min }}, {x_{\max }}], i = 1, 2, ..., D \hfill \\ \end{gathered} $ | (1) |
其中, F(x)表示优化问题的目标函数, 在单目标优化问题中, 可以理解为一个实值连续非线性目标函数从D维空间映射到一维适应度值F(x)[14].xi∈[xmin, xmax]表示边界约束, 虽然也是约束条件的一种, 但是一般来讲, 有边界约束的问题就是无约束优化问题[15].xi表示决策变量, D表示决策变量的个数(即优化问题的维数), 并且在大规模设置中, 决策变量的个数D一般大于100, 通常达到1 000维以上.本文介绍的解决方案主要针对该问题中最小化问题进行求解.
3 基于协同进化的动态多种群粒子群优化算法针对大规模优化问题, 本文提出了一种基于协同进化策略的动态多种群粒子群优化算法.对维数的动态随机分组, 不仅简化了问题的复杂度, 并且兼顾了决策变量之间的相互关系.对种群的分组, 增加了粒子的多样性, 降低了算法的收敛速度, 避免了算法陷入局部最优位置.
3.1 动态多种群粒子群优化算法不同于其他已存在的进化算法, 粒子群优化算法并不需要特别大的种群规模.特别是对于简单的问题, 3个~5个粒子的种群就可达到满意的优化结果.粒子群优化算法中除了全局优化的版本, 还有局部优化的版本.全局优化版本中, 粒子向当前代的全局最优学习; 局部优化版本和全局优化的版本有些相似, 粒子一般不向全局最优解学习, 向邻域最优解学习, 这种方法的优点是可以避免算法收敛过快, 陷入局部次优解, 增加种群的多样性.因为局部优化的版本中粒子是向其邻域最优学习的, 所以定义粒子的邻域范围比较重要.为了更好地确定邻域范围, 引入拓扑结构是十分必要的.有了拓扑结构的引入, 实验者可以根据拓扑结构确定邻域, 以便更好地找到局部最优解.这种方法在多模态优化问题上有十分优秀的效率.
在动态多种群粒子群优化算法(dynamic multi-swarm particle swarm optimizer, 简称DMS-PSO)中, 可以根据邻域结构把大种群分成很多小种群, 增强算法的局部优化能力[16].为了避免此算法不收敛, 小种群的信息必须保证可以互相交换, 因此, 这些小的种群根据不同的重组策略经常被重组.在频繁重组的过程中, 这些种群之间就在不断地交换信息.将重组周期设为R.DMS算法的搜索方式如图 1所示.

|
Fig. 1 DMS-PSO's search 图 1 DMS-PSO的搜索方法 |
如图 1所示, 假设种群规模为9, 将其随机分成3个小种群, 每个小种群中有3个粒子.使用粒子群算法的局部版本对3个小种群进行优化.在这个周期中, 9个粒子可能会收敛到3个局部最优位置.然后对整个种群进行重组, 这些新的小种群再开始他们的搜索, 这个过程一直持续到一个停止条件被满足.通过这种随机重组的方法, 小种群中的粒子的搜索空间被扩展且这些小种群更容易找到一个较好的解.
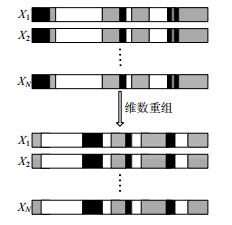
3.2 动态随机协同进化策略该策略的主要思想是将大规模复杂问题分解为一个个单维或低维的简单问题解决.协同进化(cooperative coevolution, 简称CC)策略在早期阶段是静态分组, 这种分组没有变化.但这种分组方法在解决不可分和部分可分的大规模问题上是无效的, 而且算法的结果决定于最开始的分组情况, 所以这种方法的性能非常不稳定.理论上可以将相关的决策变量分到一组, 不相关的决策变量分开优化, 但是在1 000个决策变量中, 求解决策变量之间的相关性会花费巨大的评价次数和时间, 并且还要保证求解必须十分准确, 所以在早期求解决策变量的相关性的操作并不可行.因此, 使用动态分组方法来改善这一不足之处.动态随机分组的协同进化机制如图 2所示.
|
Fig. 2 Mechanism of CC with dynamic random grouping 图 2 动态随机协同进化机制 |
如图 2所示, 种群pop(X1, X2, …, XN), 其中, N为种群规模, 首先将每个粒子的维数随机分组, 例如问题维数为20维, 随机分成3组, 每组有7维, 最后一组和第一组有1维重合, 这样设计的好处是:没有对问题的维数做出硬性规定, 可以测试多种维数的问题.然后对每组的维数进行更新.将种群中所有粒子的维数随机分成3组, 如图 2黑色部分、网状部分和白色部分所示, 每组分别使用DMS算法进行优化, 在优化时, 每组迭代次数设为Max_oneiter.所有的维数都优化过后, 重新对维数进行随机分组, 应当指出的是所有的决策变量都应该被优化.
基于协同进化策略的动态多种群粒子群优化算法的基本流程分为两部分:
首先利用协同进化策略将种群粒子的维数进行维数分组, 优化问题的总维数是D, 将维数随机分为group_D个维数小组, 每一维数小组有Dim维, 每组覆盖的维数是Diml, 即D=group_DxDim, 当没有小组之间没有维数覆盖时, Diml=0.本文设计的协同进化策略是动态随机分组的, 并没有对决策变量之间的相互关系进行求解, 所以在设计维数分组策略时加上了维数之间的叠加, 使维数连接更紧密.维数分组策略的伪代码见算法1.
算法1.动态随机协同进化算法.
1. pop(1:NP, 1:D) //随机初始化种群
2. (best, best_val)//计算适应度值, 找出当前最优解
3. While FEs < 0.95×Max_FEs
4. ind(1:D)←randperm(D)
5. index(1:2D)←repmat(2D)
6. For j←1 to group_D
7. l←(j-1)×(Dim+Diml)+1
8. U←j×(Dim+Diml)
9. pop_D←pop(:, index(l:u)) //对维数随机分组后的子部分
10. pop(:, index(l, u))←DMS-PSO(best, pop_D, Max_oneiter) //使用DMS-PSO对维数随机分组后的小组进行优化
11. (best, best_val) //计算适应度值, 找出当前最优解
12. End for
13. End while
14. While FEs≤Max_FEs
15. (best, best_val)←PSO(best, pop, Max_FEs)
16. End while
17.返回(best_val)
在上面的动态随机协同进化算法中, 主要是对粒子的维数进行分组, 要注意的是D≠group_D×Dim, 这样的设计是为了测试多种维数的问题.然后, 对已经分好组的维数小组分别使用动态多种群粒子群优化算法进行优化, 在优化每个维数小组时, 需要将整个大种群随机分为n个小种群, 每个小种群的种群规模为m, 即N=n×m, R表示种群重组的循环次数, Max_FEs表示最大评价次数, Max_oneiter表示维数分组后每组优化的最大迭代次数.动态多种群粒子群优化算法的伪代码见算法2.
算法2.动态多种群粒子群优化算法.
1. pop_D(1:N, 1:Dim) //输入的维数分组后每组的种群
2. (best_D, best_val_D)//使用gbest代替其他没有被选中优化的维数, 计算pop_D的最优解
3. gen=0
4. While gen≤max_oneiter
5. index(1:N)←randperm(N)
6. For i←1 to n
7. l’←(i-1)×m+1
8. u’←i×m
9. pop_g←pop_D(index(l’:u’), :) //将种群随机分成小种群
10. 找出pop_g的lbest
11. For d=1:Dim
12. vid=w×vid+c1xrand1id×(pbestid-xid)+c2xrand2id×(lbestid-xid)
13. vid=min(max(vid, vi, min), vi, max)
14. xid=xid+vid
15. If rand>0.5
16. xid=min(max(xid, xi, min), xi, max)
17. Else
18. If xid < xi, min
19. xid=xi, min+(xi, min-xid)
20. Else
21. xid=xi, max-(xid-xi, max)
22. End if
23. End if
24. End for
25. gen=gen+1
26. If mod(gen, R)==0
27. 对种群随机重新分组
28. End if
29. End for
30. End while
上面的DMS算法在进行粒子更新的时候使用的是粒子群优化算法的局部版本, 如步骤12.大规模优化问题的基准测试集中规定了搜索空间的上下限, 所以粒子的位置不能超过边界[Xmin, Xmax], 而粒子的速度不能超过边界[Vmin, Vmax].在本文的算法中, 设定Vmax=20%Xmax.当粒子的速度超过速度边界时, 选取边界作为更新速度, 如步骤13.当粒子位置超过位置边界时, 有50%的概率选择边界作为更新的位置, 剩下50%的概率超过边界的距离就返回相应的距离, 如步骤15~步骤23.
4 实验对比与结果分析实验选取了DECCG, SLPSO, CSO以及DMS-PSO和DMS-CC对比.和DMS-PSO对比, 是为了验证新提出的策略的有效性.DECCG在IEEE Congress on Evolutionary Computation中的大规模全局优化算法竞赛中取得了良好的结果, 而SLPSO和CSO是最近提出的两个大规模优化算法.和这些算法对比, 可以验证基于协同进化策略的动态多种群粒子群优化算法的有效性.5个算法的参数设置如下.
(1) DECCG:种群大小为100, 1 000维, 维数分为10组, 每组100维, 循环次数cycle=50;
(2) SLPSO:种群大小为100, α=0.5, β=0.01;
(3) CSO:种群大小为500, φ=0.15;
(4) DMS-PSO:种群大小为60, c1=c2=1.49445, w=0.729, 种群分为20组, 每组有3个粒子;
(5) DMS-CC:种群大小为60, c1=c2=1.49445, w=0.729, 种群分为20组, 每组有3个粒子, 维数分为20组, 循环次数Max_oneiter=100.
上面5个算法分别独立运行25次, 最大评价次数为3000×D.表 1给出了5种算法的测试结果, 结果取25次的平均值.图 3~图 6表示5种算法的15个测试函数的收敛图, 数据取25次的中值.
| Table 1 Experimental result 表 1 运行结果 |

|
Fig. 3 Convergence graph of test function F1~F6 图 3 测试函数F1~F6的收敛图 |

|
Fig. 4 Convergence graph of test function F7~F12 图 4 测试函数F7~F12的收敛图 |

|
Fig. 5 Convergence graph of test function F13~F15 图 5 测试函数F13~F15的收敛图 |
测试函数为CEC2013大规模全局优化算法测试函数集, 该测试集一共有15个测试函数, 包含了不可分、完全可分以及部分可分问题, 同时包含单模和多模特性.在实验中, 每个算法独立运行25次, 算法的最大评价次数为3000×D.除了函数F13和F14的维数设定的是905, 其他的测试函数维数设定为1 000.因为算法DECCG只能优化1 000维的问题(分组是固定的), 而算法SLPSO在选择学习目标时涉及到概率问题只能测试维数为10的倍数的测试函数, 所以这两种算法均不能测试函数F13和F14.
从结果我们可以看出DMS-CC算法在解决大规模优化问题时的有效性, 其中, 测试函数F2、F3、F5、F6、F7、F9和F10的结果比较好, 上面的7个函数均为多模态问题, 这是由于动态多种群的特点决定的, 它将种群分成多个小种群, 每个小种群在一定的搜索空间中搜索, 不同于其他算法在一开始就向一个位置靠拢, 在快速收敛的同时忽略了其他的位置, 比较容易陷入局部最优位置.它具有更好的局部搜索能力, 并且种群的多样性比较好.在测试函数F4中, 由于DECCG和DMS-CC算法都是使用了维数分组的协同进化策略, 测试函数中具有相关性的维数较多, 所以具有协同进化策略的算法普遍没有一般算法的结果好.结果比较不理想的是测试函数F1, 该测试函数的决策变量之间并没有相关性并且是单模态问题, 所以在评价次数一定的条件下, 算法收敛能力强的算法结果比较好, 由于动态多种群策略的局部搜索能力强, 牺牲了部分全局搜索能力, 使得算法的收敛能力不强, 所以算法DMS-PSO和DMS-CC的测试结果不好.在今后的工作中, 可以加上收敛能力较强的一些全局优化策略.
5 总结与展望本文针对大规模问题的高维特性, 提出了一种有效的分组策略.将大规模复杂问题分解为一个个单维或低维的简单问题来解决, 是近些年的常见策略.根据这个思想, 论文提出了将动态随机分组的协同进化机制嵌入种群分组的动态多种群算法中, 实现维数和种群的双分组, 动态维数分组可以解决决策变量多且变量之间相互关联的问题, 而动态多种群则可以解决多模态和算法收敛过快陷入局部最优的问题.最后, 将论文中提出的算法和其他算法在基准测试函数集测试进行对比实验, 验证结果的有效性.但是还存在如下一些问题, 有待在未来的工作中得到解决.
(1) 参数的调节:新算法使用的参数是固定的, 并没有对参数进行深入讨论, 增加参数的自适应机制, 减小算法的复杂度;
(2) 基于学习的协同进化策略:新算法使用了随机动态的协同进化策略, 没有解决决策变量之间的相互关系.有学者提出了基于学习的协同进化策略, 即:在算法的前期先判断决策变量之间的相互关系, 将相关的变量分到一组.但是引入学习机制会花费巨大的评价次数, 减少算法在后期优化过程中的评价次数, 所以平衡前期求解决策变量之间相关性的工作花费, 在后期有待研究;
(3) 实际应用:本文提出的算法在测试平台上有不错的结果, 但是在实际应用中的结果并没有验证, 所以算法在大规模流水线加工等实际优化问题的效果有待验证.
| [1] |
Mahdavi S, Shiri ME, Rahnamayan S. Metaheuristics in large-scale global continues optimization:A survey. Information Sciences, 2015, 295: 407–428.
[doi:10.1016/j.ins.2014.10.042] |
| [2] |
Liu JP. CMA-ES and decomposition strategy for large scale continuous optimization problem[Ph. D. Thesis]. Hefei: University of Science and Technology of China, 2014(in Chinese with nglish abstract). |
| [3] |
Potter MA. The design and analysis of a computational model of cooperative coevolution. George Mason University, 1997. |
| [4] |
Omidvar MN, Li X, Mei Y, et al. Cooperative co-evolution with differential grouping for large scale optimization. IEEE Trans. on Evolutionary Computation, 2014, 18(3): 378-393.http://ieeexplore.ieee.org/document/6595612/ |
| [5] |
Potter MA, Jong KAD. A cooperative coevolutionary approach to function optimization. In: Proc. of the Int'l Conf. on Parallel Problem Solving from Nature. Berlin, Heidelberg: Springer-Verlag, 1994. 249-257. |
| [6] |
Frans VDB, Engelbrecht AP. A cooperative approach to particle swarm optimization. IEEE Trans. on Evolutionary Computation, 2004, 8(3): 225-239.https://dl.acm.org/citation.cfm?id=2221682 |
| [7] |
Yang Z, Tang K, Yao X. Large scale evolutionary optimization using cooperative coevolution. Information Sciences, 2008, 178(15): 2985–2999.
[doi:10.1016/j.ins.2008.02.017] |
| [8] |
Li XD, Yao X. Tackling high dimensional nonseparable optimization problems by cooperatively coevolving particle swarms. In: Proc. of the IEEE Congress on Evolutionary Computation (CEC 2009). IEEE, 2009. 1546-1553.http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4983126 |
| [9] |
Li XD, Yao X. Cooperatively coevolving particle swarms for large scale optimization. IEEE Trans. on Evolutionary Computation, 2012, 16(2): 210-224.http://ieeexplore.ieee.org/document/5910380/ |
| [10] |
Mahdavi S, Rahnamayan S, Shiri ME. Multilevel framework for large-scale global optimization. In: Proc. of the Soft Computing. 2016. 1-30. |
| [11] |
Zhao SZ, Liang JJ, Suganthan PN, et al. Dynamic multi-swarm particle swarm optimizer with local search for large scale global optimization. In: Proc. of the IEEE World Congress on Computational Intelligence, IEEE Congress on Evolutionary Computation (CEC 2008). IEEE, 2008. 3845-3852. |
| [12] |
Cheng R, Jin Y. A social learning particle swarm optimization algorithm for scalable optimization. Information Sciences, 2015, 291(6): 43–60.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ0233778108 |
| [13] |
Cheng R, Jin Y. A competitive swarm optimizer for large scale optimization. IEEE Trans. on Cybernetics, 2015, 45(2): 191.http://ieeexplore.ieee.org/abstract/document/6819057/ |
| [14] |
Omidvar MN, Yang M, Mei Y, et al. DG2: A faster and more accurate differential grouping for large-scale black-box optimization. IEEE Trans. on Evolutionary Computation, 2017, 21(6): 929-942.http://ieeexplore.ieee.org/document/7911173/ |
| [15] |
Yang P, Tang K, Yao X. Turning high-dimensional optimization into computationally expensive optimization. IEEE Trans. on Evolutionary Computation, 2018, 22(1): 143-156.http://ieeexplore.ieee.org/document/7862192/ |
| [16] |
Sabar NR, Abawajy J, Yearwood J. Heterogeneous cooperative co-evolution memetic differential evolution algorithm for big data optimization problems. IEEE Trans. on Evolutionary Computation, 2017, 21(2): 315-327.http://ieeexplore.ieee.org/document/7552543/ |
| [17] |
Liang J, Song H, Qu BY, et al. Research on path planning problems based on improved particle swarm optimizer. Journal of Zhengzhou University (Engineering Science), 2014, 35(1): 34–38(in Chinese with English abstract).
[doi:10.3969/j.issn.1671-6833.2014.01.008] |
| [18] |
Yan XF, Yan JJ, Feng Y. Gradient and particle swarm optimization based hierarchical cluster algorithm in WSN. Journal of Zhengzhou University (Engineering Science), 2016, 37(2): 33–36(in Chinese with English abstract).
http://d.old.wanfangdata.com.cn/Periodical/zzgydxxb201602007 |
| [19] |
Liang JJ, Suganthan PN. Dynamic multi-swarm particle swarm optimizer with local search. In: Proc. of the 2005 IEEE Congress on Evolutionary Computation. IEEE, 2005. 522-528.http://ieeexplore.ieee.org/document/1554727/ |
| [2] |
刘金鹏. 面向大规模实值优化问题的CMA-ES算法及其分制策略研究[博士学位论文]. 合肥: 中国科学技术大学, 2014.
|
| [17] |
梁静, 宋慧, 瞿博阳, 等. 基于改进粒子群算法的路径优化问题研究. 郑州大学学报(工学版), 2014, 35(1): 34–38.
[doi:10.3969/j.issn.1671-6833.2014.01.008]
|
| [18] |
阎新芳, 严晶晶, 冯岩. WSN中基于梯度和粒子群优化算法的分级簇算法. 郑州大学学报(工学版), 2016, 37(2): 33–36.
http://d.old.wanfangdata.com.cn/Periodical/zzgydxxb201602007
|
 2018, Vol. 29
2018, Vol. 29


