2. 陕西省嵌入式系统技术重点实验室(西北工业大学), 陕西 西安 710072;
3. 北方民族大学 计算机学院, 宁夏 银川 750021
2. Shanxi Provincial Key Laboratory for embedded system(Northwestern Polytechnical University), Xi'an 710072, China;
3. College of Computer, Beifang University of Nationalities, Yinchuan 750021, China
社会学、信息科学与技术、生物学和统计物理学等领域的各种系统中存在大量的关系信息, 例如, 学术论文间的引用关系, 万维网中网页间的超链接关系, 生物细胞系统中蛋白质的物理交互关系, 航空交通网络中城市间航班往来, 社交网络中人和人的交互等.人们常常采用网络对这些复杂系统中的关系信息进行建模, 称为复杂网络.随着移动互联网、普适计算[1]、生物计算、社会感知计算[2]、城市计算等应用技术的发展, 对包含复杂关系信息的海量数据进行分析和挖掘已经成为很多行业和领域最迫切的需求, 为复杂网络分析带来了新的机遇和挑战.
贝叶斯模型作为一种重要的统计建模方法因其具有完备的理论基础和可解释性, 已经被广泛用于对网络数据进行建模和预测.可交换性假设是采用贝叶斯模型对网络数据进行建模的重要前提, 网络数据的可交换性是指节点的出现顺序不影响统计网络模型的定义.de Finetti[3]提出了随机变量序列的可交换性, 称作de Finetti表示理论; Aldous[4]和Hoover[5]提出了随机数组的可交换性, 称作Aldous-Hoover表示理论; Kallenberg[6]提出了随机测度(采用连续时间中的随机点过程表示网络数据)的联合可交换性和分部可交换性, 称作Kallenberg表示理论. Aldous-Hoover表示理论推动了贝叶斯统计模型用于网络数据建模的发展, 很多著名的随机图模型如ER模型[7]、SBM模型[8]、MMSB模型[9]、IRM模型[10]等都可以纳入这一框架(Aldous-Hoover可交换图, 简称AHEG[11]), 对这一类模型的性质和推理方法的研究也取得了很大的进展.然而, AHEG模型要么只能生成空图, 要么只能生成稠密图, 不能产生稀疏图[12], 即AHEG模型不能同时满足可交换性和稀疏性.
实证结果表明, 真实世界中的很多复杂网络都具有节点度幂律分布的稀疏特征, Barabási提出的PA (preferential attachment)模型[13]为了生成具有幂律特征的稀疏网络, 放弃了可交换性, 因而PA模型只适用于解释网络整体结构属性(如节点度分布), 不能用于进行社区发现和链路预测[14].Bollobás等人、Wolfe等人、Borgs等人提出一个折衷的方向, 基于重新调节标度的方法来产生有限可交换的稀疏图序列, 然而这类方法生成的可交换稀疏网络却不满足可投影特性, 也就不保证随机图随节点数增加产生的图序列具有一致的分布(可投影特性是采用流方式处理网络数据的重要前提), 因而基于Aldous-Hoover表示理论的统计生成模型具有先天缺陷[11].
Caron等人[15]利用随机测度和随机图间的联系提出了采用可交换随机测度来对网络数据进行建模, 将网络表示成随机点过程而不是邻接矩阵, 基于Kallenberg表示理论, Caron-Fox模型既可以生成稠密可交换图也可以生成稀疏可交换图, 解决了可交换性和稀疏性二者不可兼得的矛盾.稀疏可交换图建模由此成为学术界的研究热点, 伴随大量的相关研究工作产生了很多重要的理论和方法.
本文对稀疏可交换图建模的研究进展进行综述.第1节讨论随机图模型、Graphon模型、Graphex模型、贝叶斯非参数混合模型、可交换性表示理论、泊松点过程、完全随机测度、带独立增量的归一化随机测度、可交换分区概率函数等理论基础.第2节介绍有向多图和带自边的无向图所对应的Caron-Fox模型.第3节总结进行稀疏可交换图模型的随机模拟所涉及的截断采样和边缘化采样方法的研究发展, 重点描述通过条件采样构造CRM的Adaptive Thinning算法和通过边缘化采样构建稀疏可交换图的Pólya Ura Scheme方法.第4节对Caron-Fox模型后验推理过程采用的MCMC近似推理算法进行综述, 详细阐述哈密顿MCMC算法, 并对切片采样算法和指数倾斜稳定分布的采样进行说明.第5节对稀疏可交换图建模的最新研究进展和研究前景进行介绍.
1 相关理论 1.1 随机图模型(random graph model)随机图是利用观测数据理解复杂网络结构的重要工具, 其基本原理是:观测到的图结构是由一个潜在数据生成过程(即随机图模型)产生的, 从最大似然性思想出发, 在模型空间中寻找使观测数据具有最大出现可能性的模型, 其独特之处在于可以用概率的方法来证明所需要的图的存在性, 而不必把图真实构造出来.
定义1.1. 一个随机图模型是一族编了索引的图值(graph-valued)随机变量Gs, ϕ, s定义了图的尺寸(取值自一个完全有序集合S), ϕ是模型参数, 决定了图Gs, ϕ的一些分布特性, Gs, ϕ的分布记为gs, ϕ[11].
例1.1(ER模型):经典随机图模型由埃尔德什和莱利[7], 是n个节点上的一族简单随机图Gn, p, n∈N, 节点间连边的概率为p∈(0, 1), 边的产生是相互独立的.可以将Gn, p直观地表示成一个n×n随机邻接矩阵(一个对称的存放0, 1值的n×n数组, 其对角线全部是0), 统计分析的目标之一就是利用给定观测数据推理参数p.
为了更准确地对真实网络进行建模, 随机图模型的一个重要属性就是节点数和边数之间的关系.随机图模型Gs, ϕ, 给定参数ϕ, 记sn↑∞表示一个递增趋向于无穷大的尺寸参数序列.给定一个图G, ν=|v(G)|表示节点数, e=|e(G)|表示边数, 假设n→∞时ν→∞.若当n→∞时
例1.2(KEG):Kallenberg可交换图Gu, ϕ, 尺寸参数s不是自然数n(这是一种常用的随机图族编索引的方法), 而是一个非负实数v,
统计网络分析的固定模式是:观测到的网络gs被建模成Gs, ϕ的一个实例(参数s已知, ϕ未知), 网络分析的目的就是推理出ϕ.某些随机图模型中, 序列Gs1, f, Gs2, ϕ, ...是一个网络演化动力学模型, 尺寸s与采样大小有关, 随着采样到的观测数据的增多, 图的尺寸也在增大, 此时自然就必须考虑不同尺寸下的网络应该在分布上满足一致性(consistency).一致性可以通过要求随机图模型分布是可投影的(projective)来表述.可投影性定义在可投影系统(projective system)中, 即一族可测映射(fs, t; s≤t∈S), fs, t将尺寸为t的随机图映射到尺寸为s≤t的随机图, ft, t是同等映射, fr, t=fr, sofs, t, (r≤s≤t)[11].
定义1.2. 若存在可投影系统fs, t; s≤t∈S, 使得对于任意s < t和参数ϕ, 都有
定义1.3. Graphon是定义在概率空间上的, 在[0, 1]上取值的可测对称函数Θ:[0, 1]2→[0, 1].Graphon是无限随机图序列(Gs, ϕ)的极限[11].
例1.3(AHEG模型):Aldous-Hoover可交换图是n个节点上的一族简单随机图Gn, Θ, n仍然表示节点数, 但是参数ϕ不再是概率p, 而是一个对称可测随机函数Θ:[0, 1]2→[0, 1], 称作graphon[11].ER模型可以看做是AHEG的一个特例, 即Θ(x, y)=p是一个常graphon.
对于无限图, Aldous-Hoover表示理论断言:一个随机图具有可交换性当且仅当其分布是定义在特定的一族各态历经测度(ergodic measures)上的一个混合分布, 每一个各态历经测度就是一个graphon, 由此导致的一个必然结果是n个节点间的期望连边数为
随机图模型的一般结构:给定一个Graphon, 必定存在一个对应的具有可数无限可交换性的随机图G(n, Θ), 相应的随机邻接矩阵(Gij)ij∈N定义为
| $ \left\{ \begin{array}{l} \quad \quad \quad \;\;\mathit{\Theta } \sim \mu \quad \quad \quad \, \\ \quad \quad \quad \;{U_i}{ \sim _{iid}}Uniform[0, 1]\quad {\rm{for}}\, i \in {\bf{N}}\\ {G_{ij}}|\mathit{\Theta } , {U_i}, {U_j}{ \sim _{ind}}Bernoulli(\mathit{\Theta } ({U_i}, {U_j})) \end{array} \right. $ | (1.1) |
相应的随机邻接测度
| $ \left\{ \begin{array}{l} \quad \quad \quad \;\;\, \, {N_\alpha } \sim Poisson(c\alpha )\\ \quad \quad \;\{ {\theta _i}\} |{N_\alpha } \sim {\;_{ind}}Uniform[0, \alpha ]\\ \quad \quad \;\{ {\vartheta _i}\} |{N_\alpha } \sim {\;_{ind}}\;Uniform[0, 1]\\ ({\theta _i}, {\theta _j})|\mathit{\Theta } , {\vartheta _i}, {\vartheta _j} \sim {\;_{ind}}{\rm{ }}Bernoulli(\mathit{\Theta } ({\vartheta _i}, {\vartheta _j})) \end{array} \right. $ | (1.2) |
| $ \mathit{\Theta } ({\vartheta _i}, {\vartheta _j}) = \left\{ {\begin{array}{*{20}{l}} {1 - \exp ( - 2{{\bar \rho }^{ - 1}}({\vartheta _i}){{\bar \rho }^{ - 1}}({\vartheta _j}), }&{{\rm{if}}\;{\vartheta _i} \ne {\vartheta _j}}\\ {1 - \exp ( - {{\bar \rho }^{ - 1}}{{({\vartheta _i})}^2}), }&{{\rm{if}}\;{\vartheta _i} = {\vartheta _j}} \end{array}} \right. $ | (1.3) |
将一个分布建模成由很多简单分布混合而成, 既是一种有用的非参数密度估计方法, 又是一种对解释变量间依赖关系的潜在类进行识别的重要方法.可以采用以某个先验分布作为混合比例的层次贝叶斯框架来处理由可数无限个成份组成的混合分布, 混合比例有助于找到起决定作用的混合成份.
非参数贝叶斯估计的灵活性能够带来更好的预测性能, 原因在于其学习能力不会饱和, 从而使得预测性能可以随着观测数据的增多而持续提升[16].最大后验估计方法进行推理的目标只是找到某个特定的使后验最大的参数, 进行预测的时候只用一个模型; 而NPB估计方法进行推理的目标的则是学习参数的分布(即考虑所有可能的参数), 进行预测的时候把不同的模型都考虑进来, 无穷多种模型按相应的重要性权重一起发挥作用.令D表示观测样本集, Θ表示模型的所有参数, x*表示做预测的新样本,
| Table 1 Contrast between MAP and NPB 表 1 MAP和NPB的对比 |
1.2 可交换性表示理论
模型空间中存在大量可选的随机图模型, 然而大部分模型都只能建模出真实网络的一部分特性, 换个角度可能就变成了病态模型, 因此很难评估这些模型的统计可用性.想要找到既易于处理, 又足够灵活(可以较准确地解释真实世界中各种现象)的随机图模型, 就必须做出一定假设, 可交换性假设是非常重要的一种假设, 是指生成模型不依赖于观测样本出现的顺序, 或者说变换节点的标签不会改变图模型的概率分布(即节点的标签不提供图结构的任何信息)[11].
可交换性是最常见的一种统计不变性(invariant), 也称为概率对称(probability symmetry), 具有统计不变性的分布族, 其结构可以通过各态历经分解(ergodic decomposition)来解释, 或者说采用表示理论来更直观地刻画[11].以下首先介绍最简单的随机序列的可交换性表示理论, 然后将可交换性推广到更复杂的随机结构, 包括随机数组的可交换性表示理论、随机测度的可交换性表示理论, 并且对与可交换随机测度密切相关的可交换随机分区进行阐述.各种表示理论见表 2.
| Table 2 Overview of representation theorems 表 2 各种表示理论 |
定义1.4. 一个随机变量序列, 若对序列元素下标进行任意排列不改变序列的联合分布, 称序列是可交换的(X1, X2, ...)
定理1.1(de Finetti表示理论). 随机序列(Xi)i∈N具有可交换性当且仅当存在Χ上的一个随机概率测度Θ, 满足
从概率角度来看, Θ表示了观测数据的公共结构, 而统计推理出的条件概率Pr(Xi|Θ)则捕获了每个观测变量独有的随机性.
定义1.5. 二维随机数组X=(Xij)ij∈N称作可交换数组, 若满足(Xij)(Xπ(i)σ(j))(Xπ(i)σ(j)), 对于任意下标置换π和σ.当π=σ时, 称作联合可交换, 否则称为分部可交换[11].
定理1.2(Aldous-Hoover表示理论). 二维随机数组(Xij)ij∈N具有可交换性当且仅当存在一个随机可测函数F:[0, 1]3→
定义1.6. 空间
此时, Aldous-Hoover表示理论可以进一步简化为:无向图是可交换的, 当且仅当存在一个参数对称的随机函数Θ:[0, 1]2→[0, 1], 使定理1.2满足
Caron等人建立了随机图和对称点过程的对应关系:将随机图中的节点看作任意实数x, 将边看作

|
Fig. 1 Point process representation of a random graph 图 1 随机图的点过程表示 |
定义1.7. 一个简单无向图可以采用实平面
定义1.8.
| $ (Z({A_i}, {A_j}))\underline{\underline d} (Z({A_{\pi (i)}}, {A_{\sigma (j)}}))(Z({A_{\pi (i)}}, {A_{\sigma (j)}})) $ | (1.4) |
这里, 区间Ai=[h(i–1), hi], i=N, 考虑任意小的区间Ai以确保节点i和j不会落入同一个区间[15].
采用一个纯原子的简单随机测度来表示简单点过程更便于进行处理, 将点过程的每个点用随机测度中的每个原子来表示, 就得到了随机图的邻接测度(adjacent measure)表示, 即KEG(Kallenberg可交换图).不同于邻接矩阵表示的AHEG, KEG在连续空间取节点, 因此无限图G在某个有限区域截断得到受限图Gt=G(.I[0, t]2), 其节点个数是个随机量, 此外, KEG中节点至少要与1条边关联[11].
定义1.9.
定理1.3(Kallenberg表示理论).
| $ \xi = \sum\limits_{i, j} {f({\alpha _{}}, {\vartheta _i}, {\vartheta _j}, {\zeta _{\left\{ {i, j} \right\}}}){\delta _{{\theta _i}, {\theta _j}}}} + $ | (1.5) |
| $ \sum\limits_{j, k} {(g(\alpha , {\vartheta _j}, {{\cal X}_{jk}}){\delta _{{\theta _j}, {\sigma _{jk}}}}\, + g'(\alpha , {\vartheta _j}, {{\cal X}_{jk}}){\delta _{{\sigma _{jk}}, {\theta _j}}})} \, + $ | (1.6) |
| $\sum\limits_k {(l(\alpha , {\eta _k}){\delta _{{\rho _k}, {{\rho '}_k}}}\, + l'(\alpha , \, {\eta _k}){\delta _{{{\rho '}_k}, {\rho _k}}})} \, + $ | (1.7) |
| $\sum\limits_j {(h(\alpha , \, {\vartheta _j})({\delta _{{\theta _j}}} \otimes \Lambda )\, + h'(\alpha , \, {\vartheta _j})({\delta _{{\theta _j}}} \otimes \Lambda ))} + \beta {\Lambda _D} + \gamma {\Lambda ^2}$ | (1.8) |
因为邻接测度是纯原子的, 所有带Lebesgue成分的项必须测度为0, 因此式(1.8)取0, 式(1.7)对应了graphex的S部分, 式(1.6)对应了graphex的I部分, 式(1.5)对应了graphex的Θ部分.
| $ f({\alpha _{}}, {\vartheta _i}, {\vartheta _j}, {\zeta _{\left\{ {i, j} \right\}}}) = \left\{ {\begin{array}{*{20}{l}} {1{\rm{, }}}&{{\zeta _{\left\{ {i, j} \right\}}} \le \mathit{\Theta} ({\vartheta _i}, {\vartheta _j})}\\ {0{\rm{, }}}&{{\rm{otherwise}}} \end{array}} \right. $ | (1.9) |
| $ \mathit{\Theta} ({\vartheta _i}, {\vartheta _j}) = \left\{ {\begin{array}{*{20}{l}} {1 - \exp ( - 2{{\bar \rho }^{ - 1}}({\vartheta _i}){{\bar \rho }^{ - 1}}({\vartheta _j}){\rm{, }}}&{{\rm{if}}\;{\vartheta _i} \ne {\vartheta _j}}\\ {1 - \exp ( - {{\bar \rho }^{ - 1}}{{({\vartheta _i})}^2}){\rm{, }}}&{{\rm{if}}\;{\vartheta _i} = {\vartheta _j}} \end{array}} \right. $ | (1.10) |
随机变量X是定义在样本空间Ω上的函数, 当x是X的观测值时, 存在Ω中的ω使得x=X(w).随机向量(X1, ...Xn)是定义在样本空间Ω上的n元函数, 同时要研究更多的随机变量时, 就要引入随机过程的概念, 设T是(–∞, +∞)的子集, 则称随机变量的集合{Xt|t∈T}是随机过程, 称T为该随机过程的指标集(index set), 称{xt|xt=Xt(w), t∈T}为{Xt|t∈T}的一次观测, 当T=[0, +∞)或T=(–∞, +∞)时, {Xt|t∈T}的一次观测是一条曲线, 称作随机过程的一条轨迹(trajectory).泊松过程是一种时间连续、状态离散的随机过程[17].
定义1.10(独立增量过程(dependent incremental process)). 用随机变量N(t)表示时间段[0, t]内某类事件发生的个数, 则{N(t); t≥0}是计数过程(counting process), 满足如下条件:①对t≥0, N(t)是取非负整数值的随机变量; ②对t > s≥0, N(t)≥N(s); ③对t > s≥0, N(t)–N(s)是时间段(s, t]内的事件发生数; ④ {N(t)}的轨迹是单调不减右连续阶梯函数.若对于任意n和0≤t1 < t2 < ... < tn都有随机变量N(0), N(0, t1], N(t1, t2), ..., N(tn–1, tn)相互独立, 则这个计数过程称为独立增量过程[17].
定义1.11(平稳增量过程(stable incremental process)). 若在长度相等的时间段内, 事件发生个数的概率分布是相同的, 即对于任意s > 0, t2 > t1≥0随机变量N(t1, t2)和N(t1+s, t2+s)同分布, 则称计数过程为平稳增量过程[17].
定义1.12(泊松过程(Poisson process)). 满足条件:① N(0)=0;② {N(t)}是独立增量过程; ③对任意t, s≥0都有N(s, t+s]服从参数为λt的泊松分布, 即
常数λ取正值, 称为泊松过程的强度(intensity), 若λ不随时间变化, 则泊松过程是齐次的, 若λ随时间变化(或者说与时间有关), 则泊松过程是非齐次的[17].
定理1.4(叠加原理). 设Π1, Π2, ...是可数个相互独立的泊松点过程, 对应的计数过程分别为N1, N2, ..., 强度分别为μ1, μ2, ..., 则
定理1.5. 令Φ1, Φ2, ...是一个率为λ的泊松过程中事件发生的时间(或者位置), 给定N(t)=n, 随机变量Φ1, Φ2, ..., Φn的联合概率密度函数为
定理1.5可以通俗地解释为给定区间内事件的总数量, 事件发生的位置是某种方式的均匀分布.
定理1.6(映射原理(mapping proposition)).
任何贝叶斯模型都有一个重要的组成部分, 被表示成一个随机可测函数Θ, Θ可以用于构建贝叶斯模型的自然参数, 实现了对数据的解耦(或者说建立起数据间的联系)[11].de Finetti理论刻画了与随机序列相关的模型参数Θ, Aldous-Hoover表示理论刻画了与随机数组相关的模型参数Θ, Kallenberg表示理论刻画了与随机测度相关的模型参数Θ[18].
通过为可测函数指定先验Q, 就可以为可交换图模型指定先验.Lijoi等人2013年综述了几类非常适合作为混合模型的非参数先验Q的概率模型[19], 包括:完全随机测度(completely random measure, 简称CRM)、带独立增量的规一化随机测度(normalized random measures with independent increment, 简称NRMI)、吉布斯型先验(Gibbs-Type prior)等.很多先验都是基于CRM对进行适当的变换得到的, CRM的一个重要特性是其几乎确定的离散性, 对CRM进行变换得到的随机测度也继承了这一特性, 因此它们以概率1选择了离散分布.应用这些先验结构的方式主要有两种:①直接用于对观测数据进行建模, 当已知这些数据是由一个离散分布产生的; ②若数据是由连续分布(或者更复杂的混合分布)产生的, 先验结构就是层次混合模型的某个的构造块.
1.4.1 CRMs(完全随机测度)定义1.13.
Kingman[20]证明了一个CRM W可以分解成3个独立部分之和:不含原子的非随机的测度Wd、不含原子的非负随机质量全体Wf, 含固定原子的非负随机质量全体Wr, 并且对于不包含固定原子部分Wr和确定部分Wd的任意CRM W, 存在一个泊松过程(随机点集Π=(wi, θi)i∈N及其计数过程N(dw, dθ))使得
依据Campbell定理[20], 一个CRM由其Laplace函数唯一刻画, W(A)的Laplace变换由以下公式给出:
定义1.14. W是空间
为确保定义1.14中的规一化是良定的, T必须几乎确定是有限正值, 这一点可以由列维测度ρ的性质来保证
| $ \int_{{{\mathbb{R}}^{+}}}{\rho (\text{d}w)=+\infty }, \int_{{{\bf R}^{+}}}{(1-{{\text{e}}^{-\omega }})\rho (\text{d}w) < +\infty } $ | (1.11) |
满足(1.11)表明CRM在任意区间[0, S]有无限多个跳(对于任意的T < ∞), 称这样的CRM为无限活动CRM(infinite activity CRM)[20].
例1.4:GP(伽马过程)的列维强度有如下形式ρα(dω)μ0(dθ)=aω–1e–ωdωμ0(dθ), α > 0, 记GP为Wα, 其总质量为Tα, 列维测度ρα满足(1.11), 从而有
例1.5:广义伽马过程的列维强度如下形式
NRMI的离散分布特性很自然地引发了对生成数据的划分结构的分析, 事实上, 给定取值于某个度量空间
定义1.15. p是[n]的一族随机子集, 下标i和j同属于某个子集c当且仅当Xi=Xj, 则称π是[n]的随机分区(random partition)[11].
如将中任意子集Ai对应的唯一取值记作
定义1.16. π={A1, ..., Ak}是[n]的某个随机分区的概率
Caron和Fox利用随机测度和随机图间的联系提出了采用可交换随机测度来对网络数据进行建模, 将网络表示成随机点过程而不是邻接矩阵, 基于Kallenberg表示理论, Caron-Fox模型既可以生成稠密可交换网络也可以生成稀疏可交换图.以下介绍Caron和Fox提出的有向多图、带自边的无向图所对应的稀疏可交换图模型[15].
2.1 有向多图(directed multigraphs)可数无限多个节点的集合V=(θ1, θ2, ...), θi∈R+, 其上的有向多图(两个节点θi, θj间可以有nij≥1条边, 并且允许节点θi自己到自己有边, 边是有方向的)可以表示成R+上原子随机测度D[15].
| $D = \sum\limits_{i = 1}^\infty {} \sum\limits_{j = 1}^\infty {} {n_{ij}}\, \delta ({\theta _i}, {\theta _j})$ | (2.1) |
与每个节点θi相关联的参数ωi > 0(sociability)由一个原子随机测度W定义, W的分布是一个列维强度为ρ(dω)μ0(dθ)的齐次CRM[15].
| $ W = \sum\limits_{i = 1}^\infty {{w_i}{\delta _{{\theta _i}}}} , {\rm{ }}W \sim CRM(\rho , {\mu _0}) $ | (2.2) |
给定W, 则D由一个强度为乘积测度(product measure)
| $D|W \sim PP(W \times W)$ | (2.3) |
本质上, PP是随机点集Π及其计数过程N, 式(2.1)可以非正式地解释为:两个节点θi, θj间有边, 则位置(qi, θj)或(qj, θi)是Π中的点, 每个点的计数nij由泊松分布Poisson(wiwj)得到.
2.2 带自边的无向图(undirected graphs with self edge)对有向图
| $ \left\{ \begin{array}{l} W = \sum\limits_{i = 1}^\infty {{w_i}{\delta _{{\theta _i}}}} \quad \quad \quad \quad \quad \quad \;\quad W \sim CRM(\rho , {\mu _0})\\ D = \sum\limits_{i = 1}^\infty {} \sum\limits_{j = 1}^\infty {} {n_{ij}}\, \delta ({\theta _i}, {\theta _j})\quad \quad \quad D|W \sim PP(W \times W)\\ Z = \sum\limits_{i, j} {\min ({n_{ij}} + {n_{ji}}, 1)\, \delta ({\theta _i}, {\theta _j})} \end{array} \right. $ | (2.4) |
因为Pr(zij=1|w)=Pr(nij+nji > 0|w)并且nij和nji是相互独立的随机变量(给定W), 由泊松过程的叠加原理(superposition principle), 两个强度是wiwj的泊松随机变量相加, 得到强度是2wiwj的泊松随机变量.又因为Pr(nij+nji > 0|w)=1–Pr(nij+nji=0|w), 所以当给出节点的社交能力w=(wi)后, 也可以采用式(2.5)直接定义出无向图, 可以看到式(2.5)和式(2.4)的构建过程是等价的[15].
| $ {\rm{Pr}}({z_{ij}} = 1|w) = \left\{ {\begin{array}{*{20}{l}} {1 - \exp ( - 2{w_i}{w_j}), }&{i \ne j}\\ {1 - \exp ( - w_i^2), }&{i = j} \end{array}} \right. $ | (2.5) |
Caron等人证明了当W是一个GPP, 并且当σ≥0时, 可以得到稀疏网络.GGP具很多有非常好的特性, 比如其参数具有非常好的可解释性, GGP是条件共轭的.Hougaard[21]和Caron等人[22]对GGP进行了研究.
GGP的定义在例2.5给出, σ≥0和σ < 0的情况下, GGP具有显著不同的特性, 当σ < 0时, GGP是一个有限活动CRM(finite activity CRM), 在区间[0, α]上的跳跃的个数J依概率1有限, 并且J的分布是一个率为
稀疏可交换图的生成模型是一个非参数贝叶斯模型, 非参数贝叶斯有无限多个参数, 使得模型的复杂性随着采样尺寸的增大而增大, 由于基于随机模拟的方法需要在有限维参数空间进行采样, 因而需要通过边缘化或者截断方式对无限维参数空间进行采样.Caron等人提出了采用截断方式对GPP进行模拟, 采用边缘化对稀疏可交换图进行模拟[15].
3.1 对GGP进行随机模拟截断方法也称条件采样方法(conditional sampler), 通过合适的方法采样W的有限足够多个原子, 采用一个有限维近似来替代无限维先验.这一类方法最早由Muliere等人[23]提出, 他们证明了截断近似与无限维先验间的误差(采用总方差范式total varation norm表示)可以被选择小于某个特定值.Ishwaran等人在采用截棍方式构建NRMI
NRMI作为先验时, 对应的CRM W通常只有不含原子的非负随机质量全体Wf, 只有当给出观测数据后才会将含固定原子的非负随机质量全体Wr引入到后验中.对于Wf, 因为
算法1. Adaptive Thinning.
输入:强度为
输出:对强度为
算法步骤:
1. 令N:=Ø, t:=S
2. 迭代一些操作一直到结束
a) 从参数是1的指数分布采样得到r
b) 若r > Wt(∞), 结束; 否则令
c) 以概率
d) 令t:=t′, 进行下一轮迭代
3. 返回N(N就是对强度为[S,∞)的泊松随机测度在[S, ∞)进行的有限采样)
Thinning是从一种泊松随机测度进行采样的方法, 分为两步:首先从一个提议分布(一个比目标分布强度更高的泊松随机测度)采样出一些点, 然后以提议分布和目标分布的强度之比作为概率接受或拒绝每个采样[31].
如图 2所示, 在Adaptive Thinning算法中, 从提议分布中采样点时, 从截断级别S出发从左向右迭代进行, 令

|
Fig. 2 Asymptotic bounds used in sampling from a Poisson random measure[30] 图 2 从一个泊松随机测度进行采样时采用的渐进界限[30] |
3.1.2 通过单位率泊松过程构造CRM的逆列维方法
随机变量序列{ωi}和{qi}可以由截棍(stick breaking)过程构造[32], 也可以由单位率泊松过程构造[33].逆列维方法利用泊松随机测度的映射理论按从大到小的顺序对随机质量进行采样.对于R+上的任意单调函数f(x), 记f–1表示f(x)的右连续逆函数, 因此
定理3.1(CRMs的泊松采样). W是一个CRM, 列维强度为
给定
NRMI作为先验时, 若对应的CRM采用截棍过程表示时, 网络的生成模型为(2.4), 若对应的CRM采用unit-rate poisson表示时, 网络的生成模型为(1.2).以下介绍Caron和Fox提出的对生成模型为(2.4)的稀疏可交换图所进行的模拟[15].
3.2.1 将图限制在某个区域(graph restriction)采用邻接测度表示的随机图是一个无限图(因为W(R+)=∞), 而实际应用中所研究的网络都是有有限数量的边, 但是如何表达或者界定这个有限量是不知道的, 所以只能考虑将D或Z限制在某个区域[0, α]2得到相应的有限图Da或Zα, a作为一个模型参数通过推理得到, 相应的有CRM Wα和
| $ \text{For}~k=1,...,D_{\alpha }^{*}~\text{and}~j=1,2\\\left\{ \begin{align} & {{W}_{\alpha }}\tilde{\ }CRM(\rho ,\mu _{0}^{\alpha }) \\ & D_{\alpha }^{*}|W_{\alpha }^{*}\tilde{\ }Poisson(W{{_{\alpha }^{*}}^{2}})\left( \text{这里用到了泊松过程的叠加原理,定理1.4} \right) \\ & {{U}_{kj}}|W_{\alpha }^{*}{{\tilde{\ }}_{ind}}{{{\bar{W}}}_{\alpha }}\left( \text{这里用到了定理1.5} \right) \\ & {{D}_{\alpha }}=\sum\nolimits_{k=1}^{D_{\alpha }^{*}}{\delta ({{U}_{k1}},{{U}_{k2}})} \\ \end{align} \right. $ | (3.1) |
随机变量Ukj∈R+对应图中的节点, 节点偶对(Uk1, Uk2)对应Uk1到Uk2的一条边, 有向边的数量
由于W是一个无限活动, 所以不能直接对
| $ \text{For}\ k=1,...,D_{\alpha }^{*}\ \text{and}\ j=1,2\left\{ \begin{align} & {{W}_{\alpha }}\tilde{\ }{{P}_{W_{\alpha }^{*}}} \\ & D_{\alpha }^{*}|W_{\alpha }^{*}\tilde{\ }Poisson(W{{_{\alpha }^{*}}^{2}}) \\ & {{U}_{kj}}|W_{\alpha }^{*}{{\tilde{\ }}_{ind}}\text{Urn process}. \\ & {{D}_{\alpha }}=\sum\nolimits_{k=1}^{D_{\alpha }^{*}}{\delta ({{U}_{k1}},{{U}_{k2}})} \\ \end{align} \right. $ |
边缘化采样(marginal sampler)通过求W的边缘分布移除了由于W是无限活动带来的麻烦, 适用于预测分布体系显式给定的情形.边缘化得到的是先验的PUS表示, 这种表示可以用来定义有效的MCMC算法.MacEachern和Neal对在DPM模型上基于PUS表示的后验推理算法进行了总结, Favaro等人将这一类算法推广到了NRMI作为先验的混合模型, 这些方法的不足在于只有某些先验存在合适的PUS, 很多先验的PUS难以得到[36].
4 稀疏可交换图模型的推理稀疏可交换图的生成模型是一个以NRMI作为先验的非参数贝叶斯混合模型, 其后验分布的计算涉及到很复杂的积分, 大多不可能精确计算得到, 需要采用近似计算方法[37], 比如马尔可夫链蒙特卡洛(Markov Chain Monte Carlo, 简称MCMC)采样方法.常用的MCMC方法包括:Gibbs采样、Metropolis-Hastings采样(MH)、切片采样、哈密顿蒙特卡罗(Hamiltonian Monte Carlo, 简称HMC)、朗之万动力学方法(Langevin dynamics).
4.1 切片采样算法无限维先验不允许直接使用基于随机模拟的方法来进行后验分布推理, 因此需要对W进行截断, 仅对有限个原子进行处理.对给出X和U时CRM W的后验进行推理时, 切片采样算法引入一个辅助变量Si, 称为切片变量, 其条件分布为Si|Xi, W:Uniform(0, W({Xi}), W({Xi}表示原子Xi在W中的质量, 以Si为条件, Xi的取值对应到在W中的原子的质量肯定是大于等于Si的, 因此如果只需要有限个质量大于等于Si的原子就可以更新Xi时, Si实际上就作为了对W的截断级别[36].也就是说, 在整个数据集上, 采样的状态空间包括X, 切片变量S, CRM W和辅助变量U, 采样方法其实就是一个Gibbs采样, 迭代更新X, 然后更新U, 然后同时更新W和S.
这里只讨论对W和S的更新, W的后验既包含Wf, 又包含由观测数据引入的Wr部分, 切片变量只依赖于W中固定原子的质量, 另外我们只需要W中有限个质量大于全局截断级别S=mini∈[n]Si的位置随机的原子, 因此对W和S进行充分采样的方法是先采样Wr, 然后采样S, 最后采样Wf.对于Wr, 定理4.2表明每个固定原子对应于X中的一个唯一值
MH算法的一个主要的局限是它具有随机游走的行为, 而在状态空间中遍历的距离与步骤数量只是平方根的关系, 仅仅通过增加步长的方式是无法解决这个问题的, 因为这会使得拒绝率变高.HMC采样方法弥补了MH算法的缺陷, 可以更有效地对状态空间进行搜索.HMC起源于对哈密顿动力学(Hamiltonian dynamics)下进行变化的物理系统的行为的模拟, 通过将概率仿真转化为哈密顿系统的形式, 利用哈密顿动力学的框架能够让系统状态发生较大的改变, 同时让拒绝概率较低[38].
哈密顿动力学对应于在连续时刻T下的状态变量z={zi}的演化.经典的动力学由牛顿第二定律描述(物体的加速度正比于所受的力), 是关于时间的二阶微分方程.通过引入中间的动量变量r可以将二阶微分方程分解为两个相互耦合的一阶方程, r对应于状态变量z的变化率, 元素为
不失一般性, 将概率分布Pr(z)写成下面的形式:
哈密顿动态系统的一个重要性质是在动态系统的变化过程中, 哈密顿函数H的值是一个常数, 这一点通过求微分的方式很容易看出来, 即
考虑相空间上的联合概率分布, 其总能量是哈密顿函数, 概率分布的形式为
HMC也称混合蒙特卡罗(hybrid Monte Carlo), 是一种对连续分布进行近似的MCMC方法:给定独立观测变量集D, 后验分布Pr(z|D)∞exp(–U(z)), 势能函数
| ${\hat r_i}\left( {{\cal T} + \frac{\varepsilon }{2}} \right) = {\hat r_i}({\cal T}) - \frac{\varepsilon }{2}\frac{{\partial E}}{{\partial {z_i}}}(\hat z(r)), $ |
| ${\hat z_i}({\cal T} + \varepsilon ) = {\hat z_i}({\cal T}) + \varepsilon {\hat r_i}\left( {{\cal T} + \frac{\varepsilon }{2}} \right), $ |
| ${\hat r_i}({\cal T} + \varepsilon ) = {\hat r_i}\left( {{\cal T} + \frac{\varepsilon }{2}} \right) - \frac{\varepsilon }{2}\frac{{\partial E}}{{\partial {z_i}}}(\hat z({\cal T} + \varepsilon )).$ |
蛙跳积分对动量变量的更新形式是半步更新, 步长为ε/2, 接着是对位置变量的整步更新, 步长为ε, 然后是对动量变量的第2个半步更新.连续地使用几次蛙跳, 对动量变量的半步更新就可以结合到步长为ε的整步更新中.于是, 位置变量的更新和动量变量的更新互相之间以蛙跳的形式结合.为了将动态系统归进一个时间间隔
对于一个非零的步长ε, 蛙跳算法的离散化会在哈密顿动力学方程的积分过程中引入误差, 为了消除与离散化过程关联的数值误差, HMC将Hamiltonian动态系统框架与Metropolis算法结合在一起, 构造了一个马尔可夫链, 它由对动量r的随机更新和使用蛙跳算法对哈密顿动力系统的更新交替组成.每次应用蛙跳算法之后, 基于哈密顿函数H的值, 确定Metropolis准则, 确定生成的候选状态被接受或者拒绝.HMC完美地模拟了哈密顿动态系统, 因此每个这种候选状态都会高概率地被接受(因为H的值会保持不变)[39].HMC采样过程描述见算法2.
算法2. Hamiltonian Monte Carlo采样.
输入:起始位置z(1), 步长ε.
输出:后验分布Pr(z|D)的有限采样N.
算法步骤:
for t=1, 2, ...do
1. 对动量r进行重新采样:
2. 对离散化的对哈密顿动力系统进行采样
a)
b) for i=1 to m do
end
c)
d)
3.进行Metroplis-Hastings修正, 消除离散化带来的误差
a) 计算接受率
b) 从[0, 1]上的均匀分布采样一个μ, 若min(1, ρ) > μ, 则
End
与基本的MH方法不同, HMC能够利用到对数概率分布的梯度信息和概率分布本身的信息[40].在函数最优化领域有一个类似的情形, 大多数可以得到梯度信息的情况下, 使用哈密顿动力学方法是很有优势的.可以直观地解释为, 这种现象是由于下列的事实造成的:在n维空间中, 与计算函数本身的代价相比, 计算梯度所带来的额外计算代价通常是一个与n无关的固定因子.而与函数本身只能传递一条信息相比, n维梯度向量可以传递n条信息.
4.3 稀疏可交换图模型的后验分布的推理首先对受限CRM Wφ的条件分布Wφ|Dφ进行分析, Wφ|Dφ可以被分解成两部分之和, 一部分是全体带随机权值wi的固定位置θi的测度, 对应着观测到的网络数据中至少关联了1条边的节点全体, 另一部分是权值随机且位置随机的测度, 对应了其他节点, 用w*表示这些节点的总的随机质量.
定理4.1. 令
需要注意的是, 规一化的权值
James等人[41]通过引入一个辅助随机变量U刻画了NRMI所导出的EFFP, 令Γn是一个Gamma随机变量, 其位置参数是1, 形状参数是n, 并且独立于总质量T, 取值为正的随机变量Un=Γn/T, 容易证明对于任意的n≥1可以给出的Un密度函数
特别地,
定理4.2. 令
定理4.2表明, 在边缘采样中, CRM W被边缘后, 就可以采样得到代表X的分布的分区结构和聚类参数.
定理4.3. 令
定理4.3表明一个齐次NRMI
以下介绍Caron和Fox提出的对生成模型为(2.4)的稀疏可交换图所进行的后验推理[15].针对CRM是一个GGP的情况, 其后验推理的MCMC采样过程, 令
在观测数据是一个无向简单图的情况下, 需要推算未知的有向边数nij, 观测到zij=1(i≤j)时, 引入一个潜变量
| ${{\bar{n}}_{ij}}|z, w\sim \left\{ \begin{array}{*{35}{l}} {{\delta }_{0}}\text{, } & \text{if}\ {{z}_{ij}}=0 \\ tPoisson(2{{w}_{i}}{{w}_{j}})\text{, } & \text{if}\ {{z}_{ij}}=0, i\ne j \\ tPoisson({{w}_{i}}^{2})\text{, } & \text{if}\ {{z}_{ij}}=0, i=j \\ \end{array} \right.$ | (4.1) |
此处, tPoisson(λ)是一个零截断泊松分布, 其概率分布密度函数为
综上所述, 当稀疏可交换图是一个有向图时, 后验分布
1.给定
2.给定
3.给定
步骤1:采用HMC对
(1) 首先对辅助动量变量
(2) (w, r)为哈密顿动力系统的初始状态, 通过蛙跳离散化得到候选状态
①
②
③
(3) 以概率accep=min(1, ρ)接受
步骤2:采用MH算法对
| $ q(\widetilde \alpha , \widetilde \sigma , \widetilde \tau , {\widetilde{w}_*}|\alpha , \sigma , \tau , {w_*}) = q(\widetilde \tau |\tau )q(\widetilde \sigma |\sigma )q(\widetilde \alpha |\widetilde \sigma , \widetilde \tau , {w_*})q({\widetilde{w}_*}|\widetilde \alpha , \widetilde \sigma , \widetilde \tau , {w_*}). $ |
这里,
| $ \begin{array}{c} q(\widetilde \tau |\tau ) = \log normal(\widetilde \tau ;\log (\tau ), \sigma _\tau ^2),\\ q(\widetilde \sigma |\sigma ) = \log normal(1 - \widetilde \sigma ;\log (1 - \sigma ), \sigma _\tau ^2), \\ q(\widetilde \alpha |\widetilde \sigma , \widetilde \tau , {w_*}) = Gamma\left( {\widetilde \alpha ;{N_\varphi }, \frac{{{{\left( {\tau + 2\sum {{w_i} + {w_*}} } \right)}^{\widetilde \sigma }} - {\tau ^{\widetilde \sigma }}}}{{\widetilde \sigma }}} \right), \\ q({{\widetilde{w}}_*}|\widetilde \alpha , \widetilde \sigma , \widetilde \tau , {w_*}) = g_{\widetilde \alpha , \widetilde \sigma , \widetilde \tau + 2\sum {{w_i}} + {w_*}}^*({{\widetilde{w}}_*}) = \frac{{\exp \left( { - 2\sum {{w_i}} - {w_*}} \right)g_{\widetilde \alpha , \widetilde \sigma , \widetilde \tau }^*({{\widetilde{w}}_*})}}{{\exp ( - {\psi _{\widetilde \alpha , \widetilde \sigma , \widetilde \tau }}({{\widetilde{w}}_*}))}}. \end{array} $ |
步骤3:对潜变量
在σ≥0的情况下,
指数倾斜稳定分布是严格稳定分布天然的指数族分布, 采用指数倾斜可以在求解贝叶斯估计的近似公式时不涉及似然函数的条件最大值, 求解过程更稳定, 并且显著减少了所需要的计算时间.将严格稳定分布与指数倾斜相结合已经被证明在很多应用(例如, 重要性采样、罕见事件的模拟、保险精算等)中非常有效[44].
Brix、Rosinski、Ridout、Devroye、Hofert对指数倾斜稳定分布采样算法进行了研究, 针对分布为
Caron等人[15]采用他们提出的生成模型模拟生成了一系列随机图(s和τ取不同值情况下), 并与采用ER模型[7]、PA模型[13]、Lloyd[18]模拟生成的随机图进行了对比, 结果表明Caron-Fox模型能够模拟生成节点度分布呈现幂律分布而且具有重尾特性的稀疏图, 并且能够处理节点度分布尾部的指数截断(这一性质是进行网络数据分析时非常有用的一个重要性质), 但是采用3个作对比的生成模型模拟生成的随机图则不能表现出这些性质.
如图 3(a)所示, 在log-log坐标系下, 采用GGP作为先验的Caron-Fox模型在σ分别取0.2, 0.5, 0.8的情况下模拟生成的随机图, 其节点度分布呈现出明显的幂律分布, 而p=0.05的ER模型G(n, p)和Lloyd模型模拟生成的随机图, 其节点度分布则不能呈现出幂律分布, PA模型模拟生成的随机图的节点度分布虽然呈现出了幂律分布, 但不是可交换图, 图 3(b)所示的是当τ分别取0.1, 1, 5时的情况, 可以得到和图 3(a)类似的结论(图例中的BA表示PA模型, 因为PA模型是由Barabási和Albert共同提出的, 所以也常常被称作BA模型).
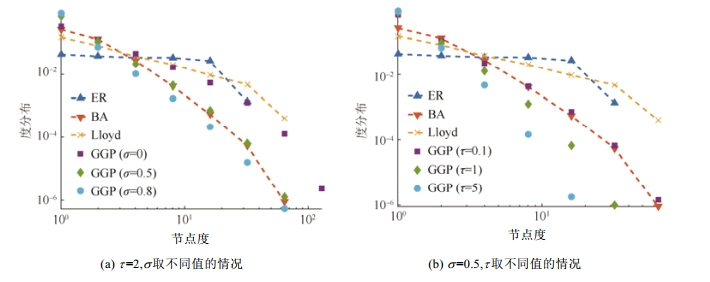
|
Fig. 3 Degree distribution on a log-log scale 图 3 Log-Log坐标系下的节点度分布图 |
如图 4所示, 采用GGP作为先验的Caron-Fox模型模拟生成的随机图表现出了这样一种特性:随着节点个数的增加, 图中度是1的节点的个数是线性增加, PA模型模拟生成的随机图有类似的性质, 但是ER模型模拟生成的随机图中度是1的节点的个数是随着节点个数的增加呈现指数减少的, Lloyd模型模拟生成的随机图则几乎没有度是1的节点.

|
Fig. 4 Number of nodes with degree 1 versus the number of nodes on a log-log scale 图 4 Log-Log坐标系下图中度是1的节点的个数随着节点个数的增加而变化的情况 |
如图 5所示, 采用GGP作为先验的Caron-Fox模型模拟生成的随机图表现出了这样一种特性:随着节点个数n的增加, 图中边的个数呈现o(n2)增加(稀疏图的特征), PA模型模拟生成的随机图有类似的性质, 但是ER模型和Lloyd模型模拟生成的随机图中, 边的个数呈现Θ(n2)增加(稠密图的特征).

|
Fig. 5 Number of edges versus the number of nodes on a log-log scale 图 5 Log-Log坐标系下图中边的个数随着节点个数的增加而变化的情况 |
实证结果表明, 当σ≥0时, 采用GGP作为先验的Caron-Fox模型可以生成稀疏可交换图, 而基于Aldous- Hoover表示理论的ER模型和Lloyd模型只能生成稠密可交换图, PA模型虽然模拟生成稀疏图, 但不是可交换的.关于实证分析的更详细过程, 可参阅文献[15].
6 最新进展与研究展望在随机图模型方面, 通过对经典Graphon的定义进行推广, Borgs等人[46]提出了Graphon process模型, Veitch等人[11]提出了Graphex模型, 这两种更广义的稀疏可交换图模型都可以对一大类可交换图进行建模, 并且将Caron-Fox模型和传统可交换稠密图作为特例纳入了一个统一的模型框架.Crane等人[47]认为, 尽管Caron-Fox模型能够生成满足可交换性的稀疏网络, 但是尚不清楚可交换性是否在各种采样策略下都能得到保证, 他们提出了一种边可交换的随机图模型(edge exchangeable model); Jacobs和Clauset[48]对各种网络生成模型从哲学思想、表示和统一性这3个方面进行了总结, 提出了网络生成模型在可解释性、同质性、优化、模型可实现、模型选择、模型检验等方面所面临的挑战和机遇, 并且指出Caron-Fox模型只能生成超线性密度(superlinear density)O(nα), 1 < α < 2的稀疏可交换图, 还不能生成更稀疏的O(n)数量级的节点数对应O(n)数量级的边数的稀疏可交换图, 还需要在理论创新和推理算法方面进行大量的研究才能使得这种基于连续空间的网络生成模型被应用到更广泛的真实网络数据分析中.
社区结构作为网络模型的重要特征刻画了网络的多种属性和功能, 对人们准确理解复杂系统的特性有十分重要的意义.从社区结构这一中观层面对复杂网络进行研究对人们准确理解复杂系统的特性有十分重要的意义, 既能够弥补宏观层面粒度过粗所造成的很多网络特性无法观察到的缺陷, 又避免了微观层面粒度过细所带来的丢失共性并且计算复杂度高等问题.社区发现作为网络数据分析的重要内容已经得到了学术界的广泛关注和深入研究, Herlau等人[14]将SBM与Caron-Fox模型相结合, 为稀疏可交换图引入了社区结构, 并提出了稀疏可交换图的非重叠静态社区发现方法; Todeschini和Caron[49]提出了稀疏可交换图的重叠静态社区发现方法, 该方法受到了Zhou[50]提出的无限边分区模型(Infinite edge partition model)的启发, 假设网络中的节点i关联了一组权重参数wik, k=1, ..., p(可以解释为节点的不同方面的社交能力), 节点i关联的权重参数是有依赖关系的混合随机测度(compound random measure)[51], 网络的生成模型为
在稀疏可交换图的动态演化方面, Palla等人[52]提出了采用动态泊松点过程对节点社交能力随时间演化的特性进行建模, 可以同时捕获节点间边的平滑演化(smooth evolution)和长程演化(long term evolution).Matias[53]指出采用离散模型对网络进行建模, 在研究网络和社区结构的动态演化时, 需要将数据聚集到预先指导的时间段以得到网络快照序列, 数据聚集会带来信息损失, 并且时间段的选择会直接影响预测结果, 但是采用随机过程作为模型参数的连续模型, 则能够很自然地将时间信息引入网络模型, 避免了上述问题.
在近似推理方法方面, 现有的关于稀疏可交换图的研究工作几乎都采用的是MCMC推理方法.相对于随机变分推理(stochastic variational inference, 简称SVI)方法, MCMC方法因为可扩展性和可并行性差从而导致其很难应用于大数据环境下的数据分析, 因此如何采用SVI对稀疏可交换图进行推理是一个非常重要的研究课题. Roychowdhury[54]提出了伽马过程(GP)的变分推理方法; Tank等人[55]提出了贝叶斯非参数混合模型的流式变分推理算法; 缘于MCMC与VI在能量函数和信息熵层面颇有渊源, Salimans等人[56]提出通过桥接二者之间的嫌隙将MCMC和VI结合起来进行推理; Wolf等人[57]提出了一种将HMC和VI相结合的算法, 把HMC步骤包含到变分下界, 以加速后验推理过程的收敛.
Caron-Fox模型中提出的“节点社交能力”这一概念可以为网络分析提供非常合理的社会学解释——节点间建立边的概率取决于两个节点潜在的社交能力, 并且正是因为具有不同方面的社交能力(或者说不同方面的潜在兴趣), 决定了一个节点可以同时隶属于不同的社区.“节点社交能力”与度纠正的随机块模型(degree- corrected SBM)[58]中的“度偏好”异曲同工, 都能使网络生成模型很好地拟合具有各种特定度分布的真实网络, 使得Caron-Fox模型与SBM模型相结合时, 不需要再进行度纠正.
稀疏可交换图模型是对传统可交换稠密图模型的扩展.关于传统可交换稠密图的研究, 从网络建模、网络演化到社区发现、社区演化, 再到链路预测、影响力分析、网络传播等各个方面的研究工作, 都已经历时弥久并且成果丰硕.尽管传统可交换稠密图的先天不足导致其无法再继续成为对真实复杂网络进行数据分析的利器, 但是很多已经被提出的研究问题和研究成果可以在进行稀疏可交换图研究时被广泛继承和发展.
综上所述, Caron等人的开创性工作为复杂网络数据分析带来了新的转机, 稀疏可交换图模型不仅解决了可交换性与稀疏性二者不可兼顾的矛盾, 并且具有很多独特的优良基因.随着对稀疏可交换图模型以及贝叶斯非参数混合模型的深入研究, 必将可以推动复杂网络数据分析, 尤其是网络社区结构动态演化研究工作的进一步发展.
致谢 文中关于哈密顿动力学方法和混合蒙特卡罗算法的部分内容引自马毅未公开发表的对文献[39]的翻译手稿, 在此向马毅表示感谢.| [1] |
Yu ZW, Zhou XS. Relocation and discussion about pervasive computing. Communications of the CCF, 2011, 7(7): 49–56(in Chinese with English abstract).
http://www.cqvip.com/QK/98258X/201603/667840033.html |
| [2] |
Yu ZW, Yu ZY, Zhou XS. Socially aware computing. Chinese Journal of Computers, 2012, 35(1): 16–26(in Chinese with English abstract).
[doi:10.3724/SP.J.1016.2012.0001] |
| [3] |
Freer CE, Roy DM. Computable exchangeable sequences have computable de Finetti measures. In: Ambos-Spies K, Lőwe B, Merkle W, eds. Proc. of the CiE 2009. LNCS 5635, Berlin, Heidelberg: Springer-Verlag, 2009. 218-231. |
| [4] |
Aldous DJ. Representations for partially exchangeable arrays of random variables. Journal of Multivariate Analysis, 1981, 11(4): 581–598.
[doi:10.1016/0047-259X(81)90099-3] |
| [5] |
Hoover DN, Keisler HJ. Adapted probability distributions. Trans. of the American Mathematical Society, 1984, 286(1): 159–201.
[doi:10.1090/S0002-9947-1984-0756035-8] |
| [6] |
Kallenberg O. Exchangeable random measures in the plane. Journal of Theoretical Probability, 1990, 3: 81–136.
[doi:10.1007/BF01063330] |
| [7] |
Erdős P, Rényi A. On the evolution of random graphs. Trans. of the American Mathematical Society, 2011, 286(1): 257–274.
http://www.ams.org/mathscinet-getitem?mr=125031 |
| [8] |
Airoldi EM, Costa TB, Chan SH. Stochastic blockmodel approximation of a graphon: Theory and consistent estimation. In: Advances in Neural Information Processing Systems, 2013, 26: 692-700.http://www.researchgate.net/publication/258312651_Stochastic_blockmodel_approximation_of_a_graphon_Theory_and_consistent_estimation |
| [9] |
Airoldi EM, Blei D, Fienberg SE, Xing E. Mixed membership stochastic blockmodels. Journal of Machine Learning Research, 2007, 9(5): 1981–2014.
https://www.ncbi.nlm.nih.gov/pubmed/21701698?dopt=Abstract |
| [10] |
Kemp C, Tenenbaum JB, Griffiths TL, Yamada T, Ueda N. Learning systems of concepts with an infinite relational model. In: Proc. of the National Conf. on Artificial Intelligence. 2006. 381-388.http://dl.acm.org/citation.cfm?id=1597600 |
| [11] |
Veitch V, Roy DM. The class of random graphs arising from exchangeable random measures. Electronic pre-print, arXiv: 1512. 03099, 2015. http://arxiv.org/abs/1512.03099http://arxiv.org/abs/1512.03099 |
| [12] |
Orbanz P, Roy DM. Bayesian models of graphs, arrays and other exchangeable random structures. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2015, 37(2): 437–461.
[doi:10.1109/TPAMI.2014.2334607] |
| [13] |
Barabási AR, Albert L. Statistical mechanics of complex networks. Reviews of Modern Physics, 2002, 74(1): 47–97.
[doi:10.1103/RevModPhys.74.47] |
| [14] |
Herlau T, Schmidt MN, Mørup M. Completely random measures for modelling block-structured sparse networks. In: Advances in Neural Information Processing Systems (NIPS). Barcelona, 2016.http://arxiv.org/abs/1507.02925 |
| [15] |
Caron F, Fox E. Sparse graphs using exchangeable random measures. Journal of the Royal Statistical Society B, 2017, 79: 1295–1366.
[doi:10.1111/rssb.2017.79.issue-5] |
| [16] |
Borgs C, Chayes JT, Cohn H, Ganguly S. Consistent nonparametric estimation for heavy-tailed sparse graphs. Electronic pre-print, arXiv: 1508. 06675, 2015. http://arxiv.org/abs/1508.06675 |
| [17] |
Kingman JFC. Poisson processes. London: Oxford University Press, 1992: 79-98.
|
| [18] |
Lloyd JR, Orbanz P, Ghahramani Z, Roy DM. Random function priors for exchangeable arrays. Advances in Neural Information Processing Systems (NIPS), 2012, 25(6): 1007–1015.
|
| [19] |
Lijoi A, Prünster I.. Models beyond the Dirichlet process. SSRN Electronic Journal, 2009, 23: 80–136.
[doi:10.2139/ssrn.1526505] |
| [20] |
Kingman JFC. Completely random measures. Pacific Journal of Mathematics, 1967, 21(1): 59–78.
[doi:10.2140/pjm.1967.21.59] |
| [21] |
Hougaard P. Survival models for heterogeneous populations derived from stable distributions. Biometrika, 1986, 73(2): 387–396.
[doi:10.1093/biomet/73.2.387] |
| [22] |
Caron F, Teh YW, Murphy TB. Bayesian nonparametric Plackett-Luce models for the analysis of preferences for college degree programmes. The Annals of Applied Statistics, 2014, 8(2): 1145–1181.
[doi:10.1214/14-AOAS717] |
| [23] |
Muliere P, Tardella L. Approximating distributions of random functionals of Ferguson-Dirichlet priors. The Canadian Journal of Statistics, 1998, 26(2): 283–297.
[doi:10.2307/3315511] |
| [24] |
Ishwaran H, Zarepour M. Exact and approximate sum represenations for the Dirichlet process. The Canadian Journal of Statistics, 2002, 30(2): 269–283.
[doi:10.2307/3315951] |
| [25] |
Ishwaran H, James L. Gibbs sampling methods for stick-breaking priors. Journal of the American Statistical Association, 2001, 96(453): 161–173.
[doi:10.2307/2670356] |
| [26] |
Papaspiliopoulos O, Roberts GO. Retrospective Markov chain Monte Carlo methods for Dirichlet process hierarchical models. Biometrika, 2008, 95(1): 169–186.
[doi:10.1093/biomet/asm086] |
| [27] |
Walker SG. Sampling the Dirichlet mixture model with slices. Communications in Statistics:Simulation and Computation, 2007, 36(1): 45–54.
[doi:10.2139/ssrn.945330] |
| [28] |
Kalli M, Griffin JE, Walker SG. Slice sampling mixture models. Statistics and Computing, 2011, 21(1): 93–105.
[doi:10.1007/s11222-009-9150-y] |
| [29] |
Favaro S, Walker SG. Slice sampling s-stable Poisson-Kingman mixture models. Journal of Computational and Graphical Statistics, 2013, 22(4): 830–847.
[doi:10.1080/10618600.2012.681211] |
| [30] |
Favaro S, Teh YW. MCMC for normalized random measure mixture models. Statistical Science, 2013, 28(3): 335–359.
[doi:10.1214/13-STS422] |
| [31] |
Lewis PAW, Shedler GS. Simulation of nonhomogeneous Poisson processes by thinning. Naval Research Logistics, 1979, 26(3): 403–413.
[doi:10.1002/nav.3800260304] |
| [32] |
Favaro S, Lijoi A, Nava C, Nipoti B, Prünster I, Teh YW. On the stick-breaking representation for homogeneous NRMIs. Bayesian Analysis, 2016, 11(3): 697–724.
[doi:10.1214/15-BA964] |
| [33] |
Orbanz P, Williamson S. Unit-Rate Poisson representations of completely random measures. Electronic Journal of Statistics, 2011, 1-12. http://stat.columbia.edu/~porbanz/reports/OrbanzWilliamson2012.pdf |
| [34] |
Ferguson TS, Klass MJ. A representation of independent increment processes without Gaussian components. The Annals of Mathematical Statistics, 1972, 43(5): 1634–1643.
[doi:10.1214/aoms/1177692395] |
| [35] |
Blackwell D, MacQueen JB. Ferguson distributions via Pólya urn schemes. The Annals of Statistics, 1973, 1(2): 353–355.
[doi:10.1214/aos/1176342372] |
| [36] |
Griffin JE. An adaptive truncation method for inference in Bayesian nonparametric models. Statistics and Computing, 2016, 26(1): 423–441.
[doi:10.1007/s11222-014-9519-4] |
| [37] |
Neal RM. Markov chain sampling methods for dirichlet process mixture models. Journal of Computational and Graphical Statistics, 2000, 9(2): 249–265.
[doi:10.1111/j.1467-9469.2008.00609.x] |
| [38] |
Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag, 2006. 548-556. |
| [39] |
Neal RM. MCMC using Hamiltonian dynamics. In: Brooks S, Gelman A, Jones G, Meng XL, eds. Handbook of Markov Chain Monte Carlo, Vol. 2. Chapman & Hall/CRC Press, 2011. 113-160.http://www.oalib.com/paper/3605346 |
| [40] |
Chen T, Fox EB, Guestrin C. Stochastic gradient Hamiltonian Monte Carlo. In: Proc. of the Int'l Conf. on Machine Learning. 2014. 1683-1691.http://arxiv.org/abs/1402.4102 |
| [41] |
James L, Lijoi A, Prünster I. Posterior analysis for normalized random measures with independent increments. Scandinavian Journal of Statistics, 2009, 36(1): 76–97.
[doi:10.1111/j.1467-9469.2008.00609.x] |
| [42] |
Hofert M. Sampling exponentially tilted stable distributions. ACM Trans. on Modeling and Computer Simulation, 2011, 22(1): Article No.3.
[doi:10.1145/2043635.2043638] |
| [43] |
Kharroubi SA, Sweeting TJ. Exponential tilting in Bayesian asymptotics. Biometrika, 2016, 103(2): 337–349.
[doi:10.1093/biomet/asw018] |
| [44] |
Hofert M. Sampling Archimedean copulas. Computational Statistics and Data Analysis, 2008, 52(12): 5163–5174.
[doi:10.1016/j.csda.2008.05.019] |
| [45] |
Devroye L. Random variate generation for exponentially and polynomially tilted stable distributions. ACM Trans. on Modeling and Computer Simulation, 2009, 19(4): 1–20.
[doi:10.1145/1596519.1596523] |
| [46] |
Borgs C, Chayes JT, Cohn H, Holden N. Sparse exchangeable graphs and their limits via graphon processes. Electronic pre-print, arXiv: 1601. 07134, 2016. http://arxiv.org/abs/1601.07134 |
| [47] |
Janson S. On edge exchangeable random graphs. Journal of Statistical Physics, 2017, 8: 1–37.
[doi:10.1007/s10955-017-1832-9] |
| [48] |
Jacobs AZ, Clauset A. A unified view of generative models for networks: Models, methods, opportunities and challenges. Electronic pre-print, arXiv: 1411. 4070, 2014. http://arxiv.org/abs/1411.4070 |
| [49] |
Todeschini A, Miscouridou X, Caron F. Exchangeable random measures for sparse and modular graphs with overlapping communities. Electronic pre-print, arXiv: 1602. 02114, 2017. http://arxiv.org/abs/1602.02114 |
| [50] |
Zhou MY. Infinite edge partition models for overlapping community detection and link prediction. In: Proc. of the 18th Int'l Conf. on Artificial Intelligence and Statistics (AISTATS). 2015. 1135-1143.http://www.oalib.com/paper/4070586 |
| [51] |
Griffin JE, Leisen F. Compound random measures and their use in Bayesian nonparametrics. Journal of the Royal Statistical Society—Series B, 2017, 79: 525–545.
[doi:10.1111/rssb.12176] |
| [52] |
Palla K, Caron F, Teh YW. Bayesian nonparametrics for sparse dynamic networks. Electronic pre-print, arXiv: 1607. 01624, 2014. http://arxiv.org/abs/1607.01624http://arxiv.org/abs/1607.01624 |
| [53] |
Matias C, Rebafka T, Villers F. A semiparametric extension of the stochastic block model for longitudinal networks. Electronic pre-print, arXiv: 1512. 07075v2, 2016. http://arxiv.org/abs/1512.07075v2 |
| [54] |
Roychowdhury A, Kulis B. Gamma processes, stick-breaking, and variational inference. In: Proc. of the 18th Int'l Conf. on Artificial Intelligence and Statistics (AISTATS). San Diego, 2015. 800-809.http://arxiv.org/abs/1410.1068 |
| [55] |
Tank A, Foti N, Fox EB. Streaming variational inference for Bayesian nonparametric mixture models. In: Proc. of the 18th Int'l Conf. on Artificial Intelligence and Statistics. 2014. 968-976.http://www.oalib.com/paper/4123343 |
| [56] |
Salimans T, Kingma DP, Welling M. Markov chain Monte Carlo and variational inference: Bridging the gap. In: Proc. of the 32nd Int'l Conf. on Machine Learning (ICML). Lille, 2015. 1218-1226.http://dl.acm.org/citation.cfm?id=3045248 |
| [57] |
Wolf C, Karl M, Smagt PVD. Variational inference with Hamiltonian Monte Carlo. Electronic pre-print, arXiv: 1609. 08203, 2016. http://arxiv.org/abs/1609.08203 |
| [58] |
Karrer B, Newman ME. Stochastic blockmodels and community structure in networks. Physical Review E, 2011, 83(2): 96–107.
[doi:10.1103/PhysRevE.83.016107] |
| [1] |
於志文, 周兴社. 普适计算的重定位与探讨. 中国计算机学会通讯, 2011, 7(7): 49–56.
http://www.cqvip.com/QK/98258X/201603/667840033.html
|
| [2] |
於志文, 於志勇, 周兴社. 社会感知计算:概念、问题及其研究进展. 计算机学报, 2012, 35(1): 16–26.
[doi:10.3724/SP.J.1016.2012.0001]
|
 2018, Vol. 29
2018, Vol. 29


