2. 上海交通大学 计算机科学与工程系, 上海 200240
2. Departmet of Computer Science and Engineering, Shanghai Jiaotong University, Shanghai 200240, China
自1962年Petri网[1]的概念提出以来, 经过半个多世纪的发展, 其已成为描述与分析并发系统最重要的形式化工具之一.除在并发程序语言形式化验证中的重要应用外, Petri网模型还被广泛应用于生物、化学、金融、网络、安全等不同领域的建模和分析[2-9].其中, Ball等人定义了并行库系统(parameterized library system, 简称PLS), 在此基础上实现了多线程程序的模型检测工具[2], 并证明了PLS系统上的一些验证问题与Petri网上的验证问题等价; Aalst用Petri网对工作流管理系统进行建模, 用Petri网理论来验证工作流过程的正确性[3]; Heiner等人[4]用Petri网对生化反应过程建模, 实现了对生化系统中短时间内的行为进行有效的分析等.国内的研究者也对类似问题进行了深入研究, 特别是将Petri网理论广泛应用于对网络及安全等领域的验证.代表性的工作包括:北京交通大学Lei教授等人用Petri网对无线网络系统建模, 以实现对无线网络的性能的有效分析[5]; 清华大学林闯教授等人在Petri网的基础上定义了私有Petri网, 对恶意软件造成的私有信息泄露行为进行分析[6]; 以及同济大学Yu教授等人用Petri网对电子商务的支付过程建模, 验证电子商务支付系统的安全性[7]等.
与Petri网等价的数学模型向量加法系统(vector addition system, 简称VAS)具有数学描述上的简洁性, 且现实中并发系统的状态和迁移往往都可以用向量描述, 故VAS本身也具有重要的理论和应用价值.VAS模型验证的核心问题之一是可达性(reachability)问题, 即对给定的VAS模型, 判断从一个初始格局出发能否到达一个指定的目标格局.令人遗憾的是:虽然关于VAS已经有了大量的理论和应用研究, 也有了一些高效的实现工具, 但对可达性问题的复杂性, 至今仍没有给出令人满意的回答.另一方面, VAS是极为简洁的系统, 在实际研究中, 人们根据不同的应用背景提出了一些重要的扩展模型(如下推向量加法系统PVAS、交互向量加法系统AVASS、分枝向量加法系统BVASS、带数据的Petri网模型PND(Petri nets with data)等).但对这些模型的相关验证问题的研究都处于初始阶段.
本文第1节形式化定义向量加法系统及一些重要的验证问题.第2节为本文重点, 总结一般VAS上可达性问题的主要结论和核心研究技术.第3节陈述当维度固定时VAS上可达性问题的主要结论和技术.第4节总结几个重要VAS扩展模型上的验证问题的结论.第5节给出现有主要验证结论一览表.本文覆盖了VAS研究领域的最新进展、关键技术和开放问题.
1 向量加法系统基础 1.1 VAS的形式化定义向量加法系统(vector addition system, 简称VAS), 可以表示为二元组V=〈d, A〉.d ∈
带状态的向量加法系统(vector addition system with states, 简称VASS)可以表示为三元组V=〈Q, d, T〉.Q是有限的状态集合, d ∈
| ${c_0}{\xrightarrow{{{t_1}...{t_n}}}_V}{c_n}$ |
针对上面两个模型, Hopcroft和Pansiot在1979年的工作[10]中证明了n维VASS可以用n+3维VAS来表达, 因此两者的可达性问题等价.
1.2 验证问题的形式化定义本节具体给出VAS模型上几个著名验证问题的形式化定义.
可达性(reachability)问题.
输入:VAS V (VASS V), 初始和结束向量u, u'(格局c, c');
问题:是否存在一次从u到u'(从c到c')的运行.
可覆盖(coverability)问题.
输入:VAS V, 初始和结束向量u, u';
问题:是否存在向量u"≥u'(u"的每一维都大于等于u'的相应维), 且存在从u到u"的运行.
有界性(boundedness)问题.
输入:VAS V, 初始向量u;
问题:u可达的向量集合是否有限.
VAS的可达性关系(reachability relation)用→*表示, 对于两个向量u, u' ∈
VAS模型上的覆盖性和有界性都已经有了确定的结论.最早是Lipton和Rackoff[11, 12]给出的EXPSPACE-完备的结果.Rosier对他们的证明做了细化, 得到了更精确的, 几乎完全匹配的上下界[13].
Lipton在1976年证明了可达性问题有EXPSPACE的算法下界[11].可判定结果则用了更长的时间:Sacerdote与Tenney在1977年给出了关于此问题的部分结论[14]; Mayr在1981年完善了原结果, 并给出了可判定性的完整证明, 但该证明非常复杂[15]; Kosaraju在1982年对证明进行了简化[16]; 1992年, Lambert在前人工作的基础上给出了清晰的可判定性证明[17].他们工作中的主要证明技术被称为KLMST分解.遗憾的是, 基于KLMST分解的算法没有给出复杂性上界.近年, 关于VAS模型可达性结论的主要进步是Leroux等人自2009年开始的一系列工作:Leroux[18]利用KLMST分解给出了基于前向递归不变量的较简洁的可达性判定算法; 基于此思想, 首次给出了不基于KLMST的判定算法[19, 20].这两个证明为VAS可达性问题建立了非常重要的几何直观, 并使得研究算法复杂性成为可能.新进展是Leroux等人在LICS 2015会议上给出的基于理想(ideal)的分解算法[21], 并首次给出了可达性问题的上界结论:
VAS上的可达性验证是领域内最受关注也最重要的问题.经过近40年的研究, 研究者已发展了一套独立、有效的研究技术.下面从验证算法的上界和下界两方面来介绍现有主要研究成果, 重点是对关键证明技术的总结和分析.
2.2.1 上界技术迄今为止, VAS可达性验证的技术可以分为两大类:2011年之前的技术都属于KLMST分解算法(或对该算法的精化)以及2011年Leroux提出的基于递归不变量的算法.下面重点陈述此类算法并对其局限和未来可能的工作做分析.
● KLMST分解算法
前文说过一般的VAS和VASS的可达性问题等价, 本节将在VAS的定义下介绍KLMST分解算法.KLMST分解算法会维护一个标记证据图序列(marked witness graph sequence)集, 对其中不满足完美(perfect)条件(等价于Kosaraju文中的q条件[16])的标记证据图作分解.如果分解结束时集合不为空, 则原可达性问题可达; 否则不可达.Leroux在2015年给出了KLMST算法的上界
首先引入大于所有自然数的元素ω, 并定义Nω=
KLMST分解算法使用的重要工具是标记证据图(marked witness graph) M=(G, cin, sin, cout, sout), 其中:G是证据图; sin, sout是G中的两个点, 代表图的输入节点(input vertices)和输出节点(output vertices);
| $\overline {{I^{in}}} = \{ 1, 2, ..., d\} \backslash {I^{in}}, \overline {{I^{out}}} = \{ 1, 2, ..., d\} \backslash {I^{out}}.$ |
ΩM表示所有的运行
标记证据图序列ξ如果满足以下3个条件, 则称ξ满足完美条件.
(1) 可泵性(pumpability):对一个标记证明图M, ΩM中存在运行使得在I中的维度都能达到无穷大, 则称M是向前可泵的(forward pumpable).类似地, 可以定义向后可泵的(backward pumpable).如果ξ中的所有标记证据图都是向前、向后可泵的, 那么称ξ满足可泵性;
(2) 边无界性(edge unboundedness):对于ξ中的每一个标记序列图Mj, Ψj表示Lξ中所有ψj的集合.对于所有e ∈Ej, 如果supΨj(e)=ω, 那么称ξ满足边无界性;
(3) 输入/输出限制无界性(input/output constraint unboundedness):对于ξ中的每一个标记序列图Mj, Uj, Vj表示Lξ中所有uj, vj的集合, 如果
KLMST分解算法将会构建标记证据图序列集合的序列Ξ0, Ξ1, Ξ2, ….初始的Ξ0={ξ0}, ξ0=M0=(G0, u, (ω, …, ω), u', (ω, …, ω)), G0=({s}, {s}xAx{s}), s=(ω, …, ω).算法的每一步, 若当前集合Ξi为空, 则算法回答“不可达”; 若Ξi不为空, 则会检测Ξi中的每一个标记证据图序列, 选出其中一个不满足完美条件的标记证据图序列ξ, 将其分解成有限的标记证据图序列集合dec(ξ), Ξi+1=(Ξi\{ξ})∪dec(ξ).如果所有标记证据图序列都满足完美条件, 则算法终止, 回答“可达”.对满足完美条件的标记证据图序列ξ最重要的结论是:
引理2.1[21].标记证据图序列ξ是否满足完美条件, 是指数空间内可判定的.
另一方面, 对不满足完美条件的标记证据图序列ξ, 将对ξ作分解.若ξ中存在一个标记证明图M是不可泵的, 假设它在第i ∈I维有上界, 那么分解后的标记证据图将具体化第i维的数值, I=I∪{i}; 若ξ不满足边无界, 其中, e出现的次数有上界, 那么会在标记证据图中去掉e这条边, 得到一个由e连接的标记证据图序列; 若ξ不满足输入限制无界, 假如第i ∈Iin维不满足, 那么将输入限制替换为有限多种可能的数值, Iin=Iin∪{i}, ξ不满足输出限制无界.为方便理解, 我们构造了具体例子介绍分解算法.
例:对V=〈3, A〉, A={a1=(2, -1, 0), a2=(0, -1, 1), a3=(-1, 1, -1), a4=(2, 1, -1)}, u=(0, 0, 3), u'=(1, 2, 0), 问u到u'是否可达.
初始的ξ0=M0如图 1所示.

|
Fig. 1 Initial marked witness graph sequence ξ0=M0 图 1 初始的标记证据图序列ξ0=M0 |
记p=(p1, p2, p3, p4) ∈
| ${M'_0} = ({G'_0}, (0, 0, 3), (\omega, \omega, \omega ), (\omega, \omega, \omega ), (\omega, \omega, \omega )), {M'_1} = ({G'_1}, (\omega, \omega, \omega ), (\omega, \omega, \omega ), (1, 2, 0), (\omega, \omega, \omega ))$ |

|
Fig. 2 Next marked witness graph sequence |
接着构造从
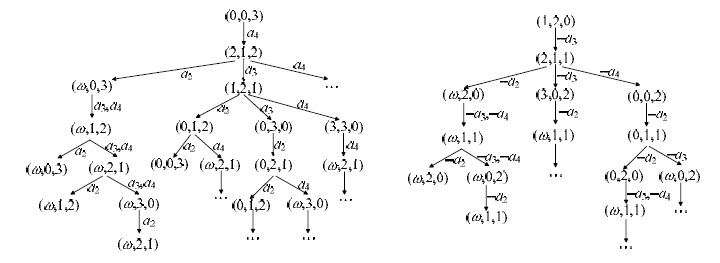
|
Fig. 3 Karp-Miller tree from (0, 0, 3) and Karp-Miller tree constructed with inverse transitions from (1, 2, 0) 图 3 从(0, 0, 3)出发的Karp-Miller树和从(1, 2, 0)出发的反向的Karp-Miller树 |

|
Fig. 4 Final marked witness graph sequence |
这里的ξ2是满足完美条件的标记证据图序列, 算法不会再对其分解.算法结束时Ξi至少包含ξ2, 因此u到u'可达.
为了说明上述计算过程会终止, 为标记证据图序列ξ定义一个秩函数(ranking function)r.这个秩函数会将ξ映射到三元组的多重集合, 包含每一个标记向量图的(|I|, |E|, |Iin|+|Iout|).例如r(ξ0)={(3, 4, 0)}, r(ξ1)={(3, 3, 3), (3, 3, 3)}, r(ξ2)={(1, 9, 1), (1, 6, 1)}.在Dershowitz定义的多重集合的序下[24], 对于所有的ξ ∈dec(ξ), 有r(ξ) > r(ξ').因为这个在多重集合上的序是一个良序(well order), 由良序的性质, 所有秩函数严格递减的ξ序列都是有限的.又因为每次对ξ分解得到的集合dec(ξ)也是有限集, 由柯尼格引理, KLMST分解算法一定终止.
下面对KLMST分解算法作复杂度分析, 这里非常重要的是引入了一类所谓的非初等(non-elementary)复杂性类, 它的定义依赖于集合论中的序数理论.
对于序列ξ0, ξ1, ξ2, …满足ξn+1 ∈dec(ξn), 有r(ξ0) > r(ξ1) > r(ξ2) > ….分解过程中, 这个序列长度的上界记做L.序数a < ε0(
我们可以把秩函数r的取值等价地看做
| ${\beta _{{\xi _0}}} = {\omega ^{{\omega ^2} \cdot 3 + \omega \cdot 4}}, {\beta _{{\xi _1}}} = {\omega ^{{\omega ^2} \cdot 3 + \omega \cdot 3 + 3}} \cdot 2, {\beta _{{\xi _2}}} = {\omega ^{{\omega ^2} + \omega \cdot 9 + 1}} + {\omega ^{{\omega ^2} + \omega \cdot 6 + 1}}.$ |
给定
例:
gk(n)=k, gω(n)=gn+1(n)=n+1, gω+1(n)=1+gω(g(n))=2+g(n).
为了研究复杂性, 还需要定义控制函数
定义gk(n)=g(gk-1(n))表示函数g迭代k次,
| ${\mathcal{F}_{ < \alpha }} = \bigcup\limits_{\beta < {\omega ^\alpha }} {FSPACE({H^\beta }(n))}, {F_{h, \alpha }} = \bigcup\limits_{p \in {\mathcal{F}_{ < \alpha }}} {SPACE({h^{{\omega ^\alpha }}}(p(n)))}, {F_\alpha } = {F_{H, \alpha }}.$ |
在KLMST分解中, 假设ξ=M0, a1, M1, …, ak, Mk, ξ' ∈dec(ξ).
可以看出, N(βξ)不超过
综上, 在KLMST分解中构造的标记证据图序列的大小有上界gL(n), 其中,
定理2.2[21]. VAS的可达性问题上界不超过
研究展望:关于KLMST分解的最新研究是2015年Leroux定义了理想的概念[21], 给出了对KLMST分解的另一个直观解释:KLMST分解是对路径集合的理想的分解.这可能对VAS的其他扩展模型的验证问题有启发作用.此外, KLMST分解的算法目前已知的上界
● 基于递归不变量(inductive invariant)的算法
基于递归不变量(inductive invariant)算法.这个算法有两个半可判定过程:第1个不断枚举所有的动作序列以证明可达, 第2个枚举所有的Presburger公式证明不可达.Leroux证明了如果向量u到向量u'不可达, 那么存在一个可以用Presburger公式表示的向量集合, 向量u在这个集合中, 而向量u'不在这个集合中[16].并且这个集合相对于可达性关系是一个前向递归不变量, 即, 所有集合中的向量的下一步依然在这个集合中.因此, 这个Presburger集合就是不可达的一个证明(witness).目前, 这个方法只有可判定的结果, 没有算法复杂性上界.
如果集合S⊆
最近, Leroux对一般情况下VAS的可达集给出了更加精确的描述.2011年, Leroux定义了Lambert集合和Petri集合的概念[19], 证明了在一般情况下, VAS的可达集是Lambert集合, 可达性关系的集合是Petri集合.其中, Petri集合一定是Lambert集合; Lambert集合一定也是Presburger集合.下面给出这些集合的定义.
集合P⊆
例:周期集合
对给定自反传递的关系R⊆
| $pos{t_R}(X) = \bigcup\limits_{x \in X} {\{ y \in {\mathbb{Z}^d}|(x, y) \in R\} }, pr{e_R}(Y) = \bigcup\limits_{y \in Y} {\{ x \in {\mathbb{Z}^d}|(x, y) \in R\} } $ |
若postR(X)⊆X, 则称X是相对于关系R的前向递归不变量(forward inductive invariant); 若preR(Y)⊆Y, 则称Y是相对于关系R的后向递归不变量(backward inductive invariant).定义R的区分(separators) (X, Y):X, Y⊆
Leroux证明了下面的重要结论:
引理2.3[19]. VAS的可达性关系是一个Petri关系.
进一步得到关于Petri关系的一个主要结论是:
引理2.4[19].若R*⊆
如果u到u'不可达,
研究展望:注意到, 基于前向递归不变量的算法不依赖于KLMST分解算法.不过, 该算法的复杂性目前仍然是公开的.这个复杂性依赖于最短的可达路径长度和最短的能够表示一个可以区分起点和终点的前向递归不变量的Presburger公式长度.值得一提的是:虽然VAS可能会有一个有限的Ackermann大小的可达集合, 但该算法中表示前向递归不变量的Presburger集合是可达集合的一个超集, 因此该算法还是可能有比Fω更好的下界.
总结:目前, VAS可达性的上界算法主要有KLMST分解算法和基于递归不变量的算法.KLMST分解算法试图去分析可达路径, 最终得到的标记证据图序列可以看出路径的结构.该算法会有Fω的下界和
Lipton在1976年给出了VAS可达性问题的EXPSPACE的算法下界.Lipton首先提出了并行程序(parallel programs)的模型, 证明了并行程序上的可接受问题(the acceptance problem)可以多项式时间归约到VAS的可达性问题.然后, 递归构造了可以模拟3个有界的计数器的并行程序(这里的计数器可以做加法、减法、测0操作), 计数器的界是这个并行程序的双指数大小.而用3个双指数大小的计数器可以来模拟任意需要指数空间的图灵机, 因此可以得到VAS的可达性问题EXPSPACE-hard的下界.
其中, Lipton用到的直观概念是并行程序(parallel programs).并行程序是三元组P=〈F, d, x〉, 其中, F是并行的流程图(flowcharts)的集合, d是维数, x=(x1, …, xd) ∈

|
Fig. 5 Four kinds of nodes in a parallel program 图 5 流程图的4种节点 |
并行程序的格局(configuration)可以表示为c=〈p1, …, pm, x1, …, xd〉, m=|F|.其中, pi表示第i个流程图当前节点的编号.并行程序的初始格局C0中, pi是第i个流程图的起始节点, xi=0.
并行程序每一步运行
(1) 存在i ∈{1, 2, …, m}, pi是起始节点,
(2) 存在i ∈{1, 2, …, m}, pi是猜测节点,
(3) 存在i ∈{1, 2, …, m}, pi是赋值节点,
用
引理2.5[11].并行程序上的可接受问题可以多项式时间归约到VAS的可达性问题.
我们可以通过研究并行程序上可接受问题的下界来回答VAS可达性问题的下界.注意, 并行程序可以模拟计数器的加法和测零操作.加法操作的模拟比较直观; 模拟测零操作的思路是用两维向量x, x' ∈
● i=1时, 程序块如图 6所示.
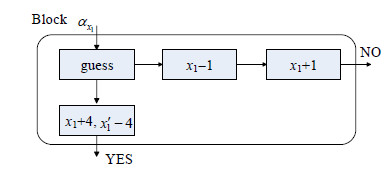
|
Fig. 6 Block |
●
i > 1时, 设置辅助变量
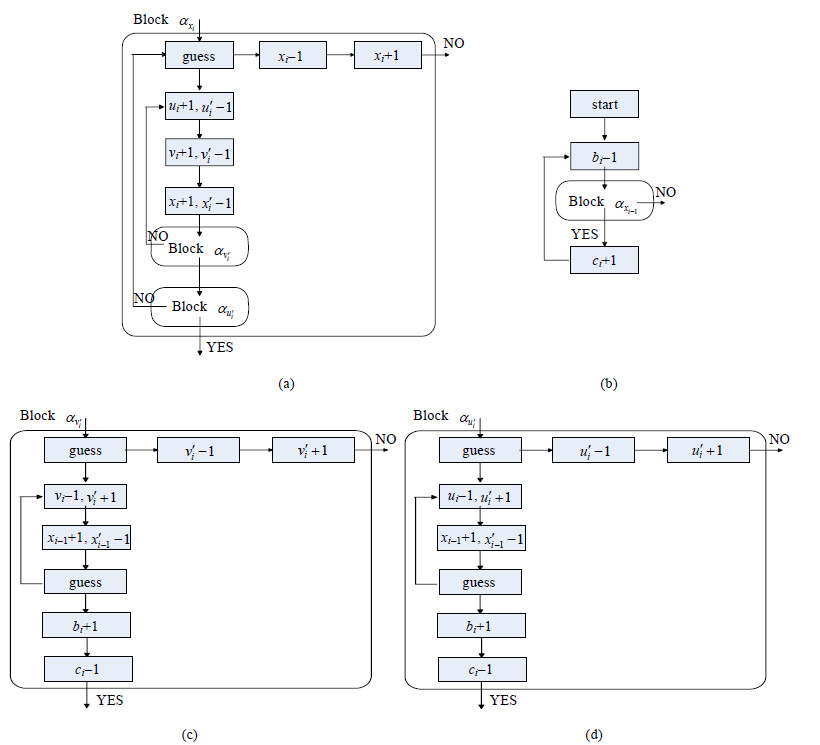
|
Fig. 7 Block |
将变量
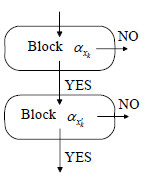
|
Fig. 8 Test zero in a parallel program 图 8 在并行程序上实现测0 |
因此, 并行程序上的可接受问题是EXPSPACE-hard.
由引理2.5, VAS可达性问题的下界也是EXPSPACE-hard.
定理2.6[11]. VAS可达性问题的下界是EXPSPACE-hard.
研究展望:在关于下界的研究方面, 已有技术的核心是VAS系统可以模拟双指数大小的计数器, 由此其可达性问题的下界是EXPSPACE-hard.类似的技术可以推广到下推向量加法系统.下推向量加法系统在向量加法系统的基础上增加了一个栈, Lazic证明了它可以模拟界是2↑↑n的计数器[28],
在前面的讨论中, 向量的维度d是输入的一部分.而在实际应用中, 问题的维度往往存在固定的上界. Hopcroft和Pansiot在1979年的工作[10]中指出:当VAS的维数在5之内时, 其可达集是一个可被有效计算的半线性集.由于n维VASS可以用n+3维VAS表示, 这就等价于得出了2维之内VASS可达性问题、等价性问题(equivalence)、包含问题(containment)等的可判定结论.他们同时用反例说明了该技术无法被应用到3维及更高维度的VASS的研究.
关于低维度VASS的研究结果主要包括:Hasse与Kreutzer等人[29]在2009年证明了1-VASS(即1维VASS, 等价于4维VAS)的可达性问题在一进制编码下是NL-完备的, 而在二进制编码下是NP-完备的.Haase在其博士论文[30]中证明了同一模型在输入是二进制编码时的有界性问题和可覆盖问题都是NP-完备的.而对2-VASS, Howell等人[31]对Hopcroft的算法进行了分析, 指出原始算法的复杂度是非确定双指数时间(2-NEXPTIME), 并进一步将算法上界改进到了确定双指数时间(2-EXPTIME).而关于二进制编码下2-VASS上可达性问题的最终结果则是在最近几年才得出:Fearnley等人[32]给出了PSPACE-hard的证明; 紧接着, Blondin等人[33]在2015年找到了PSPACE的判定算法, 从而证明了该问题实际上是PSPACE-完备的.他们工作的一个额外结论是证明了对固定维度(d≥2维)d-VASS, 有界性和可覆盖性都是PSPACE-完备的.值得一提的是, Blondin等人的工作, 本质上是对Leroux等人[34]在2004年有关2-VASS具有平坦性(flatness)证明的精化.当限制为输入是一进制编码时, 2-VASS可达性问题在2016年被证明是NL-完备的[35].到目前为止, 在可达性问题上没有关于3-VASS或更高维度模型的结果:既没有更准确的下界结论, 也没有任何非平凡(即优于
目前, 固定维度VASS的复杂性结果集中在2维及以下, 即:当向量维度大于2时, 仅有平凡结论(即2维问题的下界和维度无限制时的上界).因此, 这里集中讨论2维及2维以下模型相关的研究技术.
3.2.1 上界技术(算法) 3.2.1.1 二维VASS的平坦化(flatness)已有d维(d≤2)VASS的算法都依赖于一个重要的结论:此维度限制下的VASS是可平坦化的.对给定的VASS V=(Q, T), 其中, Q代表状态集合, T代表迁移规则集合, V的输入规模被定义为|V|=|Q|+|T|×d×log2|T|.用α0, β1, α1, …, βk, αk代表V上一组不含循环、可执行的迁移规则序列, 则一组形如

|
Fig. 9 Linear path scheme 图 9 线性路径策略 |
有限条线性路径策略的并集被称为半线性路径方案(semi-linear path scheme).若V的可达关系集合可以表示为一个半线性路径方案, 则我们称V是具有平坦性的(相应称对应的可达关系集合是平坦的).直观上讲, 平坦性意味着对应的可达路径可以被表示为一组只依次含有若干简单环的路径(即, 不存在环的嵌套), 而具有这样结构的路径所对应的可达关系是有效半线性的.对给定的二元关系RV⊆QxQ,
直到2015年, Blondin等人[33]对Leroux的研究进行了量化, 给出了上述常数c的上界(|Q|+T)O(1).并证明了如果初始格局到目标格局可达, 则在对应的平坦性的关系中, 半线性集合将由一组有效的、指数规模的线性路径策略(即
Blondin工作中一个相对独立的结果是, 证明了非确定有限自动机所识别的路径的Parikh像(Parikh image, 用于表达路径中每个字符出现的次数的函数)存在一个多项式规模的使用线性路径策略的表达方式.基于这个结论, 很容易就能证明:当将原始可达性验证问题的条件放宽到整数意义下时, 任意d维VASS上的可达性等价于存在一组有限的、多项式规模的线性路径策略.当然, 这与各维向量值都应限制为自然数下的可达性还有距离.为此, 他们将问题分成了3种子类型.
(1) 初始格局和目标格局的状态相同, 且始末状态两个计数器的值都大于常数c, 但对中间运行情况不做限制;
(2) 初始格局到目标格局的整条路径上, 两个计数器的值都大于常数c;
(3) 初始格局到目标格局的整条路径上, 至少有一个计数器的值不超过常数c.
以上3种情况分别对应于图 10中的3种不同路径类型.
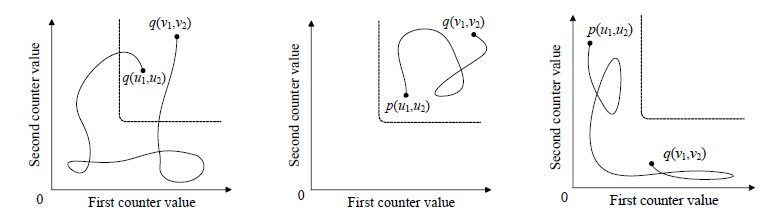
|
Fig. 10 Three kinds of reachable paths 图 10 3种类型的可达路径 |
Blondin等人证明了这3种情况下的VASS的可达关系都有指数规模的刻画.具体而言, 类型(3)可规约到维度为1的情况从而化简.类型(2)可以用类型(1)的结论推导得出.对最关键的类型(1), 与d≤2这个限制直接相关的核心技术引理是:
引理3.1[33].令b ∈Z2, P⊆Z2且b ∈P, 令Z是2维空间中的一个象限, 则有
● |Pi|≤2;
● Pi⊆(P∪L(b; P))∩Z; 且
● 存在e≤PO(1), 满足{ci}∪(Pi∩L(b; P))⊆b+cone[0, e](P).
即:在2维情况下, 对满足引理前提的线性集L(b; P), 考虑其与任意象限的交集, 结果都可以表示为一组简单的半线性路径的并; 或者更具体地说, 由一组周期(period, 即Pi)的基数为2, 且周期和基(base, 即ci)来自一个简单集合的线性路径组成.值得注意的是, 这个引理对d≥3的情况均不成立.
最后, 通过证明任意2维VASS的可达路径都可分解为多项式规模段类型为类型(1)、类型(2)、类型(3)的路径后, 就完成了2维情况下问题上界的证明.
研究展望:当维数固定时的研究, 是近年关于VASS验证研究的核心.特别值得注意的是:除了上面的引理3.1及其相关推论外, Blondin在文献[33]中的其他结论都可以被直接应用或推广到更高维的情况.因此, 对更高维情况的研究, 重点和难点是对3维及以上的情况找到类似引理3.1的降维结论.
3.2.2 下界技术下界来自对有界单计数器自动机(bounded one-counter automata)模型上可达性问题的规约.
有界单计数器自动机(可以表示为三元组V=(Q, T, b), 其中, (Q, T)就是1-VASS, 而b ∈N是用二进制表达的计数器值的上界.令B=[0, b], 对给定的初始格局p(u)和目标格局q(v), u, v ∈B.与一般的可达性问题不同的是:可达性关注是否存在从p(u)到q(v)的可行路径, 且路径上每一个中间格局对应的计数器的值都不超过b.即问关系
Fearnley等人[32]在2013年证明了有界单计数器自动机上的可达性问题是PSPACE-complete.
对任意有界单计数器自动机V=(Q, T, b), 可构造其可达性问题到2-VASS可达性问题的规约.规约的核心是利用界限参数b:构造2-VASS
模型V中
研究展望:注意, 这部分所得到的下界结论可以平凡地延伸到维度d≥3的情况.但因为目前对3维的情况了解甚少, 可优先考虑相关算法的研究, 增加对模型的认知之后, 再考虑合适的下界规约.
4 重要扩展模型随着应用领域研究的推进, 研究者们逐渐意识到现有VASS模型的局限并定义和发展了若干重要的扩展模型.鉴于篇幅限制, 这里只列举领域内近年来备受关注的几个重要模型, 并总结关于这些模型的验证问题的最新结论.
4.1 PVAS下推向量加法系统(pushdown vector addition system, 简称PVAS)是在VASS模型之上增加了栈及相应的入栈(push)和出栈(pop)操作.
PVAS上一条典型的迁移规则为:
PVAS模型是VASS的非平凡扩展.Leroux等人证明了PVAS终止性和有界性都可判定[37], 但没有进一步的上界结论; 目前仍不知道PVAS上可覆盖性和可达性问题是否可判定, 仅仅知道它们都是Tower-hard[28], 复杂性远高于VASS上的对应验证问题.
在维度固定时, 仅当维度为1时有一些进展.Leroux等人证明了1-PVAS可覆盖性是NP-hard, 上界是EXPSPACE[38, 39], 而有界性问题是NP-hard, 相应的上界是EXPTIME[39, 40].
关于PVAS非常特殊的一点是, n-PVAS的可达性, 可以规约到n+1-PVAS的可覆盖性, 即, PVAS模型下的可达性问题和可覆盖性问题难度本质上一样.这也从另一个角度说明了PVAS的特殊性.
4.2 AVASSAlternating VASS最早是由Lincoln等人在研究命题线性逻辑(propositional linear logic)的可判定性时被提出来的.AVASS是一个四元组A=Q, d, Tu, Tf.其中:Q是有限的状态集合; d ∈N代表维度; Tu⊆QxZdxQ是一元迁移规则, 如
关于AVASS的主要结论是可达性不可判定[41].Courtois等人证明了:若将求解(格局)可达性削弱为状态可达性, 则问题难度是双指数完备的[42].当AVASS模型中向量维度固定时, 状态可达性问题(及非终止性问题)难度降低为EXPTIME完备的.值得一提的是:AVASS状态可达性问题的研究可以有效地规约到BPP、VASS与有限状态系统的模拟问题上, 从而得到了新的下界结论.这也成为研究AVASS的重要原因之一.
4.3 BVASSVASS的计算过程可以理解为一个线性过程.Branching VASS[43]的计算则是一棵计算树:从叶子节点出发到根节点的过程, 每个非叶子节点的向量值被定义为:该节点的儿子节点所对应的向量值之和, 再加上一个规则向量.得到的模型可有效刻画计算语言学、逻辑、乃至XML等中的一些核心问题, 从而引起研究者的广泛重视.
Lazic[44]和Demri[45]分别研究了BVASS的可达性问题以及可覆盖性、有界性问题, 证明了前者是2-EXPSPACE-难的, 而后两个问题是2-EXPTIME-完备的.Lazic等人[46, 47]进一步证明了一般BVASS可达性问题的下界甚至是Tower-hard, 也就是Non-elementary, 即, 任何验证算法不具有现实可行性.但非常有趣的是:与对维度不做限制时的高复杂性相比, 2016年, Gller等人证明了一维BVASS上的可达性、可覆盖以及有界性问题都是多项式时间完备的[48].这些结果都表明, BVASS并非VASS的平凡扩展.
4.4 PND模型PND模型是在Petri网中引入数据与数据操作的概念而为相关建模提供了便利, PND模型中, 每个place里不再是存储同样类型的token, 而是转为存储数据, 故而迁移规则相应地变为消耗和产生数据.关于PND, 比较集中的工作是Lazic[49], Haddad[50], Rosa-Velardo[51]等人近年给出的一系列结论, 其中最重要的结论之一是证明了有序数据子模型上的可覆盖性问题是
研究展望:本节集中介绍了几个典型的VAS扩展模型, 并对这些模型上的验证问题做了较为简要的总结.这几个模型都具有理论或应用上的重要价值.从已有结论可以看出, 许多关于这些模型的验证问题都丞待解决.我们认为, 其中最值得关注的是:1维和2维PVAS可覆盖问题的上、下界、任意固定维度AVASS的验证问题的复杂性、2维BVASS的可达性问题的复杂性以及UDPN可达性问题的判定性.
5 本文总结本文总结了加法向量系统验证领域的若干核心问题、最新进展和关键技术; 特别地, 指出了本领域中若干重要开放问题及部分结论的相互联系; 并对一些扩展模型和验证问题间的相互关系做了相应探讨, 提出了未来的研究方向.我们认为:向量加法系统是一个简洁而强大的数学模型, 无论从理论还是应用上而言, 对向量加法系统及其扩展模型上验证问题的深入研究都具有极重要的价值.最后, 作为对加法向量系统验证领域研究现状的小结, 我们将本领域最新结论总结在表 1中(注意, 这里用#表示开放问题).
| Table 1 State-of-the-Art results on VASS and its extensions 表 1 VASS及其扩展模型上最新结论总结 |
| [1] |
Petri CA. Kommunikation mit Automaten. Bonn: Institut fur Instrumentelle Mathematik, Schriften des ⅡM Nr. 2, 1962. |
| [2] |
Ball T, Chaki S, Rajamani S. Parameterized verification of multithreaded software libraries. In: Proc. of the Tools and Algorithms for the Construction and Analysis of Systems. LNCS 2031, Springer-Verlag, 2001. 158-173. [doi:10.1007/3-540-45319-9_12] |
| [3] |
van der Aalst W. The application of Petri nets to workflow management. Journal of Circuits, Systems, and Computers, 1998, 8(1): 21–66.
[doi:10.1142/S0218126698000043] |
| [4] |
Heiner M, Gilbert D, Donaldson R. Petri nets for systems and synthetic biology. In: Proc. of the Formal Methods for Computational Systems Biology. 2008. 215-264. [doi:10.1007/978-3-540-68894-5_7] |
| [5] |
Lei L, Lin C, Zhong ZD. Stochastic Petri nets for wireless networks. In: Springer Briefs in Electrical and Computer Engineering, Springer-Verlag, 2015. 1-101. [doi:10.1007/978-3-319-16883-8] |
| [6] |
Fan LJ, Wang YZ, Li JY, Cheng XQ, Lin C. Privacy Petri net and privacy leak software. Journal of Computer Science and Technology, 2015, 30(6): 1318–1343.
[doi:10.1007/s11390-015-1601-7] |
| [7] |
Yu WY, Yan CG, Ding ZJ, Jiang CJ, Zhou MC. Modeling and validating E-commerce business process based on Petri nets. IEEE Trans.on Systems, Man, and Cybernetics:Systems, 2014, 44(3): 327–341.
[doi:10.1109/TSMC.2013.2248358] |
| [9] |
Jiang YX, Lin C, Qu Y, Yin H. Research on Model-Checking Based on Petri Nets. Ruan Jian Xue Bao/Journal of Software, 2004, 15(9): 1265-1276(in Chinese with English abstract)http://www.jos.org.cn/1000-9825/15/1265.htm. |
| [10] |
Hopcroft J, Pansiot JJ. On the reachability problem for 5-dimensional vector addition systems. Theoretical Computer Science, 1979, 8(2): 135–159.
[doi:10.1016/0304-3975(79)90041-0] |
| [11] |
Lipton RJ. The reachability problem is exponential-space-hard. Technical Report, 62, Department of Computer Science, Yale University, 1976. |
| [12] |
Rackoff C. The covering and boundedness problems for vector addition systems. Theoretical Computer Science, 1978, 6: 223–231.
[doi:10.1016/0304-3975(78)90036-1] |
| [13] |
Rosier L, Yen HC. A multiparameter analysis of the boundedness problem for vector addition systems. Journal of Computer and System Sciences, 1986, 32: 105–135.
[doi:10.1016/0022-0000(86)90006-1] |
| [14] |
Sacerdote GS, Tenney RL. The decidability of the reachability problem for vector addition systems (preliminary version). In: Proc. of the 9th Annual ACM Symp. on Theory of Computing. ACM Press, 1977. 61-76. [doi:10.1145/800105.803396] |
| [15] |
Mayr EW. An algorithm for the general Petri net reachability problem. In: Proc. of the STOC'81. ACM Press, 1981. 238-246. [doi:10.1145/800076.802477] |
| [16] |
Kosaraju SR. Decidability of reachability in vector addition systems. In: Proc. of the STOC'82. ACM Press, 1982. 267-281. [doi:10.1145/800070.802201] |
| [17] |
Lambert JL. A structure to decide reachability in Petri nets. Theoretical Computer Science, 1992, 99(1): 79–104.
[doi:10.1016/0304-3975(92)90173-D] |
| [18] |
Leroux J. The general vector addition system reachability problem by presburger inductive invariants. In: Proc. of the 24th IEEE Symp. on Logic in Computer Science (LICS 2009). 2009. [doi:10.1109/LICS.2009.10] |
| [19] |
Leroux J. Vector addition system reachability problem (a short self-contained proof). In: Proc. of the Principles of Programming Languages. Austin: ACM Press, 2011. 307-316. [doi:10.1145/1926385.1926421] |
| [20] |
Leroux J. Vector addition systems reachability problem (a simpler solution). In: Voronkov A, ed. Proc. of the Alan Turing Centenary Conf. (Turing-100). 2012. |
| [21] |
Leroux J, Schmitz S. Demystifying reachability in vector addition systems. In: Proc. of the 30th IEEE Symp. on Logic in Computer Science (LICS 2015). 2015. 56-67. [doi:10.1109/LICS.2015.16] |
| [22] |
Karp RM, Miller RE. Parallel program schemata. Journal of Computer and System Sciences, 1969, 3(2): 147–195.
[doi:10.1016/S0022-0000(69)80011-5] |
| [23] |
Muller H. The reachability problem for VAS. In: Proc. of the Advances in Petri Nets 1984. NCS 188. Springer-Verlag, 1985. 376-391. |
| [24] |
Dershowitz N, Manna Z. Proving termination with multiset orderings. Communications of the ACM, 1979, 22(8): 465–476.
[doi:10.1145/359138.359142] |
| [25] |
Figueira D, Figueira S, Schmitz S, Schnoebelen P. Ackermannian and primitive-recursive bounds with Dickson's Lemma. In: Proc. of the LICS 2011. IEEE Press, 2011. [10:1109/LICS:2011:39] |
| [26] |
Schmitz S. Complexity hierarchies beyond Elementary. ACM Trans. on Computation Theory, 2015. http://arxiv:org/abs/1312:5686[doi:doi:10.1145/2858784] |
| [27] |
Ginsburg S, Spanier EH. Semigroups, presburger formulas and languages. Pacific Journal of Mathematics, 1966, 16(2): 285–296.
[doi:10.2140/pjm.1966.16.285] |
| [28] |
Lazic R. The reachability problem for vector addition systems with a stack is not elementary. 2013. https://arxiv.org/pdf/1310.1767.pdf |
| [29] |
Haase C, Kreutzer S, Ouaknine J, Worrell J. Reachability in succinct and parametric one-counter automata. In: Proc. of the Concurrency Theory (CONCUR 2009). 2009. 369-383. [doi:10.1007/978-3-642-04081-8_25] |
| [30] |
Haase C. On the complexity of model checking counter automata[Ph. D. Thesis]. University of Oxford, 2012. |
| [31] |
Howell RR, Rosier LE, Huynh DT, Yen HC. Some complexity bounds for problems concerning finite and 2-dimensional vector addition systems with states. Theoretical Computer Science, 1986, 46(3): 107–140.
[doi:10.1016/0304-3975(86)90026-5] |
| [32] |
Fearnley J, Jurdzinski M. Reachability in two-clock timed automata is PSPACE-complete. In: Proc. of the 40th Int'l Colloquium on Automata, Languages, and Programming (ICALP), Vol. 2. 2013. 212-223. [doi:10.1007/978-3-642-39212-2_21] |
| [33] |
Blondin M, Finkel A, Göller S, Haase C, McKenzie P. Reachability in two-dimensional vector addition systems with states is PSPACE-complete. In: Proc. of the 30th Annual ACM/IEEE Symp. on Logic in Computer Science (LICS 2015). 2015. 32-43. [doi:10.1109/LICS.2015.14] |
| [34] |
Leroux J, Sutre G. On flatness for 2-dimensional vector addition systems with states. In: Proc. of the CONCUR 2004-15th Int'l Conf. on Concurrency Theory. 2004. 402-416. [doi:10.1007/978-3-540-28644-8_26] |
| [35] |
Englert M, Lazic P, Totzke P. Reachability in two-dimensional unary vector addition systems with states is NL-complete. In: Proc. of the LICS 2016. 2016. 477-484. [doi:10.1145/2933575.2933577] |
| [36] |
Ganty P, Majumdar R. Algorithmic verification of asynchronous programs. ACM Trans.on Programming Languages and Systems, 2012, 34(1): 1-6–48.
[doi:10.1145/2160910.2160915] |
| [37] |
Leroux J, Praveen M, Sutre G. Hyper-Ackermannian bounds for pushdown vector addition systems. In: Proc. of the Joint Meeting of the 23rd EACSL Annual Conf. on Computer Science Logic (CSL) and the 29th Annual ACM/IEEE Symp. on Logic in Computer Science (LICS) (CSL-LICS 2014). 2014. [doi:10.1145/2603088.2603146] |
| [38] |
Leroux J, Sutre G, Totzke P. On the coverability problem for pushdown vector addition systems in one dimension. In: Proc. of the ICALP, Vol. 2. 2015. 324-336. [doi:10.1007/978-3-662-47666-6_26] |
| [39] |
Finkel A, Leroux J. Recent and simple algorithms for Petri nets. Software and System Modeling, 2015, 14(2): 719–725.
[doi:10.1007/s10270-014-0426-0] |
| [40] |
Leroux J, Sutre G, Totzke P. On boundedness problems for pushdown vector addition systems. In: Proc. of the RP. 2015. 101-113. [doi:10.1007/978-3-319-24537-9_10] |
| [41] |
Lincoln P, Mitchell J, Scedrov A, Shankar N. Decision problems for propositional linear logic. Annals of Pure and Applied Logic, 1992, 56(1-3): 239–311.
[doi:10.1016/0168-0072(92)90075-B] |
| [42] |
Courtois JB, Schmitz S. Alternating vector addition systems with states. In: Proc. of the MFCS, Vol. 1. 2014. 220-231. [doi:10.1007/978-3-662-44522-8_19] |
| [43] |
Verma KN, Goubault-Larrecq J. Karp-Miller trees for a branching extension of VASS, discr. Mathematics & Theoretical Computer Science, 2005, 7: 217–230.
|
| [44] |
Lazic R. The reachability problem for branching vector addition systems requires doubly-exponential space. Information Processing Letters, 2010, 110(17): 740–745.
[doi:10.1016/j.ipl.2010.06.008] |
| [45] |
Demri S, Jurdzinski M, Lachish O, Lazic R. The covering and boundedness problems for branching vector addition systems. Journal of Computer and System Sciences, 2013, 79(1): 23–38.
[doi:10.1016/j.jcss.2012.04.002] |
| [46] |
Lazic R, Schmitz S. Non-Elementary complexities for branching VASS, MELL, and extensions. In: Proc. of the CSL/LICS. 2014. [doi:10.1145/2603088.2603129] |
| [47] |
Lazic R, Schmitz S. Non-Elementary complexities for branching VASS, MELL, and extensions. ACM Trans.on Computational Logic, 2015, 16(3): 1–30.
[doi:10.1145/2733375] |
| [48] |
Göller S, Haase C, Lazic R, Totzke P. A polynomial-time algorithm for reachability in branching VASS in dimension one. 2016, 105: 1-13. https://arxiv.org/abs/1602.05547 |
| [49] |
Lazic R, Newcomb T, Ouaknine J, Roscoe A, Worrell J. Nets with tokens which carry data. Fund Information, 2008, 88(3): 251–274.
[doi:10.1007/978-3-540-73094-1_19] |
| [50] |
Haddad S, Schmitz S, Schnoebelen P. The ordinal recursive complexity of timed-arc Petri nets, data nets, and other enriched nets. In: Proc. of the LICS. IEEE Press, 2012. 355-364. [doi:10.1109/LICS.2012.46] |
| [51] |
Rosa-Velardo F. Ordinal recursive complexity of unordered data nets. Technical Report, TR-4-14, Departamento de Sistemas Informaticosy Computacion, Universidad Complutense de Madrid, 2014.
http://www.sciencedirect.com/science/article/pii/S0890540117300160#! |
| [52] |
Hofman P, Lasota S, Lazić R, Leroux J, Schmitz S, Totzke P. Coverability trees for Petri nets with unordered data. In: Proc. of the 19th Int'l Conf. on Foundations of Software Science and Computation Structures (FoSSaCS). 2016. [doi:10.1007/978-3-662-49630-5_26] |
| [53] |
Lazic R, Totzke P. What makes Petri nets harder to verify: Stack or data? In: Proc. of the Concurrency, Security, and Puzzles 2017. 2017. 144-161. [doi:10.1007/978-3-319-51046-0_8] |
| [8] |
林闯.
随机Petri网和系统性能评价. 北京: 清华大学出版社, 2005. . |
| [9] |
蒋屹新, 林闯, 曲扬, 尹浩. 基于Petri网的模型检测研究. 软件学报, 2004, 15(9): 1265-1276. http://www.jos.org.cn/1000-9825/15/1265.htm.
|
 2018, Vol. 29
2018, Vol. 29



