数组作为一种数据结构具有简单高效的特点, 因此常常在程序中被使用.在验证数组程序正确性时, 需要分析和使用数组(及其中的元素)具有的性质.然而, 静态分析数组程序的行为是一个很有挑战的问题:首先, 数组索引会导致复杂的语义, 可能引起别名问题; 其次, 数组大小可以非常大甚至未知, 这意味着非常大数量或者未知数量的变量.因此, 分析数组程序经常需要使用和处理全称量词.
合成数组程序的不变式问题已经吸引了很多研究者的关注.谓词抽象(predicate abstraction)方法[1, 2]使用一些语法启发式方法推导用于抽象的谓词, 然后使用这些谓词推理数组程序的不变式.反例制导的精化(counter-example guided refinement)方法[3]和Craig插值(craig interpolants)方法[4]提升了谓词抽象方法的效果.文献[5]的方法将数组所有元素看做一个变量处理, 虽然提高了处理效率, 但是却会导致分析结果不精确.数组划分(array partitioning)方法[6-8]将索引域([1...n])划分为若干符号区间, 并且给每一个子数组关联一个摘要辅助变量(summary auxiliary variable), 但是该方法难以处理多维数组, 并且它基于语法信息来划分索引区间, 程序写法上的变化可能导致程序无法被处理.模板(templates)方法[9]极其强大但是代价昂贵, 并且需要用户提供数组性质模板.
针对那些通过循环控制变量的简单表达式来访问数组的程序, 本文提出了基于抽象解释框架[10]的方法来发现一类程序的全称量词性质.这些程序被称为归纳循环程序(induction loop program).这类程序中的循环控制变量在循环中每次增加或者减少一个固定常量.需要特别指出, 循环控制变量可以在一次迭代中增加/减少多次, 如图 1(d)所示的i和j.在现实中, 很多程序或者程序片段都是归纳循环程序.图 1展示了4个归纳循环程序的例子.图 1(a)和图 1(b)表示两个版本的arrayPartCopy程序.图 1(a)先进行数组操作再更新循环控制变量, 图 1(b)先更新循环控制变量再进行数组操作.图 1(c)是二维数组的例子.图 1(d)所示为QuickSort中根据阈值分划数组的程序片段, 其中的循环控制变量i和j分别在外循环的一次迭代中增加/减少多次.

|
Fig. 1 Induction loop programs 图 1 归纳循环程序 |
本文的方法能够自动发现数组元素和标量以及数组元素之间的 < , ≤=, ≠性质.例如:在两个版本的arrayPartCopy程序(如图 1(a)和图 1(b)所示)结尾处, 本文的方法可以发现数组A的所有偶数下标的元素等于对应数组B下标的元素; 在2d-ArrayCheck程序(如图 1(c)所示)结尾处, 本文的方法可以发现二维数组中的所有遍历过的元素都不等于0;在Find程序(如图 1(d)所示)结尾处, 本文的方法可以发现根据阈值x, 数组A被划分成小于x的部分和大于等于x的部分.这些性质正是这些程序期望的性质.
本文的主要贡献在于:基于抽象解释框架提出了一种完全自动化地发现数组性质的方法:首先, 通过预分析找出程序中的循环控制变量; 然后进行数组性质分析发现程序中的全称量词性质.数组性质分析会在分析过程中自动生成全称量词性质, 并根据循环控制变量的变化相应地维护和更新全称量词性质的区间.本文给出了方法的正确性证明和收敛性证明; 提出了直接以原子性质和区间量词性质集合作为抽象域的数组性质分析方法.这种抽象域具有较强的灵活性和表达能力, 能够描述一个数组区间上的元素所具有的性质; 同时能够允许区间量词的嵌套, 从而使得数组性质分析可以表示和处理多维数组的性质.
本文第1节使用一个例子直观地展示本文的方法.第2节定义归纳循环程序、数组性质以及基本知识(性质的内存域(memory scope)和迭代数据流框架).第3节描述预分析, 它给出循环控制变量的判断方法.第4节给出数组性质分析方法.第5节是工具实现和实验评估.第6节是相关工作介绍.最后总结全文, 并对未来值得关注的研究方向进行初步探讨.
1 一个例子本节将使用图 1(a)所示的arrayPartCopy程序简单展示本文所述方法.本文的方法关注区间形式的全称量词性质∀k(k ∈[e1, c, e2)⇒p(k)), 其中, 区间[e1, c, e2)表示一个集合.
| $ [{e_1}, c, {e_2}) = \left\{ {\begin{array}{*{20}{l}} {\{ {e_1} + n \times c|n \geqslant 0 \wedge {e_1} + n \times c < {e_2}\}, \;{如果}c > 0} \\ {\{ {e_1} + n \times c|n \geqslant 0 \wedge {e_1} + n \times c > {e_2}\}, \;{如果}c < 0} \end{array}} \right.. $ |
例如, 在arrayPartCopy程序结尾处, 方法能够自动发现区间全称量词性质∀k(k ∈[0, 2, size)⇒A[k]=B[k]), 即数组A的所有偶数下标的元素等于对应数组B下标的元素.这正是程序实现的功能.
本文的方法首先通过预分析找出程序中的循环控制变量、循环控制变量初始化语句和循环控制变量更新语句, 识别出循环控制变量初始值和每次改变的步长.在arrayPartCopy程序中, i是循环控制变量, 语句i=0是循环控制变量初始化语句, 语句i=i+2是循环控制变量更新语句.i的初始值是0, 步长是2.
然后, 本文的方法进行数组性质分析来发现程序中全称量词性质.数组性质分析会在分析过程中自动生成全称量词性质, 并根据循环控制变量的变化相应地维护和更新全称量词性质的区间.它的基本步骤如下.
1. 在循环控制变量初始化语句i=init之后, 数组性质分析会生成一个特殊的全称量词性质∀k(k ∈[init, c, i)⇒false), 其中, c是循环控制变量i的步长.因为循环控制变量初始化语句i=init后, [init, c, i)=∅成立, 因此∀k(k ∈[init, c, i)⇒false)成立.该性质用于生成其他全称量词性质;
2. 如果∀k(k ∈[init, c, i)⇒false)和性质p(i)在一个程序点处成立, 那么数组性质分析会在该程序点上生成全称量词性质∀k(k ∈[init, c, i+c)⇒p(k)).因为∀k(k ∈[init, c, i)⇒false)成立表明[init, c, i)是∅, 又因为循环控制变量i的步长是c, 所以[init, c, i+c)是就是集合{i}, 所以p(i)可推导出∀k(k ∈[init, c, i+c)⇒p(k));
3. 如果∀k(k ∈[init, c, i)⇒p(k))和性质p(i)在一个程序点处成立, 那么数组性质分析会在该程序点上生成全称量词性质∀k(k ∈[init, c, i+c)⇒p(k)).因为循环控制变量i的步长是c, 所以[init, c, i+c)是就是集合[init, c, i+c)∪{i}, 所以∀k(k ∈[init, c, i)⇒p(k))和p(i)可推导出∀k(k ∈[init, c, i+c)⇒p(k));
4. 在循环控制变量更新语句i=i+c之后, 数组性质分析会更新全称量词性质的区间.经过循环控制变量更新语句, ∀k(k ∈[init, c, i+c)⇒p(k))会更新成∀k(k ∈[init, c, i)⇒p(k)), ∀k(k ∈[init, c, i)⇒p(k))会更新成∀k(k ∈ [init, c, i-c)⇒p(k)).
下面将使用arrayPartCopy程序展示具体的分析过程.
假设初始时, 开始语句之前的数据流值是空集(即⊥), 其他语句之前和之后的数据流值是所有可能的性质的集合(即⊤).arrayPartCopy程序的数组性质分析过程如下.
● 第1次迭代
➢ 第3行后:∀k(k ∈[0, 2, i)⇒false)性质成立.因为循环控制变量初始化语句i=0后, [0, 2, i)=∅成立, 因此∀k(k ∈[0, 2, i)⇒false)成立;
➢ 第4行(while语句的汇点):∀k(k ∈[0, 2, i)⇒false)性质成立.第4行的性质由第3行之后和第6行之后的性质交汇得到.因为初始时第6行后的数据流值是所有可能性质的集合, 所以第4行的性质就是第3行之后的性质;
➢ 第5行后:∀k(k ∈[0, 2, i)⇒false), i < size, A[i]=B[i], ∀k(k ∈[0, 2, i+2)⇒A[k]=B[k])性质成立.性质∀k(k ∈ [0, 2, i+2)⇒A[k]=B[k])由∀k(k ∈[0, 2, i)⇒false)和A[i]=B[i]推导得到.因为∀k(k ∈[0, 2, i)⇒false)表明[0, 2, i)是∅, 因此[0, 2, i+2)就是集合{i}, 所以A[i]=B[i]可推导出∀k(k ∈[0, 2, i+2)⇒A[k]=B[k]);
➢ 第6行后:∀k(k ∈[0, 2, i)⇒A[k]=B[k])和∀k(k ∈[0, 2, i-2)⇒false)性质成立.因为循环控制变量更新语句i=i+2之后, 区间[0, 2, i+2)和[0, 2, i)分别变成[0, 2, i)和[0, 2, i-2).所以可以由第5行之后的性质∀k (k ∈[0, 2, i+2)⇒A[k]=B[k])得到∀k(k ∈[0, 2, i)⇒A[k]=B[k])在第6行之后成立.同理, 可由第5行之后的性质∀k(k ∈[0, 2, i)⇒false)得到∀k(k ∈[0, 2, i-2)⇒false)在第6行之后成立.
● 第2次迭代
➢ 在第4行(while语句的汇点):∀k(k ∈[0, 2, i)⇒A[k]=B[k])性质成立.第4行的性质由第3行之后和第6行之后的性质交汇得到.因为第3行后的性质∀k(k ∈[0, 2, i)⇒false)和第6行后的性质∀k(k ∈ [0, 2, i)⇒A[k]=B[k])交运算结果是∀k(k ∈[0, 2, i)⇒A[k]=B[k]), 所以∀k(k ∈[0, 2, i)⇒A[k]=B[k])在第4行成立;
➢ 第5行后:∀k(k ∈[0, 2, i)⇒A[k]=B[k]), i < size, A[i]=B[i], ∀k(k ∈[0, 2, i+2)⇒A[k]=B[k])性质成立.性质∀k (k ∈[0, 2, i+2)⇒A[k]=B[k])由∀k(k ∈[0, 2, i)⇒A[k]=B[k])和A[i]=B[i]推导得到.因为i的步长是2, 所以∀k(k ∈[0, 2, i)⇒A[k]=B[k])成立;
➢ 第6行后:∀k(k ∈[0, 2, i)⇒A[k]=B[k]), ∀k(k ∈[0, 2, i-2)⇒A[k]=B[k])成立.迭代收敛.
因此, 在程序结束时有:∀k(k ∈[0, 2, i)⇒A[k]=B[k]), size≤i, ∀k(k ∈[0, 2, size)⇒A[k]=B[k])性质成立.因为size≤i, 所以∀k(k ∈[0, 2, size)⇒A[k]=B[k])成立.
2 语言和预备知识 2.1 归纳循环程序(induction loop program)循环控制变量指在循环中每次增加或者减少一个固定常量的变量, 循环控制变量可以在一次迭代中增加(或者减少)多次.归纳循环程序指通过循环控制变量的简单表达式(循环控制变量与常量的加减运算)访问数组的程序.图 2给出了归纳循环程序中语句的语法.

|
Fig. 2 Syntax of statements 图 2 语句语法 |
其中, 赋值语句分为3类:赋值到一般的标量、赋值到数组元素、赋值到循环控制变量.赋值到循环控制变量又分为两类:循环控制变量初始化语句lcv=init和循环控制变量更新语句lcv=lcv(+|-) constant, 其中, lcv不出现在init中, 循环控制变量更新语句的第1个lcv和第2个lcv相同.表达式expr是没有副作用的关于常量, 标量和数组元素的+, -, *, /, %表达式(图 2没有给出它的具体语法, 本文的方法只需要expr没有副作用).数组下标表达式Iexp是常量, 循环控制变量或者循环控制变量和常量的加减运算.Iexp是expr的子集, 因为本文的很多论述都涉及到对下标表达式的处理, 因此将下标表达式作为一个独立的语法概念.条件表达式cond是析取或者合取表达式.
2.2 数组性质本文所分析的性质语法如图 3所示.

|
Fig. 3 Syntax of properties 图 3 性质语法 |
性质可以是原子性质atomProp或者全称量词性质forAllProp.原子性质atomProp是表达式之间的 < , ≤=, ≠关系.∀ID(ID ∈interval⇒false)表示一个特别的性质, 主要用于在分析过程中和其他性质一起生成新的全称量词性质.
区间interval表示一个集合, 定义如下:
| $ \begin{gathered} (exp{r_1}, constant, \exp {r_2}) = \hfill \\ \left\{ {\begin{array}{*{20}{l}} {\{ exp{r_1} + n \times constant|n > 0 \wedge exp{r_1} + n \times constant < exp{r_2}\}, {\text{ }} {如果}constant > 0} \\ {\{ exp{r_1} + n \times constant|n > 0 \wedge exp{r_1} + n \times constant > exp{r_2}\}, {\text{ }} {如果}constant < 0} \end{array}} \right., \hfill \\ [exp{r_1}, constant, exp{r_2}) = \hfill \\ \left\{ {\begin{array}{*{20}{l}} {\{ exp{r_1} + n \times constant|n \geqslant 0 \wedge exp{r_1} + n \times constant < exp{r_2}\}, {\text{ }} {如果}constant > 0} \\ {\{ exp{r_1} + n \times constant|n \geqslant 0 \wedge exp{r_1} + n \times constant > exp{r_2}\}, {\text{ }} {如果}constant < 0} \end{array}} \right., \hfill \\ (exp{r_1}, constant, exp{r_2}] = \hfill \\ \left\{ {\begin{array}{*{20}{l}} {\{ exp{r_1} + n \times constant|n > 0 \wedge exp{r_1} + n \times constant \leqslant exp{r_2}\}, {\text{ }} {如果}constant > 0} \\ {\{ exp{r_1} + n \times constant|n > 0 \wedge exp{r_1} + n \times constant \geqslant exp{r_2}\}, {\text{ }} {如果}constant < 0} \end{array}} \right., \hfill \\ [exp{r_1}, constant, exp{r_2}] = \hfill \\ \left\{ {\begin{array}{*{20}{l}} {\{ exp{r_1} + n \times constant|n \geqslant 0 \wedge exp{r_1} + n \times constant \leqslant exp{r_2}\}, {\text{ }} {如果}constant > 0} \\ {\{ exp{r_1} + n \times constant|n \geqslant 0 \wedge exp{r_1} + n \times constant \geqslant exp{r_2}\}, {\text{ }} {如果}constant < 0} \end{array}} \right.. \hfill \\ \end{gathered} $ |
内存域(memory scopes)的概念来自文献[11].对任何性质P, 它的取值只依赖于存储在有穷多个内存单元中的值.这些内存单元称为性质P的内存域M(P).内存域可以被用于判断一个性质是否可以被传播到赋值语句之后:对任何赋值语句e1:=e2, 如果性质P在该语句之前成立, 并且 & e1(即e1的地址)不属于M(P), 那么性质P在该语句之后仍然成立.
对任何表达式e, 如果e满足f(e1, …, en)的形式, 那么内存域M(e)是M(e1)∪M(e2)∪…∪M(en), 其中, f是代数运算符(e.g.+, -)或布尔运算符.表 1给出了基本形式表达式的内存域.表 2给出了不同性质的内存域.
| Table 1 Memory scope for basic forms of terms 表 1 基本表达式项的内存域 |
| Table 2 Memory scope for properties 表 2 性质的内存域 |
2.4 迭代数据流框架
迭代数据流框架[10]用于求解数据流问题.迭代数据流框架可以刻画为4元组(D, LG, ⊓G, FG), 其中, G表示控制流图(CFG).
● D是分析方向:前向或后向;
● LG是一个交半格(meet semi-lattice)描述符, 它表示待求解问题的数据流值.LG高度必须有穷;
● ⊓G是交半格LG的交操作(meet operator);
● FG是从LG到LG的流函数(flow functions)集合.流函数必须是单调的.
对任何一个数据流分析问题, 只要给出上面4个元素, 就可以通过迭代数据流分析算法进行求解.如果流函数单调, 并且格的高度有穷, 那么分析过程就必然终止[10].
本文使用了两个前向数据流分析方法.它们的分析方程都是如下形式:
| $ I{n_n} = \left\{ {\begin{array}{*{20}{l}} {BI, {\text{ }}n{\text{ is }}Start} \\ {\mathop \sqcap\limits_{p \in pred\left( n \right)} {F_p}(I{n_p}), {\text{ otherwise}}} \end{array}} \right., $ |
其中, n和p是语句, Inn是语句n之前的数据流值.Fn:LG→LG是语句n的流函数.BI表示程序开始语句Start之前的数据流值.FG由一系列Fp构成.⊓是交操作.
3 预分析对一个程序或者程序片段, 数组性质分析中需要确定哪些变量是循环控制变量、循环控制变量的初始值是什么、步长是多少.因此, 在给出数组性质分析之前, 需要进行一次预分析, 用于获取上面所说的循环控制变量的信息.
定义1(循环控制变量(loop control variable)).对于标量x, 从程序开始到某个程序点u的任何路径中, 如果每条路径中对x的赋值语句要么是将一个初始值赋值到x, 要么是将x增加(或者减少)一个固定常量, 那么x在程序点u处是循环控制变量(loop control variable).
本文设计了一种前向迭代数据流分析方法来发现循环控制变量.一个循环控制变量是一个三元组(variable, initial_value, fixed_constant_step).在这个分析中, 数据流值域LG是2(Svar, Expr, Con), 其中, Svar是待分析的CFG G中所有标量的集合, Expr是G中所有表达式的集合, Con是G中所有整数常量集合并上{⊥, ⊤}.程序开始语句之前的数据流值BI是空集.初始时其他语句之前之后的数据流值是{(v, init, ⊤)|v ∈Svar, init ∈Expr}.FG是{Fn|n is a statement}.Fn是语句n的流函数, 给定语句n之前的数据流值v, Fn(v)表示n之后的数据流值.对语句n之前的任意数据流值x, Fn(x)的定义如下:
| $ \begin{gathered} {F_n}(x){\text{ }} = {\text{ }}(x-{\text{ }}Kil{l_n}(x)) \cup Ge{n_n}(x), \hfill \\ Ge{n_n}(x) = \\ \left\{ {\begin{array}{*{20}{l}} {\{ (v, init, \top)\}, {\text{ }}n{形如}v: = init} \\ {\{ (v, init, c)\}, {\text{ }}n{形如}v: = v + c, {并且}(v, init, \top) \in x{或者}(v, init, c) \in x} \\ {\emptyset, {\text{ }}{否则}} \end{array}} \right., \hfill \\ Kil{l_n}(x) = \\ \left\{ {\begin{array}{*{20}{l}} {\{ (v, init, *)\}, {\text{ }}n{形如}{v_1}: = e, {并且}{v_1} \in \{ v\} \cup \{ init{的操作数}\}, {并且}*{是任何常量或} \bot, \top} \\ {\emptyset, {\text{ }}{否则}} \end{array}} \right.. \hfill \\ \end{gathered} $ |
对任何L1, L2 ∈LG, L1⊓GL2定义如下:
c1⊓c2定义如下:
| $ \begin{gathered} {c_1}\bar \sqcap{c_2} = \left\{ {\begin{array}{*{20}{l}} {{c_1}{\text{, }}{c_1} = {c_2}} \\ { \bot, {\text{ }}{c_1} \ne {c_2}} \end{array}, } \right.{\text{ }} \hfill \\ {c_1}\bar \sqcap \top = {c_1}{\text{, }}{c_1}\bar \sqcap \bot = \bot . \hfill \\ \end{gathered} $ |
本节给出一种前向迭代数据流分析方法来获取数组性质.
4.1 数据流值令Expr表示待分析的CFG G中所有表达式的集合(所有的变量也看作表达式).在给出数据流值域LG之前, 首先给出两个辅助定义:ProperP和
ProperP是满足下面条件的性质集合.
(1) 如果e1和e2在Expr中, 那么e1 op e2在ProperP中, 其中, op可以是 < , ≤=, ≠;
(2) 如果下面的条件都满足, 那么∀x(x ∈I⇒p1)在ProperP中, 其中, I是(e1, c, e2), [e1, c, e2), (e1, c, e2]或[e1, c, e2]:
a) e1和e2在Expr中, c是G中一个常量;
b) G中存在一个循环控制变量lcv使得p1[lcv/x]在ProperP中, 并且p1≠false;
c) p1中量词嵌套的深度小于G中循环控制变量的数量;
(3) 如果e1和e2在Expr中, 并且c是G中的一个常量, 那么∀x(x ∈[e1, c, e2)⇒false)在ProperP中.
图 4定义了运算符Op的格.Op的格图定义了运算符 < , ≤=, ≠的偏序关系⊑op和交运算⊓op.如果op2⊑opop1, 那么对于任意表达式e1和e2满足e1 op1 e2⇒e1 op2 e2.运算符的偏序关系将在下面的定义中使用.

|
Fig. 4 Lattice on Op, (Op, ⊑op, ⊓op, top, bot) 图 4 运算符Op上的格(Op, ⊑op, ⊓op, top, bot) |
下面给出
(1) p2是原子性质(e3 op2 e4), p1是原子性质(e1 op1 e2)并且e1=e3∧e2=e4∧op1⊑opop2.⊑op在图 4中定义;
(2) p1和p2都是∀x(x ∈[e3, c, e4)⇒false);
(3) p2是∀x(x ∈I1⇒p4), p1是∀x(x ∈I2⇒p3)并且下面条件之一成立.
a) I1=I2∧p4=false;
b)
I1=I2∧p3
根据上面的定义可知, p1
定义2(数组性质分析的数据流值域LG). LG的定义如下:
| $ {L_G} = \{ S|S \subseteq ProperP \wedge \forall {p_1}, {p_2} \in S, {p_1}{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } }{p_2} \Rightarrow {p_1} = {p_2}\} . $ |
直观地讲, LG的元素是性质的集合, 并且对于LG中的任意元素L, L中的两个不同性质p1, p2之间不存在
LG上的偏序关系⊑定义如下:对任何L1, L2 ∈LG, 如果对于L1中的任何性质p1, L2中都存在一个性质p2使得p1
在数组性质分析中, 程序开始语句之前的数据流值, 即BI是∅.初始时, 其他语句之前和之后的数据流值是⊤(所有可能性质的集合).
4.2 交操作(meet operation)定义LG上的交操作⊓G之前, 首先需要定义ProperP上的
(1)
其中, ⊓op定义在图 4中.
(2) 如果p1和p2都不是false, 那么:
| $ \begin{gathered} \forall x(x \in [{e_1}, {c_1}, {e_2}) \Rightarrow {p_1})\bar \sqcap\forall x(x \in [{e_3}, {c_2}, {e_4}) \Rightarrow {p_2}) = \hfill \\ \left\{ {\begin{array}{*{20}{l}} {\forall x(x \in [{e_1}, {c_1}, {e_2}) \Rightarrow {p_1}\bar \sqcap{p_2}), {\text{ }}[{e_1}, {c_1}, {e_2}) = [{e_3}, {c_2}, {e_4}) \wedge {p_1}\bar \sqcap{p_2} \ne \bot } \\ { \bot, {\text{ {否则}}}} \end{array}} \right. \hfill \\ \end{gathered} $ |
(3) ∀x(x ∈[e1, c1, e2)⇒false)⊓∀x(x ∈[e3, c2, e4)⇒p2), 其中, p2可以是false:
| $ \begin{gathered} \forall x(x \in [{e_1}, {c_1}, {e_2}) \Rightarrow false)\bar \sqcap\forall x(x \in [{e_3}, {c_2}, {e_4}) \Rightarrow {p_2}) \hfill \\ = \left\{ {\begin{array}{*{20}{l}} {\forall x(x \in [{e_1}, {c_1}, {e_2}) \Rightarrow {p_2}), {\text{ }}[{e_1}, {c_1}, {e_2}) = [{e_3}, {c_2}, {e_4})} \\ { \bot, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{否则}} \end{array}} \right. \hfill \\ \end{gathered} $ |
(4) 其他,
有上面的定义可知, 如果
⊓G定义如下:
| $ {L_1}{\sqcap_G}{L_2} = Reduce(\{ {p_1}\bar \sqcap{p_2}|{p_1} \in {L_1} \wedge {p_2} \in {L_2} \wedge {p_1}\bar \sqcap{p_2} \ne \bot \} ) $ |
对任何S ∈2ProperP, Reduce函数定义如下:
| $ Reduce\left( S \right) = S\backslash \{ p|p \in S \wedge \exists {p_1} \in S({p_1} \ne p \Rightarrow p\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } {p_1})\} . $ |
直观地讲, 对任何S ∈2ProperP, Reduce函数消除了S中具有
定理1. (LG, ⊓G, ⊑)是关于CFG G的一个交半格(meet semi-lattice), 并且高度有穷.
根据⊓G的定义, ⊓G满足交换律、幂等律和结合律, 两个元素的⊓G运算结果是这两个元素关于⊑的最大下界.因此, (LG, ⊓G, ⊑)是一个交半格.LG={S|S⊆ProperP∧∀p1, p2 ∈S, p1
语句n的流函数Fn由一系列的子函数定义.令a是语句n之前的数据流值, Fn(a)表示语句n之后的相应数据流值.在计算Fn(a)时, 首先计算语句n的语义, 并且通过传播规则产生尽可能多的性质, 该功能由Produce函数定义.如果n是数组元素赋值语句、循环控制变量初始化语句或循环控制变量更新语句, 流函数Fn(a)分别进行额外的处理:
(1) 如果n是数组元素赋值语句e1[e2]:=e3, 流函数Fn(a)会细粒度地检查全称量词性质是否会被赋值语句杀死, 如果没有被杀死, 那么该性质会传递到语句之后.该功能由Transfer函数定义;
(2) 如果n是循环控制变量初始化语句, 流函数Fn(a)产生特殊的全称量词性质.该功能由GenSpecial函数定义;
(3) 如果n是循环控制变量更新语句, 流函数Fn(a)会对全称量词的区间进行操作以产生更多的全称量词性质, 该功能由HandleInterval函数定义.
最终, 流函数Fn(a)根据一组规则产生更多全称量词性质, 该功能由GenAQ函数定义, 并使得最终的性质集合属于LG, 由Reduce函数定义.
流函数Fn由上面的子函数定义, Reduce的定义在第4.2节, 其他所有子函数的定义分别在后面的小节中详细描述.Fn的正式定义会在本节的最后描述.
4.3.1 Produce函数对任何语句n, Produce函数计算语句n的语义, 并且通过传播规则产生尽可能多的性质.Produce函数定义如下:
| $ Produce\left( {n, a} \right) = Propagated(a \cup Semantics\left( {n, a} \right)). $ |
令a是语句n之前的数据流值.函数Semantics(n, a)计算变量在语句之前和之后的关系.Semantics定义如下:
| $ Semantics(n, a) = \left\{ {\begin{array}{*{20}{l}} {\{ lh' = e\} \cup \{ lh = l{h_i}|\& lh \ne \& l{h_i} \wedge l{h_i} \in LH\}, {\text{ }}{如果}n{是}lh: = e} \\ {\{ cond\} \cup \{ lh' = l{h_i}|l{h_i} \in LH\}, {\text{ }}{如果}n{是}cond{并且在}{\text{true}}{分支处}} \\ {\{ \neg cond\} \cup \{ lh' = l{h_i}|l{h_i} \in LH\}, {\text{ }}{如果}n{是}cond{并且在}{\text{false}}{分支处}} \end{array}} \right., $ |
其中, lhi表示具有左值的表达式, LH是出现在程序中的所有具有左值的表达式的集合.无撇号表达式表示表达式在语句之前的状态, 撇号表达式表示表达式在语句之后的状态.cond表示if和while语句的条件表达式.
Semantics函数之后, propagated函数会生成尽可能多的性质.Propagated定义如下:
| $ Propagated(a \cup Semantics\left( {n, a} \right)) = Filter(ApplyRules(a \cup Semantics\left( {n, a} \right))). $ |
Propagated函数具有下面两个功能.
(1) 应用传播规则(propagation rules)来产生尽可能多的性质(ApplyRules函数);
(2) 过滤掉不需要的性质.因为propagated函数的输入是Semantics(n, a)∪a.在Semantics(n, a)中包含前置状态表达式(无撇号表达式).因此在应用传播规则之后, 需要过滤掉包含前置状态表达式(无撇号表达式)的性质, 最终留下只包含后置状态表达式(撇号表达式)的性质, 然后去掉所有的变量的撇号(Filter函数).
图 5给出了部分传播规则.

|
Fig. 5 Propagation rules 图 5 传播规则 |
注意, 所有的传播规则都需要满足下面给出的传播规则约束(propagation rules constraint).
传播规则约束.令ins表示一个规则的输入性质集合, out表示输出性质.一个传播规则可以描述为
| $ \wedge ins \Rightarrow out. $ |
传播规则需要满足如下约束:
(1) 如果ins⊆ProperP, 那么out ∈ProperP;
(2) 如果p ∈ins并且p是e1≤e2, 那么传播规则中必须包含另外两个规则:∧ins[e1 < e2/e1≤e2]⇒out1和∧ins[e1=e2/e1≤e2]⇒out2, 其中, out
(3) 如果p ∈ins并且p是e1≠e2, 那么传播规则中必须包含另外一个规则:∧ins[e1 < e2/e1≠e2]⇒out1, 其中, out
(4) 如果p ∈ins并且p是∀x(x ∈[e1, c, e2)⇒p1), 那么传播规则中必须包含另外一个规则:
| $ \wedge ins[\forall x(x \in \left[{{e_1}, c, {e_2}} \right) \Rightarrow {\text{false}})/\forall x(x \in \left[{{e_1}, c, {e_2}} \right) \Rightarrow {p_1})] \Rightarrow ou{t_1}, {其中}, out\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } ou{t_1}. $ |
传播规则约束保证了propagated函数满足单调性(证明见附录中的引理6).
例 1:考虑图 1(a)所示arrayPartCopy程序.令语句n是A[i]=B[i]、语句n之前的数据流值a={∀k(k ∈[0, 2, i)⇒ false), i < size}(第1次迭代时的性质):
| $ Semantics\left( {n, a} \right) = \{ A{\left[i \right]^{\text{'}}} = B\left[i \right], B{\left[i \right]^{\text{'}}} = B\left[i \right], {i^{\text{'}}} = i, siz{e^{\text{'}}} = size, {B^{\text{'}}} = B\} . $ |
应用传播规则并且过滤掉前置状态上的表达式(即不带'的表达式)之后, 得到性质:{A[i]'=B[i]', (∀k, k ∈[0, 2, i')⇒false), i' < size'}.去掉撇号, 最终:
| $ Propagated(a \cup Semantics\left( {n, a} \right)) = \{ A\left[i \right] = B\left[i \right], \forall k(k \in \left[{0, 2, i} \right) \Rightarrow {\text{false}}), i < size\} . $ |
如果n是e1[e2]:=e3, 而p是数据流值a中的全称量词且e1出现在p中, 根据前面对内存域的讨论, 若 & e1[e2]∉ M(p), p在n之后仍然成立.但是Produce(n, a)可能不包含p.针对这种情况, Transfer函数在 & e1[e2]∉M(p)成立时将p传递到语句n之后.Transfer(e1[e2]:=e3, a)定义如下:
Transfer(e1[e2]:=e3, a)={p|p ∈a并且p是一个全称量词性质并且 & e1[e2]∉M(p)}.
例 2:令语句n是A[i]=B[i]、语句n之前的数据流值a={∀k(k ∈[0, 2, i)⇒A[k]=B[k]), i < size}(“arrayPartCopy”程序第2次迭代时的性质):
| $ \begin{gathered} Produce(n, a) = \{ i < size\}, \hfill \\ Transfer(n, a) = \{ \forall k(k \in [0, 2, i) \Rightarrow A[k] = B[k])\} . \hfill \\ \end{gathered} $ |
因为i∉[0, 2, i), 因此 & A[i]∉M(∀k(k ∈[0, 2, i)⇒A[k]=B[k])), 所以全称量词∀k(k ∈[0, 2, i)⇒A[k]=B[k])能够传递到语句n之后.
4.3.3 GenSpecial函数对任何循环控制变量初始化语句i:=init, GenSpecial定义如下:
| $ GenSpecial\left( {i: = init} \right) = \{ \forall k(k \in \left[{init, c, i} \right) \Rightarrow {\text{false}})\} . $ |
c是循环控制变量i的步长(通过预分析获取).在循环控制变量初始化语句i:=init之后, 因为[init, c, i)是∅, 所以∀k(k ∈[init, c, i)⇒false)成立.
4.3.4 HandleInterval函数对任何循环控制变量更新语句i:=i+c, HandleInterval定义如下:
| $ \begin{gathered} HandleInterval(i: = i + c, a) = \hfill \\ \{ \forall x(x \in [ini{t_i}, c, i) \Rightarrow p)|{如果}\forall x(x \in [ini{t_i}, c, i + c) \Rightarrow p){在}a{中}\} \cup \hfill \\ \;\{ \forall x(x \in [ini{t_i}, c, i- c) \Rightarrow p)|{如果}\forall x(x \in [ini{t_i}, c, i) \Rightarrow p){在}a{中}\}, \hfill \\ \end{gathered} $ |
其中, p不包含i, p可以是false.在i:=i+c语句之后的[initi, c, i)和[initi, c, i-c)分别等价于语句之前的[initi, c, i+c)和[initi, c, i).因此当∀x(x ∈[initi, c, i)⇒p)在语句i:=i+c之前成立时, ∀x(x ∈[initi, c, i-c)⇒p)在语句之后成立.同理, 当∀x (x ∈[initi, c, i+c)⇒p)在语句之前成立时, ∀x(x ∈[initi, c, i)⇒p)在语句之后成立.
例 3:令语句n是i=i+2、语句n之前的数据流值a={∀k(k ∈[0, 2, i)⇒A[k]=B[k]), i < size, A[i]=B[i], ∀k(k ∈[0, 2, i+2)⇒A[k]=B[k])}(arrayPartCopy程序第2次迭代时的性质):
| $ \begin{gathered} Produce(n, a) = \emptyset, \hfill \\ HandleInterval(n, a) = \hfill \\ \{ (\forall k(k \in [0, 2, i- 2) \Rightarrow A[k] = B[k]), (\forall k(k \in [0, 2, i) \Rightarrow A[k] = B[k])\} . \hfill \\ \end{gathered} $ |
GenAQ函数根据现有性质产生更多的全称量词性质.对任何S ∈2ProperP, GenAQ定义如下:
| $ \begin{gathered} GenAQ(S) = \hfill \\ S \cup \{ \forall x(x \in [ini{t_i}, c, i + c) \Rightarrow \psi (..., {e_1}[{f_1}(x)], ...))|{如果}(1){或}(2){成立}\} \cup \hfill \\ \;{\text{ }}\{ \forall x(x \in [ini{t_i}, c, i) \Rightarrow \psi (..., {e_1}[{f_1}(x)], ...))|{如果}(3){或}(4){成立}\}, \hfill \\ \end{gathered} $ |
其中, ψ表示一个数组元素的性质, f1表示一个索引函数.需要特别注意, ψ(…, e1[f1(x)], …)不包含i.
| $ \forall x(x \in \left[{ini{t_i}, c, i} \right) \Rightarrow {\text{false}}){在}S{中}, {并且}ψ\left( { \ldots, {e_1}\left[{{f_1}\left( x \right)} \right], \ldots } \right){在}S{中} $ | (1) |
| $ \left. \begin{gathered} \forall x(x \in [ini{t_i}, c, i) \Rightarrow {\psi _1}(..., {e_1}[{f_1}(x)], ...)){在}S{中}, {并且}{\psi _2}(..., {e_1}[{f_1}(i)], ...){在}S{中}, \hfill \\ {并且}\psi (..., {e_1}[{f_1}(x)], ...) = {\psi _1}(..., {e_1}[{f_1}(x)], ...)\bar ⊓{\psi _2}(..., {e_1}[{f_1}(x)], ...) \hfill \\ \end{gathered} \right\} $ | (2) |
| $ \forall x(x \in [ini{t_i}, c, i- c) \Rightarrow {\text{false}}) {在}S{中}, {并且}ψ( \ldots, {e_1}[{f_1}(i-c)], \ldots ) {在}S{中} $ | (3) |
| $ \left. \begin{gathered} \forall x(x \in [ini{t_i}, c, i- c), {\psi _1}(..., {e_1}[{f_1}(x)], ...)) {在}S{中}, {并且}{\psi _2}(..., {e_1}[{f_1}(i-c)], ...) {在}S{中}, \hfill \\ {并且}\psi (..., {e_1}[{f_1}(x)], ...) = {\psi _1}(..., {e_1}[{f_1}(x)], ...)\bar \sqcap{\psi _2}(..., {e_1}[{f_1}(x)], ...) \hfill \\ \end{gathered} \right\} $ | (4) |
● 如果条件(1)成立, ∀x(x ∈[initi, c, i)⇒false)表示[initi, c, i)是∅.因此, [initi, c, i+c)就是{i}, ∀x(x ∈[initi, c, i+c)⇒ ψ(…, e1[f1(x)], …)就是ψ(…, e1[f1(i)], …).所以∀x(x ∈[initi, c, i+c)⇒ψ(…, e1[f1(x)], …)成立;
● 如果条件(2)成立, 因为ψ(…, e1[f1(x)], …)=ψ1(…, e1[f1(x)], …)⊓ψ2(…, e1[f1(x)], …), 那么:∀x(x ∈[initi, c, i)⇒ψ1(…, e1[f1(x)], …))推出∀x(x ∈[initi, c, i)⇒ψ(…, e1[f1(x)], …))成立, ψ2(…, e1[f1(i)], …)推出ψ(…, e1[f1(i)], …)成立.因此, ∀x(x ∈[initi, c, i+c)⇒ψ(…, e1[f1(x)], …))成立;
● 如果条件(3)成立, ∀x(x ∈[initi, c, i-c)⇒false)表示[initi, c, i-c)是∅成立.因此, [initi, c, i)就是{i-c}, ∀x(x ∈ [initi, c, i)⇒ψ(…, e1[f1(x)], …)就是ψ(…, e1[f1(i-c)], …).所以, ∀x(x ∈[initi, c, i)⇒ψ(…, e1[f1(x)], …))成立;
● 若条件(4)成立, 因为ψ(…, e1[f1(x)], …)=ψ1(…, e1[f1(x)], …)⊓ψ2(…, e1[f1(x)], …), 那么:∀x(x ∈[initi, c, i-c)⇒ψ1(…, e1[f1(x)], …))推出∀x(x ∈[initi, c, i-c)⇒ψ(…, e1[f1(x)], …))成立, ψ2(…, e1[f1(i-c)], …)推出ψ(…, e1[f1(i-c)], …)成立.因此, ∀x(x ∈[initi, c, i)⇒ψ(…, e1[f1(x)], …))成立.
综上所述, GenAQ新生成的性质都能够由S中的规则经过推导得到.
例 4:考虑下面两个例子.
(1) 令S={A[i]=B[i], ∀k(k ∈[0, 2, i)⇒false), i < size}:
| $ GenAQ\left( S \right) = S \cup \{ \forall k(k \in \left[{0, 2, i + 2} \right) \Rightarrow A\left[k \right] = B\left[k \right])\} . $ |
因为A[i]=B[i], ∀k(k ∈[0, 2, i)⇒false)在S中, 满足条件(1), 所以∀k(k ∈[0, 2, i+2)⇒A[k]=B[k])成立.∀k(k ∈[0, 2, i)⇒ false)表示区间[0, 2, i)=∅, 又因为循环控制变量i的步长为2, 因此[0, 2, i+2)就是{i}, 所以∀k(k ∈[0, 2, i+2)⇒A[k]= B[k])就是A[i]=B[i].
(2) 令S={A[i]=B[i], ∀k(k ∈[0, 2, i)⇒A[k]=B[k]), i < size}:
| $ GenAQ\left( S \right) = S \cup \{ \forall k(k \in \left[{0, 2, i + 2} \right) \Rightarrow A\left[k \right] = B\left[k \right])\} . $ |
因为A[i]=B[i]和∀k(k ∈[0, 2, i)⇒A[k]=B[k])在S中, 满足条件(2);又因为
令a是语句n之前的数据流值.流函数Fn(a)定义如下:
| $ {F_n}(a){\text{ }} = \left\{ {\begin{array}{*{20}{l}} {Reduce(GenAQ(Transfer(n, a) \cup Produce(n, a))), {\text{ }}{如果}n{是}{e_1}[{e_2}]: = {e_3}} \\ {Reduce(GenAQ(GenSpecial(n) \cup Produce(n, a))), {\text{ }}{如果}n{是}lcv{初始化语句}} \\ {Reduce(GenAQ(HandleInterval(n, a) \cup Produce(n, a))), {\text{ }}{如果}n{是}lcv{更新语句}} \\ {Reduce(GenAQ(Produce(n, a))), {\text{ }} {否则}} \end{array}} \right.. $ |
本文已经给出了数组性质分析的交半格(包括偏序关系和交运算)和流函数.根据文献[10]给出的迭代数据流框架, 使用该迭代数据流框架中给出的迭代数据流分析算法就可以发现程序中的数组性质.
4.4 终止性(termination)定理2.令n表示CFG G的语句.Fn是单调的.
Fn是单调的当且仅当对于LG中的任意两个元素x和y, x⊑y可以推导出Fn(x)⊑Fn(y).根据Fn的定义, 只需要证明Fn中出现的函数都是单调的.详细的证明过程见附录.
定理3.数组性质分析必然会终止.
证明:因为流函数是单调的(定理2), 并且格的高度有穷(定理1), 因此数组分析必然会终止.
4.5 正确性(soundness)令States表示程序状态集合.一个程序状态表示为二元组(ρv, ρa), 其中, ρv表示标量到值的映射, ρa表示数组到值的映射.图 6给出了归纳循环程序语句的语义, 这里使用States到States的函数

|
Fig. 6 Semantics of induction loop programs 图 6 归纳循环程序的语义 |
接下来的段落中, 使用c标记程序状态(ρv, ρa).CFG G的路径(trace) T是程序状态序列(c0, c1, ...), 其中, c0是初始状态, 并且对所有i≥0, 有G⊢ci
对于抽象值a,
定理4.令ci表示语句n之前的状态、ai表示语句n之前的数据流值.如果G⊢ci
根据Fn的定义, 只需要证明不同的语句n,
定理5.对程序的任何初始值c0,
证明:在性质分析中, BI是∅.因此对任何初始值c0,
根据定理4和定理5可知, 分析结果是正确的.
4.6 方法的灵活性在本文方法的基础上, 我们可以通过扩展抽象域LG和传播规则来发现更多的性质.这体现了我们方法的灵活性.
如果表达式a和b都出现在被分析的控制流图G中, 但a+b不出现在G中, 根据第4.1节定义的LG, 数组性质分析不能获得任何关于a+b的性质.但是通过扩展抽象域(例如, 将原来的表达式集合Expr定义为{e|e出现在G中}∪{e1+e2|e1, e2出现在G中}), 数组性质分析可以获得更多性质.
类似于抽象域, 方法也可以扩展传播规则.例如, 对Summation starts程序(如图 7所示), 因为数组性质分析算法无法根据第4.3.1节给出的传播规则来获得关于A[i]的任何性质, 所以无法获得任何全称量词性质.但是只要增加如下两个规则, 并根据传播规则约束增加相应的附属规则.
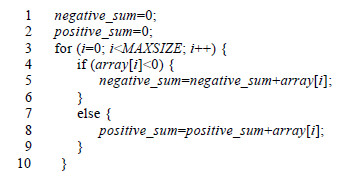
|
Fig. 7 Summation starts 图 7 Summation starts |
● e1=e2+e3∧0≤e2∧0≤e3⇒0≤e1∧e2≤e1∧e3≤e1;
● e1=e2+e3∧e2≤0∧e3≤0⇒e1≤0∧e1≤e2∧e1≤e3.
那么本文中的分析算法就可以在Summation starts的结尾处获得如下性质.
● ∀k(k ∈[0, 1, MAXSIZE)⇒A[k]≤positive_sum);
● ∀k(k ∈[0, 1, MAXSIZE)⇒negative_sum≤A[k]).
5 工具实现和实验我们已经基于clang[12]和Z3[13]实现了一个原型工具.Clang被用于在源代码层次进行数据流分析; Z3被用于分析过程中的逻辑推导, 所有的逻辑推导都只用到了Z3的线性约束求解功能.我们应用该工具在一些数组程序上发现全称量词性质, 包括图 1所示的小程序、一些常见程序(表 3)和Competition on Software Verification (SV-COMP)[14]中的array-examples benchmark.
| Table 3 Performances results 表 3 性能结果 |
5.1 小程序的分析结果
下面给出图 1中程序的分析结果.
● arrayPartCopy程序分析结果
本文给了两个版本的arrayPartCopy程序, 其中, 图 1(a)先进行数组操作再更新循环控制变量, 图 1(b)先更新循环控制变量再进行数组操作.在两个程序的结尾, 工具都可以发现下面的性质.
(1) ∀k(k ∈[0, 2, i)⇒A[k]=B[k]);
(2) ∀k(k ∈[0, 2, size)⇒A[k]=B[k]).
这些性质表明:在程序结束点上, 数组A中偶数位索引的元素和数组B中偶数位索引的元素对应相等.这正是程序所实现的功能.
● Find程序分析结果
Find程序[15]使用数组的第1个元素分割数组, 它是QuickSort中根据阈值分划数组的程序片段(如图 1(d)所示).在程序结尾, 工具可以发现下面的性质.
(1) A[I-1]=x;
(2) ∀k(k ∈[0, 1, i)⇒A[k-1] < x);
(3) ∀k(k ∈[i, 1, size-1]⇒x≤A[k]).
这些性质表明:在程序结束点上, 根据阈值x, 数组A被划分成小于x的部分和大于等于x的部分:
● 2d-ArrayCheck程序分析结果
2d-ArrayCheck程序(图 1(c)所示)用于检查2-d数组中是否包含0元素.在程序的结尾, 工具可以发现下面的性质:
| $ \forall {k_1}({k_1} \in \left[{0, 1, i} \right) \Rightarrow \forall {k_2}({k_2} \in \left[{0, 1, col} \right) \Rightarrow A\left[{{k_1}} \right]\left[{{k_2}} \right] \ne 0)). $ |
这正是期望的一个性质:当运行到程序结尾处时, 二维数组中的所有遍历过的元素都不等于0.
除了上面的程序之外, 我们的工具在一些常见的程序(片段)中合成了有用的不变式, 包括:partition程序(拷贝一个数组中小于等于和大于x的元素到两个数组中); insertion sort的内循环; arrayMax程序; 一个版本的firstNotNull程序; 1-d, 2-d和3-d数组的arrayCopy程序; 1-d, 2-d和3-d数组的arrayCheck程序.关于更多的分析结果细节, 可以访问工具和例子网址:https://github.com/libin049/InvariantSynthesisForArray_C.
表 3给出了工具在处理上面例子时的性能结果.实验运行在2.4GHz Intel处理器、4GB RAM电脑上.
表 3说明:对于1-d数组程序, 工具分析时间不超过1秒; 对于多维数组, 需要花费更多的时间去分析.这是因为对于多维数组程序, 工具需要较多的时间分析全称量词是否会被语句杀死—这个过程需要使用Z3进行逻辑推导, 相对而已比较耗时.
5.2 SV-COMP数组benchmark分析结果Competition on Software Verification(SV-COMP)[14]提供了一个数组程序的benchmark:array-examples[16]. array-examples中的程序全部使用GNU C或者ANSI C描述.它有88个文件、2 299行代码.绝大多数文件只有一个函数, 并且所有的数组都是一维数组.SV-COMP中的array-examples benchmark用来检查(不)可达性((un)reachability).在88个文件中, 有28个文件具有错误的规约, 其余的60个文件中有正确的规约.这些文件中, 所有的规约都是不包含量词的原子断言.60个包含正确规约的文件中, 有56个关于数组元素的原子断言位于循环语句内部, 这些原子断言等价于被遍历数组的全称量词性质.
表 4展示了工具在array-examples上的执行时间(time)、文件数量(#file)、每个文件平均分析时间(time/ #file)、array-examples中循环的数量(#loop)、一共在多少循环入口发现了全称量词性质(#loop(U-inv))以及一共在多少文件中发现了全称量词性质(#file(U-inv)).表 4指出每个文件平均分析时间是10s, 以及工具在304个循环入口、74个文件中发现了全称量词.
| Table 4 Analysis result of array-examples 表 4 Array-Examples分析结果 |
我们比较了工具生成的全称量词性质和60个正确规约文件中在循环内部的原子断言.在array-examples benchmark总共56个这样的原子断言.我们的工具合成了44个等价的目标全称量词性质.我们分析了其余12个没有合成目标性质的原因.其中, 有2个需要处理函数调用语句, 有4个需要将形如∀k(k ∈[e1, 1, e2)⇒p(k))的全称量词性质分解为针对两个子区间的全称量词性质, 才能够分析得到目标全称量词.另外4个目标性质不在本文方法的数据流抽象域.例如, 在standard_copyInit_true-unreach-call_ground程序(如图 8所示)中, 表达式42+incr只出现在原子断言中, 没有出现在程序中, 因此, ∀x(x ∈[0, 1, N)⇒b[x]==42+incr)不属于本文方法的抽象域.我们将在后续工作研究处理上面这几种情况的技术.

|
Fig. 8 standard_copyInit_true-unreach-call_ground 图 8 standard_copyInit_true-unreach-call_ground |
需要指出:我们的方法虽然没有合成其余的12个目标性质, 但是合成了可以用于推导出目标性质的全称量词性质.例如, 在standard_copyInit_true-unreach-call_ground程序中, 工具在第2行的for语句之前合成性质:{∀x (x ∈[0, 1, N)⇒A[x]=B[x]), ∀x(x ∈[0, 1, N)⇒A[x]=42), ∀x(x ∈[0, 1, N)⇒B[x]=42)}.这些性质可以用于推导出最终的目标性质∀x(x ∈[0, 1, N)⇒B[x]=42+incr).
5.3 与其他工具比较我们的工具与其他不变式合成工具进行了比较, 这类的工作虽然有很多, 比如文献[7, 8, 17-19], 但是只找了一个可用的工具CppInv[19].我们比较了它们合成array-examples benchmark中56个等价于全称量词性质的原子断言的个数与时间.除此之外, 本文工具也与BOOSTER[20], ESBMC[21], SMACK+Corral[22]进行了比较.其中, SMACK+Corral和ESBMC是SV-COMP2017中关于array-examples benchmark得分最高的前两个工具, BOOSTER能够直接验证量词性质.需要指出:BOOSTER, ESBMC和SMACK+Corral是程序验证工具, 它们需要给出待验证的性质.虽然BOOSTER, ESBMC和SMACK+Corral不是性质合成工具, 但是本文工具与这些工具关于合成或验证array-examples benchmark中目标断言的个数和时间的比较结果可以间接反映本文方法的有效性和可行性.
对于所有的工具, 我们比较这些工具是否可以验证或合成array-examples benchmark中56个等价于全称量词性质的原子断言的个数(第2列)、验证或合成的时间(第3列)、工具是否需要用户提供待验证的断言(第4列)、是否支持多维数组、是否能够保证分析/验证的性质一定是正确的(sound, 第5列)以及是否直接支持合成或验证量词性质(第6列).因为BOOSTER支持量词性质验证, 我们将56个断言转换成了等价的全称量词性质.每个工具在单个文件上的验证或合成时间最长是15分钟.
表 5给出了比较结果.比较结果表明, 我们的工具在合成性质的数量和时间上都优于其他工具.在这些工具中, 因为ESBMC和SMACK+Corral基于有界模型检验技术, 它们的正确性依赖于循环展开的次数; booster也用到了有界模型检验技术, 所以它们不能够保证验证结果一定是正确的.只有我们的工具和CppInv能够保证合成的性质一定是正确的, 我们的工具在合成性质的数量和时间上都明显优于CppInv, 并且能够处理多维数组.
| Table 5 Synthesis or verification results of CppInv, BOOSTER, ESBMC, SMACK+Corral and our tool 表 5 CppInv, BOOSTER, ESBMC, SMACK+Corral及我们的工具合成或验证结果 |
6 相关工作
合成数组程序不变式的相关工作可分为如下几类:数组展开(array expansion)方法、Array smashing方法、数组划分方法、谓词抽象方法、基于模板的方法、基于定理证明的方法.
● 数组展开方法[23].这个方法展开循环和数组单元来处理程序.数组展开方法优点是精确, 缺点是只能处理小尺寸的数组, 不能处理无界数组;
● Array smashing方法[5, 24].这个方法将整个数组A看作一个变量a.初始时, a被赋予一个整个数组单元都满足的已知最强的性质.A[i]:=e按照弱赋值a⊔:=e来处理.Array smashing方法的缺点是弱赋值(weak assignment⊔:=)会丢失信息, 并且无法处理关于数组单元的条件测试语句.因此, 这个方法获得的结果常常不精确;
● 数组划分方法[7, 8, 17].数组划分方法将索引域([1...n])划分为若干符号区间(e.g., I1=[1...i-1], I2=[i, i], I3= [i+1...n]), 并且给每个子数组A[Ik]关联一个辅助摘要变量(summary auxiliary variable)ak.该方法基于语法启发式[7, 8]或者预分析[17]的方法对索引域进行划分.这类方法与本文的方法类似.区别在于:本文的方法不是给每个子数组关联一个摘要变量, 而是直接将一个数组性质表示为一个或多个全称量词性质.相对于数组划分方法, 本文的方法具有更高的表达能力和灵活性.因此, 本文的方法可以非常容易地处理多维数组性质, 但是数组划分方法难以处理多维数组.此外, 数组划分方法无法处理在循环中首先进行索引更新的程序(例如图 1(b)所示的another arrayPartCopy程序), 然而在循环中首先进行索引更新的写法在实际编码中经常使用(例如A[++i]).本文的方法可以处理这类程序;
● 谓词抽象方法[1, 25, 26].谓词抽象方法会使用一些语法启发式策略推导用于抽象的谓词, 或者由用户提供谓词.它将程序抽象到谓词程序, 然后基于谓词程序合成数组性质.反例制导的精化[3]和Craig插值[4]提供了获取谓词的其他方法, 提高了谓词抽象方法的效果.谓词抽象方法中, 因为缺少有效的选择算法, 因此一些原子谓词常常必须手动提供.本文的方法不需要用户提供任何输入.此外, 谓词抽象方法需要使用约束求解器检查猜出来的量词性质是否真的成立, 而目前约束求解器对量词性质的支持有限, 因此难以处理较复杂的量词性质.本文的方法只使用到了约束求解器的线性约束求解功能, 而约束求解器(如Z3)对线性求解功能支持比较好.因此相对于这类方法, 本文的方法能够自动地分析得到更复杂的量词性质;
● 基于模板的方法[9, 27].基于模板的方法非常有用但是代价昂贵, 其基本思想是:用户提供所需要不变式的模板, 然后分析过程去搜索实例化模板参数.这个方法的过程需要用户的参与, 本文的方法是完全自动化的;
● 基于定理证明的方法[18, 28].这类方法使用定理证明器去生成循环不变式.文献[18]方法的基本思想是:将数组第i次迭代中的修改编码为一个量化事实(quantified fact), 然后运用定理证明器去推导一个封闭形式的公式.这类方法的缺点是受限于使用的定理证明器, 同时可证明的性质比较有局限性.
7 总结和未来工作本文提出了一个使用抽象解释框架自动合成数组性质的方法.该方法的特点在于抽象域是性质集合(性质包括全称量词性质和原子性质), 这种抽象域灵活并且具有较高的表达能力.该方法通过前向迭代数据流分析合成数组性质.本文证明了该方法是收敛的, 并且获得的不变式是正确的.本文也展示了方法具有一定的灵活性, 可以通过增加抽象域和传播规则来增加分析能力.本文所述分析方法的工具原型基于clang和Z3实现.该工具被用于分析一些常见程序以及SV-COMP的array-examples benchmark.array-examples benchmark共有88个文件中, 我们的工具在74个文件中发现了全称量词性质.
在未来工作中, 我们计划处理全称量词性质分裂和合成的情况(一个全称量词性质分为若干全称量词性质, 或者将若干全称量词性质合成一个全称量词性质).一个更长远的目标是处理数组和链表的全称量词和存在量词性质.
附录:证明定理1的证明
证明文中的定理1之前, 首先给出下面的推论及引理.
推论1. ProperP的势(大小)是有穷的.
推论2.对任何性质p1, p2和p3:
(1) 如果p1
(2) 如果p1
(3) 如果p1
推论3.对于任何性质p1, p2和p3:
(1) 如果
| $ \begin{gathered} {p_1}\bar \sqcap{p_2}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } {p_1} \wedge {p_1}\bar \sqcap{p_2}\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{ \prec } {p_2} \hfill \\ {p_1} \vee {p_2} \Rightarrow {p_1}\bar \sqcap{p_2}; \hfill \\ \end{gathered} $ |
(2)
(3)
推论4.对任何性质p1, p2和p3, ⊓满足下面的性质:
(1)
(2)
(3)
推论5.对任何S1, S2 ∈2ProperP:
(1) Reduce(S1) ∈LG;
(2) S1⊑Reduce(S1)∧Reduce(S1)⊑S1;
(3) S1⊑S2⇒Reduce(S1)⊑Reduce(S2).
引理1.对任何L1, L2 ∈LG, L1⊓GL2 ∈LG.
证明:结论直接来自⊓G的定义.
引理2.对任何S1, S2, S3 ∈2ProperP:
(1) S1⊓GS2⊑S1∧S1⊓GS2⊑S2;
(2) S1⊑S2∧S1⊑S3⇒S1⊑S2⊓GS3.
证明:根据推论3, 对于任何性质p1 ∈S1, p2 ∈S2, p1⊓ p2 ∈S2⊓GS2, 并且p1⊓p2
引理3.对任何L1, L2 ∈LG, L1⊑L2∧L2⊑L1⇔L1=L2.
证明:L1⊑L2∧L2⊑L1推出∀p1 ∈L1, ∃p2 ∈L2, ∃p3 ∈L1⇒p1
引理4.对任何L1, L2 ∈LG, L1⊑L2⇔L1=L1⊓GL2.
证明:要证明L1⊑L2⇔L1=L1⊓GL2, 只需证明:
1) L1⊑L2⇒L1=L1⊓GL2;
2) L1=L1⊓GL2⇒L1⊑L2.
根据引理2, 结论1)可证.令S(L1, L2)={p1⊓p2|p1 ∈L1∧p2 ∈L2∧p1⊓p2≠⊥}.根据推论5, L1⊑L2⇒L1⊑S(L1, L2)⇒L1⊑ Reduce(S(L1, L2))⇒L1⊑L1⊓GL2.根据引理2, L1⊓GL2⊑L1.根据引理3, L1⊑L1⊓GL2∧L1⊓GL2⊑L1∧L1 ∈LG∧L1⊓GL2 ∈LG推出L1=L1⊓GL2.结论2)成立.
定理1. (LG, ⊓G)是关于CFG G的一个交半格(meet semi-lattice), 并且格的高度有穷.
证明:(LG, ⊓G)是交半格当且仅当, 对所有L1, L2, L3 ∈LG:
1) L1⊓GL1=L1;
2) L1⊓GL2=L2⊓GL1;
3) (L1⊓GL2)⊓GL3=L1⊓G(L2⊓GL3);
4) L1⊑L2⇔L1=L1⊓GL2.
结论1)、结论2)和结论4)通过引理4和⊓G定义可证.令S(L1, L2)={p1⊓p2|p1 ∈L1∧p2 ∈L2∧p1⊓p2≠⊥}.要证明结论3), 只需要证明:
a) (L1⊓GL2)⊓GL3=Reduce(S(S(L1, L2), L3));
b) Reduce(S(S(L1, L2), L3))=Reduce(S(L1, S(L2, L3)));
c) Reduce(S(L1, S(L2, L3)))=L1⊓G(L2⊓GL3).
(L1⊓GL2)⊓GL3⊑L1⊓GL2⊑S(L1, L2).根据引理2, (L1⊓GL2)⊓GL3⊑S(L1, L2)⊓GL3.同理可以证明S(L1, L2)⊓GL3⊑(L1⊓G L2)⊓GL3.因此, (L1⊓GL2)⊓GL3=S(L1, L2)⊓GL3=Reduce(S(S(L1, L2), L3)).同理可以证明Reduce(S(L1, S(L2, L3)))=L1⊓G (L2⊓GL3).根据函数S的定义, S(S(L1, L2), L3)=S(L1, S(L2, L3))可证.因此, 结论3)可证.LG={S|S⊆ProperP∧∀p1, p2 ∈S, p1
定理2的证明
证明文中的定理2之前, 首先证明下面的引理:
引理5.对任何L1, L2 ∈LG, 如果L1⊑L2, 那么Semantics(n, L1)⊑Semantics(n, L2).
证明:根据Semantics的定义:
(1) 如果n是cond, 那么结论显然成立;
(2) 如果n是lh:=e, 对任何lhi ∈LH, 如果∧L1⇒ & lh≠ & lhi, 那么∧L2⇒ & lh≠ & lhi.因此:
| $ Semantics\left( {n, {L_1}} \right) \sqsubseteq Semantics\left( {n, {L_2}} \right). $ |
综上, Semantics(n, L1)⊑Semantics(n, L2).
引理6.对任何性质集合S1和S2, 如果S1⊑S2, 那么Propagated(S1)⊑Propagated(S2).
证明:对任何ins1⊆S1, 如果规则r可以应用ins1, 并且产生输出性质out1, 根据S1⊑S2和传播规则约束, 一定存在ins2⊆S2和一个对应的规则r', 使得:(a) ins1⊑ins2; (b) r'可以应用到ins2; (c)
r'和ins2产生性质out2并且out1
引理7.对任何x, y ∈LG, 如果x⊑y, Transfer(e1[e2]:=e3, x)⊑Transfer(e1[e2]:=e3, y).
证明:令TS(x)={p|p ∈x∧p是全称量词∧ & e1[e2]∉M(p)}.根据Transfer函数的定义, 只需要证明TS(x)⊑TS(y).对任何p1 ∈TS(x), 肯定存在p2 ∈y并且p1
引理8.对任何x, y ∈LG, 如果n是i:=i+c, x⊑y, 那么HandleInterval(n, x)⊑HandleInterval(n, y).
证明:下面分情况讨论:
(1) 如果∀k(k ∈[initi, c, i+c)⇒p)在x中, 那么肯定存在∀k(k ∈[initi, c, i+c)⇒p')在y中, 因为{∀k(k ∈[initi, c, i)⇒p)}⊑{∀k(k ∈[initi, c, i)⇒p')}, 因此HandleInterval(n, x)⊑HandleInterval(n, y);
(2) 如果∀k(k ∈[initi, c, i)⇒p)在x中, 那么肯定存在∀k(k ∈[initi, c, i)⇒p')在y中, 因为{∀k(k ∈[initi, c, i-c)⇒p)}⊑ {∀k(k ∈[initi, c, i-c)⇒p')}, 因此HandleInterval(n, x)⊑HandleInterval(n, y);
(3) 如果i=initi在x中, 那么肯定存在i=initi在y中, 因此HandleInterval(n, x)⊑HandleInterval(n, y);
(4) 其他情况, HandleInterval(n, x)⊑HandleInterval(n, y).
综上, HandleInterval(n, x)⊑HandleInterval(n, y).
引理9.对任何S1, S2 ∈2ProperP, 如果S1⊑S2, 那么GenAQ(S1)⊑GenAQ(S2).
证明:令ψ(k)表示ψ(…, e1[f1(k)], …)的缩写:
(1) 如果在x中条件(1)成立, GenAQ(S1)=S1∪{∀k(k ∈[initi, c, i+c)⇒ψ(k))}.S1⊑S2推出i=initi ∈S2并且∀k(k ∈ [initi, c, i)⇒false)在S2中并且ψ'(i) ∈S2, 其中, ψ(i)
(2) 如果在x中条件(2)成立, GenAQ(S1)=S1∪{∀k(k ∈[initi, c, i+c), ψ(k)}.S1⊑S2推出∀k(k ∈[initi, c, i)⇒ψ'1(k))在S2中并且ψ'2(i) ∈S2, 其中, ψ1(k)
(3) 如果在x中条件(3)和条件(4)成立, 证明过程类似条件(1)和条件(2);
(4) 其他情况, GenAQ(S1)⊑GenAQ(S2)显然成立.
综上, GenAQ(S1)⊑GenAQ(S2).
推论6.如果n是循环控制变量初始化语句, GenSpecial(n)⊑GenSpecial(n).
推论7.令G表示CFG.令a表示语句n之前的数据流值.如果a ∈LG, 那么Fn(a) ∈LG.
定理2.令n表示CFG G的语句.Fn是单调的.
证明:Fn是单调的当且仅当∀x, y ∈LG:x⊑y⇒Fn(x)⊑Fn(y).根据Fn的定义, 只需要证明Fn中出现的函数都是单调的.根据引理5~引理9和推论6、推论7, Fn是单调的.
定理4的证明
引理10.令ci表示语句n之前的状态, 令ai表示语句n之前的数据流值.如果G⊢ci
那么下面的条件成立:
1)
2) 如果n是e1[e2]:=e3, 那么
3) 如果n是循环控制变量初始化语句i:=init, 那么
4) 如果n是循环控制变量初始化语句i:=i+c, 那么
5) 对任何S ∈2ProperP, 如果
6) 对任何S ∈2ProperP, 如果
证明:
(1) 要证明结论1), 需要证明:
a) 如果n是lh:=e, 那么
b) 如果n是cond, 并且:
ⅰ
ci+1是true分支语句之前的状态, 那么
ⅱ
ci+1是false分支语句之前的状态, 那么
根据语句语义的定义, 结论a)、结论b)成立.
(2) 要证明结论2), 需要证明:
| $ \left[\kern-0.15em\left[{\{ p|p \in a \wedge p{是全称量词性质}\wedge \& {e_1}\left[{{e_2}} \right] \notin M\left( p \right)\} } \right]\kern-0.15em\right]\left( {{c_i}_{ + 1}} \right). $ |
(3) 为了证明结论3), 需要证明
(4) 为了证明结论4):
a) 如果∀x(x ∈[initi, c, i+c)⇒p)在ai中, 那么只需要证明
b) 如果(∀x(x ∈[initi, c, i)⇒p)在ai中, 那么只需要证明∀x(x ∈[initi, c, i-c)⇒p)(ci+1).∀x(x ∈[initi, c, i)⇒p)在ai中∧
c) 如果(i=initi)在ai中, 那么只需要证明
d) 其他情况, 结论4)显然成立.
综上, 结论4)成立.
(5) 为了证明结论5):
a) 如果第4.3.5节中的条件(1)或者条件(2)成立, 那么只需要证明
1)如果条件(1)成立, 那么(∧S⇒(1))∧
2)如果条件(2)成立, 那么(∧S⇒(2))∧
b) 如果第3.3.6节中的条件(3)或者条件(4)成立, 那么只需要证明
综上, 结论5)成立.
(6)
定理4.令ci表示语句n之前的状态, ai表示语句n之前的数据流值.如果G⊢ci
证明:传播规则正确, 所以
| [1] |
Flanagan C, Qadeer S. Predicate abstraction for software verification. ACM SIGPLAN Notices, 2002, 37(1): 191–202.
[doi:10.1145/565816.503291] |
| [2] |
Lahiri SK, Bryant RE. Indexed predicate discovery for unbounded system verification. In: Alur R, Peled DA, eds. Proc. of the Computer Aided Verification. Berlin: SpringerVerlag, 2004. 135-147. [doi:10.1007/978-3-540-27813-9_11] |
| [3] |
Beyer D, Henzinger TA, Majumdar R, Rybalchenko A. Path invariants. ACM SIGPLAN Notices, 2007, 42(6): 300–309.
[doi:10.1145/1273442.1250769] |
| [4] |
Jhala R, McMillan KL. Array abstractions from proofs. In: Damm W, Hermanns H, eds. Proc. of the Computer Aided Verification. Berlin: Springer-Verlag, 2007. 193-206. [doi:10.1007/978-3-540-73368-3_23] |
| [5] |
Blanchet B, Cousot P, Cousot R, Feret J, Mauborgne L, Miné A, Monniaux D, Rival X. A static analyzer for large safety-critical software. ACM SIGPLAN Notices, 2003, 38(5): 196–207.
[doi:10.1145/780822.781153] |
| [6] |
Gopan D. Numeric program analysis techniques with applications to array analysis and library summarization[Ph. D. Thesis]. Madison: University of Wisconsin, 2007. |
| [7] |
Gopan D, Reps T, Sagiv M. A framework for numeric analysis of array operations. ACM SIGPLAN Notices, 2005, 40(1): 338–350.
[doi:10.1145/1047659.1040333] |
| [8] |
Halbwachs N, Péron M. Discovering properties about arrays in simple programs. ACM SIGPLAN Notices, 2008, 43(6): 339–348.
[doi:10.1145/1379022.1375623] |
| [9] |
Gulwani S, McCloskey B, Tiwari A. Lifting abstract interpreters to quantified logical domains. ACM SIGPLAN Notices, 2008, 43(1): 235–246.
[doi:10.1145/1328897.1328468] |
| [10] |
Kam JB, Ullman JD. Monotone data flow analysis frameworks. Acta Informatica, 1977, 7(3): 305–317.
[doi:10.1007/BF00290339] |
| [11] |
Zhao JH, Li XD. Scope logic: An extension to hoare logic for pointers and recursive data structures. In: Liu ZM, ed. Proc. of the Theoretical Aspects of Computing (CICTAC 2013). Shanghai: Springer-Verlag, 2013. 409-426. [doi:10.1007/978-3-642-39718-9_24] |
| [12] | |
| [13] |
De Moura L, Bjrner N. Z3: An efficient smt solver. In: Ramakrishnan CR, Rehof J, eds. Proc. of the Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2008. 337-340. [doi:10.1007/978-3-540-78800-3_24] |
| [14] | |
| [15] |
Hoare CA. Proof of a program:Find. Communications of the ACM, 1971, 14(1): 39–45.
[doi:10.1145/362452.362489] |
| [16] | |
| [17] |
Cousot P, Cousot R, Logozzo F. A parametric segmentation functor for fully automatic and scalable array content analysis. ACM SIGPLAN Notices, 2011, 46(1): 105–118.
[doi:10.1145/1925844.1926399] |
| [18] |
Kovács L, Voronkov A. Finding loop invariants for programs over arrays using a theorem prover. In: Chechik M, Wirsing M, eds. Proc. of the Fundamental Approaches to Software Engineering. Berlin: Springer-Verlag, 2009. 470-485. [doi:10.1007/978-3-642-00593-0_33] |
| [19] |
Daniel L, Rodríguez-Carbonell E, Rubio A. SMT-Based array invariant generation. In: Giacobazzi R, Berdine J, Mastroeni I, eds. Proc. of the Verification, Model Checking, and Abstract Interpretation. Berlin: Springer-Verlag, 2013. 169-188. [doi:10.1007/978-3-642-35873-9_12] |
| [20] |
Francesco A, Ghilardi S, Sharygina N. Decision procedures for flat array properties. In: Ábrahám E, Havelund K, eds. Proc. of the Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-averlag, 2014. 15-30. [doi:10.1007/978-3-642-54862-8_2] |
| [21] |
Cordeiro L, Fischer B, Marques-Silva J. SMT-Based bounded model checking for embedded ANSI-C software. IEEE Trans. on Software Engineering, 2012, 38(4): 957-974. [doi:10.1109/TSE.2011.59] |
| [22] |
Haran A, Carter M, Emmi M, Lal A, Qadeer S, Rakamarić Z. Smack+ Corral: A modular verifier. In: Baier C, Tinelli C, eds. Proc. of the Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2015. 451-454. [doi:10.1007/978-3-662-46681-0_42] |
| [23] |
Blanchet B, Cousot P, Cousot R, Feret J, Mauborgne L, Miné A, Monniaux D, Rival X. Design and implementation of aspecialpurpose static program analyzer for safety-critical real-time embedded software. In: Mogensen TÆ, Schmidt DA, Sudborough IH, eds. Proc. of the Essence of Computation. Berlin: Springer-Verlag, 2002. 85-108. [doi:10.1007/3-540-36377-7_5] |
| [24] |
Gopan D, DiMaio F, Dor N, Reps T, Sagiv M. Numeric domains with summarized dimensions. In: Jensen K, Podelski A, eds. Proc. of the Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2004. 512-529. [doi:10.1007/978-3-540-24730-2_38] |
| [25] |
Lahiri SK, Bryant RE. Constructing quantified invariants via predicate abstraction. In: Steffen B, Levi G, eds. Proc. of the Verification, Model Checking, and Abstract Interpretation. Berlin: Springer-Verlag, 2004. 267-281. [doi:10.1007/978-3-540-24622-0_22] |
| [26] |
Lahiri SK, Bryant RE, Cook B. A symbolic approach to predicate abstraction. In: Hunt WA, Somenzi F, eds. Proc. of the Computer Aided Verification. Berlin: Springer-Verlag, 2003. 141-153. [doi:10.1007/978-3-540-45069-6_15] |
| [27] |
Srivastava S, Gulwani S. Program verification using templates over predicate abstraction. ACM SIGPLAN Notices, 2009, 44(6): 223–234.
[doi:10.1145/1543135.1542501] |
| [28] |
McMillan KL. Quantified invariant generation using an interpolating saturation prover. In: Ramakrishnan CR, Rehof J, eds. Proc. of the Tools and Algorithms for the Construction and Analysis of Systems. Berlin: Springer-Verlag, 2008. 413-427. [doi:10.1007/978-3-540-78800-3_31] |
 2018, Vol. 29
2018, Vol. 29


