2. 现代信息科学与网络技术北京市重点实验室(北京交通大学), 北京 100044
2. Beijing Key Laboratory of Advanced Information Science and Network Technology(Beijing Jiaotong University), Beijing 100044, China
随着图像修改技术的快速发展和编辑软件的广泛运用, 人们能够轻而易举地篡改伪造出逼真的图像.如果这样一张被恶意篡改的图像经过社交网络或数字媒体流传出去, 就会对社会和公众造成巨大的伤害.例如, 伊朗的”导弹齐射”事件、美国总统大选伪造图片事件、中国的华南虎事件等.这些事件不仅打破了人们“眼见为实”的传统观念, 还对军事、政治、文化等多个领域带来了严重的负面影响.因此, 检测一幅图像是否经过篡改是十分必要的, 尤其是在司法领域和军事领域.
在21世纪的今天, 各类电子产品在不断地更新换代, 使得人们可以轻易得到高分辨率的电子图片.同时, 通信设备的发展逐渐成熟化, 使得人与人之间的信息交流与共享逐渐频繁化.这样就会出现在不同设备上显示同一幅图像的情况, 而要达到这个目的, 就需要根据设备的需求对图像的尺寸进行修改.到目前为止, 效果比较好也比较新的修改图像尺寸的方法是图像内容感知缩放技术.这种技术是由Avidan[1]在2007年首次提出的.该方法消除了普通缩放技术在缩放图像时所产生的扭曲现象, 保证了原图像在经过内容感知缩放操作后, 图像中的重要内容不受到缩放操作的影响.然而, 篡改者为了将篡改的图像做得更加逼真, 他们将内容感知缩放技术也运用到了篡改图像的过程中, 这样就可以在不改变图像中重要区域内容的情况下, 去掉背景中的物体或是修改背景中的物体尺寸.因此, 检测图像中是否存在内容感知缩放操作对图像的内容取证也是具有重要意义的.
自从Avidan提出内容感知缩放技术之后, 国内外有许多学者都开始研究这一技术.2009年Sarkar[2]考虑到seam carving操作会导致图像频域特征发生变化, 而Markov转移概率矩阵能够描述出这种变化,所以提出了使用324维Markov特征来检测内容感知缩放技术.随后, 盛国瑞[3]等人发现传统的马尔可夫特征对放大比例较大的情况不够敏感, 所以提出了一种基于扩展Markov特征的seam-carving篡改检测方法, 该算法不仅克服了传统Markov特征的缺陷, 还提高了检测率.2011年, Wu[4]采用散列的预测判别方法来检测seam-carving操作.该算法是在已知原始图像散列和篡改图像散列的前提下, 使用visual word IDs对SIFT点进行配对, 并通过观察相邻匹配点间距离的变化情况, 来判断图像是否被篡改过, 但是这种方法是一种主动取证方法, 所以具有一定的局限性.2014年Wei[5]提出采用面片分析的方式来检测seam-carving, 该算法是将图像分为2×2大小的mini-squares, 然后与其所著文献[5]中提出的9种面片进行比对, 再根据比对的结果判断图像是否为篡改图像.同年, RYU[6]利用图像的能量偏差和噪声级别对原始图像和篡改图像进行区分, 在该算法中一共提出了4种能量特征、10种线特征和4种噪声特征, 并将它们放入SVM中分类.实验结果表明, 该方法优于Sarkar提出的方法.2015年Wattanachote[7]发现, 将BACM可视化后, 原始图像的BACM图是具有规律性的图案, 而被内容感知缩放操作篡改后的图像所对应的BACM图是不具有规律性的.因此, 他们提出了一种利用JPEG图像中块效应特征矩阵对称性的方法来区分原始图像和内容感知缩放图像, 并具有较好的检测效果.同年, Yin[8]考虑到原始图像会因为篡改操作而改变局部区域中的纹理特征, 又因为LBP是一种局部特征描述符, 所以提出了基于LBP的检测算法.该算法在文献[6]中所提18种特征的基础上还提出了6种新的基于半线的特征, 并具有较好的识别率.之后, Ye[9]改进了LBP的检测算法, 提出了使用LDP来检测内容感知缩放操作, 同时使用文献[8]中提到的24种特征来进行检测, 其检测结果要优于文献[6]和文献[5]中提到的方法.
如今, 由相机拍摄的照片中都存在CFA特性, 如果对这些照片做去马赛克处理, 则会改变图像像素间的相关性, 而内容感知缩放操作也会导致像素之间的相关性发生变化, 所以尝试使用CFA特性检测内容感知缩放操作.通过实验发现, 图像经过内容感知缩放操作篡改后, 原始图像中的CFA特性会被破坏, 导致篡改区域中出现许多线条, 即插入的线或删除的线.因此, 本文提出了一种基于概率Map图统计特征的内容感知缩放检测算法, 其基本思想是通过概率Map图来反映出待测图像是否被内容感知缩放操作篡改过, 并构造了4种新特征以验证该方法的识别率.
本文第1节介绍内容感知缩放技术.第2节介绍基于概率Map图的积分投影与局部统计特征的检测算法.第3节是实验结果分析.第4节是对本文的总结与展望.
1 内容感知缩放技术内容感知缩放技术分为两种, 一种是线剪裁(seam carving)操作, 另一种是线插入(seam insertion)操作.这两种操作的目的都是为了能够在不改变原图像中重要区域内容的前提下, 对原图像中的非重要区域进行缩放.针对图像中重要区域的判定方法, 本文将采用图像能量函数来进行判定, 并且定义重要区域为图像中能量较高的区域, 而非重要区域对应图像中能量较低的区域.然后, 通过计算图像中像素点与周围像素点之间的梯度值来得到每个像素点的能量值.最后, 使用线剪裁或者线插入操作对图像进行尺寸的修改.
内容感知缩放操作主要是通过移除或者增加“细缝(seam)”来达到图像缩放的目的.所谓“细缝”就是一条水平或者垂直的贯穿整幅图像的八连通像素构成的线, 并且这条线在图像中的每一行或每一列都有且只有一个像素点.当移除这样的细缝时, 就可以使图像缩小; 而当添加这样的细缝时, 就可以使图像放大.同时, 在缩放的过程中不会对图像中重要的细节信息产生很大的影响, 因此不会导致重要区域变扭曲, 其视觉效果也会更好.图 1展现了内容感知缩放技术与普通缩放技术的对比效果.从图 1可以看出, 在用普通缩放技术得到的图像中(如图 1(b)和图 1(c)所示), 重要内容都发生了形变; 而在采用内容感知缩放操作得到的图像中(如图 1(d)和图 1(e)所示), 重要内容基本上没有发生变化, 视觉效果也比普通缩放的效果要好.

|
Fig. 1 The effect picture of normal scaling and content-aware resizing 图 1 普通缩放与内容感知缩放的效果图 |
为了不影响图像中重要区域的内容, 在内容感知缩放算法[10]中对所选取的线提出了3点要求.一是选取的线是贯穿整幅图像的线, 二是图像中的每一行或每一列都有且仅有一个像素点在这条线上, 三是所选线的任意两个相邻像素点之间的横向距离不得超过一个像素点.这样, 所选线S的定义如公式(1)所示.
| $ {S^x} = \{ s_i^x\} _{i = 1}^{{N_1}} = \{ i, x(i)\} _{i = 1}^{{N_1}}, {\rm{ s}}{\rm{.t}}.\forall i, {\rm{ }}|x(i) - x(i - 1)| \le 1{\rm{ }} $ | (1) |
其中, N1代表线上所含的像素个数.为了使线S上所有像素的能量总和尽可能低, 就需要首先计算像素点的能量, 然后找出能量总和最小的线.对于一幅N1×N2大小的图像I, 利用公式(2)求得图像中像素的能量值.
| $ e(I) = \left| {\frac{\partial }{{\partial x}}I} \right| + \left| {\frac{\partial }{{\partial y}}I} \right| $ | (2) |
然后计算线S上像素点的能量之和, 并选取能量之和最小的线作为最优线S*, 其定义式如公式(3)所示.
| $ {S^ * } = \mathop {\min }\limits_S \{ E(S)\} = \mathop {\min }\limits_{S, S = \{ {s_i}\} _{i = 1}^{{N_i}}} \left\{ {\sum\limits_{i = 1}^{{N_i}} {e(I({s_i}))} } \right\} $ | (3) |
为了能够更方便地找出最优线, 本文采用动态迭代方法来实现.该迭代方法是从第2行开始计算, 一直到最后一行.对于某个特定的像素点(i, j), 其上一行中能与之构成连通的3个像素点分别为(i-1, j-1)、(i-1, j)和(i-1, j+1), 则确定最低能量线位置的公式如公式(4)所示.
| $ M(i, j) = e(i, j) + \min (M(i - 1, j - 1), M(i - 1, j), M(i - 1, j + 1)) $ | (4) |
对于缩小图像而言, 只要将能量最小的若干条线直接移除, 就可以达到缩小图像的目的.而对于放大图像而言, 则需要插入若干条最优线才能达到放大图像的目的.其方法是, 在找到能量最小的线后, 将线移走, 并且被移走的每个像素点都由两个新的像素点代替.如果最优线的位置刚好在图像的边界处, 那么最优线上的像素点将被保留, 且只添加一个新像素.
2 基于概率Map图的积分投影与局部统计特征的检测算法将CFA模型延伸到二维空间中, 并采用Bayer模型(如图 2(a)所示)来检测去马赛克操作.只考虑绿色通道, 这是因为, 人眼对绿色要比对红色和蓝色更敏感.针对绿色通道, 将一维模型中的奇偶位置转换到梅花形晶格中[11], 其中, A表示获得的的绿色值, I表示插入的绿色值(如图 2(b)所示).当存在去马赛克时, 在A处的预测误差的方差高于在I处的预测误差的方差.相反地, 如果不存在去马赛克, 则这两处的预测误差的方差会有相似的数值.因此, 通过计算A与I两位置上预测误差的方差之间的差异大小来判断图像中是否存在去马赛克操作.

|
Fig. 2 CFA model 图 2 CFA模型 |
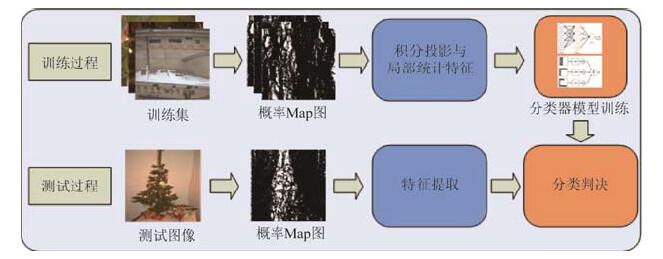
借鉴上述方法, 本文提出了一种基于概率Map图统计特征的内容感知缩放检测算法.该算法首先利用Bayer滤波马赛克模型检测待测图像中是否存在CFA特性, 并得到特征L在存在CFA特性和不存在CFA特性两种情况下的概率值P1和P2, 然后利用P2与P1的似然比来绘制概率Map图.通过分析不同类型图像的Map图之间的差异, 本文构造了4种新的统计特征来识别待测图像是否经过内容感知缩放操作, 最后将特征放入分类器中训练测试.该算法的完整流程图如图 3所示.
|
Fig. 3 The work flow of algorithm 图 3 算法流程图 |
2.1 绘制概率Map图
对于给定的一幅待测图像I(x, y), 首先需要计算出它的预测误差e(x, y), 然后采用自适应的方法来估计其方差.因为在实际情况下, 预测误差的方差只有局部是平稳的, 所以假设预测误差在(2K+1)×(2k+1)的窗口中是局部平稳的, 则预测误差的局部加权方差就由公式(5)表示, 其中, αij为权重[11].
| $ \left. \begin{array}{l} e(x, y) = s(x, y) - \sum\limits_{u, v \ne 0} {{k_{u, v}}s(x + u, y + v)} \\ \sigma _e^2(x, y) = \frac{1}{c}\left[{\left( {\sum\limits_{i, j =-K}^K {{\alpha _{ij}}{e^2}(x + i, y + j)} } \right)-{{({\mu _e})}^2}} \right]\\ {\mu _e} = \sum\nolimits_{i, j = - K}^K {{\alpha _{ij}}e(x + i, y + j)}, {\rm{ }}c = 1 - \sum\nolimits_{i, j = - K}^K {\alpha _{ij}^2} \end{array} \right\} $ | (5) |
根据上述方差的求解过程, 将待测图像分成B×B(B与贝尔模型的周期有关)大小互不重叠的块, 每块的位置由Bk, l来决定, 其中, k, l=0, ..., (N/B)-1.并且, 每一块都是由互不相交的插值像素集或获得像素集构成, 分别记作
| $ {\bf{L}}(k, l) = \log \left[{\frac{{G{M_A}(k, l)}}{{G{M_I}(k, l)}}} \right] $ | (6) |
其中, GMA(k, l)是指在获得像素处的预测误差的方差的几何平均, 而GMI(k, l)与其相似.
本文中将采用最小错误率贝叶斯决策方法, 求得L(k, l)在CFA特性存在或不存在两种情况下的似然比, 并利用似然比的值绘制出反映待测图像是否被篡改的概率Map图.假定M1和M2分别代表存在CFA特性和不存在CFA特性这两种情况, 然后计算特征L在这两种情况下的类条件概率密度, 如公式(7)所示, 其中, μ1 > 0, μ2=0.之后, 采用最大期望(EM)算法[12]对参数进行估计.
| $ \left. \begin{array}{l} {P_1}\{ {\bf{L}}(k, l)|{M_1}\} = {\rm N}({\mu _1}, \sigma _1^2), \\ {P_2}\{ {\bf{L}}(k, l)|{M_2}\} = {\rm N}(0, \sigma _2^2) \end{array} \right\} $ | (7) |
为了便于计算, 假设先验概率为
| $ L({\bf{L}}(k, l)) = \frac{{{P_2}\{ {\bf{L}}(k, l)|{M_2}\} }}{{{P_1}\{ {\bf{L}}(k, l)|{M_1}\} }} $ | (8) |
此时就可以根据图像中每块求得的似然比值来绘制概率Map图, 如图 4所示.
|
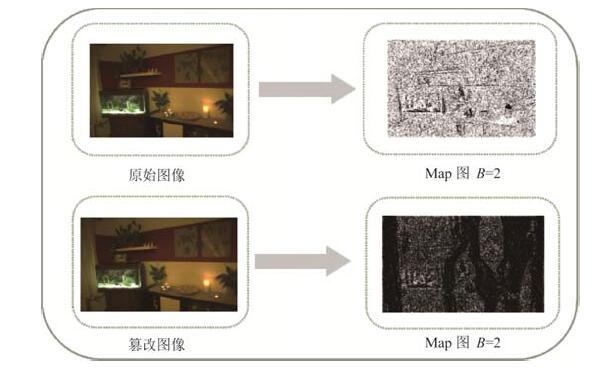
Fig. 4 The probability Map of original and tempered images 图 4 原始图像与篡改图像的Map图 |
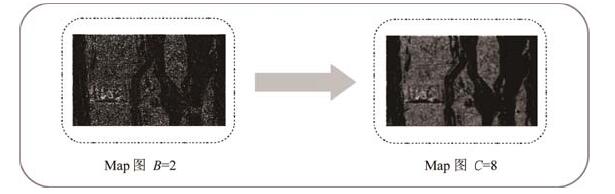
从图 4中的两幅Map图可以看出, 利用特征L在CFA存在和不存在两种情况下概率的似然比来反映待测图像是不是经过内容感知缩放操作是有明显效果的.这是由于, 一幅具有CFA特性的原始图像在经过内容感知缩放操作的篡改后, 原图像中被篡改位置上的CFA特性会因插入线或删除线而被破坏, 所以在篡改区域中原图与篡改图各自计算出的似然比值就会相差较大, 因此在可视化后, 篡改图像对应的Map图中会明显地标记出被篡改的大致位置.从Map图中还可以看出, 图中是有噪声存在的, 这样就会影响Map图中篡改位置标记的清晰度.因此, 为了降低噪声, 本文将采用放大块尺寸的方法, 即将B放大到C(C=n∙B), 此时所对应的似然比就由公式(9)给出, 实验结果表明, 当将原来的B=2扩大到C=8时, 相同图像的Map图中被标记的篡改位置会变得更加清晰, 效果图如图 5所示.
| $ {L_c}({\bf{L}}(k', l')) = \frac{{{\prod _{k, l}}{P_2}\{ {\bf{L}}(k, l)|{M_2}\} }}{{{\prod _{k, l}}{P_1}\{ {\bf{L}}(k, l)|{M_1}\} }} $ | (9) |
|
Fig. 5 The probability Map in different block size 图 5 不同块尺寸下的Map图 |
利用上述方法检测原图、内容感知缩放图和普通缩放(bicubic)图, 其对比效果如图 6所示.

|
Fig. 6 The Map of different observed images 图 6 不同待测图像对应的Map图 |
通过大量图像验证, 利用似然比可视化得到的概率Map图是能够明显地区分出待测图像是属于哪一类图像的, 并且实验结果与图 6中所展现的规律一样.如果待测图为原图, 则图像中的CFA特性没有被破坏, 所以Map图中不显示出任何黑色区域; 如果待测图是内容感知缩放图, 则在插入线或删除线位置上的CFA特性会被破坏或消失, 从而影响P1和P2间的似然比大小, 所以在Map图中会明显地显示出被篡改的大致位置; 如果待测图是普通缩放图, 则整幅图像中的CFA特性都会被破坏, 所以Map图会反映出待测图不具有CFA特性, 从而判断出待测图属于普通缩放图像.
2.2 积分投影特征分析不同类型待测图像所对应的概率Map图后可以发现:原图的Map图中所有像素值都是较高的; 内容感知缩放图的Map图中只有篡改部分具有较低的像素值, 其余位置上的像素值都较高, 但是也比原图-Map图中的像素值要低; 而对于普通缩放所对应的Map图, 由于是整体缩放图像, 所以导致原图像中CFA特性全部被破坏, 从而Map图中显现出的所有像素值都很低.由这一现象可以看出, 不同类型Map图中垂直或水平方向上的像素和是存在较大差异的, 所以本文提出了两种反映不同类型Map图中像素值之间差异的特征.而针对这两种特征, 本文是利用积分投影的方法来计算的.首先, Map图进行归一化处理.这是由于, 不同类型的Map图中像素值大部分都不处于同一个量级上, 所以需要对Map图做Z-score标准化处理.该方法利用Map图数据的均值和标准差来进行数据的标准化, 计算公式如公式(10)所示, 这样, 经过处理的数据就会符合均值为0、标准差为1的正态分布.
| $ Map\_M(i, j) = \frac{{Map(i, j) - Map\_mean}}{{Map\_std}} $ | (10) |
然后, 分别计算归一化后Map图在垂直和水平方向上的积分投影, 即分别对Map图中每列和每行求和, 将其结果可视化后得到图 7和图 8(以图库中某一张图为例).
|
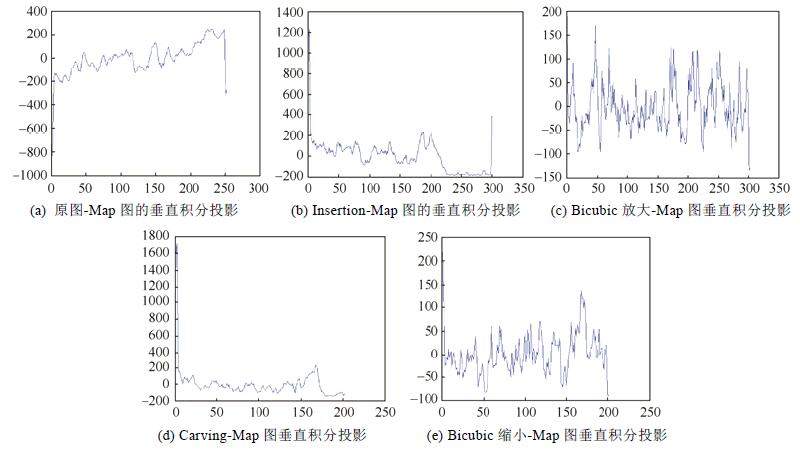
Fig. 7 The different types of Map in vertical integral projection 图 7 不同类型Map图的垂直积分投影 |
|
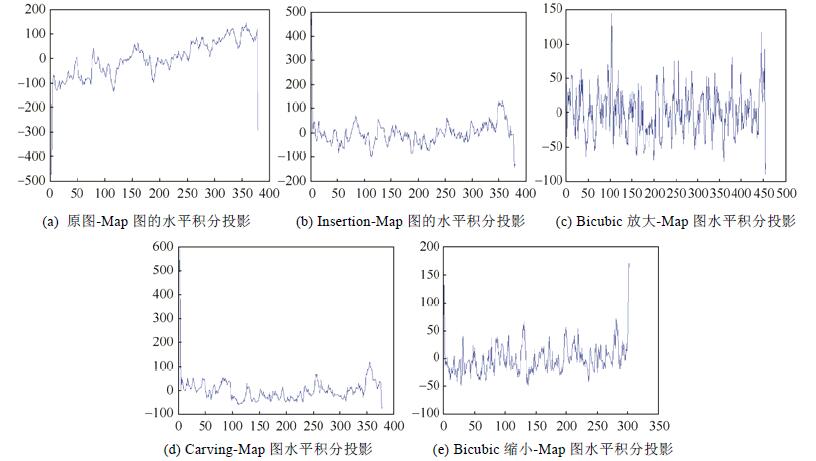
Fig. 8 The different types of Map in horizontal integral projection 图 8 不同类型Map图的水平积分投影 |
由图 7可以看出, 在原图-Map图垂直积分投影的折线图中(如图 7(a)所示), 左边缘处的值都小于–200, 且呈急剧上升趋势; 右边缘处的值都在–200~200之间, 呈急剧下降趋势; 而在中间区域的数值都分布在0值上下, 整体呈上升趋势, 但变化幅度相对较小.在insertion-Map图垂直积分投影的折线图中(如图 7(b)所示), 左边缘处的值都大于200, 且呈现急剧下降趋势.右边缘处的值在–200~400之间, 呈急剧上升趋势.而中间部分的数值同样分布在0值上下, 整体呈现下降趋势.所以, 可以根据这两种变化趋势来区分图像的类型.在bicubic放大图像对应的Map图垂直积分投影图中(如图 7(c)所示)表现出震荡趋势, 且震荡幅度很大, 而与前两者变化趋势相比有明显的不同.对于通过carving-Map图对应的折线图(如图 7(d)所示), 左边缘处的值都在200以上, 且呈大幅度下降趋势.而中间的数值都在0值上下小幅度地浮动.与图 7(a)对比, 两幅折线图不仅呈现的变化趋势不相同, 而且数值整体变化的范围也不相同, 前者的变化范围在–200~1800之间, 而后者的变化范围在–1000~400之间.图 7(e)所示的数据在0值上下振动, 且变化幅度较大, 并且与图 7(a)和图 7(d)相比, 3种图中展现出的变化趋势有显著的区别.因此, 对Map图求垂直积分有利于区分出待测图像所属的类别.
从图 8可以看出, 原图对应的水平积分投影折线图(如图 8(a)所示)所呈现的变化趋势与其在垂直方向上的变化趋势基本相同, 但是变化范围要比垂直方向上的小, 只在–500~200之间变化.而图 8(b)和图 8(d)中呈现出大致相同的变化趋势, 但是这种趋势与图 8(a)的变化趋势完全不同.经过bicubic操作的图像所对应的折线图, 如图 8(c)和图 8(e)所示, 两者的数值的变化范围都在–100~200之间, 且都围绕着0值上下振动, 但是前者的震荡幅度较大, 后者的震荡幅度相对较小.对比图 8所示的所有折线图, 可以看出水平垂直积分投影也是能够用来区别原图、内容感知缩放图和普通缩放图的.
直接采用两个方向上的积分投影作为特征来使用是不可行的, 其最主要的原因是不同类型Map图的积分投影维度是有区别的, 所以需要构造新的特征.通过对数值进行分析可以发现, 在垂直方向上, 普通缩放对应的积分投影数值变化范围最小, 中间是原图, 变化最大的是内容感知缩放图, 并且这三者之间的差异较大.而在水平方向上, 普通缩放对应的积分投影数值变化范围依然最小, 其次是原图与内容感知缩放图.这种现象表明, 如果取积分投影的方差, 则不同图像种类之间就会出现明显的差异, 因此在本文中, 将垂直方向上投影积分的方差作为特征F1, 水平方向上投影积分的方差作为特征F2.大量实验结果表明, 特征F1和F2能够较好地反映出不同Map图之间的差异, 如图 9所示.

|
Fig. 9 The scatter diagram of features F1 and F2 图 9 特征F1和F2的散点图 |
通过对比发现, 对于insertion操作, 特征F1的区分效果较好, 而对于carving操作, 特征F2的区分效果比较明显.而且对于bicubic操作而言, 这两种特征都具有良好的分类效果.在图 9所示的图例中, Y代表原图.I和C分别代表内容感知缩放操作中的insertion和carving, Bicubic中的放大和缩小操作由FD和SX分别表示, 且这4种操作的参数都为20%.数字1和数字2分别表示特征F1和F2.
2.3 局部统计特征对比5种类型图像对应的Map图可以发现, 原图的Map图中只有少量的像素值为0;而普通缩放图对应的Map图中却只有少量的值不为0;并且, 针对内容感知缩放图的Map图, 图中被篡改的区域内像素值为0或者为较小的数值, 而没有被篡改的区域内则是相对较大的数值.因此, 根据Map图之间的这些差异, 本文提出另一种构造特征的算法, 该算法的基本思路是:利用不同类型Map图中非零值个数的显著差异来判断待测图像的类型.首先, 对Map图进行分块操作.根据Map图的尺寸大小, 本文将此图分为互不重叠的若干个32×32大小的块.
在分块的过程中会遇到不能整除32的情况, 针对这种情况, 本文采用添加适当的行或列来达到整除32的目的.由于最终目的是计算非零值个数, 所以添加的行或列都为0值.然后, 计算每块中非零像素的个数, 得到矩阵M, 并将其用热点图可视化, 如图 10所示.
|
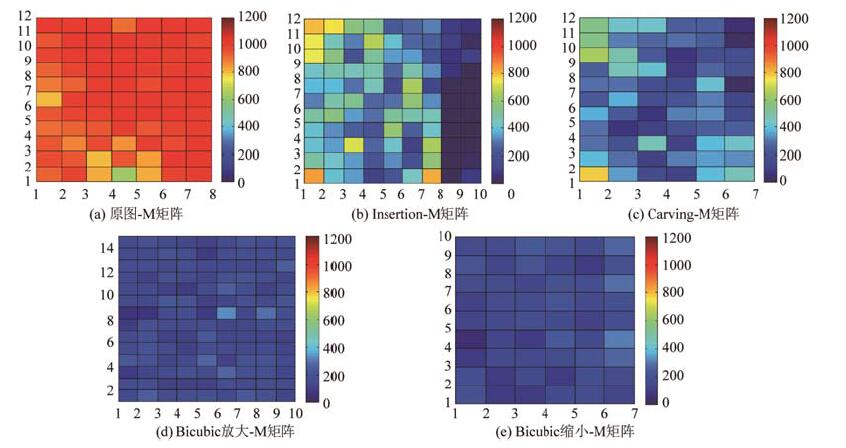
Fig. 10 The heat map of M matrix 图 10 M矩阵热点图 |
从图 10(a)中可以看出, M中大部分数据都分布在800以上, 并且每个像素值都比较大.与内容感知缩放图-M矩阵的折线图(如图 10(b)和图 10(c)所示)进行比较, 发现由于经过内容感知缩放操作后Map图中的像素值大幅度降低, 被篡改区域中出现了部分零像素值, 所以在热点图中表现出的非零像素个数大部分都在800以下, 利用此现象可以明显地分辨出Map图是属于哪一类图像的.用图 10(d)和图 10(e)与前面的3幅热点图进行对比发现, 经过普通缩放操作后, Map图中零值像素个数急剧上升, 从而使得M中的值都相对较小.因此, 利用Map图中非零值的数量来区别待测图像所属类型是有显著效果的.观察图 10中的5幅热点图可以发现, 每种情况下的均值与方差会有较大的差异, 所以在本文中采用矩阵M的均值作为特征F3, 矩阵M的方差作为特征F4, 其特征对比示意图如图 11所示.大量实验结果表明, 特征F3的分类效果十分显著(如图 11(a)和图 11(b)中第1幅和第3幅图所示).而特征F4的分类效果就不如F3.在区分内容感知缩放图与原图的情况下, F4的区分效果较为明显(如图 11(a)中的第2幅与第4幅所示); 在普通缩放图与原图进行比较时, F4只对后110幅图像具有明显的区分效果.这是由于, 这110幅图像尺寸大于前面所有图像的尺寸, 所以图像中的细节变化更明显, 检测的效果也会更好.

|
Fig. 11 The sketch map of F3 and F4 features 图 11 特征F3与F4的示意图 |
在图 11所示的图例中.数字3和4分别表示特征F3和F4.其余标识与图 9中所表示的意思一样.
2.4 分类训练集成(ensemble)分类器是将多个基础分类器的分类结果按照某种规则组合在一起来决定最终的分类结果.这种分类器不仅提高了分类时的速度, 还提高了分类效果.而神经网络分类器能够有效地解决非正太分布、非线性的评价问题.因此, 在本文中采用集成分类器对两类图像特征进行分类, 采用神经网络分类器对3类图像特征进行分类.这样就可以将区分原图、内容感知缩放图和普通缩放图问题归结为分类问题.经过分类器分类, 就可以区分出这3类图像.
3 实验结果本文中的所有实验都采用Nikon图库, 从中挑选出内容不相同的425幅图像作为原始图库.而篡改图库则由原始图库经过seam insertion、seam carving、bicubic放大和bicubic缩小4种操作得到, 其中, 参数分别为10%、20%和50%, 最终得到13个实验图库.所有实验中的结果都是测试10次结果的平均值.
3.1 区分内容感知缩放图与原图在检测seam insertion操作的实验中, 针对单个参数测试, 训练集由原始图库、I10、I20和I50图库中任选的350幅图像构成.测试集为剩余的所有图像.针对混合测试, 训练集和测试集都为所有图库中的图像, 数量与单个参数测试时的数量相同.检测seam carving操作实验中, 实验图库是原始图库、C10、C20和C50图库, 训练集与测试集的选取与检测seam insertion情况类似.实验结果见表 1和表 2(例:97.97%表示用原图库和I10图库训练出的模型检测I10图库中图像的检测率为97.97%, 其他同理).
| Table 1 Seam insertion detection accuracy for different training-testing combinations (%) 表 1 不同训练集和测试集下的seam insertion检测率(%) |
| Table 2 Seam carving detection accuracy for different training-testing combinations (%) 表 2 不同训练集和测试集下的seam carving检测率(%) |
从表 1和表 2可以看出, 本文所提方法在区分不同类型图像时具有明显的效果.通过这两个表格还可以发现, 当训练集与测试集的参数相同时, 检测率都达到了97%以上, 尤其是参数为50%时的检测率是最高的.并且, 这些数据还存在两个规律:一是训练集参数高于测试集参数时的检测率小于训练集和测试集参数相等时的检测率; 二是训练集参数低于测试集参数时的检测率高于训练集与测试集相等时的检测率.比较表格中含有混合集的数据可知, 当固定测试集时, 检测率随训练集参数的增大而减小, 并且在参数为50%时检测率仅有80%多.而当固定训练集的参数时, 检测率会随测试集参数的增大而增大, 但在参数较小时的检测率是很低的, 尤其是在检测carving操作时, 其检测率低于50%.
3.2 区分普通缩放图与原图本实验中, 针对Bicubic放大操作, 我们采用原始图库、FD10、FD20和FD50图库.针对bicubic缩小操作, 将采用原始图库、SX10、SX20和SX50图库.实验中的训练集与测试集的选取与第3.1节中的选取方法一样.实验结果见表 3和表 4.
| Table 3 Up-Scaling detection accuracy for different training-testing combinations (%) 表 3 不同训练集和测试集下的放大操作检测率(%) |
| Table 4 Down-Scaling detection accuracy for different training-testing combinations (%) 表 4 不同训练集和测试集下的缩小操作检测率(%) |
从表 3和表 4可以看出, 采用本文所提方法来区分原始图像和普通缩放图像也是有效果的, 但其效果没有检测内容感知缩放操作的效果好.这两个表格中同样显示出了一些规律:其一, 当训练集和测试集的参数相同时, 其检测率都在97%与98%之间, 并且图像放大时, 检测率随参数的增大而减小; 图像缩小时, 检测率随参数的增大而增大.其二, 在缩小图像的操作中, 对比含有混合集的检测结果可知, 当固定测试集参数时, 检测率随训练集参数的减小而减小; 当固定训练集参数时, 检测率随测试集参数的增大而减小.
3.3 区分内容感知缩放图与普通缩放图本实验中, 每次只比较经过篡改的两个图库(比如:I10与FD10图库, 其他同理), 其实验结果见表 5和表 6.
| Table 5 The detection accuracy for insertion and up-scaling images (%) 表 5 Insertion与整体放大图像的检测率(%) |
| Table 6 The detection accuracy for carving and down-scaling images (%) 表 6 Carving与整体缩小图像的检测率(%) |
由表 5和表 6可以看出, 当参数相同时, 内容感知缩放操作与普通缩放操作的检测率相差不大.在放大图像时, 检测bicubic放大操作的效果要稍好于检测insertion操作的效果; 而在缩小图像时, carving操作明显要比bicubic缩小操作的检测率高, 这说明, 所提算法在检测图像缩小操作时更有效果.从这些表中还可以看出, 在检测insertion(50%)操作时, 其检测率是最低的, 这是因为, 在原图像中插入线会使原来位置上的像素向右移动, 这样就不能与贝尔模型相匹配, 从而产生错位现象.因此, 这种情况下的Map图与普通放大操作的Map图在某些区域内具有相似的像素值, 所以在检测时增加了I50图像被判为FD50图像的几率.
3.4 区分内容感知缩放图、普通缩放图和原图在区分3类图像的实验中, 每次比较原图库和两种篡改图库(比如:原图、I10和FD10, 其他同理), 训练集与测试集的选取方式与第3.1节相同.采用神经网络分类器进行分类.实验结果见表 7~表 12.
| Table 7 The detection accuracy for original, insertion and up-scaling images (10%) 表 7 原始、insertion和放大的图像检测率(10%) |
| Table 8 The detection accuracy for original, insertion and up-scaling images (20%) 表 8 原始、insertion和放大的图像检测率(20%) |
| Table 9 The detection accuracy for original, insertion and up-scaling images (50%) 表 9 原始、insertion和放大的图像检测率(50%) |
| Table 10 The detection accuracy for original, carving and down-scaling images (10%) 表 10 原始、carving和缩小的图像检测率(10%) |
| Table 11 The detection accuracy for original, carving and down-scaling images (20%) 表 11 原始、carving和缩小的图像检测率(20%) |
| Table 12 The detection accuracy for original, carving and down-scaling images (50%) 表 12 原始、carving和缩小的图像检测率(50%) |
由表 7~表 12可以发现, 除了在参数为50%之外的4个表格中, 原图、内容感知缩放图和普通缩放图三者之间的检测率是逐渐增大的, 并且检测率都在90%以上.而在参数为50%的表 9中, 因为插入线数量较多导致错位现象比较严重, 导致I50图像被判为FD50图像的几率增大, 因此I50的检测率就相对较低.
3.5 实验对比针对Sarkar提出的基于传统Markov特征的检测方法, 本文也验证了该方法在Nikon图库中的检测效果.同时, 为了便于比较, 实验的所有设置都与第3.1节中的实验完全一致, 具体结果见表 13和表 14.
| Table 13 Seam insertion detection accuracy of Sarkar's method (%) 表 13 Sarkar方法的seam insertion检测率(%) |
| Table 14 Seam carving detection accuracy of Sarkar's method (%) 表 14 Sarkar方法的seam carving检测率(%) |
从表 13和表 14可以看出, 针对seam insertion操作, 在表格(50%, 10%)、(50%, 20%)、(50%, Mix)、(Mix, 10%)和(Mix, Mix)5个位置处, 本文所提方法的检测率都高于Sarkar方法的检测率, 尤其是在训练集参数为50%或参数混合的情况下, 这表明, 我们所提出的方法在识别测试集参数较小或混合情况下的效果较好.而表格其他位置上的检测率虽然都比Sarkar方法的检测率要低, 但是差异都较小.这是因为, 在计算Map图时出现的错位现象对提取特征时有一定的影响, 所以导致我们的检测率没有Sarkar方法高.而对seam-carving操作而言, 只有在表格(20%, 50%)、(Mix, 20%)和(Mix, 50%)这3个位置处的检测率稍低于Sarkar方法, 其余位置的检测率都比Sarkar方法的要高, 尤其是在(50%, 10%)和(Mix, 10%)两处.综上所述, 本文所提方法在检测carving操作的效果上要优于Sarkar的方法.而在检测insertion操作时, Sarkar方法的检测效果相对较好.这是由于, 本文中所提出的4种新特征在区分原图与内容感知缩放图的效果上并不是十分显著, 如图 9与图 11中前两个对比图显示的一样, 特征F2对大部分图像的区分效果不明显, 特征F4对后110幅图像的分类效果也不太明显, 因此导致本文方法的检测率稍低于Sarkar方法的检测率((50%, 10%)表示表格中训练集参数为50%, 测试集为10%.其他同理).
4 结束语本文提出了一种基于概率Map图统计特征的内容感知缩放检测算法, 该算法首先利用概率Map图来检测图像中是否存在CFA特性, 再根据检测的结果判断该图像是否经过内容感知缩放操作的篡改.并且, 通过对概率Map图进行分析, 还提出了4种新的统计特征, 用于区分不同类别的图像.将提取的特征放入两种分类器中训练, 然后进行分类测试, 结果显示出本文所提检测方法具有较高的检测效果.与Sarkar检测方法相比, 对于insertion操作, Sarkar方法的检测效果要优于我们的方法, 但在参数较小或是混合情况下, 本文所提方法的检测效果要比Sarkar方法好.而对于carving操作, 本文所提方法要好于Sarkar的检测方法.接下来, 我们将继续研究Map图, 寻找更为合适的新特征来提高检测率.
| [1] |
Avidan S, Shamir A. Seam carving for content-aware image resizing. ACM Trans. on Graph, 2007, 26(3): 10–16.
[doi:10.1145/1276377] |
| [2] |
Sarkar A, Nataraj L, Manjunath BS. Detection of seam carving and localization of seam insertions in digital images. In: Felten EW, ed. Proc. of the 11th ACM Workshop on Multimedia and Security. New York: ACM, 2009. 107-116. https://dl.acm.org/citation.cfm?id=1597837 |
| [3] |
Sheng GR, Gao TG, Fan L. Detection of content-aware image resizing for forensic applications. Int'l Journal of Digital Crime and Forensics, 2014, 6(2): 23–39.
[doi:10.4018/ijdcf.2014040102] |
| [4] |
LU W, Wu M. Seam carving estimation using forensic hash. In: Proc. of the 13th ACM Multimedia Workshop on Multimedia and Security. 2011. 9-14. [doi: 10.1145/2037252.2037255] |
| [5] |
Wei JD, Lin YJ, Wu YJ. A patch analysis method to detect seam carved images. Pattern Recognition Letter, 2014: 100–106.
[doi:10.1016/j.patrec.2013.09.026] |
| [6] |
Ryu SJ, Lee HY, Lee HK. Detecting trace seam carving for forensic analysis. IEICE Trans. Information and Systems, 2014, 1304-1311. [doi: 10.1587/transinf.E97.D.1304] |
| [7] |
Wattanachote K, Shih TK, Chang WL, Chang HH. Tamper detection of JPEG image due to seam modification. IEEE Trans. Information Forensics and Security, 2015, 2477-2491. [doi: 10.1109/TIFS.2015.2464776] |
| [8] |
Yin T, Yang GB, Li LD, Zhang DY. Detecting seam carving based image resizing using local binary patterns. Computer Security, 2015: 130–141.
[doi:10.1016/j.cose.2015.09.003] |
| [9] |
Ye JY, Shi Y Q. A local derivative pattern based image forensic framework for seam carving detection. IWDW Digital Forensics and Watermarking, 2016: 172–184.
[doi:10.1007/978-3-319-53465-7_13] |
| [10] |
Li JW, Zhao Y, Ni RR. Detection for processing history of seam insertion and contrast enhancement operation chain. In: Dai QH, Shimura T, eds. Proc. of the Int'l Conf. on Intelligent Information Hiding and Multimedia Signal Processing (ⅡH-MSP). Beijing: SPIE/COS PHOTONICS ASIA, 2015. 235-238. |
| [11] |
Ferrara P, Bianchi T, De Rose A, Piva A. Image forgery localization via fine-grained analysis of CFA artifacts. IEEE Trans. on Information Forensics and Security, 2012, 7(5): 1566-1577. [doi: 10.1109/TIFS.2012.2202227] |
| [12] |
Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, 1977, 39(1): 1–38.
|
 2018, Vol. 29
2018, Vol. 29


