2. 信息安全国家重点实验室(中国科学院 信息工程研究所), 北京 100093
2. State Key Laboratory of Information Security(Institute of Information Engineering, The Chinese Academy of Sciences), Beijing 100093, China
可逆数字水印技术通过利用多媒体信息中存在的冗余, 将水印信息(如载体特征信息、版权信息等)嵌入到数字多媒体载体当中, 并可在接收方完整地提取水印且无损地恢复原始载体[1].该技术可用于媒体的内容标识、完整性认证和版权保护等功能, 已广泛应用于对保密性、安全性以及保真度要求较高的领域, 如军事及医学图像、法律文书图片等[2].基于图像的可逆水印算法主要可以分为以下四大类:无损压缩[3]、差值扩展[4]、直方图平移[5]以及预测误差扩展[6].可逆数字水印技术一般不考虑水印的鲁棒性, 现有的大多数可逆水印算法在受到噪声干扰或经过处理后无法正确地提取嵌入的水印.实际中, 含水印的数字多媒体在网络等信道中传输时, 不可避免地会遭到各种处理或干扰, 所以, 在许多应用场景中希望嵌入的水印具有一定的鲁棒性, 在含水印的载体未受到信号处理或恶意攻击时, 在接收方能够正确地提取水印和无损地恢复原始载体; 而在含水印的载体经过一些信号处理操作时, 在接收端仍然能够正确地提取水印.近几年来, 鲁棒可逆水印技术逐渐成为了信息隐藏领域的一个重要的研究方向, 已取得一些有意义的成果[7-13].
随着互联网技术和云计算技术的快速发展, 用户可通过互联网将资料和数据上传到远程服务器或云端进行存储, 当需要时再下载使用.云存储节省了购买储存设备的开支并提高了获取资源的便利性.另外, 云服务中心的强大计算能力使得用户可以享受到第三方提供的数据处理等服务.然而, 云计算技术在方便人们生活的同时, 也引发了数据安全和隐私保护的问题[14].数据加密作为保护多媒体内容隐私的一种方式, 可以在上传到云端之前先对数据进行加密, 有效地降低内容隐私泄露的风险.为了对云端中海量的加密数据进行有效管理和安全保护, 云端管理者希望将一些用户资料相关的信息嵌入到密文数据中, 并通过提取嵌入的信息来实现密文检索和数据保护.因此, 加密域可逆水印技术成为了近年来大数据云计算背景下信息隐藏领域的研究热点.加密域可逆水印技术结合加密技术和可逆水印技术的优点, 在不暴露明文内容的情况下直接将水印嵌入到密文载体中, 并在解密及信息提取后能无损地恢复原始载体.目前的加密域图像可逆水印算法主要分为两大类:基于对称加密系统的可逆水印算法[15, 16]和基于非对称加密系统的可逆水印算法[17-20].目前, 加密域中的可逆水印算法绝大多数都不具有鲁棒性, 而在一些云计算的应用场景中, 信息隐藏者希望嵌入的水印信息不仅具有可逆性, 而且具有一定的鲁棒性, 以便在解密后图像受到处理或攻击时仍能认证媒体的版权.
与对称加密系统相比, 同态加密系统为非对称加密系统, 安全性更高, 且允许对密文进行算术运算, 更适合用于云计算背景下的第三方数据处理.本文结合同态加密系统和鲁棒可逆水印技术, 提出了一种基于同态加密系统的图像鲁棒可逆水印算法.该算法首先对原始图像进行8×8分块, 并利用Paillier加密系统[21]进行加密得到密文图像.在加密域中, 通过模乘法逆元MMI(modular multiple inverse)方法和查询密文映射表来得到每个密文分块的统计量, 然后利用同态特性对统计量进行直方图平移嵌入水印.在接收方可分别在含水印的密文图像或解密图像中得到统计量直方图并提取水印, 同时, 通过对统计量进行与嵌入过程相反的直方图平移来恢复密文图像或原始图像.另外, 解密后含水印的图像在受到一定程度的图像处理操作(如JPEG/JPEG 2000压缩和叠加高斯噪声等)后仍能正确地提取水印.该算法实现了在不对原始图像进行预处理的情况下可直接在加密后的密文图像中嵌入水印, 并可分别从加密域或明文域提取水印和恢复密文图像或原始图像, 而且嵌入的水印对常见的图像处理操作具有一定的鲁棒性.本文算法嵌入失真较小, 鲁棒性良好, 具有足够的嵌入容量来嵌入加密图像相关标签信息、版权信息或图像特征信息等, 适用于云计算中加密图像的内容标识、完整性认证及版权保护.
1 Paillier加密系统Paillier加密系统[21]是一种加性同态公钥加密系统, 这种加密技术已广泛应用于加密信号处理或第三方数据处理领域.其同态特性表现为:在加密后可直接对密文进行相应的算术运算, 其运算结果与明文域中对应的运算结果一致.其概率特性表现为:对于相同的明文, 可通过不同的加密过程得到不同的密文, 从而保证了密文的语义安全.其加密和解密机制如下.
密钥生成:随机选择两个较大的质数p和q, 计算它们的乘积N以及p-1、q-1的最小公倍数λ.然后再随机选取一个整数
| $ gcd\left( {L\left( {{g^\lambda }\bmod {N^2}} \right), N} \right) = 1 $ | (1) |
其中, 函数L(u)=(u–1)/N, 函数gcd(·)用于计算两数的最大公约数, ZN2为小于N2的整数的集合, 而
加密过程:随机选取一个整数
| $ c = E[m, r] = {g^m} \cdot {r^N}\bmod {N^2} $ | (2) |
根据Paillier加密系统的性质, 密文
解密过程:利用私钥λ, 对密文c解密后得到对应的明文m:
| $ m = D\left[c \right] = \frac{{L\left( {{c^\lambda }\bmod {N^2}} \right)}}{{L\left( {{g^\lambda }\bmod {N^2}} \right)}}\bmod N $ | (3) |
另外, Paillier加密系统具有两个重要的性质.
定理1.当g满足公式(1)时, 则c=E[m, r]是双射的, 即
本文将利用该定理实现查询密文映射表得到密文分块统计量.
同态乘法性质:对于两个明文
| $ {c_1} \cdot {c_2} = E[{m_1}, {r_1}] \cdot E[{m_2}, {r_2}] = {g^{{m_1} + {m_2}}} \cdot {\left( {{r_1} \cdot {r_2}} \right)^N}\bmod {N^2} $ | (4) |
解密后得到:
| $ D{\rm{[}}{c_1} \cdot {c_2}{\rm{]}} = D\left[{E\left[{{m_1}, {r_1}} \right] \cdot E\left[{{m_2}, {r_2}} \right]\bmod {N^2}} \right] = {m_1} + {m_2}\bmod N $ | (5) |
本文将利用该性质对密文分块统计量进行直方图平移, 实现在加密域中嵌入水印信息.
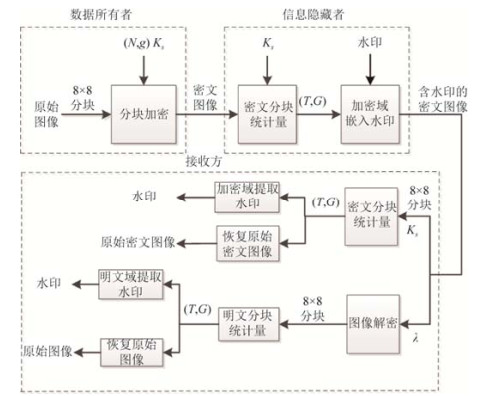
2 同态加密域图像鲁棒可逆水印算法本文提出的基于同态加密系统的图像鲁棒可逆水印算法框架如下文图 1所示.首先, 数据所有者对原始图像进行8x8分块, 并利用公钥(N, g)、密钥Ks和Paillier加密系统进行加密得到密文图像.信息隐藏者在加密域中利用Ks模乘法逆元MMI方法和查询相应密文映射表得到每个密文分块的统计量, 然后利用嵌入密钥(T, G)对统计量进行直方图平移嵌入水印.在接收方利用与嵌入过程相同的方法, 可在加密域中得到含水印的加密图像的统计量直方图, 然后利用(T, G)提取水印并通过与嵌入过程相反的直方图平移恢复密文图像.在接收方利用私钥l可对含水印的加密图像进行解密并得到统计量直方图, 然后利用(T, G)可从未受到攻击或图像处理的图像中提取水印和恢复原始图像, 或者从受到一定程度攻击的图像中提取水印.
|
Fig. 1 Sketch of the proposed robust and reversible image watermarking algorithm in encrypted image based on homomorphic cryptosystem 图 1 基于同态加密系统的图像鲁棒可逆水印算法框架 |
2.1 图像分块加密
数据所有者首先把原始图像I分为若干个互不重叠的大小为8×8的明文分块, 记第k个明文分块为P(k).然后按照第1节Paillier加密系统中描述的加密过程, 随机选取一个整数
| $ {C^{(k)}}(i, j) = E[{P^{(k)}}(i, j), {r_1}(k)] = {g^{{P^{(k)}}(i, j)}} \cdot {r_1}{(k)^N}\bmod {N^2} $ | (6) |
其中,
| $ {C'^{(k)}}(i, j) = {C^{(k)}}(i, j) \cdot E[0, {r_{(i, j)}}(k)] = {g^{{P^{(k)}}(i, j)}} \cdot {({r_1}(k) \cdot {r_{(i, j)}}(k))^N}\bmod {N^2} $ | (7) |
记改变后的密文为
| $ D[{C'^{(k)}}(i, j)] = {P^{(k)}}(i, j)\bmod N $ | (8) |
因此,
Zheng[22]提出了模乘法逆元MMI方法.对于两个互质的整数y和z, 存在整数θ满足:
| $ \theta \cdot y = 1\bmod z $ | (9) |
称θ为y的模乘法逆元, θ可根据扩展欧几里德算法[23]求得.利用MMI方法可以实现模运算中的除法.设另一个整数x, v是对x和y的乘积进行模z运算的结果:
| $ v = x \cdot y\bmod z $ | (10) |
当y已知时, 利用MMI方法可从v中求出x:
| $ v \cdot \theta = x \cdot y \cdot \theta = x\bmod z $ | (11) |
信息隐藏者接收到加密图像E[I]后, 首先把E[I]分为若干个互不重叠的大小为8×8的密文分块, 则第k个密文分块为
| $ {\theta _{Er}}(k) \cdot E[0, {r_{(i, j)}}(k)] = 1\bmod {N^2} $ | (12) |
由于
| $ {C'^{(k)}}(i, j) \cdot {\theta _{Er}}(k) = {C^{(k)}}(i, j) \cdot E[0, {r_{(i, j)}}(k)] \cdot {\theta _{Er}}(k) = {C^{(k)}}(i, j)\bmod {N^2} $ | (13) |
其中,
Zeng[11]提出了一种图像分块的统计量, 首先把图像分为若干个互不重叠的大小为m×n的明文分块, 然后定义一个大小为m×n的矩阵M:
| $ M(i, j) = \left\{ \begin{array}{l} 1, {\rm{ }}\bmod {\rm{ }}(i, 2) = \bmod {\rm{ }}(j, 2)\\ - 1, {\rm{ }}\bmod {\rm{ }}(i, 2) \ne \bmod {\rm{ }}(j, 2) \end{array} \right. $ | (14) |
其中,

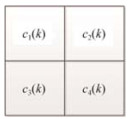
|
Fig. 2 Block M sized 2×2 图 2 2×2矩阵M示意图 |
记d(k)为第k个明文分块P(k)的统计量, P(k)(i, j)为P(k)中点(i, j)位置上的明文值, 则d(k)为
| $ {d^{(k)}} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {({P^{(k)}}(i, j) \times M(i, j))} } $ | (15) |
在加密域中, 信息隐藏者在不具有私钥λ的情况下不能将密文解密得到相应的明文, 无法直接进行明文值的运算得到统计量d(k).因此, 本文利用MMI方法和查询相应密文映射表得到密文分块统计量, 其值与对应的明文分块统计量相同.记密文分块统计量为d, d(k)是第k个密文分块C(k)的统计量.首先, 根据扩展欧几里德算法求出密文分块C(k)中密文C(k)(i, j)的模乘法逆元
| $ {\theta _{{C^{(k)}}(i, j)}} \cdot {C^{(k)}}(i, j) = 1\bmod {N^2} $ | (16) |
之后定义大小为8×8的矩阵M1和M2, 第k个矩阵
| $ {M_1}^{(k)}(i, j) = \left\{ \begin{array}{l} {C^{(k)}}(i, j), {\rm{ if }}\bmod {\rm{ }}(i, 2) = \bmod {\rm{ }}(j, 2)\\ {\theta _{{C^{(k)}}(i, j)}}, \;\;\;{\rm{ if }}\bmod {\rm{ }}(i, 2) \ne \bmod {\rm{ }}(j, 2) \end{array} \right. $ | (17) |
| $ {M_2}^{(k)}(i, j) = \left\{ \begin{array}{l} {\theta _{{C^{(k)}}(i, j)}}, \;\;{\rm{ if }}\bmod {\rm{ }}(i, 2) = \bmod {\rm{ }}(j, 2)\\ {C^{(k)}}(i, j), {\rm{ if }}\bmod {\rm{ }}(i, 2) \ne \bmod {\rm{ }}(j, 2) \end{array} \right. $ | (18) |
其中,
| $ \left\{ \begin{array}{l} {c_{d1}}\left( k \right) = \prod\limits_{i = 1}^m {\prod\limits_{j = 1}^n {{M_1}^{(k)}(i, j)\bmod {N^2}} } \\ {c_{d2}}\left( k \right) = \prod\limits_{i = 1}^m {\prod\limits_{j = 1}^n {{M_2}^{(k)}(i, j)\bmod {N^2}} } \end{array} \right. $ | (19) |
然后通过密文形式的统计量cd1(k)和cd2(k)便可在密文映射表中查询出对应的统计量d(k).下面是相应的公式推导和证明.为了方便理解, 以分块大小为2×2的密文分块加以举例证明.分块大小为2×2的第k个密文分块C(k)如图 3所示.
|
Fig. 3 Cipher block C(k) sized 2×2 图 3 2×2密文分块C(k)示意图 |
其中,
| $ \left\{ \begin{array}{l} {\theta _1}(k) \cdot {c_1}(k) = {\theta _1}(k) \cdot {g^{{P_1}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2}\\ {\theta _2}(k) \cdot {c_2}(k) = {\theta _2}(k) \cdot {g^{{P_2}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2}\\ {\theta _3}(k) \cdot {c_3}(k) = {\theta _3}(k) \cdot {g^{{P_3}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2}\\ {\theta _4}(k) \cdot {c_4}(k) = {\theta _4}(k) \cdot {g^{{P_4}(k)}} \cdot {r_1}{(k)^N} = 1\bmod {N^2} \end{array} \right. $ | (20) |
则密文分块C(k)的密文形式的统计量cd1(k)和cd2(k)为
| $ \left\{ \begin{array}{l} {c_{d1}}(k) = \prod\limits_{i = 1}^2 {\prod\limits_{j = 1}^2 {{M_1}(i, j)} = {c_1}(k)} \cdot {\theta _2}(k) \cdot {\theta _3}(k) \cdot {c_4}(k) = {g^{{P_1}(k) + {P_4}(k)}} \cdot {r_1}{(k)^{2N}} \cdot {\theta _2}(k) \cdot {\theta _3}(k)\bmod {N^2}\\ {c_{d2}}(k) = \prod\limits_{i = 1}^2 {\prod\limits_{j = 1}^2 {{M_2}(i, j)} = {\theta _1}(k) \cdot {c_2}} (k) \cdot {c_3}(k) \cdot {\theta _4}(k) = {g^{{P_2}(k) + {P_3}(k)}} \cdot {r_1}{(k)^{2N}} \cdot {\theta _1}(k) \cdot {\theta _4}(k)\bmod {N^2} \end{array} \right. $ | (21) |
根据Carmichael理论[21], 对于
| $ {a^{N\lambda }} = 1\bmod {N^2} $ | (22) |
因此, 按照第1节Paillier加密系统的描述, 对于
| $ \left\{ \begin{array}{l} {g^{N\lambda }} = 1\bmod {N^2}\\ {r_1}{(k)^{N\lambda }} = 1\bmod {N^2} \end{array} \right. $ | (23) |
并且,
| $ {g^{N\lambda }} \cdot {r_1}{(k)^{N\lambda }} = 1\bmod {N^2} $ | (24) |
根据式(20)和式(24), 可以推导出模乘法逆元的表达式:
| $ \left\{ \begin{array}{l} {\theta _1}(k) = {g^{N\lambda - {P_1}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2}\\ {\theta _2}(k) = {g^{N\lambda - {P_2}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2}\\ {\theta _3}(k) = {g^{N\lambda - {P_3}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2}\\ {\theta _4}(k) = {g^{N\lambda - {P_4}(k)}} \cdot {r_1}{(k)^{N(\lambda - 1)}}\bmod {N^2} \end{array} \right. $ | (25) |
根据式(23)和式(25)中模乘法逆元的表达式, 并考虑到统计量d(k)可能的取值, 公式(21)可以化简为
当
| $ \left\{ \begin{array}{l} {c_{d1}}(k) = {g^{{P_1} - {P_2} + {P_4} - {P_3}}}\bmod {N^2}\\ {c_{d2}}(k) = {g^{2N\lambda + {P_2} - {P_1} + {P_3} - {P_4}}}\bmod {N^2} \end{array} \right. $ | (26) |
否则,
| $ \left\{ \begin{array}{l} {c_{d1}}(k) = {g^{2N\lambda + {P_2} - {P_1} + {P_3} - {P_4}}}\bmod {N^2}\\ {c_{d2}}(k) = {g^{{P_1} - {P_2} + {P_4} - {P_3}}}\bmod {N^2} \end{array} \right. $ | (27) |
由于灰度图像中两个像素值差值的绝对值的取值范围为0~255, 则对于每个2×2分块的统计量d(k)的绝对值的取值范围为0~
| $ {c_{{d_p}}} = {g^{{d_p}}}\bmod {N^2}, {d_p} = 0, 1, ..., 255 \times \frac{{2 \times 2}}{2} + T + G $ | (28) |
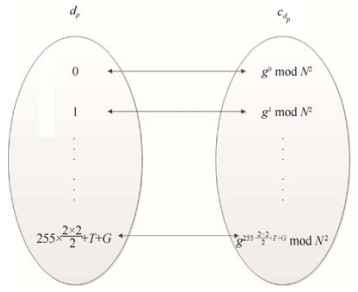
创建一个与dp一一对应的密文映射表cdp如图 4所示.
|
Fig. 4 Mapping table cdp of dp 图 4 dp的密文映射表cdp |
其中, 密文映射表cdp就是对所有统计量可能取值的绝对值dp进行加密后得到的所有密文值的集合.当
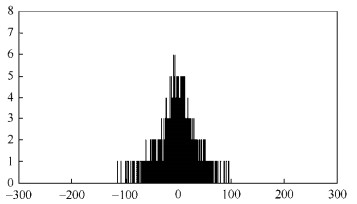
利用MMI方法和查询密文映射表的策略, 对大小为512×512的Lena灰度图像进行8×8分块和加密后得到的密文分块统计量d的直方图分布如图 5所示.
|
Fig. 5 Histogram of statistical values of the encrypted Lena image blocks 图 5 Lena图像分块在加密后的统计量直方图 |
2.2.3 统计量直方图平移
信息隐藏者首先分别选取两个正整数T和G作为嵌入密钥(T, G), 其中, T>dmax, dmax是统计量d中绝对值最大的数, 通常, T和G取为(8×8)/2的倍数.然后计算得到嵌入系数B:
| $ B = \left\lceil {\frac{{(T + G) \times 2}}{{8 \times 8}}} \right\rceil $ | (29) |
其中, 函数
| $ C_w^{(k)}(i, j) = \left\{ \begin{array}{l} {C^{(k)}}(i, j) \cdot {g^B} =\\ {g^{{P^{(k)}}(i, j) + B}} \cdot {r_1}{(k)^N}\bmod {N^2}, {\rm{ if }}\;{d^{(k)}} \in [0, T){\rm{ and}}\bmod {\rm{ }}(i, 2) = \bmod {\rm{ }}(j, 2)\\ {C^{(k)}}(i, j) \cdot {g^B} =\\ {g^{{P^{(k)}}(i, j) + B}} \cdot {r_1}{(k)^N}\bmod {N^2}, {\rm{ if }}\;{d^{(k)}} \in (- T, 0){\rm{ and}}\bmod {\rm{ }}(i, 2) \ne \bmod {\rm{ }}(j, 2)\\ {C^{(k)}}(i, j), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ else}} \end{array} \right. $ | (30) |
其中,
| $ P_w^{(k)}(i, j) = \left\{ \begin{array}{l} {P^{(k)}}(i, j) + B, {\rm{if }}\;{\rm{ }}{d^{(k)}} \in [0, T){\rm{ and}}\bmod {\rm{ }}(i, 2) = \bmod {\rm{ }}(j, 2)\\ {P^{(k)}}(i, j) + B, {\rm{if }}\;{\rm{ }}{d^{(k)}} \in (- T, 0){\rm{ and}}\bmod {\rm{ }}(i, 2) \ne \bmod {\rm{ }}(j, 2)\\ {P^{(k)}}(i, j), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{ else }} \end{array} \right. $ | (31) |
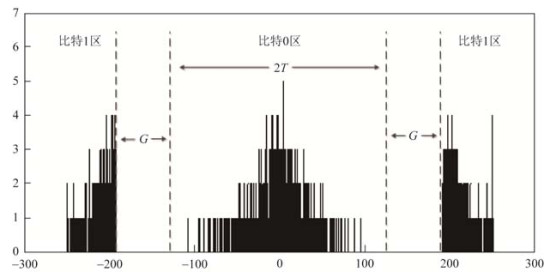
记嵌入水印后的密文分块Cw(k)的统计量为dw(k)嵌入比特0后, dw(k)在范围(-T, T)内, 因此, 称(-T, T)为比特0区; 嵌入比特1后, d(k)发生大小为平移量T+G的改变, 使dw(k)在范围
|
Fig. 6 Histogram of statistical values of the encrypted and watermarked Lena image blocks 图 6 Lena图像在加密和嵌入水印后的分块统计量直方图 |
2.3 信息提取 2.3.1 加密域提取水印和恢复加密图像
与嵌入过程相同, 接收者首先对含有水印的密文图像
| $ {w^{(k)}} = \left\{ {\begin{array}{*{20}{l}} {0,{\rm{if}}\;d_w^{(k)} \in ( - T,T)}\\ {1,\;\;{\rm{else}}} \end{array}} \right. $ | (32) |
通过对统计量dw进行与嵌入过程相反的直方图平移, 可以恢复原加密图像, 方法如下所述.首先根据扩展欧几里德算法求出gB的模乘法逆元
| $ {\theta _{{g^B}}} \cdot {g^B} = 1\bmod {N^2} $ | (33) |
对
| $ {C^{(k)}}(i,j) = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} C_w^{(k)}(i,j) \cdot {\theta _{{g^B}}} = {C^{(k)}}(i,j) \cdot {g^B} \cdot {\theta _{{g^B}}}\;\,\bmod \,\;{N^2},\\ {\rm{if}}\;d_w^{(k)} \in [T + G,2T + G)\;{\rm{and}}\;\,\bmod \,\;(i,2) = \,\bmod \,(j,2) \end{array}\\ \begin{array}{l} C_w^{(k)}(i,j) \cdot {\theta _{{g^B}}} = {C^{(k)}}(i,j) \cdot {g^B} \cdot {\theta _{{g^B}}}\;\,\bmod \,\;{N^2},\\ {\rm{if}}\;d_w^{(k)} \in [ - 2T - G, - T - G)\;{\rm{and}}\;\,\bmod \,{\kern 1pt} (i,2) \ne \;\,\bmod \,\;(j,2) \end{array}\\ {C_w^{(k)}(i,j),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if}}\;d_w^{(k)} \in ( - T,T)} \end{array}} \right. $ | (34) |
其中,
| $ {P^{(k)}}(i,j) = \left\{ {\begin{array}{*{20}{l}} {P_w^{(k)}(i,j) - B,{\rm{if}}\;{d^{(k)}} \in [T + G,2T + G)\;{\rm{and}}\,\bmod \;\,(i,2) = \,\bmod \,(j,2)}\\ {P_w^{(k)}(i,j) - B,{\rm{if}}\;{d^{(k)}} \in [ - 2T - G, - T - G)\;{\rm{and}}\,\bmod \;\,(i,2) \ne \,\bmod \,(j,2)}\\ {P_w^{(k)}(i,j),\;\;\;\;\;\;{\rm{if}}\;{d^{(k)}} \in ( - T,T)} \end{array}} \right. $ | (35) |
处理的结果使统计量
接收者在有私钥λ和嵌入密钥(T, G)的情况下, 可以对含有水印的密文图像E[Iw]进行解密后提取水印和恢复原始图像.利用λ对E[Iw]进行解密, 解密的过程如第1节所述, 记解密后的结果为Iw.首先对Iw进行8×8分块, 则第k个8×8的含水印的明文分块为
解密后含水印的图像在传递过程中可能会受到图像处理或干扰.通过将水印嵌入到分块的统计直方图, 水印算法对常见的图像处理操作(JPEG/JPEG 2000压缩和高斯噪声等)具有一定的鲁棒性.如图 6所示, 比特0区和比特1区间隔着大小为G的鲁棒区间.因此, 当解密后含水印的图像受到一定程度的图像处理或操作后, 虽然造成了分块统计量d小范围的变动但在未进入错误区间时, 接收方仍能正确提取水印.为了提高水印图像在遭受干扰或处理后提取水印的正确率, 参照文献[11, 24]的算法思路, 本文采用3种提取方案和多数投票系统策略来最终判定提取的水印比特.
提取方案 1.
| $ {w_1}^{(k)} = \left\{ \begin{array}{l} 0, {\rm{ if }}\;{d_w}^{(k)} \in ( - T, T)\\ 1, {\rm{ otherwise}} \end{array} \right. $ | (36) |
提取方案 2.重新定义比特0区为
| $ {w_2}^{(k)} = \left\{ \begin{array}{l} 0, \;\;{\rm{ if }}\;{d_w}^{(k)} \in ( - T - G/3, T + G/3)\\ 1, \;\;{\rm{ otherwise}} \end{array} \right. $ | (37) |
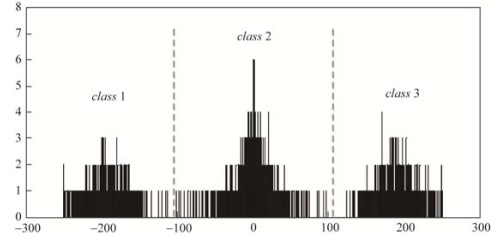
提取方案 3.利用k-means聚类[12]来提取水印比特.图 7为经过JPEG 2000压缩后分块统计量的直方图分布, 可以看出, 图像处理后分块统计量的分布大致分为3类, 分别为class 1、class 2和class 3, 则水印的提取为
| $ {w_3}^{(k)} = \left\{ {\begin{array}{*{20}{c}} {0, {\rm{ }}\;{\rm{if}}\;{d_w}^{(k)} \in class\;2\;\;\;\;\;\;\;\;\;\;\;\;\;\;}\\ {1, {\rm{ }}\;{\rm{if}}\;{d_w}^{(k)} \in \;class\;1\;{\rm{or}}\;class\;3\;} \end{array}} \right. $ | (38) |
|
Fig. 7 Histogram of statistical values of the watermarked blocks under JPEG 2000 compression 图 7 经过JPEG 2000压缩后分块统计量的直方图 |
最终通过多数投票系统来判决提取的水印比特, 多数投票判决为
| $ {w^{(k)}} = \left\{ {\begin{array}{*{20}{c}} {{w_1}^{(k)}, \;{\rm{ if}}\;{w_1}^{(k)} = {w_2}^{(k)}\;{\rm{and}}\;{w_1}^{(k)} = {w_3}^{(k)}}\\ {{w_1}^{(k)}, \;{\rm{ if}}\;{w_1}^{(k)} = {w_2}^{(k)}\;{\rm{and}}\;{w_1}^{(k)} \ne {w_3}^{(k)}}\\ {{w_2}^{(k)}, \;{\rm{ if}}\;{w_1}^{(k)} \ne {w_2}^{(k)}\;{\rm{and}}\;{w_2}^{(k)} = {w_3}^{(k)}}\\ {{w_3}^{(k)}, \;{\rm{ if}}\;{w_1}^{(k)} \ne {w_2}^{(k)}\;{\rm{and}}\;{w_1}^{(k)} = {w_3}^{(k)}} \end{array}} \right. $ | (39) |
在图像未受到干扰或处理的情况下, 公式(32)和3种提取投票系统的方案均可无损地提取水印.而在图像受到干扰或处理的情况下, 3种提取投票系统提取水印的准确率更高.因此, 本文采用3种提取方案和多数投票系统作为水印提取的方案.
2.4 溢出处理在加密域中嵌入水印后, 密文值的改变相当于其相应的明文值加上了一个大小为嵌入系数B的值, 改变后的明文值可能会超出灰度图像中像素值的范围[0, 255], 则解密后可能会出现溢出问题.E[Iw]解密后的结果Iw中值的分布有3种类型:类型1, 值在范围[0, 255]内; 类型2, 值在范围[B, 255+B]内; 类型3, 值在范围[0, 255+B]内.类型1没有溢出问题, 而类型2和类型3出现了溢出问题, 本文参照文献[11]中的算法思路, 做出相应处理.
分块统计量具有特殊性, 对于任意一个分块中的所有值加上或减去一个值, 分块统计量的值不变.因此, 对于类型2, 可以将Iw中
对于类型3, 首先统计Iw中的值属于范围[0, B]和[255, 255+B]的数量.如果值属于范围[0, B]的数量少于[255, 255+B]的数量, 则把这种类型记为类型3.1.然后把值属于范围[0, B]的位置信息标记下来, 并将全部标记位置上的值加上B, 则类型3.1转换为类型2, 然后可以再转换为类型1.最后用一种低失真的可逆水印的方案将这些标记位置信息作为附加信息嵌入图像当中得到
对于自然图像, 像素的灰度值集中于[25, 230]的范围内, 所以在一般情况下, 只要嵌入系数B的取值适当, 图像在嵌入水印后很少会出现溢出问题, 并且在绝大多数情况下不会出现类型3.根据本文的溢出处理方案, 有效地解决了可能发生的溢出情况.
3 实验结果及分析实验中首先给出以Lena图像作为载体的实验结果来验证本文算法的可行性.本文采用峰值信噪比PSNR(peak signal to noise ratio)来衡量解密后含水印的图像质量, 其值越高, 则表示嵌入水印的不可感知性越强, 图像的质量越好.假设I代表原始图像, I'代表解密后含水印的图像, (i, j)表示图像像素坐标, 则PSNR的计算公式为
| $ PSNR = 10 \times \lg \frac{{h \times w \times {{255}^2}}}{{\sum\limits_{i = 1}^h {\sum\limits_{j = 1}^w {{{[I(i, j)-I'(i, j)]}^2}} } }} $ | (40) |
其中, h和w代表图像的尺寸,

|
Fig. 8 Watermark embedding and extraction testing results with Lena 图 8 以Lena图像为载体的水印嵌入和提取测试 |
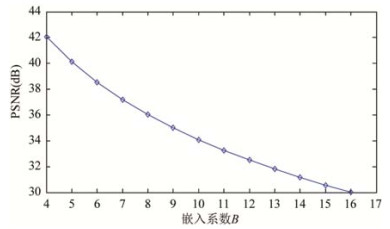
为了更进一步地评估本文算法的性能, 实验选取了如图 9所示的8幅大小为512×512的8比特灰度图像作为载体进行测试.实验中对8幅载体图像进行8×8分块, 嵌入的水印信息为4 096比特的伪随机系列.加密域嵌入水印后, 密文值的改变相当于其相应的明文值加上了一个大小为嵌入系数B的值, 因此, B直接影响到解密后图像的质量.随着B的增大, 相应的失真就越大, 导致PSNR降低.经过测试, 当8幅图像以相同的B嵌入水印时, 解密后图像的PSNR值基本相同, 嵌入系数B和PSNR值的关系如图 10所示.由图 10可知, 当B为16时, 图像的PSNR略大于30dB, 基于不可觉察度的考虑, 为了获得较好的图像质量, 本文设定最大嵌入系数Bmax=16, 即B的值不能超过16.

|
Fig. 9 Eight standard example images 图 9 8幅标准测试图像 |
|
Fig. 10 Relationship between embedding strength B and PSNR value 图 10 嵌入强度B和PSNR值的关系 |
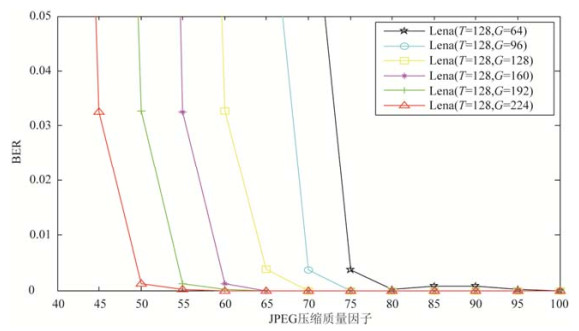
由图 6可知, 比特0区和比特1区间隔着大小为G的鲁棒区间, G越大, 则鲁棒性越强.但是, G越大会使嵌入系数B随之增大, 导致PSNR值有所降低.因此, 实际中可根据需要调节阈值G, 若需要更强的鲁棒性, 可以选择较大的阈值G; 若需要水印图像质量更好, 则可选择较小的阈值G.在JPEG压缩鲁棒性实验中, 我们采用了ACDsee 14.0软件对解密后含水印的图像进行JPEG压缩.如图 11所示, 随着压缩质量因子数值的降低(表示压缩强度逐渐增大), 提取水印的比特误差率BER逐渐升高.在同样的压缩强度下, BER随着阈值G的增大而降低, 说明随着阈值G的增大, 嵌入强度增加, 水印对JPEG压缩的鲁棒性增强.
|
Fig. 11 Effection of the value G on the robustness to JPEG compression 图 11 阈值G对水印抗JPEG压缩的影响 |
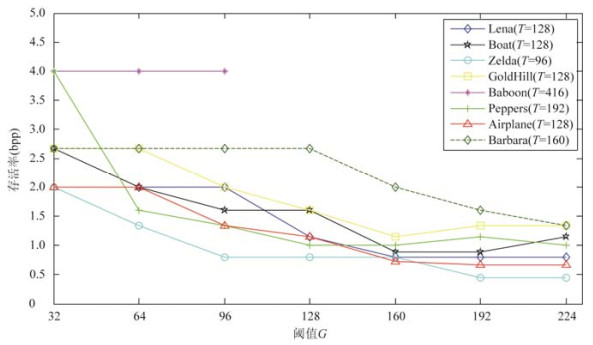
我们采用ACDsee 14.0软件对解密后的水印图像进行JPEG 2000压缩, 采用存活率(surviving bit rate)来衡量水印算法对JPEG 2000压缩的鲁棒性.存活率与最大压缩率的关系为:存活率=8/最大压缩率, 即存活率越小, 其压缩倍数越大, 鲁棒性越强.图 12所示为在不同阈值G下能够正确提取水印的最小存活率, 即在该阈值下, 若存活率高于对应的存活率, 即当压缩率更低时, 能够完全正确地提取水印.由图 12可知, 随着阈值G的增大, 最小存活率减小, 即水印对抗JPEG 2000压缩的鲁棒性增强.
|
Fig. 12 Effection of the value G on the robustness to JPEG 2000 compression 图 12 阈值G对水印抗JPEG 2000压缩的影响 |
为了测试本文算法对其他图像处理操作的鲁棒性, 本文采用MATLAB软件来对水印图像添加高斯噪声和椒盐噪声.表 1给出了8幅测试图像在设定的参数下, 嵌入4 096比特水印后的解密图像在受到不同图像处理操作后提取水印的比特误差率(BER)(%).嵌入系数B设定为16.从表 1可以看出, 对于质量因子为25的JPEG压缩, 除了Baboon图像外, BER均小于1%;对于存活率为0.67bpp的JPEG 2000压缩, 除了Baboon和Barbara图像外, BER均小于1%;对于方差为0.005的高斯噪声, 除了Baboon图像外, BER均约为5%;对于方差为0.01的椒盐噪声, 除了Baboon图像外, BER均小于5%.与其他测试图像相比, 水印以Baboon图像为载体性能较差的主要原因是Baboon图像的纹理比较复杂, 8×8分块后的dmax=388, 需要设定T=416, 即使设定G=0都会使嵌入系数B=13, 因此图像的失真较大.在本文设定的最大嵌入系数Bmax=16条件下, G最大只能取为96, 因此鲁棒性较差.由此可知, 本文算法对于比较平滑的图像有较好的性能.
| Table 1 Robustness of the proposed method against several image processing operations 表 1 本文水印算法在几种常见图像处理操作下的鲁棒性 |
由于每个密文分块都可以嵌入1比特水印, 所以图像进行分块的尺寸越小, 则嵌入容量越大.对于大小为h×w的图像并且分块大小为m×n的最大嵌入容量为[h/w]×[w/n].其中, 函数
| $ B = \left\lceil {\frac{{(T + G) \times 2}}{{m \times n}}} \right\rceil \ge \left\lceil {\frac{{(128 + G) \times 2}}{{4 \times 4}}} \right\rceil \ge 16 $ | (41) |
设T为128, 只有当G取0时, B=16才能满足本文设定的Bmax=16.为了衡量嵌入容量和图像失真以及鲁棒性的关系, 给出Lena图像以不同分块尺寸嵌入最大嵌入容量的性能, 见表 2.在不超出最大嵌入系数Bmax=16的情况下, 除分块尺寸为4×4在JPEG压缩因子为100时提取水印BER=4.52%、存活率为4时提取水印BER=3.89%, 其他分块尺寸下的JPEG压缩因子和存活率都是在给定参数下能够正确地提取水印的最小JPEG压缩因子和存活率, 并且G是能正确提取水印的最小阈值.由表 2可知, 若分块尺寸越大, 则最大嵌入容量越小, 并且图像的失真越小, 鲁棒性越强.经过实验测试, 其结果表明, 8×8分块在嵌入容量、图像失真和鲁棒性之间有较好的平衡性.
| Table 2 The performance of Lena image in different block sizes 表 2 Lena图像不同分块尺寸的性能 |
目前, 在文献中尚未有有效的加密域图像鲁棒可逆水印算法的报道, 因此无法将本文提出的同态加密域图像鲁棒可逆水印算法与前人的研究结果进行公平对比.为了进一步说明本文算法的鲁棒性, 我们与前期具有代表性的一种明文域图像鲁棒可逆水印算法[10]进行了性能比较.测试中, 使用相同的载体进行8×8分块嵌入相同的水印容量, 本文算法与文献[10]中Ni算法的鲁棒性比较见表 3.由表 3可知, 除了Baboon图像以外, 本文算法的图像质量和鲁棒性都优于文献[10].值得一提的是, 本文算法是在加密域中嵌入水印, 可以更好地在云端保护用户的数据隐私, 相比文献[10]以及其他在明文域嵌入鲁棒可逆水印的方案, 本文算法更加适用于当下大数据背景下的云计算安全领域.
| Table 3 Performance comparison of the proposed method against the Ni's method in Ref.[10] 表 3 与文献[10]中Ni算法的鲁棒性能比较 |
4 结论
加密域鲁棒可逆水印技术通过加密手段来保护数据在云端的隐私, 通过可逆水印来实现对敏感载体的完整性认证并通过鲁棒水印来进行保护数据在解密后的版权.通过结合Paillier加密系统、构造统计量和直方图平移技术, 本文提出了一种新的同态加密域图像鲁棒可逆水印算法.为了保护数据在云端的隐私并允许对密文数据进行算术操作, 数据在上传云端之前进行同态加密.为了能在云端的加密数据中嵌入水印, 对图像采用了分块加密和在加密域中构造分块统计量, 并结合Paillier加密系统的同态特性来实现基于统计量直方图平移的水印嵌入.算法的关键在于密文分块统计量的构造、模乘法逆元MMI方法的运用、利用同态特性构建密文映射表和嵌入水印, 使得在加密域中可以获得统计量直方图进行水印嵌入.
在本文中, 我们对水印算法在加密域和明文域的提取和图像的恢复进行了详细分析, 并对可能出现的溢出情况给出了处理方案.最后在实验部分, 我们选择一些标准的例子图像来测试算法的可逆性和鲁棒性.实验结果表明:(1)水印算法的嵌入失真较小, 具有良好的保真性; (2)水印算法是可逆的, 在未受到攻击的情况下水印能分别在加密域和明文域提取并且原始密文图像或原始明文图像能够无损恢复; (3)水印具有良好的鲁棒性, 解密后的含水印图像在经受一定的图像处理操作下仍能正确地提取水印.在云计算大数据背景下, 由于同态加密域鲁棒可逆水印技术在隐私保护和数据安全上的潜在应用前景, 本文算法具有很好的理论研究意义和实用
| [1] |
Honsinger CW, Jones P, Rabbani M, Stoffel JC. Lossless recovery of an original image containing embedded data. Int'l Cl: G06K 9/00 US 6278791 B1, 2001-08-21. |
| [2] |
Feng JB, Lin IC, Tsai CS, Chu YP. Reversible watermarking:current status and key issues. Int'l Journal of Network Security, 2006, 2(3): 161–171.
http://dblp.uni-trier.de/db/journals/ijnsec/ijnsec2.html#FengLTC06 |
| [3] |
Celik MU, Sharma G, Tekalp AM, Saber E. Lossless generalized-LSB data embedding. IEEE Trans. on Image Processing, 2005, 14(2): 253–266.
[doi:10.1109/TIP.2004.840686] |
| [4] |
Tian J. Reversible data embedding using a difference expansion. IEEE Trans. on Circuits and Systems for Video Technology, 2003, 13(8): 890–896.
[doi:10.1109/TCSVT.2003.815962] |
| [5] |
Ni ZC, Shi YQ, Ansari N, Su W. Reversible data hiding. IEEE Trans. on Circuits and Systems for Video Technology, 2006, 16(3): 354–362.
[doi:10.1109/TCSVT.2006.869964] |
| [6] |
Li XL, Yang B, Zeng TY. Efficient reversible watermarking based on adaptive prediction-error expansion and pixel selection. IEEE Trans. on Image Processing, 2011, 20(12): 3524–3533.
[doi:10.1109/TIP.2011.2150233] |
| [7] |
Vleeschouwer CD, Delaigle JE, Macq B. Circular interpretation of histogram for reversible watermarking. In: Proc. of the IEEE Workshop of Multimedia Signal Process. 2001. 345-350. [doi: 10.1109/MMSP.2001.962758] |
| [8] |
Vleeschouwer CD, Delaigle JE, Macq B. Circular interpretation of bijective transformations in lossless watermarking for media asset management. IEEE Trans. on Multimedia, 2003, 5(1): 97–105.
[doi:10.1109/TMM.2003.809729] |
| [9] |
Zou D, Shi YQ, Ni Z, Su W. A semi-fragile lossless digital watermarking scheme based on integer wavelet transform. IEEE Trans. on Circuits and Systems for Video Technology, 2006, 16(10): 1294–1300.
[doi:10.1109/TCSVT.2006.881857] |
| [10] |
Ni Z, Shi YQ, Ansari N, Su W, Sun Q, Lin X. Robust lossless image data hiding designed for semi-fragile image authentication. IEEE Trans. on Circuits and Systems for Video Technology, 2008, 18(4): 890–896.
[doi:10.1109/TCSVT.2008.918761] |
| [11] |
Zeng XT, Ping LD, Pan XZ. A lossless robust data hiding scheme. Pattern Recognition, 2010, 43(4): 1656–1667.
[doi:10.1016/j.patcog.2009.09.016] |
| [12] |
An L, Gao X, Li X, Tao D, Deng C, Li J. Robust reversible watermarking via clustering and enhanced pixel-wise masking. IEEE Trans. on Image Processing, 2012, 21(8): 3598–3611.
[doi:10.1109/TIP.2012.2191564] |
| [13] |
Thabit R, Khoo BE. Capacity improved robust lossless image watermarking. IET Image Processing, 2014, 8(11): 662–670.
[doi:10.1049/iet-ipr.2013.0862] |
| [14] |
Feng DG, Zhang M, Zhang Y, Xu Z. Study on cloud computing security. Ruan Jian Xue Bao/Journal of Software, 2011, 22(1): 71-83(in Chinese with English abstract). http://www.jos.org.cn/1000-9825/3958.htm[doi: 10.3724/SP.J.1001.2011.03958] |
| [15] |
Zhang XP. Reversible data hiding in encrypted image. IEEE Signal Processing Letters, 2011, 18(4): 255–258.
[doi:10.1109/LSP.2011.2114651] |
| [16] |
Zhang XP. Separable reversible data hiding in encrypted image. IEEE Trans. on Information Forensics and Security, 2012, 7(2): 826–832.
[doi:10.1109/TIFS.2011.2176120] |
| [17] |
Chen YC, Shiu CW, Horng G. Encrypted signal-based reversible data hiding with public key cryptosystem. Journal of Visual Communication and Image Representation, 2014, 25: 1164–1170.
[doi:10.1016/j.jvcir.2014.04.003] |
| [18] |
Zhang XP, Long J, Wang Z, Cheng H. Lossless and reversible data hiding in encrypted images with public key cryptography. IEEE Trans. on Circuits and Systems for Video Technology, 2016, 26(9): 1622–1631.
[doi:10.1109/TCSVT.2015.2433194] |
| [19] |
Xiang SJ, Luo XR, Shi SX. A novel reversible image watermarking algorithm in homomorphic encrypted domain. Chinese Journal of Computers, 2016, 39(3): 571–581(in Chinese with English abstract).
[doi:10.11897/SP.J.1016.2016.00571] |
| [20] |
Xiang SJ, Luo XR. Reversible data hiding in encrypted image based on homomorphic public key cryptosystem. Ruan Jian Xue Bao/Journal of Software, 2016, 27(6): 1592-1601(in Chinese with English abstract). http://www.jos.org.cn/1000-9825/5007.htm[doi: 10.13328/j.cnki.jos.005007] |
| [21] |
Paillier P. Public-Key cryptosystems based on composite degree residuosity classes. In: Proc. of the Int'l Conf. on the Theory and Application of Cryptographic Techniques Prague. 1999. 233-238. [doi: 10.1007/3-540-48910-X_16] |
| [22] |
Zheng PJ, Huang JW. Discrete wavelet transform and data expansion reduction in homomorphic encrypted domain. IEEE Trans. on Image Processing, 2013, 22(6): 2455–2468.
[doi:10.1109/TIP.2013.2253474] |
| [23] |
Donald K. The Art of Computer Programming, Volume 2. 3rd ed.. Addison-Wesley, 1997: 325–515.
https://www.bibsonomy.org/bibtex/2ee3f7d70febf87bc4d3b49640d9baa20/eutrimer |
| [24] |
Xiang SJ, Yang L, Wang Y. Robust and reversible audio watermarking by modifying statistical features in time domain. Advances in Multimedia, 2017, 2017(3): 1–10.
[doi:10.1155/2017/8492672] |
| [14] |
冯登国, 张敏, 张研, 徐震. 云计算安全研究. 软件学报, 2011, 22(1): 71-83. http://www.jos.org.cn/1000-9825/3958.htm[doi: 10.3724/SP.J.1001.2011.03958]
|
| [19] |
项世军, 罗欣荣, 石书协. 一种同态加密域图像可逆水印算法. 计算机学报, 2016, 39(3): 571–581.
[doi:10.11897/SP.J.1016.2016.00571]
|
| [20] |
项世军, 罗欣荣. 基于同态公钥加密系统的图像可逆信息隐藏算法. 软件学报, 2016, 27(6): 1592-1601. http://www.jos.org.cn/1000-9825/5007.htm[doi: 10.13328/j.cnki.jos.005007]
|
 2018, Vol. 29
2018, Vol. 29


