2. 中国科学院 计算技术研究所 智能信息处理重点实验室, 北京 100190
2. Key Laboratory of Intelligent Information Processing, Institute of Computing Technology, The Chinese Academy of Sciences, Beijing 100190, China
从监督学习的角度看, 深度学习模型在解决分类问题时可以看作是一种多层感知器.从误差曲面上看, 神经网络收敛的位置取决于权值的初始化值.在这种情况下, 如果权值是随机生成的, 那么权值可能初始化在误差曲面中比较差的位置上, 此时, 使用BP算法来训练神经网络将会得到比较差的局部最优解.深度学习可以有效地缓解这个问题.通过无监督的预训练过程, 神经网络可以调整权值初始化的位置, 有助于收敛到更好的局部最优解[1].
自深度学习提出以来, 便在学术界和工业界引起了广泛的关注.基于RBM(restricted Boltzmann machine)的DBN(deep belief net)模型是深度学习领域中的经典模型之一.RBM是一种无监督的模型, 该模型用于表达输入数据的分布规律[2-4], RBM的数学基础是概率图模型, 许多有效的方法可以用来训练RBM, 例如对比散度算法(CD)、持续的马尔可夫链(persistent Markov chain)、均匀场方法(mean field method)等.在RBM的基础上, Hinton等人在2006年提出了DBN模型[5].DBN模型通过无监督的逐层初始化, 为多层神经网络提供了一种有效的预训练方法[6].基于DBN和RBM模型, 许多研究成果被提了出来.Lee等人将RBM和卷积神经网络(CNN)相结合, 提出了一种卷积深度置信网(convolutional deep belief network)[7, 8], 为CNN的训练提供了一种有效的逐层初始化方法.基于RBM, 另一个经典的模型是深度玻尔兹曼机(DBM)[9].相比于DBN模型, DBM模型在图像的识别和重构方面十分有效[10].RBM的应用范围还包括语音识别领域, 结合递归神经网络(RNN)和RBM模型, 神经网络在语音识别中同样取得了出色的效果[11, 12].与此同时, 还有许多其他的模型可以被用于深度学习中, 例如自动编码器(AE)、极限学习机(ELM)等[13-15].
然而, 在上述的深度模型中依然存在一些不足, 其中, 过拟合问题是模型训练中常见的问题.为了防止神经网络的过拟合, 许多方法被相继提出, 其中, Dropout方法可以被使用在RBM模型中[16].然而, 通过实验我们发现: Dropout方法虽然在分类精度上取得了明显的提升, 但是Dropout RBM的图像重构能力相比于传统RBM有所下降.为了解决这个问题, 我们尝试在RBM模型中引入随机变量来替代实值变量.Weight uncertainty方法将权值随机变量引入到传统的BP算法中, 在训练神经网络时取得了比较出色的效果[17].在Weight uncertainty方法中, 通过把权值看作随机变量, 整个神经网络可以看作是一组网络的集成, 其中, 权值是服从高斯分布的随机变量.从降噪的观点上看, Dropout方法和权值随机变量均达到了非常类似的效果, 权值随机变量相当于对神经网络加入噪声, 算法训练的过程同时也是降噪的过程.在实验部分, 我们首先将权值随机变量应用到RBM中, 测试了其分类能力和图像重构能力.然后, 我们构造了WDBN模型和WDBM模型, 并与基于Dropout方法的DBN模型进行了比较.为了进一步提高模型对图像的建模能力, 我们希望更好地建模像素点之间的相关性, 因此, 我们将条件高斯分布的思想引入到模型中, 通过使用spike-and-slab Boltzmann Machine(ssRBM)模型, 并对能量函数进行微调, 最后将其作为特征提取器, 构建了相应的深度模型, 并通过实验验证了其有效性.
1 受限的玻尔兹曼机RBM是基于能量函数的, 该模型由一个可见层
| $ E(\vec{v}, \vec{h})=-\sum\limits_{i=1}^{{{n}_{v}}}{{{a}_{i}}{{v}_{i}}}-\sum\limits_{j=1}^{{{n}_{h}}}{{{b}_{j}}{{h}_{j}}}-\sum\limits_{i=1}^{{{n}_{v}}}{\sum\limits_{j=1}^{{{n}_{h}}}{{{h}_{j}}\times {{W}_{ji}}\times {{v}_{i}}}} $ | (1) |
其中,
| $ P(\vec{v}, \vec{h})=\frac{1}{Z}{{\text{e}}^{-E(\vec{v}, \vec{h})}} $ | (2) |
其中, Z表示配分函数(partition function):
| $ Z=\sum\limits_{v, h}{{{\text{e}}^{-E(\vec{v}, \vec{h})}}} $ | (3) |
我们的目标是使得概率分布函数
| $ P(\vec{v})=\sum\limits_{h}{P(\vec{v}, \vec{h})}=\frac{1}{Z}\sum\limits_{h}{{{\text{e}}^{-E(\vec{v}, \vec{h})}}} $ | (4) |
极大似然函数定义如下:
| $ {{L}_{s}}=\ln \prod\limits_{i=1}^{{{n}_{s}}}{P({{{\vec{v}}}^{(i)}})}=\sum\limits_{i=1}^{{{n}_{s}}}{\ln P({{{\vec{v}}}^{(i)}})} $ | (5) |
其中, ns是样本数.这里, 我们使用梯度上升方法来最大化似然函数.首先, 以一个样本为例对计算过程进行说明.
首先, 计算似然函数的偏导数, 令
| $ \frac{\partial \ln P(V)}{\partial \theta }=-\sum\limits_{h}{P(\vec{h}|V)}\frac{\partial E(V, \vec{h})}{\partial \theta }+\sum\limits_{v, h}{P(\vec{v}, \vec{h})}\frac{\partial E(\vec{v}, \vec{h})}{\partial \theta } $ | (6) |
其中, V表示一个输入样本, θ是要学习的参数.在RBM模型中, 当某一层的节点状态给定时, 另一层节点的激活是相互独立的, 因此有:
| $ p({{h}_{k}}=1|\vec{v})=sigmoid\left( {{b}_{k}}+\sum\limits_{i=1}^{{{n}_{v}}}{{{W}_{ki}}{{v}_{i}}} \right) $ | (7) |
| $ p({{v}_{k}}=1|\vec{h})=sigmoid\left( {{a}_{k}}+\sum\limits_{j=1}^{{{n}_{h}}}{{{h}_{j}}{{W}_{kj}}} \right) $ | (8) |
其中, hk是
Hinton等人在极大似然估计的基础上, 提出了一种对比散度(contrastive divergence, 简称CD)算法来近似求解偏导数[18]:
| $ \frac{\partial \ln P(\vec{v})}{\partial {{W}_{ij}}}\approx P({{h}_{j}}=1|{{\vec{v}}^{(0)}})\vec{v}_{i}^{(0)}-P({{h}_{j}}=1|{{\vec{v}}^{(k)}})\vec{v}_{i}^{(k)} $ | (9) |
| $ \frac{\partial \ln P(\vec{v})}{\partial {{a}_{i}}}\approx v_{i}^{(0)}-v_{i}^{(k)} $ | (10) |
| $ \frac{\partial \ln P(\vec{v})}{\partial {{b}_{i}}}\approx P({{h}_{i}}=1|{{\vec{v}}^{(0)}})-P({{h}_{i}}=1|{{\vec{v}}^{(k)}}) $ | (11) |
其中, k是K步对比散度算法(K-steps contrastive divergence algorithm, 简称CD-K)中的步数,
| $ \text{ }\!\!\Delta\!\!\text{ }{{W}_{ij}}=\eta (P({{h}_{i}}=1|{{\vec{v}}^{(0)}}){{\vec{v}}^{(0)}}-P({{h}_{i}}=1|{{\vec{v}}^{(k)}}){{\vec{v}}^{(k)}}) $ | (12) |
| $ \text{ }\!\!\Delta\!\!\text{ }{{a}_{i}}=\eta (v_{i}^{(0)}-v_{i}^{(k)}) $ | (13) |
| $ \text{ }\!\!\Delta\!\!\text{ }{{b}_{i}}=\frac{\partial \ln P(\vec{v})}{\partial {{b}_{i}}}\approx \eta (P({{h}_{i}}=1|{{\vec{v}}^{(0)}})-P({{h}_{i}}=1|{{\vec{v}}^{(k)}})) $ | (14) |
其中, 参数η是学习率.
当输入是实值数据时, 我们重新定义如下能量函数:
| $ E(\vec{v}, \vec{h})=\sum\limits_{i=1}^{{{n}_{v}}}{\frac{{{({{v}_{i}}-{{a}_{i}})}^{2}}}{2\sigma _{i}^{2}}}-\sum\limits_{j=1}^{{{n}_{h}}}{{{b}_{j}}{{h}_{j}}}-\sum\limits_{i=1}^{{{n}_{v}}}{\sum\limits_{j=1}^{{{n}_{h}}}{\frac{{{v}_{i}}}{{{\sigma }_{i}}}{{W}_{ji}}{{h}_{j}}}} $ | (15) |
其中, σ表示对角的协方差矩阵.那么, 隐藏层的激活概率可以写成如下形式:
| $ P({{h}_{k}}=1|\vec{v})=sigmoid\left( {{b}_{k}}+\sum\limits_{i=1}^{{{n}_{v}}}{{{W}_{ki}}{{v}_{i}}} \right) $ | (16) |
可见层的激活概率服从高斯分布, 如下表示:
| $ P(\vec{v}|\vec{h})=\prod\limits_{i=1}{\frac{1}{{{\sigma }_{i}}\sqrt{2\text{ }\!\!\pi\!\!\text{ }}}{{\text{e}}^{-\frac{1}{2\sigma _{i}^{2}}{{\left( {{v}_{i}}-{{a}_{i}}-{{\sigma }_{i}}\sum\nolimits_{j=1}{{{h}_{j}}{{W}_{ij}}} \right)}^{2}}}}} $ | (17) |
此时的RBM又被称为高斯RBM, 也叫均值RBM[19].
2 RBM与BM的训练算法关于RBM的训练算法有很多, 早期Hinton等人使用持续的马尔可夫链和模拟退火方法来逼近数据独立期望和数据依赖期望.目前, 针对退火、回火算法的研究仍在进行[20, 21].虽然使用退火和回火算法可以有效地逼近似然函数, 但是退火、回火算法的计算复杂性比较高, 因此在处理较大数据时比较困难.另一方面, 为了缩短RBM的训练时间, 均匀场方法被提出以替换Gibbs采样[22].在均匀场方法中, 隐藏层节点使用实值概率作为其状态值, 该方法有助于把RBM作为神经网络来训练和解释.但在实践中, 以均匀场为代表的变量方法并不适合逼近数据独立性期望.2002年, Hinton提出了对比散度算法, 这种方法虽然在迭代步长上不够准确, 但却保证了梯度方向的正确性, 并且具有较快的训练速度.随后, 在CD算法的基础上, PCD算法及其改进FPCD算法被提了出来[23, 24].在DBM的训练中, Salakhutdinov使用均匀场方法来逼近数据依赖性期望, 使用持续的马尔可夫链逼近数据独立性期望, 取得了良好的效果.
2.1 均匀场方法在概率图模型中, 均匀场推理使用一个近似的后验分布Q(h|v; λ)来替换真实的后验分布P(h|v; θ).即, 选择一个特殊的后验分布Q(h|v; λ)来最小化如下KL散度:
| $ {{\lambda }^{*}}=\underset{\lambda }{\mathop{\arg \min }}\, KL[Q(h|v)||P(h|v)] $ | (18) |
其中, KL散度定义为
对于概率函数P(v), 有:
| $ \ln P(v)=\ln \sum\limits_{h}{P(h, v)}=\ln \sum\limits_{h}{Q(h|v)\frac{P(h, v)}{Q(h|v)}}\ge \sum\limits_{h}{Q(h|v)\ln \left( \frac{P(h, v)}{Q(h|v)} \right)} $ | (19) |
对于均匀场玻尔兹曼机, 有:
| $ Q(h|v, u)=\prod\limits_{i\in H}{{{u}^{{{S}_{i}}}}{{(1-{{u}_{i}})}^{1-{{S}_{i}}}}} $ | (20) |
那么, KL散度可以写成:
| $ KL[Q||P]=\sum\limits_{i}{({{u}_{i}}\ln {{u}_{i}}+(1-{{u}_{i}})\ln (1-{{u}_{i}}))}-\sum\limits_{i<j}{{{\theta }_{ij}}{{u}_{i}}{{u}_{j}}}-\sum\limits_{i}{\theta _{i}^{c}{{u}_{i}}}+\ln {{Z}_{c}} $ | (21) |
其中, Zc是配分函数,
| $ \ln P(v;\theta )\ge \sum\limits_{i, j}{{{W}_{ij}}{{v}_{i}}{{u}_{j}}}+\sum\limits_{i}{{{b}_{i}}{{v}_{i}}}-\ln Z-\sum\limits_{j}{({{u}_{j}}\ln {{u}_{j}}+(1-{{u}_{j}})\ln (1-{{u}_{j}}))} $ | (22) |
隐藏层变量的激活值可以表示为
| $ {{u}_{i}}=sigmoid\left( \sum\limits_{j}{{{W}_{ij}}{{v}_{j}}+{{b}_{i}}} \right) $ | (23) |
持续的马尔可夫链又称为随机逼近算法, 是一种利用马尔可夫链进行分块Gibbs采样的算法.只要马尔可夫链足够长, 更新步长不太大, 马尔可夫链就可以达到稳态.持续的马尔可夫链可以有效地逼近数据独立性期望.在RBM模型中, 对于每一个样本
算法的步骤见表 1.
| Table 1 Algorithm of persistent Markov chains 表 1 持续的马尔可夫链算法步骤 |
3 深度置信网与深度玻尔兹曼机 3.1 深度置信网
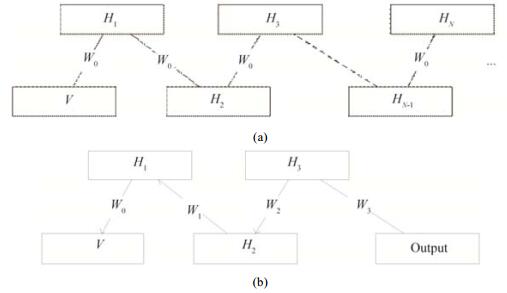
DBN是一种混合的图模型, 其顶端的两层是无向图, 用来表示关联记忆.余下的层是一个有向图, 构成一个置信网.DBN的训练是一个贪婪的逐层初始化的过程, 首先, 假设DBN是一个无限多层的模型, 而且每一层的节点数相同, 那么使用相同的权值W0来初始化整个网络, 此时, 该模型的训练可以看作是训练一个单层的RBM, 训练结束后, 固定第1层的权值W0不变, 其余层的权值使用W1来替换, 然后训练剩余的网络.在这种情况下, 先验信息会随着每一层的训练而不断更新.Hinton等人证明:在这种情况下, 每一次RBM的贪婪预训练都可以收紧变量边界, 也就是说, lnp(v|W1, W2)≥lnp(v|W1).预训练过程如图 1所示, 其中, 图 1(a)表示把DBN看作一个无限层的结构, 并且固定权值为W0, 那么DBN的训练等效于RBM的训练.然后固定第1层权值不变, 并且把V和W0的乘积作为下一个DBN的输入.重复此过程, 最后一层替换为输出层, 便得到图 1(b)所示的模型结构.将该模型的隐藏层按顺序逐层重新组织, 便得到了DBN的神经网络结构.
|
Fig. 1 Shows the diagram of training process in DBN 图 1 DBN训练过程的示意图 |
当完成逐层的预训练之后, 从神经网络的角度来看, 可以使用BP算法对网络进行权值的微调, 此时, 神经网络的各个节点的激活方式要与DBN中各个节点的激活一致.从监督学习的角度来看, 该算法有效地缓解了多层感知器极易陷入较差的局部最优解的情况, 成为深度学习的经典算法.
3.2 深度玻尔兹曼机DBM不同于DBN, 其网络结构仍然是玻尔兹曼机.在DBM的训练中, 每一层节点的激活取决于与该节点相连的上下两层的节点, 可以使用传统的玻尔兹曼机训练算法来训练DBM, 但是效果并不理想.Salakhutdinov指出, 同样可以使用逐层训练的方式初始化DBM.不同于DBN, 在每一层预训练结束后, 不是替换整个先验, 而是按比例进行替换.Salakhutdinov探究了以不同比例替换先验可以取得的不同效果, 以3层的DBM和几何均值为例, 首先对输入层和输出层加倍, 然后加倍第1个隐藏层和第2个隐藏层之间的权值W2.在DBM的预训练过程中, 替换的比例为0.5.DBM与DBN的网络结构如图 2所示.

|
Fig. 2 Structure of DBN and DBM 图 2 DBN和DBM的网络结构图 |
不同于DBN, 在DBM中, 每一个单元的激活都取决于与其直接相连的所有节点, 即, DBM中隐藏层节点的激活取决于其上下两个相邻层.因此, DBM的概率函数可以如下表示(其中, 上标表示层数, 下标表示维度坐标):
| $ p(h_{j}^{1}=1|\vec{v}, {{\vec{h}}^{2}})=sigmoid\left( \sum\limits_{i}{W_{ij}^{1}{{v}_{i}}}+\sum\limits_{m}{W_{jm}^{2}h_{m}^{2}}+b_{j}^{1} \right) $ | (24) |
| $ p(h_{m}^{2}=1|{{\vec{h}}^{1}}, {{\vec{h}}^{3}})=sigmoid\left( \sum\limits_{j}{W_{jm}^{2}h_{j}^{1}}+\sum\limits_{l}{W_{ml}^{3}h_{l}^{3}}+b_{m}^{2} \right) $ | (25) |
| $ p(h_{l}^{3}=1|{{\vec{h}}^{2}})=sigmoid\left( \sum\limits_{m}{W_{ml}^{3}h_{m}^{2}}+b_{l}^{3} \right) $ | (26) |
| $ p({v_i} = 1|{\vec h^1}) = sigmoid\left( {\sum\limits_j {W_{ij}^1h_j^1} + {b_j}} \right) $ | (27) |
对于DBM, 可以使用随机逼近算法和均匀场算法来逼近偏导数.从神经网络的角度看, DBM可以看作是一种多层感知器, 此时, 不同于DBN, 隐藏层单元的激活需要考虑与其相邻的上下两层.
4 基于权值不确定性的深度玻尔兹曼机 4.1 权值不确定性方法在上述算法中, 权值和偏置这两个参数是普通的实值变量, 这种情况下, 神经网络的训练可能会遇到过拟合问题, 在以RBM为基础的网络中, Dropout方法可以有效解决过拟合问题, 有效地实现了多个神经网络的集成, 也可以认为Dropout方法的训练过程是一个消除遮蔽噪声的过程.虽然Dropout RBM是一种非常有效的分类算法, 但是对于图像重构问题而言, 效果并不理想.我们猜测:由于对神经元的遮蔽是随机的, 遮蔽一些节点会使RBM的表达稀疏化, 这种稀疏化也许是导致网络重构图像变差的原因.
为了缓解上述问题, 我们引入随机变量的思想, 将权值看作服从高斯分布的随机变量.只要求得其期望和方差, 那么根据该期望和方差生成的采样权值是相对稳定的.同时, 每一次权值的采样也可以看作是一个子模型的构建过程.因此, 基于权值随机变量的网络模型也可以看作是多个网络的集成.
在Blundell等人的研究中, 对于神经网络模型, 所有的权值都被表示为随机变量.此时, 神经网络的目标函数可以如下表示:
| $ {\theta }'=\underset{\theta }{\mathop{\arg \min }}\, KL[q(W|\theta )||P(W|\theta )]=\\ \underset{\theta }{\mathop{\arg \min }}\, KL[q(W|\theta )||P(W)]-{{E}_{q(w|\theta )}}[\log P(D|W)] $ | (28) |
根据极大后验估计的思想, 令:
| $ f(W, \theta )=\log q(W|\theta )-\log P(W)P(D|W) $ | (29) |
其中, 先验公式可以表达为高斯分布.在RBM中, 为了获得更加出色的图像重构效果和分类效果, 我们引入了权值随机变量, 这样, RBM的代价函数可以写为极大似然估计p(v|W)或者极大后验估计p(W|v)的形式.RBM自身的目标函数为p(v), 同时也是概率图模型的极大似然函数, 因此, 为了方便计算, 减少超参数的数量, 在随机变量的前提下, 我们使用极大似然估计的方法来计算RBM的激活概率.假设权值W是符合高斯分布的, 其均值为μ, 标准差为σ=log(1+exp(ρ)), 假设ε~N(0, I).为了方便计算, 那么权值可以写成W=μ+log(1+exp(ρ))
| $ \frac{\partial \log p({{W}_{ij}})}{\partial {{W}_{ij}}}\times \frac{\partial {{W}_{ij}}}{\partial \mu }=\left( P({{h}_{j}}=1|\vec{v}){{v}_{i}}-\sum\limits_{v, h}{P(v)P({{h}_{j}}=1|\vec{v}){{v}_{i}}} \right)\times 1 $ | (30) |
| $ \frac{\partial \log p({{W}_{ij}})}{\partial {{W}_{ij}}}\times \frac{\partial {{W}_{ij}}}{\partial \rho }=\left( P({{h}_{j}}=1|\vec{v}){{v}_{i}}-\sum\limits_{v, h}{P(v)P({{h}_{j}}=1|\vec{v}){{v}_{i}}} \right)\times \frac{\varepsilon }{1+\exp (-\rho )} $ | (31) |
在实验部分, 我们基于权值随机变量构建了DBM模型, 然后与传统的DBM进行比较.同时, 为了与Dropout方法进行对比, 我们在实验中测试了Dropout DBN和WDBN的分类能力以及图像的重构误差.通过实验我们发现, 权值随机变量在分类精度上达到了与Dropout方法近似的效果.同时, 我们的方法具有更低的图像重构误差.
4.2 Boosted CD算法Boosted CD算法是一种有效的正则化技术, 该算法首先被提出用于解决DNA的计算问题[26].在Boosted CD算法中, 目标函数可以写成
| $ \frac{\partial L}{\partial W}\approx \text{Eq}.(2)+\frac{1}{N}\sum\nolimits_{n=1}^{N}{f(v_{n}^{(k)})h_{n}^{(k-1)}} $ | (32) |
| $ \frac{\partial L}{\partial b}\approx \frac{1}{N}\sum\nolimits_{n=1}^{N}{(\vec{v}_{n}^{(0)}-\vec{v}_{n}^{(k)}+f(v_{n}^{(k)}))} $ | (33) |
其中,
目前, 基于条件高斯分布对图像进行建模的方法主要有高斯-二值受限的玻尔兹曼机(mRBM)、Factored 3 way Boltzmann Machine(cRBM)[27]以及spike and slab Boltzmann Machine(ssRBM)[28, 29].其中, mRBM建模的是条件高斯分布的均值, 然而mRBM的建模能力比较差, 不能很好地还原输入数据的分布.cRBM建模的是条件高斯分布的协方差, 此时, 建模的精度相比GRBM有所提高.然而, 在cRBM中, 协方差矩阵是一个非对角矩阵, 不能采用分块的Gibbs采样, 因此在cRBM中, 使用的是混合的蒙特卡洛采样(HMC)方法, 然而HMC方法的缺点是参数过多、运行时间长.在ssRBM中, 可以同时建模高斯分布的均值和协方差, 为了保证可见层单元所服从分布的协方差矩阵是一个对角矩阵, ssRBM引入了两个随机变量s和h, 在给定s和h的状态时, v服从条件高斯分布, 并且可以使用分块的Gibbs采样, 修改的能量函数可以如下表示:
| $ E(v, s, h) = \frac{1}{2}{v^T}\mathit{\Lambda} v-\sum\nolimits_{i = 1}^N {\left( {{v^T}{W_i}{s_i}{h_i}-\frac{1}{2}s_i^T{\alpha _i}{s_i} + {b_i}{h_i}} \right)} =\\ \frac{1}{2}\sum\nolimits_{d = 1}^D {v_d^2{\mathit{\Lambda} _d}}-\sum\nolimits_{i = 1}^N {\left( {{v^T}{W_i}{s_i}{h_i} - \frac{1}{2}s_i^T{\alpha _i}{s_i} + {\alpha _i}{\mu _i}{h_i}{s_i} + {b_i}{h_i}} \right)} $ | (34) |
其中, Λ和α是对角矩阵; W为可见层单元与隐藏层单元之间的权值矩阵, 每一个隐藏层节点i关联2个变量, 即si和hi; μ是一个参数, 表示变量s的均值.此时, 条件概率可以表达如下:
| $ P(v|s, h) = \frac{{P(v, s, h)}}{{P(s, h)}} = N({\mathit{\Lambda} ^{-1}}\sum\nolimits_{i = 1}^N {({W_i}{s_i}{h_i})}, {\mathit{\Lambda} ^{-1}}) $ | (35) |
| $ P({h_i} = 1|v) = sigmoid\left( {\frac{1}{2}{v^T}{W_i}{h_i}\alpha _i^{-1}W_i^T{h_i}v + {v^T}{W_i}{\mu _i} + {b_i}} \right) $ | (36) |
| $ P(s|v, h) = \prod\limits_{i = 1}^N {N(\alpha _i^{-1}{v^T}{W_i}{h_i} + {\mu _i}{h_i}, \alpha _i^{-1})} $ | (37) |
我们的ssRBM在原始的模型基础上进行了修正, 在使用参数μ的同时, 尽量避免过多的参数影响计算.为了建模二值数据, 可见层单元的条件概率可以进行如下修改:
| $ p({v_j} = 1|s, h) = sigmoid\left( {\sum\limits_i {{W_{ij}}{s_i}{h_i} + {\mathit{\Lambda} _i}} } \right) $ | (38) |
将ssRBM作为我们模型的第1层, 其余2层使用WRBM模型.输入为像素点组成的向量, 经过第1个ssRBM之后, 使用隐藏层单元h的状态作为第2个WRBM的输入.然后重复该传递过程, 直到完成预训练.
5 实验及分析实验环境如下:CPU:Intel i7 4710hq, 内存:16g, GPU:GTX 970m.由于之前并没有权值随机变量在RBM中应用的先例, 所以我们首先分析了RBM和WRBM的分类能力和重构能力.使用两个不同大小的MNIST数据集来测试RBM和WRBM的分类和重构能力.为了方便比较权值随机变量的作用, 我们使用单层的RBM和WRBM以及BP算法训练.为了形式上的统一, 接下来的实验中, BP过程使用共轭梯度法, 迭代次数为100.在浅层模型中, 我们使用的隐藏层节点数为1 000, 模型的学习速率参数选择为0.005, 预训练的迭代次数为200.在单层RBM的实验中, 我们使用两个数据集, 分别为MNIST-Basic和Rectangles.在多层模型的对比实验中, 我们用基于Dropout方法建立的深度模型作为对比模型.其中, Dropout DBM和Dropout DBN是在DBM模型和DBN模型的基础上引入Dropout方法构建的深度模型.数据集的属性见表 2.
| Table 2 Attributes of data sets 表 2 实验数据的属性 |
我们首先测试了单层模型来验证权值随机变量的有效性.在这一步的实验中, 使用的数据集是MNIST-Basic和Rectangles.
测试精度见表 3, 记录的是数据的分类错误率.
| Table 3 Number of misclassifications in shallow models 表 3 单层模型的测试精度对比 |
接下来, 我们测试了模型的图像重构能力, 记录的是数据的重构误差.
从表 4中我们可以看出:相对于Dropout RBM和RBM, WRBM取得了最好的图像重构效果.Dropout RBM和WRBM的重构图像如图 3所示.
| Table 4 Reconstruction errors of RBM and WRBM 表 4 RBM和WRBM的模型重构误差 |

|
Fig. 3 Reconstructed images of Dropout RBM and weight uncertainty RBM 图 3 Dropout RBM和weight uncertainty RBM的重构图像对比 |
在多层模型中, 使用的网络结构为784-1000-1000-10, 为了方便比较, 我们使用BP算法进行权值的微调, 循环次数为100, MNIST-Basic的训练样本数为10 000, 测试样本数为50 000, MNIST数据集的训练样本数为60 000, 测试样本数为10 000.
从表 5中我们可以看出:相对于DBM, WDBM在3个数据集上的分类能力均有所提升.同时, 对于DBN模型, WDBN达到了与Dropout DBN相近的分类能力.最后, 我们测试WSDBM在MNIST数据集的分类能力和图像重建能力.重建图像如图 4所示.
| Table 5 Number of misclassifications of DBN and DBM 表 5 DBN和DBM分类精度对比 |

|
Fig. 4 Reconstructed image of WSDBM 图 4 WSDBM的重构图像 |
在最后的实验中, 我们希望在第1个RBM中既可以提取像素点之间的相关性信息, 而且可以进行精确的推理.因此, 我们引入ssRBM作为第1层, 构建基于权值随机变量的深度模型WSDBM.见表 6.
| Table 6 Classification accuracies of the algorithms 表 6 分类精度对比 |
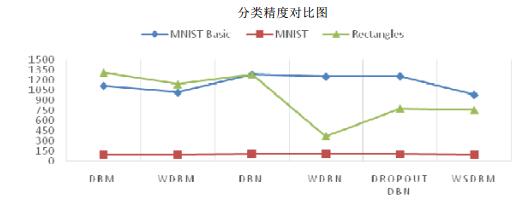
分类精度的对比图如图 5所示.
|
Fig. 5 Figure of accuracies 图 5 分类精度对比图 |
该模型还可以结合卷积操作, 被用于处理实数值的图像.我们利用卷积操作测试了模型的特征提取能力, 在能量函数中加入卷积操作, 将RBM中输入数据与权值的乘积转换为卷积RBM中输入图像与权值的卷积.卷积层的单元数为40, 卷积核尺寸为5×5.以MNIST数据集为例, 融合稀疏编码, 我们得到如图 6所示的特征图(在训练时, 我们没有对数据进行二值化处理, 而是使用实数值进行表示).

|
Fig. 6 Features of real-valued data 图 6 实值数据的特征图像 |
6 结论
本文中, 为了缓解神经网络过拟合的问题, 提高RBM模型的分类能力和图像重构能力, 我们引入了WRBM.在我们的实验中, 与Dropout方法相比, 权值随机变量是有效的.基于实验的表现, 我们对模型进一步改进, 引入ssRBM模型, 对能量函数进行略微调整, 可以成功地建模实值图像和二值图像.融合卷积和稀疏编码, 我们可以成功地提取图像的边缘特征.在接下来的工作中, 我们将重点研究实数值图像的分类和重构问题, 目前的研究工作也为我们提供了很好的理论基础.
| [1] |
Erhan D, Bengio Y, Courville A, Manzagol PA, Vincent P, Bengio S. Why does unsupervised pre-training help deep learning. Journal of Machine Learning Research, 2010, 11(3): 625–660.
http://www.doc88.com/p-2595988881841.html |
| [2] |
Hinton GE. Training products of experts by minimizing contrastive divergence. Neural Computation, 2002, 14(8): 1771–1800.
[doi:10.1162/089976602760128018] |
| [3] |
Roux N, Bengio Y. Representational power of restricted Boltzmann machines and deep belief networks. Neural Computation, 2008, 20(6): 1631–1649.
[doi:10.1162/neco.2008.04-07-510] |
| [4] |
Liu JW, Liu Y, Luo XL. Research and development on Boltzmann machine. Journal of Computer Research and Development, 2014, 51(1): 1–16(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.2014.20121044] |
| [5] |
Hinton GE, Osindero S, Th Y. A fast learning algorithm for deep belief nets. Neural Computation, 2006, 18(7): 1527–1554.
[doi:10.1162/neco.2006.18.7.1527] |
| [6] |
Hinton GE, Salakhutdinov R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504–507.
[doi:10.1126/science.1127647] |
| [7] |
Lee H, Pham PT, Yan L, Ng A. Unsupervised feature learning for audio classification using convolutional deep belief networks. In: Bengio Y, Schuurmans D, Lafferty JD, Williams CKI, Culotta A, eds. Proc. of the Advances in Neural Information Processing Systems. 2009. 1096-1104. https://papers.nips.cc/book/advances-in-neural-information-processing-systems-22-2009 |
| [8] |
Norouzi M, Ranjbar M, Mori G. Stacks of convolutional restricted Boltzmann machines for shift-invariant feature learning. In: Proc. of the Computer Vision and Pattern Recognition. 2009. 2735-2742. [doi: 10.1109/CVPR.2009.5206577] |
| [9] |
Salakhutdinov R, Larochelle H. Efficient learning of deep Boltzmann machines. Journal of Machine Learning Research, 2010, 9(8): 693–700.
http://dspace.mit.edu/bitstream/handle/1721.1/57474/MIT-CSAIL-TR-2010-037.pdf?sequence=1 |
| [10] |
Salakhutdinov R, Hinton GE. An efficient learning procedure for deep Boltzmann machines. Neural Computation, 2012, 24(8): 1967–2006.
[doi:10.1162/NECO_a_00311] |
| [11] |
Boulanger-Lewandowski N, Bengio Y, Vincent P. Modeling temporal dependencies in high-dimensional sequences:Application to polyphonic music generation and transcription. Chemistry a European Journal, 2012, 18(13): 3981–3991.
[doi:10.1002/chem.v18.13] |
| [12] |
Hu Z, Fu K, Zhang CS. Audio classical composer identification by deep neural network. Journal of Computer Research and Development, 2014, 51(9): 1945–1954(in Chinese with English abstract).
[doi:10.7544/issn1000-1239.2014.20140189] |
| [13] |
Zhang J, Ding SF, Zhang N, Shi ZZ. Incremental extreme learning machine based on deep feature embedded. Int'l Journal of Machine Learning and Cybernetics, 2016, 7(1): 111–120.
[doi:10.1007/s13042-015-0419-5] |
| [14] |
Zhang N, Ding SF, Shi ZZ. Denoising Laplacian multi-layer extreme learning machine. Neurocomputing, 2016, 171(C): 1066–1074.
[doi:10.1016/j.neucom.2015.07.058] |
| [15] |
Ding SF, Zhang N, Xu XZ, Guo LL, Zhang J. Deep extreme learning machine and its application in EEG classification. In: Proc. of the Mathematical Problems in Engineering. 2015. 1-11. [doi: 10.1155/2015/129021] |
| [16] |
Srivastava N, Hinton GE, Krizhevsky A. Dropout:A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 2014, 15(1): 1929–1958.
|
| [17] |
Blundell C, Cornebise J, Kavukcuoglu K. Weight uncertainty in neural networks. In: Bach F, Blei D, eds. Proc. of the 32nd Int'l Conf. on Machine Learning. Lille, 2015. http://proceedings.mlr.press/v37/ |
| [18] |
Hinton GE. A practical guide to training restricted Boltzmann machines. Momentum, 2010, 9(1): 926.
[doi:10.1007/978-3-642-35289-8_32] |
| [19] |
Krizhevsky A, Hinton GE. Learning multiple layers of features from tiny images. Technical Report, University of Toronto, 2009.
http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf |
| [20] |
Salakhutdinov RR. Learning in Markov random fields using tempered transitions. In: Bengio Y, Schuurmans D, Lafferty JD, et al., eds. Proc. of the Advances in Neural Information Processing Systems. Curran Associates Inc., 2009. 1598-1606. |
| [21] |
Desjardins G, Courville AC, Bengio Y, Vincent P, Delalleau O. Tempered Markov chain Monte Carlo for training of restricted Boltzmann machines. In: Lawrence N, Whye TY, Titterington M, eds. Proc. of the Int'l Conf. on Artificial Intelligence and Statistics, Vol. 9. 2010. 145-152. |
| [22] |
Peterson C. A mean field theory learning algorithm for neural network. Complex Systems, 1987, 1(3): 995–1019.
|
| [23] |
Tieleman T. Training restricted Boltzmann machines using approximations to the likelihood gradient. In: Proc. of the 25th Int'l Conf. on Machine Learning. ACM Press, 2008. 1064-1071. [doi: 10.1145/1390156.1390290] |
| [24] |
Tieleman T, Hinton GE. Using fast weights to improve persistent contrastive divergence. In: Proc. of the 26th Int'l Conf. on Machine Learning. ACM Press, 2009. 1033-1040. [doi: 10.1145/1553374.1553506] |
| [25] |
Bengio Y. Learning deep architectures for AI. Foundations & Trends in Machine Learning, 2009, 2(1): 1–127.
[doi:10.1561/2200000006] |
| [26] |
Lee T, Yoon S. Boosted categorical restricted Boltzmann machine for computational prediction of splice junctions. In: Bach F, Blei D, eds. Proc. of the Int'l Conf. on Machine Learning. 2015. 2483-2492. |
| [27] |
Ranzato M, Krizhevsky A, Hinton GE. Factored 3-way restricted Boltzmann machines for modeling natural images. Journal of Machine Learning Research, 2010, 9: 621–628.
https://www.researchgate.net/publication/220320634_Factored_3-Way_Restricted_Boltzmann_Machines_For_Modeling_Natural_Images |
| [28] |
Courville AC, Bergstra J, Bengio Y. A spike and slab restricted Boltzmann machine. Journal of Machine Learning Research, 2011, 15(15): 233–241.
https://www.researchgate.net/profile/Y_Bengio/publication/220320195_A_Spike_and_Slab_Restricted_Boltzmann_Machine/links/546cd25e0cf2a7492c55ab2a/A-Spike-and-Slab-Restricted-Boltzmann-Machine.pdf |
| [29] |
Courville AC, Desjardins G, Bergstra J, Bengio Y. The spike-and-slab RBM and extensions to discrete and sparse data distributions. IEEE Trans. on Software Engineering, 2014, 36(9): 1874–1887.
[doi:10.1109/TPAMI.2013.238] |
| [4] |
刘建伟, 刘媛, 罗雄麟. 玻尔兹曼机研究进展. 计算机研究与发展, 2014, 51(1): 1–16.
[doi:10.7544/issn1000-1239.2014.20121044]
|
| [12] |
胡振, 傅昆, 张长水. 基于深度学习的作曲家分类问题. 计算机研究与发展, 2014, 51(9): 1945–1954.
[doi:10.7544/issn1000-1239.2014.20140189]
|
 2018, Vol. 29
2018, Vol. 29


