2. 成都信息工程大学 网络空间安全学院, 四川 成都 610225
2. School of Cybersecurity, Chengdu University of Information Technology, Chengdu 610225, China
随着社会快速发展, 人们之间的社交关系形成了非常复杂的数据集合, 而这些数据集内部的数据相互之间存在着一定的联系, 使得每个数据集可以映射为图.与之类似的例子还有很多, 如生物中的各种分子之间的关联、交通网络以及天文星体网络等.其中, 社区聚类挖掘是近年来研究的热点.传统的社交网络数据挖掘研究内容主要是如何对社交对象间频繁发生某种交互进行聚类, 获得的社区仅表示这类交互的一个聚集紧密度, 不能表示社交对象间的真实关系.
社交对象间的真实关系往往是最具价值的信息.举例来说, 两个频繁交互(如通过手机联系)的对象可能是夫妻或亲友关系, 也可能是某种临时性的工作关系(如外卖送餐), 而两种关系在对象间的亲疏上代表的意义完全不同, 外卖的聚类发现基本不具备应用价值, 这就需要分析更多维度的信息以获得对象间的真实关系.
现实中, 社交数据往往是巨大的, 对象间的联系是多维度的, 体现了对象交互的多样性[1, 2].例如, 人群的社交方式包括电话、见面、即时通信软件(微信、QQ)、E-mail等.如图 1所示, 图 1(a)为真实世界的社交关系, 其中, 5个对象的各类交互用虚线表示.通常传统的聚类算法将各类交互进行特征抽取, 分别映射成图数据, 使用相应算法进行挖掘, 即, 将图 1(a)中的交互区分为3类, 分别是通话(绿线代表)、微信(黑线代表)以及见面(红线代表), 映射成为图 1(b)中的3个子图后, 分别进行单维度的聚类分析.

|
Fig. 1 Mapping between social relationships and complex graph data 图 1 现实社交关系与复杂关系图数据的映射 |
通过上述分析得知:仅对某一种特定社交方式的聚类挖掘, 反映的是对象在这种交互上的亲疏关系, 这种单维度关系分析通常不能显示对象间的真实社会关系[3].要挖掘对象间的真实关系, 需要在聚类挖掘中引入更多维度的交互.如图 1(c)所示, 将图 1(b)中的3个单维度的图数据进行组合, 同时在多个维度对图数据进行挖掘将会获得更多价值的信息.例如:仅对对象间的通话进行聚类, 得到的聚类反映对象间通话的频率; 同理, 仅聚类对象间的见面关系, 反映的是碰面的频次.以上两种聚类仅能表示对象间的亲疏关系.但如果结合通话与见面两个关系进行挖掘分析, 得到聚类(通话与见面都频繁)中社交对象间的关系更紧密, 更有可能体现对象间的真实社交关系.
对象间的交互关系在映射的图中表现为不同类型的边, 如在图 1(c)中共存在3种不同类型的边.本文将图中边类型称为维度, 简称维, 用d表示, 如图 1(c)中, d=3, 即有3个维度.不同维度间的组合称为子空间, 子空间共有2d-1种组合, 如图 1(c)中的子空间包括通话、见面、微信、通话+见面、通话+微信、见面+微信、通话+见面+微信共7种组合.
综上, 本文提出了子空间聚类算法SCA(subspace cluster algorithm), 该算法可以对多维度图进行聚类挖掘, 算法自底向上发现复杂社交图数据中所有子空间下的聚类集合, 探索通过分析对象间多维度交互, 来挖掘真实社交关系的方法.
本文的主要贡献总结如下:
(1) 首次在图数据上研究子空间的结构聚类;
(2) 通过各个子空间聚类的数据挖掘, 探索真实社交关系朋友圈;
(3) 提出了可对多维度图进行挖掘的子空间聚类算法SCA;
(4) 自底向上进行多维聚类时, 对核心节点、候选子空间进行剪枝优化, 提出优化算法SCA+.
本文第1节介绍传统社交图数据挖掘模型和多维聚类的相关工作.第2节对SCA相关问题进行描述, 进一步解释SCA模型, 同时给出8个关键定义与子空间单调性的证明.第3节描述SCA算法及伪代码执行的过程.第4节介绍通过对核节点、候选子空间进行剪枝, 给出优化算法SCA+.第5节在3个数据集上分别运行SCA, SCA+, 并分析对比算法在各种参数下的时间效率.第6节在真实数据集上进行实例分析, 验证算法的正确性.最后, 在第7节总结全文并给出未来的工作.
1 相关工作社区搜索拥有巨大的潜在价值, 产生了众多优秀的聚类算法, 包括k-团[4]、k-plex[5]、LS集[6-8]、k-核[9]、k-truss[10, 11].在无权图中, k-团表示一个子图, 其任意两个顶点之间的最短路径的长度都小于或等于k条边.k-plex是由r个顶点诱导的子图, 其任意顶点的度都至少为r-k.LS集为顶点集合的子集, 该子集具有以下特性:子集中的顶点与其补集中的顶点相连接的边数, 少于该子集的任意真子集中的顶点与其相应的补集中的顶点相连的边数.而且, 该子集是具备这种特性的最大子集.这里着重讨论两种模型:k-核与k-truss.
k-核的概念是由Seidman首次提出的[9].k-核是一个诱导子图, 该子图中节点的度都大于或等于k, 且该子图是具备这种性质的最大子图.为了求解大图数据的k-核分解问题, Vladimir和Matjaz率先提出了一种线性时间算法[12].该算法依次从图中删除度最小的节点, 并利用类似于桶排序的数据结构存储节点, 从而实现快速的k-核计算.该算法首先发现核数较低的节点, 然后依次发现核数较高的节点.因为k-核模型主要关注图中度数较高的节点, 往往会忽略一些度数较低、但是却在现实中有关联的社区.
相对于k-核, k-truss是较新的概念, 由Cohen首次提出[10].同样, k-truss也是一个诱导子图, 该子图中的任意一条边都至少包含在(k-2)个三角形中, 且该子图是具备这种性质的最大子图.值得注意的是:一个k-truss是(k-1)-核, 反之不一定成立.由此可见, k-truss是一种精炼的k-核结构.然而与k-核不同的是, k-truss的定义是基于图中顶点所形成的三角形结构.
另外一个重要的算法是基于结构的聚类算法SCAN(structural clustering algorithm for network)[13], 算法在处理分析现实数据形成的图时取得了很好的效果, 并在此基础上提出了一系列剪枝算法, 诸如SCAN++[14], pSCAN[15]等.在大规模社交网络的结构聚类上, 也提出了相关算法[16], 社交网络数据挖掘研究一直是大数据研究的热门领域.
目前, 对多维数据聚类的处理大多采用降维的方式[17, 18], 即:将多维数据映射到多个单维, 将繁多复杂的关系简单化.但降维聚类操作有几个重大的缺陷[19]:对象间多维关系在降维简单化后, 往往不代表任何实际意义; 在某些情况下, 降维后不能直接聚类; 多维数据降维后, 只能使用SCAN等聚类算法针对单维关系数据进行挖掘, 目前还没有有效的聚类算法能够对多维数据聚类.
文献[20]提出了一种基于密度连接的子空间聚类, 聚类对象主要为空间多维数据, 没有涉及结构化数据.
可以看出, 当前的研究工作忽视了对结构化数据多维度交互关系的聚类, 导致无法辨析社交数据挖掘中聚类结果的价值.本文针对此问题提出的多维度图聚类的社交网络挖掘算法SCA, 通过对多维子空间的聚类得到对象交互更紧密的社区, 为挖掘对象间的真实社交关系提供了解决方案.
2 问题描述及相关定义基于结构的聚类算法在图数据挖掘和分析中具有重要的意义, 尤其在社区搜索应用中取得了很好的效果, 因此吸引了大量学者在这方面进行相关研究.
2.1 关键定义存在图G=(V, ε), 任意两个顶点u, v之间最多存在d种不同类型的边(维度), 即代表它们之间的交互类型最多为d种.设定Ed={e1…ed}为图G中所有维度的集合, 任意子集S⊆Ed称为子空间(subspace).S的基数|S|称为S的度.本文将度值大的子空间称为高维子空间, 度值小的称为低维子空间.例如图 1(c)中, d=3, E3={通话, 见面, 微信}.如S={通话, 见面}, 则S的度等于2.ε为实数, μ为整数.
定义1(顶点结构相似性).若顶点u, v之间存在边ei=(u, v), 则u和v在ei(1≤i≤d)上的结构相似性的值为
| $ {\sigma ^{{e^i}}}\left( {v,u} \right)\frac{{\left| {{\mathit{\Gamma }^{{\mathit{e}^\mathit{i}}}}\left( v \right) \cap {\mathit{\Gamma }^{{\mathit{e}^\mathit{i}}}}\left( u \right)} \right|}}{{\sqrt {\left| {{\mathit{\Gamma }^{{\mathit{e}^\mathit{i}}}}\left( v \right)\left\| {{\mathit{\Gamma }^{{\mathit{e}^\mathit{i}}}}\left( u \right)} \right.} \right|} }} $ | (1) |
其中,
由此引申出u和v在S上的结构相似性的值为
| $ {\sigma ^s}\left( {u,v} \right) - \left\{ {{e^i} \in S\left| {\min \left( {{\sigma ^{{e^i}}}} \right)} \right.} \right\} $ | (2) |
即, u, v在S中各个维度下的相似性最小值.如在图 1(c)中, 取S={通话, 见面, 微信}, 则:
σs(u, v)={min(σ通话(u, v), σ见面(u, v), σ微信(u, v))}.
定义2(ε邻居).顶点u在S下的ε邻居, 即S下与u之间结构相似性大于等于阈值ε的顶点的集合:
| $ N_\varepsilon ^S\left( u \right) = \left\{ {w \in {\mathit{\Gamma }^S}\left( \mathit{u} \right)\left| {{\sigma ^S}\left( {u,w} \right)} \right. \ge \varepsilon } \right\} $ | (3) |
定义3(核心节点).假设顶点u在S下的ε邻居的个数大于等于阈值μ, 则u为核心节点:
| $ Core_{\varepsilon ,\mu }^S\left( u \right) \Leftrightarrow \left| {N_\varepsilon ^S\left( u \right)} \right| \ge \mu $ | (4) |
定义4(直接结构可达).顶点u在S下直接结构可达顶点v, 当且仅当u在S下是核心顶点且u和v之间在S下的结构相似性大于等于ε(即, v是u的ε-邻居):
| $ DirREACH_{\varepsilon ,\mu }^S\left( {u,v} \right) \Leftrightarrow Core_{\varepsilon ,\mu }^S\left( u \right) \wedge v \in N_\varepsilon ^S\left( u \right) $ | (5) |
定义5(结构可达).假设在S下顶点p∈V结构可达顶点q∈V当且仅当存在p1, …, pn, p1=q, pn=p, 并且pi+1与pi直接结构可达, 即:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {REACH} \end{array}_{\varepsilon ,\mu }^S\left( {q,p} \right) \Leftrightarrow \exists {p_1}, \cdots {p_n} \in V:{\mathit{p}_1} = q \wedge {p_n} = p \wedge \forall i \in \left\{ {1 \ldots n - 1} \right\}:\\ \begin{array}{*{20}{l}} {DirREACH} \end{array}_{\varepsilon ,\mu }^S\left( {{p_i},{\mathit{p}_\mathit{i}}_{ + 1}} \right) \end{array} $ | (6) |
定义6(结构连接).给顶点p, q在S下结构连接, 当且仅当存在节点o, p与q在S下分别与o结构可达:
| $ \begin{array}{*{20}{l}} {CONNECT} \end{array}_{\varepsilon ,\mu }^S\left( {q,p} \right) \Leftrightarrow \exists o \in V:\begin{array}{*{20}{l}} {REACH_{\varepsilon ,\mu }^S} \end{array}\left( {q,o} \right) \wedge \begin{array}{*{20}{l}} {REACH} \end{array}_{\varepsilon ,\mu }^S\left( {o,p} \right) $ | (7) |
定义7(结构连接集).设C是非空节点集合, 如果C中的所有节点在S下结构连接, 则C称为S下的结构连接集:
| $ CONSET_{\varepsilon ,\mu }^S\left( C \right) \Leftrightarrow \forall p,q \in C:CONNECT_{\varepsilon ,\mu }^S\left( {p,q} \right) $ | (8) |
定义8(子空间聚类).给定一个图G, 非空子图G'在S下的子空间聚类当且仅当G'满足如下两个条件.
(1) G'中每个顶点之间在S下满足结构可达;
(2) G'最大.
2.2 子空间聚类的单调性按照上述定义, 最直接地搜索各个子空间上的结构聚类方法就是在所有子空间S上使用聚类算法.本文提出的SCA就是基于这种思想, 采取从低维到高维自下而上的搜索策略挖掘各个子空间上的聚类, 探索发现对象间真实的社交关系.
值得注意的是:子空间聚类并不具备单调性, 即, 低维的聚类在高维不一定是聚类, 这是因为部分节点在高维上不满足结构可达; 反之, 高维的聚类顶点在低维上必定结构可达, 但不一定满足最大性原则.
但在子空间聚类过程中, 核心节点、直接结构可达、结构可达、结构连接以及结构连接集都具备单调性, 即, 高维子空间上的核心节点u在低维子空间上一定是核心节点, 节点u, v在高维子空间直接结构可达, 在低维子空间同样直接结构可达, 以此类推.于是有如下的单调性引理.
引理1(单调性).设ε为实数, μ为整数, C是非空节点集合, 即C≠Ø, o, q∈V, S⊆Ed, T⊆S, 有如下的单调性规则.
(1)
(2)
(3)
(4)
(5)
引理1的证明如下.
(1) 核心节点o在子空间S上为核心节点, 则对于子空间T⊂S, o在T上也是核心节点.这是因为在S上所有维的
| $ \begin{array}{l} Core_{\varepsilon ,\mu }^S\left( o \right) \Leftrightarrow \left| {N_\varepsilon ^S\left( o \right)} \right| \ge \mu \Leftrightarrow \mathop {\min }\limits_{{e^i} \in S} \left( {{\sigma ^{{e^i}}}} \right) \ge \mu \mathop \Rightarrow \limits^{\left( {T \subset S} \right)} \mathop {\min }\limits_{{e^i} \in T} \left( {{\sigma ^{{e^i}}}} \right) \ge \mu \Leftrightarrow \\ \left| {N_\varepsilon ^T\left( o \right)} \right| \ge \mu \Leftrightarrow Core_{\varepsilon ,\mu }^T\left( o \right). \end{array} $ |
(2) 节点o, q在子空间S上直接结构可达, 则对于子空间T⊂S, o, q在T上也直接结构可达.这是因为o在T上是核心节点, q在T上同时是o的ε-邻居:
| $ \begin{array}{l} DirREACH_{\varepsilon ,\mu }^S\left( {o,\mathit{q}} \right) \Leftrightarrow Core_{\varepsilon ,\mu }^S\left( o \right) \wedge q \in N_\varepsilon ^S\left( o \right) \Leftrightarrow Core_{\varepsilon ,\mu }^S\left( o \right) \wedge {\sigma ^S}\left( {o,q} \right) \ge \varepsilon \Leftrightarrow \\ Core_{\varepsilon ,\mu }^S\left( o \right) \wedge \mathop {\min }\limits_{{e^i} \in S} \left( {{\sigma ^{{e^i}}}} \right) \ge \mu \mathop \Rightarrow \limits^{\left( {T \subset S} \right)} Core_{\varepsilon ,\mu }^T\left( o \right) \wedge \mathop {\min }\limits_{{e^i} \in S} \left( {{\sigma ^{{e^i}}}} \right) \ge \mu \Leftrightarrow \\ Core_{\varepsilon ,\mu }^T\left( o \right) \wedge {\sigma ^T}\left( {o,\mathit{q}} \right) \ge \varepsilon \Leftrightarrow Core_{\varepsilon ,\mu }^T\left( o \right) \wedge \mathit{q} \in \mathit{N}_\varepsilon ^T\left( o \right) \Leftrightarrow DirEACH_{\varepsilon ,\mu }^T\left( {o,\mathit{q}} \right). \end{array} $ |
(3) 节点o, q在子空间S上结构可达, 则对于子空间T⊂S, o, q在T上结构可达.这是因为在S上存在p1, …, pn, p1=q, pn=p, 并且pi+1与pi直接结构可达, 根据定义5与引理1的证明(2), 上述条件在T上亦成立.
| $ \begin{array}{l} REACH_{\varepsilon ,\mu }^S\left( {o,\mathit{q}} \right) \\\mathop \Leftrightarrow \limits_{T \subset S} \exists{p_1}, \cdots {p_n} \in V:{p_1} = o \wedge {p_n} = q \wedge \forall i \in \left\{ {1, \ldots n - 1} \right\}:REACH_{\varepsilon ,\mu }^S\left( {{p_i},{p_{i + 1}}} \right)\\ \Rightarrow \exists {p_1}, \ldots ,{p_n} \in V,{p_1} = o \wedge {p_n} = q \wedge \forall i \in \left\{ {1, \ldots n - 1} \right\}:REACH_{\varepsilon ,\mu }^T\left( {{p_i},{p_{i + 1}}} \right)\\ \Leftrightarrow REACH_{\varepsilon ,\mu }^T\;\left( {o,\mathit{q}} \right). \end{array} $ |
(4) 节点o, q在子空间S上结构连接, 则对于子空间T⊂S, o, q在T上结构连接.这是根据在S上存在的x使得o, q分别与之结构可达, 则在T上, x与o, q分别结构可达, 根据定义6与引理1的证明(3)得证.
| $ \begin{array}{l} CONNECT_{\varepsilon ,\mu }^S\left( {o,\mathit{q}} \right)\mathop \Leftrightarrow \limits_{T \subset S} \exists x \in V:REACH_{\varepsilon ,\mu }^s\left( {x,o} \right) \wedge REACH_{\varepsilon ,\mu }^s\left( {x,\mathit{q}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Rightarrow \exists x \in \;\;V:REACH_{\varepsilon ,\mu }^T\left( {x,o} \right) \wedge REACH_{\varepsilon ,\mu }^T\left( {x,\mathit{q}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Leftrightarrow CONNECT_{\varepsilon ,\mu }^T\left( {o,\mathit{q}} \right). \end{array} $ |
(5) 设C是非空节点集合, 并且C在子空间S上为结构连接集, 则对于子空间T⊂S, C在T上亦为结构连接集.根据定义7与引理1的证明(4)得证:
| $ CONNECT_{\varepsilon ,\mu }^S\left( C \right) \Leftrightarrow \forall o,\mathit{q} \in C:CONNECT_{\varepsilon ,\mu }^S\left( {o,\mathit{q}} \right)\mathop \Rightarrow \limits^{T \subset S} \forall o,\mathit{q} \in C:\\CONNECT_{\varepsilon ,\mu }^T\left( {o,\mathit{q}} \right) \Leftrightarrow CONNECT_{\varepsilon ,\mu }^T\left( C \right). $ |
上述单调性是自底向上的子空间聚类算法剪枝优化的核心思想.对于如何将单调性运用于算法优化, 本文将在第4节中详细讨论.
3 子空间聚类算法子空间聚类算法基于结构聚类算法SCAN, 加入维度与子空间的概念, 其思想是自底向上、从低维到高维搜索所有子空间的结构聚类.首先介绍算法的基本思想.
3.1 算法的基本思想SCA算法的基本思想是自底向上地在各个子空间上使用SCAN进行聚类.SCAN在发现社区的同时, 还能够检测到Hub节点和离群节点, 使得该算法在图聚类中具备特殊的优势.SCAN在聚类的过程中需要指定两个阈值:判断相连节点之间是否满足结构相似性的阈值ε以及判断节点是否为核心顶点的阈值μ.在聚类过程中, 需要对每条边计算其两个端点之间的结构相似性.算法的复杂度是O(m1.5)[9], 当聚类数据过于庞大时, 计算全图节点的结构相似性极为耗时.
SCA对子空间的图聚类过程如图 2所示, 设聚类社交图数据中包含3种类型的边(通信、见面、微信), 即, 图数据维度为3.算法需要在3个维度上, 自底向上分别对7个子空间进行运算.即:算法首先进行一维聚类(通话、见面、微信), 其次为二维聚类(通话+见面、通话+微信、见面+微信), 最后是三维聚类(通话+见面+微信).

|
Fig. 2 Cluster diagram of SCA 图 2 SCA算法聚类示意图 |
3.2 SCA代码分析
算法1为SCA的伪代码, 首先将代码中的部分变量解释如下.
(1) Si:G中所有的子空间组合, i=1, 2, …, 2d-1;
(2) CoreSi:Si下所有核心节点;
(3) Dk:k维度下的所有核心节点集k=1, 2, …, d;
(4) Sk:k维度下的所有子空间k=1, 2, …, d;
(5) CSi :Si下所有聚类集合.
首先, 算法1在第1次迭代生成一维度下所有子空间的组合CanS1(第4行), 如在图 2中为一维聚类的3个子空间:通信、见面、微信.接着, 选取CanSk中的所有子空间Scan, 分别在参数ε, μ下使用定义1的结构相似性公式, 结合定义2、定义3求出核心节点, 并存于CoreSscan中(第5行~第9行).算法首先计算子空间内所有节点的ε-邻居数NεScan (v), 如满足|NεScan (v)|≥μ, 则将v存放到CoreSscan中, 如计算的是通信子空间, 则存于CoreS通信中.当子空间所有节点ε-邻居计算完成后, 调用算法2(GenerateCluster(CoreScan, Scan))生成一维度上的所有子空间的聚类(第10行~第12行).对于图 2来说, 就是生成了一维度下3个子空间的3个聚类集(有可能为空集, 即, 该子空间不存在聚类).下一步迭代计算高一维空间的聚类(第13行), 直到完成第d维下所有子空间的聚类, 在图 2中, d=3.
算法1. SCA(G, ε, μ).
输入:多维度图G, 参数ε, μ;
输出:子空间聚类集合C.
1.初始化集合C;
2.k=1
3.while k≤d do
4.计算所有k维度子空间组合CanSk;
5.for each Scan∈CanSk do //求每个子空间的核心节点
6. CoreScan= Ø;
7. for each v∈V(Scan) do //对属于该子空间的节点进行计算
8. compute NεScan (v)
9.if |NεScan (v)|≥μ then CoreScan:=CoreScan∪{v}; //将核心节点存放CoreScan中
10.if CoreScan = Ø then
11.CScan GenerateCluster(CoreScan, Scan) //通过Scan维度的核心节点进行聚类
12.C:=C∪CScan
13.k=k+1
算法2是根据核心节点集CoreSi在子空间Si下生成聚类的算法, 算法首先遍历CoreSi中所有的核心节点(第2行), 如果发现该节点v没有被标记, 对v节点生成一个新的聚类, 并进行标记, 然后将NεSi(v)中不包括v的全部节点加入队列Q并标记聚类(第3行~第5行).算法的第6行~第10行为生成核心节点v的聚类过程, 首先从队列中取出y节点, 假如y是核心节点, 则继续将y的ε-邻居NεSi(y)中没有被标记的顶点加入队列Q(第9行、第10行), 重复迭代上述过程, 直到队列Q为空集, 算法返回的ClusterSi为子空间Si的聚类集.
算法2. GenerateCluster(CoreSi, Si).
1.ClusterSi=Ø
2.foreach v∈CoreSi do //遍历所有核心节点
3. if v is not classified then //对没有标记的核心节点聚类
4.ClusterID={v};
5. insert x ∈NεSi(v) and x≠v into queue Q and classify x; //NεSi(v)入队并标记聚类
6.while Q≠ Ø do
7. y=Q.pop();
8. ClusterID:=ClusterID∪{y};
9. if y∈Corei then
10. insert z∈NεSi(y) and z is unclassified into queue Q and classify z; //标记节点z
11.ClusterIDSi:=ClusterIDSi∪ClusterID;
12.return ClusterIDSi
因需要计算每条边对应节点的结构相似性, 故算法1的时间复杂度同SCAN算法, 为O(m1.5)[9], 证明从略.
4 改进的子空间聚类算法SCA算法提出了计算多维度图数据子空间聚类的方法, 但是子空间的组合包含(2d-1)种可能, 当d很大时, 暴力穷举导致算法效率过低.另外, SCA在每个子空间都要重复计算核心节点, 提升了算法时间复杂度.本节通过分析第2.2节子空间聚类单调性, 提出一种剪枝优化的升级算法SCA+.
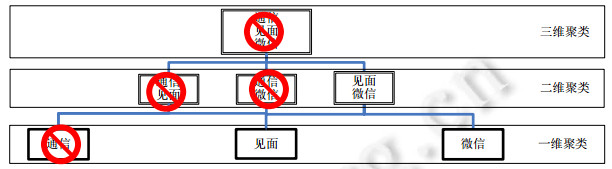
从上述第2.2节的单调性证明可得:u与v在子空间S上为核心节点/(直接)结构可达/结构相连, 必然得到u与v在子空间T ⊆S上为核心节点/(直接)结构可达/结构相连.如果在子空间T不存在聚类, 则子空间S中也不存在聚类, 即, S不是需要计算聚类的子空间.如图 3所示:在自底向上计算子空间聚类时, 设在一维度的子空间通信中没有发现聚类, 则根据单调性, 在所有涉及通信的子空间都不存在聚类, 即, 子空间通信+见面、通信+微信、通信+见面+微信中都不存在聚类, 算法仅需考虑见面、微信、见面+微信这3个子空间的聚类计算.
|
Fig. 3 Candidate subspace pruning 图 3 候选子空间剪枝 |
另外, 根据v在子空间S上为核心节点, 在子空间T⊆S上亦为核心节点的单调性, 算法在计算每个子空间的核心节点时, 无需对每个节点进行相似性计算, 改为仅计算组成S的低维子空间核心节点的交集.例如, 要计算图 2中通信+见面子空间的核心节点, 按照SCA, 需要遍历所有节点来确定该子空间上的核心节点Core通信+见面.
在SCA+中, 根据核心节点的单调性, 仅需遍历子空间通信、见面的核心节点Core通信与Core见面的交集Core通信∩Core见面, 因为Core通信+见面⊆(Core通信⊆Core见面).
算法3是对上述两个剪枝(候选子空间、候选核心节点)的实现, 首选通过对核心节点的求交集计算, 获得候选核心节点CoreSscan(第1行~第3行); 通过k维子空间生成(k+1)维候选子空间集, 其中, Scan为计算出候选核节点CoreSscan所在的子空间, 然后, 将所生成k+1维下的候选子空间和候选核节点分别加入集合CanSk+1与CanDk+1中(第4行~第6行), 算法返回候选子空间CanSk+1与候选核心节点CanDk+1.
算法3. GenerateCandidate(Dk, Sk).
1.for i from 1 to |Dk|-1 do
2. for j from 2 to |Dk| do
3. CoreSscan:=Dk[i]∩Dk[j];
4.if CoreScan≠Ø and Scan∉CanSk+1 and |Scan|=k+1 do //对没有计算过的k+1维下子空
5. CanSk+1:=CanSk+1∪Scan; //间和该维中的核心节点分别加入
6. CanDk+1:=CanDk+1∪CoreScan //CanSk+1和CanDk+1中
7.return (CanSk+1, CanDk+1);
算法4是剪枝算法SCA+, 在一维度子空间聚类的计算上与SCA没有很大区别, 只是增加了保存一维子空间的核心节点于D1中(第8行); 在高维度(k≥2)的子空间聚类上, SCA+不会对所有子空间进行聚类, 而是分别对候选子空间以及候选核心节点进行剪枝优化(第14行).另外, 在核心节点的查找上, 不会对所有的节点进行遍历重新计算核心节点, 仅对算法3生成的候选核心节点, 利用定义1引申相似性定义计算相似性, 并根据相似性求出ε-邻居, 如果ε-邻居大于等于μ则为真核(第17行、第18行).最后, 根据所求的真核CoreSscan使用算法2进行聚类(第19行~第22行), 并且保存真核于Dk+1中, 用于循环迭代(第20行).
算法4. SCA+(G, ε, μ) //剪枝算法.
输入:多维度图G, 参数ε, μ;
输出:子空间聚类集合C.
1.初始化集合C, D1;
2.for i form 1 to d do //对各个一维空间聚类
3. CoreSi=Ø;
4. for each v∉V(Si) do
5. compute NεSi(v)
6.if |NεSi(v)| ≥μ then CoreSi=CoreSi∪{v};
7. if CoreSi≠Ø then
8.D1:=D1∪CoreSi //每个维度空间的核心节点集合存放于D1
9.CoreSi =GenerateCluster(CoreSi, Si);
10.C:=C∪CSi;
11. k=1
12. while Dk ≠Ø do
13.初始化Dk+1, CanSk+1, CanDk+1;
14.(CanSk+1, CanDk+1)=GenerateCandidate(Dk, Sk); //获取候选维度以及该维度上的核心节点
15.for each CanCorecan∈ CanDk+1 do
16.CoreScan=Ø;
17.for each v∈ CanCorecan do //判断该节点在候选维度空间上是否为真正的核心节点
18. if |NεScan(v)| ≥μ then CoreScan:= CoreScan∪{v}
19.if CoreScan:=Ø then
20. Dk+1:=Dk+1∪CoreScan
21.CScan=GenerateCluster(CoreScan, Scan)
22. C:=C∪CScan
23.k=k+1
剪枝算法SCA+同样需要在一维聚类时对所有边的节点进行结构相似性计算, 所以算法的时间复杂度亦为O(m1.5).但SCA+减少了子空间与核心节点的计算, 在一些节点稀疏的多维度图中, 可以减少接近50%的子空间聚类计算.如图 3所示, 因为在计算通信子空间中未发现聚类, 所以子空间通信+见面、通信+微信、通信+见面+微信不需要计算, 仅需计算剩余的3个子空间, 减少了57%的子空间聚类计算; 如果在计算图 3中见面子空间中也未发现聚类, 则所有高维度(k≥2)的子空间都不存在聚类.
5 实验分析本节首先介绍实验所用的数据集, 然后简要说明实验平台和设置方法, 最后给出程序运行结果和详细分析.由于目前学术界还没有能够运行在大规模多维结构图数据上的图聚类算法, 因此在本实验中, 主要是SCA与SCA+在参数ε, μ下的性能对比.
5.1 实验数据集介绍本实验将使用3个真实的数据集, 分别来源于斯坦福大学的官方数据集(http://snap.stanford.edu/data/)和科布伦茨网络收集数据集(http://konect.uni-koblenz.de/).3个数据都包含多种属性的无向边, 即为多维度图数据.数据集的相关信息见表 1.
| Table 1 Experimental datasets 表 1 实验数据集 |
5.2 实验平台介绍
本文所有程序均用C++语言实现, 实验环境为Intel(R) Xeon(R) CPU E5-2630 v3@2.40GHz, 该服务器具有双CPU, 每个CPU为八核, 并且支持超线程技术, 系统内存为32GB, 系统搭载的操作系统为Linux(Ubuntu16).
5.3 实验结果与分析实验共分两部分:第1部分(实验(1)), ε, μ不变, 在3个数据集上分别运行SCA与SCA+, 比较两种算法运行时间, 结果如图 4所示; 第2部分(实验(2)~实验(7)), 通过分别改变ε, μ的值, 在3个数据集上运行SCA与SCA+, 通过运行时间比较, 分析算法在参数改变下的稳定性, 结果如图 5所示.

|
Fig. 4 Comparison of operation efficiency between SCA and SCA+ in different datasets 图 4 不同数据集中SCA与SCA+算法效率对比 |

|
Fig. 5 Operational efficiency between SCA and SCA+ when ε=0.4, μ=3, 4, 5 & ε=0.3, 0.4, 0.5, μ=4 图 5 ε=0.4, μ=3, 4, 5与ε=0.3, 0.4, 0.5, μ=4时, SCA与SCA+的算法效率 |
(1) 分别取ε=0.4, μ=4, 在3个数据集上分别运行SCA与SCA+算法, 分析对比算法的运行时间.从结果来看, ego-Facebook数据集(8万条边)运行时间为SCA(1243ms), SCA+(823ms), 共获得各维度聚类417个; Flickr(230万条边)运行时间为SCA(120575ms), SCA+(96295ms), 获得聚类5 109个; 而Skitter(1100万条边)运行时间为SCA(586605ms), SCA+(540183ms), 共获得聚类190 080个.从结果图 4可以看出: SCA与SCA+在各种级别数据集上运行的效率对比, SCA+相对SCA有平均20%的效率提升;
(2) 分别取ε=0.4, μ=3, 4, 5, 在数据集ego-Facebook运行SCA与SCA+算法, 结果如图 5(a)所示:SCA分别为1326ms, 1243ms, 1216ms; SCA+分别为917ms, 823ms, 807ms;
(3) 分别取ε=0.4, μ=3, 4, 5, 在数据集Flickr运行SCA与SCA+算法, 结果如图 5(b)所示:SCA分别为128459ms, 120575ms, 122893ms; SCA+分别为100342ms, 96295ms, 96174ms;
(4) 分别取ε=0.4, μ=3, 4, 5, 在数据集Skitter运行SCA与SCA+算法, 结果如图 5(c)所示:SCA分别为585608ms, 586605ms, 598531ms; SCA+分别为545608ms, 540183ms, 558531ms;
(5) 分别取ε=0.3, 0.4, 0.5, μ=4, 在数据集ego-Facebook运行SCA与SCA+算法, 结果如图 5(d)所示:SCA分别为1325ms, 1243ms, 1176ms; SCA+分别为958ms, 823ms, 798ms;
(6) 分别取ε=0.3, 0.4, 0.5, μ=4, 在数据集Flickr运行SCA与SCA+算法, 结果如图 5(e)所示:SCA分别为128432ms, 120575ms, 117864ms; SCA+分别为97986ms, 96295ms, 95813ms;
(7) 分别取ε=0.3, 0.4, 0.5, μ=4, 在数据集Skitter运行SCA与SCA+算法, 结果如图 5(f)所示:SCA分别为554973ms, 586605ms, 591069ms; SCA+分别为541756ms, 540183ms, 538389ms.
从实验(2)~实验(7)可以看出各参数改变时, SCA与SCA+算法的稳定性.
从图 4结果可以看出:在ego-Facebook上, SCA+性能优化得最为明显, 这是因为SCA+相比SCA少遍历了约32%的子空间; 在Skitter下, SCA+仅提升了8.6%的效率, 这是因为两种算法遍历的子空间数相同(每个子空间都有聚类, 没有出现候选子空间的剪枝).SCA+的性能提升来自于减少了核心节点的计算数量, 而Flickr上SCA+的性能改善分别来自于候选子空间与候选核心节点的剪枝.
从图 5(a)、图 5(d)可以看出:在保持ε恒定、改变μ值与保持μ恒定、改变ε值的情况下, SCA+与SCA相比, 效率提升都超过30%.这是因为在数据稀疏的情况下, 某些子空间无法挖掘出社区聚类, 候选子空间的剪枝发生概率较大, 算法效率提升明显.
对图 5(b)、图 5(e)的结果进行分析可以看出, 算法运行保持稳定, 不会出现特别异常的聚类结果, 也没有出现异常的算法运行时间, 算法效率提升介于中间.
从图 5(c)、图 5(f)可以看出:在保持ε恒定、改变μ值的情况下, 算法保持稳定, SCA+与SCA相比, 效率提升都不超过10%.这个结果与实验(1)的结果类似, 在大数据集上, 因为各个子空间都不存在无聚类的情况, 所以没有发生候选子空间的剪枝, 算法效率提升都集中在候选核心节点的剪枝上.
6 实例分析为了验证本文提出算法的有效性与正确性, 即, 是否能够从多维子空间聚类中获得真实的社交关系, 本文与某通信运营商合作, 获取部分脱敏数据, 运行SCA+算法聚类后分析本文第1作者(节点3725)以及部分样本节点所在的各子空间聚类的社交圈.
实验数据集为经过运营商脱敏处理的社交数据, 数据为文本格式, 大小超过120G, 涵盖9个月连续的本地交互数据(不含外地交互数据), 主要包含3个维度的社交关系:通话(移动电话)、见面(处于同一基站扇区)、微信(移动电话号码匹配).根据数据情况, 使用SCA+分别生成3个维度下共7个子空间的聚类(包含点3725), 如图 6~图 8所示.图 6~图 8中, 聚类结果中不同维度的聚类用不同颜色的点表示, 例如, 图 6为一维聚类的结果, 黑色的节点仅在一维聚类中(如节点3934).绿色的节点不仅出现在一维聚类, 还在二维聚类中(如节点3917, 存在图 7(a)).红色的节点存在于一维、二维、三维的聚类(如点3725, 分别存在于图 6(a)、图 7(a)、图 8中).

|
Fig. 6 Clusters in 1st-demention 图 6 一维聚类 |

|
Fig. 7 Clusters in 2nd-demention 图 7 二维聚类 |

|
Fig. 8 Clusters in 3rd-demention 图 8 三维聚类(通话+见面+微信) |
实例分析的结果证明了算法的可行性与正确性:在一维聚类结果中, 存在很多与作者(节点3725)频繁交互但并不熟悉的人, 如外卖员、快递员等出现在通话聚类中; 二维聚类的人与作者较为紧密, 但也存在部分陌生人, 如在通话+微信聚类中有网店卖家, 作者曾与其多次通话和微信进行联系; 三维聚类结果中, 都是作者的家人或同事等关系紧密的社交对象.
为了更进一步分析、证明算法的正确性, 继续选取的几个有代表性的节点(节点2578, 2970, 3710)样本进行分析, 包含样本节点的三维聚类结果, 如图 9(a)~图 9(c)所示.
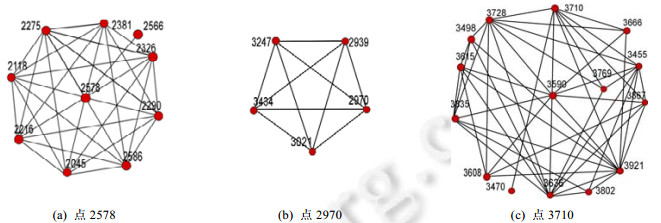
|
Fig. 9 Clusters of nodes 2578, 2970, 3710 in 3rd-demention 图 9 点2578, 2970, 3710的三维聚类 |
在图 9(a)中的样本节点2578为高中学生, 满足三维聚类亲密关系的节点大都为他的同学.可以看到:其他大部分节点都互为三维关系, 但点2566为2578的母亲(单亲家庭), 没有与其他节点存在联系.
图 9(b)展现的是样本节点2970的三维聚类, 2970为一个初创公司的技术合伙人, 三维聚类中, 其他4个节点都为公司同事, 聚类中没有父母、家人等是因为2970为单身青年, 另外, 父母在农村老家, 无使用手机习惯.
图 9(c)中的样本节点3710为某公司业务员, 可以在图中看出:与她进行多维度交互的人员较多, 交互对象多为其客户, 点3470为其配偶, 在聚类中只与3710发生交互.但是聚类中并无其父母, 这是因为实验所用的数据集中无3710与其父母在本地见面的联系(父母在外地).据3710证实, 9个月内并未和父母在本地见面(实验数据中的见面联系特定发生在本地).
从实例分析结果可以证明算法SCA在真实社交关系挖掘中的正确性与可行性.
7 总结及未来的工作本文首先简述传统的结构聚类算法在发现真实社交关系上的缺陷, 提出了在社交关系图数据上多维度挖掘概念.在此基础上, 首次提出了基于结构聚类的子空间聚类算法SCA, 算法能够自底向上、低维至高维地搜索出各维度的聚类集.接着分析了子空间聚类的算法单调性并加以证明, 在此基础上, 通过候选子空间剪枝与候选核心节点剪枝对SCA进行性能优化, 提出了改进算法SCA+, 实验和实例证明了算法的正确性和可行性以及SCA+在性能上相对SCA的提升与改善.
受限于实验数据的不完备性, 部分联系紧密的节点并未在聚类中体现.接下来, 我们将使用更大更完备的数据对算法进行测试.为了更深层[21, 22]地挖掘社交数据中的真实对象关系, 还将引入更多的数据信息对算法进行改进, 比如加入见面时间(白天、黑夜)、地点(写字楼、住宅区)等判断因素, 可以对社交关系进一步的明确.另外, 由于现实世界中所形成的图数据总是在不断发生变化、不断地进行更新, 所以有必要对已有的聚类进行动态维护, 未来我们也将在这方便展开相关研究.
| [1] |
Ye X, Huang Q, Li W. Integrating big social data. Computing and Modeling for Spatial Social Science, 2017, 43(5): 377–378.
[doi:10.1080/15230406.2016.1212302] |
| [2] |
Peng S, Wang G, Xie D. Social influence analysis in social networking big data:Opportunities and challenges. IEEE Network, 2017, 31(1): 11–17.
[doi:10.1109/MNET.2016.1500104NM] |
| [3] |
Bello-Orgaz G, Jung JJ, Camacho D. Social big data:Recent achievements and new challenges. Information Fusion, 2016, 28: 45–59.
[doi:10.1016/j.inffus.2015.08.005] |
| [4] |
Mokken RJ. Cliques, clubs and clans. Quality & Quantity, 1979, 13: 161–173.
[doi:10.1007/BF00139635] |
| [5] |
Seidman SB, Foster BL. A graph-Theoretic generalization of the clique concept. Journal of Mathematical Sociology, 1978, 6: 139–154.
[doi:10.1080/0022250X.1978.9989883] |
| [6] |
Borgatti SP, Everett MG, Shirey PR. LS sets, lambda sets and other cohesive subsets. Social Networks, 1990, 12: 337–357.
[doi:10.1016/0378-8733(90)90014-Z] |
| [7] |
Seidman SB. Internal cohesion of LS sets in graphs. Social Networks, 1983, 5: 97–107.
[doi:10.1016/0378-8733(83)90020-5] |
| [8] |
Seidman SB. LS sets as cohesive subsets of graphs and hypergraphs. Mathematical Social Sciences, 1983, 6: 87–91.
[doi:10.1016/0165-4896(83)90048-3] |
| [9] |
Seidman SB. Network structure and minimum degree. Social Networks, 1983, 5: 269–287.
[doi:10.1016/0378-8733(83)90028-X] |
| [10] |
Cohen JD. Trusses:Cohesive subgraphs for social network analysis. National Security Agency Technical Report, 2008.
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.505.7006 |
| [11] |
Wang J, Cheng J. Truss decomposition in massive networks. Proc. of the VLDB Endowment (PVLDB), 2012, 5: 812–823.
[doi:10.14778/2311906.2311909] |
| [12] |
Batagelj V, Zaversnik M. An O(m) algorithm for cores decomposition of networks. Computer Science, 2003, 1(6): 34–37.
https://arxiv.org/abs/cs/0310049 |
| [13] |
Xu X, Yuruk N, Feng Z, Schweiger TAJ. SCAN: A structural clustering algorithm for networks. In: Proc. of the ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. ACM Press, 2007. 824-833. [doi: 10.1145/1281192.1281280] |
| [14] |
Shiokawa H, Fujiwara Y, Onizuka M. SCAN++:Efficient algorithm for finding clusters, hubs and outliers on large-scale graphs. VLDB Endowment, 2015, 8(11): 1178–1193.
[doi:10.14778/2809974.2809980] |
| [15] |
Chang L, Li W, Lin X, Qin L, Zhang W. pSCAN:Fast and exact structural graph clustering. IEEE Trans. on Knowledge & Data Engineering, 2017, 29(2): 387–401.
[doi:10.1109/TKDE.2016.2618795] |
| [16] |
Chen JM, Chen JJ, Liu J, Huang YL, Wang Y, Feng X. Clustering algorithm for large scale social network based on structure similarity. Journal of Electronics and Information, 2015, 37(2): 449–454(in Chinese with English abstract).
[doi:10.11999/JEIT140512] |
| [17] |
Chen G, Huang RZ, Zhong WL. Multi-Dimensional text representation based on social features. Computer Engineering and Science, 2016, 38(11): 2348–2355(in Chinese with English abstract).
[doi:10.3969/j.issn.1007-130X.2016.11.029] |
| [18] |
Lu J, Peng X, Deng W, Mian A. Regularization techniques for high-dimensional data analysis. Image & Vision Computing, 2017, 60: 1–3.
[doi:10.1016/j.imavis.2017.03.001] |
| [19] |
He L, Cai YC, Yang Z. Survey of clustering algorithms for high-dimensional data. Application Research of Computers, 2010, 27(1): 23–26(in Chinese with English abstract).
[doi:10.3969/j.issn.1001-3695.2010.01.006] |
| [20] |
Kröger P, Kriegel HP, Kailing K. Density-Connected subspace clustering for high-dimensional data. In:Proc. of the Siam Int'l Conf. on Data Mining. 2004. 246-257.[doi:10.1137/1.9781611972740.23] |
| [21] |
Andris C. Integrating social network data into GISystems. Int'l Journal of Geographical Information Science, 2016, 30(10): 1–23.
[doi:10.1080/13658816.2016.1153103] |
| [22] |
Gao Q, Zhang FL, Wang RJ, Zhou F. Track data:A survey of key technologies in data processing. Ruan Jian Xue Bao/Journal of Software, 2017, 28(4): 959–992(in Chinese with English abstract).
http://www.jos.org.cn/jos/ch/reader/view_abstract.aspx?file_no=5143&flag=1 [doi:10.13328/j.cnki.jos.005143] |
| [16] |
陈季梦, 陈佳俊, 刘杰, 黄亚楼, 王嫄, 冯霞. 基于结构相似度的大规模社交网络聚类算法. 电子与信息学报, 2015, 37(2): 449–454.
[doi:10.11999/JEIT140512]
|
| [17] |
陈功, 黄瑞章, 钟文良. 基于社交特征的多维度文本表示方法. 计算机工程与科学, 2016, 38(11): 2348–2355.
[doi:10.3969/j.issn.1007-130X.2016.11.029]
|
| [19] |
贺玲, 蔡益朝, 杨征. 高维数据聚类方法综述. 计算机应用研究, 2010, 27(1): 23–26.
[doi:10.3969/j.issn.1001-3695.2010.01.006]
|
| [22] |
高强, 张凤荔, 王瑞锦, 周帆. 轨迹大数据:数据处理关键技术研究综述. 软件学报, 2017, 28(4): 959–992.
http://www.jos.org.cn/jos/ch/reader/view_abstract.aspx?file_no=5143&flag=1 [doi:10.13328/j.cnki.jos.005143]
|
 2018, Vol. 29
2018, Vol. 29


