2. 大数据存储与管理工业和信息化部重点实验室(西北工业大学), 陕西 西安 710129
2. Key Laboratory of Big Data Storage and Management(Northwestern Polytechnical University), Ministry of Industry and Information Technology, Xi'an 710129, China
随着信息提取和数据库管理系统的不断发展, 构建大规模知识库已成为工业界和学术界的研究热点, 典型系统有Yago[1]、Freebase[2]、Google knowledge graph[3]、DBPedia[4]、NELL[5]等.知识库构建(knowledge base construction, 简称KBC)的主要过程为:从结构和非结构数据源(比如文本、表格、图片)中获取关系型事实.比如, 谷歌知识图谱主要从Freebase、维基百科以及大规模网页内容中抽取知识, 到2016年底, 它已包含700亿条实体关系.这种以结构化形式存储信息的方式能够促进信息的有效处理和查询.
然而, 由于信息提取算法固有的概率特性和人类知识的局限性, 知识库系统通常存在不确定性和不完全性.因此, 通常需要以概率的方式去推断知识库中的缺失事实.而马尔可夫逻辑网(Markov logic network, 简称MLN)[6]是将一阶逻辑(first-order logic)和概率图模型(probabilistic graph model)相结合的一种统计关系型模型, 它可用于处理不确定的规则和事实.于是, 基于MLNs的概率知识库系统运用而生, 典型用例有Deepdive[7]、Elementary[8]、ProbKB[9]等.它们主要采用命题推断的思想, 其过程包括两个阶段:1)实例化(grounding)阶段——基于MLNs构建因子图; 2)推断(inference)阶段——在因子图上执行边缘推断.在Inference阶段, 已有的大多数概率知识库系统主要采用基于马尔可夫链蒙特卡罗(Markov chain Monte Carlo, 简称MCMC)的算法[10](比如吉布斯采样)在整个因子图上执行边缘推断(批量式), 即计算因子图中每个变量的边缘概率.
目前, 我们正采用MLN模型构建商品决策支持系统Poolside[11].其主要目标是:为用户提供针对性的推荐服务, 并可支持含有模糊概念的查询, 比如推荐一款性价比高的华为手机.在响应用户的查询时, 若采用以上批处理的方式执行边缘推断则耗时较多(商品数目通常较多), 而且也没有必要(用户并不可能对所有商品都感兴趣).尽管基于查询驱动的k-hop算法[12, 13]可加快推理过程, 但它很难同时在时间和精度上取得权衡:若跳跃步数k取值较大则精度较高, 但推理较慢; 若跳跃步数k取值较小则推理较快, 但精度较差.但事实上, 随着用户的不断访问, 概率知识库中的已推断事实会逐渐增加, 若能重复利用它们的推断结果计算其他查询事实的概率, 则可在保证精度的情况下降低计算量.
基于以上分析, 本文提出了一种基于近似因子的在线推理方法(online inference based on approximate factors), 记为OIAF算法.OIAF算法主要包括3个步骤:子图提取、添加并估算近似因子和边缘推断.其具体过程为:首先, 从因子图中提取查询变量的子图(含已推断变量); 然后, 为子图中的已推断变量添加近似因子以模拟子图外变量的影响, 并基于已推断变量的概率估算近似因子的取值; 最后, 采用团树算法在含有近似因子的子图上执行边缘推断.本文的主要贡献总结如下.
1) 针对概率知识库的在线查询场景, 提出了一种基于近似因子的在线推理算法.它主要利用已推断结果计算查询变量的边缘概率.
2) 在真实和模拟数据集上进行大量实验, 进而说明相对于k-hop算法, OIAF算法可在时间和精度上取得较好的权衡.
本文第1节综述概率知识库推理技术的相关工作.第2节介绍概率知识库的背景知识, 包括马尔可夫逻辑网及其推理过程的两个阶段:Grounding阶段和Inference阶段.第3节给出本文的研究问题和相关的符号定义, 并对OIAF算法的工作流程进行介绍.第4节通过实验说明OIAF算法可在时间和精度上取得较好的权衡.第5节对本文内容进行总结.
1 相关工作目前, 概率知识库的推理主要基于马尔可夫逻辑网模型, 它已广泛应用在社交网络分析(social network analysis)[14]、实体解析(entity resolution)[15]、信息提取(information extraction)[16]等领域.MLNs是将一阶逻辑与概率图模型相结合的一种统计关系型模型.它主要包括两种类型的推断方法:命题推断(propositional inference)和合一推断(lifted inference).命题推断主要采用概率图模型的推理算法[17], 比如置信传播、变分推断以及马尔可夫链蒙特卡罗等, 其主要思想为:基于MLNs构建概率图模型(比如因子图、马尔可夫网), 然后采用以上方法执行边缘推断.合一推断则基于一阶逻辑推理的思想, 主要算法有合一一阶置信传播(lifted first-order belief propagation)[18]、加权一阶模型计算(weighted first-order model counting, 简称WFOMC)[19]等.相对于合一推断, 目前, 命题推断的应用较为广泛.
本文主要采用命题推断的思想, 其过程主要包括两部分:Grounding阶段和Inference阶段.基于它的概率知识库系统主要有Alchemy[20], Tuffy[21], ProbKB[9], Deepdive[22]等.最初的Alchemy系统提出了一系列算法, 主要用于马尔可夫逻辑网的统计关系学习和概率逻辑推断, 并且主要在内存中实现.然而Alchemy系统的推理过程耗时较多, 为此Tuffy提出了混合架构的思想:Grounding阶段在RDBMS中实现, Inference阶段在内存中执行.但Tuffy并不适用于含有大规模规则的MLN, 于是, ProbKB通过利用关系表存储规则的方式实现了推理规则的批量式应用.另外, 考虑到概率知识库的推理过程通常是增量式的(随着新数据的到来), Deepdive提出了增量式构建知识库(incremental knowledge base construction)的方法.然而, 以上系统并未支持概率知识库的在线推理.
针对概率知识库的在线推理, 文献[12, 13]提出了基于查询驱动的k-hop算法, 但它很难同时在时间和精度上取得权衡.针对以上挑战, 本文提出了一种基于近似因子的在线推理方法.
2 概率知识库简介概率知识库是支持不确定型事实和规则的知识库, 是基于马尔可夫逻辑网进行定义的[9].本节主要介绍马尔可夫逻辑网及其推理过程的两个阶段:Grounding阶段和Inference阶段.
2.1 马尔可夫逻辑网马尔可夫逻辑网[6]是表示不确定事实和规则的数学模型.它由一阶加权子句构成, 其权重反映了该一阶子句成立的可能性.MLN的一个简单例子为
| $ 3.0\;\;smoke\left( x \right) \wedge friends\left( {x, y} \right) \Rightarrow smoke\left( y \right), \;\;\;2.0\;\;smoke\left( x \right) \Rightarrow cancer\left( x \right) $ | (1) |
其中, 第1个规则蕴含抽烟者的朋友也抽烟, 而另外一个规则蕴含抽烟会患癌症.然而, 这两条规则并不是绝对成立, 权重3.0和2.0分别用于度量规则成立的可能性程度:权重值越大, 说明规则越不容易被违反.下面给出MLNs的形式化定义.
定义1(马尔可夫逻辑网). MLNs是由一组加权子句{(Fi, wi), i=1, …, n}构成的集合, 其中, Fi为一阶子句, 而wi为其权重且
在概率知识库中, 基于MLNs构建因子图的过程称为Grounding.首先介绍因子图的相关知识.因子图由变量节点X={x1, x2, …., xN}和因子节点Φ={ϕ1, ϕ2, …, ϕM}组成, 其中, 因子ϕi为定义在Xi⊂X(Xi为X的子集)上的函数, 主要用于表示Xi中元素之间的关系.在Grounding阶段构建的因子图中, 变量节点表示概率知识库中的事实, 因子节点表示事实之间的因果关系.然后举例说明如何基于MLNs构建因子图.图 1以Friends & Smokers为例, 简单阐述了Grounding的基本过程.
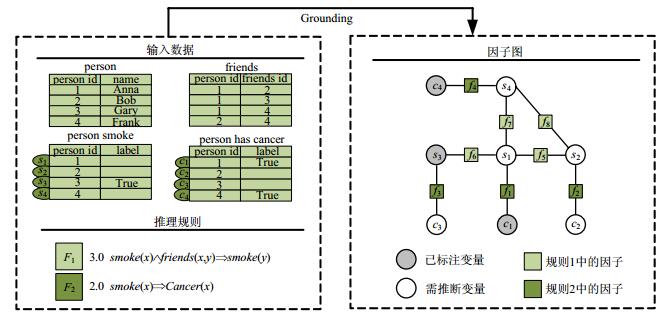
|
Fig. 1 Schematic illustration of grounding 图 1 Grounding示意图 |
比如, 在规则F2“2.0 smoke(x)⇒cancer(x)”中, 若x取值为Anna, 则可得到2个变量节点smoke(Anna)和cancer(Anna)(分别记为s1, c1, 如图 1所示)以及1个因子节点f1(s1, c1), 其函数值取决于规则的权重且表示为
| $ {f_1}\left( {{s_1}, {c_1}} \right) = \left\{ \begin{array}{l} 1, \;\;\;\;{\rm{if}}\left( {{s_1}, {c_1}} \right) = \left( {1, 0} \right)\\ {{\rm{e}}^{2.0}}, \;{\rm{otherwise}} \end{array} \right. $ | (2) |
依此类推, 实例化规则F1和F2中的变量, 进而可构建如图 1右半部分所示的因子图.
下面给出Grounding的形式化定义.
定义2(Grounding).给定马尔可夫逻辑网L={(Fi, wi), i=1, …, n}及常量集C, 则规则Fi的Grounding结果集为
Grounding阶段构建的因子图定义了一个关于随机变量X的概率分布[9]:
| $ P(X = x) = \frac{1}{Z}\prod\limits_i {{f_i}({X_i})} = \frac{1}{Z}\exp \left( {\sum\limits_i {{w_i}{n_i}(x)} } \right) $ | (3) |
其中, ni(x)=|{g|g∈G(Fi), x|=g}|, 即为G(Fi)中命题子句成立的数目; Z为规范化常数.Inference阶段的主要任务为:基于此概率分布, 计算因子图中变量节点的边缘概率.
在因子图中, 计算边缘概率的方法主要分为两种类型:精确计算和近似计算.精确计算方法主要有变量消除、团树算法等, 而近似计算方法主要有马尔可夫链蒙特卡罗和变分推断等.另外, 概率图模型中的精确推理和近似推理都是NP难问题[23].
3 OIAF算法本节首先给出本文的研究问题和相关的符号定义(第3.1节), 然后详细介绍OIAF算法的基本流程(第3.2节), 最后分析算法的复杂度(第3.3节).
3.1 问题描述及符号定义问题描述.给定概率知识库Grounding阶段构建的全局因子图和已推断变量, 本文的目标是利用已推断结果计算查询变量的概率.
第3.2节需涉及到k-hop子图的概念(示意图可参见后文图 3), 在此给出其形式化定义[13].

|
Fig. 3 An illustration of extracting subgraph 图 3 提取子图示意图 |
定义3(k-hop子图).给定因子图F中的因子节点{fi|0≤i≤N}、查询变量vq以及跳跃步数k, 若因子节点
针对以上研究问题, 本节提出了OIAF算法, 其基本流程如图 2所示.
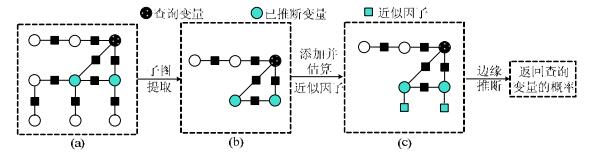
|
Fig. 2 Workflow of OIAF 图 2 OIAF算法的基本流程 |
它主要包括3个步骤:(1)子图提取; (2)添加并估算近似因子; (3)边缘推断.OIAF算法首先从全局因子图(如图 2(a)所示)中提取查询变量的子图(含已推断变量, 如图 2(b)所示); 然后, 为子图中的已推断变量添加近似因子以模拟子图外变量的影响(如图 2(c)所示), 并基于已推断变量的概率估算近似因子的取值; 最后, 在含有近似因子的子图(如图 2(c)所示)上执行边缘推断并返回查询变量的边缘概率.下面将详细介绍这3部分内容.
3.2.1 子图提取在因子图中, 若假定所有变量都一样, 则变量p和q之间的重要性[13]可表示为
| $ {I_p}\left( q \right) = \left\{ \begin{array}{l} C, \;\;\;\;\;\;\;\;\;\;{\rm{if}}\;d\left( {p, q} \right) = 1\\ C/{d^N}, \;\;\;{\rm{if}}\;d\left( {p, q} \right) > 1 \end{array} \right. $ | (4) |
其中, C为常数, N为正实数, d(p, q)为变量p和q之间需要跳跃的最小步数.也就是说, 随着两节点之间距离的增大, 它们之间的相互影响将会减弱.已有的k-hop算法正是基于此思想.它通过在查询变量的k-hop子图(如图 3(b)所示)上执行边缘推断, 从而实现概率知识库的在线推理.然而, 此算法通常存在以下两种情况:(1)若跳跃步数k的取值较大, 则推理精度较高, 但时间会较长; (2)若跳跃步数k的取值较小, 则推理较快, 但精度相对较低.对此, 本节提出了受约束的kcons-hop子图(如图 3(c)所示), 它本质上是k-hop子图(如图 3(b)所示)剪枝之后的结果.
kcons-hop子图的提取原则为:以查询变量为中心, 若在搜索路径上(k跳之内)遇到已推断变量, 则搜索停止; 否则执行最大跳跃步数k.虽然受约束kcons-hop子图相对于k-hop子图较小, 但通过利用已推断变量的信息可进一步提高推理的精确性, 详见第3.2.2节.提取kcons-hop子图的具体过程如算法1所示.
算法1.子图提取.
输入:全局因子图F, 查询变量vq, 跳跃步数k.
输出:kcons-hop子图Fsg.
1. BEGIN
2. Fsg=breadthFirstSearch(F, vq, k) //利用广度优先搜索提取子图
3. RERURN Fsg
4. END
3.2.2 添加并估算近似因子若直接在提取的受约束kcons-hop子图上执行边缘推断, 则会忽略子图之外变量的影响, 从而导致误差较大.为了进一步提高推理的精确度, 则可借助子图中已推断变量的概率信息.假定子图中已推断变量的概率较为精确, 则其在一定程度上反映了全局因子图中变量对它的影响.若通过给kcons-hop子图中已推断变量添加近似因子的方式能够使在含有近似因子的子图上推断得到的已推断变量的概率与已知概率相等, 近似因子则从一定程度上反映了子图之外变量的影响, 这是本文算法的基本原理.在概率知识库中, 因子图中的因子往往对应于相应的规则, 故添加近似因子相当于增加了相应的规则.另外, 我们将含有近似因子(approximate factor)的子图简称为AF子图.本文采用非线性方程组的思想求解近似因子的权重(即为近似因子相应规则的权重), 下面给出其形式化表示.
假定提取的kcons-hop子图为Fsg={fi|i=1, …, n}、子图中的已推断变量集为Isg={vj|j=1, …, m}及其相应的概率为Psg={p(vj)|vj∈Isg}、添加的近似因子集为
| $ f_j^*\left( {{v_j}} \right) = \left\{ \begin{array}{l} 1, \;\;\;\;\;{v_j} = 0\\ {{\rm{e}}^{{w_j}}}, \;\;{v_j} = 1 \end{array} \right. $ | (5) |
可记为
| $ \left\{ \begin{array}{l} \frac{1}{Z}\sum\limits_{V\backslash {v_1}} {\left[{\prod\limits_{i, j} {{f_i}f_j^*} } \right]} = p({v_1})\\ ...\\ \frac{1}{Z}\sum\limits_{V\backslash {v_m}} {\left[{\prod\limits_{i, j} {{f_i}f_j^*} } \right]} = p({v_m}) \end{array} \right. $ | (6) |
其中, Z为规范化常数, V为子图中的变量集.此方程组中未知变量的个数取决于已推断变量(近似因子)的数目, 且未知变量为
下面通过例子说明非线性方程组的具体构建过程.比如图 4(a)为原始因子图, 其中, 变量x1, x3为已推断变量, 变量x5为查询变量.假定提取的kcons-hop(k取值为2)子图如图 4(b)所示, 为了使查询变量x5的推断概率较为精确, 分别为已推断变量x1, x3添加近似因子

|
Fig. 4 An illustration of adding approximate factors 图 4 添加近似因子示意图 |
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{Z}\sum\limits_{{x_2}} {\sum\limits_{{x_3}} {\sum\limits_{{x_5}} {{f_1}({x_1}, {x_2}){f_2}({x_2}, {x_3}){f_3}({x_1}, {x_5}){f_4}({x_2}, {x_5})f_1^ * ({x_1})f_2^ * ({x_3})} } } = p({x_1})}\\ {\frac{1}{Z}\sum\limits_{{x_1}} {\sum\limits_{{x_2}} {\sum\limits_{{x_5}} {{f_1}({x_1}, {x_2}){f_2}({x_2}, {x_3}){f_3}({x_1}, {x_5}){f_4}({x_2}, {x_5})f_1^ * ({x_1})f_2^ * ({x_3})} } } = p({x_3})} \end{array}} \right. $ | (7) |
其中,
添加并估算近似因子的具体过程如算法2所示.此算法以kcons-hop子图Fsg和子图中已推断变量集Isg的概率为输入, 输出为AF子图
算法2.添加并估算近似因子.
输入:kcons-hop子图Fsg, 子图中已推断变量集Isg的概率.
输出:AF子图
1. BEGIN
2.
3. FOR EACH v∈Isg DO
4.
5.
6. END FOR
7. create equations like Eq.(6) and solve it
8. instantiation of the parameters in Faf
9.
10. RETURN
11. END
优化方案.在算法2中, 我们采用子图中的所有变量联合求解近似因子的权重, 但当子图较大或已推断变量较多时, 求解过程耗时较多.事实上, 在求解近似因子的权重时, 子图中变量的影响程度与距离有关:距离较近的变量影响较大, 距离较远的变量则影响较小.比如在图 5(a)中, 变量x2与近似因子

|
Fig. 5 An illustration of grouping 图 5 分组示意图 |
3.2.3 边缘推断
最后, 在AF子图上执行边缘推断, 进而返回查询变量的边缘概率.目前, 大部分概率知识库系统主要采用基于马尔可夫链蒙特卡罗的算法(比如吉布斯抽样)在大规模因子图上执行边缘推断任务.然而当因子图较小时, 若想获得较为精确的结果, 采样算法通常比精确推理算法(比如团树算法)耗时要多.考虑到本文提取的AF子图通常较小, 故采用团树算法执行边缘推断.边缘推断的具体过程如算法3所示.它以AF子图
算法3.边缘推断.
输入:AF子图
输出:查询变量的边缘概率p(vq).
1. BEGINE
2.
3. RETURN p(vq)
4. END
3.3 复杂度分析本节主要分析OIAF算法的复杂度.不妨设子图提取、添加并估算近似因子和边缘推断的时间复杂度分别为T1, T2, T3.下面分别对它们进行分析.
(1) 令全局因子图为F, 最大跳跃步数为k, 则利用广度优先搜索提取kcons-hop子图Fsg的时间复杂度为T1=O(bk+1)(https://en.wikipedia.org/wiki/Breadth-first_search)(k的取值通常较小, 默认值为2), 其中, b为图F的分支系数.
(2) 估算近似因子的过程主要包括两部分:构建方程组和求解方程组.令在分组求解中估算近似因子的组数为n, 各组中变量节点的最大阈值为Nvars, 则构建非线性方程组所需的时间为
(3) 文献[23]指出, 概率图模型中的精确推理和近似推理都是NP难问题, 故本文所采用的团树算法在最坏情况下需要指数时间.然而, 实际中提取的2cons-hop子图通常较小, 故可有效执行推理.另外, 该算法的空间复杂度为S=O(bd+1+m2).
4 实验及分析本文第4.1节对实验配置(包括运行环境、数据集等)进行详细说明.第4.2节为OIAF算法和k-hop算法的对比实验.第4.3节和第4.4节分别说明跳跃步数k和分组优化技术对OIAF算法性能的影响.
4.1 实验配置实验所用的编程语言为Python, 且运行环境配置为Intel(R) Core(TM) i5-6300HQ 2.30GHz处理器, 16GB内存, Ubuntu 16.04 LTS 64位操作系统.实验选用了两部分数据集:(1) Poolside商品知识库[11], 主要为用户提供针对性的推荐服务; (2) Friends & Smokers知识库[18], 主要用于社交网络.数据集的相关统计信息见表 1.
| Table 1 Statistics of the datasets used in the experiment 表 1 实验中所用数据集的统计信息 |
在实验中, 若选取因子图中的所有变量作为查询变量, 则耗时较多且没有必要.于是, 本文分别从Poolside和Friends & Smokers中随机选取83和153个变量作为查询节点.已有在线推理算法的精度评估标准为:在线推理结果与全局推断结果的绝对误差.但若仅仅将这些查询变量的平均绝对误差作为精确性的评估标准, 则很难得知OIAF算法(或k-hop算法)在低误差和高误差区间上的具体分布情况.于是, 我们将误差区间[0, 1]切分为7部分(如后文图 6所示):第1部分为[0, 0.005](低误差区间); 最后一部分为(0.03, 1](简记为others, 高误差区间); 其余部分为(0.005, 0.01], (0.01, 0.015]), (0.015, 0.02], (0.02, 0.025]和(0.025, 0.03];并分别统计了在各误差区间上查询变量所占的比例.同理, 时间区间[0, ∞)(单位为s)被划分为6部分:第1部分为[0, 2](低响应区间); 最后一部分为[10, +∞)(简记为others, 高响应区间); 其余部分为(2, 4], (4, 6], (6, 8]和(8, 10].以上数据集中已推断变量的选取比例均为20%.另外, 考虑到精度和时间之间的相互影响(类似于信息检索中精确率和召回率之间的关系), 本文对它们的权衡采取类似的准则:Fβ=(1+β2)pept/(β2pe+pt), 其中, pe为低误差区间[0, 0.005]内的百分比(精度的度量), pt为低响应区间[0, 2]内的百分比.由于相对于精度, 在线算法的时间响应更为重要, 因此本文选取β=2.F2的取值越大, 说明精度和时间之间的权衡越好.

|
Fig. 6 Comparison results of error and time on Poolside (OIAF vs. k-hop) 图 6 Poolside上各误差和时间的对比结果(OIAF vs. k-hop) |
OIAF算法的默认设置为kcons-hop子图中的跳跃步数k为2, 采用分组优化技术求解近似因子的权重.
4.2 OIAF算法vs. k-hop算法本节主要通过OIAF算法和k-hop算法在Poolside和Friends & Smokers数据集上的对比实验来说明OIAF算法可以在精度和时间上取得较好的权衡.
图 6为两种算法在Poolside数据集上误差和时间的对比结果, 表 2为此对比实验在各误差和时间区间内所占百分比的详细信息, 表 3为误差和时间的相关统计信息(比如均值和标准差).
| Table 2 Percentage of each error and time interval on Poolside (OIAF vs. k-hop) 表 2 Poolside上各误差和时间区间内所占的百分比(OIAF vs. k-hop) |
| Table 3 Statistics of error and time on Poolside (OIAF vs. k-hop) 表 3 Poolside上误差和时间的统计信息(OIAF vs. k-hop) |
误差对比结果如图 6(a)所示, 其横坐标为误差区间, 纵坐标为在每个误差区间上查询变量所占的百分比.分析得知:OIAF算法在低误差区间[0, 0.005]上的比例高达67.47%, 而在高误差区间内的比例较低(仅为6.02%); 1-hop算法则正好相反, 它在低误差区间上的比例极低, 而在高误差区间上的比例极高(高达79.52%); 2-hop算法相对于1-hop算法, 精确性虽然有所提升, 但它在低误差区间和高误差区间上的表现均没有OIAF算法好.时间对比结果如图 6(b)所示, 其横坐标为时间区间, 纵坐标为在每个时间区间上查询变量所占的百分比.结果表明: 1-hop算法的推理速度最快(集中在低响应区间[0, 2]上的比例为100%); OIAF算法的推理速度次之, 它在低响应区间上的比例达到93.98%;而2-hop算法的推理速度相对较慢.分析得知:1-hop算法的推理速度较快但误差较大; 2-hop算法虽然在准确性上有所提升但推理相对较慢, 而OIAF算法在时间和精度上的表现均较好.另外, 在精度和时间的权衡方面, OIAF, 1-hop和2-hop算法的F2值分别为0.871 3, 0.0和0.284 5.综合分析可知, OIAF算法可在时间和精度上取得较好的权衡.
图 7为两种算法在Friends & Smokers数据集上的误差和时间对比结果, 表 4为此对比实验在各误差和时间区间内所占百分比的详细信息, 表 5为误差和时间的相关统计信息(比如均值和标准差).

|
Fig. 7 Comparison results of error and time on Friends & Smokers (OIAF vs. k-hop) 图 7 Friends & Smokers上误差和时间的对比结果(OIAF vs. k-hop) |
| Table 4 Percentage of each error and time interval on Friends & Smokers (OIAF vs. k-hop) 表 4 Friends & Smokers上各误差和时间区间内所占的百分比(OIAF vs. k-hop) |
| Table 5 Statistics of error and time on Friends & Smokers (OIAF vs. k-hop) 表 5 Friends & Smokers上误差和时间的统计信息(OIAF vs. k-hop) |
图 7(a)和图 7(b)表明:相对于k-hop算法(k分别取1, 2, 3), OIAF算法在低误差区间上的比例明显较高, 且推理速度也相对较快(仅慢于1-hop算法).另外, 在评测精度和时间之间的权衡时, OIAF, 1-hop, 2-hop和3-hop算法的F2值分别为0.832 1, 0.031 7, 0.174 2和0.153 6.由此可进一步说明, 相对于k-hop算法, OIAF算法可在精度和时间上取得较好的权衡.
4.3 跳跃步数k对OIAF算法的影响本节实验主要比较不同跳跃步数k对OIAF算法的影响.在上述实验中, k的默认取值为2.图 8测评了k取不同值(1, 2, 3)时, OIAF算法在Friends & Smokers数据集上误差和时间的对比结果, 表 6为此对比实验在各误差和时间区间内所占百分比的详细信息.
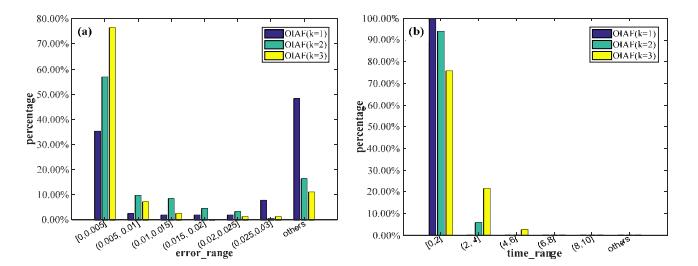
|
Fig. 8 Comparison results of error and time for OIAF (k=1, 2, 3) on Friends & Smokers 图 8 OIAF(k=1, 2, 3)在误差和时间上的对比结果(Friends & Smokers) |
| Table 6 Percentage of each error and time interval for OIAF (k=1, 2, 3) on Friends & Smokers 表 6 OIAF(k=1, 2, 3)在各误差和时间区间内所占的百分比(Friends & Smokers) |
图 8(a)表明:在低误差区间[0, 0.005]上, k=1时比例最低, k=2时次之, k=3时最高.图 8(b)表明:整体来看, k=1时推理速度最快, k=2时次之, k=3时推理相对较慢.另外, 当k取1, 2, 3时, 计算得知, OIAF算法的F2值分别为0.731 7, 0.832 1和0.759 5.综合分析得知:当k=2时, OIAF算法在精度和时间上的均衡较好.
4.4 分组求解对OIAF算法的影响本节实验主要说明分组求解优化技术对OIAF算法的影响.图 9给出了在数据集Friends & Smokers上, 分组优化技术对OIAF算法的影响, 表 7为此对比实验在各误差和时间区间内所占百分比的详细信息.
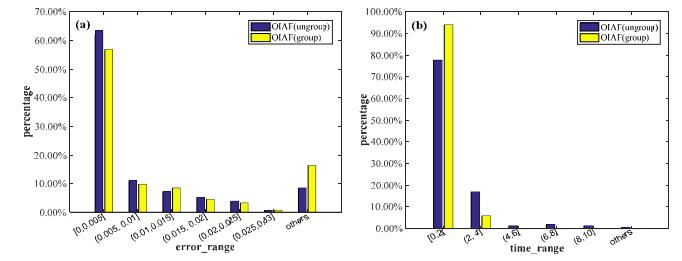
|
Fig. 9 Performance for the OIAF approach with the optimization technique on Friends & Smokers 图 9 分组求解优化技术对OIAF算法的影响(Friends & Smokers) |
| Table 7 Percentage of each error and time interval for OIAF (ungroup/group) on Friends & Smokers 表 7 OIAF(ungroup/group)在各误差和时间区间内所占的百分比(Friends & Smokers) |
图 9(a)表明:若采用分组优化技术, 则在低误差区间的比例只有稍微下降.但从图 9(b)可以看出, 分组优化技术明显加快了推理过程.另外, 在权衡精度和时间时, OIAF算法在未分组和分组情形下的F2值分别为0.744 0和0.832 1.综合分析得知, 分组求解对OIAF算法具有一定的有效性.
5 总结针对概率知识库的在线查询场景, 本文提出了一种基于近似因子的在线推理方法.其主要思想为:重复利用已推断结果计算查询变量的概率.该算法通过子图提取和添加近似因子的方式, 在含有近似因子的子图上执行边缘推断, 进而计算查询变量的概率.相对于已有算法, 该算法能够在时间和精度上取得较好的权衡.另外, 在对概率知识库进行增量式推理时, 需要根据已推断结果来更新节点信息, 故本文算法可进一步推广到增量式推理场景中.
| [1] |
Suchanek FM, Kasneci G, Weikum G. Yago: A core of semantic knowledge. In: Proc. of the 16th Int'l Conf. on World Wide Web (WWW 2007). Banff: ACM Press, 2007. 697-706. [doi: 10.1145/1242572.1242667] |
| [2] |
Bollacker K, Evans C, Paritosh P, Sturge T, Taylor J. Freebase: A collaboratively created graph database for structuring human knowledge. In: Proc. of the ACM SIGMOD Int'l Conf. on Management of Data (SIGMOD 2008). Vancouver: ACM Press, 2008. 1247-1250. [doi: 10.1145/1376616.1376746] |
| [3] |
Singhal A. Introducing the Knowledge Graph:Things, Not Strings. Official Google Blog, 2012.
https://link.springer.com/content/pdf/10.1007/978-3-319-49493-7_1.pdf |
| [4] |
Auer S, Bizer C, Kobilarov G, Lehmann J, Cyganiak R, Ives Z. Dbpedia: A nucleus for a Web of open data. In: Proc. of the 6th Int'l Semantic Web Conf., 2nd Asian Semantic Web Conf. (ISWC2007, ASWC 2007). Busan: Springer-verlag, 2007. 722-735. [doi: 10.1007/978-3-540-76298-0_52] |
| [5] |
Carlson A, Betteridge J, Kisiel B, Settles B, Hruschka ER, Mitchell TM. Toward an architecture for never-ending language learning. In: Proc. of the 24th AAAI Conf. on Artificial Intelligence (AAAI 2010). Atlanta: AAAI Press, 2010. 1306-1313. |
| [6] |
Richardson M, Domingos P. Markov logic networks. Machine Learning, 2006, 62(1): 107–136.
[doi:10.1007/s10994-006-5833-1] |
| [7] |
Zhang C. DeepDive:A data management system for automatic knowledge base construction. Madison: University of Wisconsin-Madison, 2015.
|
| [8] |
Niu F, Zhang C, Ré C, Shavlik J. Elementary:Large-Scale knowledge-base construction via machine learning and statistical inference. Int'l Journal on Semantic Web and Information Systems, 2012, 8(3): 42–73.
[doi:10.4018/jswis.2012070103] |
| [9] |
Chen Y, Wang DZ. Knowledge expansion over probabilistic knowledge bases. In: Proc. of the 2014 ACM SIGMOD Int'l Conf. on Management of Data (SIGMOD 2014). Snowbird: ACM Press, 2014. 649-660. [doi: 10.1145/2588555.2610516] |
| [10] |
Wick M, Mccallum A, Miklau G. Scalable probabilistic databases with factor graphs and MCMC. Proc. of the Vldb Endowment, 2010, 3(1): 794–804.
[doi:10.14778/1920841.1920942] |
| [11] |
Zhong P, Li ZH, Chen Q, Wang YY, Wang LP, Ahmed MHM, Fan FF. Poolside: An online probabilistic knowledge base for shopping decision support. In: Proc. of the 26th ACM Int'l Conf. on Information and Knowledge Management (CIKM 2017). Singapore: ACM Press, 2017. 2559-2562. [doi: 10.1145/3132847.3133168] |
| [12] |
Zhou X, Chen Y, Wang DZ. ArchimedesOne:Query processing over probabilistic knowledge bases. Proc. of the VLDB Endowment, 2016, 9(13): 1461–1464.
[doi:10.14778/3007263.3007284] |
| [13] |
Li K, Zhou X, Wang DZ, Grant C, Dobra A, Dudley C. In-Database batch and query-time inference over probabilistic graphical models using UDA-GIST. The VLDB Journal, 2017, 26(2): 177–201.
[doi:10.1007/s00778-016-0446-1] |
| [14] |
Singla P, Kautz H, Luo J, Gallagher A. Discovery of social relationships in consumer photo collections using Markov logic. In: Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPRW 2008). Anchorage: IEEE Computer Society, 2008. 1-7. [doi: 10.1109/CVPRW.2008.4563047] |
| [15] |
Singla P, Domingos P. Entity resolution with Markov logic. In: Proc. of the 6th Int'l Conf. on Data Mining (ICDM 2006). Hong Kong: IEEE Computer Society, 2006. 572-582. [doi: 10.1109/ICDM.2006.65] |
| [16] |
Poon H, Domingos P. Joint inference in information extraction. In: Proc. of the 22nd AAAI Conf. on Artificial Intelligence. Vancouver: AAAI Press, 2007. 913-918. |
| [17] |
Bishop CM. Pattern Recognition and Machine Learning (Information Science and Statistics). New York: Springer-Verlag, 2006.
|
| [18] |
Singla P, Domingos P. Lifted first-order belief propagation. In: Proc. of the 23th AAAI Conf. on Artificial Intelligence. Chicago: AAAI Press, 2008. 1094-1099. |
| [19] |
Van den Broeck G, Taghipour N, Meert W, Davis J, De Raedt L. Lifted probabilistic inference by first-order knowledge compilation. In: Proc. of the 22nd Int'l Joint Conf. on Artificial Intelligence. Barcelona: IJCAI Press, 2011. 2178-2185. [doi: 10.5591/978-1-57735-516-8/IJCAI11-363] |
| [20] |
Kok S, Singla P, Richardson M, Domingos P. The Alchemy system for statistical relational AI. 2007. http://www.cs.washington.edu/ai/alchemy |
| [21] |
Niu F, Ré C, Doan AH, Shavlik J. Tuffy:Scaling up statistical inference in Markov logic networks using an RDBMS. Proc. of the VLDB Endowment, 2011, 4(6): 373–384.
[doi:10.14778/1978665.1978669] |
| [22] |
Shin J, Wu S, Wang F, De SC, Zhang C, Ré C. Incremental knowledge base construction using deepdive. Proc. of the VLDB Endowment, 2015, 8(11): 1310–1321.
[doi:10.14778/2809974.2809991] |
| [23] |
Koller D, Friedman N, Wrote; Wang FY, Han SQ, Trans. Probabilistic Graph Model. Beijing: Tsinghua University Press, 2015(in Chinese). |
| [23] |
Koller D, Friedman N, 著; 王飞跃, 韩素青, 译. 概率图模型. 北京: 清华大学出版社, 2015.
|
 2018, Vol. 29
2018, Vol. 29


