2. 安徽大学 计算机科学与技术学院, 安徽 合肥 230601;
3. 合肥工业大学 计算机科学与信息工程学院, 安徽 合肥 230009;
4. School of Computing and Informatics, University of Louisiana at Lafayette, Lafayette 70503, USA
2. School of Computer Science and Technology, Anhui University, Hefei 230601, China;
3. School of Computer Science and Information Engineering, Hefei University of Technology, Hefei 230009, China;
4. School of Computing and Informatics, University of Louisiana at Lafayette, Lafayette 70503, USA
随着大数据时代的到来, 模式匹配技术已被广泛应用到生物信息学[1]、空气质量监测[2]、数据流挖掘[3]以及信息检索与过滤等重要领域[4].在生物信息学方面, 研究者利用模式匹配技术, 借助TATA框, 能够快速地从数以亿计的DNA序列中定位内含子的起始位置, 通常会在CAATCT后30个~50个字符出现, 可以表示成…CAATCT[30, 50]TATA…[5]; 在空气质量监测方面, 通过空气质量传感器可以实时地监测一个城市周边的空气质量指数, 地理位置相近的传感器检测到的空气质量指数变化往往具有相关性, 利用模式匹配技术监测变化是否具有周期性的特点, 可以帮助人们找到该城市空气污染的主要因素并采取措施防止污染扩散[2]; 在数据流挖掘方面, 利用模式匹配技术能够找出模式在数据序列中出现的位置, 有效地预测数据流的变化规律[3]; 在信息检索方面, 可通过带间隙的模式匹配技术从网络上大量的文本信息中正确检索出用户所需要的信息[6].
Fischer等人首次在模式匹配中提出了通配符的概念[7].通配符可以代表任意的字符, 记为Φ, 如aΦcΦΦg随后, Manber等人[5]将通配符的个数从固定值变为可变值, 但没有限制字符个数的最大长度.Chen等人[8]提出了独立通配符的概念, 形如P=p0[min0, max0]p1…pj…[minm-2, maxm-2]pm-1, 其中, minj和maxj分别指pj和pj+1之间通配符个数的最小值和最大值, 当各个间隙区间都相同时, 称为周期间隙[9].Liu等人[10]对带间隔约束与one-off条件的序列模式匹配问题进行了研究, 通过CluTree结构, 提高了匹配解的完备性.
上述研究讨论的均是非负间隙的模式匹配, 即在进行匹配过程中, 子模式pj一定出现在pj+1之前.由于序列的有序性, 采用非负间隙的模式匹配技术无疑禁止了子模式串次序颠倒现象的发生.然而在实际生活中, 这种次序颠倒的现象普遍存在, 若采用非负间隙进行模式匹配, 就会漏掉一些有价值的信息.例如, 通过检测人体的某段DNA序列中含有CAATCT基因片段的数目, 可以判断是否患有某种疾病.由于基因片段在转录的过程中发生变异, 片段"AT"和"CT"出现了位置颠倒, 同时, 变异后的基因与原基因具有相同的致病效果, 我们进行模式匹配时不仅要统计DNA序列中CAATCT出现的次数, 而且还要统计变异后出现的次数.此时, 如果利用非负间隙模式匹配进行统计, 则会忽略变异情况; 如果利用一般间隙模式匹配, 则可以准确地进行统计.Fredriksson等人[11, 12]对间隙可以为负情况下(称为一般间隙)的模式匹配进行了研究, 但未对序列中的每个位置能否被多次使用进行讨论.之后, 柴欣等人[13]采用网树结构, 在一般间隙模式匹配问题上进行研究, 允许序列中的每个位置能够被多个出现使用; 文献[14]中考虑了one-off条件, 即模式的任意两次出现都不共享序列中的相同位置[13]. one-off条件更加符合实际需要, 如上述的生物学的例子, 由于基因在转录过程中形成特定的RNA, 所以DAN序列中的位置最多只能被致病基因匹配1次.
综上所示, 利用一般间隙与one-off条件的模式匹配进行序列挖掘, 能够发现更多有价值的信息, 更符合实际应用的需要.由于序列模式匹配是序列挖掘的关键步骤, 本文对基于一般间隙与one-off条件的序列模式匹配(sequential pattern matching with general gaps and one-off condition, 简称SPMGOO)进行研究.该问题有如下5个特点:是NP-Hard问题; 是一种精确的模式匹配; 是一种严格的模式匹配; 是基于one-off条件的模式匹配; 模式串中的间隔可以为负值.
一般间隙模式匹配通过并、或运算可以分解成非负间隙模式匹配[15].而相对于非负间隙约束, 一般间隙约束更具有灵活性, 因为非负间隙约束都需要在前一事件发生在后一事件之前的理想情况下进行模式匹配.然而在实际生活中, 事件发生的顺序是可以改变的, 如上述对DNA中致病基因的分析.同时, one-off条件也更加符合实际需要, 如典型的序列模式挖掘的例子, 购买了手机, 一段时间后很可能购买手机配件, 则每一次购买手机与手机配件应该只作为1次出现统计.因此, 利用一般间隙的模式匹配进行序列挖掘能够发现更多有价值的信息, 具有更大的实际应用价值.本文的主要贡献如下.
(1) 提出了一般间隙与one-off条件的序列模式匹配问题SPMGOO.
在具有间隙约束的模式串中, 允许子模式串之间的间隙为负值; 同时加入了one-off条件, 允许序列串中任意位置的字符最多使用1次的精确的严格模式匹配.之后, 通过理论证明了SPMGOO问题为NP-Hard问题.
(2) 首次使用线性表解决SPMGOO问题, 并且在模式匹配的过程中首次提出对模式串结构以及符号集S中各个元素在序列串中的频度进行分析, 判断是否需要转置操作, 使模式与序列达到最佳匹配状态.
(3) 提出了基于一般间隙与one-off条件的最大数目的序列模式匹配算法MSAING.
MSAING算法首先采用Reverse策略判断是否需要转置操作; 然后, 利用线性表的结构进行模式匹配, 具体分为Locate阶段、Forward阶段、Backward阶段, 使MSAING算法在模式匹配过程中消耗的时间和内存大为减少, 同时, 在Backward阶段使用回溯机制, 使匹配的成功率大幅度提高; 最后, 提出了inside_Checking机制判断模式串是否会产生内部重复现象, 以及如果产生内部重复会在模式串的哪个位置产生, 从而有效地提高了MSAING算法的运行效率.经过理论分析得出, MSAING算法的时间复杂度为O(MSAING)=O(n+kmg(l+m)), 空间复杂度为O(lm).其中, n为序列串的长度, k表示字符pm-1在序列串S中出现的频度, m为模式串P的长度,
(4) 从理论上证明了MSAING算法的正确性和完备性, 并对比测试了MSAING算法的性能.
SPMGOO问题为NP-Hard问题, 本文首先从理论上证明了MSAING算法比目前已有算法具有更好的完备性, 对于不含重复的模式能够取得完备解; 其次, 本文在真实的生物数据集以及文本上, 与DCNP等多种相关的改进算法进行了对比实验, 通过实验结果验证了MSAING算法具有较高的准确性和较低的时空复杂度, 并对实验结果及其意义进行了分析.
本文第2节对相关工作进行总结.第3节给出SPMGOO问题的定义和相关理论分析.第4节介绍MSAING算法设计的过程, 并分析算法的时间和空间复杂度以及算法的正确性与完备性.第5节通过大量对比实验验证MSAING算法的性能.第6节给出结论.
1 相关工作目前, 对于带有间隙约束的模式匹配问题的研究可以分为以下6个方面:是周期模式匹配还是具有多个可变间隙的模式匹配; 是精确匹配还是近似匹配; 是严格模式匹配还是宽松模式匹配; 一般间隙与否; 是否具有one-off条件; 是否具有长度约束[13].
Fischer等人在1974年首次在模式匹配中提出了通配符的概念[7].在研究模式匹配过程中, 根据通配符的不同形成了5类研究成果:最先开始研究的是连续的模式匹配问题[7], 即子模式串之间不含通配符; 子模式串之间通配符的个数是非负且固定的[16]; 子模式串之间通配符的个数范围为0~∞[17], 用[0, ∞]表示, 如ac[0, ∞]t表示ac和t之间可以有无穷多个通配符; 子模式串之间通配符的个数范围是上下限可变的非负数[8], 其中的特例是, 当每个间隙的变化范围相同时, 称为带周期间隙的模式匹配[18], 如a[1, 2]c[1, 2]t; 若子模式串之间的通配符的变化范围可以为负数时称为一般间隙模式[15], 如例1中的模式串为一般间隙模式串.对于带通配符的模式匹配的研究发展过程如图 1所示.

|
Fig. 1 Development process of pattern matching with wildcard 图 1 带通配符的模式匹配的发展过程 |
近几年来, 随着带一般间隙模式匹配问题研究的深入, 人们逐渐意识到一般间隙模式匹配问题的重要性. Myers[19]最早对一般间隙模式匹配问题进行了研究, 接着, Fredriksson等人[11, 12]分别在2006年和2008年对一般间隙模式匹配问题进行研究, 并应用到蛋白质序列匹配和音乐信息检索等领域.武等人在网树结构的基础上做了大量模式匹配方面的研究, 其中, 在文献[20]中通过将SGSP算法和SRMP算法相结合提出了SBO算法, 并在对一般间隙及one-off条件的严格模式匹配问题进行研究的基础上[13]提出了DCNP算法.但是, 基于网树结构的算法在模式匹配过程中时间和空间开销较大, 而且算法仅考虑到局部最优而忽略了模式以及序列本身所具有的特性.
在文献[8]中, Chen等人提出了SAIL算法.该算法在one-off条件约束下进行模式匹配, 利用one-off条件过滤掉大量冗余信息, 提高了匹配的效率.但是算法只适合在线的模式匹配, 在离线的模式匹配情况下, 解的完备性较差.Lam等人[21]利用one-off条件对压缩序列模式挖掘问题进行了研究.表 1对比了几种具有间隙的模式匹配算法.
| Table 1 Comparison of pattern matching with gap constraints 表 1 几种具有间隙约束的模式匹配对比 |
从表 1可以看出, 本文与文献[8, 13]的研究工作比较接近, 但本文与文献[8]主要区别在间隙的类型不相同.文献[8]为非负间隙与one-off条件下的在线模式匹配, 因为在非负间隙的条件下, 模式子串pj对应序列串中字符的位置一定在pj+1之前, 因此在匹配出现解的过程中, 只需要从前向后单向扫描即可.本文研究的是间隙可以为负的一般间隙的模式匹配, 而在一般间隙的条件下, 模式子串pj对应在序列串中字符的位置可能在pj+1之后, 从而在一个出现中可能有内部重复的现象.因此, 本文提出的MSAING算法不仅需要考虑如何避免出现与出现之间的位置重复, 还要考虑如何避免出现的内部重复, 求解难度更大, 也更具有实际意义.
本文与文献[13]的区别在于:文献[13]一次性地在整个序列串上建立网树结构, 当序列串或模式串较长时, 将消耗大量的时间和内存空间; 文献[13]中提出的DCNP算法属于贪心算法, 容易陷入局部最优, 从而无法获得全局最优解.本文提出利用线性表解决SPMGOO问题, 通过线性表对序列分段存储、分段匹配, 减少了时间和空间的消耗; 本文所提出的MSAING算法通过对模式串、序列串的整体形式分析, 使模式匹配的解尽可能地达到全局最优, 并且利用回溯的方法提高匹配的成功率, 采用检测机制提高执行效率, 所以与DCNP相比效率更高, 更加接近匹配的完备解.
2 SPMGOO问题 2.1 问题定义定义1.序列串S={(s0s1…si…sn-1)|si∈Σ, 1≤i≤n-1}, 其中, n表示序列串S的长度.si∈S代表符号集, 应用场景不同, Σ代表的符号也不相同, 如, DNA序列中的符号集合Σ是由{A, C, G, T}构成的; 而在音乐信息检索方面, Σ由音符构成.
定义2.具有间隙约束的模式P可表示成
| $ P = \{ ({p_0}\left[{{\rm{mi}}{{\rm{n}}_0}, {\rm{ma}}{{\rm{x}}_0}} \right]{p_1} \ldots [{\rm{mi}}{{\rm{n}}_j}_{-1}, {\rm{ma}}{{\rm{x}}_j}_{-1}\left] {{p_j} \ldots } \right[{\rm{mi}}{{\rm{n}}_m}_{-2}, {\rm{ma}}{{\rm{x}}_m}_{-2}]{p_m}_{ - 1})|{p_j} \in \mathit{\Sigma }\}, $ |
其中, m表示模式串的长度; minj, maxj为给定的整数值, 分别表示pj和pj+1之间间隙的最小值和最大值, 且满足minj≤maxj.若模式串P中的间隙满足{∃mini<0|0≤i≤m-1}的条件, 则模式串P称为一般间隙模式串; 否则, 模式串P称为非负间隙的模式串.
定义3.给定模式串P=p0[min0, max0]p1…pj…[minm-2, maxm-2]pm-1, 如果pi=pj, 其中, 0≤i.j≤m-1且i≠j, 则模式串P称为带重复字符的模式串, 简写为R模式(pattern with recurring characters), 如a[0, 1]c[0, 2]c[0, 1]t; 否则称为不含重复字符的模式串, 简写为NR模式.若p0=p1=…=pj成立, 则模式串P称为首部重复的模式串, 简写为RH模式, 如a[0, 1]a[0, 2]c; 同理, 如果pi=pi+1=…=pm-1, 则模式串P称为尾部重复的模式串, 简写为RT模式, 如a[0, 1]c[0, 2]c.
定义4.若一个序列S中的位置索引occ=<o0, o1, …, oj, …, om-1>, 其中, 0≤j≤m-1, 0≤oj≤n-1满足以下的条件:
| $ {S_{{o_j}}} = {p_j} $ | (1) |
| $ {o_j}_{ - 1} \ne {o_j} $ | (2) |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\min }_{j - 1}} \le {o_j} - {o_{j - 1}} - 1 \le {{\max }_{j - 1}}, {\rm{ if }}{o_{j - 1}} < {o_j}}\\ {{{\min }_{j - 1}} \le {o_j} - {o_{j - 1}} \le {{\max }_{j - 1}}, \;\;\;\;\;{\rm{ if }}{o_{j - 1}} > {o_j}} \end{array}} \right. $ | (3) |
则称occ是模式串P在序列串S中满足间隙约束的一个出现.
定义5.给定一个出现occ=<o0, …, oj, …, om-1>, 若ok=oq(k≠q, 0≤k, q≤m-1)的情况存在, 则称为有内部重复的出现; 否则, 称为无内部重复的出现.
定义6.给定两个无内部重复的出现
定义7.令集合OCCSPMGOO表示模式串P在序列串S中的满足一般间隙与one-off条件的出现, 其大小用|OCCSPMGOO|表示, 本文即计算具有one-off条件的一般间隙的最大模式匹配数目, 即求|OCCmax|的最大值.
2.2 理论分析一般间隙约束的模式匹配存在内部重复的可能, 但并不是所有的模式匹配都会出现内部重复.下面分析在哪些情况下可能出现内部重复.
(1) 非负间隙的模式串不会有内部重复的出现, 因为模式串中的字符pj一定在pj-1的后面出现, 如a[0, 1]c[0, 3]a.
(2) NR模式不会有内部重复的出现, 因为模式串中的每个字符不可能在序列串中占用相同的位置, 如Pt=a[0, 2]c[-1, 1]t.
(3) 只有在一般间隙约束下的R模式才可能有内部重复的出现, 即pj=pi(0<j, i≤m-1), 并且pj可能出现在pi之后, 如P=a[0, 1]c[-1, 2]c[-1, 2]c.
为了避免有内部重复的出现以及提高算法的执行效率, 针对可能出现内部重复的情况, 本文提出了内部重复检测机制.引理1说明了需要进行内部重复检测的条件.
引理1.在一般间隙模式匹配中, 当模式串P的长度大于等于2时, 如果pj=pj+k+1, 并且满足
证明:给定模式串P=p0[min0, max0]p1…[minj-1, maxj-1]pj…[minm-2, maxm-2]pm-1, pj出现的位置设为h, pj到pj+k+1的间隙约束为[minj, maxj]…[minj+k, maxj+k], 所以pj+k+1出现的最小位置为
定理1.一般间隙与one-off条件的模式匹配的判定问题的计算复杂性为NP-Complete问题.
证明:文献[13]给出了具体的计算复杂性的证明, 此处从略.
由于一般间隙与one-off条件的模式匹配的判定问题的计算复杂性为NP-Complete问题, 所以一般间隙与one-off条件的序列模式匹配的优化问题为NP-Hard问题.如何匹配出最优的完备性的解集以及大幅度地降低时空消耗, 是本文的核心任务.同时, 在一般间隙模式匹配问题中如何有效地避免出现与出现之间的重复, 判断内部重复可能产生的范围并有效地消除范围被放大的影响, 这就是本文处理SPMGOO问题中比较复杂的环节.下面将通过介绍MSAING算法给出这些问题的解决方案.
3 MSAING算法分析及设计 3.1 SAING算法Chen等人[8]提出了SAIL算法在非负间隙约束下解决在线模式匹配问题, 在NR模式的情况下取得了完备的解, 而R模式的情况下匹配结果较差.因此, 本文在此基础上提出了SAING算法, 在一般间隙与one-off条件下, 使R模式匹配取得完备解, NR模式匹配取得最优解.
SAING算法包括3个部分:Locate phase, Forward phase, Backward phase[8].Locate阶段查找序列串中位置i, 满足{i|si=pm-1}, 即模式串的尾字符pm-1在序列串中匹配的位置; Forward phase判断能否建立搜索表; 如果搜索表建立成功, 则Backward phase找出一个最优出现.由于Locate phase比较简单, 所以下面将分别从算法1: Forward phase以及算法3:Backward phase具体地介绍SAING算法.其中, Backward phase根据一般间隙的特性需要考虑内部重复出现[13]、回溯机制提高解的完备性.
3.1.1 Forward phase算法的设计Forward phase主要是判断能否建立搜索表, 算法返回值是布尔型.在第1行中, 对能否成功建立搜索表的标记位进行初始化, 初值为false; 第2行计算模式串匹配的范围, 设定可达到的最大位置为limit, 最小位置为start; 第3行初始化一个长度为limit-start+1的搜索表table, 如图 2所示.通过对搜索表进行遍历(第4行、第5行), 首先找出p0可能出现的位置, 即如果sj未被使用, 并且与p0相同, 则对位置j标记(第6行、第7行); 第8行~第14行找出p1~pm-1的所有出现:如果sj未被使用, 与pi相同, 并且搜索表table中在[mini-1, maxi-1]范围内pi-1已被标记, 则表明在间隙约束范围内有pi的出现, 对pi也进行标记; 只有当pm-1在end处被标记时, 才完成搜索表的建立, 否则无法建立搜索表(第17行~第19行).
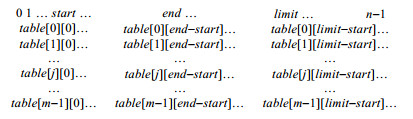
|
Fig. 2 Search table 图 2 搜索表 |
算法1. Forward phase.
输入:标志数组used, pm-1在序列中的位置end.
输出:flage_table.
1. falg_table=false;
2. 计算模式串匹配的范围为[start, limit];
3. creat_table(); //创建一个长度为len=limit-start+1的线性表
4. for i=0 to m-1
5. for j=start to limit
6. if (!used[j] and sj=pi and i=0) then
7. table[i][j-start]=1;
8. else if (!used[j] and sj=pi) then
9. for k=mini-1 to maxi-1
10. if (table[i-1][j-k-start]=1) then
11. table[i][j-start]=1
12. end if
13. end for
14. end if
15. end for
16. end for
17. if (table[m-1][end-start]=1)
18. flag_table=true;
19. end if
20. return flag_table
文献[8]提出了使用线性表解决非负间隙模式匹配问题, 并且极大减少了空间的消耗.然而, 由于一般间隙模式匹配相对于传统的非负间隙问题更加复杂, 因此本文重新设计了线性表的长度计算, 并首次提出了利用线性表解决SPMGOO问题, 建立的搜索表如图 2所示.该搜索表的行数为模式串的长度, 列数为模式串在序列串中可能匹配的范围的大小, 即limit-start+1, 不大于序列串的长度n, 从而有效地节约了内存空间.
3.1.2 内部重复出现检测机制通过引理1的分析证明可知, 一般间隙与one-off条件的模式匹配问题需要考虑内部重复出现的情况.因此, 本文提出了内部检测机制, 通过减少重复检测的次数来提高执行效率.具体检测过程如算法2所示.本文采用线性表的结构, 并增加了一个布尔型的标志数组incheck, 用于标记pj和pi的出现位置是否有重复的可能(其中, 0≤j<i≤m-1), incheck的初始值为false(第1行).由上述分析可知, 如果模式串中间隙全为非负间隙, 或者不包含重复字符则不会有内部重复的情况出现(第2行~第6行); 否则, 从pm-2开始依次向前查找, 检查pm-2是否会与pm-1发生重复.如果pm-2=pm-1并且minm-2<0, 则将pm-2的incheck设置为true, 否则继续向前检测pm-3.以此类推, 直到检测完p0为止(第8行~第15行).如, P=a[-2, 3]c[0, 4]a[-1, 3]a[-1, 5]g[0, 1]g, 标记incheck={1, 0, 1, 0, 0, 0}, 即当匹配模式串的0, 2位置上的字符时, 需要内部重复检测.
算法2. inside_Checking.
输入:模式串P.
输出:标志数组incheck.
1.初始化incheck标志数组全为false
2. if (∀mini≥0, 0≤i≤m-2) then
3. return incheck;
4. end if
5. if (∀pi≠pj, 0≤i, j≤m-1, i≠j) then
6. return incheck;
7. else
8. for i=m-2 downto 0
9. for j=i+1 to m-1
10. if
11. incheck[i]=true;
12. break;
13. end if
14. end for
15. end for
16. end if
17. return incheck
3.1.3 回溯机制一般间隙约束的模式匹配比非负间隙约束的模式匹配更为复杂, 这是由于在非负间隙约束的模式匹配中, 模式是顺序匹配的, 即pj+1匹配的位置一定在pj之后; 而在一般间隙约束的模式匹配中, pj+1可能出现在pj之前.为了提高解的完备性, 本文提出了回溯机制, 即当pj+1的一次匹配不成功时, 回溯到上一层pj重新选择一条路径再次进行匹配, 直至回溯到pm-1时还没有找到满足条件的路径时, 则结束本次匹配.具体思路如例1所示.
例1:将序列串S=aacccccccacc, 模式串P=a[-1, 2]c[-1, 2]c[-1, 2]c转置, 即得到序列串S'=ccacccccccaa, 模式串p'为c[-1, 2]c[-1, 2]c[-1, 2]a, 进行模式匹配.当end=2时, 如图 3所示, 按照文献[8]提出的SAIL算法, 即最左优先策略, 所匹配的路径为图中点线圆形箭头的指向, 则出现数为0.这时, 需要利用回溯机制回到
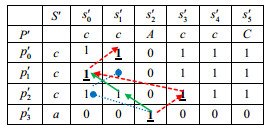
|
Fig. 3 Search table for sequence S' and pattern p' 图 3 序列S'和模式p'对应的搜索表 |
算法3. Backward phase.
输入:table搜索表, pm-1在序列中的位置end.
输出:出现occ.
1. occm-1=end
2. back_flag=false;
3. 计算标志数组incheck //算法2 inside_Checking
4. for i=m-2 to 0
5. if (!back_flag) then计算kmin, kmax
6. else kmin=occi+1
7. end if
8. for k=kmin to kmax
9. if (table[i][k-start]=1) then
10. if (incheck[i] & & 内部重复) then continue; //只有当incheck[i]为真时, 才判断是否内部重复
11. else
12. occi=k
13. back_falg=false;
14. break;
15. end if
16. end if
17. end for
18. if (k>kmax) then
19. if (i=m-1) then return occ=NULL;
20. else then
21. back_flag=true;
22. i=i+2; //回溯机制回溯
23. end if
24. end if
25. end for
26. return occ;
Forward phase完成搜索表的建立后, 启动Backward phase, 按照最左优先匹配策略, 返回一个出现occ.首先从pm-1开始向左进行匹配, 因此, 第1行~第3行将pm-1在序列中的位置end存放于occm-1, 设置回溯标志位back_flag初值为false, 并调用算法2 inside_Checking内部重复检查, 以判断模式串中需要检查的字符位置; 然后遍历模式串并按照最左优先匹配的策略进行模式匹配(第4行~第25行), 其中, 第5行、第6行计算pi可以匹配的范围, kmin, kmax分别为pi可以到达的最小值和最大值, 由于间隙[mini, maxi]的范围不同, 可分为mini≥0, maxi<0, mini<0≤maxi这3种情况计算, 当需要回溯时, 则回溯到pi+1位置, 由上次pi+1选择的后一个节点开始; 然后, 在[kmin, kmax]范围内遍历搜索表(第8行), 如果搜索表在此范围内有标记, 则需要判断incheck[i]是否为真.
● 如果incheck[i]为真, 则需要内部检测才进行内部重复的判断, 而如果内部有重复, 则进入[kmin, kmax]范围内的下一位置的判断(第9行、第10行).
● 如果incheck[i]为假, 或者incheck[i]为真而不存在内部重复, 则位置k作为pi匹配的位置(第11行~第14行).
如果超出[kmin, kmax]范围还没有pi匹配的位置, 则需要回溯机制(第18行~第24行).其中, 如果已经回溯到pm-1, 则该搜索表上的匹配不成功, 出现为空(第19行); 否则, 将back_flag标记为真, 回溯到pi+1重新匹配(第20行~第23行).
3.1.4 SAING算法设计SAING为主程序, 获得所有出现以及出现的个数, 具体设计如算法4所示.首先对序列串S由s0开始扫描, 当序列串中某个字符与模式串的尾字符相同时, 完成Locate阶段(第2行).第3行利用Forward phase判断搜索表能否成功建立:如果能够成功建表, 则启动Backward phase, 找出一个最优出现(第4行~第6行).如果Backward phase匹配的解不为空, 则把本次查找到的出现occ加入到出现集合OCC中, 并将出现中的位置标记为已使用(第7行~第12行), 继续向后扫描, 扫描至序列串S结束为止.
算法4. SAING.
输入:P=p0[min0, max0]p1…[minm-2, maxm-2]pm-1, S=s0s1…sn-1.
输出:|OCCSPMGOO|.
1. for i=0 to i<n
2. if (si=pm-1) then //Locate phase
3. flag_table=Forward phase(); //算法1
4. if (flag_table)
5. occ=Backward phase(); //算法3
6. end if
7. if (occ)
8. OCCSPMGOO=OCCSPMGOO∪occ
9. for j=0 to m-1
10. used[occj]=true
11. end for
12. end if
13. end if
14. end for
15. return |OCCSPMGOO|
SAING算法是利用线性表的结构实现一般间隙与one-off条件下的模式匹配, 为了进一步提高匹配的完备性, 本文在SAING算法的基础上, 采用Reverse策略提出了MSAING算法.该算法通过对模式串结构以及符号集S中各个元素在序列串中的频度进行分析, 判断模式串是否需要转置处理, 以使出现数目达到最大值.
3.2 Reverse策略与MSAING算法 3.2.1 Reverse策略定理2.对序列串S、模式串P同时执行转置操作, 不影响出现的正确性.
证明:给定序列串S=s0…sn-1, 模式串P=p0…pm-1, 同时对其执行转置操作, 分别表示成
引理2.在模式匹配的过程中, 使频度较大的字符出现在模式前端, 可以提高匹配的成功率.
证明:形如P=p0[min0, max0]p1…[minj-1, maxj-1]pj…[minm-2, maxm-2]pm-1, 当pm-1=sj完成定位时, 即end=j, 开始启动Forward阶段建立搜索表.建立搜索表的过程由p0开始建立, p0出现的频率越高, 可供p1选择的范围越大, 匹配的位置越多.而p1匹配的位置越多, 相应地, p2选择的范围越大, 匹配的位置就越多.以此类推, 建立的搜索表能够形成的回溯路径越多, 则Backward阶段可供选择的路径增加, 得到的匹配解的个数也会增多.
引理3.若模式串P为RT模式, 将模式串P与序列串S同时转置, 可以提高匹配的完备性.
证明:给定序列串S=s0…sstart…send…slimit…sn-1, 其中, 0≤start<limit≤n-1, 给定RT模式P为P=p0[min0, max0]…pi…[minm-2, maxm-2]pm-1, 其中, pi=pi+1=…=pm-1.假设pm-1=send, pi匹配的位置为sj(start≤j≤limit).如果在[sstart, slimit]有一个出现occ, 当间隙区间较小时, 由于对于序列串S继续向后扫描, [sj, slimit]相对集中出现了字符pm-1, 导致S中的其他字符因为不满足间隙约束, 在[sstart, sj]区间匹配的概率大为降低.间隙区间越小, 重复的字符数目越多, 匹配的完备性就越差.
模式串P、序列串S分别转置为P', S', 表示为S'=sn-1…slimit…send…sstart…s0, P'=pm-1[minm-2, maxm-2]… pi…[min0, max0]p0, 其中, 1≤i≤m-1, pm-1=pm-2=…=pi, 则模式P'为RH模式.pi匹配的位置为sj(start≤j≤limit), 同理可得, [slimit, sj]相对集中出现pm-1, [sj, sstart]区间内字符分布均匀, 所以在下一次匹配过程中, [sj, sstart]区间内未被使用的位置可被其他字符使用.引理3得证.对于Reverse策略, 通过例2进行说明.
例2:给定序列串S=aacccccccacc, 模式串P=a[-1, 2]c[-1, 2]c[-1, 2]c, SAING算法首先对模式串建立标志位数组incheck={0, 1, 1, 0};然后, 在定位阶段扫描序列串S, 找到s2=pm-1=p3, 所以end=2;启动Froward阶段, 根据模式串的间隙, 计算模式串在序列串上可以匹配的范围为[0, 5], start=0, limit=5, 建立搜索表len=6, 如图 4所示.

|
Fig. 4 Search table when end=2 图 4 end=2时的搜索表 |
由于end=2位置可以标记为1, 则启动Backward阶段匹配出最优出现, 从p3=2开始, 然后按照最左优先的策略匹配, 在执行p2时, 由于s0, s1均标记为0, 且incheck[2]=1, 需要内部检测是否重复, 而s2已经被p3占用, 所以若s2不满足条件则选择s3, 同理可得p1选择s4, p0选择s1.图 4中, 加粗、下划线的<1, 4, 3, 2>即表示为一次出现, 将序列串中的位置<1, 4, 3, 2>标记为已使用.继续向后扫描序列, 当end=5时, 进入Forward阶段, 计算start=0, limit=8, 建立len=9的搜索表, p0在s0标记为1, 但由于序列中<1, 4, 3, 2>已经被使用, 所以在[-1, 2]的间隙内p1无法标记, 因此搜索表无法成功建立, 不启动Backward阶段.继续扫描向后扫描序列, 当end=6时, 计算start=0, limit=9, 建立len=10的搜索表, 如图 5所示(其中带*的列, 表示已被使用), 序列中<9, 8, 7, 6>的位置为一次出现.同理, 继续向后扫描, 若都不满足条件, 则结束程序.出现集合为{<1, 4, 3, 2>, <9, 8, 7, 6>}, |OCCSPMGOO|=2.

|
Fig. 5 Search table when end=6 图 5 end=6时的搜索表 |
例2中的模式串P为RT模式, 并且序列串字符"c"出现的频度较高, 符合Reverse策略.因此, 对序列串S、模式串P同时进行转置操作, 分别得到S'=ccacccccccaa, 模式串p'=c[-1, 2]c[-1, 2]c[-1, 2]a.然后, 再按照SAING算法进行模式匹配, 扫描序列串S', 当end=2时,
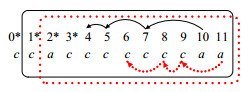
|
Fig. 6 Pattern matching when end=10, 11 图 6 end=10, 11时的模式匹配 |
3.2.2 MSAING算法
由例2可知, 通过对模式串P的形式分析, 判断是否需要转置, 可以在很大程度上提高SAING算法的完备性.对于给定的模式串P, 可分为以下几种情况来讨论.
1) 模式串P是RT模式不是RH模式, 则需要对模式串和序列执行转置操作(第1行~第3行).
2) 模式串P不是RT模式而是RH模式, 不需要转置..
3) 模式串P既是RT模式又是RH模式, 这时需要进一步比较模式前端与后端字符重复的数目:如果后端相同字符数目较多, 则需要对模式串与序列串执行转置操作; 如果前端相同字符数目较多, 则不需要转置; 如果前端与后端相同字符数目相同, 则需比较两端重复字符在序列串中的频度, 如果后端频度大, 则需要转置, 否则不需要转置(第4行~第15行).
4) 模式串P既不是RT模式又不是RH模式, 需要比较模式前端与后端第1个不相同的字符在序列串中出现的频度:如果后端出现的频度大, 则需要转置; 否则不需要转置(第16行~第20行).具体详细过程见算法5.
算法5. MSAING算法.
输入:P=p0[min0, max0]p1…[minm-2, maxm-2]pm-1, S=s0s1…sn-1.
输出:最大的出现数目|OCCmax|.
1. if (RT(P) and!RH(P)) then
2. reverse(P, S) //转置P, S
3. end if
4. if (RT(P) and RH(P)) then
5. hcount={i|p0=p1=…=pi, 1≤i≤m-2} //首字符重复的数目
6. tcount={m-j|pj=pj+1=…=pm-1, 1≤j≤m-2} //尾字符重复的数目
7. if (tcount>hcount) then
8. reverse(P, S)
9. end if
10. if (tcount=hcount) then
11. if (frequence(p0)<frequence(pm-1))
12. reverse(P, S)
13. end if
14. end if
15. end if
16. if (!RT(P) and!RH(P))
17. if (frequence(pi)<frequence(pm-1-i)) //pi为首尾两端第1个不相同的字符
18. reverse(P, S)
19. end if
20. end if
21.调用算法4:SAING算法
22. return |OCCmax|
3.3 算法分析通过对以上5种算法的介绍可知, MSAING算法的时间复杂度等于SAING算法复杂度.SAING算法时间主要消耗在定位阶段、Forward阶段和Backward阶段.其中, 定位阶段时间复杂度为O(n), 主要对序列的一次完整的扫描; Forward阶段时间复杂度为O(lmg), 其中,
引理4.给定序列串S, 模式串P, occ为模式串P在序列串S上满足一般间隙约束的一个出现, 若occ没有被MSAING算法作为一个出现, 则occ与出现集合OCC中至少一个出现不满足one-off条件.
证明:为了方便证明, 不妨证明其逆否命题.假设OCC为MSAING算法输出的出现集合, occ与OCC中的任意一个出现都满足one-off条件, 则occ一定会被MSAING算法作为一个出现的解.
由于MSAING算法在Forward阶段将所有满足条件的位置进行标记, Backward阶段是由pm-1开始按照最左优先进行模式匹配, 则occ中的位置为线性表中的一组匹配.由one-off条件的性质可知, occ中的任意位置都没有被使用, 则在匹配的过程中由occm-1开始, 根据假设, 在匹配过程中occ未被作为出现, 则一定是由于另一个出现occ'选择了occ的位置, 其中,
定理3.在NR模式情况下, MSAING算法取得完备解.
证明:利用反证法进行证明.设OSM为MSAING算法计算的解, 而OSC为完备解.假设|OSM|<|OSC|, 为了简化证明不妨假设|OSM|=1, 而|OSC|=2, 其中, OSM={O}, OSC={A, B}:
● O={o0, o1, …, om-1};
● A={a0, a1, …, am-1};
● B={b0, b1, …, bm-1}.
若O与{A, B}满足one-off条件, 则|OSC|=3, 与假设矛盾; 由引理4知, O与A、O与B不满足one-off条件.
所以, ∃0≤u, w, i, k<m, 使得au=oi, bw=ok (ⅰ)
则
因此, pu=pi, pw=pk.
下面分两种情况分别加以讨论.
1.当u≠i或者w≠k时, 模式P为R模式, 与P为NR模式条件相矛盾.
2.当u=i, w=k时, 下面再分为情况(1)、情况(2)两种情况来讨论.
(1) 当u=w时, 由(ⅰ)可知, au=oi=ou, bw=ok=ow, 而u=w, 则au=oi=ok=bw.
所以, 当u=w时, 出现A与出现B不满足one-off条件, 与假设相矛盾.
(2) 当u≠w时, 为了不失一般性, 不妨假设u<w,
由于O是MSAING算法采用最左优先策略匹配的解,
所以, ou=bu, ow=aw. (ⅱ)
所以, 由(ⅰ)、(ⅱ)得:au<bu, bw<aw, 则出现A, B可以表示为如下的形式:
| $ \begin{array}{c} A = ....{a_u}.............................{a_w}..., \\ B = .............{b_u}..........{b_w}... \end{array} $ |
所以, ∃t, u≤t<m满足下面的条件; 又由于模式P为一般间隙约束, 则可以分为形式①~形式④这4种
形式进行分析:
① at<bt<bt+1<at+1, 则bt+1-bt<at+1-bt<at+1-at;
② at<bt+1<bt<at+1, 则bt+1-bt<at+1-bt<at+1-at;
③ at+1<bt<bt+1<at, 则at+1-at<at+1-bt<bt+1-bt;
④ at+1<bt+1<bt<at, 则at+1-at<at+1-bt<bt+1-bt.
上述4种情况表明, at+1, bt之间满足间隙约束条件, 所以, <b0, …, bu, …, bt, at+1, …, aw, …, am-1>是模式串P在序列串S上, 与出现O满足间隙约束与one-off条件的另一个出现, 而与引理4相矛盾.故假设不成立, 定理3得证.
4 实验结果及分析 4.1 实验环境本节采用真实生物数据对比SAIL_Gen, RSAIL_Gen, SGSP_Gen, SBO_Gen, RBCT_Gen, DCNP和MSAING算法的性能, 其中, 前4种算法分别为在一般间隙约束下对文献[8, 10, 13, 20, 24]中算法SAIL, RSAIL, SGSP, SBO, RBC的改进, 即不改变算法的执行步骤, 只是扩展间隙约束的范围, 使其可以在一般间隙约束条件下进行模式匹配; DCNP来自于文献[13]实验运行的软、硬件环境为:Intel(R) Core(TM)i3-4170 CPU@3.70GHz, 4.0GB内存, 操作系统为Window7, 64位操作系统, 程序使用C++语言编写, 并且采用Microsoft Visual Studio 2013集成开发环境进行编译和运行.为了验证算法的性能, 本文采用文献[13]所使用的真实数据——序列数据库SDB1作为测试序列.同时, 为了更好地验证算法在实际应用中大规模的数据上的性能, 实验还分别采用了表 2中描述的序列数据库SDB2, SDB3, SDB4, 其中, SDB2, SDB3在文献[25]中作为大规模的数据集, 用于算法性能检测.表 2中所有的DNA片段、DNA序列库都可以从美国国家生物计算信息中心的网站下载(http://www.ncbi.nlm.nih.gov/).蛋白质序列库可以从http://gi.cebitec.uni-bielefeld.de/comet/force/indexOld.html上下载.表 3描述的是文献[13]中的序列数据库SDB1包含的12个序列的特征.
| Table 2 Characteristic of experimental data 表 2 实验数据集特征 |
| Table 3 Sequences of real biological data in SDB 表 3 SDB1真实生物数据片段 |
4.2 实验结果及分析 4.2.1 DNA片段上算法的比较
DNA控制RNA的转录以及遗传信息, 因此, 通过对DNA片段进行特定的模式匹配, 找出匹配解的个数, 对于致病基因以及遗传信息的检测、病毒传播的预防等起着重要的作用.一般间隙模式匹配有利于灵活地找出模式匹配个数的精确解, 通过对匹配解的数目分析, 对生物学中基因遗传的研究具有重要的价值.下面将具体介绍MSAING以及对比算法在DNA片段上的性能.为了分别对比测试MSAING算法在模式串不存在重复字符以及存在重复字符时的求解性能, 选取了P1~P4模式为不存在重复字符的4种模式, P5~P9模式为存在重复字符的5种模式, 具体模式串在表 4中给出.这7种算法的模式串的测试结果见表 5, 其中给出了各种算法在不同模式下得到的出现数的总和; 表 6给出了各种算法在不同模式以及序列下的消耗时间总和.
| Table 4 Patterns 表 4 模式串 |
| Table 5 Comparison of the number of occurrences of P1~P9 between 7 algorithms 表 5 7种算法在P1~P9上的出现个数 |
| Table 6 Comparison of the running time on P1~P9 between 7 algorithms (s) 表 6 7种算法在P1~P9上的运行时间 (s) |
(1) 在模式串中不存在重复字符的情况下, MSAING, SAIL_Gen, RSAIL_Gen均属于完备算法.文献[8, 24]证明了这种情况, 从表 5中可以看出, MSAING能够达到完备的情况, 与定理2的理论分析相一致.
(2) 在模式串中有重复字符的情况下, MSAING算法性能最好, DCNP算法性能次之, SAIL_Gen算法性能最差.p5~p9模式串中具有重复的字符, 其中, p8为首部重复模式, p9为尾部重复模式, 从表 5可以清晰地看到, SAIL-Gen不能在任何实例上取得最好的结果; 而且模式串p5~p9在12个序列的出现总和中, SAIL-Gen算法取得了最小值, 占MSAING算法匹配数的88%, 而DCNP算法获得了次优匹配, 占MSAING算法匹配数的97%.这充分说明, 对于R模式不宜采用SAIL-Gen算法进行求解.DCNP算法在处理RH模式和RT模式上完备性较低, 产生这种现象的原因是:DCNP算法在SBO_Gen算法的基础上动态更新节点属性, 采取每次选择出现相关数较少的策略, 因而其可以很好地解决one-off条件下一般间隙的模式匹配问题.但是, 由于只是局部最优的贪婪算法, 因此未必能够达到全局最优, 这种缺陷在连续重复字符的模式串, 如RH和RT模式串上表现更为明显.而MSAING算法通过最左侧匹配以及回溯方法使每次匹配达到局部最优, 同时采用内部检测机制避免内部重复, 利用Reverse策略对模式串的结构以及符号集S中各个元素在序列串中的频度进行分析, 使其达到最佳的匹配状态, 保证匹配达到全局最优.
(3) 根据表 6时间消耗可知, DCNP算法消耗时间最长, RBCT_Gen算法消耗时间最少; 而在不存在重复字符的模式串中, MSAING算法消耗的时间次之; 在存在重复字符的模式串中, SAIL-Gen算法消耗的时间次之.SAIL是文献[8]提出的一种在线算法, 具有最好的时间性能来解决非间隙模式匹配问题, SAIL-Gen和MSAING算法继承了这种特性, 当模式串不存在重复字符, 进行一般间隙模式匹配时, SAIL-Gen需要判断是否内部重复, 消耗了大量的时间, 而MSAING算法具有内部检查机制使时间消耗减少; 在存在重复字符的模式串匹配中, MSAING算法为了提高解的完备性, 增加了回溯的功能, 使消耗的时间变多.虽然SAIL-Gen耗时较少, 但是基于一般性模式匹配问题时, 求解性能很差, 因此不宜采用SAIL-Gen算法进行求解.同理, RBCT_Gen利用CluTree结构, 在匹配的过程中减少了时间的消耗, 但是相对于MSAING和DCNP算法, 求解性能较差.DCNP算法在SBO_Gen算法的基础上动态更新节点属性, 因此所用的时间最长.综上所述, MSAING算法解的性能优于DCNP和SBO_Gen算法.
通过将MSAING算法与其他各种算法在SDB1数据集上进行对比可知:MSAING算法的匹配解比DCNP提高了2%, 比SAIL_Gen提高了12%.MSAING算法是通过Reverse策略提高匹配解的数目的, 下面将通过实验进一步验证Reverse机制的有效性.
4.2.2 Reverse机制有效性验证为了验证Reverse机制的有效性, 在数据集SDB1上选取需要转置的模式串p5, p6, p9, 计算每个模式串在12条DNA片段上解的和.由图 7可知, MSAING算法转置后的解的完备性较高, 说明了Reverse机制的有效性.这是由于MSAING算法通过对模式串结构的分析以及序列串中个字符元素的频度的计算, 找出最佳的模式匹配形式, 使解的完备性得到了提高.
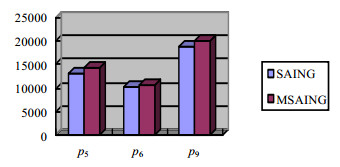
|
Fig. 7 Validation of effectiveness of Reverse strategy 图 7 Reverse机制有效性验证 |
本实验验证了Reverse策略的有效性, 使匹配解的平均数目提高了5.6%.下面将通过在序列数据库中比较算法的性能, 证明MSAING算法能够在较大规模的数据库上进行有效的模式匹配.
4.2.3 序列库中算法性能的比较随着蛋白质产品在人们日常生活中应用的普及, 蛋白质检测在生物学领域得到了广泛的研究.食品中营养蛋白的检测、药物中蛋白酶以及胰岛素的检测以及蛋白质中氨基酸序列的检测等, 都需要对蛋白质序列进行某些特定的模式串匹配.一般间隙的模式匹配能够灵活地找出匹配解的数量, 在生物学中某种蛋白质含量的监测中有着重要的应用.下面的实验将比较MSAING与其他算法在DNA库以及蛋白质库中的性能.
为了更有效地对比各种算法匹配解的个数以及运行的速度, 在DNA序列库WO02059377、蛋白质序列库ASTRAL95_1_161上做了对比实验.
在DNA序列库上的模式匹配, 模式串为表 3中的p1~p9, 计算每个模式串在整个序列库中解的和.由图 8可知:在NR模式串p1~p4的匹配中, SAIL_Gen, MSAING取得了完备解; 在R模式串p5~p9中, MSAING取得了最优解, 而SAIL_Gen算法解的完备性最差.这是由于SAIL_Gen算法只适合在线的模式匹配, 在离线的情况下仅利用最左优先策略, 而没有考虑回溯的情况, 导致完备性较差.图 9中可以看出:MSAING, SAIL_Gen和RBCT_Gen算法的运行消耗的时间都比较少, 而DCNP消耗的时间最多.这是由于DCNP, SBO_Gen都需要建立网树结构, 消耗了大量的时间.

|
Fig. 8 Comparison of the number of occurrences on DNA sequence database 图 8 DNA序列库上出现的数目对比 |

|
Fig. 9 Comparison of the running time on DNA sequence database 图 9 DNA序列库上运行时间对比 |
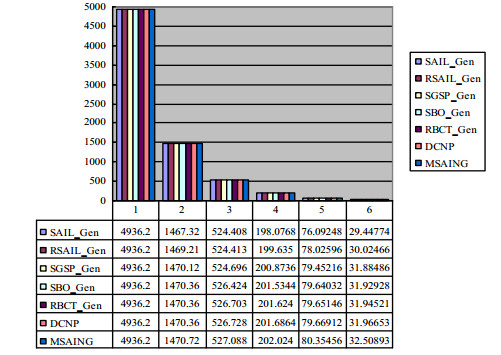
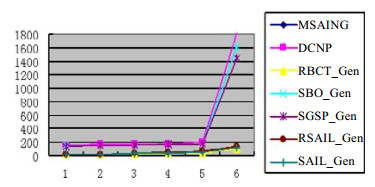
在蛋白质序列库上, 分别选择长度为1~6、间隙为[-2, 7]的模式串, 其中, 长度为1模式串为{a, c, d, e, f}, 长度为2模式串是由长度为1的字符组合而成的25条模式串, 模式长度为3的模式串125条, 以此类推, 模式串长度为6的15 625条模式串; 然后, 求相同长度的模式串在蛋白质序列库上出现解的和, 并计算其平均值.通过图 10可知:随着模式长度的变大, 每个模式串出现的平均个数在减小.这是由于长度为(m+1)的模式串是在长度为m的模式串的基础上满足pm的匹配.因此, 模式越长, 出现解的概率越低.其中, MSAING算法的完备性最高, DCNP算法的完备性次之.图 11中比较的是各种算法的完备性, 图中纵坐标是各种算法解的数目比上MSAING算法解的数目所获得的百分数.随着模式长度的增加, MSAING算法的完备性相对于其对比算法的完备性越来越高.这是由于随着模式长度的增加, 模式串中含有重复的字符越来越多, DCNP, RBCT_Gen, SBO_Gen, SGSP_Gen, RSAIL_ Gen, SAIL_Gen算法只是利用局部最优策略, 而没有考虑到模式串的结构与序列串中各个字符出现的频度之间的关系, 导致模式串长度越大, 解的完备性就越差.图 12为每条模式串在蛋白质序列库上运行的平均时间, 可以看出:随着模式越来越长, 模式匹配消耗的时间越来越多.其中, RBCT_Gen, SAIL_Gen, MSAING增长速度比较缓慢; 而DCNP, SBO_Gen, SGSP_Gen增长速度较快, 消耗时间较多.
|
Fig. 10 Comparison of the number of occurrences on protein sequence database 图 10 在蛋白质序列库上出现的对比 |

|
Fig. 11 Percentage of each algorithm with MSAING on protein sequence database 图 11 在蛋白质序列库上各算法的出现与MSAING算法的百分比 |
|
Fig. 12 Comparison of the running time on protein sequence database 图 12 蛋白质序列库中运行时间对比 |
在生物序列上的实验, 验证了MASING算法进行较大规模数据库模式匹配时的性能.为了进一步证明该算法解决某些实际问题的有效性, 本文把它应用在文本信息的检索中.
4.2.4 文本信息检索中的应用在文本信息检索中考虑一般间隙更具有实际意义, 例如在文献[26]中, 出现frequent closed subsequence与带负间隔的模式closed frequent subsequence表示相同的意思.通过统计文本中模式出现的次数, 可以实现文本中关键词的抽取.带一般间隙的模式匹配将文本中单词、短语视为模式串, 通过提高文本中模式出现解的完备性, 从而可以进一步提高关键词抽取的精确度, 在文本信息检索的过程中获得更多有价值的信息.
以文献[26]作为信息检索文本, 分别检索data mining, closed subsequence, frequent closed subsequence在文本中出现的次数, 由表 7可知:一般间隙的模式匹配出现的次数更多, 更具有灵活性.为了更好地验证一般间隙的性质, 计算在文献[26]中所有长度为2的模式串出现的次数之和, 非负间隙将给定的间隙的最小值设为0.从图 15可以看出:随着模式串的间隙的增大, 解的个数不断增多, 一般间隙比非负间隙获得更多的解.这是由于一般间隙在非负间隙的基础上又考虑了负间隙的情况, 即模式串中字符的顺序发生颠倒的情况; 同时, 间隙越大, 满足匹配出现的概率也越大, 解的个数也就越多.
| Table 7 Comparison of the number of occurrences about no-negative gap with general gap 表 7 非负间隙与一般间隙出现个数比较 |

|
Fig. 13 Comparison of the number of occurrences about no-negative gap with general gap 图 13 非负间隙与一般间隙解的出现对比 |
5 结论
本文提出了一般间隙与one-off条件约束的模式匹配问题——SPMGOO问题.该问题的研究允许用户更加灵活地设定模式串.该问题具有如下特点:间隙可以为负; 同时, 序列串中任何字符最多只能使用1次.本文把线性表应用于该问题的求解, 并基于线性表的结构提出了MSAING算法.算法首先采用Reverse策略使模式与序列达到最佳的匹配状态, 克服了某些算法容易陷入局部最优的缺点; 其次, 利用线性表的结构使匹配过程中的时间和空间消耗大为减少, 并利用回溯的方法提高匹配的成功率; 最后, 根据inside_Checking机制判断模式串内部是否会产生重复现象, 有效提高算法运行效率.最后, 本文从理论和实验两个方面验证了MSANIG算法匹配的有效性.
本文只是对一般间隙与one-off条件的模式匹配问题进行了研究, 而模式匹配是序列模式挖掘的基础, 因此, 下一步将对一般间隙的序列模式挖掘问题进行研究.该研究将有助于挖掘更多有价值的频繁模式.此外, 在实际应用中有很多模式匹配是近似模式匹配, 这不但具有实际意义, 而且研究难度也会更大, 这些问题均是未来研究的方向.
| [1] |
Wu XD, Zhu XQ, He Y, Arslan AN. PMBC:Pattern mining from biological sequences with wildcard constraints. Computers in Biologyand Medicine, 2013, 43(5): 481–492.
[doi:10.1016/j.compbiomed.2013.02.006] |
| [2] |
Zhang C, Zheng Y, Ma XL, Han JW. Assembler: Efficient discovery of spatial co-evolving patterns in massive geo-sensory data. In: Proc. of the 21th ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. New York: ACM Press, 2015. 1415-1424. [doi: 10.1145/2783258.2783394] |
| [3] |
Shokoohi-Yekta M, Chen YP, Campana B, Hu B, Zakaria J, Keogh E. Discovery of meaningful rules in time series. In: Proc. of the ACM SIGKDD Int'l Conf. 2015. 1085-1094. [doi: 10.1145/2783258.2783306] |
| [4] |
Chou CP, Jea KF, Liao HH. A syntactic approach to twig-query matching on XML streams. Journal of Systems and Software, 2011, 84(6): 993–1007.
[doi:10.1016/j.jss.2011.01.033] |
| [5] |
Manber U, Baeza-Yates R. An algorithm for string matching with a sequence of don't cares. Information Processing Leters, 1991, 37(3): 133–136.
[doi:10.1016/0020-0190(91)90032-d] |
| [6] |
Bille P, Gørtz IL, Vildhøj HW, Wind DK. String matchingwith variable length gaps. In: Chavez E, et al., eds. Proc. of the 17th Int'l Conf. on String Processing and Information Retrieval. Berlin: Springer-Verlag, 2010. 385-394. [doi: 10.1007/978-3-642-16321-0_40] |
| [7] |
Fischer MJ, Paterson MS. String matching and other products. In: Proc. of the String-Matching and Other Products. Cambridge: Massachusetts Institute of Technology, 1973. 113-125. |
| [8] |
Chen G, Wu XD, Zhu XQ, Arslan AN, He Y. Efficient string matching with wildcards and length constraints. Knowledge and Information Systems, 2006, 10(4): 399–419.
[doi:10.1007/s10115-006-0016-8] |
| [9] |
Zhu XQ, Wu XD. Discovering relational patternsacross multiple databases. In: Proc. of the IEEE 23rd Int'l Conf. on Data Engineering. 2007. 726-735. [doi: 10.1109/ICDE.2007.367918] |
| [10] |
Liu YL, Wu XD, Hu XG, Gao J. A matching algorithm in PMWL based on CluTree. New Generation Computing, 2014, 32(2): 95–122.
[doi:10.1007/s00354-014-0201-3] |
| [11] |
Fredriksson K, Grabowski S. Efficient algorithms for pattern matching with general gaps and character classed. In: Crestani F, et al., eds. Proc. of the Int'l Conf. on String Processing and Information Retrieval. Berlin: Springer-Verlag, 2006. 267-278. [doi: 10.1007/11880561_22] |
| [12] |
Fredriksson K, Grabowski S. Efficient algorithms for pattern matching with general gaps, character classes, and transposition invariance. Information Retrieval, 2008, 11(4): 335–357.
[doi:10.1007/s10791-008-9054-z] |
| [14] |
Wu YX, Fu S, Jiang H, Wu XD. Strict approximate pattern matching with general gaps. Applied Intelligence, 2014, 42(3): 1–15.
[doi:10.1007/s10489-014-0612-3] |
| [16] |
Kalai A. Efficient pattern-matching with don't cares. In: Proc. of the 13th ACM-SIAM Symp. on Discrete Algorithms. Society for Industrial and Applied Mathematics, 2002. 655-656. |
| [17] |
Kucherov G, Rusinowitch M. Matching a set of strings with variable length don't cares. In: Nivat M, et al., eds. Proc. of the Theoretical Computer Science. Berlin: Springer-Verlag, 1995. 230-247. [doi: 10.1007/3-540-60044-2_46] |
| [18] |
Wu YX, Wang LL, Ren JD, Ding W, Wu XD. Mining sequential patterns with periodic wildcard gaps. Applied Intelligence, 2014, 41(1): 99–116.
[doi:10.1007/s10489-013-0499-4] |
| [19] |
Myers EW. Approximate matching of network expressions with spacers. Journal of Computational Biology, 2009, 3(1): 33–51.
[doi:10.1089/cmb.1996.3.33] |
| [20] |
Wu YX, Wu XD, Jiang H, Min F. A heuristic algorithm for MPMGOOC. Chinese Journal of Computers, 2011, 34(8): 1452–1462(in Chinese with English abstract).
[doi:10.3724/SP.J.1016.2011.01452] |
| [21] |
Lam H, Morchen F, Fradkin D, Calders T. Mining compressing sequential patterns. Statistical Analysis and Data Mining, 2012, 7(1): 34–52.
[doi:10.1002/sam.11192] |
| [22] |
He D, Wu XD, Zhu XQ. SAIL-APPROX: An efficient on-line algorithm for approximate pattern matching with wildcards and length constraints. In: Proc. of the 2007 IEEE Int'l Conf. on Bioinformatics and Biomedicine. Washington: IEEE Computer Society, 2007. 151-158. [doi: 10.1109/BIBM.2007.48] |
| [23] |
Ding B, Lo D, Han JW, Khoo SC. Efficient mining of closed repetitive gapped subsequences from a sequence database. In: Proc. of the 2009 IEEE Int'l Conf. on Data Engineering. Washington: IEEE Computer Society, 2009. 1024-1035. [doi: 10.1109/ICDE.2009.104] |
| [24] |
Wang HP, Xie F, Hu XG, Li PP, Wu XD. Pattern matching with flexible wildcards and recurring characters. In: Proc. of the 2010 IEEE Int'l Conf. on Granular Computing. Washington: IEEE Computer Society, 2010. 782-786. [doi: 10.1109/GrC.2010.156] |
| [25] |
Zhou K. Mining sequential patterns with periodic general gap constraints[MS. Thesis]. Shijiazhuang: Hebei University of Technology, 2014(in Chinese with English abstract). |
| [26] |
Li C, Wang JY. Efficiently mining closed subsequences with gap constraints. In: Proc. of the SIAM Int'l Conf. on Data Mining. 2008. 313-322. [doi: 10.1137/1.9781611972788.28] |
| [13] |
柴欣, 贾晓菲, 武优西, 江贺, 吴信东. 一般间隙及一次性条件的严格模式匹配. 软件学报, 2015, 26(5): 1096–1112.
http://www.jos.org.cn/jos/ch/reader/view_abstract.aspx?flag=1&file_no=4707&journal_id=jos [doi:10.13328/j.cnki.jos.004707]
|
| [15] |
武优西, 刘亚伟, 郭磊, 吴信东. 子网树求解一般间隙和长度约束严格模式匹配. 软件学报, 2013, 24(5): 915–932.
http://www.jos.org.cn/jos/ch/reader/view_abstract.aspx?flag=1&file_no=4381&journal_id=jos [doi:10.3724/SP.J.1001.2013.04381]
|
| [20] |
武优西, 吴信东, 江贺, 闵帆. 一种求解MPMGOOC问题的启发式算法. 计算机学报, 2011, 34(8): 1452–1462.
[doi:10.3724/SP.J.1016.2011.01452]
|
| [25] |
周坤. 一般周期间隙约束的序列模式挖掘[硕士学位论文]. 石家庄: 河北工业大学, 2014.
|
 2018, Vol. 29
2018, Vol. 29


