装填问题研究的是给定一个待布局区域和若干待装填物体(以下简称装填物), 问如何将这些装填物合理地摆放在布局区域中, 以满足必要的约束条件(如干涉性约束、性能约束等).例如, 给定一些集装箱和有限多的物件, 装填问题研究的是如何将所有物件相互间没有嵌入地放入集装箱中, 并且要求使用的集装箱数量最少^{[1, 2]}.此问题和经典的背包问题、cutting stock问题及loading问题非常类似, 以至于很难精确地划分它们之间的界限, 如存在于裁衣、木料、钢材、玻璃和纸张等行业的cutting stock问题^[3], 它和装填问题的最终目标都是在满足一定约束的前提下, 使得边角废料最小, 从而给企业带来最大的效益.除此之外, 装填问题还涉及现实生活中的许多其他方面和行业, 如大规模电路装填设计、房屋装修设计、工厂设备布局、航空航天设备装载^[4-6]等.

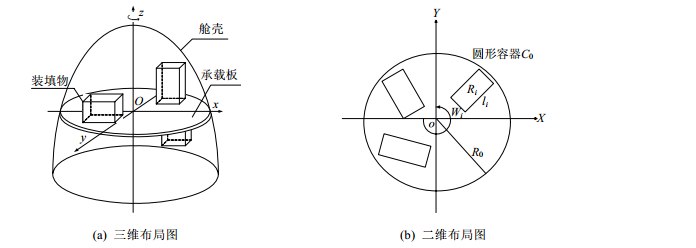
装填问题从布局区域的维数来分, 可分为二维、三维和四维问题^[7]等; 从布局区域的形状来分, 可分为圆形、矩形、三角形和任意的多边形区域等; 从装填物的种类来分, 可分为圆形、矩形、三角形和不规则形状物体; 对于矩形装填物, 从放置的方式来分, 可分为正交放置和任意放置; 从布局系统有无性能(如平衡性、惯性、稳定性等)约束来分, 又可分为不带性能约束的布局和带性能约束的布局.关于装填问题, 目前多数文献[8-11]是研究二维或三维矩形物体在矩形容器中的装填布局, 而且多为不带性能约束的装填问题.本文主要研究带平衡性能约束的任意矩形的装填问题.该问题是一类Non-Deterministic Polynomial(NP)难度问题^[12], 且有着深刻的应用背景.在一个带自旋的返回式卫星舱内(如图 1(a)所示), 要求将一些事先给定的装填物(如仪器、设备等有效部件)分配到旋转的卫星舱内.假设各装填物均为长方体, 且在卫星舱的垂直于舱的中心轴线的圆形承载板上进行布局.当考虑问题的二维形式, 即长方体简化为矩形装填物时, 简化卫星舱布局问题就转变为带静不平衡性能约束的矩形装填问题^[13], 如图 1(b)所示.

对于带性能约束的矩形装填问题, 近年来一些学者进行了研究, 并提出了一些求解算法.1999年, 冯恩民等人^[13]应用图论和群论等数学知识描述了装填问题的一些内在性质, 首次给出了带性能约束的矩形装填问题的一种全局优化算法.同年, 翟金刚等人^[14]给出并证明了矩形图元装填优化不干涉性的判别定理, 并据此构造了求解矩形装填问题的不干涉遗传算法.2001年, 滕弘飞等人^[15]对于矩形的动态不干涉判断问题, 应用不适合多边形(no-fit-polygon, 简称NFP)法, 提出了相对运动的矩形与矩形装填物之间的动态不干涉的判别条件, 并给出了其NFP顶点的简洁计算公式和相应的不干涉算法.2007年, Xu等人^[16]首先采用压缩算法产生合法的初始格局, 然后应用粒子群算法进行装填优化.2010年, 徐义春等人^[17]设计了一种布局定位的构造方法, 并将其与经过特别设计的遗传算法相结合, 提出了一种基于遗传算法的布局顺序寻优算法.2011年, 黄振东等人^[18]将带压缩策略的动态匹配算法与粒子群优化算法相结合, 并将整个装填过程分为4个阶段, 相应地将圆形容器分为8个区域, 构造了一种混合算法.2012年, Zeng等人^[19]采用启发式策略将圆形容器划分为4个部分, 然后根据最左最底填充策略去放置矩形布局物, 构造了一种启发式萤火虫优化算法.2012年, Liu等人^[20]提出了一种结合占角和二分搜索策略的改进的禁忌搜索算法.2014年, Li等人^[21]针对带质量平衡约束的正交矩形布局问题, 提出了一种基于拟物策略的动态调整布局方法.

Wang-Landau抽样算法^[22]是一种基于频数直方图抽样的Monte Carlo算法.该算法通过面向搜索空间的随机抽样而得到一个近似平坦的频数直方图来确定布局系统的状态密度函数.本文将基于矩形的启发式格局更新策略、局部搜索机制、质心平移策略等启发式策略与Wang-Landau抽样算法相结合, 提出了一种用于解决带静不平衡约束的矩形装填问题的启发式布局算法.通过对文献中的两组共10个算例进行测试, 计算结果表明, 所提出的布局算法是一种有效算法.

1 问题描述与模型转化

本文主要研究以卫星舱装填为背景的带静不平衡约束的任意矩形装填问题.该问题要求在圆形容器(即卫星舱圆形承载板)上布置若干矩形装填物, 需要满足如下的约束要求.

(a)   装填物与装填物之间, 装填物与圆形容器之间互不干涉;

(b)   装填物尽量向圆形容器中心聚集;

(c)   装填后整个系统满足静不平衡约束.

问题具体描述如下:给定n个矩形装填物R_i(i=1, 2, ..., n), 其长度、宽度和质量分别为l_i, w_i和m_i, 要求将它们相互之间不干涉地任意放置于半径为R₀的圆形容器C₀中(如图 1(b)所示), 且在放置后整个装填系统满足静不平衡约束(即$J = \sqrt {{{\left( {\sum\limits_{i = 1}^n {{m_i}{x_i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^n {{m_i}{y_i}} } \right)}^2}} \le \delta ( > 0)$)的条件下, 使得容器的半径R₀尽可能地小.静不平衡约束, 即J≤δ的物理意义是, 由圆形容器(即卫星舱的旋转承载板)内各矩形装填物的偏心质量所产生的静不平衡量J(或不平衡的离心力的大小)是在允许值范围内.J的值越小, 整个系统就越满足静平衡约束; 当J=0时, 整个系统处于静平衡.

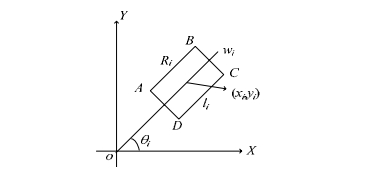
以圆形容器C₀的中心为坐标原点, 建立如图 2所示的笛卡尔坐标系.

用(x_i, y_i)表示矩形装填物R_i的中心坐标, 用θ_i表示矩形装填物R_i的长边所在直线与x轴正向所形成的夹角.用D(o, i)表示矩形装填物R_i的4个顶点A, B, C, D到坐标原点o(0, 0)的最大距离.令X=(x₁, y₁, θ₁, x₂, y₂, θ₂, …, x_n, y_n, θ_n)表示所有矩形装填物的位置及放置方式, 也就是表示一个格局.

借鉴拟物思想^[23], 将圆形容器和所有矩形装填物均视为弹性物体.令u_ij(i < j, i, j=1, …, n)表示矩形装填物R_i与R_j之间的挤压弹性势能, u_0j(j=1, …, n)表示圆形容器C₀与矩形装填物R_j之间的挤压弹性势能.d_ij(i, j=1, …, n, i≠j)表示矩形装填物R_i与R_j之间的干涉量, d_0j(j=1, 2, …, n)表示圆形容器C₀与矩形装填物R_j之间的干涉量.显然, d_ij=d_ji, d_0j=d_j0.当矩形装填物R_i与R_j(或矩形装填物R_j与圆形容器C₀)之间相互嵌入时, ${u_{ij}} = \mu d_{ij}^2$(i < j, i, j=0, 1, …, n), 其中, μ是一个弹性系数, 本文不妨设μ=1.这样, 整个装填系统的挤压弹性势能可定义为

$ {U_1}(X) = \sum\limits_{i = 0}^{n-1} {\sum\limits_{j = i + 1}^n {{u_{ij}}} } = \sum\limits_{i = 0}^{n-1} {\sum\limits_{j = i + 1}^n {d_{ij}^2} } . $

为了使装填系统满足静不平衡约束, 引入一个静不平衡势能函数U₂(X)作为惩罚项:

$ {U_2}(X) = l{J^2} = l\left[{{{\left( {\sum\limits_{i = 1}^n {{m_i}{x_i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^n {{m_i}{y_i}} } \right)}^2}} \right], $

其中, l是惩罚系数, 根据经验, 一般取l∈[10^-6, 10^-4]之间的一个正数.这样, 整个系统的势能为

$ U(X) = {U_1}(X) + {U_2}(X) = \sum\limits_{i = 0}^{n- 1} {\sum\limits_{j = i + 1}^n {d_{ij}^2} } + l\left[{{{\left( {\sum\limits_{i = 1}^n {{m_i}{x_i}} } \right)}^2} + {{\left( {\sum\limits_{i = 1}^n {{m_i}{y_i}} } \right)}^2}} \right]. $

显然, 当U(X)=0时, 整个装填系统的挤压弹性势能和静不平衡量均等于0, 此时, 格局X同时满足原来带静不平衡约束的任意矩形装填问题的不干涉性约束和静不平衡约束.因此, 如果能够提出一种优化算法, 当运用该算法对minimize U(X)进行求解时, 若能找到一个格局X^*, 使得U(X^*)近似为0, 我们就能得到原来问题的一个可行解; 然后, 再用二分法或质心平移法等有效方法得到圆形容器的最小半径.

下面我们将讨论如何计算d_ij.

2 干涉性判断和干涉量计算

有限包络圆族法^[24-26]是由西北工业大学张卫红等人针对多边形装填问题提出的一种自动化建模方法, 它的核心思想是将装填物统一划分为圆形装填物.这是由于圆形装填物之间几何关系相对简单, 通过圆心距离和圆的半径就可以判断两个圆形装填物之间是否干涉, 并能给出相应的干涉量.相对来说, 矩形装填物之间的干涉性判断就要复杂得多, 特别是对于任意的放置方式, 更是难以判断.因此, 如果能将矩形装填物转化为圆形装填物, 那么问题的难度将会大为降低.

有限包络圆族法通过二分法、三步划分法和带间隙的改进的三步划分法将矩形装填物划分为大小不同、数量有限的包络圆族.这种方式使得划分的圆族和原来的矩形装填物的轮廓基本相当, 能够接近于原来矩形装填物的尺寸.但是如果采用这个办法, 在实际的装填过程中, 无论是确定圆族中每个包络圆的半径, 还是圆心坐标都比较困难, 计算量也特别大, 所以不利于实际运用.鉴于此, 本文对矩形装填物提出了一种更加简单的划分方式, 虽然在外包络精度上不及原始有限包络圆族法, 但在实际运用上要简单得多, 便于实现, 实验结果表明, 该改进方法也非常有效.

改进的有限包络圆族法去除了原有的三步划分等繁琐步骤, 直接根据矩形装填物的边长和中心对其进行划分.为了便于理解, 我们首先将矩形装填物分为正方形和长方形, 然后分别针对正方形和长方形, 采用有限圆族进行划分, 具体步骤如下.

Step 1.  比较矩形装填物两相邻边长度, 若两边长度相等, 则为正方形, 转Step 2;否则为长方形, 转Step 3.

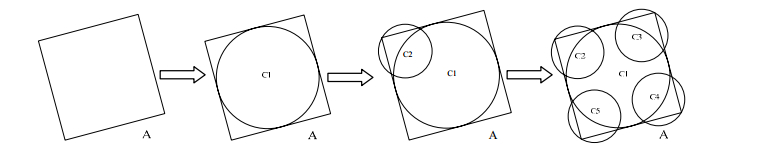
Step 2.  如图 3所示, 以正方形A的中心为圆心、边长的1/2为半径, 画一个内切圆c₁.然后, 以正方形的一个角的角平分线上的一点为圆心、边长的1/4为半径, 画一个过此角的顶点及其相邻两条边的角圆c₂.同理可以得到其他3个角的角圆c₃, c₄和c₅.这样, 得出的圆族将正方形A进行了近似划分.

Step 3.  如图 4所示, 首先, 以长方形B的一个角的角平分线上的一点为圆心, 画一个过此角顶点和过其相邻短边的中点的角圆c₁(如图 4(b)所示).同理可画出其他3个角的角圆c₂, c₃和c₄(如图 4(c)所示).然后, 以长方形两条长边c, d的对称轴上一点为圆心、长方形宽的1/2为半径, 画一个与短边a和两条长边c, d内切的圆c₅(如图 4(d)所示).接着, 在这个圆的基础上, 画一个过圆c₅的圆心并且与两条长边内切的圆c₆(如图 4(e)所示).依此方法画圆c_i(7≤i≤k), 即圆c_i经过圆c_(i-1)的圆心, 并与两条长边相切, 直至圆c_k.若圆c_k与短边b相交, 则放弃圆c_k, 重新画与b和两条长边相切的圆c_k.最后, 以圆c_k、圆c_(k-1)的圆心连线的中点为圆心, 画与两条长边相切的圆c_(k+1).从而得到一系列圆c₁, c₂, …, c_(k+1).显然, 圆族(c₁, c₂, …, c_(k+1))将长方形B进行了近似划分.

例如, 在图 4(e)中, 由于圆c₇与短边b相交, 所以放弃圆c₇, 重新从边b开始, 画一个与边b和两条长边c, d内切的圆c₇(如图 4(f)所示).然后, 以圆c₇和圆c₆圆心之间连线的中点为圆心、长方形宽的1/2为半径, 画一个圆c₈(如图 4(g)所示).这样, 得到的圆族(c₁, c₂, …, c₈)将长方形B进行了划分.

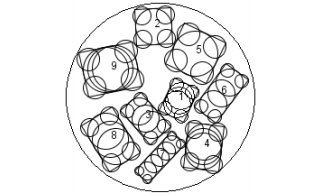
对于其他长方形可类似地得到相应的划分圆族.图 5列举了一个算例在采用改进的有限包络圆族法时的实际划分示意图.显然, 采用上述有限圆族划分方法对矩形装填物进行划分, 可得到原矩形装填物的近似轮廓.这样, 两矩形装填物的干涉性判断和干涉量计算即可通过圆族的干涉性判断和干涉量计算来得到.需要注意的是:在将矩形装填物划分为若干圆形后, 这些圆形将作为一个整体进行相应的运动(移动、转动等).

划分圆族后的矩形装填物的干涉性判断与干涉量的计算过程如下.

若矩形装填物R_s和R_t划分后的圆族分别为M(M₁, …, M_i, …, M_m)和N(N₁, …, N_j, …, N_n), 这里, m, n分别代表所划分圆族中包含的圆形个数.判断矩形装填物R_s和R_t之间是否干涉的伪代码如下.

for (i=1; i≤m; i++)

  for (j=1; j≤n; j++){

  if (${r_{{M_i}}} + {r_{{N_j}}} > \sqrt {{{({x_{{M_i}}}-{x_{{N_j}}})}^2} + {{({y_{{M_i}}}-{y_{{N_j}}})}^2}} $); //此式表示两圆M_i和N_j的半径${r_{{M_i}}}, {r_{{N_j}}}$之和大于其圆心距离

    return两矩形装填物R_s和R_t之间存在干涉;

  }

return两矩形装填物R_s和R_t之间不干涉.

若判断出矩形装填物R_s和R_t之间存在干涉, 则它们之间的干涉量可通过如下伪代码求得.

令d_st=0; //这里, d_st表示矩形装填物R_s和R_t之间的干涉量

for (i=1; i≤m; i++)

  for (j=1; j≤n; j++){

    ${d_{st}} = {d_{st}} + {r_{{M_i}}} + {r_{{N_j}}}-\sqrt {{{({x_{{M_i}}}-{x_{{N_j}}})}^2} + {{({y_{{M_i}}}-{y_{{N_j}}})}^2}} $

  }

return d_st;

根据圆形装填物之间的干涉性判断方法, 将矩形装填物R_s划分圆族M中的每个圆M_i与矩形装填物R_t划分圆族N中的每个圆N_j分别进行判断, 若它们之间存在干涉, 则计算相应的干涉量, M中所有圆的干涉量之和就是矩形装填物R_s和R_t之间的干涉量d_st.采用类似方法可求得矩形装填物R_t和R_s之间的干涉量d_ts, 显然, d_st=d_ts.矩形装填物R_s与其他所有矩形装填物之间的干涉量之和为$\sum\limits_{i = 1, i \ne s}^n {{d_{si}}}, $这里, n为所有矩形装填物的个数.

判断矩形装填物R_s和圆形容器C₀之间是否干涉的伪代码如下.

for (i=1; i≤m; i++){

  if ($\sqrt {x_{{M_i}}^2 + y_{{M_i}}^2} > {R_0}-{r_{{M_i}}}$); //此式表示两圆心的距离大于圆形容器C₀的半径R₀与圆族中圆M_i的半径r_Mi的差

    return矩形装填物R_s和圆形容器C₀干涉;

}

return矩形装填物R_s和圆形容器C₀之间不存在干涉;

若判断出矩形装填物R_s与圆形容器C₀之间存在干涉, 则它们之间的干涉量由下面的伪代码求得.

令d_s0=0; //这里, d_s0表示矩形装填物R_s和圆形容器C₀之间的干涉量

for (i=1; i≤m; i++){

    ${d_{s0}} = {d_{s0}} + {r_{{M_i}}}-{R_0} + \sqrt {x_{{M_i}}^2 + y_{{M_i}}^2} $

}

return d_s0;

显然, d_s0=d_0s, 且矩形装填物R_s的干涉量${D_s} = \sum\limits_{i = 0, i \ne s}^n {{d_{si}}} .$

3 任意矩形装填问题的启发式Wang-Landau抽样算法 3.1 Wang-Landau抽样算法

Wang-Landau(WL)抽样算法是由Wang和Landau^[22]于2001年提出的一种蒙特卡罗(MC)方法.传统的MC算法只能在固定的温度下产生正则分布, 要想得到高质量的解, 必须在不同的温度下运行多次(如模拟退火算法), 非常耗时; 而WL抽样算法与温度无关, 它是通过一定的接受准则在整个能量空间随意行走而得到一个平坦的能量直方图, 从而确定系统的能量状态密度g(E), 这样就可以有效地减少计算时间.WL抽样算法的理论基础是, 能量E被访问的概率与其能量状态密度g(E)的倒数1/g(E)成正比.

在WL抽样算法的开始阶段, 所有可能的能量和状态密度函数g(E(X))都是未知的.状态密度函数在算法迭代过程中自适应地更新.如果一次MC随机行走找到了一个新的能量, 我们就将该能量标记为已访问过的能量, 并把它的状态密度和相应的直方图函数设置为1.因为本文中能量的值为正实数, 所以我们把所有可能的能量划分到有限的区间内.例如, 把[0, 5000)划分成5 000个独立的区间, 所有大于等于5 000的能量划分到一个单独的能量区间, 从而得到5 001个能量区间:[0, 1), [1, 2), …, [4999, 5000), [5000, 5000+).为简单起见, 把能量区间[⌊E(X)⌋, ⌈E(X)⌉)标记为[E(X)], 其中, ⌊E(X)⌋是E(X)的向下取整值, ⌈E(X)⌉是E(X)的向上取整值.例如, E(X)=4.523处于能量区间[4, 5)中, 记为[4.523].将WL抽样算法应用于本文任意矩形装填问题, 其基本过程如下.

首先, 随机产生一个初始格局X₁, 然后通过启发式格局更新策略(见第3.2节)产生新的格局X₂.格局X₂被接受的概率为:$p({X_1} \to {X_2}) = \min (g(E({X_1}))/g(E({X_2})),1) = \min ({{\rm{e}}^{\ln g(E({X_1})) - \ln g(E({X_2}))}},1).$如果X₂被接受, 那么将g(E(X₂))乘以一个修正因子f_i, 并将其直方图函数H(E(X₂))加1, 即g(E(X₂))=f_i×g(E(X₂)), H(E(X₂))=H(E(X₂))+1(i的初始值为0);如果X₂没有被接受, 那么令g(E(X₁))=f_i×g(E(X₁)), H(E(X₁))=H(E(X₁))+1.在本文中, 我们设置f₀=e=2.7182.WL抽样算法的收敛速度是由直方图的平坦度控制的, 然而实际操作中, 想要获得一个绝对平坦的直方图是非常困难的.在WL抽样算法中, 所谓平坦的直方图是指所有H(E(X))的值不小于直方图的平均值〈H([E(X)])〉的k(0 < k < 1)倍, 其中, k是由系统的复杂度和期待的g(E(X))的准确度决定的.在本文中, 我们设置k=0.8, 并在每10³次MC迭代后检查直方图是否近似平.如果直方图近似平坦, 则使用某单调递减函数(如${f_{i + 1}} = \sqrt {{f_i}} $)将修正因子f_i缩小为一个更小的值, 然后将所有访问过的能量区间[E(X)]所对应的H([E(X)])清零, 然后开始下一次随机行走.当修正因子f_i小于阈值f_final时, 算法终止.此时, g(E(X))以某一精度收敛于其真实值.f_final是g(E(X))的控制参数, 并决定了WL抽样算法的MC迭代次数.如果f_final过小, 那么模拟过程将花费很长的时间; 反之, 如果f_final过大, g(E(X))就不能收敛于其真实值.在本文中, 我们设置f_final=0.0001.另外, 由于在实际计算中g(E(X))的值会变得很大, 以至于超出双精度的数字所能表示的范围, 所以本文选择用包含有对数的公式来更新g(E(X)), 即令

lng(E(X_i))=lnf_i+lng(E(X_i)), i=1或2.

3.2 启发式格局更新策略

在Wang-Landau抽样算法执行过程中, 需要不断产生新的格局, 本文根据矩形装填物的特点, 提出了如下启发式格局更新策略.

策略1.  挑选出当前格局X中相对挤压弹性势能E_i/S_i最大的矩形装填物R_i, 并将其重新放置, 其中,

${E_i} = \sum\limits_{j = 0}^n {d_{ij}^2} $表示第i个矩形装填物受到的挤压弹性势能, S_i为第i个矩形装填物的面积.

策略2.  在圆形容器内随机产生100个空位点(空位点表示该点位于圆形容器内, 但不在任何矩形装填物内), 将挑选出的矩形装填物R_i的中心“试放”在每一个空位点上, 这里, “试放”包括该矩形装填物的长边与x轴水平或垂直放置两种方式, 找出使R_i挤压弹性势能最小的空位点及相应的放置方式, 并正式将R_i的中心放在该空位点上, 产生一个新的格局X^*.

策略3.  对于挑选的相对挤压弹性势能最大的矩形装填物R_i, 若通过策略2(即每次均从100×2个试放位置中挑出挤压弹性势能最小的方位)正式放置3次, 每次均没有得到可接受的格局, 则下次将不再挑选该矩形装填物, 而是从其他矩形装填物中任选一个进行重新放置.这种策略可以避免算法在执行的过程中反复挑选同一个矩形装填物而找不到合适的放置位置, 避免死循环.

3.3 局部搜索机制

当用启发式格局更新策略产生新的格局X^*后, 为了得到X^*附近势能更低的格局, 本文在X^*基础上执行局部搜索算法——基于自适应步长的梯度法GM(X^*)^{[27, 28]}, 以加速Wang-Landau抽样算法对全局最优格局的搜索.

3.4 质心平移

为了使装填后的系统满足约束条件, 且使静不平衡量尽可能地小, 我们将执行Wang-Landau抽样算法得到的合法格局X'(称满足E(X') < 10^-10的格局X'为合法格局)进行质心平移, 并计算平移后新格局的外包络圆半径.具体步骤如下.

Step 1.  计算格局X'的质心o'(x₀, y₀), 其中,

$ {x_0} = \frac{{\sum\limits_{i = 1}^n {{m_i}{x_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}, {y_0} = \frac{{\sum\limits_{i = 1}^n {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }} $

这里, x_i和y_i分别表示矩形装填物R_i中心的横坐标和纵坐标, m_i表示R_i的质量.

Step 2.  将新得到的格局的质心o'(x₀, y₀)平移至原始坐标系中心o(0, 0)上, 同时, 将所有矩形装填物看作一个整体进行相应的平移.

Step 3.  计算中心o到每个矩形装填物R_i的4个顶点的最大距离D(o, i), 令${R_{\max }} = \mathop {\max }\limits_{i \in \left\{ {1, 2, ..., n} \right\}} \{ D(o, i)\} .$这样, 新得到的格局的外包络圆半径即为R_max.

3.5 启发式Wang-Landau抽样算法步骤描述

以Wang-Landau抽样算法作为全局搜索算法, 并结合上述的启发式策略和局部搜索机制, 即得到本文求解带静不平衡约束的任意矩形装填问题的布局算法——启发式Wang-Landau(hWL)抽样算法.算法具体步骤如下.

Step 1.  随机产生一个初始格局X₁, 将格局中的所有矩形装填物采用改进的有限包络圆族法进行划分, 并计算相应的能量U(X₁).令访问过的能量所在能量区间的集合S={[U(X₁)]}, 令状态密度函数g(U(X₁))=1, 直方图函数H([U(X₁)])=1.令i=0, l=0, f₀=e > 1, k=0.8, ε=10^-10.

Step 2.  在当前格局X₁中挑选E_i/S_i最大的矩形装填物R_i, 这里, E_i为第i个矩形装填物受到的挤压弹性势能, S_i为第i个矩形装填物的面积.备份当前格局X₁.

Step 3.  采用启发式格局更新策略2将挑选出的矩形装填物R_i进行重新放置, 得到一个新的格局X^*.

Step 4.  基于X^*执行自适应步长梯度法, 得到格局X₂, 计算U(X₂), 令g(U(X₂))=1, H([U(X₂)])=1, l=l+1.

Step 5.  若U(X₂) < ε, 即X₂为合法格局, 则在格局X₂基础上进行质心平移, 得到新的格局X₃, 计算新格局的外包络圆半径R_max, 保存X₃及格局图形, 成功退出; 否则, 转Step 6.

Step 6.  如果[U(X₂)]∉S, 则令S=S∪{[U(X₂)]}.

Step 7.  判断新格局是否被接受, 接受概率为

$ p({X_1} \to {X_2}) = \min \left( {\frac{{g(U({X_1}))}}{{g(U({X_2}))}}, 1} \right) = \min \left( {{{\rm{e}}^{\ln g(U({X_1}))-g(U({X_2}))}}, 1} \right). $

如果random(0, 1) < $\min ({{\rm{e}}^{\ln g(U({X_1}))-g(U({X_2}))}}, 1), $则接受X₂; 否则, 不接受X₂.

Step 8.  更新状态密度函数g(U(X))和直方图函数H([U(X)]), 具体方法如下.

●  若X₂被接受, 则令ln(g(U(X₂)))=lnf_i+ln(g(U(X₂))), H([U(X₂)])=H([U(X₂)])+1;

●  否则, 令ln(g(U(X₁)))=lnf_i+ln(g(U(X₁))), H([U(X₁)])=H([U(X₁)])+1.转Step 9;

Step 9.  如果l%1000=0, 则转Step 10;否则, 转Step 2.

Step 10.  如果H([U(X)])变得近似平, 即对能量区间集S中所有的[U(X)], 如果H([U(X)])≥k〈H([U(X)])〉, 这里, 〈H([U(X)])〉表示平均直方图, 即所有直方图频数的平均值, 则转Step 11;否则, 转Step 2.

Step 11.  令${f_{i + 1}} = \sqrt {{f_i}}, $i=i+1.

Step 12.  如果f_i < 1.0001, 则失败停机; 否则, 对能量区间集S中所有[U(X)], 恢复H([U(X)])=0, 而g(U(X))值保留, 转Step 2.

4 实验结果与分析

为了检验启发式Wang-Landau抽样算法在解决带静不平衡约束的任意矩形装填问题上的性能, 我们在Myeclipse平台上, 采用Java语言编程实现该算法, 并在Core2, 2.94GHz CPU, 2GB RAM的PC机上运行.本文分别测试了两组算例:第1组包含8个算例, 装填物皆为矩形; 第2组包含2个算例, 装填物既有矩形也有圆形.这10个算例既包含小规模算例, 又包含大规模算例, 是测试带静不平衡性能约束的任意矩形装填问题的典型算例.

4.1 任意矩形装填物布局的结果与分析

表 1列举了第1组8个算例的矩形数以及各矩形装填物的长、宽和质量.

我们使用hWL算法对每个算例分别运行5次.将5次运行获得的平均圆形容器半径R₀(mm)、平均静不平衡量J(g.mm)和平均运行时间T(s)分别列于表 2中, 并与文献中遗传算法(GA)^[14]、粒子群(PSO)算法^[29]、带压缩策略并结合局部搜索的粒子群(CA-PSLS)算法^[29]、改进的遗传算法(IGA)^[30]和模拟退火算法(SA)^[29]的计算结果形成对比.

从表 2不难看出, 由于任意矩形装填问题(不同于正交矩形装填问题)的复杂性, 所以多年来的研究成果并不是很多.在已有的研究成果中, GA和IGA只计算了较小规模的算例.文献中, 研究者使用复杂的数学知识, 通过推导、证明, 然后判断两个矩形装填物之间是否干涉, 并构造了相应的不干涉判别算法.这种方法在装填物个数较小的情况下能够适用, 并且可以取得较好的解; 但当装填物的个数逐渐增多时, 由于计算的复杂性, 整个装填过程一般要花费大量的时间, 所以不适于大规模矩形装填物.PSO, CA-PSLS和SA采用矩形装填物内切圆或外包络圆的方式进行干涉性判断和干涉量计算, 当算例规模逐渐增大时, 从表 2可以看出, 装填后得到的整个圆形容器的半径非常大, 甚至有的比本文得到的结果大4倍多.本文采用的是改进的有限包络圆族的方式进行干涉性判断和干涉量计算, 并结合Wang-Landau抽样算法进行全局搜索.在小规模算例上, hWL算法所求得的外包络圆半径相对于GA和IGA优势并不是特别明显, 比如对于算例1和算例3, 并没有得到最优结果, 但是和最优结果相差不多.图 6是本文算法得到的算例1~算例3的一个典型最优装填图.

随着问题规模的不断扩大, 本文算法的优势就逐渐体现出来.对于算例4, 本文算法得到的平均圆形容器半径比当今文献中的最好结果减小了(31.680-27.769)/31.680×100%=12.34%;对于算例5, 本文算法得到的平均圆形容器半径比当今文献中的最好结果减小了(174.586-153.013)/174.586x100%=12.35%.图 7是本文算法得到的算例4和算例5的一个典型最优装填图.

对于算例6~算例8, 本文所得到的平均圆形容器半径明显优于目前文献中的最优结果.以算例8为例, 本文算法得到的平均圆形容器半径比当今文献中的最好结果减小了(423.087-192.909)/423.087x100%=54.40%, 即减少了一半还多, 足以表明本文算法在解决大规模算例上的优势.图 8列举了算例6~算例8的一个典型最优装填图.在静不平衡量方面, 文献中部分算法没有明确给出计算结果, 本文得到的静不平衡量基本接近于0, 完全满足静不平衡约束的要求.

4.2 任意矩形和圆形混合装填物布局的结果与分析

为了验证本文所提出的算法的有效性, 我们又进一步计算了包含矩形和圆形混合装填物的两个算例——算例9和算例10.算例9包含10个装填物, 该算例引自于文献[31], 其中, 装填物1~5为矩形, 装填物6~10为圆形(其中, 第10个圆不能移动).表 3详细列出了每个装填物的尺寸和质量.运用本文算法对算例9独立运行20次, 并将获得的最小圆形容器半径R₀(mm)及其相对应的静不平衡量J(g.mm)、运行时间t(s)列于表 4中, 并与文献中遗传算法(GA)^[31]、人机交互遗传算法(HCIGA)^[31]和基于案例推理的遗传算法(CBR-GA)^[31]给出的结果进行比较.从表 4可以看出, 本文方法在解决算例9上具有非常好的效果.对于最小圆形容器半径R₀, 本文得到的结果比目前文献中的最好结果减小了(741.09-727.59)/741.09=1.8%.在静不平衡量J上, 本文得到的结果基本接近于0, 明显优于文献给出的结果.另外, 在表 4中, 我们也给出了本文hWL算法获得的平均静不平衡量(avg.)J(g.mm)和平均运行时间(avg.)t(s).表 5列出了本文算法得到的算例9的一个最优格局的数据.图 9是本文hWL算法得到的算例9的最优布局图.

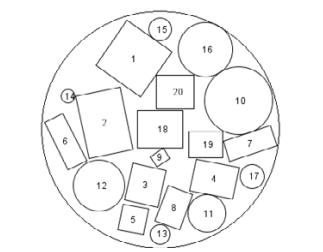
算例10包含20个装填物, 该算例引自于文献[32], 其中, 装填物1~9为矩形; 装填物10~17为圆形; 装填物18~20也是矩形, 但是这3个矩形装填物不能移动.表 6详细列出了每个装填物的尺寸和质量.运用本文所提出的算法对算例10独立运行20次, 并将计算结果与文献中并行遗传算法(PGA)^[32]、带免疫的粒子群算法(PSO-IA)^[32]和基于免疫的人机交互粒子群算法(HCPSO-IO)^[32]给出的结果进行比较.

从表 7可以看出, 本文方法在解决算例10上同样达到了较好的效果.对于最小圆形容器半径R₀(mm), 本文得到的结果比目前文献中的最好结果减小了(1587.58-1577.94)/1587.58=0.6%.在静不平衡量J上, 无论是最优格局的静不平衡量J(kg.mm), 还是平均静不平衡量(avg.)J(kg.mm), 本文的优势都很明显.图 10给出了本文算法得到的算例10的最优布局图.表 8给出了算例10的最优格局数据.

关于两组算例的计算时间, 考虑到执行各算法所使用的计算机的性能和实现算法的编程语言不同, 本文不做详细对比, 但从表 2、表 4和表 7不难看出, 对于两组共10个算例, hWL算法均能在较短时间内得到计算结果.

5 结论

对于带静不平衡性能约束的任意矩形装填问题, 本文通过改进有限包络圆族法, 提出了针对矩形装填物的一种新的划分方式.通过将任意矩形装填问题转化为圆形装填问题, 从而使得任意矩形装填物之间的干涉性判断和干涉量计算更加简单.通过将基于矩形的启发式格局更新策略、局部搜索机制、质心平移策略与Wang-Landau抽样算法相结合, 提了一种用于解决带静不平衡约束的任意矩形装填问题的启发式布局算法.通过对文献中的若干算例进行测试, 计算结果表明, 所提出的布局算法是一种有效算法.