2. 计算机科学国家重点实验室(中国科学院 软件研究所), 北京 100190;
3. 北京大学 数学科学学院, 北京 100871
2. State Key Laboratory of Computer Science(Institute of Software, The Chinese Academy of Sciences), Beijing 100190, China;
3. School of Mathematical Sciences, Peking University, Beijing 100871, China
在信息安全领域中被大量采用的RSA, ElGamal等公钥密码体制中, 模缩减、模乘、模幂等核心运算模块得到了广泛使用.而大整数乘法是构成这些模块的重要基础之一, 其时间复杂度较高, 耗时较多.此外, 大整数乘法还被用来精确计算某些常数如自然对数底数e和圆周率π等, 以及求取大规模素数的运算中[1].
大整数乘法运算有多种不同的快速算法, 比如基线乘法算法、Comba算法、Karatsuba算法[2]、Toom-Cook算法[3]、基于Cooley-Tukey的乘法算法[4]、基于傅里叶变换的大整数乘法、Sch nhage-Strassen算法(简称SSA)[5-7]和Fürer算法[8, 9]等.基线乘法就是传统的笔乘算法, 是最基础的乘法算法, 时间复杂度为O(n2).其实现简单, 但因需要传递进位, 使得嵌套循环的顺序性强, 难以进行并行计算.Comba算法于1990年提出, 它以列为计算单位, 并通过延迟进位解决嵌套计算问题, 虽然其时间复杂度与基线乘法相同, 但是其更易于并行实现.Karatsuba算法和Toom-Cook算法都利用了分治递归思想, 将两个大整数分别拆分成k个较小的大整数进行递归求解, 其时间复杂度为
1969年, Cook利用Toom算法(将大整数分为k部分(k≥2)进行递归)提出一种以动态分治递归方式来加快计算机程序, 称为Toom-Cook乘法算法, 但当k值较大时, 该算法变得相当复杂, 因而在实际应用中较少采用.基于Cooley-Tukey的乘法算法和SSA算法都是利用与傅里叶变换相关的快速算法实现大整数乘法的算法, 其时间复杂度能降低到O(nlogn·loglogn).其中, 基于Cooley-Tukey的乘法算法的基础是快速傅里叶变换, 它由Cooley和Tukey于1965年提出; SSA算法由Sch nhage和Strassen于1971年提出, 它通过引入数论变换, 使用整数模运算代替基于Cooley-Tukey的乘法算法中的浮点运算.2007年, Fürer算法被提出, 是目前最快的大整数乘法算法, 但因其仅适用于超大整数, 实际应用很少[1].
国际上有多个优秀的大数运算库, 如GMP(GNU multiple precision arithmetic library), LibTomMath, Crypto++, Miracl, Cryptlib, OpenSSL, Flint, HugeCalc等.其中, GMP关注于数学运算功能, 其他库则主要应用于密码学等方面.GMP被称为地球上最快的大整数算法库, 它包括了任意精度的整数、浮点数的各种基本运算操作, 主要应用方向是密码学、网络安全、代数系统、计算科学等.GMP支持的大整数规模较大, 但其目前只支持串行运算.随着多核处理器日益普及, 以GMP等优秀的大整数运算库为基础, 发展支持多核并行化的大整数运算软件, 具有重要应用意义.
在大整数乘法的并行算法研究方面, 国内外的研究人员已经开展了大量工作.如:
● 文献[10]中, 作者在Intel Xeon Phi平台上实现了大整数传统手乘算法的众核并行优化, 但由于该算法的时间复杂度高, 当规模大于2 048比特时, 该实现比GMP库运行速度慢;
● 文献[11, 12]主要开展了Karatsuba算法的多核并行研究;
● 文献[11, 13]主要开展了Toom-Cook算法的并行化研究, 包括CPU和GPU两种平台;
● 文献[14-16]均是针对基于傅里叶变换的大整数乘法算法开展研究:文献[14]主要关注在GPU平台对该算法进行细致的并行优化, 文献[15]主要借助中国剩余定理来实现多核并行, 而文献[16]则是实现在GPU平台利用数论转换和中国剩余定理技术在有限域上并行优化;
● 文献[17, 18]主要开展了SSA算法的并行研究, 但其是基于karatsuba算法的分治思想实现并行的, 相当于将karatsuba算法与SSA算法相结合.实验表明:当规模大于4百万比特时, 其运算速度比在64位CPU平台上串行运行慢;
● 文献[19]从硬件的角度提高大整数乘法算法的性能.作者定制出一个有效计算百万比特位乘法的硬件架构, 并基于Cooley-Tukey技术来加快SSA算法中数论转换部分, 实现以7.74ms完成百万比特位级的乘法运算.
由此可知, 目前国内外主要针对时间复杂度较高的大整数乘法算法在多核和众核平台进行并行优化, 对时间复杂度较好的SSA算法进行并行优化的工作相对较少.已有的SSA算法并行主要是从粗粒度的角度进行, 但其性能效果并不理想, 目前还没有工作对SSA算法进行深度剖析, 并从细粒度的角度进行并行优化.本文深度剖析了SSA算法的递归过程, 借助递归分解策略对SSA算法进行比较细致地并行化, 从而更充分利用硬件的多核资源, 提高运行效率.
1 大整数乘法SSA算法简介 1.1 大整数数据结构大整数一般采用基存储的方式, 以R为基的n位大整数可表示为
| $a = {({a_0}, {a_1}, ..., {a_{n - 1}})_R} = \sum\nolimits_{i = 0}^{n - 1} {{a_i}{R^i}} $ | (1) |
其中, ai(0≤i≤n-1)为0或正整数, 且0≤ai < R, 最高位an-1≠0.大整数与多项式在形式上基本一致, 可将大整数看做是某种特殊类型的多项式A(x), 其中, x=R, 其值:
| $ A(R) = \sum\nolimits_{i = 0}^{n-1} {{a_i}{R^i}} $ | (2) |
其中, ai的条件同公式(1)[1].
大整数数位的数据类型(单位可用limb表示)和大整数数据结构的定义如下:
typedef unsigned long mp_limb_t; //定义大整数数位的数据类型
typedef struct //定义大整数数据结构
{ int _mp_alloc //大整数动态数组的长度
int _mp_size; //大整数动态数组已用的长度和符号
mp_limb_t* _mp_d; //大整数动态数组首地址指针
}mpz_struct; //定义存储大整数的数据结构
其中, limb的大小一般和处理器位数相关, 比如64位处理器, 1 limb等于64位bit, 其最大值的10进制数表示为18 446 744 073 709 551 615.本文涉及的大整数乘法SSA算法是基于大整数多项式模型进行分析研究的.
1.2 算法原理大整数可以用多项式来表示, 那么大整数乘法也就是多项式乘法, 其实质是求两个向量的卷积.根据卷积定理[20, 21], 向量卷积的傅里叶变换是向量傅里叶变换的乘积.另外, 傅里叶变换有快速算法(fast fourier transformation, 简称FFT), 可以将算法的复杂度降低到O(nlogn), 因此能利用FFT来求解大整数乘法.但是根据循环卷积和线性卷积的定义, 傅里叶变换对应的是循环卷积而不是线性卷积[22], 这就需要一些额外操作完成求解.
假设要求解大整数a和b的乘积, a的多项式表示为
| $ A(R) = {({a_0}, {a_1}, ..., {a_{n-1}})_R} = \sum\nolimits_{i = 0}^{n-1} {{a_i}{R^i}} $ | (3) |
其中, ai的条件同公式(1), 其向量表示为(a0, a1, …, an-1).b的多项式表示为
| $ B(R) = {({b_0}, {b_1}, ..., {b_{m-1}})_R} = \sum\nolimits_{i = 0}^{m-1} {{b_i}{R^i}} $ | (4) |
其中, bi(0≤i≤m-1)为或正整数, 且0≤bi < R, 最高位bm-1≠0, a和b的向量表示为(a0, a1, …, an-1)和(b0, b1, …, bm-1).众所周知, 最高次数为n-1的多项式与最高次数为m-1的多项式相乘, 其结果的最高次数为n+m-2, 所以a和b的乘积c是一个最高次数为n+m-2的多项式[23].但是根据傅里叶变换的定义, 大整数a(a0, a1, …, an-1)和b(b0, b1, …, bm-1)的傅里叶变换结果分别是n点序列和m点的序列, 那么要想应用傅里叶变换求解多项式a和b的乘积, 就需要对a和b两个向量进行扩充, 也即将a和b两个向量的长度扩充到n+m-2, 具体方式见算法1.
算法 1.基于FFT的大整数乘法算法.
Input:大整数a(n位)和b(m位);
Output: c=a×b.
1.
2.
3.
4.
5.对c进行进位操作
算法1的第1步对a和b两个向量高阶部分进行补零操作, 完成扩充; 第2步分别对扩充后的两个向量进行FFT计算; 第3步对得到的FFT两个序列进行逐点相乘操作; 第4步对点乘结果做快速傅里叶逆变换IFFT; 最后对第4步得到的序列做进位等操作, 得到结果c.
上面的算法已经实现了利用FFT计算大整数乘法, 但是仍存在两个主要缺陷:其一是对a和b两个向量需要进行扩充操作, 在一定程度上增加了计算量; 其二是传统的FFT算法是基于复数上的n次单位根ωn=cos(2π/n)+isin(2π/n)的, 因此必须要进行三角函数类的浮点运算, 从而会有一定程度的截断误差.
对于扩充问题, 可以利用求循环卷积或者负循环卷积来代替求线性卷积来解决.循环卷积和负循环卷积的定义在文献[24, 25]中有比较详细的介绍, 下面主要介绍利用FFT计算循环卷积和负循环卷积的方法:假设a=[a0, a1, …, an-1]T和b=[b0, b1, …, bn-1]T是长度为n的列向量.ω是主n次单位根, 并且ψ2=ω.假设n有一个乘法的逆, 那么,
| $ a{和}b{的循环卷积} = IFFT(FFT(a) \cdot FFT(b)) $ | (5) |
| $ a{和}b{的负循环卷积} = {\psi ^{-1}} \cdot IFFT(FFT(\psi \cdot a) \cdot FFT(\psi \cdot b)) $ | (6) |
其中, ψ称为权重因子.由于计算负循环卷积的过程与计算循环卷积的过程类似, 因此用循环卷积或负循环卷积代替线性卷积, 都能很好地解决扩充问题.
对于截断误差问题, 可以利用快速数论变换(fast number theoretic transforms, 简称FNT)技术来解决.数论变换具有与傅里叶变换相似的结构, 但其是利用整数根代替复指数单位根, 且所有运算按整数模来定义.数论变换实际只是傅里叶变换在有限域的一种表现形式, 即:傅里叶变换的插值是取复数域内的N次方根, 数论变换的插值是取某个剩余系内的N次方根, 其余的运算和傅叶变换基本一致.数论变换同样具有循环卷积性质, 并且在某些情况下可以只利用加法和移位操作来计算, 可以显著减少计算量, 而且相比于傅里叶变换可以精确地计算卷积而没有舍入误差.
大整数乘法SSA算法就是采用上面两种方法对基于傅里叶变换的大整数乘法算法进行优化的.为了实现递归求解, 即:在对得到的傅里叶变换后的两个序列进行逐点相乘操作时, 可以递归地调用此算法来求解, 选取的是求解负循环卷积来解决扩充问题; 同时, 利用FNT技术, 在有限域上求解负循环卷积来解决截断误差问题, 具体内容见算法2.
算法2.大整数乘法SSA算法.
Input:大整数a(n位)和b(m位);
Output: c=a×b.
1.
2.
3.
4.
5.
6.对c进行进位操作
算法2中, 第1步对a和b进行分解操作, 其实质就是将a和b两个大整数转化成多项式的过程, 并对两个向量乘以权重因子; 第2步对a和b两个向量进行快速数论变换; 第3步对得到的变换后的两个序列进行逐点相乘操作, 当点乘的规模很大时, 递归调用SSA算法; 第4步对第3步中得到的乘积序列做快速数论逆变换(IFNT); 第5步对第4步中得到的结果除以权重因子; 最后对第5步得到的序列做进位等操作, 得到结果c.
1.3 热点分析利用SSA算法求取负循环卷积的计算过程可以分成4个步骤进行计算, 分别是分解(decompose)、快速数论转换、点乘(MUL)和快速数论逆转换.运行串行SSA算法, 对规模为上万limbs的两个随机生成的大整数进行实验, 测试并统计各步骤占总计算时间的比重, 见表 1所示.表中数据显示:点乘操作占比最大超过60%, 这4个步骤占用时间百分比超过90%.因此, 这些是SSA算法并行优化的研究热点.
| Table 1 Percent of operation time 表 1 运算时间百分比 |
2 大整数乘法SSA算法多核并行实现
SSA算法并行方案是从算法的内部进行多核并行, 其核心是需对SSA算法的各个核心步骤进行详细地分析, 然后根据分析结果分别对每个步骤定制最优的多核并行方案, 其优势在于能够充分利用平台的CPU资源.
2.1 分解并行方案设计分解操作的主要工作是根据大整数的规模将其进行分解, 以得到大整数的多项式形式, 然后对得到的多项式序列乘以权重因子, 其采用循环for的方式实现.分解过程任务间没有依赖关系, 所以可以直接对这部分进行细粒度的多核并行优化.但当规模较小的时候, 该并行方式开销较大, 需采用粗粒度的优化方案.粗粒度方案是对SSA算法中a和b的分解操作利用OpenMP中的section并行方式, 两个任务并行执行; 细粒度方案是利用OpenMP中的for循环迭代进行多核并行.
2.2 FNT和IFNT并行方案设计根据规模的大小, 采用粗粒度和细粒度两种并行方案进行.对于小规模, 采用粗粒度方式, 利用OpenMP中的section并行方式对函数接口内部进行优化, 因其实现采用的是时域抽取法, 故只对递归的第1层进行并行, 即函数内部的两次递归调用过程利用section方式两个线程并行执行.对于大规模, 采用细粒度方式, 其采用递归分解的策略进行, 如图 1所示.以8线程为例, 可将其前两层的递归调用从递归过程中拆分出来, 即消除第1层递归调用和第2层递归调用, 当递归调用开始时, 直接进入第3层递归, 然后每次递归调用再按原方式进行.

|
Fig. 1 Analysis diagram of the parallelization of the FNT (#threads=8) 图 1 以8线程为例, FNT并行方案分析图 |
当对递归过程进行如上的改变后, 需要进行相应的合并操作以得到正确的结果值, 其具体过程如图 1中的合并1~合并7操作.同时, 每层合并操作可多线程并行执行.另外, 本方案会根据大整数规模通过调整递归分解策略选择合适的并行方案, 以达到最好的并行效果.
IFNT其并行方案与FNT的并行方案相同.
2.3 点乘并行方案设计点乘部分所需的计算时间最长, 并且会随着规模的增加而增大, 其主要是利用OpenMP中的for循环迭代进行多核并行, 因任务间没有依赖关系, 可以根据线程数直接进行任务划分, 然后多个线程分别执行所负责的子任务.但是需要注意的是:SSA算法本身是递归算法, 当进行点乘的数据规模很大时, 多个线程内的每对元素的乘法调用串行SSA算法进行.
2.4 SSA算法并行方案设计通过算法2的介绍可知:这4步之间存在严格的时间先后关系, 并且不存在线程嵌套的情况.根据上面对本方案并行策略的介绍, 其多核并行方案流程图如图 2所示.

|
Fig. 2 Flow chart of theparallel SSA algorithm 图 2 SSA算法并行方案流程图 |
图 2中, SSA-*代表SSA算法中的操作, PSSA(1)-*代表SSA算法并行方案中各操作的粗粒度并行方式, PSSA(2)-*代表SSA算法并行方案中各操作的细粒度并行方式, DECP表示分解操作.
3 实验结果和分析 3.1 实验准备实验分别在两个平台进行:平台1为某IntelX86平台, 平台2为浪潮TS850服务器, 信息见表 2.
| Table 2 Information of test platform 表 2 测试平台信息 |
实验基于大整数运算开源库GMP-5.1.3进行算法的正确性验证和性能测试, 选取大整数的基R为264, 大整数的规模以unsigned long int(limb)类型为基本单位.选取了10组大整数进行实验, 每组测试数据都是规模为从几十万到上千万limbs的两个大整数, 所有测试数据均随机产生.
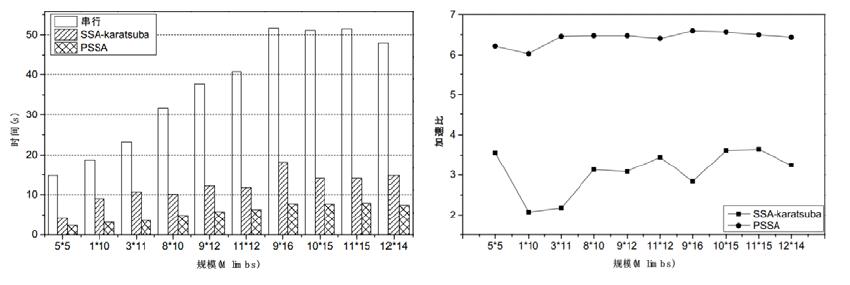
3.2 并行算法加速比和可扩展性实验1在某Intel X86平台主要测试了SSA算法多核并行方案8线程时的性能以及GMP-5.1.3库相应串行程序的性能, 为了与文献[17, 18]中方案进行对比, 我们还实现了karatsuba+SSA的并行方案, 其测试结果如图 3所示.图中PSSA代表SSA算法并行方案在8线程时性能, SSA-karatsuba代表karatsuba算法与SSA算法结合的并行方案在8线程时性能, 大整数规模的单位为百万limbs.实验结果表明:SSA算法并行方案得到了较好的加速性能, 其性能优于karatsuba算法与SSA算法结合的并行方案, 其平均加速比为6.41, 最大加速比可达到6.59.
|
Fig. 3 Performance comparison of two parallel schemes for SSA algorithm 图 3 SSA算法两种并行方案性能对比 |
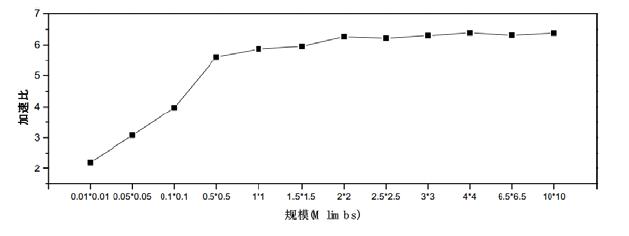
另外, 本文还测试了加速比与规模的关系, 如图 4所示.当规模较少时, 加速比比较低; 随着规模的增大, 加速比逐渐增大; 并且当规模大于2Mlimbs时, 加速比趋于稳定.
|
Fig. 4 Relationship of speedup and scale 图 4 加速比与规模的关系图 |
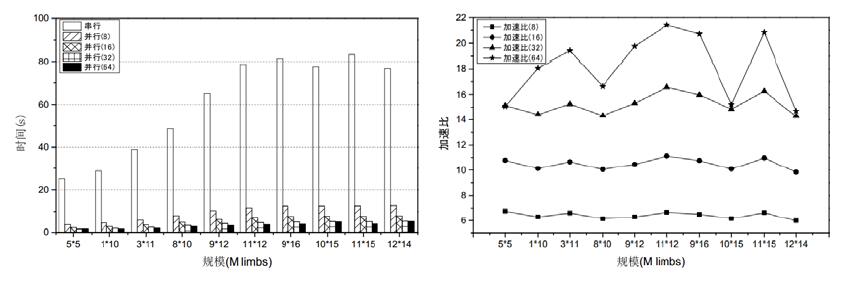
实验2在浪潮TS850服务器对SSA算法并行方案的扩展性进行测试, 实验分别以8线程、16线程、32线程和64线程以及GMP-5.1.3库中相应串行程序进行, 其性能如图 5所示.图中并行(*)代表SSA算法并行方案在8, 16, 32, 64线程时的性能, 加速比(*)代表此方案在8, 16, 32, 64线程时的加速比.实验结果表明:此方案具有一定的扩展性, 加速比会随着线程数的增加而增大, 并且16线程的加速比最大能达到11.14, 32线程的加速比最大能达到16.58, 64线程的加速比最大能达到21.42.
|
Fig. 5 Scalability of the parallel SSA algorithm 图 5 SSA算法并行方案扩展性 |
3.3 实验结果分析
采用阿姆达尔定律[26]来分析并行SSA算法的加速比.大整数乘法SSA算法的基础虽然是FFT算法, 但是该算法比FFT算法更复杂, SSA算法中的大部分运算都可以并行, 但是仍有一小部分计算不能并行.另外, 在FNT和IFNT操作中采用的是递归算法, 在并行算法中额外引入了合并过程, 这部分开销也需要考虑.整体加速比上限可以用如下公式进行计算:设SSA中需要串行计算的部分运行时间为Ws, 可并行计算部分的运行时间为Wp, p为线程数, Wo为并行算法引入的开销, 则:
| $ Speedu{p_{SSA}} = \frac{{{W_s} + {W_p}}}{{{W_s} + \frac{{{W_p}}}{p} + {W_o}}}. $ |
不同计算规模Ws和Wo占总串行时间的比例不同, 当计算规模较大时(大于5Mlimbs), SSA算法中Ws约占总串行时间的2%, Wo约占总串行时间的0.4%, 即:
● 当p=8时, SpeedupSSA=1/(0.02+0.98/8+0.004)=6.83;
● 当p=64时, SpeedupSSA=1/(0.02+0.98/64+0.004)=25.44.
本文的SSA并行算法8线程时最大加速比为6.59, 64线程时最大加速比为21.42, 考虑到并行区开启的开销, 该加速比已经接近加速比上限, 所以说本文的加速效果是比较理想的.
3.4 SSA并行算法特点大整数乘法SSA算法的运算流程比较复杂, 本文针对其运算流程中的每步精心设计了性能更高的并行方案, 如图 2所示.本文的并行方案有两个主要特点:1) SSA算法中大量使用了递归, 本文根据线程数对递归层进行拆解并行, 并采用高效的合并以快速得到正确的结果; 2) SSA算法并行过程中采用自适应的思想, 根据运算规模选用不同的并行方案, 以取得更好的性能.这两点对大整数运算中其他递归算法的并行优化均有一定的借鉴意义, 如大整数分解、GCD等算法.
本文提出的SSA并行方案在SSA算法实现本身存在多种递归实现以至于难以并行优化的条件下仍取得较为理想的加速效果, 充分说明本文的研究内容具有一定的实际应用意义.
4 结束语大整数乘法SSA算法的并行优化具有重要的研究价值和应用意义.本文详细介绍了该算法的一种并行方案, 对SSA算法的各个核心步骤进行细粒度的多核并行优化, 得到了良好的加速性能.下一步工作拟从以下两个方面展开:一方面, 从算法实现上来进行进一步优化, 例如可将算法中的递归实现改成迭代实现, 也可以充分利用中国剩余定理, 将算法以更利于并行优化的方式实现; 另一方面, 将本文的技术与众核并行化相结合, 在众核平台上综合考虑算法级和代码级两个层次优化来进一步改进算法性能.
| [1] |
Sang B. Research and fast implementation of large integers multiplication algorithm[MS. Thesis]. Guangzhou: South China University of Technology, 2012(in Chinese with English abstract).
|
| [2] |
Karatsuba A, Ofman Y. Multiplication of multidigit numbers on automata. Soviet Physics-Doklady, 1963, 7: 595-596.
https://www.researchgate.net/publication/2370542_Multidigit_Multiplication_For_Mathematicians |
| [3] |
Toom AL. The complexity of a scheme of functional elements realizing the multiplication of ISSntegers. Soviet Mathematics Doklady, 1963, 3: 714-716.
https://www.sciencedirect.com/science/article/pii/0196885880900135 |
| [4] |
Cooley JW, Tukey JW. An algorithm for the machine calculation of complex Fourier series. Mathematics of Computation, 1965, 19: 297-301.
[doi:10.1090/S0025-5718-1965-0178586-1] |
| [5] |
Schönhage A, Strassen V. Schnelle multiplikation großer zahlen. Computing, 1971, 7(3-4): 281-292.
[doi:10.1007/BF02242355] |
| [6] |
Gaudry P, Kruppa A, Zimmermann P. A GMP-based implementation of Schönhage-Strassen's large integer multiplication algorithm. In: Proc. of the 2007 Int'l Symp. on Symbolic and Algebraic Computation. ACM Press, 2007. 167-174.
|
| [7] |
Sze TW. Schönhage-Strassen algorithm with MapReduce for multiplying terabit integers. In: Proc. of the 2011 Int'l Workshop on Symbolic-Numeric Computation. ACM Press, 2012. 54-62.
|
| [8] |
Fürer M. Faster integer multiplication. In: Proc. of the 39th ACM Symp. on Theory of Computing. 2007. 57-66.
|
| [9] |
Fürer M. Faster integer multiplication. SIAM Journal on Computing, 2009, 39(3): 979-1005.
[doi:10.1137/070711761] |
| [10] |
Keliris A, Maniatakos M. Investigating large integer arithmetic on Intel Xeon Phi SIMD extensions. In: Proc. of the 9th Int'l Conf. on Design & Technology of Integrated Systems in Nanoscale Era (DTIS 2014). Santorini: IEEE, 2014. 1-6.
|
| [11] |
Tembhurne JV, Sathe SR. Performance evaluation of long integer multiplication using OpenMP and MPI on shared memory architecture. In: Proc. of the 20147th Int'l Conf. on Contemporary Computing (IC3). IEEE, 2014. 283-288.
|
| [12] |
Jebelean T. Using the parallel karatsuba algorithm for long integer multiplication and division. In: Proc. of the Euro-Par'97 Parallel Processing. Berlin, Heidelberg: Springer-Verlag, 1997. 1169-1172.
|
| [13] |
Mansouri F. On the parallelization of integer polynomial multiplication[MS. Thesis]. University of Western Ontario, 2014.
|
| [14] |
Xu L, Wang Z. Fast large integer multiplication based on CUDA. Computer Engineering and Applications, 2013, 49(16):221-225(in Chinese with English abstract).
|
| [15] |
Chmielowiec A. Fast, parallel algorithm for multiplying polynomials with integer coefficients. In: Proc. of the World Congress on Engineering. 2012.
|
| [16] |
Emeliyanenko P. Efficient multiplication of polynomials on graphics hardware. In: Proc. of the Advanced on Parallel Processing Technologies. Berlin, Heidelberg: Springer-Verlag, 2009. 134-149.
|
| [17] |
Emmart N, Weems C. High precision integer multiplication with a graphics processing unit. In: Proc. of the 2010 IEEE Int'l Symp. on Parallel & Distributed Processing, Workshops and Phd Forum (IPDPSW). IEEE, 2010. 1-6.
|
| [18] |
Emmart N, Weems C. High precision integer multiplication with a GPU. In: Proc. of the 2011 IEEE Int'l Symp. on Parallel and Distributed Processing Workshops and Phd Forum (IPDPSW). IEEE, 2011. 1781-1787.
|
| [19] |
Doroz Y, Ozturk E, Sunar B. Evaluating the hardware performance of a million-bit multiplier. In: Proc. of the 2013 Euromicro Conf. on Digital System Design (DSD). IEEE, 2013. 955-962.
|
| [20] |
Jiang CJ, Jiang Y. Fast Fourier Transform and C Procedures. Hefei: University of Science and Technology of China Press, 2004.
|
| [21] |
Nussbaumer HJ. Fast polynomial transform algorithms for digital convolution. IEEE Trans. on Acoustics, Speech, and Signal Processing, 1980, 28(2): 205-215.
[doi:10.1109/TASSP.1980.1163372] |
| [22] |
Hu GS. Digital Signal Processing:Theory, Arithmetic and Realization. 2nd ed. Beijing: Tsinghua University Press, 2003.
|
| [23] |
Cormen TH, Leiserson CE, Rivest RL, Stein C. Introduction to Algorithms. 3rd ed. Cambridge: The MIT Press, 2009: 900-905.
|
| [24] |
Proakis JG, Rader CM, Ling F, Nikias CL, Moonen M, Proudler IK. Algorithms for Statistical Signal Processing. London: Prentice Hall, 2002: 63-67.
|
| [25] |
Crandall R, Fagin B. Discrete weighted transforms and large-integer arithmetic. Mathematics of Computation, 1994, 62(205): 305-324.
[doi:10.1090/S0025-5718-1994-1185244-1] |
| [26] |
Amdahl GM. Validity of the single processor approach to achieving large scale computing capabilities. In: Proc. of the Spring Joint Computer Conf. ACM Press, 1967. 483-485.
|
| [1] |
桑波.大整数乘法算法的研究与快速实现[硕士学位论文].广州: 华南理工大学, 2012.
|
| [14] |
许亮, 王震.基于CUDA的快速大整数乘法.计算机工程与应用, 2013, 49(16): 221-225.
|
| [20] |
蒋长锦, 蒋勇. 快速傅里叶变换及其C程序. 合肥: 中国科学技术大学出版社, 2004.
|
| [22] |
胡广书. 数字信号处理:理论、算法与实现. 第2版. 北京: 清华大学出版社, 2003.
|
 2018, Vol. 29
2018, Vol. 29


