2. Department of Computer Science and Software Engineering, Swinburne University of Technology, Melbourne VIC3122, Australia
2. Department of Computer Science and Software Engineering, Swinburne University of Technology, Melbourne VIC3122, Australia
工作流中, 人力资源的分配方式直接影响业务流程中任务执行的质量.特别地, 在一个业务流程执行过程中, 相邻的两个任务之间往往需要大量的交互, 而执行这些任务的员工(执行者)之间协作能力的高低, 一般在很大程度上会影响整个流程的执行效率.比如在一个软件开发流程中, 如果编码工程师能够与测试工程师很好地合作, 整个软件的开发进度就有可能加快[1, 2].
通常, 工作流系统会从资源模型的角度(有能力执行某些活动的角色、员工)分析一个流程的执行情况.目前已有的资源分配方法大都是基于角色的分配方法.然而这种资源分配方法往往是“粗粒度”的[3], 在某些情况下可能无法适用.例如, 某制造业生产流程中的“生产计划”活动预定义由角色“生产计划设计者”执行, 但是在实际分配中, 可能需要将活动分配给该角色中的一个或多个更具有资格的员工而并非是该角色对应的所有员工.除此之外, 也有一些人力资源分配方法关注适应度、紧急程度、符合度以及可用性等方面[4, 5], 但很少关注不同员工之间的协作水平.而现有的少数关于协作方面的研究, 忽略了员工之间的协作能力会受到他们当前执行活动的影响.为了度量业务流程中员工之间的合作能力, Kumar等人[6]提出了“协作度”这一概念.他们认为, 有效的员工分配, 能够使得流程整体协作度达到最大.事实上, 我们认为, 在员工分配时, 不能仅根据员工之间的协作度大小进行分配, 因为在员工之间的协作度会由于他们执行活动的不同而有所差别.不仅如此, 这种仅通过计算员工之间的协作度进行员工分配的结果, 就有可能会出现分配给某活动的员工并不具备执行该活动的权限.另一方面, 这种员工之间的协作能力的度量显然也只能从历史流程实例中挖掘得到.事实上, 从这些历史的日志中可以得到很多隐含的更富有实际意义的信息, 如某活动可以很好地由某些员工执行(这些员工应该是属于角色对应的一部分更具有资格或者能力更强的员工)等.
为了解决以上问题, 本文首先引入了实体(即活动和执行者的混合体)和实体协作度(即不同员工在执行不同任务之间的协作水平)的概念, 然后在此基础上提出如何从流程运行的历史日志中挖掘出具有高协作能力的员工分配模式(即高协作水平的协作模式), 最后, 使用编码的方式将这些模式与待分配员工的流程快速匹配选出可使流程协作水平达到最优的员工分配方式.
本文的主要贡献在于:
(1) 提出了一种基于挖掘得到的高协作模式进行快速、有效的员工分配方法;
(2) 提出了实体协作度的概念, 可用于度量不同员工在执行不同任务时彼此之间的协作水平;
(3) 构建了已分配员工的流程整体协作度计算模型;
(4) 提出了基于两种序列编码的匹配方式, 用以快速获取基于高协作模式的最优员工分配方案.
本文第1节概述相关研究现状.第2节介绍相关的定义和问题描述.第3节详细介绍本文提出的员工分配方法框架、步骤以及算法.第4节基于合成数据集和真实的业务流程数据集进行实验评估与分析对比.第5节对全文的研究工作进行总结, 并展望未来工作.
1 相关研究现状分析近年来, 已经有大量从资源管理的角度出发研究员工分配问题[7-9]的工作, 特别是研究如何通过自动化实现合理的员工分配[10].如, Ly等人[11]提出了从历史数据和组织模型中挖掘员工分配的规则作为决策树学习方法的输入进行员工分配; Liu等人[12]提出了一种半自动的方法, 使用机器学习算法从历史事件日志中学习哪些员工能够执行哪些活动; Xu等人[13]提出了一种基于高斯领域的挖掘方法, 可实现半自动化的员工分配.等等.这些方法都是使用机器学习中的学习方法对历史数据进行学习, 然后根据学习的内容进行员工分配.另外, Cheng等人[14]通过使用模糊数的理论解决了由于不同经验和能力的员工、任务的循环执行、优先级约束以及资源的限制等造成的不同的执行模式时实现最优的员工分配模型.除此之外, 很多研究者关注员工分配的优化方法, 例如:Liu等人[15]提出了一种数据挖掘的方法找到事件日志的频繁模式, 并根据预定义的关联规则生成资源分配的约束条件来解决员工分配问题, 从而改善工作流资源管理的效率; Kumar等人[6]提出了计算员工之间协作度的模型, 用以员工分配; 许荣斌等人[16]在此基础上提出了基于最大依赖度及最小冗余度的员工协作优化策略.然而, 这类仅根据员工之间的协作度进行员工分配的方法忽略了员工之间的协作度在他们协作执行不同活动时会发生变化的情况.
另一方面, 也有一些通过研究协作模式来提高流程的性能的工作, 因为工作流中的一些好的协作模式往往代表着活动之间、员工之间具有良好的交互, 其可以被用作分配员工时的一种经验参考.这方面的典型工作包括:Meddah等人[17]提出使用流程挖掘的方法挖掘协作模式; Smirnov等人[18]研究类似于协作模式的行为模式及其之间的关系; Verginadis等人[19]论述了与协作相关的模式方法、模型和语言的研究结果, 并提出使用已有的模式可以更好地为实现协作提供解决方案.此外, Diamantini等人[20]提出一种使用图挖掘的理论知识在流程实例构成的图中挖掘协作模式的方法, 但是这类基于子图挖掘理论进行模式挖掘的方法在时间复杂度上仍是一个挑战.然而, 这些研究都仅仅只是挖掘出协作模式, 并没有从协作能力的角度度量这些协作模式的协作水平.
2 问题和定义 2.1 基础概念定义1.流程模型BPM=(A, C)是由一系列的活动组成, 它们通过获取一些资源(如执行者), 按照活动之间的先后次序来执行, 从而达到一个特定的目标, 其中, A={a1, a2, …, ai, …, an}表示该流程中所有活动的集合, C⊆(A×A)表示该流程中活动与活动之间的先后发生次序.
如图 1所示, 某制造业采购流程模型包括以下活动:采购申请(PP)、采购审批(PA)、供应商选择(SS)、价格谈判(QN)、订单签订(PS)、交货付款(DP), 即A={PP, PA, SS, QN, PS, DP}, C={〈PP, PA〉, 〈PA, SS〉, 〈SS, QN〉, 〈QN, PS〉, 〈PS, DP〉}.它的每次执行都会得到一个对应的流程实例, 这些流程实例会以日志的形式记录在流程管理系统中.

|
Fig. 1 Purchasing process model in manufacturing 图 1 制造业采购流程模型 |
定义2.事件e=(#startTime(e), #endTime(e), #activity(e), #resource(e)), 其中, #startTime(e), #endTime(e), #activity(e), #resource(e)为事件e的属性, 分别表示开始时间戳属性、结束时间戳属性、活动名称属性和资源属性.用L表示某一流程在运行时产生的事件日志, 其中,
事件e是流程模型中活动的实例化, 事件日志L是由EL中一系列流程实例中的事件组成的.如表 1所示, 其中, 第1行表示实例ID为1, 事件ID为1的事件e有6个不同的属性:实例ID属性、事件ID属性、开始时间戳属性和结束时间戳属性(表示该事件开始于2010/08/01 10:26:00, 结束于2010/08/02 14:06:00)、活动属性(该事件对应的是采购申请活动)和执行者属性(如Sathish完成该事件).
| Table 1 An event log of the purchasing process in manufacturing 表 1 制造业采购流程的事件日志 |
定义3.轨迹
如上述表 1所示, 相同实例ID、不同事件ID的所有事件属于同一个流程实例, 因此, 实例ID为1的轨迹可表示为〈采购申请; 采购审批; 供应商选择; 价格谈判; 订单签订; 付款交货〉, 简单记作T1=〈PP; PA; SS; QN; PS; DP〉.
定义4. “活动-执行者”实体(简称实体)entity={(ai|ri)|ai∈AL, ri∈RL}表示事件日志L中执行者(员工)ri执行活动ai; 实体轨迹
如上述表 1中的第1行所示, 实例ID为1、事件ID为1的事件就可以表示为:采购申请|Sathish(或PP|M1), 代表员工Sathish执行采购申请活动, 该实例的实体轨迹可表示为ET1=〈PP|M1;PA|M2;SS|M3;QN|M4;PS|M5;DP| M6〉.
定义5.序列对齐是通过使用空格占位符和移动序列中元素的位置, 尽可能地花费最小的代价实现序列中相同元素对齐的一种方式, 从而发现相同的子序列, 如, 两条序列GCATTCA和GATTACA可能会得到如下的一种对齐:
| $ \begin{array}{l} G\;C\;A\;T\;T - \;C\;A\\ G - A\;T\;T\;A\;C\;A \end{array} $ |
实体轨迹对齐根据序列对齐的思想将实体轨迹序列实现对齐, 从而快速发现相同的子实体序列.比如, 两条实体轨迹ET1=〈PP|M1;PA|M2;SS|M3;QN|M4;PS|M5;DP|M6〉和ET2=〈PP|M1;PA|M2;SS|M3;QN|M4;SS|M3;QN|M4; PS|M5;DP|M6〉, 可以得到如下的对齐:
| $ \begin{array}{l} PP|M1\;PA|M2\;SS|M3\;QN|M4\;\;\; - \;\;\; - \;\;\;PS|M5\;\;\;DP|M6\\ PP|M1\;PA|M2\;SS|M3\;QN|M4\;SS|M3\;QN|M4\;PS|M5\;DP|M6 \end{array} $ |
如某个流程的事件日志L中有n个流程实例, 即可以得到n条实体轨迹.根据上述的对齐思想, 可以得到对齐的实体轨迹矩阵:
| $A{M_{n \times m}} = {({a_{i, j}}|{r_{i, j}})_{n \times m}} = \left[ {\begin{array}{*{20}{c}} {{a_{0, 0}}|{r_{0, 0}}}&{{a_{0, 1}}|{r_{0, 1}}}&{...}&{{a_{0, m - 1}}|{r_{0, m - 1}}} \\ {{a_{1, 0}}|{r_{1, 0}}}&{{a_{1, 1}}|{r_{1, 1}}}&{...}&{{a_{1, m - 1}}|{r_{1, m - 1}}} \\ {...}&{...}&{...}&{...} \\ {{a_{n - 1, 0}}|{r_{n - 1, 0}}}&{{a_{n - 1, 1}}|{r_{n - 1, 1}}}&{...}&{{a_{n - 1, m - 1}}|{r_{n - 1, m - 1}}} \end{array}} \right]$ . |
其中, ai, j|ri, j表示对齐后的第i条实体轨迹的第j列的元素, 该元素为某一实体或者“-”, 同一列的所有非“-”实体对应的活动相同.
定义6.参考活动序列Ras=〈a·, 0; a·, 1; …; a·, j; …; a·, m-1〉(a·, j∈AL)表示对齐的实体轨迹矩阵AMn×m中最长的一条活动序列, 即, 将矩阵的每一列中所有非“-”实体对应的同一个活动作为该列的活动, 最后得到的m个活动组成的活动序列.待分配活动流程aP=〈a1; a2; …; ai〉(ai∈AL)表示针对某个流程模型正在实例化的一个流程实例, 即, 一个待分配员工的活动序列(仅有活动信息).
根据上述定义, 对于上述对齐的两条实体轨迹ET1和ET2, 我们可以得到参考活动序列为〈PP; PA; SS; QN; SS2; QN2; PS; DP〉.
定义7.活动协作度
| $coo{p_{{a_1}, {a_2}}} = \frac{1}{{1 + {{\text{e}}^{ - k({c_{{a_1}, {a_2}}} - \bar c)}}}}({a_1} \ne {a_2}, {a_1}{ > _L}{a_2})$ | (1) |
其中,
定义8.活动序列协作度Coopas表示一个活动序列as=〈ak; ak+1; …; aj; …; al〉(0≤k < l≤m, aj∈AL)中所有有协作关系的连续活动之间总的协作程度:
| $Coo{p_{as}} = \sum\nolimits_{\forall ({a_1}, {a_2}) \in as} {coo{p_{{a_1}, {a_2}}}} $ | (2) |
定义9.实体协作度
| $compatibilit{y_{{a_1}|{r_1}, {a_2}|{r_2}}} = \frac{1}{{1 + {{\text{e}}^{ - k({{\bar t}_{{a_1}|., {a_2}|.}} - {{\bar t}_{{a_1}|{r_1}, {a_2}|{r_2}}})}}}}({a_1} \ne {a_2}, {r_1} \ne {r_2};{a_1}|{r_2}{ > _L}{a_2}|{r_2})$ | (3) |
其中,
定义10.实体序列协作度Compatibilityes表示事件日志L中一个已分配员工的活动序列, 即实体序列es=〈ak|rk; ak+1|rk+1; …; aj|rj; …; al|rl〉(0≤k < l≤m-1, aj∈AL, rj∈RL)的整体协作能力.
| $Compatibilit{y_{es}} = \sum\nolimits_{\forall ({a_1}|{r_1}, {a_2}|{r_2}) \in es} {(coo{p_{{a_1}, {a_2}}} \times compatibilit{y_{{a_1}|{r_1}, {a_2}|{r_2}}})} $ | (4) |
定义11.高协作模式用一个二元组集合〈es, cpt〉表示, 其中, es=〈ak|rk; ak+1|rk+1; …; aj|rj; …; al|rl〉(0≤k < l≤m-1, aj∈AL, rj∈RL)表示事件日志L中协作能力较高的实体序列, cpt=Compatibilityes表示该实体序列的协作度值.高协作模式代表历史流程实例中的员工在协作完成活动时的协作能力比较高的一种方式.
定义12.基于最大协作度的员工分配(最优员工分配)策略用一个三元组集合表示, 其中,
● aP=〈a1; a2; …; ai〉(ai∈AL)表示由用户提供的待分配活动流程;
● eP=〈a1|r1; a2|r2; …; ai|ri〉(ai∈AL, ri∈RL)表示针对该活动流程中的活动分别进行员工分配后使得整体协作度最大的实体序列;
● cpt=CompatibilityeP表示相应的分配策略所对应的协作度值.
2.2 问题描述对制造业采购流程系统来说, 一旦采购经办人成功发起了采购申请, 即正确填写了采购的相关信息, 采购经理就需要对此次采购请求进行审批; 如果审批通过, 采购人员需要根据采购单和报价选择相应的供应商; 选定合适的供应商后, 财务部人员需要与供应商进行价格谈判; 待双方达成一致意见后, 业务人员需要与供应商签订订单; 订单签订成功后, 供应商可以开始按照订单生产; 最后交货时, 需要财务人员付款.显然, 整个采购流程需要由来自不同部门的员工共同协作才能完成.在这个过程中, 若采购经办人员非常了解采购经理审批的依据, 那么他在填写采购申请单时就可以避免错误, 从而快速实现采购申请的批准.同样地, 如果采购人员与财务人员的协作水平较好, 那么他就可以在选择供应商的时候尽可能地选择财务人员更能认可的供应商.这样就可以极大地提高整个采购流程的效率.因此, 本文从协作的角度研究员工分配问题:一方面, 为了最大程度地提高流程执行的性能, 文中提出了一种使流程整体协作度最大的员工分配方法; 另一方面, 历史流程执行日志中隐含地存在一些协作较好的员工执行活动的模式, 这种分配方式应该被发现并运用在优化员工分配问题中, 所以本文提出了一种方法用来挖掘协作水平较高的协作模式.基于这些协作模式, 以整体协作度最大为目标, 实现员工最优分配.
目前, 从协作的角度实现员工最优分配的研究是基于员工之间的协作能力来进行分配的, 因为忽略了员工之间的协作水平会由于执行不同的活动而影响, 这种分配方法会出现不合理的分配.比如, 某事件日志有员工集合{r1, r2, r3, r4}和活动集合{a1, a2, a3, a4}, 根据日志统计:员工r1和r2协作执行活动a1和a2(即a1:r1, a2:r2)的协作度为0.6, 协作执行活动a3和a4(即a3:r1, a4:r2)的协作度为0.2, 员工r3和r4协作执行活动a3和a4(即a3:r3, a4:r4)的协作度为0.3.然后, 在此基础上对活动序列〈a3; a4〉分配员工, 如果仅根据员工之间的协作度来进行最大协作度分配就会出现a3:r1, a4:r2的不合理分配(因为r1和r2之间的平均协作度为0.4, r3和r4之间的平均协作度为0.3, 实际上r3和r4在协作执行a3和a4时的协作度更高一些).
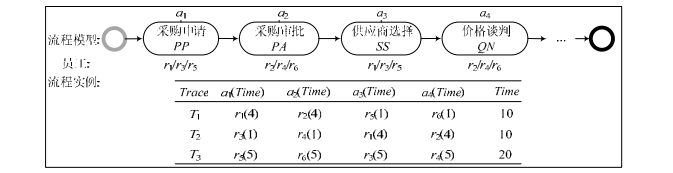
为了解决这种不合理分配问题, 本文首先提出了活动协作度和实体协作度的计算, 对员工之间协作执行不同活动的协作水平进行准确度量.根据这种度量方式, 挖掘历史日志中存在的具有高协作水平的员工分配模式, 然后参考这些模式, 将待分配员工的活动流程实现合理有效的流程最大化协作的员工分配.下面用一个简单的例子说明本文是如何实现协作最优员工分配以及最优分配的意义(a1(Time)表示员工完成活动a1所需的时间).
根据图 2、表 2和表 3, 可以分别计算出不同员工分配方法分配后的实体序列的协作度.假如待分配活动流程为4个活动组成的序列〈a1; a2; a3; a4〉.
|
Fig. 2 Example of execution traces of purchasing process in manufacturing 图 2 制造业采购流程的执行轨迹示例 |
|
Table 2 Compatibility table of two activities |
|
Table 3 Compatibility table of two entities |
● 第1种情况:随机员工分配
活动a1:员工r5; 活动a2:员工r6; 活动a3:员工r3; 活动a4:员工r4; 即
| $ es = \langle a1|r5;a2|r6;a3|r3;a4|r4\rangle , \\Compatibilityes = 0.5 \times 0.034 + 0.5 \times 0.034 + 0.5 \times 0.034 = 0.052; $ |
● 第2种情况:基于最大协作度的员工分配
活动a1:员工r1; 活动a2:员工r2; 活动a3:员工r5; 活动a4:员工r6; 即
| $ es = \langle a1|r1;a2|r2;a3|r5;a4|r6\rangle , \\Compatibilityes = 0.5 \times 0.209 + 0.5 \times 0.841 + 0.5 \times 0.991 = 1.020. $ |
从这个示例中可以看出, 这两种不同的分配方法得到的整体协作度差别很大, 说明了最优员工分配研究对流程执行性能的重要性.
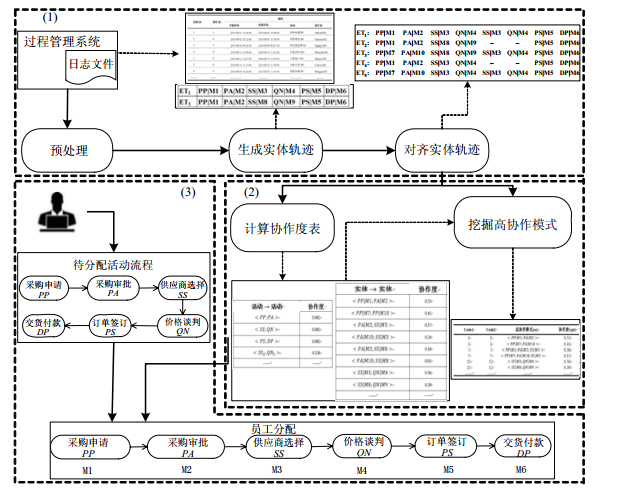
3 协作最优的员工分配方法基于最大协作度(协作最优)的员工分配方法FOSA(fast optimal staff assignment)总体框架如图 3所示, 其整体过程可概述如下.
|
Fig. 3 Framework of staff assignment approach for maximizing compatibility 图 3 基于最大协作度的员工分配方法框架 |
(1) 首先, 预处理历史流程执行日志得到标准事件日志, 并将一条条的流程实例转换成实体轨迹; 然后, 再使用Needleman-Wunsch算法[21]对齐实体轨迹得到对齐矩阵.
(2) 其次, 根据对齐的实体轨迹矩阵和协作度计算方法可以得到活动-活动、实体-实体的协作度表(见表 2和表 3); 然后, 基于Apriori算法思想实现高协作模式挖掘(后文算法1), 以得到代表高协作能力的员工分配模式表.
(3) 最后, 根据步骤(1)、步骤(2)中得到的活动-活动协作度表、实体-实体协作度表以及高协作模式表, 使用本文提出的协作最优员工分配算法(后文算法2)可以实现快速、有效的员工分配.
3.1 预处理日志文件和对齐实体轨迹流程管理系统记录的流程执行日志文件中往往存在着由不当操作造成的噪声数据和大量的冗余数据.本文通过对日志中关键属性值的提取、时间戳属性的标准化、异常值的剔除等一些基本的预处理操作可以得到标准的事件日志.然后再根据上文的定义, 将事件日志转换成一条条的实体轨迹.
本文使用经典的Needleman-Wunsch算法[21]实现实体轨迹对齐.
3.2 计算协作度和挖掘高协作模式为了度量分配员工后的整个流程的协作度(即实体序列协作度), 根据公式(4), 本文提出一种方法来计算需要协作完成的活动-活动之间的协作度以及在协作完成活动时的实体-实体之间的协作度.另外, 从一些复杂的(有循环、分支结构)或者未知的流程模型运行日志中生成的实体轨迹个体之间差异较大, 为了能够挖掘得到过去的最佳实践的员工分配, 基于对齐的实体轨迹, 本文提出了挖掘高协作模式的算法.
3.2.1 计算协作度为了度量两个活动之间的协作度
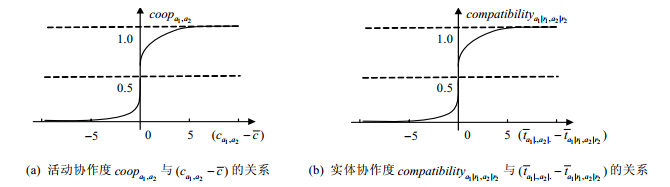
图 4分别表示
|
Fig. 4 Variation curves of activity compatibility and entity compatibility 图 4 活动协作度和实体协作度的变化曲线 |
从图 4(a)中可以发现:频繁度
为了快速计算实体序列协作模式, 确定公式中的参数k后, 需要将事件日志L中所有具有协作关系的活动的协作度以及所有协作执行的实体的协作度进行计算并存储, 最后可以得到一个所有类型的活动-活动的协作度表和一个所有类型的实体-实体的协作度表(与第2.2节类似).
3.2.2 挖掘高协作模式为了挖掘历史日志中协作度较高的员工分配, 本节基于对齐的实体轨迹实现了算法1.该算法首先计算所有的活动序列及其协作度(第2行~第7行)、所有的实体序列及其协作度(第8行~第10行); 然后, 通过最小协作支持度阈值过滤得到具有高协作度的活动序列; 再在这些活动序列中通过最小协作置信度阈值过滤得到具有高协作度的子实体序列即高协作模式(第11行~第17行).
算法1.挖掘高协作模式.

|

|
基于算法1得到的高协作模式〈es, cpt〉(见定义11), 本文提出了如图 5所示的两种编码方式(以上文提到的制造业采购流程为例).

|
Fig. 5 Two kinds of encoding: binary encoding and adjoint binary encoding 图 5 两种不同的编码方式:二进制编码和伴随二进制编码 |
(a) 二进制编码:首先, 根据实体轨迹对齐得到的参考活动序列(如图 5中的〈PP; PA; SS; QN; SS2; QN; SS2; QN2; PS; DP〉)对流程中的所有活动按位置进行编码(如第1个活动PP的编码为20, 第2个活动PA的编码为21, …, 以此类推); 然后, 根据活动编码可将待分配活动流程〈PP; PA; SS; QN; PS; DP〉进行编码, 得到一个编码序列11110011和编码值207(如图 5所示).对高协作模式进行二进制编码, 即根据其对应的活动序列进行编码, 如高协作模式对应的活动序列为〈SS; QN; PS; DP〉, 我们可以得到其二进制编码序列为00110011.
(b) 伴随二进制编码:将高协作模式的二进制编码(如00110011)中相邻的两个1中的0全部取反, 即可得到它的伴随二进制编码(即00111111).
基于事件日志挖掘出来的每个高协作模式, 可分别得到它的二进制编码值code1和伴随二进制编码值code2.每个协作模式用一个四元组〈code1, code2, es, cpt〉表示, 挖掘得到的所有协作模式存在一个表中, 即高协作模式表, 见表 4.
| Table 4 Example of high collaboration patterns 表 4 高协作模式的示例 |
最后, 根据一定的匹配规则(如图 5所示), 可以快速确定可与待分配活动流程匹配的高协作模式.这些高协作模式将作为员工分配的候选方案.
3.3 员工分配算法为了找到能使待分配活动流程达到最大协作度的最优员工分配方案, 基于第3.2节中得到的员工分配的候选方案(候选方案中的高协作模式都是子实体序列, 只能作为部分活动的候选分配方案), 本文定义了如公式(5)所示的目标函数:
| ${\text{Minimize}}\sum\nolimits_{\forall ({a_1}|{r_1}, {a_2}|{r_2}) \in entityProList} {(1 - coo{p_{{a_1}, {a_2}}} \times compatibilit{y_{{a_1}|{r_1}, {a_2}|{r_2}}})} $ | (5) |
其中, entityProList表示已经分配员工的活动流程(即实体序列).根据该函数, 可从候选方案中选择使得整体协作度最大的一种分配方案.具体实现如算法2所示.
● 首先, 对待分配流程进行二进制编码并记录当前未分配的活动序列的编码(第1行、第2行);
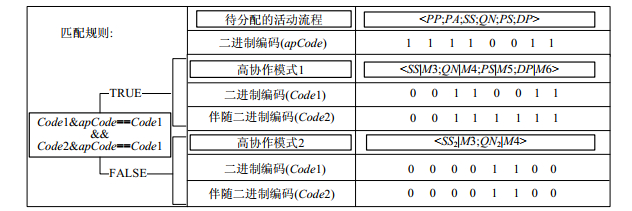
● 然后, 根据图 6的匹配规则快速得到能作为候选的员工方案的高协作模式(第4行~第8行);
|
Fig. 6 Matching rule between high collaboration patterns and activity process 图 6 高协作模式和活动流程的匹配规则 |
● 最后, 以整体协作度最大为目标, 在已有候选分配方案的部分活动的基础上, 通过遍历协作度表CTap和CTep对没有候选分配方案的活动子序列选择一种协作度最大的分配方案(第9行~第16行).
如图 6所示, 高协作模式1能与待分配的活动流程成功匹配, 说明它可以作为候选分配方案对SS(供应商选择)、QN(价格谈判)、PS(订单签订)、DP(交货付款)活动进行分配.
算法2.协作最优员工分配.

|
为了验证本文提出的员工分配方法FOSA的可行性和有效性, 分别在两个不同的数据集(合成数据集和真实数据集)上, 根据实体之间的协作度对比, 使用不同的分配算法对所有可能出现的待分配活动流程进行员工分配, 最后对比分配后的协作度以及分配所需的时间.对比的算法主要有贪婪启发式分配算法GHWA(greedy heuristic work assignment)、随机分配算法RWA(random work assignment)以及暴力求解算法BFWA(brute forth work assignment).
另外, 为了验证本文基于实体间协作度进行员工分配的效果比仅考虑员工之间协作度进行分配的效果更好, 在第4.3节中使用真实数据集, 分别基于实体之间的协作度计算(CMEA)和基于员工之间的协作度(CMA)[6]计算, 并使用BFWA算法(消除分配算法不同而带来的影响)分配员工, 然后对比分配后的效果.上述算法均使用Java语言开发实现, 实验运行环境是Windows 7+Intel Xeon E5-2620+2.00GHz主频+64GB内存.
4.1 合成数据集本节使用CPNTools (http://cpntools.org/)工具, 根据着色Petri网合成了一个软件开发流程(如图 7所示)的日志数据集, 包含10 000条流程实例、106 500个活动、21种不同的实体.

|
Fig. 7 Software development process model 图 7 软件开发流程模型 |
该流程中的某些复杂活动如编写代码(WriteCode)经常由多个员工共同协作完成, 针对这种情况, 本文将完成同一个活动的员工看作一个整体, 使用实体(编码|员工1, 员工2, 员工3)表示, 然后, 在此基础上计算协作度.在该数据集上, 将本文提出的FOSA算法与其他3种算法(RWA, GHWA, BFWA)的实验结果进行对比, 结果见表 5.该表统计了在计算实体间协作度的基础上, 使用不同的分配算法对所有可能出现的待分配活动流程(即活动个数范围为2~6)进行协作最优员工分配, 最后得到分配方案对应的协作度以及分配所需时间的平均值.从表 5中可以看出, 综合考虑协作度和算法运行时间, 本文提出的FOSA算法是最优的.
| Table 5 Comparison results of four staff assignment methods based on synthetic dataset 表 5 基于合成数据集的4种员工分配算法结果对比 |
4.2 真实数据集
本文使用的真实数据集是由Disco(https://fluxicon.com/disco/)提供的一个复杂采购流程(如图 8所示, 与图 1不同)日志.该日志包含99条实例、24种不同的活动、27名员工, 活动和员工构成的实体类型为145种(其中, 每种类型的活动都可由2个~14个员工执行).与第4.1节中进行相同的实验, 结果见表 6(由于对比的BFWA算法的时间随着分配活动个数的增加会变得非常大, 因此只统计了活动个数为2~10的待分配活动流程).

|
Fig. 8 Complex purchasing process model 图 8 复杂采购流程模型 |
| Table 6 Comparison results of four staff assignment methods based on real dataset 表 6 基于真实数据集的4种员工分配算法结果对比 |
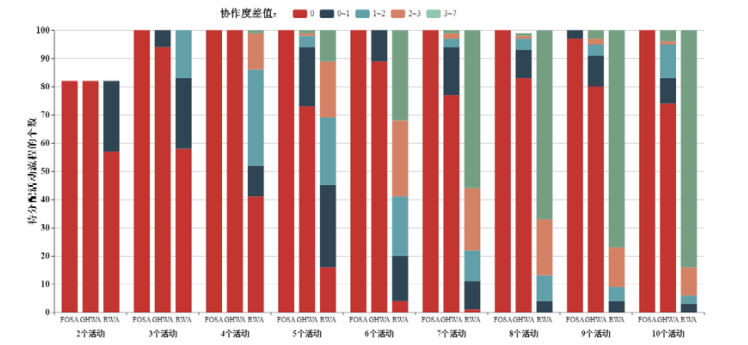
从表 6中可以发现, FOSA算法的执行结果非常接近BFWA算法的最优分配结果(理论上最优), 而时间上却有绝对的优势, 因此可以说明本文的方法能够实现快速而有效的员工分配.为了更好地对比算法效果, 本文使用堆积柱状图展示随着待分配活动流程中活动个数的增加, FOSA算法与RWA, GHWA算法对每一个待分配流程个体分配的结果(协作度)与BFWA算法所得的理论上最大的协作度之间的差值分布情况, 如图 9所示.我们首先将协作度差值划分为5类, 分别为0, 0~1, 1~2, 2~3, 3~7, 然后统计使用不同的分配方法将待分配活动流程个体分配结果的协作度与理论上能取得的最大协作度(BFWA算法)的差值分布.从图中可以看出, 使用本文提出的FOSA算法进行员工分配时的协作度几乎能够达到理论的最优值; 而另外两种分配算法随着活动个数的增加, 分配结果与理论最优的分配方案的协作度差值越来越大.
|
Fig. 9 Comparison results of three staff assignment methods for activity processes with different number of activities 图 9 使用3种不同的算法对不同活动个数的活动流程分配员工的结果比较 |
4.3 有效性验证
为了验证本文提出的根据实体之间的协作度(CMEA)进行员工分配的结果比根据员工之间的协作度(CMA)进行分配的结果更合理, 本文在真实数据集上分别基于这两种不同的协作度计算方法, 对所有可能出现的待分配活动流程(按流程中的活动个数分类)使用BFWA算法进行员工分配, 然后比较每条待分配活动流程在两种不同的员工分配结果时, 整个流程的执行时间(参考历史日志中员工执行活动的平均时间), 如图 10所示.

|
Fig. 10 Comparison results of staff assignment between CMEA and CMA 图 10 基于实体协作度(CMEA)和基于员工协作度(CMA)的员工分配结果比较 |
图 10(a)中的折线图表示不同活动个数的所有待分配活动流程, 分别基于CMEA+BFWA得到的员工分配方案对应的流程执行时间与基于CMA+BFWA的分配方案对应的流程执行时间的比值(记作“流程执行时间比”, 用TR=Time(CMEA+BFWA)/Time(CMA+BFWA)表示)的分布情况.图中的每个折线图上有很多个数值点, 每个数值点代表一条待分配活动流程, 横坐标值代表流程中的活动个数, 纵坐标值代表两种不同方案得到的流程执行时间比, 图中的加粗黑色虚线代表TR等于1, 即两种分配方案的效果一样.从图中可以发现:不管活动个数为多少, TR小于1(即CMEA+BFWA的流程执行时间比CMA+BFWA流程执行时间少)的数值点个数比TR大于1(即CMEA+BFWA的流程执行时间比CMA+BFWA流程执行时间多)的数值点要多.这说明大多数情况下, 基于实体协作度CMEA进行员工分配后的流程执行时间比基于员工协作度CMA进行员工分配后的流程执行时间要少, 进一步说明了基于实体协作度进行员工分配的效果更好.
图 10(b)中的柱状图是对图 10(a)中的流程执行时间比TR的进一步分析, 它表示不同活动个数的所有待分配活动流程中执行时间比TR小于1(即CMEA比CMA优)、TR大于1(即CMA比CMEA优)的流程个数占流程总数的比值分布情况.从图中可以发现:不管待分配流程中的活动个数是多少, CMEA比CMA优的流程占总比的值都要比CMA比CMEA优的流程占总比的值大.这进一步说明了使用实体协作度计算进行员工分配比考虑员工之间的协作度的分配效果要好.
5 结论和未来工作本文提出了一种通过参考历史日志中的高协作模式实现最大协作度的员工分配方法.特别地, 在计算员工与员工之间的协作度时也考虑了活动本身对其协作水平的影响.本文提出了两种编码方式, 用于快速匹配待分配的活动流程和挖掘得到的高协作模式, 并将匹配成功的模式作为员工分配的候选方案, 然后从中选出使得整个流程的协作度达到最大的一种员工分配方案.大量的对比实验, 验证了该方法的可行性和有效性.
由于对比实验选择了暴力求解算法, 这使得实验中待分配活动流程中的流程个数必须较少, 否则无法运行.未来我们准备基于其他算法、使用活动个数更多的流程来验证本文方法.此外, 由于挖掘得到的高协作模式的质量高低会影响后续员工分配方案的选择和效率, 所以需要进一步通过实验对比来选择最合适的协作模式挖掘算法.最后, 我们也将基于A*算法的思想, 通过综合考虑各个因素研究工作流最优员工分配问题.
| [1] |
Noll J, Beecham S, Richardson I. Global software development and collaboration:Barriers and solutions. Association for Computing Machinery, 2010, 1(3): 66–78.
[doi:10.1145/1835428.1835445] |
| [2] |
Magdaleno AM. A maturity model to promote collaboration in business processes. Journal of Business Process Integration & Management, 2009, 4(2): 111–123.
[doi:10.1504/IJBPIM.2009.027779] |
| [3] |
Liu TY, Cheng YL, Ni ZH. Mining event logs to support workflow resource allocation. Knowledge-Based Systems, 2012, 35(15): 320–331.
[doi:10.1016/j.knosys.2012.05.010] |
| [4] |
Aalst WVD. Process mining. Communications of the ACM, 2012, 55(8): 76–83.
[doi:10.1145/2240236.2240257] |
| [5] |
Bose RPJC, Aalst WVD. Trace alignment in process mining: Opportunities for process diagnostics. In: Hull R, Mendling J, Tai S, eds. Proc. of the 2010 Int'l Conf. on Business Process Management. Berlin: Springer-Verlag, 2010. 227-242.[doi:10.1007/978-3-642-15618-2_17] |
| [6] |
Kumar A, Dijkman RM, Song M. Optimal resource assignment in workflows for maximizing cooperation. In: Daniel F, Wang J, Weber B, eds. Proc. of the 2013 Int'l Conf. on Business Process Management. Berlin: Springer-Verlag, 2013. 235-250.[doi:10.1007/978-3-642-40176-3_20] |
| [7] |
Xie Y, Chien CF, Tang RZ. A method for estimating the cycle time of business processes with many-to-many relationships among the resources and activities based on individual worklists. Computers & Industrial Engineering, 2013, 65(2): 194–206.
[doi:10.1016/j.cie.2013.02.015] |
| [8] |
Xie Y, Chien CF, Tang RZ. A dynamic task assignment approach based on individual worklists for minimizing the cycle time of business processes. Computers & Industrial Engineering, 2015, 99: 401–414.
[doi:10.1016/j.cie.2015.11.023] |
| [9] |
Bessai K, Charoy F. Business process tasks-assignment and resource allocation in crowdsourcing context. In: Proc. of the 2016 IEEE Int'l Conf. on Collaboration and Internet Computing. New York: IEEE, 2016. 11-18.[doi:10.1109/CIC.2016.016] |
| [10] |
Reijers HA, Jansenvullers MH, Muehlen MZ, Appl W. Workflow management systems+swarm intelligence=dynamic task assignment for emergency management applications. In: Alonso G, Dadam P, Rosemann M, eds. Proc. of the 2007 Int'l Conf. on Business Process Management. Berlin: Springer-Verlag, 2007. 125-140.[doi:10.1007/978-3-540-75183-0_10] |
| [11] |
Ly LT, Rinderle S, Dadam P, Reichert M. Mining staff assignment rules from event-based data. In: Bussler CJ, Haller A, eds. Proc. of the 2005 Business Process Management Workshops. Berlin: Springer-Verlag, 2005. 177-190.[doi:10.1007/11678564_16] |
| [12] |
Liu YB, Wang JM, Yang Y, Sun JG. A semi-automatic approach for workflow staff assignment. Computers in Industry, 2008, 59(5): 463–476.
[doi:10.1016/j.compind.2007.12.002] |
| [13] |
Xu RB, Liu X, Xie Y, Yuan D, Yang Y. A Gaussian fields based mining method for semi-automating staff assignment in workflow application. In: Proc. of the 2014 Int'l Conf. on Software and System Process. New York: ACM Press, 2014. 178-182.[doi:10.1145/2600821.2600843] |
| [14] |
Cheng H, Chu XN. Task assignment with multiskilled employees and multiple modes for product development projects. Journal of Advanced Manufacturing Technology, 2012, 61(1-4): 391–403.
[doi:10.1007/s00170-011-3686-7] |
| [15] |
Liu TY, Cheng YL, Ni ZH. Mining event logs to support workflow resource allocation. Knowledge-Based Systems, 2012, 35(15): 320–331.
[doi:10.1016/j.knosys.2012.05.010] |
| [16] |
Xu RB, Bao GH, Yang PQ, Wang XM, Xie Y. Staff collective optimization strategy based on maximal dependency and minimal redundancy. Journal of Computer Integrated Manufacturing Systems, 2017, 23(5): 1014–1019(in Chinese with English abstract).
[doi:10.13196/j.cims.2017.05.012] |
| [17] |
Meddah I, Khaled B. Discovering patterns using process mining. Journal of Rough Sets & Data Analysis, 2016, 3(4): 21–31.
[doi:10.4018/IJRSDA.2016100102] |
| [18] |
Smirnov S, Weidlich M, Mendling J, Weske M. Action patterns in business process model repositories. Computers in Industry, 2009, 63(2): 115–129.
[doi:10.1016/j.compind.2011.11.001] |
| [19] |
Verginadis Y, Papageorgiou N, Apostolou D, Mentzas G. A review of patterns in collaborative work. In: Proc. of the 16th ACM Int'l Conf. on Supporting Group Work (Group 2010). New York: ACM Press, 2010. 283-292.[doi:10.1145/1880071.1880118] |
| [20] |
Diamantini C, Genga L, Potena D, Storti E. Discovering behavioral patterns in knowledge-intensive collaborative processes. In: Appice A, Ceci M, Loglisci C, Manco G, Masciari E, Ras Z, eds. Proc. of the New Frontiers in Mining Complex Patterns. Berlin: Springer-Verlag, 2015. 149-163.[doi:10.1007/978-3-319-17876-9_10] |
| [21] |
Needleman SB, Wunsch CD. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology, 1970, 48(3): 443–453.
[doi:10.1016/0022-2836(70)90057-4] |
| [16] |
许荣斌, 鲍广华, 杨培全, 汪欣梅, 谢莹. 基于最大依赖度及最小冗余度的员工协作优化策略. 计算机集成制造系统, 2017, 23(5): 1014–1019.
[doi:10.13196/j.cims.2017.05.012]
|
 2018, Vol. 29
2018, Vol. 29


