2. 数学工程与先进计算国家重点实验室(解放军信息工程大学), 河南 郑州 450001
2. State Key Laboratory of Mathematical Engineering and Advanced Computing(PLA Information Engineering University), Zhengzhou 450001, China
物联网通过在物品上嵌入电子标签、条形码等标识, 从而可达到对物品进行跟踪、监控等智能化管理的目的.但随着物联网的高速发展, 人们对信息数据的安全性需求也越来越多.从典型的物联网硬件平台(如RFID芯片、无线传感器)来看, 直接采用现在广泛应用的分组密码(AES、SHA等), 并不能完全适应其计算资源受限的硬件环境.因此, 越来越多的密码学家开始设计能适应这种环境中的分组密码, 并提出了许多轻量级分组密码算法, 如PRESENT[1]、PRINCE[2]、KATANTAN[3]、PRIDE[4]等.轻量级分组密码算法的分组和密钥长度一般较短, 非线性组件规模较小, 但迭代次数较高, 从而便于软硬件的快速实现.
SIMON[5]算法是2013年由NSA提出的一簇轻量级分组密码算法, 自提出以来, 就受到密码分析者的广泛关注.Abed等人[6]利用低重量的差分路径对SIMON进行了差分攻击.接着, Alkhzaimi等人[7]利用差分分析对SIMON的安全性进行了估计.此外, Alizadeh等人在文献[8]中对SIMON进行了线性攻击, 并得到关于SIMON更好的线性分析结果.Abed等人[6, 9, 10]将攻击轮数拓展到SIMON整个轮数的一半.Biryukov等人在文献[11]中利用分支边界算法对SIMON和SPECK差分路径进行搜索.2015年, Yu等人[12]利用零相关线性分析的方法对缩减轮数的SIMON进行了攻击.在2015美密会, Kölbl等人[13]详尽分析了SIMON轮函数的性质, 并利用SAT/SMT求解器给出了自动化搜索SIMON差分和线性路径的算法.
不可能差分分析[14]最早由Biham等人提出, 与差分分析寻找一条概率最大的差分路径不同, 不可能差分的分析目的在于寻找一条概率为零的差分路径来排除错误的候选密钥, 从而恢复正确密钥, 目前被广泛地应用到了各种结构的分组密码攻击中, 在AES[15], MISTY1[16]等密码上有非常好的攻击效果.零相关线性分析方法[17]由Bogdanov等人于2012年提出, 零相关线性分析的第1步是构造密码算法的零相关线性逼近关系, 我们通常让线性掩码在非零偏差下从两头向中间传播, 并在中间相遇, 若任何一个位置产生矛盾, 则找到一条零相关线性逼近.构造完密码算法的零相关线性逼近关系后, 接下来就可以对密钥进行恢复.
除中间相错技术外, 目前还存在几种自动化搜索不可能差分路径的算法, 如μ-method[18], UID-method[19], MILP[20]等.然而它们均未能充分考虑非线性组件与的性质, 所以不能精确给出每一轮的差分传播特征.
布尔可满足性问题(SAT)是当今计算机科学研究的核心问题, 很多不容易处理的问题都可以通过某些途径转换成SAT问题, 从而进行求解.本文提出了一种基于SAT的普适性的SIMON不可能差分和零相关路径自动化搜索算法.利用该算法, 我们共搜索到32条11轮不可能差分和零相关路径.该算法除用于自动化搜索不可能差分(零相关)路径外, 还可以在短时间内判断任意一对输入输出差分(掩码)是否构成一条不可能差分(零相关)路径.此外, SIMON设计者并未给出其轮函数中循环移位常数(a, b, c)的选取依据, 我们尝试从抵抗不可能差分攻击的角度, 对该常数的选取进行分析.
本文第1节给出SIMON算法介绍.第2节给出SIMON不可能差分路径搜索算法.第3节给出SIMON零相关路径搜索算法.第4节给出不可能差分路径搜索算法的其他应用.第5节总结全文.
1 SIMON算法介绍 1.1 概念与性质我们用F2代表二元有限域;
SIMON的轮函数表示如下:
| $ {{f}_{a}}_{,b,c}\left( x \right)={{S}^{a}}\left( x \right)\odot {{S}^{b}}\left( x \right)\oplus S{{c}^{a}}\left( x \right), $ |
其中, 循环移位常数(a, b, c)为(8, 1, 2).
为研究轮函数f的线性传播性质, 我们首先给出如下概念.
定义1. 对于n元布尔函数
| $ \hat f(\alpha ,\beta ) = \sum\limits_x {\mu (\langle \beta ,f\rangle + \langle \alpha ,x\rangle )} . $ |
为方便书写, 我们定义μ(x)=(-1)x.
定义2. 对于n元布尔函数
| $ {C^2}(\alpha \to \beta ) = {\left( {\frac{{\hat f(\alpha ,\beta )}}{{{2^n}}}} \right)^2}. $ |
定义3. 给定输入输出差分α, β, 则α通过f输出β的概率为
| $ \Pr (\alpha \to \beta ) = \frac{{|\{ x|f(x) \oplus f(x \oplus \alpha ) = \beta \} |}}{{{2^n}}}. $ |
最后, 我们用Dom(f)表示f的定义域, 用Img(f)代表其值域.
1.2 SIMON算法SIMON类算法是典型的Feistel结构, 其轮函数f(x)采用按位与运算、循环移位运算和异或运算, 其分组规模为2n(n=16, 24, 32, 48, 64), 密钥规模为mn, 根据不同的主密钥规模m, 取2, 3或4, 称为SIMON 2n/mn.SIMON类算法结构如图 1所示.
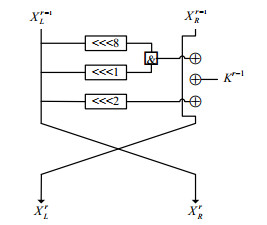
|
Fig. 1 r-Round structure of SIMON 图 1 SIMON第r轮结构 |
2 SIMON不可能差分路径搜索
针对不同的密码算法, 存在几种搜索不可能差分路径的方法, 包括μ-method, UID-method等.但这些算法也存在一些缺点和不足, 由于没充分考虑非线性组件的性质, 往往不能准确描述密码算法的差分传播性质.
本节, 我们提出一种基于SAT的SIMON不可能差分路径自动搜索算法.利用该算法, 可快速给出SIMON的32条11轮不可能差分路径.第2.1节介绍SIMON轮函数的差分传播性质; 第2.2节给出基于SAT的SIMON不可能差分路径搜索方法; 第2.3节给出SIMON的32条11轮不可能差分路径, 并用中间相错方法对其进行验证.
2.1 SIMON轮函数的差分传播性质在2015年的美密会, Kölbl等人深入研究了SIMON中的AND组件, 给出了准确的轮函数差分传播特性.
定理1[13]. 给定输入输出差分α, β, 则α通过函数f(x)=x⊙Sa(x)输出为β的概率pα, β为
| $ {p_{\alpha ,\beta }} = \left\{ {\begin{array}{*{20}{l}} {2 - n - d,{\text{ if }}\beta \oplus \alpha \odot {S^8}(\alpha ) \in Img({L_\alpha })} \\ {0, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\text{else}}} \end{array}} \right., $ |
其中, d=dimker(Lα), Lα(x)=x⊙Sa(α)⊕α⊙Sa(x).
定理2[13]. 令
| $ P(\alpha \to \beta ) = \left\{ {\begin{array}{*{20}{l}} {{2^{ - n + 1}}, \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\text{if }}\alpha = 1{\text{ and }}wt(\beta ) \equiv 0{\text{ }}\bmod {\text{ }}2} \\ {{2^{ - wt(varibits \oplus doublebits)}},{\text{ if }}\alpha \ne 1{\text{ and }}\beta \odot \overline {\operatorname{var} ibits} = 0 {\text{ and }}(\beta \oplus {S^1}(\beta )) \\ \ \ \ \ \ \ \ \odot doublebits = 0} \\ {0,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\text{else}}} \end{array}} \right.. $ |
为了得到一条有效的差分路径, 根据第2.1节中的定理, 我们构造出α和β需满足的如下约束式:
| $ \left. \begin{array}{1} {\text{if }}\alpha ! = 1 \hfill \\ \ \ \ \ \ varibits = {S^8}(\alpha ) \vee {S^1}(\alpha ) \hfill \\ \ \ \ \ \ doublebits = {S^1}(\alpha ) \odot \overline {{S^8}(\alpha )} \wedge {S^{15}}(\alpha ) \hfill \\ \ \ \ \ \ \beta \odot varibits = 0 \hfill \\ \ \ \ \ \ (\beta \oplus {S^7}(\beta )) \odot doublebits = 0 \hfill \\ {\text{else}} \hfill \\ \ \ \ \ \ wt(\beta ) \equiv 0{\text{ }}\bmod {\text{ }}2 \hfill \\ \end{array} \right\} $ | (1) |
再根据SIMON的算法结构, 利用约束式(1)写出n轮差分的传播约束式; 接着, 对特定集合下的每一对差分, 利用SAT求解器, 对其n轮差分传递的有效性进行验证.该算法如算法1所示.
算法1. SIMON不可能差分路径搜索.

|
算法1为遍历算法, 其复杂度与输入输出差分对的选取集合有关.对于分组长度为32的密码算法, 遍历起来不现实, 我们通常选取特定集合来遍历.其中的dispose函数, 将所列的约束式转化为合取范式(CNF), 再将CNF送入特定的SAT求解器, 验证其可否满足.目前存在多种SAT求解器, 本文采用的是CryptoMiniSat4.对于不同求解器, 其求解效率也存在差异.
2.3 11轮SIMON的不可能差分路径目前, 关于SIMON的3条11轮不可能差分路径由Wang等人[21]利用中间相错技术给出, 本文利用基于SAT的自动化搜索算法给出了32条11轮不可能差分路径, 接着又用中间相错技术对其进行了验证.
2.3.1 32条11轮不可能差分路径SIMON的分组长度是32, 遍历所有可能的差分对复杂度太高, 所以我们只考虑输入、输出差分重量均为1的情况.利用该算法, 我们在短时间内给出32条SIMON的11轮不可能差分路径, 结果见表 1, 其中, vi(0≤i≤7)代表只有第i bit为1.而0则代表一个字节中所有bit均为0.
| Table 1 Impossible differential trails of SIMON 表 1 SIMON不可能差分路径 |
搜索在一台Intel Core i7-6700笔记本上进行, 时间为29s.
2.3.2 32条不可能差分路径验证中间相错技术的基本原理是:加密方向

|
Fig. 2 Schematic diagram of miss-in-the-middle 图 2 中间相错示意图 |
我们利用中间相错技术, 对32轮不可能差分结果进行了验证, 例如(0, 0, 0, v7)→(v6, 0, 0, 0)这条路径, 验证结果在表 2中给出, 表 2中的问号, 即代表我们无法确定该比特位是1还是0.
| Table 2 Result of miss-in-the-middle 表 2 中间相错结果 |
从表 2中可以看到, 差分(ΔL0, ΔR0)(即(0, 0, 0, v7))向下传递6轮与差分(ΔL11, ΔR11)(即(v6, 0, 0, 0))向上传递5轮以后, 在(ΔL6, ΔR6)相遇.观察差分前后传递得到的ΔR6值, (1, ?, ?, ?, ?, ?, ?, 0, ?, 0, ?, ?, ?, ?, ?, ?)与(0, ?, 0, ?, ?, ?, ?, ?, ?, 1, ?, ?, ?, ?, ?, ?)在最高比特位构成矛盾.
3 SIMON零相关路径搜索目前, 关于SIMON的11轮零相关路径由Wang等人[21]给出.本节提出一种基于SAT的SIMON零相关路径自动搜索算法, 利用该算法, 可以快速地给出SIMON的32条11轮不可能差分路径.第3.1节介绍SIMON轮函数的线性传播性质; 第3.2节给出基于SAT的SIMON零相关路径搜索方法; 第3.3节给出SIMON条11轮零相关路径.
3.1 SIMON轮函数的线性传播性质与(AND)运算对SIMON线性掩码的传递有着重要影响, Kölbl等人[13]对非线性组件与进行了深入的研究, 并给出了一些能够精确描述SIMON轮函数线性传播性质的表达式.
定理3[13]. SIMON算法中,
| $ C(u \to v) = \left\{ {\begin{array}{*{20}{l}} {{2^{ - n + 2}}{\text{, if }}v = 1{\text{ and }}u \in {U_{1/v}}} \\ {{2^{ - \theta (v)}}{\text{, if }}v \ne 1{\text{ and }}u \in {U_{1/v}}} \\ {0, \ \ \ \ \ \ \ \ {\text{else}}} \end{array}} \right.. $ |
本节中, 首先构造描述SIMON轮函数线性传播性质的约束式, 然后, 利用约束式构造一个用于自动搜索SIMON零相关路径的算法.
由第3.1节可知, 若u→v有效当且仅当u∈U1/v.为得到一条有效的线性路径, 我们构造如下的约束式:
| $ \left. \begin{array}{1} u = u \oplus {S^{ - c}}(v) \hfill \\ (({S^{ - a}}(v)|{S^{ - b}}(v)) \oplus u) \odot u! = 0 \hfill \\ {\text{if }}(f,v = = ({2^n} - 1)) \hfill \\ \ \ \ \ t,l = u,0 \hfill \\ \ \ \ \ {\text{while }}t! = 0 \hfill \\ \ \ \ \ \ \ \ \ l = l \oplus (t \odot 3) \hfill \\ \ \ \ \ \ \ \ \ t = (t \gg 2) \hfill \\ \ \ \ \ l = 0 \hfill \\ {\text{else}} \hfill \\ \ \ \ \ tmp = v \hfill \\ \ \ \ \ abits = v \hfill \\ \ \ \ \ {\text{while }}tmp! = 0 \hfill \\ \ \ \ \ \ \ \ \ tmp = v \odot {S^{ - (a - b)}}(tmp) \hfill \\ \ \ \ \ \ \ \ \ abits = abits \oplus tmp \hfill \\ \ \ \ \ sbits = {S^{ - (a - b)}}(v) \odot ( - v) \odot ( - {S^{ - (a - b)}}(abits)) \hfill \\ \ \ \ \ sbits = {S^{ - b}}(sbits) \hfill \\ \ \ \ \ pbits = 0 \hfill \\ \ \ \ {\text{while }}sbits! = 0 \hfill \\ \ \ \ \ \ \ \ \ pbit{{s}^{\wedge }} = sbits \odot u \hfill \\ \ \ \ \ \ \ \ \ sbits = {S^{a - b}}(sbits) \odot {S^{ - b}}(v) \hfill \\ \ \ \ \ \ \ \ \ sbits = {S^{a - b}}(sbits) \hfill \\ \ \ \ \ \ \ \ \ pbits = {S^{2*(a - b)}}(pbits) \hfill \\ \ \ \ \ pbits = 0 \hfill \\ \end{array} \right\} $ | (2) |
结合约束式(2), 我们构造了一种用于搜索SIMON零相关路径的算法.该算法是一种遍历算法, 通过穷举特定的输入输出掩码集合(Δ, Γ), 判断每一对输入输出掩码是否构成一条有效线性路径:若否, 则输出一条零相关路径.考虑到SIMON的分组长度.我们无法遍历所有可能的输入输出掩码, (Δ, Γ)只是掩码全集中的一个子集, 该算法如算法2所示.
算法2. SIMON零相关路径搜索.

|
类似于搜索不可能差分, 我们只考虑输入输出掩码重量均为1的情况.利用第3.2节中的算法, 我们共找到32条零相关路径, 见表 3.
| Table 3 Zero-Correlation linear trails of SIMON 表 3 SIMON零相关路径 |
由于线性传播特性刻画复杂, 上述结果的搜索时间约为17min.
4 不可能差分路径搜索算法的其他应用 4.1 SIMON不可能差分存在性证明本文提出的算法除用于自动化搜索不可能差分外, 还可以快速判断给定的输入输出差分是否能构成一条有效路径.我们将输入差分分成左右两部分(左右各为16bit), 并将左半部分设为0x0000, 右半部分从0x0000遍历到0xFFFF, 接着设定输出差分重量为1.通过遍历上述集合中所有可能的输入输出差分, 我们确定在该集合下SIMON最长不可能差分的轮数确为11轮.上述结果的搜索时间为21h, 如果计算能力允许, 还可给出比现有结果更强的结论.
4.2 SIMON循环移位常数选取分析SIMON设计者从未给出图 1中循环移位常数(8, 1, 2)的选取思路.我们尝试从抵抗不可能差分的角度, 来分析循环移位常数对SIMON安全性的影响, 希望能起到一些抛砖引玉的作用.
Kölbl等人[13]主要从抵抗差分攻击的角度对循环移位常数的选取进行了分析.通过研究SIMON循环移位常数对其扩散性的影响, 文献[13]从所有可能的移位常数(a, b, c)中选出一个集合Δ, 由Δ中元素构成的SIMON32, SIMON48, SIMON64算法, 均有类似于标准算法的10轮差分概率, 具有较好的扩散性和抵抗差分攻击能力.Δ见表 4.
| Table 4 Cyclic shift constant set of SIMON 表 4 SIMON循环移位常数选取集合 |
分别对Δ中元素构成的SIMON算法进行不可能差分路径搜索, 以测试其抵抗不可能差分攻击的能力.利用自动搜索算法, 设定输入输出重量均为1, 分别对Δ中元素构成的SIMON算法进行11轮不可能差分路径搜索, 结果见表 5; 利用自动搜索算法, 设定输入输出重量均为1, 分别对Δ中元素构成的SIMON算法进行12轮不可能差分路径搜索, 结果见表 6.
| Table 5 Impossible differential trails of 11-round SIMON with different parameters 表 5 SIMON不同参数11轮不可能差分路径 |
| Table 6 Impossible differential trails of 12-round SIMON with different parameters 表 6 SIMON不同参数12轮不可能差分路径 |
由第2.3节可知, 用原始移位参数(8, 1, 2)搜索SIMON的11轮不可能差分路径条数为32条, 搜索到12轮不可能差分路径条数为0条, 结果均小于或等于Δ中元素搜索到的条数.可见, SIMON原始参数更能抵抗不可能差分攻击.
5 总结本文提出了一种SIMON不可能差分及零相关路径自动化搜索算法.利用该算法, 我们能够快速地搜索到更多条数的11轮SIMON不可能差分及零相关路径.该算法还可以准确地判断任意差分对(掩码对)能否构成一条不可能差分(零相关路径).此外, 我们还给出了特定输入输出差分集合下, SIMON算法不存在12轮不可能差分路径的结论.最后, 我们从抵抗不可能差分攻击的角度, 对SIMON循环移位参数的安全性进行估计, 并验证了相对于其他参数, SIMON原始参数具有更强的抵抗不可能差分攻击能力.在后续工作中, 我们拟对该算法做出进一步的优化, 并将其推广到其他结构的分组密码上.
| [1] |
Bogdanov A, Knudsen LR, Leander G, Paar C, Poschmann A, Robshaw MJB, Seurin Y, Vikkelsoe C. PRESENT: An ultralightweight block cipher. In: Proc. of the CHES 2007. LNCS 4727, Berlin: Springer-Verlag, 2007. 350-466.https://link.springer.com/chapter/10.1007%2F978-3-540-74735-2_31 |
| [2] |
Borghoff J, Canteaut A, Gneysu T, Lender G, et al. PRINCE-A low-latency block cipher for pervasive computing applications: Extended abstract. In: Proc. of the ASIACRYPT 2012. LNCS 7658, Berlin: Springer-Verlag, 2012. 208-225. |
| [3] |
De Canniére C, Dunkelman O, Knezevic M. KATAN and KTANTAN: A family of small and efficient hardware-oriented block ciphers. In: Proc. of the CHES 2009. LNCS 5747, Berlin: Springer-Verlag, 2009. 272-288.https://www.mendeley.com/catalogue/katan-ktantan-family-small-efficient-hardwareoriented-block-ciphers/ |
| [4] |
Albrecht MR, Driessen B, Kavun EB, Leander G, Paar C, Yalcn T, et al. Block ciphers-focus on the linear layer (feat. PRIDE). In: Proc. of the CRYPTO 2014. LNCS 8616, Berlin: Springer-Verlag, 2014. 57-76.https://link.springer.com/chapter/10.1007%2F978-3-662-44371-2_4 |
| [5] |
Beaulieu R, Shors D, Smith J, Clark ST, Weeks B, Wingers L. The SIMON and SPECK families of lightweight block ciphers. Technical Report, 2013/404, 2013.http://ieeexplore.ieee.org/document/7167361/ |
| [6] |
Abed F, List E, Lucks S, Wenzel J. Differential and linear cryptanalysis of reduced-round SIMON. Technical Report, 526, 2013. |
| [7] |
Alkhzaimi H, Lauridsen M. Cryptanalysis of the SIMON family of block ciphers. Technical Report, 543, 2013. |
| [8] |
Alizadeh J, Bagheri N, Gauravaram P, Kumar A, Sanadhya SK. Linear cryptanalysis of round reduced SIMON. Technical Report, 663, 2013.https://eprint.iacr.org/2013/663.pdf |
| [9] |
Abed F, List E, Lucks S, Wenzel J. Cryptanalysis of the SPECK family of block ciphers. Technical Report, 568, 2013.http://pdfs.semanticscholar.org/1878/bc8ec45c6fbacf50b5dafcc4f8579142aed1.pdf |
| [10] |
Abed F, List E, Lucks S, Wenzel J. Differential cryptanalysis of round-reduced SIMON and SPECK. In: Proc. of the FSE 2014. LNCS 8540, Berlin: Springer-Verlag, 2014. 525-545.https://link.springer.com/chapter/10.1007%2F978-3-662-46706-0_27 |
| [11] |
Biryukov A, Roy A, Velichkov V. Differential analysis of block ciphers SIMON and SPECK. In: Proc. of the FSE 2014. LNCS 8540, Berlin: Springer-Verlag, 2014. 546-570.https://link.springer.com/chapter/10.1007/978-3-662-46706-0_28 |
| [12] |
Yu XL, Wu WL, Shi ZQ, Member S, Shi ZQ, Zhang J, Zhang L, Wang YF. Zero-Correlation linear cryptanalysis of reduced-round SIMON. Journal of Computer Science and Technology, 2015, 30(6): 1358–1369.
[doi:10.1007/s11390-015-1603-5] |
| [13] |
Köbl S, Leander G, Tiessen T. Observations on the SIMON block cipher family. In: Proc. of the CRYPTO 2015. LNCS 9215, Berlin: Springer-Verlag, 2015. 161-185.https://link.springer.com/chapter/10.1007/978-3-662-47989-6_8 |
| [14] |
Biham E, Biryukov A, Shamir A. Cryptanalysis of skipjack reduced to 31 rounds using impossible differentials. In: Proc. of the EUROCRYPT'99. Berlin, Heidelberg: Springer-Verlag, 1999. 12-23.https://link.springer.com/chapter/10.1007%2F3-540-48910-X_2 |
| [15] |
FIPS PUB 197. Announcing the Advanced Encryption Standard (AES). Washington: National Institute of Standards and Technology, 2001. |
| [16] |
Matsui M. New block encryption algorithm MISTY. In: Proc. of the FSE'97. LNCS 1267, Berlin: Springer-Verlag, 1997. 64-67. |
| [17] |
Bogdanov A, Rijmen V. Linear hulls with correlation zero and linear cryptanalysis of block ciphers. Designs, Codes and Cryptography, 2014, 70(3): 369–383.
[doi:10.1007/s10623-012-9697-z] |
| [18] |
Kim J, Hong S, Lim J. Impossible differential cryptanalysis using matrix method. Discrete Mathematics, 2010, 310(5): 988–1002.
[doi:10.1016/j.disc.2009.10.019] |
| [19] |
Luo YY, Lai XJ, Wu ZM, Gong G. A unified method for finding impossible differentials of block cipher structures. Information Sciences, 2014, 263(1): 211–220.
http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ0232403371 |
| [20] |
Cui TT, Jia KT, Fu K, Chen SY, Wang MQ. New automatic search tool for impossible differentials and zero-correlation linear approximations. IACR Cryptology ePrint Archive, 2016. https://eprint.iacr.org/2016/689.pdf |
| [21] |
Wang QJ, Liu ZQ, Varici K, Sasaki Y, Rijmen V, Yosuke T. Cryptanalysis of reduced-round SIMON32 and SIMON48. In: Proc. of the INDOCRYPT 2014. LNCS 8885, Berlin: Springer-Verlag, 2014. 143-160.https://link.springer.com/chapter/10.1007%2F978-3-319-13039-2_9 |
 2018, Vol. 29
2018, Vol. 29


