2. 中国科学院大学, 北京 100190;
3. 计算机科学国家重点实验室(中国科学院 软件研究所), 北京 100190
2. University of Chinese Academy of Sciences, Beijing 100190, China;
3. State Key Laboratory of Computer Science(Institute of Software, The Chinese Academy of Sciences), Beijing 100190, China
机器学习问题通常会转换成一个目标函数去求解, 优化算法是求解目标函数中参数的重要工具[1].目前, 机器学习常用的优化算法主要包括梯度下降(gradient decent, 简称GD)算法[1]、二阶优化(second-order)算法[1]、邻近梯度(proximal gradient, 简称PG)算法[2]、坐标下降(cooridinate decent, 简称CD)算法[3]、交替方向乘子(alternating direction method of multipliers, 简称ADMM)算法[4], 分别适用于不同类型的优化问题:梯度法和二阶法适用于可微凸函数、邻近梯度法适用于可微凸函数与不可微凸函数的和问题、坐标法适用于不可求导凸函数问题、交替方向乘子法适用于有约束的凸函数问题.然而, 在大数据环境下, 单线程优化算法已经不能适应大规模机器学习应用的需求, 基于不同计算模型的并行与分布式优化算法成为研究热点.在多核环境下, 研究者们提出了基于共享存储的并行优化算法, 通过对样本数据或者模型参数的划分, 使用多线程并行训练更新共享内存中的模型参数.但是单机存储的数据量非常有限, 为了应对大数据量难以存储、单机计算量有限的问题, 分布式优化算法逐渐涌现出来, 基于不同的并行计算模型解决多节点任务划分和参数更新的问题, 同时尽可能地降低通信成本.
为研究可扩展机器学习的优化算法在并行与分布式环境下的优化策略, 本文对多种机器学习优化算法进行分析总结.首先介绍本文对算法的分析维度、原始优化算法基本原理和并行计算模型, 然后对GD、Second-order、PG、CD和ADMM这5种优化算法分别从单机多核并行优化和分布式并行优化角度进行阐述, 并从模型特性、输入数据特性、算法评价标准和并行计算模型对每种算法的具体优化策略进行对比分析.通过综述研究发现:各种优化算法大多是对传统机器学习的凸函数问题进行优化, 不同算法再根据自身特点对目标函数的不同特性进行优化, 对于非凸函数的优化求解研究较少; 在多核、分布式环境下, 基于不同并行计算模型对不同算法进行改进, 通过并行化来提高运行速率, 解决大规模数据处理问题; 输入数据样本大多具有稀疏性, 从而保证特征之间关联程度较小, 便于多节点并行训练更新, 保证算法收敛.同时, 算法的更新策略需要依赖于不同计算模型的具体平台, 因此, 本文分类研究流行的可扩展机器学习系统, 总结其中实现的算法, 进而了解各优化算法在目前系统的实际实现和部署情况.最后绘制了根据目标函数进行分类的多层次分类图, 对论文中介绍的各优化算法进行划分, 帮助开发者根据目标函数选择优化算法, 交叉探索应用优化算法到新的目标函数类型上.
本文第1节介绍算法分析维度、原始优化算法和并行计算模型.第2节~第6节分别综述各优化算法并行与分布式改进.第7节综述现有机器学习系统优化算法实现情况.第8节给出全文算法的多层次分类图, 对目前优化算法存在的问题进行分析, 并展望未来的研究工作.第9节进行总结.
1 基础知识简介在机器学习的模型训练中, 要优化的目标函数一般都可以表示为以下形式:
| $ \min J(x, \theta )\ {\rm{ or }}\ \max J(x, \theta ), 其中, J(x, \theta )=f(\{{{x}_{i}}, {{y}_{i}}\}_{i=1}^{N};\theta )+r(\theta ) $ | (1) |
其中, 函数J(θ)为目标函数, f为表示真实值与拟合值之差的损失函数, r(θ)为正则项(为防止参数过拟合问题)[5].各种优化算法通过不同的方式求解该方程以得到使J(θ)最优的参数θ.为了更加清晰地理解优化算法的求解过程, 本节首先对优化算法的分析维度进行拆分介绍; 随后, 从优化算法解决的问题域出发, 对5种优化算法的原始单线程版本进行简要介绍, 分析对比它们的收敛率、求解优势和存在的不足, 为后续的并行与分布式算法改进提供算法理论基础.同时, 在设计并行与分布式算法时, 算法需要依赖于具体平台, 系统软件层次的并行计算模型是算法设计者与体系结构研究者之间的一个桥梁, 是影响算法逻辑的重要因素之一, 因此, 对4种常见的并行计算模型进行介绍, 为理解与平台相结合的并行与分布式算法改进提供计算模型理论基础.
1.1 算法分析维度简介针对不同算法, 本文从4个维度——模型特性(目标函数特性)、输入数据特性、算法评价标准(收敛率和扩展性)、所应用平台的计算模型进行说明.下文中, 每类算法的对比分析表格即根据这4个维度, 按照时间顺序对每种算法进行比较.对于表格中的方法一栏, 如果在论文中对算法名称有说明, 则为算法名称加年份; 否则, 为作者姓名加年份.对于表格中的单横线, 表示论文没有分析该维度, 无法客观评价进行填写.下面对各个维度进行介绍.
1.1.1 模型特性机器学习问题中建立的优化模型通常可以转换为一个目标函数, 因此, 模型特性即指目标函数特性, 是优化算法要解决的目标.本文将目标函数按照属性特征分为凸函数和非凸函数两大类, 其中, 凸函数分为强凸函数与非强凸函数:强凸是指在到达极小值区域时函数曲线陡峭, 而非强凸函数是指在到达极小值区域时函数曲线平缓.传统的机器学习问题通常为凸函数优化问题, 其又可细分为对变量有约束的凸函数和对变量无约束的凸函数.凸函数根据多项式各变量是否可以求导分为可微和不可微凸函数, 其中, 函数连续可微则称函数平滑.神经网络相关的深度学习问题的损失函数通常为非凸函数, 由于目前非凸函数的优化算法的理论研究较少, 本文仅包含几种深度学习领域中的非凸函数优化算法.
目标函数从组成上包含损失函数和正则项, 其中, 损失函数表示真实值与拟合函数值之间的差值; 正则项是对模型参数规范化, 从而达到避免函数过拟合或者简化函数的目的.损失函数可按照上述函数属性来进行细分.正则项主要分为L1正则项(‖θ‖)、L2正则项(‖θ‖2)和弹性网正则项(L1+L2正则项).可以看出, 正则项都为凸函数.其中, L2正则项可微分, 而L1正则项不可微分.
1.1.2 数据特性训练模型输入样本数据的不同将带来不同的运行效果, 是影响算法结果、性能的重要因素.本文按照稀疏性、维数、规模来对数据特性进行评价:稀疏性是指样本特征值非零的比例, 分为稀疏和稠密; 维数是指样本特征的个数, 分为高维和低维; 规模是指模型训练数据样本的多少, 在分布式环境下, 数据规模通常是大规模.
1.1.3 评价标准优化算法的评价体系一般包括收敛率、扩展性、时间复杂度、空间复杂度、通信复杂度和结果准确率等.通常, 论文中会证明算法的收敛率, 从理论上说明算法的正确性, 所以, 是否收敛是我们重要的评价标准.部分算法会对扩展性进行说明, 由于如何划分算法来并行更新是并行与分布式实现的重点, 因此, 将扩展性纳入到评价标准中.时间、空间、通信复杂度和结果准确度在大多数优化算法论文中都没有进行理论说明, 但是部分算法在实验验证部分对这些指标进行了对比.由于机器学习问题与实验数据有关, 不同的实验数据所需要的循环迭代次数、运行结果会有所不同, 部分数据的结果对这些指标概括性不足会造成以偏概全, 因此, 我们不对这些指标进行详细分析.
收敛率是指连续两次误差的比值的极限, 可以表示为下式:
| $ {{\lim }_{k\to \infty }}\frac{|{{J}_{k+1}}-{{J}^{*}}|}{|{{J}_{k}}-{{J}^{*}}{{|}^{q}}}=\mu $ | (2) |
其中, Jk为每一轮目标函数的更新结果, J*为目标函数J的最优值.依照定义, 可以确定这个比值μ小于1, 否则发散.根据q与μ值的不同, 可以得出不同的收敛结果.
(1) 如果q=1, k无穷大, μ收敛到0, 则为次线性收敛;
(2) 如果q=1, k无穷大, μ收敛到0至1, 则为以收敛比μ线性收敛;
(3) 如果q > 1, k无穷大, μ收敛到0至1, 或q=1且μ=0, 则为q次超线性收敛.例如, 当q=2时, 为二次收敛.
扩展性是指算法是否随着线程的增加, 或者系统的物理(内、外存)资源、计算框架的扩展, 或者样本数据的增加达到一定程度的加速比, 其中, 加速比是指同一个任务在单处理器系统和并行处理器系统中运行所消耗的时间的比率, 用来衡量并行系统或程序并行化的性能和效果.
(1) 线性加速比是指p个处理器运行算法的时间是1个处理器运行算法时间的p倍, 又称为理想加速比;
(2) 超线性加速比是指p个处理器运行算法的时间大于1个处理器运行算法时间的p倍;
(3) 病态加速比是指p个处理器运行算法的时间小于1个处理器运行算法时间的p倍.
1.1.4 计算模型并行计算模型是并行算法设计和分析的基础.为提高系统性能, 研究者们提出多种并行计算模型:第1代为单机多核环境下的共享存储计算模型; 第2代为分布式存储模型, 包括整体同步并行计算模型(BSP)[6]、延迟同步并行计算模型(SSP)[5]和异步并行计算模型(ASP)[5]等.由于本文中介绍的优化算法目前广泛使用共享存储、BSP、SSP和ASP计算模型, 在第2.3节将详细介绍这4类模型.
1.2 原始单线程机器学习优化算法本节简要介绍梯度下降算法[1]、二阶优化算法[1]、邻近梯度算法[2]、坐标下降算法[3]和交替方向乘子算法[4]的未改进的原始单线程版本的基本原理, 便于以此为基础理解其并行与分布式版本.
1.2.1 梯度下降算法[7]梯度下降法是求解无约束优化问题最常用的方法, 存在大量改进的算法变种.梯度下降法是沿梯度下降的方向, 即以负梯度方向作为搜索方向, 不断迭代求解目标函数的最优值.由于梯度下降法需要求解目标函数导数, 因此理论上, 梯度下降法主要解决可微凸函数.当目标函数为连续可微强凸函数时, 算法是线性收敛的.当放松目标函数属性条件为利普希茨连续凸函数时, 收敛率会降低至次线性.
梯度下降法的计算过程如下.
(1) 对参数θ赋初值θk, 计算目标函数的梯度, 即目标函数J(θ)在θk处的导数为
| $ \nabla J({{\theta }_{k}}) $ | (3) |
(2) 改变θ的值, 使得J(θ)按梯度下降的方向进行减少, 即:
| $ {{\theta }_{k}}_{+1}={{\theta }_{k}}-\alpha \nabla J({{\theta }_{k}}) $ | (4) |
其中, α表示梯度负方向上的搜索步长, 步长一般通过线性搜索算法来确定.
(3) 将θk+1对公式(3)中的θk赋值, 然后按照步骤(1)~步骤(3)反复迭代直至收敛, 从而经过多轮迭代后, 得到最优值θk+1.
在原始梯度下降法中, 由于需要计算所有样本的梯度, 耗时大、易陷入局部最优解等问题, 相继有研究者提出批量梯度下降法(batch GD)[8]、随机梯度下降法(SGD)[9]; 针对计算新一轮梯度, 步长难以确定的问题, 研究者们提出学习率自动更新算法等[10]; 针对训练样本不均衡、存在噪音, 标准随机梯度下降法只能获得次线性收敛率的问题, 研究者们提出噪音消减算法等[11, 12].同时, 不同改进策略结合不同的目标函数属性进行算法实现.
1.2.2 二阶优化算法[7]二阶优化算法与梯度下降法的问题域相同, 但梯度下降法主要利用目标函数的局部性质, 即求解目标函数的一阶导数, 具有一定的“盲目性”.二阶优化算法的代表算法——牛顿法, 利用目标函数的一阶和二阶导数信息, 带有一定的全局性, 因此牛顿法的收敛速率更快.当目标函数二阶可导且导数连续时可以获得二次收敛率.
牛顿法的计算过程如下.
(1) 将目标函数J(θ)在点θk的某邻域内展开成泰勒级数:
| $J(\theta )=J({{\theta }_{k}})+{J}'({{\theta }_{k}})(\theta -{{\theta }_{k}})+1/2!\cdot {J}''({{\theta }_{k}}){{(\theta -{{\theta }_{k}})}^{2}}+{{R}_{n}}(\theta ) $ | (5) |
(2) 取其前3项, 对方程求导求其最小值, 即J'(θ)=0的解:
| $ {{\theta }_{k}}_{+1}={{\theta }_{k}}-{{({{\nabla }^{2}}J({{\theta }_{k}}))}^{-1}}\nabla J({{\theta }_{k}}) $ | (6) |
其中, 将函数的二阶导表示为Hesse矩阵(假设其可逆), 函数的一阶导表示为Jacobi矩阵, 上述等式可改写为
| $ {{\theta }_{k}}_{+1}={{\theta }_{k}}-Hess{{e}^{-1}}\cdot Jacobi $ | (7) |
(3) 将θk+1对公式(5)中的θk赋值, 按照步骤(1)~步骤(3)反复迭代, 直至收敛.
原始牛顿法中, 由于Hesse矩阵的逆矩阵可能不存在, 同时, 由于Hesse矩阵计算复杂性高、存储消耗大等原因, 相继有一些研究者提出改进算法, 如阻尼牛顿法、拟牛顿法、L-BFGS算法等[13-15].
1.2.3 邻近梯度算法[16]梯度下降法和二阶优化算法通常只能解决整体可微凸函数, 对于目标函数J(θ)是由平滑凸函数f(θ)和非平滑凸函数g(θ)组成的情况:
| $ J(\theta )=f(\theta )+g(\theta ) $ | (8) |
则使用次梯度法[17]来优化, 但是, 次梯度法存在求解慢、不会产生稀疏解等问题.而在凸优化领域, 基于邻近点算子的邻近梯度算法被证明适合求解该问题.一般地, f(θ)和g(θ)分别代表损失函数和目标函数的正则项.当f(θ)为平滑凸函数且具有利普希茨连续导数、g(θ)为非平滑凸函数时, 算法是次线性收敛.
首先定义函数g(θ)的邻近点算子为
| $ pro{{x}_{g}}(u)=\arg {{\min }_{\theta }}\ g(\theta )+(1/2)\, \cdot \, ||\theta -u||_{2}^{2} $ | (9) |
即, 在当前点u的周围寻找极小化f(θ)的邻近点θ, 因此, 可以通过设置初始点, 不断地迭代获得θ的最优解.
邻近梯度法的计算过程如下.
(1) 对参数θ赋初值θk.
(2) 利用邻近点梯度算法的迭代公式, 求得新的θk+1:
| $ {{\theta }_{k}}_{+1}=prox({{\theta }_{k}}-\eta \nabla f({{\theta }_{k}})) $ | (10) |
通常, g(θ)为L1正则项, 则proxg代表g的软阈值函数.μ为步长, ∇f(θk)为f(θ)的在θk处的一阶导数.
(3) 将θk+1代入公式(10), 按照步骤(2)、步骤(3)反复迭代, 直至收敛.
1.2.4 坐标下降算法[18]不同于上述算法需要计算目标函数的梯度、存在步长难确定等问题, 坐标下降法是一种非梯度优化算法, 并且不用设定步长.在每次迭代中, 在当前点处沿一个坐标方向进行一维线搜索, 固定其他坐标方向, 以求得目标函数的一个局部最小值, 循环使用不同的坐标方向.一个周期的一维搜索迭代过程相当于一个梯度迭代.当目标函数连续可微且每个子问题均可解或非平滑部分可分离时, 算法是次线性收敛.
坐标下降法的计算过程如下.
(1) 沿一个方向寻求多变量目标函数J(θ)的局部最小值, 即, 固定θi以外的坐标, 求θi方向的最小值.例如, 从θ1开始以线性空间的一组基θ1k-1, θ2k-1, …, θnk-1作为搜索方向, 求得新的θ1k.
| $ \theta _{1}^{k}\in \arg \min J({{\theta }_{1}}, \theta _{2}^{k-1}, ..., \theta _{i}^{k-1}, ..., \theta _{n}^{k-1}) $ | (11) |
(2) 循环最小化各个坐标方向上的目标函数值:
| $ \theta _{n-1}^{k}\in \arg \min J(\theta _{1}^{k}, \theta _{2}^{k}, ..., \theta _{i}^{k}, ..., {{\theta }_{n-1}}, \theta _{n}^{k-1}) $ | (12) |
(3) 从一个初始的q1值可以求得函数J的局部最优值, 然后迭代获得θ1, θ2, …, θn的序列.
(4) 将θk对公式(11)中的θk-1赋值, 按照步骤(1)~步骤(3)反复迭代直至收敛.
原始坐标下降法中, 按序求解每一维的最小值可能最终的结果并不是全局最优解.如何选择求解方向, 使得目标函数结果最优, 相继有研究者提出随机坐标法[19]、贪婪坐标法[20]和循环坐标法[21]等.
1.2.5 交替方向乘子法[4]上述算法通常解决无约束问题.对于有约束的凸函数问题, Gabay和Mercier[4]提出了交替方向乘子法, 融合了对偶上升法的可分解性与拉格朗日乘子法优秀的收敛性质.对于目标函数为f(x)+g(z) subject to Ax+Bz=c的形式, 通常, f(x)为目标函数, g(z)为正则项.ADMM将目标函数与约束进行融合, 构造相应的增广Lagrange目标函数形式:
| $ {{L}_{\rho }}(x, z, \lambda )=f(x)+g(z)+\lambda (Ax+Bz-c)+(\rho /2)\, \cdot \, ||Ax+Bz-c||_{2}^{2} $ | (13) |
其中, x表示原始变量, z表示对偶变量, λ表示Lagrange乘子变量, ρ为常数.然后对增广Lagrange函数中涉及的变量进行分解与轮流优化, 具体迭代形式为如下公式:
| $ {{x}^{k}}^{+1}={\rm{argmin}}_{x} f\left( x \right)+{{L}_{\rho }}(x, {{z}^{k}}, {{\lambda }^{k}})~~ $ | (14) |
| $ {{z}^{k}}^{+1}={\rm{argmin}}_{z}{{L}_{\rho }}({{x}^{k}}^{+1}, z, {{\lambda }^{k}})~ $ | (15) |
| $ {{\lambda }^{k}}^{+1}={{\lambda }^{k}}+\rho (A{{x}^{k}}^{+1}+B{{z}^{k}}^{+1}-c) $ | (16) |
不断循环迭代公式(14)~公式(16), 直至收敛.当目标函数为闭实集上的凸函数时为次线性收敛.同时, 该形式便于在对目标函数更一般的属性条件下并行优化, 因此, ADMM适用于大规模分布式优化问题.
表 1分析比较了5类优化算法原始单线程版本的优势、不足以及收敛率.该表格中仅说明算法原始未改进的初始版本所存在的优势及其不足, 同时指明不同的函数属性在原始算法下所对应的收敛率.
| Table 1 Comparison of optimization algorithms 表 1 优化算法对比 |
1.3 计算模型简介
随着单机多核系统的发展, 处理器写共享内存速度可达12GB/s, 延迟可达纳秒级别, 并行计算的优势逐渐得到体现[22].因此在多核兴起时代, 基于共享存储计算模型的并行优化算法被提了出来.但是, 随着数据量的不断剧增, 单个机器无法存储全部数据, 分布式优化算法又成为热点, 研究者们提出了基于整体同步(BSP)[6]、延迟同步(SSP)[5]和异步(ASP)[5]等并行计算模型的并行优化算法.在不同的并行计算模型下, 优化算法通常可以分为数据划分和模型划分.数据划分是指将样本数据进行行拆分, 每条数据分别存储在不同的节点上, 每个节点利用本地数据进行全部模型参数训练, 集群节点并行更新参数; 模型划分是指将模型参数进行列拆分, 不同列的数据分别存储在不同的节点上, 每个节点利用本地数据对分配的参数进行更新, 集群节点并行更新参数.
并行计算模型作为并行算法设计和分析的基础, 本节主要介绍与论文中优化算法实现相关的流行的并行计算模式, 即共享存储、BSP、SSP和ASP计算模型.
1.3.1 共享存储计算模型共享存储计算模型即为共享内存模型, 其计算模型如图 1所示[23].

|
Fig. 1 Shared memory model 图 1 共享存储计算模型 |
某个进程对共享内存中数据的改动, 将立即影响到可以访问同一段共享内存的任何其他进程.数据的共享不需要进程间的数据传送, 而是直接访问内存, 加快了程序效率.共享存储模型根据多线程锁机制又可细分为同步、异步模式.结合数据划分, 同步模式可解释为:各线程利用部分数据对全局模型参数进行计算, 计算完成后, 将结果同步到共享内存中进行聚合操作; 随后, 各线程读取更新后的全局参数.结合模型划分、异步模式可解释为:各线程更新部分模型参数, 计算完成后即更新共享内存中参数的值, 其他线程在下一次读取模型参数时, 可直接读取到更新的参数.由于目前普通机器均为多核CPU, 因此大多分布式系统中的单一节点也均采用这种计算模型.
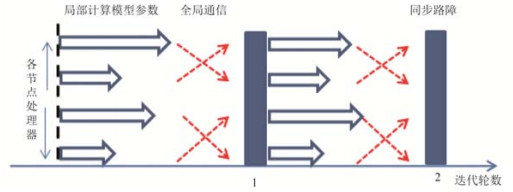
1.3.2 整体同步并行计算模型整体同步并行计算模型BSP(bulk synchronous parallel)是由一组具有局部内存的分布式处理器和支持所有处理单元间全局同步的路障组成, 其计算模型如图 2所示[23].同步更新流程为:多个处理器单元以相同迭代轮次对模型进行更新, 多处理器单元完成一轮迭代后根据路障机制在主节点进行同步等待, 主节点对模型统一更新, 并将更新后的参数发送给各处理器单元, 进行新一轮迭代.这样的好处是能够保证模型的收敛性.结合数据划分可解释为:每个节点利用本地数据进行全部模型参数更新, 等到所有节点计算完成后, 在主节点处进行汇总, 主节点分发新一轮全局模型参数给各节点进行下一轮更新.常见的BSP模型系统包括Mahout[24]、Spark[24]等.
|
Fig. 2 Bulk synchronous parallel model 图 2 整体同步并行计算模型 |
1.3.3 异步并行计算模型
异步并行计算模型ASP(asychronous parallel)是由具有局部内存的分布式处理器和管理全局参数的总节点组成, 其计算模型如图 3所示[23].

|
Fig. 3 Asynchronous parallel model 图 3 异步并行计算模型 |
异步更新流程为:各节点以不同步调在主节点上对模型进行更新.结合数据划分可解释为:各节点利用本地数据对全部模型参数进行计算, 节点计算完一轮后, 即可在主节点处对模型进行参数更新, 然后从主节点处获取最新全局参数进行下一轮更新, 各节点不需要互相等待.但是对各节点的迭代轮数差不加限制会造成结果最终不收敛, 为了解决ASP模型计算结果的不稳定性, 提出下面的延迟同步并行计算模型.
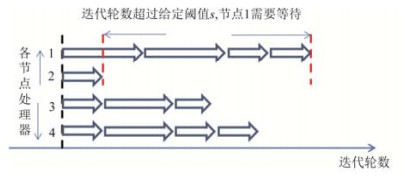
1.3.4 延迟同步并行计算模型延迟同步并行计算模型SSP(staleness synchronous parallel)是由具有局部内存的分布式处理器、总节点和延迟参数(stale)组成, 其计算模型如图 4所示[23].半异步更新流程为:各节点以不同轮次在主节点上对模型进行更新, 但需稍加限制——最快、最慢节点参数的迭代轮次不得大于stale.从而既能减轻慢节点拖慢整个系统运行速度的程度, 又能保证模型参数的最终收敛.结合模型划分可解释为:每个节点更新分配到的模型参数, 节点计算完成后即传送计算结果到主节点对该参数进行更新, 然后获取主节点处的最新全部参数进行下一轮更新.如果不同节点的更新轮次大于给定阈值, 则最快的节点需要等待, 直到更新轮数的差小于阈值才能再次更新.常见的SSP模型系统包括Petuum[23]、深度学习系统[25-27]等.
|
Fig. 4 Staleness synchronous parallel model 图 4 延迟同步并行计算模型 |
2 并行与分布式梯度下降算法 2.1 并行GD算法
并行GD算法的优化主要基于多线程不同的锁操作模式进行改进.通过对共享内存中管理全局模型的锁机制进行优化, 从而加快算法的运行速度.
John等人提出的Round-robin[28]方法是最早的并行GD算法, 该算法使用同步更新策略, 通过对共享内存中的全局模型加锁实现并发控制, 每个线程串行更新模型, 收敛率仅为次线性.Round-robin是并行GD算法的基础.
由于Round-robin的加锁并发控制使得算法收敛速率较慢, Niu等人提出了无锁并行随机梯度下降算法Hogwild![29].针对稀疏数据, 算法采用无锁异步更新策略, 每个线程进行更新操作时只会对很少的特征进行更新, 冲突较少; 当冲突发生时, 算法提供部分写锁对可能产生多次冲突的变量不更新, 保证重写不会发生.虽然Hogwild!收敛率依旧为次线性, 但实验结果表明, Hogwild!收敛比大于Round-robin.
针对Hogwild!只能获取次线性的收敛率, Zhao等人提出了无锁线性收敛的AsySVRG[30], 该方法是对Johnson等人提出的SVRG[11]的并行实现.所有线程计算模型平均梯度, 然后, 每个线程分别计算本地梯度, 同时利用平均梯度进行修正, 最后, 多线程异步更新全局模型, 多次迭代直到收敛.该算法的关键在于提高了每次用于模型更新的梯度质量, 从而快速收敛.并且理论和实验均表明了这种更新策略优于Hogwild!.
表 2对GD算法的并行改进算法进行了总结.
| Table 2 Comparison of parallel gradient descent algorithms 表 2 并行梯度下降算法对比 |
2.2 分布式GD算法
分布式GD算法主要是对标准SGD算法、异步SGD算法、噪声削减方法的分布式实现, 以及对提高结果准确度及运行效率等其他方面的优化进行改进.
在标准SGD算法的基础上, Martin等人开创性地提出了基于MapReduce计算模型的分布式SGD算法[9].该算法利用节点的本地数据进行参数计算, 对I/O延迟不敏感, 最后在主节点进行模型的合并.这些特点使其非常适合分布式大规模机器学习.实验结果表明:相比单机串行算法, 分布式SGD算法可以大大缩短运行时间.以该算法作为分布式SGD算法的基础, 随后, Meng等人基于Spark平台实现了分布式机器学习算法库MLlib[8], 其实现的标准Mini-Batch SGD经常作为分布式机器学习优化算法性能测试的基准.
在标准SGD的迭代过程中, 同步往往造成较大的延迟.为了避免这个问题, Meng等人提出异步SGD算法AASGD[31], 并通过理论证明了该异步算法的线性收敛性.同时, Meng指出:噪声去除、坐标块采样以及牛顿法是互补的, 集成在一起能发挥各自的优势.然而相比标准SGD, AASGD能取得的加速比严重受限于数据稀疏性, 对于非稀疏数据, 很难取得较好的加速比.
由于标准SGD易受噪声梯度影响而降低收敛速度, 于是, 基于SGD的噪声去除方法大量涌现.基于原始单线程去噪方法SVRG, Jason等人提出分布式去噪随机梯度下降法DSVRG[32], 并证明在数据随机划分的条件下, 相比其他一阶优化方法, DSVRG可取得最优的运行时间、最少的通信次数等.但该算法是利用单机多线程模拟集群环境, 每个线程代表一个计算节点, 通过节点之间相互传递消息实现参数的更新.本质上讲, 这种循环更新模式是串行的, 当一个机器更新模型时, 其他机器会存在等待情况, 这不是真正意义上的分布式并行.因此, Soham等人基于真正的主从集群环境, 提出了去噪方法SAGA的分布式实现CentralVR[33].通过证明可得:该算法具有线性收敛率, 并且随着集群节点的增加, 可达到线性加速比.类似地, Zhao等人提出了串行去噪方法SVRG的分布式实现SCOPE[22], 并且大量实验结果表明:在很多数据集上, SCOPE和CentralVR具有类似的实验效果.
为了提高标准SGD算法的准确度和效率, Zhang等人提出了Splash[34].其核心思想是:首先, 将集群中的计算单元分成k组; 然后, 每个计算单元使用本地数据计算本地模型, 每个组分别合并组内的模型, 通过交叉验证选择k组中结果最好的模型.相比Spark上的Mini-Batch SGD, 该算法一般可实现10~20倍的加速.
表 3对GD算法的分布式改进算法进行了总结.
| Table 3 Comparison of distributed gradient descent algorithms 表 3 分布式梯度下降算法对比 |
3 并行与分布式二阶优化算法 3.1 并行Second-Order算法
并行二阶优化算法主要对原始的牛顿法及其变种进行改进, 利用数据特征划分使得算法适用于多核环境, 从而解决应用问题.原始的截断牛顿法运用于非线性网络优化问题中, Stephen等人提出改进后的截断牛顿法使其适用于大规模问题的求解[35].在每轮迭代中, 利用基于共轭梯度法的块迭代法来计算近似牛顿等式的搜索方向, 从而避免牛顿法中Hesse矩阵及其逆矩阵的计算消耗.Stavros等人将截断牛顿法应用于大规模稀疏线性方程组的求解中[36].根据网络的结构特性, 将方程组划分为若干独立的模块, 从而并行更新原始方程.
表 4对Second-Order算法的并行改进算法进行了总结.
| Table 4 Comparison of parallel second order optimization algorithms 表 4 并行二阶优化算法对比 |
3.2 分布式Second-Order算法
原始牛顿法中, 由于二阶导数Hesse矩阵过于庞大, 使得计算、存储、通信成为算法瓶颈, 因此, 其分布式优化主要关注于减少Hesse矩阵的计算、存储和通信消耗.
在大规模逻辑回归问题, 即目标函数为凸函数的问题中, Lin等人发现:对于梯度难以收敛到最优以及目标函数二阶导数Hesse矩阵太大难以存储的情况, 分别可以通过信任域方法和共轭梯度迭代法来解决.因此, Lin等人提出信任域牛顿法[37].利用共轭梯度法找到近似牛顿方向(即截断牛顿法), 通过信任域方法调整牛顿方向的步长来加快收敛.在实际应用中, Spark平台上主要采用牛顿法变种——限制内存BFGS法(L-BFGS)[15]来解决逻辑回归问题.通过5步迭代——利用m个历史向量对(权重之差、梯度之差)计算梯度下降方向、搜索选择步长、更新权重、计算当前向量对(权重之差、梯度之差)、保存最近m个历史向量对, 从而解决Hesse矩阵计算和存储问题.对于大、中规模数据, 随着存储历史向量对个数m的增加, 迭代次数减少, 运行加快.实验结果表明, L-BFGS的收敛率要大于Spark平台上的SGD算法.尽管Spark平台已在MLlib库中实现了效果较好的分布式L-BFGS, Chen等人为加快计算过程, 提出改进版的VL-BFGS(vector free L-BFGS)算法[38], 将原始的L-BFGS算法中所有向量操作转换为标量操作:对特征向量进行列切分, 即对模型进行特征划分.每个节点对一维特征的梯度∇f(X)进行计算, 多个节点对不同维度并行化进行更新; 然后, 通过一个聚合操作合成一个完整的梯度向量.这样可以基于MapReduce计算模式中的一次Map-Reduce过程来计算整个矩阵, 从而加快计算.
对于平滑凸函数, 为了获得更好的通信效率, Zhang等人提出分布式不精确阻尼牛顿法DISCO[39], 利用分布式的预处理共轭梯度法来计算近似牛顿等式.由于共轭梯度法在通信时只需传递一个矩阵向量, 从而减少了通信的数据量.当正则化参数满足
表 5对Second-order算法的分布式改进算法进行了总结.
| Table 5 Comparison of distributed second order optimization algorithms 表 5 分布式二阶优化算法对比 |
4 并行与分布式邻近梯度算法 4.1 并行PG算法
并行邻近梯度法主要用来解决应用问题, 在多核环境下, 对数据特征进行拆分来加速求解过程.Pustelnik等人将邻近梯度法应用于噪音图像处理领域[40], 提出加速版的并行邻近梯度法(accelerated PPXA).当目标函数为凸函数、正则项为混合空间领域和微波领域知识的非平滑函数时, 通过划分整体正则项为子函数的方法来解决整体正则项的邻近算子难以计算的情况.Kamilov将邻近梯度法应用于信号处理领域[41, 42], 利用并行邻近梯度法求解包含总变差正则项的最小二乘问题.通过计算几个简单独立的邻近算子来替换总变差正则项的总邻近算子, 从而在不增加内部迭代的情况下达到收敛.
表 6对PG算法的并行改进算法进行了总结.
| Table 6 Comparison of parallel proximal gradient algorithms 表 6 并行邻近梯度算法对比 |
4.2 分布式PG算法
分布式邻近梯度法主要是基于不同的并行计算模型, 针对数据不均衡等问题进行优化以及分布式实现, 从而提高算法运行效率.
在分布式计算环境中, 各节点数据的差异可能带来各节点计算结果的不均衡, 从而影响最终结果.Chen等人针对该问题提出快速分布式邻近梯度法Accelerated PG[43].在每轮迭代中, 集群节点首先在本地计算目标函数的可微部分; 然后, 节点间交换计算结果, 利用简单的线性运算进行多节点“共识”, 使得每个节点目标函数的可微部分结果相差不大; 接着, 每个节点通过邻近算子操作在本地计算不可微部分得出梯度, 并利用Nesterov加速法得到新一轮的参数.通过增加节点间的“共识”操作平衡计算结果, 从而达到次线性收敛率.随后, Lin和Zhang将梯度下降法中的采样策略——全采样Full-GD、随机采样SGD、随机平均梯度SAG、随机对偶坐标上升SDCA和随机噪音消减梯度SVRG等优化策略移植到邻近梯度法中来, 以缓解数据不均衡问题[44], 并通过实验验证:将邻近梯度法与SVRG的优化策略进行结合(Prox-SVRG), 可以获得最好的更新效率.
上述优化工作基于同步并行计算模型, 随后, 诸多学者对邻近梯度法进行异步、半异步计算模型下的分布式优化.在延迟同步模型下, Li等人基于参数服务器提出分布式延迟同步邻近梯度法[45].首先, 将数据按列存储在各个节点上, 每个节点更新其数据块梯度; 然后, 传递给参数服务器进行聚合, 再返回给各节点.当各节点的迭代轮数之差在一定阈值内时, 算法收敛.随后, Zhou等人提出异步邻近梯度算法msPG[46].参数服务器(总节点)将模型划分并存储于不同的节点上, 每个节点传递子梯度给总节点, 总节点通过汇总后再将全部参数传递给子节点.同时, 每个节点保存本地时钟——记录本地与其他节点的时钟差, 总节点保存一个时钟向量——记录各节点的最大时钟差, 从而保证各节点更新延迟在固定范围之内.通过将该算法部署在基于SSP模型的Petuum平台上进行实验, 验证算法的收敛率满足次线性.在异步模型下, Aybat等人提出去中心化的异步邻近梯度法DFAL[47].结合随机采样更新中计算部分梯度的结果比计算全部梯度要更高效, 同时, 在所有节点上寻求共识均衡计算结果的思想, 该算法通过使用由相邻节点传递的“本地”决策来实现最佳决策, 从而消除中心节点.DFAL在每个节点利用给定公式计算本地损失函数的邻近梯度, 如果某个节点的计算结果满足一次迭代停止的要求, 则将其计算结果发送给邻居节点, 终止其邻居节点的计算, 进入下一轮迭代, 从而最终结果用部分节点的计算结果来表示, 获得更高的效率.
表 7对PG算法的分布式改进算法进行了总结.
| Table 7 Comparison of distributed proximal gradient algorithms 表 7 分布式邻近梯度算法对比 |
5 并行与分布式坐标下降算法 5.1 并行CD算法
并行CD算法主要是对传统单线程下的随机坐标下降法[19]、贪婪坐标下降法[20]以及结合其他优化算法优势的混杂坐标下降方法的并行实现, 同时, 这些优化对不同的目标函数有不同的改进.
对于随机坐标下降法, 原始的串行随机坐标下降法是每轮迭代随机地从所有特征中选取一维特征进行更新, 多轮迭代直到收敛.Bradley等人基于原始随机坐标下降法提出并行随机坐标下降算法Shotgun[48], 每轮迭代中, p个处理器从所有特征中随机选取p个进行并行更新.实验结果表明:在各维特征关联性较小的情况下, Shotgun可扩展到p=d/2ρ个节点(d为数据维数, ρ为数据矩阵谱半径), 运行速度与p呈线性关系, 迭代次数可减少为普通坐标下降法的1/p.但当节点数超过p时, 收敛速率将会降低甚至发散.Richtarik等人针对Shotgun的问题, 提出并行随机块坐标下降法PCDM[49].随机地选取一维特征, 通过概率选择可以与该特征并行更新的多个特征组成坐标块, 对坐标块并行更新以加速求解过程.其加速程度与目标函数中平滑函数的可拆分程度, 即各维特征的关联程度有关.理想情况是平滑函数可分, 运行速度与处理器的个数正相关.同时, 该方法可以任意选择每次迭代的坐标块维数.在上述共享内存同步算法的基础上, Liu等人提出异步并行随机坐标下降法AsySCD, 用来求解无约束平滑或有约束可分函数的最优值问题[50].随机选取特征并行更新, 线程在参数计算结束后异步写入内存, 各线程不互相等待.当损失函数满足基本强凸属性时, 收敛率可达线性; 当函数为一般凸函数时, 收敛率可达次线性.在无约束条件下处理器个数为O(n1/2), 或在可分有约束条件下处理器个数为O(n1/4), 加速比可达次线性(n为变量个数).
随机坐标下降法是随机地选择特征进行更新, 在特征关联的情况下并行更新会出现收敛速度慢甚至发散的问题, 贪婪坐标下降法对其进行了改进:选择可以迅速减少目标函数值的特征进行模型更新.Scherrer等人提出块-贪婪坐标下降算法族Block-Greedy CD[51], 首先将特征聚类成坐标块, 保证块间的不关联性, 再从各坐标块中选择可迅速减少目标函数值的特征进行并行更新以加速求解过程.该算法族可以用两个参数B, P(P≤B)来表示, 其中, B代表特征聚类后划分为B个坐标块, P表示在一个节点上进行一次迭代时从坐标块中选择的特征个数.在B=P的情况下, 对于平滑函数与可分凸函数之和的问题, 当坐标块的谱半径ρ小于2时, 算法收敛率均满足O(1/(2-ρ)k)(其中, ρ为坐标块谱半径, k为迭代次数)[52].然而, 同步并行存在等待问题, You等人提出异步贪婪坐标下降算法AGCD[53], 以解决有约束平滑函数最小值问题.每个节点在每轮迭代中异步更新特征, 从而保证每个核不会空闲等待, 可达到线性收敛率.同时, 该方法已应用在基于共享内存的核支持向量机的求解问题中.
Liu等人将坐标下降法与邻近梯度法相结合, 提出异步随机邻近坐标下降算法ASYSPCD[54].随机选取多个特征, 利用邻近梯度法对选取的特征进行并行更新.并证明:当函数满足强凸性时, 收敛率可达线性; 当函数为一般凸函数时, 收敛率可达次线性.如果处理器个数为O(n1/4), 则加速比可达次线性(其中, n为变量个数).
由于同步环境下并行对偶坐标下降法收敛速度慢, Hsieh等人提出了异步并行随机对偶坐标下降算法PASS-CoDe[55], 用来解决正则项为L2的目标函数最小化问题.每个线程循环地选择一个对偶变量, 并对存储在共享内存中的原始变量进行更新.在对共享内存进行原子操作的情况下, 算法的收敛率可提升为线性.
表 8对CD算法的并行改进进行了总结.
| Table 8 Comparison of parallel coordinate descent algorithms 表 8 并行坐标下降算法对比 |
5.2 分布式CD算法
线性支持向量机(SVM)、线性回归(Lasso)等模型是处理大规模稀疏高维数据应用的很好的工具, 而坐标下降法可以利用分块求解的特性去求解高维数据模型.因此, 在大数据环境下, 优化集中在对其变种——随机对偶坐标下降法、块坐标下降、混杂优化以及网络扩展上的改进, 从而更好地求解线性SVM和Lasso模型.
SVM模型通常利用对偶坐标下降法求解, Hsieh等人提出改进版的分布式对偶坐标下降法DCD-SVM[56].通过投影梯度法来求解原函数的对偶方程, 可经过O(log(1/ε))次迭代达到ε精度.作为对偶坐标下降法的相似算法, 诸多学者也对随机对偶坐标上升法进行了研究.Yang提出了分布式随机对偶坐标上升法DisDCA[57].集群中K个节点并行更新特征, 每个节点在本地序列化更新m个对偶变量, 每轮迭代后, 通过聚合操作汇总到总节点; 最后, 将更新后的变量广播给各节点.通过权衡网络节点数K与本地更新变量数m来平衡通信与计算间的代价.随后, Yang等人[58]对DisDCA的收敛率进行理论分析后发现:增加每轮迭代中对偶变量的数量m, 收敛速度将趋近于指数级; 增加节点数量K, 则收敛速度将趋近于线性.Martin等人针对分布式对偶上升法的通信瓶颈问题, 提出有效的通信框架CoCoA[59].每个节点在本地进行多轮迭代更新后再进行全局梯度聚合更新, 从而减少了通信次数.该框架基于Spark平台加以实现, 在相同精度情况下, CoCoA的运行速度比Spark上的Mini-Batch SGD快25倍.
对于Lasso模型求解, Mahajan等人提出了分布式块坐标下降法DBCD[60]:首先, 对目标函数进行Taylor二阶展开; 然后, 集群每个节点选择要更新的坐标块, 并对二阶展开式进行多节点并行计算; 最后, 汇总更新.通过增加本地的计算以减少通信消耗, 加速求解过程.为了彻底避免通信, Peter等人提出了混杂坐标下降方法Hydra来解决线性分类问题[61].算法中的混杂是指集群包括多个节点, 每个节点又分为多个并行处理器.首先, 按照特征将数据划分并分配到不同的节点上; 在每一轮迭代中, 每个节点随机选择本地特征子集独立地进行运算, 利用多个处理器并行更新本地特征块, 直到收敛.这样, 多个节点多个处理器可以并行更新每一列的特征值, 从而不用进行节点间的通信, 但是算法运行迭代的上限依赖于数据及其划分.
对于广义线性模型, 收敛率通常会随着集群节点的数目而发生变化.同时, 当集群数量发生变化时, 分布式随机梯度法不能随着节点的增加而呈线性扩展, 尤其是在共享云环境下, 很难预测算法运行效率等.因此, Steffen等人提出了可扩展坐标下降法SCD[62].将集群分为master-worker-workers架构, 并对特征和数据进行划分. Master每次随机选择一个特征块给一组workers进行计算, workers对该特征块进行数据并行更新, 计算完成后, 在worker处汇总, 再由worker将汇总结果传递给master.由于划分给各节点的特征块维数不变, 从而无论机器节点的数目和计算环境怎样变化, 其收敛率总是保持次线性.线性加速比可以保证将单机算法扩展到上千核, 适用于低成本的云环境.
表 9对CD算法的分布式改进进行了总结.
| Table 9 Comparison of distributed coordinate descent algorithms 表 9 分布式坐标下降算法对比 |
6 交替方向乘子算法
ADMM算法独特的分布式结构使其非常适用于分布式环境, 通常用来并行求解大规模问题.因此, 本文只对ADMM算法的分布式改进加以总结.
6.1 分布式ADMM算法在分布式环境下, ADMM算法的优化不关注于算法结构的改变, 主要关注于如何结合不同的体系结构进行算法的部署及应用, 包括主从网络(中心化)结构下以及去中心化(图)结构下的同步和异步更新.
基于主从结构的同步计算模型, Sauptik等人[63]假设虚拟对偶变量为z, 使得原始变量x与对偶变量z满足等式x=z, 构造约束条件x-z=0, 从而将无约束线性分类等模型转换为带约束的问题.利用ADMM算法中原始变量和对偶变量交替更新的形式, 多节点先利用本地数据并行求解原始变量, 主节点进行汇总后分发原始变量更新值给各节点, 多节点再利用原始变量更新值并行求解对偶变量, 多轮迭代直到收敛.通过在Spark平台上进行实验(ADMM on spark)发现, ADMM算法相较Spark平台上的SGD优化算法的运行速度快近25倍.为改进同步等待问题, Zhang等人基于延迟同步模式提出分布式异步ADMM算法Async-ADMM[64].每个节点利用本地数据更新全部参数, 并且允许中心节点至多等待k个节点完成计算就可以完成一轮更新, 更新后的全局变量值只需传递k个节点, 从而节约网络带宽.实验结果表明:异步减少了网络等待, 加快了收敛速度.
主从结构下的计算模型总会存在延迟等待、单节点压力过大等问题, 因此, 诸多学者对ADMM算法的去中心化分布式优化展开研究.
对于有约束的强凸目标函数, Shi等人提出去中心双边图模型下的分布式ADMM算法[65].集群节点利用本地数据及其邻居节点上一轮原始变量计算结果来计算原始变量; 然后, 利用本地数据及其邻居节点的新一轮原始变量计算结果计算乘子变量, 多轮循环直到有节点收敛.虽然该算法拥有线性收敛率, 但网络拓扑结构的图半径等因素会对算法收敛率产生影响.随后, Mota等人将强凸函数分为多个节点相等的私有函数及私有约束条件之和的形式, 提出图节点排序的分布式异步ADMM算法D-ADMM[66].将集群节点分为不同的组, 每组等级不同.同一组内先计算乘子变量总和γ, 每个节点利用本地数据、γ、序号小于该组的新一轮原始变量计算结果, 以及序号大于该组的上一轮原始变量计算结果来并行计算原始变量, 一组内选出结果最小的原始变量作为该组所有节点新一轮的原始变量计算结果, 并发送给其邻居节点; 然后, 一组内所有节点利用本地及其邻居节点新一轮原始变量计算结果并行计算乘子变量γ, 多轮循环直到有节点收敛, 从而达到去中心化的目的.通过理论证明:该方法在双边网络或强凸函数情况下, 收敛率为线性; 与已有算法相比, 可以在通信更少的情况下达到相同精度.
对于有线性约束的可分目标函数, Wei等人提出了基于边通信的去中心化异步ADMM算法[67].将目标函数拆解为多节点子函数之和的形式, 每个节点的约束条件表示其与不同节点之间的约束关系, 保存在关系矩阵中.在每一轮迭代中, 集群随机选取部分约束条件, 更新该约束条件对应的变量(又称为激活变量).激活变量所对应的节点计算原始变量, 并与其边相连的邻居节点交换更新后的原始变量, 再根据边相连节点的约束函数来异步计算对偶变量, 进行多轮迭代直到收敛.相较于利用次梯度算法求解, 该方法的收敛率可达次线性.但是, 基于边相连的通信模式需要保存网络中边的信息, 即, 每个节点保存其与不同节点约束条件的关系矩阵, 浪费了存储空间, 因此, Ali等人提出了基于顶点通信的分布式ADMM方法[68].将集群中每个节点的约束条件划分为多个子约束条件, 每个子约束条件分别与该节点的一个邻居变量相关, 因此, 节点无需知道更新顺序就可并行更新变量.每个节点利用所有的邻居节点的上一轮原始变量和对偶变量计算该节点的原始变量, 并找到最小的计算结果作为该节点新一轮的原始变量值; 随后, 节点只需广播该节点的原始变量给其邻居节点, 每个节点利用该数据并行更新本节点的对偶变量; 然后进入下一轮迭代.从而不需要维护基于边的对偶变量, 减少了存储需求.
ADMM算法通常求解有约束问题, 而Wei等人利用ADMM算法求解无约束问题, 提出了基于节点排序的分布式ADMM算法[69].该方法通过假设虚拟对偶变量为z, 构造x-z=0的约束条件, 将目标函数转换为约束条件下的损失函数.函数先拆分为子目标函数之和的形式, 再分配子目标函数给各节点.对于每个子节点, 将序号小于该节点的新一轮原始变量计算结果、本节点以及大于该节点的上一轮原始变量计算结果用来更新原始变量, 将本节点和小于该节点的新一轮原始变量计算结果用来更新对偶变量, 相邻节点间异步并行更新.通过优化, 与利用次梯度方法求解相比, 该算法收敛率可达次线性.
除了传统机器学习的凸函数问题外, ADMM算法也可用于神经网络非凸函数的训练.针对大规模数据集、集群, 传统的随机梯度优化方法对非凸函数不能很好地加以扩展, Gavin等人提出, 将ADMM算法与Bregman方法迭代地结合起来[70], 利用多核GPU进行并行计算.该算法避免了梯度法在非凸问题上收敛慢的问题, 并对二次惩罚项函数保证收敛.同时, 在分布式环境下拥有强扩展性, 即使划分到上千处理核上仍拥有线性加速比.
表 10对ADMM算法的分布式改进进行了总结.
| Table 10 Comparison of distributed alternating direction method of multipliers algorithms 表 10 分布式交替方向乘子算法对比 |
7 可扩展机器学习系统中的优化算法
为了应对大数据机器学习问题, 出现了一批采用分布式架构的可扩展的机器学习系统.分布式架构大致可以分为两类:第1类是不含参数服务器架构的系统, 其大多为整体同步并行计算模型; 第2类是采用参数服务器架构的系统, 也是目前机器学习系统的主流发展方向, 主要为延迟同步并行计算模型.在原始的主从架构平台中, 从节点在完成计算后需要和主节点进行交互.然而在大数据环境下, 单一节点难以存储大规模参数集, 同时对节点通信、参数计算等造成单点瓶颈, 因此, 为应对分布式环境下的大规模数据集, 参数服务器架构应运而生.参数服务器架构是指模型的参数采用一个统一的分布式服务器组作为主节点来进行存储管理, 参数服务器组中的每个服务器分别对应不同的从节点组, 从而不存在单点故障.由于算法的实现离不开平台, 因此, 本节对分布式平台进行简介, 包括其实现的适用于该系统的分布式优化算法, 并总结分析不同平台中算法的应用场景.
第1类中, 基于整体同步并行计算模型的机器学习系统主要包括Hadoop Mahout[24]、Spark MLlib[25]和GraphLab[71].其中, Mahout和Spark主要采用MapReduce编程模型.通过Mahout系统最新版本介绍, 其实现了一种采用SGD算法的逻辑回归模型, 并没有单独的SGD算法实现, 也没有其他模型来使用该算法.Spark MLlib实现了Mini-Batch SGD算法、L-BFGS算法和PG算法.其中, PG算法用来求解L1正则化问题, Mini-Batch SGD算法和L-BFGS算法都适用于MLlib算法库中模型的求解.但是, 由于L-BFGS算法的运行速率快于Mini-Batch SGD算法, 因此最新版本中的MLlib库通常使用L-BFGS算法作为求解算法.然而, Spark等开源系统不支持参数服务器架构, 在模型规模上都无法支持互联网级别机器学习模型训练的需求.同时, 大量优化算法在大量数据集上的收敛速度均比Spark上实现的原始SGD算法快几十倍, 因此, Spark上的优化算法有很大的改进空间.CMU开发的GraphLab[71]采用gather-apply-scatter的图计算模型, 从节点从相邻节点收集信息, 并将该信息发送到主节点进行汇总, 主节点将更新后的值传给从节点; 最后, 从节点更新相邻边信息进行新一轮计算.作为分布式图模型, 实现了SGD算法, 以及由于GraphLab平台的协同过滤工具箱的需要实现的Bias-SGD算法.虽然GraphLab用图来作抽象可以解决大部分机器学习问题, 但仍然有很多问题无法高效求解, 比如深度学习中的多层结构.
第2类机器学习系统都采用参数服务器架构加SSP更新策略, 主要包括CMU的Parameter Server[24]和Petuum[23], 它们均实现了一种新的分布式SGD算法.腾讯的Angel机器学习平台也是基于参数服务器架构, 以实现多种业界最新技术和腾讯自主研发技术, 如异步分布式SGD、多线程参数共享模式Hogwild!等方法.作为机器学习的延伸, 采用参数服务器架构的深度学习系统逐渐涌起.Google Distbelief[26]是Google第1代分布式深度学习平台, 主要实现了改进的分布式随机梯度下降法(downpour SGD)以及对深度学习有很好效果的L-BFGS算法.随后, Google公司第2代分布式深度学习平台Tensorflow[27]实现了若干添加学习率优化器的梯度下降法, 包括GradientDescentOptimizer、AdadeltaOptimizer、AdagradOptimizer、MomentumOptimizer、AdamOptimizer、FtrlOptimizer、RMSPropOptimizer等.同时, Li等人的MxNet[25]平台也是类似的实现方式, 主要实现了GD算法和PG算法.
综合来看, 大多数分布式机器学习平台都实现了SGD算法, 但是仅限于基本的Mini-Batch SGD, 用于求解机器学习问题.其中, 新一代的机器学习平台都采用了分布式参数服务器架构, 实现了数据并行和模型并行, 这些架构本身就是一种新的算法实现, 不同于本文前面介绍的算法理论.从深度学习角度来看, 由于非凸函数的求解理论研究不足, 目前, 实验结果表明, 添加自适应学习率的SGD算法可以满足求解要求, 是主流的方法.Google Distbelief和Spark MLlib都还实现了L-BFGS算法, 同时, 实验结果还表明:在一些情况下, 其运行效率要优于SGD.但是, 为了避免系统过于复杂, Tensorflow并未实现L-BFGS算法.虽然各个平台都可以解决机器学习问题, 但是具体问题的求解需要考虑具体的应用场景, 例如数据特性、数据规模、运行结果需求等.同时, 可以结合具体系统的特性与其已有的优化算法来进行平台与算法的选择.例如, 想要保证结果的准确性, 对运行时间没有太高要求, 则可优先选择BSP模型的平台.对于决定了运行平台, 选择哪种优化算法来求解具体模型, 可根据求解模型和数据的特性来选择优化算法.例如, 如果模型是SVM, 则可选择实现坐标下降法; 如果带有约束条件, 则可选择ADMM算法.
表 11总结了现有机器学习平台其优化算法实现的情况.
| Table 11 Implementation of optimization algorithms on existing machine learning platforms 表 11 现有机器学习平台优化算法实现情况 |
8 分析与讨论
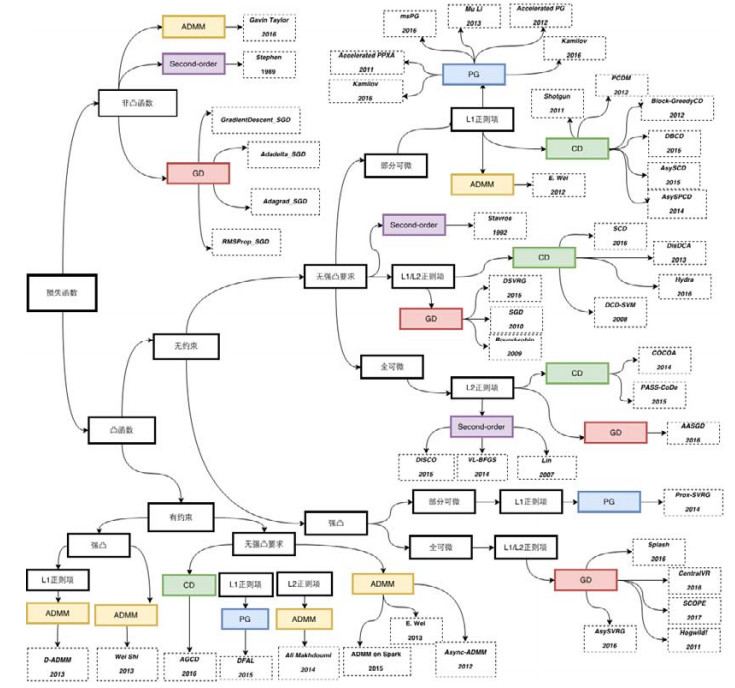
飞速增长的数据量使得模型处理需要更快的速度, 机器学习算法的效率是最关键的问题之一.而机器学习算法的效率更多地依赖于优化方法的改进, 因此, 优化算法作为机器学习的重要组成部分, 近年来在并行与分布式机器学习领域获得了广泛关注, 取得了诸多研究成果, 得到了快速发展.本文从模型训练优化角度出发, 对梯度下降算法、二阶优化算法、邻近梯度算法、坐标下降算法和交替方向乘子算法这5种不同类型的优化算法的并行与分布式优化策略进行综述.通过层次化分类, 将各种算法按照目标函数类型总结为如图 5所示.
|
Fig. 5 Hierarchical classification of optimization algorithm by objective functions 图 5 基于目标函数类型的优化算法层次化分类 |
图中箭头表示论文中该算法可用于求解此类目标函数, 不代表其不能求解其他类型的目标函数, 只是每一种算法针对目标函数从理论上有一定的优势, 实际应用中的性能还需基于数据集进行评测分析.从图中可知:大部分优化算法求解的问题域与其原始理论解释保持一致, 部分算法突破了原有设定, 进行了相关的改进.通过查看图 5, 从本质上加深了对算法优化技巧的理解, 帮助开发者求解模型时对优化算法的选择, 为相关优化算法的并行与分布式实现提供参考, 并且可以交叉探索将优化算法应用到新的目标函数类型上.对算法综述的同时, 调研分析了现有分布式学习平台优化算法的实现程度, 全面总结了优化算法从理论到实际的发展情况.通过总结发现, 5类分布式优化算法都可以适用于分布式环境下大规模问题的求解.其中, 梯度下降法、二阶优化算法、交替方向乘子法可以解决凸函数与非凸函数的问题:梯度下降法的使用范围更广, 在现有分布式学习平台上均有部署, 求解简单且性能较好, 基本上可以满足机器学习与深度学习的需求; 二阶优化算法求解效率更高, 虽然计算稍复杂些, 但对于传统机器学习, 该方法很受欢迎, 部署范围较广; 交替方向乘子法独特的算法架构很适合于分布式环境, 但在求解无约束问题时, 需要构造约束条件, 将无约束问题转换为有约束问题来求解.目前, 在实际应用中还处于研究阶段; 邻近梯度法主要解决L1正则化带来的不可求导问题, 只有少数平台实现了该算法; 坐标下降法适合于分布式环境下求解多维数据或者函数不可求导问题, SVM模型通常利用该算法求解, 性能较好, 但是由于梯度法或邻近梯度法可以对其进行替换, 在实际平台中没有应用.
尽管机器学习优化算法在并行与分布式方面取得了众多的进展, 但仍然存在如下几点不足.
(1) 在算法使用多样性方面.
在现有大规模数据环境下, 应用最广泛、关注最多的优化算法是梯度下降法, 因为其实现简单, 使用场景广泛.但是由于应用的精细化, 不同的应用场景需要不同的机器学习模型, 对于不同的目标函数、数据规模可能需要不同的优化策略, 不能一概而论.然而, 其他优化算法在实际应用中并不常见, 如何结合各种优化算法的特性、提高具体应用的运行效率, 还有待进一步加以研究.
(2) 在算法扩展性方面.
对于分布式算法, 扩展性作为重要指标在现有分布式算法中没有得到重视.随着数据规模的扩大, 在分布式环境下可以配置更多的机器, 如何有效地利用这些计算资源, 分布式机器学习优化算法的可扩展性至关重要.
(3) 在与系统结合方面.
随着集群机器的普通化, 异构环境下不同机器的速度不一, 同步将会造成大量的同步等待, 从而越来越多的研究转变到异步更新策略上.对于更新策略为异步的情况, 高维稀疏数据往往能取得更好的加速效果.因此, 如何更好地利用现有系统、如何将现有算法移植到异步环境下、如何应用到稠密数据上还有待研究.
(4) 在非凸函数优化方面.
现有优化算法的目标函数主要针对凸函数, 然而关注度逐渐升高的深度学习的目标函数主要为非凸函数.目前, 非凸函数的主要求解策略是添加自适应学习率的随机梯度下降法.虽然梯度下降法能够较好地解决问题, 但是对于求解大规模深度学习问题仍存在较大难度, 存在收敛速度较慢等不足.利用其他优化算法求解神经网络相关的非凸函数问题仍有待进一步加以研究.
由于机器学习优化方法的研究方兴未艾, 对其所进行的研究工作尚不完善, 在与平台相结合的并行与分布式方面仍需要做大量工作.未来的研究方向主要可以从如下几个方面加以展开.
(1) 与系统相结合的分布式优化算法.
随着数据体量的增大, 与系统相结合的分布式优化算法进行模型求解将需要更大的内存以及更快的计算效率.然而现有分布式算法大多只是理论研究, 基于真实应用平台的分布式算法研究仍处于探索阶段.未来可以基于真实的分布式机器学习平台运行多种优化算法, 找出影响运行速度的优化算法或平台因素, 从而进行相应的改进.
(2) 与深度学习相关的优化算法.
现有分布式优化算法对非凸函数的研究较少, 主要是利用添加自适应学习率的随机梯度下降法, 但是梯度下降法并不能解决全部的深度学习问题.因此, 针对非凸优化机器学习问题, 还需要大量的理论研究.同时, 还需要基于分布式深度学习平台进行实例测试, 从理论和实践上改进非凸函数的优化求解问题.
9 总结综上所述, 现有并行与分布式优化方法已经取得了较好的科研和实际应用成果, 不同的优化算法在并行与分布式环境下针对不同的目标函数有不同的改进, 对于不同的应用也可以得到较高的处理效率, 在实际应用平台上部署效果较好.但仍有创新的空间, 如果在现有优化算法优化策略的基础上, 将优化策略与现有并行与分布式机器学习平台相结合, 推出更加适用于不同应用场景的优化算法, 将会形成更多创新的算法, 有利于大规模机器学习问题的优化求解, 满足实际应用需求, 使其应用前景更加广阔.
| [1] |
Léon B, Frank EC, Jorge N. Optimization methods for large-scale machine learning. arXiv:1606.04838v1, 2016. |
| [2] |
Neal P, Stephen B. Proximal algorithms. Foundations and Trends in Optimization, 2014, 1(3): 127–239.
[doi:10.1561/2400000003] |
| [3] |
Stephen JW. Coordinate descent algorithms. arXiv:1502.04759v1, 2015. |
| [4] |
Stephen B, Neal P, Eric C, Borja P, Jonathan E. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning, 2011, 3(1): 1–122.
https://stanford.edu/~boyd/papers/admm_distr_stats.html |
| [5] |
Eric X, Qirong H, Xie PT, Wei D. Strategies and principles of distributed machine learning on big data. Engineering, 2016, 2(2): 179–195.
[doi:10.1016/J.ENG.2016.02.008] |
| [6] |
Frédéric L, Frédéric G, David B. Bulk synchronous parallel ML:Modular implementation and performance prediction. In:Proc. of the Int'l Conf. on Computational Science. 2005. 1046-1054.[doi:10.1007/11428848_132] |
| [7] |
Nesterov Y. Introductory Lectures on Convex Optimization:A Basic Course. Springer-Verlag, 2004: xviii-236.
|
| [8] |
Meng XR, Joseph B, Burak Y, Evan S, Shivaram V, Davies L, Jeremy F, DB T, Manish M, Sean O, Doris X, Reynold X, Michael JF, Reza Z, Matei Z, Ameet T. MLlib:Machine learning in apache spark. The Journal of Machine Learning Research, 2016, 17(1): 1235–1241.
http://dl.acm.org/citation.cfm?id=2946679& |
| [9] |
Martin AZ, Markus W, Alexander S, Li LH. Parallelized stochastic gradient descent. In:Advances in Neural Information Processing Systems. 2010. 2595-2603. http://papers.nips.cc/paper/4006-parallelized-stochastic-gradient-descent.pdf |
| [10] |
Leen TK, Orr GB. Optimal stochastic search and adaptive momentum. In:Advances in Neural Information Processing Systems. 1994. 477-484. http://papers.nips.cc/paper/772-optimal-stochastic-search-and-adaptive-momentum.pdf |
| [11] |
Rie J, Zhang T. Accelerating stochastic gradient descent using predictive variance reduction. In:Advances in Neural Information Processing Systems. 2013. 315-323. http://papers.nips.cc/paper/4937-accelerating-stochastic-gradient-descent-using-predictive-variance-reduction.pdf |
| [12] |
Aaron D, Francis B, Simon LJ. SAGA:A fast incremental gradient method with support for non-strongly convex composite objectives. In:Advances in Neural Information Processing Systems. 2014. 1646-1654. http://papers.nips.cc/paper/5258-saga-a-fast-incremental-gradient-method-with-support-for-non-strongly-convex-composite-objectives.pdf |
| [13] |
Nicol S, Yu J, Simon G. A stochastic quasi-newton method for online convex optimization. The Journal of Machine Learning Research, 2007, 2: 436–443.
http://www.mendeley.com/catalog/stochastic-quasinewton-method-online-convex-optimization/ |
| [14] |
Goldfarb D. A family of variable metric updates derived by variational means. Mathematics of Computation, 1970, 24(109): 23–26.
[doi:10.1090/S0025-5718-1970-0258249-6] |
| [15] |
Liu DC, Nocedal J. On the limited memory BFGS for large scale optimization. Mathematical Programming, 1989, 45(1): 503–528.
[doi:10.1007/BF01589116] |
| [16] |
Combettes PL, Wajs VR. Signal recovery by proximal forward-backward splitting. Multiscale Modeling & Simulation, 2005, 4(4): 1168–1200.
[doi:10.1137/050626090] |
| [17] |
Ram SS, Nedich A, Veeravalli VV. Incremental stochastic subgradient algorithms for convex optimization. SIAM Journal on Optimization, 2009, 20(2): 691–717.
[doi:10.1137/080726380] |
| [18] |
Luo ZQ, Tseng P. On the convergence of the coordinate descent method for convex differentiable minimization. Journal of Optimization Theory and Applications, 1992, 72(1): 7–35.
[doi:10.1007/BF00939948] |
| [19] |
Nesterov Y. Efficiency of coordinate descent methods on huge-scale optimization problems. SIAM Journal on Optimization, 2012, 22(2): 341–362.
[doi:10.1137/100802001] |
| [20] |
Dhillon IS, Ravikumar P, Tewari A. Nearest neighbor based greedy coordinate descent. In:Advances in Neural Information Processing Systems. 2011. 2160-2168. http://papers.nips.cc/paper/4425-nearest-neighbor-based-greedy-coordinate-descent.pdf |
| [21] |
Canutescu A, Dunbrack R. Cyclic coordinate descent:A robotics algorithm for protein loop closure. Protein Science, 2003, 12(5): 963–972.
[doi:10.1110/ps.0242703] |
| [22] |
Zhao SY, Xiang R, Shi YH, Gao P, Li WJ. SCOPE:Scalable composite optimization for learning on spark. In:Proc. of the Association for the Advancement of Artificial Intelligence. 2017. 2928-2934. |
| [23] |
Qirong H, James C, Jin K, Seunghak L, Phillip G, Garth G, Gregory G, Eric X. More effective distributed ML via a stale synchronous parallel parameter server. In:Advances in Neural Information Processing Systems. 2013. 1223-1231. http://papers.nips.cc/paper/4894-more-effective-distributed-ml-via-a-stale-synchronous-parallel-parameter-server.pdf |
| [24] |
Mu L, David A, Jun P, Alexander S, Amr A, Vanja J, James L, Eugene S, Bor-Yiing S. Scaling distributed machine learning with the parameter server. OSDI, 2014, 1(10.4): 3.
[doi:10.1145/2640087.2644155] |
| [25] |
Chen TQ, Li M, Li YT, Lin M, Wang NY, Wang MJ, Xiao TJ, Xu B, Zhang CY, Zhang Z. MXNet:A flexible and efficient machine learning library for heterogeneous distributed systems. arXiv:1512.01274, 2015. |
| [26] |
Jeffrey D, Greg C, Rajat M, Chen K, Matthieu D, Quoc VL, Mark M, Marc R, Andrew S, Paul T, Yang K, Andrew NG. Large scale distributed deep networks. In:Proc. of the Advances in Neural Information Processing Systems. 2012. 1223-1231. http://papers.nips.cc/paper/4687-large-scale-distributed-deep-networks.pdf |
| [27] |
Martin A, Ashish A, Paul B, Eugene B, Chen ZF, Craig C, Greg C, Andy D, Jeffrey D, Matthieu D, Sanjay G, Ian G, Andrew H, Geoffrey I, Michael I, Jia YQ, Rafal J, Lukasz K, Manjunath K, Josh L, Dan M, Rajat M, Sherry M, Derek M, Chris O, Mike S, Jonathon S, Benoit S, Ilya S, Kunal T, Paul T, Vincent V, Vijay V, Fernanda V, Oriol V, Pete W, Martin W, Martin W, Yu Y, Zheng XQ. TensorFlow:A system for large-scale machine learning. In:Proc. of the USENIX Symp. on Operating Systems Design and Implementation, Vol.16. 2016. 265-283. https://www.usenix.org/system/files/conference/osdi16/osdi16-abadi.pdf |
| [28] |
John L, Alexander S, Martin Z. Slow learners are aast. In:Advances in Neural Information Processing Systems, Vol.22. 2009. 2331-2339. https://papers.nips.cc/paper/3888-slow-learners-are-fast.pdf |
| [29] |
Feng N, Recht B, Re C, Wright SJ. Hogwild!:A lock-free approach to parallelizing stochastic gradient descent. In:Advances in Neural Information Processing Systems, Vol.24. 2011. 693-701. http://papers.nips.cc/paper/4390-hogwild-a-lock-free-approach-to-parallelizing-stochastic-gradient-descent.pdf |
| [30] |
Zhao SY. Fast asynchronous parallel stochastic gradient descent:A lock-free approach with convergence guarantee. In:Proc. of the Association for the Advancement of Artificial Intelligence. 2016. 2379-2385. http://www.aaai.org/ocs/index.php/AAAI/AAAI16/paper/download/12442/11887 |
| [31] |
Meng Q, Chen W, Yu JC, Wang TF, Ma ZM, Liu TY. Asychronous accelerated stochastic gradient descent. In:Proc. of the Int'l Joint Conf. on Artificial Intelligence. 2016. 1853-1859. https://www.ijcai.org/Proceedings/16/Papers/265.pdf |
| [32] |
Jason L, Lin QH, Ma TY, Yang TB. Distributed stochastic variance reduced gradient. arXiv:1507.07595v2, 2015. |
| [33] |
Soham D, Tom G. Efficient distributed SGD with variance reduction. In:Proc. of the 16th IEEE Int'l Conf. on Data Mining (ICDM). IEEE, 2016. 111-120.[doi:10.1109/ICDM.2016.0022] |
| [34] |
Zhang YC, Michael IJ. Splash:User-Friendly programming interface for parallelizing stochastic algorithms. arXiv:1506.07552, 2015. |
| [35] |
Steffen R, Dennis F, Eugene JS, Su BY. Robust large-scale machine learning in the cloud. In:Proc. of the 22nd ACM SIGKDD Int'l Conf. on Knowledge Discovery and Data Mining. ACM Press, 2016. 1125-1134.[doi:10.1145/2939672.2939790] |
| [36] |
Stavros Z, Mustafa CP. Parallel block-partitioning of truncated newton for nonlinear network. SIAM Journal on Scientific and Statistical Computing, 1992, 13(5): 1173–1193.
[doi:10.1137/0913068] |
| [37] |
Lin CJ, Ruby CW, Keerthi SS. Trust region newton method for large-scale logistic regression. In:Proc. of the 24th Int'l Conf. on Machine Learning. ACM Press, 2007. 561-568.[doi:10.1145/1390681.1390703] |
| [38] |
Chen WZ, Wang ZH, Zhou JR. Large-Scale L-BFGS using MapReduce. In:Advances in Neural Information Processing Systems, Vol.27. 2014. 1332-1340. http://papers.nips.cc/paper/5333-large-scale-l-bfgs-using-mapreduce.pdf |
| [39] |
Zhang YC, Lin X. DiSCO:Distributed optimization for self-concordant empirical loss. The Journal of Machine Learning Research, 2015, 37: 362–370.
http://proceedings.mlr.press/v37/zhangb15.html |
| [40] |
Nelly P, Caroline C, Jean-Christophe P. Parallel proximal algorithm for image restoration using hybrid regularization. IEEE Trans. on Image Processing, 2011, 20(9): 2450–2462.
[doi:10.1109/TIP.2011.2128335] |
| [41] |
Kamilov US. Parallel proximal methods for total variation minimization. In:Proc. of the 2016 IEEE Int'l Conf. on Acoustics, Speech and Signal Processing (ICASSP). IEEE, 2016. 4697-4701.[doi:10.1109/ICASSP.2016.7472568] |
| [42] |
Kamilov US. A parallel proximal algorithm for anisotropic total variation minimization. IEEE Trans. on Image Processing, 2017, 26(2): 539–548.
[doi:10.1109/TIP.2016.2629449] |
| [43] |
Chen AI, Asuman O. A fast distributed proximal-gradient method. In:Proc. of the 50th Annual Allerton Conf. on Communication, Control, and Computing (Allerton). IEEE, 2012. 601-608.[doi:10.1109/Allerton.2012.6483273] |
| [44] |
Lin X, Zhang T. A proximal stochastic gradient method with progressive variance reduction. SIAM Journal on Optimization, 2014, 24(4): 2057–2075.
[doi:10.1137/140961791] |
| [45] |
Mu L, David A, Alexander S. Distributed delayed proximal gradient methods. In:Proc. of the NIPS Workshop on Optimization for Machine Learning. 2013. 3. http://www.cs.cmu.edu/afs/cs/user/muli/www/file/ddp.pdf |
| [46] |
Zhou Y, Yu YL, Dai W, Liang YB, Eric X. On convergence of model parallel proximal gradient algorithm for stale synchronous parallel system. The Journal of Machine Learning Research, 2016, 51: 713–722.
http://www.cs.cmu.edu/~epxing/papers/2016/Zhou_Yu_Liang_Xing_aistats16.pdf |
| [47] |
Aybat NS, Wang Z, Iyengar G. An asynchronous distributed proximal gradient method for composite convex optimization. arXiv:1409.8547v2, 2015. |
| [48] |
Mota JF, Xavier JM, Aguiar PM, Püschel M. D-ADMM:A communication-efficient distributed algorithm for separable optimization. IEEE Trans. on Signal Processing, 2013, 61(10): 2718–2723.
[doi:10.1109/TSP.2013.2254478] |
| [49] |
Peter R, Martin T. Parallel coordinate descent methods for big data optimization. Mathematical Programming, 2016, 156(1-2): 433–484.
[doi:10.1007/s10107-015-0901-6] |
| [50] |
Liu J, Stephen JW, Christopher R, Victor B, Srikrishna S. An asynchronous parallel stochastic coordinate descent algorithm. The Journal of Machine Learning Research, 2015, 16(1): 285–322.
http://dl.acm.org/citation.cfm?id=2789282&CFID=567164344&CFTOKEN=11661950 |
| [51] |
Scherrer C, Tewari A, Halappanavar M, Haglin D. Feature clustering for accelerating parallel coordinate descent. In:Advances in Neural Information Processing Systems. 2012. 28-36. http://papers.nips.cc/paper/4674-feature-clustering-for-accelerating-parallel-coordinate-descent.pdf |
| [52] |
Scherrer C, Tewari A, Halappanavar M, Haglin D. Scaling up coordinate descent algorithms for large L1 regularization problems. In:Proc. of the 29th Int'l Conf. on Machine Learning. Omnipress, 2012. 355-362. |
| [53] |
Yang Y, Lian XR, Liu J, Yu HF, Dhillon IS, Demmel J, Hsieh CJ. Asynchronous parallel greedy coordinate descent. In:Advances in Neural Information Processing Systems. 2016. 4682-4690. http://papers.nips.cc/paper/6070-asynchronous-parallel-greedy-coordinate-descent.pdf |
| [54] |
Liu J, Stephen JW. Asynchronous stochastic coordinate descent:Parallelism and convergence properties. SIAM Journal on Optimization, 2015, 25(1): 351–376.
[doi:10.1137/140961134] |
| [55] |
Hsieh CJ, Yu HF, Dhillon IS. PASSCoDe:Parallel asynchronous stochastic dual co-ordinate descent. The Journal of Machine Learning Research, 2015, 37: 2370–2379.
https://arxiv.org/abs/1504.01365 |
| [56] |
Hsieh CJ, Chang KW, Lin CJ, Keerthi SS, Sundarajan S. A dual coordinate descent method for large-scale linear SVM. In:Proc. of the 25th Int'l Conf. on Machine Learning. ACM Press, 2008. 408-415.[doi:10.1145/1390156.1390208] |
| [57] |
Yang TB. Trading computation for communication:Distributed stochastic dual coordinate ascent. In:Advances in Neural Information Processing Systems. 2013. 629-637. http://papers.nips.cc/paper/5114-trading-computation-for-communication-distri-buted-stochastic-dual-coordinate-ascent.pdf |
| [58] |
Yang TB, Zhu SH, Jin R, Lin YQ. Analysis of distributed stochastic dual coordinate ascent. arXiv:1312.1031, 2013. |
| [59] |
Martin J, Virginia S, Martin T, Joathan T, Sanjay K, Thomas H, Michael IJ. Communication-Efficient distributed dual coordinate ascent. In:Advances in Neural Information Processing Systems. 2014. 3068-3076. http://papers.nips.cc/paper/5599-communi-cation-efficient-distributed-dual-coordinate-ascent.pdf |
| [60] |
Mahajan D, Keerthi SS, Sundararajan S. A distributed block coordinate descent method for training L1 regularized linear classifiers. arXiv:1405.4544, 2014. |
| [61] |
Dhar S, Yi C, Ramakrishnan N, Shah M. ADMM based scalable machine learning on spark. In:Proc. of the 2015 IEEE Int'l Conf. on Big Data. IEEE. 2015. 1174-1182.[doi:10.1109/BigData.2015.7363871] |
| [62] |
Stephen GN, Ariela S. Block truncated-newton methods for parallel optimization. Mathematical Programming, 1989, 45(1): 529–546.
[doi:10.1007/BF01589117] |
| [63] |
Gavin T, Ryan B, Xu Z, Bharat S, Ankit P, Tom G. Training neural networks without gradients:A scalable ADMM approach. The Journal of Machine Learning Research, 2016, 48: 2722–2731.
http://dl.acm.org/citation.cfm?id=3045677 |
| [64] |
Zhang R, Kwok JT. Asynchronous distributed ADMM for consensus optimization. In:Proc. of the 31st Int'l Conf. on Machine Learning. 2014. 1701-1709. http://proceedings.mlr.press/v32/zhange14.pdf |
| [65] |
Shi W, Ling Q, Yuan K, Wu G, Yin W. On the linear convergence of the ADMM in decentralized consensus optimization. arXiv:1307.5561v4, 2014.[doi:10.1109/TSP.2014.2304432] |
| [66] |
Bradley JK, Kyrola A, Bickson D, Guestrin C. Parallel coordinate descent for L1-regularized loss minimization. arXiv:1105.5379, 2011. |
| [67] |
Wei E, Asuman O. On the O(1/k) convergence of asynchronous distributed alternating direction method of multipliers. In:Proc. of the 2013 IEEE Global Conf. on Signal and Information Processing. IEEE, 2013. 551-554.[doi:10.1109/GlobalSIP.2013.6736937] |
| [68] |
Ali M, Asuman O. Broadcast-Based distributed alternating direction method of multipliers. In:Proc. of the 52nd Annual Allerton Conf. on Communication, Control, and Computing (Allerton). IEEE, 2014. 270-277.[doi:10.1109/ALLERTON.2014.7028466] |
| [69] |
Wei E, Asuman O. Distributed alternating direction method of multipliers. In:Proc. of the 51st IEEE Annual Conf. on Decision and Control (CDC). IEEE, 2012. 5445-5450.[doi:10.1109/CDC.2012.6425904] |
| [70] |
Peter R, Martin T. Distributed coordinate descent method for learning with big data. The Journal of Machine Learning Research, 2016, 17(1): 2657–2681.
https://arxiv.org/pdf/1310.2059 |
| [71] |
Low Y, Gonzalez JE, Kyrola A, Bickson D, Guestrin CE, Hellerstein J. Graphlab:A new parallel framework formachine learning. Computer Science, 2014. https://arxiv.org/ftp/arxiv/papers/1408/1408.2041.pdf |
 2018, Vol. 29
2018, Vol. 29


