1 引言

大数据中的信息挖掘, 是当今计算机科学领域中的一个热门研究领域.然而, 绝大多数大数据中都包含了很多敏感的个人隐私信息, 如医疗记录、搜索引擎记录、电子商务数据、社会网络数据等^{[1, 2]}.如何以隐私保持的方式在隐私敏感数据集中挖掘有用信息, 在近二、三十年中一直是一个很活跃的研究领域^[3].特别地, 随着差分隐私模型的引入, 隐私保持信息分析和挖掘在近年中得到了迅速的发展^[4-8].然而, 这个领域还处于比较初级的发展阶段, 很多关键问题还没能得到解决.尽管差分隐私是一个有严格数学定义的隐私模型, 通过其可对数据集中的个人隐私信息进行很好的保护, 但是, 差分隐私模型也因其较差的数据有用性而得到很多批评——经差分隐私处理后数据的有用性要比经类k-匿名(如k-匿名、$\ell $ -多样性、t-邻近性等)模型处理后数据的有用性差^{[9, 10]}(当然, 类k-匿名模型的隐私保护程度差也是其重大缺陷).然而, 经差分隐私处理后数据的有用性较弱的原因一直没能被充分研究.也就是说, 没有比较完整的结论, 说明经差分隐私处理后数据有用性差的问题是因为差分隐私模型的特性, 还是因为现在的研究还没能找到更好的相关差分隐私算法, 或者是因为隐私保护本身的特性而与隐私模型选择无关.关于这个问题, 学者们从不同的角度(直接或间接地)进行了研究, 如统计学习角度^[11-13]、数据类型角度^{[14, 15]}、数据分析角度^[16]、最优机制角度^[17-19]等.本文的工作属于最优机制研究, 即:对一个特定的查询问题, 我们试图在保持差分隐私的条件下达到最优的数据有用性.本文构造了一些基本的分析方法来对差分隐私的最优机制问题进行分析.

对多查询问题(即同时对多个查询进行处理), 从查询函数的角度, (广义)最优机制问题可分为两个方面:函数压缩和(狭义)最优机制.函数压缩关注不同查询之间的相关性问题, 如线性相关性.函数压缩试图将相关性很高的多查询问题压缩为相关性较低的少量查询问题, 然后通过寻找后者的差分隐私机制来求解前者的差分隐私机制, 由此来减小噪声复杂度^[20-22].(狭义)最优机制关注于低相关性函数查询的最优机制寻找问题.函数压缩问题可表述如下:对于相关性较高的m个查询问题g₁(x), …, g_m(x), 经过某种压缩算法, 可将其压缩为n( < m)个相关性很低的查询函数f₁(x), …, f_n(x).最简单情形, 存在一个m×n实值矩阵A, 满足g(x)=Af(x), 其中, g(x)=(g₁(x), …, g_m(x))^T, f(x)=(f₁(x), …, f_n(x))^T.若矩阵A是一个小元素矩阵(即A的每个元素都很小), 则通过研究关于查询函数f(x)的差分隐私机制, 就可以以后处理(post-processing)原理^[5]通过表达式g(x)=Af(x)来找到g(x)的差分隐私机制.与文献[18]类似, 本文主要讨论(狭义)最优机制问题.也就是说:对于相关性很低的函数f(x), 需要找到最优差分隐私机制, 从而得到数据有用性最高的(或最精确的)对f(x)的查询反馈.在本文以下的分析中, 我们都假定多查询函数是低相关的, 因此无需关注其函数压缩.

1.1 本文贡献

本文试图构造一些基本的分析方法来对差分隐私的最优机制问题进行分析.

首先, 不同于文献[18-24]中将最优机制问题归结为一个单目标函数优化问题, 本文引入了多目标函数优化模型来求解最优机制.这种多目标函数模型与其他单目标函数模型相比, 如Min-Max目标函数模型^{[18, 19]}, 具有很大优点:多目标模型将不同数据集对应分布的有用性的权衡问题剥离出了最优差分隐私机制问题, 这为分析差分隐私机制的最优性提供了方便.

其次, 本文引入了一种新的最优差分隐私机制分析方法.该分析方法受到了文献[25]中的梯子函数(ladder function)的启发, 将概率分布通过集合切分及合理测度赋值来达到数据有用性和隐私性的权衡.

最后, 针对线性查询问题, 本文寻找到了线性查询问题的一种近似最优机制(定理2).据我们所知, 定理2是关于线性查询最优机制的最全面的结论.并且, 本文的大部分分析方法对分析非线性查询问题的最优机制也是适用的, 比如, 第3节、第4节的内容都没有对函数类型进行限定.本文的深层目的是探讨差分隐私的深层数学结构.本文发现:一个数据集的邻居集合对应的查询函数值集合里面包含了差分隐私的一些非常重要的特征, 而敏感度只是该集合的极值特性.本文通过研究该集合中点的分布情况来探讨差分隐私的深层特征, 相关内容请参考第6节的讨论.

1.2 相关工作

差分隐私的研究主要从3个关注点展开:数据隐私性、数据有用性(或噪声复杂度)及算法复杂度.对一个查询问题, 这三者之间相互冲突, 需要在他们之间进行权衡.

本文的研究关注于数据隐私性及数据有用性之间的权衡问题, 不考虑相关算法的复杂度问题.即:考虑在隐私保护程度确定的条件下, 获得有用性最高的查询结果时的机制寻找问题(即最优机制问题).前人分别从不同的角度对一些特殊的线性查询的最优机制问题进行了研究, 如单输出值查询^{[18, 19, 24, 29]}、多输出连续实值查询^[23]、多输出值查询噪声复杂度上下界及其逼近^{[17, 28]}等.不同于先前的工作, 本文对一般的线性查询问题寻找最优机制, 并得出了相关结果(定理2), 扩展了在线性查询最优机制方面的结论.本文的分析方法其实是为了分析非线性查询问题而发展起来的一套分析理论, 因此也可以对非线性查询问题进行分析.

如第1节的分析, 另一类研究关注于多线性查询问题中各查询之间的相关性(如线性相关性)问题, 并试图将相关性很高的多查询问题压缩为相关性很低的少量查询以降低噪声复杂度^[20-22].这一类研究关注于线性查询相关算法的隐私性、数据有用性及算法复杂度这3方面的权衡, 但并不强调相关机制的(噪声复杂度)最优性.

从统计学习的角度, 很多学者试图将关于数据集x的多线性查询转化为一个关于数据集y的对应多线性查询^[30-32].该方法的理论基础是基于查询函数的统计特性及自变量的数据集的特性.这类研究关注噪声复杂度、计算复杂度的估计及与隐私之间的权衡, 没有强调最优机制问题.

敏感度方法是差分隐私中的一类重要方法, 如全局敏感度^[27]、平滑敏感度^[26]及局部敏感度^[25]等.现在的绝大多数差分隐私算法都是通过敏感度方法来进行隐私分析的.本文的分析方法受到了文献[25]中梯子函数(ladder function)的极大启发.但文献[25]中梯子函数的方法还是基于(局部)敏感度, 而本文将该方法进行了改进, 使其脱离了敏感度方法, 并发展出一套与文献[25]完全不同的分析方法.并且, 文献[25]并不讨论机制的最优性及方法的推广.关于本文方法与敏感度方法之间的优劣比较见本文第6节的讨论.据我们所知, 本文方法是第一个不基于敏感度而能对非线性查询最优机制进行分析的方法.

2 问题形式化

在本文中, 数据集(dataset)是一些记录(行向量)的多重集(multiset), 每个记录代表个体信息, 其形式化表示为^{[5, 17, 21]}:设$\chi $是所有不同记录的集合, 且设一个数据集x是$\chi $中一些记录的(多重)集合.本文将数据集x表示为直方图$x\in {{\mathbb{N}}^{|\mathcal{X}|}}$, 其中, 每个分量x_i表示数据集x中类型$i\in \chi $的个数($\mathbb{N}$表示包含0的自然数集, |$\chi $ |表示$\chi $中元素的(可以不可数)个数).两个数据集x, y的距离定义为他们直方图表示的差值的${{\ell }_{{{1}^{-}}}}$范数, 即||x-y||₁.若||x-y||₁=1, 则称x, y为邻居或相邻数据集.数据集x的所有邻居的集合记为${\mathcal{N}^{x}}$.设${\mathcal{D}^{x}}\subseteq {{\mathbb{N}}^{|\chi |}}$是所有可允许的数据集的集合, 则${\mathcal{N}^{x}}=\{{x}'\in \mathcal{D}:||x-{x}'|{{|}_{1}}=1\}$.

本文主要研究线性查询(linear query)的最优机制.线性查询是一类很广泛的查询函数^{[5, 17, 21]}, 包括计数函数、列联表(contingency table)及范围查询(range query)等.线性查询f定义为f:$\chi \to {\mathit{\mathbb{R}}}$, 且对有限元素数据集x(当$\chi $为离散集合时):

$ f(x)=\sum\limits_{i=1}^{|\mathcal{X}|}{{{x}_{i}}}f({{\mathcal{X}}_{i}}), $

或(当$\chi $为连续集合时):

$ f(x)=\sum\limits_{i=1}^{|\mathcal{Y}|}{{{y}_{i}}}f({{\mathcal{Y}}_{i}}), $

其中, $\mathcal{Y}$表示有限元素数据集x中非零元的不同类型的集合, y_i是类型$\mathcal{Y}_{i}$的个数.我们称函数f关于数据集x的邻居集为$\{f({x}'):{x}'\in {\mathcal{N}^{x}}\}$, 记为$\mathcal{V}$^x.显然, 若f为线性函数, 则${\mathcal{V}^{x}}=f\left( x \right)\pm \{f\left( y \right):y\in \chi \}$, 因为$\{f\left( y \right):y\in \chi \}$只与f有关, 我们称其为线性函数f的邻居集, 记为$\mathcal{V}$.集合$\mathcal{V}$中包含了很多重要的差分隐私所需的特征, 如(全局或局部)敏感度$\Delta f={{\max }_{a, b\in \mathcal{V}}}|a-b|$.本文试图通过集合V的其他特性(集合中点的分布)来理解差分隐私的一些深层数学结构.

n个线性查询f₁(x), …, f_n(x)可定义为一个多输出值线性函数f的查询问题.当$\chi $为离散集合时, 定义:

$ f\left( x \right)=Ax, $

其中, 矩阵A的元素a_ij=f_i($\chi $_j), 数据集x为其直方图表示的列向量.当$\chi $为连续集合时, 定义:

$ f\left( x \right)=Ay, $

其中, y为数据集x(有限集)的直方图表示中非零元组成的列向量(y₁, …, y_k)^T, 矩阵A的元素${{a}_{ij}}={{f}_{i}}({\mathcal{Y}_{j}}), {\mathcal{Y}_{j}}$代表非零元y_j对应的记录类型.因此, 一个(多)线性查询函数可统一记为f: $\chi \to {{\mathit{\mathbb{R}}}^{n}}$; 或为了表述的方便, 记为f: $\mathcal{D}\to {{\mathit{\mathbb{R}}}^{n}}$, 其中, $\mathcal{D}$为所有可允许的取值于$\chi $的数据集的集合.

差分隐私机制^[5]是一类随机函数, 其输出是一个随机变量.设$\mathcal{D}$为所有可允许的数据集的集合, 且对查询函数f, 设$\mathcal{R}=\{f\left( x \right):x\in \mathcal{D}\}$.

定义1.  以$\mathcal{D}$为定义域, 以$\mathcal{R}$为值域的随机函数$\mathcal{M}$关联了一个确定性函数M: $\mathcal{D}\to \Delta \left( \mathcal{R} \right)$, 其中, $\Delta \left( \mathcal{R} \right)$代表所有$\mathcal{R}$上的概率分布的集合.当输入为$x\in \mathcal{D}$时, $\mathcal{M}$输出随机变量$\mathcal{M}$ (x), 其服从概率分布M(x). $\mathcal{M}$满足$\varepsilon $ -差分隐私, 如果对任意的相邻数据集x, y及对任意的可测集$S\subseteq \mathcal{R} $, 满足:

$ \text{Pr}[M\left( x \right)\in S]\le \text{exp}(\varepsilon )\times \text{Pr}[M\left( y \right)\in S]. $

定义1说明, 差分隐私机制$\mathcal{M}$给每一个数据集x对应了一个概率分布M(x), 而相邻数据集所对应的概率分布需满足定义1中的不等式.因此, 差分隐私机制$\mathcal{M}$与概率分布族{M(x):x∈ $\mathcal{D}$}是一一对应的.若$\{M\left( x \right):x\in \mathcal{D}\}$是连续概率分布族, 其密度函数族为$\{{{p}_{x}}:x\in \mathcal{D}\}$, 则差分隐私机制M与密度函数族$\{{{p}_{x}}:x\in \mathcal{D}\}$一一对应.在以下的分析中, 如果没有特殊说明, 本文将$\mathcal{M}$与其密度函数族$\{{{p}_{x}}:x\in \mathcal{D}\}$视为相同的量.

当$\mathcal{R}={{\mathit{\mathbb{R}}}^{n}}$时, 我们定义函数f: $\mathcal{D}\to {{\mathit{\mathbb{R}}}^{n}}$关于x的局部${{\ell }_{p}}$敏感度为${{\max }_{{x}'\in {{\mathcal{N}}^{x}}}}\|f(x)-f({x}'){{\|}_{p}}$, 定义f的全局${{\ell }_{p}}$敏感度为${{\max }_{x\in \mathcal{D}}}{{\max }_{{x}'\in {{\mathcal{N}}^{x}}}}\|f(x)-f({x}'){{\|}_{p}}$, 其中, ||·||_p代表p-范数.

2.1 效用模型

本文以连续情形为例进行分析, 离散情形可类似处理.对于线性查询函数f: $\mathcal{D}\to {{\mathit{\mathbb{R}}}^{n}}$及数据集x, 根据定义1, 不同的差分隐私机制对应了不同的$ {{\mathit{\mathbb{R}}}^{n}}$上的密度函数族, 也就对应了不同的查询反馈值.本文研究满足$\varepsilon - $差分隐私的所有机制中查询反馈最精确的那个密度函数族.下面定义效用模型, 用其来衡量差分隐私输出的有用性.

在差分隐私的研究中, 有几种常用的衡量差分隐私输出有用性的模型, 最常用的为Min-Max模型^{[17, 18, 23]}, 即:

$ \underset{\mathcal{M}}{\mathop{\arg \min }}\, \ \underset{x\in \mathcal{D}}{\mathop{\sup }}\, \int_{r\in {{\mathbb{R}}^{n}}}{\|f(x)-r{{\|}_{p}}{{p}^{x}}(r)\text{d}r}. $

不同于Min-Max等单目标函数优化模型, 本文使用多目标函数优化模型, 即:

$ \underset{\mathcal{M}}{\mathop{\arg \min }}\, \{\int_{r\in {{\mathbb{R}}^{n}}}{\|f(x)-r{{\|}_{p}}{{p}^{x}}(r)\text{d}r}:x\in \mathcal{D}\}, $

其中, p^x(r)代表$\mathcal{M}\left( x \right)$的密度函数, ||·||_p代表p-范数(p是一个常量).多目标函数模型意在寻找对所有数据集x都达到最优的差分隐私机制.而Min-Max等单目标函数模型需要对不同数据集对应输出的有用性进行权衡, 这增加了问题分析的复杂度.也就是说, 多目标模型将不同数据集对应输出的有用性权衡问题剥离出了优化机制问题, 这为分析差分隐私机制的最优性提供了方便.

2.2 最优化问题

现在将最优差分隐私机制问题归纳为如下的多目标优化问题.

$ \left. \begin{align} &\underset{{{p}_{x}}:x\in \mathcal{D}}{\mathop{\arg \min }}\, \left\{ \int_{r\in {{\mathit{\mathbb{R}}}^{n}}}{\parallel f\left( x \right)-r\parallel _{p}\left. {{p}_{x}}\left( r \right)\text{d}r\in \mathcal{D} \right\}} \right. \\ &\text{s}\text{.t}\text{.对任意邻居}x, {x}'\text{及任意可测集}S\subseteq {{\mathit{\mathbb{R}}}^{n}}, \\ &\Pr \left[\mathcal{M}\left( x \right)\in S \right]\le \exp \left( \varepsilon \right)\times \Pr \left[\mathcal{M}\left( {{x}'} \right)\in S \right] \\ \end{align} \right\} $

(1)

上面的优化问题等价于:

$ \left. \begin{align} &\underset{{{p}_{x}}:x\in \mathcal{D}}{\mathop{\arg \min }}\, \left\{ \int_{r\in {{\mathit{\mathbb{R}}}^{n}}}{\parallel f\left( x \right)-r{{\parallel }_{p}}\left. {{p}^{_{x}}}\left( r \right)\text{d}r\in \mathcal{D} \right\}} \right. \\ &\text{s}\text{.t}\text{.对任意邻居}x, {x}'\text{任意}\ r\subseteq {{\mathit{\mathbb{R}}}^{n}}\backslash B, \mu \left( B \right)=0 \\ &{{p}^{_{x}}}\left( r \right)\le {{e}^{\varepsilon }}{{p}^{_{{{x}'}}}}\left( r \right) \\ \end{align} \right\} $

(2)

其中, μ代表${{\mathit{\mathbb{R}}}^{n}}$上的Lebesgue-Stieltjes测度, B $\in {{\mathit{\mathbb{R}}}^{n}}$.为了表述的简洁性, 在本文中设B=∅.p是一个常量.

对多目标函数优化问题(1) 或(2), 需要寻找(可能多个)密度函数族$ \{{{p}_{x}}:x\in \mathcal{D}\}$, 其对优化问题(1) 或(2) 具有Pareto最优性.更多关于多目标函数优化问题的知识见文献[33].

3 差分隐私机制分解

对于集合$\mathcal{R}$上的密度函数p^x(r), 可以将其表示为exp(εq(x, r))的形式, 其中, $q(x, r)=\frac{1}{\varepsilon }\ln {{p}_{x}}(r)$并设置ln0=-∞.因此, 若函数$q:\mathcal{D}\times \mathcal{R}\to \mathit{\mathbb{R}}\_$, 其中, $\mathit{\mathbb{R}}\_$表示非正实数集与-∞的并集, 则对于数据集x, exp(εq(x, r))可表示任何一个$\mathcal{R}$上的密度函数.因此, 记密度函数p^x(r)=exp(εq(x, r)), 其中, $q:\mathcal{D}\times \mathcal{R}\to \mathit{\mathbb{R}}\_$称为p^x(r)的质量函数.

对于数据集x及相应密度函数p^x(r)=exp(εq(x, r)), 下面根据质量函数q(x, r)的值对集合$\mathcal{R}$进行切分.对数据集x, 设q(x, r)的值域为$\mathcal{Q}$^x.对任意一个z∈$\mathcal{Q}$^x, 记$\mathcal{R}_{z}^{x}=\{r\in \mathcal{R}:q(x, r)=z\}$.则$\mathcal{R}=\bigcup\nolimits_{z\in \mathcal{Q}}{\mathcal{R}_{z}^{x}}\mathcal{R}_{z}^{x}\cap \mathcal{R}_{{{z}'}}^{x}=\varnothing $, 其中z, z∈$\mathcal{Q}$^x且z≠z'.记${{\mathcal{R}}^{x}}=\{\mathcal{R}_{z}^{x}:z\in {{\mathcal{Q}}^{x}}\}$, 则p^x(r)与集合对($\mathcal{Q}$^x, $\mathcal{R}$^x)一一对应.因此, 差分隐私机制$\{{{p}_{x}}:x\in \mathcal{D}\}$与集合对族{($\mathcal{Q}$, $\mathcal{R}$):x∈ $\mathcal{D}$ }形成一一对应.不同的集合对族{($\mathcal{Q}$, $\mathcal{R}$):x∈$\mathcal{D}$ }对应了不同的差分隐私机制.

对数据集x∈ $\mathcal{D}$, 当$\mathcal{Q}$^x是一个可数点的集合时, 记$\mathcal{Q}$^x={z₀, z₁, …}及${{\mathcal{R}}^{x}}=\{\mathcal{R}_{0}^{x}, \mathcal{R}_{1}^{x}, ...\}$, 其中, $\mathcal{R}_{i}^{x}=\mathcal{R}_{{{z}_{i}}}^{x}$.则优化问题(2) 等价于下面优化问题(3):

$ \left. \begin{align} & \underset{\left( {{\mathcal{Q}}^{x}},{{\mathcal{R}}^{x}} \right):x\in \mathcal{D}}{\mathop{\arg \min }}\,\left\{ \sum\limits_{i=0}^{\infty }{\frac{\exp \left( \varepsilon z_{i}^{x} \right)}{{{\alpha }_{x}}}}\int_{r\in \mathbb{R}_{i}^{x}}{\parallel f\left( x \right)-r{{\parallel }_{p}}\text{d}r:x\in \mathcal{D}} \right\} \\ & \text{s}\text{.t}\text{.对任意邻居}x,{x}'\text{任意}\ i,j\subseteq \mathbb{N}\text{且满足}\mathcal{R}_{i}^{x}\cap R_{i}^{{{x}'}}\ne \varnothing ,\text{有} \\ & \exp \left( \varepsilon \left( z_{i}^{x}-z_{i}^{{{x}'}}-1 \right) \right)\le \frac{{{\alpha }_{x}}}{{{\alpha }_{{{x}'}}}} \\ \end{align} \right\} $

(3)

其中, ${{\alpha }_{x}}=\sum\limits_{j=0}^{\infty }{\exp (\varepsilon z_{j}^{x})\int_{r\in \mathcal{R}_{j}^{x}}{\text{d}r}}.$此时, 记${{a}_{j}}=\int_{r\in \mathcal{R}_{j}^{x}}{||f(x)-r|{{|}_{p}}\text{d}r}, {{b}_{j}}=\int_{r\in \mathcal{R}_{j}^{x}}{\text{d}r}.$

对数据集x∈ $\mathcal{D}$, 当$\mathcal{Q}$是一个连续点集时, 优化问题(2) 等价于下面优化问题(4):

$ \left. \begin{align} & \underset{\left( {{\mathcal{Q}}^{x}},{{\mathcal{R}}^{x}} \right):x\in \mathcal{D}}{\mathop{\arg \min }}\,\left\{ \int_{z\in {{\mathcal{Q}}^{x}}}{\frac{\exp \left( \varepsilon z \right)}{{{\alpha }_{x}}}\sum\limits_{r\in \mathcal{R}_{z}^{x}}{\parallel f\left( x \right)-r{{\parallel }_{p}}}\text{d}z:x\in \mathcal{D}} \right\} \\ & \text{s}\text{.t}\text{.对任意邻居}x,{x}'\text{任意}\ i,j\subseteq \mathbb{N}\text{且满足}\mathcal{R}_{i}^{x}\cap R_{i}^{{{x}'}}\ne \varnothing ,\text{有} \\ & \exp \left( \varepsilon \left( z_{i}^{x}-z_{i}^{{{x}'}}-1 \right) \right)\le \frac{{{\alpha }_{x}}}{{{\alpha }_{{{x}'}}}} \\ \end{align} \right\} $

(4)

其中, ${{\alpha }_{x}}=\int_{z\in {{\mathcal{Q}}^{x}}}{\exp }(\varepsilon {{z}^{x}})|\mathcal{R}_{z}^{x}|\text{d}z.$

4 极小差分隐私集序列

根据上一节的结论, 差分隐私机制与集合对族{($\mathcal{Q}$, $\mathcal{R}$):x∈ $\mathcal{D}$}一一对应.因此, 只需要研究集合对族的性质就可以研究清楚差分隐私机制的性质.本节讨论{$\mathcal{R}$:x∈ $\mathcal{D}$}的构造问题, 也就是说, 研究满足差分隐私的对应机制中对值域$\mathcal{R} $ ={f(x):x∈ $\mathcal{D}$}的切分问题.首先给出一个假设, 该假设说明:当查询值是f(x)时, 密度函数p^x(r)应在r=f(x)点达到最大.

假设1.  对任意数据集x∈ $\mathcal{D}$及任意r∈ $\mathcal{R}$, 有p^x(f(x))≥p^x(r), 且$f(x)\in \mathcal{R}_{0}^{x}, z_{0}^{x}=0.$

注:假设1中, $z_{0}^{x}=0$可能导致整个值域$\mathcal{R}$上的概率和(或积分)不为1, 因此需要进行归一化处理.这在第5节有所体现.

基于假设1, 构造一类集合切分$\mathcal{R}=\bigcup\nolimits_{t}{I_{t}^{x}}, x\in \mathcal{D}$, 这一类集合切分将相邻数据集的函数值尽可能放到同一个子集合或相邻的子集合, 这样就便于分析和构造差分隐私机制.具体构造如下:对任一x∈ $\mathcal{D}$, 设置$I_{0}^{x}=\{f(x)\}$及$I_{t}^{x}=\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{I_{t-1}^{{{x}'}}}\backslash \bigcup\nolimits_{i=0}^{t-1}{I_{i}^{x}}, t>0$.这种集合切分构造借鉴了文献[25]中梯子函数的构造方法.该构造有如下性质.

引理1.对任意的邻居x, x'∈ $\mathcal{D}$, 及对任意的|t-s| > 1, 有$I_{t}^{x}\cap I_{s}^{{{x}'}}=\varnothing \mathcal{R}=\bigcup\nolimits_{i=0}^{\infty }{I_{i}^{x}}.$

证明:首先定义集合$A_{t}^{x}=\{f({x}'):{x}'\in \mathcal{D}, \|x-{x}'{{\|}_{1}}\le t\}$.下面证明$A_{t}^{x}=\bigcup\nolimits_{i=0}^{t}{I_{i}^{x}}$.首先, 对每个i≤t, $I_{i}^{x}$是一些与x的距离小于等于i的数据集的函数值的集合, 而$A_{t}^{x}$是所有与x的距离小于等于t的数据集的函数值的集合, 因此$ \bigcup\nolimits_{i=0}^{t}{I_{i}^{x}}\subseteq A_{t}^{x}$.下面使用数学归纳法来证明$A_{t}^{x}\subseteq \bigcup\nolimits_{i=0}^{t}{I_{i}^{x}}$.当t=0时, $A_{0}^{x}=\bigcup\nolimits_{i=0}^{t}{I_{i}^{x}}=\{f(x)\}$显然成立; 假设对所有t < k, 有$A_{t}^{x}\subseteq \bigcup\nolimits_{i=0}^{t}{I_{i}^{x}} $; 当t=k时, 对任意$r\in A_{k}^{x}$, 存在一个数据集y及整数j, 满足||x-y||₁=j≤k且f(y)=r.显然, $r\in A_{j}^{x}.$若j < k, 根据假设, 有$r\in \bigcup\nolimits_{i=0}^{j}{I_{i}^{x}}.$若j=k, 则存在x', 满足||x-x'||₁=1且||x'-y||₁=k-1.根据假设, 有$r\in A_{k-1}^{{{x}'}}\subseteq \bigcup\nolimits_{i=0}^{k-1}{I_{i}^{{{x}'}}}.$再由$I_{k}^{x}$的定义, 有$r\in I_{k}^{x}$.因此, $A_{k}^{x}\subseteq \bigcup\nolimits_{i=0}^{k}{I_{i}^{x}}.$从而, 对任意t≥0, x∈ $\mathcal{D}$, 有$A_{t}^{x}=\bigcup\nolimits_{i=0}^{t}{I_{i}^{x}}.$

由$A_{t}^{x}=\bigcup\nolimits_{i=0}^{t}{I_{i}^{x}}$, 易得$\mathcal{R}=\bigcup\nolimits_{i=0}^{\infty }{I_{i}^{x}}I_{t}^{x}=\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{I_{t-1}^{{{x}'}}}\backslash A_{t-1}^{x}$.下面证明$I_{t}^{x}\cap I_{s}^{{{x}'}}=\varnothing $.因为$I_{t}^{x}=\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{I_{t-1}^{{{x}'}}}\backslash A_{t-1}^{x}, $则对任意$r\in I_{t}^{x}$, 存在y∈ $\mathcal{D}$, 满足||x-y||₁=t及r=f(y), 且对任何满足||x-y‘||₁≤t-1的y’∈ $\mathcal{D}$, 有r≠f(y').另一方面, 对任意$r\in I_{t}^{x}$', 存在$\hat{x}\in \mathcal{D}$, 满足$\|\hat{x}-{x}'{{\|}_{1}}=s$及${r}'=f(\hat{x})$.再由s≤t-2 < t-1, 有$I_{t}^{x}\cap I_{s}^{{{x}'}}=\varnothing .$

记${{I}^{x}}=\{I_{i}^{x}:i\in \mathbb{N}\}$.引理1说明:对任意的邻居x, x'∈ $\mathcal{D}$, 每个点r∈$\mathcal{R}$在I^x和I^x'中的对应集合序列的位置至多错一位.这个性质为分析机制的差分隐私性提供了极大的方便.并且, 这个错位值(即1) 不能再提升到0了, 否则, 或者f(x), x∈ $\mathcal{D}$是恒等函数, 或者$I_{0}^{x}=\mathcal{R}, x\in \mathcal{D}.$

另外, {I^x:x∈ $\mathcal{D}$}是所有满足假设1和引理1的切分序列中最“瘦”的——从$I_{1}^{x}$开始, 每个$I_{i}^{x}$仅包含了那些与x的距离为i的邻居的函数值.这个极小性质为分析机制的输出数据有用性提供了方便.

我们的目的是对所有$I_{i}^{x}$中的点, 赋值以相同的概率密度值.这样, 由引理1的性质, 当判断是否机制满足差分隐私时, 只需要判断当|t-s|≤1且$I_{t}^{x}\cap I_{s}^{{{x}'}}\ne \varnothing $时, $I_{t}^{x}\cap I_{s}^{{{x}'}}\ne \varnothing $中相应点的概率值是否满足差分隐私, 而无需考虑其他的点了.

5 线性查询的一种近似最优机制

本节讨论线性查询的最优机制问题.首先讨论当集合序列是极小集合序列{I^x:x∈ $\mathcal{D}$}时, 质量序列{$\mathcal{Q}$^x:x∈ $\mathcal{D}$}的最优问题.

线性查询具有特殊的性质:对所有x∈ $\mathcal{D}$及所有i∈$\mathbb{N} $, 集合$I_{i}^{x}-f(x)$都是相同的.这是因为:

$ I_{0}^{x}-f(x)=\varnothing, I_{1}^{x}-f(x)=\{f({x}')-f(x):{x}'\in {{\mathcal{N}}^{x}}\}=\{\pm f(s):s\in \mathcal{X}\}, $

再由$I_{i}^{x}$的对称递归构造过程可得.

这个性质为构造对应的值序列提供了方便.将序列{I^x:x∈ $\mathcal{D}$}代入(替换{$\mathcal{R}$^x:x∈ $\mathcal{D}$})优化问题(3) 中, 发现对不同的x∈ $\mathcal{D}$, 他们有相同的a_i和b_i, i∈ $\mathit{\mathbb{N}} $.因此, 对所有x, y∈ $\mathcal{D}$, 为了让所有目标函数极小值, 对质量序列{$\mathcal{Q}$^x:x∈ $\mathcal{D}$}, 应设$z_{i}^{x}=z_{i}^{y}:={{z}_{i}}, i\in \mathbb{N}.$从而, 对所有x, y∈ $\mathcal{D}$, α_x=α_y.这样, 优化问题(3) 等价于如下的优化问题(5).

$ \left. \begin{align} &\underset{{{z}_{i}}, i\in \mathbb{N}}{\mathop{\arg \min }}\, \left\{ \frac{\sum\limits_{i=0}^{\infty }{\exp }(\varepsilon {{z}_{i}})\int_{r\in I_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}}{\sum\limits_{j=0}^{\infty }{\exp }(\varepsilon {{z}_{j}})\int_{r\in I_{j}^{x}}{\text{d}r}}:x\in \mathcal{D} \right\} \\ &\text{s}\text{.t}\text{. }对任意邻居x, {x}', 任意i, j\in \mathbb{N}且满足|i-j|\le 1及 \\ &\text{ }I_{i}^{x}\cap I_{j}^{{{x}'}}\ne \varnothing, 有{{z}_{i}}-{{z}_{j}}\le 1 \\ \end{align} \right\} $

(5)

下面分析质量序列{z_i:i∈ $\mathbb{N} $ }的最优取值问题.首先给出两个引理.

引理2.设$g(x)=\frac{{{\alpha }_{0}}x+{{\alpha }_{1}}}{{{\beta }_{0}}x+{{\beta }_{1}}}$ :若α₀β₁ > α₁β₀, 则g(x)是非减函数; 若α₀β₁ < α₁β₀, 则g(x)是非增函数.

证明:由于g(x)的导数${g}'(x)=\frac{{{\alpha }_{0}}{{\beta }_{1}}-{{\alpha }_{1}}{{\beta }_{0}}}{{{({{\beta }_{0}}x+{{\beta }_{1}})}^{2}}}$, 从而可得结论.

引理3.设f: $\chi \to {{\mathit{\mathbb{R}}}^{n}}$为一线性查询函数, 且设${{a}_{i}}=\int_{r\in I_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}, {{b}_{i}}=\int_{r\in I_{i}^{x}}{\text{d}r}$, 则对j > i, 有$\frac{{{a}_{i}}}{{{b}_{i}}}\le \frac{{{a}_{j}}}{{{b}_{j}}}.$

证明:该结论是积分中值定理的一个推论.

由引理3, 可得如下推论。

推论1.对所有t∈ $\mathbb{N}$, 有$\frac{\sum\limits_{i=0}^{t-1}{\exp }(-\varepsilon i){{a}_{i}}}{\sum\limits_{i=0}^{t-1}{\exp }(-\varepsilon i){{b}_{i}}}\le \frac{{{a}_{t}}}{{{b}_{t}}}.$

定理1.设假设1成立, 则优化问题(5) 的最优质量序列为${{\{z_{i}^{x}=-i\}}_{i\in \mathbb{N}}}, x\in \mathcal{D}. $

证明:本定理使用数学归纳法证明, 其证明思路简述如下.

首先, 根据推论1、引理2及z₀=0, 可得优化问题(6) 的最优解为z₁=-1.

$ \left. \begin{align} &\underset{{{z}_{1}}}{\mathop{\arg \min }}\, \left\{ \frac{\sum\limits_{i=0}^{1}{\exp }(\varepsilon {{z}_{i}})\int_{r\in I_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}}{\sum\limits_{j=0}^{1}{\exp }(\varepsilon {{z}_{j}})\int_{r\in I_{j}^{x}}{\text{d}r}}:x\in \mathcal{D} \right\} \\ &\text{s}\text{.t}\text{. }对任意邻居x, {x}', 任意i, j\in \{0, 1\}满足 \\ &\text{ }I_{i}^{x}\cap I_{j}^{{{x}'}}\ne \varnothing, 有{{z}_{i}}-{{z}_{j}}\le 1 \\ \end{align} \right\} $

(6)

接着, 设对所有t < k, 有z_t=-t.下面证明z_k=-k是如下优化问题(7) 的解, 而这个结论是推论1及假设(t < k时, 有z_t=-t)的推论.

$ \left. \begin{align} &\underset{{{z}_{t}}}{\mathop{\arg \min }}\, \left\{ \frac{\sum\limits_{i=0}^{t}{\exp }(\varepsilon {{z}_{i}})\int_{r\in I_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}}{\sum\limits_{j=0}^{t}{\exp }(\varepsilon {{z}_{j}})\int_{r\in I_{j}^{x}}{\text{d}r}}:x\in \mathcal{D} \right\} \\ &\text{s}\text{.t}\text{. }对任意邻居x, {x}', 任意i\in \{t-1, t\}满足 \\ &\text{ }I_{i}^{x}\cap I_{t}^{{{x}'}}\ne \varnothing, 有{{z}_{i}}-{{z}_{t}}\le 1 \\ \end{align} \right\} $

(7)

集合序列{I^x:x∈ $\mathcal{D}$}是优化问题(3) 的极小集合序列, 但并不一定是优化问题(3) 的最优集合序列.经过本节的研究已经发现:对线性查询问题, $z_{t}^{x}=-t, t\in \mathbb{N}, x\in \mathcal{D}$是(3) 的最优质量序列.现在来研究对$z_{t}^{x}=-t, t\in \mathbb{N}, x\in \mathcal{D}$寻

找最优的集合序列, 即, 满足优化问题(8) 的最优解.

$ \left. \begin{align} &\underset{{{\mathcal{R}}^{x}}:x\in \mathcal{D}}{\mathop{\arg \min }}\, \left\{ \frac{\sum\limits_{i=0}^{\infty }{\exp }(-\varepsilon i)\int_{r\in \mathcal{R}_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}}{\sum\limits_{j=0}^{\infty }{\exp }(-\varepsilon j)\int_{r\in \mathcal{R}_{j}^{x}}{\text{d}r}}:x\in \mathcal{D} \right\} \\ &\text{s}\text{.t}\text{. }对任意邻居x, {x}', 任意i, j\in \mathbb{N}满足 \\ &\text{ }\mathcal{R}_{i}^{x}\cap \mathcal{R}_{j}^{{{x}'}}\ne \varnothing, 有|i-j|\le 1 \\ \end{align} \right\} $

(8)

我们从极小序列{I^x:x∈ $\mathcal{D}$}出发来构造最优集合序列{$\mathcal{R}$^x:x∈ $\mathcal{D}$}.现在对极小集合序列{I^x:x∈ $\mathcal{D}$}进行调整以减小目标函数.根据引理2及引理3的结论, 可将单位球{r∈ $\mathit{\mathbb{R}}$ⁿ:||f(x)-r||_p≤1}中的点添入$I_{0}^{x}$ (也就是增加了单位球中点的输出概率)以减小目标函数值.但由于$I_{t}^{x}=\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{I_{t-1}^{{{x}'}}}\backslash A_{t-1}^{x}, t>0 $, 对集合$I_{0}^{x}$的改变会导致$I_{t}^{x}, t>0$相应的变化.这些因素综合的结果对目标函数的增减影响难以用简单的分析判断出来.因此, 我们设置一个参数δ, 通过解决一个优化问题来决定将哪些点添入$I_{0}^{x}$中.设$\mathcal{R}_{0}^{x}=\{r\in {{\mathbb{R}}^{n}}:\|f(x)-r{{\|}_{p}}\le \delta \}, \mathcal{R}_{i}^{x}=\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{\mathcal{R}_{i-1}^{{{x}'}}}\backslash \bigcup\nolimits_{j=0}^{i-1}{\mathcal{R}_{j}^{x}}$, 我们需要找到最优的δ, 使得目标函数达到最小.与集合序列{I^x:x∈ $\mathcal{D}$}类似, 集合序列{$\mathcal{R}$^x:x∈ $\mathcal{D}$}也有类似于引理1的性质, 如引理4所示.引理4的证明与引理1的证明类似, 在此不再详述.

引理4.对任意的邻居x, x'∈ $\mathcal{D}$, 及对任意的|t-s| > 1, 有$\mathcal{R}_{t}^{x}\cap \mathcal{R}_{s}^{{{x}'}}=\varnothing 且\mathcal{R}=\bigcup\nolimits_{i=0}^{\infty }{\mathcal{R}_{i}^{x}}.$

根据引理4及优化问题(8), 可构造无约束优化问题(9), 以求解参数δ:

$ \underset{\delta }{\mathop{\arg \min }}\, \frac{\sum\limits_{i=0}^{\infty }{\exp }(-\varepsilon i)\int_{r\in \mathcal{R}_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}}{\sum\limits_{j=0}^{\infty }{\exp }(-\varepsilon j)\int_{r\in \mathcal{R}_{j}^{x}}{\text{d}r}} $

(9)

5.1 小结

下面就概率密度族{($\mathcal{Q}$^x, $\mathcal{R}$^x):x∈ $\mathcal{D}$}对优化问题(5) 的近似最优性进行分析, 其中,

$ \mathcal{R}_{0}^{x}=\{r\in \mathcal{R}:d(f(x),r)\le {{\delta }^{*}}\},\mathcal{R}_{i}^{x}=\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{\mathcal{R}_{i-1}^{{{x}'}}}\backslash \bigcup\nolimits_{j=0}^{i-1}{\mathcal{R}_{j}^{x}},z_{i}^{x}=-i,i\in \mathbb{N},x\in \mathcal{D}. $

δ^*为优化问题(9) 的最优解.由于δ^*是通过求解优化问题(9) 来找到的, 因此$\mathcal{R}_{i}^{x}$是这种递归构造序列中最优的集合序列.又因为$z_{i}^{x}=-i, i\in \mathbb{N}, x\in \mathcal{D}$是满足不等式$z_{i}^{x}-z_{j}^{{{x}'}}\le 1, |i-j|\le 1且\mathcal{R}_{i}^{x}\cap \mathcal{R}_{j}^{{{x}'}}\ne \varnothing $的最大间距的序列, 若将一些点集从$\mathcal{R}_{j}^{x}$转入$\mathcal{R}_{i}^{x}$, j > i, 这样就会增大该点集出现的概率, 从而增大目标函数.若将一些点集从$\mathcal{R}_{i}^{x}$转入$\mathcal{R}_{j}^{x}$, j > i, 则就会使得差分隐私不等式约束不满足.并且对任意邻居数据集x, x', 密度函数($\mathcal{Q}$^x, $\mathcal{R}$^x)与($\mathcal{Q}$^x', $\mathcal{R}$^x')在所有点集$\mathcal{R}_{i}^{x}\cap \mathcal{R}_{i-1}^{{{x}'}}$都达到了差分隐私不等式$z_{i}^{x}-z_{i-1}^{{{x}'}}\le 1$的边界.综上所述, 概率密度族{($\mathcal{Q}$^x, $\mathcal{R}$^x):x∈ $\mathcal{D}$}是优化问题(5) 的一个近似Pareto最优解.

现在将线性函数相关的最优机制问题归纳为如下的结论.

定理2.设假设1成立.设f: $\chi \to {{\mathit{\mathbb{R}}}^{n}}$是任意线性查询函数, 则其关于优化问题(2) 的一个近似Pareto最优解为{p^x=($\mathcal{Q}$^x, $\mathcal{R}$^x):x∈ $\mathcal{D}$}, 其中,

$ {{\mathcal{Q}}^{x}}=\{z_{i}^{x}=-i:i\in \mathbb{N}\},{{\mathcal{R}}^{x}}=\{\mathcal{R}_{i}^{x}:i\in \mathbb{N}\},\mathcal{R}_{0}^{x}=\{r:\|r-f(x){{\|}_{p}}\le \delta *\},\mathcal{R}_{i}^{x}={\bigcup\nolimits_{{x}'\in {{\mathcal{N}}^{x}}}{\mathcal{R}_{i-1}^{{{x}'}}}}/{\bigcup\nolimits_{j=0}^{i-1}{\mathcal{R}_{j}^{x}}}\; $

及

$ {{\delta }^{*}}=\underset{\delta }{\mathop{\arg \min }}\,\frac{\sum\limits_{i=0}^{\infty }{\exp }(-\varepsilon i)\int_{r\in \mathcal{R}_{i}^{x}}{\|f(x)-r{{\|}_{p}}\text{d}r}}{\sum\limits_{j=0}^{\infty }{\exp }(-\varepsilon j)\int_{r\in \mathcal{R}_{j}^{x}}{\text{d}r}}. $

注释:本文使用先实现差分隐私再提高有用性的策略来达到隐私和有用性之间的权衡.首先, 我们寻找实现差分隐私所需设置的最小点集.具体说来, 对数据集x, 我们将x的邻居集对应的函数值的集合设置为$I_{1}^{x}$, 而$I_{0}^{x}=\{f(x)\}$.依此类推, $I_{i}^{x}$包含了$I_{i-1}^{x}$对应的数据集的邻居集合的函数值(需要去掉一些与前面集合的重复点).这样, 我们只需要让$I_{i}^{x}$集合中的点与$I_{i-1}^{x}$集合中的点的密度函数值满足差分隐私不等式就可以实现差分隐私了.这种实现差分隐私的方法称为最小点集实现法.在实现差分隐私的基础上, 我们接着来提高机制的有用性, 这通过引入一个f(x)的δ邻域来实现.具体思路是, 让f(x)附近的点获得较高的密度函数值.这就是构造集合序列$\{\mathcal{R}_{i}^{x}:i\in \mathbb{N}\}$的原因.这种将差分隐私实现机制通过拆分、组合的方式来实现的方法, 可以更精确地对隐私和有用性进行权衡, 相关实验也证明了这种方法的合理性.

不过, 需要说明的是, 本文的方法没能实现真正意义上的机制最优性.最优机制需要找到一个密度函数族{p^x(r):x∈ $\mathcal{D}$}, 其比其他任何密度函数族都具有更好的数据有用性, 而每个密度函数族都具有无穷多条密度函数.这是一个非常复杂的泛函优化问题, 且是否存在这种真正意义上的最优机制现在还有疑问.这也是本文以一种近似最优而非最优来限定本文最优性的意图, 文献[18]中的不合理结论也充分说明了这个问题.关于差分隐私最优机制的存在性及如何合理定义差分隐私机制最优性, 还需要进一步的研究.

6 实例分析

本节通过实际例子来解释本文的方法并分析其性质.

设f: $\chi \to \mathit{\mathbb{R}}$为线性查询函数.对数据集x∈ $\mathcal{D}$, 设 $\mathcal{N}$^x是x的所有邻居的集合, 则$\mathcal{N}$^x对应的函数值的集合为{f'∈(x):x'∈$\mathcal{N}$^x}=f(x)±{f(y):y∈ $\chi $}.记$\mathcal{V}$={f(y):y∈$\chi $}, 则集合$\mathcal{V}$由该查询函数唯一确定.我们称$\mathcal{V}$为查询函数的邻居集, 我们下面研究集合$\mathcal{V}$的结构对查询结果的影响.显然, $\mathcal{V}$对应查询函数的局部敏感度和全局敏感度都相同, 且等于$\mathcal{V}$中最大元素和最小元素相差的值, 即$\Delta f={{\max }_{a, b\in \mathcal{V}}}|a-b| $.本文的算法试图通过研究$\mathcal{V}$的内部结构来达到构造低噪声差分隐私机制的目的.

考虑$\mathcal{V}$是两个不同区间并的情形, 即$\mathcal{V}$ =[a, b]∪[b, c], 其中, 0 < a < b < c.显然, 敏感度Δf=c且$\mathcal{V}$的Lebesgue测度μ($\mathcal{V}$)=a+c-b.我们试图通过对a, b, c赋以不同的值, 从而控制Δf及μ($\mathcal{V}$)的值, 然后研究其对噪声复杂度的影响.对本节的特例, 本文构造差分隐私机制的算法见算法1所示, 其输出f(x)=0对应数据集x的密度函数.对应密度函数给所有$\mathcal{R}$_i中的点赋以相同的密度值p_i(r)=exp(-iε)/α.

算法1.生成概率密度函数.

输入:3个递增的正实数a, b, c, 正实数δ及ε, 迭代次数n;

//设集合序列{$\mathcal{R}$_i:i∈ $\mathbb{N}$}在第n步后收敛;

输出:概率密度函数{(p_i(r), R_i):i∈$\mathbb{N} $}.

步骤1:设置I₀={0};

步骤2://计算集合序列I_i

For i=1 to n{

  对每个区间[s, e]∈I_i-1 {

  将4个区间[s, e+a], [s+b, e+c], [s-a, e], [s-c, e-b]存入集合I_i中;

  }

  计算${{I}_{i}}={{I}_{i}}-\bigcup\nolimits_{j=0}^{i-1}{{{I}_{j}}}$; //去掉I_i中与前面集合重复点集;

}

步骤3: //计算集合序列$\mathcal{R}$_i

For i=0 to n {

  对每个区间[s, e]∈I_i {

  将区间[s-δ, e+δ]存入集合$\mathcal{R}$_i中;

  }

  计算${{\mathcal{R}}_{i}}={{\mathcal{R}}_{i}}-\bigcup\nolimits_{j=0}^{i-1}{{{\mathcal{R}}_{j}}}$; //去掉$\mathcal{R}$_i中与前面集合重复点集;

}

//设$\mathcal{R}$_n={[-a_n, -Δf, -a_n], [a_n, a_n+Δf]}

步骤4:计算$sum1=\sum\limits_{i=0}^{n}{\exp (-i\varepsilon )\mu ({{\mathcal{R}}_{i}})}$及sum2=2Δf*exp(-ε(n+1))/(1-exp(-ε));

步骤5:计算α=sum1+sum2;

步骤6:设置p_i(r)=exp(-iε)/α, 其中, r∈R_i, i∈$\mathbb{N} $;

步骤7:Return {(p_i(r), R_i):i∈$\mathbb{N} $}.

算法1需要下面的集合序列收敛性质:

定义2.设$\mathcal{R}$ =$\mathit{\mathbb{R}}$.对数据集x∈ $\mathcal{D}$, 称集合序列{$\mathcal{R}$_i:i∈$\mathbb{N} $}在第n∈$\mathbb{N} $步收敛, 如果存在a_n∈ $\mathcal{R}$, 有:

$ {\mathcal{R}_{n}}=\pm ({{a}_{n}}+[0,\Delta f])且{\mathcal{R}_{n}}_{+1}=\pm ({{a}_{n}}+[\Delta f,2\Delta f]). $

我们的实验设计如下:首先, 计算算法1生成的密度函数的数学期望值$ mean=\sum\limits_{i=0}^{\infty }{{{p}_{i}}}\times \int_{r\in {{\mathcal{R}}_{i}}}{r\mu (\text{d}r)};$然后, 与Laplace机制^[27]的期望值Δf/ε及Staircase机制^[18]的期望值Δf×exp(ε/2)/(exp(ε)-1) 进行比较, 越小的期望值代表噪声复杂度越低.由于发现Staircase机制的期望值比Laplace机制的期望值小, 因此, 本实验只比较mean与Staircase机制期望值Δf×exp(ε/2)/(exp(ε)-1) 的大小, 即rate=mean×(exp(ε)-1)/(Δf×exp(ε/2)).rate值小于1, 代表算法1对应机制优于Staircase机制; 反之, 则差于Staircase机制.

我们构造两组实验:第1组使用相同的敏感度及不同的函数邻居集测度, 第2组使用不同的敏感度及相同的函数邻居集测度.第1组实验有4个不同的查询函数f₁, f₂, f₃, f₄, 其邻居集分别为$\mathcal{V}$ ₁=[0, 1]∪[1000, 1001], $\mathcal{V}$₂=[0, 100]∪[1000, 1001], $\mathcal{V}$₃=[0, 500]∪[1000, 1001], $\mathcal{V}$₄=[0, 1001].4个不同集合可以理解为4个不同单位的工资分布情况:$\mathcal{V}$₁代表了工资两级分化极其严重的单位; $\mathcal{V}$₄代表了该单位的工资虽然最高工资和最低工资差距很大, 但是高中低档工资都可以出现; 其他两个集合代表了折中的情形.实验结果如图 1所示.

图 1的4个子图分别代表了$\mathcal{V}$₁, $\mathcal{V}$₂, $\mathcal{V}$₃, $\mathcal{V}$₄的实现效果图.其中, 横坐标表示δ的取值, 纵坐标表示ε的取值, 坐标点(δ, ε)对应的值表示相应的rate的值.从图 1可以发现:随着邻居集测度μ($\mathcal{V}$_i)的增大, rate的值相应增大, 从而说明算法1中机制的优势是随μ($\mathcal{V}$_i)的增大而递减的.

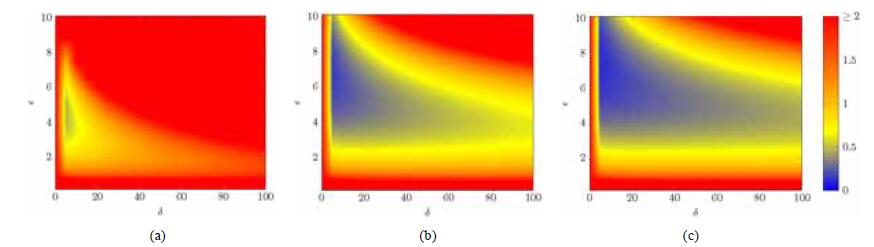
第2组实验有3个查询函数, 其邻居集分别为$\mathcal{V}$₅=[0, 1]∪[100, 101], $\mathcal{V}$₆=[0, 1]∪[1000, 1001], $\mathcal{V}$₇=[0, 1]∪[2000, 2001].显然, 3个函数的全局(及局部)敏感度分别为101, 1001, 2001, 但有相同的邻居集测度μ($\mathcal{V}$_i)=2.其实验结果如图 2所示.

图 2的3个子图分别代表了$\mathcal{V}$₅, $\mathcal{V}$₆, $\mathcal{V}$₇的实现效果图.与图 1一样, 每个子图中坐标点(δ, ε)对应的值表示相应的rate的值.从图 2可以发现:当敏感度增加的时候, 算法1中机制的噪声复杂度要比Staircase机制的复杂度相对越来越小.也就是说:在函数邻居集的测度不变化的条件下, 随着敏感度的增加, 算法1中机制的噪声复杂度要比Staircase等敏感度方法的噪声复杂度越来越小.

综合图 1、图 2的结果, 我们可以得到如下的结论:若查询函数的邻居集V的敏感度Δf与其测度μ($\mathcal{V}$)的比率Δf/μ($\mathcal{V}$)越来越大时, 敏感度方法将添加越来越大的噪声.而本文的方法会极大地降低这个比率带来的噪声复杂度升高的问题, 这也是本文的方法优于敏感度方法的最显著特征.

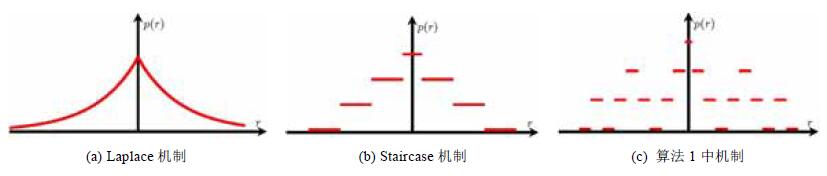
Laplace机制、Staircase机制及算法1中机制的密度函数如图 3所示.图 3(c)的密度函数与前两个密度函数的显著区别是:密度函数并不是从中心向两边递减的, 而是总体递减, 但是局部有增的密度函数.这种密度函数更适合于Δf/μ($\mathcal{V}$)很大的情形, 因为其波浪状形态可以不受全局敏感度的限制而更适合于邻居集的(不同查询函数的)多变特性.

算法2是算法1生成的密度函数的随机变量生成算法.

算法2.生成随机变量.

输入:敏感度Δf、迭代次数n、{ $\mathcal{R}$_i:i∈{0, 1, …, n}}、a_n、α=sum1+sum2;

//设$\mathcal{R}$_n={[-a_n, -Δf, -a_n], [a_n, a_n+Δf]}, 即, 算法从第n步后收敛;

输出:随机变量X.

步骤1:以exp(-iε)μ($\mathcal{R}$_i)/α的概率输出i, i∈{0, 1, …, n}; 以概率sum2/α输出n+1;

步骤2:If步骤1输出值i∈{0, 1, …, n} then

  在$\mathcal{R}$_i中均匀抽样出一个数x;

    Return x;

  Else

    从参数为1-exp(-ε)的几何分布中抽样出一个整数j;

    从[-a_n-(j+1)Δf, -a_n-jΔf]∪[a_n+jΔf, a_n+(j+1)Δf]中均匀随机抽样出一个数y;

    Return y;

6.1 时间复杂度

算法1和算法2的时间复杂度由集合序列{ $\mathcal{R}$_i:i∈$\mathbb{N} $}的收敛性决定.本节的例子中, 该序列都在2 200步内达到了收敛.但是对一般线性查询函数, 我们还没能有方法证明其一定在有限步内收敛.不过, 我们相信这个结论是对的.

若{ $\mathcal{R}$_i:i∈$\mathbb{N} $}在第n步收敛, 且max_{i∈{0, 1, …, n}}N_i=N, 其中, N_i是$\mathcal{R}$_i中区间的个数, 则算法1的时间复杂度为O(n²×N²), 算法2的时间复杂度为O(n).

7 结论

传统的观点认为, 查询函数的(全局或局部)敏感度是查询函数噪声复杂度的(最主要)标志.本文的结论发现:敏感度其实只是查询函数的邻居集$\mathcal{V}$^x的一个极值特征, 还有很多敏感度无法刻画的特征(如该集合中点的分布).本文的方法可根据$\mathcal{V}$^x中点的分布情形, 构造适合于该分布的差分隐私机制, 相应的密度函数类似于图 3(c)所示.与敏感度方法(如图 3(a)、图 3(b)所示)不同, 本文机制的密度函数不是(向两边)全局递减的, 而是以局部有起伏的方式(向两边)递减的, 这种递减方式更具灵活性, 更适合于$\mathcal{V}$^x中点的不规则分布情形.

第6节的实际例子也说明, 本文的方法一般要比Laplace机制及Staircase机制更精确.但是本文的方法具有很高的时间复杂度, 不适合于直接使用在大数据集上.如何通过本文的方法和结论构造低时间复杂度的非敏感度方法, 将作为未来的一项工作.

另外, 本文的很多分析方法和结论(如第3节、第4节中的内容都没有设定函数类型)也可对非线性查询问题^{[15, 16, 34-36]}进行分析, 因为非线性查询问题具有更加复杂的邻居集.至于其分析有效程度如何, 还需要进一步探索.非线性查询问题将具有更加复杂的最优机制, 不同数据集将对应形状各异的密度函数, 对非线性函数的非敏感度机制研究将作为未来的另一项工作.

致谢 本文作者感谢匿名审稿专家对本文初稿提出的宝贵建议和意见, 这些建议和意见对本文的完整性及易读性有很大的帮助.同时, 这些建议和意见促使我们发现了初稿中的一个证明错误.