2. 武汉大学 计算机学院, 湖北 武汉 430072;
3. 武汉大学 国际软件学院, 湖北 武汉 430072;
4. 云南大学 信息工程学院, 云南 昆明 650091
2. Computer School, Wuhan University, Wuhan 430072, China;
3. International School of Software, Wuhan University, Wuhan 430072, China;
4. School of Information Science and Engineering, Yunnan University, Kunming 650091, China
近年来, 随着互联网的兴起, 由此形成的可观测社会网络为研究信息传播、疾病扩散等现象提供了前所未有的平台和机遇.其中, 受舆情控制、病毒式营销、疾病预防等应用的驱动, 影响最大化问题受到广泛的关注[1-4].该问题旨在从给定的网络中寻找一组有限子集, 并根据影响的级联传递, 使得该子集的影响力传播最大.目前, 现有研究大都以实体点(如个人或博客)为分析对象, 并基于点的影响关系, 设计算法搜索最具影响力的k-点组合[3-12].但在很多现实场景下, 人们往往更关注团体(如各类人群、社区等)组合的影响力而并非点组合的影响力.
一个关注于团体影响力的典型例子是:埃博拉病毒在非洲蔓延, 世界卫生组织有限的资源建立k个防疫站.由于防疫站针对的是一个地区的所有居民, 为达到全局最佳的防疫效果, 世界卫生组织希望找出期望传染力最强的k个区域(而不是针对k个居民)建立防疫站.在此, 区域传染力可抽象为团体的影响力.类似情况还大量出现在户外广告、电视营销等场景中.由此可见, 团体影响力的研究具有广泛的现实意义.本文研究了团体影响最大化问题, 即给定大小k, 在网络中寻找k个团组成的集合(简称为k-团体组合), 使其影响力传播最大.
通常, 一个团体的影响力可视为其内所有“感染”(或采纳谣言、购买产品等)点的影响力之和.因此, 我们可以依据点的影响力对团体影响力进行估计, 并简单扩展现有点影响最大化方法求解团体影响最大化问题.然而, 点影响力估计需要非常高的代价, 以至于在使用该方法解决由大量点组成的团体影响传播问题时存在明显的效率缺陷.例如, 依据传统的传播模型(如独立级联模型[3]), 在一个仅仅由72万个点组成的网络中寻找20个最有影响力的点就需要数天时间[5].方法效率的低下不仅会增加硬件的投入, 而且不适用于诸如疾病防疫等具有时效性的应用.此外, 点影响最大化方法需要以点影响关系作为输入, 但在多数情况下, 我们仅能观测到点的状态而不能观测点的相互影响.例如, 防疫站可以判断某人是否染病, 但并不能确定他受谁传染.综上所述, 面向点影响的最大化方法从效率和应用实际上来看, 不能很好地解决团体影响最大化问题.
为了避免点分析法的局限性, 我们可以将团体看作整体, 通过建立团体粒度上传播模型来解决该问题.由于网络中团体的数量远少于点的数量, 这种粗粒度的分析策略将显著提高运行效率.然而, 团体粒度传播模型的建立面临以下两个方面的挑战.
(1) 首先, 团体间的影响本质上是团体间点的影响, 而粗粒度上点影响关系的不可见, 使得团体间影响存在不确定性.例如, 在点粒度上(如图 1(a)所示), 我们可以根据点影响关系(图中边)看出, 团体B中的点{b1, b2, b3, b4}受A影响, 而{b5, b6}受C影响, 所以A, C对B的总影响分别为4和2, 但在团体粒度上(如图 1(b)所示), 点影响关系的遗失使我们不能确定B中的“感染”点(如b1)是受A或受C影响, 从而难以通过计数计算A, C分别对B的总影响.

|
Fig. 1 An example of influence relationship of nodes 图 1 点影响关系实例 |
(2) 其次, 作为点的集合, 团体可被多个邻居同时影响且状态为连续取值, 例如, 团体A中有30%的点感染.该特性使得在动态模拟团体影响传递时, 需要建立相对于布尔取值的点来说更复杂的规则来计算影响大小.由此可见, 如何表达团体的不确定性影响, 并描述团体影响传递过程是团体传播模型建立的关键与难点.
为了粗粒度地求解团体影响最大化, 以反映团体影响的不确定性为出发点, 本文用概率关联的形式描述团体影响的不确定性, 并通过对团体历史“感染”数据(见第3.1节)进行统计, 计算得到团体影响的量值, 由此提出了一种基于概率关联的团体传播模型GIC(group influence cascade).特别指出:由于多个团体影响是一种网状的结构, 所以本文定义的概率关联是一种结构化关联.GIC的核心思想是:将同一团体内点看作“感染”概率相同的随机变量, 通过变量集(团体)在历史数据上的条件概率独立描述团体的结构化关联, 进而根据关联强弱推测其间不确定性影响, 并结合团体“感染”程度动态计算团体影响范围.借助于GIC模型, 本文给出了CGIM(cascade group influence maximization)算法快速搜索影响力top-k团体组合.该算法利用了GIC模型的子模性质, 可从理论上保证返回1-1/e的最优解.值得指出的是, 当我们将一个点看作一个团体时, 本文方法同样可以用于解决点影响最大化问题.
本文的主要贡献包括:
(1) 给出了团体影响关联的定义, 并用图结构对关联进行建模;
(2) 基于团体关联图, 给出了动态计算团体影响力的传播模型GIC;
(3) 利用GIC模型影响函数的单调、子模性, 给出贪心算法CGIM搜索影响力k-团组合.
本文第1节介绍相关工作.第2节定义团体影响关联, 并基于关联给出团体传播模型GIC.第3节证明GIC模型上影响函数的子模性, 并提出CGIM算法.第4节验证并对比分析CGIM算法的效率和效果.第5节总结本文工作并探讨未来研究方向.
1 相关工作与本文相关的工作主要有:点影响最大化方法和实体影响建模.因此, 本节将就这两个方面进行简要介绍.
1.1 点影响最大化方法点影响最大化可定义为:根据特定传播模型, 如何从网络中搜寻出一组最具传播力的点集, 其大小为k.该问题被证明是NP-hard的.从模型的角度看, IC模型(independent cascade model, 简称IC)[3]和LT(linear thresholds)[3]模型是目前研究该问题的两种基础模型.而从算法的角度看, 目前主要采用贪心搜索方法[3-7]和启发式搜索方法[8-12]求解该问题.由于本文传播模型的基础是IC模型, 在此, 主要介绍基于IC模型的点影响最大化方法.
● 基于贪心搜索的方法
Kempe等人[3]基于IC模型的子模性质, 利用贪心算法(又名KK算法)来求解该问题.尽管KK算法的效果具有理论保证, 但由于依赖于大量的蒙特卡洛模拟, 该算法的运行十分耗时.此后, Leskovec等人[4]通过延迟点边际收益计算对KK算法进行了优化, 提出基于剪枝的CELF算法.Wang等人[5]利用局部搜索降低KK算法的开销, 并提出了CGA算法.研究结果表明:CELF算法效果好于KK算法, 但依然存在效率低下的问题[5]; CGA算法依赖的社区划分问题其本身就需要耗费大量计算时间[6], 所以它们均无法适用于大规模网络.Borgs等人[7]给出了一种基于随机抽样的RIS算法, 并证明了该算法能够在Θ(k(n+m)logn/ε3)的时间复杂度以1-ε的误差逼近KK算法.TIM算法[8]进一步将时间复杂度降为O((k+l)(n+m)logn/ε2).虽然RIS和TIM已逼近线性时间, 然而这些算法为记录随机抽样结果需要大量的空间耗费, 使其在面对大规模网络时依然存在难以解决的现实问题.作为大量点的集合, 求解团体的最大化问题依赖于非常高效的点最大化方法.但就目前的情况来看, 现有基于贪心搜索的点最大化方法都难以避免种子集规模增加带来的效率或空间开销问题.因此, 使用这些方法求解团体最大化问题并不是一种理想的选择.
● 启发式搜索方法
随着社交网络规模的不断增大, 研究者开始关注在大规模环境下影响最大化的计算问题[9-12].这些工作主要采用启发式算法来提高问题求解的效率和可扩展性, 但不能在理论上保证准确性.例如, Chen等人[9]提出了基于度数的degreeDiscount启发算法; Chen等人[10]根据IC模型上的点影响的局部树结构提出了PMIA算法; IRIE算法[11]根据全局影响力排名算法(influence ranking)计算每个点的影响力排名, 并基于排序值选择最具影响力点.曹等人[12]将网络中K-core的作为影响力较大的种子, 提出了基于K-core的最大化算法.相对于基于贪心搜索的方法来说, 启发式方法比较简单且具有效率优势, 可以在较短时间输出符合其启发规则的团体种子集.但在面对具有整体性质的团体时, 面向点的启发式规则是否能够避免团体内点的影响重叠从而准确估计团体影响力, 依然是个开放性问题.不仅如此, 这些方法大都依赖于点影响关系的获取, 所以如何在点影响关系未知的情况下定位最有影响力的团体, 仍然是一个亟待解决的问题.
1.2 实体影响建模目前, 一些工作开始关注在实体影响关系不可观测的情况下推测实体影响关系.这些工作主要分为点和点集影响关系建模两个方面.
点影响关系建模的方法[13-16]大都基于IC模型, 且一般需要点的历史“感染”状态和时间作为输入.它们大多假设一对“感染”间隔小的点其影响可能性大, 并通过建立概率生成模型从历史数据中发现点的影响关系.例如, Myers等人[13]基于点的历史“感染”时间将点的影响关系推测形式化为凸优化问题, 并基于生存函数(survival function)提出了NETRATE模型.Gomez等人[15]同样基于点的历史“感染”时间提出期望最大化的NETINF模型, 用于发现在网络中最强top-k影响关系.然而, 这些基于点“感染”时间间隔的方法难以用于团体影响建模.原因主要有两点.
1) 同一团体中不同点的“感染”时间存在较大差异, 以至于团体间的“感染”间隔无法被准确量化;
2) 团体状态取值的连续性, 使得概率生成模型难以反映团体状态与影响之间的数量关系, 从而给影响推测带来困难.
关于点集影响关系建模的研究有文献[17, 18].其中, Mehmood等人[17]提出的CSI模型其实质是点影响关系建模方法的扩展.该模型认为, 点集的影响关系即跨集合间点的影响关系.而一个简单的事实是:点集内的点同样会发生影响传递, 所以CSI模型不能准确描述团体影响关系.Hu等人[18]提出了COLD模型, 该模型是一种基于主题分析的团体影响推测方法.然而, COLD模型所表示的影响不能转化为传统影响最大化问题所依赖的图结构, 所以该工作研究的问题实则与本文并不相同.
由第2.1节和第2.2节的分析可知, 现有影响最大化算法和影响建模方法不能很好地用于解决本文研究的问题.由此, 本文将从建模和算法两个层面给出适应于团体影响最大化问题的解决办法.
2 团体影响传播建模本节定义了团体影响关联, 并基于关联给出GIC传播模型.首先, 我们简要介绍方法所依赖的团体历史“感染”数据.
2.1 团体历史“感染”数据在社会网络中, “疾病”的每次出现引起一次传播过程.我们用cl表示第l次“疾病”, 并将网络中总共发生的|C|次“疾病”用集合C={c1…c|C|}表示.当cl∈C传播停止后, 网络中团体集M={m1, …, m|M|}的“感染”程度记为
| Table 1 Historical records 表 1 历史数据 |
| Table 2 Probability computation of pl 表 2 pl概率计算 |
2.2 IC模型
实体影响力的估计依赖于相应传播模型.IC模型作为本文模型的基础, 是一种点传播模型.在该模型中, 点有“未感染”或“感染”两种状态, 且点一旦“感染”则状态不再变化.其具体描述如下.
设S为种子集, G(V, E, P)为社会网络对应的点影响关系图.IC模型将传播划分为T个离散时刻进行模拟:设At为在t时刻的“感染”点集, A0=S.在t+1时刻, 每个点u∈At有唯一一次机会尝试以pu, v的概率激活G中邻居点
从统计的角度来看, 存在影响的团体其间必然存在某种关联, 反之亦然.所以团体影响关系对应的关联是一种结构化关联, 可用图IG(M, I, W)的形式表示, 其中, M, I, W分别表示团体集、影响关联集和关联程度.本节基于H上团体“感染”的概率关系, 给出团体影响关联的定义, 并用图的形式建模.
在“疾病”cl下, 网络中点xj的最终状态(是否“感染”)可认为是cl对xj的不确定性影响造成的, 则xj可视为二元随机变量, 并记xj“感染”cl的概率为pl(xj), “未感染”cl的概率为1-pl(xj).虽然pl(xj)的取值无法获得, 但将同一团体内的点看作同质时[16](简称为同质性假设), 我们可以认为pl(xj)=Hli, 当且仅当xj∈mi(x), 其中, mi(x)表示mi对应的点集.例如, 在某次埃博拉病暴发时, 我们观测到某个区域有10%的居民感染, 那么说明该病有10%的可能“感染”该区域中的任一个居民.由此, 表 1等价于一张表示点“感染”概率的表, 其中, 第l行第i列表示∀xj∈mi(x)“感染”cl的概率.已知点的“感染”概率, 我们可以对cl下点集状态取值的概率进行计算.设点集X={x1, …, xJ}的状态取值为Ex=(x1=e1, …, xJ=eJ).那么在cl∈C下, X以Ex出现的概率为
| $ {p_l}(X = {E_x}) = \prod\limits_{{e_j} = 1}^J {{p_l}({x_j})\prod\limits_{{e_j} = 0}^J {(1-{p_l}({x_j}))} } $ | (1) |
其中, ej为二元变量, ej=1表示xj的状态为“感染”, ej=0表示xj的状态为“未感染”.表 2给出了一个pl(X=Ex)的计算实例.根据公式(1), 在整个“疾病”集C:={c1…c|C|}中, X以状态取值Ex出现的概率为
| $ p(X = {E_x}) = \sum\limits_{l = 1}^{|C|} {{p_l}(X = {E_x})} /|C| $ | (2) |
根据公式(2), 我们可以获得同质性假设下H上点集状态的完备概率空间D.由概率论可知, 点集对的关联可用点集对的概率独立性进行表达.例如, 对于点集X, Y的任意状态取值x, y, 都有p(x, y)=p(y)p(x), 则说明X和Y不存在关联; 反之, 则存在关联.自然地, 作为特定点集, 团体对的关联同样可以用概率独立描述.但值得注意的是, 概率独立并不具有结构化特征, 不能描述团体影响对应的关联图IG.原因是团体影响有直接和间接之分, 而概率独立不能从语义上区别这两种影响所形成的关联.
例1:设X, Y和Z为3个点集, X与Y存在直接影响记为X~Y, 且假设有X~Z~Y, X
定义1.设变量集U={a, b, …}的概率分布为D, 且集合X, Y, Z⊂U.X和Y在分布D上关于Z条件概率独立记作I〈X, Z, Y〉, 其中, I〈X, Z, Y〉是指对于X, Y, Z的任意状态取值x, y, z, 都有p(x, y|z)=p(y|z)p(x|z).特别地, 当Z=∅时, I〈X, Z, Y〉退化为概率独立I〈X, Y〉.
定义1描述变量间的相对独立性.相对独立性的物理含义反映了排除条件变量(Z)的中介作用后, 测试变量(X, Y)的相关性, 即反映了测试变量的直接相关性.所以, 我们可以通过I〈X, Z, Y〉的真值来判断例1中X和Y是否直接相关来获得其间结构化关联:I〈X, Z, Y〉为真, 即说明X
根据信息论理论, 条件互信息熵常用来定量描述变量的条件独立程度.
定义2. X和Y关于Z的条件互信息熵记为Inf((X, Y)|Z), 其中,
| $ Inf((X, Y)|Z) = \sum\limits_{X, Y, Z的所有状态取值} {p(x, y, z){{\log }_2}\frac{{p(x, y|z)}}{{p(x|z)p(y|z)}}} $ | (3) |
Inf((X, Y)|Z)表示Z确定之后, Y与X的互信息熵.Inf((X, Y)|Z)=0表示I〈X, Z, Y〉, 且其值越大, 说明X和Y关于Z的直接关联性越强.特别指出:当Z=∅时, Inf((X, Y)|Z)退化为互信息熵Inf(X, Y).
根据以上论述, 团体直接影响关联的形式化定义如下.
定义3.设M为社会网络G(V, E)上的团体集, 团体mi, mj∈M, mi对应的点集记为mi(x), 且有
我们可以根据定义3构建IG.然而, 这种直观的构建方法不能运用于较大规模的网络.其原因是:定义3中, wij的计算需考虑集合mi(x), mj(x), V-{mi(x), mj(x)}的所有状态取值; 集合的状态取值数是该集合大小的指数倍, 例如, 当网络点数量|V|=n, |mi(x)|+|mj(x)|=a时, V-{mi(x), mj(x)}的状态取值就有2n-a种, 由此可见, wij的计算复杂度为O(2n).为此, 我们将利用同质性假设条件, 通过建立团体关联和单点关联的关系, 给出一种wij的快速计算方法.在介绍我们的方法之前, 我们首先引入条件概率独立相关的数学性质来说明方法的思路.
引理1[19].设X, Y, Z, Q是分布D上两两不相交的变量集, 则I〈X, Z, Y〉满足:
(1) 对称律:I〈X, Z, Y〉⇒I〈Y, ZQ, X〉.
(2) 分解律:I〈X, Z, Y〉∧I〈X, Z, Q〉⇔I〈X, Z, Y∪Q〉.
在同质性假设下, 团体和点的直接影响关联存在如下关系.
定理1. M={m1, …, m|M|}为团体集, X={x1, …, x|M|}为点集, 且xi∈mi(x), i∈1, …, |M|.在同质性假设下, 在历史观测数据H上有ind(xi, xj)=0, 当且仅当ind(mi, mj)=0.
证明:设mi(x)=x1∪…∪xi,
定理1说明点集X和团体M的关联图同构, 所以我们可使用如下的办法快速构建IG(M, I, W).
● 给定一个以团体为节点(为与社会网络G区别, 此处将IG图中的点称为节点)的完全图IG*(M, I, W), 如果在分布D上有Inf(xi, xj)≤ε(其中, xi∈mi(x)), 说明mi, mj独立(不存在关联), 则直接删去边Ii, j;
● 否则, 需根据条件概率独立进一步判断关联类型:如果ind(xi, xj)=0, 则说明在mi, mj不存在直接关联, 删掉该边; 如果ind(xi, xj) > 0, 则说明在mi, mj存在直接关联, 将Ii, j的权值设置为wi, j=ind(xi, xj).
当所有无关联的边被删除后, IG*(M, I, W)即同构于IG(M, I, W).显然, 在该过程中, 我们最多需要|M|(|M|-1)/2次条件独立计算, 且每次计算的复杂性为2|M|.所以在M远小于n的情况下, 该方法可被看作线性时间.算法1用伪码的形式清晰地描述了上述过程.
算法1.团体关联图构建.
输入:团体集M“感染”的历史观测数据D.
输出:团体关联图IG(M, I, W).
1:初始化图IG*(M, I, W)为无向完全图; i←0
2: while ∀xi∈mi and mi.visited=false
3: mi.visited←true
4: for each mi and mj.visited=false //根据条件独立关系删边
If Inf(xi, xj)≥ε
5: if w←ind((xi, xj)|X-(xi, xj)) > 0 //X={x1, …, x|M|}, xj∈mj
6: wij←w
7: else
8: I←I-eij
else
I←I-eij
9: i++
10: return IG*(M, I, W)
2.4 GIC传递规则关联程度越高的团体, 其间点发生影响传递的可能性越高.根据此特征, 本节将基于IG给出一种粗粒度的影响传递规则.
给定团体关联图IG(M, I, W), 记团体m∈M的邻居集为N(m).N(m)将对m产生影响, 且如果团体u, u'∈N(m)有wu, m > wu', m, 那么点xi∈u(x)比xj∈u'(x)有更大可能激活xm∈m.自然地, 我们可以用
| $ {\eta _u}_{ \to m} = {\eta _u}×{p_u}_{, m}×\left( {1-{\eta _m}} \right) $ | (4) |
特别指出, 当u中没有点“感染”(ηu=0) 或m中点已全部被“感染”(1-ηm=0) 时, u对m的传递影响比例为0.
根据公式(4), GIC模型的动态传递规则如下.
GIC将影响传播过程划分为t(t=0, 1, 2, ...)个离散时间片进行模拟.为在G上激活一次传播, t=0时刻, 我们向种子团体集S以广播的方式散布“疾病”, 并假设mi∈S以固定比例Ri“感染”(很多现实场景下, Ri是可以获得的, 例如用户的点击率可被预测).当传播被激活后, S在t > 0时刻将迭代的把影响传递给其邻居, 乃至其邻居的邻居. IC模型约定:t时刻的“感染”点仅在t+1时刻具有“传染”性.类似地, 在动态模拟团体影响传播过程中, 我们将记录团体mi在t时刻“感染”的比例
例2:在图 2中, 设S={a}, l=1, 且
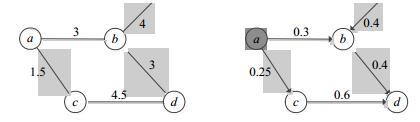
|
Fig. 2 Example of influence diffusion 图 2 影响传播示例 |
● 当t=1时, a将影响邻居b, c.其中,
| $ \begin{array}{c} \eta _b^1 = \eta _{a \to b}^1 = \eta _a^0 \times {p_{a, b}} \times (1-\eta _b^0) = 30\% \times \frac{3}{{3 + 3 + 4}} \times (1-0) = 9\%, \\ \eta _c^1 = \eta _{a \to c}^1 = 30\% \times \frac{{1.5}}{{1.5 + 4.5}} \times (1-0) = 7.5\% . \end{array} $ |
● 在t=2时刻, b, c将共同影响d, 有
可以看出, GIC是IC模型的扩展, 其主要区别有两点.
1) IC模型中点的状态为布尔取值, 最多能够被1个邻居影响, 而GIC模型将节点(团体)状态扩展为连续取值(比例), 能够被多个邻居共同影响.
2) IC模型中点间的影响的用概率表示, 而GIC模型中节点间的影响用激活点数的期望比例表示.
3 团体影响最大化算法基于GIC模型, 本节从算法角度定义了团体影响最大化问题, 并给出了一种贪心算法快速求解该问题.
3.1 问题定义给定网络G上的团体关联图IG(M, I, W), 整数k和团体的初始“感染”率Ri作为输入, 根据GIC模型的模拟传播结果, 在IG中搜索k个团体S⊂M作为种子集, 使其期望的影响范围σ(S)最大.
定理2.团体影响最大化是NP-hard问题.
证明:已知点影响最大化问题是NP-hard.当网络中的每个团体仅包含1个点时, 团体影响最大化即退化为点影响最大化问题, 所以团体影响最大化是NP-hard问题.
由定理2可知, 在P≠NP的假设下, 不存在多项式时间的算法能够得到团体最大化问题的精确解.
3.2 函数子模性与贪心选择定义4(子模性)[21]. F是定义域为集合U的函数, 给定S1, S2为U上的2个子集.F具有子模性, 如果F满足:
F(S1∪{u})-F(S1)≥F(S2∪{u})-F(S2),
其中, u⊂U, S1⊆S2⊆U.
引理2[21].如果一个最优问题的优化目标(函数)F满足单调性和子模性, 那么使用贪心策略求解该问题所获得的结果能够保证返回(1-1/e)的最优.
引理2为近似求解特殊优化问题提供了理论支持.本节通过证明团体最大化问题的影响函数σ(S)满足单调、子模性, 给出了一种具有保证的贪心算法.首先, 我们基于GIC模型给出σ(S)的函数表达式.
在GIC模型中, ∀mj∈V/S能够被S影响, 当且仅当S到mj(在IG中)至少存在1条轨(如果路径u≥v中的顶点各不相同, 则该路径称为u到v的一条轨).记Γ={G1, Γ2, …}为S到mj的轨集, Γq=〈mi=w1, w2, …, wm=mj〉表示Γ中第q条轨, 其中, w1∈S且wu∉S, 2≤u≤m.由此, 我们可基于轨给出一种特殊的树结构(简称为Tr)来辅助分析mj受S影响的大小, 如图 3所示.
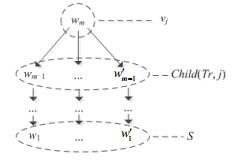
|
Fig. 3 Tr tree 图 3 Tr树 |
在Tr中, mj和S分别作为树的根和叶子, 如果Γq∈Γ中mj的直接前驱为mk, 则mk为mj的儿子节点, 依此类推.
显然, 在Tr中, mj只能被其儿子节点mk∈chlid(Tr, j)直接影响.当不考虑重复激活时, mk对mj的期望影响为ηk→j=ηS→k×pk, j×(1-0).又由于chlid(Tr, j)中团体对mj的影响相互独立, 所以我们可以合并所有chlid(Tr, j)对mj的影响, 得到ηS≥j的递推式:
| $ {\eta _{S \to j}} = \left\{ {\begin{array}{*{20}{l}} {{R_j}, }\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&{{o_j} \in S}\\ {1-\prod\nolimits_{k \in chlid(Tr, j)} {(1-{\eta _{S \to k}} \times {p_{k, j}})}, }&{{o_j} \notin S} \end{array}} \right. $ | (5) |
设|mj|表示mj所包含的点数, 根据公式(5), 影响范围函数σ(S)可表示为
| $ \sigma (S) = \sum\nolimits_{{m_j} \in M} {|{m_j}| \times {\eta _{S \to j}}} $ | (6) |
推论1.影响函数σ(S)具有单调性.
证明:给定IG(V, E, W), S⊆W⊆V.W-S到∀mj∈M的轨集数量|Gw-s|≥0, 所以有Γw⊇Γs, chlid(TrW, j)⊇chlid(TrS, j).我们首先归纳证明ηx≥y的单调性.当mj∈S时, 根据公式(5) 直接有ηW→j=ηS→j=Rj, 所以ηW≥j≥ηS≥j成立.当mj∉S时, 假设对于∀mk∈chlid(TrW, j)都有ηW≥k≥ηS≥k成立.因为chlid(TrW, j)⊇chlid(TrS, j), 对于mj∉S有:
| $ {\eta _{W \to j}} =\\ 1-\prod\nolimits_{k \in chlid(T{r_W}, j)} {(1-{\eta _{W \to k}} \times {p_{k, j}})} \ge 1-\prod\nolimits_{k \in chlid(T{r_S}, j)} {(1 - {\eta _{W \to k}} \times {p_{k, j}})} . $ |
又已假设ηW→k≥ηS→k, 有
推论2. 影响函数σ(S)具有子模性.
为了证明σ(S, T)满足子模性, 我们首先归纳证明ηx≥y满足子模性, 即证:对于任意mi∈M, 有ηS'≥j-ηS≥j≥ηW'≥j-ηW≥j成立, 其中S'=S∪mi, W'=W∪mi, S⊂W.当mj∈S时, 显然有ηS'≥j-ηS≥j=hW'→j-ηW→j=0, 子模性成立.当mj∉S时, 假设对于S的任意前驱mk∈chlid(TW'r, j)都有ηS'≥k-ηS≥k≥ηW'≥k-ηW≥k.根据公式(5) 有:
| $ {\eta _{S' \to j}}-{\eta _{S \to j}} =\\ 1-{p_{k, j}} \times \prod\nolimits_{k \in chlid(T{r_{S'}}, j)} {((1-{\eta _{S' \to k}}) - (1 - {\eta _{S \to k}}))} = \\{p_{k, j}} \times \prod\nolimits_{k \in chlid(T{r_{S'}}, j)} {({\eta _{S' \to k}} - {\eta _{S \to k}})} . $ |
等式两边取对数得
又ηS'→k-ηS→k≥ηW'→k-ηW→k, 有
如上所述, 在假设团体的邻居满足子模性后, 该团体同样满足子模性, 根据归纳法, 有ηx→y满足子模性成立.又已知子模函数的和函数同样是子模的, 所以σ(S)具有子模性.
3.3 CGIM算法根据推论1和推论2, 我们将给出一种贪心算法来快速求解团体影响最大化问题, 具体描述如算法2所示.
算法2. CGIM.
输入:IG(M, I, W), k, R={R1, …, Rn}.
输出: seed set S.
1: S←∅
2: while |S| < k do
3: for each mi in M-S
4:
5: S←S∪mj
6: return S
初始时, CGIM算法将种子集S初始化为空集.每一轮迭代中, 我们以S∪mi作为备选种子, 通过GIC模型估计S∪mi的影响范围σ(S∪mi), 并选取边际影响收益σ(S∪mi)-σ(S)最大的mi加入S.重复此过程, 直到S的大小为k, 则返回.
CGIM算法每次迭代需计算一次所有备选种子的边际收益, 总共k轮迭代, 一共需要O(k×|M|)次.每次边际收益的计算需要通过一次GIC传播模拟过程来确定收益大小.最坏情况下, GIC传播模拟需要遍历IG(M, I, W)中所有点和边, 时间复杂度为O(|M|+|I|).由此, 算法2的总的时间复杂度为O(k×|M|×(|M|+|I|)).由于团体的规模|M|远小于社会网络中点的规模n, 所以该方法时间复杂度相对于n仍可看作线性时间.
4 实验分析● 人工数据集
采用LFR(lancichinetti fortunato radicchi)算法[15]生成的人工网络.特别指出:LFR算法在生成网络的同时, 能够自动给出社区划分基准, 而社区是团体一种自然表现形式, 属于本文研究对象的范畴.LFR算法的关键参数说明如下:n表示模拟网络的点个数, m表示模拟网络的边数, w表示社区数量.在本文实验中, 我们将通过调节算法参数生成多种规模网络来对CGIM算法进行测试, 见表 3.
| Table 3 Experimental network 表 3 实验网络 |
● 真实数据集
采用作者合作网络, 其中, 节点表示作者, 边表示两个作者之间存在合作关系.我们从DBLP中2012年计算机领域的700个期刊或会议中抽取了83 450个作者、343 261条合作关系.为获得该合作网络中的团体划分, 我们视一个期刊或者会议为一个团体, 并将作者划分至投稿次数最高的团体.如, 作者A向会议(或期刊)L1, L2的投稿次数分别为3, 5, 那么A将被划分至L2.
● 历史观测数据集生成
为了获得历史观测数据, 我们将通过以下方式生成.
假定实验网络中点的传播概率p相同.在每次“疾病”传播过程中, 我们从测试网络中随机的选择1%的点作为“感染”点, 并根据IC模型进行影响传播模拟.在传播模拟结束后, 我们记录各个团体的“感染”状态作为一条记录, 并生成多条记录作为本文实验的观测数据集.
为了验证CGIM算法的性能, 我们将在点的粒度上使用多种传统方法求解团体影响最大化问题, 并以此作为对比基准.实验中, 算法的效果好坏可通过各算法输出种子的影响范围(即σ(S), 见公式(6))来评价, 其中, 种子的影响范围越大, 说明算法效果越好.特别指出:为了避免不同传播模型对影响范围估计的差异, 本文将统一在IC模型下对各算法输出种子的影响范围进行计算.由相关工作的分析可知:贪心算法的优势在于选点质量高, 而启发算法的优势在于效率, 所以本文将选取CELF算法、TIM算法和degreeDis算法作为比对算法.
在本文实验中, 我们在不同k值下对比了各算法的影响范围和运行时间.此外, 我们还测试了团体大小、数量对算法的影响.本文程序采用Java编写, 实验环境为Quad-Core 2.0 GHz CPU, 8GB内存的个人电脑.
4.1 实验结果 4.1.1 影响范围对比为了验证网络特征变化对算法效果的影响, 本文首先考虑团体规模的因素, 并分别在团体平均大小不等的人工网络上验证了各算法输出种子的影响范围.
● 由图 4(a)所示, 当团体平均大小Avg-s为25时, CELF, TIM在net1上的影响范围明显高于其他算法, 其次是DegreeDis, CGIM的效果较差.
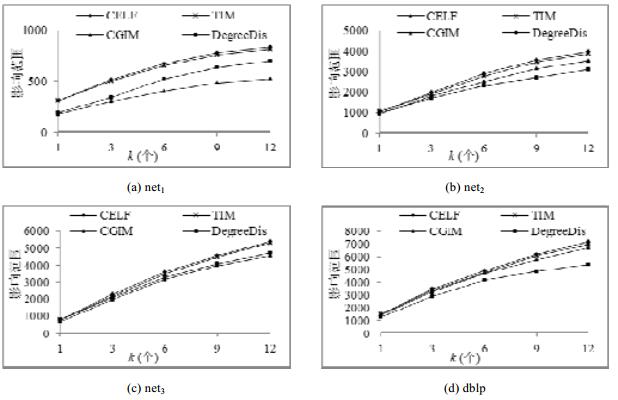
|
Fig. 4 Comparison of influence 图 4 影响力对比 |
● 当Avg-s=50时(如图 4(c)所示), CELF, TIM相对于其他算法的优势逐渐减弱, 而CGIM与DegreeDis的差距被拉近.
● 当Avg-s=100时(如图 4(b)所示), CELF, TIM的影响范围依然保持领先, 但CGIM的表现已明显好于DegreeDis.
由此可见, 团体规模大小对算法效果的影响显著.DegreeDis的影响范围随团体规模的增大出现了下降的原因是:在规模较大的团体中, 度数较高的点之间有很大可能在多跳之后存在较严重的影响重叠, 所以度启发规则的选种策略存在单个种子影响力大而总体影响力小的问题.CGIM的影响范围随团体规模的增大明显增加的原因是:团体中点数越多, 单个点的状态变化对整体的影响就越小, 即在同质性假设下, 点的概率值更贴近团体“感染”比例.所以, 基于GIC更能反映团体的影响关系, 从而间接提高了CGIM选点的质量.此外, 我们还注意到:图 4(a)中, DegreeDis的影响曲线在k=3和k=6之间存在明显跳动.该现象反映了DegreeDis算法存在不稳定的问题. CELF和CGIM的曲线随着k的增大平缓增加, 反映出基于传播模型的算法相对于度启发式算法更具稳定优势.
为了验证CGIM算法的实用性, 我们在DBLP网络上进行对比测试, 如图 4(d)所示.图中显示:CGIM的效果随k变化始终较为贴近CELF, 而DegreeDis在k≥6时效果较差.从各算法曲线的对比观察中可以发现:DegreeDis随着k增大, 其影响范围增长缓慢, 这是该算法效果不佳的主要因素.这是由于DBLP网络中存在较为明显的领域性质, 例如, 同属于数据库领域的Sigmod会议和VlDB会议往往对其领域内的其他会议和期刊同时造成影响.因为属于同一个领域的团体(会议)间往往存在较大的影响重叠, 该特点直接导致了度启发规则的效果不佳.
4.1.2 效率对比图 5(a)~图 5(c)分别显示了在net1, net2, net3上各算法的执行时间.特别指出:由于不同算法的执行时间相差较大, 我们选择对数刻度描述时间轴.实验结果印证了CELF的低效性.如图 5(a)所示, CELF在小规模网络(net1)上选取1个团体种子的时间即为分钟级别, 且随着k的增大, 执行时间增加明显, 效率远远低于TIM, CGIM和DegreeDis; CGIM的效率明显高于CELF, TIM而略低于DegreeDis.这说明当团体数目远小于点的数量时(net1: n=10k, w=0.2k), GIC模型相对于IC模型在估计团体边际收益时的效率优势明显.此外, 我们还注意到, 当k增大时, CGIM的执行时间基本保持不变.这是由于net1中团体数仅为200, 以至于CGIM选择局部最优解所消耗的时间相对于扫描历史观测数据来说基本可以忽略引起的.

|
Fig. 5 Comparison of execution time 图 5 执行时间对比 |
横向对比图 5(a)~图 5(c)我们发现, CGIM执行时间对网络团体数量规模变化敏感.例如, 当团体数同为w=200时, CGIM的执行时间在net2上(如图 5(b)所示)与在net1上(如图 5(a)所示)相比基本无变化, 而在w=2000的net3上(如图 5(c)所示), CGIM的执行时间相对于net1上升了51倍.由此可见, 团体数目对CGIM的效率影响较大.为此, 我们保持点、边规模不变(n=20k, m=50k), 在w={1k, 2k, 3k, 4k, 5k}的网络上进一步验证团体数对CGIM效率的影响.由图 5(d)可知, CGIM在w={1k, 2k, 3k, 4k, 5k}时的执行时间分别为{21, 73, 179, 913, 2445}s.可以看出, CGIM随着团体个数增加, 执行时间成指数级上升.造成该问题的原因是CGIM依赖于团体关联图的构建, 而当团体数量较多时, 计算团体间条件概率独立需要大量的时间开销.由此可得出结论:CGIM算法在团体数目较多的网络上, 效率优势不明显, 相比之下, 更适合处理点数规模较大而团体规模相对较小的网络.
5 结论本文提出并研究了团体影响最大化问题, 通过发现历史“感染”数据中团体的概率关联, 建立了团体传播模型GIC, 由此给出了一种高效的团体最大化算法CGIM.与传统的面向点的影响最大化方法不同的是, 本文方法不依赖于点影响关系的获取, 即可快速定位最有影响力的团体种子集.实验结果表明:当网络中团体数量远小于点数量时, CGIM算法比CELF, TIM算法更高效, 且比degreeDis算法更准确, 适合于处理点数规模较大而团体规模相对较小的网络.
未来可行的研究方向包括以下4个方面.
1) 针对本文团体关联图构建算法(算法1) 不适用于团体数量规模较大网络的问题, 我们将研究如何利用概率性质对关联计算进行剪枝, 从而提高该算法的效率.
2) 本文工作假设团体之间的点互不重叠, 如何在考虑重叠情况下对团体最大化问题进行快速求解, 则是我们试图研究的第2个问题.
3) 我们还将考虑社会网络的动态性, 研究如何在点随时加入、退出团体的情况下求解团体最大化问题.
4) 最后, 我们还将试图给出CGIM的并行版本, 并基于hadoop, spark等平台进一步提高算法的可扩展性.
| [1] | Guille A, Hacid H, Favre C, Zighed DA. Information diffusion in online social networks:A survey. ACM SIGMOD Record, 2013, 42(2): 17–28 . [doi:10.1145/2503792.2503797] |
| [2] | Lü L, Zhang YC, Yeung CH, Zhou T. Leaders in social networks, the delicious case. PloS One, 2011, 6(6): e21202 . [doi:10.1371/journal.pone.0021202] |
| [3] | Kempe D, Kleinberg J, Tardos É. Maximizing the spread of influence through a social network. In:Lise G, Ted ES, Pedro MD, Christos F, eds. Proc. of the Int'l Conf. on Knowledge Discovery and Data Mining. Washington:ACM Press, 2003. 137-146.[doi:10.1145/956750.956769] |
| [4] | Leskovec J, Krause A, Guestrin C, Faloutsos C, VanBriesen J, Glance N. Cost-Effective outbreak detection in networks In:Pavel B, Rich C, Xindong W, eds. Proc. of the Int'l Conf. on Knowledge Discovery and Data Mining. San Jose:ACM Press, 2007. 420-429.[doi:10.1145/1281192.1281239] |
| [5] | Wang Y, Cong G, Song G, Xie K. Community-Based greedy algorithm for mining top-k influential nodes in mobile social networks. In:Bharat R, Balaji K, Andrew T, Qiang Y, eds. Proc. of the Int'l Conf. on Knowledge Discovery and Data Mining. Washington:ACM Press, 2010. 1039-1048.[doi:10.1145/1835804.1835935] |
| [6] | Fortunato S. Community detection in graphs. Physics Reports, 2009, 486(3-5):75-174.[doi:10.1016/j.physrep.2009.11.002] |
| [7] | Borgs C, Brautbar M, Chayes J, Lucier B. Maximizing social influence in nearly optimal time. In:Chandra C, ed. Proc. of the Symp. on Discrete Algorithms. Portland:SIAM, 2014. 946-957. |
| [8] | Tang Y, Xiao X, Shi Y. Influence maximization:Near-Optimal time complexity meets practical efficiency. In:Curtis ED, Feifei L, Özsu MT, eds. Proc. of the Int'l Conf. on Management of Data. Snowbird:ACM Press, 2014. 75-86.[doi:10.1145/2588555.2593670] |
| [9] | Chen W, Wang Y, Yang S. Efficient influence maximization in social networks. In:John FEI, Françoise F, Peter AF, Mohammed JZ, eds. Proc. of the Int'l Conf. on Knowledge Discovery and Data Mining. Paris:ACM Press, 2009. 199-208.[doi:10.1145/1557019.1557047] |
| [10] | Chen W, Wang C, Wang Y. Scalable influence maximization for prevalent viral marketing in large-scale social networks. In:Bharat R, Balaji K, Andrew T, Qiang Y, eds. Proc. of the Int'l Conf. on Knowledge Discovery and Data Mining. Washington:ACM Press, 2010. 1029-1038.[doi:10.1145/1835804.1835934] |
| [11] | Jung K, Heo W, Chen W. Irie:Scalable and robust influence maximization in social networks. In:Zaki MJ, Siebes A, Yu JX, Goethals B, Webb GI, Wu XD, eds. Proc. of 2012 IEEE the 12th Int'l Conf. on Data Mining. Brussels:IEEE Computer Society, 2012. 918-923.[doi:10.1109/ICDM.2012.79] |
| [12] | Cao JX, Dong D, Xu S, Zheng X, Liu B, Luo JZ. A K-core based algorithm for influence maximization in social networks. Chinese Journal of Computers, 2015, 38(2): 238–248 (in Chinese with English abstract). [doi:10.3724/SP.J.1016.2015.00238] |
| [13] | Myers S, Leskovec J. On the convexity of latent social network inference. In:John DL, Christopher KIW, John S, Richard SZ, Aron C, eds. Proc. of the Neural Information Processing Systems. Vancouver:Curran Associates, Inc., 2010. 1741-1749. |
| [14] | Gomez-Rodriguez M, Balduzzi D, Schölkopf B. Uncovering the temporal dynamics of diffusion networks. In:Lise G, Tobias S, eds. Proc. of the Int'l Conf. on Machine Learning. Washington:Omni Press, 2011. 561-568. |
| [15] | Gomez Rodriguez M, Leskovec J, Krause A. Inferring networks of diffusion and influence. In:Bharat R, Balaji K, Andrew T, Qiang Y, eds. Proc. of the Int'l Conf. on Knowledge Discovery and Data Mining. Washington:ACM Press, 2010. 1019-1028.[doi:10.1145/2086737.2086741] |
| [16] | Gomez Rodriguez M, Leskovec J, Schölkopf B. Structure and dynamics of information pathways in online media. In:Stefano L, Alessandro P, Paolo F, Aristides G, eds. Proc. of the 6th ACM Int'l Conf. on Web Search and Data Mining. Rome:ACM Press, 2013. 23-32.[doi:10.1145/2433396.2433402] |
| [17] | Mehmood Y, Barbieri N, Bonchi F, Ukkonen A. CSI:Community-Level Social Influence Analysis. Springer-Verlag, 2013: 48–63 . [doi:10.1007/978-3-642-40991-2_4] |
| [18] | Hu Z, Yao J, Cui B, Xing E. Community level diffusion extraction. In:Timos KS, Susan BD, Zachary GI, eds. Proc. of the Int'l Conf. on Management of Data. Melbourne:ACM Press, 2015. 1555-1569.[doi:10.1145/2723372.2723737] |
| [19] | Pearl J. Probabilistic Reasoning in Intelligent Systems:Networks of Plausible Reasoning. Morgan Kaufmann Publishers, 1988: 84–86 . http://www.mendeley.com/catalog/probabilistic-reasoning-intelligent-systems-networks-plausible-inference/ |
| [20] | Roughgarden T, Tardos E, Vazirani VV. Algorithmic Game Theory. Cambridge: Cambridge University Press, 2007: 648-651. |
| [21] | Nemhauser GL, Wolsey LA, Fisher ML. An analysis of approximations for maximizing submodular set functions-Ⅰ. Mathematical Programming, 1978, 14(1): 265–294 . [doi:10.1007/BF01588971] |
| [12] | 曹玖新, 董丹, 徐顺, 郑啸, 刘波, 罗军舟. 一种基于k-核的社会网络影响最大化算法. 计算机学报, 2015, 38(2): 238–248. [doi:10.3724/SP.J.1016.2015.00238] |
 2017, Vol. 28
2017, Vol. 28


