软件可靠性工程为高质量软件系统的开发和应用带来了前所未有的机遇.在最近几十年, 数量激增的软件系统开发出来, 为用户提供了极大的便利.随着这些软件系统日益成熟和复杂, 其可靠性评估被定义为在一定条件和特定时间下无故障运行的概率^[1], 成为开发商预测系统行为的关键和艰巨任务.

软件可靠性增长模型(software reliability growth model, 简称SRGM)使用故障检测时间或在特定时间内的故障数来评价系统的可靠性.故障检测过程被普遍认为是一个非齐次泊松过程(NHPP)^[2-6], 并对故障检测率(fault detection rate, 简称FDR)有不同的假设.Goel等人^[7]扩展了Jelinsky和Moranda^[8]的早期工作, 并提出了经典指数SRGM, 俗称为Goel-Okumoto模型(G-O模型).一些学者^[9-13]随后断言G-O模型无法准确模拟故障检测的动态过程; 取而代之, 他们提出一个依赖时间的FDR来反映其随时间光滑/规律的变化.SRGM包括延迟型模型^[9]、拐点S形模型^[10], 包括工作量方程的SGRM^[11]和扩展的具有变化点功能的G-O模型.总而言之, 大多数模型假定软件测试检测到的累计故障数和检测时间存在一个确定的关系.

然而, 在不确定性环境中, 上述假设FDR为确定性的假设不再有效.在实际软件开发过程中, FDR随着环境、人员和资源的变化而变化, 而且未知突然变化, 即不确定变化, 从而显著影响传统故障检测模型.为了应对这些挑战, 1994年, Yamada等人^[14]首次将不确定性干扰因素建模为白色噪音, 提出了新的模型(白色噪音模型), 也是最早使用白色噪音的模型.随后的大多数随机NHPP类模型都是在此基础上扩展的.这些模型一般将环境的集体因素描述为白色噪音, 即马尔可夫噪音.与传统模型相比, 这种假设噪音具有马尔可夫性的方法毫无疑问地通过采用简单的数学方法使模型更接近现实.而在实践中, 噪音出现非马尔可夫性是普通现象, 而噪音呈现马尔可夫性仅仅是例外^{[15, 16]}.在许多真实情况下, 白色噪声的理想化假设是不足的:真正的不规则因素总是相关性的, 且相应的随机波动通常为相关性噪声.这类相关性噪声符合非马尔可夫随机过程.在实际应用中, 多个不具有可加性的相关性噪音是不可避免的.例如, 来自环境等诸多干扰信号^[16].故障检测过程中的FDR从时域上看在任意两个相邻时刻的状态是相关的, 即非马尔可夫噪音, 使得FDR呈现为非马尔可夫相关性噪音.而只有更贴近实际的量化不确定性干扰因素, 才能建立更贴近实际的软件可靠性模型, 也才能更真实地描述故障检测过程, 并计算软件可靠性和相关的性质.

在本文中, 我们提出了用一个替代的随机框架来描述故障检测过程的模型, 并且考虑了环境干扰因素的影响, 将其建模为任意分布和时间相关性的噪音.第1节介绍研究现状.第2节对新的随机模型进行详细说明.第3节通过4组历史数据验证我们的方法并与传统方法进行比较.最后的结论在第4节中给出.

到目前为止, 各种NHPP类SGRM提出用以描述故障检测过程, 进而评估系统可靠性.基于Jelinsky和Moranda^[8]的早期工作, Goel和Okumoto提出了一个指数型的软件可靠性模型(G-O模型).模型假定检测到的故障的均值与剩余的故障数是成比例的, 并且故障检测率FDR是一个恒定的数.这种模型提供了一类数学简化方法, 不过, 鉴于软件测试过程的复杂性, 这种常数的FDR过于简化了故障检测过程的动态特征.

为了解决这个问题, 平稳变化的FDR被结合到后来的模型中.Yamada等人^[9]发现, 故障检测率符合S型生长曲线, 并提出了延迟的S形的软件可靠性增长模型.采用软件故障检测过程中的学习现象, Ohba^[10]后来提出了另一个S形的拐点的软件可靠性增长模型.Yamada等人^[11]进一步将工作量函数与检测故障数的关系相结合集成到模型中.总体而言, 平稳变化的FDR的假设在一定程度上符合观察结果, 并在许多测试情况下显示了预测的有效性和准确性.

除了测试工作量, 许多其他因素, 如工作资源的分布、策略和运行环境等, 都会影响故障检测过程, 因此, 软件FDR可能呈现规律性变化^[17].Huang等人^[13]指出, 软件故障检测与修复过程在开发与运行中是不同的.他们提出将统一理论和多重因素一起合并到NHPP类SRGM中, 并发现FDR在检测过程中的平稳变化特征.Zhao等人^[18]将环境因素纳入其模型中.考虑到故障检测和修正的时间延迟, Huang等人^[12]提出了有限和无限的排队论的不完美软件可靠性增长模型.后来, Huang等人^[19]还使用多个变化点来处理不完美的调试问题.软件FDR呈现规律性变化的可靠性模型是早期模型的改进^[20-22], 它们通过改变点前后两个不同的FDR来描述故障点前后的环境变化.换句话说, 当环境因素在故障检测阶段发生改变时, FDR也可能明显地非单调变化^[23].

在不确定的环境中, 我们不能再假定FDR是确定性的.Yamada等人^[14]断言, 如果软件系统的规模很大, 则在故障排除阶段检测到的故障数也随之增大.同时, 在故障检测过程中被校正和检测的故障数的差与初始的故障数相比很小.在实际故障检测过程中, FDR随着环境、人员和资源的变化而变化, 而且未知突然变化, 即不确定变化.为描述这些不确定因素, 1994年, Yamada等人^[14]首次将不确定性干扰因素建模为白色噪音, 提出了白色噪音模型, 也是最早使用白色噪音的模型.随后提出的大多数NHPP模型都是在此基础上扩展的, 如2005年Kapur等人^[24]提出的SGRM, 2009年Kapur等人^[25]提出的模型和2010年Tamura等人^[26]提出的NHPP模型等.白色噪声过程是一种理想化的数学模型, 在任意两个相邻时刻的状态是不相关的, 即随时间的起伏变化极快, 将白色噪音定义为一维Wiener过程来描述故障检测过程, 即故障检测过程中的失效率受白色噪音影响的过程或称为马尔可夫过程.这种随机模型毫无疑问地在数学方法上采用了更简单的故障估计理论.

从上面的讨论我们可以发现, 已有的随机NHPP模型假设FDR的随机干扰因素为白色噪音.在实践中, 噪音出现非马尔可夫性是普通现象, 而噪音出现马尔可夫性仅仅是例外^{[15, 16]}.基于白色噪声的过程通常称为马尔可夫随机过程.然而, 在许多实际情况下, 白色噪声的理想化假设是不足的:真正的不规则因素总是相关性的, 且相应的随机波动通常为相关性噪声.这类相关性噪声符合非马尔可夫随机过程^[15].在实际应用中, 多个不具有可加性的相关性噪音是不可避免的, 例如, 来自环境等诸多干扰信号^[16].故障检测过程中的失效率从时域上看在任意两个相邻时刻的状态是相关的, 即非马尔可夫噪音, 使得软件FDR呈现出基于非马尔可夫噪音的相关且不规律变化.因此, 研究在具有时间相关性噪音影响下的NHPP类SRGM符合实际的软件故障检测过程, 具有重要的理论意义和实际价值.在研究过程中, 我们希望引入时间相关性的环境噪声来进一步改善这种模型.

在本文中, 我们采用连续时间NHPP^[24-26]来建模故障计数过程{N(t), t≥0}.NHPP已广泛使用在许多实际领域^[11], 这一模型假设:

(1) 软件故障检测过程是一个具有连续状态空间的随机过程;

(2) 系统的故障由系统中的剩余故障在一个随机时间引起;

(3) 在时间区间(t, δt)内, 检测的平均故障数与剩余故障数是成比例的;

(4) 一个检测的故障被发现后即被排除且没有带来新的故障.

那么, NHPP过程可以表示为

其中, M(t)是时间区间(0, t]内检测的故障数, M(t)的时间演化经常被描述为故障失效强度函数λ(t).

其中, a为初始故障总数, 非负函数r代表在时间t的故障检测率.

由于故障检测率r(t)受一些随机环境影响^[16], 我们遵循以往的研究^{[14, 24-26]}, 将r(t)表示为一个平均值〈r(t)〉和一个均值为0(随机)的波动r′(t)的和.

与早期的将随机波动建模为白色噪音的方法不同, 我们扩展了这个假设并描述噪音的两点协方差为

其中, σ_r²代表噪音的强度, ρ表示相关性方程, t与s为两个不同时间点, τ为相关性时间长度.当噪音的相关性时间无限小时, 相关性方程变成狄拉克函数(Dirac Delta function)并被称为“白色噪音”; 其他时候, 它被称为“彩色噪音”.

将式(3) 代入式(2) 中, 我们得到一个不确定性FDR的随机微分等式:

故障检测率〈r(t)〉表示一个故障的平均失效率, 在不同的模型中有不同的表现形式.在表 1中, 本文列出了5个基于NHPP模型的具有确定性〈r(t)〉的数学表达式, 即Goel-Okumoto SRGM(G-O model), generalized G-O SRGM(gG-O Model), Delay S-shaped SRGM(DSS model), Inflection S-shaped SRGM(ISS model), Model with change-point(CP)和Log-Exponential SRGM(log-exp).其中, b为r(t)中的常量, d为r(t)中的塑形因子, w为权重, t_cp为改变点的时间, b₁和b₂分别为改变点t_cp前后的FDRs.

表 1(Table 1)

Table 1 The FDR (fault detection rate) of deterministic SRGMs 表 1 确定性SRGMs的故障检测率FDR〈r(t)〉 模型 FDR〈r(t)〉 Goel-Okumoto SRGM (G-O model) b generalized G-O SRGM (gG-O Model) btd Delay S-shaped SRGM (DSS model) b2t/(1+bt) Inflection S-shaped SRGM (ISS model) b/(1+we-bt) Model with change-point (CP) $\left\{ {\begin{array}{*{20}{c}} {{b_1}, {\rm{ }}t < {t_{cp}}}\\ {{b_2}, {\rm{ }}t > {t_{cp}}} \end{array}} \right.$ Log-Exponential SRGM (log-exp) ${\rm{d}}b{{\rm{e}}^b}t{\rm{ }}{({{\rm{e}}^b}t -1)^{(d -1)}}/[1 + {({{\rm{e}}^b}t -1)^d}]$

Table 1 The FDR (fault detection rate) of deterministic SRGMs 表 1 确定性SRGMs的故障检测率FDR〈r(t)〉

这里需要指出的是, 故障检测率模型(5) 描述了一个完美的调试过程.在许多情况下, 时间延迟、故障排除失败和新故障的引入, 将导致出现不完美的调试问题^{[12, 13, 18, 19]}.在目前的研究中, 我们的重点在于提出一个量化环境因素不确定性的框架.为不失一般性, 此框架随后也可以扩展到不完美的调试过程.

我们采用广义G-O模型^[27]中的方法来表示平均故障检测率与剩余的故障数关系的函数.

其中, d是一个塑形参数, 而常量b代表了故障检测率, 且b∈(0, 1).其中, b→0说明模型的故障检测能力很差.

使用分离变量法, 一个累计故障数M的解析解可推导为

值得一提的是, 解(7) 包括一个随机干扰随时间的积分, ${I_{r'}} = \int_0^t {r'} (t'){\rm{d}}t', $因而变成了一个随机积分问题.在相关性时间长度t与我们关注的时间t的基础上, 我们采用3个不同的近似方案^[28]来计算随机积分的概率密度函数${f_{{I_{r'}}}}$.详细的推导过程在附录A1中给出.

现在, 故障数M的均值和方差可推导为

这里, 我们注意到噪音的分布函数${f_{r'}}$或噪音的相关性方程ρ没有进一步的假设.在随后的数值研究中, 除非特别说明, 否则均用一个高斯函数来描述随机干扰, 即r′~N(0, s_r²), 且噪音的相关性方程为指数函数, 即r(s, t; t)=exp(–|t–s|/t).

为了验证模型, 我们用4组软件失效数据集:(1) DS1来自一个基于Web的集成会计ERP系统; (2) DS2来自一个开源项目管理软件^{[29, 30]}; (3) DS3和(4) DS4来自坦丁姆计算机公司(Tandem Computers Inc.)的第1次和第4次软件发布版本^[31].在4组数据中, 两个基于广域网的系统(DS1和DS2) 更容易受环境因素影响, 而Tandem软件在一个更封闭和稳定的环境中开发.因此, 我们通过噪声方差来体现这种差异, 即基于Web的系统具有更大的噪声σ_r².数据集DS1, DS2, DS3和DS4的测试时间分别为60(months), 29(weeks), 20(weeks)和19(weeks).如需详细信息, 请参考列于附录A2中的失效数据.

我们的相关性模型中有5个输入参数:初始故障总数a, 故障检测率b, 塑形参数d, 噪音的强度σ_r²和相关时间t.给定一组数据, 前3个参数可以使用矩估计法、最小二乘法、最大似然法和贝叶斯方法获得^[32-34]且相应的支持工具包括SPSS等.对于噪声参数, 我们的相关性噪音强度σ_r²继承了之前的白色噪声研究中的强度^{[14, 24, 25]}; 关于噪声的相关时间, 由于故障修复时间以天为单位^[35], 因此, 我们设置τ=0.1(month)或(week)供以后分析使用.

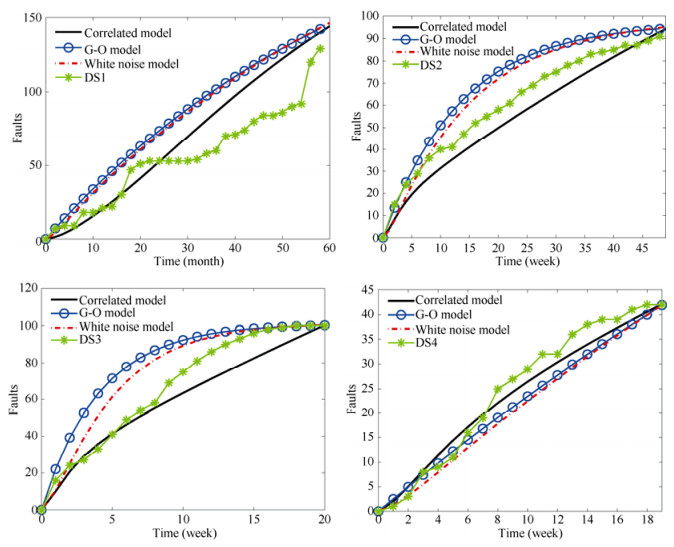
为了验证时间相关性模型(correlated model), 本文与经典的确定性SGRM模型(G-O model)和流行的白色噪声随机模型(white-noise model)进行了对比.图 1展示了在不同的数据集和测试时间上, 相关性模型、G-O模型和白色噪声模型对故障数〈M〉的预测结果.所有3个模型的参数都已经调整为最适合它们的数值.如图 1所示, 虽然相关的模型高估了DS1的故障数, 也低估了DS2, DS3和DS4的故障数, 但是整体上, 与G-O模型和白色噪声模型相比, 本文的预测结果最匹配于4组实际数据.

图 1

Fig. 1

Fig. 1 Expected number of faults, 〈M〉, computed from the correlated model, G-O model and white-noise model, are compared with four data sets 图 1 在4个数据集基础上, 相关性的模型、G-O模型及白噪声模型分别计算出的预期故障数〈M〉

为了更好地验证相关性模型的性能, 我们采用如下5个评价标准.

a)预测相对误差(predicted relative error, 简称PRE)

PRE是在时间t时观察值和估计值的相对距离, 通常被称为预测效度.

其中, q是观测数据中t时刻的故障均值.一个完美的数据拟合使得PRE(t)=0.^{[36, 37]}

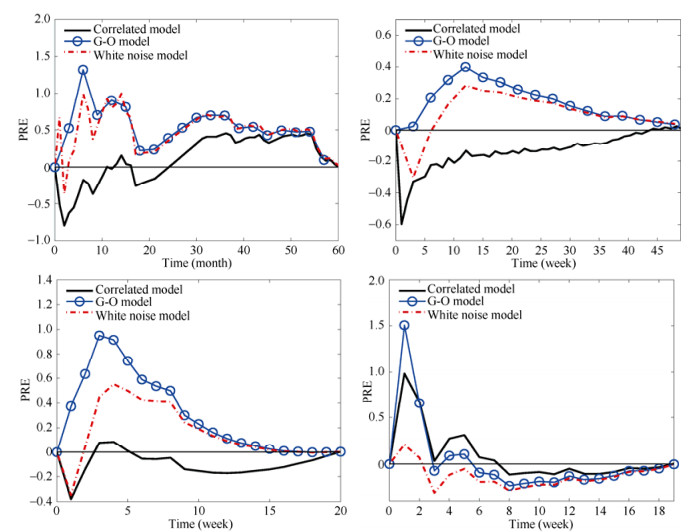
图 2展示了在不同的测试时间上, 相关性模型、G-O模型和白色噪声模型的PRE结果.3个模型具有类似的趋势:开始时具有很大的预测误差(距0的偏差), 稍后逐渐趋于可观测值.这个结果是符合预期的, 因为在早期只有很少的数据来衡量模型的参数; 随着时间的消耗, 更多的数据变得可用, 模型的精度有所提高, 因此, 它们的PRE接近0.总体而言, 相关性模型产生的PRE最小.

图 2

Fig. 2

Fig. 2 Predicted relative error (PRE) for correlated model, G-O model and white-noise model, from four data sets 图 2 在4个数据集上分别计算相关性模型、G-O模型与白噪声模的预测相对误差PRE值

b)均方误差(mean square error, 简称MSE)

这里, K代表观测点的总数.MSE的值越小说明模型的预测性越好^{[26, 37]}.

c)决定系数(coefficient of determination, 简称R²)

R²度量模型如何线性回归逼近真实的数据点.R²=1说明模型的预测结果完美地接近实际.

d)误差均方根(root mean square prediction error, 简称RMSPE)

RMSPE包含两个附加指标:平均的预测错误(the average of prediction errors, 简称Bias)和平均相对误差(the predicted relative variation, 简称PRV).

其中,

Bias, PRV和RMSPE的值越小, 代表模型越接近实际.

相关性模型、G-O模型和白色噪声模型在数据集DS1, DS2, DS3和DS4上的评估结果展示在表 2中.尽管在DS1中PRV有一个较高的值, 但是相关性模型在4个数据集上对所有指标都展示出了对实际数据的最好的拟合度(goodness-of-fit).

表 2(Table 2)

Table 2 The MSE, R2, Bias, PRV and RMSPE results of correlated model, G-O model and white noise model for DS1, DS2, DS3 and DS4 表 2 相关性模型、G-O模型和白色噪音模型在DS1, DS2, DS3与DS4上的MSE, R2, Bias, PRV及RMSPE结果 模型 数据集 参数设置 MSE R2 Bias PRV RMSPE 相关性 模型 DS1 a=445, b=0.04047, d=0.028, σr2=0.0002236, t=0.1 411.840 4 0.653 1 12.542 7 16.088 4 20.399 9 DS2 a=308, b=0.5446, d=0.026, σr2=0.0002228, t=0.1 46.194 3 0.913 3 –5.944 2 3.329 8 6.813 3 DS3 a=618, b=0.846, d=0.025, σr2=0.0002219, t=0.1 78.658 2 0.903 2 –6.675 6 5.990 8 8.969 5 DS4 a=269, b=0.3046, d=0.024, σr2=0.0002207, t=0.1 5.928 4 0.968 2 –0.974 3 2.292 6 2.491 0 G-O模型 DS1 a=249, b=0.0146 847.959 9 0.285 8 25.617 9 13.961 9 29.175 5 DS2 a=97, b=0.0746 123.789 6 0.767 8 9.694 0 5.517 1 11.154 0 DS3 a=101, b=0.246 318.577 2 0.608 1 13.575 3 11.889 3 18.045 6 DS4 a=173, b=0.0146 15.314 7 0.917 8 –2.714 6 2.896 1 3.969 4 白色噪音 模型 DS1 a=522, b=0.0126, d=0.028, σr2=0.0002236 816.378 4 0.312 4 24.601 8 14.654 3 28.635 6 DS2 a=197, b=0.06246, d=0.026, σr2=0.0002228 82.049 3 0.846 1 7.077 5 5.711 7 9.094 8 DS3 a=203, b=0.226, d=0.025, σr2=0.0002219 157.913 9 0.805 8 8.832 9 9.170 6 12.732 6 DS4 a=377, b=0.0126, d=0.024, σr2=0.0002207 20.409 4 0.890 5 –3.698 1 2.666 1 4.558 9

Table 2 The MSE, R2, Bias, PRV and RMSPE results of correlated model, G-O model and white noise model for DS1, DS2, DS3 and DS4 表 2 相关性模型、G-O模型和白色噪音模型在DS1, DS2, DS3与DS4上的MSE, R2, Bias, PRV及RMSPE结果

我们已在4组数据集上验证了相关性模型, 现在着手利用这个模型来预测评估软件可靠性.由于环境噪音r(t)的影响, 检测到故障的累积数量在一个时间跨度内将不会是确定的值.软件可靠性是从在NHPP模型基础上的故障累计数和检测时间计算而来.换言之, 环境的不确定性影响了故障计数过程(NHPP), 并进一步影响了软件的可靠性.本节的目的是估算在这个不确定性调试过程下的软件可靠性.为不失一般性, 随后的研究中, 相关性模型将采用以下参数:a=308, b=0.005446, d=0.026, σ_r²=0.0002228和τ=0.1.

软件可靠性R(t; T)被广泛地定义为在时间区间[T, T+t]内软件不发生故障的概率.基于NHPP的软件可靠性可以表示为

使用相关性模型, 软件可靠性R(t; T)在时间T=2, 10和50周的3个截图如图 3所示.根据表达式(13), 当在T固定且在相对于T的时间t=0时, $R(t; T) = {{\rm{e}}^{-\left[{\left\langle {M\left(T \right)} \right\rangle-\left\langle {M\left(T \right)} \right\rangle } \right]}} = {{\rm{e}}^0} = 1$.在3个时间戳上的可靠性在初始时具有峰值, 但是随后逐渐减慢, 最后在t→∞时R(t; T)接近于0.这是我们预计的结果, 因为在早期, 大部分的故障尚未被检测到; 随着时间的流逝, 更多的bug被检测出来, 导致软件可靠性的下降; 当系统所有的故障都被清除时, R(t; T)达到平稳状态.

图 3

Fig. 3

Fig. 3 Temporal evolutions of software reliability, R(t; T), and reliability growth rate, RGR(t; T), at time T=2, 10, 50 weeks, using the correlated model with parameters a=308, b=0.005 446, d=0.026, σr2=0.0002228, and τ=0.1 图 3 软件可靠性R(t; T)和软件可靠性的增长速度RGR(t; T), 在时间T=2, 10, 50周, 使用参数为a=308, b=0.005 446, d=0.026, σr2=0.0002228和τ=0.1的相关性模型的时间演化

为了更进一步地研究可靠性, 我们现在评估软件可靠性的增长率RGR(t; T).当时间间隔t趋近于0时, 平均增长率的极限称为瞬时增长率.此时, RGR(t; T)也可表示为

软件可靠性增长率与可靠性无必然联系, 可靠性增长率很大时, 可靠性可以很小; 可靠性很大时, 可靠性增长率也可以很小.当软件的可靠性增长率加速度为0时, 软件的可靠性就均匀增加.当软件的可靠性增长率保持大小不变时, 软件的可靠性就匀速改变.在软件调试过程中, 如果软件的可靠性增长率不为0, 则软件的可靠性就处于变化状态.如果软件的可靠性增长率大于0, 则其可靠性快速增加; 如果软件的可靠性增长率小于0, 则其可靠性快速减小.将软件可靠性增长率作为可靠性变化的度量标准, 是观察软件可靠性是否稳定的指标.

以本文的相关性模型为例, RGR(t; T)可通过模型公式解(8a)和(8b)来计算.

其中, 方差dσ_I/dt的推导可参见附录A1中的表 3.

表 3(Table 3)

Table 3 Approximation of distribution for the random integral: ${I_{r'}} = \int_0^t {r'(t')} {\rm{d}}t' = \sum\nolimits_{i = 1}^N {{I_i}} = \sum\nolimits_{i = 1}^N {\int_{\left({i -1} \right)\Delta }^{i\Delta } {r'(t'){\rm{d}}t} } $, where Δ=t/N 表 3 随机积分${I_{r'}} = \int_0^t {r'(t')} {\rm{d}}t' = \sum\nolimits_{i = 1}^N {{I_i}} = \sum\nolimits_{i = 1}^N {\int_{\left({i -1} \right)\Delta }^{i\Delta } {r'(t'){\rm{d}}t} } $的分布近似, 其中, Δ=t/N Cases t≪t t≫t Others Distribution fI fr' Gaussian Gaussian Mean 0 0 0 Variance σI2 σr2t2 2σr2t $2N\sigma _r^2\left[ {\int_0^\Delta {(\Delta -t')\rho \left({t'} \right){\rm{d}}t' + \sum\nolimits_{i = 2}^N {\int_0^\Delta {\int_{(i -1)\Delta }^{i\Delta } {\rho (t' -t''){\rm{d}}t'{\rm{d}}t''} } } } } \right]$ $\frac{{{\rm{d}}{\sigma _I}}}{{{\rm{d}}t}}(t; T)$ ${\sigma _r}$ $\frac{1}{{\sqrt {2(T + t)} }}$ $\begin{array}{*{20}{c}} {\frac{1}{{{\sigma _I}}}\left\{ {\int_0^\Delta {\rho \left({t'} \right){\rm{d}}t' + \sum\nolimits_{i = 2}^N {\left[ {\int_0^\Delta i \rho \left({i\Delta -t''} \right){\rm{d}}t'' -} \right.} } } \right.}\\ {\left. {\left. {\int_0^\Delta {\left({i -1} \right)} \rho \left[ {\left({i -1} \right)\Delta -t''} \right]{\rm{d}}t'' + \int_{\left({i -1} \right)\Delta }^{i\Delta } {\rho \left({t' -\Delta } \right)} {\rm{d}}t'} \right]} \right\}} \end{array}$

Table 3 Approximation of distribution for the random integral: ${I_{r'}} = \int_0^t {r'(t')} {\rm{d}}t' = \sum\nolimits_{i = 1}^N {{I_i}} = \sum\nolimits_{i = 1}^N {\int_{\left({i -1} \right)\Delta }^{i\Delta } {r'(t'){\rm{d}}t} } $, where Δ=t/N 表 3 随机积分${I_{r'}} = \int_0^t {r'(t')} {\rm{d}}t' = \sum\nolimits_{i = 1}^N {{I_i}} = \sum\nolimits_{i = 1}^N {\int_{\left({i -1} \right)\Delta }^{i\Delta } {r'(t'){\rm{d}}t} } $的分布近似, 其中, Δ=t/N

图 3显示了通过模型(15) 计算的T=2, 10和50周时对应的软件可靠性增长率RGR.尽管最初表现为上升趋势, 但是3个时段的RGR随后都收敛到0并保持平稳.这也和故障调试过程是一致的, 由于更多的故障随着检测时间的推进被排除.当所有的故障都被排除时, 软件可靠性增长率RGR达到0.根据表达式(15), 当RGR的初始值为0时, 在我们的例子中, 是第80周.

传统的软件可靠性评估依赖于平均故障检测〈M〉, 通过提出一个随机FDR, 人们可以得到M完整的统计信息, 从而可以对软件系统进行概率风险评估.对公式解(7) 进行统计分析, 我们能够获得故障移除的概率分布密度函数(probabilistic density function, 简称PDF)f_M(m; t)和累积密度函数(cumulative density function, 简称CDF)f_M(m; t)且${f_M}{\rm{d}}m = {f_{{I_{r'}}}}{\rm{d}}{I_{r'}}$.

其中, erf(*)∈[-1, 1], 代表误差函数(error function), σ_I²表示随机积分I_r′的方差, 可见附录A1.

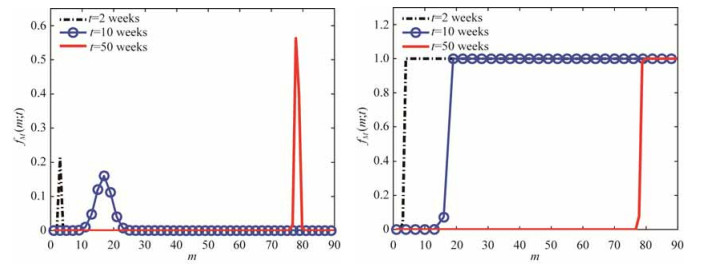
使用参数a=308, b=0.005446, d=0.026, σ_r²=0.0002228和τ=0.1时, PDF和CDF在时间t=2, 10和50周的3个快照分别如图 4所示.

图 4

Fig. 4

Fig. 4 Snapshots of the PDF, fM(m; t) and the CDF, FM(m; t), at time t=2, 10 and 50 weeks, using parameters a=308, b=0.005446, d=0.026, σr2=0.0002228, and τ=0.1 图 4 在时间t=2, 10和50周, 使用参数a=308, b=0.005446, d=0.026, σr2=0.0002228和τ=0.1时, 概率密度函数(PDF)和累积密度函数(CDF)的快照

计算PDF和CDF的主要目的是研究故障数在受到环境不确定性噪声r(t)影响时的概率分布情况.由于故障PDF和CDF是根据随机微分等式(5) 逐步推导而来, 根据随机微分等式可知初始条件时间t对PDF和CDF的值有较大的影响.我们可以使用时间t来观测, 在t=2, 10或50周时故障数的可能情况.通过给定的初始条件时间t, 模型可以计算t=2, 10或50周时故障的概率密度函数.以t=2为例, t=2时的PDF给出了此时故障数的可能的分布情况; t=2时的概率密度函数也给出了t+8的故障数的确定值和这个值的概率, 但是这个确定值是在t=2时的初始条件下计算出的结果.在t=10的初始条件下计算的故障数也是一个概率密度函数, 这个概率密度函数和t=2时计算的2+8时所计算的故障数的确定值可能不存在等同关系.

由于受不确定性噪音的影响, 故障数不再是一个确定值, 变成了一个连续型随机变量(PDF).我们预测的不确定性展示在PDF宽度上.因为PDF给出了每个给定的时间条件下故障的可能性, 所以每个估计的故障下限和上限可通过跟踪PDF得到.通过分析一个特定时间的PDF, 可找到检测故障最小数目和最大数目.例如, 它们在10周时分别是4和21.CDF的值先从2周增加到10周; 之后落在50周, 因为此时大部分的故障都已被检测到.图 4所示的PDF和CDF给出了在噪音影响下T时刻故障数的可能性.当不确定性噪音对故障检测过程影响消失时.即PDF宽度为0时, 说明几乎所有的故障都已被检测到, 而这个时间是80周.

现有的NHPP类SRGM假定检测到故障的累积数和软件调试的时间之间存在确定性的关系, 应用具有一定的局限性.对于不确定环境影响, 本文将环境因素统一表示成任意分布和相关性结构的噪声, 提出了一种用于量化环境中软件故障检测过程不确定性的相关性模型, 并进一步推导了故障检测数的显式解:均值、方差、PDF和CDF.经本文分析后可以得出以下主要结论:(1) 在4组实际数据集上, 本文所提出的软件可靠性增长模型比经典的G-O模型和白色噪声模型具有更好的拟合度; (2) 本文所提出的软件可靠性增长模型在预测初期不确定性较大, 但随着检测时间的推进而逐渐减少, 因此初始阶段需要更多的维护; (3) 故障检测人员可借助本文所提出的软件可靠性增长模型评估检测过程中的小概率事件, 以完成软件的不确定性风险评估.

A1 随机场积分

这里, 我们采用文献[28]的结果来计算随机积分Ir′, 并列在表 3中.

当t≪τ时, 随机积分可以近似为一个常数, 即I_r′≈r′t.它的分布类型就是积分部分f_r'.

当t≫τ时, 随机积分可以是近似为不相关的随机波动的和, 其中, ρ(r"-t′)=δ(r"-t′), 且不相关的随机波动具有相同的分布.

对于所有其他情况, 我们可以使用文献[39]中的方法和将积分区间[0, t]分成N个区间, 使得每个子区间的长度为Δ=t/N.

已知环境噪音r′(t)是一个有连续样本函数的固定过程, 所有的随机项(i=1, …, N)具有相同的均值和方差.

我们可以计算区间之间的两点协方差:

依据相关性随机参数的中心极限定理^{[40, 41]}, ${I_{r'}}(t) = \sum\nolimits_{i = 1}^N {{I_i}} $是(N→∞)接近均值为0和方差为NV的高斯型, 其中,

A2 数据集

用于模型验证的4个数据集的数值分别列于表 4~表 7中.

表 4(Table 4)

Table 4 The failure data of Web-based accounting ERP system (DS1) from August 2003 to July 2008 表 4 基于Web的会计ERP系统(DS1) 从2003年8月~2008年7月的失效数据 Time unit (month) Detected faults 1 1 2 7 3 7 4 9 5 9 6 9 7 12 8 18 9 18 10 18 11 18 12 21 13 22 14 22 15 27 16 30 17 45 18 47 19 49 20 51 21 53 22 53 23 53 24 53 25 53 26 53 27 53 28 53 29 53 30 53 31 53 32 54 33 56 34 58 35 59 36 60 37 63 38 70 39 71 40 71 41 72 42 74 43 74 44 80 45 84 46 84 47 84 48 84 49 85 50 86 51 89 52 90 53 90 54 92 55 108 56 120 57 128 58 129 59 139 60 146

Table 4 The failure data of Web-based accounting ERP system (DS1) from August 2003 to July 2008 表 4 基于Web的会计ERP系统(DS1) 从2003年8月~2008年7月的失效数据

表 5(Table 5)

Table 5 The failure data of open source project management software (DS2) from August 2007 to July 2008 表 5 The failure data of open source project management software (DS2) from August 2007 to July 2008 Time unit (week) Detected faults 1 9 2 15 3 19 4 24 5 28 6 29 7 32 8 36 9 36 10 40 11 41 12 41 13 45 14 47 15 49 16 52 17 52 18 55 19 57 20 58 21 61 22 61 23 64 24 66 25 67 26 69 27 70 28 73 29 74 30 75 31 75 32 78 33 79 34 80 35 82 36 83 37 83 38 84 39 84 40 85 41 85 42 87 43 87 44 87 45 89 46 89 47 91 48 91 49 94 - - - - - -

Table 5 The failure data of open source project management software (DS2) from August 2007 to July 2008 表 5 The failure data of open source project management software (DS2) from August 2007 to July 2008

表 6(Table 6)

Table 6 The failure data of Tandem software (DS3) from the first release 表 6 Tandem软件(DS3) 第1版发布的失效数据 Time unit (week) Detected faults 1 16 2 24 3 27 4 33 5 41 6 49 7 54 8 58 9 69 10 75 11 81 12 86 13 90 14 93 15 96 16 98 17 99 18 100 19 100 20 100

Table 6 The failure data of Tandem software (DS3) from the first release 表 6 Tandem软件(DS3) 第1版发布的失效数据

表 7(Table 7)

Table 7 The failure data of Tandem software (DS4) from the fourth release 表 7 Tandem软件(DS4) 第4版发布的失效数据 Time unit (week) Detected faults 1 1 2 3 3 8 4 9 5 11 6 16 7 19 8 25 9 27 10 29 11 32 12 32 13 36 14 38 15 39 16 39 17 41 18 42 19 42 - -

Table 7 The failure data of Tandem software (DS4) from the fourth release 表 7 Tandem软件(DS4) 第4版发布的失效数据