在经典逻辑中, 推理是单调的, 即在已知的前提中添加新的信息, 不会使其推导出的集合缩小.与之相反, 非单调逻辑中, 推导关系(⊢)的单调性是不成立的.在已有的知识库中添加新的知识后, 可能会推翻之前的推论.即推导出的集合不会随着前提的增加而扩大.典型的非单调逻辑有缺省逻辑、封闭世界假设、限定推理(circumscription)和单调模态逻辑等.信念修正也可以被看作是一种非单调逻辑.

经典逻辑可以准确地表明一个事物为真还是为假, 但在现实世界中, 很多事物都是一般情况下为真, 但是有特殊情况的存在.比较经典的例子是“鸟通常会飞”, 在经典逻辑中, 我们只能将其表示为“所有的鸟都会飞”, 这显然是假的, 因为还有类似于鸵鸟等特例的存在.但是, 如果表示为“存在鸟会飞”又不符合我们想要表达的含义.因此, 我们必须表示为“除了鸵鸟、企鹅...之外, 所有的鸟都会飞”.缺省逻辑的目的在于形式化这样的推导规则.

缺省逻辑^[1]是由Reiter于1980年首先提出来的, 是缺省推理的一种形式化方法.缺省逻辑中的缺省规则是基于假设的, 并且在许多领域有着广泛的应用^[2].包括非单调继承网络(nonmonotomnic inheritance network)^[3]、信息检索^[4]和常识推理^[5]等.在缺省规则中, 我们可以把上述情形形式化地表示为一个推导规则, 即“缺省的, 鸟会飞”, 不需要列出所有的例外.

缺省逻辑的语言是基于一阶逻辑的, 公式的定义在缺省逻辑与一阶逻辑中是相同的.一个缺省规则是形如$\frac{{Bird:Flying}}{{Flying}}$的表达式, 其含义为“缺省的, 鸟会飞”.一个缺省理论Γ是一个二元组(T, Δ), 其中, T是公式的集合, Δ是缺省规则的集合.缺省理论的扩展是缺省推理中重要的概念, 它由缺省理论和缺省推理定义.Ƚukaszewicz^[6]给出了一种缺省逻辑的语义, 但在这种语义中, 缺省逻辑的模型实际上是满足扩展中所有一阶逻辑公式的模型, 并没有对缺省规则进行解释, 因此这种模型仍然是一阶逻辑的模型.

在实际应用方面, 缺省逻辑存在着一定的局限性.研究人员提出一些缺省逻辑的变体(variant)来获得某些特定的性质或者赋予扩展更为直观的解释, 亦或为了解决计算复杂度的问题.例如, 在使用缺省规则对知识库进行扩充时, 显式或者隐式地制定优先顺序^[7]; 证实缺省逻辑(justified default logic)^[8]和受限缺省逻辑(constrained default logic)^[9]确保扩展的存在; 为了降低计算扩展的难度, 一些缺省逻辑的变体使用命题逻辑语言^[10]、描述逻辑语言^[11]以及OWL-DL语言^[12]等可判定语言.近年来, 臧良俊还提出了分层的缺省逻辑^[13]和分层的缺省描述逻辑^[14], 将缺省规则由公式层面拓展到了规则层面, 为缺省逻辑引入了分层的概念.

考虑如下例子, 给定一个缺省理论(T, Δ), 其中, T={Man(Jone), ¬ HasArm(Jone)}, 表达某个人Jone没有胳膊; Δ由一个缺省规则$\frac{{{\rm{Man(}}x{\rm{)}}:{\rm{HasArm(}}x{\rm{)}} \wedge {\rm{HasLeg}}(x)}}{{{\rm{HasArm(}}x{\rm{)}} \wedge {\rm{HasLeg}}(x)}}$组成, 该缺省规则的含义是:缺省地, 人是有胳膊和腿的.在缺省逻辑中, 缺省理论(T, Δ)只有一个扩展${\rm{Th}}(\{ {\rm{Man(Jone)}}, \neg {\rm{HasArm(Jone)}}\})$, 即我们不能获得该人是否具有腿的信息.事实上, 我们希望能够从上述的缺省理论中推导出没有胳膊的Jone是缺省的有腿的.形式化地表示为由${\rm{Man(Jone)}}, \neg {\rm{HasArm(Jone)}}, \frac{{{\rm{Man(}}x{\rm{)}}:{\rm{HasArm(}}x{\rm{)}} \wedge {\rm{HasLeg}}(x)}}{{{\rm{HasArm(}}x{\rm{)}} \wedge {\rm{HasLeg}}(x)}}$缺省地推导出HasLeg(Jone).

本文将提出一种贪婪缺省逻辑, 使得在贪婪缺省逻辑中, 缺省理论的扩展(我们称其为GD-扩展)要尽可能地保留缺省规则中结论公式中所蕴含的信息.为了表达缺省理论中公式和扩展的关系, 参照子公式的概念, 我们引入了伪子公式的概念.并且, 一个公式的子公式一定是该公式的伪子公式, 反之, 结论不成立.例如, 上述的例子, 在贪婪缺省逻辑中, 我们会将公式q^r的伪子公式r添加到扩展中去, 即保留了公式q^r与{p, ¬ q}协调的部分.本文将给出贪婪缺省逻辑中的推导规则, 建立了贪婪缺省逻辑的推演系统—GD系统.类似于经典逻辑中的Gentzen推演系统^[15], 缺省逻辑推演系统—GD系统的推导规则通过分解连接词的方法, 将每个缺省规则的结论部分拆分为原子公式或者原子公式的否定, 判断原子公式(原子公式的否定)是否保留或者删除, 将保留的原子公式(原子公式的否定)重新按照原有的连接词进行复合, 得到结论公式的伪子公式.本文给出了贪婪缺省逻辑扩展的构造方法, 并对贪婪缺省逻辑的扩展和缺省逻辑的GD-扩展进行了比较, 证明了如果一个缺省理论存在扩展E, 则存在一个GD-扩展E′, 使得E⊆ E′.反之不成立.

本文第1节给出缺省逻辑的基本定义和伪公式的定义.第2节给出贪婪缺省逻辑的推演系统—GD系统.第3节讨论贪婪缺省逻辑的推演系统—GD系统的性质.第4节通过例子对贪婪缺省逻辑的扩展(即GD-扩展)和缺省逻辑的扩展进行比较.第5节总结全文.

为了简化讨论, 我们使用命题逻辑的语言作为缺省逻辑的语言.

定义1.1. 给定命题逻辑的语言L, L包含下列符号.

● 命题变量:p₀, p₁, …;

● 逻辑连接词:¬ , ∧ , ∨ .

公式定义如下:

在本文中, 否定连接词“¬ ”仅出现在原子公式的前面.因为由德摩根律, 我们可以将一般公式化简为否定连接词限定只能出现在原子公式前的形式.

模型M是一个赋值v.我们称公式Φ在模型M下是可满足的, 记为${\boldsymbol{\rm{M}}} \models \phi $, 如果

定义1.2(缺省规则). 缺省规则δ是形如$\frac{{\phi :{\psi _1}, ..., {\psi _n}}}{\chi }$的表达式, 其中,

●  Φ, ψ₁, ..., ψ_n, χ为公式;

●  Φ称为δ的前提条件, 记为pre(δ);

●  ψ₁, ..., ψ_n称为δ的检验条件, 记为just(δ);

●  χ称为δ的结论, 记为cons(δ).

一个缺省规则δ是正则的, 如果δ形如$\frac{{\phi :\psi }}{\psi }, $通常, 为了便于表示, 我们记为$\phi \rightsquigarrow \psi.$

定义1.3(缺省理论). 缺省理论Γ是一个二元组(T, Δ), 其中, T是公式的集合, Δ是缺省规则的集合.如果Δ中的缺省规则都是正则的, 则称缺省理论Γ=(T, Δ)为正则缺省理论.

定义1.4(∧ _Γ演算). 给定缺省理论Γ=(T, Δ), A是公式的集合, ∧ _Γ(A)是满足下列条件的最小集合.

● ${ \wedge _\Gamma }1).\; T \subseteq { \wedge _\Gamma }(A); $

● ${ \wedge _\Gamma }2).\; Th({ \wedge _\Gamma }(A)) = { \wedge _\Gamma }(A); $

● ${ \wedge _\Gamma }3).$对于任意的$\delta = \frac{{\phi :{\psi _1}, ..., {\psi _n}}}{\chi } \in \Delta, $如果$\phi \in { \wedge _\Gamma }(A)$, $\neg {\psi _1}\not \in A, ..., \neg {\psi _n}\not \in A, $则$\chi \in { \wedge _\Gamma }(A).$

Th(A)表示A的理论闭包.

定义1.5(扩展). 给定缺省理论Γ和一个公式集合E, 如果E是∧ _r的固定点, 即E=∧ _r(E), 则称E为Γ的一个扩展.

定义1.6. 给定公式的集合E和缺省理论Γ=(T, Δ).定义

E_0=T,

${E_{i + 1}} = Th({E_i}) \cup \left\{ {\chi |\frac{{\phi :{\psi _1}, ..., {\psi _n}}}{\chi } \in \Delta, \phi \in {E_i}, \neg {\psi _1}, ..., \neg {\psi _n}\not \in E} \right\}, $

则E是缺省理论Γ=(T, Δ)的扩展当且仅当$E = \bigcup\limits_{i = 0}^\infty {{E_i}}.$

定义1.7(子公式). 给定公式Φ, 公式ψ是Φ的子公式, 记作ψ≤Φ, 如果Φ=ψ或者

(ⅰ)如果Φ=¬ Φ₁, 则ψ≤Φ₁;

(ⅱ)如果Φ=Φ₁∨ Φ₂或Φ₁∧ Φ₂, 则ψ≤Φ₁或ψ≤Φ₂.

令Φ=(p∨ q)∧ (r∨ s), 则有p∨ q, r∨ s≤Φ和p∧ r, q∧ r, p∧ (r∨ s)≤Φ.

为了区分形如p∧ r, q∧ r, p∧ (r∨ s)这种既是公式Φ的一部分, 但又不是Φ的子公式的公式, 我们引入伪子公式的概念.

定理1.8(伪子公式). 给定公式Φ[ψ₁, …, ψ_n], 其中, ψ_i是ψ_i在Φ中的一次出现, 令公式ψ=Φ[ψ₁/λ, ..., ψ_n/λ], 即将Φ中的ψ_i替换为空公式λ, 我们称ψ为Φ的伪子公式, 记作$\psi \subseteq \phi.$ψ为Φ的伪子公式, 如果$\psi \subseteq \phi $且$\psi \ne \phi.$

令Φ=(p∨ q)∧ (r∨ s), 则有p∨ q, r∨ s, p∧ r, q∧ r, p∧ (r∨ s)⊆ Φ.

命题1.9. 给定公式Φ₁, Φ₂, ψ₁和ψ₂,

(ⅰ) ψ₁≤Φ₁蕴含ψ₁≤Φ₁∨ Φ₂并且ψ₁≤Φ₁∧ Φ₂;

(ⅱ) ψ₁⊆ Φ₁与ψ₂⊆ Φ₂蕴含¬ ψ₁⊆ ¬ Φ₁, ψ₁∨ ψ₂⊆ Φ₁∨ Φ₂与ψ₁∧ ψ₂⊆ Φ₁∧ Φ₂.

命题1.10. 对于任意公式Φ和ψ, 如果ψ≤Φ, 则ψ⊆ Φ.

命题1.11.  ≤和⊆ 是定义在公式集合上的偏序关系.

给定公式Φ, 令P(Φ)为Φ的所有伪子公式构成的集合.每一个公式ψ∈ P(Φ)都由一个集合t(ψ)={[p₁], ..., [p_n]}来决定, 其中, [p_i]是原子公式p_i在Φ中的一次出现, 满足ψ=Φ([p₁]/λ, …, [p_n]/λ).

给定任意ψ₁, ψ₂∈ P(Φ), 定义:

命题1.12. 对于任意的伪子公式ψ₁, ψ₂∈ P(Φ), ψ₁∩ ψ₂和ψ₁∪ ψ₂都是存在的.P(Φ)=(P(Φ), ∪ , ∩ , Φ, λ)是具有最大元Φ和最小元λ的格.

命题1.13. 对于任意的伪子公式ψ₁, ψ₂∈ P(Φ), ψ₁⊆ ψ₂当且仅当τ(ψ₁)⊇ τ(ψ₂), 并且有

在本节中, 我们考虑的缺省规则均为正则缺省规则.考虑缺省理论:Γ=(T, Δ), 其中,

在经典缺省逻辑中, Γ的扩展为E=Th({Man(Jone), ¬ HasArm(Jone)}).我们从已知的缺省规则中不能获得更多的信息, 并且因为HasArm(Jone)∧ HasLeg(Jone)与¬ HasArm(Jone)矛盾而将HasLeg(Jone)也一同舍弃了.一般来说, 一个没有手的人是有腿的, 这是符合我们日常认知的.因此我们提出贪婪缺省逻辑, 使得在贪婪缺省逻辑中, E' =Th({Man(Jone), ¬ HasArm(Jone), HasLeg(Jone)})为缺省理论Γ的扩展(GD-扩展).

定义2.1. 缺省矢列式是形如T₁|Δ₁⇒ T₂|Δ₂的表达式.其中, T₁, T₂是公式的集合, Δ₁, Δ₂是缺省规则的序列.

表达式Δ₁, δ, Δ₂表示Δ₂≤δ≤Δ₁, 其中, Δ₁和Δ₂是缺省规则的序列, δ是缺省规则, 即Δ₁中的缺省规则的序优于δ, 并且δ的序优于Δ₂中的缺省规则.

缺省矢列式T|Δ₁, δ, Δ₂⇒ T, θ|Δ₁, Δ₂的含义为:缺省表达式T|D₁, δ, D₂可以通过作用缺省规则δ规约为T, θ|Δ₁, Δ₂.

在这里, 我们要求对于任意的公式Φ∈ pre(Δ₁)pre(Δ₁), $T\not \vdash \phi $; 并且$T \vdash $pre(δ).

在缺省逻辑中, 缺省规则作用的思路是:给定一个缺省规则$\phi \rightsquigarrow \psi $和公式集合T, 我们首先判断条件$T\vdash \phi $是否成立, 如果条件成立, 再判断ψ与T是否协调; 若协调, 则将ψ添加到集合T中去.因此, 改变现有集合T的是公式ψ而不是Φ.

如果将T看作是一个知识系统, 公式Φ可以看作是规则的启动条件, 它不对原有的系统的内容进行扩展.并且, 如果启动条件得到满足, 已有的知识与ψ不矛盾的话, 我们就可以将ψ作为一条新的知识添加到系统中去.但是, 如果ψ与原有的知识矛盾, 在缺省逻辑中我们会将ψ舍去.而缺省规则$\phi \rightsquigarrow \psi, $它实际上是一条经验规则, 其含义, 是当Φ成立时, 通常有ψ成立.公式ψ的结构也可能不是简单的原子公式, 而是通过逻辑连接词复合而成的复杂公式.正如上面的例子一样, 即使ψ在系统中不成立, 但ψ中可能还有一些与原系统不矛盾的信息, 因此, 我们希望能够通过分解连接词的方法, 尽可能地保留ψ中与T不矛盾的信息.

贪婪缺省推演系统—GD系统:推导规则.

在下列所有的推导规则中, T是公式集合, Δ₁和Δ₂是缺省规则的序列, 并且对于Δ₁中的任意缺省规则$\delta =\phi \rightsquigarrow \psi, $都有$T\not \vdash \phi.$

定义2.2. Atomic⁺-rule:

公式θ可能是属于T的, 但是我们仍记为$T|{{\Delta }_{1}}, \phi \rightsquigarrow \psi, {{\Delta }_{2}}\Rightarrow T, \theta |{{\Delta }_{1}}, {{\Delta }_{2}}$来表示该θ是通过作用缺省规则产生的.

定义2.3. Atomic-rule:

原子公式和原子公式的否定形式是公式的最基本形式, 如果协调, 则将公式添加到集合T中去.如果不协调, 则表明T可以推导出公式的否定, 由于原子公式不能再继续分解, 因此将公式舍去.

定义2.4. ∧ ^↓ -rule:

∧ ^↓ -rule是指对于缺省规则$\phi \rightsquigarrow {{\psi }_{1}}\wedge {{\psi }_{2}}, $如果$T\vdash \phi $成立, 集合T作用缺省规则$\phi \rightsquigarrow {{\psi }_{1}}$可以得到$T\cup \{{{\psi }_{1}}\}, T\cup \{{{\psi }_{1}}\}$作用缺省规则$\phi \rightsquigarrow {{\psi }_{2}}$可以得到$T\cup \{{{\psi }_{1}}, {{\psi }_{2}}\}, $则集合T作用缺省规则$\phi \rightsquigarrow {{\psi }_{1}}\wedge {{\psi }_{2}}$可以得到$T\cup \{{{\psi }_{1}}\wedge {{\psi }_{2}}\}.$

事实上, ∧ ^↓ -rule还有另外一种形式:

即如果$T\vdash \phi $成立, 集合T作用缺省规则$\phi \rightsquigarrow {{\psi }_{1}}$可以得到$T\cup \{{{\psi }_{2}}\}, T\cup \{{{\psi }_{2}}\}$作用缺省规则$\phi \rightsquigarrow {{\psi }_{1}}$可以得到$T\cup \{{{\psi }_{1}}, {{\psi }_{2}}\}, $则集合T作用缺省规则$\phi \rightsquigarrow {{\psi }_{1}}\wedge {{\psi }_{2}}$可以得到$T\cup \{{{\psi }_{1}}\wedge {{\psi }_{2}}\}.$因为对于集合T和公式\[{{\psi }_{1}}, {{\psi }_{2}}, T\cup \{{{\psi }_{1}}, {{\psi }_{2}}\}\]是协调的, 所以这两条规则是等价的, 我们只保留其中的一条.并且, 我们在之后的定理中也证明, 如果ψ可以全部保留, 则ψ与集合T是协调的.

定义2.5. ∧ ^↑ -rule:

其中, θ₁和θ₂分别是ψ₁和ψ₂的伪子公式.

在∧ ^↑ -rule中, 缺省规则$\phi \rightsquigarrow \psi $作用在集合T上得到的是ψ的一个伪子公式.这说明, ψ本身与集合T是不协调的.ψ的最外层逻辑联结词是合取符号, 即ψ=ψ₁∧ ψ₂.于是有ψ₁∧ ψ₂与T是不协调的, 缺省规则$\phi \rightsquigarrow {{\psi }_{1}}$和$\phi \rightsquigarrow {{\psi }_{2}}$作用的顺序不同, 则可能产生的伪子公式不同.例如, 最简单的情况, 令$T=\{p\}, \phi \rightsquigarrow {{\psi }_{1}}\wedge {{\psi }_{2}}=p\rightsquigarrow q\wedge \neg q.$先作用$p\rightsquigarrow q$产生的集合为{p, q}, 而先作用$p\rightsquigarrow \neg q$产生的集合为$\{p, \neg q\}.$

所以上述规则并不是等价的, 需要一一列出.

定义2.6. ∨ ^↓ -rule:

在∨ ^↓ -rule中, 如果T和ψ₁或者ψ₂是协调的, 则T与ψ₁∨ ψ₂是协调的.因此只要满足上述条件之一, 我们即可把ψ₁∨ ψ₂添加到T当中去.即当ψ与集合T是协调的, 则将ψ全部保留.

定义2.7. ∨ ^↑ -rule:

其中, θ₁和θ₂分别是ψ₁和ψ₂的真伪子公式.

在∨ ^↓ -rule中, 公式ψ₁∨ ψ₂与集合T是不协调的.因此公式ψ₁和ψ₂与集合T都是不协调的.即集合T作用$\phi \rightsquigarrow {{\psi }_{1}}$和$\phi \rightsquigarrow {{\psi }_{2}}$产生的新公式都是ψ₁和ψ₂的伪子公式, 考虑到公式ψ₁和ψ₂与集合T都是不协调的, 我们不将

任何公式添加到＄T＄中去.

定义2.8. TR-rule:

直观上, TR-rule表明缺省矢列式是具有传递性的, 即如果矢列式T₁|Δ₁⇒ T₂|Δ₂成立, 且有T₂|Δ₂⇒ T₃|Δ₃成立, 则有T₁|Δ₁⇒ T₃|Δ₃成立.

定义2.9(证明). 给定公式的集合S₁和S₂, 缺省规则的集合Δ₁和Δ₂(Δ₂可能是∅ ).我们称缺省矢列式S₁|Δ₁⇒ S₂|Δ₂是GD-可证的, 记为${{\vdash }^{\mathbf{GD}}}{{S}_{1}}|{{\Delta }_{1}}\Rightarrow {{S}_{2}}|{{\Delta }_{2}}$, 当且仅当存在一棵以S₁|Δ₁⇒ S₂|Δ₂为根节点的证明树T, 满足:

1) T的非叶节点都是缺省矢列式;

2) T的所有叶节点都是Axiom的上层;

3) T中除了根节点以外的所有节点都是某一个推导规则的上层, 且其直接后继节点为该缺省规则的下层.

显然, 证明树T的任意子树也是证明树.

例如:给定缺省理论$\Gamma =(T, \Delta), $其中, $T=\{p\}, \Delta =\{p\rightsquigarrow q, q\rightsquigarrow r\}, $则

为T|Δ⇒ p, q, r的一棵证明树, 即T|Δ⇒ p, q, r是可证的.

命题2.10. 给定缺省矢列式S₁|Δ₁⇒ S₂|Δ₂, 如果S₁|Δ₁⇒ S₂|Δ₂是GD-可证的, 则有Δ₂⊆ Δ₁, S₁⊆ S₂.

定义2.11(公式的序L下可证性). 给定缺省理论Γ=(T, Δ)和一个定义在Δ上的全序L, 其中, L=δ₁, δ₂, ..., δ_n, ....公式ψ是关于缺省理论Γ=(T, Δ)在序L下可证的, 如果存在一个Δ中的缺省规则的序列${{{\delta }'}_{1}}, {{{\delta }'}_{2}}, …, {{{\delta }'}_{j}}$, 使得:

…

…

其中, ${{\Delta }_{0}}=\Delta ={{\Delta }_{{{0}'}}}\cup {{\Delta }_{{{0}''}}}, {{\Delta }_{i}}={{\Delta }_{i-1}}-\{{{\delta }_{{{i}'}}}\}={{\Delta }_{{{i}'}}}\cup {{\Delta }_{{{i}''}}}; $对于任意的缺省规则$\delta \in {{\Delta }_{{{i}'}}}, $$\delta {{\ge }^{L}}{{\delta }_{i+{{1}^{\prime }}}}$并且${{T}_{i}}\not{\vdash }\text{pre}(\delta); $同时, 对于任意的缺省规则$\delta \in {{\Delta }_{{{i}''}}}, $都有${{\delta }_{i+{1}'}}{{\ge }^{L}}\delta.$

从公式的可证性我们了解到, 缺省规则的作用依赖于给定的严格偏序, 每一步作用的缺省规则都是活动的, 并且具有最优先的序.在每次作用完之后, 我们就将这个缺省规则从原有的集合中移除.我们要求每一步的矢列式都是缺省可证的, 并且由这些矢列式组成了一个连续可证的缺省矢列式的序列, 使得可证的公式可以被矢列式当中的某一个集合T' 推导出来.这样按照严格偏序去一步一步地作用缺省规则而生成的公式, 都是在该序下关于缺省理论Γ可证的公式, 那么包含所有这些公式的集合, 我们定义为GD-扩展, 定义如下.

定义2.12(GD-扩展). 给定缺省理论Γ=(T, Δ), 其中, T是协调的公式集合, Δ是缺省规则的集合.公式的集合E是缺省理论Γ=(T, Δ)的一个GD-扩展, 如果存在一个Δ上的全序L=δ₀, δ₁, δ₂, …, δ_i, …, 使得

…

…

其中, ${{T}_{0}}=T, {{T}_{i}}={{T}_{i-1}}\cup \{{{\theta }_{i}}\}; $${{\Delta }_{0}}=\Delta ={{\Delta }_{{{0}'}}}\cup {{\Delta }_{{{0}''}}}, {{\Delta }_{i}}={{\Delta }_{i-1}}-\{{{\delta }_{{{i}'}}}\}={{\Delta }_{{{i}'}}}\cup {{\Delta }_{{{i}''}}}; $对于任意的缺省规则$\delta \in {{\Delta }_{i-{1}'}}, $$\delta {{\ge }^{L}}{{\delta }_{{{i}'}}}, $并且${{T}_{i-1}}\not{\vdash }$pre(δ); 同时, 对于任意的缺省规则$\delta \in {{\Delta }_{i-{1}''}}, $都有${{\delta }_{{{i}'}}}{{\ge }^{L}}\delta.$

我们称E是缺省理论Γ=(T, Δ)的一个关于序L的GD-扩展.并且, 对于任意公式$\phi \in \text{pre}\left(\bigcap\limits_{i=0}^{\infty }{{{\Delta }_{i}}} \right), E\not{\vdash }\phi.$

不同于缺省逻辑, 贪婪缺省逻辑的GD-扩展的定义是构造型的.在贪婪缺省逻辑中, 由于随着作用集合的变化, 作用相同的缺省规则产生的伪子公式是不尽相同的; 即便是将缺省规则作用在最终生成的GD-扩展上所生成的公式与在生成扩展的过程中作用于该规则所产生的公式也未必相同.而在缺省逻辑中, 即使集合发生变化, 作用相同的缺省规则产生的公式要么是其本身, 要么是一个空公式; 并且, 将缺省规则作用在最终生成的扩展上生成的公式与在生成扩展的过程中作用于该规则上产生的公式是相同的.因此, 我们不能把GD-扩展不动点型定义为类似于缺省逻辑中形式, 即${{\wedge }_{\Gamma }}(S)=Th(T\cup \{\phi :S\vdash \phi, E\not{\vdash }\neg \psi, \phi \rightsquigarrow \psi \in \Delta \}), $其中, E是扩展.

例2.13:给定缺省理论Γ=(T, Δ), $T=\{{{p}_{1}}, \neg {{p}_{2}}\}, \Delta =\{{{p}_{3}}\rightsquigarrow {{p}_{4}}, {{p}_{1}}\rightsquigarrow {{p}_{2}}\wedge {{p}_{3}}, {{p}_{4}}\rightsquigarrow {{p}_{2}}\}.$L是定义在Δ上的全序, 其中, $L={{p}_{3}}\rightsquigarrow {{p}_{4}}, {{p}_{1}}\rightsquigarrow {{p}_{2}}\wedge {{p}_{3}}, {{p}_{4}}\rightsquigarrow {{p}_{2}}.$我们构造缺省理论Γ=(T, Δ)的一个关于序L的GD-扩展如下.

Step 1.

因为

故而有${{\vdash }^{\mathbf{D}}}{{T}_{0}}|{{\Delta }_{{{0}'}}}, {{\delta }_{{{k}_{0}}}}, {{\Delta }_{{{0}''}}}\Rightarrow {{T}_{0}}, {{\theta }_{{{k}_{0}}}}|{{\Delta }_{{{0}'}}}, {{\Delta }_{{{0}''}}}$, 其中, ${{\theta }_{{{k}_{0}}}}={{p}_{3}}.$

Step 2.

因为

故而有${{\vdash }^{\mathbf{D}}}{{T}_{1}}|{{p}_{3}}\rightsquigarrow {{p}_{4}}, {{\Delta }_{{{1}''}}}\Rightarrow {{T}_{1}}, {{p}_{4}}|{{\Delta }_{{{1}''}}}, $其中, ${{\theta }_{{{k}_{1}}}}={{p}_{4}}.$

Step 3.

因为

故而有${{\vdash }^{\mathbf{D}}}{{T}_{2}}|{{p}_{4}}\rightsquigarrow {{p}_{2}}\Rightarrow {{T}_{2}}, \lambda, $其中, ${{\theta }_{{{k}_{2}}}}=\lambda.$

故而Th(T₂)是缺省理论Γ=(T, Δ)的一个关于序L的GD-扩展, 并且公式p₃, p₄都是于缺省理论Γ=(T, Δ)在序λ下可证的.

例3.1:给定公式集合$S=\{p, \neg {{q}_{2}}, \neg {{q}_{4}}\}$和缺省规则$\delta =p\rightsquigarrow ({{q}_{1}}\wedge {{q}_{2}})\wedge ({{q}_{3}}\wedge {{q}_{4}}).$首先, 因为$S\vdash p, $缺省规则δ是可作用于集合S上的; 之后, 按照贪婪缺省逻辑的推导规则, 将缺省规则δ作用在集合S上.

我们可以得到公式q₁∧ q₃.q₁∧ q₃并不是(q₁∧ q₂)∧ (q₃∧ q₄)的子公式, 而是(q₁∧ q₂)∧ (q₃∧ q₄)的伪子公式.

从上述的例子中我们发现, 在贪婪缺省逻辑中, 作用缺省规则δ而产生的公式是cons(δ)的伪子公式.正如接下来的定理3.2.

定理3.2.  给定协调的公式集合S, 缺省规则集合Δ₁, Δ₂和缺省规则$\delta =\phi \rightsquigarrow \psi; $其中, 对于任意的公式${{\phi }_{1}}\in \text{pre}({{\Delta }_{1}}), $都有$S\not{\vdash }{{\phi }_{1}}$.那么, 如果$S|{{\Delta }_{1}}, \phi \rightsquigarrow \psi, {{\Delta }_{2}}\Rightarrow S, \theta |{{\Delta }_{1}}, {{\Delta }_{2}}$是GD-可证的, 则θ是ψ的伪子公式.

证明:我们对公式ψ的结构进行归纳证明.

基始:如果ψ=p或者ψ=¬ p, 根据推导规则的定义, θ的形式要么是ψ本身, 要么是空公式.显然, ψ和空公式λ都是ψ的伪子公式, 结论成立.

归纳步骤:假设结论在结构比公式ψ简单的公式上成立.

如果${{\vdash }^{\mathbf{GD}}}S|{{\Delta }_{1}}, \phi \rightsquigarrow \psi, {{\Delta }_{2}}\Rightarrow S, \theta |{{\Delta }_{1}}, {{\Delta }_{2}}, $根据证明的定义, 存在一棵以$S|{{\Delta }_{1}}, \phi \rightsquigarrow \psi, {{\Delta }_{2}}\Rightarrow S, \theta |{{\Delta }_{1}}, {{\Delta }_{2}}$为根节点的证明树.那么存在以下几种情形.

情形1:ψ=ψ₁∨ ψ₂.

根据证明树的定义, 证明树的最低两层有以下3种可能:

对于第1种和第2种可能, 显然, ψ₁∨ ψ₂是其本身的伪子公式, 结论成立.第3种情形是一种特殊的情形, 空公式是所有公式的伪子公式.

情形2:ψ=ψ₁∧ ψ₂.

根据证明树的定义, 证明树的最低两层有以下3种可能:

对于第1种情形, 显然, ψ₁∧ ψ₂是其本身的伪子公式, 结论成立.我们下面将对第2种情形进行讨论.

因为缺省矢列式$S|{{\Delta }_{1}}, \phi \rightsquigarrow {{\psi }_{1}}, {{\Delta }_{2}}\Rightarrow S, {{\theta }_{1}}|{{\Delta }_{1}}, {{\Delta }_{2}}$和$S, {{\theta }_{1}}|{{\Delta }_{1}}, \phi \rightsquigarrow {{\psi }_{2}}, {{\Delta }_{2}}\Rightarrow S, {{\theta }_{1}}, {{\theta }_{2}}|{{\Delta }_{1}}, {{\Delta }_{2}}$都是GD-可证的; 由归纳假设, θ₁与θ₂分别是ψ₁与ψ₂的伪子公式.根据证明树的定义, θ=θ₁∧ θ₂.又根据伪子公式的定义, θ₁∧ θ₂是ψ₁∨ ψ₂的伪子公式, 故而结论成立.

第3种情形与第2种类似.

定理3.3. 给定协调的公式集合S, 缺省规则集合Δ₁, Δ₂和缺省规则$\delta =\phi \rightsquigarrow \psi; $其中, 对于任意的公式${{\phi }_{1}}\in \text{pre}({{\Delta }_{1}}), $都有$S\not{\vdash }{{\phi }_{1}}.$那么, $S|{{\Delta }_{1}}, \phi \rightsquigarrow \psi, {{\Delta }_{2}}\Rightarrow S, \psi |{{\Delta }_{1}}, {{\Delta }_{2}}$是GD-可证的, 当且仅当$S\vdash \phi, $并且$S\not{\vdash }\neg \psi.$

证明:我们对公式ψ的结构进行归纳证明.

基始:如果ψ=p或者Φ=¬ p, 根据推导规则的定义, 结论成立.

归纳步骤:假设结论在结构比公式ψ简单的公式上成立.

情形1:ψ=ψ₁∨ ψ₂.

(⇒ )如果S|δ⇒ S, ψ是可证的, 则存在一棵以S|δ⇒ S, ψ为根节点的证明树, 使得该证明树的最底部的两层为

根据证明的定义, 可以得到矢列式$S|\phi \rightsquigarrow {{\psi }_{1}}\Rightarrow S, {{\psi }_{1}}$或者$S|\phi \rightsquigarrow {{\psi }_{2}}\Rightarrow S, {{\psi }_{2}}$是可证的.由归纳假设$S\cup \{{{\psi }_{1}}\}$或者$S\cup \{{{\psi }_{2}}\}$是协调的.因此$S\cup \{{{\psi }_{1}}\vee {{\psi }_{2}}\}$是协调的.即$S\not{\vdash }\neg \psi.$

(⇐ )如果$S\not{\vdash }\neg \psi, $则有$S\not{\vdash }\neg {{\psi }_{1}}\wedge \neg {{\psi }_{2}}.$即$S\not{\vdash }\neg {{\psi }_{1}}$或者$S\not{\vdash }\neg {{\psi }_{2}}.$不妨假设$S\not{\vdash }\neg {{\psi }_{1}}.$由归纳假设, $S|\phi \rightsquigarrow {{\psi }_{1}}\Rightarrow S, {{\psi }_{1}}$是可证的.故而由推导规则∨ ^↓ , 有

可以知道, $S|\phi \rightsquigarrow {{\psi }_{1}}\vee {{\psi }_{2}}\Rightarrow S, {{\psi }_{1}}\vee {{\psi }_{2}}$是可证的.同样地, 如果$S\not{\vdash }\neg {{\psi }_{2}}, $则有$S|\phi \rightsquigarrow {{\psi }_{1}}\vee {{\psi }_{2}}\Rightarrow S, {{\psi }_{1}}\vee {{\psi }_{2}}$是可证的.

即结论在情形1的情况下成立.

情形2:ψ=ψ₁∧ ψ₂.

(⇒ )如果S|δ⇒ S, ψ是可证的, 则存在一棵以$S|\delta \Rightarrow S, \psi $为根节点的证明树, 使得该证明树的最底两层为

根据证明树的定义, $S|\phi \rightsquigarrow {{\psi }_{1}}\Rightarrow S, {{\psi }_{1}}$是可证的, 由归纳假设可知$S\cup \{{{\psi }_{1}}\}$是协调的.同理, $S, {{\psi }_{1}}|\phi \rightsquigarrow {{\psi }_{2}}\Rightarrow $S, ψ₁, ψ₂也是可证的, 再次使用归纳假设可知, $S\cup \{{{\psi }_{1}}\}\cup \{{{\psi }_{2}}\}$是协调的.因此, $S\cup \{{{\psi }_{1}}\wedge {{\psi }_{2}}\}$是协调的, 故而$S\not{\vdash }\neg \psi.$

(⇐ )如果$S\not{\vdash }\neg \psi, $则$S\not{\vdash }\neg {{\psi }_{1}}\vee \neg {{\psi }_{2}}.$即$S\not{\vdash }\neg {{\psi }_{1}}$且$S\not{\vdash }\neg {{\psi }_{2}}.$因为$S\cup \{{{\psi }_{1}}, {{\psi }_{2}}\}$是协调的, 所以, $S, {{\psi }_{1}}\not{\vdash }\neg {{\psi }_{2}}.$由归纳假设, $S|\phi \rightsquigarrow {{\psi }_{1}}\Rightarrow S, {{\psi }_{1}}$和$S, {{\psi }_{1}}|\phi \rightsquigarrow {{\psi }_{2}}\Rightarrow S, {{\psi }_{1}}, {{\psi }_{2}}$都是可证的.使用推导规则∧ ^↓ , 有

可知$S|\phi \rightsquigarrow {{\psi }_{1}}\wedge {{\psi }_{2}}\Rightarrow S, {{\psi }_{1}}\wedge {{\psi }_{2}}$是可证的.

即结论在情形2的情况下成立.

定理3.4. 给定协调的公式集合S, 缺省规则集合Δ₁, Δ₂和缺省规则$\delta =\phi \rightsquigarrow \psi; $其中, 对于任意的公式${{\phi }_{1}}\in \text{pre}({{\Delta }_{1}}), $都有$S\not{\vdash }{{\phi }_{1}}.$如果$S|{{\Delta }_{1}}, \phi \rightsquigarrow \psi, {{\Delta }_{2}}\Rightarrow S, \theta |{{\Delta }_{1}}, {{\Delta }_{2}}$是GD-可证的, 则$S\cup \{\theta \}$是协调的.

证明:我们对ψ的公式结构进行归纳假设.

基始:如果ψ=p或者Φ=¬ p, 由推导规则定义可知, 结论成立.

归纳步骤:假设结论在结构比公式ψ简单的公式上成立.

情形1:ψ=ψ₁∨ ψ₂.

子情形1.1:q=ψ₁∨ ψ₂,

由定理3.3可知, 结论成立.

子情形1.2:θ=λ, 结论成立.

情形2:ψ=ψ₁∧ ψ₂.

子情形2.1:θ=θ₁∧ θ₂.

如果$S|\phi \rightsquigarrow \psi \Rightarrow S, {{\theta }_{1}}\wedge {{\theta }_{2}}$是可证的, 则存在一棵以$S|\phi \rightsquigarrow \psi \Rightarrow S, {{\theta }_{1}}\wedge {{\theta }_{2}}$为根节点的证明树, 使得该证明树的最底两层为

其中, 在公式(1) 中出现的θ₁和θ₂与公式(2) 中出现的θ₁和θ₂不一定相同.

由式(1) 可知, $S|\phi \rightsquigarrow {{\psi }_{1}}\Rightarrow S, {{\theta }_{1}}$是可证的, 故由归纳假设可知$S\cup \{{{\theta }_{1}}\}$是协调的.同理, $S, {{\theta }_{1}}|\phi \rightsquigarrow {{\psi }_{2}}\Rightarrow S, {{\theta }_{1}}, {{\theta }_{2}}$也是可证的, 因此, $S\cup \{{{\theta }_{1}}\}\cup \{{{\theta }_{2}}\}$是协调的.故而$S\cup \{{{\theta }_{1}}\wedge {{\theta }_{2}}\}$是协调的.

式(2) 的情形与式(1) 类似.

子情形2.2:θ=ψ₁∧ θ₂与θ=θ₁∧ ψ₂.

与子情形2.1类似.

子情形2.3:θ=ψ₁∧ ψ₂.

由定理3.3可知, 结论成立.

推论3.5. 给定缺省理论Γ=(T, Δ), 其中, T是协调的公式集合, Δ是缺省规则的集合.对于任意的公式集合E, 如果E是缺省理论Γ=(T, Δ)的一个GD-扩展, 则E是协调的.

证明:根据GD-扩展的定义, 我们对自然数n进行归纳.

基始:当n=0时, 由于T₀=T, T是协调的, 因此＄T_0＄是协调的公式集合.结论成立.

归纳步骤:假设当＄n=k＄时, 结论成立, 即T_k是协调的公式集合.当n=k+1时, 令δ是序最优的, 并且是可以被作用的缺省规则.根据缺省规则的推导规则,

并且${{T}_{k+1}}={{T}_{k}}\cup \{\theta \}.$由定理3.4, T_k+1是协调的.并且根据GD-扩展的定义过程, 对于任意的自然数i, j, 如果i≤j, 则有T_i⊆ T_j.因此, $\bigcup\limits_{i=0}^{k+1}{{{T}_{i}}}={{T}_{k+1}}.$于是, 对于任意的自然数n, 都有T_n和$\bigcup\limits_{i=0}^{n}{{{T}_{i}}}$均是协调的.又因为GD-扩展$E=Th\left(\bigcup\limits_{i=0}^{\infty }{{{T}_{i}}} \right), $因此E是协调的.

在第2节中, 我们给出了贪婪缺省逻辑中GD-扩展的定义.自然而然地, 我们会产生疑问, 对于缺省理论Γ, Γ在贪婪缺省逻辑中的GD-扩展E和缺省逻辑中的扩展E' 存在怎样的区别与联系呢?

可以发现, 贪婪缺省逻辑GD-扩展的定义与缺省逻辑扩展的构造定理是类似的, 且贪婪缺省逻辑的目标是尽可能地保留缺省规则中的信息.那么, 对于GD-扩展E, 是否存在扩展E' 使得E' ⊆ E?亦或对于扩展E' ,是否存在GD-扩展E使得E' ⊆ E?

首先, 回到本文开始部分提出的问题, Jone是一个没有腿的人和人是缺省的有胳膊并且有腿的; 其次, 我们使用贪婪缺省逻辑的推导规则, 是否可以得到我们想要的结果?

例4.1:给定缺省理论Γ=(T, Δ), 其中, $T=\{\text{Man(Jone)}, \neg \text{HasLeg(Jone)}\}$, $\Delta =\{\text{Man}(x)\rightsquigarrow \text{HasLeg}(x)\wedge \text{HasArm}(x)\}.$

构造关于缺省理论Γ的证明树如下:

于是, 缺省理论的GD-扩展为Th({Man(Jone), ¬ HasLeg(Jone), HasArm(Jone)}).因此, 通过人是缺省的有胳膊和腿的这条规则以及Jone是一个没有腿的人推导出Jone是有胳膊而没有腿的.

下面我们将通过给出的几个具体例子来探讨贪婪缺省逻辑的扩展与缺省逻辑扩展之间的关系.

例4.2:给定缺省理论Γ=(T, Δ), T={p}, D={δ₁, δ₂}, 其中, ${{\delta }_{1}}=p\rightsquigarrow \neg {{q}_{1}}, {{\delta }_{2}}=p\rightsquigarrow {{q}_{1}}\wedge {{q}_{2}}.$

我们可以写出两棵关于该缺省理论的证明树.

根据证明树, 可以得到缺省理论Γ的两个GD-扩展:${{E}_{1}}=Th(\{p, \neg {{q}_{1}}, {{q}_{2}}\}), {{E}_{2}}=Th(\{p, {{q}_{1}}\wedge {{q}_{2}}\}).$另一方面, 根据缺省理论扩展的定义, 缺省理论Γ有两个扩展:${{E}_{3}}=Th(\{p, \neg {{q}_{1}}\}), {{E}_{4}}=Th(\{p, {{q}_{1}}\wedge {{q}_{2}})\}, $且有${{E}_{3}}\subseteq {{E}_{1}}$和E₂=E₄.

即缺省理论的扩展可能是其GD-扩展, 也可能是其GD-扩展的子集.

接下来, 我们考虑一个公式结构稍微复杂些的例子.

例4.3:给定缺省理论$\Gamma =(T, \Delta), T=\{p\}, \Delta =\{{{\delta }_{1}}, {{\delta }_{2}}, {{\delta }_{3}}, {{\delta }_{4}}\}, $其中, ${{\delta }_{1}}=p\rightsquigarrow \neg {{q}_{1}}, $${{\delta }_{2}}=p\rightsquigarrow \neg {{q}_{3}}, $${{\delta }_{3}}=p\rightsquigarrow \neg {{q}_{4}}$以及${{\delta }_{4}}=p\rightsquigarrow (({{q}_{1}}\wedge {{q}_{2}})\wedge {{q}_{3}})\vee {{q}_{4}}.$

以序列L=δ₁, δ₂, δ₃, δ₄构造的证明树为例.

首先分解左边的这一支S₁, 可以得到

再来分解S₂这一支, 可以得到(为了简化标记, 我们使用符号T' 表示集合$T\cup \{\neg {{q}_{1}}, \neg {{q}_{3}}, \neg {{q}_{4}}\}$):

节点S₅, S₆, S₈, S₁₀, S₁₁和S₁₂的上层公式都是Atomic规则, 即它们都是叶子节点, 其他节点都是中间节点, 它们都是通过联结词的分解规则亦或是传递规则联结起来的.这样即构成了一棵以$T|{{\delta }_{1}}, {{\delta }_{2}}, {{\delta }_{3}}, {{\delta }_{4}}\Rightarrow T, \neg {{q}_{1}}, \neg {{q}_{3}}, \neg {{q}_{4}}, {{q}_{2}}$为根节点的证明树.

我们给出图 1证明树的结构示意图以帮助理解.

图 1

Fig. 1

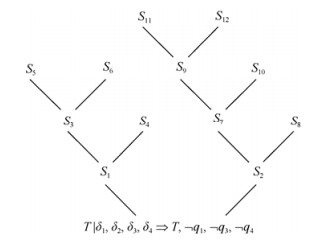
Fig. 1 Structure of proof tree 图 1 证明树结构示意图

根据证明树与GD-扩展的定义, 我们可以得到缺省理论Γ的一个GD-扩展${{E}_{1}}=Th(\{p, \neg {{q}_{1}}, \neg {{q}_{3}}, \neg {{q}_{4}}\}).$

类似地, 我们可以得到缺省理论Γ在其他23种序列下的证明树, 由于数目较多, 这里我们不再一一列举.从24种不同序列的证明树中, 我们可以根据定义得到缺省理论Γ的3个不同的GD-扩展.

根据缺省逻辑扩展的定义, E₁, E₂和E₃都是缺省理论Γ的扩展.即在这个缺省理论中, E₁, E₂和E₃既是缺省理论的扩展, 又是缺省理论的GD-扩展.并且, Γ任意的两个不同的GD-扩展的并集都是不协调的.

下面的例子则说明, 可能存在某些GD-扩展, 并不存在扩展, 使得这些GD-扩展与扩展之间有包含关系.

例4.4:给定缺省理论$\Gamma = (T, \Delta), T = \{ p\}, \Delta = \{ {\delta _1}, {\delta _2}, {\delta _3}\}, $其中, ${{\delta }_{1}}=p\rightsquigarrow {{q}_{1}}\wedge {{q}_{2}}, $${{\delta }_{2}}=p\rightsquigarrow \neg {{q}_{1}}$以及${{\delta }_{3}}=p\rightsquigarrow \neg {{q}_{2}}.$

与例4.3类似, 可以得到缺省理论Γ在6种序列下的证明树, 因此下面的缺省矢列式都是GD-可证的.

根据GD-扩展的定义, 我们可以得到缺省理论Γ的4种不同的GD-扩展.

根据缺省逻辑中扩展的定义, Γ的扩展为

从而有E₁=E₅, E₃=E₆, 即E₁和E₃既是缺省理论的扩展, 又是缺省理论的GD-扩展.但是, 不同于例4.3, 在该例子中, GD-扩展E₂和E₄并不包含该缺省理论的扩展.

那么贪婪缺省逻辑中缺省理论的GD-扩展是否也与扩展一样具有半单调性呢?我们先看下面的例子.

例4.5:给定缺省理论$\Gamma = (T, \Delta)$和$\Gamma ' = (T, \Delta '), $$T = \{ p\}, \Delta = \{ {\delta _1}\}, \Delta ' = \{ {\delta _1}, {\delta _2}\}; $其中, ${{\delta }_{1}}=p\rightsquigarrow {{q}_{1}}\wedge {{q}_{2}}, $${{\delta }_{2}}=p\rightsquigarrow \Subset \neg {{q}_{1}}.$

分别构造缺省理论Γ与Γ' 的证明树.Γ只有1棵证明树如下:

缺省理论Γ ' 有两棵证明树, 分别为

因此, 缺省理论Γ只有一个GD-扩展:$E=Th(\{p, {{q}_{1}}\wedge {{q}_{2}}\}), $缺省理论Γ' 有两个GD-扩展${{{E}'}_{1}}=Th(\{p, {{q}_{1}}\wedge {{q}_{2}}\})$和${{{E}'}_{2}}=Th(\{p, \neg {{q}_{1}}, {{q}_{2}}\}), $其中, $E={{{E}'}_{1}}.$

根据上述的例子, 我们可以得到下面的定理.

定理4.6(GD-扩展的存在性). 一个缺省理论至少有一个GD-扩展.

定理4.7(GD-扩展的半单调性). 给定缺省理论Γ₁=(T, Δ)和缺省理论Γ=(T, Δ' ), 满足D⊆ D' .如果E是缺省理论Γ₁的一个GD-扩展, 那么一定存在缺省理论Γ₂的一个GD-扩展E' ,使得E⊆ E' .

证明:因为E是缺省理论Γ₁的一个GD-扩展, 根据GD-扩展的定义, 一定存在序列T₁, T₂, …, T_i, …(T_i的定义见定义2.12), 使得$E=Th\left(\bigcup\limits_{i=0}^{\infty }{{{T}_{i}}} \right).$下面我们证明存在E' ,使得E⊆ E' .

因为根据GD-扩展的定义, 对于每一个集合T_i, 都对应一个缺省规则δ_i+1, 并且δ₁, δ₂, …, δ_i, …是缺省规则集合Δ上的一个全序L.定义Δ^–=Δ' –Δ和Δ' 上的一个全序L' , L' 满足

● 对于任意δ₁, δ₂∈ Δ, 如果${{\delta }_{1}}{{\succcurlyeq }^{L}}{{\delta }_{2}}, $则${{\delta }_{1}}{{\succcurlyeq }^{{{L}'}}}{{\delta }_{2}}; $

● 对于任意δ∈ Δ和δ' ∈ Δ^–, 都有$\delta {{\succcurlyeq }^{{{L}'}}}{\delta }'.$

因此根据定义, 按照序列L' 生成的GD-扩展E' 满足对于任意T_i, 都有T_i⊆ E' .故而$Th\left(\bigcup\limits_{i=0}^{\infty }{{{T}_{i}}} \right)\subseteq {E}', $即E⊆ E' .

定理4.8. 给定缺省理论Γ=(T, Δ), 如果存在公式的集合E是Γ的扩展, 则存在Γ的一个GD-扩展E' ,使得E⊆ E.反之不成立.

证明:因为集合E是Γ的扩展, 根据定理1.6, 存在一个集合的序列E₀, …, E_i, …, 使得

故而, 令

则有${E_{i + 1}} = Th({E_i}) \cup \{ \psi |\phi \psi \in {\Delta _i}\}.$并且, 对于每个${\Delta _i} = \{ {\delta _{i1}} = {\phi _{i1}}{\psi _{i1}}, {\delta _{i2}} = {\phi _{i2}}{\psi _{i2}}, ...\}, $都有:

并且, $\{\psi |\phi \rightsquigarrow \psi \in {{\Delta }_{i}}\}=\bigcup\limits_{j=1}^{\infty }{\{{{\psi }_{ij}}\}}, $即${{E}_{i+1}}=Th({{E}_{i}})\cup \bigcup\limits_{j=1}^{\infty }{\{{{\psi }_{ij}}\}}.$

我们将Δ中缺省规则的序列定义为$L::{{\delta }_{01}}, {{\delta }_{02}}, ...{{\delta }_{i1}}, {{\delta }_{i2}}, ...{{{\delta }'}_{1}}, ..., {{{\delta }'}_{i}}, ...$, 其中, ${{\delta }_{ij}}\in \bigcup\limits_{k=0}^{\infty }{{{\Delta }_{k}}}, {{\delta }_{{{i}'}}}\in \Delta -\bigcup\limits_{k=0}^{\infty }{{{\Delta }_{k}}}.$故而由L生成的序列E' 满足$E\subseteq {E}'.$

反之不成立, 见例4.4.在例4.4中, Th({p, q₁∧ q₂})和Th({p, ¬ q₁, ¬ q₂})是Γ的GD-扩展, 又是Γ的扩展, 但是GD-扩展Th({p, ¬ q₁, q₂})和Th({p, ¬ q₂, q₁})都不是Γ的扩展.

我们可以得出贪婪缺省逻辑是不能退化为缺省逻辑的, 故而我们得到下面的定理.

定理4.9(不可退化性). 存在一个缺省理论Γ, 对于任意的集合E, 都有E是缺省理论Γ的扩展当且仅当E是缺省理论Γ的GD-扩展.

本文提出了一种贪婪缺省逻辑, 旨在构造扩展时能尽可能地保留缺省规则中的信息, 并给出了贪婪缺省逻辑的推演系统—GD系统和贪婪缺省逻辑的GD-扩展的构造型定义.证明了贪婪缺省逻辑的存在性、半单调性和不可退化性等性质, 说明了贪婪缺省逻辑与经典缺省逻辑是两种不同的逻辑.