2. 可信软件国际联合研究中心 (华东师范大学), 上海 200062;
3. 上海市高可信重点实验室 (华东师范大学), 上海 200062
2. International Joint Research Center of Trustworthy Software (East China Normal University), Shanghai 200062, China;
3. Shanghai Key Laboratory of Trustworthy Computing (East China Normal University), Shanghai 200062, China
信息-物理融合系统 (cyber-physical system, 简称CPS)[1]是一类综合计算、网络和物理环境的多维复杂系统, 在健康医疗、智能交通、航空电子、智能建筑等领域有着广泛的应用前景.与传统系统不同, CPS是一个交叉领域学科, 除计算机外, 还融合了机械、环境、土木、电子、生物、化学、航空等诸多工程领域的模型和方法.CPS是一种运行在开放环境中的复杂异构系统, 存在大量不确定性因素, 如运行环境、信号误差、人的行为等.CPS具有以下两个特点:1) CPS的应用大都安全攸关或功耗要求严苛, 在保证系统功能正确的前提下, 还需要满足非功能性需求约束, 如吞吐量、能耗、时间等; 2) CPS是异构的混成系统, 融合了连续的物理过程和离散的系统行为, 且其运行的开放环境具有不确定性、随机性.因此, 如何使用现有的模型检测技术分析验证CPS的正确性及量化评估系统性能指标, 是当前面临的挑战.
传统的模型检测技术通过对系统的状态空间进行全遍历, 能够自动验证、分析系统行为的安全性、可靠性, 但是它存在状态空间爆炸的问题 (即随着系统规模的增加, 系统的状态空间呈指数级增长).随着系统规模的扩大, 传统的模型检测算法[2-4]很难验证、分析复杂系统行为的正确性、可靠性, 也无法进行定量评估分析.因此, 使用传统的模型检测技术分析验证CPS的可靠性、定量评估系统的性能面临着巨大困难.统计模型检测技术 (statistical model checking, 简称SMC)[5]能够有效评估系统模型满足目标约束的概率区间, 可用于定量分析系统模型的性能指标, 能够有效缓解状态空间爆炸问题.统计模型检测技术主要使用统计方法分析复杂系统的模拟执行路径, 优点是效率高、执行速度快, 该项技术的关键点在于:首先生成系统的模拟路径, 并对其进行伯努利实验, 判断模拟路径是否满足给定的系统约束; 其次, 使用假设检验的方法对系统模拟路径的样本空间进行统计分析, 评估系统满足约束的概率区间.对于大型、复杂的系统而言, 生成系统模拟路径要更快、更容易, 而不需要将系统模型转换为验证工具的输入语言.因此, 统计模型检测技术为大型、复杂的CPS的正确性、可靠性分析和性能评估提供了广阔的研究前景.目前, SMC技术已引起学术界和工业界的广泛关注, 成功应用于分析实时调度[6]、生物系统[7]、能耗感知的智能家居 (energy-aware building)[8, 9]等领域.
虽然SMC无需遍历状态空间, 但当结果的精度要求较高或者检测小概率事件时, 仍需生成大量系统执行路径才能使统计算法收敛.随着系统规模的增加, 路径的生成和验证十分耗时.因此, 如何有效减少SMC收敛所需的路径数量, 提供一个高效实用的SMC验证方案, 是对CPS进行有效验证的重要问题.针对该问题, 我们的工作贡献主要包括以下3个方面.首先, 通过对已有SMC算法的原理分析和实验比较, 得出贝叶斯区间估计算法是实用性和效率最好的算法.但其存在实际概率趋于0.5时所需路径数量剧增的问题, 为弥补贝叶斯区间估计算法的不足, 我们提出了基于抽象和学习的统计模型检测方法, 旨在减少统计分析所需的路径数量, 提高SMC的效率.其次, 我们提出了一种自适应的SMC算法框架, 可根据系统满足目标约束的概率估值, 动态地在BIE和基于抽象和学习的统计模型检测算法之间选择合适的算法.该算法框架为CPS的验证问题提供了一种效率较高的验证途径.最后, 我们通过几个典型的CPS案例对单纯的BIE算法和自适应SMC算法进行对比, 实验数据表明, 使用自适应SMC算法框架能够有效提高SMC的效率, 并将误差控制在一定范围内.
1 现有统计模型检测算法的分析比较统计模型检测技术建立在蒙特卡洛模拟 (Monte Carlo) 技术之上, 它能够有效评估系统模型满足目标约束的概率区间, 对系统进行验证分析.SMC算法主要分为定性和定量两类, 定性类算法包括3种:Single Sampling Plan (SSP), Sequential Probability Ratio Test (SPRT) 和Bayesian Hypothesis Testing (BHT), 用以验证“系统S满足BLTL约束φ'的概率是否大于或等于某个概率阈值θ(θ∈(0, 1))”这类问题, 即SP≥θ(φ'); 定量类算法包括Approximate Probabilistic Model Checking (APMC) 和Bayesian Interval Estimation (BIE), 用以解决“系统S满足约束φ'的概率是多少”这类问题, 即SP=?(φ').不同类型的SMC算法的主要区别在于统计参数的计算和置信度满足条件的判断上, 由于SSP算法可用性不高, 且与SPRT算法的原理类似, 下面我们主要针对统计参数的计算和置信度满足的判断条件两部分, 对其余4种SMC算法进行简要的原理分析和性能评估.
1.1 4种SMC算法的原理分析定性类算法都基于假设检验.通过随机取样并检验原假设 (即被检验的假设)H0:P≥θ与备择假设H1:P < θ(P是S满足φ'的真实概率) 来判断某条路径是接受H0还是拒绝H0.这种方法并不能保证结论完全正确, 只能通过参数限定来减少犯错的机率.
定量算法可以直接返回S满足φ'的概率p, 并将误差限定在某一范围内.APMC和BIE两种算法都可被看作返回一个概率区间, 即 (p-δ, p+δ), 但两种算法计算获得p和δ的方式不同.
1.1.1 SPRT算法最初Wald提出的SPRT方法[10]基于简单假设 (如H:p=0.8), 在错误率同等的条件下, 最小化所需样本总数, 此时, SPRT可达到最优.然而SMC所验证的问题都是基于复合假设 (如H:p≥0.8) 的, 因此, Younes等人将SPRT扩展到复合假设检验[11], 引入无差异区域 (p1, p0), 但此时的SPRT已无法达到最优.SPRT需要选择两个参数A和B(A > B) 来保证检验强度, 并计算概率比, 即
| $ \frac{{{p_{1n}}}}{{{p_{0n}}}} = \prod {\frac{{\Pr ({B_i} = {b_i}|p = {p_1})}}{{\Pr ({B_i} = {b_i}|p = {p_0})}}} = \frac{{p_1^x{{(1-{p_1})}^{n-x}}}}{{p_0^x{{(1-{p_0})}^{n - x}}}} $ | (1) |
当
基于贝叶斯的假设检验方法BHT[12]同样利用一个概率比值来衡量H0和H1的相对倾向程度, 称为贝叶斯因子 (Bayes factor), 它最早由Jeffreys[13]提出.对于原假设H0和备择假设H1, 贝叶斯因子B被定义为两者的似然比, 它在数理统计中是一个能够同时反映灵敏度与特异度的综合指标, 即
| $ B = \frac{{P({d_n}|{H_0})}}{{P({d_n}|{H_1})}} $ | (2) |
这里, dn表示样本路径集.在BHT算法中, 我们通常还会预设一个常数阈值T(要求T > 1), 如果B > T, 则接受H0假设; 如果B < T, 则接受H1假设.贝叶斯统计的难点在于复杂的条件概率计算, 这可以利用共轭分布来简化计算.由于SMC所验证的参数θ是 (0, 1) 上的值, 所以适合使用Beta分布 (定义在 (0, 1) 上有两个参数α, β > 0的概率分布), Beta概率密度函数表达如下:
| $ {g_{(\alpha, \beta )}}(u) = \frac{1}{{B(\alpha, \beta )}}{u^{\alpha-1}}{(1-u)^{\beta-1}} $ | (3) |
其中, B(α, β) 为Beta函数:
| $ B(\alpha, \beta ) = \int_{{\kern 1pt} 0}^{{\kern 1pt} 1} {{t^{\alpha-1}}{{(1-t)}^{\beta-1}}{\rm{d}}t} $ | (4) |
通过调整Beta函数, 可以近似模拟许多 (0, 1) 上的光滑单峰概率密度.特别地, 当α=β=1时, 其实是 (0, 1) 上的均匀分布, 通常被用作BHT计算的默认先验分布.
1.1.3 APMC算法最早由Thomas等人[14]提出的APMC算法通过计算x/n(x表示实际正样本数, n表示总样本路径数) 来获得概率p, 并通过Chernoff-Hoeffding界来保证其准确性.Hoeffding在文献[12]中证明, 通过统计获得的
| $ p = x/n $ | (5) |
与真实概率P之间满足
| $ \Pr (|P-p| \le \varepsilon ) \ge 1-\delta, 当N \ge 4\log \left( {\frac{2}{\delta }} \right)/{\varepsilon ^2} $ | (6) |
此外, APMC算法需要两个参数ε(近似参数), d(置信参数) 来保证结果准确性, 并可以计算出所需的路径样本数量n.
1.1.4 BIE算法BIE算法[15]是一种基于贝叶斯统计理论的SMC算法.与APMC不同, BIE算法不直接计算其值, 而是寻找包含真实概率的区间, 然后, 取估值区间 (假定为 (t0, t1)) 的中间值作为概率p, 即p=t0+x=t1-x.这里, x是预设的半区间大小.
因此, BIE算法的核心为区间估计.当给定一个目标阈值 (区间覆盖系数
| $ \int_{{\kern 1pt} {t_0}}^{{\kern 1pt} {t_1}} {f(u|{d_n}){\rm{d}}u} = c $ | (7) |
由于区间 (t0, t1) 包含了真实概率P, 所以在满足公式 (7) 的条件下尽量缩小区间.然而, 并非所有分布都能保证找到这样的最优区间, 对于Beta分布这样的单峰概率密度, 可取后验概率的均值作为所求区间的中心, 再通过预设的δ得到区间端点.对于参数为α, β的Beta先验分布, 后验概率的均值为p=(x+α)/(n+α+β), 后验概率分布函数如下:
| $ \int_{{\kern 1pt} {t_0}}^{{\kern 1pt} {t_1}} {f(u|{d_n}){\rm{d}}u} = {F_{x + \alpha, n-x + \beta }}({t_1})-{F_{x + \alpha, n-x + \beta }}({t_0}) $ | (8) |
其中, dn表示样本路径集, F(·) 为Beta分布函数.
1.2 4种SMC算法的性能比较SMC算法的总体性能取决于仿真器和统计分析器的性能.对于大多数模型而言, 路径的产生与验证耗时占SMC总体耗时的90%左右[15].仿真器的性能直接决定了每条执行路径产生的效率, 不同模型和工具差异较大, 且与SMC的统计分析效率无关.我们将使用取随机数的方式来模拟不同的概率空间, 将仿真器对SMC算法性能的影响降到最低, 以准确评估SMC算法本身的性能。此外, 我们还对比算法终止时所需的路径数量 (可看作SMC算法对仿真器性能的依赖程度).下面将从算法所需的路径数和统计计算的耗时两个方面, 对4种SMC算法进行性能比较.
图 1(a)和图 1(b)分别展示了真实概率P为0.3和0.5时, 执行100次SPRT算法所需的平均路径数量.由图 1可知:随着置信度 (α, β) 的提高, 所需路径数会增加; 并且概率阈值θ越接近真实概率, 所需路径越多.

|
Fig. 1 Traces needed for SPRT algorithm at different confidence and probability threshold θ 图 1 不同置信度和概率阈值θ下, SPRT算法所需的路径数量 |
图 2展示了真实概率P为0.3和0.5时, 执行100次BHT算法所需的平均路径数量.规律与SPRT类似:随着贝叶斯因子的可接受阈值T的增大, 所需样本数量呈指数增长.实验中, 当BHT算法的θ约等于真实概率时, 所需路径数接近正无穷.

|
Fig. 2 Traces needed for BHT algorithm at different confidence and probability threshold θ 图 2 不同置信度和概率阈值θ下, BHT算法所需的路径数量 |
图 3对比了SPRT与BHT在同一置信度下所需的路径数量 (SPRT的δ=0.01, BHT的T=10000).当θ远离真实概率时, BHT算法所需路径数少于SPRT算法; 但当θ接近真实概率时, BHT所需路径数急剧增大, 可能远大于SPRT所需路径数.

|
Fig. 3 Traces needed for SPRT and BHT algorithm with the same confidence (δ=0.01, T=10000) 图 3 同一置信度下SPRT与BHT算法所需路径数量的对比 (δ=0.01, T=10000) |
图 4(a)展示了执行100次APMC算法所需的平均路径数量.如图 4所示, APMC在检验不同概率值时, 所需路径数量相等; 但随精度要求提高, 所需路径数量也急剧上升.

|
Fig. 4 Traces needed for APMC and BIE algorithm at different probabilities under different accuracy 图 4 不同精度下, APMC和BIE算法检验不同概率值所需的路径数量 |
图 4(b)展示了执行100次BIE算法所需的平均路径数量.由图可知, BIE在真实概率P为0.5时所需路径最多, 而接近0或1时所需路径数最少.对比发现, BIE所需路径数在精度较高时明显小于APMC所需路径数 (当δ= 0.01, BIE中的c=0.9, 即APMC中的1-ε=0.9时, BIE所需最大路径数为17 000, 而APMC所需路径数为212 000).
图 5则更直观地比较了APMC与BIE在同一精度下所需的路径数量.

|
Fig. 5 Traces needed for APMC and BIE algorithm with the same accuracy (δ=0.01, c=1-ε=0.9) 图 5 同精度下APMC与BIE算法所需路径数对比 (δ=0.01, c=1-ε=0.9) |
接下来分析比较4种SMC算法的耗时情况.表 1为4种SMC算法在1 000次迭代下统计计算部分的耗时对比.其中, BHT和BIE在不同积分步长下耗时差异显著, 可见, 积分是贝叶斯类SMC算法的主要耗时部分, 具体应用中, 我们应根据需要选择合适的积分步长; 而SPRT与APMC算法的耗时都小于1ms.尽管BHT与BIE的统计过程耗时严重, 但仍远小于仿真路径的生成和验证所需的时间.例如, BIE在积分步长为10 000时, 单次迭代耗时仅0.02s, 而仿真软件生成一条路径的耗时普遍在0.3s~3s, 可见, 实际应用中, BIE的积分过程并不会成为性能瓶颈.由以上实验数据分析可知, BIE与BHT所需路径数量较少, 因此实际应用中的总体性能将优于SPRT与APMC.
| Table 1 Time consuming of different SMC algorithms' computation part (at 1 000 iterations) 表 1 SMC算法统计计算部分的耗时对比 (1 000次迭代) |
综上, 我们可以得出以下结论:
(1) 定性类算法 (SPRT和BHT) 得出验证结果所需的路径数要小于定量类算法 (APMC和BIE), 但定量类算法能够评估出系统满足目标约束的概率区间, 可以有效地对系统的性能进行定量评估, 这在实际中更有用.
(2) SPRT和BHT算法在验证真实概率接近概率阈值的约束时性能最差, 其中, BHT所需路径数量将急剧增大, 接近无穷, 几乎无法完成验证; 而BIE在检验真实概率P接近0.5的约束时性能最差, 因此, 使用中应尽量避免这两类情况出现.
(3) APMC算法的统计分析效率高于BIE算法, 而BIE算法所需路径数少于APMC算法.对于大多数模型, 路径的生成和验证都为主要耗时部分, 所以BIE算法在实际应用中性能更好.
2 基于抽象和学习的SMC算法通过对现有的4种SMC算法的原理分析和实验数据的总结可知, 在实际应用中, BIE算法可定量确定目标约束的概率区间且效率较高.但在实际概率接近0.5时, BIE算法所需路径数量急剧增加, 由于路径的生成和验证为SMC算法的主要耗时部分, 这将严重影响算法的性能.为了在整个概率区间内都能有效地使用SMC算法对CPS进行约束验证, 我们提出了一种基于抽象和学习的SMC算法 (AL-SMC), 以解决BIE算法在真实概率P接近0.5时所需路径数目剧增的问题.
2.1 基于抽象和学习的统计模型检测为了避免直接计算最终概率, 可采用分解模型的方式, 使得每一个子模型计算的概率远离0.5.基于此思想, 我们提出了一种基于抽象和学习的SMC算法.
2.1.1 基本思想通过对SMC算法分析路径过程的研究可知, 每条路径在某一时间点上即可判断满足或不满足φ'.而对于不同模型, 该点在时间轴上的分布情况不同.假设对于n个样本路径 (时间长度为t), 最终在时间[0, t]上满足φ'的概率为p, 且存在m≥1段子路径 (时间段分别为
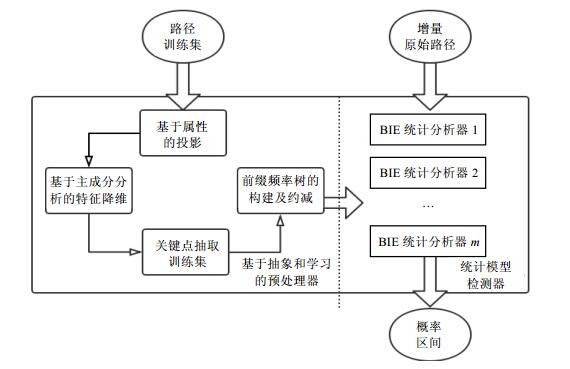
AL-SMC算法的核心思想如图 6所示.
|
Fig. 6 Framework of the optimized SMC algorithm 图 6 优化的统计模型检测算法框架 |
● 首先, 取少量的样本路径 (样本数量可根据不同的精度需求自定) 作为路径训练集, 并将其作为基于抽象和学习的路径预处理器的输入.
● 接着执行预处理器.它主要包括4个功能模块:基于约束的投影、基于主成分分析的特征降维、关键点抽取以及前缀频率树的构建与约减.
● 经过预处理器处理后得到的PFT和增量原始路径一起作为统计模型检测器的输入, 借助多个普通的SMC (如BIE) 算法同时进行统计分析, 再求和得到最终概率.
下面, 我们将简单介绍AL-SMC算法中两个阶段的核心步骤, 更详尽的算法过程参见文献[16].
2.1.2 抽象阶段抽象阶段利用不同的抽象技术对原始路径δ0进行简化, 其详细代码描述如图 7所示.

|
Fig. 7 Abstraction and simplification of Trace 图 7 路径的简化和抽象 |
如算法1中所描述, 路径的简化和抽象主要分为3个关键步骤, 即算法中的traceDiscretization(·) 函数 (对应于图 6中的基于属性的投影模块)、pcaDimensionReduction(×) 函数 (对应于图 6中的主成分分析模块) 和traceExtraction(·) 函数 (对应于图 6中的前缀频率树的构建和降维模块).下面我们简要介绍这3个函数的基本思想.
1) traceDiscretization(·) 函数
在CPS中, 存在大量离散和连续变量, 设变量集合为SV=L∪X; 一条原始路径δ0是k维向量v的集合 (k=#(SV), 即SV的元素个数).由于离散变量改变的状态点对应于系统的关键状态点, 基于此, 分两步对原始路径进行处理:
(1) 基于离散变量分段.找到路径中所有离散变量有变化的时间点ti, 对路径进行第1次分段, 并增加两个维度sChk; tChk:sChk表示子段路径是否满足φ', tChk表示整段路径目前是否满足φ'.
(2) 面向目标约束对连续变量投影.当检验某一确定约束公式 (如φ') 时, 只考虑某些连续变量在路径的哪一点使约束满足, 因此将约束中不包含的连续变量删去, 其余连续变量投影到上面新增的两维上去.投影方法类似于检查给定路径段上φ'是否满足, sChk只检验子路径满足情况, tChk从第1个sChk变为1的时刻开始, 之后都为1.
2) pcaDimensionReduction(·) 函数
经过traceDiscretization(·) 函数处理后, 路径中只留下离散变量.由于对某一具体的公式φ', 影响系统满足该约束的核心变量并不多, 可利用变量之间的相关性来进一步减少变量.我们借助机器学习中常用的一种降维算法——主成分分析 (principal components analysis, 简称PCA)[17], 继续对路径进行投影抽象.
首先将特征的概念引入CPS模型中, 并利用方差贡献来建立目标评价模型, 计算每个成分 (即变量) 的综合得分, 然后排序.在经过标准化、计算协方差矩阵、计算特征值和特征向量、求主成分和计算综合得分等步骤后, 即可求得问题的主成分变量, 从而减少路径中的变量总数.
3) traceExtraction(·) 函数
经过抽象之后, 状态已经相对较少, 但并非所有状态量都对计算最终概率有用, 还需将对路径中的状态点进行筛选.关键点提取方法的具体步骤是:
(1) 关键点必包含每条路径中判断其满足φ'的点 (即tChk=1的点), 这是计算满足概率的直接相关点.
(2) 经PCA降维后的变量不再是二值, 而是多值, 因此, 我们选择训练样本集下频率总和有较大覆盖的取值 (如频率和≥0.8) 即可.
2.1.3 学习阶段经过前3个步骤的抽象简化后, 路径的复杂度大为降低.接下来是学习阶段, 通过构造用于统计模型检测分析的前缀频率树来划分出概率更平均的路径段, 前缀频率树的定义如下.
定义 (前缀频率树 (prefix frequency tree, 简称PFT)).一棵前缀频率树T是一个元组T=(D, R, d0), 其中,
● D代表树结点的集合.每个结点可表示为d=(id, f, n), 其中, id是这个状态向量唯一编号 (用0/1串表示), f记录在此结点终止的路径数, n记录所有经过此结点的路径数, 所以任意结点都满足f≤n.
● R代表结点之间的关系, 可表示为 (d, d'); 除根结点外, 每个结点对于R来说都有且仅有1个前驱结点, 但可以有0个或多个后继结点.
● d0∈D为树的根结点, 有且仅有1个, 对于d0来说没有前驱结点.
根据文献[18]中的随机文法推断方法 (用于从句子回推文法自动机), 可将系统的离散路径看作一种语言的句子来构造前缀频率树.我们规定不满足目标约束的样本路径为空句, 即在PFT的根结点终止; 满足目标约束的样本路径在某一非根结点终止.如此即可构建出一棵PFT, 它实际上是原系统的一个高度离散化的抽象模型, 并具有如下性质:
● n(dleaf)=f(dleaf), 即所有叶子结点的f与n相等;
●
●
尽管抽象阶段已对路径做了简化处理, 但直接利用路径δ3构造出的PFT仍然十分庞大, 因此, 可通过前缀频率树的横向、纵向约减来有效减小PFT的规模, 便于之后的分析.如图 8所示, 在构造初始PFT之后, 调用reduce1_recur(·) 函数, 通过检验、判断每个结点的孩子结点的n和f值来进行横向合并; 然后, 根据每个结点是否有分支和f值的情况, 进行结点的纵向合并, 即reduce2_recur(×) 函数, 完成进一步约减.

|
Fig. 8 Construction and reductions of PFT 图 8 前缀频率树的构建及约减算法 |
经过两步约减后, PFT各终止结点上的路径样本数更加平均, 即划分出了概率更平均的路径段.若将终止结点数/总结点数定义为前缀频率树的结点有效率, 则使用约减算法能够提高结点的有效率.
2.1.4 最终概率的统计分析约减后的PFT即T', 可看作对原系统在概率空间上进行了划分的抽象模型.假设T'含有m个非根终止结点 (f > 0), 考虑到在大样本量的情况下会有未被T'接受的正样本, 我们设置m+1个BIE分析器, 并发执行BIE统计模型检测算法, 对在不同结点终止的路径分别进行统计.当所有BIE分析器都终止时, 整个算法终止.最后, 对每个BIE分析器重新执行一次计算, 并分别进行如下处理:
1) 若pi > δ, 即pi超过半区间大小, 则表明pi值较准确, 不修正;
2) 若pi≤δ, 则表明pi不准确, 执行修正pi=xi/N.
最终概率为

|
Fig. 9 Multi-BIEs calculation of the final probability 图 9 最终概率的多BIE统计算法 |
2.2 算法分析
AL-SMC算法从原始路径 (σ0) 抽象简化至最终的前缀频率树 (T') 构建、约减的过程, 对于目标约束φ'而言, φ'是否满足以及何时满足的信息并无丢失, 只是变换了观察视角.即:对于φ'的概率空间来说, 系统模型间存在等价关系:
| $ {P_M}({d^0}) = {P_M}({d^1}) = {P_M}(T') $ | (9) |
因此, 最终概率评估的误差取决于BIE统计分析的过程.
AL-SMC算法中各阶段的时间复杂度与空间复杂度见表 2.由表 2可知:1) 基于PCA的特征降维的复杂度取决于PCA算法本身所需的特征数; 2) 两种递归算法在PFT复杂时可能会出现递归栈溢出, 可通过调整参数来有效地控制PFT的规模来解决这一问题; 3) 最终概率的多BIE分析算法所需迭代次数因实际情况而定, 而单次迭代的时间主要取决于积分步长.
| Table 2 Time and space complexity of AL-SMC algorithm 表 2 AL-SMC算法的时间与空间复杂度 |
3 自适应的统计模型检测框架
AL-SMC算法可以有效缓解BIE算法在实际概率值接近0.5时遇到的性能问题, 因此, 结合BIE和AL-SMC算法, 可以对[0, 1]区间上的任意概率进行有效验证.在此基础上, 本文提出了一种动态的自适应SMC算法框架, 对于一个CPS实例, 可根据概率值的预估, 灵活选择SMC算法, 其算法流程图如图 10所示.

|
Fig. 10 Framework of the self-adaptive SMC algorithm 图 10 自适应SMC算法框架 |
首先, 根据有无先验分布, 选择定性算法SPRT或BHT, 进行概率区间预估计 (通常可以在100条~200条路径内完成).为了快速预估计概率, 我们对[0, 1]概率区间进行划分, 有t1=0.15, t2=0.5, t3=0.85这3个点.同时检验3个约束公式P1:P≥0.15(φ'), P2:P≥0.5(φ'), P3:P≥0.85(φ'), 通过它们的满足情况选择合适的SMC算法, 再进行定量评估. SPRT或BHT分析的误差概率取0.1, 以保证P1, P2, P3中至少能有2个约束可在250条路径内完成, 若有某一约束在250条路径内尚未完成, 则说明真实概率在其对应的概率区间内.
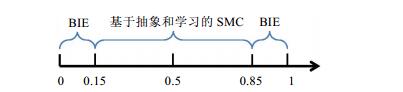
图 11为最终定量算法的选择区间.这里有两种定量类算法可选:BIE算法与AL-SMC算法.当所检验概率在[0+δ, 0.5-η]和[0.5+η, 1-δ]范围时 (η一般取0.3~0.35, δ为半区间大小), 选择BIE算法; 否则, 选择AL-SMC算法. AL-SMC算法弥补了BIE算法的不足, 可以更高效地检验真实概率P接近0.5左右的概率约束, 但需要保证P不超过0.5.
|
Fig. 11 Selection interval of the final algorithm 图 11 最终定量算法的选择区间 |
下面给出详细的算法选择过程.P1, P2, P3的检验结果可分为7种情况.
(1) P1, P2, P3都不满足, 表明P∈[0, 0.15), 选择BIE;
(2) P1未完成且P2, P3不满足, 表明P接近0.15, 选择AL-SMC;
(3) P1满足且P2, P3不满足, 表明P∈(0.15, 0.5), 选择AL-SMC;
(4) P2未完成且P1满足P3不满足, 表明P接近0.5, 选择AL-SMC;
(5) P1, P2满足且P3不满足, 表明P∈(0.5, 0.85), 约束取反, 选择AL-SMC;
(6) P1, P2满足且P3未完成, 表明P接近0.85, 约束取反, 选择AL-SMC;
(7) P1, P2, P3都满足, 表明P∈(0.85, 1], 选择BIE.
最后, 根据自适应SMC算法框架所选择的算法, 完成最终概率的统计分析.本算法中虽然多次调用SMC算法, 但可以重用已生成的路径, 因此整体效率较高.其中, 概率的划分和选择也基于大量实验结果, 具有一定的通用性.自适应SMC方法的详细伪代码如图 12所示.

|
Fig. 12 Pseudocode of the self-adaptive SMC algorithm 图 12 自适应SMC算法框架伪代码 |
4 案例分析
为了对自适应统计模型检测方法进行实际应用分析, 我们对智能温控系统、移动机器人路径规划和蓝牙协议进行了约束验证, 并根据实验结果分析比较了自适应SMC算法框架和单纯的BIE算法的性能.待验证的约束公式见表 3(每个公式都在两种参数设定下进行验证:(1) δ=0.05, c=0.99;(2) δ=0.02, c=0.9).
| Table 3 Constraint formula of three benchmarks 表 3 3个案例的目标约束公式 |
其中, φ1和φ2表示在移动机器人路径规划问题中的能量和时间的约束检验, φ3和φ4表示对智能温控系统中能量消耗和不舒服度的检验, φ5和φ6表示在蓝牙协议中对能量消耗的检验.
为了形象地阐述自适应统计模型检测框架在实例中的应用, 我们借助智能温控系统对公式φ4(0.05, 0.99) 的验证来简单解释这一过程:首先, 根据先验分布, 选择BHT算法在200条路径内来验证P1, P2, P3, 由于P2未完成 (即前述情况4), 可知真实概率P在0.5左右, 故选择AL-SMC进行验证.经过对路径训练集的抽象和学习过程, 再利用增量原始路径, 使用多BIE统计分析器可计算出最终的概率结果.
我们对每个案例进行了100次重复实验, 并将实验结果取最小值、最大值、平均值这3种情况进行分析.表 4为不同情况下, 自适应SMC方法和BIE算法所需的路径数目.由表 4可知, 采用自适应SMC算法框架可有效减少实验所需的路径数, 即提高了性能, 但是这种性能的提高并不稳定 (如对公式φ4, 可减少40%的路径数; 而对于公式φ1, 只能减少16%的路径数, 从理论上来说, 这取决于PFT的叶子结点的分布).
| Table 4 Comparison of required Traces between BIE and self-adaptive SMC algorithm of three benchmarks 表 4 3个案例中BIE和自适应SMC方法所需路径数的比较 |
表 5为自适应SMC算法和BIE算法的实验结果对比, 经过简单分析, 我们得出, 自适应SMC算法的概率误差被限制在一个区间内, 其准确度是可接受的.对于误差分析, 在文献[16]中我们做了更严谨的讨论.在实际应用过程中, 可以针对具体情况, 通过动态调整r(r为约减参数, 其值表示前缀频率树的约减程度) 值来控制自适应SMC算法的准确度.因此从实用角度来说, 相对于单纯的BIE算法, 自适应SMC算法的效率更高.
| Table 5 Comparison of result between BIE and self-adaptive SMC algorithm of three benchmarks 表 5 3个案例中BIE和自适应SMC的结果比较 |
5 相关工作
人们利用统计知识分析系统由来已久, SMC技术建立在蒙特卡洛模拟、假设检验等统计方法之上, 通过统计分析系统仿真运行的路径来验证系统满足约束的情况.它最早被Sen等人提出, 用来验证黑盒系统[19], 即SSP算法的雏形, 其难点在于确定算法收敛所需的路径总样本数量N以及接受原假设的阈值C.Younes等人[20]提出一种基于二叉搜索的算法来近似得到所需的N和C, 并指出了文献[21]中验证黑盒系统方法的一些错误.Younes等人还在Wald的SPRT原理的基础上提出了基于对数的SPRT实现算法[11, 20], 以最小化算法所需路径的样本数量.SSP与SPRT都用来解决定性验证问题, 即, 回答“系统S满足约束φ'的概率是否大于或等于某个概率阈值”这个问题, 即SP≥θ(f').与定性算法不同, 定量算法可以直接返回S满足φ'的概率p, 如APMC[14], 通过计算x/n来计算p(其中, x和n分别表示所需的路径正样本数量和总数量), 并通过Chernoff-Hoeffding界来限定结果的误差范围.随后, Zuliani, Clarke等人基于贝叶斯统计又提出了两种新SMC算法:BHT和BIE[12, 15], 前者基于贝叶斯假设检验解决定性验证问题, 后者基于贝叶斯区间估计解决定量评估问题.
从SSP, SPRT, APMC到BHT, BIE, SMC算法所需路径数量逐渐减少, 效率逐渐提高.为了进一步探索SMC技术, 人们将数值方法与统计方法相结合[22, 23], 以进一步提升SMC效率或解决一些SMC难以解决的问题, 如非确定性问题 (non-determinism).研究SMC非确定性算法的还有Henriques, 其博士学位论文讨论了如何用概率方式近似解决非确定性问题[24].目前, SMC主要验证有界 (通常指时间约束, 即time-bounded) 的约束, 因此, 如何验证传统模型检测中的无界“Until”约束, 也成了SMC研究热点之一, He, Jennings等人提出了一种将无界“Until”验证转化为有界“Until”的方法以解决此问题[25, 26].此外, 由于SMC针对系统仿真结果进行分析, 所以也不可避免地引入了仿真领域的问题, 比如小概率事件在路径中出现概率极低, 使得验证过程需要产生路径的数量过多而效率低.针对该问题, Jegourel, Legay等人基于重要性取样 (importance sampling) 和重要性分割 (importance splitting) 技术提出了面向小概率约束验证的SMC算法[27, 28], 极大地减少了验证所需的路径样本数量; 解决类似问题还可以借助于机器学习技术, 我们之前的研究工作[29]中提到的借助支持向量机预测事件、Kumar在文献[30]中借助贝叶斯推断预测事件, 都可以提高SMC的效率.
Ymer[31]和Vesta[32]是最早实现SMC的验证工具.Vesta采用了极易实现并行化的SSP算法的一个变种, Ymer采用的SPRT算法很快也被Younes证明同样能够被并行化.Vesta支持了无界“Until”的验证, 但Ymer在实验中的效率高于Vesta.此外, UPPAAL-SMC[33]和Prism[34]的最新版本也支持SMC技术, 二者都实现了定性的SPRT算法, 同时也实现了基于置信区间 (confidence interval, 简称CI)[35]的定量算法 (文献[36]对不同版本的CI统计算法进行了对比, 并根据需求的不同给出了方法选择的建议).其中, UPPAAL-SMC支持使用SHA模型建模CPS的随机行为, 并支持使用SMC算法定量评估系统的性能; Prism则使用Reactive Modules Language (RML) 建模, 对随机 (如马尔科夫链) 和非确定性 (如马尔科夫决策过程) 模型的验证支持较好.Plasma Lab[37]是新出现的一款纯SMC工具, 同样支持RML建模, 并实现了多种SMC算法 (包括重要性取样和分割等面向小概率事件的算法).Plasma Lab允许用户以插件集成的方式为其添加新的模型输入和验证算法, 如Simulink的集成.
6 总结统计模型检测技术能够有效地分析、验证CPS的正确性、可靠性, 并能对系统的性能进行定量评估.然而, 随着系统规模的日益增大, 如何有效地提高使用统计模型检测技术分析、验证CPS的效率, 是使用模型检测技术验证、分析CPS所面临的主要问题之一.针对该问题, 我们提出了一套有效的解决方案.主要工作贡献包括:
1) 首先, 对已有SMC算法的原理进行了剖析, 通过实验分析, 详细比较已有的SMC算法的性能, 总结出现有SMC算法的局限性和性能瓶颈.针对贝叶斯区间估计算法的不足, 提出了基于抽象和学习的统计模型检测方法, 以有效解决真实概率P接近0.5时的目标约束验证问题.
2) 其次, 提出了一种自适应的SMC算法框架, 能够根据系统满足目标约束的概率估值, 动态地、灵活地选择合适的SMC算法, 旨在从整体上提高SMC技术的性能, 提供一整套面向CPS的SMC检测方案.
3) 具体案例分析, 通过3个实例, 将自适应的SMC算法与单纯的BIE算法的效率做对比, 同时给出了谨慎的误差分析.
不足之处在于:本文的方法是将概率空间划分后, 分别统计再进行累加, 与直接统计分析整个概率空间相比有一定的误差.大量实验结果表明, 该方法误差极小, 属于可接受范围.我们下一步的工作是继续优化、改进自适应SMC算法, 并对算法的误差分析进行精确的量化评估.
| [1] | Lee EA. Cyber physical systems: Design challenges. In: Proc. of the 2008 11th IEEE Int'l Symp. on Object Oriented Real-Time Distributed Computing (ISORC). 2008. 363-369. [doi: 10.1109/ISORC.2008.25] |
| [2] | Baier C, Katoen JP, Baier C, Katoen JP. Principles of Model Checking. Cambridge: MIT Press, 2008. . |
| [3] | Platzer A. Differential dynamic logic for hybrid systems. Journal of Automated Reasoning, 2008, 41(2): 143–189 . [doi:10.1007/s10817-008-9103-8] |
| [4] | Platzer A, Clarke EM. Computing differential invariants of hybrid systems as fixedpoints. In: Proc. of the Computer Aided Verification. 2008. 176-189. [doi: 10.1007/978-3-540-70545-1_17] |
| [5] | Legay A, Delahaye B, Bensalem S. Statistical model checking: An overview. In: Proc. of the Runtime Verification. 2010. 122-135. [doi: 10.1007/978-3-642-16612-9_11] |
| [6] | Chen M, Yue D, Qin X, Fu X, Mishra P. Variation-Aware evaluation of MPSoC task allocation and scheduling strategies using statistical model checking. In: Proc. of the Design, Automation & Test in Europe Conf. & Exhibition (DATE). 2015. 199-204. |
| [7] | Jha SK, Clarke EM, Langmead CJ, Legay A, Platzer A, Zuliani P. A bayesian approach to model checking biological systems. In: Proc. of the Computational Methods in Systems Biology. 2009. 218-234. [doi: 10.1007/978-3-642-03845-7_15] |
| [8] | Chen MS, Gu P, Xu SY, Chen XH. Formal evaluation of scheduling strategies for smart building air-conditioning systems under uncertain environment. Ruan Jian Xue Bao/Journal of Software, 2016, 27(3): 655–669 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/4987.htm [doi:10.13328/j.cnki.jos.004987] |
| [9] | Cheng B, Wang X, Liu JF, Du DH. Modana: An integrated framework for modeling and analysis of energy-Aware CPSs. In: Proc. of 2015 IEEE the 39th Annual Computer Software and Applications Conf. (COMPSAC). IEEE, 2015. 127-136. [doi: 10.1109/COMPSAC.2015.68] |
| [10] | Wald A. Sequential tests of statistical hypotheses. The Annals of Mathematical Statistics, 1945, 16(2): 117–186 . [doi:10.1214/aoms/1177731118] |
| [11] | Younes HL, Simmons RG. Statistical probabilistic model checking with a focus on time-bounded properties. Information and Computation, 2006, 204(9): 1368–1409 . [doi:10.1016/j.ic.2006.05.002] |
| [12] | Hoeffding W. Probability inequalities for sums of bounded random variables. Journal of the American Statistical Association, 1963, 58(301): 13–30 . [doi:10.1080/01621459.1963.10500830] |
| [13] | Jeffreys H. The Theory of Probability. OUP Oxford, 1998. |
| [14] | Hérault T, Lassaigne R, Magniette F, Peyronnet S. Approximate probabilistic model checking. In: Proc. of the Verification, Model Checking, and Abstract Interpretation. 2004. 73-84. [doi: 10.1007/978-3-540-24622-0_8] |
| [15] | Zuliani P, Platzer A, Clarke EM. Bayesian statistical model checking with application to Stateflow/Simulink verification. Formal Methods in System Design, 2013, 43(2): 338–367 . [doi:10.1007/s10703-013-0195-3] |
| [16] | Jiang KQ, Huang P, Zan H, Du DH. AL-SMC: Optimizing statistical model checking by automatic abstraction and learning. Int'l Journal of Software and Informatics, 2016, 10(4): 54–69 . [doi:10.21655/ijsi.1673-7288.00235] |
| [17] | Dunteman GH. Principal Components Analysis. Sage, 1989. |
| [18] | Carrasco RC, Oncina J. Learning stochastic regular grammars by means of a state merging method. In: Proc. of the Grammatical Inference and Applications. Springer-Verlag, 1994. 139-152. [doi: 10.1007/3-540-58473-0_144] |
| [19] | Sen K, Viswanathan M, Agha G. Statistical model checking of black-box probabilistic systems. In: Proc. of the Computer Aided Verification. 2004. 202-215. |
| [20] | Younes HL. Verification and Planning for Stochastic Processes with Asynchronous Events. DTIC Document, 2005. |
| [21] | Sen K, Viswanathan M, Agha G. Statistical model checking of black-box probabilistic systems. In: Proc. of the Computer Aided Verification. 2004. 202-215. [doi: 10.1007/978-3-540-27813-9_16] |
| [22] | Bogdoll J, Fioriti LMF, Hartmanns A, Hermanns H. Partial order methods for statistical model checking and simulation. In: Proc. of the Formal Techniques for Distributed Systems. Springer-Verlag, 2011. 59-74. [doi: 10.1007/978-3-642-21461-5_4] |
| [23] | Pavese E, Braberman V, Uchitel S. Automated reliability estimation over partial systematic explorations. In: Proc. of 2013 the th Int'l Conf. on Software Engineering (ICSE). 2013. 602-611. [doi: 10.1109/ICSE.2013.6606606] |
| [24] | Henriques D. Statistical model checking for markov decision processes [Ph.D. Thesis]. General Motors, 2012. |
| [25] | He R, Jennings P, Basu S, Ghosh AP, Wu HQ. A bounded statistical approach for model checking of unbounded until properties. In: Proc. of the IEEE/ACM Int'l Conf. on Automated Software Engineering. 2010. 225-234. [doi: 10.1145/1858996.1859043] |
| [26] | Jennings P, Ghosh AP, Basu S. A two-phase approximation for model checking probabilistic unbounded until properties of probabilistic systems. ACM Trans. on Software Engineering and Methodology (TOSEM), 2012, 21(3): 18 . [doi:10.1145/2211616.2211621] |
| [27] | Jegourel C, Legay A, Sedwards S. Cross-Entropy optimisation of importance sampling parameters for statistical model checking. In: Proc. of the Computer Aided Verification. 2012. 327-342. [doi: 10.1007/978-3-642-31424-7_26] |
| [28] | Jegourel C, Legay A, Sedwards S. Importance splitting for statistical model checking rare properties. In: Proc. of the Computer Aided Verification. 2013. 576-591. [doi: 10.1007/978-3-642-39799-8_38] |
| [29] | Du DH, Cheng B, Liu J. Statistical model checking for rare-event in safety-critical system. Ruan Jian Xue Bao/Journal of Software, 2015, 26(2): 305–320 (in Chinese with English abstract). http://www.jos.org.cn/1000-9825/4783.htm [doi:10.13328/j.cnki.jos.004783] |
| [30] | Kumar JA, Ahmadyan SN, Vasudevan S. Efficient statistical model checking of hardware circuits with multiple failure regions. IEEE Trans. on Computer-Aided Design of Integrated Circuits and Systems, 2014, 33(6): 945–958 . [doi:10.1109/TCAD.2014.2299957] |
| [31] | Younes HL. Ymer: A statistical model checker. In: Proc. of the Computer Aided Verification. 2005. 429-433. [doi: 10.1007/11513988_43] |
| [32] | Sen K, Viswanathan M, Agha GA. VESTA: A statistical model-checker and analyzer for probabilistic systems. In: Proc. of the QEST, Vol.5. 2005. 251-252. [doi: 10.1109/QEST.2005.42] |
| [33] | Bulychev PE, David A, Larsen KG, Mikucionis M, Poulsen DB, Legay A, Wang Z. Uppaal-SMC: Statistical model checking for priced timed automata. arXiv preprint arXiv:1207.1272, 2012. [doi: 10.4204/EPTCS.85.1] |
| [34] | Kwiatkowska M, Norman G, Parker D. PRISM 4.0: Verification of probabilistic real-time systems. In: Proc. of the Computer aided Verification. 2011. 585-591. [doi: 10.1007/978-3-642-22110-1_47] |
| [35] | Brown LD, Cai TT, Dasgupta A. Interval estimation for a binomial proportion. In: Proc. of the Statistical Science. 2001. 101-117. |
| [36] | Pires AM, Amado C. Interval estimators for a binomial proportion: Comparison of twenty methods. REVSTAT-Statistical Journal, 2008, 6(2): 165–197 . |
| [37] | Boyer B, Corre K, Legay A, Sedwards S. PLASMA-Lab: A flexible, distributable statistical model checking library. In: Proc. of the Quantitative Evaluation of Systems. Springer-Verlag, 2013. 160-164. [doi: 10.1007/978-3-642-40196-1_12] |
| [8] | 陈铭松, 顾璠, 徐思远, 陈小红. 不确定环境下智能大厦空调系统调度策略评估. 软件学报, 2016, 27(3): 655–669. http://www.jos.org.cn/1000-9825/4987.htm [doi:10.13328/j.cnki.jos.004987] |
| [29] | 杜德慧, 程贝, 刘静. 面向安全攸关系统中小概率事件的统计模型检测. 软件学报, 2015, 26(2): 305–320. http://www.jos.org.cn/1000-9825/4783.htm [doi:10.13328/j.cnki.jos.004783] |
 2017, Vol. 28
2017, Vol. 28


